Gravity Waves in Planetary Atmospheres: Their Effects and Parameterization in Global Circulation Models
Abstract
1. Introduction
2. Atmospheric Gravity Waves
2.1. Physics of Gravity Waves
2.2. Linear Theory of Gravity Waves
2.3. Wave Generation and Sources of Gravity Waves
2.4. Observations of Gravity Waves
3. Methods of Parameterizing Gravity Waves in General Circulation Models
3.1. Principles of Parameterization
3.2. Instability Threshold
3.3. Spectral Schemes
3.4. Nonlinear Spectral Schemes
3.5. Whole Atmosphere Gravity Wave Scheme
3.6. Stochastic Modifications of Parameterizations
4. Modeling Gravity Wave Effects in Planetary Atmospheres
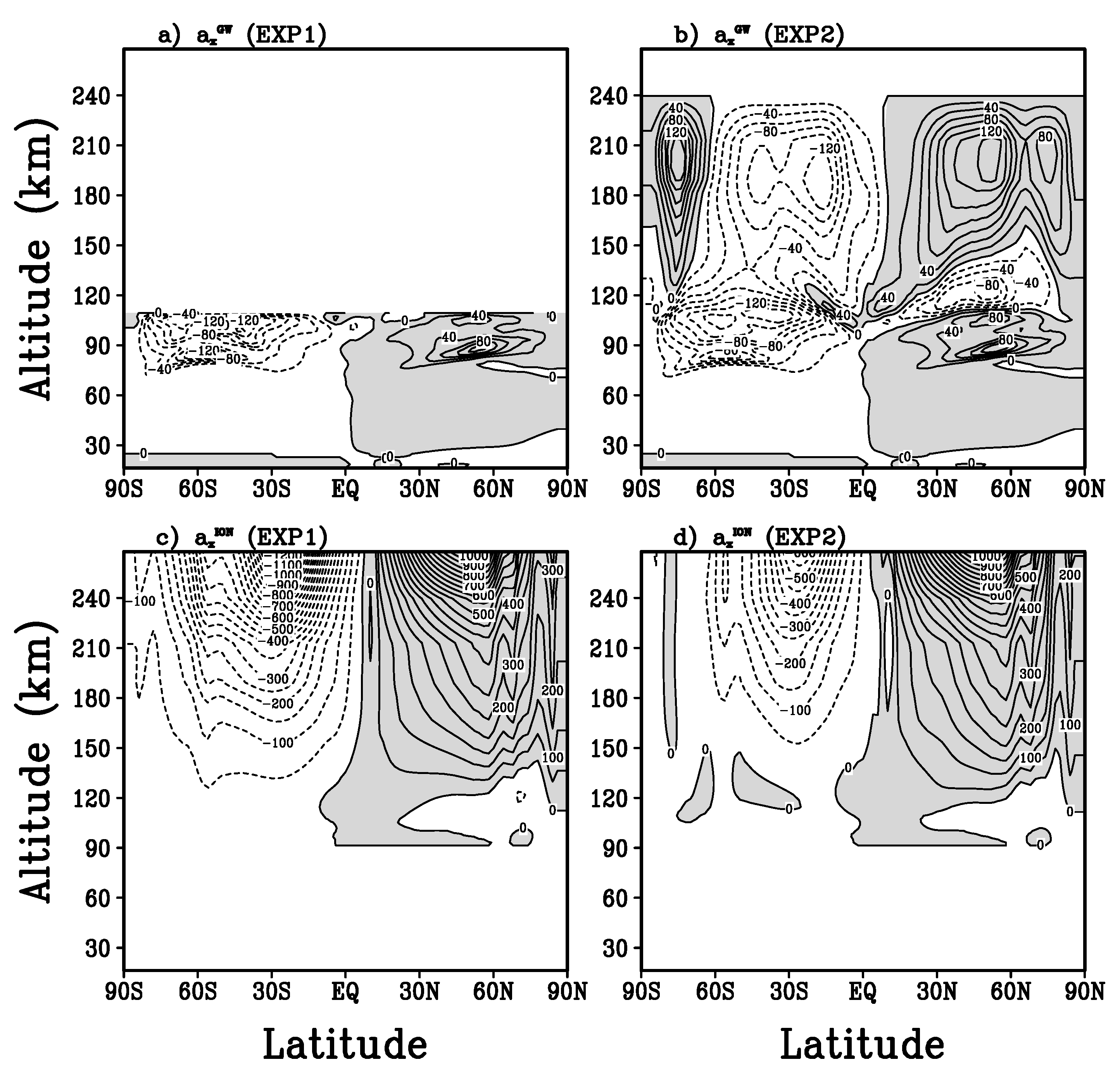
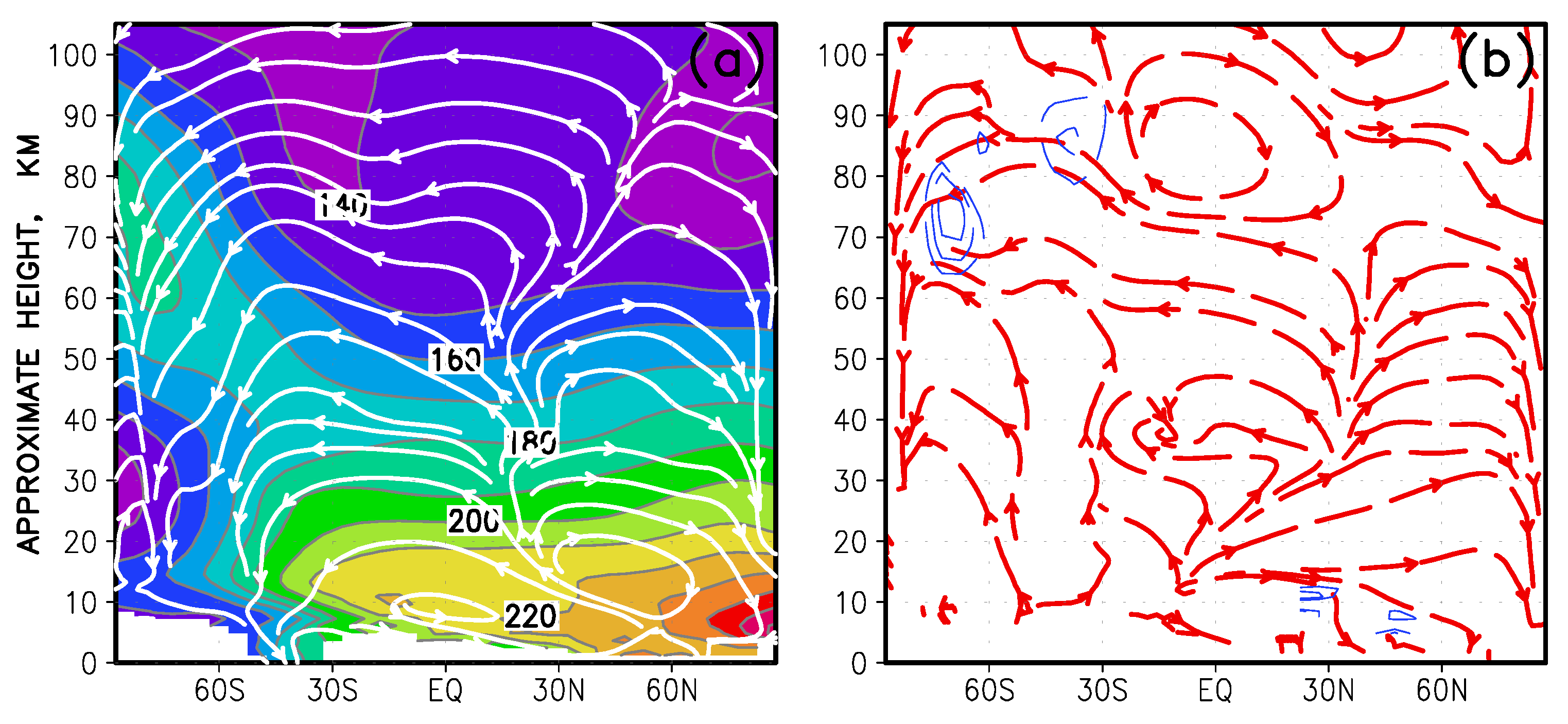
4.1. Dynamical Effects
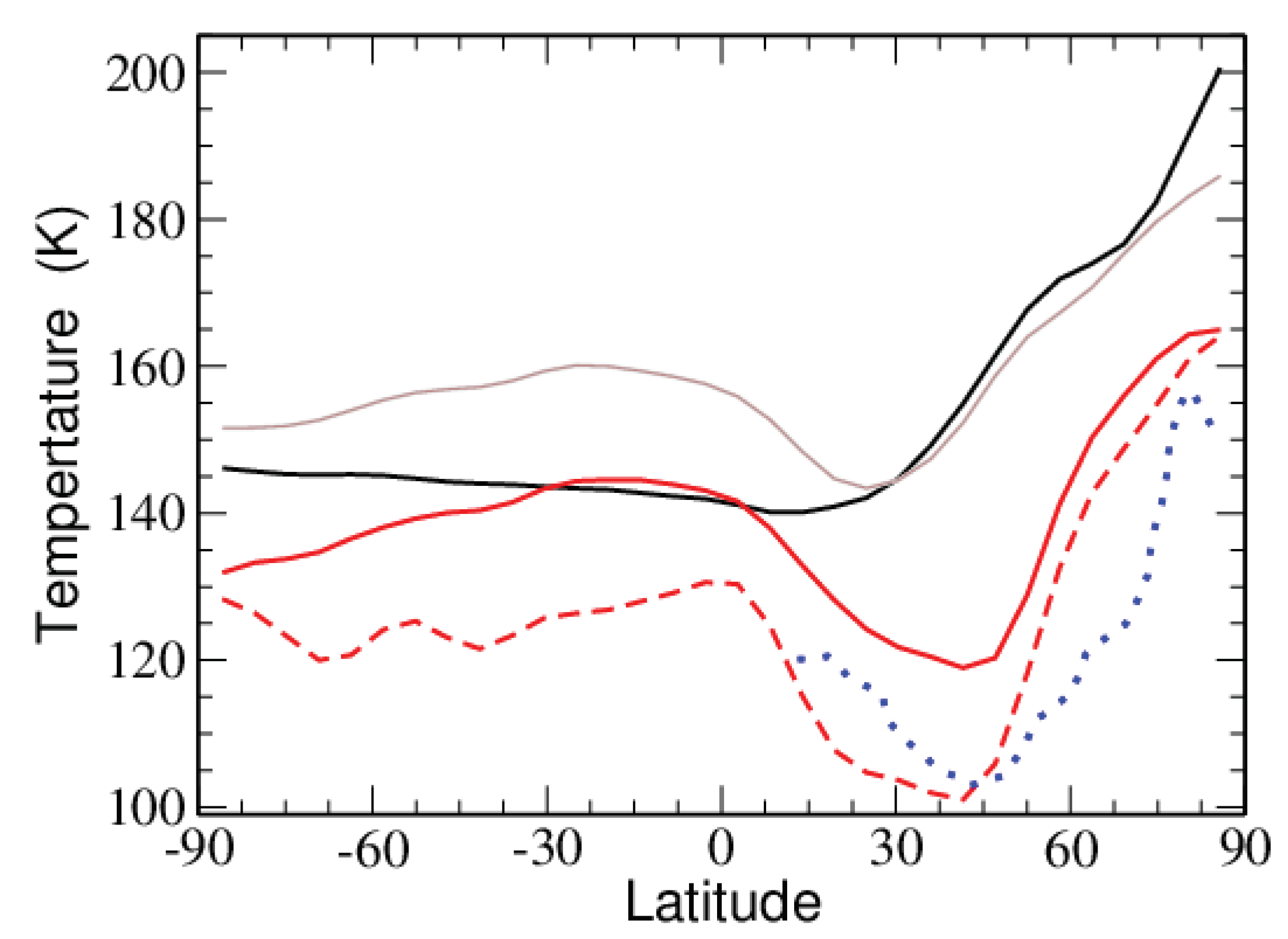
4.2. Thermal Effects
5. Phenomena Associated with Gravity Waves in Planetary Atmospheres
5.1. Sudden Stratospheric Warmings
5.2. Martian Polar Warmings
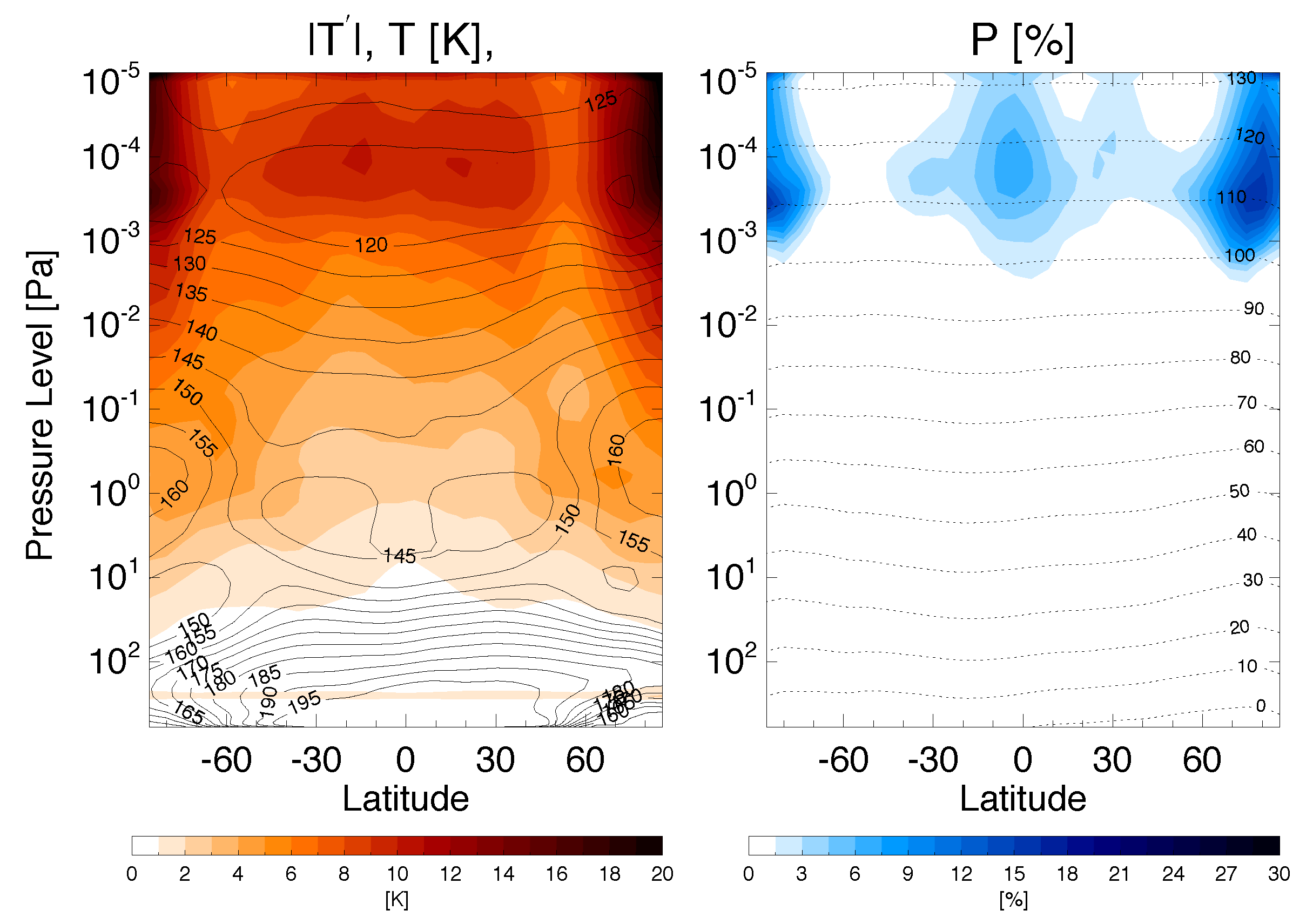
5.3. Gravity Waves and Ice Clouds
5.4. Ionospheric Effects
6. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| GWs | Gravity waves |
| GCM | General (or global) circulation models |
| MAVEN | Mars Atmosphere and Volatile Evolution |
| WKB | Wentzel–Kramer–Brilloin |
| SSW | Sudden stratospheric warming |
| TIDs | Traveling ionospheric disturbances |
References
- Yiğit, E.; Medvedev, A.S. Internal wave coupling processes in Earth’s atmosphere. Adv. Space Res. 2015, 55, 983–1003. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41. [Google Scholar] [CrossRef]
- Kim, Y.J.; Eckermann, S.E.; Chun, H.Y. An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models. Atmos. Ocean 2003, 41, 65–98. [Google Scholar]
- Hoffmann, L.; Xue, X.; Alexander, M.J. A global view of stratospheric gravity wave hotspots located with Atmospheric Infrared Sounder observations. J. Geophys. Res. 2013, 118. [Google Scholar] [CrossRef]
- Spiga, A.; González-Galindo, F.; López-Valverde, M.A.; Forget, F. Gravity waves, cold pockets and CO2 clouds in the Martian mesosphere. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Kuroda, T.; Medvedev, A.S.; Yiğit, E.; Hartogh, P. A global view of gravity waves in the Martian atmosphere inferred from a high-resolution general circulation model. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Kuroda, T.; Medvedev, A.S.; Yiğit, E.; Hartogh, P. Global distribution of gravity wave sources and fields in the Martian atmosphere during equinox and solstice inferred from a high-resolution general circulation model. J. Atmos. Sci. 2016, 73, 4895–4909. [Google Scholar] [CrossRef]
- Kuroda, T.; Yiğit, E.; Medvedev, A.S. Annual cycle of gravity wave activity derived From a high-resolution Martian general circulation model. J. Geophys. Res. Planets 2019, 124, 1618–1632. [Google Scholar] [CrossRef]
- Fukuhara, T.; Futaguchi, M.; Hashimoto, G.; Horinouchi, T.; Imamura, T.; Iwagaimi, N.; Kouyama, T.; Murakami, S.Y.; Nakamura, M.; Ogohara, K.; et al. Large stationary gravity wave in the atmosphere of Venus. Nat. Geosci. 2017, 10, 85–88. [Google Scholar] [CrossRef]
- Balme, M.; Greeley, R. Dust devils on Earth and Mars. Rev. Geophys. 2006, 44. [Google Scholar] [CrossRef]
- Colaïtis, A.; Spiga, A.; Hourdin, F.; Rio, C.; Forget, F.; Millour, E. A thermal plume model for the Martian convective boundary layer. J. Geophys. Res. Planets 2013, 118, 1468–1487. [Google Scholar] [CrossRef]
- Cantor, B.A.; Pickett, N.B.; Malin, M.C.; Lee, S.W.; Wolff, M.J.; Caplinger, M.A. Martian dust storm activity near the Mars 2020 candidate landing sites: MRO-MARCI observations from Mars years 28-34. Icarus 2019, 321, 161–170. [Google Scholar] [CrossRef]
- Leroy, S.S.; Ingersoll, A.P. Convective generation of gravity waves in Venus’s atmosphere: Gravity wave spectrum and momentum transport. J. Atmos. Sci. 1995, 52, 3717–3737. [Google Scholar] [CrossRef]
- Plougonven, R.; Zhang, F. Internal gravity waves from atmospheric jets and fronts. Rev. Geophys. 2014, 52, 33–76. [Google Scholar] [CrossRef]
- Orton, G.S.; Hansen, C.; Caplinger, M.; Ravine, M.; Atreya, S.; Ingersoll, A.P.; Jensen, E.; Momary, T.; Lipkaman, L.; Krysak, D.; et al. The first close-up images of Jupiter’s polar regions: Results from the Juno mission JunoCam instrument. Geophys. Res. Lett. 2017, 44, 4599–4606. [Google Scholar] [CrossRef]
- Pichon, A.; Blanc, E.; Hauchecorne, A. Infrasound Monitoring for Atmospheric Studies: Challenges in Middle Atmosphere Dynamics and Societal Benefits; Springer: New York, NY, USA, 2018. [Google Scholar]
- Seiff, A.; Kirk, D.B. Structure of Mars’ atmosphere up to 100 kilometers from the entry measurements of Viking 2. Science 1976, 194, 1300–1303. [Google Scholar] [CrossRef]
- Young, L.A.; Yelle, R.V.; Young, R.; Seiff, A.; Kirk, D.B. Gravity Waves in Jupiter’s Thermosphere. Science 1997, 276, 108–111. [Google Scholar] [CrossRef]
- Lorenz, R.D.; Young, L.A.; Ferri, F. Gravity waves in Titan’s lower stratosphere from Huygens probe in situ temperature measurements. Icarus 2014, 227, 49–55. [Google Scholar] [CrossRef]
- Niemann, H.B.; Kasprzak, W.T.; Hedin, A.E.; Hunten, D.M.; Spencer, N.W. Mass spectrometric measurements of the neutral gas composition of the thermosphere and exosphere of Venus. J. Geophys. Res. Space Phys. 1980, 85, 7817–7827. [Google Scholar] [CrossRef]
- Sagdeev, R.Z.; Llinkin, V.M.; Blamont, J.E.; Preston, R.A. The VEGA Venus balloon experiment. Science 1986, 231, 1407–1408. [Google Scholar] [CrossRef]
- Creasey, J.E.; Forbes, J.M.; Keating, G.M. Density variability at scales typical of gravity waves observed in Mars’ thermosphere by the MGS accelerometer. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Fritts, D.C.; Wang, L.; Tolson, R.H. Mean and gravity wave structures and variability in the Mars upper atmosphere inferred from Mars Global Surveyor and Mars Odyssey aerobraking densities. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Müller-Wodarg, I.C.F.; Yelle, R.V.; Borggren, N.; Waite, J.H. Waves and horizontal structures in Titan’s thermosphere. J. Geophys. Res. Space Phys. 2006, 111, A12315. [Google Scholar] [CrossRef]
- Yiğit, E.; England, S.L.; Liu, G.; Medvedev, A.S.; Mahaffy, P.R.; Kuroda, T.; Jakowky, B. High-altitude gravity waves in the Martian thermosphere observed by MAVEN/NGIMS and modeled by a gravity wave scheme. Geophys. Res. Lett. 2015, 42. [Google Scholar] [CrossRef]
- Terada, N.; Leblanc, F.; Nakagawa, H.; Medvedev, A.S.; Yiğit, E.; Kuroda, T.; Hara, T.; England, S.L.; Fujiwara, H.; Terada, K.; et al. Global distribution and parameter dependences of gravity wave activity in the Martian upper thermosphere derived from MAVEN/NGIMS observations. J. Geophys. Res. Space Phys. 2017. [Google Scholar] [CrossRef]
- Siddle, A.; Mueller-Wodarg, I.; Stone, S.; Yelle, R. Global characteristics of gravity waves in the upper atmosphere of Mars as measured by MAVEN/NGIMS. Icarus 2019, 333, 12–21. [Google Scholar] [CrossRef]
- Hinson, D.P.; Simpson, R.A.; Twicken, J.D.; Tyler, G.L.; Flasar, F.M. Initial results from radio occultation measurements with Mars Global Surveyor. J. Geophys. Res. Planets 1999, 104, 26997–27012. [Google Scholar] [CrossRef]
- Häusler, B.; Pätzold, M.; Tyler, G.; Simpson, R.; Bird, M.; Dehant, V.; Barriot, J.P.; Eidel, W.; Mattei, R.; Remus, S.; et al. Radio science investigations by VeRa onboard the Venus Express spacecraft. Planet. Space Sci. 2006, 54, 1315–1335. [Google Scholar] [CrossRef]
- Ando, H.; Imamura, T.; Tsuda, T. Vertical wavenumber spectra of gravity waves in the Martian atmosphere obtained from Mars Global Surveyor radio occultation data. J. Atmos. Sci. 2012, 69, 2906–2912. [Google Scholar] [CrossRef]
- Ando, H.; Imamura, T.; Tsuda, T.; Tellmann, S.; Pätzold, M.; Häusler, B. Vertical wavenumber spectra of gravity waves in the Venus atmosphere obtained from Venus Express radio occultation data: Evidence for saturation. J. Atmos. Sci. 2015, 72, 2318–2329. [Google Scholar] [CrossRef]
- Kalisch, S.; Preusse, P.; Ern, M.; Eckermann, S.D.; Riese, M. Differences in gravity wave drag between realistic oblique and assumed vertical propagation. J. Geophys. Res. Atmos. 2014, 119, 10081–10099. [Google Scholar] [CrossRef]
- Song, I.S.; Chun, H.Y. A Lagrangian spectral parameterization of gravity wave drag induced by cumulus convection. J. Atmos. Sci. 2008, 65, 1204–1224. [Google Scholar] [CrossRef]
- Hodges, R.R. Generation of turbulence in the upper atmosphere by internal gravity waves. J. Geophys. Res. 1967, 72, 3455–3458. [Google Scholar] [CrossRef]
- Lindzen, R.S. Turbulence and stress owing to gravity waves and tidal breakdown. J. Geophys. Res. 1981, 86, 9707–9714. [Google Scholar] [CrossRef]
- Fritts, D.C. A review of gravity wave saturation processes, effects, and variability in the middle atmosphere. Pageoph 1989, 130, 343–371. [Google Scholar] [CrossRef]
- Dunkerton, T.I. Theory of internal gravity wave saturation. Pageoph 1989, 130, 373–397. [Google Scholar] [CrossRef]
- Lund, T.S.; Fritts, D.C. Numerical simulations of gravity wave breaking in the lower thermosphere. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Alexander, M.J.; Dunkerton, T.J. A spectral parameterization of mean-flow forcing due to breaking gravity waves. J. Atmos. Sci. 1999, 56, 4167–4182. [Google Scholar] [CrossRef]
- Lindzen, R.S.; Holton, J.R. A theory of the quasi-biennial oscillation. J. Atmos. Sci. 1968, 25, 1095–1107. [Google Scholar] [CrossRef]
- Warner, C.; McIntyre, M. On the propagation and dissipation of gravity wave spectra through a realistic atmosphere. J. Atmos. Sci. 1996, 53, 3213–3235. [Google Scholar] [CrossRef]
- Warner, C.D.; McIntyre, M.E. An ultrasimple spectral parameterization for nonorographic gravity waves. J. Atmos. Sci. 2001, 58, 1837–1857. [Google Scholar] [CrossRef]
- Scinocca, J.F. An accurate spectral nonorographic gravity wave drag parameterization for general circulation models. J. Atmos. Sci. 2003, 60, 667–682. [Google Scholar] [CrossRef]
- Majdzadeh, M.; Klaassen, G.P. An Analysis of the Hines and Warner-McIntyre-Scinocca nonorographic gravity wave drag parameterizations. Q. J. R. Meteorol. Soc. 2019, 145, 2308–2334. [Google Scholar] [CrossRef]
- Hines, C.O. The saturation of gravity waves in the middle atmosphere. Part2: Development of Doppler-spread theory. J. Atmos. Sci. 1991, 48, 1360–1379. [Google Scholar]
- Hines, C.O. Doppler spread parameterization of gravity wave momentum deposition in the middle: 1. Basic formulation. J. Atmos. Sol.-Terr. Phys. 1997, 59, 371–386. [Google Scholar] [CrossRef]
- Charron, M.; Manzini, E.; Warner, C.D. Intercomparison of gravity wave parameterizations: Hines doppler-spread and Warner and McIntyre ultra-simple schemes. J. Meteor. Soc. Jpn. 2002, 80, 335–345. [Google Scholar] [CrossRef][Green Version]
- McLandress, C.; Scinocca, J.F. The GCM response to current parameterizations of nonorographic gravity wave drag. J. Atmos. Sci. 2005, 62, 2394–2413. [Google Scholar] [CrossRef]
- Hines, C.O. Theory of the Eulerian tail in the spectra of atmospheric and oceanic internal gravity waves. J. Fluid Mech. 2001, 448, 289–313. [Google Scholar] [CrossRef]
- Klaassen, G.P.; Sonmor, L.J. Does kinematic advection by superimposed waves provide an explanation for quasi-universal gravity-wave spectra? Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Klaassen, G.P. Testing Lagrangian theories of internal wave spectra. Part I: Varying the amplitude and wavenumbers. J. Atmos. Sci. 2009, 66, 1077–1100. [Google Scholar] [CrossRef]
- Klaassen, G.P. Testing Lagrangian theories of internal wave spectra. Part II: varying the number of waves. J. Atmos. Sci. 2009, 66, 1101–1125. [Google Scholar] [CrossRef]
- Weinstock, J. Nonlinear theory of acoustic-gravity waves 1. Saturation and enhanced diffusion. J. Geophys. Res. 1976, 81, 633–652. [Google Scholar] [CrossRef]
- Weinstock, J. Nonlinear theory of gravity waves: Momentum deposition, generalized rayleigh friction, and diffusion. J. Atmos. Sci. 1982, 39, 1698–1710. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Klaassen, G.P. Vertical evolution of gravity wave spectra and the parameterization of associated wave drag. J. Geophys. Res. 1995, 100, 25841–25853. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Klaassen, G.P. Parameterization of gravity wave momentum deposition based on nonlinear wave interactions: Basic formulation and sensitivity tests. J. Atmos. Sol.-Terr. Phys. 2000, 62, 1015–1033. [Google Scholar] [CrossRef]
- Yiğit, E.; Aylward, A.D.; Medvedev, A.S. Parameterization of the effects of vertically propagating gravity waves for thermosphere general circulation models: Sensitivity study. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Extending the parameterization of gravity waves into the thermosphere and modeling their effects. In Climate and Weather of the Sun-Earth System (CAWSES); Lübken, F.J., Ed.; Springer: Heidelberg, Germany, 2012; pp. 467–480. [Google Scholar]
- Eckermann, S.D.; Ma, J.; Zhu, X. Scale-dependent infrared radiative damping rates on Mars and their role in the deposition of gravity-wave momentum flux. Icarus 2011, 211, 429–442. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Yiğit, E.; Hartogh, P. Estimates of gravity wave drag on Mars: indication of a possible lower thermosphere wind reversal. Icarus 2011, 211, 909–912. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Yiğit, E.; Hartogh, P. Ion friction and quantification of the geomagnetic influence on gravity wave propagation and dissipation in the thermosphere-ionosphere. J. Geophys. Res. Space Phys. 2017, 122, 12464–12475. [Google Scholar] [CrossRef]
- Eckermann, S.D. Explicitly stochastic parameterization of nonorographic gravity wave drag. J. Atmos. Sci. 2011, 68, 1749–1765. [Google Scholar] [CrossRef]
- Lott, F.; Guez, L.; Maury, P. A stochastic parameterization of non-orographic gravity waves: Formalism and impact on the equatorial stratosphere. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- de la Càmara, A.; Lott, F.; Hertzog, A. Intermittency in a stochastic parameterization of nonorographic gravity waves. J. Geophys. Res. Atmos. 2014, 119, 11905–11919. [Google Scholar] [CrossRef]
- Serva, F.; Cagnazzo, C.; Riccio, A.; Manzini, E. Impact of a stochastic nonorographic gravity wave parameterization on the stratospheric dynamics of a general circulation model. J. Adv. Model. Earth Syst. 2018, 10, 2147–2162. [Google Scholar] [CrossRef]
- Leovy, C. Simple models of thermally driven mesospheric circulation. J. Atmos. Sci. 1964, 21, 327–341. [Google Scholar] [CrossRef]
- Hodges, R.R. Eddy diffusion coeffients due to instabilities in internal gravity waves. J. Geophys. Res. 1969, 74, 4087–4090. [Google Scholar] [CrossRef]
- Holton, J.R.; Wehrbein, W.M. A numerical model of the zonal mean circulation of the middle atmosphere. Pageoph 1980, 118, 284–306. [Google Scholar] [CrossRef]
- Holton, J.R. The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere. J. Atmos. Sci. 1982, 39, 791–799. [Google Scholar] [CrossRef]
- Garcia, R.R.; Solomon, S. The effect of breaking gravity waves on the dynamics and chemical composition of the mesosphere and lower thermosphere. J. Geophys. Res. 1985, 90, 3850–3868. [Google Scholar] [CrossRef]
- Hertzog, A.; Boccara, G.; Vincent, R.A.; Vial, F.; Cocquerez, P. Estimation of gravity wave momentum flux and phase speeds from quasi-Lagrangian stratospheric balloon flights. Part II: Results from the Vorcore campaign in Antarctica. J. Atmos. Sci. 2008, 65, 3056–3070. [Google Scholar] [CrossRef]
- Alexander, M.J.; Geller, M.; McLandress, C.; Polavarapu, S.; Preusse, P.; Sassi, F.; Sato, K.; Eckermann, S.; Ern, M.; Hertzog, A.; et al. Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 2010, 136, 1103–1124. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S.; Aylward, A.D.; Hartogh, P.; Harris, M.J. Modeling the effects of gravity wave momentum deposition on the general circulation above the turbopause. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef]
- Klostermeyer, J. Influence of viscosity, thermal conduction, and ion drag on the propagation of atmospheric gravity waves in the thermosphere. Z. Geophys. 1972, 38, 881–890. [Google Scholar]
- Vadas, S.L.; Fritts, D.C. Thermospheric responses to gravity waves: Influences of increasing viscosity and thermal diffusivity. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Miyoshi, Y.; Fujiwara, H. Gravity waves in the thermosphere simulated by a general circulation model. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Influence of parameterized small-scale gravity waves on the migrating diurnal tide in Earth’s thermosphere. J. Geophys. Res. Space Phys. 2017, 122. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Kshevetskii, S.P. Three-dimensional numerical simulation of nonlinear acoustic-gravity wave propagation from the troposphere to the thermosphere. Earth Planets Space 2014, 66. [Google Scholar] [CrossRef]
- Gavrilov, N.M.; Kshevetskii, S.P.; Koval, A.V. Propagation of non-stationary acoustic-gravity waves at thermospheric temperatures corresponding to different solar activity. J. Atmos. Sol.-Terr. Phys. 2018, 172, 100–106. [Google Scholar] [CrossRef]
- Heale, C.J.; Snively, J.B.; Hickey, M.P.; Ali, C.J. Thermospheric dissipation of upward propagating gravity wave packets. J. Geophys. Res. Space Phys. 2014, 119, 3857–3872. [Google Scholar] [CrossRef]
- Heale, C.J.; Walterscheid, R.L.; Snively, J.B. Localization effects on the dissipation of gravity wave packets in the upper mesosphere and lower thermosphere. J. Geophys. Res. Atmos. 2018, 123, 8915–8935. [Google Scholar] [CrossRef]
- Vadas, S.L.; Fritts, D.C.; Alexander, M.J. Mechanism for the generation of secondary waves in wave breaking regions. J. Atmos. Sci. 2003, 60, 194–214. [Google Scholar] [CrossRef]
- Becker, E.; Vadas, S.L. Secondary gravity waves in the winter mesosphere: Results from a high-resolution global circulation model. J. Geophys. Res. Atmos. 2018, 123, 2605–2627. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Obscure waves in planetary atmospheres. Phys. Today 2019, 6, 40–46. [Google Scholar] [CrossRef]
- Barnes, J.R. Possible effects of breaking gravity waves on the circulation of the middle atmosphere of Mars. J. Geophys. Res. 1990, 95, 1401–1421. [Google Scholar] [CrossRef]
- Théodore, B.; Lellouch, E.; Chassefiére, E.; Hauchecorne, A. Solstial temperature inversions in the Martian middle atmosphere: Observational clues and 2-D modeling. Icarus 1993, 105, 512–528. [Google Scholar] [CrossRef]
- Joshi, M.M.; Lawrence, B.N.; Lewis, S.R. Gravity wave drag in three-dimensional atmospheric models of Mars. J. Geophys. Res. 1995, 100, 21235–21245. [Google Scholar] [CrossRef]
- Joshi, M.M.; Lawrence, B.N.; Lewis, S.R. The effect of spatial variations in unresolved topography on gravity wave drag in the Martian atmosphere. Geophys. Res. Lett. 1996, 23, 2927–2930. [Google Scholar] [CrossRef]
- Collins, M.; Lewis, S.R.; Read, P.L. Gravity wave drag in a global circulation model of the Mars atmosphere: Parameterization and validation. Adv. Space Res. 1997, 19, 1245–1254. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S.; Aylward, A.D.; Ridley, A.J.; Harris, M.J.; Moldwin, M.B.; Hartogh, P. Dynamical effects of internal gravity waves in the equinoctial thermosphere. J. Atmos. Sol.-Terr. Phys. 2012, 90–91, 104–116. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Yiğit, E.; Hartogh, P.; Becker, E. Influence of gravity waves on the Martian atmosphere: General circulation modeling. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Nakagawa, H.; Mockel, C.; Yiğit, E.; Kuroda, T.; Hartogh, P.; Terada, K.; Terada, N.; Seki, K.; Schneider, N.M.; et al. Comparison of the Martian thermospheric density and temperature from IUVS/MAVEN data and general circulation modeling. Geophys. Res. Lett. 2016, 43, 3095–3104. [Google Scholar] [CrossRef]
- Bougher, S.; Dickinson, R.; Ridley, E.; Roble, R. Venus mesosphere and thermosphere: III. Three-dimensional general circulation with coupled dynamics and composition. Icarus 1988, 73, 545–573. [Google Scholar] [CrossRef]
- Zalucha, A.M.; Brecht, A.S.; Rafkin, S.; Bougher, S.W.; Alexander, M.J. Incorporation of a gravity wave momentum deposition parameterization into the Venus Thermosphere General Circulation Model (VTGCM). J. Geophys. Res. Planets 2013, 118, 147–160. [Google Scholar] [CrossRef]
- Hoshino, N.; Fujiwara, H.; Takagi, M.; Kasaba, Y. Effects of gravity waves on the day-night difference of the general circulation in the Venusian lower thermosphere. J. Geophys. Res. Planets 2013, 118, 2004–2015. [Google Scholar] [CrossRef]
- Gilli, G.; Lebonnois, S.; González-Galindo, F.; López-Valverde, M.; Stolzenbach, A.; Lefèvre, F.; Chaufray, J.; Lott, F. Thermal structure of the upper atmosphere of Venus simulated by a ground-to-thermosphere GCM. Icarus 2017, 281, 55–72. [Google Scholar] [CrossRef]
- Walterscheid, R.L. Dynamical cooling induced by dissipating internal gravity waves. Geophys. Res. Lett. 1981, 8, 1235–1238. [Google Scholar] [CrossRef]
- Becker, E. Direct heating rates associated with gravity wave saturation. J. Atmos. Sol.-Terr. Phys. 2004, 66, 683–696. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Klaassen, G.P. Thermal effects of saturating gravity waves in the atmosphere. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Heating and cooling of the thermosphere by internal gravity waves. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Yiğit, E. Thermal effects of internal gravity waves in the Martian upper atmosphere. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Bougher, S.W.; Bell, J.M.; Murphy, J.R.; López-Valverde, M.A.; Withers, P.G. Polar warming in the Mars thermosphere: Seasonal variations owing to changing insolation and dust distributions. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Medvedev, A.S.; González-Galindo, F.; Yiğit, E.; Feofilov, A.G.; Forget, F.; Hartogh, P. Cooling of the Martian thermosphere by CO2 radiation and gravity waves: An intercomparison study with two general circulation models. J. Geophys. Res. Planets 2015, 120, 913–927. [Google Scholar] [CrossRef]
- Hickey, M.P.; Walterscheid, R.L.; Schubert, G. Gravity wave heating and cooling in Jupiter’s thermosphere. Icarus 2000, 148, 266–281. [Google Scholar] [CrossRef]
- Hickey, M.P.; Schubert, G.; Walterscheid, R.L. Acoustic wave heating of the thermosphere. J. Geophys. Res. Space Phys. 2001, 106, 21543–21548. [Google Scholar] [CrossRef]
- Scherhag, R. Die explosionsartige Stratosphärenerwärmung des Spätwinters 1951–1952. Ber. Deut. Wetterdienstes 1952, 6, 51–63. [Google Scholar]
- Matsuno, T. A dynamical model of the stratospheric sudden warming. J. Atmos. Sci. 1971, 28, 1479–1494. [Google Scholar] [CrossRef]
- Schoeberl, M.R. Stratospheric warmings: observation and theory. Rev. Geophys. 1978, 16, 521–538. [Google Scholar] [CrossRef]
- Holton, J.R. The dynamics of stratospheric warmings. Ann. Rev. Earth Planet. Sci. 1980, 8, 169–190. [Google Scholar] [CrossRef]
- Andrews, D.G.; Holton, J.R.; Leovy, C.B. Middle Atmosphere Dynamics; International Geophysics Series; Academic Press: Cambridge, MA, USA, 1987; Volume 40. [Google Scholar]
- Liu, H.L.; Roble, R.G. A study of a self-generated stratospheric sudden warming and its mesospheric-lower thermospheric impacts using the coupled TIME-GCM/CCM3. J. Geophys. Res. 2002, 107, 15–1, 15–18. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Gravity waves in the thermosphere during a sudden stratospheric warming. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S.; England, S.L.; Immel, T.J. Simulated variability of the high-latitude thermosphere induced by small-scale gravity waves during a sudden stratospheric warming. J. Geophys. Res. Space Phys. 2014, 119. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S. Role of gravity waves in vertical coupling during sudden stratospheric warmings. Geosci. Lett. 2016, 3, 1–13. [Google Scholar] [CrossRef]
- Nayak, C.; Yiğit, E. Variation of small-scale gravity wave activity in the ionosphere during the major sudden stratospheric warming event of 2009. J. Geophys. Res. Space Phys. 2019, 124, 470–488. [Google Scholar] [CrossRef]
- Ern, M.; Trinh, Q.T.; Kaufmann, M.; Krisch, I.; Preusse, P.; Ungermann, J.; Zhu, Y.; Gille, J.C.; Mlynczak, M.G.; Russell, J.M., III; et al. Satellite observations of middle atmosphere gravity wave absolute momentum flux and of its vertical gradient during recent stratospheric warmings. Atmos. Chem. Phys. 2016, 16, 9983–10019. [Google Scholar] [CrossRef]
- Barnes, J.R.; Hollingsworth, J.L. Dynamical modeling of a planetary wave mechanism for a Martian polar warming. Icarus 1987, 71, 313–334. [Google Scholar] [CrossRef]
- Wilson, R.J. A general circulation model simulation of the Martian polar warming. Geophys. Res. Lett. 1997, 24, 123–126. [Google Scholar] [CrossRef]
- Hartogh, P.; Medvedev, A.S.; Jarchow, C. Middle atmosphere polar warmings on Mars: simulations and study on the validation with sub-millimeter observations. Planet. Space Sci. 2007, 55, 1103–1112. [Google Scholar] [CrossRef]
- Kurodo, T.; Medvedev, A.S.; Hartogh, P.; Takahashi, M. On forcing the winter polar warmings in the Martian middle atmosphere during dust storms. J. Meteor. Soc. Japan 2009, 87, 913–921. [Google Scholar] [CrossRef]
- Keating, G.M.; Theriot, M.; Tolson, R.; Bougher, S.; Forget, F.; Forbes, J. Brief review on the results obtained with the MGS and Mars Odyssey 2001 Accelerometer Experiments. In International Workshop: Mars Atmosphere Modeling and Observations; Inst. de Astrofis. de Andalucia: Granada, Spain, 2003. [Google Scholar]
- Bell, J.M.; Bougher, S.W.; Murphy, J.R. Vertical dust mixing and the interannual variations in the Mars thermosphere. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Medvedev, A.S.; Yiğit, E.; Kuroda, T.; Hartogh, P. General circulation modeling of the Martian upper atmosphere during global dust storms. J. Geophys. Res. Planets 2013, 118, 1–13. [Google Scholar] [CrossRef]
- Clancy, R.T.; Sandor, B.J. CO2 ice clouds in the upper atmosphere of Mars. Geophys. Res. Lett. 1998, 25, 489–492. [Google Scholar] [CrossRef]
- Määttänen, A.; Montmessin, F.; Gondet, B.; Scholten, F.; Hoffmann, H.; González-Galindo, F.; Spiga, A.; Forget, F.; Hauber, E.; Neukum, G.; et al. Mapping the mesospheric CO2 clouds on Mars: MEx/OMEGA and MEx/HRSC observations and challenges for atmospheric models. Icarus 2010, 209, 452–469. [Google Scholar] [CrossRef]
- González-Galindo, F.; Määtänen, A.; Forget, F.; Spiga, A. The martian mesosphere as revealed by CO2 cloud observations and general circulation modeling. Icarus 2011, 216, 10–22. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S.; Hartogh, P. Gravity waves and high-altitude CO2 ice cloud formation in the Martian atmosphere. Geophys. Res. Lett. 2015, 42, 4294–4300. [Google Scholar] [CrossRef]
- Yiğit, E.; Medvedev, A.S.; Hartogh, P. Influence of gravity waves on the climatology of high-altitude Martian carbon dioxide ice clouds. Ann. Geophys. 2018, 36, 1631–1646. [Google Scholar] [CrossRef]
- Jiang, F.Y.; Yelle, R.V.; Jain, S.K.; Cui, J.; Montmessin, F.; Schneider, N.M.; Deighan, J.; Gröller, H.; Verdier, L. Detection of mesospheric CO2 ice clouds on Mars in southern summer. Geophys. Res. Lett. 2019. [Google Scholar] [CrossRef]
- Määttänen, A.; Pérot, K.; Montmessin, F.; Houchecorne, A. Mesopheric clouds on Mars and on Earth. In Comparative Climatology of Terrestrial Planets; Mackwell, S.J., Ed.; Univ. of Arizona: Tucson, AZ, USA, 2013; pp. 393–413. [Google Scholar]
- Listowski, C.; Määtänen, A.; Montmessin, F.; Spiga, A.; Lefévre, F. Modeling the microphysics of CO2 ice clouds within wave-induced cold pockets in the martian mesosphere. Icarus 2014, 237, 239–261. [Google Scholar] [CrossRef]
- Hines, C.O. Internal gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Nelson, R.A. Response of the ionosphere to the passage of neutral atmospheric waves. J. Atmos. Terr. Phys. 1968, 30, 825–835. [Google Scholar] [CrossRef]
- Kirchengast, G.; Hocke, K.; Schlegel, K. The gravity wave-TID relationship: insight via theoretical model-EISCAT data comparison. J. Atmos. Terr. Phys. 1996, 58, 233–243. [Google Scholar] [CrossRef]
- Kirchengast, G. Characteristics of high-latitude TIDs from different causative mechanisms deduced by theoretical modeling. J. Geophys. Res. 1997, 102, 4597–4612. [Google Scholar] [CrossRef]
- Hunsucker, R. Atmospheric gravity waves generated in the high-latitude ionosphere: A review. Rev. Geophys. 1982, 20, 293–315. [Google Scholar] [CrossRef]
- Collinson, G.; McFadden, J.; Mitchell, D.; Grebowsky, J.; Benna, M.; Espley, J.; Jakosky, B. Traveling ionospheric disturbances at Mars. Geophys. Res. Lett. 2019, 46, 4554–4563. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, W.; Hickey, M.P. Ionospheric signatures of gravity waves produced by the 2004 Sumatra and 2011 Tohoku tsunamis: A modeling study. J. Geophys. Res. Space Phys. 2017, 122, 1146–1162. [Google Scholar] [CrossRef]
- Matcheva, K.I.; Strobel, D.F.; Flasar, F. Interaction of Gravity Waves with Ionospheric Plasma: Implications for Jupiter’s Ionosphere. Icarus 2001, 152, 347–365. [Google Scholar] [CrossRef]
- Barrow, D.J.; Matcheva, K.I. Modeling the effect of atmospheric gravity waves on Saturn’s ionosphere. Icarus 2013, 224, 32–42. [Google Scholar] [CrossRef]
- Haider, S.A.; Mahajan, K.K.; Kallio, E. Mars ionosphere: A review of experimental results and modeling studies. Rev. Geophys. 2011, 49. [Google Scholar] [CrossRef]
- Jones, P.W.; Hamilton, K.; Wilson, R.J. Very high resolution general circulation model simulation of the global circulation in austral winter. J. Atmos. Sci. 1997, 54, 1107–1116. [Google Scholar] [CrossRef]
| Earth | Mars | Venus | Jupiter | Saturn | |
|---|---|---|---|---|---|
| Rotational frequency , s | 7.29 × 10 | 7.09 × 10 | 2.99 × 10 | 1.76 × 10 | 1.64 × 10 |
| Acceleration of gravity g, m s | 9.81 | 3.72 | 8.87 | 24.79 | 10.44 |
| Scale height H, km | 5.5–9 | 7.5–11.5 | 5–16 | 27 | 60 |
| Buoyancy frequency N, s | ∼2 × 10 | ∼2 × 10 | ∼2 × 10 | ∼2 × 10 | ∼2 × 10 |
| Max horizontal phase velocity, , m s | 220–360 | 300–460 | 200–640 | 1080 | 2400 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Medvedev, A.S.; Yiğit, E. Gravity Waves in Planetary Atmospheres: Their Effects and Parameterization in Global Circulation Models. Atmosphere 2019, 10, 531. https://doi.org/10.3390/atmos10090531
Medvedev AS, Yiğit E. Gravity Waves in Planetary Atmospheres: Their Effects and Parameterization in Global Circulation Models. Atmosphere. 2019; 10(9):531. https://doi.org/10.3390/atmos10090531
Chicago/Turabian StyleMedvedev, Alexander S., and Erdal Yiğit. 2019. "Gravity Waves in Planetary Atmospheres: Their Effects and Parameterization in Global Circulation Models" Atmosphere 10, no. 9: 531. https://doi.org/10.3390/atmos10090531
APA StyleMedvedev, A. S., & Yiğit, E. (2019). Gravity Waves in Planetary Atmospheres: Their Effects and Parameterization in Global Circulation Models. Atmosphere, 10(9), 531. https://doi.org/10.3390/atmos10090531






