Abstract
This study proposes a new algorithm termed rain cell identification and tracking (RCIT) to identify and track rain cells from high resolution weather radar data. Previous algorithms have limitations when tracking non-consequent rain cells owing to their use of maximum correlation coefficient methods and their lack of an alternative way to handle the variation stages of rain cells during their life cycles. To address these deficiencies, various methods are implemented in the new algorithm. These include the particle image velocimetry (PIV) method for motion estimation and the rain cell matching rule to obtain the stage changes of rain cells. High resolution (5 min and 1 km) radar data from three rainy days over the German federal state North Rhine Westphalia (NRW) are used in this study. The performance of the identification module for the new algorithm is accessed by two object-oriented verification methods: structure–amplitude–location (SAL) and geometric index, while the performance of the tracking module is compared with TREC and SCOUT tracking algorithms and evaluated by the contingency table verification approach. Results suggest that the performance of the new algorithm is better than reference tracking method. Application of the RCIT algorithm to the selected cases shows that the inner structure of rainfall events in the experimental region present extreme value distributions, with most rainfall events having a short duration with less intensity. The new algorithm can effectively capture the stage changes of rain cells during their life cycles. The proposed algorithm can serve as the basis for further hydro-meteorological applications such as spatial and temporal analysis of rainfall events and short-term flood forecasting.
1. Introduction
Precipitation is a key process in Earth’s water circle. Acquiring explicit knowledge about its inner behavior is critical to assisting us in understanding its interaction with hydrological processes. Rainfall events are characterized by several elements, such as duration, intensity, velocity, and spatial and temporal variability [1]. The variability of rainfall events can be defined as “the variability derived from having multiple spatially-distributed rainfall fields for a given point in time” [2]. In hydro-meteorological applications, elements of rainfall events (e.g., duration, covering area, intensity, velocity) always vary over the life cycle of events. As a consequence, the responses of hydrology models are sensitive to this variation. Modeling rainfall events and analyzing their spatial and temporal information is necessary, in order to improve the accuracy of short-term rainfall forecasting and to lower the uncertainties of hydrological modeling from the variability of rainfall inputs.
For rainfall event monitoring, intensity and cumulative value are the two most common indices and they are usually measured using a rain gauge, which is the standard instrument for providing direct observations. Nevertheless, a rain gauge cannot directly detect variability in rainfall events, it is also subject to errors owing to topography and wind effects. As a possible alternative, weather radars have played a major role in recent years owing to their high spatial and temporal resolution. This is advantageous in terms of (i) acquiring spatial and temporal patterns when modeling rainfall events and (ii) undertaking short-term rainfall forecasting at fine scales. Identifying and tracking rainfall events is a common task in radar-based meteorological and hydrological applications [3,4,5,6].
Broadly speaking, the corresponding algorithms for radar-based rainfall event identification and tracking can be classified into pixel- and object-based approaches. The pixel-based approaches are also referred to as advection field tracking. These are pattern matching approaches for extracting global motion vectors by searching for the maximum correlation coefficient of rain cells in two consecutive radar images. Pixel-based algorithms are more effective when they are applied in convective rainfall nowcasting, which is usually found in frontal systems [7]. Algorithms of this kind are capable of distinguishing between large scale convective and stratiform rainfall, although they are not so effective for individual rain cell tracking. Herein, a rain cell is defined as the closed contours over which rainfall intensity exceeds a given threshold during one rainfall event [8]. Representative algorithms can be listed as follows: TREC [9], TITAN [10], COTREC [11], and SWIRLS [12]. Object-based approaches (also termed cell tracking) include (i) a detecting algorithm for searching a discrete rain cell’s properties (e.g., centroid, area, echo-tops, and vertical-integrated) in consecutive radar images and (ii) a matching algorithm for tracking cell motion and stage changes (e.g., merging and splitting). Representative algorithms can be listed as follows: SCOUT [13], SCIT [14], Trace3D [15], and PERsiann-ForeCAST [16].
Despite the thorough application of these rain cell tracking algorithms, they have the following deficiencies. For pixel-based approaches, they cannot identify and analyze the properties of rain cells, and motion estimates are mostly based on the maximum correlation coefficient, which may yield non-continuous results when fast decay of rainfall occurs. Object-based approaches can quantify the characteristics of rain cells and reflect their dynamics, however, motion estimates obtained from the rain cell center of mass may lack accuracy owing to the random center of mass displacement problem. This problem occurs when the shape of rain cells changes rapidly. As a consequence of motion estimate inaccuracies, these algorithms may also encounter difficulties when handling merging and splitting scenarios [17], whereas a rain cell can begin its life cycle by simply emerging at a location with no rain. For handling false merger and splits issues in rain cell tracking, some recently developed tracking algorithms use object-oriented discriminant methods based on some judging parameters (e.g., overlaps of rain cells in successive radar images, intensity difference of rain cells, maximum matching distance or search radius factors) [18,19,20,21].
This study attempts to make a further step to solve the issues of non-continuous motion estimation and false rain cell stage assignments in rain cell tracking, and a new algorithm: Rain Cell Identification and Tracking (RICT) is proposed. This paper is organized as follows. The RCIT algorithm is illustrated in Section 2. An introduction to the study area and radar data is given in Section 3. Section 4 presents application results of the RCIT algorithm to selected rainfall events that occurred in North Rhine Westphalia (NRW). The discussion is given in Section 5. In Section 6, the main conclusions and further expectations of this work are given.
2. Methodology
The aim of the RCIT is to analyze rainfall events by fully utilizing the merits of weather radar. It involves two modules: rain cell identification and tracking, as presented in Figure 1. The new algorithm combines pixel and object tracking approaches. However, it uses instantaneous flow velocity measuring methods to estimate global motion vectors instead of the maximum correlation coefficient method. This can avoid the non-continuous motion estimation results. A child rain cell matching rule is also defined, which uses rain cell features (i.e., overlap, difference between centroid and average global motion vector, and area difference) to get rain cell tracking results. The inputs to the proposed algorithm are radar reflectivity images and the outputs are the properties of rain cells such as area, intensity, and trajectory.
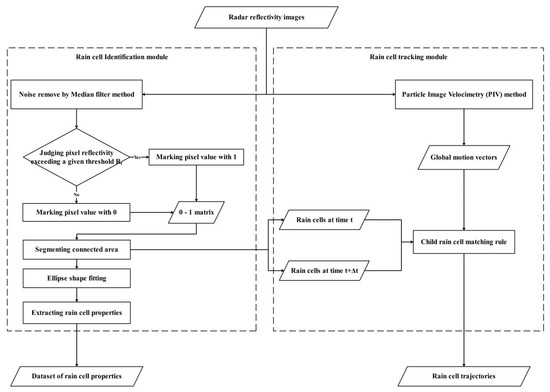
Figure 1.
Step illustration of RCIT algorithm.
2.1. Rain Cell Identification Module
Similar to most object-based tracking algorithms, the rain cell identification module of the RCIT is based on discerning a connected domain above a given threshold. As presented in the left portion of Figure 1, each selected radar reflectivity image is initially filtered by the median filtering method [22] to remove noisy pixels (pixels with abnormally high reflectivity). Then, pixels above a given reflectivity threshold are assigned the value one, with the remainder assigned the value zero. A segmenting process is implemented to assemble and cluster pixels sharing the same reflectivity threshold into a connected area. In the segmenting process, the following rules suggested by [23] are obeyed: (i) if the reflectivity of a rainy pixel is lower than a given threshold Rt, then it is set to null. (ii) For each rainy pixel and its eight neighbors, if more than five of them are null, then it is set to null. (iii) If the pixel is spurred, then it is set to null. Herein, spur pixels are those isolated pixels whose reflectivity is different to others along the horizontal and vertical directions in the labeled binary image. (iv) If the area of a connected region is smaller than 9 km2, then it is ignored. All the segmented regions are then labeled and fitted with an ellipse shape. Their properties are extracted and stored in a relational database. The extracted properties are as follows:
- Area (km2)—sum value for the number of pixels contained in one rain cell.
- Areal rainfall depth (mm)—cumulative precipitation of one rain cell over a 5-min interval.
- Maximum intensity (mm·h−1)—peak intensity of one rain cell.
- Areal mean rainfall depth (mm·km−2)—ratio of the areal rainfall depth and area.
- Eccentricity—ratio of minor and major axes, which are acquired from the fitted eclipse. Used to describe the shape of one rain cell with a value range from 0 to 1.
- Center of mass (km)—center of mass of a rain cell, which is weighted by the reflectivity of rainy pixels.
Property calculation: Areal rainfall depth, maximum intensity, and areal mean rainfall depth are based on the reflectivity (Z) and rain rate (R) converting function: Z = aRb.
2.2. Rain Cell Tracking Module
The rain cell tracking module is established based on a hybrid approach, as illustrated in the right portion of Figure 1. In the first procedure, motion vectors are estimated by implementing the particle image velocimetry (PIV). This is an optical method of flow visualization that is used to obtain instantaneous velocity measurements and related properties of fluids [24,25,26]. It consists of a class of flow measuring mechanisms that are characterized by recording the displacement of small particles embedded in a region of fluid. Figure 2 shows a PIV application in motion vector estimation. In the first step, a window box of size r × r is initially defined, which divides radar images into several sub-blocks. In the second step, a searching distance, d = 2 × vmax + 1, is defined, where vmax is the preset maximum velocity. The minimum quadric difference (MQD), as suggested by [27], is employed in searching the optimal grid points at time t + Δt, as in Equation (1):
where R1(Xi,Yj) and R2(Xi,Yj) are the reflectivity of grid points contained within the window boxes of radar images at time t and t + Δt, respectively; Δx and Δy (Δx, Δy ∈ d) are the locations of minimum reflectivity difference in the east-west and north-south directions separately. The minimum reflectivity differences of grid points within the window boxes are reversed to simplify the calculation. In order to guarantee that the solitary peak locations can be calculated, Δx and Δy are corrected separately in the east-west and north-south directions by fitting a second-order polynomial to the logarithm of the maximum reflectivity of the grid point and its three direct neighbors, as in Equation (2). In this way, the optimal grid points at time t + Δt are identified, with their locations presented as . In the final step, the calculated motion vectors are smoothed by the median filter algorithm.
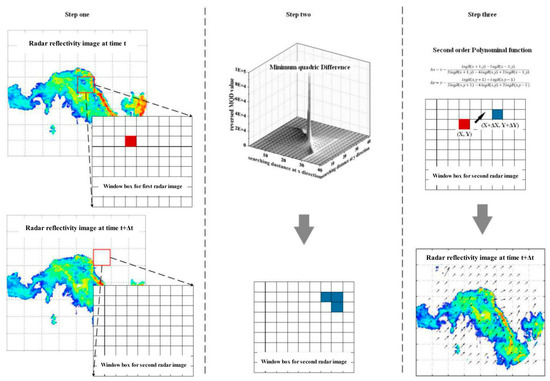
Figure 2.
Illustration of particle image velocimetry (PIV) application in rain cell motion estimation. Step one: window boxes with the area of r × r are defined (rectangular with red color); step two: for any grid point in the window box at a previous timepoint (red block), the minimum quadric difference (MQD) algorithm is applied to deduce the minimum reflectivity differences, and grid points with minimum value in the next window box are identified (blue blocks); step three: the solitary locations of reversed MQD value, Δx and Δy, are corrected by applying Equation (2). The locations of the optimal grid point at the next timepoint are calculated using the second-order polynomial function, and the global motion vectors are extracted and smoothed by the median filter method.
In the second procedure, rain cells at time t and t + Δt are identified. Finally, a child rain cell matching rule is defined in this work for identifying the most-matched rain cells. Before introduction of the child rain cell matching rule, certain definitions were identified: (i) for two radar images at time t and t + Δt, rain cells identified from radar images at t are termed parent cells and (ii) rain cells identified from radar images at t + Δt are termed child cells. The child rain cell matching scheme considers the stage changes of rain cells between successive radar images (e.g., merge, split), using certain indexes for determination such as overlap, area diversification, distance, and angle difference for center of mass. The matching rule can be depicted as follows:
- A boundary box of a parent cell is defined, with a horizontal length of (10 + max(posx), min(posx) − 10) and vertical length of (10 + max(posy), min(posy) − 10), where posx and posy are Cartesian coordinates of pixels in the parent cell.
- The number of child cells falling into the boundary box is determined and their properties, e.g., area, areal rainfall depth, max intensity, areal mean rainfall depth, and center of mass, are selected.
- If only one child cell is searched in the boundary box and it overlaps with a parent cell, then it is the most-matched rain cell. If this child cell does not overlap with a parent cell and the distance and angle difference for the center of mass between it and the parent cell are less than 3 × mean (Vmotion_vector) and 3 × θmotion_vector, it is also the most-matched rain cell, where mean (Vmotion_vector) and θmotion_vector are the mean value of velocity and the prevailing direction of the motion vector, respectively.
- If two or more child cells fall into the boundary box without overlapping a parent cell, the matching rule is changeless; however, one extra condition is included, i.e., child cells whose areas have minimum absolute differences with the parent cell are the most-matched rain cells.
3. Study Area and Data
The study area is the federal state of NRW (Figure 3). Two main types of landscape can be found in NRW, namely the North German lowlands, with elevations just a few meters above sea level, and the North German low mountain range, with elevations of up to 850 m. The lowland areas comprise the Rhine-Ruhr area, which is one of the largest metropolitan areas, with a population of approximately 10 million. The circulation pattern of NRW is mainly affected by the air mass from the Atlantic Ocean along the direction toward the mainland. When arriving at the southern high mountain regions, the air mass stops and rises; this leads to more cloudiness and precipitation. On the eastern side of the mountain regions, drier air masses result in less cloudiness and less precipitation.
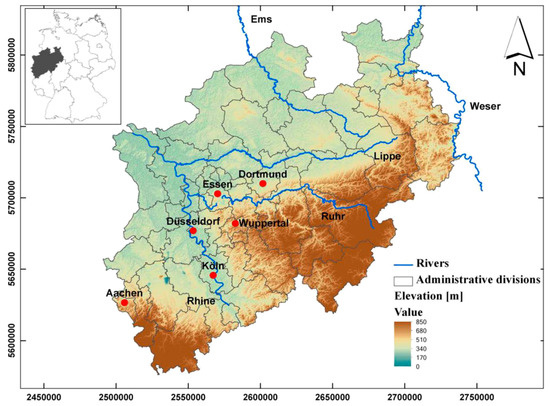
Figure 3.
Study area of North Rhine Westphalia (NRW) and its location in Germany. The main administrative cities are marked with red dots.
Radar data were obtained from the Essen radar deployed in Essen City, NRW. The Essen radar has been deployed over the study area and is a part of the radar network of the German weather service (DWD). The Essen radar is a dual-polarimetric C-band Doppler radar. It delivers radar volume scans (frequency: 800/1200 Hz, maximum range: 124 km) every 15 min for the Doppler velocity, together with intensity volume scans (frequency: 500 Hz, maximum range: 256 km) and precipitation scans (frequency: 600 Hz, maximum range: 150 km) every 5 min for the precipitation echo, with a high spatial resolution of 1 km in range and 1° in azimuth. For this study, the Essen radar provided precipitation scans (time step: 5 min) with an elevation of 0.8° and a range of 128 km. The output reflectivity was selected with a plan position indicator (PPI) display type.
As radar measures precipitation in an indirect manner, the quality of radar data must be carefully checked. The sources that affect the quality of the Essen radar data include ground clutter and speckle, beam blockage, and attenuation. The corresponding quality correction methods in this work follow [28]. After quality checking, an open source package “Wradlib” [29] was applied to project the raw radar image onto a 256 × 256 km2 Cartesian map with 1-km resolution. In order to access the performance of the RCIT algorithm, selected rainfall events for testing should be those with fast growing and decaying intensities and distinct moving directions. In total, 864 radar reflectivity images for three rainy days (26 May 2007; 19 July 2008; and 26 July 2008), were selected to evaluate the performance of the proposed algorithm. The daily rainfall distributions of these rainy days are shown in Figure 4.
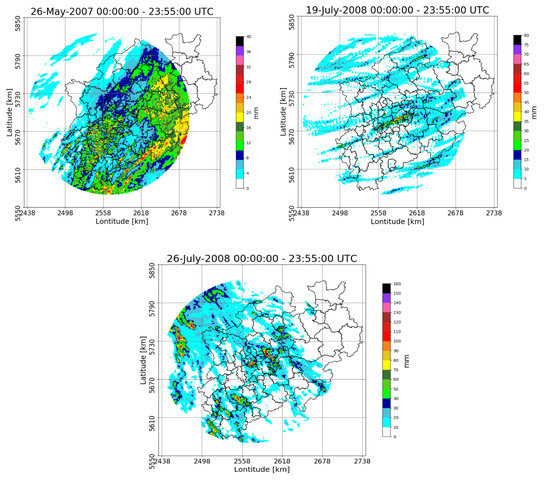
Figure 4.
Daily rainfall distribution for selected rainy days. Radar reflectivity was converted into rain rate according to the German weather service standard Z–R relationship.
4. Results
In the algorithm application process, the reflectivity threshold for rain cell identification was set to 19 dBZ, which was based on the classification of DWD presented by [30], as in Table 1. For the German weather radar system, two common Z–R relationships were used by [30]: one is categorized for the RADOLAN product and the other uses constants a and b with values of 256 and 1.42, respectively. Although the DWD has stated that the categorized relationship statistically shows better results over long time periods, the standard relationship can be more compatible with local cases when a correction factor is added [31]. Based on the above considerations, we applied the DWD standard Z–R relationship to radar reflectivity–rain rate conversion in the application cases.

Table 1.
Conversion of radar reflectivity to rain rates using the Z–R relationship (a = 256, b = 1.42) with thresholds according to the classification of the DWD.
There were 10,346 rain cells identified from the selected radar reflectivity images. Descriptive statistics of their properties are given in Table 2. It was found that a high standard deviation existed for the areas of these rain cells, with values ranging from 9 to 18,734 km2 (most were less than 38 km2). For areal rainfall depth, values ranged from 0.36 to 8861 mm and a high standard deviation again existed. For the max intensity property, a high standard deviation (34.08 mm·h−1) was also found; the median was 2.83 mm·h−1 and the range of values was 0.48 to 397.75 mm·h−1. Areal mean rainfall depth was from 0.04 to 4.4 mm·km−2. Eccentricity ranged from 0 to 1, with a median over 0.5.

Table 2.
Descriptive statistics of rain cell properties. Indexes used for the statistics are minimum value, maximum value, standard deviation, and median value.
Inner structures of the selected events were described by statistically analyzing the physical and geometric properties of the rain cells. RCIT simulation results indicated that the properties (e.g., area, areal rainfall depth, max intensity, and areal mean rainfall depth) of the identified rain cells presented a wide range of values. The shape of the rain cells was somewhat elliptical, with a median value over 0.5. Histograms of the log10-transformed rain cell properties are given as in Figure 5. To determine the best theoretical distributions describing the empirical distributions, a multi-goodness of fit testing (GOF) approach combined with the Akaike information criterion (AIC), the Bayesian information criterion (BIC), and the Kolmogorov–Smirnov (K–S) test methods was applied (see Appendix A). Figure 6 shows their fitted cumulative distributions. Empirical distributions of the log10-transformed properties (area, areal rainfall depth, maximum intensity, and areal mean rainfall depth) could be fitted with the generalized Pareto distribution (GPD) presented in Equation (3), and the extreme value distribution (EVD) was found to fit the eccentricity property shown in Equation (4).
where k is the shape parameter, and μ and α are location and scale parameters, respectively. For μ < 0, k is above zero, and for μ < x < α, k is below zero. At the limit for k = 0, the GPD is the exponential distribution.
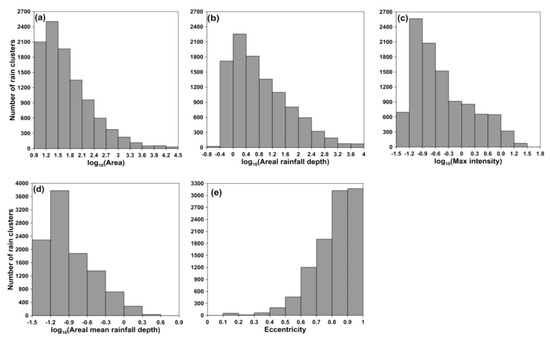
Figure 5.
Histograms of log10-transformed rain cell properties: (a) area, (b) areal rainfall depth, (c) maximum intensity, (d) areal mean rainfall depth and property, (e) eccentricity for identified rain fields.
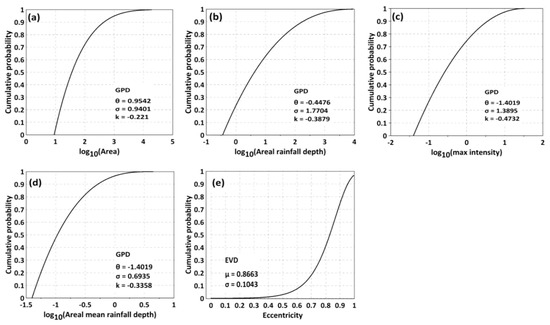
Figure 6.
Cumulative curves of fitted probability density functions for log10-transformed rain cell properties: (a) area, (b) areal rainfall depth, (c) maximum intensity, (d) areal mean rainfall depth and property, (e) eccentricity.
For , when k > 0, the generalized EVD is the Frchet distribution; k < 0 corresponds to the Weibull distribution; at the limit for k = 0, it is the Gumbel distribution.
A total of 1107 rain cell trajectories were exploited. Histograms of their duration and motion vectors are presented in Figure 7. All rain cells held a mean duration of 40 min. For all the identified rain cells, the median value of their life cycles was 15 min, with an average moving speed of 11.59 m·s−1. The moving directions of the rain cells were consistently toward the motion direction observed in the radar images.
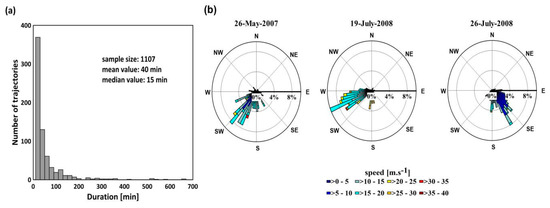
Figure 7.
(a) Histograms of rain cell duration for identified rain fields, (b) wind rose plot of the rain cell motion estimation result, which is sorted by three rainy days.
These results were in agreement with the study of [32], in which the structures of convective rainfall events were analyzed and presented an extreme value distribution statistically. Statistical analysis of the rain cell properties suggests that the inner structures of the selected rainy days can be expressed by the extreme value distribution. This suggests that most rainfall events had a limited covering area with less intensity and short duration; rainfall events with a long duration had a large covering area and high intensity.
During the life cycle of a rainfall event, the physical and geometrical features of rain cells continually change. Three common stages reflect these variations: cumulus, mature, and dissipating [33]. In fact, the stage changes of rain cells are not only associated with its internal growth and decay but also with other rain cells (e.g., merging or splitting). Five rain cell life stages could be confirmed by references; their definitions are listed as follows (Figure 8a–e):
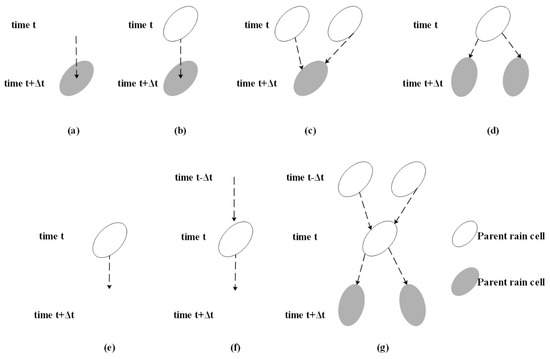
Figure 8.
Five rain cell life stages of rain cells: (a) Initial, (b) Tracking, (c) Merging, (d) Splitting, (e) Dissipating, (f) 5-min life cycle, (g) Complex stage.
- Initial: A rain cell having no parent cell is termed an initial rain cell.
- Tracking: A rain cell with only one parent cell and having no interaction with other rain cells during its life cycle is termed a tracking rain cell.
- Merge: A rain cell with at least two parent cells is termed a merged rain cell.
- Split: A rain cell with only one parent cell but at least two child cells is termed a split rain cell.
- Dissipate: A rain cell with at least one parent cell but no child cells is termed a dissipate rain cell.
Additionally, other two stages named ‘5-min life cycle’ and ‘Complex stage’ were firstly defined in this study (Figure 8f,g). A rain cell with a life cycle of only 5 min is termed 5-min life cycle stage. A rain cell for which merging and splitting simultaneously exist during its life cycle is termed complex stage.
The number of rain cells with different stages over their life cycles is summarized in Table 3. Rain cells with “5-min life cycle” and “tracking” stages were dominant. The “merging”, “splitting”, and “complex stage” cells occurred in isolated cases, indicating a stable inner structure of the identified cells. For the cases of 19 July 2008 and 26 July 2008, the number of rain cells in the “tracking” stage was even greater, indicating that the rainfall events occurring on these two days had long duration. The number of rain cells in the “merging” and “splitting” stages was greater in the 26 July 2008 case. This suggests that there were more convective rainfall events on that day since rain cells merge or split more frequently under such conditions.

Table 3.
Number of rain cells with different life stages, sorted by selected rain day.
5. Discussion
Assessing the performance of the RCIT algorithm involves three parts: evaluating the performance of the rain cell identification module, assessing the performance of motion estimation against the TREC tracking algorithm, and rain cell merging and splitting evaluation against the SCOUT algorithm.
5.1. Evaluation of Rain Cell Identification Module by Feature-Based Verification Methods
Grid-point related error measurement is problematic for the rain cell tracking algorithm. A classic example illustrating this problem is the well-known “Double Penalty” problem [34], in which prediction of a precipitation object at the correct size and structure might yield very poor verification scores. For example, one rain cell is displaced slightly in space, but the categorical verification scores heavily penalize such a situation. In traditional verification methods, a displacement simply leads to a false alarm, and it is also very poorly rated owing to its large root mean squared error [35]. On the other hand, despite a great deal of effort in the statistical validation of grid-based rainfall estimated results, verification associated with the geometry patterns of rain cells has not been well researched or applied.
As an alternative, feature-based verification methods have been built upon the idea of identifying rainfall events as “objects”. With this perspective, simulated and observed rainfalls are not compared directly at the same location; rather, objects of interest are extracted from simulated and observed data and then compared together so that verification statistics are obtained. A number of spatial verification methods have been proposed [36,37]. In the present work two feature-based verification methods, structure–amplitude–location (SAL) [38] and geometric index [39], were implemented to evaluate the identification module of the RCIT algorithm. A detailed introduction to the SAL and geometric index methods is presented in Appendix B. The inputs for these two methods are radar reflectivity images (termed obs_ref) and reflectivity images of pixel sets for rain cells, these kind images are generated from the RCIT algorithm (termed sim_ref).
Figure 9 shows the SAL verification results, which are arranged based on the three selected rainy days. For each SAL plot presented in Figure 9, the vertical axis denotes the A component, the horizontal axis denoted the S component, the dots represent values of the S and A components, and the color scale of the dots denotes the L component. Median values of the SAL components are presented as dashed lines. It can be seen that all S and A values are concentrated close to zero, as are most L component values. Table 4 gives three geometric index values calculates from the sim_ref and obs_ref data sets respectively. All values were again organized based on the three selected rainy days. It is evident that the index differences between the sim_ref and obs_ref data sets were less than 0.05.
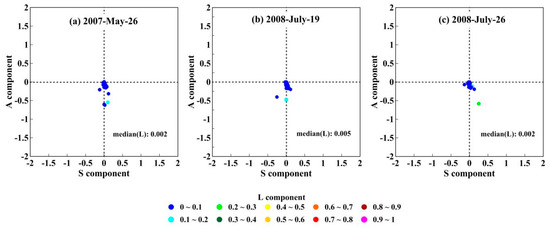
Figure 9.
Value distributions of the three structure–amplitude–location (SAL) components. Dashed lines in the vertical and horizontal directions in each sub-figure represent the median values of the S and A components, respectively, and dot color represents the L component value. Results are sorted by selected rain days: (a) 26 May 2007; (b) 19 July 2008; (c) 26 July 2008.

Table 4.
Results of three geometric index components for sim_ref and obs_ref data sets. Values are sorted at 5, 50, and 75 percentile levels.
According to the definition of SAL, values of S and A components range from −2 to 2, and 0 denotes a very good match for the simulated data set to the observed data set. The SAL verification results suggested that rain cells from the RCIT algorithm can be well matched to rainfall fields as manually observed from radar reflectivity images. It was also suggested that there were no rain cells (area threshold > 9 km2) not identified from the RCIT algorithm. Geometric index verification results indicated that spatial pattern difference between rain cells from the RCIT algorithm and manually observed rainfall fields from radar reflectivity images were not obvious. In general, the rain cell identification module for the RCIT algorithm performed well based on the two feature-based verification results.
5.2. Assessing the Performance of Motion Estimation against the TREC Algorithm
The performance of the rain cell tracking module is compared to the pixel-based tracking algorithm: TREC by operating a deterministic persistence forecasting [17]. The forecasting performance can reflect the motion estimation accuracy by neglecting growth and decay process [40]. In this work, eight short-term rainfall events were selected from three rainy days, as listed in Table 5. The forecasting is done as follows: motion vectors at time t - Δt and t were generated by RCIT and TREC algorithm separately, then radar reflectivity images at time t were extrapolated with a leading time up to 2 h by using the motion vectors derived from their corresponding tracking schemes. The reflectivity threshold for the forecasting is 19 dBZ, which is the same with the reflectivity threshold used in the rain cell identification module.

Table 5.
Precipitation statics of selected events with 5 min accumulated data from the Essen radar. The static parameters are Max. Total Rainfall, Max. Intensity.
Forecasting performance is accessed by contingency table approach [10], which calculates three skill scores, i.e., the probability of detection (POD), the false alarm rate (FAR), and the critical success index (CSI). If rainfall appears on both of the forecast results and radar images, they are recorded as hit. If it only appears on radar images, it is marked as miss, and if it only appears on forecast results, it is regarded as false. By counting all the hits, misses, and false, POD, FAR, and CSI can be calculated according to the following formula, respectively. The higher value of POD and CSI, or the lower value of FAR, the better the tracking algorithm.
Figure 10 gives the averaged value of these three skill scores for forecasting results. When the leading time was less than 30 min, skill score value differences were not obvious for forecasting results from both tracking algorithms, while the higher POD and CSI but lower FAR scores were found for the RCIT algorithm compared to the TREC algorithm as leading time increased. It indicated that identified motion vectors from the RCIT algorithm were more credible.
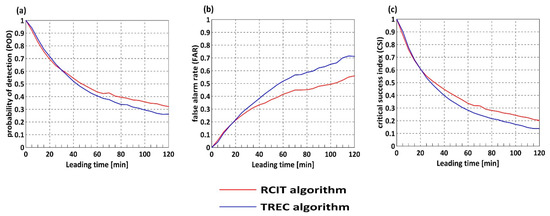
Figure 10.
Averaged value of three contingency table skill scores for forecasting results by two tracking algorithms. (a) POD; (b) FAR; (c) CSI. The red solid lines in each subplot represent results for the RCIT algorithm, the blue solid lines represent results for the TREC algorithm.
5.3. Rain Cell Merging and Splitting Evaluation against the SCOUT Algorithm
Performance of rain cell merging and splitting assignment for the new algorithm is compared with the object-based tracking approach: SCOUT. The performance is also evaluated by contingency table, which follows the accessing method listed in [17]. We firstly acquired tracks of rain cells manually from selected eight rainfall events, then tracks from RCIT and SCOUT approaches were also acquired. These tracks are compared to those manually acquired, number of hit, miss, and false were counted and POD, FAR, and CSI were calculated for RCIT and SCOUT algorithms respectively. Table 6 shows three skill scores for two tracking algorithms. A look at the results in Table 6 indicated a good fit between the visual inspection and what the new algorithm captures for rain cells. The higher POD and CSI values for rain cells with ‘Merge’ and ‘Split’ obtained by the new algorithm reflected an improvement in the RCIT algorithm with respect to the SCOUT tracking approach. Moreover, lower FAR values for the new algorithm also suggested better capability to avoid wrong rain cell assignment for the RCIT algorithm.

Table 6.
POD, FAR, and CSI scores for rain cell assignments from RCIT and SCOUT tracking approaches, respectively.
6. Conclusions
This study develops a new algorithm, RCIT, which utilizes the advantages of high resolution weather radar data. The proposed algorithm provides the following improvements:
- It uses the PIV method in rain cell motion estimation. Rain cell motion estimation by past algorithms is mainly based on the maximum correlation coefficient method, which may lead to nonconsecutive motion when the shape and volume of a rain cell change rapidly. The PIV method avoids this situation.
- A rain cell matching rule is proposed to discern the life cycle and stage change of rain cells. Some other algorithms focus mainly on analyzing feature changes of rain cells (e.g., overlap, area, intensity) by some object methods in dealing with cell merge and splits. The proposed rain cell matching rule put global motion vector as one judging parameter in rain cell stage analysis, this can be easily operated, and various stages of rain cells can also be discerned effectively.
The performance of rain cell identification for the RCIT algorithm is accessed by using two feature-based verification methods, SAL and geometric index; performance of rain cell tracking for the new algorithm is compared to pixel and object based tracking algorithms (TREC and SCOUT) by using the contingency table method. It is shown that the new algorithm improves the capabilities of motion estimation and rain cell tracking. Practical applications of the RCIT algorithm in analyzing the inner structure of historical rainfall events that occurred in the NRW is presented. Results show that the properties of rain cells in this region presented an extreme value distribution, indicating that the selected rainfall events had a short duration with low intensity. Long duration events with high intensity are rarely found and the stage changes of rain cells vary between events.
It should be noted that inputs for the proposed algorithm are not limited to radar data; other 2D remote sensing data will also be used as the algorithm inputs, suggesting the versatility of the proposed algorithm. In future application, it is intended that this algorithm will analyze the spatial–temporal variation of rainfall in small regions; this will lead to the determination of rainfall inputs with proper spatial and temporal scales for hydro-meteorological applications. The proposed algorithm will also be applied to rainfall nowcasting. However, it must be noted that the new algorithm is designed without considering the internal growth and decay of rainfall events. This will limit the forecasting accuracy in some convective scenarios (e.g., tropical cyclone). In addition, the features of the rain cell output from this algorithm can be used in sensitivity analyses of urban runoff in relation to short-term rainfall events, which will improve flood forecasting precision in small–medium catchments.
Author Contributions
Conceptualization, T.H. and T.E.; methodology, T.H.; software, T.H.; validation, T.H. and J.Z.; resources, T.E.; writing—review and editing, J.H. and Y.C.
Funding
This research was funded by the INTERNATIONAL SCIENCE & TECHNOLOGY COOPERATION PROGRAM OF CHINA, grant number 2012DFG22140.
Acknowledgments
Authors would like to thank WUPPERVERBAND (water management in Wupper area) for radar data support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The GOF test determines whether a data set is well fitted with a predefined distribution that gives the highest probability of producing the observed data. As such, a series of fit testing methods was developed, with the commonly applied tests as follows:
- The K–S test is based on the empirical cumulative distribution function (ECDF). Given N ordered data points Y1, Y2, …., Yn, their ECDF is defined as:where n(i) is the number of points less than Yi and Yj, which are ordered from the smallest to largest value. This is a step function that increases by 1/N at the value of each ordered data point. The K–S test was developed according to the following hypotheses: H0—the data follow a specified distribution; H1—the data do not follow the specified distribution.
- AIC [41] is based on the use of Kullback–Leible information as the discrepancy measure between the true distribution and the approximating distributions: Mi = gi(x, p1, p2, …, pn). The AIC for the ith candidate distribution can be computed as:where stands for the maximum log-likelihood of the sample of the data set, p is the parameter’s number of candidate distributions when the sample size n is small with respect to the number of the estimated parameter Pi. The smaller the value of AIC, the better fitting the result for the candidate distribution is.
- BIC [42] serves as an asymptotic approximation to a transformation of the Bayesian posterior probability of a candidate model. It is based on the empirical log-likelihood and does not require the specification of priors. BIC is defined as:where the symbols are the same as those in Equation (A2). A small value of BIC means that the candidate distribution fits well with the empirical distribution.
Appendix B
Two feature-based verification methods, structure–amplitude–location (SAL) and geometric index, were applied to evaluate the performance of the RCIT algorithm and nowcasting methods. In SAL, term structure denotes the similarity in the shapes of modeled and observed rain cells; its value range is from −2 to 2. Amplitude denotes the similarity in the total precipitation values of modeled and observed rain cells; its value range is from −2 to 2. Location denotes the similarity of the center of mass for the modeled and observed rain cells; its value varies from 0 to 2. The accuracy of nowcasting methods can be evaluated based on the value of the three SAL components and a perfect nowcasting is confirmed by S, A, and L values of 0. More details on the SAL method can be found in [39].
Geometric index is a quantitative assessment method for the spatial patterns of rain cells [40]. It compares the geometric features of modeled and observed rain cells via three indexes:
- Connectivity index: This is defined to compare simulated rain cells with respect to a reference object (e.g., observed rain cells). Its value is calculated based on the number of rain cells (NC) and the total number of non-zero pixels or pixels above a given threshold (NP), as in Equation (A4).where Cindex is the connectivity index, NP is the number of rainy pixels above a given threshold, and NC is the number of rain cells.
- Shape index: This index is introduced to quantitatively describe the shape discrepancy of rain cells, as in Equation (A5).where Sindex is the single index, Pmin is the theoretical minimum perimeter, and P is the actual perimeter of the rain cell.
- Area index: This is defined to depict the dispersiveness between the modeled and observed rain cells. Its value is the ratio of the area of its convex hull (the boundary of the minimal convex set containing a finite set of points in the rain cell), as in Equation (A6).where Aindex is the area of the rain cell and AConvex is the area of the convex hull.
References
- Cristiano, E.; Veldhuis, M.C.T.; Giesen, N.V.D. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 1–34. [Google Scholar] [CrossRef]
- Peleg, N.; Blumensaat, F.; Molnar, P.; Fatichi, S.; Burlando, P. Partitioning the impacts of spatial and climatological rainfall variability in urban drainage modeling. Hydrol. Earth Syst. Sci. 2017, 21, 1–20. [Google Scholar] [CrossRef]
- Moseley, C.; Berg, P.; Haerter, J.O. Probing the precipitation life cycle by iterative rain cell tracking. J. Geophys. Res. Atmos. 2013, 118, 13361–13370. [Google Scholar] [CrossRef]
- Novo, S.; Martínez, D.; Puentes, O. Tracking, analysis, and nowcasting of Cuban convective cells as seen by radar. Meteorol. Appl. 2014, 21, 585–595. [Google Scholar] [CrossRef]
- Guinard, K.; Mailhot, A.; Caya, D. Projected changes in characteristics of precipitation spatial structures over North America. Int. J. Climatol. 2015, 35, 596–612. [Google Scholar] [CrossRef]
- Yeung, J.K.; Smith, J.A.; Baeck, M.L.; Villarini, G. Lagrangian Analyses of Rainfall Structure and Evolution for Organized Thunderstorm Systems in the Urban Corridor of the Northeastern US. J. Hydrometeorol. 2015, 16, 1575–1595. [Google Scholar] [CrossRef]
- Moral, A.D.; Rigo, T.; Llasat, M.C. A radar-based centroid tracking algorithm for severe weather surveillance: Identifying split/merge processes in convective systems. Atmos. Res. 2018, 213, 110–120. [Google Scholar] [CrossRef]
- Féral, L.; Sauvageot, H.; Castanet, L.; Lemorton, J.; Cornet, F.; Leconte, K. Large-scale modeling of rain fields from a rain cell deterministic model. Radio Sci. 2006, 41, 1–21. [Google Scholar] [CrossRef]
- Rinehart, R.E.; Garvey, E.T. Three-dimensional storm motion detection by conventional weather radar. Nature 1978, 273, 287–289. [Google Scholar] [CrossRef]
- Dixon, M.; Wiener, G. TITAN: Thunderstorm Identification, Tracking, Analysis, and Nowcasting—A Radar-based Methodology. J. Atmos. Ocean. Technol. 1993, 10, 785–797. [Google Scholar] [CrossRef]
- Li, L.; Schmid, W.; Joss, J. Nowcasting of Motion and Growth of Precipitation with Radar over a Complex Orography. J. Appl. Meteorol. 1995, 34, 1286–1300. [Google Scholar] [CrossRef]
- Li, P.W.; Lai, E.S.T. Applications of radar-based nowcasting techniques for mesoscale weather forecasting in Hong Kong. Meteorol. Appl. 2004, 11, 253–264. [Google Scholar] [CrossRef]
- Einfalt, T.; Denoeux, T.; Jacquet, G. A radar rainfall forecasting method designed for hydrological purposes. J. Hydrol. 1990, 114, 229–244. [Google Scholar] [CrossRef]
- Johnson, J.T.; Mackeen, P.L.; Witt, A.; Mitchell, E.D.W.; Stumpf, G.J.; Eilts, M.D.; Thomas, K.W. The Storm Cell Identification and Tracking Algorithm: An Enhanced WSR-88D Algorithm. Weather Forecast. 1998, 13, 263–276. [Google Scholar] [CrossRef]
- Handwerker, J. Cell tracking with TRACE3D—A new algorithm. Atmos. Res. 2002, 61, 15–34. [Google Scholar] [CrossRef]
- Zahraei, A.; Hsu, K.L.; Sorooshian, S.; Gourley, J.J.; Hong, Y.; Behrangi, A. Short-term quantitative precipitation forecasting using an object-based approach. J. Hydrol. 2013, 483, 1–15. [Google Scholar] [CrossRef]
- Munoz, C.; Wang, L.P.; Willems, P. Enhanced object-based tracking algorithm for convective rain storms and cells. Atmos. Res. 2017, 201, 144–158. [Google Scholar] [CrossRef]
- Jung, S.H.; Lee, G. Radar-based cell tracking with fuzzy logic approach. Meteorol. Appl. 2015, 22, 716–730. [Google Scholar] [CrossRef]
- Shah, S.; Notarpietro, R.; Branca, M. Storm Identification, Tracking and Forecasting Using High-Resolution Images of Short-Range X-Band Radar. Atmosphere 2015, 6, 579–606. [Google Scholar] [CrossRef]
- Hou, J.; Wang, P. Storm Tracking via Tree Structure Representation of Radar Data. J. Atmos. Ocean. Technol. 2017, 34, 729–747. [Google Scholar] [CrossRef]
- Zan, B.; Yu, Y.; Li, J.; Zhao, G.; Zhang, T.; Ge, J. Solving the storm split-merge problem—A combined storm identification, tracking algorithm. Atmos. Res. 2019, 218, 335–346. [Google Scholar] [CrossRef]
- Anoraganingrum, D. Cell Segmentation with Median Filter and Mathematical Morphology Operation. In Proceedings of the 10th International Conference on Image Analysis and Processing, Venice, Italy, 27–29 September 1999; p. 1043. [Google Scholar]
- Peleg, N.; Morin, E. Convective rain cells: Radar-derived spatiotemporal characteristics and synoptic patterns over the eastern Mediterranean. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Merzkirch, W. Particle Image Velocimetry. In Optical Measurements: Techniques and Applications; Mayinger, F., Feldmann, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 341–357. [Google Scholar]
- Adrian, R.J. Twenty years of particle image velocimetry. Exp. Fluids 2005, 39, 159–169. [Google Scholar] [CrossRef]
- Westerweel, J.; Elsinga, G.E.; Adrian, R.J. Particle Image Velocimetry for Complex and Turbulent Flows. Annu. Rev. Fluid Mech. 2013, 45, 409. [Google Scholar] [CrossRef]
- Gui, L.C.; Merzkirch, W. A method of tracking ensembles of particle images. Exp. Fluids 1996, 21, 465–468. [Google Scholar] [CrossRef]
- Golz, C.; Einfalt, T.; Galli, G. Radar data quality control methods in VOLTAIRE. Meteorol. Z. 2006, 15, 497–504. [Google Scholar] [CrossRef]
- Heistermann, M.; Jacobi, S.; Pfaff, T. Technical Note: An open source library for processing weather radar data (wradlib). Hydrol. Earth Syst. Sci. 2013, 17, 863–871. [Google Scholar] [CrossRef]
- Weusthoff, T.; Hauf, T. The life cycle of convective-shower cells under post-frontal conditions. Q. J. R. Meteorol. Soc. 2010, 134, 841–857. [Google Scholar] [CrossRef]
- Frerk, I.; Treis, A.; Einfalt, T.; Jessen, M. Ten years of quality controlled and adjusted radar precipitation data for north rhine-westphalia–methods and objectives. In Proceedings of the 9th International Workshop on Precipitation in Urban Areas: Urban Challenges in Rainfall Analysis, Pontresina, Switzerland, 2012. [Google Scholar]
- Barnolas, M.; Rigo, T.; Llasat, M.C. Characteristics of 2-D convective structures in Catalonia (NE Spain): An analysis using radar data and GIS. Hydrol. Earth Syst. Sci. 2010, 14, 129–139. [Google Scholar] [CrossRef]
- Byers, H.R.; Braham, R.R. Thunderstorm structure and circulation. J. Meteorol. 1948, 5, 71–86. [Google Scholar] [CrossRef]
- Zhao, B.; Zhang, B. Assessing Hourly Precipitation Forecast Skill with the Fractions Skill Score. J. Meteorol. Res. 2018, 32, 135–145. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-Based Verification of Precipitation Forecasts. Part I: Methodology and Application to Mesoscale Rain Areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Gilleland, E.; Ahijevych, D.; Brown, B.G.; Casati, B.; Ebert, E.E. Intercomparison of Spatial Forecast Verification Methods. Weather Forecast. 2009, 24, 1416–1430. [Google Scholar] [CrossRef]
- Ebert, B.; Fowler, T.; Gill, P.; Goeber, M.; Joslyn, S.; Mittermaier, M.; Nurmi, P.; Watkins, A.; Weigel, A. Progress and challenges in forecast verification. Meteorol. Appl. 2013, 20, 129. [Google Scholar] [CrossRef]
- Wernli, H.; Paulat, M.; Hagen, M.; Frei, C. SAL—A Novel Quality Measure for the Verification of Quantitative Precipitation Forecasts. Mon. Weather Rev. 2008, 136, 4470–4487. [Google Scholar] [CrossRef]
- Aghakouchak, A.; Nasrollahi, N.; Li, J.; Imam, B.; Sorooshian, S. Geometrical Characterization of Precipitation Patterns. J. Polym. Environ. 2011, 19, 818. [Google Scholar] [CrossRef]
- Germann, U.; Zawadzki, I.; Turner, B. Predictability of Precipitation from Continental Radar Images. Part IV: Limits to Prediction. J. Atmos. Sci. 2006, 63, 2092–2108. [Google Scholar] [CrossRef]
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–213. [Google Scholar]
- Schwarz, G. Estimating the Dimension of a Model. Annal. Stat. 2005, 6, 15–18. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).