Seasonal Forecasting of the Onset of the Rainy Season in West Africa
Abstract
1. Introduction
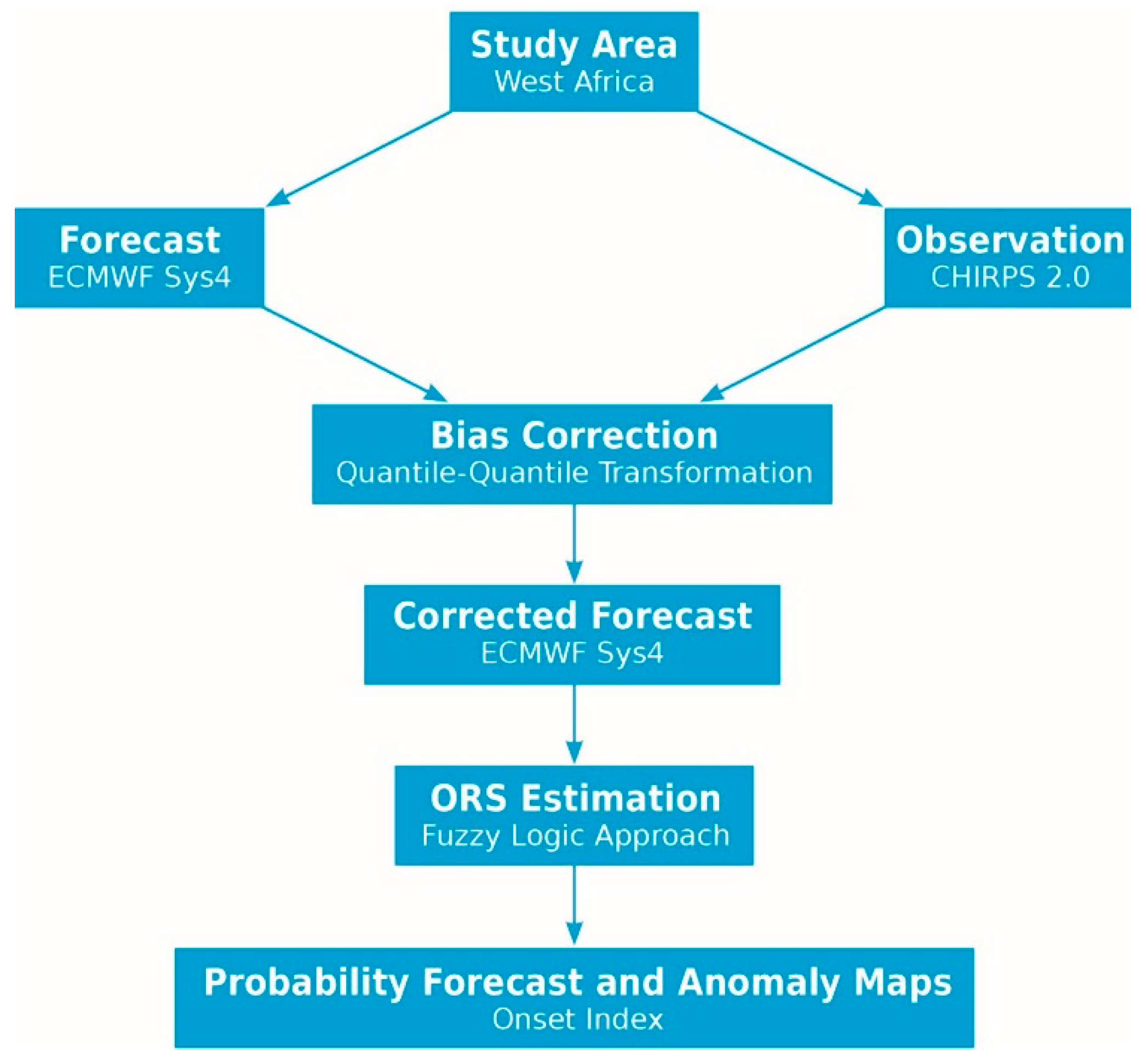
2. Data and Study Area
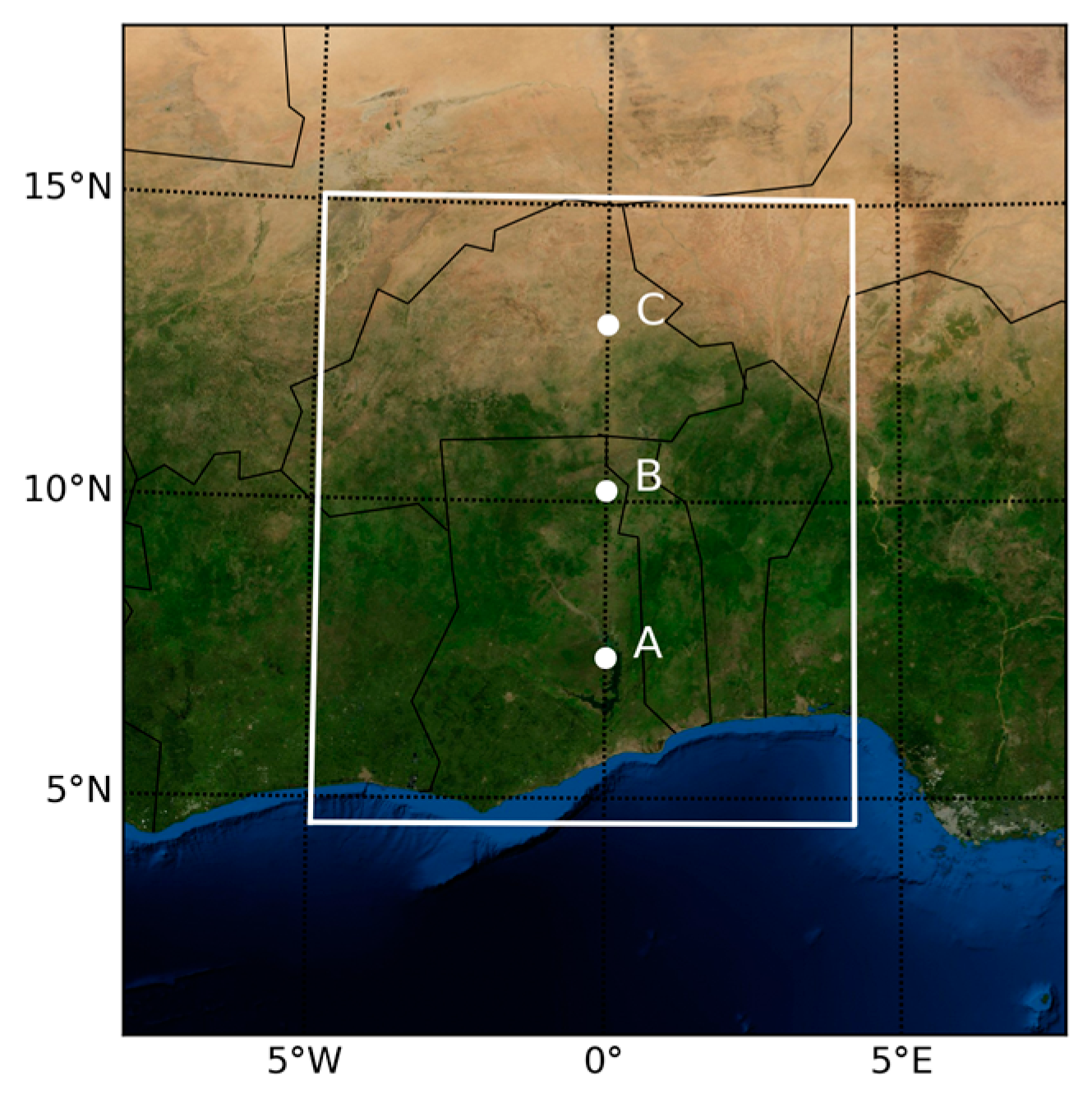
2.1. Study Area
2.2. ECMWF SYS4 Precipitation Hindcasts
2.3. CHIRPS Observations
3. Forecasting Methodology and Verification
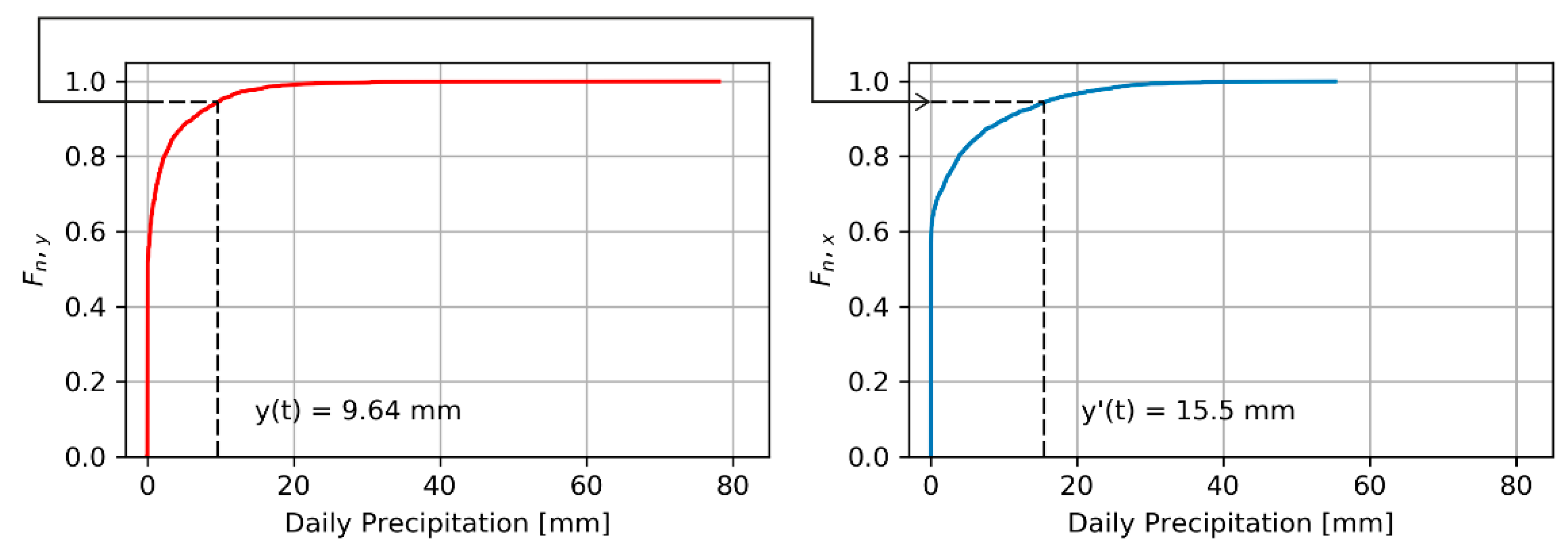
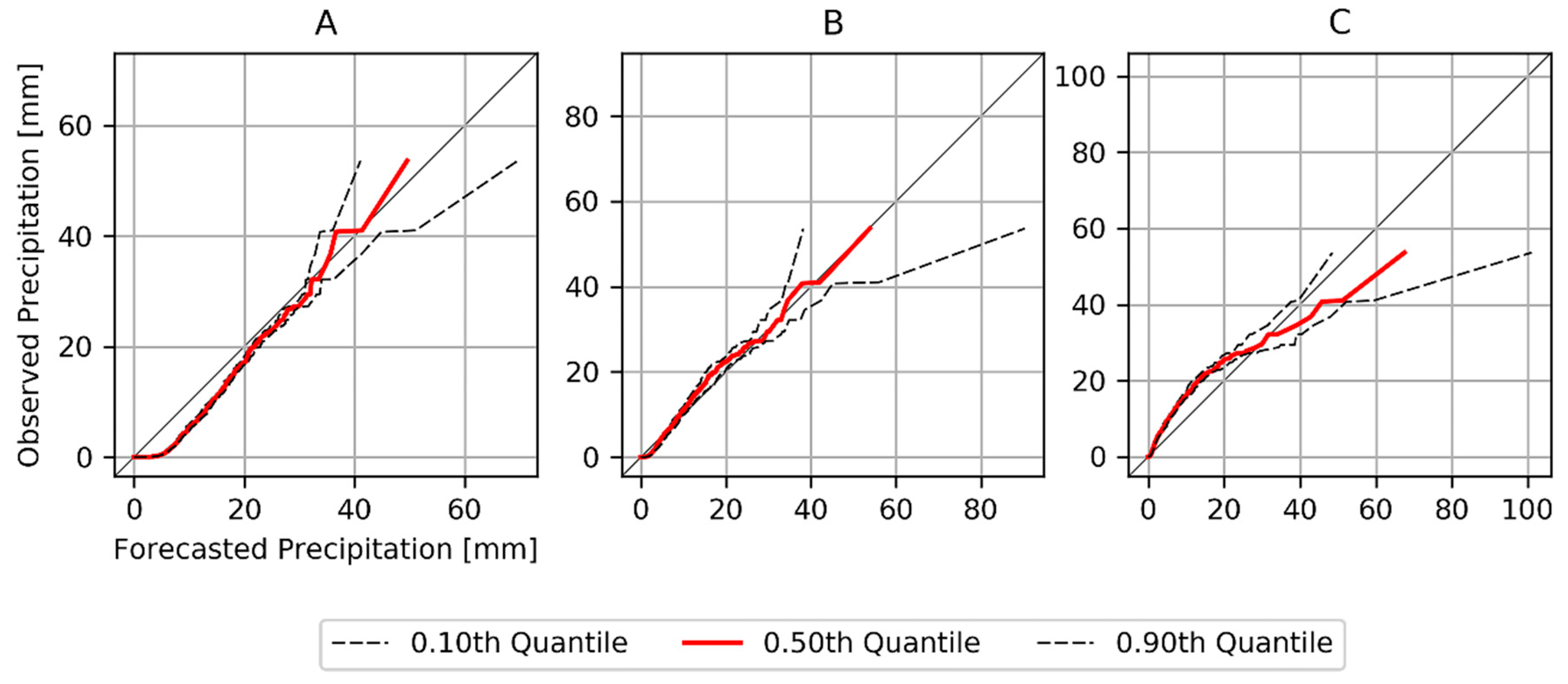
3.1. Bias Correction of Ensemble Precipitation Forecasts
- Sort the daily observed values for the investigation period (1 February–31 February, 2000–2010) in an ascending order.
- Determination of the rank for each observation with and number of observations.
- Determining the empirical cumulative distribution function of the observations by calculating the cumulative frequencies for each observation using the formula ).
- Sort the daily forecast values of an ensemble member for the investigation period (1.02–31.08, 2000–2010) in an ascending order.
- Determination of the rank for each forecast with and number of forecasts.
- Determining the empirical cumulative distribution function of the forecasts by calculating the cumulative frequencies for each forecast using the formula
- Determine the corrected prediction value for each with the inverse cumulative distribution function of the observations .
- Repeat steps 4–7 for each ensemble member and each grid point.
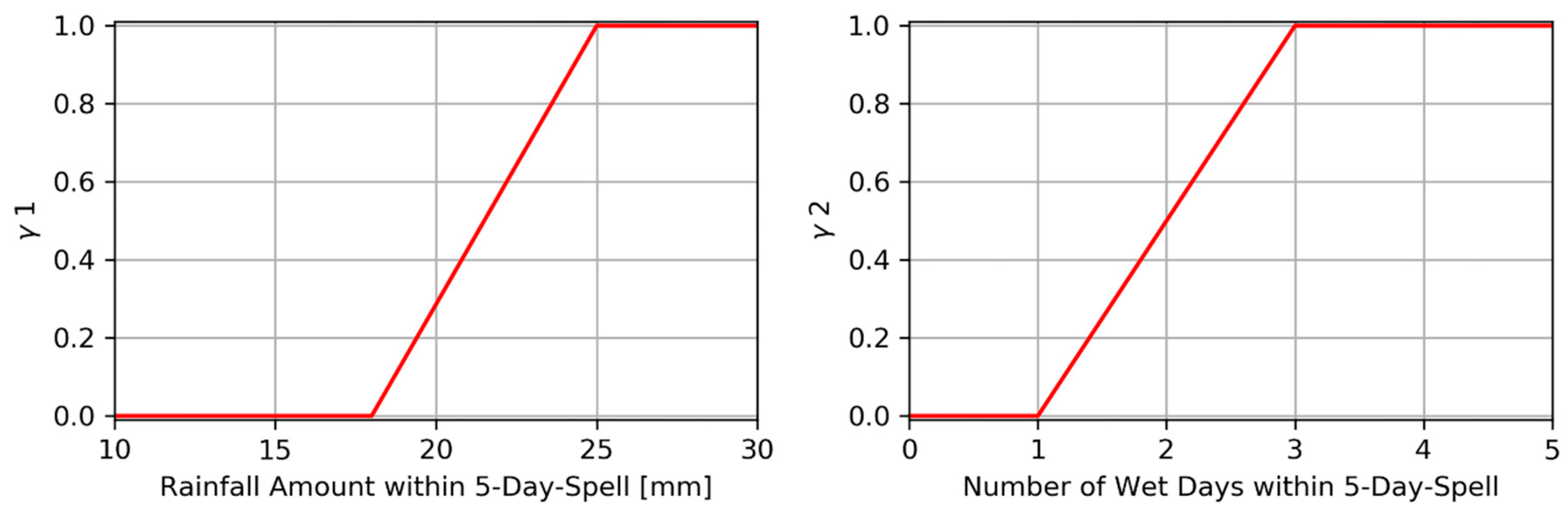
3.2. Calculation of the ORS Dates Using Fuzzy Rules
- ORS is defined by local precipitation events and is based on dry and wet periods.
- ORS is defined by large-scale changes of the WAM system, indicated by e.g., circulation patterns or specific atmospheric variables like long-wave radiation fluxes.
- The accumulated sum of precipitation in five consecutive days is at least 25 mm.
- Within this pentad, at least two more days must exceed a precipitation amount of 1 mm.
- There is no period of consecutive 7 dry days or longer within the next 30 days (false start criterion). A dry day is defined as a day with less than 1 mm precipitation.
3.3. Verification of the Spatial ORS Fields
3.4. Calculation of the ORS Index
- Calculation of the observed ORS dates from CHIRPS for the period from 1981–2010.
- Determination of the quantiles and from the observed ORS dates to define the tercile-based ORS categories.
- Calculation of the ORS dates from the bias-corrected SYS4 precipitation hindcasts for each ensemble member of a given year.
- Classification of the 15 ORS ensemble members into the three tercile-based categories: Below average, if yij (t) < , near average, if ≤ yij (t) ≤ and above average, if yij (t) > .
- Calculation of the corresponding forecast probabilities pk for each ORS category.
- Calculation of the ORS index value based on Equation (3).
- Step 3 to 6 are repeated, if the forecasts probabilities are determined for other years.
4. Results and Discussion
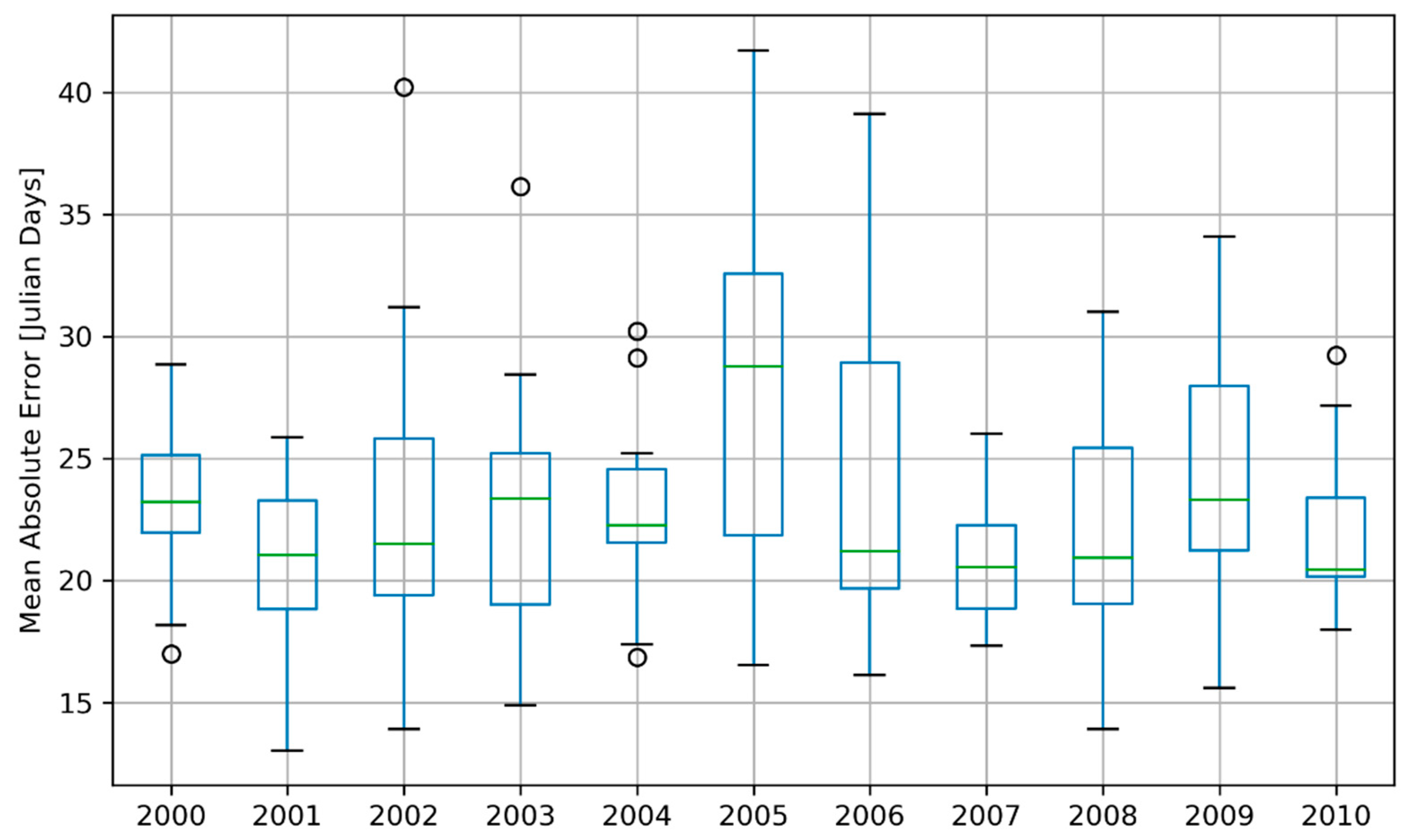
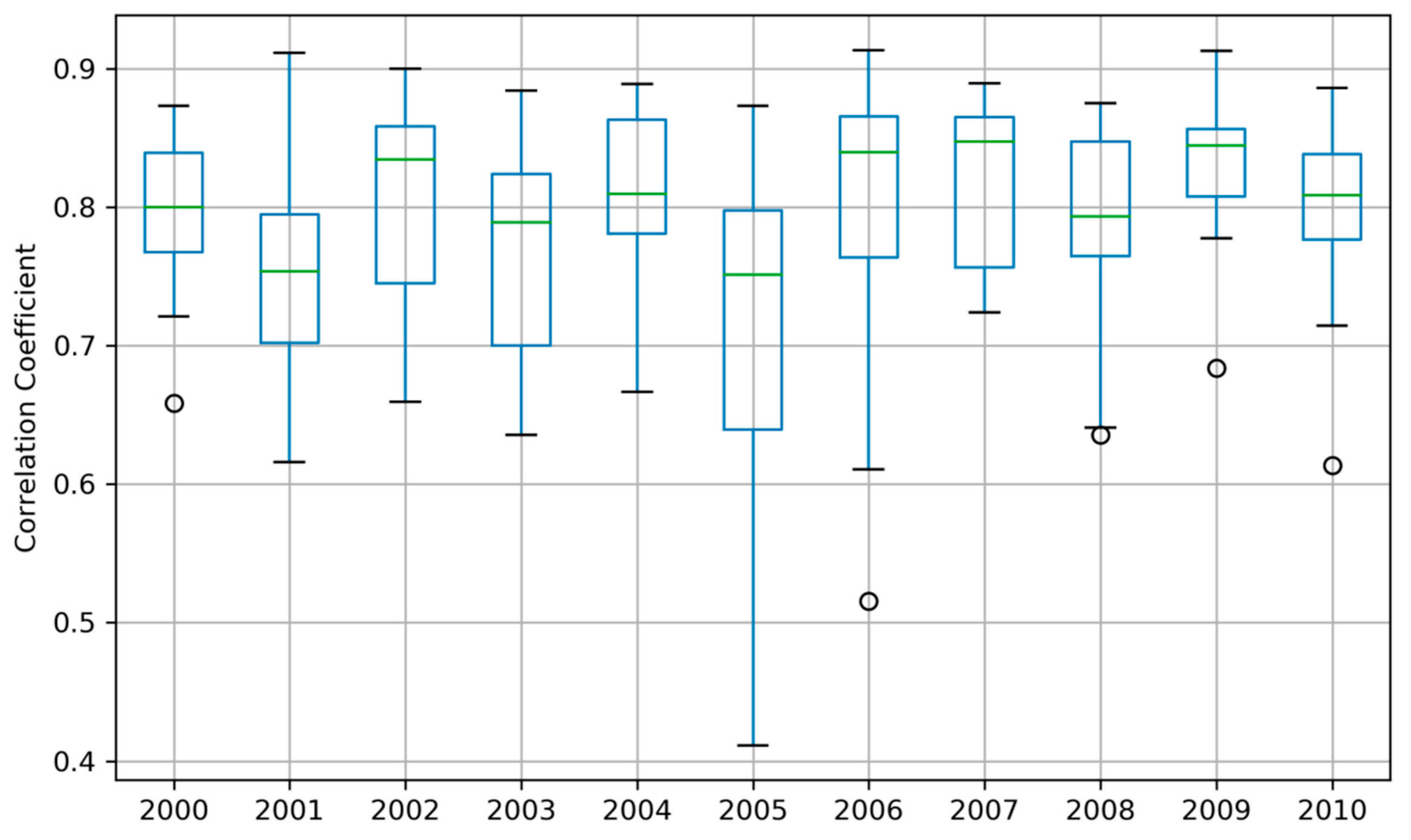
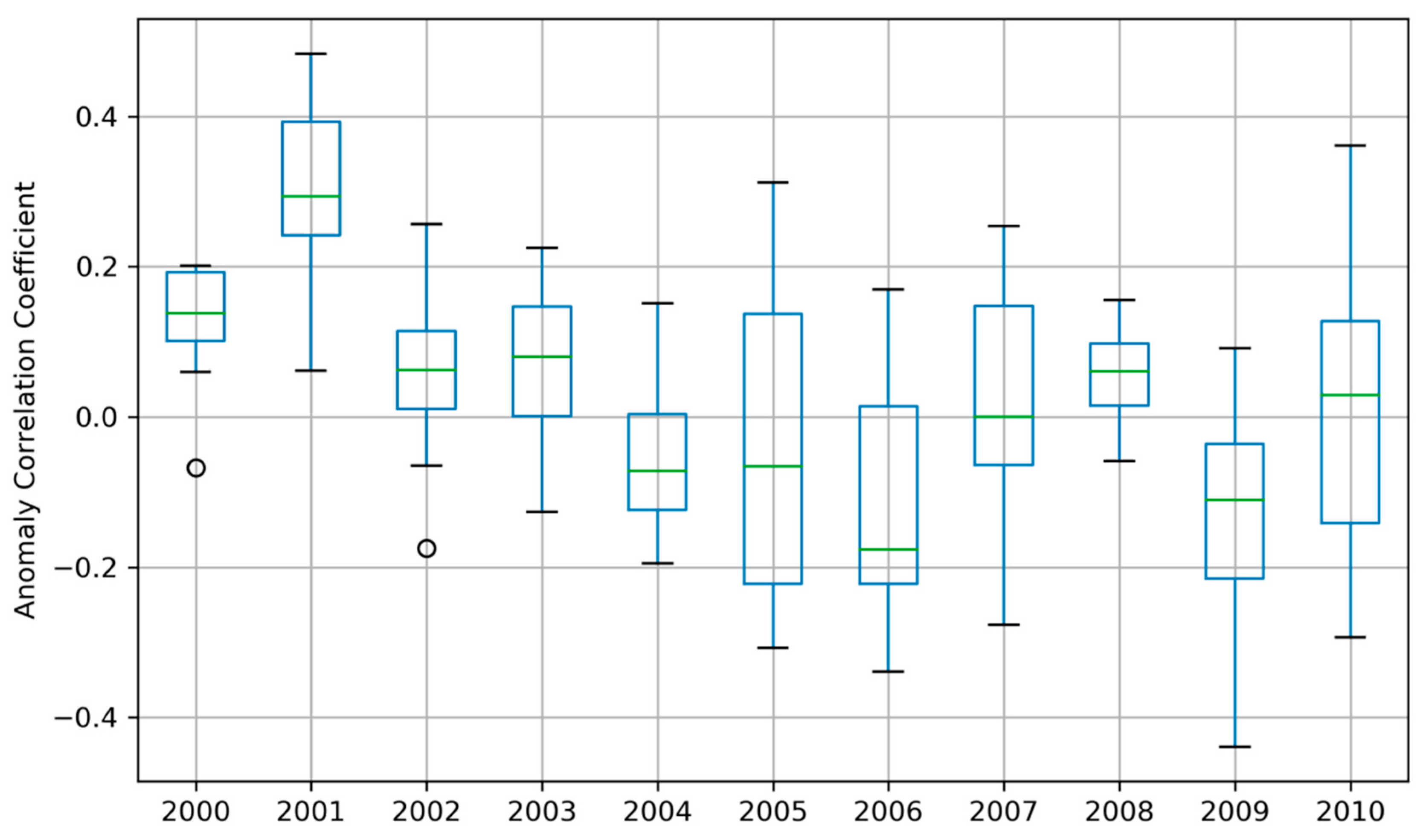
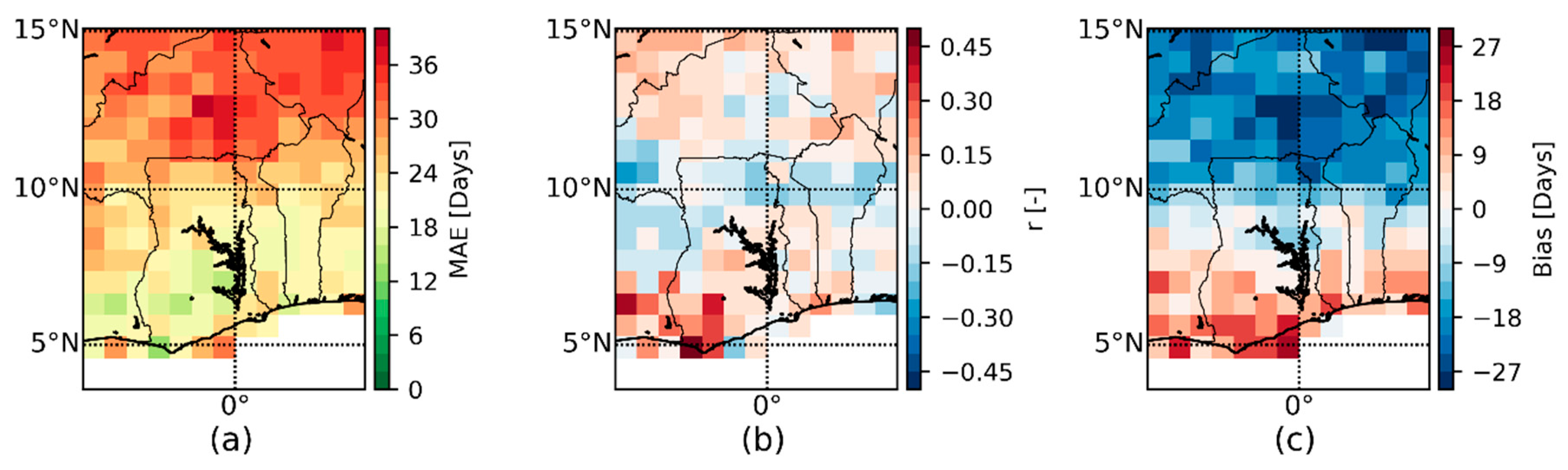
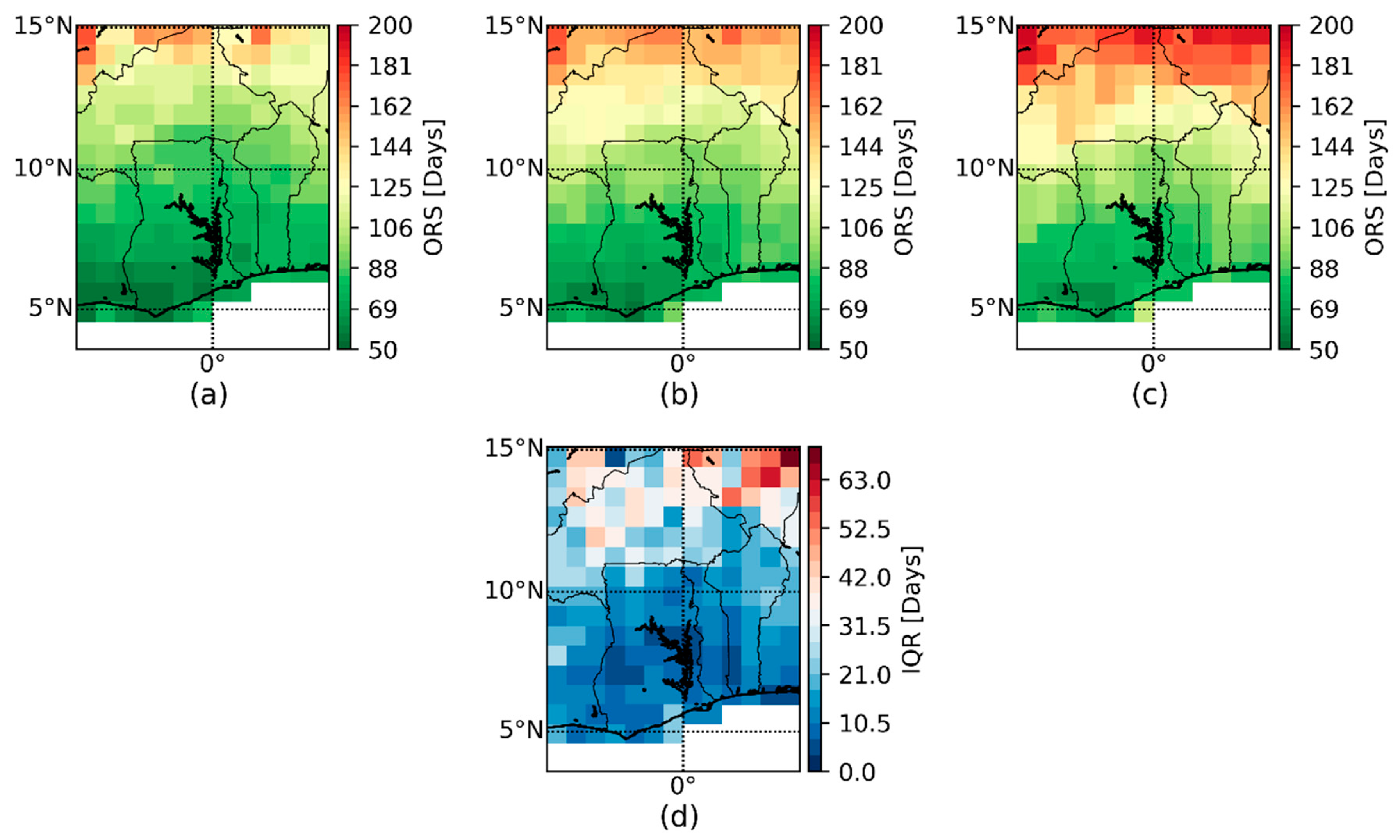
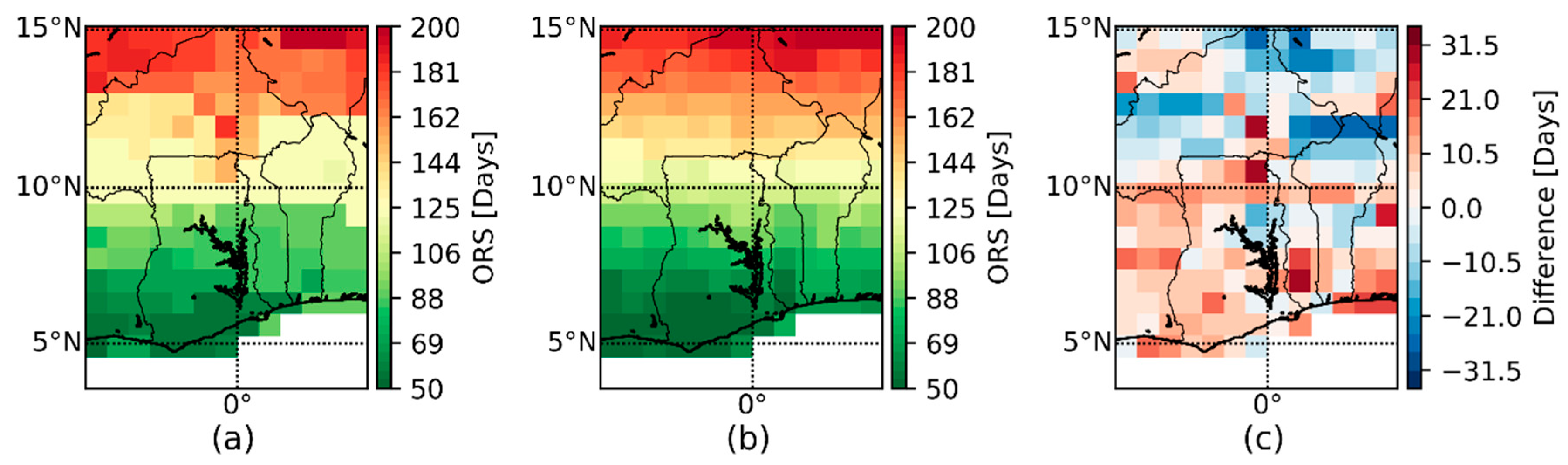
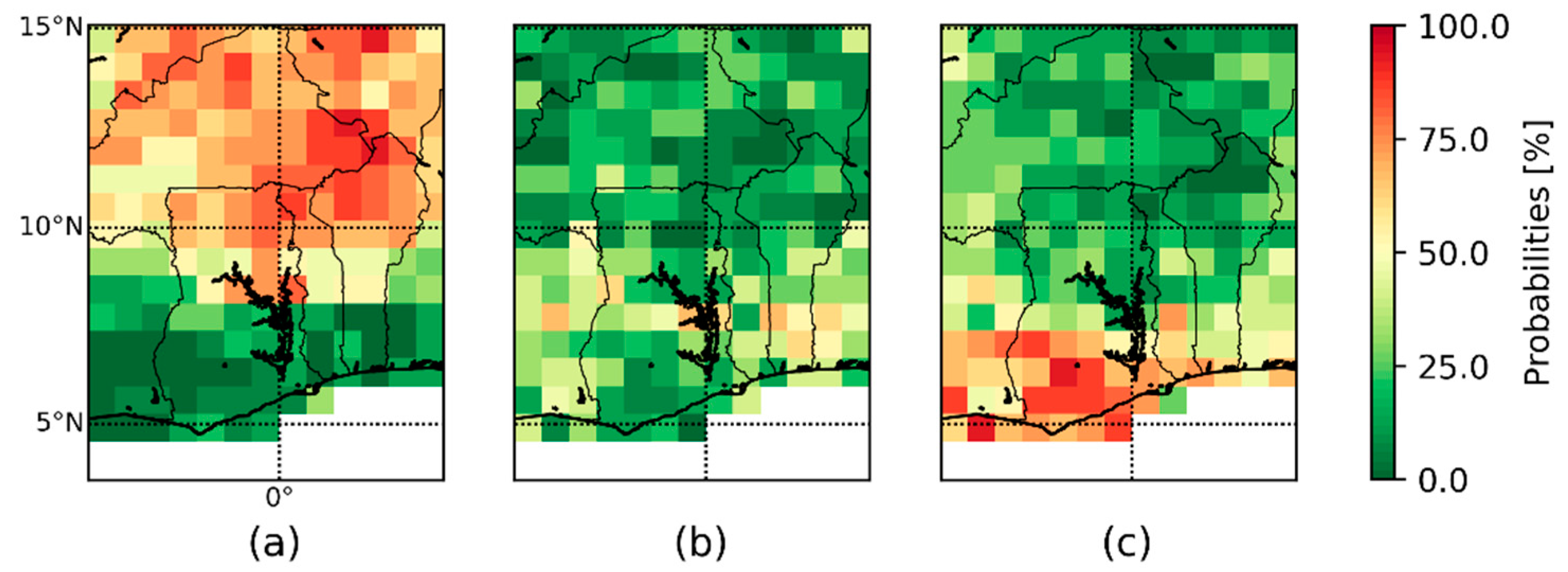
4.1. Spatiotemperal Verification of the ORS Fields
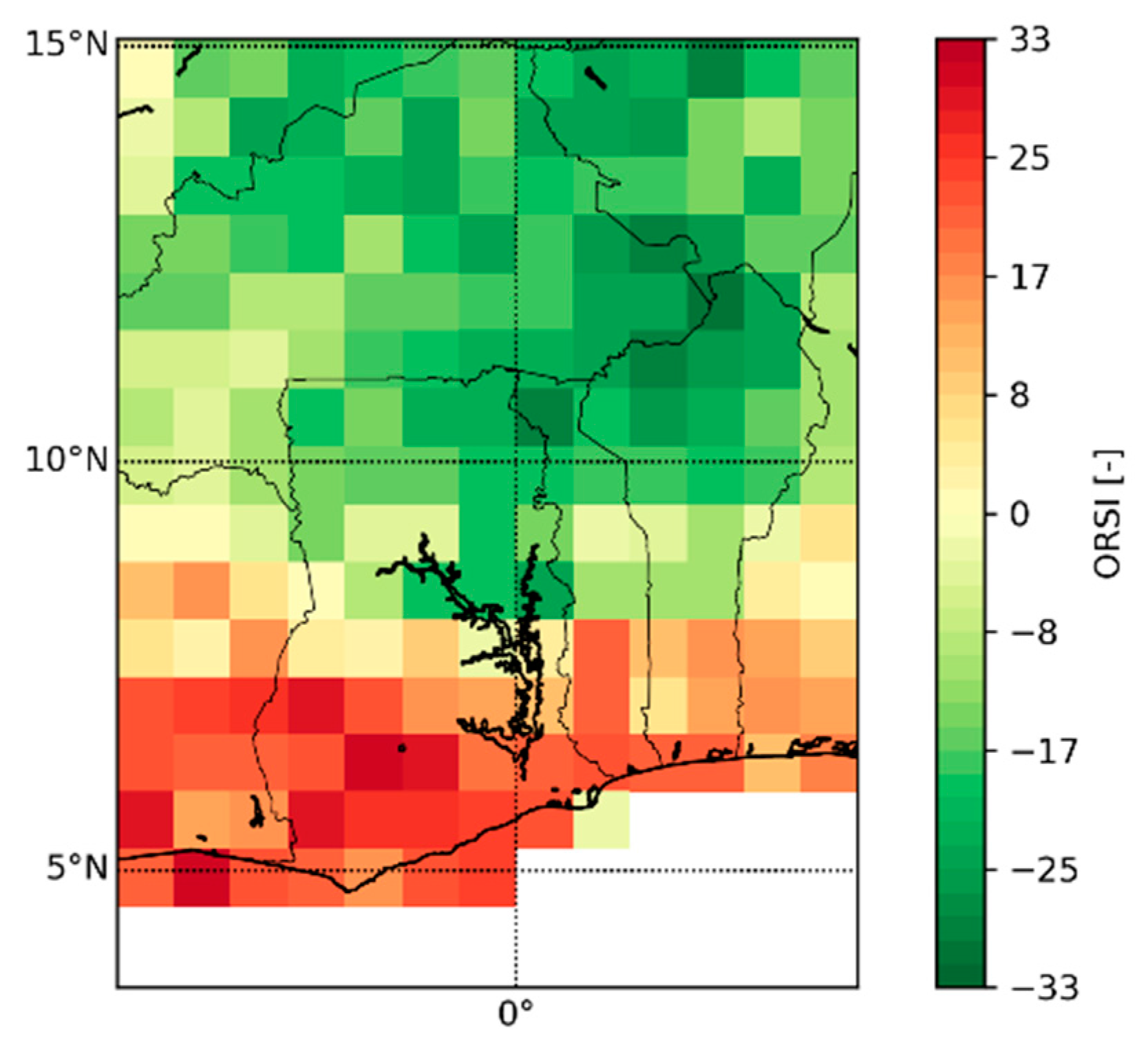
4.2. Visualisation of the ORS Fields
5. Summary and Conclusions
- Better adapting the ORS approach to the location-specific conditions in the region, i.e., considering the heterogeneous rainfall conditions across the region. This can be achieved by coupling the ORS approach to a process-based crop model to derive location-specific planting rules (ORS criteria), as done in [2,63]. Based on seasonal predictions, it is also possible to incorporate the false-start criterion in the ORS predictions;
- Testing the skills of other GSEPS such as the Climate Forecast System Version 2 or the ECMWF SYS5, which is e.g., improved in terms of the spatial resolution and the number of ensemble members compared to the SYS4 [64]. Since the probabilistic forecast depends strongly on the size of the ensemble members (e.g., [64]), the increase of the ensemble members may possibly lead to improved ORS predictions;
- Incorporating longer lead times in the analysis. Longer lead times would increase preparation time for farmers. On the other hand, increasing the lead time would result in reduced forecast periods for the rainy season;
- Further reducing the biases in the forecasts, either by improving the statistical bias correction method or by dynamically downscaling the forecasts. The former could e.g., be achieved by applying the corrections separately for the different months (e.g., [65]) or for different large-scale atmospheric circulation patterns (e.g., [66]).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| Shapiro-Wilk test | 0.962 | 0.953 | 0.913 | 0.941 | 0.948 | 0.968 | 0.888 | 0.945 | 0.909 | 0.976 | 0.912 |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| 2000 | 0.0000 | 0.6857 | 4.4401 | 3.2395 | 0.4457 | 11.4124 | 10.4689 | 0.0046 | 4.2194 | 4.7732 | 0.2915 |
| 2001 | 0.6857 | 0.0000 | 2.4402 | 1.3479 | 0.0128 | 7.5099 | 6.7862 | 0.9765 | 1.6950 | 2.0575 | 0.1180 |
| 2002 | 4.4401 | 2.4402 | 0.0000 | 0.2468 | 2.5807 | 0.6076 | 0.4680 | 4.9639 | 0.3073 | 0.2046 | 3.3129 |
| 2003 | 3.2395 | 1.3479 | 0.2468 | 0.0000 | 1.4816 | 1.9600 | 1.6680 | 3.7898 | 0.0006 | 0.0082 | 2.1308 |
| 2004 | 0.4457 | 0.0128 | 2.5807 | 1.4816 | 0.0000 | 7.6105 | 6.8992 | 0.6338 | 1.8393 | 2.2029 | 0.0415 |
| 2005 | 11.4124 | 7.5099 | 0.6076 | 1.9600 | 7.6105 | 0.0000 | 0.0099 | 12.8651 | 2.3825 | 2.0390 | 9.4714 |
| 2006 | 10.4689 | 6.7862 | 0.4680 | 1.6680 | 6.8992 | 0.0099 | 0.0000 | 11.7991 | 2.0297 | 1.7165 | 8.6121 |
| 2007 | 0.0046 | 0.9765 | 4.9639 | 3.7898 | 0.6338 | 12.8651 | 11.7991 | 0.0000 | 5.1484 | 5.7892 | 0.4753 |
| 2008 | 4.2194 | 1.6950 | 0.3073 | 0.0006 | 1.8393 | 2.3825 | 2.0297 | 5.1484 | 0.0000 | 0.0163 | 2.7800 |
| 2009 | 4.7732 | 2.0575 | 0.2046 | 0.0082 | 2.2029 | 2.0390 | 1.7165 | 5.7892 | 0.0163 | 0.0000 | 3.2528 |
| 2010 | 0.2915 | 0.1180 | 3.3129 | 2.1308 | 0.0415 | 9.4714 | 8.6121 | 0.4753 | 2.7800 | 3.2528 | 0.0000 |
| Year | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | 2010 |
| 2000 | 0.0000 | 1.8406 | −0.2189 | 0.1816 | 0.1690 | −2.3839 | −0.7848 | 2.1129 | 0.4895 | −0.8831 | 0.9980 |
| 2001 | −1.8406 | 0.0000 | −1.3634 | −1.1451 | −1.5163 | −3.3723 | −1.8394 | −0.0538 | −0.9283 | −2.1992 | −0.8811 |
| 2002 | 0.2189 | 1.3634 | 0.0000 | 0.3171 | 0.3161 | −1.7477 | −0.4627 | 1.4119 | 0.5372 | −0.4430 | 0.8145 |
| 2003 | −0.1816 | 1.1451 | −0.3171 | 0.0000 | −0.0500 | −2.1811 | −0.8006 | 1.1985 | 0.2338 | −0.8509 | 0.5113 |
| 2004 | −0.1690 | 1.5163 | −0.3161 | 0.0500 | 0.0000 | −2.3958 | −0.8554 | 1.6783 | 0.3311 | −0.9561 | 0.7306 |
| 2005 | 2.3839 | 3.3723 | 1.7477 | 2.1811 | 2.3958 | 0.0000 | 1.2399 | 3.5143 | 2.4388 | 1.5009 | 2.9086 |
| 2006 | 0.7848 | 1.8394 | 0.4627 | 0.8006 | 0.8554 | −1.2399 | 0.0000 | 1.9046 | 1.0226 | 0.0879 | 1.3350 |
| 2007 | −2.1129 | 0.0538 | −1.4119 | −1.1985 | −1.6783 | −3.5143 | −1.9046 | 0.0000 | −0.9712 | −2.3518 | −0.9699 |
| 2008 | −0.4895 | 0.9283 | −0.5372 | −0.2338 | −0.3311 | −2.4388 | −1.0226 | 0.9712 | 0.0000 | −1.1259 | 0.2509 |
| 2009 | 0.8831 | 2.1992 | 0.4430 | 0.8509 | 0.9561 | −1.5009 | −0.0879 | 2.3518 | 1.1259 | 0.0000 | 1.5821 |
| 2010 | −0.9980 | 0.8811 | −0.8145 | −0.5113 | −0.7306 | −2.9086 | −1.3350 | 0.9699 | −0.2509 | −1.5821 | 0.0000 |
References
- Dobor, L.; Barcza, Z.; Hlásny, T.; Árendás, T.; Spitkó, T.; Fodor, N. Crop planting date matters: Estimation methods and effect on future yields. Agric. For. Meteorol. 2016, 223, 103–115. [Google Scholar] [CrossRef]
- Waongo, M.; Laux, P.; Traoré, S.B.; Sanon, M.; Kunstmann, H. A crop model and fuzzy rule based approach for optimizing maize planting dates in Burkina Faso, West Africa. J. Appl. Meteor. Climatol. 2014, 53, 598–613. [Google Scholar] [CrossRef]
- Nicholson, S.E. Climatic and environmental change in Africa during the last two centuries. Clim. Res. 2001, 17, 123–144. [Google Scholar] [CrossRef]
- Nicholson, S.E.; Funk, C.; Fink, A.H. Rainfall over the African continent from the 19th through the 21st century. Glob. Planet. Chang. 2018, 165, 114–127. [Google Scholar] [CrossRef]
- Adegoke, J.; Bamba Sylla, M.; Bossa, A.; Ogunjobi, K.; Adounpke, J. On the 2017 rainy season intensity and subsequent flood events over West Africa. In Regional Climate Change Series: Floods; WASCAL Publishing: Accra, Ghana, 2019; pp. 10–14. [Google Scholar]
- Markantonis, V.; Farinosi, F.; Dondeynaz, C.; Ameztoy, I.; Pastori, M.; Marletta, L.; Ali, A.; Carmona Moreno, C. Assessing floods and droughts in the Mékrou River basin (West Africa): A combined household survey and climatic trends analysis approach. Nat. Hazards Earth Syst. Sci. 2018, 18, 1279–1296. [Google Scholar] [CrossRef]
- Munich Re. NatCat Service; Munich Re: Munich, Germany, 2019. [Google Scholar]
- Ingram, K.T.; Roncoli, M.C.; Kirshen, P.H. Opportunities and constraints for farmers of West Africa to use seasonal precipitation forecasts with Burkina Faso as a case study. Agric. Syst. 2002, 74, 331–349. [Google Scholar] [CrossRef]
- Amegnaglo, C.J.; Anaman, K.A.; Mensah-Bonsu, A.; Onumah, E.E.; Gero, F.A. Contingent valuation study of the benefits of seasonal climate forecasts for maize farmers in the Republic of Benin, West Africa. Clim. Serv. 2017, 6, 1–11. [Google Scholar] [CrossRef]
- Ouédraogo, M.; Barry, S.; Zougmoré, R.; Partey, S.; Somé, L.; Baki, G. Farmers’ willingness to pay for climate information services: Evidence from Cowpea and Sesame producers in Northern Burkina Faso. Sustainability 2018, 10, 611. [Google Scholar] [CrossRef]
- Bliefernicht, J.; Waongo, M.; Salack, S.; Seidel, J.; Laux, P.; Kunstmann, H. Quality and value of seasonal precipitation forecasts issued by the West African regional climate outlook forum. J. Appl. Meteorol. Climatol. 2019, 58, 621–642. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Regional Climate Outlook Forums. Available online: https://library.wmo.int/doc_num.php?explnum_id=3191 (accessed on 27 June 2019).
- Siegmund, J.; Bliefernicht, J.; Laux, P.; Kunstmann, H. Toward a seasonal precipitation prediction system for West Africa: Performance of CFSv2 and high-resolution dynamical downscaling. J. Geophys. Res. Atmos. 2015, 120, 7316–7339. [Google Scholar] [CrossRef]
- African Centre of Meteorological Application for Development (ACMAD). Regional climate outlook forum PRESASS-06. Available online: http://acmad.net/rcc/atelier/bulletin_PRESASS06_eng.pdf (accessed on 27 June 2019).
- Omotosho, J.B.; Balogun, A.A.; Ogunjobi, K. Predicting monthly and seasonal rainfall, onset and cessation of the rainy season in West Africa using only surface data. Int. J. Climatol. J. R. Meteorol. Soc. 2000, 20, 865–880. [Google Scholar] [CrossRef]
- Laux, P.; Wagner, S.; Wagner, A.; Jacobeit, J.; Bárdossy, A.; Kunstmann, H. Modelling daily precipitation features in the Volta Basin of West Africa. Int. J. Climatol. J. R. Meteorol. Soc. 2009, 29, 937–954. [Google Scholar] [CrossRef]
- Laux, P.; Kunstmann, H.; Bárdossy, A. Predicting the regional onset of the rainy season in West Africa. Int. J. Climatol. J. R. Meteorol. Soc. 2008, 28, 329–342. [Google Scholar] [CrossRef]
- Omotosho, J.B. Long-range prediction of the onset and end of the rainy season in the West African Sahel. Int. J. Climatol. 1992, 12, 369–382. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, UK, 2011; ISBN 0123850223. [Google Scholar]
- Vellinga, M.; Arribas, A.; Graham, R. Seasonal forecasts for regional onset of the West African monsoon. Clim. Dyn. 2013, 40, 3047–3070. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M. The NCEP climate forecast system version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Batté, L.; Déqué, M. Seasonal predictions of precipitation over Africa using coupled ocean-atmosphere general circulation models: Skill of the ENSEMBLES project multimodel ensemble forecasts. Tellus A Dyn. Meteorol. Oceanogr. 2011, 63, 283–299. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Forecast verification: A Practitioner’s Guide in Atmospheric Science; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 1119961076. [Google Scholar]
- Lebel, T.; Diedhiou, A.; Laurent, H. Seasonal cycle and interannual variability of the Sahelian rainfall at hydrological scales. J. Geophys. Res. Atmos. 2003, 108, 1–11. [Google Scholar] [CrossRef]
- Fink, A.H. Das Westafrikanische Monsunsystem. Promet 2006, 32, 114–122. [Google Scholar]
- Masih, I.; Maskey, S.; Mussá, F.E.F.; Trambauer, P. A review of droughts on the African continent: A geospatial and long-term perspective. Hydrol. Earth Syst. Sci. 2014, 18, 3635–3649. [Google Scholar] [CrossRef]
- Salack, S.; Klein, C.; Giannini, A.; Sarr, B.; Worou, O.N.; Belko, N.; Bliefernicht, J.; Kunstman, H. Global warming induced hybrid rainy seasons in the Sahel. Environ. Res. Lett. 2016, 11, 104008. [Google Scholar] [CrossRef]
- Taylor, C.M.; Belušić, D.; Guichard, F.; Parker, D.J.; Vischel, T.; Bock, O.; Harris, P.P.; Janicot, S.; Klein, C.; Panthou, G. Frequency of extreme Sahelian storms tripled since 1982 in satellite observations. Nature 2017, 544, 475–478. [Google Scholar] [CrossRef] [PubMed]
- Dunning, C.M.; Black, E.; Allan, R.P. Later wet seasons with more intense rainfall over Africa under future climate change. J. Clim. 2018, 31, 9719–9738. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF). System 4 User Guide. Available online: https://www.ecmwf.int/sites/default/files/medialibrary/2017-10/System4_guide.pdf (accessed on 27 June 2019).
- Mwangi, E.; Wetterhall, F.; Dutra, E.; Di Giuseppe, F.; Pappenberger, F. Forecasting droughts in East Africa. Hydrol. Earth Syst. Sci. 2014, 18, 611–620. [Google Scholar] [CrossRef]
- Winsemius, H.C.; Dutra, E.; Engelbrecht, F.A.; van Archer Garderen, E.; Wetterhall, F.; Pappenberger, F.; Werner, M.G.F. The potential value of seasonal forecasts in a changing climate in Southern Africa. Hydrol. Earth Syst. Sci. 2014, 18, 1525–1538. [Google Scholar] [CrossRef]
- Weisheimer, A.; Palmer, T.N. On the reliability of seasonal climate forecasts. J. R. Soc. Interface 2014, 11, 20131162. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.-M.; Webster, P.J.; Curry, J.A.; Toma, V.E. Asian summer monsoon prediction in ECMWF System 4 and NCEP CFSv2 retrospective seasonal forecasts. Clim. Dyn. 2012, 39, 2975–2991. [Google Scholar] [CrossRef]
- Dutra, E.; Di Giuseppe, F.; Wetterhall, F.; Pappenberger, F. Seasonal forecasts of droughts in African basins using the Standardized Precipitation Index. Hydrol. Earth Syst. Sci. 2013, 17, 2359–2373. [Google Scholar] [CrossRef]
- Rodrigues, L.R.L.; García-Serrano, J.; Doblas-Reyes, F. Seasonal forecast quality of the West African monsoon rainfall regimes by multiple forecast systems. J. Geophys. Res. Atmos. 2014, 119, 7908–7930. [Google Scholar] [CrossRef]
- Molteni, F.; Stockdale, T.; Balmaseda, M.; Balsamo, G.; Buizza, R.; Ferranti, L.; Magnusson, L.; Mogensen, K.; Palmer, T.; Vitart, F. The New ECMWF Seasonal Forecast System (System 4); European Centre for Medium-Range Weather Forecasts: Reading, UK, 2011. [Google Scholar]
- Climate Hazards Group. What Is CHIRPS? Available online: http://chg.geog.ucsb.edu/data/chirps/index.html (accessed on 2 July 2018).
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Dembélé, M.; Zwart, S.J. Evaluation and comparison of satellite-based rainfall products in Burkina Faso, West Africa. Int. J. Remote Sens. 2016, 37, 3995–4014. [Google Scholar] [CrossRef]
- Novella, N.S.; Thiaw, W.M. African rainfall climatology version 2 for famine early warning systems. J. Appl. Meteorol. Climatol. 2013, 52, 588–606. [Google Scholar] [CrossRef]
- Hsu, K.-L.; Gao, X.; Sorooshian, S.; Gupta, H.V. Precipitation estimation from remotely sensed information using artificial neural networks. J. Appl. Meteorol. 1997, 36, 1176–1190. [Google Scholar] [CrossRef]
- Herman, A.; Kumar, V.B.; Arkin, P.A.; Kousky, J.V. Objectively determined 10-day African rainfall estimates created for famine early warning systems. Int. J. Remote Sens. 1997, 18, 2147–2159. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T. TRMM and Other Data Precipitation Data Set Documentation; NASA: Greenbelt, MD, USA, 2013; Volume 28, p. 1.
- Maraun, D. Bias correcting climate change simulations-a critical review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Feudale, L.; Tompkins, A. A simple bias correction technique for modeled monsoon precipitation applied to West Africa. Geophys. Res. Lett. 2011, 38, 1–5. [Google Scholar] [CrossRef]
- Bogner, K.; Pappenberger, F.; Cloke, H.L. The normal quantile transformation and its application in a flood forecasting system. Hydrol. Earth Syst. Sci. 2012, 16, 1085–1094. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Weisheimer, A.; Déqué, M.; Keenlyside, N.; McVean, M.; Murphy, J.M.; Rogel, P.; Smith, D.; Palmer, T.N. Addressing model uncertainty in seasonal and annual dynamical ensemble forecasts. Q. J. R. Meteorol. Soc. 2009, 135, 1538–1559. [Google Scholar] [CrossRef]
- Fitzpatrick, R.G.J.; Bain, C.L.; Knippertz, P.; Marsham, J.H.; Parker, D.J. The West African monsoon onset: A concise comparison of definitions. J. Clim. 2015, 28, 8673–8694. [Google Scholar] [CrossRef]
- Stern, R.D.; Dennett, M.D.; Garbutt, D.J. The start of the rains in West Africa. J. Climatol. 1981, 1, 59–68. [Google Scholar] [CrossRef]
- Dieng, D.; Laux, P.; Smiatek, G.; Heinzeller, D.; Bliefernicht, J.; Sarr, A.; Gaye, A.T.; Kunstmann, H. Performance analysis and projected changes of agroclimatological indices across West Africa based on high-resolution regional climate model simulations. J. Geophys. Res. Atmos. 2018, 123, 7950–7973. [Google Scholar] [CrossRef]
- Bliefernicht, J. Probability Forecasts of Daily Areal Precipitation for Small River Basins. Ph.D. Thesis, Institut fur Wasserbau, Universität Stuttgart, Stuttgart, Germany, 2011. [Google Scholar]
- Murphy, A.H. Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Weather Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Welch, B.L. The generalization of student’s problem when several different population variances are involved. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Welch, B.L. On the comparison of several mean values: An alternative approach. Biometrika 1951, 38, 330–336. [Google Scholar] [CrossRef]
- Fink, A.H.; Vincent, D.G.; Ermert, V. Rainfall types in the West African Sudanian zone during the summer monsoon 2002. Mon. Weather Rev. 2006, 134, 2143–2164. [Google Scholar] [CrossRef]
- Demeritt, D.; Nobert, S.; Cloke, H.; Pappenberger, F. Challenges in communicating and using ensembles in operational flood forecasting. Meteorol. Appl. 2010, 17, 209–222. [Google Scholar] [CrossRef]
- Dettinger, M.D. From climate-change spaghetti to climate-change distributions for 21st-century California. San Franc. Estuary Watershed Sci. 2005, 3, 1–14. [Google Scholar]
- Ferstl, F.; Bürger, K.; Westermann, R. Streamline variability plots for characterizing the uncertainty in vector field ensembles. IEEE Trans. Vis. Comput. Graph. 2015, 22, 767–776. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the continuous ranked probability score for ensemble prediction systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Bartels, J.; Bliefernicht, J.; Seidel, J.; Bárdossy, A.; Kunstmann, H.; Johst, M.; Demuth, N. Assessment of Ensemble Discharge Forecasts for Operational Flood Warnings. Hydrol. Wasserbewirtsch. 2017, 61, 297–310. [Google Scholar] [CrossRef]
- Gilleland, E.; Ahijevych, D.; Brown, B.G.; Casati, B.; Ebert, E.E. Intercomparison of spatial forecast verification methods. Weather Forecast. 2009, 24, 1416–1430. [Google Scholar] [CrossRef]
- Laux, P.; Jäckel, G.; Tingem, R.M.; Kunstmann, H. Impact of climate change on agricultural productivity under rainfed conditions in Cameroon—A method to improve attainable crop yields by planting date adaptations. Agric. For. Meteorol. 2010, 150, 1258–1271. [Google Scholar] [CrossRef]
- European Centre for Medium-Range Weather Forecasts (ECMWF). SEAS 5 User Guide. Available online: https://www.ecmwf.int/sites/default/files/medialibrary/2017-10/System5_guide.pdf (accessed on 16 August 2018).
- Jakob Themeßl, M.; Gobiet, A.; Leuprecht, A. Empirical-statistical downscaling and error correction of daily precipitation from regional climate models. Int. J. Climatol. 2011, 31, 1530–1544. [Google Scholar] [CrossRef]
- Bárdossy, A.; Pegram, G. Downscaling precipitation using regional climate models and circulation patterns toward hydrology. Water Resour. Res. 2011, 47, 1–18. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- Levene, H. Contributions to Probability and Statistics: Essays in Honor of Harold Hotelling; Stanford University Press: Palo Alto, CA, USA, 1960; pp. 278–292. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rauch, M.; Bliefernicht, J.; Laux, P.; Salack, S.; Waongo, M.; Kunstmann, H. Seasonal Forecasting of the Onset of the Rainy Season in West Africa. Atmosphere 2019, 10, 528. https://doi.org/10.3390/atmos10090528
Rauch M, Bliefernicht J, Laux P, Salack S, Waongo M, Kunstmann H. Seasonal Forecasting of the Onset of the Rainy Season in West Africa. Atmosphere. 2019; 10(9):528. https://doi.org/10.3390/atmos10090528
Chicago/Turabian StyleRauch, Manuel, Jan Bliefernicht, Patrick Laux, Seyni Salack, Moussa Waongo, and Harald Kunstmann. 2019. "Seasonal Forecasting of the Onset of the Rainy Season in West Africa" Atmosphere 10, no. 9: 528. https://doi.org/10.3390/atmos10090528
APA StyleRauch, M., Bliefernicht, J., Laux, P., Salack, S., Waongo, M., & Kunstmann, H. (2019). Seasonal Forecasting of the Onset of the Rainy Season in West Africa. Atmosphere, 10(9), 528. https://doi.org/10.3390/atmos10090528






