GIS Application for Determining Geographical Factors on Intensity of Erosion in Serbian River Basins. Case Study: The River Basin of Likodra
Abstract
:1. Introduction
- to provide data for the verification model erosion;
- to assess the damage caused by erosion;
- to raise the population’s awareness of the possible risks caused by erosion processes;
- to improve the management process of river basin sediments.
2. Research Methods
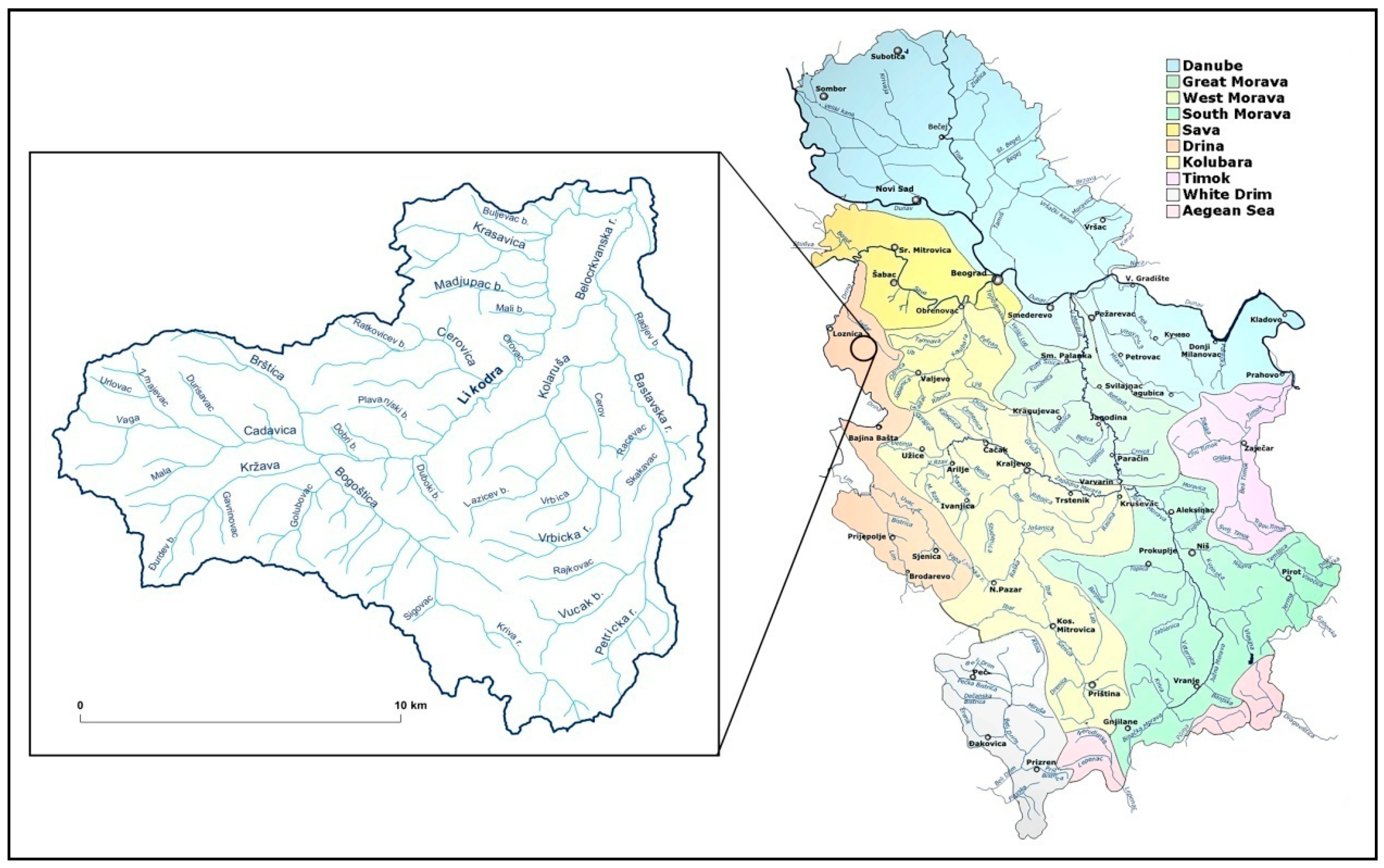
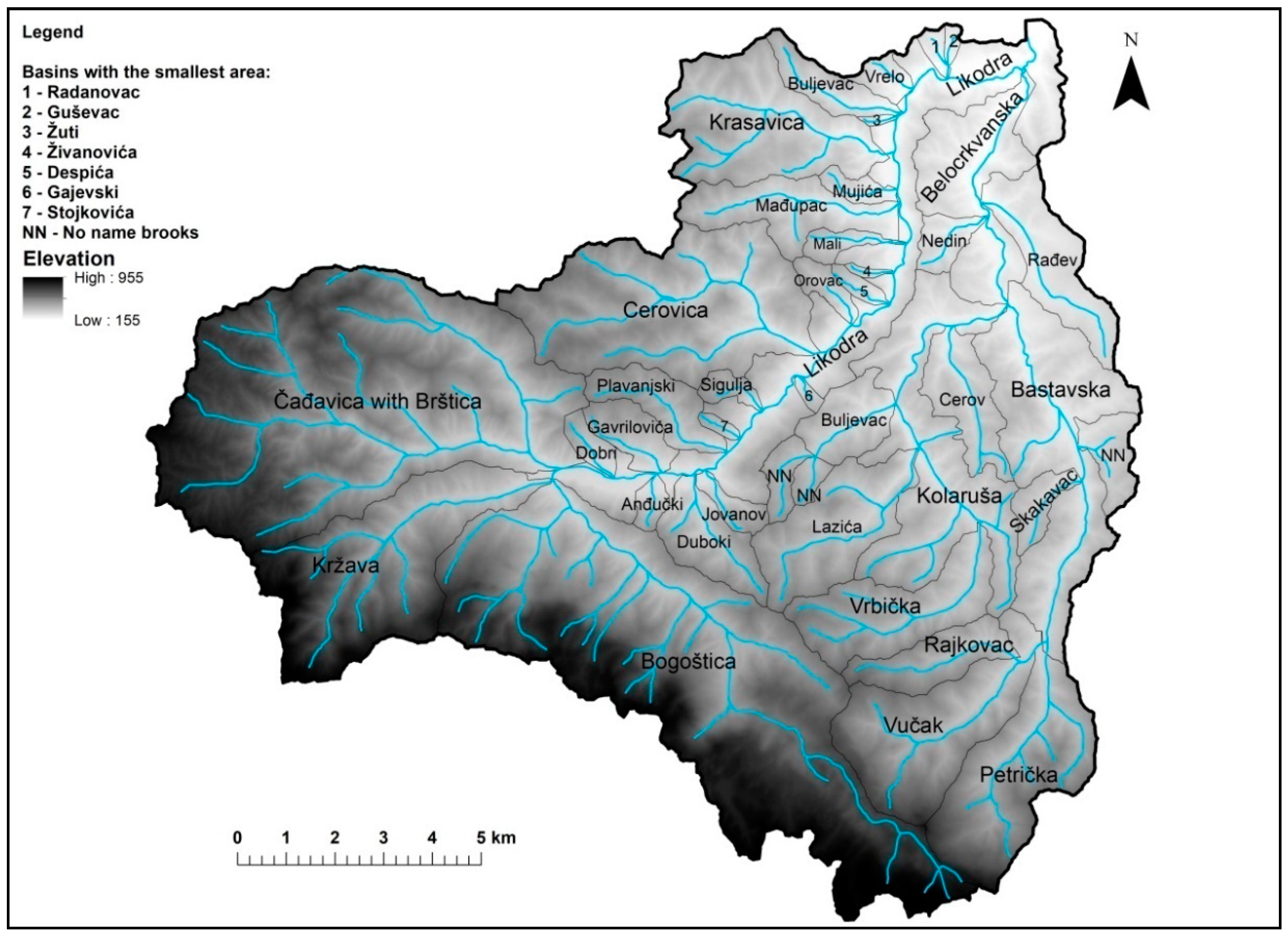
3. Geographical Location and Characteristic of the Basin
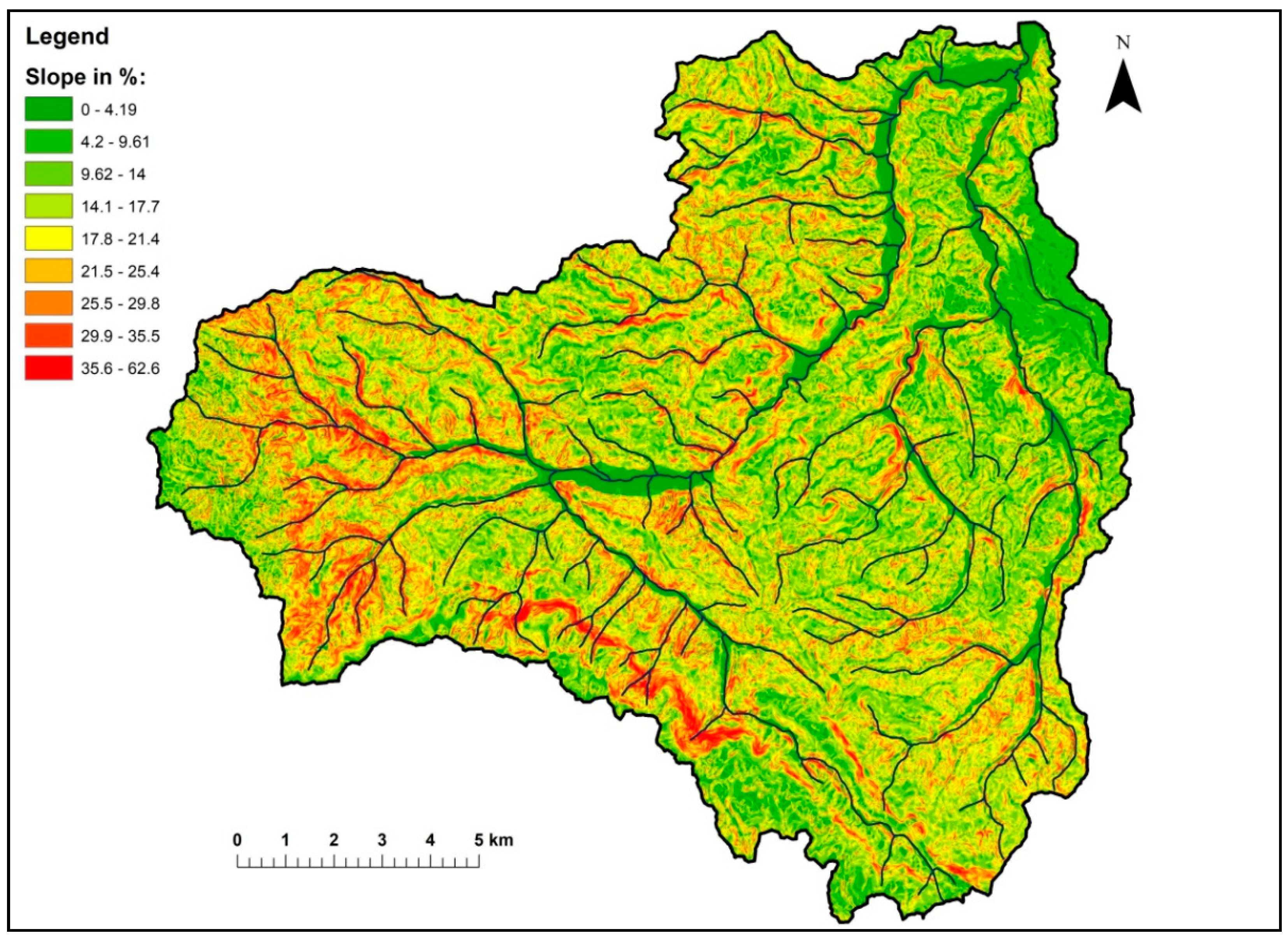
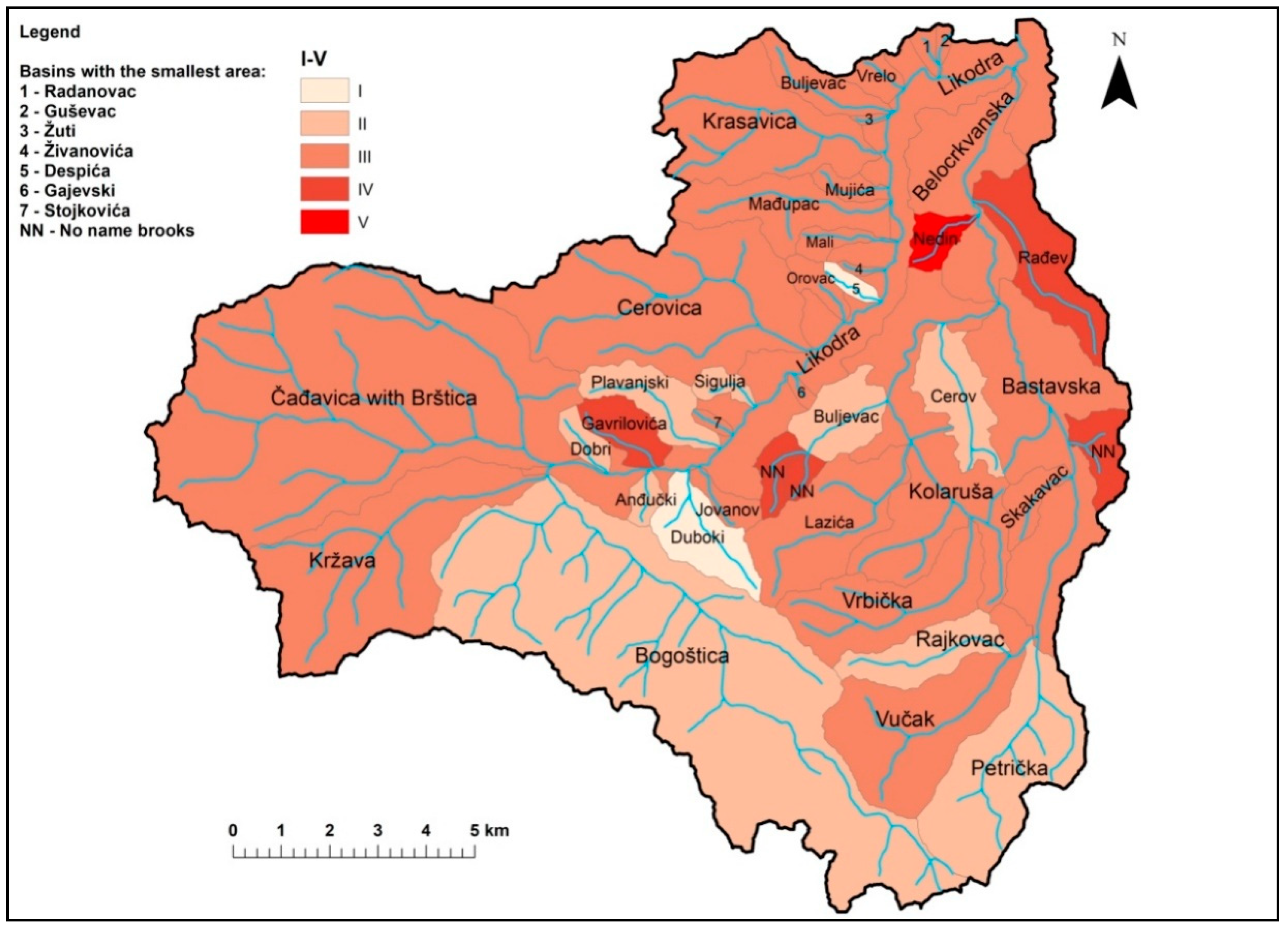
4. Results
5. Discussion
- To regulate the riverbed of torrential streams that threaten the settlements and industrial facilities;
- To plant forests on the terrains affected by I and II erosion process categories (excessive and strong erosion processes);
- To introduce advanced agro-technical measures in the areas with III and IV erosion process category, and to exceptionally permit crops in the areas with above 25° inclination with the obligatory introduction of contour bunding practice in agriculture;
- To take advantage of all the benefits of cross-sections in torrential stream beds for intensive construction of small water reservoirs to prevent the flooding and the economic exploitation of waterfrom torrential streams for local irrigation, development of tourism, fishery and other economic purposes;
- To combat the deep erosion processes in torrential stream beds (landslides, landslips, rockfall, and ravines) by building a series of appropriate modern dams: partition structure and leachate drainage system.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Index | Quantitative Indicators | Measure |
|---|---|---|
| F | Torrential catchment area | km2 |
| L | Length of the main torrential flow | km |
| O | Length watershed basin | km |
| D | Average height difference of basin or area covered by erosion | m |
| A | Coefficient of basin shape | - |
| S1 | Coefficient of water-permeability | - |
| S2 | Coefficient of vegetation covering | - |
| W | Analytic expression of retention | m2/km |
| Qmax | Maximum quantity of water | m3/sec |
| G | Production of deposit from one km2 of the basin | m3/km |
| Z | Erosion coefficient | |
| ∑L | Length of the main contour lines | km |
| Isr | Intermediate slope basin | |
| T0 | Average annual temperature | |
| Hgod | Mean annual rainfall | mm |
| Lhm | Length tributary I and II | km |
| Lgt | Length of the main torrential flow | km |
| K | Climatic and topographical coefficient | - |
| Hk | Hydrographic class | A,B,C,D,E,F |
References
- Ristić, R. Redefining the policy of torrential flood prevention in Serbia. J. Public Policy 2014, 8, 23–28. [Google Scholar]
- Staut, M. Recent Erosional Processes in the Catchment of the Dragonja River. Unpublished graduate thesis, University of Ljubljana, Ljubljana, Slovenia, 2004. [Google Scholar]
- Cook, H.L. The nalure and controlling variables of the water erosion process. Soil Sci. Soc. Am Proc. 1936, 1, 60–64. [Google Scholar]
- Zingg, A.W. Degree and length of land slope as it affects soil loss in runoff. J.Agric. Eng. 1940, 21, 59–64. [Google Scholar]
- Smith, D.D. Interpretation of soil conservation data for field use. J. Agric. Eng. 1941, 22, 173–175. [Google Scholar]
- Poljakov, B.V. Problemi Ruslovih Processov; Moskva, Russia, 1953. (In Russian) [Google Scholar]
- Herheulidze, I. Ovraniei Selevie Vinosi; Moskva, Russia, 1947. (In Russian) [Google Scholar]
- Browning, G.M.; Parish, C.L.; Glass, J. A method for determining the use and limitations of rotation and conservation practices in the control of soil erosion in Iowa. J. Am. Soc. Agron. 1947, 39, 65–73. [Google Scholar] [CrossRef]
- Silvestrov, S.I. Reljefi Zemljedelijev Erozionih Rajonah; Moskva, Russia, 1955. (In Russian) [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall-Erosion Losses from Cropland East of Rocky Mountains—Guide for Selection of Practices for Soil and Water Conservation; U.S. Department of Agriculture, Agricultural Handbook 282; Agricultural Research Service: Washington, DC, USA, 1965.
- De Vente, J.; Poesen, J. Predicting soil erosion and sediment yieldat the basin scale: Scale issues and semi-quantitative models. Earth-Sci. Rev. 2005, 71, 95–125. [Google Scholar] [CrossRef]
- Eisazadeh, L.; Sokouti, R.; Homaee, M.; Pazira, E. Comparison ofempirical models to estimate soil erosion and sediment yield inmicro catchments. Eurasian J. Soil Sci. 2012, 1, 28–33. [Google Scholar]
- Dragičević, N.; Karleuša, B.; Ožanić, N. A review of the Gavrilović method (erosion potential method) application. Građevinar J. Croat. Assoc. Civ. Eng. 2016, 68, 715–725. [Google Scholar]
- Gavrilović, S. A method for estimating of the average annual quantity of sediments according to the potency of erosion. J. Fac. For. 1962, 26, 151–168. [Google Scholar]
- Gavrilović, S. Modern methods of calculating torrents sediment and production of erosion maps. In Erosion, Torrents and Alluvial Deposits, Proceeding of the Seminar Erosion, Torrents and Sediment; Belgrade, Serbia, 1970; pp. 85–100. [Google Scholar]
- Gavrilović, S. Engineering of torrents and erosion, Special edition. J. Constr. 1972, 1–292. [Google Scholar]
- Lazarević, R. Scientific-research work and problems in prevention measures against soil erosion and torrential erosion. In Proceedings of the Symposium on the Problems of Erosion in the Federal Republic of Serbia, Beograd, Serbia, 25–28 October 1967; pp. 35–46. [Google Scholar]
- Lazarević, R. The new method for erosion coefficient determination—Z. Erosion-Prof. Inf. Bull. 1985, 13, 54–61. [Google Scholar]
- Pintar, J.; Mikoš, M.; Verbovšek, V. Elements of the water management—Alternative to narrowing of live natural processes in rigid objects. In Second Congress of the Waters of Yugoslavia; Simonović, S., Ed.; Yugoslav Society for Drainage and Irrigation: Belgrade, Serbia, 1986; Volume 4, pp. 800–814. [Google Scholar]
- Amini, S.; Rafiei, B.; Khodabakhsh, S.; Heydari, M. Estimation of еrosion and sediment yield of Ekbatan Dam drainage basin with EPM, using GIS. Iran. J. Earth Sci. 2010, 2, 73–180. [Google Scholar]
- Gavrilović, Z.; Stefanović, M.; Milovanović, I.; Čotrić, J.; Milojević, M. Torrent classification—base of rational management of erosive regions. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2008; Volume 4, pp. 1–8. [Google Scholar]
- Tošić, R.; Dragićević, S. Methodology update for determination ofthe erosion coefficient. J.Serb. Geogr. Soc. 2012, 92, 11–26. [Google Scholar]
- Globevnik, L.; Holjević, D.; Petkovšek, G.; Rubinić, J. Applicability of the Gavrilović method in erosion calculation using spatial data manipulation techniques. In Erosion Prediction in Ungauged Basins: Integrating Methods and Techniques, IAHS publication 279; De Boer, D.H., Ed.; International Association of Hydrological Sciences: Wallingford/Oxfordshire, UK, 2003; pp. 224–233. [Google Scholar]
- Ristanović, B.; Miljanović, B.; Cimbaljević, M.; Pankov, N.; Živković, M.; Popovic, A. Determining hydrological problems using GIS, Case study Krasavica. In Proceedings of the 47th Annual conference of the Serbian Water Pollution Control Society, WATER 2018, Soko Banja, Serbia, 12–14 June 2018; pp. 255–262. [Google Scholar]
- Mikoš, M.; Fazarinc, R.; Ribičič, M. Sediment production and delivery from recent large landslides and earthquake-induced rock falls in the Upper Soča River Valley, Slovenia. Eng. Geol. 2006, 86, 198–210. [Google Scholar] [CrossRef]
- Gavrilović, Z. The importance of laboratory tests in the experimental study of soil erosion. In Irrigation and Drainage in Serbia, Proceedings of Counseling; Svilajnac, Serbia, 1994; pp. 327–331. [Google Scholar]
- Gavrilović, Z. The use of empirical method (erosion potential method) for calculating sediment production and transportation in unstudied or torrential streams. In International Conference on River Regime; White, W.R., Ed.; Hydraulics Research Limited: Wallingford/Oxfordshire, UK, 1988; pp. 411–422. [Google Scholar]
- Water Base River Jadar; Water Management Organization “Loznica”: Loznica, Serbia, 1970; Volume IV, p. 123.
- Lazarević, R. Landslides; Yugoslav Society for the Protection of the torrent: Beograd, Serbia, 2000. [Google Scholar]
- Lièbault, F.; Gómez, B.; Page, M.; Marden, M.; Peacock, D.; Richard, D.; Trotter, C.M. Land-use change, sediment production and channel response in upland region. Rivers Res. Appl. 2005, 21, 739–756. [Google Scholar]
- Keesstra, S.D.; Van Dam, O.; Verstraeten, G.; van Huissteden, J. Changing sediment dynamics due to natural reforestation in the Dragonja catchment, SW Slovenia. Catena 2009, 78, 60–72. [Google Scholar] [CrossRef]
- Piégay, H.; Walling, D.E.; Landon, N.; He, Q.; Liébault, F.; Petiot, R. Contemporary changes in sediment yield in an alpine mountain basin due to afforestation (the upper Drôme in France). Catena 2004, 20, 183–212. [Google Scholar]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling-Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Singh, R.B. Land use/cover changes, extreme events and ecohydrological responses in the Himalayan region. Hydrol. Process. 1999, 12, 2043–2055. [Google Scholar] [CrossRef]
- Lenhart, T.; Fohrer, N.; Frede, H.G. Effects of land use changes on the nutrient balance in mesoscale catchments. Phys. Chem. Earth Parts A/B/C 2003, 28, 1301–1309. [Google Scholar] [CrossRef]
- Vanacker, V.; Vanderschaeghe, M.; Govers, G.; Willems, E.; Poesen, J.; Deckers, J.; De Bievreet, B. Linking hydrological, infinite slope stability and land-use change models through GIS for assessing the impact of deforestation on slope stability in high Andean watersheds. Geomorphology 2003, 52, 299–315. [Google Scholar] [CrossRef]
- Varela, M.E.; Blas, E.D.; Benito, E. Physical soil degradation induced by deforestation and slope modification in a temperate–humid environment. Land Degrad. Dev. 2001, 12, 477–484. [Google Scholar] [CrossRef]
- Martínez-Casasnovas, J.A.; Sánchez-Bosch, I. Impact assessment of changes in land use/conservation practices on soil erosion in the Penedès–Anoia vineyard region (NE Spain). Soil Tillage Res. 2000, 57, 101–106. [Google Scholar] [CrossRef]
- Erskine, W.D.; Mahmoudzadeh, A.; Myers, C. Land use effects on sediment yields and soil loss rates in small basins of Triassic sandstone near Sydney, NSW, Australia. Catena 2002, 49, 271–287. [Google Scholar] [CrossRef]
- Ristanović, B.; Živković Bubalo, M.; Tanasić, J.; Popović, A. Monograph of Municipality Krupanj; Department of Geography, Tourism and Hotel Menagment: Novi Sad, Serbia, 2016. [Google Scholar]
| Average altitude of basin or erosive area | Nsr = (f1 × h1 + f2 × h2 +…….fn × hn)/F |
| Average height difference of basin or area covered by erosion | D = Nsr − Nu |
| Coefficient of basin shape | A = O/L × ( + 2) = 0,195 × O/L |
| Average basin fall | Jsr = WL × h/F |
| Coefficient of water-permeability | S1 = 0,4 × fp + 0,7 × fpp + fnp |
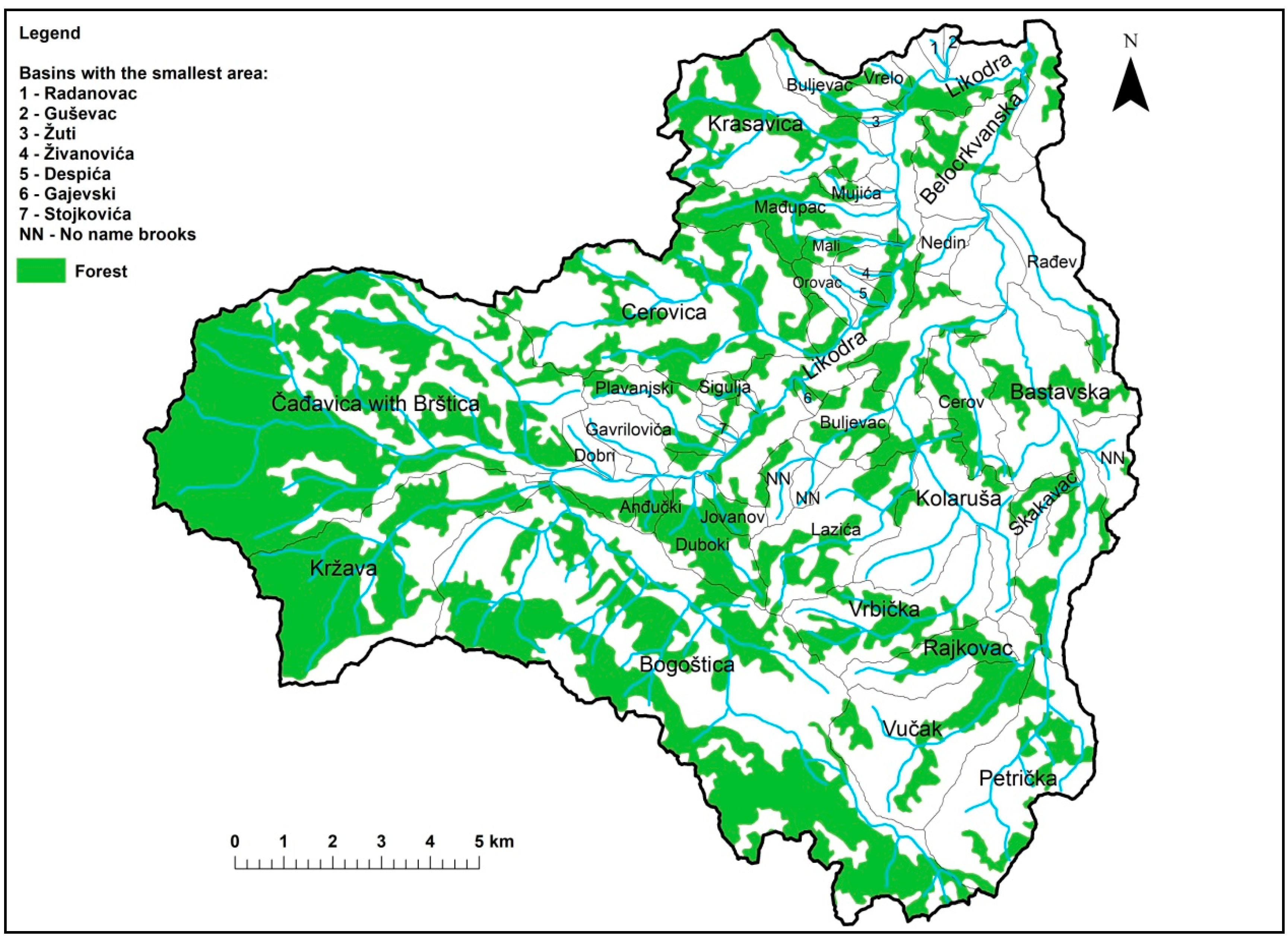
| Coefficient of vegetation covering | S2 = 0,6 × fš + 0,8 × ft + 1,0 × fg/F |
| Analytic expression of retention | W = y × h2/L |
| Maximum quantity of water (which runs out by erosive basin) | Qmax = A × S1 × S2 × W × |
| Production of deposit from one km2 of the basin | G = To × Hgod × × Z3/2 |
| Confluence | F (km2) | L (km) | O (km) | D (m) | A | S1 | S2 | W | Qmax | G | Z | ΣL | ISR | To | Lhm + 1 Lgt + 1 | K | Hk | I–V | A–F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Slope and Interconfluences from Emptier to Orovac Brook | 3.75 | ||||||||||||||||||
| Radanovac Brook | 0.47 | 1.00 | 3.00 | 37 | 0.58 | 0.70 | 0.88 | 0.72 | 4.81 | 1238.18 | 0.55 | 1.00 | 0.21 | 1.044 | 0.50 | 0.47 | 0.06 | III | E |
| Guševac Brook | 0.30 | 0.75 | 2.00 | 60 | 0.52 | 0.70 | 0.90 | 0.73 | 4.50 | 1238.18 | 0.55 | 0.40 | 0.13 | 1.044 | 0.66 | 0.37 | 0.04 | III | F |
| Brelo Brook | 0.57 | 1.75 | 3.50 | 92 | 0.39 | 0.61 | 0.79 | 0.72 | 4.35 | 1238.18 | 0.55 | 1.25 | 0.22 | 1.044 | 0.66 | 0.49 | 0.07 | III | E |
| Buljevac Brook | 1.84 | 3.20 | 6.75 | 139 | 0.41 | 0.74 | 0.88 | 0.71 | 13.54 | 826.26 | 0.42 | 5.50 | 0.30 | 1.044 | 0.25 | 0.57 | 0.11 | III | D |
| Žuti Brook | 0.12 | 0.70 | 1.70 | 63 | 0.47 | 0.61 | 0.72 | 0.73 | 1.83 | 1446.22 | 0.61 | 0.30 | 0.25 | 1.044 | 0.71 | 0.52 | 0.02 | III | F |
| Krasavica | 8.50 | 5.25 | 12.25 | 160 | 0.46 | 0.40 | 0.85 | 0.70 | 18.09 | 1590.78 | 0.65 | 21.0 | 0.25 | 1.044 | 0.83 | 0.52 | 1.69 | III | C |
| Mujića Brook | 0.57 | 1.30 | 3.75 | 69 | 0.56 | 0.55 | 0.85 | 0.72 | 5.28 | 1517.93 | 0.63 | 1.25 | 0.22 | 1.044 | 0.50 | 0.49 | 0.08 | III | E |
| Mađupac Brook | 3.60 | 4.60 | 11.50 | 169 | 0.49 | 0.55 | 0.86 | 0.71 | 17.98 | 1105.59 | 0.51 | 11.0 | 0.31 | 1.044 | 0.55 | 0.58 | 0.56 | III | D |
| Mali Brook | 0.11 | 1.00 | 2.50 | 57 | 0.49 | 0.55 | 0.86 | 0.72 | 1.87 | 1238.18 | 0.55 | 0.50 | 0.45 | 1.044 | 0.50 | 0.70 | 0.02 | III | F |
| Živanovića Brook | 1.05 | 1.75 | 4.75 | 101 | 0.53 | 0.55 | 0.75 | 0.72 | 7.21 | 1238.18 | 0.55 | 3.20 | 0.30 | 1.044 | 0.36 | 0.57 | 0.11 | III | D |
| Otavice Brook | 0.23 | 0.90 | 2.50 | 96 | 0.54 | 0.55 | 0.86 | 0.72 | 3.88 | 1238.18 | 0.55 | 1.00 | 0.43 | 1.044 | 0.36 | 0.68 | 0.03 | III | F |
| Despića Brook or Gumina | 0.32 | 1.10 | 3.00 | 92 | 0.53 | 0.40 | 0.84 | 0.72 | 3.12 | 4242.34 | 1.25 | 1.25 | 0.39 | 1.044 | 0.36 | 0.65 | 0.04 | I | F |
| Orovac | 0.87 | 2.00 | 4.00 | 129 | 0.39 | 0.74 | 0.82 | 0.72 | 8.02 | 2378.86 | 0.85 | 3.00 | 0.34 | 1.044 | 0.52 | 0.609 | 0.11 | III | D |
| Slope and Interconfluences from Orovac Brook to Čađavica | 0.33 | ||||||||||||||||||
| Cerovica | 15.18 | 7.50 | 19.00 | 186 | 0.49 | 0.60 | 0.83 | 0.70 | 40.20 | 855.94 | 0.43 | 44.0 | 0.29 | 1.044 | 1.94 | 0.56 | 8.11 | III | C |
| Točine | 0.12 | 0.50 | 1.50 | 135 | 0.58 | 0.46 | 0.87 | 0.73 | 3.03 | 2378.86 | 0.85 | 0.50 | 0.42 | 1.044 | 0.98 | 0.67 | 0.05 | II | E |
| Milinovača Brook | 0.26 | 0.70 | 2.50 | 130 | 0.70 | 0.47 | 0.73 | 0.73 | 4.52 | 1238.18 | 0.55 | 1.00 | 0.38 | 1.044 | 0.62 | 0.64 | 0.07 | III | E |
| Sigulja | 0.52 | 1.50 | 2.75 | 164 | 0.36 | 0.46 | 0.91 | 0.72 | 4.47 | 2378.86 | 0.85 | 2.00 | 0.38 | 1.044 | 0.52 | 0.64 | 0.06 | II | E |
| Stojkovića Brook | 0.29 | 0.90 | 2.75 | 156 | 0.60 | 0.60 | 0.74 | 0.72 | 5.79 | 1238.18 | 0.55 | 1.25 | 0.43 | 1.044 | 0.57 | 0.68 | 0.07 | III | E |
| Plavanjski Brook | 2.30 | 3.50 | 8.00 | 165 | 0.44 | 0.72 | 0.88 | 0.71 | 17.18 | 2900.00 | 0.97 | 7.00 | 0.30 | 1.044 | 0.55 | 0.57 | 0.32 | II | D |
| Gavrilovića Brook | 1.70 | 2.00 | 4.75 | 147 | 0.46 | 0.77 | 0.91 | 0.72 | 16.30 | 683.19 | 0.37 | 4.00 | 0.24 | 1.044 | 0.82 | 0.51 | 0.33 | IV | E |
| Dobri Brook | 0.50 | 1.25 | 3.00 | 98 | 0.47 | 0.81 | 0.89 | 0.72 | 7.64 | 2295.39 | 0.83 | 2.00 | 0.40 | 1.044 | 0.51 | 0.66 | 0.08 | II | A |
| Čađavica with Brštica | 34.34 | 9.25 | 24.50 | 252 | 0.52 | 0.83 | 0.76 | 0.69 | 94.07 | 1340.86 | 0.58 | 98.5 | 0.29 | 1.044 | 4.95 | 0.56 | 49.68 | III | C |
| Kržava | 12.18 | 8.00 | 19.00 | 321 | 0.39 | 0.57 | 0.69 | 0.69 | 29.70 | 826.26 | 0.42 | 40.5 | 0.33 | 1.044 | 2.03 | 0.60 | 5.79 | III | A |
| Bogoštica | 32.54 | 13.50 | 35.50 | 292 | 0.51 | 0.51 | 0.81 | 0.68 | 62.31 | 2091.13 | 0.78 | 114.00 | 0.35 | 1.044 | 3.03 | 0.61 | 31.08 | II | A |
| Interconfluences from Bogoštica to Jovanov Brook | 4.37 | ||||||||||||||||||
| Vujin Brook | 0.30 | 0.90 | 2.50 | 86 | 0.54 | 0.82 | 0.85 | 0.72 | 6.17 | 2591.81 | 0.90 | 1.80 | 0.60 | 1.044 | 1.05 | 0.80 | 0.14 | II | D |
| Anđučki Brook | 0.50 | 1.40 | 3.40 | 87 | 0.47 | 0.79 | 0.85 | 0.72 | 6.72 | 2378.86 | 0.85 | 2.25 | 0.45 | 1.044 | 0.62 | 0.70 | 0.10 | II | D |
| Duboki Brook | 2.86 | 3.00 | 7.50 | 138 | 049 | 0.76 | 0.91 | 0.71 | 21.38 | 4242.34 | 1.25 | 8.50 | 0.30 | 1.044 | 1.47 | 0.57 | 1.18 | I | C |
| Jovanov Brook | 0.60 | 1.50 | 4.50 | 71 | 0.59 | 0.75 | 0.85 | 0.72 | 7.88 | 1340.85 | 0.58 | 3.00 | 0.50 | 1.044 | 1.14 | 0.73 | 0.30 | III | D |
| Slope | 1.77 | ||||||||||||||||||
| Gajevski Brook | 0.30 | 0.80 | 2.20 | 84 | 0.54 | 0.45 | 0.79 | 0.73 | 3.12 | 885.97 | 0.44 | 0.50 | 0.17 | 1.044 | 0.83 | 0.43 | 0.06 | III | E |
| Slope | 1.76 | ||||||||||||||||||
| Belocrkvanska River | 73.86 | 18.50 | 45.50 | 268 | 0.48 | 0.64 | 0.75 | 0.67 | 96.92 | 1138.27 | 0.52 | 136.8 | 0.19 | 1.044 | 3.50 | 0.45 | 56.46 | III | A |
| Slope | 1.40 | ||||||||||||||||||
| Likodra River | 212.5 | 27.00 | 77.50 | 171 | 0.56 | 0.67 | 0.82 | 0.66 | 171.71 | 1238.18 | 0.55 | 80.3 | 0.03 | 1.044 | 5.38 | 0.18 | 115.8 | III | A |
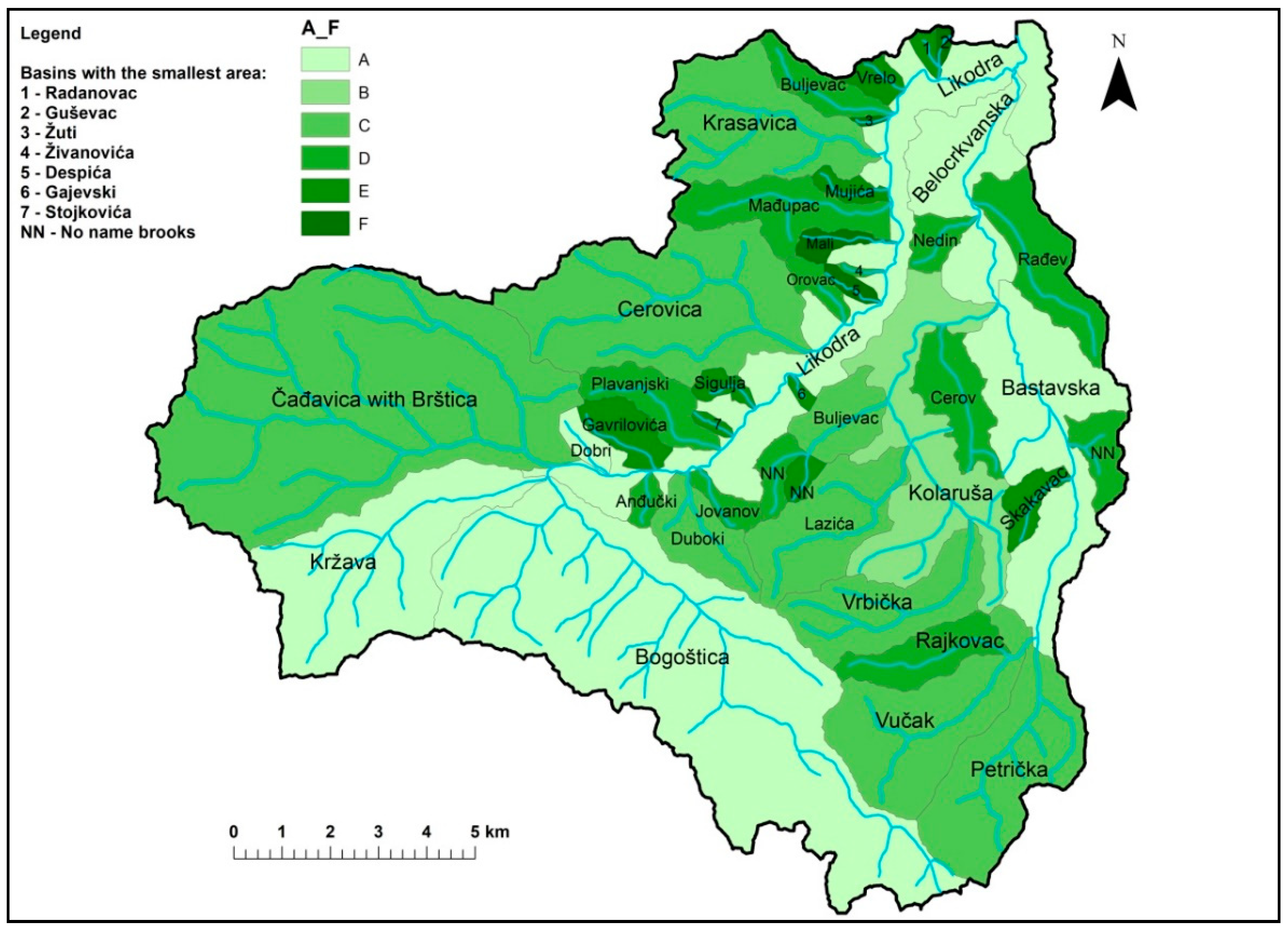
| River Basin | Hydrographic Classes | Σ | Intensity Erosion Categories | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | D | E | F | I | II | III | IV | V | ||
| Likodra | 4 | - | 4 | 9 | 9 | 5 | 31 | 2 | 8 | 20 | 1 | - |
| Belocrkvanska River | 1 | 1 | 5 | 8 | 3 | 2 | 20 | - | 4 | 6 | 10 | - |
| Total | 5 | 1 | 9 | 17 | 12 | 7 | 51 | 2 | 12 | 26 | 11 | - |
| % | 9.80 | 1.96 | 17.64 | 33.33 | 23.53 | 13.72 | 100 | 3.92 | 23.52 | 50.98 | 21.56 | 0.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ristanović, B.; Cimbaljević, M.; Miljković, Đ.; Ostojić, M.; Fekete, R. GIS Application for Determining Geographical Factors on Intensity of Erosion in Serbian River Basins. Case Study: The River Basin of Likodra. Atmosphere 2019, 10, 526. https://doi.org/10.3390/atmos10090526
Ristanović B, Cimbaljević M, Miljković Đ, Ostojić M, Fekete R. GIS Application for Determining Geographical Factors on Intensity of Erosion in Serbian River Basins. Case Study: The River Basin of Likodra. Atmosphere. 2019; 10(9):526. https://doi.org/10.3390/atmos10090526
Chicago/Turabian StyleRistanović, Branko, Marija Cimbaljević, Đurđa Miljković, Miloš Ostojić, and Renata Fekete. 2019. "GIS Application for Determining Geographical Factors on Intensity of Erosion in Serbian River Basins. Case Study: The River Basin of Likodra" Atmosphere 10, no. 9: 526. https://doi.org/10.3390/atmos10090526
APA StyleRistanović, B., Cimbaljević, M., Miljković, Đ., Ostojić, M., & Fekete, R. (2019). GIS Application for Determining Geographical Factors on Intensity of Erosion in Serbian River Basins. Case Study: The River Basin of Likodra. Atmosphere, 10(9), 526. https://doi.org/10.3390/atmos10090526




