Comparison Analysis of Total Precipitable Water of Satellite-Borne Microwave Radiometer Retrievals and Island Radiosondes
Abstract
1. Introduction
2. Data and Methods
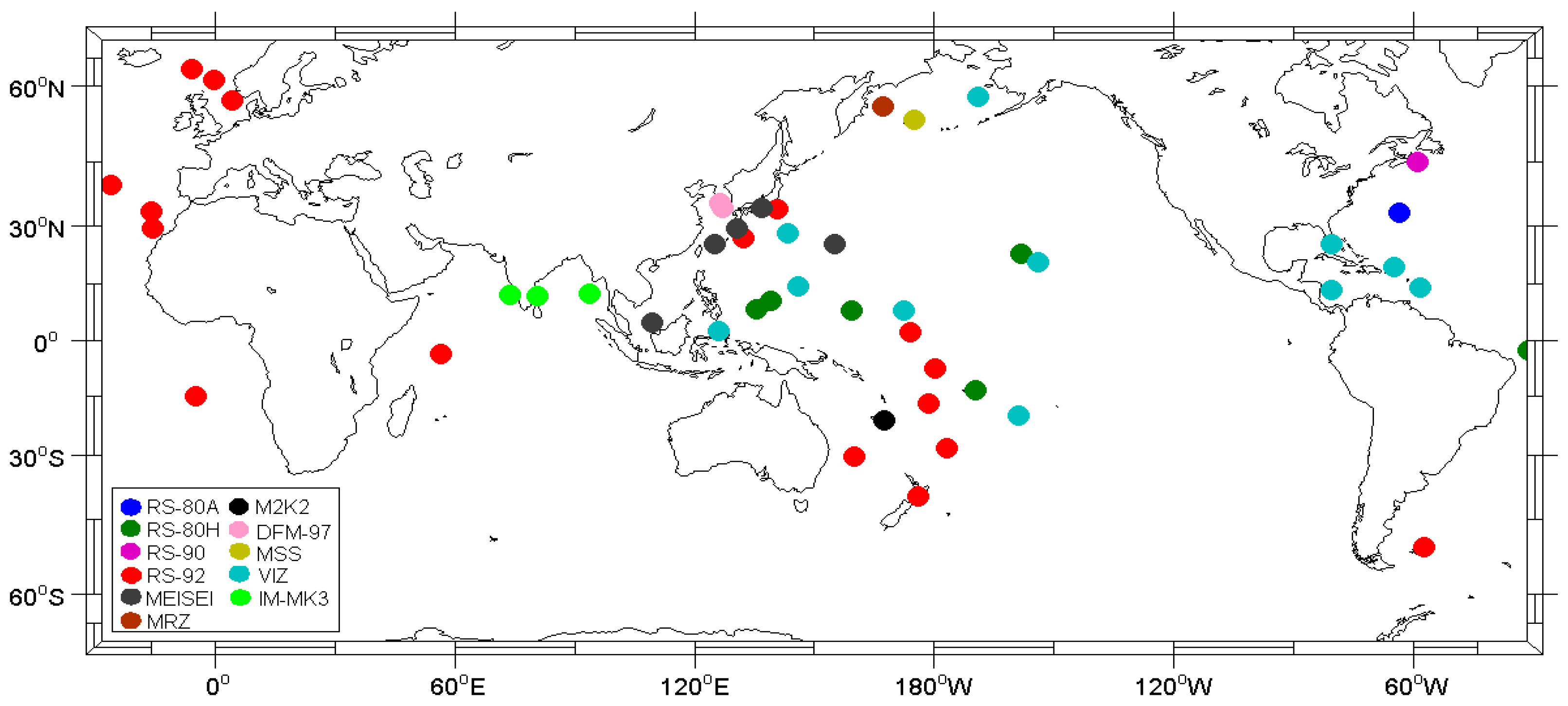
2.1. Radiosonde TPW
2.2. TPW Retrieval of Satellites
2.3. Data Matching Methods
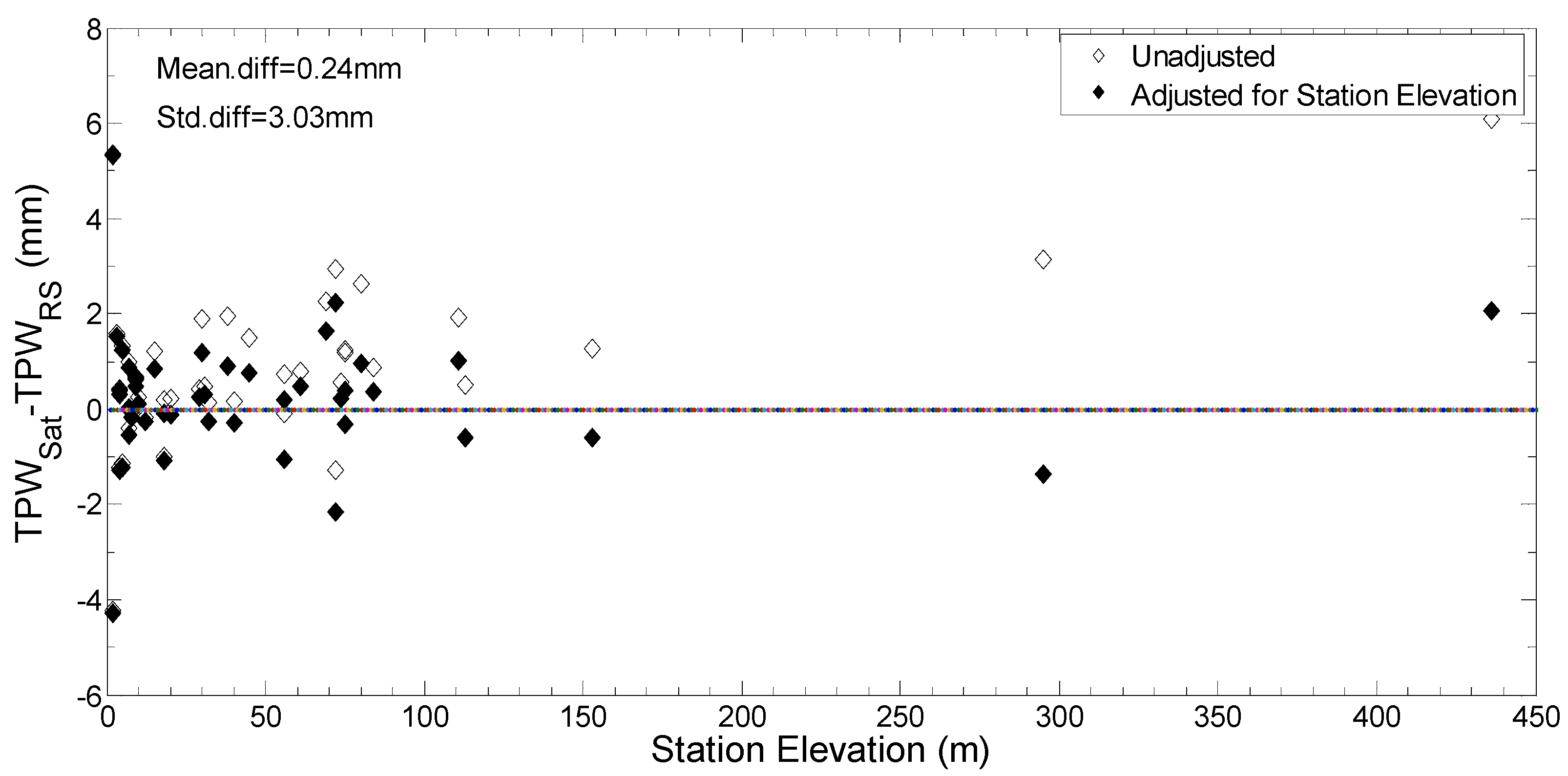
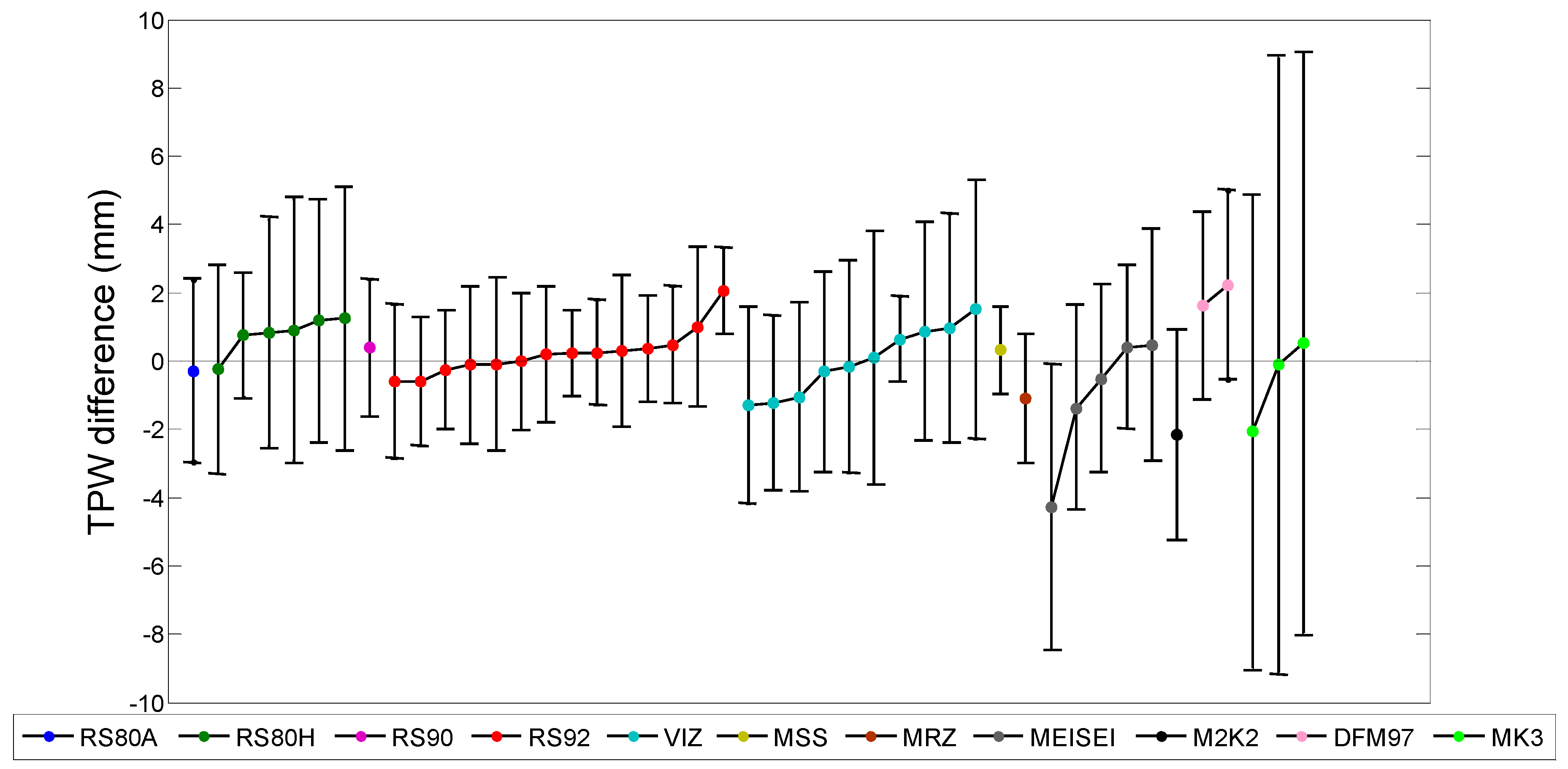
2.4. Correction for Altitude Difference
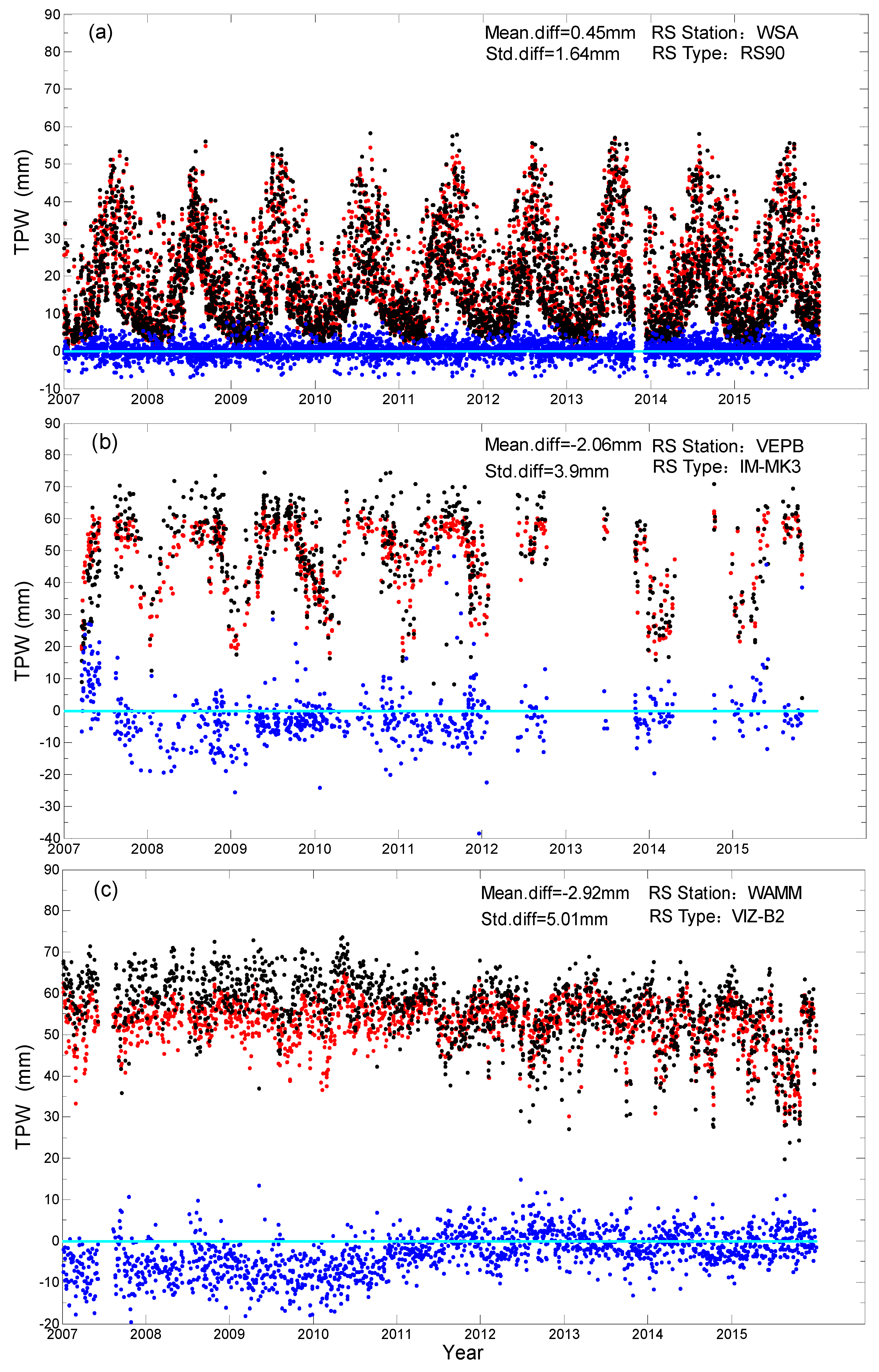
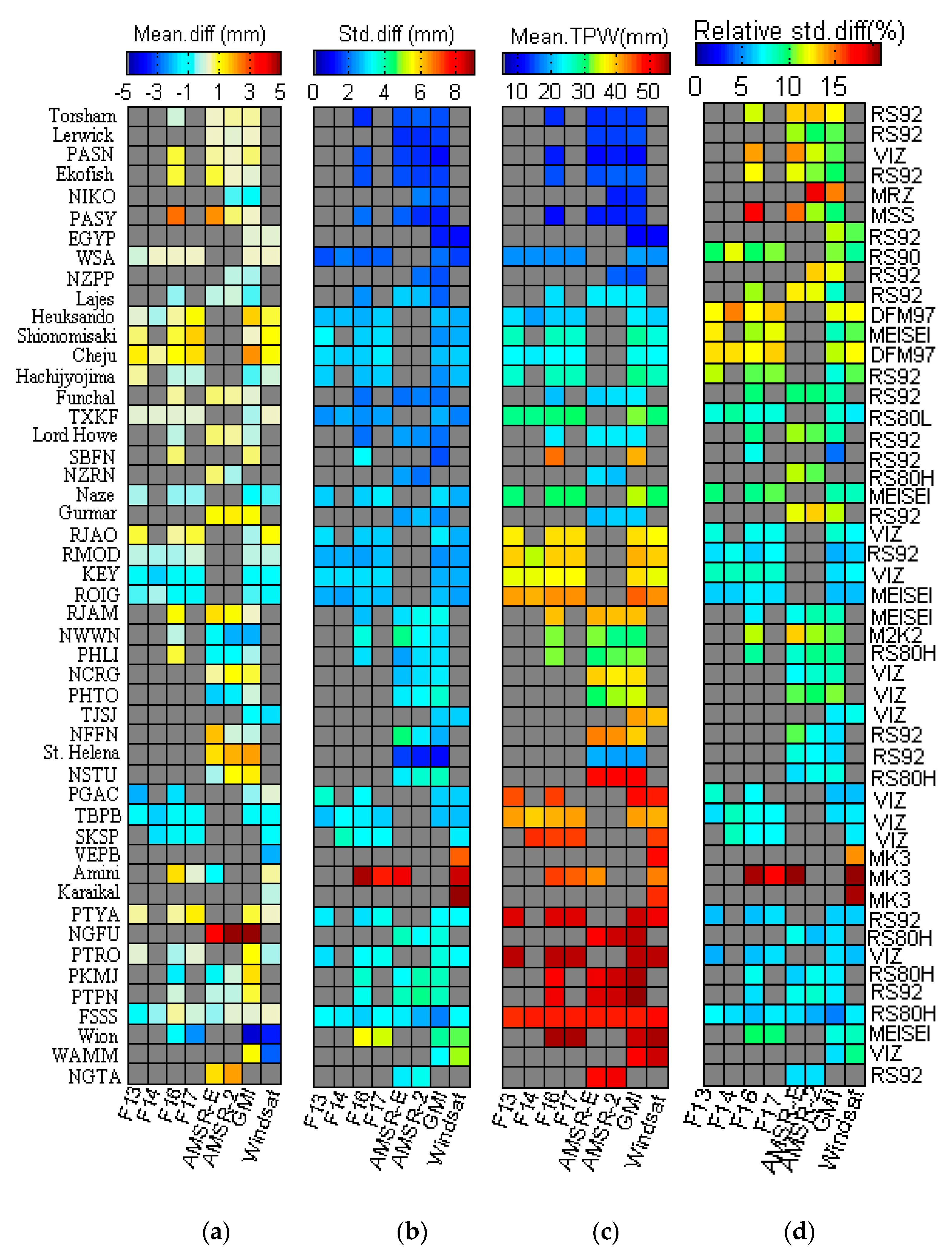
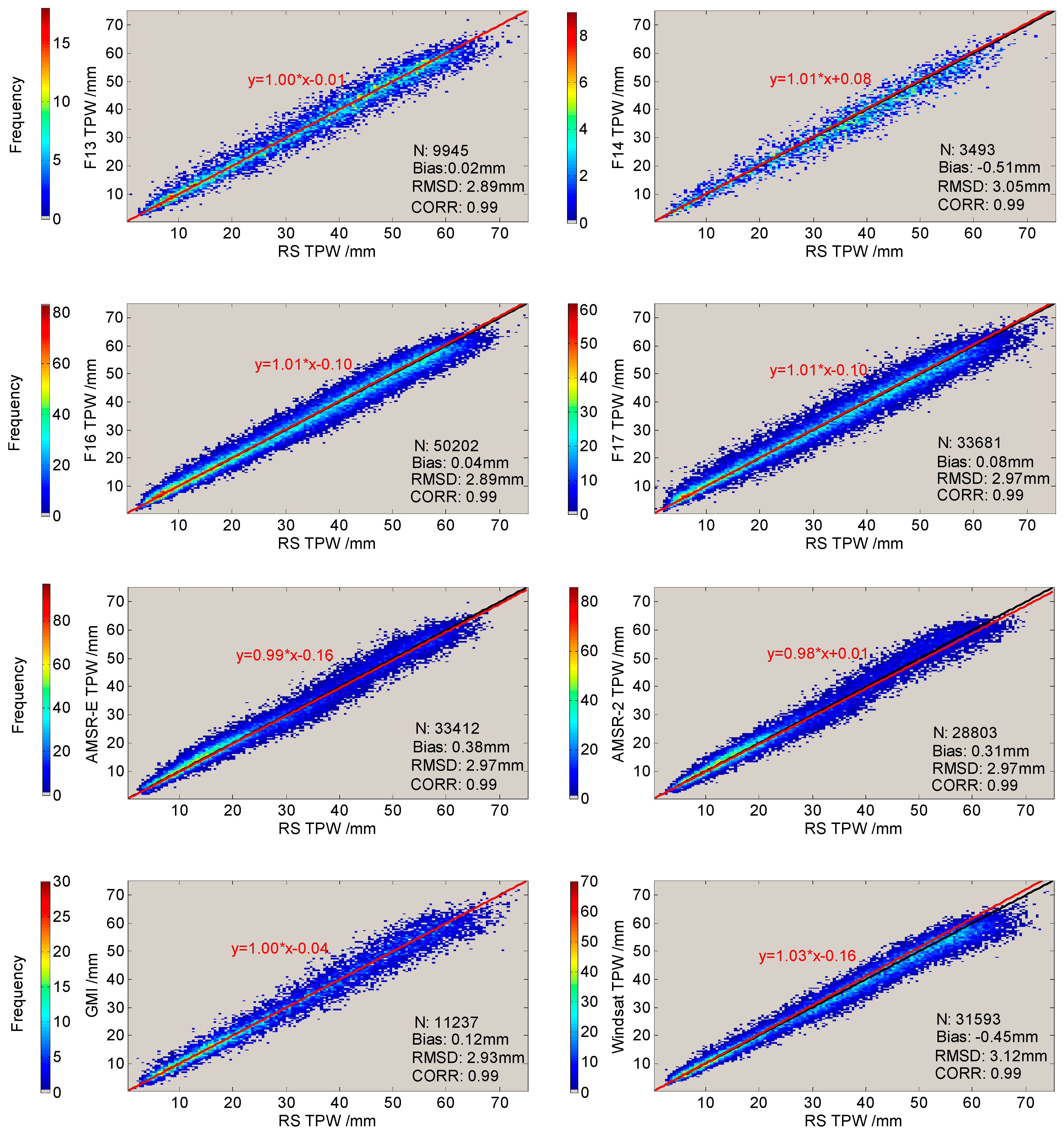
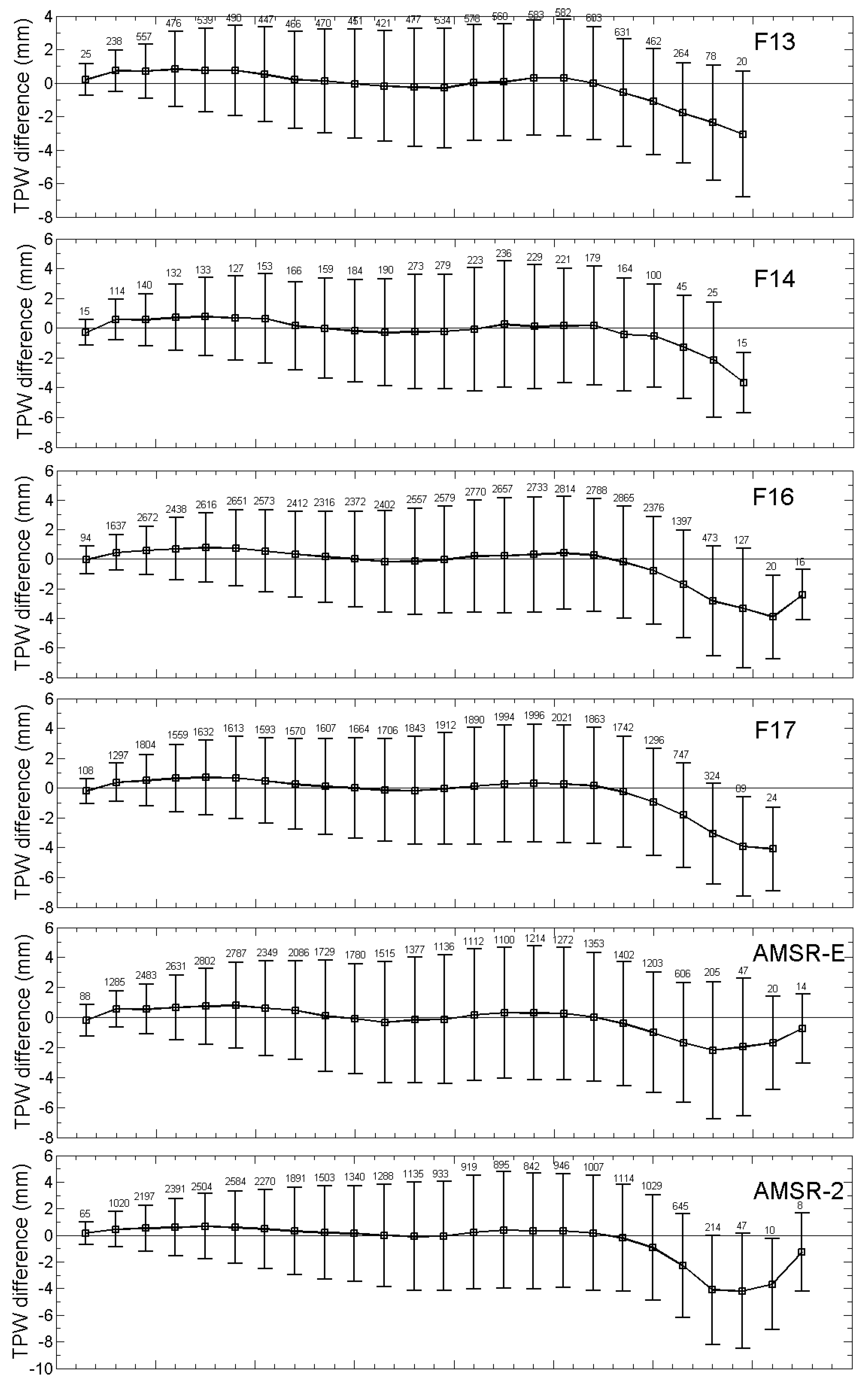
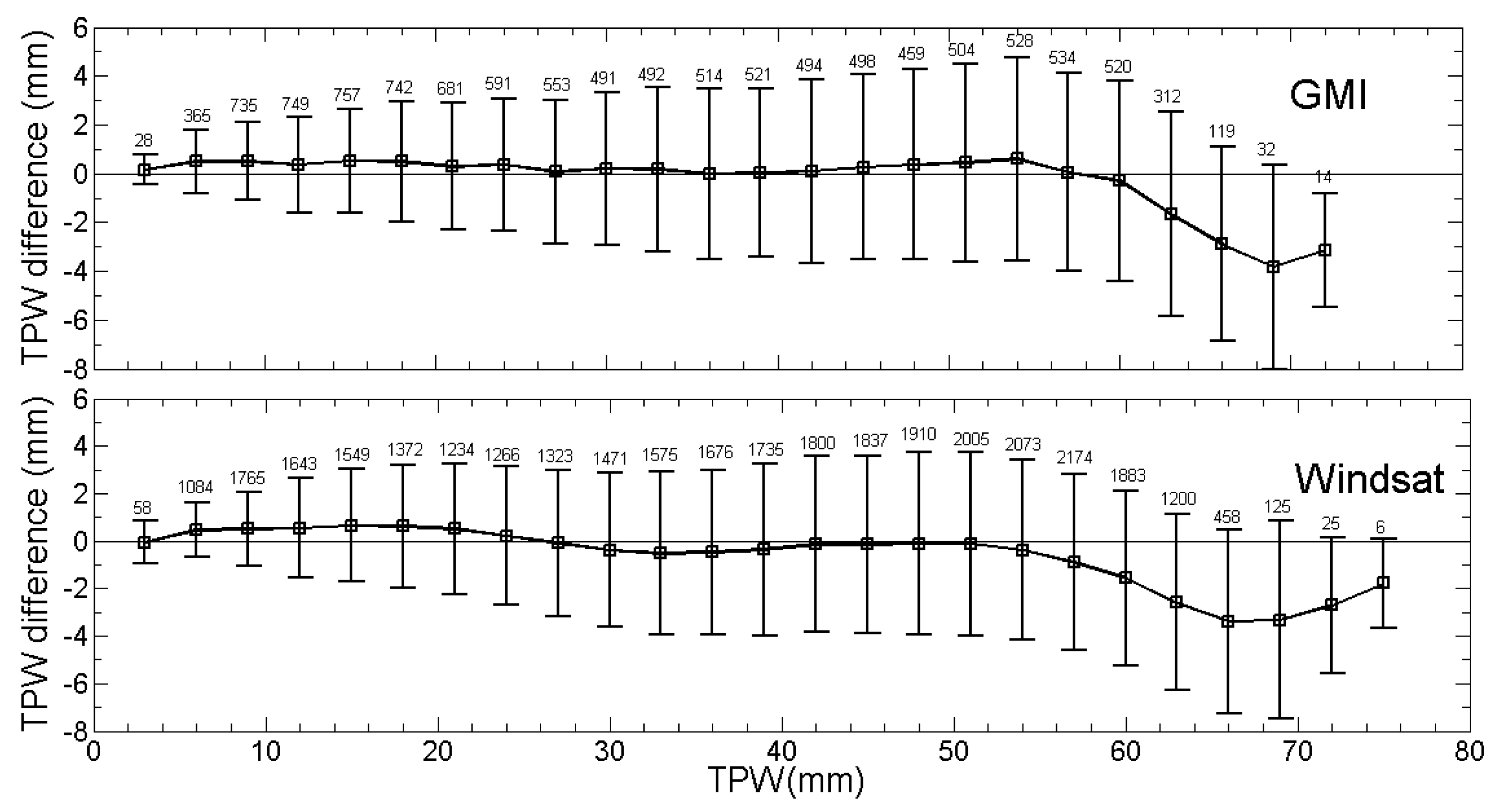
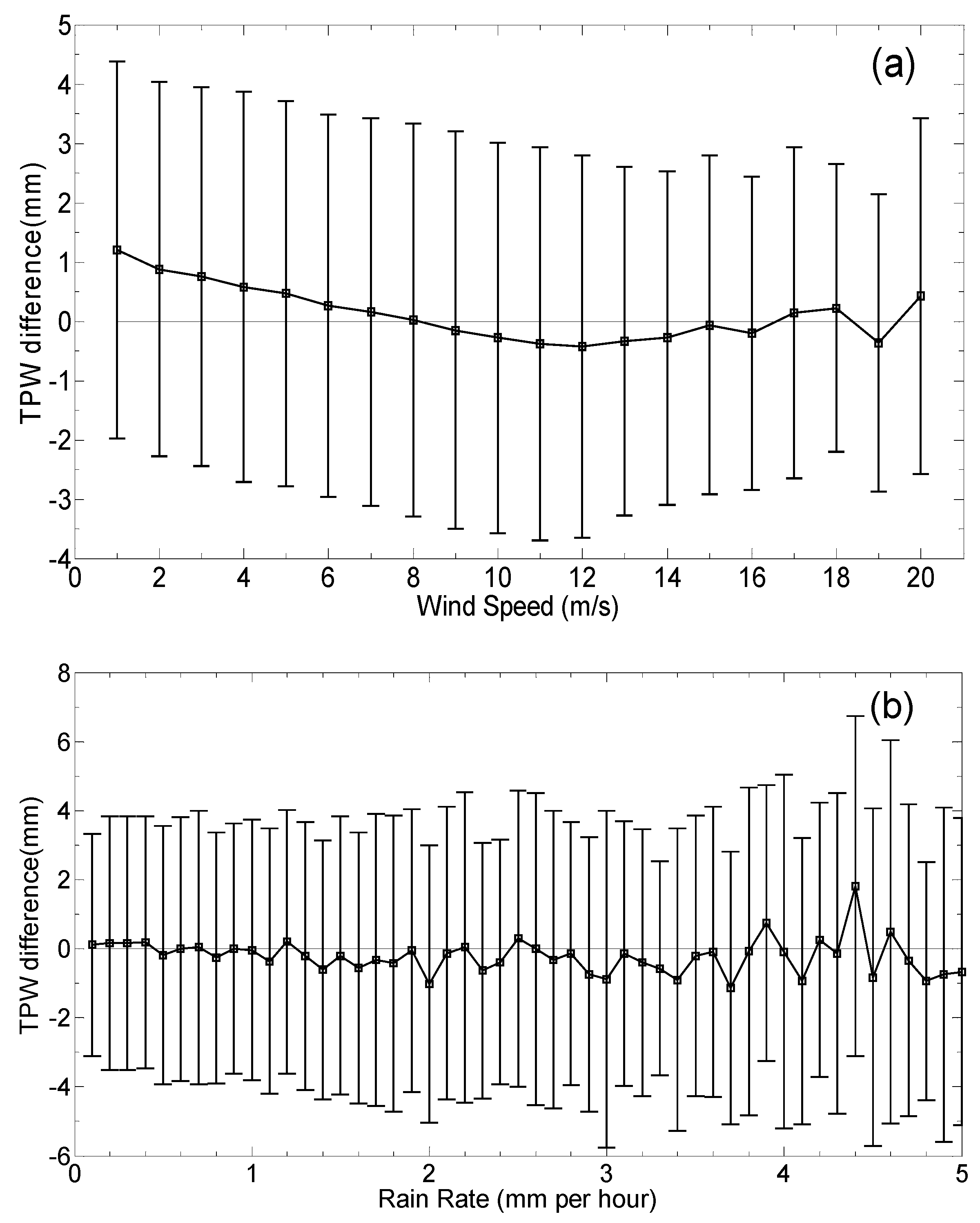
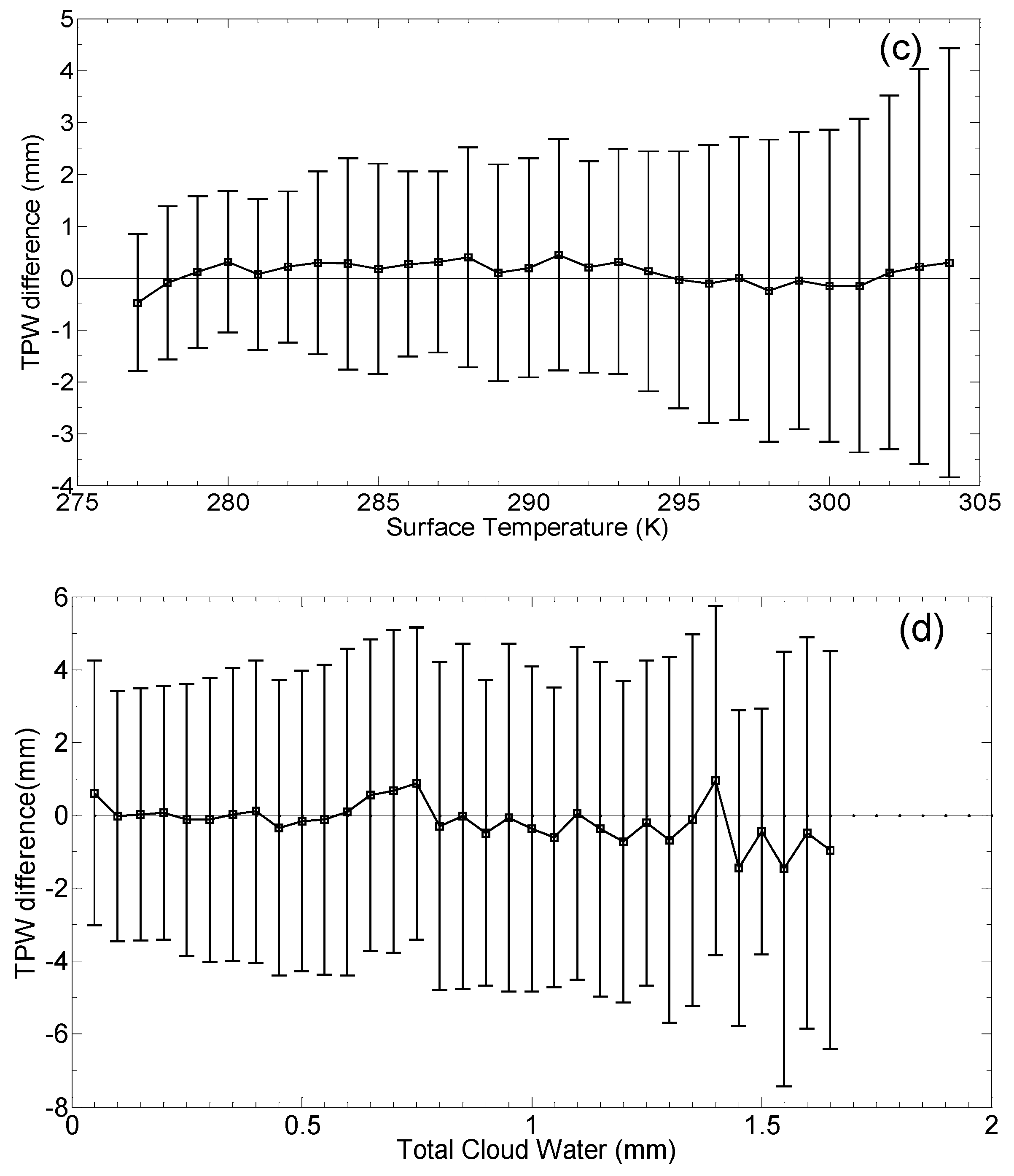
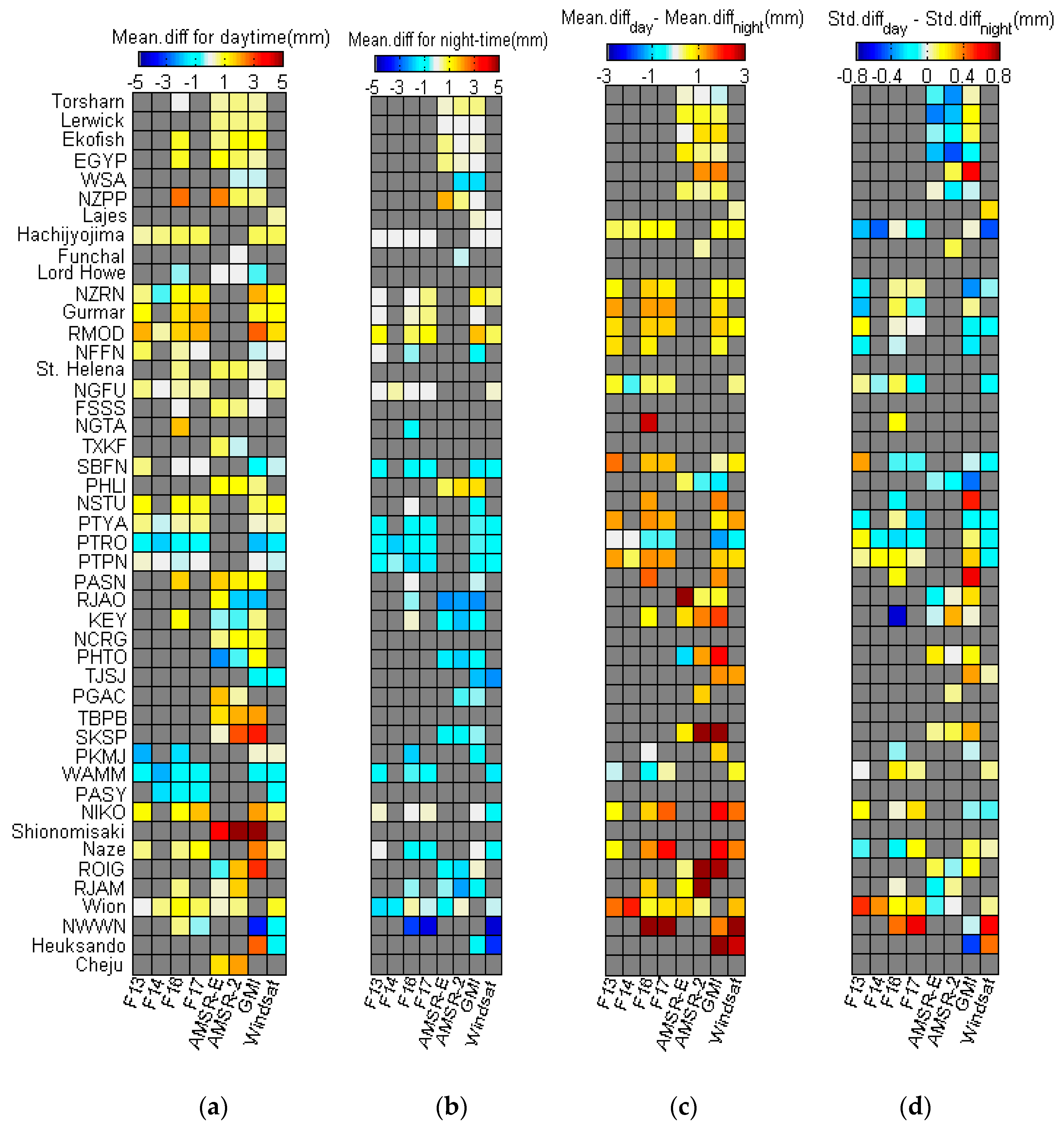
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, J.; Zhang, L. Climate applications of a global, 2-hourly atmospheric precipitable water dataset derived from IGS tropospheric products. J. Geod. 2009, 83, 209–217. [Google Scholar] [CrossRef]
- Mears, C.A.; Santer, B.D.; Wentz, F.J.; Taylor, K.E.; Wehner, M.F. Relationship between temperature and precipitable water changes over tropical oceans. Geophys. Res. Lett. 2007, 34, 497–507. [Google Scholar] [CrossRef]
- Mccarthy, M.P.; Thorne, P.W.; Titchner, H.A. An analysis of tropospheric humidity trends from radiosondes. J. Clim. 2009, 22, 5820–5838. [Google Scholar] [CrossRef]
- Santer, B.D.; Taylor, K.E.; Gleckler, P.J.; Bonfils, C.; Barnett, T.P.; Pierce, D.M.; Mears, C.; Wentz, F.J.; Brüggemann, W.; Gillett, N.P.; et al. Incorporating model quality information in climate change detection and attribution studies. Proc. Natl. Acad. Sci. USA 2009, 106, 14778–14783. [Google Scholar] [CrossRef] [PubMed]
- Van Malderen, R.; Brenot, H.; Pottiaux, E.; Beirle, S.; Hermans, C.; De Mazière, M.; Wagner, T.; De Backer, H.; Bruyninx, C. A multi-site intercomparison of integrated water vapour observations for climate change analysis. Atmos. Meas. Tech. 2014, 7, 1075–1151. [Google Scholar] [CrossRef]
- MengistuTsidu, G.; Blumenstock, T.; Hase, F. Observations of precipitable water vapour over complex topography of ethiopia from ground-based GPS, FTIR, radiosonde and ERA-interim reanalysis. Atmos. Meas. Tech. 2015, 8, 3277–3295. [Google Scholar] [CrossRef]
- Racette, P.E.; Westwater, E.R.; Han, Y.; Gasiewski, A.J.; Klein, M.; Cimini, D.; David, C.J.; Will, M.; Edward, J.K.; James, R.W.; et al. Measurement of low amounts of precipitable water vapor using ground-based millimeter-wave radiometry. J. Atmos. Ocean. Technol. 2003, 22, 317–337. [Google Scholar] [CrossRef]
- Ferrare, R.A.; Melfi, S.H.; Whiteman, D.N.; Evans, K.D.; Schmidlin, F.J.; Starr, D.O. A comparison of water vapor measurements made by ramanlidar and radiosondes. J. Atmos. Ocean. Technol. 1995, 12, 1177–1195. [Google Scholar] [CrossRef]
- Behrendt, A.; Wulfmeyer, V.; Girolamo, P.D.; Kiemle, C.; Bauer, H.S.; Schaberl, T.; Summa, D.; Wang, J.; Browell, E.V. Intercomparison of water vapor data measured with lidar during ihop_2002. Part I: Airborne to ground-based lidar systems and comparisons with chilled-mirror hygrometer radiosondes. J. Atmos. Ocean. Technol. 2007, 24, 3–21. [Google Scholar] [CrossRef]
- Bokoye, A.I.; Royer, A.; Cliche, P.; O’Neill, N. Calibration of sun radiometer based atmospheric water vapor retrievals using GPS meteorology. J. Atmos. Ocean. Technol. 2007, 24, 964–979. [Google Scholar] [CrossRef]
- Van Baelen, J.; Aubagnac, J.P.; Dabas, A. Comparison of near-real time estimates of integrated water vapor derived with GPS, radiosondes, and microwave radiometer. J. Atmos. Ocean. Technol. 2005, 22, 201–210. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Dai, A.; Van Hove, T.; Van Baelen, J. A near-global, 2-hourly data set of atmospheric precipitable water from ground-based GPS measurements. J. Geophys. Res. Atmos. 2007, 112, 236–242. [Google Scholar] [CrossRef]
- Bock, O.; Willis, P.; Wang, J.; Mears, C. A high-quality, homogenized, global, long-term (1993–2008) DORIS precipitable water data set for climate monitoring and model verification. J. Geophys. Res. Atmos. 2014, 119, 7209–7230. [Google Scholar] [CrossRef]
- Niell, A.E.; Coster, A.J.; Solheim, F.S.; Mendes, V.B.; Toor, P.C.; Langley, R.B.; Upham, C.A. Comparison of measurements of atmospheric wet delay by radiosonde, water vapor radiometer, GPS, and VLBI. J. Atmos. Ocean. Technol. 1972, 18, 830–850. [Google Scholar] [CrossRef]
- King, M.D.; Menzel, W.P.; Grant, P.S.; Myers, J.S.; Arnold, G.T.; Platnick, S.E.; Liam, E.; Tsay, S.-I.; Moeller, C.C.; Fitzgerald, M.; et al. Airborne scanning spectrometer for remote sensing of cloud, aerosol, water vapor, and surface properties. J. Geophys. Res. Atmos. 2009, 13, 777–794. [Google Scholar] [CrossRef]
- Gunshor, M.M.; Schmit, T.J.; Menzel, W.P. Intercalibration of the infrared window and water vapor channels on operational geostationary environmental satellites using a single polar-orbiting satellite. J. Geophys. Res. Atmos. 2004, 21, 61–68. [Google Scholar] [CrossRef]
- Wentz, F.J. A well-calibrated ocean algorithm for special sensor microwave/imager. J. Geophys. Res. Atmos. 1997, 102, 8703–8718. [Google Scholar] [CrossRef]
- Soden, B.; Lanzante, J. An Assessment of Satellite and Radiosonde Climatologies of Upper-Tropospheric Water Vapor. J. Climate. 1995, 9, 1235–1250. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Schreiner, W.S.; Wang, J.; Rossiter, D.L.; Zhang, Y. Comparison of GPS radio occultation soundings with radiosondes. Geophys. Res. Lett. 2005, 32, 215–236. [Google Scholar] [CrossRef]
- Yang, J.; Qiu, J.A. Method for estimating precipitable water and effective water vapor content from ground humidity parameters. Chin. J. Atmos. Sci. 2002, 26, 9–22. [Google Scholar]
- Soden, B.J.; Lanzante, J.R. An assessment of satellite and radiosondeclimatologiesof upper-tropospheric water vapor. J. Clim. 1996, 9, 1235–1250. [Google Scholar] [CrossRef]
- Wentz, B.F.J.; Meissner, T. Algorithm Theoretical Basis Document (ATBD) Version 2: AMSR Ocean Algorithm (RSS Technology Proposal No.121599A1); Remote Sensing System: Santa Rosa, CA, USA, 2000.
- Thao, S.; Eymard, L.; Obligis, E.; Picard, B. Trend and variability of the atmospheric water vapor: A mean sea level issue. J. Atmos. Ocean. Technol. 2014, 31, 1881–1901. [Google Scholar] [CrossRef]
- Mears, C.A.; Wang, J.; Smith, D.; Wentz, F.J. Intercomparison of total precipitable water measurements made by satellite-borne microwave radiometers and ground-based GPS instruments. J. Geophys. Res. Atmos. 2015, 120, 2492–2504. [Google Scholar] [CrossRef]
- Wentz, F.J. SSM/I Version 7 Calibration Report (RSS Technology Report No. 011012); Remote Sensing System: Santa Rosa, CA, USA, 2013. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L. Systematic errors in global radiosondeprecipitable water data from comparisons with ground-based GPS measurements. J. Clim. 2008, 21, 2218–2238. [Google Scholar] [CrossRef]
- Alishouse, J.C.; Snyder, S.A.; Vongsathorn, J.; Ferraro, R.R. Determination of oceanic total precipitable water from the SSM/I. IEEE Trans. Geosci. Remote Sens. 1990, 28, 811–816. [Google Scholar] [CrossRef]
- Sohn, B.J.; Smith, E.A. Explaining sources of discrepancy in SSM/I water vapor algorithms. J. Clim. 2003, 16, 3229–3255. [Google Scholar] [CrossRef]
- Bock, O.; Bouin, M.; Walpersdorf, A.; Lafore, J.P.; Janicot, S.; Guichard, F.; Agusti-Panareda, A. Comparison of ground-based GPS precipitable water vapour to independent observations and NWP model reanalyses over africa. Q. J. R. Meteorol. Soc. 2010, 133, 2011–2027. [Google Scholar] [CrossRef]
- Buehler, S.A.; Stman, S.; Melsheimer, C.; Holl, G.; Eliasson, S.; John, V.O.; Mendrok, J.A. multi-instrument comparison of integrated water vapour measurements at a high latitude site. Atmos. Chem. Phys. Discuss. 2012, 12, 21013–21063. [Google Scholar] [CrossRef]
- Wang, Y.; Fu, Y.; Liu, G.; Liu, Q.; Sun, L. A new water vapor algorithm for TRMM microwave imager (TMI) measurements based on a log linear relationship. J. Geophys. Res. Atmos. 2009, 114, 6149–6150. [Google Scholar] [CrossRef]
- University of Wyoming College of Engineering/ Upperair Air Data/ Soundings Page. Available online: http://weather.uwyo.edu/upperair/sounding.html (accessed on 11 July 2019).
- Thorne, P.W.; Parker, D.E.; Tett, S.F.B.; Jones, P.D.; Mccarthy, M.; Coleman, H.; Brohan, P. Revisiting radiosonde upper air temperatures from 1958 to 2002. J. Geophys. Res. Atmos. 2005, 110, 812–821. [Google Scholar] [CrossRef]
- Chelton, D.B.; Esbensen, S.K.; Schlax, M.G.; Thum, N.; Freilich, M.H.; Wentz, F.J.; Schopf, S. Observations of coupling between surface wind stress and sea surface temperature in the eastern tropical pacific. J. Clim. 1913, 14, 1479–1498. [Google Scholar] [CrossRef]
- Wang, J. Understanding and Correcting Humidity Measurement ErrorsfromVaisala RS80 and VIZ Radiosondes. (Radiosonde Workshop, Hampton University). Available online: http://www.eol.ucar.edu/homes/junhong/paper/RadiosondeWS02.pdf (accessed on 11 July 2019).
- Liu, H.; Tang, S.; Zhang, S.; Hu, J. Evaluation of modis water vapour products over china using radiosonde data. Int. J. Remote Sens. 2015, 36, 680–690. [Google Scholar] [CrossRef]
- Vömel, H.; Selkirk, H.; Miloshevich, L.; Valverdecanossa, J.; Valdés, J.; Kyrö, E.; Diaz, J.A. Radiation dry bias of the vaisala RS92 humidity sensor. J. Atmos. Ocean. Technol. 2007, 24, 953–963. [Google Scholar] [CrossRef]
- Nash, J.; Smout, R.; Oakley, T.; Pathack, B.; Kurnosenko, S. WMO Intercomparison of High Quality Radiosonde Systems: Final Report. Available online: http://www.wmo.int/pages/prog/www/IMOP/intercomparisons/RSO-2005/RSO-IC-2005_Final_Report.pdf (accessed on 11 July 2019).
| Satellite | Instrument | Start Date | End Date |
|---|---|---|---|
| DMSP-F13 | SSM/I | May 1995 | November 2009 |
| DMSP-F14 | SSM/I | May 1997 | August 2008 |
| DMSP-F16 | SSMI/S | October 2003 | Present |
| DMSP-F17 | SSMI/S | December 2006 | Present |
| NASA Aqua | AMSR-E | June 2002 | October 2011 |
| GCOM-W1 | AMSR-2 | May 2012 | Present |
| GPM | GMI | February 2014 | Present |
| Coriolis | WindSat | February 2003 | Present |
| Mean.Diff(mm) | Std.Diff(mm) | |||
|---|---|---|---|---|
| Daytime | Night-Time | Daytime | Night-Time | |
| F13 | 0.21 | −0.21 | 2.94 | 2.91 |
| F14 | −0.54 | −0.50 | 2.84 | 3.12 |
| F16 | 0.42 | −0.25 | 2.90 | 2.86 |
| F17 | 0.36 | −0.22 | 3.03 | 2.90 |
| AMSR-E | 0.68 | 0.11 | 3.17 | 2.70 |
| AMSR-2 | 0.86 | −0.20 | 3.09 | 2.73 |
| GMI | 0.66 | −0.34 | 3.02 | 2.77 |
| WindSat | 0.01 | −0.80 | 2.84 | 3.22 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, J.-P.; Yin, Y.-T.; Zhang, L.-F.; Wang, J.-N.; Zhang, M.-Y. Comparison Analysis of Total Precipitable Water of Satellite-Borne Microwave Radiometer Retrievals and Island Radiosondes. Atmosphere 2019, 10, 390. https://doi.org/10.3390/atmos10070390
Guan J-P, Yin Y-T, Zhang L-F, Wang J-N, Zhang M-Y. Comparison Analysis of Total Precipitable Water of Satellite-Borne Microwave Radiometer Retrievals and Island Radiosondes. Atmosphere. 2019; 10(7):390. https://doi.org/10.3390/atmos10070390
Chicago/Turabian StyleGuan, Ji-Ping, Yan-Tong Yin, Li-Feng Zhang, Jing-Nan Wang, and Ming-Yang Zhang. 2019. "Comparison Analysis of Total Precipitable Water of Satellite-Borne Microwave Radiometer Retrievals and Island Radiosondes" Atmosphere 10, no. 7: 390. https://doi.org/10.3390/atmos10070390
APA StyleGuan, J.-P., Yin, Y.-T., Zhang, L.-F., Wang, J.-N., & Zhang, M.-Y. (2019). Comparison Analysis of Total Precipitable Water of Satellite-Borne Microwave Radiometer Retrievals and Island Radiosondes. Atmosphere, 10(7), 390. https://doi.org/10.3390/atmos10070390




