Historical Winter Storm Atlas for Germany (GeWiSA)
Abstract
1. Introduction
2. Material and Methods
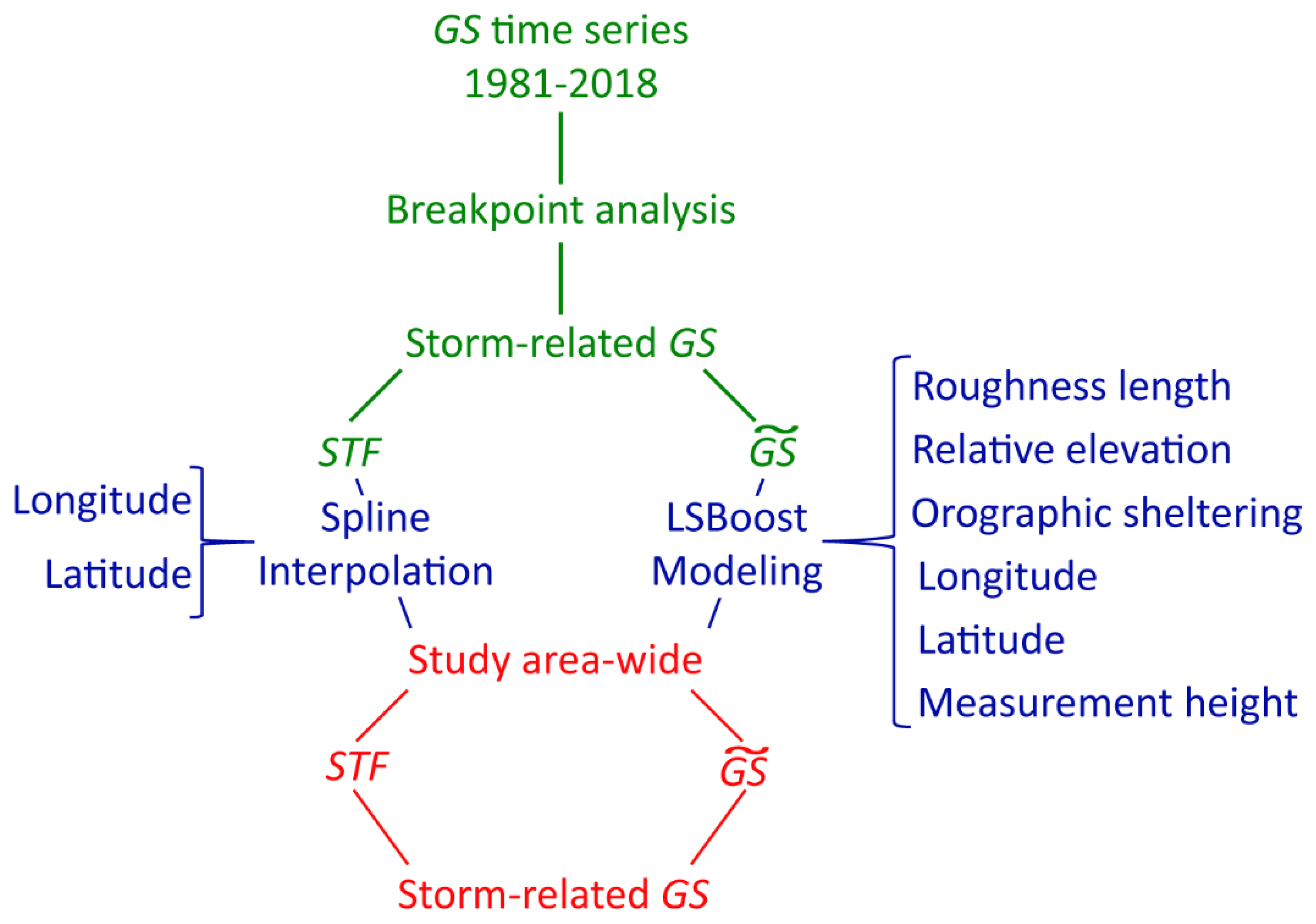
2.1. Overview
2.2. Study Area and Evaluated Winter Storms
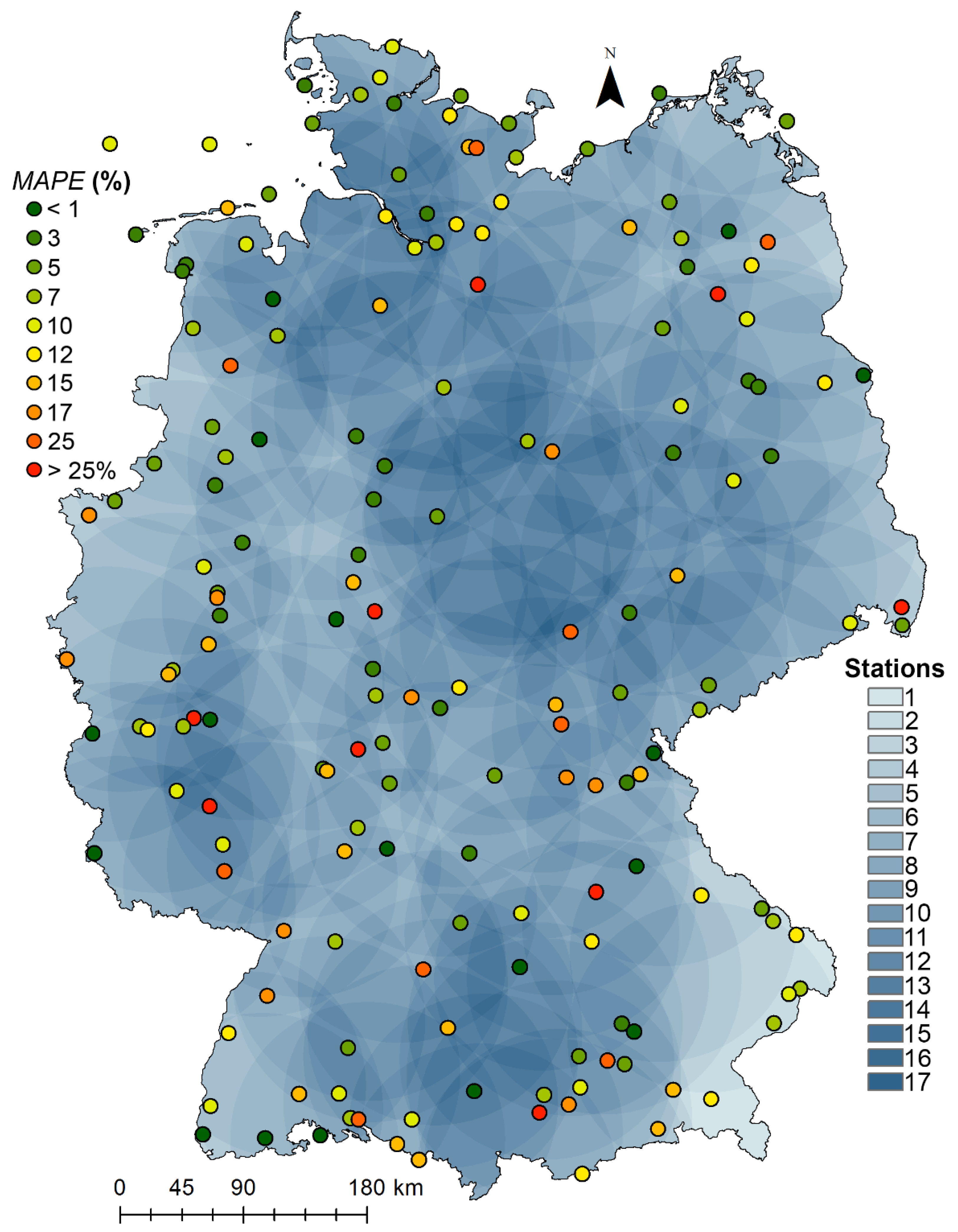
2.3. Gust Speed (GS) Data
2.4. Predictor Variables (PV)
2.5. LS-Boost Modeling (LSBoost)
2.6. Thin Plate Spline Interpolation (TPS)
3. Results and Discussion
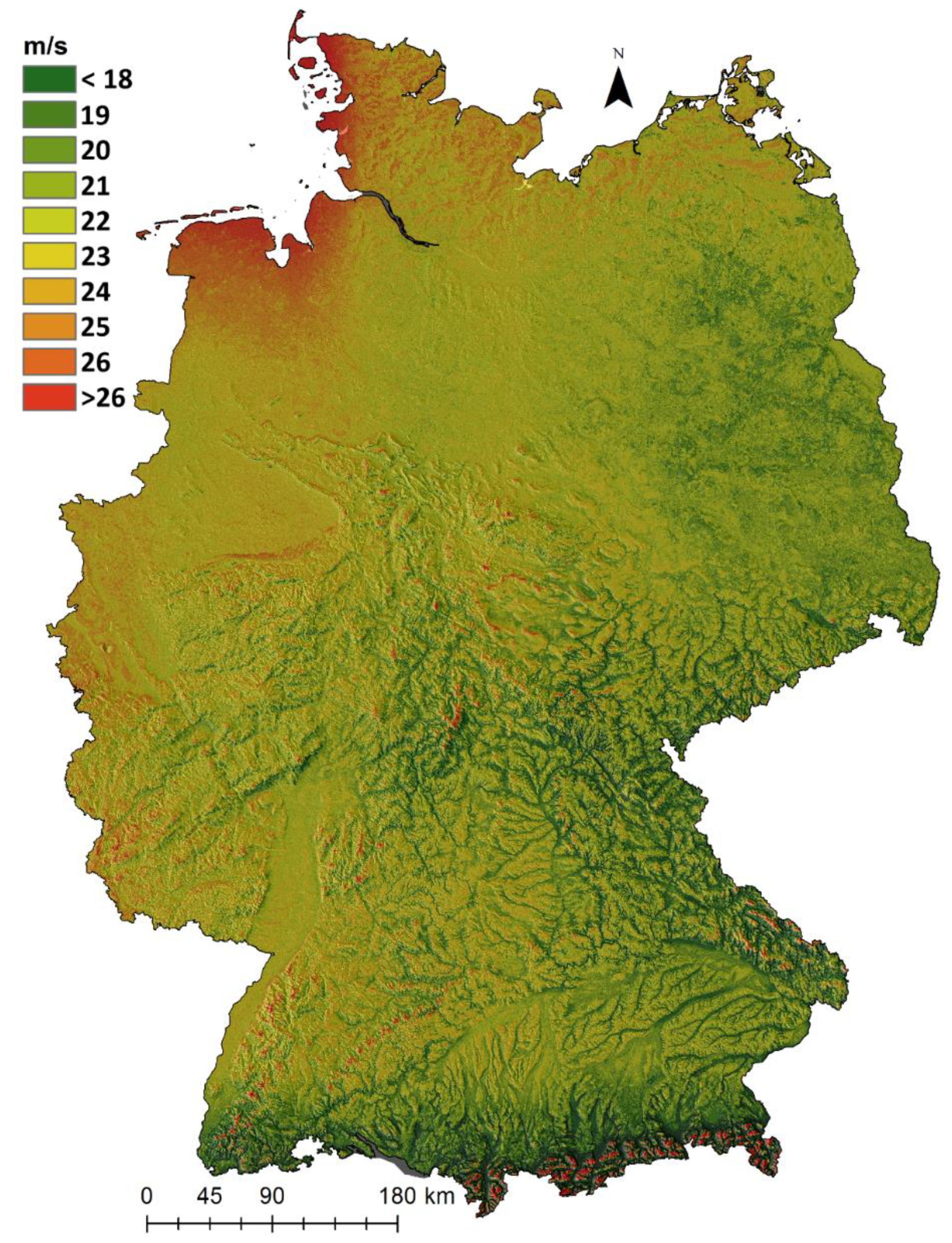
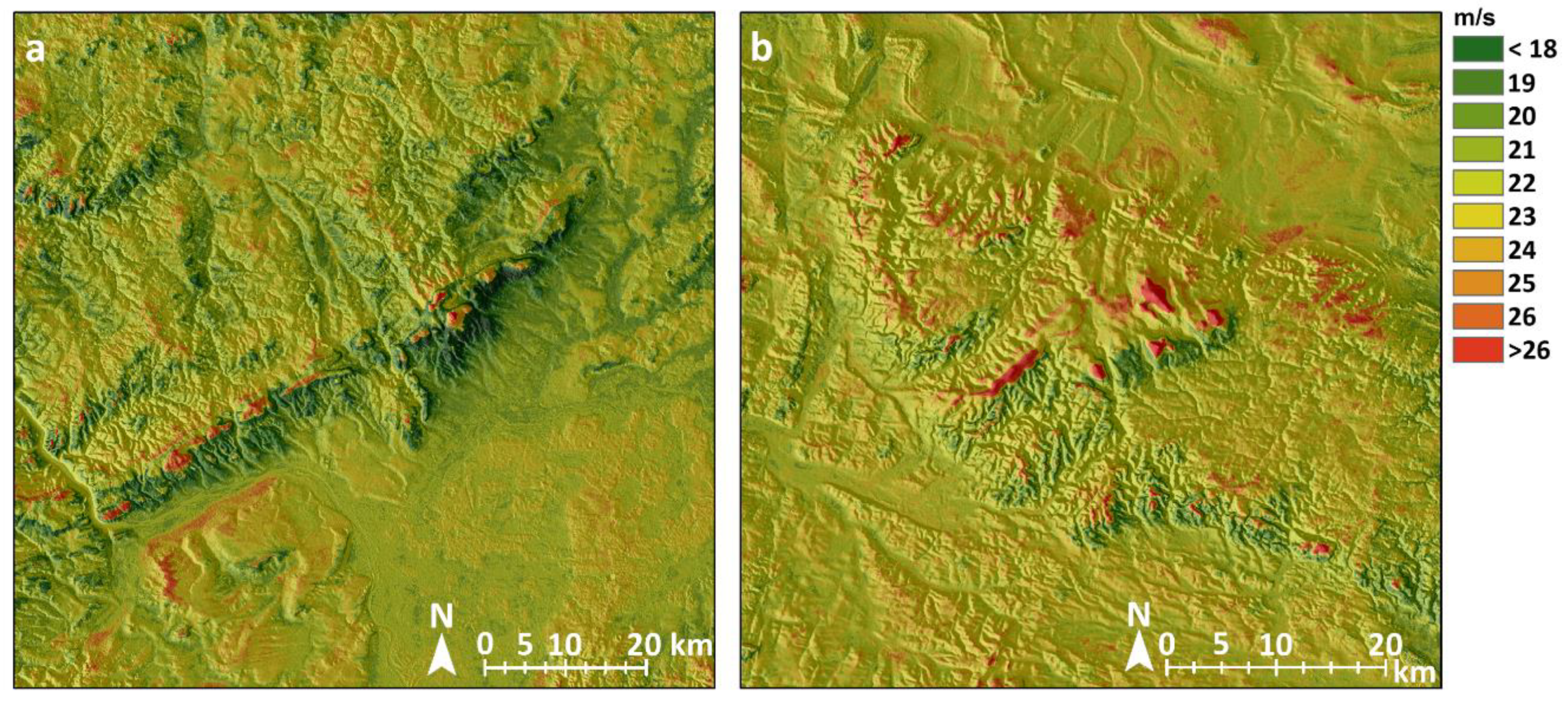
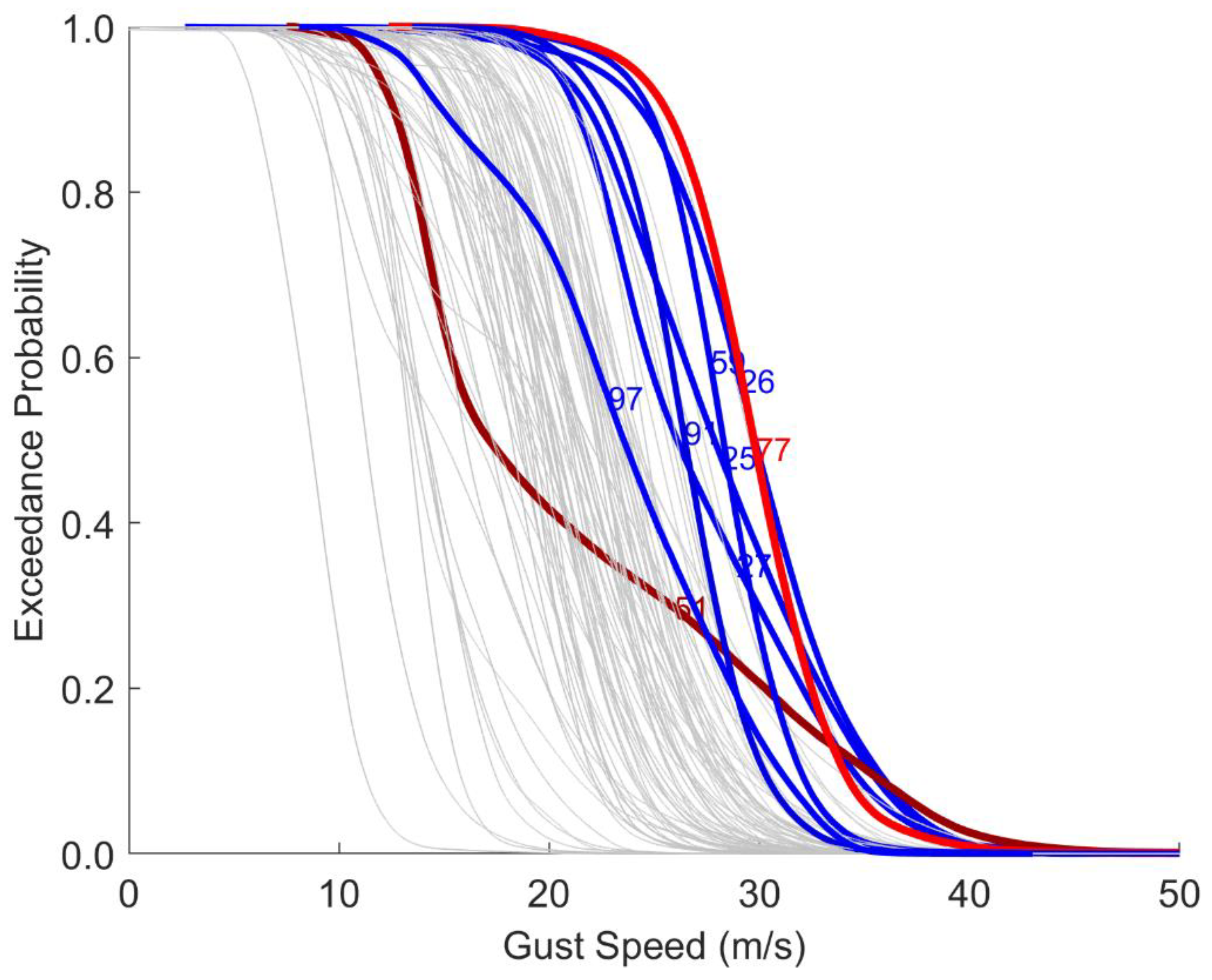
3.1. Median Gust Speed
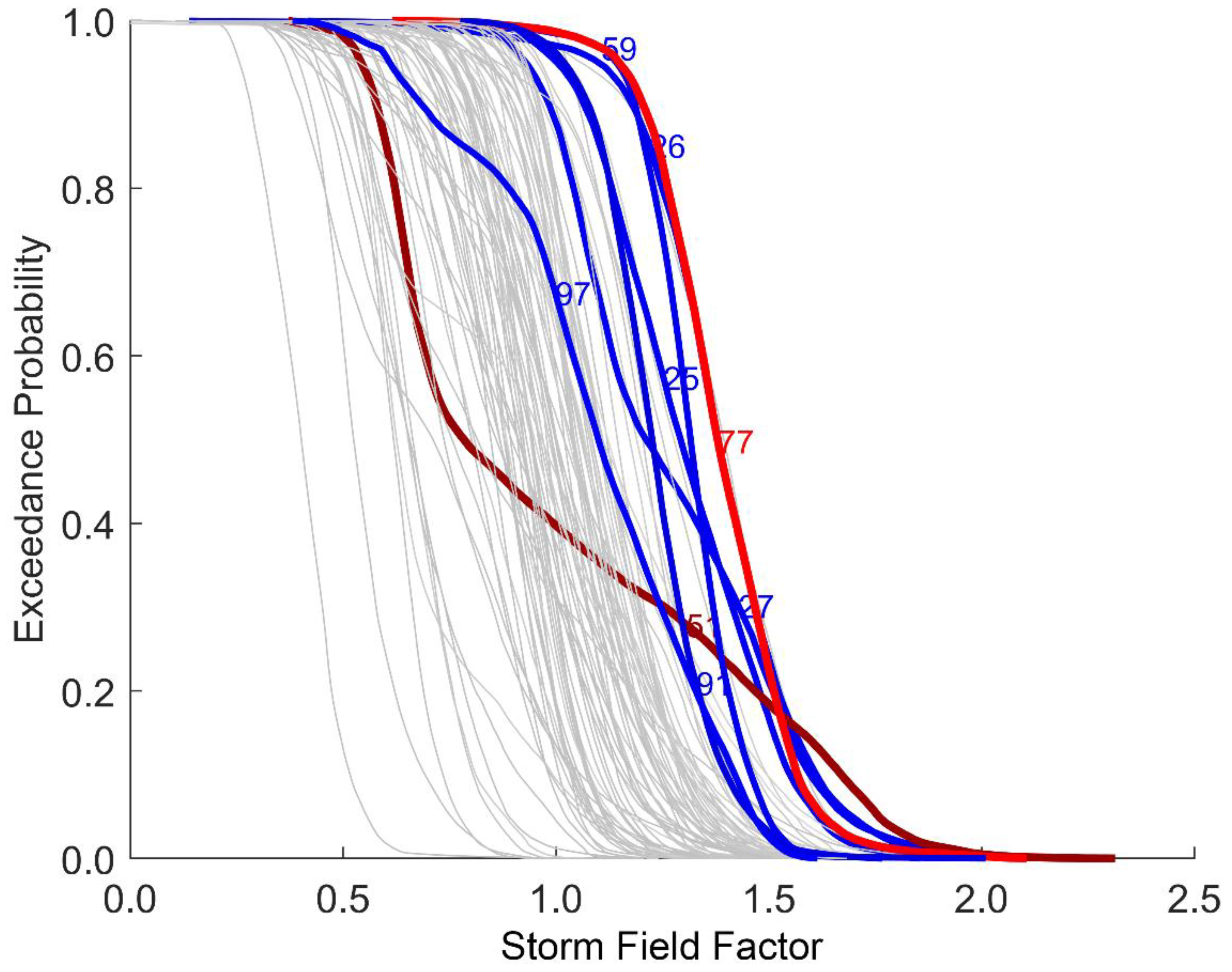
3.2. Storm Field Factor (STF)
3.3. Winter Storm-Related Gust Speed
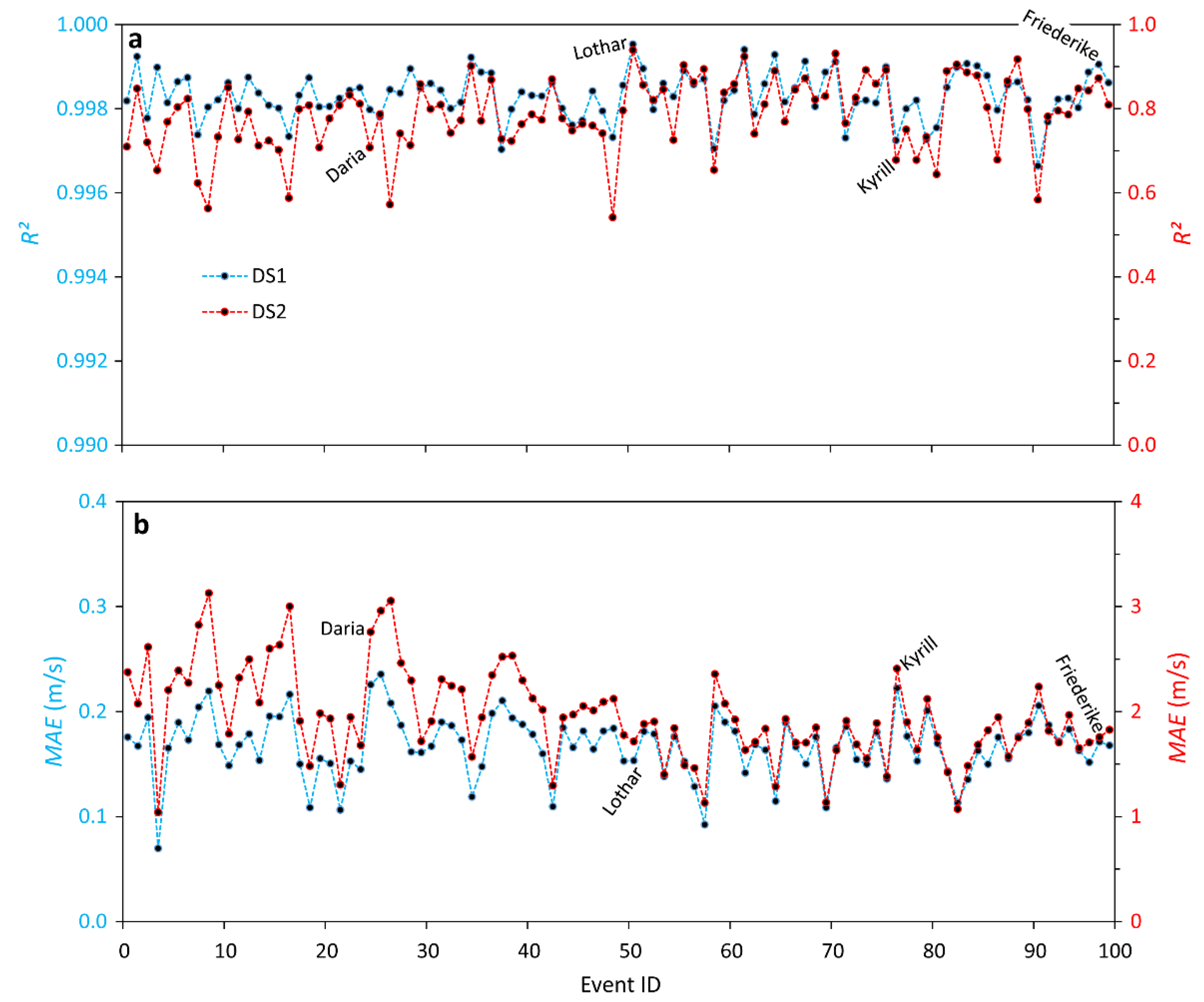
3.4. Model Comparison
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Munich RE NatCatSERVICE. Available online: https://natcatservice.munichre.com/ (accessed on 28 May 2019).
- Jung, C.; Schindler, D.; Buchholz, A.; Laible, J. Global Gust Climate Evaluation and Its Influence on Wind Turbines. Energies 2017, 10, 1474. [Google Scholar] [CrossRef]
- Hagen, M.; Bartenschlager, B.; Finke, U. Motion characteristics of thunderstorms in southern Germany. Meteorol. Appl. 1999, 6, 227–239. [Google Scholar] [CrossRef]
- Kunz, M. The skill of convective parameters and indices to predict isolated and severe thunderstorms. Nat. Hazards Earth Syst. Sci. 2007, 7, 327–342. [Google Scholar] [CrossRef]
- Kunz, M.; Sander, J.; Kottmeier, C.H. Recent trends of thunderstorm and hailstorm frequency and their relation to atmospheric characteristics in southwest Germany. Int. J. Climatol. 2009, 29, 2283–2297. [Google Scholar] [CrossRef]
- Pilorz, W.; Laskowski, I.; Łupikasza, E.; Taszarek, M. Wind Shear and the Strength of Severe Convective Phenomena—Preliminary Results from Poland in 2011–2015. Climate 2016, 4, 51. [Google Scholar] [CrossRef]
- Gregow, H.; Laaksonen, A.; Alper, M.E. Increasing large scale windstorm damage in Western, Central and Northern European forests, 1951–2010. Sci. Rep. 2017, 7, 46397. [Google Scholar] [CrossRef]
- Donat, M.G.; Leckebusch, G.C.; Pinto, J.G.; Ulbrich, U. Examination of wind storms over Central Europe with respect to circulation weather types and NAO phases. Int. J. Climatol. 2010, 30, 1289–1300. [Google Scholar] [CrossRef]
- Rasilla, D.; García-Codron, J.C.; Garmendia, C.; Herrera, S.; Rivas, V. Extreme Wave Storms and Atmospheric Variability at the Spanish Coast of the Bay of Biscay. Atmosphere 2018, 9, 316. [Google Scholar] [CrossRef]
- Basu, S.; Zhang, X.; Wang, Z. A Modeling Investigation of Northern Hemisphere Extratropical Cyclone Activity in Spring: The Linkage between Extreme Weather and Arctic Sea Ice Forcing. Climate 2019, 7, 25. [Google Scholar] [CrossRef]
- Durst, C.S. Wind speeds over short periods of time. Meteorol. Mag. 1960, 89, 181–186. [Google Scholar]
- Shanmuganathan, S.; Sallis, P. Data Mining Methods to Generate Severe Wind Gust Models. Atmosphere 2014, 5, 60–80. [Google Scholar] [CrossRef]
- Schelhaas, M.-J.; Nabuurs, G.-J.; Schuck, A. Natural disturbances in the European forests in the 19th and 20th centuries. Glob. Chang. Biol. 2003, 9, 1620–1633. [Google Scholar] [CrossRef]
- Schindler, D.; Grebhan, K.; Albrecht, A.; Schönborn, J.; Kohnle, U. GIS-based estimation of the winter storm damage probability in forests: A case study from Baden-Wuerttemberg (Southwest Germany). Int. J. Biometeorol. 2012, 56, 57–69. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D.; Albrecht, A.; Buchholz, A. The Role of Highly-Resolved Gust Speed in Simulations of Storm Damage in Forests at the Landscape Scale: A Case Study from Southwest Germany. Atmosphere 2016, 7, 7. [Google Scholar] [CrossRef]
- Valverde, L.J., Jr.; Convertino, M. Insurer Resilience in an Era of Climate Change and Extreme Weather: An Econometric Analysis. Climate 2019, 7, 55. [Google Scholar] [CrossRef]
- Hang, J.; Li, Y. Ventilation strategy and air change rates in idealized high-rise compact urban areas. Build. Environ. 2010, 45, 2754–2767. [Google Scholar] [CrossRef]
- Liu, L.; Wen, Y.; Liang, Y.; Zhang, F.; Yang, T. Extreme Weather Impacts on Inland Waterways Transport of Yangtze River. Atmosphere 2019, 10, 133. [Google Scholar] [CrossRef]
- Manasseh, R.; Middleton, J.H. The surface wind gust regime and aircraft operations at Sydney Airport. J. Wind Eng. Ind. Aerodyn. 1999, 79, 269–288. [Google Scholar] [CrossRef]
- Etienne, C.; Lehmann, A.; Goyette, S.; Lopez-Moreno, J.I.; Beniston, M. Spatial predictions of extreme wind speeds over Switzerland using generalized additive models. J. Appl. Meteorol. Climatol. 2010, 49, 1956–1970. [Google Scholar] [CrossRef]
- Augter, G.; Roos, M. Berechnung von Sturmintensitäten für Deutschland; Berichte des Deutschen Wetterdienstes; Deutscher Wetterdienst: Offenbach am Main, Germany, 2011; No. 236. (In German)
- Jung, C.; Schindler, D. Modelling monthly near-surface maximum daily gust speed distributions in Southwest Germany. Int. J. Climatol. 2016, 36, 4058–4070. [Google Scholar] [CrossRef]
- Schindler, D.; Jung, C.; Buchholz, A. Using highly resolved maximum gust speed as predictor for forest storm damage caused by the high-impact winter storm Lothar in Southwest Germany. Atmos. Sci. Lett. 2016, 17, 462–469. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Sensitivity analysis of the system of wind speed distributions. Energy Convers. Manag. 2018, 177, 376–384. [Google Scholar] [CrossRef]
- Jung, C. High Spatial Resolution Simulation of Annual Wind Energy Yield Using Near-Surface Wind Speed Time Series. Energies 2016, 9, 344. [Google Scholar] [CrossRef]
- Wan, H.; Wang, X.; Swail, V.R. Homogenization and trend analysis of Canadian near-surface wind speeds. J. Clim. 2010, 23, 1209–1225. [Google Scholar] [CrossRef]
- Walshaw, D. Getting the most from your extreme wind data: A step by step guide. J. Res. NIST 1994, 99, 399–411. [Google Scholar] [CrossRef]
- Wieringa, J. Does representative wind information exist? J. Wind Eng. Ind. Aerodyn. 1996, 65, 1–12. [Google Scholar] [CrossRef]
- Petersen, E.L.; Mortensen, N.G.; Landberg, L.; Højstrup, J.; Frank, H.P. Wind power meteorology. Part I: Climate and turbulence. Wind Energy 1998, 1, 25–45. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. Development of a statistical bivariate wind speed-wind shear model (WSWS) to quantify the height-dependent wind resource. Energy Convers. Manag. 2017, 149, 303–317. [Google Scholar] [CrossRef]
- CORINE Land Cover. Available online: https://land.copernicus.eu/pan-european/corine-land-cover (accessed on 28 May 2019).
- CDC (Climate Data Center). Available online: https://cdc.dwd.de/portal/ (accessed on 28 May 2019).
- Wang, X.L. Accounting for autocorrelation in detecting mean-shifts in climate data series using the penalized maximal t or F test. J. Appl. Meteorol. Climatol. 2008, 47, 2423–2444. [Google Scholar] [CrossRef]
- Wang, X.L. Penalized maximal F-test for detecting undocumented mean shifts without trend-change. J. Atmos. Ocean. Technol. 2008, 25, 368–384. [Google Scholar] [CrossRef]
- EU DEM. Available online: https://land.copernicus.eu/imagery-in-situ/eu-dem (accessed on 28 May 2019).
- Wilson, J.D. Determining a topex score. Scott. For. 1984, 38, 251–256. [Google Scholar]
- European Settlement Map. Available online: https://land.copernicus.eu/pan-european/GHSL (accessed on 28 May 2019).
- Silva, J.; Ribeiro, C.; Guedes, R. Roughness length classification of Corine Land Cover classes. In Proceedings of the European Wind Energy Conference, Milan, Italy, 7–10 May 2007. [Google Scholar]
- Friedman, J. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Van Heijst, D.; Potharst, R.; van Wezel, M. A support system for predicting eBay end prices. Decis. Support Syst. 2008, 44, 970–982. [Google Scholar] [CrossRef]
- Jung, C.; Schindler, D. 3D statistical mapping of Germany’s wind resource using WSWS. Energy Convers. Manag. 2018, 159, 96–108. [Google Scholar] [CrossRef]
- Wood, S.N. Thin-plate regression splines. J. R. Stat. Soc. Ser. B 2003, 65, 95–114. [Google Scholar] [CrossRef]
- Heneka, P.; Hofherr, T.; Ruck, B.; Kottmeier, C. Winter storm risk of residential structures—Model development and application to the German state of Baden-Württemberg. Nat. Hazards Earth Syst. Sci. 2006, 6, 721–733. [Google Scholar] [CrossRef]



| ID | Winter Storm | Duration | Losses (US$m) | ID | Winter Storm | Duration | Losses (US$m) |
|---|---|---|---|---|---|---|---|
| 1 | - | 3 January 81 | 51 | 50 | Winnie | 24–25 October 98 | 130 |
| 2 | - | 3 February 81 | 25 | 51 | Lothar | 26 December 99 | 2200 |
| 3 | - | 15–16 December 82 | 26 | 52 | Anatol | 3–4 December 99 | 410 |
| 4 | - | 9 October 82 | 13 | 53 | Lara | 4–6 February 99 | 140 |
| 5 | - | 10 December 82 | 8 | 54 | Ginger | 28 May 00 | 310 |
| 6 | - | 18 January 83 | 130 | 55 | Kerstin | 29–30 January 00 | 120 |
| 7 | - | 26–28 November 83 | 130 | 56 | Oratia | 29–30 October 00 | 93 |
| 8 | - | 1 February 83 | 110 | 57 | - | 10–11 December 00 | 15 |
| 9 | - | 22–24 November 84 | 220 | 58 | - | 9 November 01 | 31 |
| 10 | - | 3 January 84 | 58 | 59 | Jeanett | 26–28 October 02 | 1700 |
| 11 | - | 20 October 84 | 29 | 60 | Anna | 26–27 February 02 | 730 |
| 12 | - | 7–8 February 84 | 3 | 61 | Jennifer | 28–29 January 02 | 410 |
| 13 | - | 6 December 85 | 44 | 62 | Calvann | 2–3 January 03 | 360 |
| 14 | - | 6 November 85 | 29 | 63 | January | 21 December 03 | 120 |
| 15 | - | 19–20 December 86 | 430 | 64 | Hanne | 12–14 January 04 | 330 |
| 16 | - | 20–23 October86 | 430 | 65 | - | 17 December 04 | 320 |
| 17 | - | 19–20 January86 | 430 | 66 | Oralie | 20–21 March 04 | 270 |
| 18 | - | 12 November 87 | 9 | 67 | Queenie | 31 January–1 February 04 | 170 |
| 19 | - | 29 February–1 March 88 | 86 | 68 | Gerda | 12–13 January 04 | 140 |
| 20 | - | 7–8 October 88 | 26 | 69 | Cyrus | 15–16 December 05 | 530 |
| 21 | - | 8–9 October88 | 17 | 70 | Thorsten | 25–27 November 05 | 320 |
| 22 | - | 6 December 88 | 9 | 71 | Erwin | 8–9 January 05 | 160 |
| 23 | - | 19 December 88 | 5 | 72 | Ulf | 12–13 February 05 | 140 |
| 24 | - | 4–6 April 89 | 18 | 73 | Ingo | 21 January 05 | 74 |
| 25 | Daria | 25–26 January 90 | 1800 | 74 | Britta | 31 October–2 November 06 | 520 |
| 26 | Vivian | 25–27 February 90 | 1800 | 75 | - | 30 December 06–1 January 07 | 130 |
| 27 | Wiebke | 28 February–1 March 90 | 1800 | 76 | Vera | 8 December 06 | 67 |
| 28 | Herta | 3–4 February 90 | 900 | 77 | Kyrill | 18–19 January 07 | 5100 |
| 29 | Ottilie/Polly | 13–15 February 90 | 270 | 78 | Franz | 11–12 January 07 | 93 |
| 30 | Nora | 17–18 October 91 | 30 | 79 | Fridtijof | 2–3 December 07 | 51 |
| 31 | Undine | 6–9 January 91 | 7 | 80 | Emma | 1–2 March 08 | 840 |
| 32 | Ismene | 26 November 92 | 730 | 81 | Kristen | 12 March 08 | 250 |
| 33 | Coranna | 11–12 November 92 | 280 | 82 | Resi | 31 January–1 February 08 | 4 |
| 34 | - | 13 March 92 | 7 | 83 | Annette | 23–24 February 08 | 3 |
| 35 | Wilma | 26 October 92 | 4 | 84 | Quinten | 9–10 February 09 | 53 |
| 36 | - | 2–3 December 92 | 3 | 85 | Xynthia | 28 February 10 | 920 |
| 37 | Verena | 13–14 January 93 | 500 | 86 | Joachim | 16–17 December 11 | 200 |
| 38 | Barbara | 23–24 January 93 | 240 | 87 | Andrea | 5–6 January 12 | 240 |
| 39 | Quena | 8–9 December 93 | 200 | 88 | Ulli/Emil | 3 January 12 | 82 |
| 40 | Victoria | 19–21 December 93 | 160 | 89 | Christian | 27–29 October 13 | 830 |
| 41 | Agnes | 22–23 January 93 | 150 | 90 | Xaver | 5–7 December 13 | 260 |
| 42 | Lore | 27 January 94 | 520 | 91 | Niklas | 30 March–1 April 15 | 1200 |
| 43 | Grace | 4–5 November 95 | 7 | 92 | Elon/Felix | 8–11 January 15 | 260 |
| 44 | Sonja | 27–29 March 97 | 260 | 93 | Xavier | 5 October 17 | 500 |
| 45 | Daniela | 19–20 February 97 | 210 | 94 | Herwart | 29 October 17 | 290 |
| 46 | Gisela/Heidi | 25 February 97 | 100 | 95 | Sebastian | 13–14 September 17 | 160 |
| 47 | - | 13–14 February 97 | 78 | 96 | Egon | 12–13 January 17 | 120 |
| 48 | Xylia | 27–29 October 98 | 370 | 97 | Friederike | 18 January 18 | 1900 |
| 49 | - | 4–5 March 98 | 270 | 98 | Burglind | 3 January 18 | 240 |
| Symbol | Name | Sector (°) | Distance (m) | Data Source | Original Resolution |
|---|---|---|---|---|---|
| h | measuring height | - | - | DWD | - |
| lon | longitude | - | - | - | - |
| lat | latitude | - | - | - | - |
| ε | elevation | - | - | EU-DEM v.1 | 20 m × 20 m |
| η1000 | relative elevation | 1–360 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| η3000 | relative elevation | 1–360 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| η5000 | relative elevation | 1–360 | 5000 | EU-DEM v.1 | 20 m × 20 m |
| η7500 | relative elevation | 1–360 | 7500 | EU-DEM v.1 | 20 m × 20 m |
| ηn | relative elevation | 337.5–22.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηne | relative elevation | 22.5–67.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηe | relative elevation | 67.5–112.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηse | relative elevation | 112.5–157.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηs | relative elevation | 157.5–202.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηsw | relative elevation | 202.5–247.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηw | relative elevation | 247.5–292.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| ηnw | relative elevation | 292.5–337.4 | 3000 | EU-DEM v.1 | 20 m × 20 m |
| σn | sheltering | 337.5–22.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σne | sheltering | 22.5–67.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σe | sheltering | 67.5–112.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σse | sheltering | 112.5–157.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σs | sheltering | 157.5–202.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σsw | sheltering | 202.5–247.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σw | sheltering | 247.5–292.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σnw | sheltering | 292.5–337.4 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| σsum | sheltering | 1–360 | 1000 | EU-DEM v.1 | 20 m × 20 m |
| z0,25 | roughness length | 1–360 | 25 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,100 | roughness length | 1–360 | 100 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,200 | roughness length | 1–360 | 200 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,400 | roughness length | 1–360 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,n | roughness length | 337.5–22.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,ne | roughness length | 22.5–67.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,e | roughness length | 67.5–112.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,se | roughness length | 112.5–157.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,s | roughness length | 157.5–202.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,sw | roughness length | 202.5–247.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,w | roughness length | 247.5–292.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| z0,nw | roughness length | 292.5–337.4 | 400 | ESM 2012 R 2017 | 2.5 m × 2.5 m |
| Name | z0 (mm) |
|---|---|
| BU Buildings | 1600 |
| BU Area-Street Green NDVI | 100 |
| BU Area-Green Urban Atlas | 500 |
| BU Area-Green NDVI | 500 |
| BU Area-Streets | 100 |
| BU Area-Open Space | 1 |
| NBU Area-Street Green NDVI | 100 |
| NBU Area-Green NDVI | 750 |
| NBU Area-Streets | 100 |
| NBU Area-Open Space | 30 |
| Railways | 100 |
| Water | 1 |
| PVC | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | lon | lat | h | η5000 | ηsw | σne | z0,sw |
| 2 | lon | lat | h | η7500 | ηs | σsum | z0,400 |
| 3 | lon | lat | h | η7500 | ηs | σs | z0,sw |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, C.; Schindler, D. Historical Winter Storm Atlas for Germany (GeWiSA). Atmosphere 2019, 10, 387. https://doi.org/10.3390/atmos10070387
Jung C, Schindler D. Historical Winter Storm Atlas for Germany (GeWiSA). Atmosphere. 2019; 10(7):387. https://doi.org/10.3390/atmos10070387
Chicago/Turabian StyleJung, Christopher, and Dirk Schindler. 2019. "Historical Winter Storm Atlas for Germany (GeWiSA)" Atmosphere 10, no. 7: 387. https://doi.org/10.3390/atmos10070387
APA StyleJung, C., & Schindler, D. (2019). Historical Winter Storm Atlas for Germany (GeWiSA). Atmosphere, 10(7), 387. https://doi.org/10.3390/atmos10070387





