Weather Based Strawberry Yield Forecasts at Field Scale Using Statistical and Machine Learning Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Measurement Sensors
2.3. Strawberry Yield Data
2.4. Meteorological Data
2.5. Statistical Analysis
2.5.1. Correlation and Regression Analysis
2.5.2. Principal Component Analysis
2.6. Predictive Models
2.6.1. Predictive Principal Component Regression (PPCR)
2.6.2. Neural Network (NN)
2.6.3. Random Forest (RF)
2.6.4. Performance Strategies
3. Results and Discussion
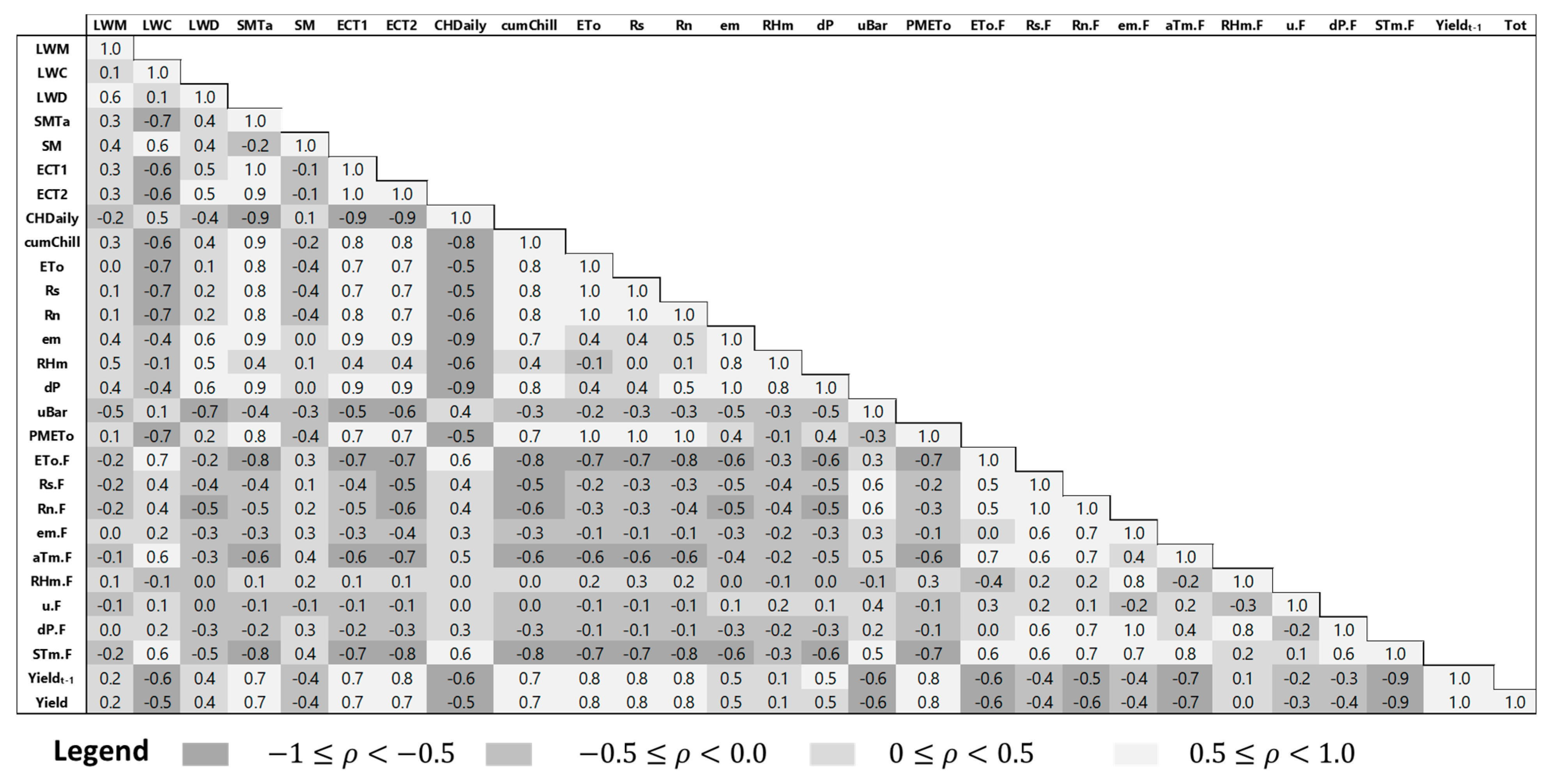
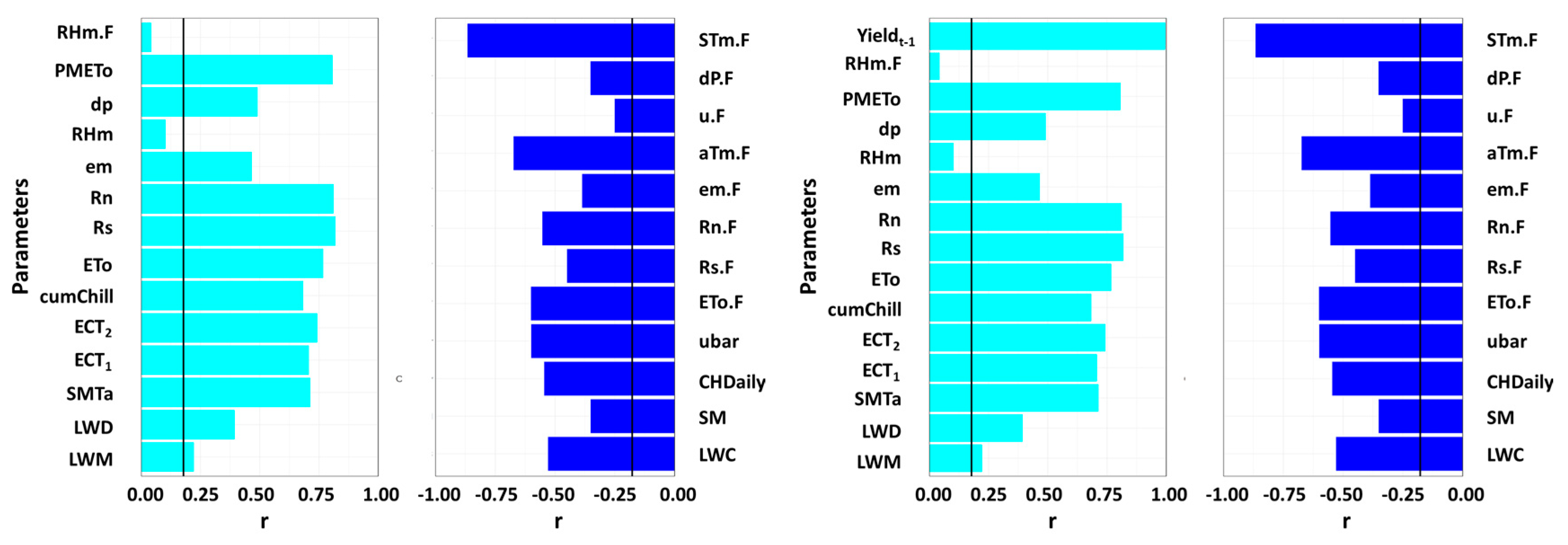
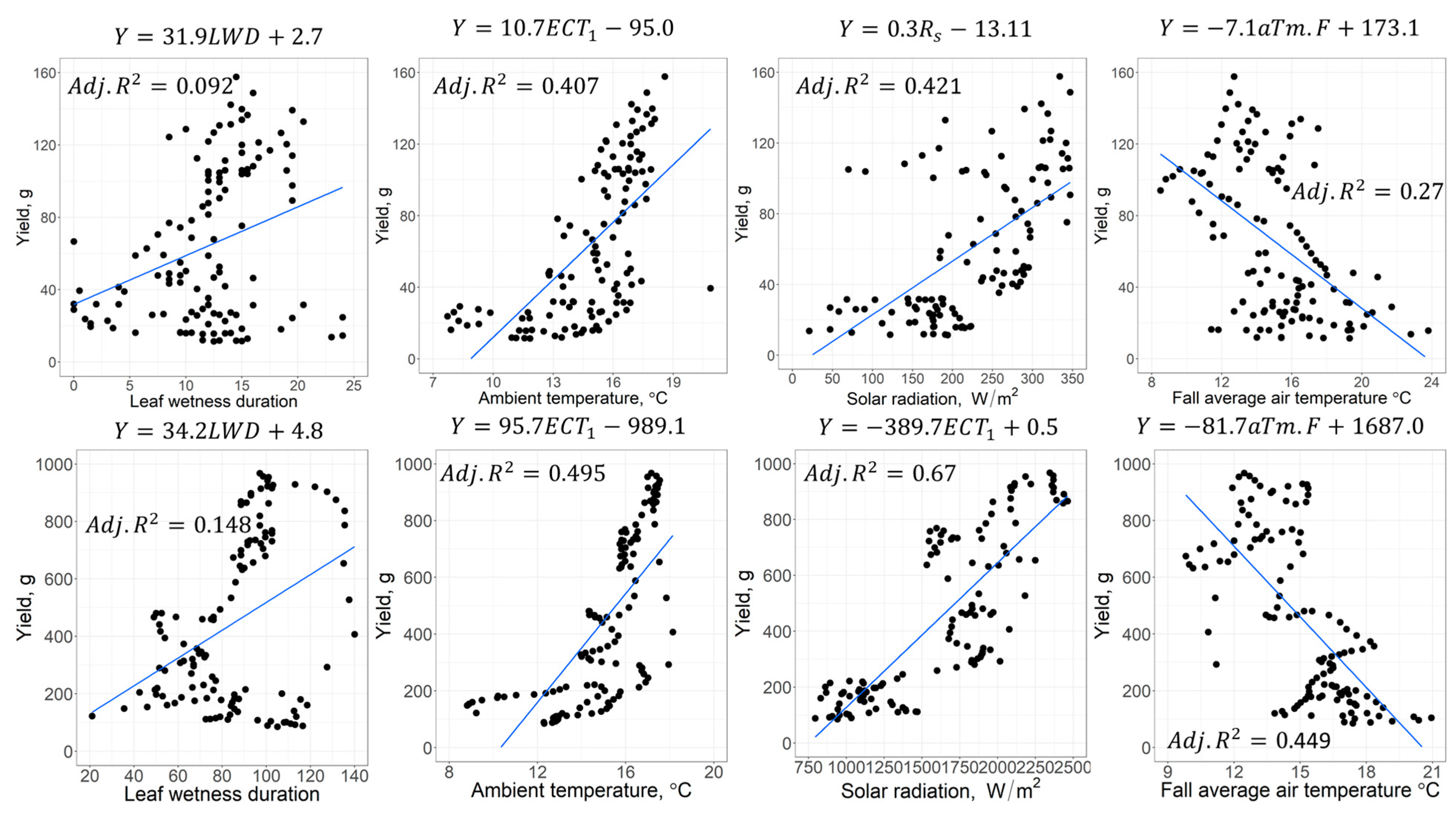
3.1. Statistical Analysis
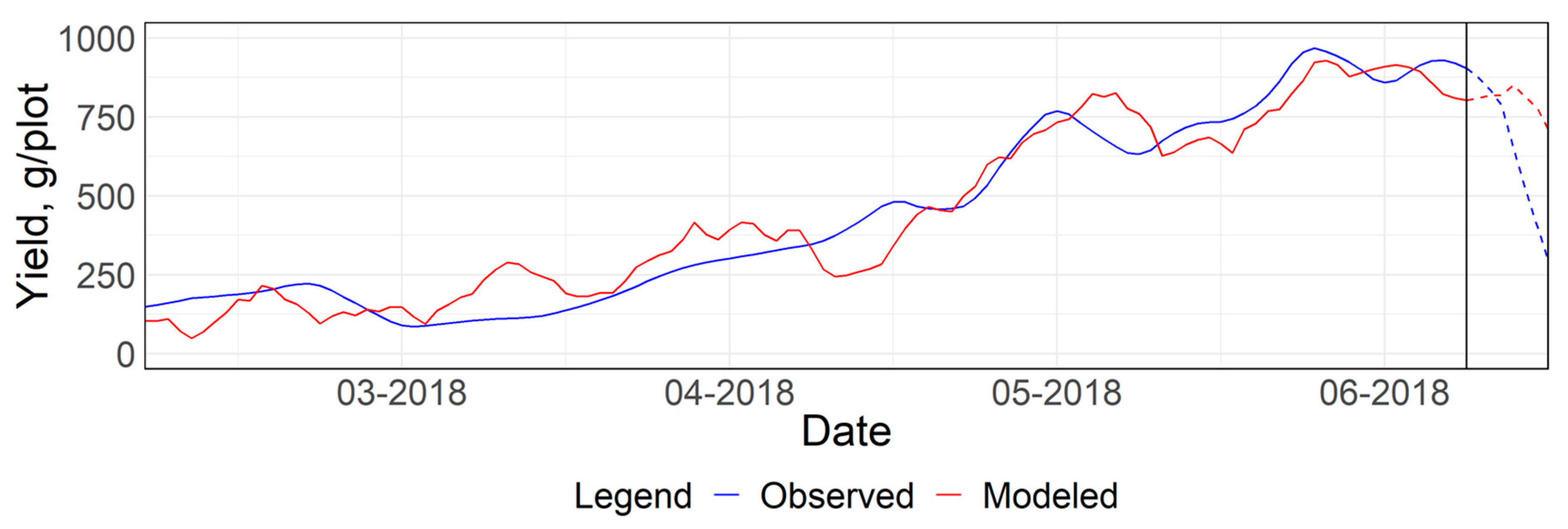
3.2. Weekly Prediction of Strawberry Yield
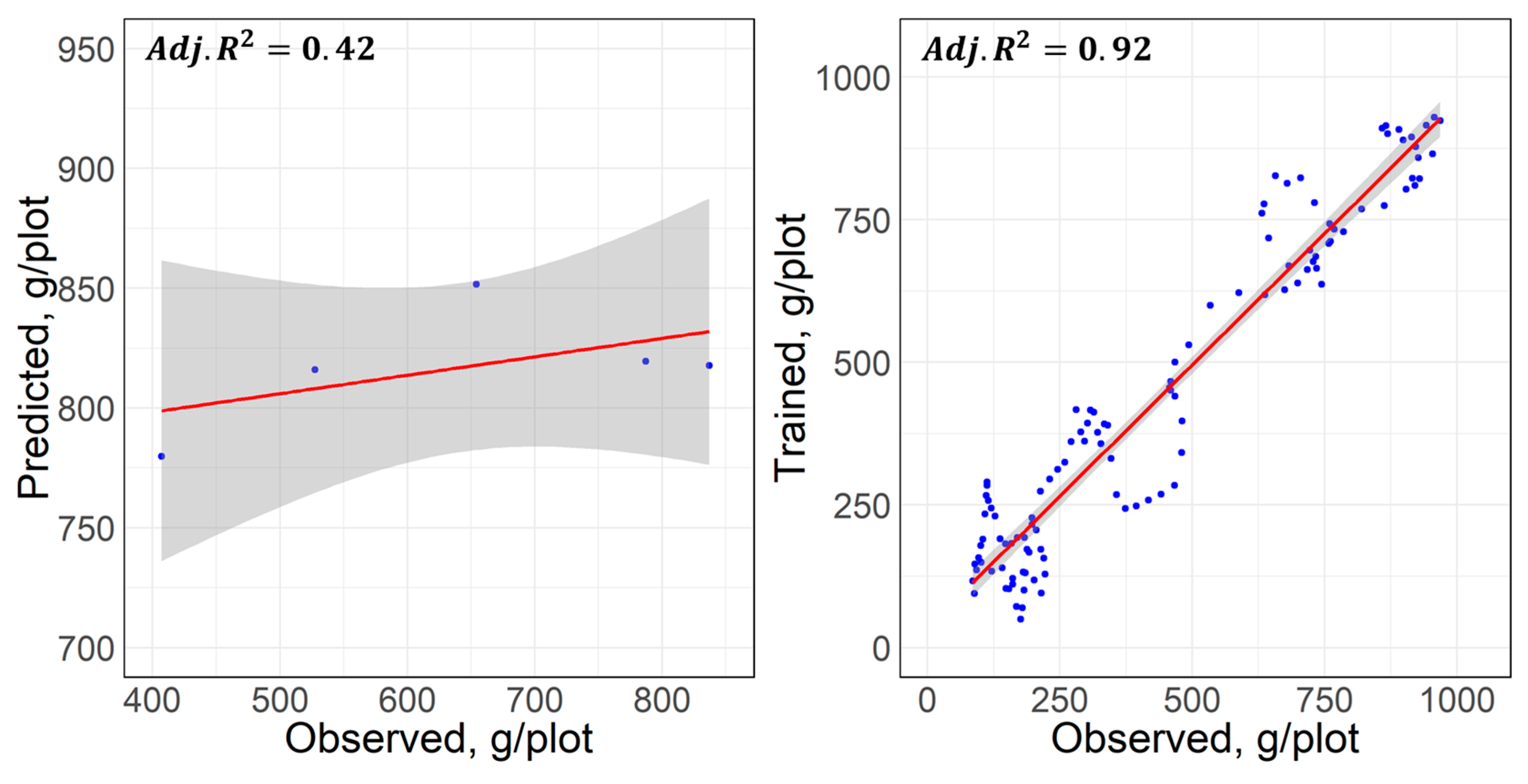
3.2.1. Predictive Principal Component Regression (PPCR)
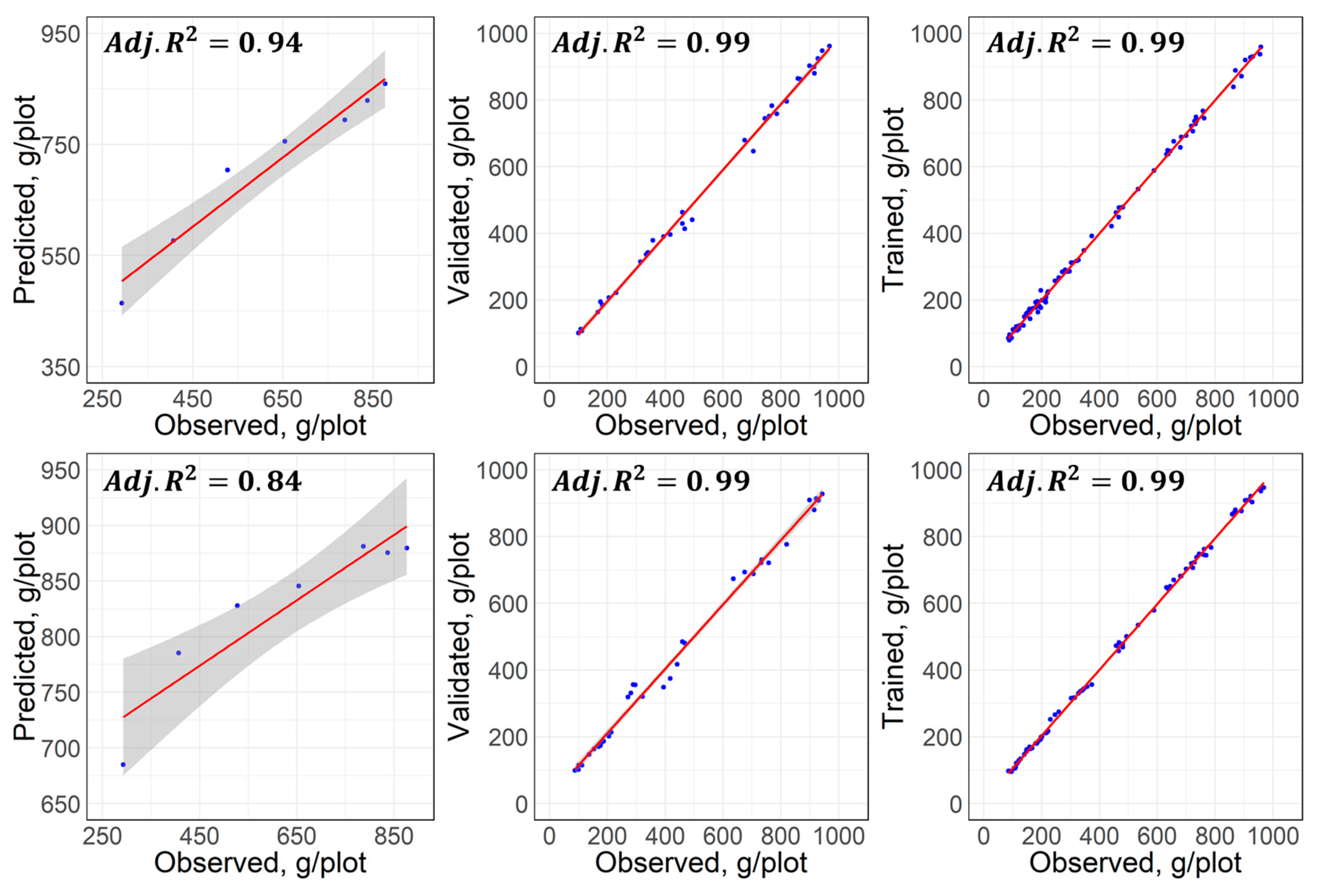
3.2.2. Machine Learning Approaches
4. Conclusions and Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Palencia, P.; Martínez, F.; Medina, J.J.; López-Medina, J. Strawberry yield efficiency and its correlation with temperature and solar radiation. Hortic. Bras. 2013, 31, 93–99. [Google Scholar] [CrossRef][Green Version]
- UCANR. Crop Profile for Strawberries in California. Available online: https://ucanr.edu/datastoreFiles/391-501.pdf (accessed on 1 April 2019).
- Pathak, T.B.; Dara, S.K.; Biscaro, A. Evaluating correlations and development of meteorology based yield forecasting model for strawberry. Adv. Meteorol. 2016, 2016. [Google Scholar] [CrossRef]
- CDFA. CDFA—Statistics. Available online: https://www.cdfa.ca.gov/statistics/ (accessed on 16 March 2019).
- USDS/NASS. USDA/NASS 2018 State Agriculture Overview for California. Available online: https://www.nass.usda.gov/Quick_Stats/Ag_Overview/stateOverview.php?state=CALIFORNIA (accessed on 6 April 2019).
- California Strawberry Commission. 2018 California Strawberry Acreage Survey Update; California Strawberry Commission: Watsonville, CA, USA, 2018. [Google Scholar]
- California Strawberry Commission. FARMING—California Strawberry Commission. Available online: https://www.calstrawberry.com/Portals/2/Reports/Industry%20Reports/Industry%20Fact%20Sheets/California%20Strawberry%20Farming%20Fact%20Sheet%202018.pdf?ver=2018-03-08-115600-790 (accessed on 5 April 2019).
- Pathak, T.; Maskey, M.; Dahlberg, J.; Kearns, F.; Bali, K.; Zaccaria, D. Climate change trends and impacts on California agriculture: A detailed review. Agronomy 2018, 8, 25. [Google Scholar] [CrossRef]
- Rieger, M. Introduction to Fruit Crops; CRC Press: Boca Raton, FL, USA, 2006; ISBN 1-4822-9805-8. [Google Scholar]
- Condori, B.; Fleisher, D.H.; Lewers, K.S. Relationship of strawberry yield with microclimate factors in open and covered raised-bed production. Trans. ASABE 2017, 60, 1511–1525. [Google Scholar] [CrossRef]
- Casierra-Posada, F.; Peña-Olmos, J.E.; Ulrichs, C. Basic growth analysis in strawberry plants (Fragaria sp.) exposed to different radiation environments. Agron. Colomb. 2012, 30, 25–33. [Google Scholar]
- Li, H.; Li, T.; Gordon, R.J.; Asiedu, S.K.; Hu, K. Strawberry plant fruiting efficiency and its correlation with solar irradiance, temperature, and reflectance water index variation. Environ. Exp. Bot. 2010, 68, 165–174. [Google Scholar] [CrossRef]
- Waister, P. Wind as a limitation on the growth and yield of strawberries. J. Hortic. Sci. 1972, 47, 411–418. [Google Scholar] [CrossRef]
- MacKerron, D. Wind damage to the surface of strawberry leaves. Ann. Bot. 1976, 40, 351–354. [Google Scholar] [CrossRef]
- Grace, J. 3. Plant response to wind. Agric. Ecosyst. Environ. 1988, 22, 71–88. [Google Scholar] [CrossRef]
- Lobell, D.; Cahill, K.; Field, C. Weather-based yield forecasts developed for 12 California crops. Calif. Agric. 2006, 60, 211–215. [Google Scholar] [CrossRef]
- Hansen, J.W. Integrating seasonal climate prediction and agricultural models for insights into agricultural practice. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 2037–2047. [Google Scholar] [CrossRef] [PubMed]
- Jones, J.W.; Hansen, J.W.; Royce, F.S.; Messina, C.D. Potential benefits of climate forecasting to agriculture. Agric. Ecosyst. Environ. 2000, 82, 169–184. [Google Scholar] [CrossRef]
- Newlands, N.K.; Zamar, D.S.; Kouadio, L.A.; Zhang, Y.; Chipanshi, A.; Potgieter, A.; Toure, S.; Hill, H.S. An integrated, probabilistic model for improved seasonal forecasting of agricultural crop yield under environmental uncertainty. Front. Environ. Sci. 2014, 2, 17. [Google Scholar] [CrossRef]
- Basso, B.; Cammarano, D.; Carfagna, E. Review of Crop Yield Forecasting Methods and Early Warning Systems. In Proceedings of the First Meeting of the Scientific Advisory Committee of the Global Strategy to Improve Agricultural and Rural Statistics, FAO Headquarters, Rome, Italy, 18–19 July 2013; pp. 18–19. [Google Scholar]
- Vangdal, E.; Meland, M.; Måge, F.; Døving, A. Prediction of fruit quality of plums (Prunus domestica L.). In Proceedings of the III International Symposium on Applications of Modelling as an Innovative Technology in the Agri-Food Chain, Leuven, Belgium, 29 May–2 June 2005; Volume MODEL-IT 674, pp. 613–617. [Google Scholar]
- Hoogenboom, G.; White, J.W.; Messina, C.D. From genome to crop: Integration through simulation modeling. Field Crops Res. 2004, 90, 145–163. [Google Scholar] [CrossRef]
- Døving, A.; Måge, F. Prediction of strawberry fruit yield. Acta Agric. Scand. 2001, 51, 35–42. [Google Scholar] [CrossRef]
- Khoshnevisan, B.; Rafiee, S.; Mousazadeh, H. Application of multi-layer adaptive neuro-fuzzy inference system for estimation of greenhouse strawberry yield. Measurement 2014, 47, 903–910. [Google Scholar] [CrossRef]
- Pathak, T.; Dara, S.K. Influence of Weather on Strawberry Crop and Development of a Yield Forecasting Model. Available online: https://ucanr.edu/blogs/strawberries-vegetables/index.cfm?start=13 (accessed on 26 April 2019).
- Liakos, K.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef]
- Lobell, D.B.; Burke, M.B. On the use of statistical models to predict crop yield responses to climate change. Agric. For. Meteorol. 2010, 150, 1443–1452. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.; Mouazen, A.M. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Drummond, S.T.; Sudduth, K.A.; Joshi, A.; Birrell, S.J.; Kitchen, N.R. Statistical and neural methods for site-specific yield prediction. Trans. ASAE 2003, 46, 5. [Google Scholar] [CrossRef]
- Fortin, J.G.; Anctil, F.; Parent, L.-É.; Bolinder, M.A. A neural network experiment on the site-specific simulation of potato tuber growth in Eastern Canada. Comput. Electron. Agric. 2010, 73, 126–132. [Google Scholar] [CrossRef]
- Effendi, Z.; Ramli, R.; Ghani, J.A.; Rahman, M. A Back Propagation Neural Networks for Grading Jatropha curcas Fruits Maturity. Am. J. Appl. Sci. 2010, 7, 390. [Google Scholar] [CrossRef][Green Version]
- Misaghi, F.; Dayyanidardashti, S.; Mohammadi, K.; Ehsani, M. Application of Artificial Neural Network and Geostatistical Methods in Analyzing Strawberry Yield Data; American Society of Agricultural and Biological Engineers: Minneapolis, MN, USA, 2004; p. 1. [Google Scholar]
- Liu, J.; Goering, C.; Tian, L. A neural network for setting target corn yields. Trans. ASAE 2001, 44, 705. [Google Scholar]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.-M.; Gerber, J.S.; Reddy, V.R. Random forests for global and regional crop yield predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef] [PubMed]
- Mutanga, O.; Adam, E.; Cho, M.A. High-density biomass estimation for wetland vegetation using WorldView-2 imagery and random forest regression algorithm. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 399–406. [Google Scholar] [CrossRef]
- Fukuda, S.; Spreer, W.; Yasunaga, E.; Yuge, K.; Sardsud, V.; Müller, J. Random Forests modeling for the estimation of mango (Mangifera indica L. cv. Chok Anan) fruit yields under different irrigation regimes. Agric. Water Manag. 2013, 116, 142–150. [Google Scholar] [CrossRef]
- Lee, M.; Monteiro, A.; Barclay, A.; Marcar, J.; Miteva-Neagu, M.; Parker, J. A framework for predicting soft-fruit yields and phenology using embedded, networked microsensors, coupled weather models and machine-learning techniques. BiorXiv 2019. [Google Scholar] [CrossRef]
- Leaf Wetness Sensor from Decagon Devices: Campbell Update 1st. Available online: https://www.campbellsci.com/leaf-wetness-article (accessed on 7 April 2019).
- Meter PHYTOS 31. Available online: http://library.metergroup.com/Manuals/20434_PHYTOS31_Manual_Web.pdf (accessed on 4 July 2019).
- Kim, K.; Gleason, M.; Taylor, S. Forecasting site-specific leaf wetness duration for input to disease-warning systems. Plant Dis. 2006, 90, 650–656. [Google Scholar] [CrossRef]
- Sentelhas, P.; Monteiro, J.; Gillespie, T. Electronic leaf wetness duration sensor: Why it should be painted. Int. J. Biometeorol. 2004, 48, 202–205. [Google Scholar] [CrossRef]
- METER. Legacy Soil Moisture Sensors | METER. Available online: https://www.metergroup.com/environment/articles/meter-legacy-soil-moisture-sensors/ (accessed on 17 June 2019).
- Bolda, M. Chilling Requirements in California Strawberries. Available online: https://ucanr.edu/blogs/blogcore/postdetail.cfm?postnum=722 (accessed on 30 April 2019).
- ECH2O 5TM | Soil Moisture and Temperature Sensor | METER Environment. Available online: https://www.metergroup.com/environment/products/ech2o-5tm-soil-moisture/ (accessed on 7 April 2019).
- California Farms California Strawberries, Strawberry Fields, Crops and Events. Available online: http://www.seecalifornia.com/farms/california-strawberries.html (accessed on 7 April 2019).
- Snyder, R.; Spano, D.; Pawu, K. Surface renewal analysis for sensible and latent heat flux density. Bound. Layer Meteorol. 1996, 77, 249–266. [Google Scholar] [CrossRef]
- Marino, G.; Zaccaria, D.; Snyder, R.L.; Lagos, O.; Lampinen, B.D.; Ferguson, L.; Grattan, S.R.; Little, C.; Shapiro, K.; Maskey, M.L. Actual Evapotranspiration and Tree Performance of Mature Micro-Irrigated Pistachio Orchards Grown on Saline-Sodic Soils in the San Joaquin Valley of California. Agriculture 2019, 9, 76. [Google Scholar] [CrossRef]
- CIMIS, California Irrigation Mangagement Information System; Department of Water Resources: Sacramento, CA, USA, 1982. Available online: https://cimis.water.ca.gov/ (accessed on 7 April 2019).
- Becker, R.; Chambers, J.; Wilks, A. The New S Language; Wadsworth & Brooks/Cole; Pacific: Wisconsin, IL, USA, 1988. [Google Scholar]
- Sellam, V.; Poovammal, E. Prediction of crop yield using regression analysis. Indian J. Sci. Technol. 2016, 9, 1–5. [Google Scholar] [CrossRef]
- Jackson, J.E. A User’s Guide to Principal Components; John Willey Sons Inc.: New York, NY, USA, 1991; p. 40. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Compiting: Vienna, Austria, 2018. [Google Scholar]
- Li, A.; Liang, S.; Wang, A.; Qin, J. Estimating crop yield from multi-temporal satellite data using multivariate regression and neural network techniques. Photogramm. Eng. Remote Sens. 2007, 73, 1149–1157. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The Rprop Algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; Volume 1993, pp. 586–591. [Google Scholar]
- Günther, F.; Fritsch, S. Neuralnet: Training of neural networks. R J. 2010, 2, 30–38. [Google Scholar] [CrossRef]
- Mendes, C.; da Silva Magalhes, R.; Esquerre, K.; Queiroz, L.M. Artificial neural network modeling for predicting organic matter in a full-scale up-flow anaerobic sludge blanket (UASB) reactor. Environ. Model. Assess. 2015, 20, 625–635. [Google Scholar] [CrossRef]
- Manzini, N. Single Hidden Layer Neural Network. Available online: https://www.nicolamanzini.com/single-hidden-layer-neural-network/ (accessed on 8 April 2019).
- Chan, M.-C.; Wong, C.-C.; Lam, C.-C. Financial Time Series Forecasting by Neural Network Using Conjugate Gradient Learning Algorithm and Multiple Linear Regression Weight Initialization. In Computing in Economics and Finance; The Hong Kong Polytechnic University: Kowloon, Hong Kong, 2000; Volume 61, pp. 326–342. [Google Scholar]
- Hayashi, Y.; Sakata, M.; Gallant, S.I. Multi-Layer Versus Single-Layer Neural Networks and An Application to Reading Hand-Stamped Characters; Springer: Dordrecht, the Netherlands, 1990; pp. 781–784. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the thirteenth international conference on artificial intelligence and statistics, Sardinia, Italy, 13–15 May 2010; 2010; pp. 249–256. [Google Scholar]
- Bergstra, J.; Desjardins, G.; Lamblin, P.; Bengio, Y. Quadratic Polynomials Learn Better Image Features (Technical Report 1337); Département d’Informatique et de Recherche Opérationnelle, Université de Montréal: Montréal, QC, Canada, 2009. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Everingham, Y.; Sexton, J.; Skocaj, D.; Inman-Bamber, G. Accurate prediction of sugarcane yield using a random forest algorithm. Agron. Sustain. Dev. 2016, 36, 27. [Google Scholar] [CrossRef]
- Crane-Droesch, A. Machine learning methods for crop yield prediction and climate change impact assessment in agriculture. Environ. Res. Lett. 2018, 13, 114003. [Google Scholar] [CrossRef]
- Narasimhamurthy, V.; Kumar, P. Rice Crop Yield Forecasting Using Random Forest Algorithm. Int. J. Res. Appl. Sci. Eng. Technol. IJRASET 2017, 5, 1220–1225. [Google Scholar] [CrossRef]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? Springer: Berlin, Germany, 2012; pp. 154–168. [Google Scholar]
- RColorBrewer, S.; Liaw, M.A. Package ‘Randomforest’; University of California, Berkeley: Berkeley, CA, USA, 2018. [Google Scholar]
- Khanh, P.D. Caret Practice. Available online: https://rpubs.com/phamdinhkhanh/389752 (accessed on 25 March 2019).
- Liaw, A.; Wiener, M. Classification and regression by random forest, R News, vol. 2/3, 18–22. R News 2002, 2, 18–22. [Google Scholar]
- Aly, M. What Is the Difference between Random Search and Grid Search for Hyperparameter Optimization?—Quora. Available online: https://www.quora.com/What-is-the-difference-between-random-search-and-grid-search-for-hyperparameter-optimization (accessed on 9 April 2019).
- Galili, T.; Meilijson, I. Splitting matters: How monotone transformation of predictor variables may improve the predictions of decision tree models. arXiv 2016, arXiv:161104561. [Google Scholar]

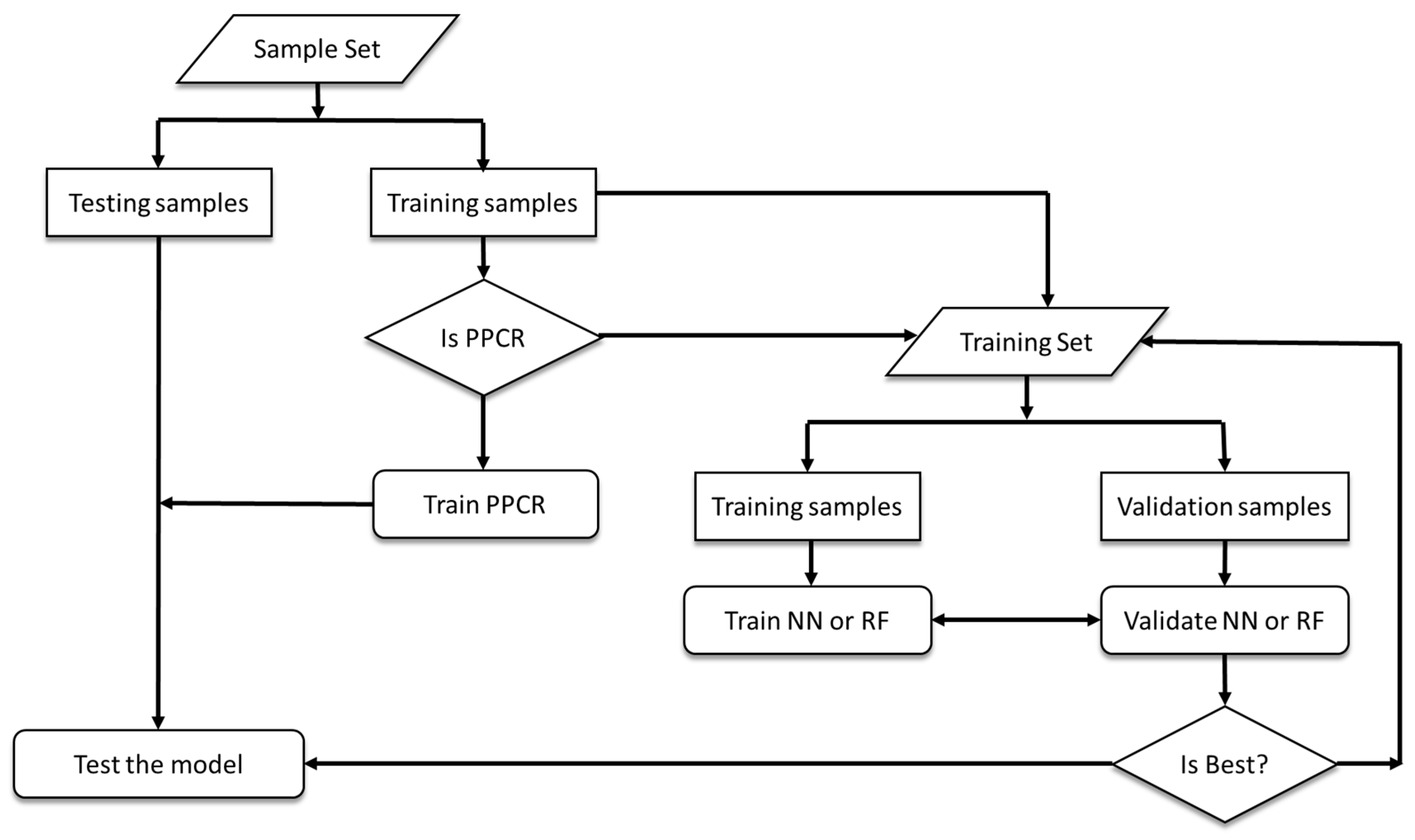
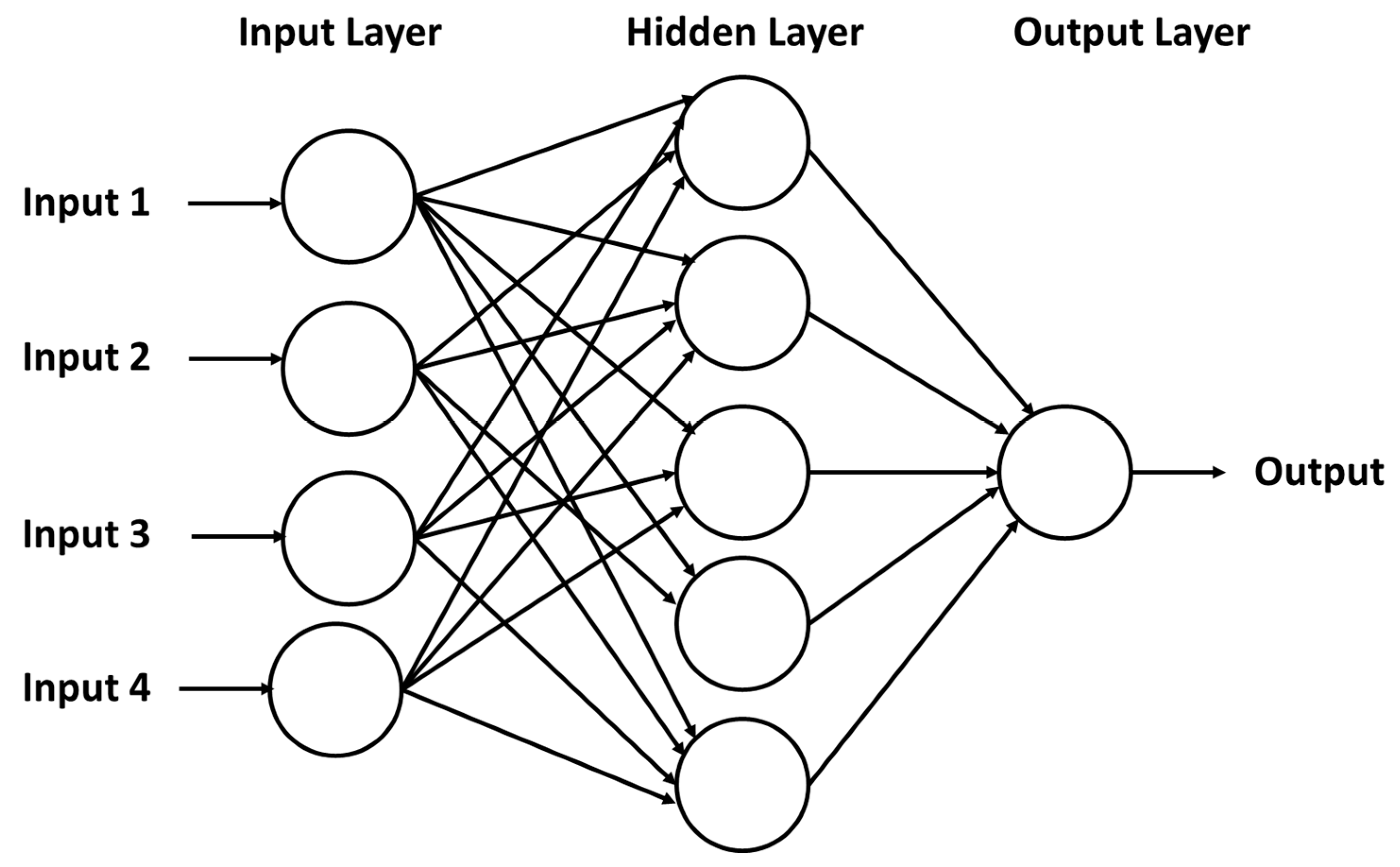


| Neural Network (NN) | Random Forest (RF) |
|---|---|
| layers: 3 (input, hidden, & neurons) | mtry: varied from to 27 |
| hidden neurons: half of the total parameters | where is a number of available predictors |
| activation function: logistic, hyperbolic tangent and softmax function error function: logistic function | |
| algorithm: resilient backpropagation | ntree: 100 to 500 with increment in 25 trees |
| learning rate: 0.01 | giving 17 scenarios |
| thresholds: 0.05 | |
| stepmax: 106 | |
| maximum seed = 500 | seed: 100 |
| Statistics | Sensor 1 | Sensor 2 | Temperature | Soil Moisture Content | ||||
|---|---|---|---|---|---|---|---|---|
| Count | Minutes | Count | Minutes | Ambient | Canopy | Soil | ||
| Minimum | 360 | 0 | 436 | 0 | −2 | −1 | 6 | 0.11 |
| Average | 450 | 26 | 463 | 55 | 15 | 14 | 17 | 0.13 |
| Maximum | 961 | 1960 | 863 | 1998 | 33 | 30 | 32 | 0.32 |
| Id | Parameters | Units | Notation | Daily | Moving Weekly |
|---|---|---|---|---|---|
| 1 | Average leaf wetness minutes | minutes | LWM | 0.004 | 0.041 |
| 2 | Average leaf wetness count | LWC | 0.120 | 0.274 | |
| 3 | Average leaf wetness duration | LWD | 0.092 | 0.148 | |
| 4 | Ambient temperature | °C | ECT1 | 0.460 | 0.505 |
| 5 | Canopy temperature | °C | ECT2 | 0.030 | 0.116 |
| 6 | Soil temperature | °C | SMTa | 0.407 | 0.495 |
| 7 | Volumetric soil moisture | m3/m3 | SM | 0.417 | 0.547 |
| 8 | Daily chill hours | hours | CHDaily | 0.189 | 0.292 |
| 9 | Cumulated chill hours | hours | cumChill | 0.431 | 0.462 |
| 10 | Reference evapotranspiration | mm | ETo | 0.338 | 0.585 |
| 11 | Solar Radiation | Wm-2 | Rs | 0.421 | 0.667 |
| 12 | Net Radiation | Wm-2 | Rn | 0.439 | 0.656 |
| 13 | Average vapor pressure | kPa | em | 0.134 | 0.210 |
| 14 | Average relative humidity | % | RHm | 0.000 | 0.002 |
| 15 | Dew point | °C | dP | 0.157 | 0.234 |
| 16 | Average wind speed | ms-1 | uBar | 0.261 | 0.354 |
| 17 | Penmann-Montieth Evapotranspiration | mm | PMETo | 0.384 | 0.648 |
| 18 | Fall reference evapotranspiration | mm | ETo.F | 0.244 | 0.356 |
| 19 | Fall solar radiation | Wm-2 | Rs.F | 0.129 | 0.196 |
| 20 | Fall net radiation | Wm-2 | Rn.F | 0.242 | 0.300 |
| 21 | Fall average vapor pressure | kPa | em.F | 0.084 | 0.143 |
| 22 | Fall average air temperature | °C | aTm.F | 0.270 | 0.449 |
| 23 | Fall average relative humidity | % | RHm.F | –0.005 | –0.006 |
| 24 | Fall average wind speed | ms-1 | u.F | 0.020 | 0.055 |
| 25 | Fall dew point | °C | dP.F | 0.071 | 0.116 |
| 26 | Fall average soil temperature | °C | STm.F | 0.739 | 0.748 |
| Data Set | Statistics | Predictive model | ||
|---|---|---|---|---|
| PPCR | NN | RF | ||
| Training | RMSE, g | 81.83 | 11.47 | 9.87 |
| Adjusted | 0.92 | 0.99 | 0.99 | |
| EF, % | 16.10 | 2.20 | 1.74 | |
| Validation | RMSE, g | 20.85 | 27.49 | |
| Adjusted | 0.99 | 0.99 | ||
| EF, % | 1.43 | 2.72 | ||
| Testing | RMSE, g | 250.90 | 119.58 | 249.07 |
| Adjusted | 0.51 | 0.95 | 0.84 | |
| EF, % | 30.20 | 15.49 | 29.27 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maskey, M.L.; Pathak, T.B.; Dara, S.K. Weather Based Strawberry Yield Forecasts at Field Scale Using Statistical and Machine Learning Models. Atmosphere 2019, 10, 378. https://doi.org/10.3390/atmos10070378
Maskey ML, Pathak TB, Dara SK. Weather Based Strawberry Yield Forecasts at Field Scale Using Statistical and Machine Learning Models. Atmosphere. 2019; 10(7):378. https://doi.org/10.3390/atmos10070378
Chicago/Turabian StyleMaskey, Mahesh L., Tapan B Pathak, and Surendra K. Dara. 2019. "Weather Based Strawberry Yield Forecasts at Field Scale Using Statistical and Machine Learning Models" Atmosphere 10, no. 7: 378. https://doi.org/10.3390/atmos10070378
APA StyleMaskey, M. L., Pathak, T. B., & Dara, S. K. (2019). Weather Based Strawberry Yield Forecasts at Field Scale Using Statistical and Machine Learning Models. Atmosphere, 10(7), 378. https://doi.org/10.3390/atmos10070378






