Py4CAtS—PYthon for Computational ATmospheric Spectroscopy
Abstract
1. Introduction
2. Theory and Methods
2.1. Molecular Absorption and Radiative Transfer
2.2. Numerics
2.2.1. Lbl Molecular Absorption Cross Sections: Multigrid Voigt Function
2.2.2. Integration of the Beer and Schwarzschild Equations
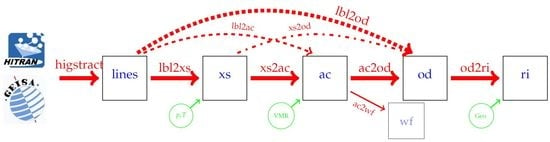
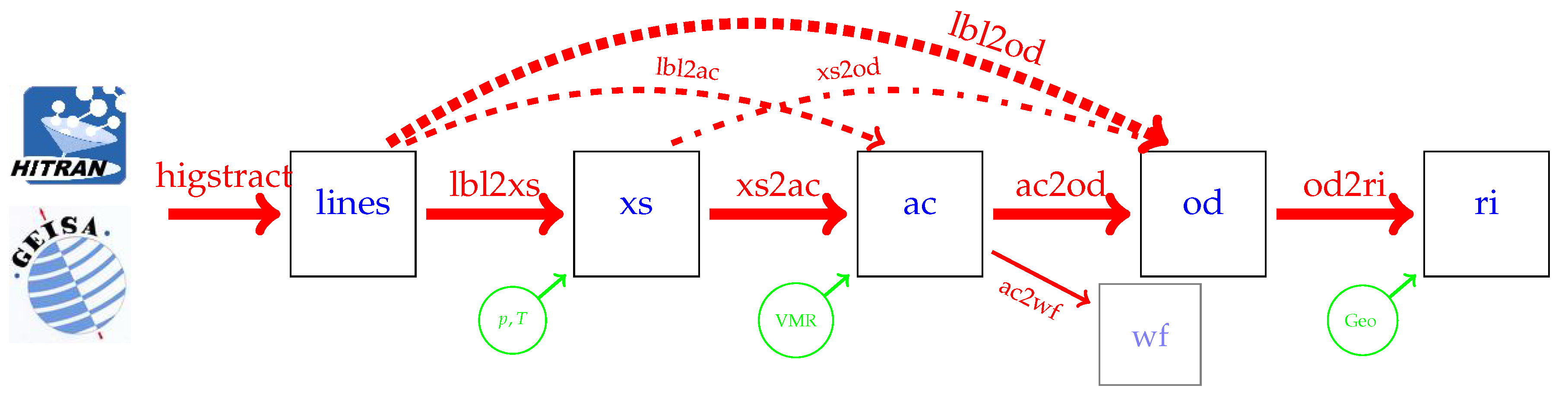
3. The Package: Usage and Implementation
- higstract: extract (select) lines of relevant molecules in the spectral range of interest;
- lbl2xs: compute lbl cross sections for given pressure(s) and temperature(s): Equation (1);
- xs2ac: multiply cross sections with number densities and sum over all molecules: Equation (6);
- ac2od: integrate absorption coefficients along the line-of-sight through the atmosphere to the vertical optical depth (7);
3.1. Running Py4CAtS in the Classical Console
- lbl2ac compute lbl cross sections and combine to absorption coefficients;
- lbl2od compute lbl cross sections and absorption coefficients, then integrate to optical depth.
- xs2od multiply cross sections with densities, sum over molecules, and integrate to optical depth.
3.2. Py4CAtS Used within the (I)Python and Jupyter Shell
3.2.1. Atmospheric Data
3.2.2. Line Data
3.2.3. Cross Sections
3.2.4. Absorption Coefficients
3.2.5. Optical Depths
3.2.6. Weighting Functions
3.2.7. Radiance/Intensity
3.2.8. Shortcuts
4. Discussion
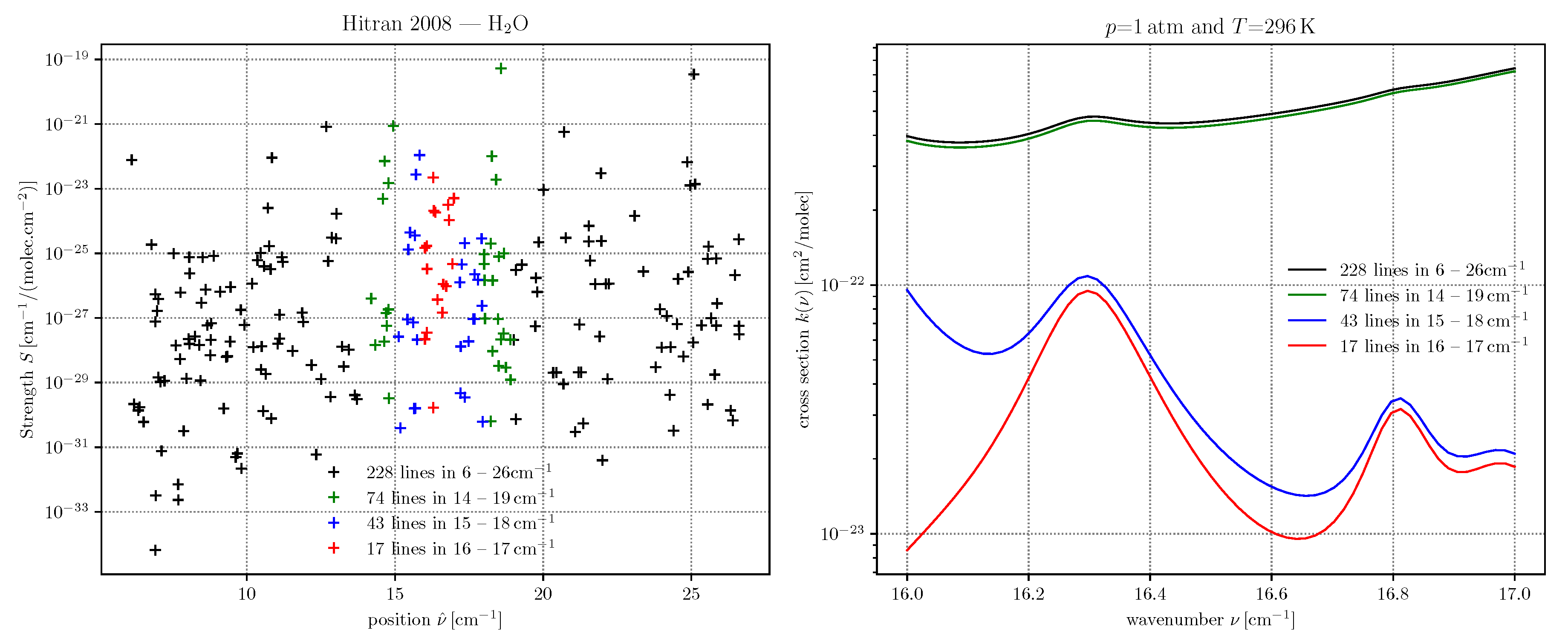
4.1. Selection of Spectral Range, Contributions from Line Wings
4.2. Optical Depths, Transmissions, and Weighting Functions for a Horizontal View
4.3. Arbitrary Observer Positions
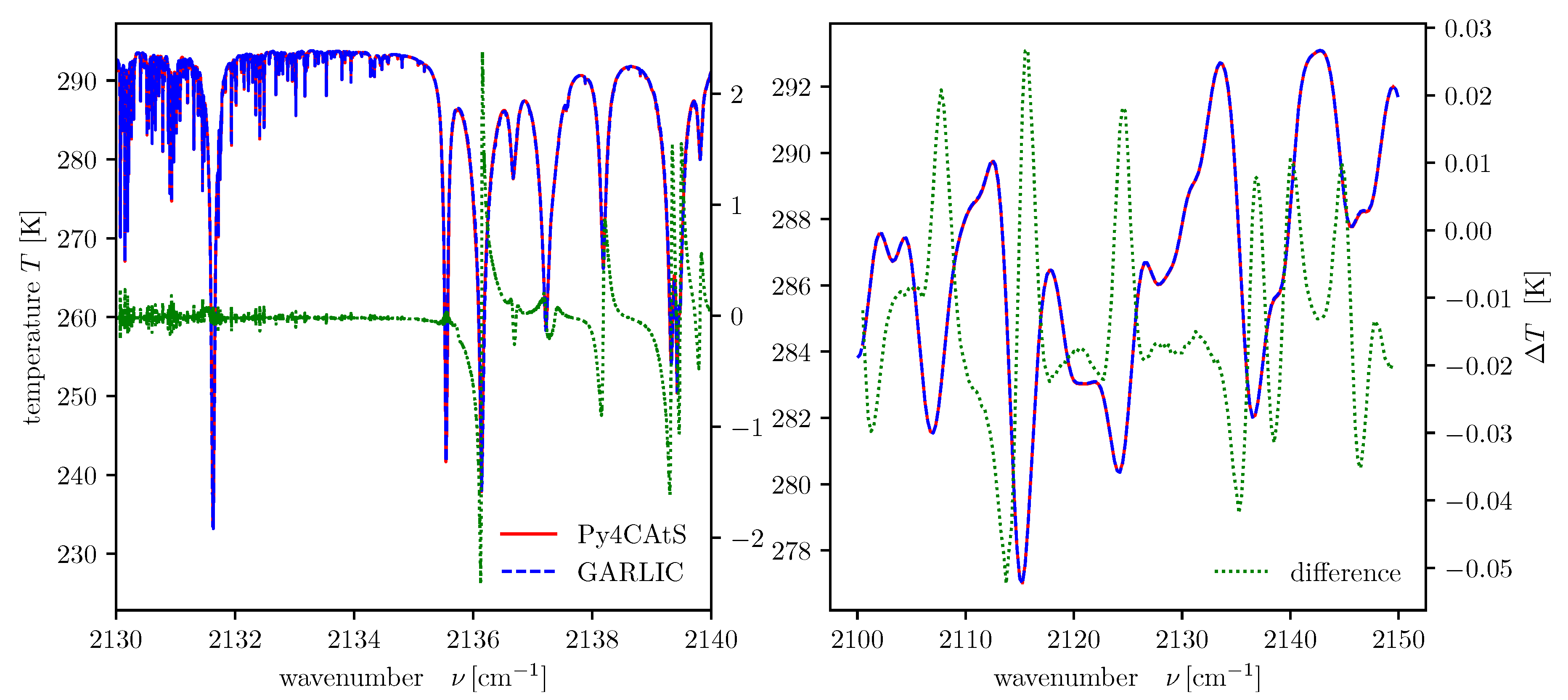
4.4. GARLIC vs. Py4CAtS
4.5. Batch Processing
4.6. Current limitations—What Py4CAtS Cannot Do
- Spherical atmospheres: modeling radiance and/or transmission for limb sounding is not possible; Py4CAtS is assuming a plane-parallel atmosphere. Please note that the quadrature schemes of Section 2.2.2 also work for limb geometry.
- Jacobians: Several tools have been developed for automatic differentiation of Python code (see http://www.autodiff.org), so derivatives of spectra w.r.t. atmospheric parameters etc. could be implemented similar to the approach used in GARLIC [94]. This is currently not foreseen.
- Other line parameter databases (see also http://hitran.org/links/): In addition to HITRAN/HITEMP and GEISA, further databases have been developed such as ExoMol [19] and databases dedicated to specific spectral regions (e.g., JPL and CDMS catalogs, Pickett et al. [16], Endres et al. [18]), specific molecules (e.g., [95,96,97]), or satellite missions [96,98]. Some of these databases have a format similar to HITRAN and GEISA and an appropriate reader could be readily implemented, whereas an implementation of other databases would require some more effort because of their different organization. Please note that a Python script ExoMol_to_HITRAN.py has been developed by the ExoMol consortium, see https://github.com/xnx/ExoMol_to_HITRAN.
- Predefined cross sections: Both HITRAN and GEISA include a large collection of IR (and UV) cross sections esp. for heavy molecules that can be relevant for atmospheric absorption. Reading and further processing of these data is not yet implemented in Py4CAtS.
- Py4CAtS stores only the “core” line parameters required for cross section modeling. In contrast, HAPI [34] can also keep track of line assignments, transition IDs etc. However, Py4CAtS has been developed with atmospheric spectroscopy as target application, but not molecular spectroscopy.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BoA | Bottom of Atmosphere |
| GARLIC | Generic Atmospheric Radiation Line-by-line Infrared Code |
| HWHM | half width half maximum |
| IR | infrared |
| lbl | line-by-line |
| Py4CAtS | PYthon scripts for Computational ATmospheric Spectroscopy |
| ToA | Top of Atmosphere |
| ac | absorption coefficient |
| od | optical depth |
| ri | radiance intensity |
| wf | weighting function |
| vmr | volume mixing ratio |
| xs | cross section |
Appendix A. Implementation
Appendix A.1. Input/Output
Appendix A.2. Visualization
Appendix A.3. Recursive Functions
- a single lineArray holding the line parameters (position, strengths, …) of a single molecule and a single pair (that defaults to STP );
- a dictionary or list of lineArray’s and a single pair;
- a single lineArray and a list/array of pressures and/or a list/array of temperatures (if both p and T are arrays (or lists), their length must be identical!);
- a dictionary (list) of lineArray’s and (a list/array of) pressure(s) and temperature(s).
Appendix A.4. The Subclassed NumPy Arrays
- xs.info()
- — print “essential” information;
- xs.dx()
- — compute the grid point spacing (essentially xs.x.size()/(len(xs)-1));
- xs.grid()
- — returns the uniform wavenumber grid array;
- xs.regrid(n)
- — interpolate to a denser uniform grid (usually n is larger than len(xs));
- xs.__eq__(other)
- — compare two cross sections using the == operator, i.e., xs1==xs2 returns True if the wavenumber intervals, pressure, temperature, and the spectra itself agree (approximately).
Appendix A.5. Structured Arrays
Appendix A.6. Conversion of Physical Units: The cgsUnits Module
Appendix A.7. The Option Parser Module command_parser.py
Appendix A.8. Input/Output Utilities: The aeiou.py Module
Appendix A.9. The pairTypes.py Module
References
- Goody, R.; Yung, Y. Atmospheric Radiation—Theoretical Basis, 2nd ed.; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Liou, K.N. An Introduction to Atmospheric Radiation; Academic Press: Orlando, FL, USA, 1980. [Google Scholar]
- Zdunkowski, W.; Trautmann, T.; Bott, A. Radiation in the Atmosphere—A Course in Theoretical Meteorology; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Wiscombe, W. Atmospheric Radiation: 1975–1983. Rev. Geophys. Space Phys. 1983, 21, 997. [Google Scholar] [CrossRef]
- Schläpfer, D. MODO: An interface to MODTRAN for the simulation of imaging spectrometry at-sensor signals. In Proceedings of the Tenth Jet Propulsion Laboratory Airborne Earth Science Workshop, Pasadena, CA, USA, 27 February–2 March 2001; Green, R., Ed.; Volume JPL-02-1, pp. 343–350. [Google Scholar]
- Berk, A.; Anderson, G.; Acharya, P.; Bernstein, L.; Muratov, L.; Lee, J.; Fox, M.; Adler-Golden, S.; Chetwynd, J.; Hoke, M.; et al. MODTRAN 5: A reformulated atmospheric band model with auxiliary species and practical multiple scattering options: Update. In Proceedings of the Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Orlando, FL, USA, 28 March–1 April 2005; Shen, S., Lewis, P., Eds.; Volume 5806, pp. 662–667. [Google Scholar] [CrossRef]
- Wilson, R. Py6S: A Python interface to the 6S radiative transfer model. Comput. Geosci. 2013, 51, 166–171. [Google Scholar] [CrossRef]
- Vermote, E.; Tanré, D.; Deuzé, J.; Herman, M.; Morcette, J.J. Second Simulation of the Satellite Signal in the Solar Spectrum, 6S: An Overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Lacis, A.; Oinas, V. A Description of the Correlated k Distribution Method for Modeling Nongray Gaseous Absorption, Thermal Emission, and Multiple Scattering in Vertically Inhomogeneous Atmospheres. J. Geophys. Res. 1991, 96, 9027–9063. [Google Scholar] [CrossRef]
- Wiscombe, W.; Evans, J. Exponential-sum fitting of radiative transmission functions. J. Comput. Phys. 1977, 24, 416–444. [Google Scholar] [CrossRef]
- Heng, K.; Marley, M. Radiative Transfer for Exoplanet Atmospheres. In Handbook of Exoplanets; Deeg, H.J., Belmonte, J.A., Eds.; Springer International Publishing: New York, NY, USA, 2018; pp. 2137–2152. [Google Scholar]
- Madhusudhan, N. Atmospheric Retrieval of Exoplanets. In Handbook of Exoplanets; Deeg, H.J., Belmonte, J.A., Eds.; Springer: New York, NY, USA, 2018. [Google Scholar]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN2016 molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Rothman, L.; Gordon, I.; Barber, R.; Dothe, H.; Gamache, R.; Goldman, A.; Perevalov, V.; Tashkun, S.; Tennyson, J. HITEMP, the high-temperature molecular spectroscopic database. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 2139–2150. [Google Scholar] [CrossRef]
- Jacquinet-Husson, N.; Armante, R.; Scott, N.A.; Chédin, A.; Crépeau, L.; Boutammine, C.; Bouhdaoui, A.; Crevoisier, C.; Capelle, V.; Boonne, C.; et al. The 2015 edition of the GEISA spectroscopic database. J. Mol. Spectrosc. 2016, 327, 31–72. [Google Scholar] [CrossRef]
- Pickett, H.; Poynter, R.; Cohen, E.; Delitsky, M.; Pearson, J.; Müller, H. Submillimeter, millimeter, and microwave spectral line catalog. J. Quant. Spectrosc. Radiat. Transf. 1998, 60, 883–890. [Google Scholar] [CrossRef]
- Müller, H.; Schlöder, F.; Stutzki, J.; Winnewisser, G. The Cologne Database for Molecular Spectroscopy, CDMS: A useful tool for astronomers and spectroscopists. J. Mol. Struct. 2005, 742, 215–227. [Google Scholar] [CrossRef]
- Endres, C.P.; Schlemmer, S.; Schilke, P.; Stutzki, J.; Müller, H.S. The Cologne Database for Molecular Spectroscopy, CDMS, in the Virtual Atomic and Molecular Data Centre, VAMDC. J. Mol. Spectrosc. 2016, 327, 95–104. [Google Scholar] [CrossRef]
- Tennyson, J.; Yurchenko, S.N.; Al-Refaie, A.F.; Barton, E.J.; Chubb, K.L.; Coles, P.A.; Diamantopoulou, S.; Gorman, M.N.; Hill, C.; Lam, A.Z.; et al. The ExoMol database: Molecular line lists for exoplanet and other hot atmospheres. J. Mol. Spectrosc. 2016, 327, 73–94. [Google Scholar] [CrossRef]
- Clough, S.; Kneizys, F.; Rothman, L.; Gallery, W. Atmospheric transmittance and radiance: FASCOD1B. Proc. SPIE 1981, 277, 152–166. [Google Scholar] [CrossRef]
- Scott, N.; Chédin, A. A Fast Line-by-Line Method for Atmospheric Absorption Computations: The Automatized Atmospheric Absorption Atlas. J. Appl. Meteorol. 1981, 20, 802–812. [Google Scholar] [CrossRef]
- Buehler, S.A.; Eriksson, P.; Kuhn, T.; von Engeln, A.; Verdes, C. ARTS, the atmospheric radiative transfer simulator. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 65–93. [Google Scholar] [CrossRef]
- Eriksson, P.; Buehler, S.A.; Davis, C.; Emde, C.; Lemke, O. ARTS, the atmospheric radiative transfer simulator, version 2. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1551–1558. [Google Scholar] [CrossRef]
- Buehler, S.A.; Mendrok, J.; Eriksson, P.; Perrin, A.; Larsson, R.; Lemke, O. ARTS, the atmospheric radiative transfer simulator—Version 2.2, the planetary toolbox edition. Geosci. Model Dev. 2018, 11, 1537–1556. [Google Scholar] [CrossRef]
- Schreier, F.; Gimeno García, S.; Hedelt, P.; Hess, M.; Mendrok, J.; Vasquez, M.; Xu, J. GARLIC—A General Purpose Atmospheric Radiative Transfer Line-by-Line Infrared-Microwave Code: Implementation and Evaluation. J. Quant. Spectrosc. Radiat. Transf. 2014, 137, 29–50. [Google Scholar] [CrossRef]
- Edwards, D. Atmospheric transmittance and radiance calculations using line–by–line computer models. In Proceedings of the Modelling of the Atmosphere, Orlando, FL, USA, 4–8 April 1988; Volume 928, pp. 94–116. [Google Scholar] [CrossRef]
- Stiller, G.; von Clarmann, T.; Funke, B.; Glatthor, N.; Hase, F.; Höpfner, M.; Linden, A. Sensitivity of trace gas abundances retrievals from infrared limb emission spectra to simplifying approximations in radiative transfer modelling. J. Quant. Spectrosc. Radiat. Transf. 2002, 72, 249–280. [Google Scholar] [CrossRef]
- Clough, S.; Shephard, M.; Mlawer, E.; Delamere, J.; Iacono, M.; Cady-Pereira, K.; Boukabara, S.; Brown, P. Atmospheric radiative transfer modeling: A summary of the AER codes. J. Quant. Spectrosc. Radiat. Transf. 2005, 91, 233–244. [Google Scholar] [CrossRef]
- Gordley, L.; Marshall, B.; Chu, D. LINEPAK: Algorithms for modeling spectral transmittance and radiance. J. Quant. Spectrosc. Radiat. Transf. 1994, 52, 563. [Google Scholar] [CrossRef]
- Dudhia, A. The Reference Forward Model (RFM). J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 243–253. [Google Scholar] [CrossRef]
- Amato, U.; Masiello, G.; Serio, C.; Viggiano, M. The σ–IASI code for the calculation of infrared atmospheric radiance and its derivatives. Environ. Model. Softw. 2002, 17, 651–667. [Google Scholar] [CrossRef]
- Bailey, J.; Kedziora-Chudczer, L. Modelling the spectra of planets, brown dwarfs and stars using VStar. Mon. Not. R. Astron. Soc. 2012, 419, 1913–1929. [Google Scholar] [CrossRef]
- Hill, C.; Gordon, I.E.; Kochanov, R.V.; Barrett, L.; Wilzewski, J.S.; Rothman, L.S. HITRANonline: An online interface and the flexible representation of spectroscopic data in the HITRAN database. J. Quant. Spectrosc. Radiat. Transf. 2015, 177, 4–14. [Google Scholar] [CrossRef]
- Kochanov, R.; Gordon, I.; Rothman, L.; Wcisło, P.; Hill, C.; Wilzewski, J. HITRAN Application Programming Interface (HAPI): A comprehensive approach to working with spectroscopic data. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 15–30. [Google Scholar] [CrossRef]
- Goldenstein, C.; Miller, V.; Spearrin, R.; Strand, C. SpectraPlot.com: Integrated spectroscopic modeling of atomic and molecular gases. J. Quant. Spectrosc. Radiat. Transf. 2017, 200, 249–257. [Google Scholar] [CrossRef]
- Villanueva, G.; Smith, M.; Protopapa, S.; Faggi, S.; Mandell, A. Planetary Spectrum Generator: An accurate online radiative transfer suite for atmospheres, comets, small bodies and exoplanets. J. Quant. Spectrosc. Radiat. Transf. 2018, 217, 86–104. [Google Scholar] [CrossRef]
- Smette, A.; Sana, H.; Noll, S.; Horst, H.; Kausch, W.; Kimeswenger, S.; Barden, M.; Szyszka, C.; Jones, A.M.; Gallenne, A.; et al. Molecfit: A general tool for telluric absorption correction. Astron. Astrophys. 2015, 576, A77. [Google Scholar] [CrossRef]
- Bertaux, L.; Lallement, R.; Ferron, S.; Boonne, C.; Bodichon, R. TAPAS, a web-based service of atmospheric transmission computation for astronomy. Astron. Astrophys. 2014, 564, A46. [Google Scholar] [CrossRef]
- Schreier, F.; Böttger, U. MIRART, A Line-By-Line Code for Infrared Atmospheric Radiation Computations incl. Derivatives. Atmos. Ocean. Opt. 2003, 16, 262–268. [Google Scholar]
- Ernst, T.; Rother, T.; Schreier, F.; Wauer, J.; Balzer, W. DLR’s Virtual Lab: Scientific Software just a mouse click away. Comput. Sci. Eng. 2003, 5, 70–79. [Google Scholar] [CrossRef]
- von Clarmann, T.; Echle, G. Selection of Optimized Microwindows for Atmospheric Spectroscopy. Appl. Opt. 1998, 37, 7661–7669. [Google Scholar] [CrossRef]
- Echle, G.; von Clarmann, T.; Dudhia, A.; Flaud, J.M.; Funke, B.; Glatthor, N.; Kerridge, B.; López-Puertas, M.; Martin-Torres, F.; Stiller, G. Optimized Spectral Microwindows for Data Analysis of the Michelson Interferometer for Passive Atmospheric Sounding on the Environmental Satellite. Appl. Opt. 2000, 39, 5531–5540. [Google Scholar] [CrossRef]
- Dudhia, A.; Jay, V.; Rodgers, C. Microwindow selection for high-resolution-sounders. Appl. Opt. 2002, 41, 3665–3673. [Google Scholar] [CrossRef]
- Rabier, F.; Fourrié, N.; Chafai, D.; Prunet, P. Channel Selection Methods for Infrared Atmospheric Sounding Interferometer Radiances. Quart. J. R. Met. Soc. 2002, 128, 1011–2027. [Google Scholar] [CrossRef]
- Crevoisier, C.; Chedin, A.; Scott, N.A. AIRS channel selection for CO2 and other trace-gas retrievals. Quart. J. R. Met. Soc. 2003, 129, 2719–2740. [Google Scholar] [CrossRef]
- Kuai, L.; Natraj, V.; Shia, R.; Miller, C.; Yung, Y. Channel selection using information content analysis: A case study of CO2 retrieval from near infrared measurements. J. Quant. Spectrosc. Radiat. Transf. 2010, 111, 1296–1304. [Google Scholar] [CrossRef]
- Dubois, P.; Hinsen, K.; Hugunin, J. Numerical Python. Comput. Phys. 1996, 10, 262–267. [Google Scholar] [CrossRef]
- Watters, A.; van Rossum, G.; Ahlstrom, J.C. Internet Programming with Python; M & T Books: New York, NY, USA, 1996. [Google Scholar]
- Oliphant, T. Python for Scientific Computing. Comput. Sci. Eng. 2007, 9, 10–20. [Google Scholar] [CrossRef]
- Langtangen, H.P. Python Scripting for Computational Science, 3rd ed.; Texts in Computational Science and Engineering; Springer: New York, NY, USA, 2008; Volume 3. [Google Scholar]
- van der Walt, S.; Colbert, S.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Pérez, F.; Granger, B.; Hunter, J. Python: An Ecosystem for Scientific Computing. Comput. Sci. Eng. 2011, 13, 13–21. [Google Scholar] [CrossRef]
- Lin, J.W.B. Why Python is the next wave in earth sciences computing. Bull. Am. Met. Soc. 2012, 93, 1823–1824. [Google Scholar] [CrossRef]
- Raspaud, M.; Hoese, D.; Dybbroe, A.; Lahtinen, P.; Devasthale, A.; Itkin, M.; Hamann, U.; Rasmussen, L.Ø.; Nielsen, E.; Leppelt, T.; et al. PyTroll: An Open-Source, Community-Driven Python Framework to Process Earth Observation Satellite Data. Bull. Am. Met. Soc. 2018, 99, 1329–1336. [Google Scholar] [CrossRef]
- Astropy Collaboration; Robitaille, T.P.; Tollerud, E.J.; Greenfield, P.; Droettboom, M.; Bray, E.; Aldcroft, T.; Davis, M.; Ginsburg, A.; Price-Whelan, A.; et al. Astropy: A community Python package for astronomy. Astron. Astrophys. 2013, 558, A33. [Google Scholar] [CrossRef]
- Parker, S.; Johnson, C.; Beazley, D. Computational Steering Software Systems and Strategies. IEEE Comput. Sci. Eng. 1997, 4, 50–59. [Google Scholar] [CrossRef]
- Dubois, P.; Yang, T.Y. Extending Python with Fortran. Comput. Sci. Eng. 1999, 1, 66–73. [Google Scholar] [CrossRef]
- Peterson, P. F2PY: A tool for connecting Fortran and Python programs. Int. J. Comput. Sci. Eng. 2009, 4, 296–305. [Google Scholar] [CrossRef]
- Norton, R.; Rinsland, C. ATMOS data processing and science analysis methods. Appl. Opt. 1991, 30, 389–400. [Google Scholar] [CrossRef]
- Armstrong, B. Spectrum Line Profiles: The Voigt Function. J. Quant. Spectrosc. Radiat. Transf. 1967, 7, 61–88. [Google Scholar] [CrossRef]
- Varghese, P.; Hanson, R. Collisional narrowing effects on spectral line shapes measured at high resolution. Appl. Opt. 1984, 23, 2376–2385. [Google Scholar] [CrossRef]
- Tennyson, J.; Bernath, P.; Campargue, A.; Császár, A.; Daumont, L.; Gamache, R.; Hodges, J.; Lisak, D.; Naumenko, O.; Rothman, L.; et al. Recommended isolated-line profile for representing high-resolution spectroscopic transitions (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 1931–1943. [Google Scholar] [CrossRef]
- Schreier, F. Computational Aspects of Speed-Dependent Voigt Profiles. J. Quant. Spectrosc. Radiat. Transf. 2017, 187, 44–53. [Google Scholar] [CrossRef]
- NIST Digital Library of Mathematical Functions; Online companion to [65]; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2010.
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. (Eds.) NIST Handbook of Mathematical Functions; Print companion to [64]; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Ralston, A.; Rabinowitz, P. A First Course in Numerical Analysis, 2nd ed.; McGraw–Hill Book Company: New York, NY, USA, 1978. [Google Scholar]
- Cuyt, A.; Petersen, V.; Verdonk, B.; Waadeland, H.; Jones, W. Handbook of Continued Fractions for Special Functions; Springer: New York, NY, USA, 2008. [Google Scholar]
- Humlíček, J. An efficient method for evaluation of the complex probability function: The Voigt function and its derivatives. J. Quant. Spectrosc. Radiat. Transf. 1979, 21, 309–313. [Google Scholar] [CrossRef]
- Humlíček, J. Optimized computation of the Voigt and complex probability function. J. Quant. Spectrosc. Radiat. Transf. 1982, 27, 437–444. [Google Scholar] [CrossRef]
- Weideman, J. Computation of the Complex Error Function. SIAM J. Num. Anal. 1994, 31, 1497–1518. [Google Scholar] [CrossRef]
- Schreier, F. Optimized Implementations of Rational Approximations for the Voigt and Complex Error Function. J. Quant. Spectrosc. Radiat. Transf. 2011, 112, 1010–1025. [Google Scholar] [CrossRef]
- Whiting, E. An empirical approximation to the Voigt profile. J. Quant. Spectrosc. Radiat. Transf. 1968, 8, 1379–1384. [Google Scholar] [CrossRef]
- Schreier, F. Optimized evaluation of a large sum of functions using a three-grid approach. Comput. Phys. Commun. 2006, 174, 783–802. [Google Scholar] [CrossRef]
- Schreier, F.; Milz, M.; Buehler, S.A.; von Clarmann, T. Intercomparison of three microwave/infrared high resolution line-by-line radiative transfer codes. J. Quant. Spectrosc. Radiat. Transf. 2018, 211, 64–77. [Google Scholar] [CrossRef]
- von Clarmann, T.; Höpfner, M.; Funke, B.; López-Puertas, M.; Dudhia, A.; Jay, V.; Schreier, F.; Ridolfi, M.; Ceccherini, S.; Kerridge, B.; et al. Modeling of Atmospheric Mid–Infrared Radiative Transfer: The AMIL2DA Algorithm Intercomparison Experiment. J. Quant. Spectrosc. Radiat. Transf. 2003, 78, 381–407. [Google Scholar] [CrossRef]
- Melsheimer, C.; Verdes, C.; Buehler, S.A.; Emde, C.; Eriksson, P.; Feist, D.; Ichizawa, S.; John, V.; Kasai, Y.; Kopp, G.; et al. Intercomparison of General Purpose Clear Sky Atmospheric Radiative Transfer Models for the Millimeter/Submillimeter Spectral Range. Radio Sci. 2005, 40, RS1007. [Google Scholar] [CrossRef]
- Hunter, J. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Anderson, G.; Clough, S.; Kneizys, F.; Chetwynd, J.; Shettle, E. AFGL Atmospheric Constituent Profiles (0–120 km); Technical Report TR-86-0110; AFGL: Hanscom AFB, MA, USA, 1986. [Google Scholar]
- Fortems-Cheiney, A.; Chevallier, F.; Pison, I.; Bousquet, P.; Carouge, C.; Clerbaux, C.; Coheur, P.F.; George, M.; Hurtmans, D.; Szopa, S. On the capability of IASI measurements to inform about CO surface emissions. Atmos. Chem. Phys. 2009, 9, 8735–8743. [Google Scholar] [CrossRef]
- George, M.; Clerbaux, C.; Bouarar, I.; Coheur, P.F.; Deeter, M.; Edwards, D.; Francis, G.; Gille, J.; Hadji-Lazaro, J.; Hurtmans, D.; et al. An examination of the long-term CO records from MOPITT and IASI: Comparison of retrieval methodology. Atmos. Meas. Tech. 2015, 8, 4313–4328. [Google Scholar] [CrossRef]
- McMillan, W.; Barnet, C.; Strow, L.; Chahine, M.; McCourt, M.; Warner, J.; Novelli, P.; Korontzi, S.; Maddy, E.; Datta, S. Daily global maps of carbon monoxide from NASA’s Atmospheric Infrared Sounder. Geophys. Res. Lett. 2005, 32, L11801. [Google Scholar] [CrossRef]
- Park, J.; Rothman, L.; Rinsland, C.; Richardson, D.; Namkung, J. Atlas of Absorption Lines from 0 to 17,900 cm-1; Reference Publication 1188; NASA: Washington, DC, USA, 1987.
- Murtagh, D.; Frisk, U.; Merino, F.; Ridal, M.; Jonsson, A.; Stegman, J.; Witt, G.; Eriksson, P.; Jiménez, C.; Megie, G.; et al. An overview of the Odin atmospheric mission. Can. J. Phys. 2002, 80, 309–319. [Google Scholar] [CrossRef]
- Hughes, R.; Bernath, P.; Boone, C. ACE infrared spectral atlases of the Earth’s atmosphere. J. Quant. Spectrosc. Radiat. Transf. 2014, 148, 18–21. [Google Scholar] [CrossRef]
- Bernath, P.F. The Atmospheric Chemistry Experiment (ACE). J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 3–16. [Google Scholar] [CrossRef]
- Schreier, F.; Städt, S.; Hedelt, P.; Godolt, M. Transmission Spectroscopy with the ACE-FTS Infrared Spectral Atlas of Earth: A Model Validation and Feasibility Study. Mol. Astrophys. 2018, 11, 1–22. [Google Scholar] [CrossRef]
- Richard, C.; Gordon, I.; Rothman, L.; Abel, M.; Frommhold, L.; Gustafsson, M.; Hartmann, J.M.; Hermans, C.; Lafferty, W.; Orton, G.; et al. New section of the HITRAN database: Collision-Induced Absorption (CIA). J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1276–1285. [Google Scholar] [CrossRef]
- Clough, S.; Kneizys, F.; Davies, R. Line Shape and the Water Vapor Continuum. Atmos. Res. 1989, 23, 229–241. [Google Scholar] [CrossRef]
- Tipping, R.; Ma, Q. Theory of the water vapor continuum and validations. Atmos. Res. 1995, 36, 69–94. [Google Scholar] [CrossRef]
- Green, P.D.; Newman, S.M.; Beeby, R.J.; Murray, J.E.; Pickering, J.C.; Harries, J.E. Recent advances in measurement of the water vapour continuum in the far-infrared spectral region. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 2637–2655. [Google Scholar] [CrossRef][Green Version]
- Mlawer, E.; Payne, V.; Moncet, J.L.; Delamere, J.; Alvarado, M.; Tobin, D. Development and recent evaluation of the MT-CKD model of continuum absorption. Philos. Trans. R. Soc. Lond. Ser. A 2012, 370, 2520–2556. [Google Scholar] [CrossRef]
- Shine, K.; Ptashnik, I.; Rädel, G. The Water Vapour Continuum: Brief History and Recent Developments. Surv. Geophys. 2012, 33, 535–555. [Google Scholar] [CrossRef]
- Shine, K.; Campargue, A.; Mondelain, D.; McPheat, R.; Ptashnik, I.; Weidmann, D. The water vapour continuum in near-infrared windows—Current understanding and prospects for its inclusion in spectroscopic databases. J. Mol. Spectrosc. 2016, 327, 193–208. [Google Scholar] [CrossRef]
- Schreier, F.; Gimeno García, S.; Vasquez, M.; Xu, J. Algorithmic vs. finite difference Jacobians for infrared atmospheric radiative transfer. J. Quant. Spectrosc. Radiat. Transf. 2015, 164, 147–160. [Google Scholar] [CrossRef]
- Tashkun, S.A.; Perevalov, V.I.; Teffo, J.L.; Bykov, A.D.; Lavrentieva, N.N. CDSD-1000, the high-temperature carbon dioxide spectroscopic databank. J. Quant. Spectrosc. Radiat. Transf. 2003, 82, 165–196. [Google Scholar] [CrossRef]
- Nikitin, A.; Lyulin, O.; Mikhailenko, S.; Perevalov, V.; Filippov, N.; Grigoriev, I.; Morino, I.; Yoshida, Y.; Matsunaga, T. GOSAT-2014 methane spectral line list. J. Quant. Spectrosc. Radiat. Transf. 2015, 154, 63–71. [Google Scholar] [CrossRef]
- Tashkun, S.; Perevalov, V.; Lavrentieva, N. NOSD-1000, the high-temperature nitrous oxide spectroscopic databank. J. Quant. Spectrosc. Radiat. Transf. 2016, 177, 43–48. [Google Scholar] [CrossRef]
- Brown, L.; Gunson, M.; Toth, R.; Irion, F.; Rinsland, C.; Goldman, A. 1995 Atmospheric Trace Molecule Spectroscopy (ATMOS) Linelist. Appl. Opt. 1996, 35, 2828–2848. [Google Scholar] [CrossRef]
- Stamnes, K.; Tsay, S.C.; Wiscombe, W.; Jayaweera, K. Numerically Stable Algorithm for Discrete–Ordinate–Method Radiative Transfer in Multiple Scattering and Emitting Layered Media. Appl. Opt. 1988, 27, 2502–2509. [Google Scholar] [CrossRef]
- Mayer, B.; Kylling, A. Technical note: The libRadtran software package for radiative transfer calculations— Description and examples of use. Atmos. Chem. Phys. 2005, 5, 1855–1877. [Google Scholar] [CrossRef]
- Emde, C.; Buras-Schnell, R.; Kylling, A.; Mayer, B.; Gasteiger, J.; Hamann, U.; Kylling, J.; Richter, B.; Pause, C.; Dowling, T.; et al. The libRadtran software package for radiative transfer calculations (version 2.0.1). Geosci. Model Dev. 2016, 9, 1647–1672. [Google Scholar] [CrossRef]
- Schreier, F. The Voigt and complex error function: Humlíček’s rational approximation generalized. Mon. Not. R. Astron. Soc. 2018, 479, 3068–3075. [Google Scholar] [CrossRef]
- Rothman, L.; Gamache, R.; Goldman, A.; Brown, L.; Toth, R.; Pickett, H.; Poynter, P.; Flaud, J.M.; Camy-Peyret, C.; Barbe, A.; et al. The HITRAN database: 1986 edition. Appl. Opt. 1987, 26, 4058. [Google Scholar] [CrossRef]


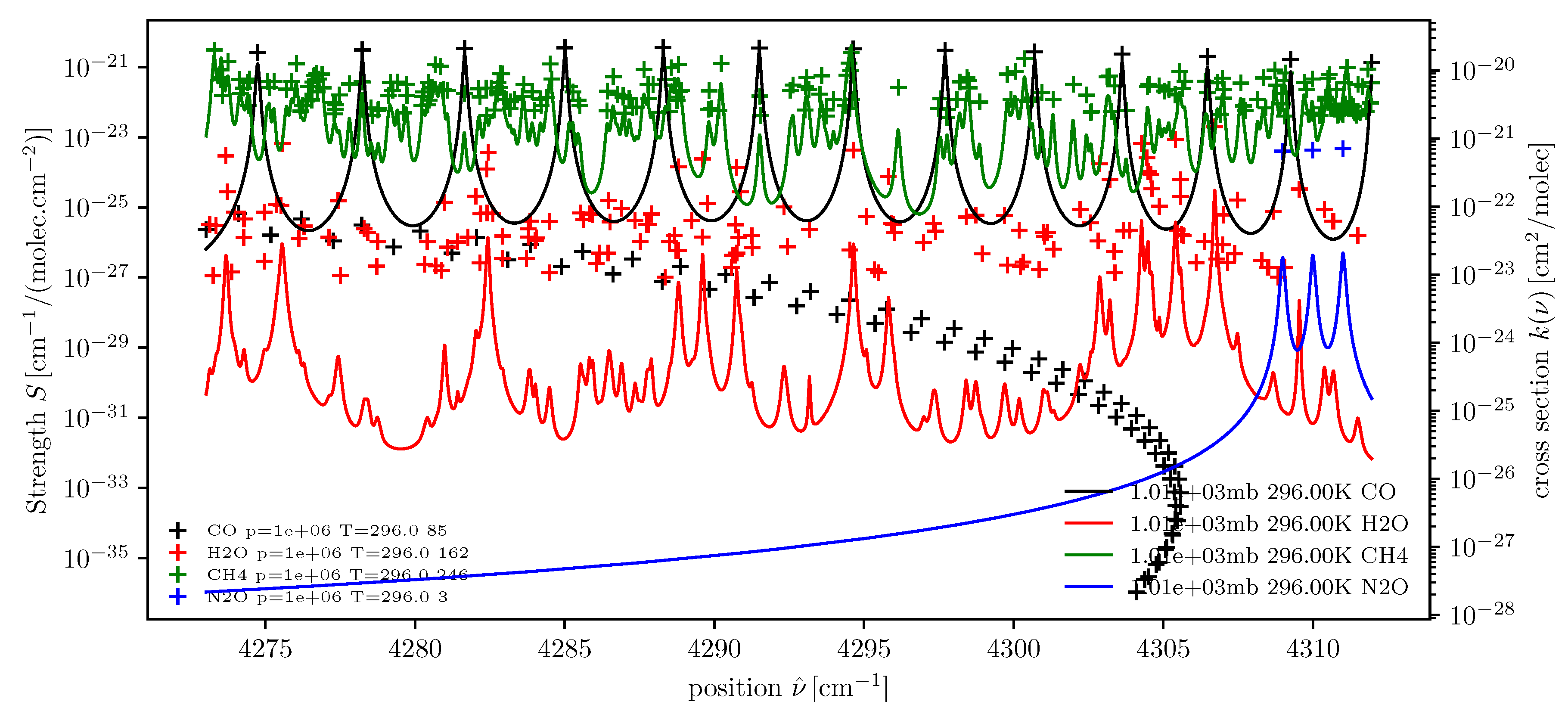
dll = higstract(’/data/hitran/2000/lines’,(4273,4312), ’main’) # dict of line lists xss = lbl2xs(dll) # dict of cross sections atlas(dll); twinx(); xsPlot(xss)
dll = higstract(’/data/hitran/2000/lines’,(4273,4312), ’main’) # dict of line lists xss = lbl2xs(dll) # dict of cross sections atlas(dll); twinx(); xsPlot(xss)
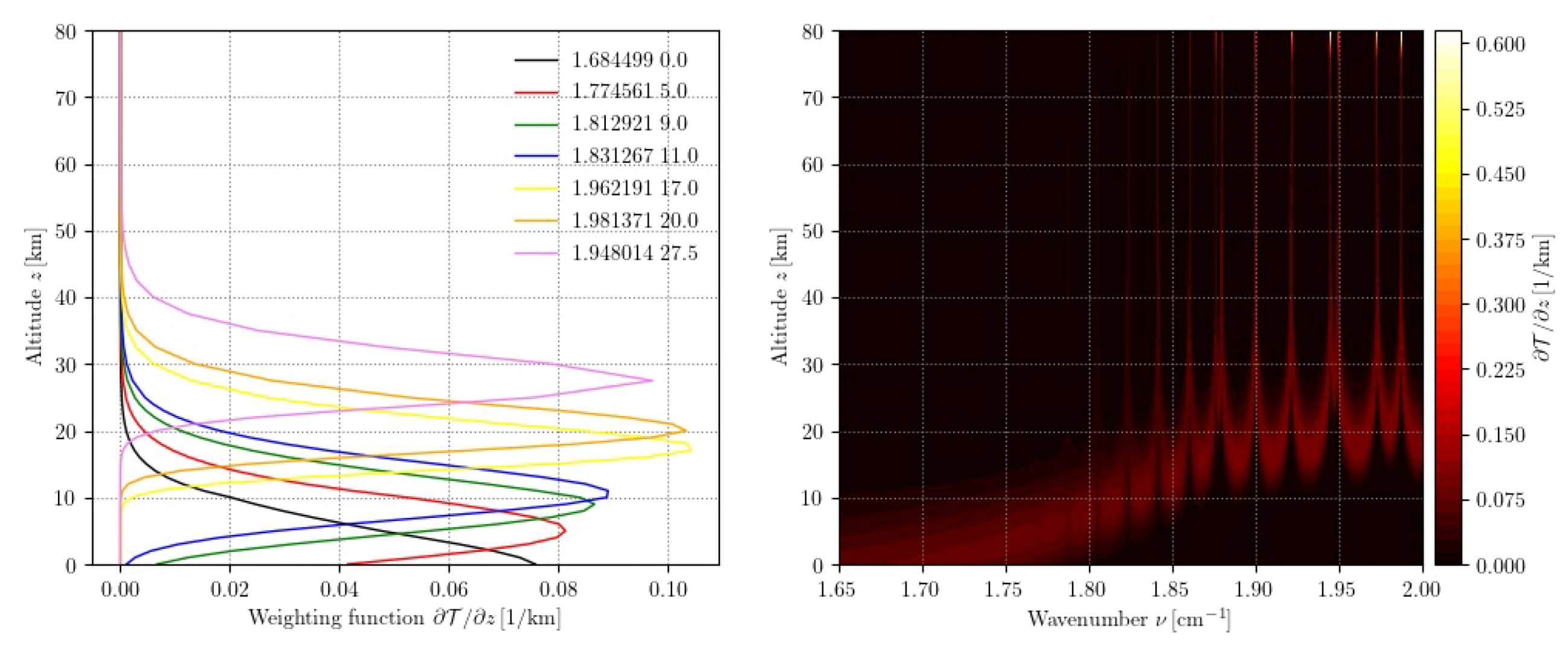
sas = atmRead(’/data/atmos/50/subarcticSummer.xy’, zToA=80) dll = higstract(’/data/hitran/2000/lines’,(0,10), ’main’); del dll[’CO’] acList = lbl2ac(sas, dll, (1.65,2)) wgtFct = ac2wf(acList, 180) ssmtFreqs=array([50.5, 53.2, 54.35, 54.9, 58.825, 59.4, 58.4,])*1e9/c subplot(121); wfPlot(wgtFct, wavenumber=ssmtFreqs) subplot(122); wfPlot(wgtFct, nLevels=50)
sas = atmRead(’/data/atmos/50/subarcticSummer.xy’, zToA=80) dll = higstract(’/data/hitran/2000/lines’,(0,10), ’main’); del dll[’CO’] acList = lbl2ac(sas, dll, (1.65,2)) wgtFct = ac2wf(acList, 180) ssmtFreqs=array([50.5, 53.2, 54.35, 54.9, 58.825, 59.4, 58.4,])*1e9/c subplot(121); wfPlot(wgtFct, wavenumber=ssmtFreqs) subplot(122); wfPlot(wgtFct, nLevels=50)
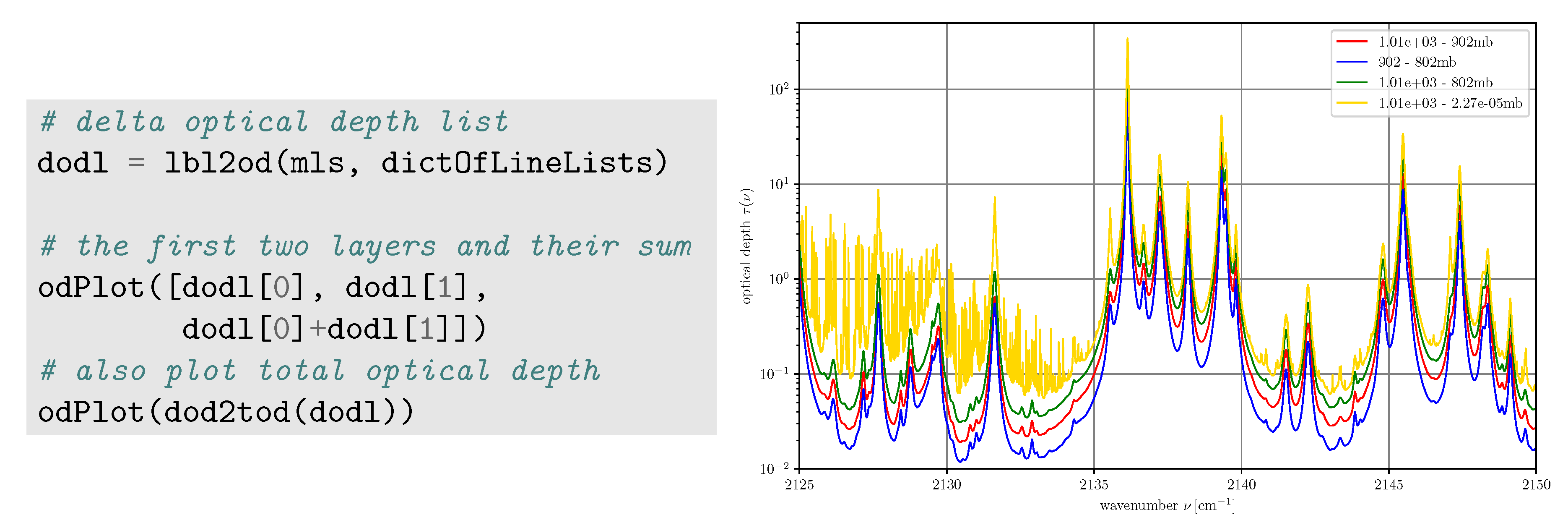
vLimits = Interval(2100.0,2150.0) mls = atmRead(’/data/atmos/50/mls.xy’, zToA=100) dll = higstract(’/data/hitran/2000/lines’,vLimits+20, ’main’) # dict. of line lists radNadir = dod2ri(lbl2od(mls,dll,vLimits+5),180.,mls[’T’][0]) # monochrom radiance radNadirG = radNadir.convolve(1.0,’G’) # Gauss spectral response btNadir = radiance2Kelvin(radNadir.grid(),radNadir) # equ brightness temperature btNadirG = radiance2Kelvin(radNadirG.grid(),radNadirG)
vLimits = Interval(2100.0,2150.0) mls = atmRead(’/data/atmos/50/mls.xy’, zToA=100) dll = higstract(’/data/hitran/2000/lines’,vLimits+20, ’main’) # dict. of line lists radNadir = dod2ri(lbl2od(mls,dll,vLimits+5),180.,mls[’T’][0]) # monochrom radiance radNadirG = radNadir.convolve(1.0,’G’) # Gauss spectral response btNadir = radiance2Kelvin(radNadir.grid(),radNadir) # equ brightness temperature btNadirG = radiance2Kelvin(radNadirG.grid(),radNadirG)
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schreier, F.; Gimeno García, S.; Hochstaffl, P.; Städt, S. Py4CAtS—PYthon for Computational ATmospheric Spectroscopy. Atmosphere 2019, 10, 262. https://doi.org/10.3390/atmos10050262
Schreier F, Gimeno García S, Hochstaffl P, Städt S. Py4CAtS—PYthon for Computational ATmospheric Spectroscopy. Atmosphere. 2019; 10(5):262. https://doi.org/10.3390/atmos10050262
Chicago/Turabian StyleSchreier, Franz, Sebastián Gimeno García, Philipp Hochstaffl, and Steffen Städt. 2019. "Py4CAtS—PYthon for Computational ATmospheric Spectroscopy" Atmosphere 10, no. 5: 262. https://doi.org/10.3390/atmos10050262
APA StyleSchreier, F., Gimeno García, S., Hochstaffl, P., & Städt, S. (2019). Py4CAtS—PYthon for Computational ATmospheric Spectroscopy. Atmosphere, 10(5), 262. https://doi.org/10.3390/atmos10050262