Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models
Abstract
:1. Introduction
2. Methods
2.1. SEB Models
2.1.1. SEBAL
2.1.2. SSEB
2.1.3. S-SEBI
2.1.4. SEBS
2.2. BMA Method
2.3. Statistical Analysis
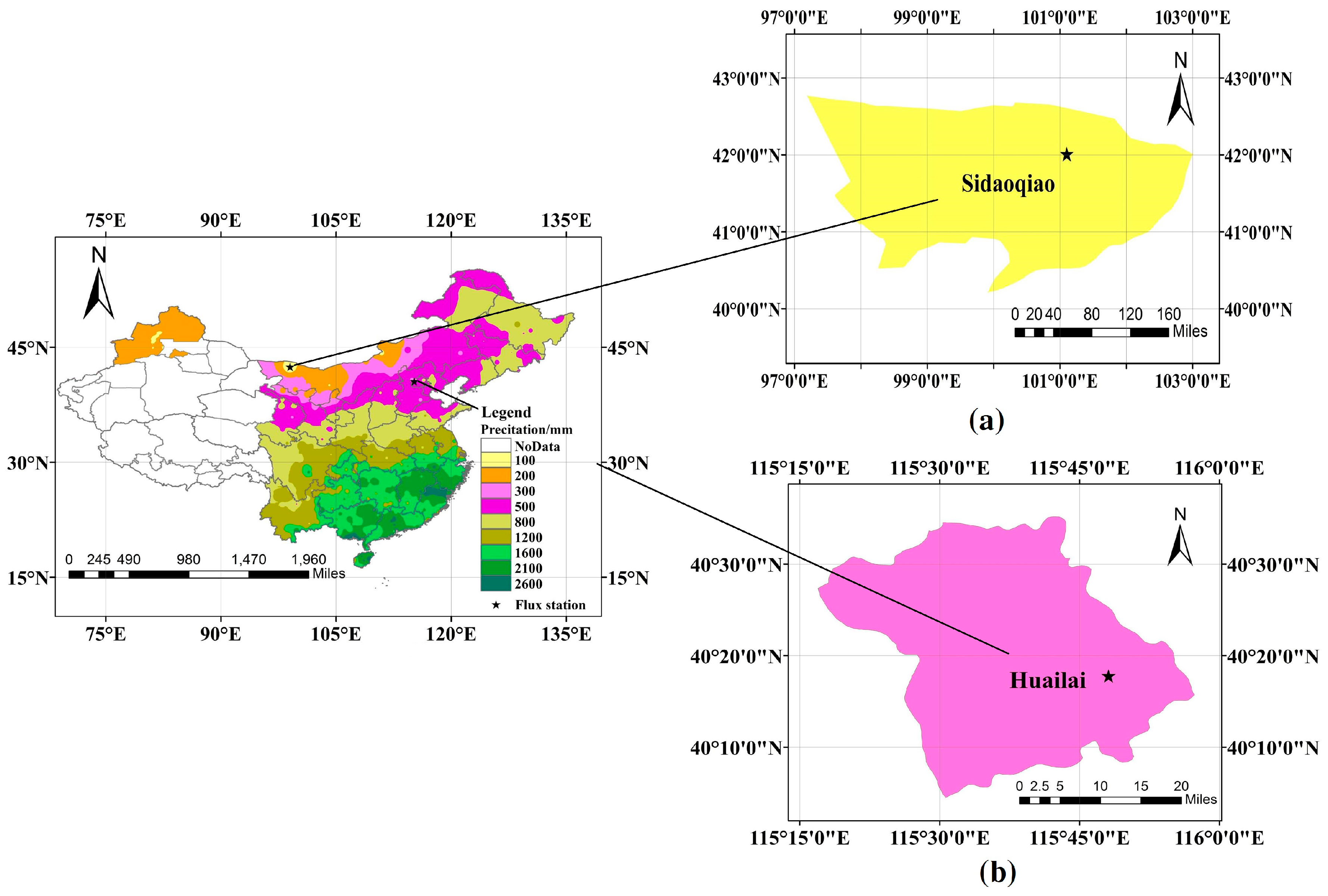
2.4. Study Areas
2.5. Data for the Study Areas
2.5.1. Remote Sensing Data
2.5.2. Flux Tower Data
3. Results and Discussions
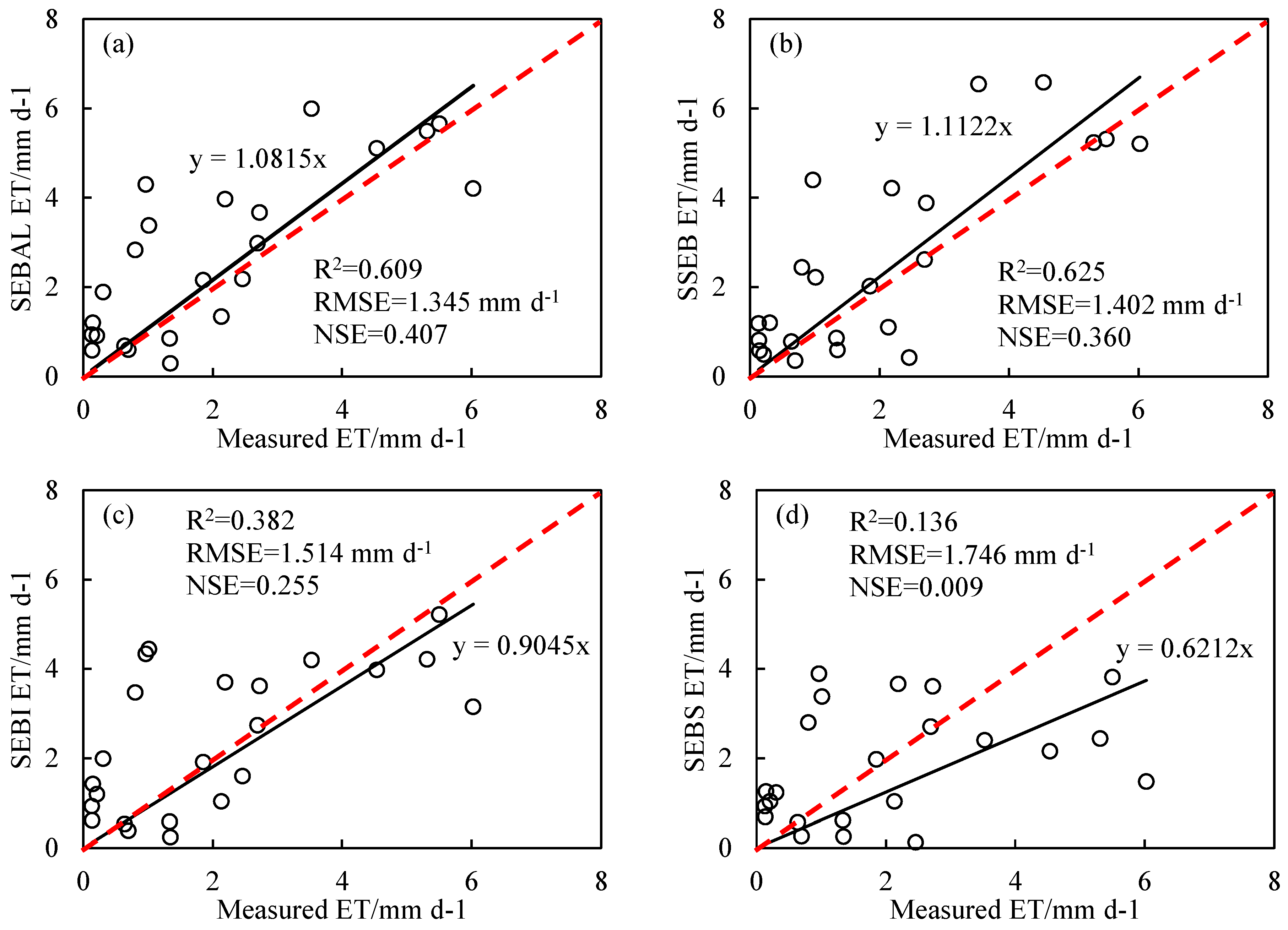
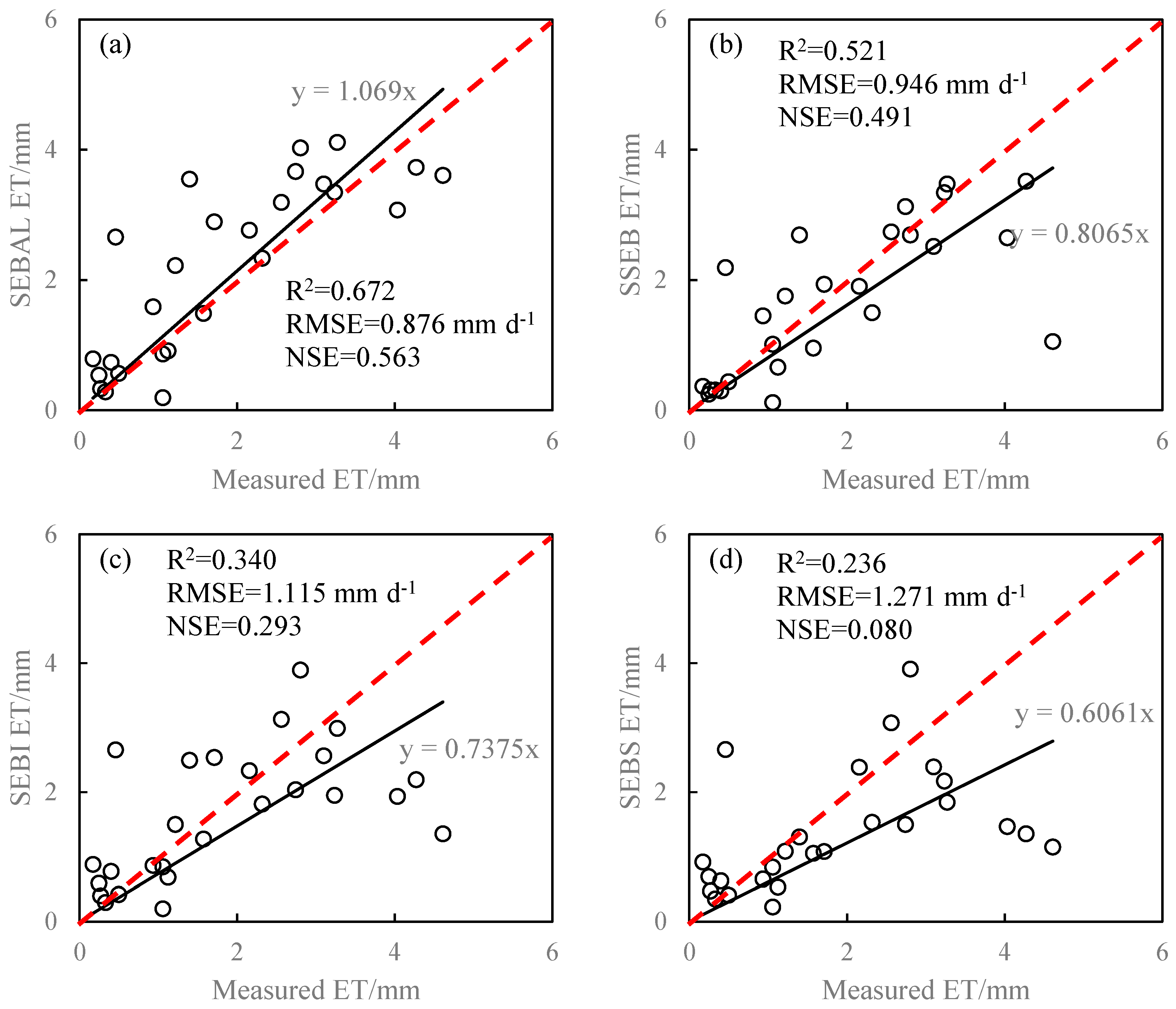
3.1. Single Model Performance in Two Study Areas
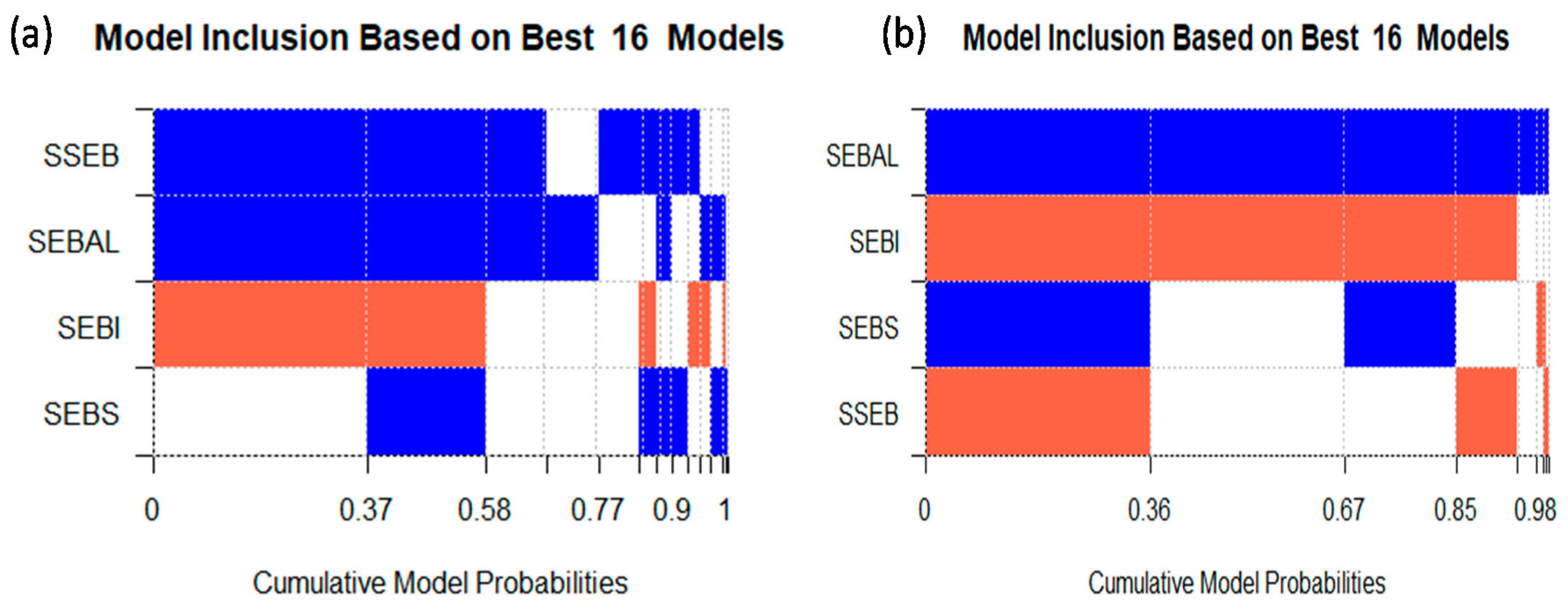
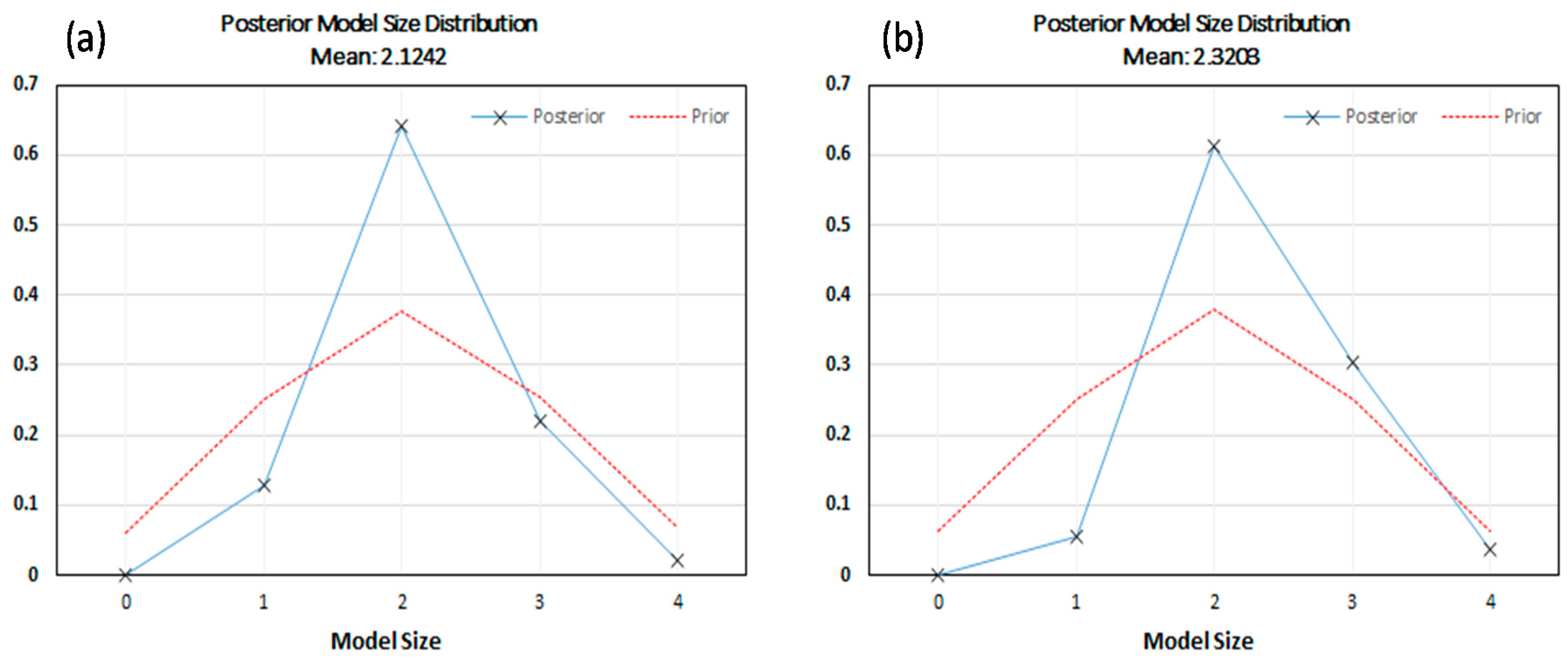
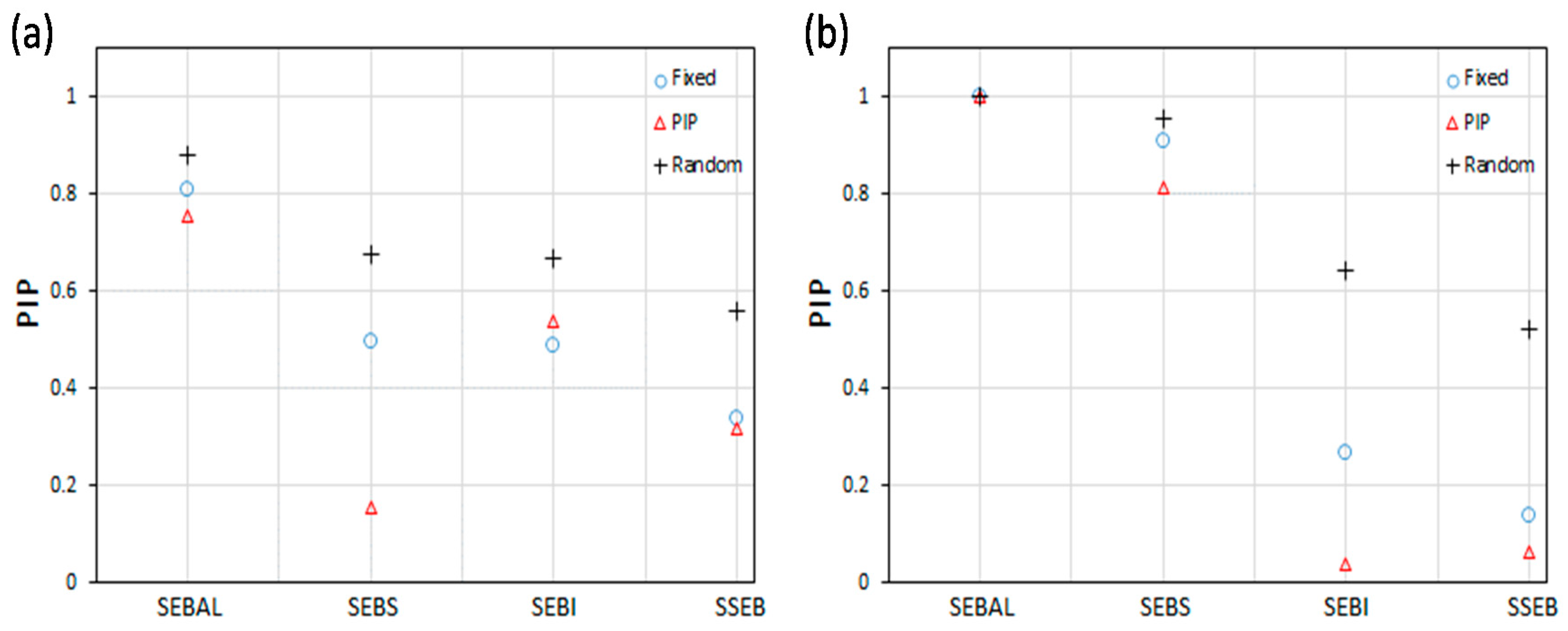
3.2. Effect of Model Priors
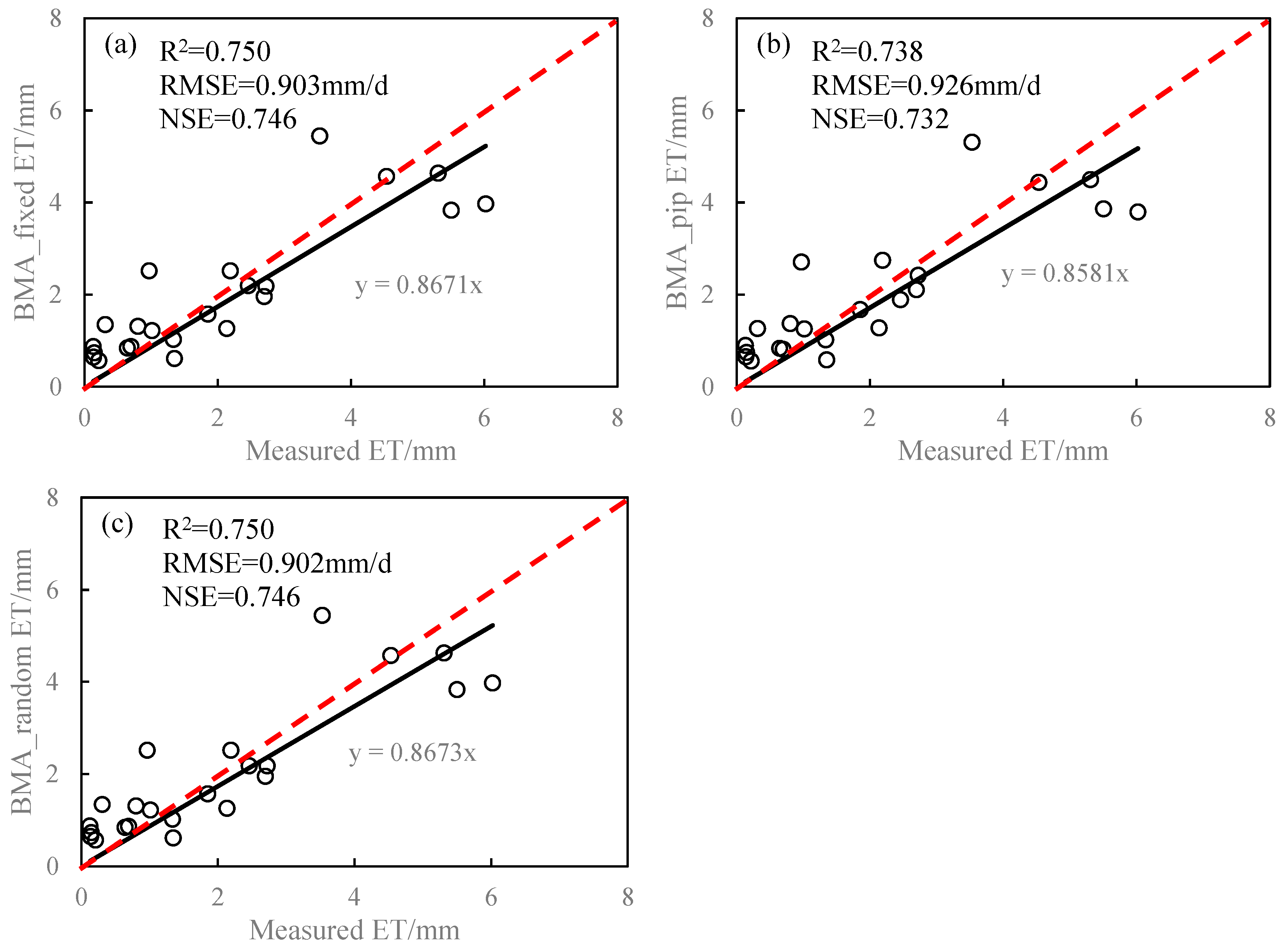
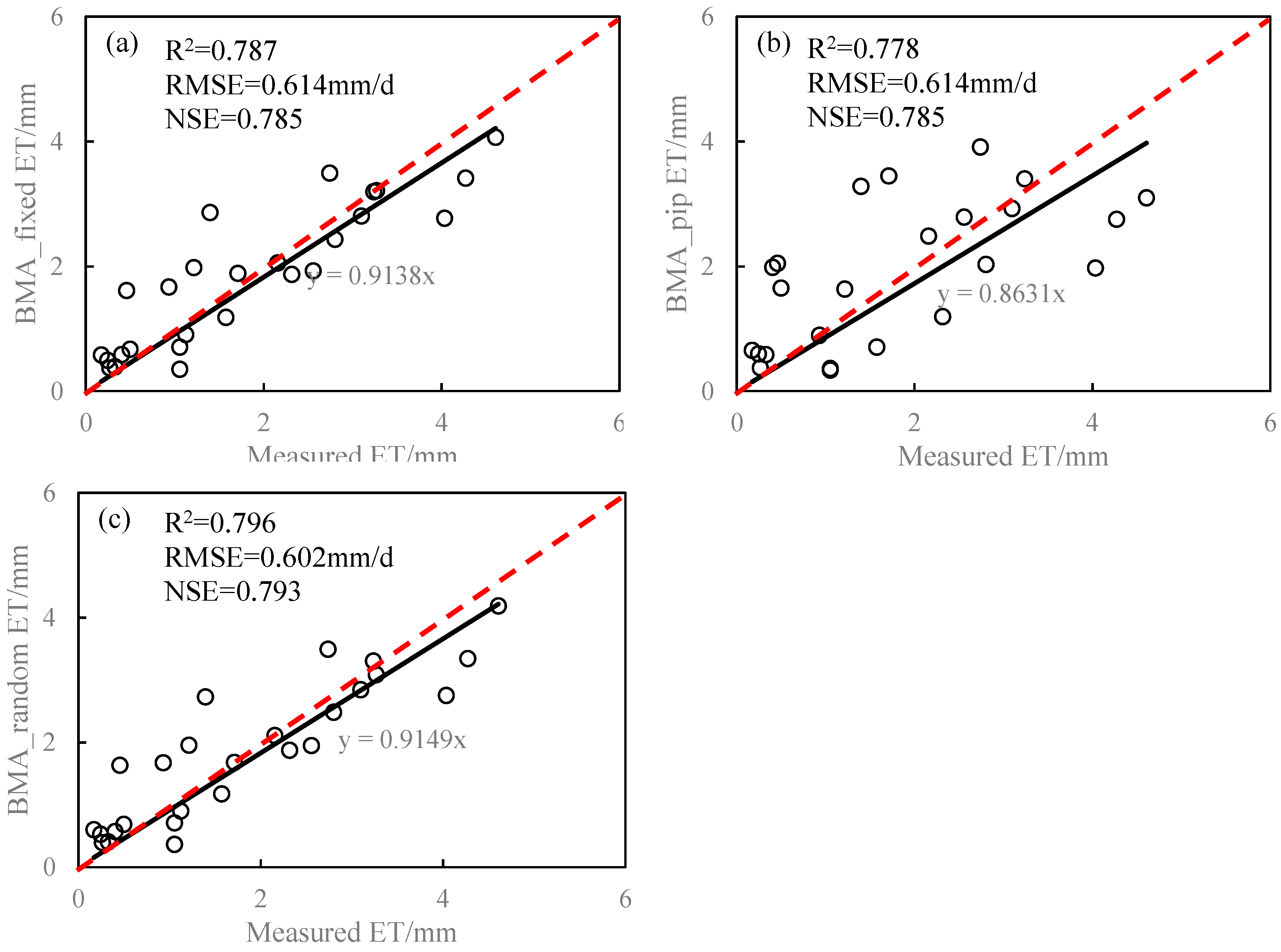
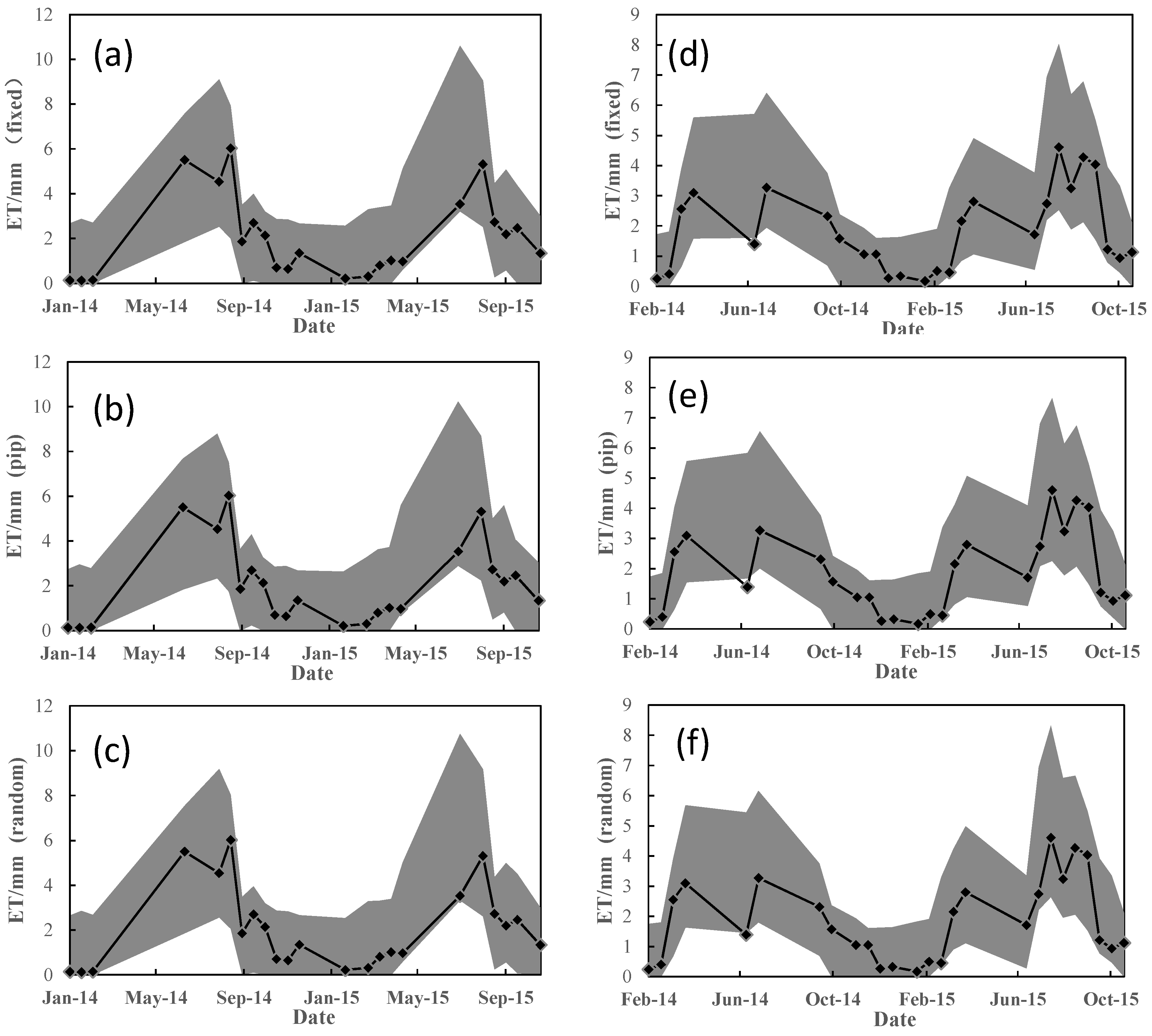
3.3. Performances of the BMA Methods
4. Conclusions
Author Contributions
Funding
Acknowledgements
Conflicts of Interest
References
- Wang, K.C.; Dickinson, R.E. A Review of Global Terrestrial Evapotranspiration: Observation, Modeling, Climatology and Climatic Variability. Rev. Geophys. 2012, 50, RG2005. [Google Scholar] [CrossRef]
- Shiklomanov, A.I. World Water Resources: A New Appraisal and Assessment for the Twenty-First Century: A Summary of the Monograph “World Water Resources”; Reports; UNESCO: Paris, France, 1998; 37p. [Google Scholar]
- Yuan, W.P.; Liu, S.G.; Liang, S.L.; Tan, Z.X.; Liu, H.P.; Young, C. Estimations of Evapotranspiration and Water Balance with Uncertainty over the Yukon River Basin. Water Resour. Manag. 2012, 26, 2147–2157. [Google Scholar] [CrossRef]
- Liu, Y.; Ye, L.; Qin, H.; Hong, X.; Ye, J.; Yin, X. Monthly streamflow forecasting based on hidden Markov model and Gaussian Mixture Regression. J. Hydrol. 2018, 561, 146–159. [Google Scholar] [CrossRef]
- Zhang, Y.R.; Sun, A.; Sun, H.W.; Gui, D.W.; Xue, J.; Liao, W.H.; Yan, D.; Zhao, N.; Zeng, X.F. Error adjustment of TMPA satellite precipitation estimates and assessment of their hydrological utility in the middle and upper Yangtze River Basin, China. Atmos. Res. 2019, 216, 52–64. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L. Recent Decline in the Global Land Evapotranspiration Trend Due to Limited Moisture Supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F.; Roderick, M.L. Little Change in Global Drought Over the Past 60 years. Nature 2012, 491, 435–438. [Google Scholar] [CrossRef] [PubMed]
- Yan, D.; Jia, Z.W.; Xue, J.; Sun, H.W.; Gui, D.W.; Liu, Y.; Zeng, X.F. Inter-Regional Coordination to Improve Equality in the Agricultural Virtual Water Trade. Sustainability 2018, 10, 4561. [Google Scholar] [CrossRef]
- Ma, W.Q.; Ma, Y.M.; Ishikawa, H. Evaluation of the SEBS for upscaling the evapotranspiration based on in-situ observations over the Tibetan Plateau. Atmos. Res. 2014, 138, 91–97. [Google Scholar] [CrossRef]
- Xue, J.; Gui, D.; Lei, J.; Sun, H.; Zeng, F.; Mao, D.; Zhang, Z.; Jin, Q.; Liu, Y. Oasis microclimate effects under different weather events in arid or hyper arid regions: A case analysis in southern Taklimakan desert and implication for maintaining oasis sustainability. Theor. Appl. Climatol. 2018, 8, 1–13. [Google Scholar] [CrossRef]
- Yin, J.; Zhan, C.S.; Ye, W. An Experimental Study on Evapotranspiration Data Assimilation Based on the Hydrological Model. Water Resour. Manag. 2016, 30, 5263–5279. [Google Scholar] [CrossRef]
- Guo, D.; Westra, S.; Maier, H.R. An R package for modelling actual, potential and reference evapotranspiration. Environ. Model. Softw. 2016, 78, 216–224. [Google Scholar] [CrossRef]
- McMahon, T.A.; Finlayson, B.L.; Peel, M.C. Historical developments of models for estimating evaporation using standard meteorological data. WIREs Water 2016, 3, 788–818. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Li, X.; Chen, J.; Liu, S.; Jia, K.; Zhang, X.; Xiao, Z.; Fisher, J.B.; Mu, Q.; et al. Improving global terrestrial evapotranspiration estimation using support vector machine by integrating three process-based algorithms. Agric. For. Meteorol. 2017, 242, 55–74. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global Estimates of the Land-atmosphere Water Flux Based on Monthly AVHRR and ISLSCP-II data, Validated at 16 FLUXNET Sites. Remote Sens. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Fisher, J.B.; Malhi, Y.; Bonal, D.; Da Rocha, H.R.; De Araujo, A.C.; Gamo, M.; Goulden, M.L.; Hirano, T.; Huete, A.R.; Kondo, H.; et al. The Land-atmosphere Water Flux in the Tropics. Glob. Chang. Biol. 2009, 15, 2694–2714. [Google Scholar] [CrossRef]
- Badgley, G.; Fisher, J.B.; Tu, K.P.; Vinukollu, R.K. On Uncertainty in Global Evapotranspiration Estimates from Choice of Input Forcing Datasets. Hydrometeorology 2015, 16, 1449–1455. [Google Scholar] [CrossRef]
- Verma, M.; Fisher, J.B.; Mallick, K.; Ryu, Y.; Kobayashi, H.; Guillaume, A.; Moore, G.; Ramakrishnan, L.; Hendrix, V.; Wolf, S.; et al. Global Daily Surface Net-radiation at 5 km from MODIS. Remote Sens. 2016, 8, 739. [Google Scholar] [CrossRef]
- Lian, J.J.; Huang, M.B. Evapotranspiration Estimation for an Oasis Area in the Heihe River Basin Using Landsat-8 Images and the METRIC Model. Water Resour. Manag. 2015, 29, 5157–5170. [Google Scholar] [CrossRef]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar] [CrossRef]
- French, A.N.; Hunsaker, D.J.; Thorp, K.R. Remote sensing of evapotranspiration over cotton using the TSEB and METRIC energy balance models. Remote Sens. Environ. 2015, 158, 281–294. [Google Scholar] [CrossRef]
- Sun, H.; Gui, D.; Yan, B.; Liu, Y.; Liao, W.; Zhu, Y.; Lu, C.; Zhao, N. Assessing the potential of random forest method for estimating solar radiation using air pollution index. Energy Convers. Manag. 2016, 119, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Roula, B.; Inga, M.; Andres, M.; Ticlavilca, W.R. Wavelet-Multivariate Relevance Vector Machine Hybrid Model for Forecasting Daily Evapotranspiration. Stoch. Environ. Res. Risk Assess. 2016, 30, 103–117. [Google Scholar] [CrossRef]
- Dormann, C.F.; Calabrese, J.M.; Guillera-Arroita, G.; Matechou, E. Model averaging in ecology: A review of Bayesian, information-theoretic, and tactical approaches for predictive inference. Ecol. Monogr. 2018, 88, 485–504. [Google Scholar] [CrossRef]
- Raftery, A.E.; Gneiting, T.; Balabdaoui, F.; Polakowski, M. Using Bayesian Model Averaging to Calibrate Forecast Ensembles. Mon. Weather Rev. 2005, 133, 1155–1174. [Google Scholar] [CrossRef] [Green Version]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model Ensemble Hydrologic Prediction Using Bayesian Model Averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Ellison, A.M. Bayesian Inference in Ecology. Ecol. Lett. 2004, 7, 509–520. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Robinson, B.A. Treatment of Uncertainty Using Ensemble Methods: Comparison of Sequential Data Assimilation and Bayesian Model Averaging. Water Resour. Res. 2007, 43, W01411. [Google Scholar] [CrossRef]
- Liu, Y.; Xue, J.; Gui, D.; Lei, J.; Sun, H.; Lv, G.; Zhang, Z. Agricultural Oasis Expansion and Its Impact on Oasis Landscape Patterns in the Southern Margin of Tarim Basin, Northwest China. Sustainability 2018, 10, 1957. [Google Scholar] [CrossRef]
- Liang, Z.M.; Wang, D.; Guo, Y.; Zhang, Y.; Dai, R. Application of Bayesian Model Averaging Approach to Multi-Model Ensemble Hydrologic Forecasting. J. Hydrol. Eng. 2011, 18, 1426–1436. [Google Scholar] [CrossRef]
- Zhu, G.F.; Li, X.; Zhang, K.; Ding, Z.Y. Multi-model Ensemble Prediction of Terrestrial Evapotranspiration Across North China Using Bayesian Model Averaging. J. Hydrol. Process. 2016, 30, 2861–2879. [Google Scholar] [CrossRef]
- Chen, Y.; Yuan, W.P.; Xia, J.Z.; Joshua, B. Fisher, Using Bayesian Model Averaging to Estimate Terrestrial Evapotranspiration in China. J. Hydrol. 2015, 52, 537–549. [Google Scholar] [CrossRef]
- Allen, R.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A Remote Sensing Surface Energy Balance Algorithm for Land (SEBAL). J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Allen, R.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.; Bastiaanssen, W.; Kramber, W.; Lorite, I.; Robison, C. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)-Applications. J. Irrig. Drain. Eng. 2007, 133, 395–406. [Google Scholar] [CrossRef]
- Senay, G.B.; Budde, M.E.; Verdin, J.P. Enhancing the Simplified Surface Energy Balance (SSEB) Approach for Estimating Landscape ET: Validation with the METRIC Model. Agric. Water Manag. 2011, 98, 606–618. [Google Scholar] [CrossRef]
- Roerink, G.J.; Su, Z.; Menenti, M. S-SEBI: A Simple Remote Sensing Algorithm to Estimate the Surface Energy Balance. Phys. Chem. Earth 2000, 25, 147–157. [Google Scholar] [CrossRef]
- Su, Z.; Schmugge, T.; Kusts, W.P. An Evaluation of Two Models for Estimation of the Roughness Height for Heat Transfer between the Land Surface and Atmosphere. J. Appl. Meteorol. 2001, 40, 1933–1951. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for Estimation of Turbulent Heat Fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian Model Averaging: A Tutorial. Stat. Sci. 1999, 14, 382–417. [Google Scholar]
- Ley, E.; Steel, M.F. On the Effect of Prior Assumptions in Bayesian Model Averaging with Applications to Growth Regressions. J. Appl. Econom. 2009, 24, 651–674. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the Use of ‘goodness-of-fit’ Measures in Hydrologic and Hydroclimatic Model Validation. Water Resource. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Jackson, R.D. Estimation of daily evapotranspiration from one time-day measurements. Agric. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Tian, F.; Qiu, G.; Yang, Y.; Lü, Y.; Xiong, Y. Estimation of evapotranspiration and its partition based on an extended three-temperature model and MODIS products. J. Hydrol. 2013, 498, 210–220. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S. FLUXNET: A New Tool to Study the Temporal and Spatial Variability of Ecosystem-scale Carbon Dioxide, Water Vapor and Energy Flux Densities. Bull. Am. Meteorol. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Ke, Y.; Im, J.; Park, S.; Gong, H. Downscaling of MODIS One Kilometer Evapotranspiration Using Landsat-8 Data and Machine Learning Approaches. Remote Sens. 2016, 8, 215. [Google Scholar] [CrossRef]
- Bhattarai, N.; Mallick, K.; Brunsell, N.A.; Sun, G.; Jain, M. Evapotranspiration from An Image-Based Implementation of the Surface Temperature Initiated Closure(STIC1.2) Model and Its Validation across an Aridity Gradient in the Conterminous US. Hydrol. Earth Syst. Sci. 2018, 22, 2311–2341. [Google Scholar] [CrossRef]
- Vinukollu, R.K.; Wood, E.F.; Ferguson, C.R.; Fisher, J.B. Global estimates of evapotranspiration for climate studies using multi-sensor remote sensing data: Evaluation of three process-based approaches. Remote Sens. Environ. 2011, 115, 801–823. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Veroustraete, F. Experimental Sentinel-2 LAI estimation using parametric, non-parametric and physical retrieval methods—A comparison. ISPRS J. Photogramm. Remote Sens. 2015, 108, 260–272. [Google Scholar] [CrossRef]
- Wang, J.M.; Zhuang, J.X.; Wang, W.Z.; Liu, S.M.; Xu, Z.W. Assessment of Uncertainties in Eddy Covariance Flux Measurement Based on Intensive Flux Matrix of HiWATER-MUSOEXE. IEEE Geosci. Remote Sens. 2014, 12, 259–263. [Google Scholar] [CrossRef]
- Masseroni, D.; Corbari, C.; Mancini, M. Validation of theoretical footprint models using experimental measurements of turbulent fluxes over maize fields in PoValley. Environ. Earth Sci. 2014, 72, 1213–1225. [Google Scholar] [CrossRef]
- Masseroni, D.; Corbari, C.; Mancini, M. Limitations and improvements of the energy balance closure with reference to experimental data measured over a maize field. Atmósfera 2014, 27, 335–352. [Google Scholar] [CrossRef] [Green Version]
| ET Model Name | Input Parameters | Assumption of Estimating H | Advantages | Disadvantages |
|---|---|---|---|---|
| SEBAL | Ts, Rn, , , , , , u, G | a linear relationship between and Ts | Less measured ground data, have internal self-calibration mechanism | Require flat underlying surface, uncertainty in pixel selection |
| SSEB | Ts, Rn, G | a linear relationship between ET fraction and LST | Do not need ground measured data input | Uncertainty in Pixel selection |
| S-SEBI | Ts, , albedo, Rn, G | linear relationship between Ts and albedo | Do not need ground measured data input | Need to select a specific location as Thot and Tcold |
| SEBS | Ts, , u, , , Rn, G | The atmospheric similarity theory | Accurately calculate roughness height instead of using fixed values | Excessive input parameters, complicated calculation of turbulent heat flux |
| Site Name | Huailai | Sidaoqiao |
|---|---|---|
| Location (lat./long.) | 40.3491° N/115.7880° E | 42.0048° N/101.1138° E |
| Elevation (m) | 480 | 875 |
| EC tower above canopy (m) | 5 | 3.5 |
| Climate zone | Semiarid | Arid/semiarid |
| Vegetation type | Cropland (corn) | Cropland (muskmelon) |
| Data collected years | 2014~2015 | 2014~2015 |
| Area | Path/Row: Image Dates (Expressed as Month/Day/Year) |
|---|---|
| Huailai | 124/32: 01/14/2014, 01/30/2014, 02/15/2014, 06/23/2014, 08/10/2014, 08/26/2014, 09/11/2014, 09/27/2014, 10/13/2014, 10/29/2014, 11/14/2014, 11/30/2014, 02/02/2015, 03/06/2015, 03/22/2015, 04/07/2015, 04/23/2015, 07/12/2015, 08/13/2015, 08/29/2015, 09/14/2015, 09/30/2015, 11/01/2015, 12/03/2015 |
| Sidaoqiao | 133/31: 02/14/2014, 03/02/2014, 03/18/2014, 04/03/2014, 06/22/2014, 07/08/2014, 08/09/2014, 08/25/2014, 09/26/2014, 10/12/2014, 11/13/2014, 11/29/2014, 12/15/2014, 12/31/2014, 02/01/2015, 02/17/2015, 03/05/2015, 03/21/2015, 04/06/2015, 06/25/2015, 07/11/2015, 07/27/2015, 08/12/2015, 08/28/2015, 09/13/2015, 09/29/2015, 10/15/2015, 10/31/2015 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, H.; Yang, Y.; Wu, R.; Gui, D.; Xue, J.; Liu, Y.; Yan, D. Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models. Atmosphere 2019, 10, 188. https://doi.org/10.3390/atmos10040188
Sun H, Yang Y, Wu R, Gui D, Xue J, Liu Y, Yan D. Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models. Atmosphere. 2019; 10(4):188. https://doi.org/10.3390/atmos10040188
Chicago/Turabian StyleSun, Huaiwei, Yong Yang, Ruiying Wu, Dongwei Gui, Jie Xue, Yi Liu, and Dong Yan. 2019. "Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models" Atmosphere 10, no. 4: 188. https://doi.org/10.3390/atmos10040188
APA StyleSun, H., Yang, Y., Wu, R., Gui, D., Xue, J., Liu, Y., & Yan, D. (2019). Improving Estimation of Cropland Evapotranspiration by the Bayesian Model Averaging Method with Surface Energy Balance Models. Atmosphere, 10(4), 188. https://doi.org/10.3390/atmos10040188





