Arctic Sea Ice Decline in the 2010s: The Increasing Role of the Ocean—Air Heat Exchange in the Late Summer
Abstract
1. Introduction
2. Data and Methods
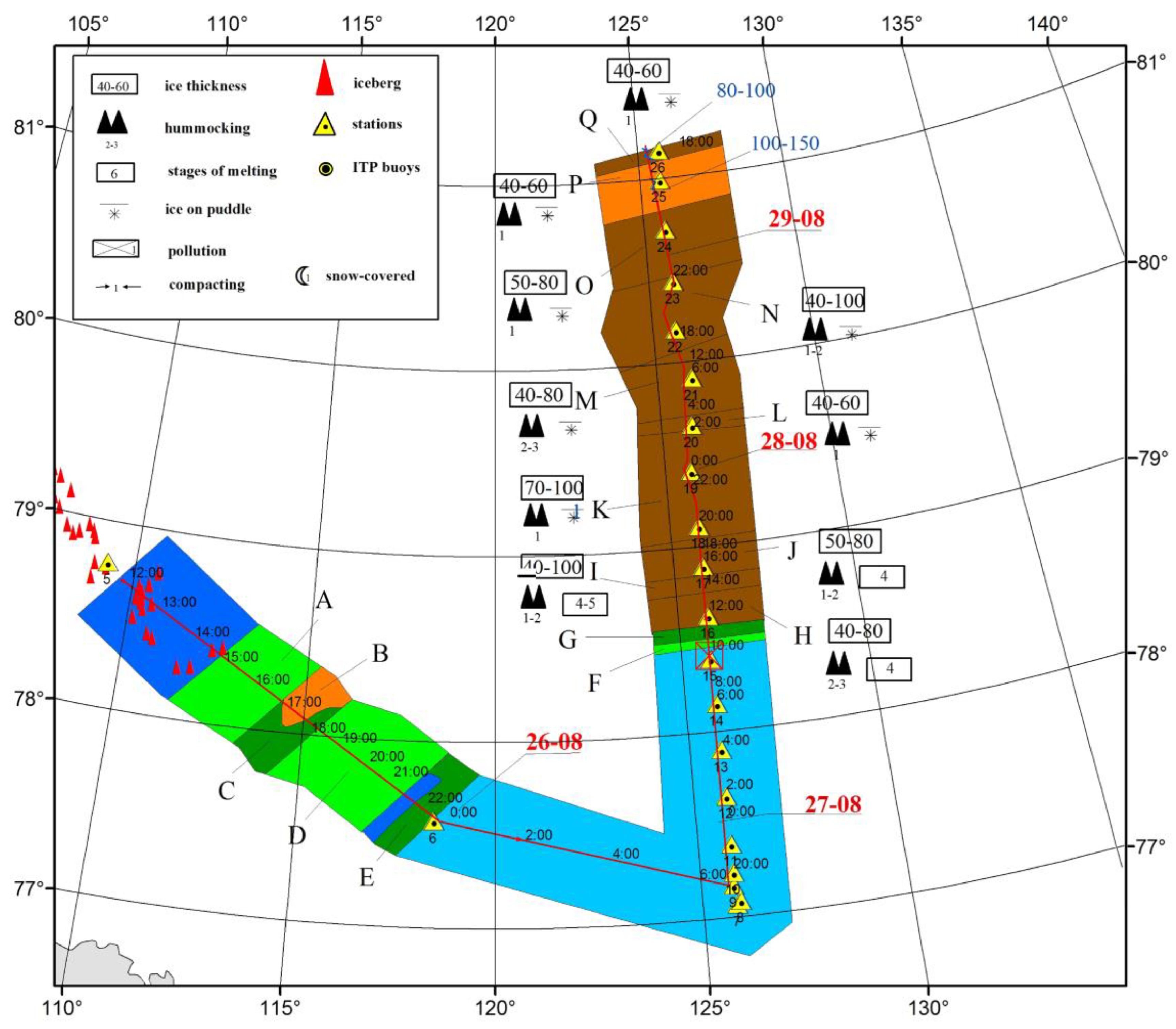
3. Ice and Hydrometeorological Conditions in the Central Laptev Sea in Summer
3.1. Ice Conditions
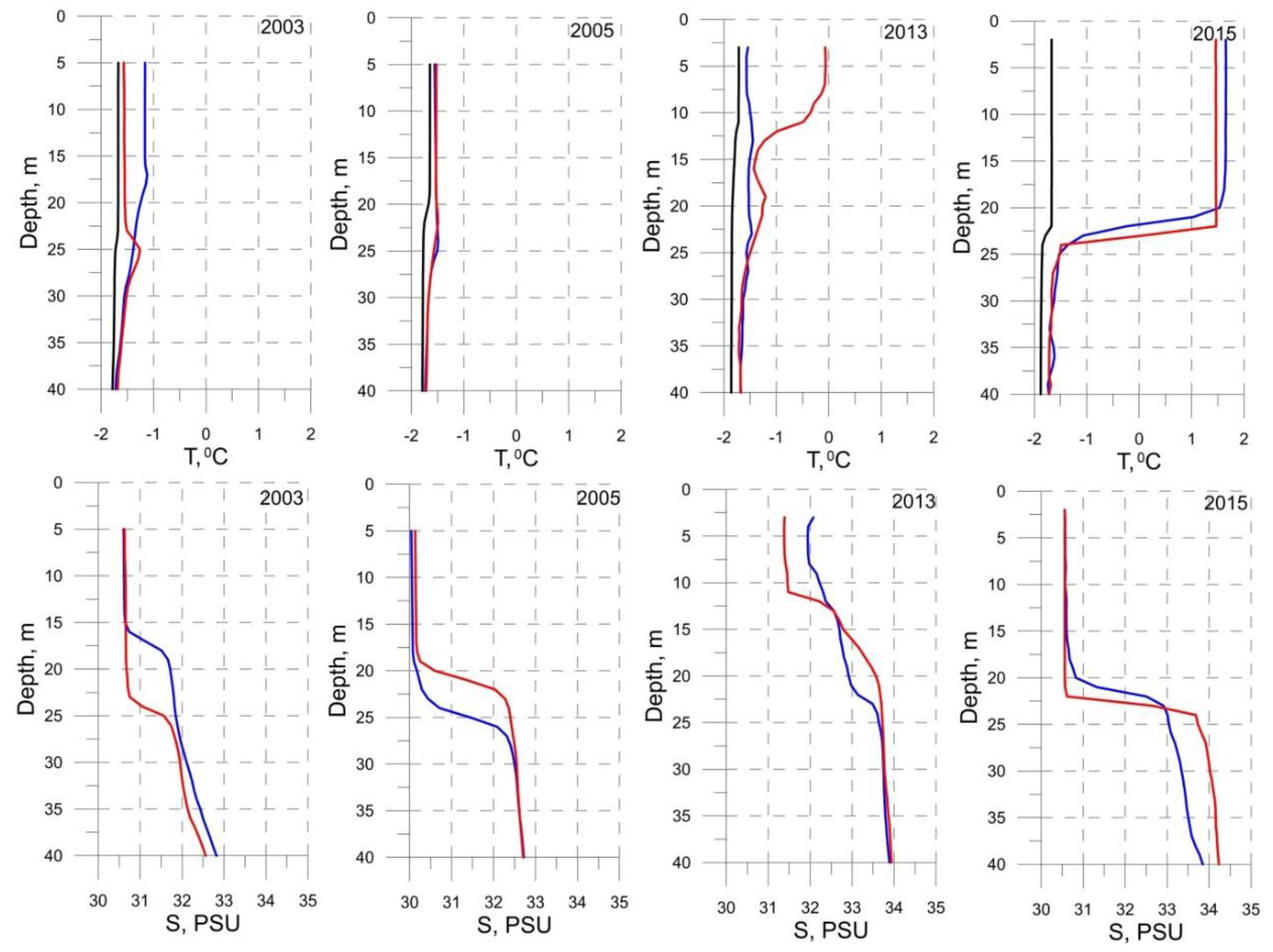
3.2. Hydrographic Conditions
3.3. Weather Conditions
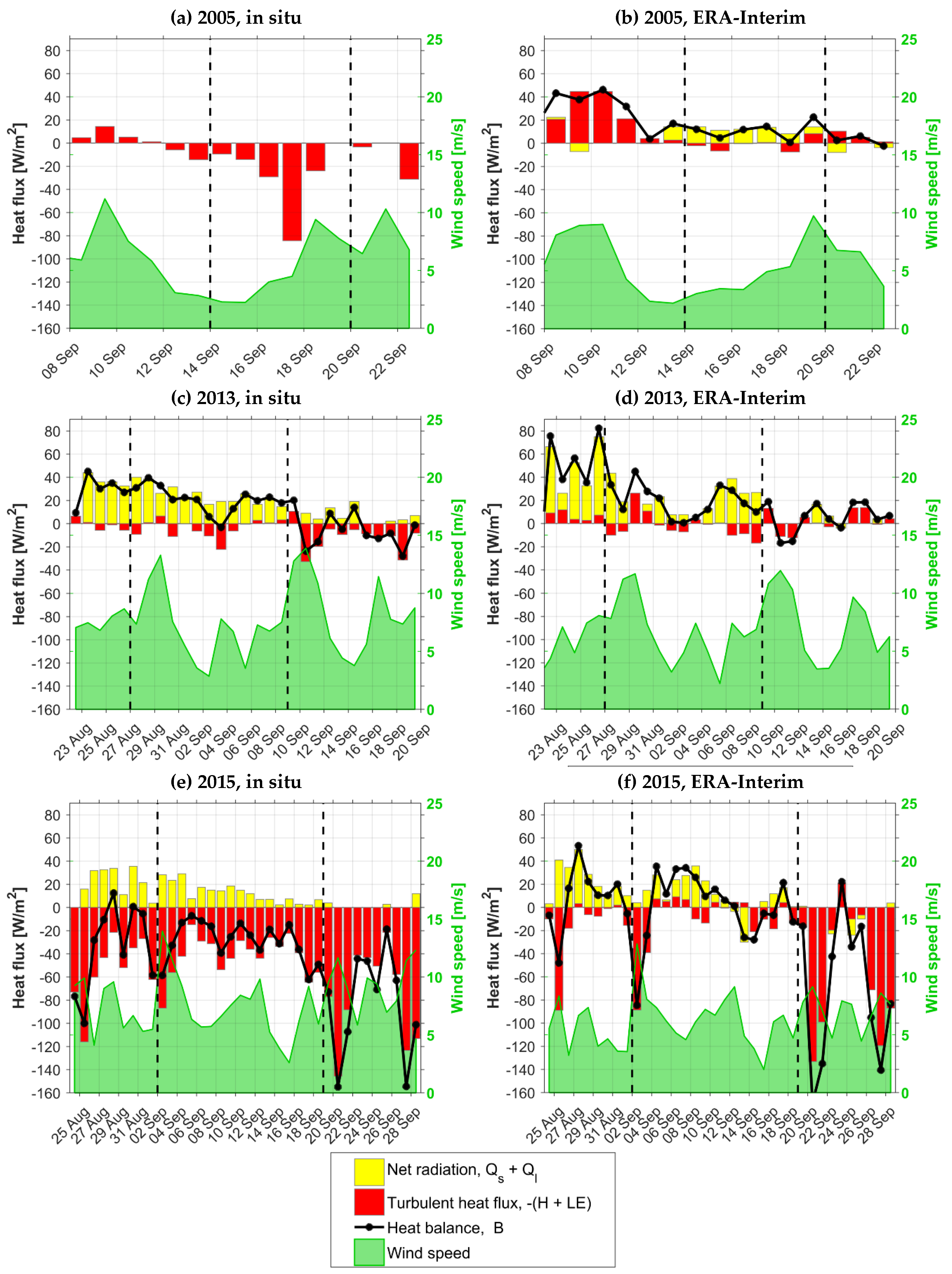
3.4. Ocean–Air Energy Exchange
3.5. Heat Accumulation in the UML
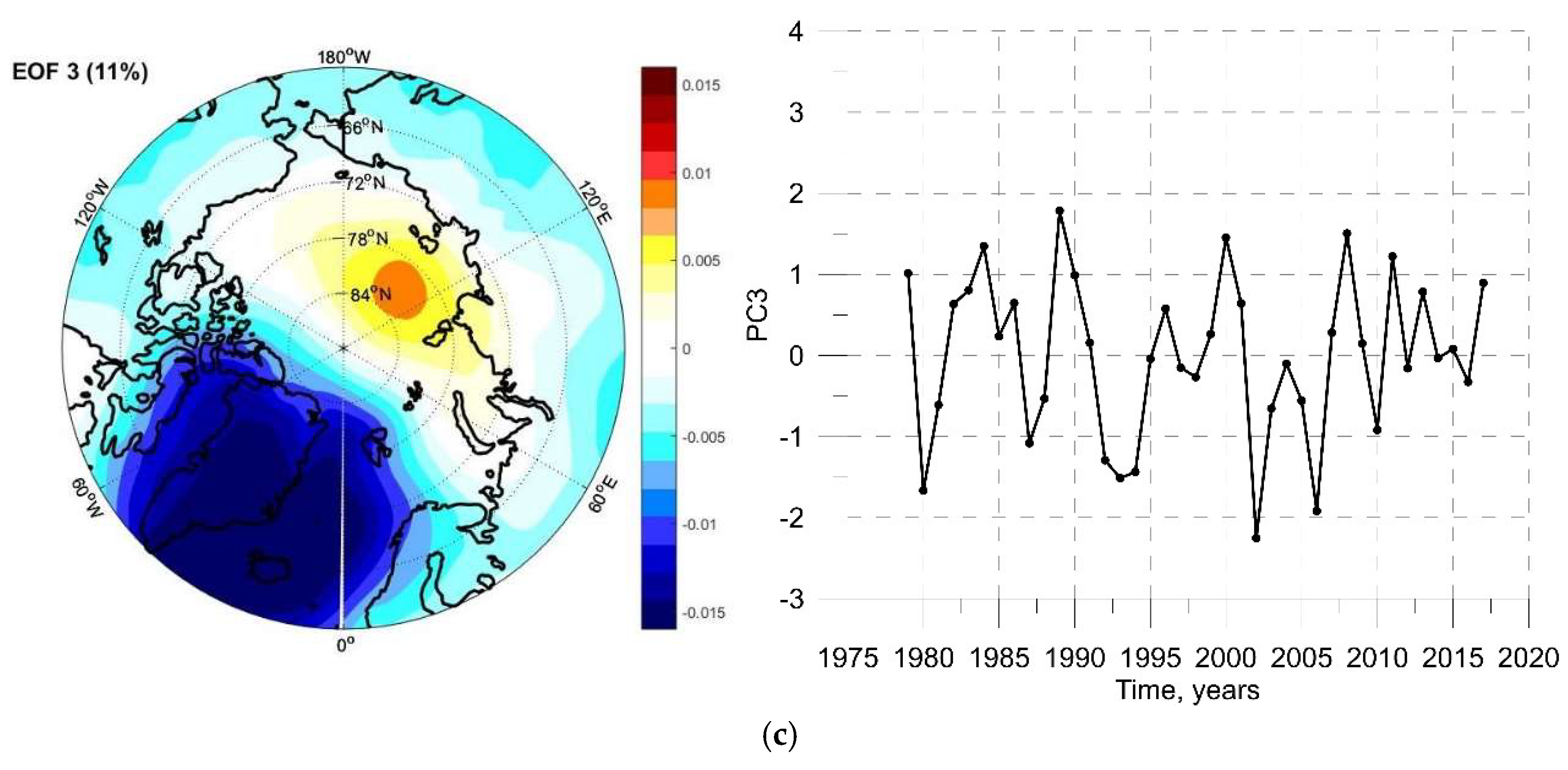
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix
A.1. Observational Techniques
| Observed Parameter | Measurement Instrument | |
|---|---|---|
| NABOS-2013 | NABOS-2015 | |
| Fluctuations of air temperature and three components of wind speed | Acoustic three-component anemometer Gill Wind Master, installed at the foredeck, 10 Hz frequency | Acoustic three-component anemometer METEK Sonic-3 Scientific, installed at the foredeck, 10 Hz frequency |
| Upward and downward fluxes of the shortwave and longwave radiation | Instrument cluster Kipp & Zonen (two pyrgeometers CGR-3 and two pyranometers CMP-21), installed at the crossbar on the upper deck, 1 min frequency | |
| Meteorological parameters (temperature, pressure, humidity, wind speed) | (1) Aanderaa AWS2700 automatic weather station (spaced apart left and right shipboards), 1 min frequency (2) Ship weather station | (1) Marine automatic weather station Airmar WX150 with an internal GPS, compass, inclinometer, and accelerometers, installed at the foredeck, 1 Hz frequency (2) Ship weather station |
| Characteristics of ship movement (speed, location, inclination) | Three-axis accelerometer ADXL330, inclinometer, GPS-receiver of Garmin 17N standard | |
| Sea surface temperature | Infrared radiometer HEITRONICS KT19.82, 1 Hz frequency | |
| Air temperature profile in the lower troposphere | Microwave temperature profiler MTP-5, installed at the upper deck at a height of 25 m above sea level, 5 min frequency, vertical resolution 50 m | |
| Vertical range 0–600 | Vertical range 0–1000 | |
A.2. Data Processing Techniques
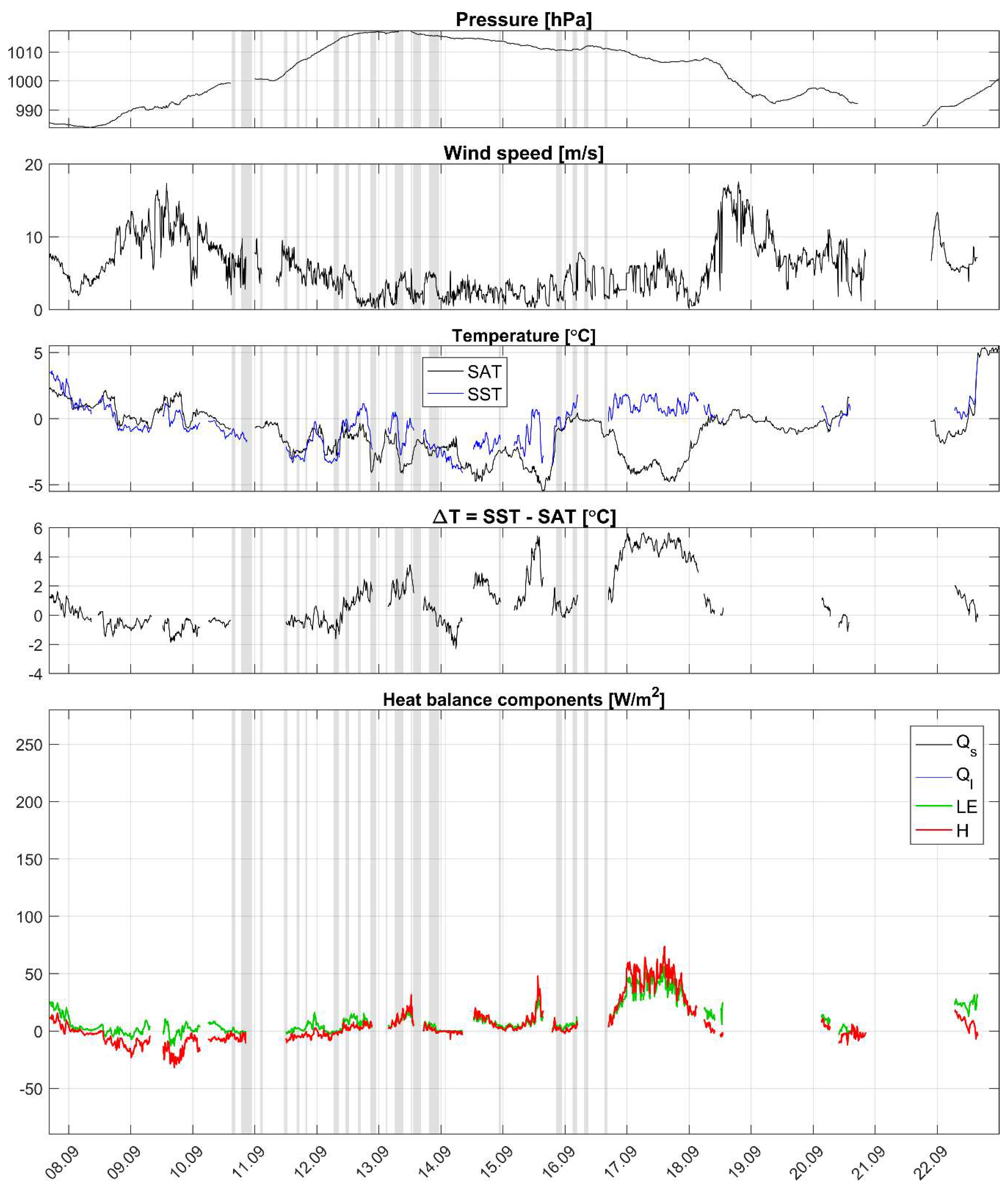
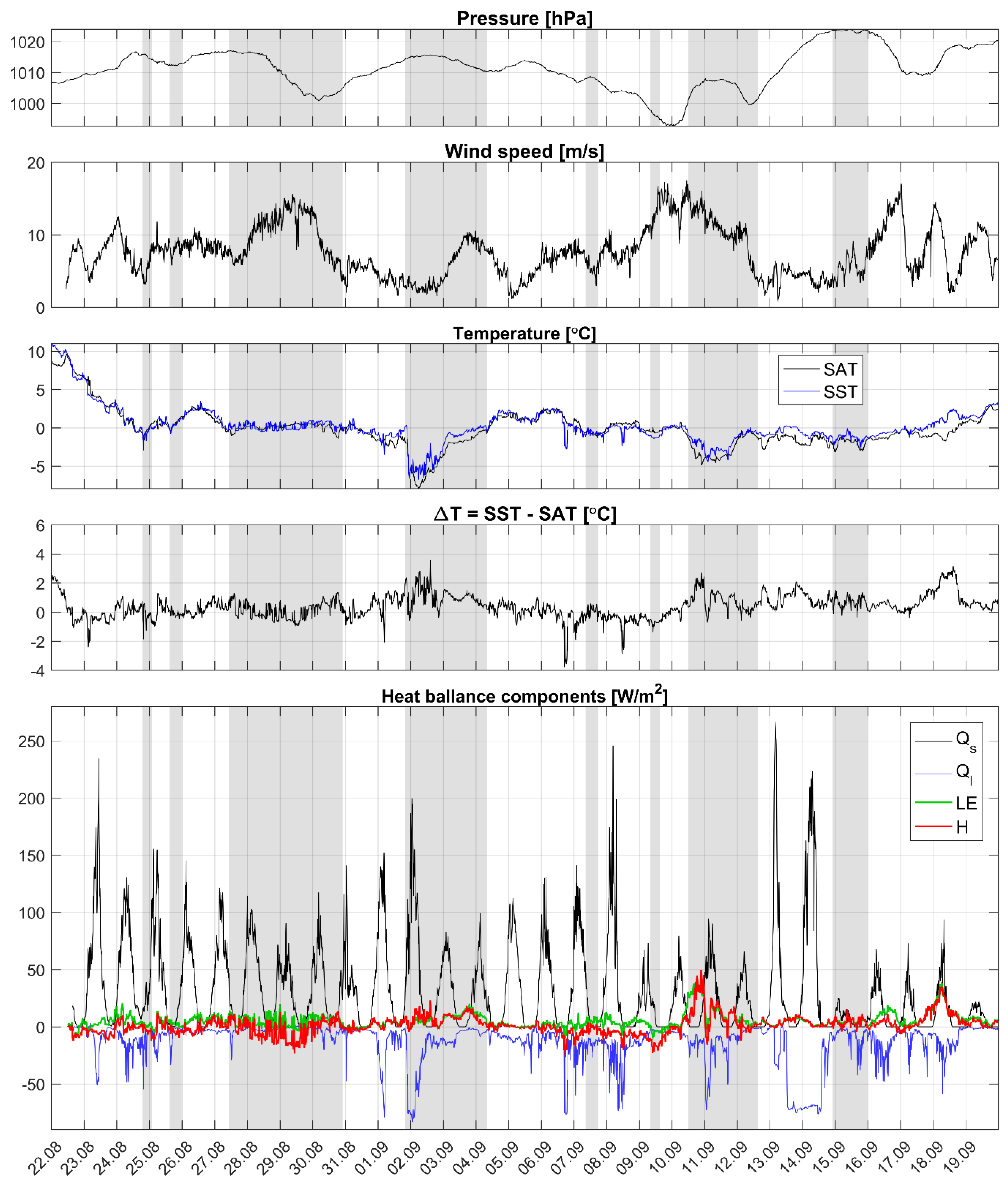
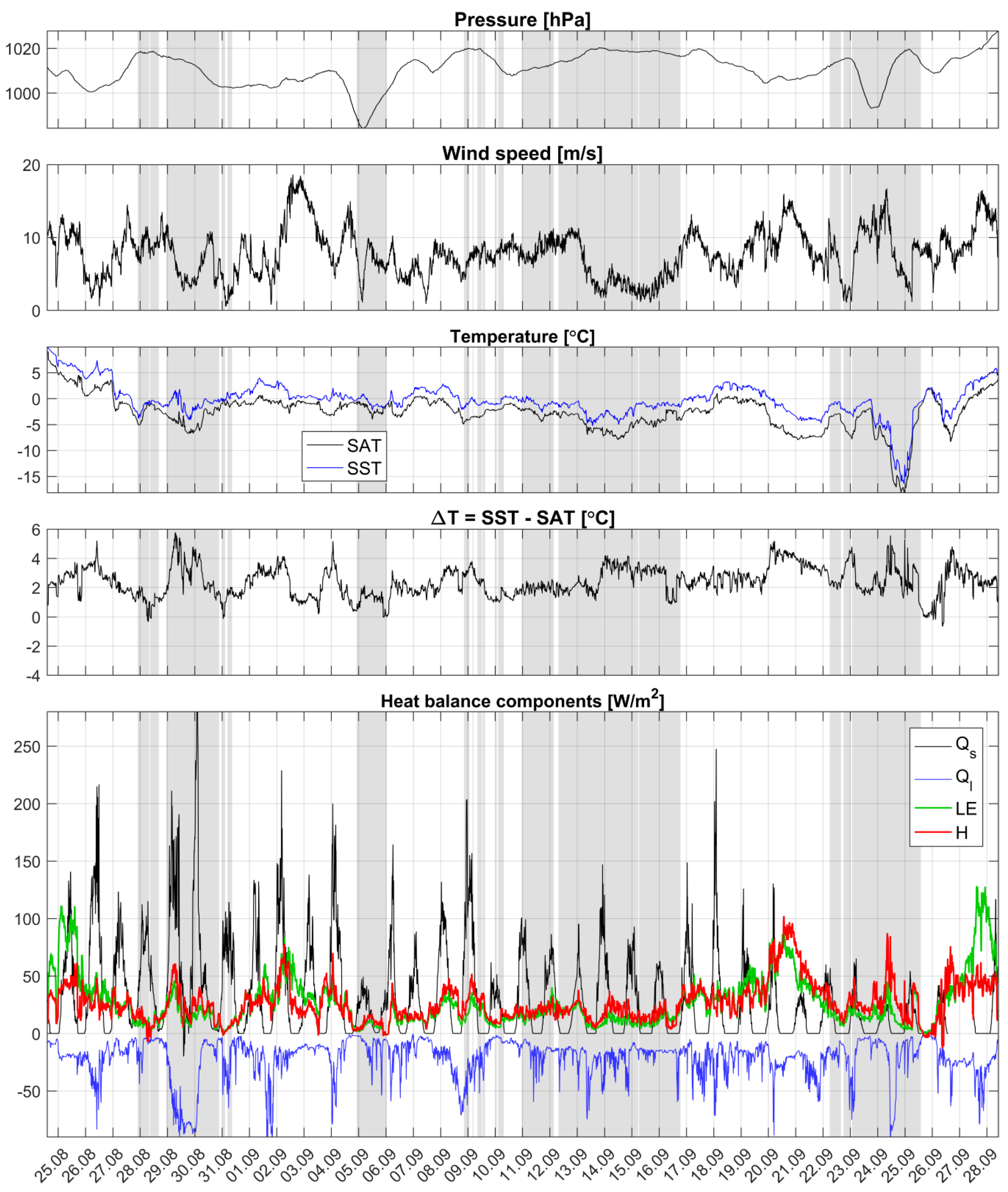
A.3. Observed Time Series of Meteorological Parameters and Their Comparison with Reanalysis Data
References
- Climate Change 2014–Synthesis Report. Contribution of Working Groups I, II 2366 and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Kwok, R.; Cunningham, G.F.; Wensnahan, M.; Rigor, I.; Zwally, H.J.; Yi, D. Thinning and volume loss of the Arctic Ocean sea ice cover: 2003–2008. J. Geophys. Res. Phys. 2009, 114. [Google Scholar] [CrossRef]
- Ivanov, V.; Alexeev, V.; Koldunov, N.V.; Repina, I.; Sandø, A.B.; Smedsrud, L.H.; Smirnov, A. Arctic Ocean heat impact on regional ice decay—A suggested positive feedback. J. Phys. Oceanogr. 2016, 46, 1437–1456. [Google Scholar] [CrossRef]
- Polyakov, I.V.; Pnyushkov, A.V.; Alkire, M.B.; Ashik, I.M.; Baumann, T.M.; Carmack, E.C.; Goszczko, I.; Guthrie, J.; Ivanov, V.V.; Kanzow, T.; et al. Greater role for Atlantic inflows on sea-ice loss in the Eurasian Basin of the Arctic Ocean. Science 2017, 356, 285–291. [Google Scholar] [CrossRef] [PubMed]
- Lind, S.; Ingvaldsen, R.B.; Furevik, T. Arctic warming hotspot in the northern Barents Sea linked to declining sea-ice import. Nat. Clim. Chang. 2018, 8, 634–639. [Google Scholar] [CrossRef]
- Timmermans, M.-L.; Toole, J.; Krishfield, R. Warming of the interior Arctic Ocean linked to sea ice losses at the basin margins. Sci. Adv. 2018, 4, eaat6773. [Google Scholar] [CrossRef] [PubMed]
- Kay, J.E.; Malanik, J.; Barrett, A.P.; Stroeve, J.C.; Serreze, M.C.; Holland, M.M. The Arctic’s rapidly shrinking sea ice cover: A research synthesis. Clim. Chang. 2011, 110, 1005–1027. [Google Scholar]
- Kraus, E.; Turner, J. A non-dimensional model of the seasonal thermocline. The general theory and its consequences. Tellus 1967, 19, 98–106. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Cavalieri, C.; Glo, D.; Parkinson ersen, P.; Zwally, H.J. Sea Ice Concentrations from Nimbus-7 SMMR and DMSP SSM/I-SSMIS Passive Microwave Data, 1979–2010; National Snow and Ice Data Center: Boulder, CO, USA, 1996; updated yearly. Digital media. [Google Scholar] [CrossRef]
- Lüpkes, C.; Vihma, T.; Jakobson, E.; Tetzlaff, A.; König-Langlo, G. Meteorological observations from ship cruises during summer to the central Arctic: A comparison with reanalysis data. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Lindsay, R.; Wensnahan, M.; Schweiger, A.; Zhang, J. Evaluation of Seven Different Atmospheric Reanalysis Products in the Arctic*. J. Clim. 2014, 27, 2588–2606. [Google Scholar] [CrossRef]
- Tikhonov, V.; Repina, I.; Raev, M.; Sharkov, E.; Ivanov, V.; Boyarskii, D.; Alexeeva, T.; Komarova, N.A. physical algorithm to measure sea ice concentration from passive microwave remote sensing data. Adv. Res. 2015, 56, 1578–1589. [Google Scholar] [CrossRef]
- Marcq, S.; Weiss, J. Influence of sea ice lead-width distribution on turbulent heat transfer between the ocean and the atmosphere. Cryosphere 2012, 6, 143–156. [Google Scholar] [CrossRef]
- Ivanov, V.V.; Alexeev, V.A.; Repina, I.A. Increase of Atlantic water impact on the Arctic sea ice. In Turbulence and Climate Dynamics, Proceedings of International Conference Dedicated to the Memory of Academician A.M. Obukhov, Moscow, Russia, 13–16 May 2013; Golitsyn, G.S., Mokhov, I.I., Kulichkov, S.N., Kurgansky, M.V., Chkhetiani, O.G., Chernokulsky, A.V., Eds.; GEOS: Moscow, Russia, 2014; pp. 336–345. [Google Scholar]
- Gaspar, P. Modeling the Seasonal Cycle of the Upper Ocean. J. Phys. Oceanogr. 1988, 18, 161–180. [Google Scholar] [CrossRef]
- Zubov, N.N. Arctic Ice (In Russian: L’dy Arktili); Isdatel’stvo Glavsevmorputi: Moscow, Russia, 1945; p. 360. [Google Scholar]
- Atlas of the Arctic (In Russian: Atlas Arktiki); GUGK: Moscow, Russia, 1985; p. 204.
- Иванoв, B.B.; Aлексеев, B.A.; Aлексеева, T.A.; Кoлдунoв, H.B.; Репина, И.A.; Смирнoв, A.B. Aрктический ледянoй пoкрoв станoвится сезoнным? Исследoвания Земли из Кoсмoса 2013, 2013, 50–65. [Google Scholar] [CrossRef]
- Björnsson, H.; Venegas, S.A. A manual for EOF and SVD analyses of climatic data. CCGCR Rep. 1997, 97, 112–134. [Google Scholar]
- Lorenz, E.N. Empirical Orthogonal Functions and Statistical Weather Prediction. Technical report; Statistical Forecast Project Report 1; Dept. of Meteor. MIT: Cambridge, MA, USA, 1956; p. 49. [Google Scholar]
- Thompson, D.W.J.; Wallace, J.M. The Arctic oscillation signature in the wintertime geopotential height and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef]
- Wang, M.; Overland, J.E. Large-scale atmospheric circulation changes are associated with the recent loss of Arctic sea ice. Tellus A: Dyn. Meteorol. Oceanogr. 2010, 62, 1–9. [Google Scholar]
- Ogi, M.; Tachibana, Y.; Yamazaki, K. The summertime annular mode in the Northern Hemisphere and its linkage to the winter mode. J. Geophys. Res. Phys. 2004, 109. [Google Scholar] [CrossRef]
- Ogi, M.; Rysgaard, S.; Barber, D.G. Importance of combined winter and summer Arctic Oscillation (AO) on September sea ice extent. Environ. Res. Lett. 2016, 11, 34019. [Google Scholar] [CrossRef]
- Quadrelli, R.; Wallace, J.M. A Simplified Linear Framework for Interpreting Patterns of Northern Hemisphere Wintertime Climate Variability. J. Clim. 2004, 17, 3728–3744. [Google Scholar] [CrossRef]
- Overland, J.E.; Wang, M. The third Arctic climate pattern: 1930s and early 2000s. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Overland, J.E.; Francis, J.A.; Hanna, E.; Wang, M. The recent shift in early summer Arctic atmospheric circulation. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Wu, B.; Yang, K.; Francis, J.A. Summer Arctic dipole wind pattern affects the winter Siberian High. Int. J. Clim. 2016, 36, 4187–4201. [Google Scholar] [CrossRef]
- LeGates, D.R. The effect of domain shape on principal components analyses: A reply. Int. J. Clim. 1993, 13, 219–228. [Google Scholar] [CrossRef]
- Sluggish Ice Growth in the Arctic. National Snow & Ice Data Center, Arctic Sea Ice New & Analysis. 02.11.2016. Available online: http://nsidc.org/arcticseaicenews/2016/11/ (accessed on 4 April 2019).
- Ivanov, V.; Smirnov, A.; Alexeev, V.; Koldunov, N.V.; Repina, I.; Semenov, V. Contribution of Convection-Induced Heat Flux to Winter Ice Decay in the Western Nansen Basin. J. Geophys. Res. Oceans 2018, 123, 6581–6597. [Google Scholar] [CrossRef]
- Burba, G. Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates; LI-COR Biosciences: Lincoln, KY, USA, 2013; p. 331. [Google Scholar]
- Moncrieff, J.B.; Clement, R.; Finnigan, J.; Meyers, T. Averaging detrending and filtering of eddy covariance time series. In Handbook of Micrometeorology: A Guide for Surface Flux Measurements; Lee, X., Massman, W.J., Law, B.E., Eds.; Kluwer Academic: Dordrecht, The Netherlands, 2004; pp. 7–31. [Google Scholar]
- Van Dijk, A.; Moene, A.F.; de Bruin, H.A.R. The Principles of Surface Flux Physics: Theory, Practice and Description of the ECPack Library; Meteorology and Air Quality Group, Wageningen University: Wageningen, The Netherlands, 2004; p. 99. [Google Scholar]
- Vickers, D.; Mahrt, L. Quality Control and Flux Sampling Problems for Tower and Aircraft Data. J. Atmos. Ocean. Technol. 1997, 14, 512–526. [Google Scholar] [CrossRef]
- Edson, J.B.; Hinton, A.A.; Prada, K.E.; Hare, J.E.; Fairall, C.W. Direct Covariance Flux Estimates from Mobile Platforms at Sea*. J. Atmos. Ocean. Technol. 1998, 15, 547–562. [Google Scholar] [CrossRef]
- Repina, I.A. Methods of Determination of Turbulent Fluxes above the Sea Surface; Space Research Institute: Moscow, Russia, 2007; p. 36. (In Russian) [Google Scholar]
- Andreas, E.L.; Jordan, R.E.; Makshtas, A.P. Parameterizing turbulent exchange over sea ice: The ice station weddell results. Bound.-Layer Meteorol. 2005, 114, 439–460. [Google Scholar] [CrossRef]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Grachev, A.; Fairall, C.; Larsen, S. On the Determination of the Neutral Drag Coefficient in the Convective Boundary Layer. Bound.-Layer Meteorol. 1998, 86, 257–278. [Google Scholar] [CrossRef]
- Holtslag, A.A.M.; de Bruin, H.A.R. Applied modelling of the nighttime surface energy balance over land. J. Appl. Meteorol. 1988, 27, 689–704. [Google Scholar] [CrossRef]
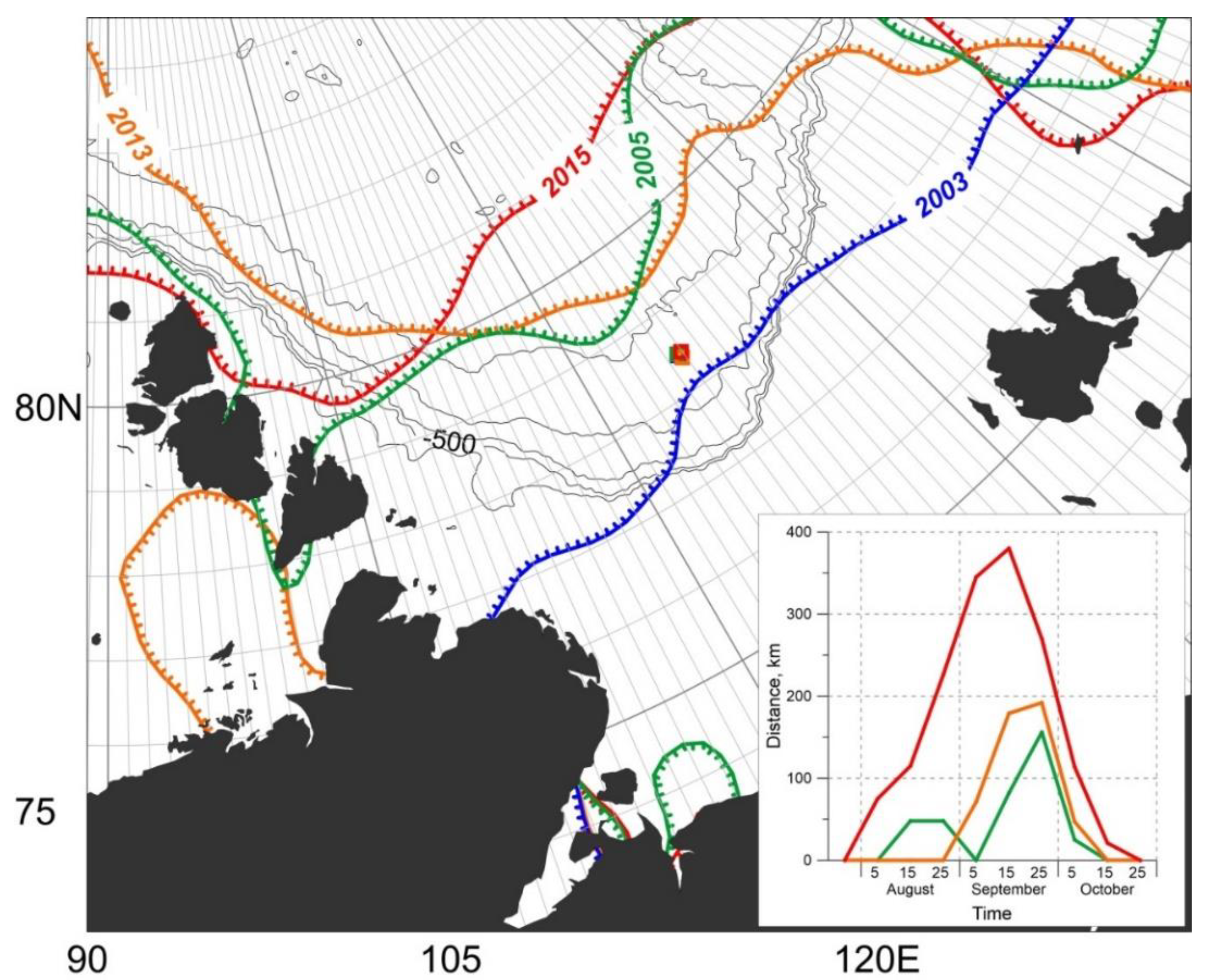
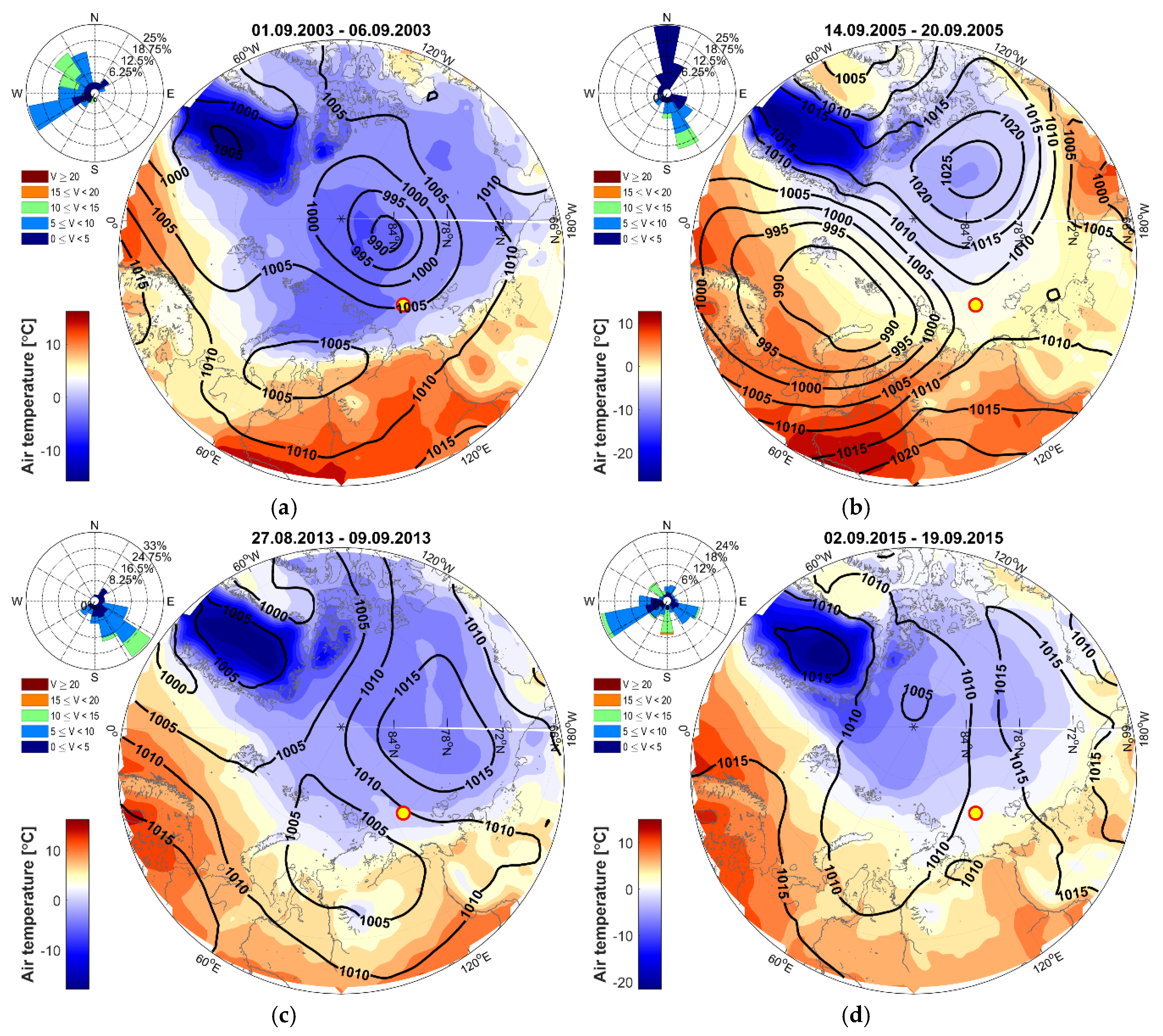
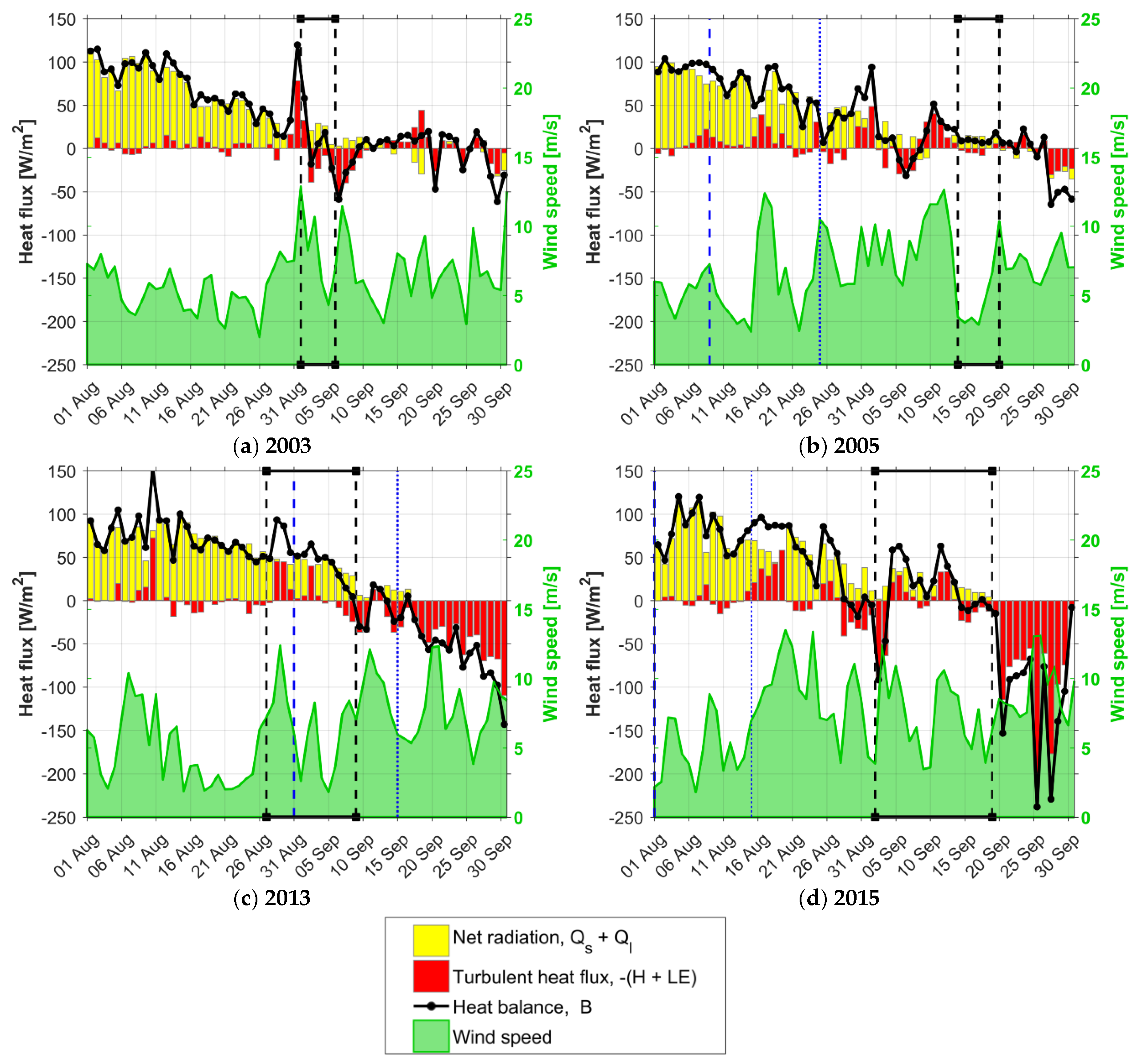
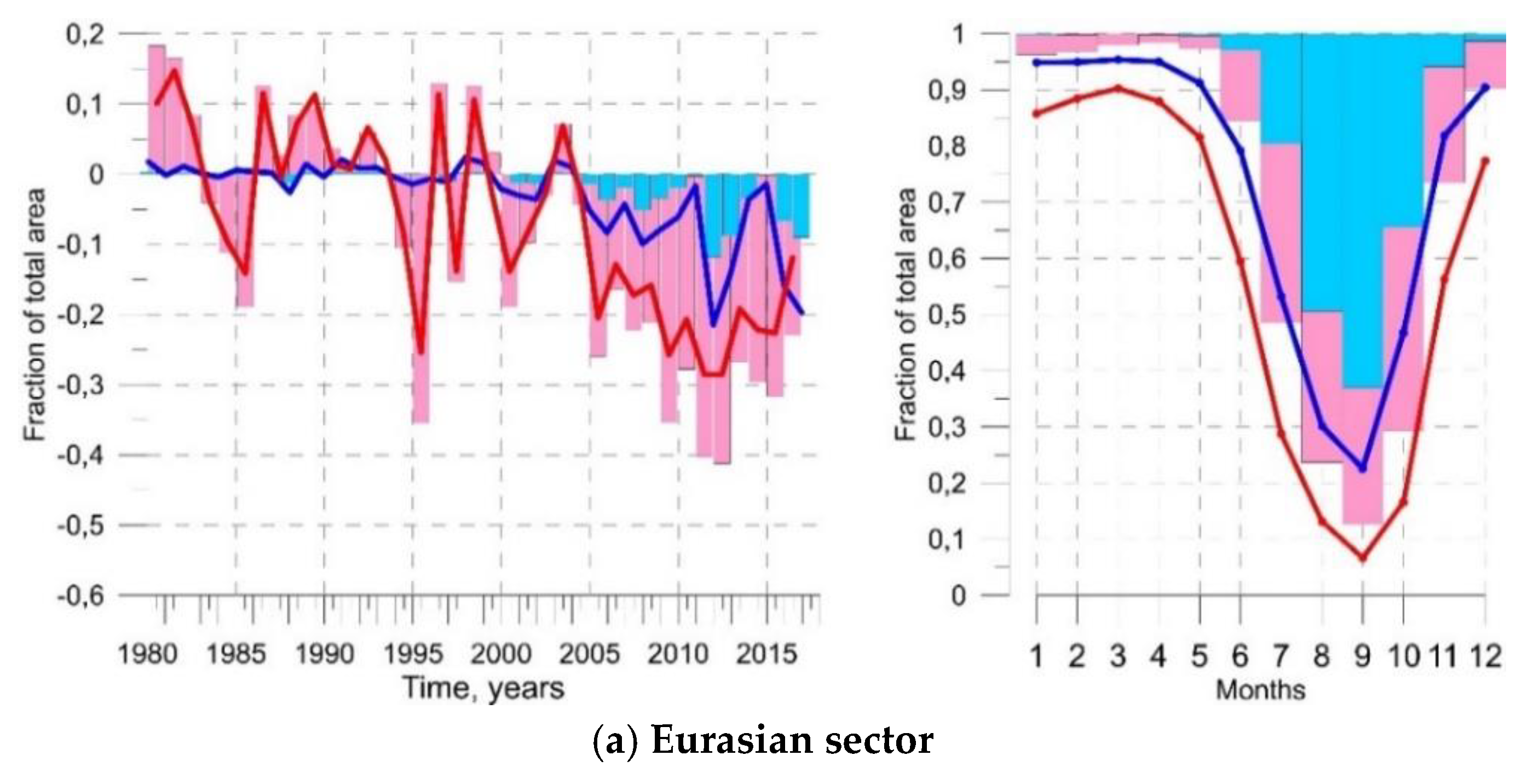
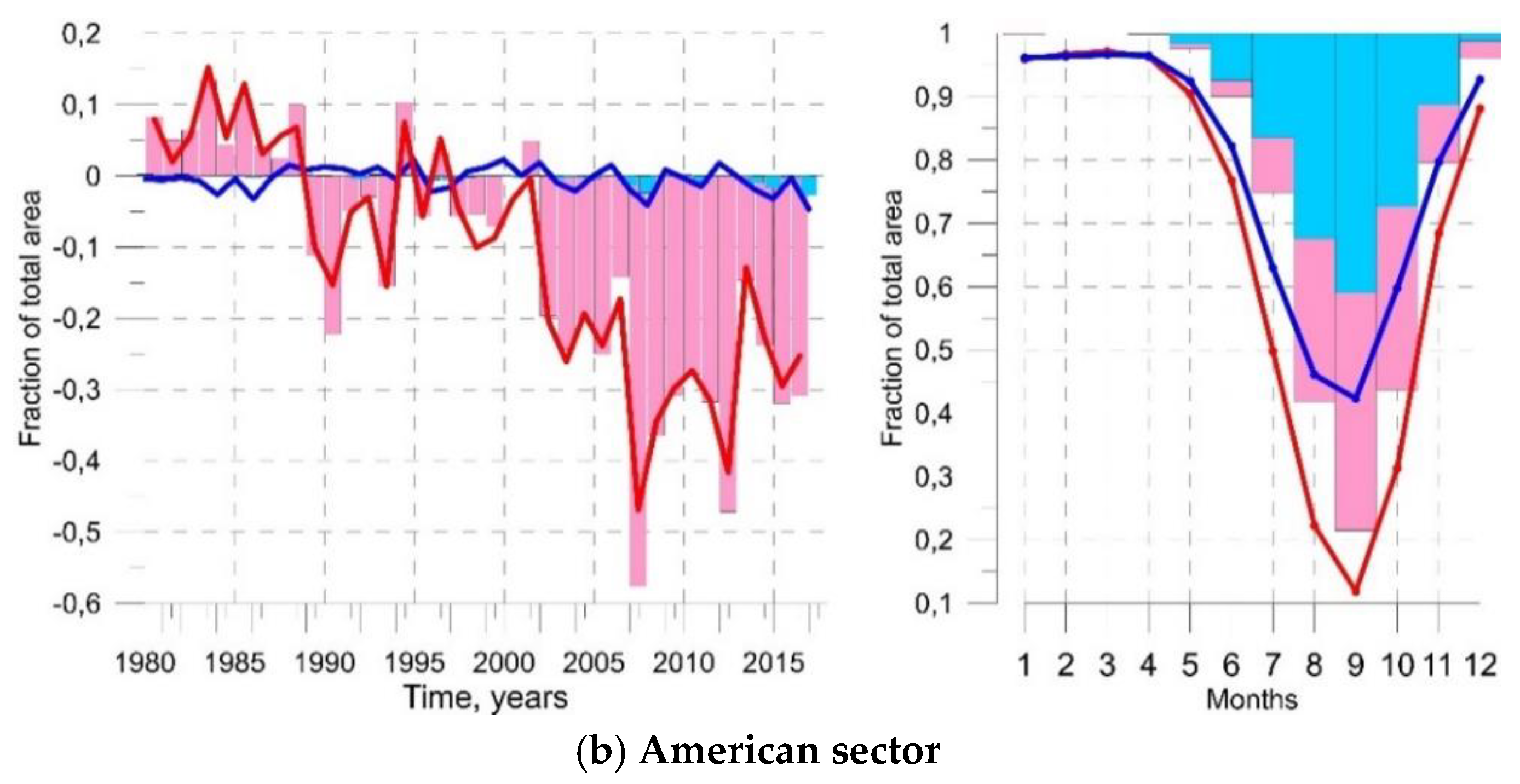
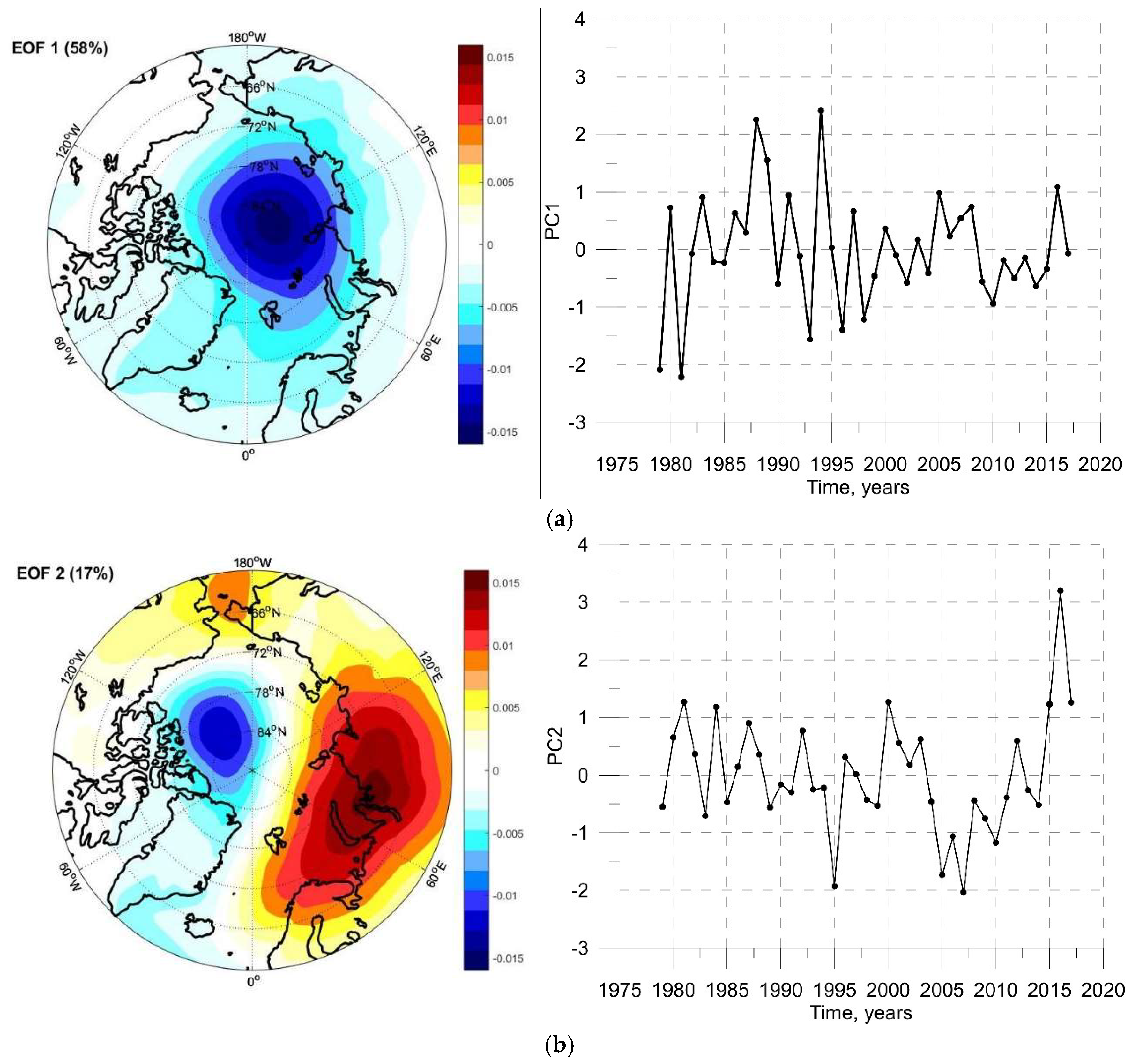
| Year | Date-1 | Date-2 | Lat., ° | Long., ° | Date of Opening, ±5 Days | Date of Closing, ±5 Days | Duration of Open Water, ±10 Days | Mean Distance to the Ice Edge, km |
|---|---|---|---|---|---|---|---|---|
| 2003 | 01.09 | 06.09 | 78.445 | 125.662 | n/a | n/a | n/a | n/a |
| 2005 | 14.09 | 20.09 | 78.464 | 125.668 | 25.08 | 05.10 | 40 | 60 |
| 2013 | 27.08 | 07.09 | 78.395 | 125.785 | 30.08 | 05.10 | 35 | 122 |
| 2015 | 02.09 | 19.09 | 78.460 | 125.930 | 30.07 | 20.10 | 80 | 193 |
| Region of Averaging | Year | SAT | SST | ΔT = SST − SAT |
|---|---|---|---|---|
| Average over ice-free water along the whole cruise tracks | 2013 | 0.68 | 1.03 | 0.34 |
| 2015 | −1.33 | 1.08 | 2.41 | |
| Average over ice-free water in Laptev sea region (100–150 °E) | 2013 | 0.35 | 0.43 | 0.08 |
| 2015 | −2.14 | 0.41 | 2.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ivanov, V.; Varentsov, M.; Matveeva, T.; Repina, I.; Artamonov, A.; Khavina, E. Arctic Sea Ice Decline in the 2010s: The Increasing Role of the Ocean—Air Heat Exchange in the Late Summer. Atmosphere 2019, 10, 184. https://doi.org/10.3390/atmos10040184
Ivanov V, Varentsov M, Matveeva T, Repina I, Artamonov A, Khavina E. Arctic Sea Ice Decline in the 2010s: The Increasing Role of the Ocean—Air Heat Exchange in the Late Summer. Atmosphere. 2019; 10(4):184. https://doi.org/10.3390/atmos10040184
Chicago/Turabian StyleIvanov, Vladimir, Mikhail Varentsov, Tatiana Matveeva, Irina Repina, Arseniy Artamonov, and Elena Khavina. 2019. "Arctic Sea Ice Decline in the 2010s: The Increasing Role of the Ocean—Air Heat Exchange in the Late Summer" Atmosphere 10, no. 4: 184. https://doi.org/10.3390/atmos10040184
APA StyleIvanov, V., Varentsov, M., Matveeva, T., Repina, I., Artamonov, A., & Khavina, E. (2019). Arctic Sea Ice Decline in the 2010s: The Increasing Role of the Ocean—Air Heat Exchange in the Late Summer. Atmosphere, 10(4), 184. https://doi.org/10.3390/atmos10040184








