Abstract
A two-dimensional mathematical model of moist air convection in the sub-cloud and cloud layers is proposed. A theoretical analysis of the influence of near ground atmospheric parameters on the development of sub-cloud and cloud convection is provided, and the criteria of convection development are considered. As a rule, this relationship is parameterized in general circulation, regional or mesoscale models of the atmosphere. Therefore, achieving a more complete and correct understanding of this relationship can lead to an improvement in the accuracy of weather forecasts. The mathematical model describes the system of the equations of motion, heat conductivity and the continuity equations for a two-dimensional vertical plane. The approximate analytical solution of the system of equations is obtained. Expressions for the estimation of the convection height and height of maximum velocity are derived for vertical and horizontal components of updraft wind and for vertical distribution of temperature. From the expressions obtained, the criterion of sub-cloud convection development is derived. The expressions for the convection parameters at a condensation level have also been formulated, from which the criterion of cloud development through convection is derived. It is established that the development of cloud convection depends on absolute values of the dew point deficit in a near-surface layer and, in a greater degree, on vertical gradients of water vapor mass fraction. It is shown that at certain critical values of a vertical gradient of water vapor mass fraction “explosive convective growth” is observed. The application of the obtained results to artificial stimulation of convection by means of air heating in the near-ground atmosphere has shown that the success of such an application and the required air heating-up depend on: (i) the vertical temperature gradient; (ii) the vertical dew-point gradient; and (iii) the value of the dew point deficit in the near-ground layer. The analysis performed has shown the possibility of successful stimulation of artificial convection under specific favorable atmospheric conditions.
1. Introduction
The formation of clouds and precipitation is known to be conditioned by the rise of moist air, its cooling, and condensation of the water vapor. The upward motion of air is triggered by either free air convection due to thermal instabilities of the atmosphere, or by the effect of the dynamic factors, associated with the passage of atmospheric fronts or flows around orographic heterogeneities.
This work is devoted to thermal convection, including: (i) convection of moist unsaturated air in the sub-cloud layer; and (ii) convection above the condensation level, where water vapor reaches the dew point and may pass into the liquid phase.
A number of studies have examined the development mechanisms of free thermal convection depending on the characteristics of the near-surface atmospheric layer (air temperature, moisture, and their vertical profiles). The effects of the vertical profile of moisture on the development of convection have been experimentally substantiated [1]. The effects of the near-surface layer on the vertical profiles of the temperature and moisture on the state of the free troposphere have been investigated [2]. Convection is believed to start from the formation of thermals, which, similar to phase transition, begins from the formation, under certain conditions, of a critical size thermal [3]. If the size of the thermal is subcritical, the thermal is unstable, and dissipates over time, while supercritical size thermals are stable, lifts off the ground and grows. Attempts to determine the critical size of thermals relied exclusively on the balance between the buoyancy force and Stokes’ resistance force; however, the theory requires further development.
Small-scale processes that are parameterized in the common circulation, regional, or mesoscale models, including shallow convection, add further complexities to the topic. The quality of these models depends largely upon the degree of understanding of the physics and adequate description of these processes [4,5]. The sub-cloud convection determines the vertical distribution of the moisture and temperature, and plays a key role in the global hydrological and energy cycles [6,7,8,9,10,11]. To deepen the understanding of the role of the sub-cloud convection in the climate models, simple one-dimensional models have been applied [2,12,13,14,15,16]; their improvement is also a vital task.
The moist (cloud) convection triggers severe storms that lead to showery rains, thunderstorms, hail, squalls, tornadoes, flash floods, and inundations [17]. Convective storms are usually local [18], hence, forecasting the locations, timings, and causes of their development are the most difficult challenges in weather forecasting [19]. Current operational numerical models are still generally unable to forecast the location and onset time of cloud convection initiated by the sub-cloud layer processes due to the poor representation of these processes in the model physics. It has been shown in [20,21] that the sub-cloud convection seriously affects the development of the cloud convection. Hence, forecasting the initiation of cloud (deep) convection requires knowledge on the sub-cloud layer thermodynamics.
Field surveys have provided insights on cloud convection initiation processes [21,22,23,24]. The understanding of the general dynamics of the processes under study is in place, whereas the initial stage of development of the convection cells remains insufficiently studied [25]. Some studies [1,26] have indicated that cloud convection initiation is quite sensitive to the sub-cloud layer temperature and moisture variations, whose field of moisture is a key factor to initiate the precipitation-forming convection [27]. Even slight variations of the water vapor mass fraction can promote or inhibit the development of storms (e.g. 1 g/kg variation of the water vapor mass fraction may lead to strictly antipodal forecasts: no convection or intensive convection [1]). The moisture of the underlying surface largely affects the sub-cloud layer water content [28,29], because a moist soil enriches the air of the near-surface layer with water vapor [30,31].
Hence, the effective forecast of storm events relies on the accurate determination of the initial thermodynamic characteristics and moisture of the sub-cloud layer. However, traditional meteorological observation systems do not permit a detailed structure of the near-surface atmosphere layer parameters. According to [24], the critical factor that limits forecasting convectional precipitation is the uncertainty of water vapor vertical distribution measurements. Radiosonde measurements are insufficient for these purposes, as they provide information on vertical profiles in distant locations, usually only twice a day, and are subject to significant errors [32,33].
To improve knowledge of the initiation of storms, two significant European studies have been conducted: the Convective Storms Initiation Project (CSIP) [19] in the south United Kingdom in summer 2005, and the Convective and Orographically-induced Precipitation Study (COPS) [34,35] in the south-west Germany and east France in summer 2007. The main purpose of these experiments was to observe the atmospheric boundary layer using a dense observation network consisting of radiosondes, wind profilers, and Global Positioning System (GPS) to determine water vapor contents, and automated weather stations. The findings highlighted the necessity to further refine theoretical concepts of the relationship between cloud convection and the processes in sub-cloud and near-surface layers. This will potentially improve the convective phenomena forecasting methods, while taking into account the aforementioned limitations of traditional weather observation systems.
In [36], the effect of the size of sub-cloud rising streams on the perturbation of the vertical velocity in cloud convection is studied. Simple analytical solutions were obtained, for which the following assumptions are made:
- the vertical component of the pressure disturbance gradient is ignored;
- the solution is sought for in the Boussinesq approximation, where the undisturbed air density is assumed to be constant;
- the solution is sought for in the form of the stationary two-dimensional wave.
It should be noted that such simple analytical solutions are necessary to understand the physics of the process, as well. In particular Weisman et al. (1997) [37] used solutions in the form of normal modes of the linearized two-dimensional Boussinesq equations of motion, equations of continuity, and equations of thermodynamics to draw a simple expression for the vertical velocity W0 in the sub-cloud layer:
where and are the amplitudes of the normal modes for the vertical velocity and buoyancy respectively; is the Brunt-Väisälä frequency; and are the horizontal and vertical wave numbers respectively.
Much of the previous work has dealt with the characteristics of the near-surface layer and their effect on the development of large-scale circulation [38,39] and cloud convection [40]. Studies dealing with the artificial stimulation of convection [41,42], where the sub-cloud layer was studied within the framework of the simple one-dimensional model, may be associated with the above. Nevertheless, convective motion is among the most common types of the atmospheric motions, while many gaps still exist in the physics of the process and its mathematical description.
The objectives of this work are to describe the sub-cloud and cloud convections within the framework of a two-dimensional model, analyze the effects of the near-surface layer on the development of the sub-cloud and cloud convections, and reveal the criteria of their development.
2. Definition of Problem
Radiosonde measurements, plotted on the aerological diagram, are commonly used to forecast cloud convection parameters. The routine assumption made is that the velocity of the rising streams and temperature excess of a buoyant parcel at the condensation level are equal to zero. However, this assumption does not always hold. Therefore, it appears important to determine how the near-surface layer parameters affect those of the cloud convection at the level of condensation. In the approach of artificial stimulation of convection, the major uncertainty lies in the parameter values of the near-surface layer that are reached when artificially stimulated convection reaches the condensation level for cloud formation.
In [43] the analytical solution of the two-dimensional model of thermal convection in the atmosphere of absolutely dry air was derived. In [44] the analytical solution was obtained for a two-dimensional model of the moist saturated air convection. Hence, we have analytical solutions for the two-dimensional models of the dry air convection that will be referred to as “sub-cloud” convection, and an analytical solution for the moist air convection model that will be referred to as “cloud” convection. In the present study, we attempt to apply the results of [43,44] to analyze the effects of the characteristics of the near-surface layer of atmosphere on the development of the cloud convection.
To describe the cloud convection we need to know such parameters as the temperature excess of a buoyant parcel, velocities of the rising flows, and mass fraction of the water vapor at the level of condensation. These parameters can be found by the examination of the sub-cloud convection determined by the characteristics of the surface layer. Therefore, the nature of cloud convection relates to the characteristics of the near-surface layer of atmosphere. The objective of this work consists of establishing this relationship. Here we perform analytical research on this problem within the framework of the two-dimensional nonlinear model of convection, based on earlier analytical solutions for dry and moist saturated air convection.
3. Equations of Thermal Convection or Moist Unsaturated Air
The sub-cloud air is not dry, requiring us to apply the previously described illustrations of convection of moist unsaturated air. Similar to (Zakinyan et al., 2015) [43], where the analytical solution for the two-dimensional model of dry air convection was obtained, we now derive the solution for the convection of moist unsaturated air, considering the effects of the near-surface layer on the values of the convection parameter at the level of condensation. For this we proceed with a stepwise approach to the conclusion made in [43], but taking into account the air moisture.
The equation of motion is considered in the plane. The pressure is presented as the sum of the static state pressure and its disturbance: . We define the moist air density by the expression:
where is the density of the disturbed air in atmosphere; is the density of the air in the static atmosphere; is the air thermal expansion coefficient ; is the temperature excess of a buoyant parcel; , are the air temperatures in the disturbed and undisturbed atmospheres respectively; is the mass fraction of the water vapor; is the oversaturation function; z is the altitude; ; is the molar weight of the dry air; and is the molar weight of the water vapor. Here index “p” denotes “parcel characteristics” and index ”e”—“environment”, “d”—“dry”, ”v”—“vapor”.
The rise of an air parcel is assumed to be adiabatic in the ambient undisturbed atmosphere where . In other words, we assume that in approximation (2) the air density depends on the temperature and mass fraction of the water vapor and is pressure independent [3,45]. The temperature excess of a buoyant parcel equals to:
where is the value of the temperature excess of a buoyant parcel near the ground surface ; , where is the air temperature gradient of the undisturbed static atmosphere; is the dry adiabatic temperature gradient; is the disturbed atmosphere air temperature near the ground surface; is the undisturbed static atmosphere air temperature near the ground surface.
In Equation (3) we assume that the air temperature of the undisturbed atmosphere varies linearly. This assumption differs from the actual vertical temperature profile with the presence of inhibiting layers, but it solves the problem analytically.
The mass fraction of water vapor in an adiabatically rising unsaturated air parcel remains constant and , where is the mass fraction of water vapor near the ground surface. Let the mass fraction of water vapor in a static undisturbed atmosphere decreases linearly:
where is the gradient of the mass fraction of water vapor. Then the expression for the oversaturation function is
where is the oversaturation near the ground surface. By substituting expressions (3) and (5) into Equation (2) the expression for the air parcel density will have the form
Find from here the level of equalization of the air density in an air parcel and in an undisturbed atmosphere from condition :
Assuming formally , we obtain from Equation (7) the expression for the level of equalization of the temperatures (the level of neutral buoyancy), that follows directly from Equation (3). It follows from here that for a moist parcel the level of equalization of the air densities is higher than that for the temperatures.
Advance evaluation of the temperatures equalization level is done with the following atmospheric parameters [45]: , where we get . Here we assumed the vertical temperature gradient equal to (for the standard atmosphere ) Average value of temperature excess of a buoyant parcel is . The warm season water vapor mass fraction gradient for middle latitudes is assumed to be equal to , also assume . For these parameter values, the level of equalization of densities is , that is, higher than that for the temperatures [45]. However, it follows from (7) that if the water vapor mass fraction gradient approaches a certain critical value equal to , then the level of equalization of the densities will go to infinity, with the so-called “explosive” intensification of convection. The real atmosphere presents many stability layers that would prevent convection from reaching arbitrary height levels. This is a distinctive feature of the moist atmosphere convection compared to the dry air convection. Hence, we see that the absolute value of the near-surface water vapor mass fraction is not critical for the convection, but its vertical gradient is.
Taking into account the static equation valid for the undisturbed atmosphere, the set of equations that describes the thermal convection of stationary moist unsaturated air has the form:
where and are the horizontal and vertical components of the air velocity. Here in Equation (9) it was assumed analogously to [36] that .
Note that the air motion in our model is described by the equation of motion of an ideal (nonviscous) fluid. In addition, we do not consider turbulent motion and consequently turbulent mechanism of air entrainment. Entrainment is taken into account only due to the continuity Equation (10). It should also be noted that, in contrast to equations for an incompressible fluid, in Equation (8) the density of air is a function of altitude. It can be seen from Equation (9) that the level of density equalization is the level of neutral buoyancy.
It follows from continuity Equation (10) that the stream function may be introduced as follows:
Comparing this system with the set of equations for the dry air thermal convection [43], one can see that they differ only in the right part of Equation (9). Hence, the solution for the set of Equations (8)–(10) is found similarly to that for the dry air set of equations.
The critical gradient for the water vapor mass fraction can be found from (7) at the condition :
Solving the system of Equations (8)–(11) for the moist unsaturated air convection by analogy with [43], we obtain the stream function in the form
From here with account of Equation (11), for the velocity projections we get:
Then, from Equation (15) under condition , for the moist unsaturated air convection level , the following expression is obtained
It should be noted that when predicting the convection parameters using an aerological diagram, it is assumed that the level of convection coincides with the level of temperature equalization (the level of neutral buoyancy). But in the framework of the adiabatic model of convection, this is not the case. The level of neutral buoyancy corresponds to the maximum velocity and the air continues its movement. There is an analogy with the oscillations of a pendulum. In our case, the air oscillates about an equilibrium position with the Brunt-Väisälä frequency.
It can be seen in Equation (16) that the level of convection depends on both the temperature excess of a buoyant parcel and oversaturation in the near-surface layer, and the vertical gradients of the temperature and the water vapor mass fraction. According to Equation (16), the following limiting cases can take place. At the convection development is more affected by the air temperature excess near the earth surface. Contrary, at the convection development is more affected by the air moisture near the earth surface.
It can also be seen in Equation (16) that the water vapor mass fraction gradient is the most significant factor. If the water vapor mass fraction gradient approaches the critical level, the “explosive” intensification of convection occurs, that is, the level of convection grows and goes to infinity. This is due to that our model of convection considers the equation of motion of an ideal liquid without taking into account the viscosity of the air. The air viscosity limits the level of convection.
The maximal velocities level may be found from the condition: . Having taken the derivative with respect to variable z in expression (15), we get
and call the value
Brunt-Väisälä frequency for the moist unsaturated air oscillations. This formula shows that at the critical water vapor mass fraction gradient the Brunt-Väisälä frequency equals zero, hence, the period of oscillations goes to infinity. It follows from Equation (17) that the maximal velocities level coincides with the densities equalization level: .
Substituting the expression for into Equation (15), we get for the maximal velocity of the rising moist unsaturated air flows the equation
The expression for the moist unsaturated air rising flows velocity square is:
It follows from here that, if , that is, the air densities in the near-surface disturbed and undisturbed atmospheres coincide, then the development of convection in a moist atmosphere follows the condition . In particular, for a dry atmosphere, the known condition of the convection development follows: . In a moist atmosphere the convection develops even under the condition .
Then we get for the rising flows velocity:
i.e., the rising flows velocity will grow with altitude following the linear law, and no convection level will be reached even if . It is clear that this result is an idealization. In a real atmosphere, the inversion layers and air viscosity will not allow for such a pattern.
The expression for the rising flow maximal velocity amplitudes in a moist atmosphere has the form:
Hence, expression (22) obtained for the rising flow velocity amplitude shows that the vertical velocity depends on the instability of the atmosphere, water vapor mass fraction gradient in the ambient atmosphere and near-surface temperature excess of a buoyant parcel . It is also seen from Equation (22) that at the critical water vapor mass fraction the maximum velocity goes to infinity (“explosive growth”).
4. Parameters of Convection on Condensation Level
Determine [45] the level of condensation from following equation:
where is the near-surface dew point; is the near-surface dew point deficit ; and is the dew point gradient. Equation (23) is known to give understated levels of condensation due to not taking into account the entrainment of the ambient environment by the rising air. Taking, for example, the vertical temperature gradient equal to , dew-point gradient equal to , and dew point deficit , we get the condensation level equal to . Note that over most of the European and North American territory, the maximum repeatability of the cloud-base height for warm season in the afternoon falls on the values of 1.2–1.6 km [46,47].
For the further analysis, only the dependence between the level of condensation and the near-surface dew point deficit is of importance.
Substitute Equation (23) into Equation (15), at the level of condensation the expression for the rising flows velocity will have the form:
Substitute Equation (23) into Equation (3), and get the formula for the condensation level temperature excess of a buoyant parcel
Substitute Equation (23) into Equation (5), for the condensation level oversaturation function, we get
It can be seen in Equations (24) and (25) that the critical near-surface dew point deficit values exist, at which both the condensation level temperature excess of a buoyant parcel and the rising air flow velocities equal zero:
It follows from Equation (28) that the sub-cloud layer moisture will promote the development of the cloud convection. It also follows from this formula that at the water vapor mass fraction gradient equal to the critical value , the critical near-surface dew point deficit goes to infinity, and, hence, the sub-cloud convection will always “break through” the condensation level, that is, . This once again underlines the important role of such a parameter as the water vapor mass fraction vertical gradient for the development of convection.
The found criteria determine the initial conditions of the cloud convection.
- If the near-surface dew point deficit equals the second critical value , the condensation level temperature excess of a buoyant parcel will be negative (Figure 1a)and the rising flow velocity at the same level will equal zero . Hence, in this case, the sub-cloud layer will not promote the cloud convection development. At such near-surface dew point deficit the atmosphere is not moist enough, and rising air will not break through the sub-cloud layer (Figure 1a). Formally assuming , we get the condensation level temperature excess of a buoyant parcel for a dry sub-cloud atmosphere. This result is known from the dry air convection adiabatic model [45].
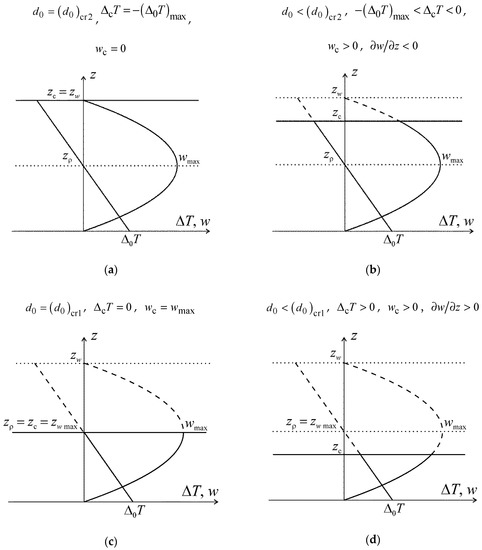 Figure 1. Distributions of rising flows velocity and temperature excess of a buoyant parcel with altitude depending on different near-surface dew point deficits. Graphs are shown schematically for moist unsaturated air. (a) , , ; (b) , , , ; (c) , , ; (d) , , , .
Figure 1. Distributions of rising flows velocity and temperature excess of a buoyant parcel with altitude depending on different near-surface dew point deficits. Graphs are shown schematically for moist unsaturated air. (a) , , ; (b) , , , ; (c) , , ; (d) , , , . - If the near-surface dew point deficit is , then the condensation level temperature excess of a buoyant parcel is negative, but its absolute value is lesser in magnitude than the maximal value , while the rising flow velocity at the same level is positive. In this case, the rising sub-cloud flow will break through the level of condensation: this promotes the cloud convection development (Figure 1b).
- If the near-surface dew point deficit equals the first critical value , then the condensation level temperature excess of a buoyant parcel equals zero , and the rising flow velocity equals (lesser than maximum), that is, the velocity equals the value at the level of equalization of temperatures:or
It should be noted that in this case the condensation level coincides with that of equalization of temperatures: . Similarly, the oversaturation function is equal to that at the same level :
Hence, in this case, the conditions for the cloud convection development will be in place (Figure 1c).
If the near-surface dew point deficit is lower than the first critical deficit , then the condensation level temperature excess of a buoyant parcel is positive , while the rising flow velocity level is positive, but lesser than maximum: these may promote the cloud convection development, as well (Figure 1d).
It can be seen in Equation (24), that if the ambient atmosphere water vapor mass fraction gradient becomes critical , then the condensation level rising flows velocity is positive at any near-surface dew point deficit and equals:
Hence, taking into account that the moisture of the sub-cloud layer leads to not only the qualitative changes of the criteria that determine the condensation level cloud convection parameters, but to quantitative changes, as well. We see that the cloud convection parameters at the level of condensation are affected by the water vapor mass fraction gradient in the sub-cloud layer, rather than by the sub-cloud layer absolute moisture. This is physically explained by that the rising air is moister in relation to the undisturbed atmosphere in this case.
Hence, the analytical expressions obtained for the two-dimensional model of convection have allowed for the analysis of the effects of the characteristics of near-surface layer of atmosphere on the development of the cloud convection.
5. Cloud Convection
In the work [44] the analytical solution for the two-dimensional model of the moist saturated air convection has been obtained. See the major provisions and assumptions that had served the bases for the analytical solution in [44]. The moist saturated air temperature gradient has the form:
where is the condensation level moist-adiabatic temperature gradient, known function of the temperature and pressure [45]; is the specific heat of condensation; is the specific thermal capacity at constant pressure; is the saturated water vapor mass fraction; is constant; and is a certain function of , condensation level water vapor mass fraction, also assumed constant. Here index “m” denotes “moist”, “ma”—“moist-adiabatic”, “mac”—“moist-adiabatic on the condensation level”.
The temperature excess of a buoyant parcel will be written as [44]:
where is the temperature excess of a buoyant parcel at the level of condensation; is the difference between the undisturbed atmosphere air temperature gradient and that of a rising parcel at the level of condensation. On the aerological diagram determines the angle between the condition curve and stratification curve at the level of condensation. Comparison of calculations using Equation (35) with the curve of the wet adiabat on the aerological diagram shows satisfactory agreement in the range of heights of our concern. This, in turn, indicates the admissibility of the approximation (34).
The expression for the oversaturation function is [44]:
where is the oversaturation at the level of condensation.
The formula for the air parcel density has the form [44]
where
The level of equalization of the air densities in a cloud air parcel and ambient atmosphere is [44]:
The level of equalization of the temperatures is determined by the expression [44]:
The thermal convection of the moist saturated air is described by the set of equations
Note that air density in Equation (40) is a function of altitude. Solving this set of equations, we get for the stream function [44]:
where [44]:
is the Brunt-Väisälä frequency for the moist saturated air;
For the vertical velocity we get [44]:
The thickness of the convection cell (“cloud”) is found from the condition ; for the case when the velocity at the condensation level equals zero , it equals [44]:
Because according to Equation (34) , it can be seen in Equation (49) that in the case of the cloud convection the critical ambient water vapor mass fraction gradient that promotes the development of the cloud convection exists, as well:
Even more clearly in Equations (47) and (49) it is seen that when , that is, the atmosphere is moist-stable and the convection is, according to the traditional concepts, impossible, when the water vapor mass fraction gradients exceed the critical ones, the convection becomes possible.
In Figure 2, the stream function for the sub-cloud convection was calculated from Equation (13), and for the cloud convection, it was calculated from Equation (45). Figures show that the growth of moisture in the near-surface layer (drop of dew point deficit ) leads to the development of the cloud convection.
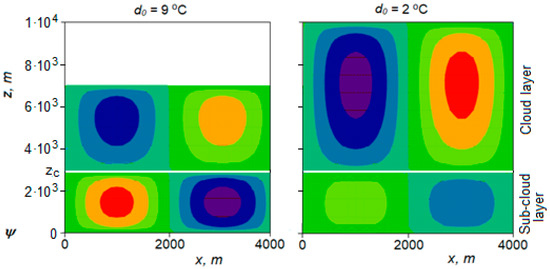
Figure 2.
Interaction between sub-cloud and cloud convections. Left—in a dry atmosphere, when the dew point deficit in the surface layer is equal to d0 = 9.0 °C; right—in a moist atmosphere, when the dew point deficit in the surface layer is equal to d0 = 2.0 °C.
Hence, the expressions for the cloud convection parameters show that this convection depends on the temperature excess of a buoyant parcel and rising flows velocity at the level of condensation; these ones are themselves dependent upon the characteristics of the near-surface atmosphere layer.
6. Artificial Stimulation of Convection
For many arid regions of the world, the idea of artificial stimulation of convection to create clouds and precipitation is highly attractive [41,42]. From above it follows that it is necessary to increase the temperature and moisture of the near-surface layer of the atmosphere in order to achieve the criterion value of the dew point deficit. However, in the problem of the artificial stimulation of convection we cannot sufficiently influence the moisture; hence, consider for the criterion the near-surface temperature excess of a buoyant parcel .
It can be seen in Equations (24) and (25) that the critical near-surface temperature excess of a buoyant parcel values exist, at which both the condensation level temperature excess of a buoyant parcel and the rising air flows velocity (at the level of condensation) equal zero:
It has already been noted that Equation (23) gives understated values for the level of condensation. This is due to the near-surface layer having impeding layers, in addition to the rising air mixing with the ambient environment. Hence, assuming the complete mixing, Equation (23) is written as
As , we will take the first criterion as the necessary and sufficient criterion of convection, i.e.,
The calculations for the vertical temperature gradient , and dew point deficit , yield .
It follows from Equation (54) that the required temperature excess of a buoyant parcel is a function of the vertical temperature gradient. If , then the temperature excess of a buoyant parcel equals zero, and the convection develops by itself. If, however, , that is, the vertical gradient of the temperature is equal to that of the dew point, the temperature excess of a buoyant parcel equals infinity. In other words, even without the temperature inversion, the temperature gradient equals to makes the convection impossible. Hence, if the near-surface layer of atmosphere, from the ground surface level to the level of condensation has the temperature gradient equal to , any attempts to artificially stimulate the convection by heating are ineffective. However, if the thickness of the impeding layers is greater than that of the layer mentioned, they may be broken through.
7. Discussion of the Results
In Section 3, the two-dimensional mathematical model of thermal convection of moist unsaturated air in the atmosphere is proposed. An analytical solution is obtained for stream function, horizontal and vertical velocity components, the level of convection, maximal vertical component of air velocity. It is shown that, as in the case of dry air, the atmosphere is unstable under the condition , that is, when the vertical temperature gradient is greater than the dry-adiabatic gradient. However, convection can develop in a stable atmosphere as well, if there is an air temperature excess of a buoyant parcel near the ground surface , that is, if there is some air volume warmer than the ambient atmosphere.
In contrast to the dry air convection, the convection of moist unsaturated air depends on the oversaturation near the ground surface , that is, on the excess of the water vapor mass fraction of warm air relative to the air of the ambient atmosphere. In addition, the convection of moist unsaturated air strongly depends on the vertical gradient of the water vapor mass fraction in the ambient atmosphere. At some critical value of this parameter , the so-called “explosive growth” occurs, that is, the atmosphere becomes wet-unstable, being dry-stable.
An analytical solution of a quite complicated problem under study was obtained for an idealized atmosphere in which the ambient air temperature decreases with the height according to the linear law, and the temperature of the air particle decreases with the height according to the dry-adiabatic law. At the same time, we did not take into account the presence of intercepting layers. The analytical solution is obtained under the condition that the water vapor mass fraction gradient in the surrounding atmosphere decreases linearly with the height, and the moisture of the adiabatically rising air particle remains constant. It is assumed that the air viscosity can be neglected. The neglection of viscosity is the reason for the convection "explosive growth" at the critical value of the water vapor mass fraction gradient in the obtained solution.
On the basis of the proposed model of moist unsaturated air convection, called “sub-cloud convection”, in Section 4 the values of the convection parameters (temperature excess of a buoyant parcel and vertical velocity ) at the level of condensation are obtained. In the further analysis we assumed that the dew point temperature vertical gradient is constant. It is shown that the values of these parameters depend on the value of the dew point deficit near the ground surface , that is, on the difference between the temperature of warm moist air and the dew point temperature.
It is shown that there is a critical value of the dew point deficit at which the temperature excess of a buoyant parcel at the condensation level is zero . At accepted atmosphere parameters the value corresponds to the first critical value the dew point deficit. It is to remind that the water vapor mass fraction vertical gradient is assumed to be less than critical value , as at a condition the atmosphere is unstable. When temperature excess of a buoyant parcel at the condensation level will be positive; this will promote the cloud convection development. If the air is not moist enough and , it will be colder than the environment at the level of condensation; this will exclude the development of cloud convection.
The same is the case with the critical value , which determines the value of the upstream velocity at the condensation level. At the abovementioned atmosphere parameters, the value corresponds to the second critical value of the dew point deficit. At , the velocity of upward flows at the condensation level is zero and the upper bound of the sub-cloud convection coincides with the lower bound of the cloud convection. At , i.e., at the condensation level, there will be some positive upstream velocity, which will be the initial upstream velocity for cloud convection.
Note that at , although the upstream velocity at the condensation level is positive, the temperature excess of a buoyant parcel will be negative, that is, air is colder than the environment. In this case the sub-cloud convection will influence the development of cloud convection, but this influence will not be optimal. If (i.e., when the air is not moist enough), then the sub-cloud convection does not reach the level of condensation and does not contribute to the development of cloud convection. Therefore, the conditions presented in Figure 1c when will be the most optimal case. In this case, although the temperature excess of a buoyant parcel is equal to zero, the upstream velocity at the condensation level is highest.
In Section 5 a mathematical model of moist saturated air convection developed in [43] and called in this paper “cloud convection” is presented. The analytical solution is obtained under the assumption that the vertical gradient of moist saturated air temperature depends linearly on altitude (Equation (34)). Unlike the convection of dry air and moist unsaturated air, the convection pattern of moist saturated air is vertically asymmetrical. The level of maximal velocities is not in the middle of the convective cell, but in the upper half. It is shown that the level of cloud convection depends on the values of the temperature excess of a buoyant parcel and the initial velocity at the condensation level. These values are calculated using a sub-cloud convection model.
Thus, cloud convection depends on the parameters of the atmosphere at the level of condensation, which in turn depend on the values of the atmospheric parameters at the near-surface layer. Figure 2 shows how the value of the dew point deficit near the ground surface affects the development of cloud convection. The development of cloud convection is significantly affected by the vertical gradient of the water vapor mass fraction in the ambient atmosphere.
Section 6 examines the possibilities of convection stimulation to create artificial convective clouds and precipitation. It is shown that under the favorable conditions it is possible to successfully stimulate the development of artificial convection, contributing to the development of cloud convection.
8. Conclusions
Based on the analytical solutions from [43,44] of the dry and moist saturated air convection equations, and upon the analytical solution for the moist unsaturated air convection, the effects of the atmosphere near-surface layers parameters on the development of the cloud convection have been shown. The analytical expressions for the dew point deficits in the near-surface layer determining the temperature excess of a buoyant parcel and rising flows velocities at the level of condensation have been obtained. The value of the water vapor mass fraction has been shown to significantly affect the development of the sub-cloud convection. It has been established that at the close to critical gradients of the water vapor mass fraction the “explosive” growth of the convection cells in the sub-cloud layer is observed. It has also been shown that the critical gradient of the water vapor mass fraction exists, that promotes the development of the sub-cloud convection.
Hence, the findings from the proposed model agree with the experimental and theoretical data on the effects of the moisture of the near-surface layer of atmosphere on the development of the convection. The specificity of the proposed model is that, first, it deals with not only the absolute value of the near-surface layer moisture, but also with the crucial role of the water vapor mass fraction gradient. Moreover, the analysis is based upon the solution of the two-dimensional nonlinear convection model. The drawback of the proposed model is that it is stationary and does not account for the viscosity of the air.
Author Contributions
Conceptualization and writing—review and editing, M.T.A.; performing theoretical analysis and writing—original draft, R.G.Z.; funding acquisition and discussion of applications, A.M.A.; formal analysis, Q.S.K.A.-O. and L.M.K.; formal analysis and reviewed the manuscript, A.R.Z.; proofread and reviewed the manuscript, Y.W., L.Y., S.F. and A.A.M.
Funding
This work was supported by the National Center of Meteorology, Abu Dhabi, UAE under the UAE Research Program for Rain Enhancement Science (UAEREP, grant No APP-REP-2017-02120); and the Russian Foundation for Basic Research (grants No: 17-05-00965 and BRICS 18-55-80020).
Conflicts of Interest
The authors declare no conflict of interest. Any opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Center of Meteorology, Abu Dhabi, UAE, funder of the research.
References
- Crook, N.A. Sensitivity of moist convection forced by boundary layer processes to low-level thermodynamic fields. Mon. Weather Rev. 1996, 124, 1767–1785. [Google Scholar] [CrossRef]
- Van Zanten, M.C.; Duynkerke, P.; Cuijpers, J. Entrainment parameterization in convective boundary layers. J. Atmos. Sci. 1999, 56, 813–828. [Google Scholar] [CrossRef]
- Emanuel, K.A. Atmospheric Convection; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Hu, X.-M.; Nielsen-Gammon, J.W.; Zhang, F. Evaluation of three planetary boundary layer schemes in the WRF Model. J. Appl. Meteorol. Climatol. 2010, 49, 1831–1844. [Google Scholar] [CrossRef]
- Stensrud, D.J. Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Arakawa, A. The cumulus parameterization problem: Past, present, and future. J. Clim. 2004, 17, 2493–2525. [Google Scholar] [CrossRef]
- Bony, S.; Dufresne, J.L. Marine boundary layer clouds at the heart of tropical cloud feedback uncertainties in climate models. Geophys. Res. Lett. 2005, 32, L20806. [Google Scholar] [CrossRef]
- Hohenegger, C.; Bretherton, C.S. Simulating deep convection with a shallow convection scheme. Atmos. Chem. Phys. 2011, 11, 10389–10406. [Google Scholar] [CrossRef]
- Plant, R.S. A review of the theoretical basis for bulk mass flux convective parameterization. Atmos. Chem. Phys. 2010, 10, 3529–3544. [Google Scholar] [CrossRef]
- Von Salzen, K.; McFarlane, N.; Lazare, M. The role of shallow convection in the water and energy cycles of the atmosphere. Clim. Dyn. 2005, 25, 671–688. [Google Scholar] [CrossRef]
- Yano, J.-I.; Plant, R. Interactions between shallow and deep convection under a finite departure from convective quasi equilibrium. J. Atmos. Sci. 2012, 69, 3463–3470. [Google Scholar] [CrossRef]
- Bellon, G.; Stevens, B. On bulk models of shallow cumulus convection. J. Atmos. Sci. 2005, 62, 3286–3302. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A new bulk shallow-cumulus model and implications for penetrative entrainment feedback on updraft buoyancy. J. Atmos. Sci. 2008, 65, 2174–2193. [Google Scholar] [CrossRef]
- Deardorff, J.W. Prediction of convective mixed-layer entrainment for realistic capping inversion structure. J. Atmos. Sci. 1979, 36, 424–436. [Google Scholar] [CrossRef]
- Gentine, P.; Betts, A.K.; Lintner, B.R.; Findell, K.L.; van Heerwaarden, C.C.; D’Andrea, F. A probabilistic bulk model of coupled mixed layer and convection. Part II: Shallow convection case. J. Atmos. Sci. 2013, 70, 1557–1576. [Google Scholar] [CrossRef]
- Rio, C.; Hourdin, F. A thermal plume model for the convective boundary layer: Representation of cumulus clouds. J. Atmos. Sci. 2008, 65, 407–425. [Google Scholar] [CrossRef]
- Pardo, S.K. High-Resolution Analysis of the Initiation of Deep Convection Forced by Boundary-Layer Processes; KIT Scientific Publishing: Karlsruhe, Germany, 2015. [Google Scholar]
- Abshaev, M.T.; Abshaev, A.M.; Malkarova, A.M.; Zharashuev, M.V. Automated radar identification, measurement of parameters, and classification of convective cells for hail protection and storm warning. Russ. Meteorol. Hydrol. 2010, 35, 182–189. [Google Scholar] [CrossRef]
- Browning, K.; Blyth, A.; Clark, P.; Corsmeier, U.; Morcrette, C.; Agner, J.; Bamber, D.; Barthlott, C.; Bennett, L.; Beswick, K.; et al. The convective storm initiation project. Bull. Am. Meteorol. Soc. 2007, 1939–1955. [Google Scholar] [CrossRef]
- Purdom, J.F.W. Subjective interpretation of geostationary satellite data for nowcasting. In Nowcasting; Browning, K.A., Ed.; Academic Press: London, UK, 1982; pp. 149–166. [Google Scholar]
- Wilson, J.; Crook, N.; Mueller, C.; Sun, J.; Dixon, M. Nowcasting thunderstorms: A status report. Bull. Am. Meteorol. Soc. 1998, 79, 2079–2100. [Google Scholar] [CrossRef]
- Jorgensen, D.P.; Weckwerth, T.M. Forcing and organization of convective systems. In Radar and Atmospheric Science: A Collection of Essays in Honor of Davis Atlas; Wakimoto, R.M., Srivastava, R.C., Eds.; American Meteorological Society: Boston, MA, USA, 2003; pp. 75–104. [Google Scholar]
- Wakimoto, R.M. Convectively driven high wind events. In Severe Convective Storms; Doswell, C., Ed.; American Meteorological Society: Boston, MA, USA, 2001; pp. 255–298. [Google Scholar]
- Weckwerth, T.M.; Parsons, D.B. A Review of Convection Initiation and Motivation for IHOP 2002. Mon. Weather Rev. 2006, 134, 5–21. [Google Scholar] [CrossRef]
- Bennett, L.J.; Browing, K.A.; Blyth, A.M.; Parker, D.J.; Clark, P.A. A review of the initiation of precipitating convection in the United Kingdom. Q. J. R. Meteorol. Soc. 2006, 132, 1001–1020. [Google Scholar] [CrossRef]
- Brooks, H.E.; Doswell, C.A.; Wicker, L.J. STORM-TIPE: A forecasting experiment using a three-dimensional cloud model. Weather Forecast. 1993, 8, 352–362. [Google Scholar] [CrossRef]
- Lauscaux, F.; Richard, E.; Keil, C.; Bock, O. Impact of the MAP reanalysis on the numerical simulation of the MAP-IOP2a convective system. Meteorol. Z. 2004, 13, 49–54. [Google Scholar] [CrossRef]
- Sun, W.-Y.; Ogura, Y. Boundary-layer forcing as a possible trigger to a squall-line formation. J. Atmos. Sci. 1979, 36, 235–254. [Google Scholar] [CrossRef]
- Zhou, X.; Geerts, B. The influence of soil moisture on the planetary boundary layer and on cumulus convection over an isolated mountain. Part I: Observations. Mon. Weather Rev. 2013, 141, 1061–1078. [Google Scholar] [CrossRef]
- Betts, A.K.; Ball, J.H.; Beljaars, A.C.M.; Miller, M.J.; Viterbo, P.A. The land surface-atmosphere interaction: A review based on observational and global modeling perspectives. J. Geophys. Res. Atmos. 1996, 101, 7209–7225. [Google Scholar] [CrossRef]
- Eltahir, E.A.B. A soil moisture–rainfall feedback mechanism. Part I: Theory and observations. Water Resour. Res. 1998, 34, 765–776. [Google Scholar] [CrossRef]
- Turner, D.D.; Lesht, B.M.; Clough, S.A.; Liljegren, J.C.; Revercomb, H.E.; Tobin, D.C. Dry bias and variability in Vaisala RS80-H radiosondes: The ARM experience. J. Atmos. Ocean. Technol. 2003, 20, 117–132. [Google Scholar] [CrossRef]
- Wang, J.; Cole, H.L.; Carlson, D.J.; Miller, E.R.; Beierle, K.; Paukkunen, A.; Laine, T.K. Corrections of humidity measurement errors from the Vaisala RS80 radiosonde: Application to TOGA COARE data. J. Atmos. Ocean. Technol. 2002, 19, 981–1002. [Google Scholar] [CrossRef]
- Kottmeier, C.; Kalthoff, N.; Barthlott, C.; Corsmeier, U.; Van Baelen, J.; Behrendt, A.; Behrendt, R.; Blyth, A.; Coulter, R.; Crewell, S.; et al. Mechanisms initiating deep convection over complex terrain during COPS. Meteorol. Z. 2008, 17, 931–948. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Behrendt, A.; Bauer, H.-S.; Kottmeier, C.; Corsmeier, U.; Blyth, G.C.A.; Schumann, U.; Hagen, M.; Crewell, S.; Girolamo, P.D.; et al. The convective and orographically-induced precipitation study. Bull. Am. Meteorol. Soc. 2008, 89, 1477–1486. [Google Scholar]
- Morrison, H. Impacts of updraft size and dimensionality on the perturbation pressure and vertical velocity in cumulus convection, Part 1: Simple, generalized analytic solutions. J. Atmos. Sci. 2015, 73, 1441–1454. [Google Scholar] [CrossRef]
- Weisman, M.L.; Skamarock, W.C.; Klemp, J.B. The resolution dependence of explicitly modeled convective systems. Mon. Weather Rev. 1997, 125, 527–548. [Google Scholar] [CrossRef]
- Alekseev, V.V.; Gusev, A.M. Free convection in geophysical processes. Sov. Phys. Uspekhi 1983, 26, 906–922. [Google Scholar] [CrossRef]
- Scorer, R.S. Environmental Aerodynamics; Ellis Horwood Limited: Chichester, UK, 1978. [Google Scholar]
- Bluestein, H.B. Severe Convective Storms and Tornadoes; Springer: Chichester, UK, 2013. [Google Scholar]
- Vulfson, N.I.; Levin, L.M. Meteotron as a Means to Influence the Atmosphere; Gidrometeoizdat: Leningrad, Russia, 1987. (In Russian) [Google Scholar]
- Kachurin, L.G. Physical Basis of Atmospheric Process Modification; Gidrometeoizdat: Leningrad, Russia, 1990. (In Russian) [Google Scholar]
- Zakinyan, R.G.; Zakinyan, A.R.; Lukinov, A.A. Two-dimensional analytical model of dry air thermal convection. Meteorol. Atmos. Phys. 2015, 127, 451–455. [Google Scholar] [CrossRef]
- Zakinyan, R.G.; Zakinyan, A.R.; Ryzhkov, R.; Avanesyan, K. Convection of moist saturated air: Analytical study. Atmosphere 2016, 7, 8. [Google Scholar] [CrossRef]
- Matveev, L.T. Fundamentals of General Meteorology: Physics of the Atmosphere; Israel Program for Scientific Translations: Jerusalem, Israel, 1967. [Google Scholar]
- Sengupta, M.; Clothiaux, E.E.; Ackerman, T.P. Climatology of warm boundary layer clouds at the ARM SGP site and their comparison to models. J. Clim. 2004, 17, 4760–4782. [Google Scholar] [CrossRef]
- Costa-Surós, M.; Calbó, J.; González, J.A.; Martin-Vide, J. Behavior of cloud base height from ceilometer measurements. Atmos. Res. 2013, 127, 64–76. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).