Next Article in Journal
On the Relationship between Gravity Waves and Tropopause Height and Temperature over the Globe Revealed by COSMIC Radio Occultation Measurements
Next Article in Special Issue
Atmospheric Response to Oceanic Cold Eddies West of Luzon in the Northern South China Sea
Previous Article in Journal
Spatial Distribution, Chemical Speciation and Health Risk of Heavy Metals from Settled Dust in Qingdao Urban Area
Previous Article in Special Issue
Ensemble Sensitivity Analysis-Based Ensemble Transform with 3D Rescaling Initialization Method for Storm-Scale Ensemble Forecast
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 10
Issue 2
10.3390/atmos10020074
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Impact of Cumulus Parameterization on Model Convergence of Tropical Cyclone Destructive Potential Simulation at Grey-Zone Resolutions: A Numerical Investigation

by
Chen Ma
1,
Yuan Sun
2,*,
Jia Liu
1,
Tim Li
1,3 and
Zhong Zhong
2
1
Key Laboratory of Meteorological Disaster, Ministry of Education (KLME)/Joint International Research Laboratory of Climate and Environmental Change (ILCEC)/Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disasters (CIC-FEMD), Nanjing University of Information Science and Technology, Nanjing 210044, China
2
College of Meteorology and Oceanography, National University of Defense Technology, No.60, Shuanglong Rd., Nanjing 211101, China
3
International Pacific Research Center and Department of Atmospheric Sciences, School of Ocean and Earth Science and Technology, University of Hawaii, Honolulu, HI 96822, USA
*
Author to whom correspondence should be addressed.
Atmosphere 2019, 10(2), 74; https://doi.org/10.3390/atmos10020074
Submission received: 18 December 2018 / Revised: 30 January 2019 / Accepted: 7 February 2019 / Published: 12 February 2019
(This article belongs to the Special Issue Advancements in Mesoscale Weather Analysis and Prediction)
Browse Figures
Versions Notes

Abstract

:
The Weather Research Forecast model (WRF) is used to examine the destructive potential of tropical cyclone (TC) Shanshan (2006) at various horizontal resolutions (7.5 km–1 km) with different cumulus parameterization (CP) schemes. It is found that the calculated Power Dissipation Index (PDI) increases while the size-dependent destructive potential (PDS) decreases as the grid spacing decreases for all CP-scheme simulations, which indicates a weak model convergence in both PDI and PDS calculations. Moreover, it is change of the storm intensity and inner-core size that lead to the non-convergence of PDI and PDS respectively. At a higher resolution, convection becomes more explicitly resolved, which leads to larger diabatic heating. As a result, the radial pressure gradient force (PGF) increases, and the radius of maximum wind (RMW) decreases. The area of strong diabatic heating subsequently becomes closer to the TC center, which further increases the TC intensity and the PGF near the eyewall. With such a positive feedback loop, the PGF increases and the RMW decreases as the resolution increases. Note that a perfect model should converge well in the simulation of both TC intensity and size, and thus converge in the PDS. For some CP experiments, the calculated PDS convergence is relatively strong, but it is a result of offset between the non-convergent simulations of TC intensity and size. In contrast, the Grell–Freitas scheme exhibits a stronger convergence in the simulations of TC intensity and size, although the convergence in PDS is relatively weak, but is closer to the truth.

1. Introduction

Tropical cyclones (TCs) are highly destructive natural disasters that occur on tropical oceans [1,2]. Zhai and Jiang investigate the US hurricane economic loss on TC intensity and size based on National Hurricane Center (NHC) Extended Best Track database which TC size data on North Atlantic is available since 1988 [3]. However, the TC size data on West North Pacific and East North Pacific is available since 2001 in Joint Typhoon Warning Center (JTWC) dataset. Compared with the TC intensity and track data in best track datasets, the historical record of TC size is much less. Owing to the lack of TC size information in observational data, the previous studies often ignored the effect of TC size on its destructiveness and assumed a fixed TC dimension in calculating the TC destructiveness. The power dissipation index (PDI), which is proposed by Emanuel [4], is widely used to estimate the TC destructive potential [5,6,7]. However, as the PDI of a TC is defined as the sum of the cube of the maximum wind speed (MWS), which is integrated during the TC lifetime, the PDI does not take into account the effect of the TC size. Sun et al. defined an index of size-dependent destructive potential (PDS) [8], which is dependent on both the TC intensity and TC size, in particular, the inner-core size of TC.
With advances in computation capability, numerical weather prediction models are able to run at horizontal grid intervals within the range of 1–10 km [9]. Whether the high-resolution numerical model can improve the simulation of TCs, however, remains a controversial issue. Sun et al. argued that with increases in the model resolution [10], a key issue in numerical weather prediction is the appropriateness of various cumulus parameterization (CP) schemes. Hammarstrand pointed out that the prerequisite for the application of CP scheme is that the spatial scale of the convective updraft must be much smaller than the horizontal grid interval of the model [11]. Most of the CP schemes primarily used at present are designed based on the above concept proposed by Hammarstrand [11]. This assumption in the design of CP scheme induces many arguments about whether it is still necessary to use CP scheme in high-resolution numerical weather prediction models. On the one hand, Gerard proposed the concept of “grey-zone resolution”, which is used to describe the resolution at which it is uncertain whether the CP scheme should be applied [12]. Yu and Lee further suggested that the “grey-zone resolution” ranges with 1–5 km [13]. On the other hand, many studies showed problems such as irresolvable convection and under prediction or over prediction of precipitation in high-resolution simulations without the application of CP scheme. Thereby, it is suggested that the CP scheme is still needed even in high-resolution simulations [14,15]. For high-resolution TC simulations, Fierro et al. indicated that it is impossible to effectively improve the TC simulation by solely increasing the model resolution without improving the description of various physical processes [16]. Results of the previous studies showed that, the CP scheme is closely related to the model convergence in simulating TC intensity [10,17]. They also suggested that, a perfect numerical model should produce convergent TC structure and intensity simulation as the model resolution increases, despite of the fact that the converged solution does not necessarily approach the truth. Therefore, finding or designing a proper CP scheme which makes the model solution converged, is a prerequisite for a perfect model. According to the results of large-eddy simulation of idealized TC, Rotunno et al. pointed out that the simulated TC intensity increases significantly with increasing resolution and becomes non-convergent especially under high-resolutions [18]. Bryan et al. conducted squall lines simulation with grid spacing below 1 km, and found that the simulated squall lines varies with model resolution [19]. Sun et al. revealed different convergent features of high-resolution TC intensity simulation using several different CP schemes and analyzed the possible mechanisms behind [10,17]. They found a weak convergence in simulations with most of the CP schemes, whereas the convergence is relatively strong in the simulations with the Grell–Freitas (GF) scheme [20], which is a scale-aware scheme designed for any resolution.
The studies mentioned above have revealed that the simulated TC intensity increases with increased resolution, eventually leading to non-convergent TC intensity simulation. However, the property of convergence related to TC structure like the TC size has not been well studied. Since the TC PDS is determined by not only the TC intensity but also the TC size, how the TC PDS will respond to increasing resolution and how different the PDS is compared to the PDI remains unclear. In the present study, we investigate the convergence of TC PDS simulation based on the case study of typhoon Shanshan (2006) with several different CP schemes. Section 2 describes the model configuration and experimental design. Section 3 shows the results of simulations using various CP schemes and at different resolutions. Possible physical mechanisms that affect the convergence of TC PDS simulation are explored in Section 4. Conclusions and discussion are presented in Section 5.

2. Model Configuration and Experimental Design

Typhoon Shanshan was formed over the northwestern Pacific (16.7° N, 134.9° E) at 1200 UTC 10 September 2006. In the following 2 days, Shanshan continued to move westward and was upgraded to an extremely severe typhoon by the Joint Typhoon Warning Center (JTWC) at 0000 UTC 12 September. It then moved northward and reached eastern Taiwan Island (20.7° N, 124.6° E) at 1800 UTC 14 September. Subsequently, Shanshan turned to northeast and made landfall in Japan about 1000 UTC 17 September. Overall, Shanshan has a typical recurving track with high intensity and long lifetime, which is illustrated by the JTWC best-track data [21]. Due to the high intensity and long duration, Shanshan inflicted enormous life and property losses over Japan and its outlying Pacific islands. The loss of $2.5 billion caused by TC Shanshan made it the sixth costliest disaster in the world in 2006.
In this study, the Weather Research and Forecasting model version 3.5 (WRFV3.5) is employed to conduct a series of numerical experiments. Some important physical schemes include Monin–Obukhov surface-layer scheme [22,23], Yonsei University planetary boundary layer scheme [24], and Lin microphysical scheme [25]. The initial and boundary conditions are obtained from the 1° × 1° National Centers for Environment Prediction final analysis data at 6-h intervals [26]. The TC bogus scheme in the WRF model is used to refine the initial field [27].
Four suites of experiments are carried out in this study. The difference among them lies on CP schemes in the innermost domain, which are as follows: (1) without the CP scheme (NOCP), (2) the Kain–Fritsch CP (KFEX) scheme [28,29] is applied, (3) the Betts–Miller–Janjić CP (BMJ) scheme is used [30,31,32,33] and (4) the Grell and Freitas (GF) scheme is employed [20]. Each suite of experiments includes simulations at resolutions of 1, 3, 5, and 7.5 km in the innermost domain. Table 1 lists the model domain setting, which is triply-nested with the two inner domains (DM2, DM3) movable [27]. An extra nesting domain (DM4) with the highest resolution of 1 km is added for some high-resolution experiments. The domain configuration can be found in Figure S1. During the integration, all the inner domains (DM2, DM3, and DM4) can move following the movement of typhoon Shanshan. In order to keep the parent domains consistent between all these suites, DM1 and DM2 cover the same areas in all the experiments. The size of DM4 in the 1-km resolution runs is the same as that of the DM3 in 3 km, 5 km and 7.5 km resolution runs. All physical schemes and dynamical setup in the innermost domain are the same in these suites of experiments except the CP scheme, which makes it convenient for us to compare the performance of different CP schemes. Note that the GF scheme is a scale-aware scheme, which is different from other CP schemes. As the model resolution increases, the GF scheme produces smaller tendencies and more convection is resolved by the microphysical scheme. This scheme can sufficiently remove moist instability for the entire grid point, and thus is somewhat different from other conventional CP schemes. Sun et al. indicated that the GF scheme could yield convergent simulation of TC intensity [17]. Thereby, in the following sections we pay more attention to the performance of the GF scheme in the simulations of TC size and destructive potential in the high-resolution runs.

3. Performance of Different CP Schemes

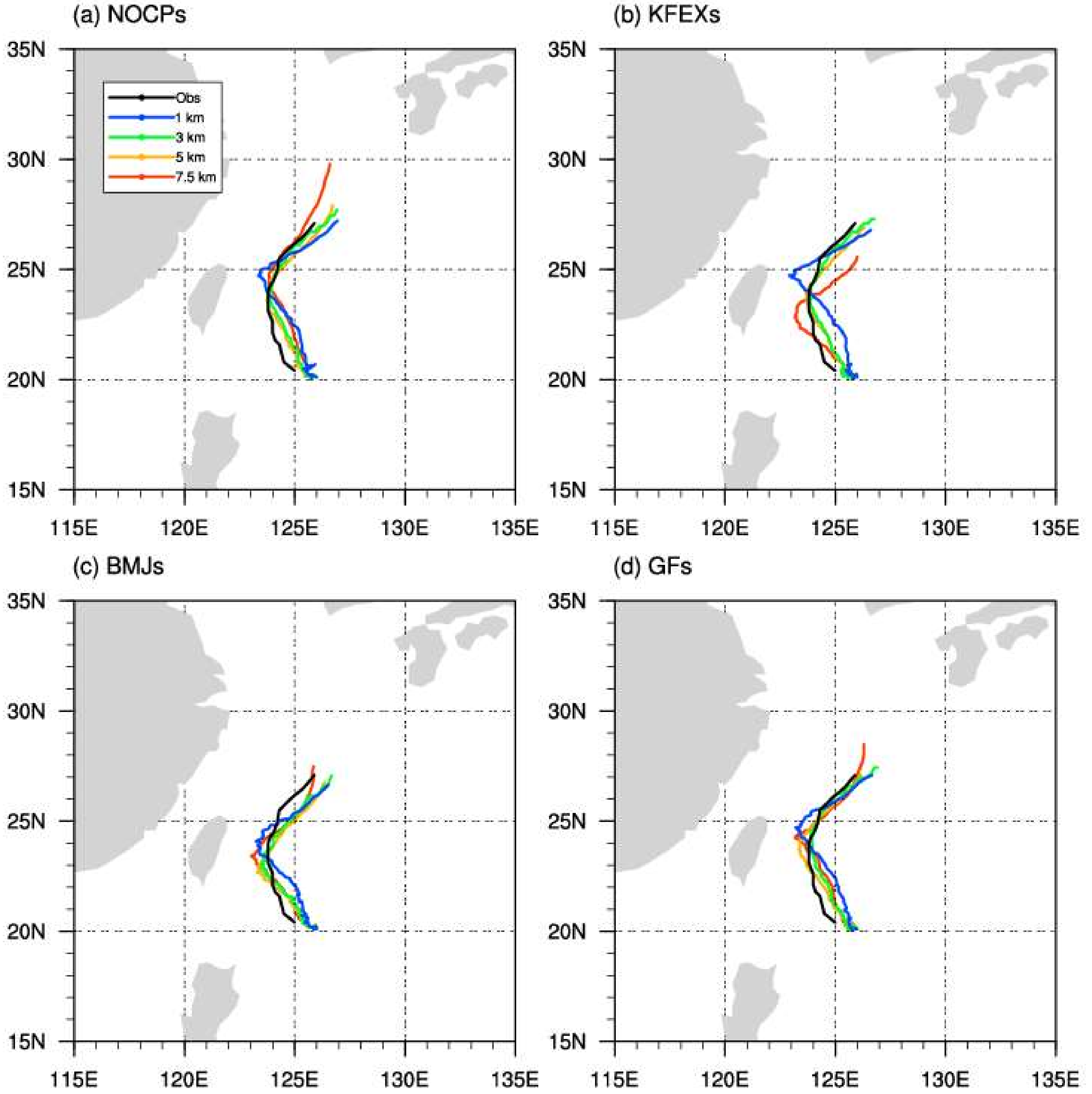
In this study, the simulated storms in all the experiments share a similar track (Figure 1), which effectively reduces uncertainties caused by the effect of large-scale environmental field in these experiments [34,35]. This makes it trustworthy to examine the sensitivity of the simulated TC structure to the choice of horizontal resolution and CP scheme. Meanwhile, the simulated TC intensity and size are also sensitive to the CP scheme and model resolution (Figures S2–S4). Since the simulated TC reaches its maximum intensity at 0000 UTC 16 September, we define the period from 1800 UTC 15 September to 0600 UTC 16 September as the TC mature stage. Unless specified otherwise, this period is used as the TC mature stage hereafter.
Emanuel defined a simplified power dissipation index as [4]:
PDI = ∫ 0 τ V max 3 d t
where Vmax is the maximum wind speed and τ is the lifetime of TC. Although the PDI index has been widely applied, this index cannot account for the effect of TC size. The storm size is an important parameter in estimating the extent of TC-induced damage. The TC size here we referred to is the mean radius of hurricane-force wind (R33), which is an important damage potential parameter and thus more suitable for the assessment of TC destructive potential. To take into account the TC size effect, the storm size-dependent TC destructive potential (PDS) index proposed by Sun et al. is used in the present study [8]:
PDS = ∫ 0 τ ∫ 0 A 0 C D ρ V 3 d A d t
where CD is the surface drag coefficient, ρ is the surface air density, A0 is the area of hurricane-force wind, |V| is the magnitude of surface wind, and τ is the lifetime of TC. The PDS represents the total power of hurricane-force winds over its lifetime. Compared with changes in the PDI that only considers the effect of TC intensity, changes in the TC PDS that considers effects of both the TC intensity and TC size with increasing resolution might be different.
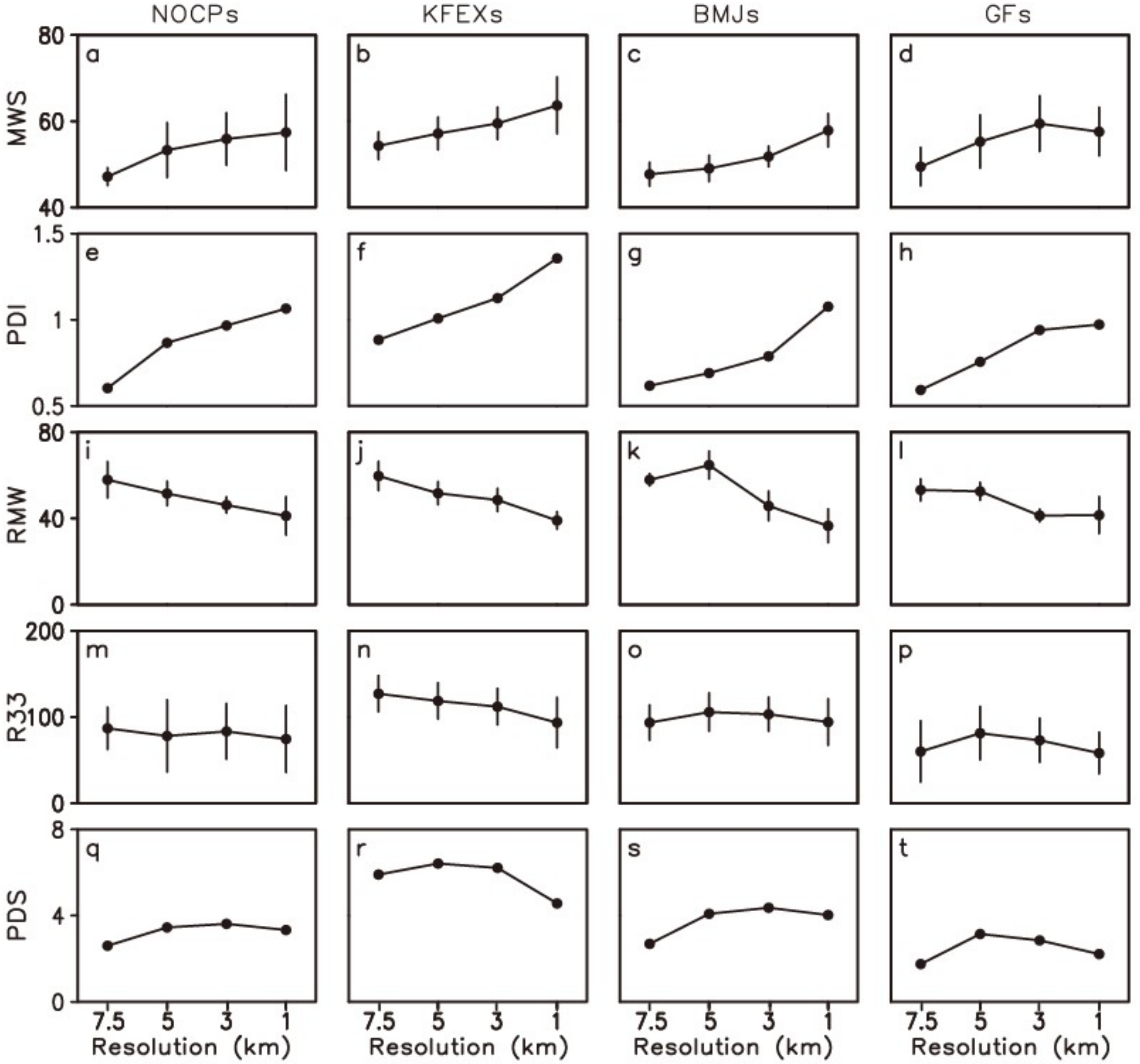
Figure 2 presents changes in the domain-averaged MWS, PDI, radius of maximum wind (RMW), R33 and PDS with increasing resolution in the innermost domain simulated with different CP schemes and averaged in the TC mature stage from 1800 UTC 15 September to 0600 UTC 16 September. The reason of using TC mature stage here is that, the destructive potential of a TC is a time integral of TC intensity and size. Only when the intensity and size of TC reach its peak in the mature stage, making the TC destructive potential meaningful. It shows clearly that the simulated TC intensifies with increasing resolution (i.e., from 7.5 km to 5 km) in all the experiments with various CP schemes, which is attributed to the intensification of convection. In the NOCP, KFEX and BMJ runs, the simulated TC intensity and PDI index keep increasing with increases in the resolution, and the model becomes non-convergent. In the GF runs, the simulated TC intensity and PDI remain relatively stable as the resolution increases from 3 km to 1 km (Figure 2d,h), suggesting that the GF scheme converges well in the simulation of TC intensity and PDI. As the resolution of the GF experiment is increased from 3 km to 1 km, the MWS is decreasing while the PDI is increasing (Figure 2d,h). This is because the PDI is a time integration variable that covers the whole TC lifetime rather than only the TC mature stage, and the simulated MWS in the 1-km resolution run is stronger than that in the 3-km resolution run in the TC developing phase (Figure S3d).
When considering the effect of the TC size, the calculated PDS at high-resolutions (i.e., from 3 km to 1 km) in the NOCP, KFEX, BMJ and GF runs all decrease with increased resolution, which is opposite to the changes of the PDI (Figure 2e–h, and Figure 2q–t). It can be seen from the distribution of the mean and standard deviation that the decrease of TC size is an objective phenomenon, rather than the individual low values lowering the overall time average. Since the inner-core size is considered in the PDS definition, we compare the model convergence for the simulations of RMW and R33, which are two indexes that reflect the TC inner-core features. Note that R33 is more complicated than RMW since it is related to not only RMW, but also other factors like MWS. As shown in Figure 2, the model convergence in the NOCP, KFEX, and BMJ runs is weak in terms of both the RMW and R33. Further analysis shows a relatively strong convergence of the RMW simulation in the GF experiment. However, the simulated R33 decreases with increased resolution, which is possibly because the simulated TC intensity slightly decreases under high-resolution (Figure 2d). Thereby, the PDS simulation is also non-convergent in the GF experiment. Compared to the non-convergent PDI, the non-convergent PDS is largely attributed to the non-convergent simulation of the TC inner-core size. Due to the strong impact of TC inner-core size on the PDS convergence, it is necessary to investigate the weak convergence of TC size in the four suites of experiments with different CP schemes.
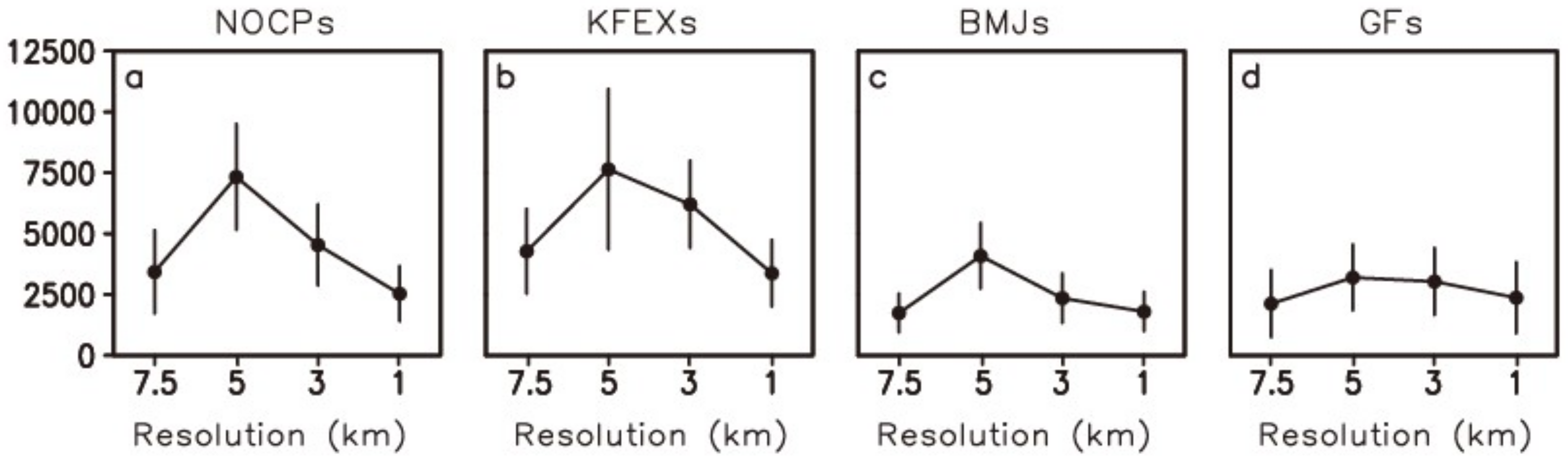
To further confirm the non-convergent feature in the simulation of the TC inner-core size with various CP schemes, Figure 3 is presented to display changes in the heavy precipitation area with resolutions from 7.5 km to 1 km in all the experiments with different CP schemes in the TC mature stage from 1800 UTC 15 September to 0600 UTC 16 September. As strong convection near the TC eyewall area is often accompanied by heavy precipitation, here we use the area with precipitation larger than 50 mm h−1 as the standard to measure the inner-core size. Similar to the situation for RMW, R33 and PDS, heavy precipitation area keeps decreasing with increased resolution in all the experiments using the four CP schemes. The model convergence is especially weak in the NOCP, KFEX, and BMJ experiments based on the degree of decrease in the heavy precipitation area with increased resolution. The model convergence in the GF experiment is relatively strong, but the heavy precipitation area still decreases with increased resolution, which is consistent with the model simulation of RMW and R33. Thereby, in terms of the heavy precipitation area, the model is non-convergent in the simulation of TC inner-core size with all the four CP schemes.
Overall, the calculated TC PDS becomes non-convergent at high resolution when using all the four CP schemes, which would lead to biases in the estimation of TC destructive potential. The major reason for the non-convergent simulation of TC PDS is that the simulation of the TC inner core size is not convergent. In the next section, we will further explore the possible reasons for the weak model convergence in the simulation of the TC inner-core size.

4. Reasons for The Non-Convergent Simulation of TC Inner Core Size with Different CP Schemes

Generally speaking, the tangential wind profile of the TC is largely determined by the TC intensity (i.e., MWS), TC inner-core size (i.e., RMW) and tangential wind slope outside the RMW. Based on the theoretical study of Carr and Elsberry [36], the tangential wind slope outside the RMW is related to the Coriolis parameter f, which actually reflects the latitude where the TC is located. In the present study, the simulated typhoon tracks in all the experiments are similar (Figure 1), suggesting that the tangential wind slopes outside the RMW are similar as well in these experiments. Sun et al. also indicated that stronger convection along the TC eyewall leads to stronger outward flows in the upper troposphere, which can induce raindrop evaporation in the middle troposphere and promote the formation of new convection in the TC outer region and thus lead to the slope difference [8]. In other words, the slope outside RMW is somehow related to the TC intensity. In order to disentangle the contributions of RMW and MWS to the TC R33, Table 2 shows the statistics of regressions of R33 from all the experiments data onto the RMW and MWS. Although the regression residual of RMW to R33 is small, the multiple regression coefficients are statistically significant and explain 34% of the R33 when RMW and MWS indices together. Thereby, the R33 is largely affected by the RMW and MWS. It is relatively easy to understand why the MWS increases following the increase of model resolution. As suggested by Sun et al., more convection within the TC eyewall can be resolved with increasing resolution [10]. The MWS increases as convection intensifies within the eyewall. However, the mechanisms for changes in the TC size (RMW) are more complicated compared to that for TC intensity (MWS). Thereby, we will further investigate reasons for the weak convergence of simulated R33 from the perspective of the MWS and RMW, and focus on the mechanism that affects the convergence of RMW. The simulations of the four CP experiments are divided into two categories, i.e., results of the NOCP, KFEX and BMJ experiments are the first category, and results of the GF experiments are the second category. In the first category, the simulated TC intensity gradually increases while the RMW and R33 gradually decrease with increasing resolution. In the second category, following the increase in model resolution, relatively small changes are found in the simulated MWS and RMW while the R33 gradually decreases.
Following the increase of model resolution, the subgrid-scale convection may become grid-scale convection that can be resolved by the model, thus more convection is resolved, resulting in larger diabatic heating, which directly drives the development of convection in the TC eyewall region and induces the secondary circulation of typhoon [37]. The above processes are expected to contribute to not only the TC intensity (e.g., MWS) but also the TC structure (e.g., TC size). In all the suites of experiments in the present study, the distribution of diabatic heating is always sensitive to model resolution and CP scheme. Horizontal distributions of diabatic heating at 700 hPa simulated in these experiments are displayed in Figure 4. Note that the diabatic heating here includes four terms, which is caused by microphysics, by cumulus scheme, by radiation scheme and by boundary layer parameterization [38]. As expected, a similar feature is found in all the four CP experiments, i.e., following the increase in the model resolution, maximum diabatic heating in the TC eyewall region increases but its horizontal distribution becomes more fragmented. Meanwhile, the radius of the TC eyewall exhibits various degrees of decrease as the resolution increases (Figure 4m–p), especially when the model resolution increases from 3 km to 1 km. Furthermore, obvious double eyewall structure can be found in the KFEX and BMJ experiments (Figure 3o and Figure 4n). This double eyewall feature can also be seen in the observed satellite imagery (Figure S5). Following the occurrence of the outer eyewall, the radius of the inner eyewall decreases greatly from 50–60 km to 20–40 km in KFEX and BMJ runs when the resolution increases form 7.5 km to 1 km.
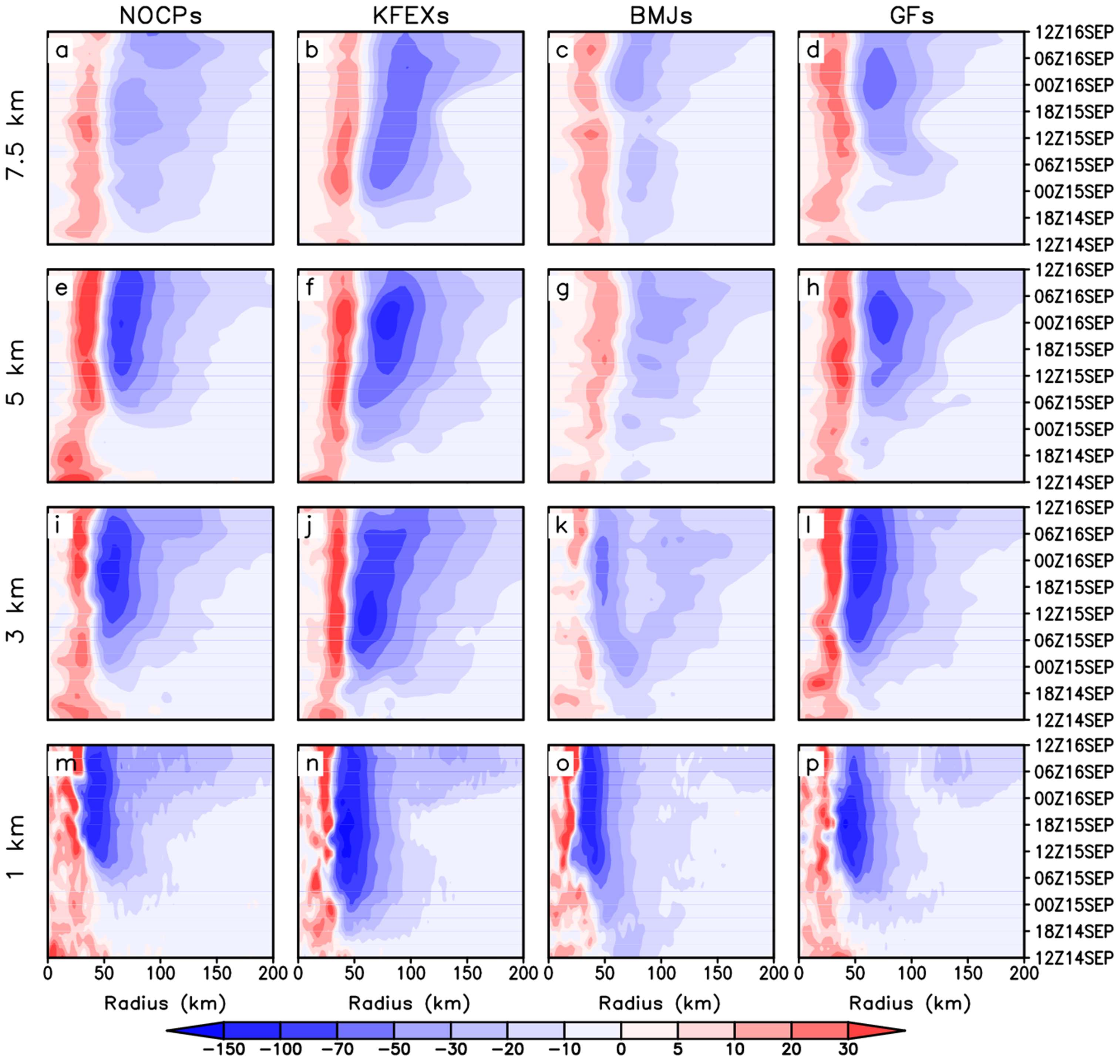
To further confirm the close relationship between simulated TC inner-core size and diabatic heating, Figure 5 is presented to show the azimuthal-means and time-averaged cross sections of the model simulated diabatic heating. Similar to those shown in Figure 4, when the resolution increases form 7.5 km to 5 km, diabatic heating intensifies in all the four CP experiments as expected. This is because when the resolution increases, more convection is resolved within the TC eyewall and diabatic heating increases subsequently. When the model resolution further increases, i.e., grid spacing decreases from 5 km to 1 km, diabatic heating in the TC eyewall area continues to intensify in the first three experiments; meanwhile, the maximum heating is located closer to the TC center. This result is consistent with the variations of model-simulated rainfall shown by Gentry and Lackmann [39]. In addition, the eyewall slope represented by the solid line decreases with height, indicating a decreased TC inner core size. Hazelton and Hart use the radar reflectivity data to analyze the relationship between azimuthal mean slope and TC intensity. Their result shows that the eye slope is more upright in the stronger storms [40]. In fact, as the resolution increases, the eye slope of the simulated TCs decreases in our first three experiments and the intensity is indeed enhanced. In the GF experiment (Figure 5l,p), however, when the resolution increases from 3 km to 1 km, the maximum diabatic heating value becomes smaller, and its distance to the TC center changes little, resulting in a relatively small change in the horizontal distribution of diabatic heating. This may be an important reason for the relatively strong convergence in the RMW simulation of the GF runs, which will be further discussed later.
Figure 6 shows the Hovmöller diagram of azimuthal-mean radial pressure gradient at 100-m height. Note that the spatial and temporal distributions of diabatic heating are quite similar to those of radial pressure gradient (figure omitted). As suggested by Hack and Schubert, the closer the position of diabiatic heating to TC center, the larger the contribution it makes to the TC central pressure fall [41]. In the simulations with coarse resolutions, e.g., 7.5 km and 5 km, the simulated maximum value of diabatic heating is relatively small and located farther from the TC center. This contributes to the smaller fall of the TC central pressure, and thus leads to weaker pressure gradient near the eyewall [10,42]. In contrast, when the model resolution increases to 3 km and 1 km, the opposite is true. The simulated maximum value of diabatic heating increases significantly and is located closer to the TC center in the NOCP, KFEX and BMJ experiments, leading to great increases in the TC intensity and thus the radial pressure gradient near the TC eyewall. In order to better understand the relationship between the intensified radial pressure gradient and the decreased RMW as the grid spacing decreases (see Figure 2), diagnostic analysis of radial velocity is conducted. The diagnostic equation used in the present study is similar to that in Gopalakrishnan et al. [43], which is expressed as:
d u r d t = − 1 ρ ∂ p ∂ r + v t v t r + f v t − D u r
where r is the radial distance from the TC center, ur and vt are azimuthal-mean radial and tangential winds, respectively, f is the Coriolis parameter, ρ and p are the air density and pressure, Dur is parameterized subgrid scale diffusion term which includes friction and horizontal diffusions. The inflow of radial wind is mainly concentrated below the height of 1 km (Figure S6), thereby the vertical level of the radial velocity equation diagnosis is selected at the height of 100 m above the surface. Previous studies have shown that the horizontal diffusion term above 100 m is quite small and negligible in storm simulation. Equation (3) reflects the gradient wind imbalance outside the eyewall [44,45]. This imbalance intensifies as the resolution increases, which is attributed to the increase in pressure gradient force (Figure 6). Following the increase in model resolution, the stronger radial pressure gradient force accelerates the radial inflow and leads to an inward contraction of the RMW (Figure 6). This indicates that the decrease of RMW is contributed by the increase of pressure gradient force as the model resolution increases. Figure 7 shows the azimuthal-mean net radial forcing term. As the model resolution increases to 1 km, the diabatic heating near the eyewall increases in the NOCP, KFEX and BMJ experiments, which reduces the pressure at the TC center and increases the pressure gradient force (Figure 6m–o). In this situation, the net radial forcing term also becomes larger according to Equation (3). As a result, the TC eyewall shrinks inward and the RMW reduces. Moreover, due to the decrease in the RMW, the area of diabatic heating shifts closer to the TC center and further decreases the TC central pressure [41]. The above results indicate that with the increase in the model resolution, a positive feedback develops between decreases in the RMW and increases in the pressure gradient, which leads to TC intensification and further decreases the RMW. The simulation of RMW eventually becomes non-convergent as shown in Figure 2, which presents the results of the experiments of NOCP, KFEX and BMJ. Meanwhile, the contraction of the RMW leads to large centrifugal force and thus decelerates the radial inflow, preventing further contraction of the RMW [46]. Thereby, such a positive feedback loop keeps increasing the pressure gradient and decreasing the RMW until a new equilibrium of radial force in the eyewall is reached. Nevertheless, for the GF scheme, the diabatic heating only slightly decreases as the model resolution increases, and the area of diabatic heating changes little (Figure 5p). With small changes in net radial forcing term, the simulation of the RMW remains convergent.
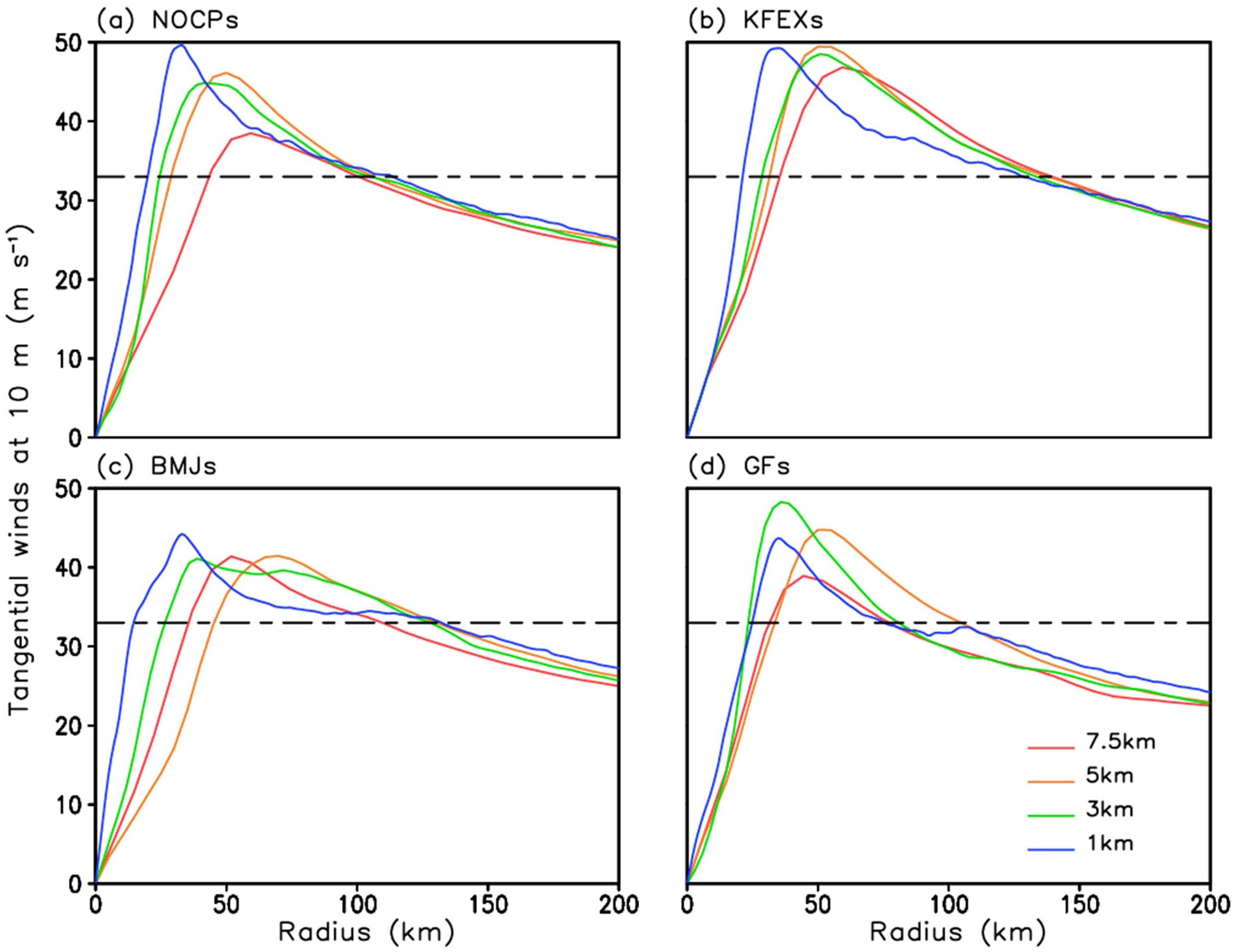
In the GF experiment, only small changes are found in the TC inner core size (i.e., RMW) as the resolution increases. However, the calculated PDS is still non-convergent because of the decrease in the R33, which is determined by both the MWS and RMW. Figure 8 shows the azimuthal-mean radial distribution of tangential wind at 10-m height above the ground. The dashed line represents the tangential wind speed of 33 m s−1. When the model resolution increases from 7.5 km to 3 km, the simulated RMW decreases but the maximum tangential wind increases in all the experiments. However, when the model resolution increases from 3 km to 1 km, simulations with different CP schemes become quite different. Contrary to the results simulated with the other three CP schemes, the diabatic heating simulated with the GF scheme decreases as the resolution increases, especially the diabatic heating in the eyewall (Figure 5p). This is because the relatively strong outer convection suppresses the development of inner convection in the TC eyewall [44], which leads to relatively weak TC intensity in the 1-km run. Meanwhile, the RMW remains unchanged in the 1-km resolution run compared to that in the 3-km resolution run. The above features contribute to the convergence of the RMW simulation with the GF scheme (Figure 2). It is exactly that R33 becomes smaller based on the theory of Carr and Elsberry [36], as the RMW remains unchanged and the intensity (MWS) decreases in the GF experiment when the model resolution increases to the finest (i.e., 1 km). This eventually leads to the non-convergent simulation of PDS. In the other three suites of experiments with different CP schemes (Figure 8a–c), the RMW decreases and the MWS increases as the model resolution increases. Simulations of the above two factors (i.e., RMW and MWS), which affect the simulation convergence of R33, are not convergent. Thereby, compared to that in the GF experiment, the relatively strong convergence of R33 simulation in the NOCP and BMJ experiments is obtained by wrong reasons and thus are not trustworthy. Comparison of the four CP schemes reveals that the NOCP and BMJ schemes cannot well simulate the TC intensity and TC size; thereby, their relatively better performance in the convergence of calculated PDS is a result of offset between counteracting behaviors of other variables. A perfect model should be able to yield strong convergent simulation of both the TC intensity and TC size, and thus strong convergent simulation of PDS. Compared to the other three CP schemes, the simulation of the GF scheme is more trustworthy.

5. Summary and Discussion

The present study investigates the convergence of WRF simulation of the destructive potential of TC Shanshan (2006) using four different CP schemes. It is found that as the model resolution increases, the PDI increases while the PDS decreases to various degrees in all the experiments with the four CP schemes. The differences in the simulation convergence between the two TC destructive potential indexes lie in the fact that the TC inner core size is considered in the PDS computation but not in the PDI. Apparently, the TC inner-core size imposes great impacts on the PDS simulation. The increase in the calculated PDI at higher resolution is attributed to larger TC intensity at higher resolution. When considering the TC inner core size, decreases in the PDS at higher resolution are associated with decreases in the TC inner-core size at higher resolution.
Since the TC inner-core size makes great contributions to the non-convergence of the TC PDS simulation, the present study is focused on the convergence issue of TC inner-core size simulation, especially the RMW. Physical mechanisms for the non-convergent PDS, which decreases as the resolution increases, are explored (Figure 9). Diagnostic analysis of radial winds is conducted to investigate the reasons for different features of convergence in the TC inner-core size simulation using different CP schemes. It is found that in the NOCP, KFEX, and BMJ experiments, when the resolution gradually increases from 7.5 km to 1 km, more convection is resolved, and the simulated maximum diabatic heating near the TC eyewall becomes larger, leading to rapid pressure decrease and pressure gradient increase in the corresponding area. On the one hand, the above processes keep increasing the simulated TC intensity, and result in stronger non-convergence of the PDI simulation. On the other hand, larger pressure gradient force would reduce the RMW according to the gradient wind balance equation. The area of diabatic heating becomes closer to the TC center due to the decrease in the RMW, leading to larger pressure decrease in the TC center. Such a positive feedback loop keeps increasing the pressure gradient and decreasing the RMW until a new stable equilibrium of radial force in the eyewall is reached. As a result, the model simulation of the TC inner core size becomes non-convergent, which eventually leads to non-convergent PDS simulation.
Contrary to the simulations with the above three CP schemes, the RMW simulation converges well with the GF scheme. With this scheme, the area of diabatic heating does not shrink inward as the resolution increases, and the maximum diabatic heating only changes slightly. As a result, the model well converges for simulations of the RMW, TC intensity, and PDI. However, the convergence of the PDS simulation is less satisfactory. This is because the simulated TC intensity weakens as the resolution increases since the simulated maximum diabatic heating becomes smaller. As a result, the R33 keeps decreasing and the simulation becomes non-convergent. Comparison of the four CP schemes reveals that the NOCP and BMJ schemes cannot well simulate the TC intensity and TC size; thereby, their relatively better performance in the convergence of PDS simulation is a result of cancelation between other variables. A perfect model should be able to yield strong convergent simulation of both the TC intensity and TC size, and thus strong convergent simulation of the PDS. Compared to the other three CP schemes, the simulation of the GF scheme is more trustworthy.

Supplementary Materials

The following are available online at https://www.mdpi.com/2073-4433/10/2/74/s1, Figure S1: Setting of nested model domains for 1 km resolution experiments. The movable domains D2, D3 and D4 are shown at their initial positions. Figure S2: Temporal evolutions of minimum sea level pressure (MSLP) in the sensitivity experiments: (a) NOCPs, (b) KFEXs, (c) BMJs, and (d) GFs. The black line is the observation data from JTWC. Figure S3: Temporal evolutions of maximum 10-meter wind speed (MWS) in the sensitivity experiments: (a) NOCPs, (b) KFEXs, (c) BMJs, and (d) GFs. The black line is the observation data from JTWC. Figure S4: Temporal evolutions of the radius of maximum wind at 10-meter height (RMW) in the sensitivity experiments: (a) NOCPs, (b) KFEXs, (c) BMJs, and (d) GFs. The black line is the observation data from JTWC. Figure S5: Rainfall rate (inches h-1) from TRMM TMI/PR at 0431 UTC 16 September 2006. Figure S6: Azimuthal- and time-averaged cross-sections of radial wind (m s-1) in the TC mature stage.

Author Contributions

Data curation, C.M. and J.L.; Formal analysis, C.M., Y.S. and J.L.; Funding acquisition, T.L.; Investigation, C.M., Y.S., J.L., T.L. and Z.Z.; Methodology, C.M., Y.S., T.L. and Z.Z.; Project administration, Y.S.; Writing—original draft, C.M.

Funding

This work was jointly supported by China NSF grant 41605072, NSFC grants 41630423, Jiangsu projects BK20160768, China National Key R&D Program 2015CB453200, NOAA NA18OAR4310298, NSF AGS-1643297, NSFC grants 41875069, NRL grant N00173-16-1-G906, and NSF 41675077. This work was supported in part by China Scholarship Council (CSC) under the Grant CSC N201808320282. This is SOEST contribution number 10650, IPRC contribution number 1363, and ESMC contribution number 249.

Acknowledgments

The authors thank the three reviewers and the academic editor for their constructive comments which benefit to improve the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Pielke, A., Jr.; Gratz, J.; Landsea, C.W.; Collins, D.; Saunders, M.; Musulin, R. Normalized hurricane damage in the United States: 1900–2005. Nat. Hazards Rev. 2008, 9, 29–42. [Google Scholar] [CrossRef]
  2. Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
  3. Zhai, A.R.; Jiang, J.H. Dependence of U.S. hurricane economic loss on maximum wind speed and storm size. Environ. Res. Lett. 2014, 9, 064019. [Google Scholar] [CrossRef]
  4. Emanuel, K.A. Increasing destructiveness of tropical cyclones over the past 30 years. Nature 2005, 436, 686–688. [Google Scholar] [CrossRef] [PubMed]
  5. Vecchi, G.A.; Swanson, K.L.; Soden, B.J. Whither hurricane activity? Science 2008, 322, 687–689. [Google Scholar] [CrossRef] [PubMed]
  6. Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.K.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157–163. [Google Scholar] [CrossRef] [Green Version]
  7. Lin, Y.; Zhao, M.; Zhang, M. Tropical cyclone rainfall area controlled by relative sea surface temperature. Nat. Commun. 2015, 6, 6591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  8. Sun, Y.; Zhong, Z.; Li, T.; Yi, L.; Hu, Y.; Wan, H.; Chen, H.; Liao, Q.; Ma, C.; Li, Q. Impact of ocean warming on tropical cyclone size and its destructiveness. Sci. Rep. 2017, 7, 8154. [Google Scholar] [CrossRef] [PubMed]
  9. Lean, H.W.; Clark, P.A.; Dixon, M.; Roberts, N.M.; Fitch, A.; Forbes, R.; Halliwell, C. Characteristics of highresolution versions of the Met Office Unified Model for forecasting convection over the United Kingdom. Mon. Weather Rev. 2008, 136, 3408–3424. [Google Scholar] [CrossRef]
  10. Sun, Y.; Yi, L.; Zhong, Z.; Hu, Y.; Ha, Y. Dependence of model convergence on horizontal resolution and convective parameterization in simulations of a tropical cyclone at greyzone resolutions. J. Geophys. Res. Atmos. 2013, 118, 7715–7732. [Google Scholar] [CrossRef]
  11. Hammarstrand, U. Questions involving the use of traditional convection parameterization in NWP models with higher resolution. Tellus 1998, 50A, 265–282. [Google Scholar] [CrossRef]
  12. Gerard, L. An integrated package for subgrid convection, clouds and precipitation compatible with meso-gamma scales. Q. J. R. Meteor. Soc. 2007, 133, 711–730. [Google Scholar] [CrossRef]
  13. Yu, X.; Lee, T.-Y. Role of convective parameterization in simulations of a convection band at grey-zone resolutions. Tellus 2010, 62, 617–632. [Google Scholar] [CrossRef]
  14. Kotroni, V.; Lagouvardos, K. Evaluation of MM5high resolution real-time forecasts over the urban area of Athens, Greece. J. Appl. Meteorol. 2004, 43, 1666–1678. [Google Scholar] [CrossRef]
  15. Deng, A.; Stauffer, D.R. On improving 4-km mesoscale model simulations. J. Appl. Meteorol. Climatol. 2006, 45, 361–381. [Google Scholar] [CrossRef]
  16. Fierro, A.O.; Rogers, R.F.; Marks, F.D. The impact of horizontal grid spacing on the microphysical and kinematic structures of strong tropical cyclones simulated with the WRF-ARW model. Mon. Weather Rev. 2009, 137, 3717–3743. [Google Scholar] [CrossRef]
  17. Sun, Y.; Yi, L.; Zhong, Z.; Ha, Y. Performance of a new convective parameterization scheme on model convergence in simulations of a tropical cyclone at gray-zone resolutions. J. Atmos. Sci. 2014, 71, 2078–2088. [Google Scholar] [CrossRef]
  18. Rotunno, R.; Chen, Y.; Wang, W.; Davis, C.; Dudhia, J.; Holland, G.J. Large-eddy simulation of an idealized tropical cyclone. Bull. Amer. Meteor. Soc. 2009, 90, 1783–1788. [Google Scholar] [CrossRef]
  19. Bryan, G.H.; Wyngaard, J.C.; Fritsch, J.M. Resolution requirements for the simulation of deep moist convection. Mon. Weather Rev. 2003, 131, 2394–2416. [Google Scholar] [CrossRef]
  20. Grell, G.A.; Freitas, S. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. Discuss. 2014, 14, 5233–5250. [Google Scholar] [CrossRef] [Green Version]
  21. Joint Typhoon Warning Center Best Track Data. Available online: http://www.metoc.navy.mil/jtwc/jtwc.html?western-pacific (accessed on 20 December 2018).
  22. Paulson, C.A. The mathematical representation of wind speed and temperature profiles in the unstable atmospheric surface layer. J. Appl. Meteorol. 1970, 9, 857–861. [Google Scholar] [CrossRef]
  23. Beljaars, A.C.M. The parameterization of surface fluxes in large-scale models under free convection. Q. J. R. Meteor. Soc. 1994, 121, 255–270. [Google Scholar] [CrossRef]
  24. Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
  25. Lin, Y.-L.; Farley, R.D.; Orville, H.D. Bulk parameterization of the snow field in a cloud model. J. Clim. Appl. Meteorol. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
  26. NCEP FNL Operational Model Global Tropospheric Analyses, continuing from July 1999. Available online: https://rda.ucar.edu/datasets/ds083.2/index.html?hash=!access (accessed on 17 April 2018).
  27. Skamarock, W.C.; , and Coauthors. A Description of the Advanced Research WRF Version 3. NCAR Tech. Note NCAR/TN-4751STR. 2008, p. 113. Available online: http://www.mmm.ucar.edu/people/skamarock/ (accessed on 18 December 2018).
  28. Kain, J.S. The Kain-Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
  29. Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
  30. Betts, A.K. A new convective adjustment scheme. Part I: Observational and theoretical basis. Q. J. R. Meteor. Soc. 1986, 112, 677–692. [Google Scholar] [CrossRef]
  31. Betts, A.K.; Miller, M.J. A new convective adjustment scheme. Part II: Single column tests using GATE wave, BOMEX, ATEX and arctic air-mass data sets. Q. J. R. Meteor. Soc. 1986, 112, 693–709. [Google Scholar] [CrossRef]
  32. Janjić, Z.I. The step-mountain eta coordinate model: Further developments of the convection, viscous sublayer and turbulence closure schemes. Mon. Weather Rev. 1994, 122, 927–945. [Google Scholar] [CrossRef]
  33. Janjić, Z.I. Comments on “Development and evaluation of a convection scheme for use in climate models”. J. Atmos. Sci. 2000, 57, 3686. [Google Scholar] [CrossRef]
  34. Ma, Z.; Fei, J.; Huang, X.; Cheng, X. Contributions of surface sensible heat fluxes to tropical cyclone. Part I: evolution of tropical cyclone intensity and structure. J. Atmos. Sci. 2015, 721, 120–140. [Google Scholar] [CrossRef]
  35. Ma, Z.; Fei, J.; Cheng, X.; Wang, Y.; Huang, X. Contributions of surface sensible heat fluxes to tropical cyclone. Part II: The sea spray processes. J. Atmos. Sci. 2015, 72, 4218–4236. [Google Scholar] [CrossRef]
  36. Carr, L.E.; Elsberry, R.L. Models of tropical cyclone wind distribution and beta-effect propagation for application to tropical cyclone track forecasting. Mon. Weather Rev. 1997, 125, 3190–3209. [Google Scholar] [CrossRef]
  37. Wang, B.; Li, T. A simple tropical atmosphere model of relevance to short-term climate variations. J. Atmos. Sci. 1993, 50, 260–284. [Google Scholar] [CrossRef]
  38. Sun, Y.; Zhong, Z.; Lu, W.; Hu, Y. Why are tropical cyclone tracks over the western North Pacific sensitive to the cumulus parameterization scheme in regional climate modeling? A case study for Megi (2010). Mon. Weather Rev. 2014, 142, 1240–1249. [Google Scholar] [CrossRef]
  39. Gentry, M.S.; Lackmann, G.M. Sensitivity of simulated tropical cyclone structure and intensity to horizontal resolution. Mon. Weather Rev. 2010, 138, 688–704. [Google Scholar] [CrossRef]
  40. Hazelton, A.T.; Hart, R.E. Hurricane eyewall slope as determined from airborne radar reflectivity data: Composites and case studies. Wea. Forecast. 2013, 28, 368–386. [Google Scholar] [CrossRef]
  41. Hack, J.J.; Schubert, W.H. Nonlinear response of atmospheric vortices to heating by organized cumulus convection. J. Atmos. Sci. 1986, 43, 1559–1573. [Google Scholar] [CrossRef]
  42. Black, P.G.; Holland, G.J. The boundary layer of Tropical Cyclone Kerry (1979). Mon. Weather Rev. 1995, 123, 2007–2028. [Google Scholar] [CrossRef]
  43. Gopalakrishnan, S.G.; Marks, F., Jr.; Zhang, X.J.; Bao, J.-W.; Yeh, K.-S.; Atlas, R. The experimental HWRF system: A study on the influence of horizontal resolution on the structure and intensity changes in tropical cyclones using an idealized framework. Mon. Weather Rev. 2011, 139, 1762–1784. [Google Scholar] [CrossRef]
  44. Wang, Y. How do outer spiral rainbands affect tropical cyclone structure and intensity? J. Atmos. Sci. 2009, 66, 1250–1273. [Google Scholar] [CrossRef]
  45. Emanuel, K.A. An air–sea interaction theory for tropical cyclones. Part 1: Steady-state maintenance. J. Atmos. Sci. 1986, 43, 585–604. [Google Scholar] [CrossRef]
  46. Xu, J.; Wang, Y. Sensitivity of tropical cyclone innercore size and intensity to the radial distribution of surface entropy flux. J. Atmos. Sci. 2010, 67, 1831–1852. [Google Scholar] [CrossRef]
Atmosphere 10 00074 g001 550
Figure 1. Storm tracks at various resolutions simulated by (a) NOCPs, (b) KFEXs, (c) BMJs, (d) GFs. The black line is the observation data from JTWC.
Figure 1. Storm tracks at various resolutions simulated by (a) NOCPs, (b) KFEXs, (c) BMJs, (d) GFs. The black line is the observation data from JTWC.
Atmosphere 10 00074 g001
Atmosphere 10 00074 g002 550
Figure 2. Changes of time-averaged (a–d) MWS (m s−1), (e–h) PDI (1016 m3 s−2), (i–l) RMW (km), (m–p) R33 (km), (q–t) PDS (1014 kg m2 s−2) with resolution in the experiments using four CP schemes in the TC mature stage from 1800UTC 15 September to 0600 UTC 16 September. The time-average interval is one hour. The bar line is a range of one standard deviation.
Figure 2. Changes of time-averaged (a–d) MWS (m s−1), (e–h) PDI (1016 m3 s−2), (i–l) RMW (km), (m–p) R33 (km), (q–t) PDS (1014 kg m2 s−2) with resolution in the experiments using four CP schemes in the TC mature stage from 1800UTC 15 September to 0600 UTC 16 September. The time-average interval is one hour. The bar line is a range of one standard deviation.
Atmosphere 10 00074 g002
Atmosphere 10 00074 g003 550
Figure 3. Changes of time-averaged heavy precipitation (greater than 50 mm h−1) area (km2) with resolution in the experiments simulated by (a) NOCPs, (b) KFEXs, (c) BMJs, (d) GFs. The time-average interval is one hour. The bar line is a range of one standard deviation.
Figure 3. Changes of time-averaged heavy precipitation (greater than 50 mm h−1) area (km2) with resolution in the experiments simulated by (a) NOCPs, (b) KFEXs, (c) BMJs, (d) GFs. The time-average interval is one hour. The bar line is a range of one standard deviation.
Atmosphere 10 00074 g003
Atmosphere 10 00074 g004 550
Figure 4. Horizontal cross sections of time-averaged diabatic heating (°C h−1) in the TC mature stage. The time-average interval is one hour. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Figure 4. Horizontal cross sections of time-averaged diabatic heating (°C h−1) in the TC mature stage. The time-average interval is one hour. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Atmosphere 10 00074 g004
Atmosphere 10 00074 g005 550
Figure 5. Azimuthal- and time-averaged cross-sections of the model-simulated diabatic heating (°C h−1; shaded) and the solid line represents the 5 °C h−1 contour line of simulated diabatic heating in the TC mature stage. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Figure 5. Azimuthal- and time-averaged cross-sections of the model-simulated diabatic heating (°C h−1; shaded) and the solid line represents the 5 °C h−1 contour line of simulated diabatic heating in the TC mature stage. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Atmosphere 10 00074 g005
Atmosphere 10 00074 g006 550
Figure 6. Hovmöller diagrams of the azimuthal-averaged radial pressure gradient (kg m−2 s−1 h−1) at 100 m height. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Figure 6. Hovmöller diagrams of the azimuthal-averaged radial pressure gradient (kg m−2 s−1 h−1) at 100 m height. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Atmosphere 10 00074 g006
Atmosphere 10 00074 g007 550
Figure 7. Hovmöller diagrams of the azimuthal-averaged net radial forcing term (m s−1 h−1) at 100 m height. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Figure 7. Hovmöller diagrams of the azimuthal-averaged net radial forcing term (m s−1 h−1) at 100 m height. The model resolution is 7.5 km (a–d), 5 km (e–h), 3 km (i–l) and 1 km (m–p) respectively.
Atmosphere 10 00074 g007
Atmosphere 10 00074 g008 550
Figure 8. Radial distributions of the azimuthal-mean tangential wind (m s−1) at 10-m height in the TC mature stage simulated by (a) NOCPs, (b) KFEXs, (c) BMJs, (d) GFs. The dash line represents 33m s−1.
Figure 8. Radial distributions of the azimuthal-mean tangential wind (m s−1) at 10-m height in the TC mature stage simulated by (a) NOCPs, (b) KFEXs, (c) BMJs, (d) GFs. The dash line represents 33m s−1.
Atmosphere 10 00074 g008
Atmosphere 10 00074 g009 550
Figure 9. Schematic diagram summarizing the possible reasons for the dependence of model convergence in simulations of the TC PDI and PDS. Blue shading indicates the positive feedback of smaller RMW on central pressure fall.
Figure 9. Schematic diagram summarizing the possible reasons for the dependence of model convergence in simulations of the TC PDI and PDS. Blue shading indicates the positive feedback of smaller RMW on central pressure fall.
Atmosphere 10 00074 g009
Table
Table 1. Domain settings for the four suites of simulations with different horizontal resolutions.
Table 1. Domain settings for the four suites of simulations with different horizontal resolutions.
CaseGrid SpacingDM1DM2DM3DM4
7.5 km45-15-7.5 km55 × 75100 × 100105 × 105none
5 km45-15-5 km55 × 75100 × 100157 × 157none
3 km45-15-3 km55 × 75100 × 100261 × 261none
1 km45-15-5-1 km55 × 75100 × 100157 × 157501 × 501
Table
Table 2. The residuals of the regression of R33 onto the RMW, MWS and the residuals of the bivariate regression of R33 onto the RMW and MWS indices for the all experiments data. The correlation coefficient between R33 and RMW is 0.19 and 0.39 between R33 and MWS.
Table 2. The residuals of the regression of R33 onto the RMW, MWS and the residuals of the bivariate regression of R33 onto the RMW and MWS indices for the all experiments data. The correlation coefficient between R33 and RMW is 0.19 and 0.39 between R33 and MWS.
RMWMWSRMW + MWS
R20.040.150.34
p-value<0.001<0.001<0.001
Corr0.190.39

Share and Cite

MDPI and ACS Style

Ma, C.; Sun, Y.; Liu, J.; Li, T.; Zhong, Z. Impact of Cumulus Parameterization on Model Convergence of Tropical Cyclone Destructive Potential Simulation at Grey-Zone Resolutions: A Numerical Investigation. Atmosphere 2019, 10, 74. https://doi.org/10.3390/atmos10020074

AMA Style

Ma C, Sun Y, Liu J, Li T, Zhong Z. Impact of Cumulus Parameterization on Model Convergence of Tropical Cyclone Destructive Potential Simulation at Grey-Zone Resolutions: A Numerical Investigation. Atmosphere. 2019; 10(2):74. https://doi.org/10.3390/atmos10020074

Chicago/Turabian Style

Ma, Chen, Yuan Sun, Jia Liu, Tim Li, and Zhong Zhong. 2019. "Impact of Cumulus Parameterization on Model Convergence of Tropical Cyclone Destructive Potential Simulation at Grey-Zone Resolutions: A Numerical Investigation" Atmosphere 10, no. 2: 74. https://doi.org/10.3390/atmos10020074

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop