Hierarchical Modeling of Solar System Planets with Isca
Abstract
1. Introduction
- There are so many planets that constructing a comprehensive model for each is simply infeasible.
- The observational data available for solar system planets are orders of magnitude less than that for Earth in terms of spatial and temporal coverage, even with modern missions to other planets such as the Venus Express or Juno. The data available for exoplanets are orders of magnitude less still. Thus, were we to choose to use a highly complex model to model a given planet, we would be in danger of having to make too many choices about important parameters and processes that are, at the very least, under-constrained by the observations. We would therefore run the risk of over-interpreting matches between model output and observations when the solutions could be highly non-unique, thus running the risk of “over-fitting” the data to the model.
- Although there is a diversity of planetary atmospheres, they obey the same physical laws. This, and the desire to understand as well as simulate (a desire that also holds for Earth) suggests that we should use models that take advantage of that commonality and build from there, with appropriate complexity for the problem at hand.
2. Isca, the Modeling Framework
- A spectral, primitive equation dynamical core in spherical co-ordinates.
- The shallow water equations on the sphere.
- The barotropic vorticity equation on the sphere [13].
- Optional inclusion of moisture and other tracers.
- A thermal relaxation scheme, in particular the Held–Suarez scheme and variants about it [14].
- A thermal relaxation scheme based on an analytic radiative-convective equilibrium state, with variable tropopause height depending on optical depth and other parameters, and a seasonal cycle.
- A thermal relaxation scheme based on an analytic radiative equilibrium state.
- A radiation scheme with two bands in the infra-red [17].
- The multi-band, comprehensive RRTM (Rapid Radiative Transfer Model) scheme [18].
- The multi-band, comprehensive SOCRATES scheme [19].
- A slab mixed-layer ocean, with or without Q-fluxes (that is, specified horizontal heat fluxes) to mimic heat transport (see e.g., [26]).
- Evaporative resistance over land, or a simple bucket model with evaporation dependent on how full the bucket is.
- Configurable land outlines, or land outline taken from a dataset (e.g., ERA-interim reanalysis for Earth [27]).
- Configurable topography, or topography taken from a dataset (for Earth or Mars).
3. Earth
3.1. A Simple Thermal-Relaxation Model
3.2. An Intermediate Complexity Model
3.3. A More Comprehensive Model
4. Mars
4.1. A Simple Model
4.2. An Intermediate Complexity Model
4.3. A More Comprehensive Model
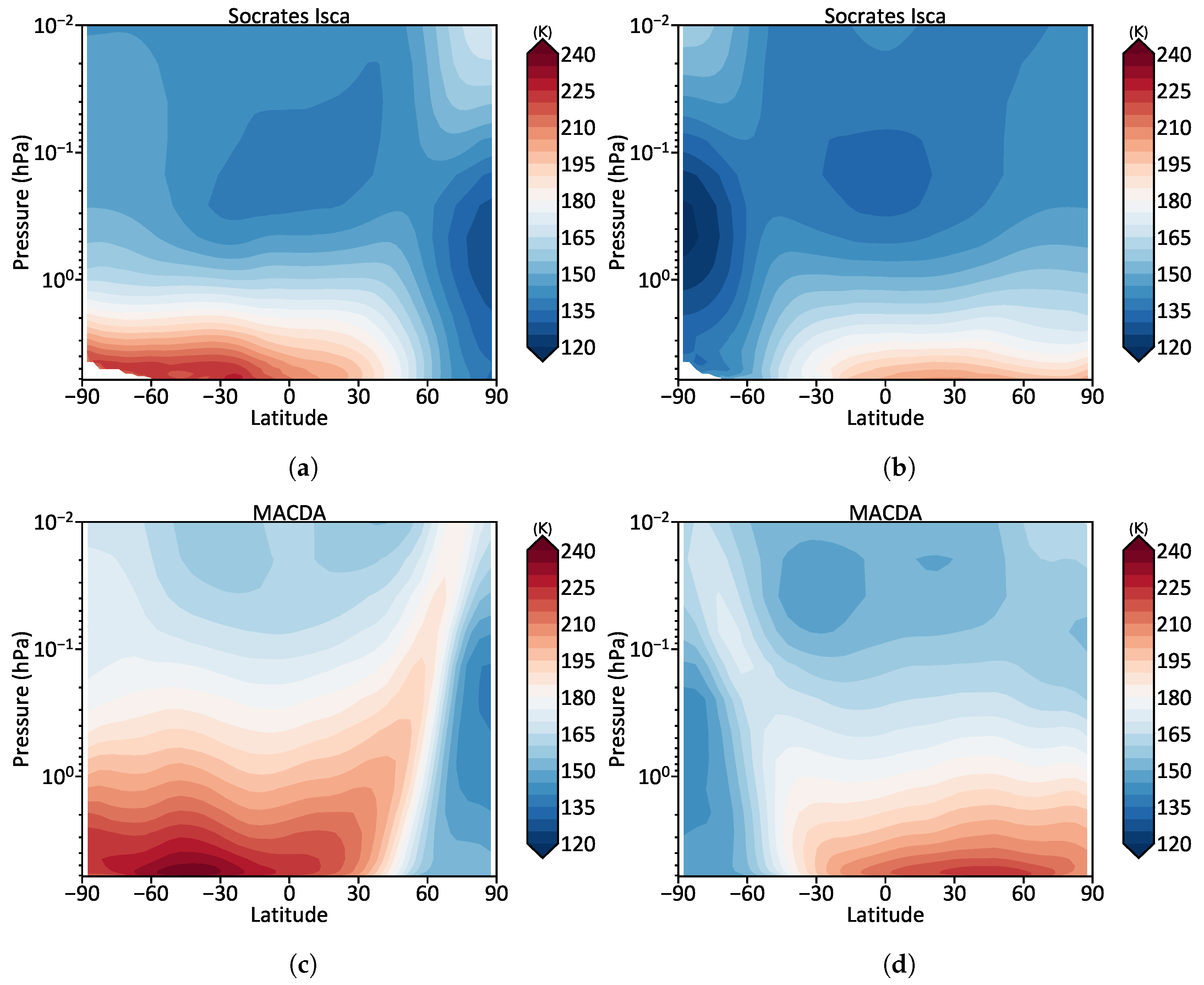
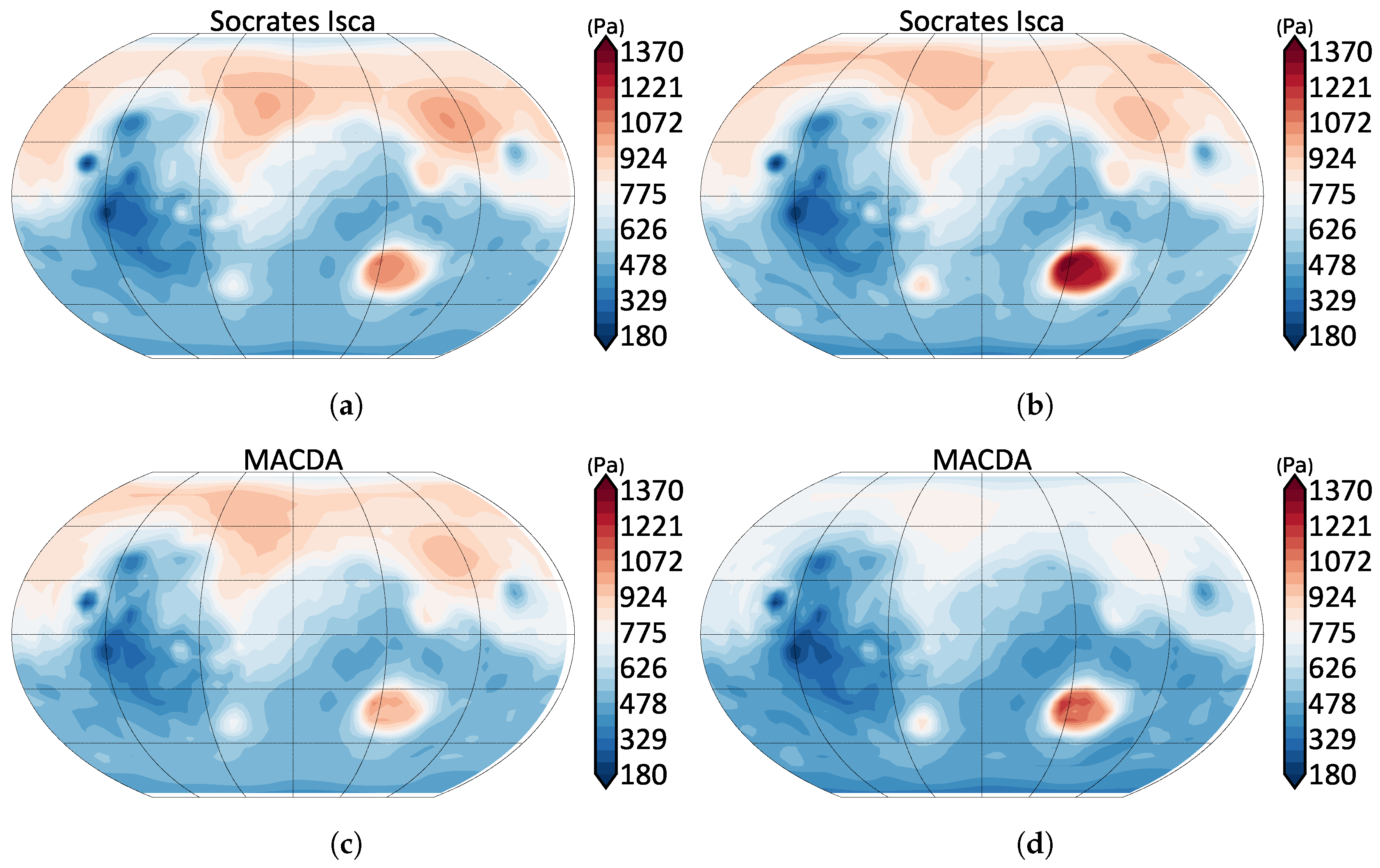
4.4. Comparison of Models and Observations
5. Jupiter
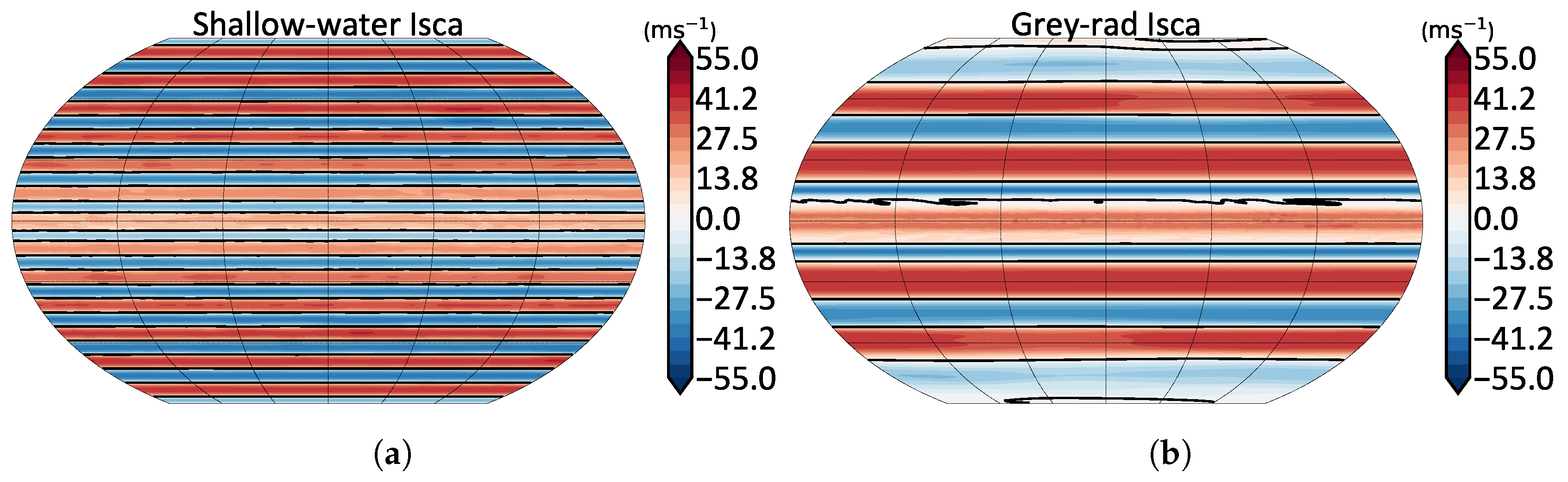
5.1. A Simple Model
5.2. An Intermediate Complexity Model
5.3. Toward a More Comprehensive Model
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Correia, A.C.M.; Laskar, J. Mercury’s capture into the 3/2 spin-orbit resonance as a result of its chaotic dynamics. Nature 2004, 429, 848–850. [Google Scholar] [CrossRef] [PubMed]
- Taylor, F.W.; Svedhem, H.; Head, J.W. Venus: The Atmosphere, Climate, Surface, Interior and Near-Space Environment of an Earth-Like Planet. Space Sci. Rev. 2018, 214, 35. [Google Scholar] [CrossRef]
- Sánchez-Lavega, A.; Lebonnois, S.; Imamura, T.; Read, P.; Luz, D. The Atmospheric Dynamics of Venus. Space Sci. Rev. 2017, 212, 1541–1616. [Google Scholar] [CrossRef]
- Laskar, J.; Correia, A.; Gastineau, M.; Joutel, F.; Levrard, B.; Robutel, P. Long term evolution and chaotic diffusion of the insolation quantities of Mars. Icarus 2004, 170, 343–364. [Google Scholar] [CrossRef]
- Armstrong, J.C.; Leovy, C.B.; Quinn, T. A 1 Gyr climate model for Mars: New orbital statistics and the importance of seasonally resolved polar processes. Icarus 2004, 171, 255–271. [Google Scholar] [CrossRef]
- Read, P.L.; Lewis, S.R. The Martian Climate Revisited: Atmosphere and Environment of a Desert Planet; Springer Praxis Books: Geophysical Sciences; Springer: Berlin/Heidelerg, Germany, 2004; Volume 26. [Google Scholar]
- Akeson, R.L.; Chen, X.; Ciardi, D.; Crane, M.; Good, J.; Harbut, M.; Jackson, E.; Kane, S.R.; Laity, A.C.; Leifer, S.; et al. The NASA Exoplanet Archive: Data and Tools for Exoplanet Research. Publ. Astron. Soc. Pac. 2013, 125, 989–999. [Google Scholar] [CrossRef]
- Bouchy, F.; Udry, S.; Mayor, M.; Moutou, C.; Pont, F.; Iribarne, N.; Da Silva, R.; Ilovaisky, S.; Queloz, D.; Santos, N.C.; et al. ELODIE metallicity-biased search for transiting Hot Jupiters. Astron. Astrophys. 2005, 444, L15–L19. [Google Scholar] [CrossRef]
- Seager, S.; Deming, D. Exoplanet Atmospheres. Annu. Rev. Astron. Astrophys. 2010, 48, 631–672. [Google Scholar] [CrossRef]
- Maher, P.; Gerber, E.P.; Medeiros, B.; Merlis, T.; Sherwood, S.; Sheshadri, A.; Sobel, A.; Vallis, G.K.; Voigt, A.; Zurita-Gotor, P. Model Hierarchies for Understanding Atmospheric Circulation. Rev. Geophys. 2019, 57, 250–280. [Google Scholar] [CrossRef]
- Vallis, G.K.; Colyer, G.; Geen, R.; Gerber, E.; Jucker, M.; Maher, P.; Paterson, A.; Pietschnig, M.; Penn, J.; Thomson, S.I. Isca, v1.0: A Framework for the Global Modelling of the Atmospheres of Earth and Other Planets at Varying Levels of Complexity. Geosci. Model Dev. 2018, 11, 843–859. [Google Scholar] [CrossRef]
- Donner, L.J.; Wyman, B.L.; Hemler, R.S.; Horowitz, L.W.; Ming, Y.; Zhao, M.; Golaz, J.C.; Ginoux, P.; Lin, S.J.; Schwarzkopf, M.D.; et al. The dynamical core, physical parameterizations, and basic simulation characteristics of the atmospheric component AM3 of the GFDL global coupled model CM3. J. Clim. 2011, 24, 3484–3519. [Google Scholar] [CrossRef]
- Vallis, G.K.; Gerber, E.P.; Kushner, P.J.; Cash, B.A. A Mechanism and Simple Dynamical Model of the North Atlantic Oscillation and Annular Modes. J. Atmos. Sci. 2004, 61, 264–280. [Google Scholar] [CrossRef]
- Held, I.M.; Suarez, M.J. A Proposal for the Intercomparison of the Dynamical Cores of Atmospheric General Circulation Models. Bull. Am. Meteorol. Soc. 1994, 75, 1825–1830. [Google Scholar] [CrossRef]
- Frierson, D.M.W.; Held, I.M.; Zurita-Gotor, P. A Gray Radiation Aquaplanet Moist GCM. Part 1: Static Stability and Eddy Scales. J. Atmos. Sci. 2006, 63, 2548–2566. [Google Scholar] [CrossRef]
- Byrne, M.P.; O’Gorman, P.A. Land–ocean warming contrast over a wide range of climates: Convective quasi-equilibrium theory and idealized simulations. J. Clim. 2013, 26, 4000–4016. [Google Scholar] [CrossRef]
- Geen, R.; Czaja, A.; Haigh, J.D. The effects of increasing humidity on heat transport by extratropical waves. Geophys. Res. Lett. 2016, 43, 8314–8321. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Manners, J.; Edwards, J.M.; Hill, P.; Thelen, J.C. SOCRATES Technical Guide: Suite Of Community RAdiative Transfer Codes Based on Edwards and Slingo; Technical Report; Met Office: Exeter, UK, 2017. [Google Scholar]
- O’Gorman, P.A.; Schneider, T. The hydrological cycle over a wide range of climates simulated with an idealized GCM. J. Clim. 2008, 21, 3815–3832. [Google Scholar] [CrossRef]
- Lambert, F.H.; Lewis, N.; Boutle, I. The Lambert–Lewis Convection Scheme; Technical Report; Unified Model Documentation Paper 041; Met Office: Exeter, UK, 2017. [Google Scholar]
- Betts, A.K. A new convective adjustment scheme. Part I: Observational and theoretical basis. Q. J. R. Meteorol. Soc. 1986, 112, 677–691. [Google Scholar]
- Betts, A.K.; Miller, M.J. The Betts–Miller scheme. In The Representation of Cumulus Convection in Numerical Models; Emanuel, K., Raymond, D., Eds.; Meteorological Monographs—American Meteorological Society: Boston, MA, USA, 1986; pp. 107–121. [Google Scholar]
- Frierson, D.M.W.; Held, I.M.; Zurita-Gotor, P. A Gray Radiation Aquaplanet Moist GCM. Part 2: Energy transports in altered climates. J. Atmos. Sci. 2007, 64, 1680–1693. [Google Scholar] [CrossRef]
- Moorthi, S.; Suarez, M.J. Relaxed Arakawa-Schubert. A parameterization of moist convection for general circulation models. Mon. Weather Rev. 1992, 120, 978–1002. [Google Scholar] [CrossRef]
- Russell, G.L.; Miller, J.R.; Tsang, L.C. Seasonal oceanic heat transports computed from an atmospheric model. Dyn. Atmos. Oceans 1985, 9, 253–271. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Thomson, S.I.; Vallis, G.K. Atmospheric Response to SST anomalies. Part I: Background-state dependence, teleconnections and local effects in winter. J. Atmos. Sci. 2018, 75, 4107–4124. [Google Scholar] [CrossRef]
- Thomson, S.I.; Vallis, G.K. Atmospheric Response to SST anomalies. Part II: Background-state dependence, teleconnections and local effects in summer. J. Atmos. Sci. 2018, 75, 4125–4138. [Google Scholar] [CrossRef]
- Geen, R.; Lambert, F.H.; Vallis, G.K. Regime Change Behavior During Asian Monsoon Onset. J. Clim. 2018. [Google Scholar] [CrossRef]
- Jiménez-Esteve, B.; Domeisen, D. Nonlinearity in the North Pacific atmospheric response to a linear ENSO forcing. Geophys. Res. Lett. 2019, 46, 2271–2281. [Google Scholar] [CrossRef]
- Vallis, G.K.; Zurita-Gotor, P.; Cairns, C.; Kidston, J. The response of the large-scale structure of the atmosphere to global warming. Q. J. R. Meteorol. Soc. 2015, 141, 1479–1501. [Google Scholar] [CrossRef]
- Schneider, E.K. A Note on the Annual Cycle of Sea Surface Temperature at the Equator; COLA Report; COLA: Calverton, MD, USA, 1996; Volume 36, 16p. [Google Scholar]
- Jucker, M. The surface of an aquaplanet GCM. Iceberg 2019, 1–4. [Google Scholar] [CrossRef]
- Donohoe, A.; Frierson, D.M.W.; Battisti, D.S. The effect of ocean mixed layer depth on climate in slab ocean aquaplanet experiments. Clim. Dyn. 2014, 43, 1041–1055. [Google Scholar] [CrossRef]
- Kobayashi, S.; Ota, Y.; Harada, Y.; Ebita, A.; Moriya, M.; Onoda, H.; Onogi, K.; Kamahori, H.; Kobayashi, C.; Endo, H.; et al. The JRA-55 Reanalysis: General specifications and basic characteristics. J. Meteorol. Soc. Jpn. Ser II 2015, 93, 5–48. [Google Scholar] [CrossRef]
- Taylor, K.E.; Williamson, D.; Zwiers, F. The Sea Surface Temperature and Sea-Ice Concentration Boundary Conditions for AMIP II Simulations; PCMDI Report No. 60; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2000; 25p. [Google Scholar]
- Thomson, S.I.; Vallis, G.K. The effects of gravity on the climate and circulation of a terrestrial planet. Q. J. R. Meteorol. Soc. 2019. [Google Scholar] [CrossRef]
- Greybush, S.J.; Wilson, R.J.; Hoffman, R.N.; Hoffman, M.J.; Miyoshi, T.; Ide, K.; McConnochie, T.; Kalnay, E. Ensemble Kalman filter data assimilation of Thermal Emission Spectrometer temperature retrievals into a Mars GCM. J. Geophys. Res. (Planets) 2012, 117, E11. [Google Scholar] [CrossRef]
- Montabone, L.; Marsh, K.; Lewis, S.R.; Read, P.L.; Smith, M.D.; Holmes, J.; Spiga, A.; Lowe, D.; Pamment, A. The Mars Analysis Correction Data Assimilation (MACDA) Dataset V1.0. Geosci. Data J. 2014, 1, 129–139. [Google Scholar] [CrossRef]
- Mitchell, D.M.; Montabone, L.; Thomson, S.; Read, P.L. Polar vortices on Earth and Mars: A comparative study of the climatology and variability from reanalyses. Q. J. R. Meteorol. Soc. 2014. [Google Scholar] [CrossRef] [PubMed]
- Seviour, W.J.M.; Waugh, D.W.; Scott, R.K. The Stability of Mars’s Annular Polar Vortex. J. Atmos. Sci. 2017, 74, 1533–1547. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T. Principles of Planetary Climate; Cambridge University Press: Cambridge, UK, 2010; p. 652. [Google Scholar]
- Vallis, G.K. Essentials of Atmospheric and Oceanic Dynamics; Cambridge University Press: Cambridge, UK, 2019; p. 356. [Google Scholar] [CrossRef]
- Martin, T.Z.; Peterfreund, A.R.; Miner, E.D.; Kieffer, H.H.; Hunt, G.E. Thermal infrared properties of the Martian atmosphere: 1. Global behavior at 7, 9, 11, and 20 μm. J. Geophys. Res. 1979, 84, 2830. [Google Scholar] [CrossRef]
- Haberle, R.M.; Houben, H.; Barnes, J.R.; Young, R.E. A simplified three-dimensional model for Martian climate studies. J. Geophys. Res. Planets 1997, 102, 9051–9067. [Google Scholar] [CrossRef]
- Way, M.J.; Aleinov, I.; Amundsen, D.S.; Chandler, M.A.; Clune, T.L.; Genio, A.D.D.; Fujii, Y.; Kelley, M.; Kiang, N.Y.; Sohl, L.; et al. Resolving Orbital and Climate Keys of Earth and Extraterrestrial Environments with Dynamics (ROCKE-3D) 1.0: A General Circulation Model for Simulating the Climates of Rocky Planets. Astrophys. J. Suppl. Ser. 2017, 231, 12. [Google Scholar] [CrossRef]
- Gruszka, M.; Borysow, A. Computer simulation of the far infrared collision induced absorption spectra of gaseous CO2. Mol. Phys. 1998, 93, 1007–1016. [Google Scholar] [CrossRef]
- Baranov, Y.I.; Lafferty, W.; Fraser, G. Infrared spectrum of the continuum and dimer absorption in the vicinity of the O2 vibrational fundamental in O2/CO2 mixtures. J. Mol. Spectrosc. 2004, 228, 432–440. [Google Scholar] [CrossRef]
- Wordsworth, R.; Forget, F.; Eymet, V. Infrared collision-induced and far-line absorption in dense CO2 atmospheres. Icarus 2010, 210, 992–997. [Google Scholar] [CrossRef]
- Perrin, M.; Hartmann, J. Temperature-dependent measurements and modeling of absorption by CO2-N2 mixtures in the far line-wings of the 4.3 μm CO2 band. J. Quant. Spectrosc. Radiat. Transf. 1989, 42, 311–317. [Google Scholar] [CrossRef]
- Smith, D.E.; Zuber, M.T.; Solomon, S.C.; Phillips, R.J.; Head, J.W.; Garvin, J.B.; Banerdt, W.B.; Muhleman, D.O.; Pettengill, G.H.; Neumann, G.A.; et al. The Global Topography of Mars and Implications for Surface Evolution. Science 1999, 284, 1495–1503. [Google Scholar] [CrossRef] [PubMed]
- Williams, G.P. Planetary circulations: 1. Barotropic representation of Jovian and terrestrial turbulence. J. Atmos. Sci. 1978, 35, 1399–1426. [Google Scholar] [CrossRef]
- Williams, G.P. Planetary circulations: 2. The Jovian quasi-geostrophic regime. J. Atmos. Sci. 1979, 36, 932–969. [Google Scholar] [CrossRef]
- Heimpel, M.; Aurnou, J.; Wicht, J. Simulation of equatorial and high-latitude jets on Jupiter in a deep convection model. Nature 2005, 438, 193–196. [Google Scholar] [CrossRef]
- Scott, R.K.; Polvani, L.M. Forced-Dissipative Shallow-Water Turbulence on the Sphere and the Atmospheric Circulation of the Giant Planets. J. Atmos. Sci. 2007, 64, 3158–3176. [Google Scholar] [CrossRef]
- Showman, A.P. Numerical Simulations of Forced Shallow-Water Turbulence: Effects of Moist Convection on the Large-Scale Circulation of Jupiter and Saturn. J. Atmos. Sci. 2007, 64, 3132–3157. [Google Scholar] [CrossRef]
- Li, L.; Ingersoll, A.P.; Huang, X. Interaction of moist convection with zonal jets on Jupiter and Saturn. Icarus 2006, 180, 113–123. [Google Scholar] [CrossRef]
- Dowling, T.E.; Ingersoll, A.P. Jupiter’s Great Red Spot as a shallow water system. J. Atmos. Sci. 1989, 46, 3256–3278. [Google Scholar] [CrossRef]
- Heimpel, M.; Gastine, T.; Wicht, J. Simulation of deep-seated zonal jets and shallow vortices in gas giant atmospheres. Nat. Geosci. 2016, 9, 19–23. [Google Scholar] [CrossRef]
- Thomson, S.; McIntyre, M.E. Jupiter’s unearthly jets: A new turbulent model exhibiting statistical steadiness without large-scale dissipation. J. Atmos. Sci. 2016, 73, 1119–1141. [Google Scholar] [CrossRef]
- Schneider, T.; Liu, J. Formation of jets and equatorial superrotation on Jupiter. J. Atmos. Sci. 2009, 66, 579–601. [Google Scholar] [CrossRef]
- Kaspi, Y.; Flierl, G.R.; Showman, A.P. The deep wind structure of the giant planets: Results from an anelastic general circulation model. Icarus 2009, 202, 525–542. [Google Scholar] [CrossRef]
- Kaspi, Y.; Galanti, E.; Hubbard, W.B.; Stevenson, D.J.; Bolton, S.J.; Iess, L.; Guillot, T.; Bloxham, J.; Connerney, J.E.P.; Cao, H.; et al. Jupiter’s atmospheric jet streams extend thousands of kilometres deep. Nature 2018, 555, 223–226. [Google Scholar] [CrossRef]
- Kong, D.; Zhang, K.; Schubert, G.; Anderson, J.D. Origin of Jupiter’s cloud-level zonal winds remains a puzzle even after Juno. Proc. Natl. Acad. Sci. USA 2018, 115, 8499–8504. [Google Scholar] [CrossRef]
- Dowling, T. The Explicit Planetary Isentropic-Coordinate (EPIC) Atmospheric Model. Icarus 1998, 132, 221–238. [Google Scholar] [CrossRef]
- Thomson, S.I. The Influence of Deep Jets on Jupiter’s Weather Layer in a 1.5-layer Shallow-Water Model. Q. J. R. Meteorol. Soc. Submitted.
- Young, R.M.; Read, P.L.; Wang, Y. Simulating Jupiter’s weather layer. Part I: Jet spin-up in a dry atmosphere. Icarus 2019, 326, 225–252. [Google Scholar] [CrossRef]
- Lian, Y.; Showman, A.P. Deep jets on gas-giant planets. Icarus 2008, 194, 597–615. [Google Scholar] [CrossRef]
- Palotai, C.; Dowling, T.E. Addition of water and ammonia cloud microphysics to the EPIC model. Icarus 2008, 194, 303–326. [Google Scholar] [CrossRef]
- Gierasch, P.; Ingersoll, A.; Banfield, D.; Ewald, S.; Helfenstein, P.; Simon-Miller, A.; Vasavada, A.R.; Breneman, H.; Senske, D.; Team, G. Observation of moist convection in Jupiter’s atmosphere. Galileo Imaging Team. Nature 2000, 403, 628–630. [Google Scholar] [CrossRef] [PubMed]
- Ingersoll, A.P.; Gierasch, P.J.; Banfield, D.; Vasavada, A.R. Moist convection as an energy source for the large-scale motions in Jupiter’s atmosphere. Nature 2000, 403, 630–632. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.H.; Dickinson, R.E. Climate Modeling. Rev. Geophys. Space Phys. 1974, 12, 447–493. [Google Scholar] [CrossRef]
- Hoskins, B.J. Dynamical processes in the atmosphere and the use of models. Q. J. R. Meteorol. Soc. 1983, 109, 1–21. [Google Scholar] [CrossRef]
- Held, I.M. The gap between simulation and understanding in climate modeling. Bull. Am. Meteorol. Soc. 2005, 86, 1609–1614. [Google Scholar] [CrossRef]
- Vallis, G.K. Geophysical Fluid Dynamics: Whence, whither and why? Proc. R. Soc. A 2016, 472, 23. [Google Scholar] [CrossRef]
- Korablev, O.; Montmessin, F.; Trokhimovskiy, A.; Fedorova, A.A.; Shakun, A.V.; Grigoriev, A.V.; Moshkin, B.E.; Ignatiev, N.I.; Forget, F.; Lefèvre, F.; et al. The Atmospheric Chemistry Suite (ACS) of Three Spectrometers for the ExoMars 2016 Trace Gas Orbiter. Space Sci. Rev. 2018, 214, 7. [Google Scholar] [CrossRef]
- Bolton, S.J.; Adriani, A.; Adumitroaie, V.; Allison, M.; Anderson, J.; Atreya, S.; Bloxham, J.; Brown, S.; Connerney, J.E.P.; DeJong, E.; et al. Jupiter’s interior and deep atmosphere: The initial pole-to-pole passes with the Juno spacecraft. Science 2017, 356, 821–825. [Google Scholar] [CrossRef]
- Voosen, P. NASA to fly drone on Titan. Science 2019, 365, 15. [Google Scholar] [CrossRef] [PubMed]
- Penn, J.; Vallis, G.K. Atmospheric Dynamics and Thermal Phase-Curve Offset on Tidally and Nontidally Locked Exoplanets. Astrophys. J. 2018, 868, 147. [Google Scholar] [CrossRef]
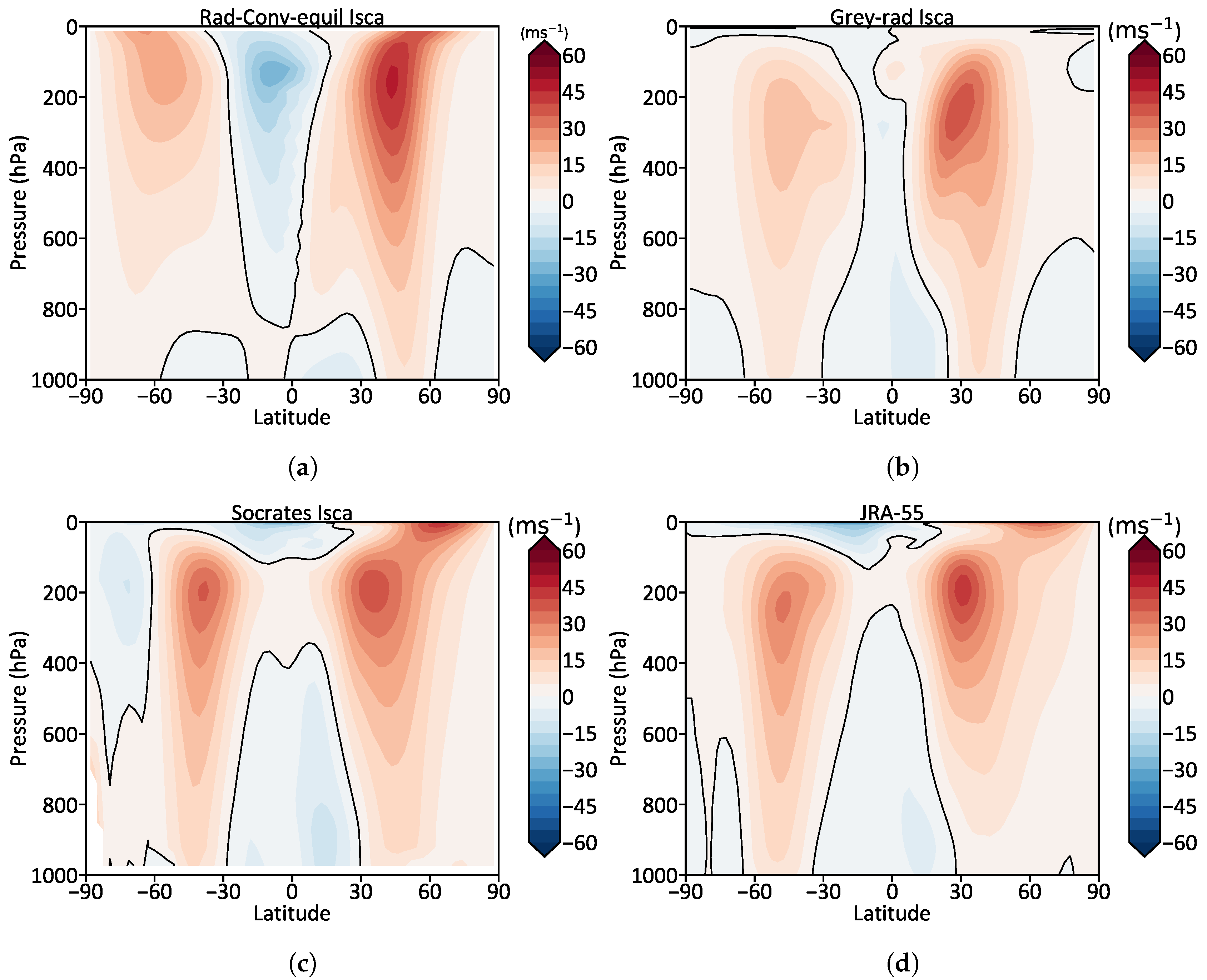
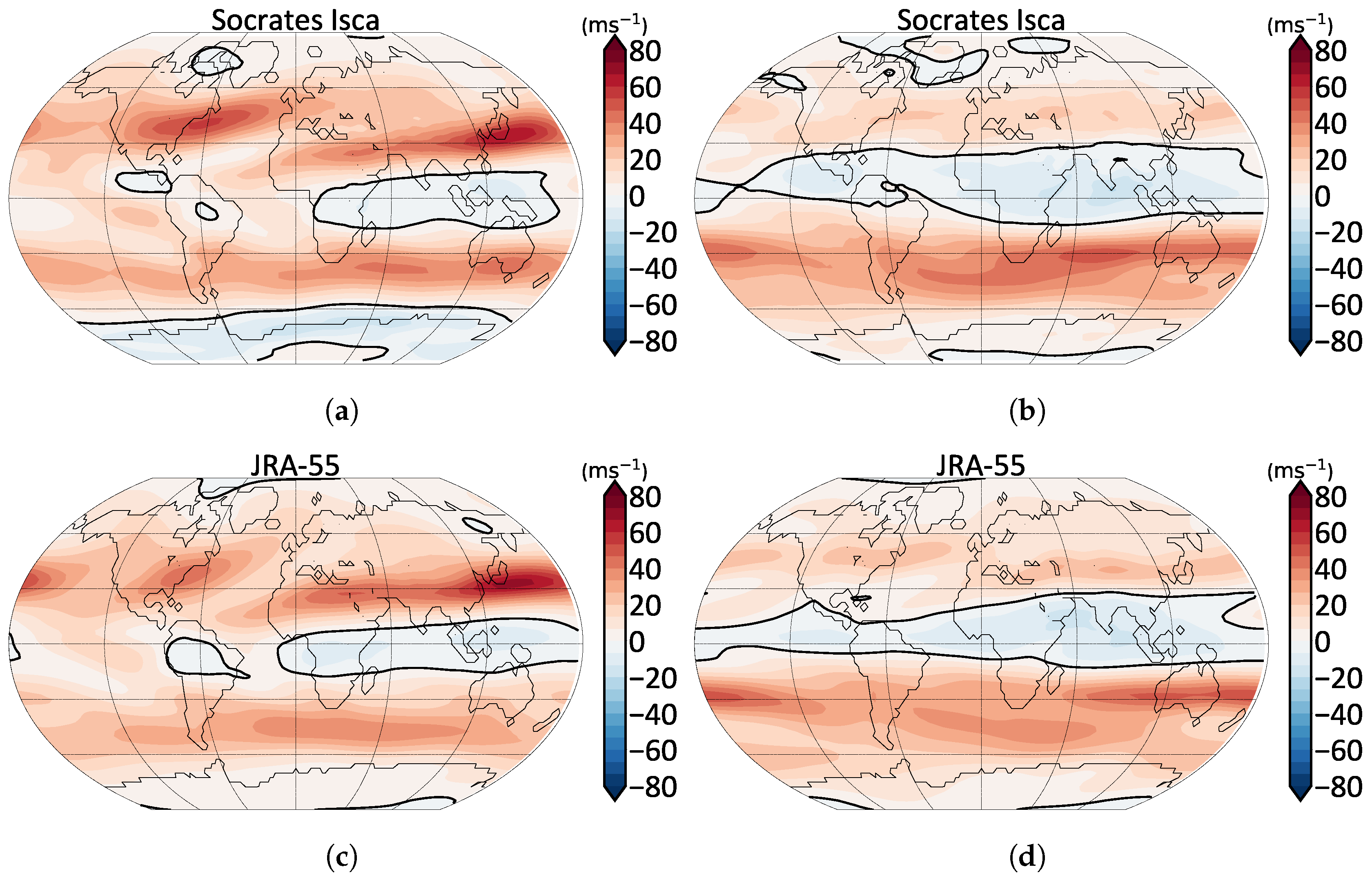
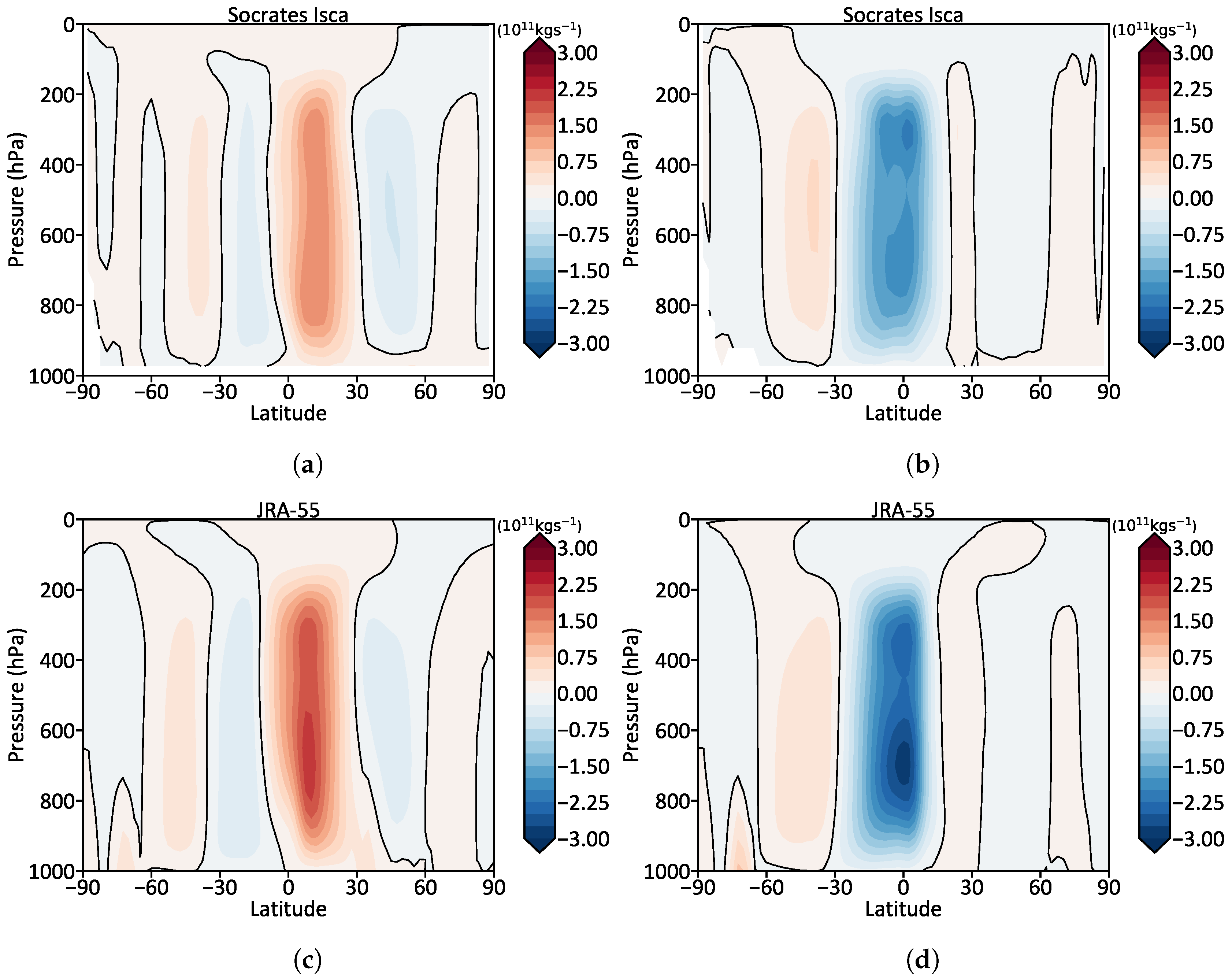
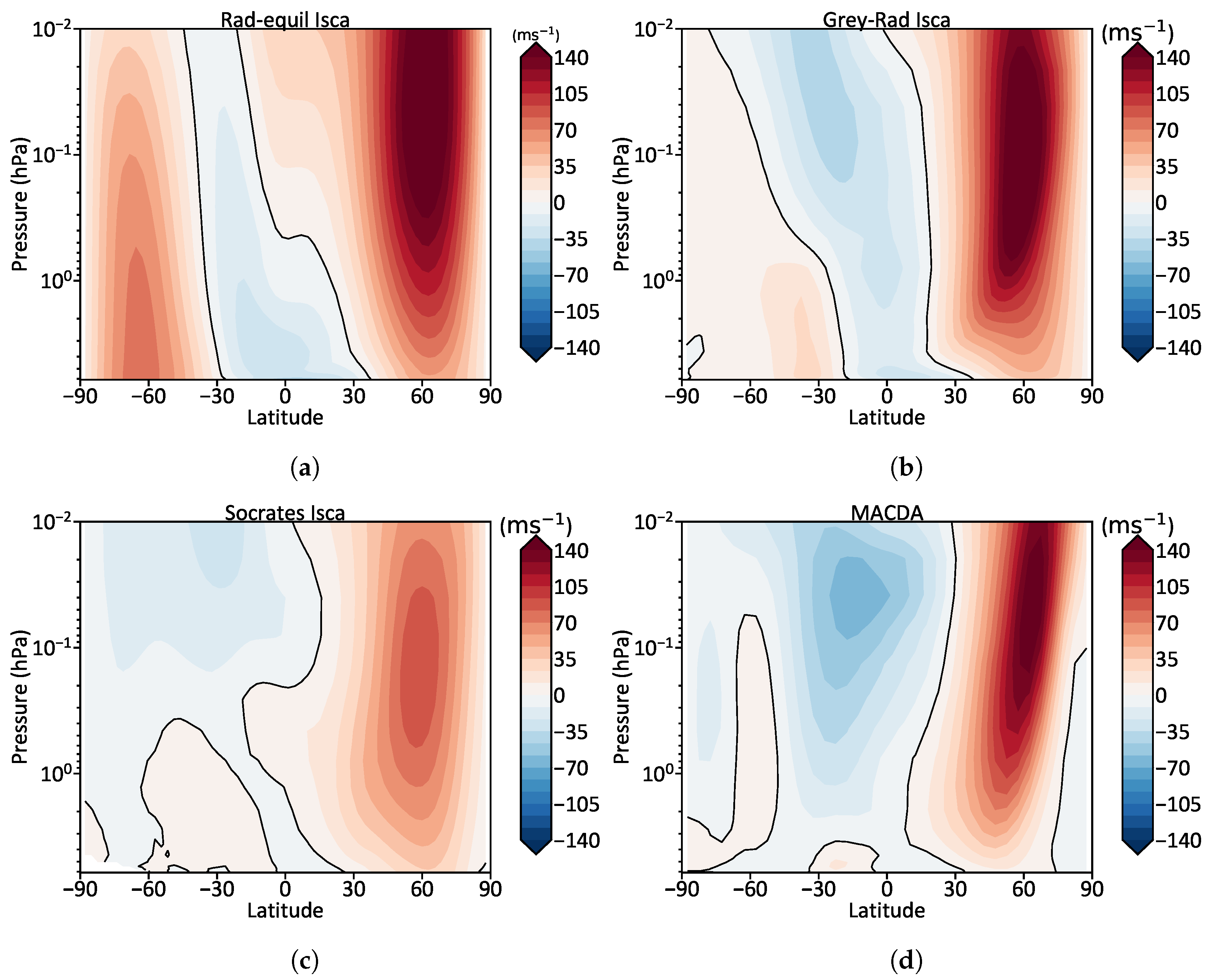

| Planet | E-S | E-I | E-C | M-S | M-I | M-C | J-S | J-I |
|---|---|---|---|---|---|---|---|---|
| Dynamics | Prim. | Prim. | Prim. | Prim. | Prim. | Prim. | SW | Prim. |
| Rad. Scheme | Newt. Relax | Grey | Socrates | Newt. Relax | Grey | Socrates | N/A | Grey |
| Seasons | Y | Y | Y | Y | Y | Y | N | N |
| Number of levels | 30 | 25 | 40 | 25 | 25 | 25 | 1.5 | 60 |
| Horiz. resolution | T42 | T42 | T42 | T42 | T42 | T42 | T341 | T213 |
| Surf. Pressure (hPa) | 1013.25 | 1013.25 | 1013.25 | 6.1 | 6.1 | 6.1 | N/A | 15,000 |
| Rot. Rate () | 7.29 | 7.29 | 7.29 | 7.12 | 7.12 | 7.12 | 17.6 | 17.6 |
| Radius (km) | 6376 | 6376 | 6376 | 3396 | 3396 | 3396 | 69,911 | 69,911 |
| Ocean depth | 20 m | 20 m | 20 m | N/A | N/A | N/A | N/A | N/A |
| Land depth | N/A | N/A | 2 m | 2 m | 2 m | 2 m | N/A | N/A |
| Fixed SSTs | N | N | Y | N | N | N | N | N |
| Topography | N | N | Y | N | N | Y | N/A | N |
| Conv Scheme | None | SBM | SBM | None | None | None | N/A | Dry |
| (s) | N/A | 7200 | 7200 | N/A | N/A | N/A | N/A | 21,600 |
| , | 2.4, 16 | 1.2, 16 | 6.3, 16 | 14.5, 16 | 8, 16 | 16.4, 32 | 7, 32 | 124, 64 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thomson, S.I.; Vallis, G.K. Hierarchical Modeling of Solar System Planets with Isca. Atmosphere 2019, 10, 803. https://doi.org/10.3390/atmos10120803
Thomson SI, Vallis GK. Hierarchical Modeling of Solar System Planets with Isca. Atmosphere. 2019; 10(12):803. https://doi.org/10.3390/atmos10120803
Chicago/Turabian StyleThomson, Stephen I., and Geoffrey K. Vallis. 2019. "Hierarchical Modeling of Solar System Planets with Isca" Atmosphere 10, no. 12: 803. https://doi.org/10.3390/atmos10120803
APA StyleThomson, S. I., & Vallis, G. K. (2019). Hierarchical Modeling of Solar System Planets with Isca. Atmosphere, 10(12), 803. https://doi.org/10.3390/atmos10120803





