Next Article in Journal
Radar Remote Sensing of Precipitation in High Mountains: Detection and Characterization of Melting Layer in the Grenoble Valley, French Alps
Previous Article in Journal
Influence of Individual Household Heating on PM2.5 Concentration in a Rural Settlement
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 10
Issue 12
10.3390/atmos10120783
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of Aerosols as Ice Nuclei on the Dynamics, Microphysics and Precipitation of Severe Storm Clouds

by
Huiling Yang
1,*,
Hui Xiao
1,2 and
Chunwei Guo
3
1
Key Laboratory of Cloud Precipitation Physics and Severe Storms (LACS), &Center of disaster Reduction, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China
2
University of Chinese Academy of Sciences, Beijing 100049, China
3
Institute of Urban Meteorology, China Meteorological Administration, Beijing 100089, China
*
Author to whom correspondence should be addressed.
Atmosphere 2019, 10(12), 783; https://doi.org/10.3390/atmos10120783
Submission received: 13 November 2019 / Revised: 2 December 2019 / Accepted: 3 December 2019 / Published: 6 December 2019
(This article belongs to the Section Aerosols)
Browse Figures
Versions Notes

Abstract

:
The Regional Atmospheric Modeling System (RAMS) is used to investigate the effect of aerosols acting as ice nuclei (IN) on the formation and growth of hydrometeor particles as well as on the dynamics and precipitation of a severe storm in Northern China. The focus of this study is to determine how the overall dynamics and microphysical structure of deep convective clouds are influenced if IN concentrations are somehow altered in a storm environment that is otherwise unchanged. Ice mixing ratios tend to increase and liquid mixing ratios tend to decrease with increasing IN concentrations. High concentrations of IN reduce the mean hail diameter and hail particles with smaller diameters melt more easily, which leads to a decrease in ground hailfall and an increase in surface rainfall. Liquid water plays a more important role in the process of hail formation, while the role of ice particles in the process of hail formation decreases with higher IN concentrations. The role of small cloud droplets in the formation of raindrops is increased and the role of hail melting in the process of raindrops formation is weakened with enhanced IN concentrations. Both latent heat release and absorption significantly increase with increasing IN concentrations. Increasing the concentration of IN by an appropriate amount is beneficial for increasing the total water content and strengthening the updraft, leading to enhancement of a storm, but excessive IN concentrations will inhibit the development of a storm.

1. Introduction

The effects of aerosols on cloud dynamical structures, microphysical processes and precipitation have attracted much attention over the past 50 years. Observations and numerical simulation results have shown that aerosols can modify cloud microphysical processes and dynamical processes, and can consequently alter the location, intensity and type of rainfall by acting as cloud condensation nuclei (CCN) and ice nuclei (IN) [1,2]. The impacts of aerosols on solar radiation, cloud microphysical processes and precipitation are uncertain [3,4]. The main uncertainty in regard to the influence of aerosols on precipitation comes from the uncertainty in the ice phase process in clouds.
Statistical studies have shown that more than 50% of mid-latitude precipitation comes from the melting of ice particles [5]. The mutual transformation of ice phase particles in clouds plays an important role in the formation of precipitation [6,7,8,9]. Over the past three decades, there have been many studies aimed at understanding the effects of aerosols on cloud droplets, but relatively few studies have been investigated the impacts of aerosols on the formation of ice crystals. The IN concentrations in the atmosphere are very low relative to the concentration of aerosols; there is approximately one IN for every 105 aerosol particles at −20 °C. Unlike CCN, IN are usually insoluble particles, such as certain mineral dusts (mineral dustis atmospheric aerosols originated from the suspension of minerals constituting the soil. It is composed of various oxides and carbonates), carbonaceous aerosols and various biogenic particles [10,11,12,13,14,15]. The effects of IN on the ice phase processes in strong convective clouds are extremely complex: there are no definite conclusions about the net effects of IN on severe storm clouds [7]. Model studies show that dust from Asia and Africa acting as IN can affect the formation of ice crystals in mixed clouds, which in turn affect cloud microphysical properties [16,17] (including the hydrometeor phases and particle sizes), and ultimately alter the characteristics of precipitation.
The influence of IN on cloud microphysical processes is affected by the change of the atmospheric thermodynamic environment and will ultimately affect latent heat release, dynamic processes and precipitation characteristics [18,19]. At present, there are no definite conclusions on the effects of IN on strong convective precipitation, which vary by case and region [7]. In recent years, research results have mainly drawn the following four conclusions: (1) The change of IN number concentrations has little effect on precipitation [20]. (2) The increase of IN concentration is beneficial to the increase of surface precipitation [21]. Observations [22] have shown that there was still a large amount of supercooled water at −21 °C in clouds with abundant IN. The dust and biological particles transported over long distances can act as IN to enhance orographic rainfall in California [23,24,25]. Simulations demonstrated that increasing IN concentrations enhanced the riming rate, and dramatically reduced the supercooled water content and increased the cloud glaciations temperature. Clouds with higher IN concentrations glaciated at much warmer temperatures [14,23,26]. Increasing IN concentrations can produce more rimed mass and enhance the Wegener-Bergeron-Findeisen (WBF) process due to enhanced ice formation, thus increasing precipitable ice particles such as snow [27]. Crystals can aggrade rime after colliding with supercooled cloud droplets [15,17,28,29,30,31], especially in more turbulent clouds [32]. Increasing the IN concentrations increase latent heat release through the freezing of small cloud droplets, strengthening the convective process and resulting in increased hail and rain precipitation [33,34]. (3) An increase in IN will lead to a decrease in surface precipitation. The number of graupel particles decreases but the number of hail particles increases with increasing IN concentrations [35]. (4) The effects of IN are varied at different developmental stages of storm clouds. Increasing IN increases the initial concentration of ice crystals. In the developing and early maturation stages of hail clouds, a large number of ice crystals compete for water vapor with increasing IN, and this competition prevents ice crystals from growing into snowflakes and inhibits the formation and growth of hail embryos. During the later mature stage, updrafts intensify and more supercooled water is transported above the freezing level, which is beneficial for the production and growth of hail particles [2]. Increasing IN favors the formation of hail at this developmental stage. Increasing IN concentrations produces more surface precipitation in the early development stage of convective clouds, but less precipitation in the mature and dissipation stage of the storm [36]. Thus, it is necessary to study the impact of IN on severe storms in different areas.
Although the influences of CCN on precipitation suppression are well understood [37,38,39], the combined effects of CCN and IN on precipitation in mixed-phase clouds are not well established [40]. Although previous studies have shown that aerosols have possible effects on clouds and precipitation, it is difficult to distinguish the effects of different influencing factors, including the meteorological environment, cloud organization, and aerosol concentration. The ice particle formation mechanism may differ from one mixed phase cloud to another. How squall line clouds respond to a change of IN is highly uncertain. Considering that many microphysical processes are sensitive to the type of aerosol (CCN or IN), the effects of aerosols on cloud microphysics could be complicated depending on cloud dynamics and thermodynamics. Our current understanding of the influence of IN on supercooled water and the cloud phase in various meteorological environments is poor. Therefore, it is essential to study the effects of IN on clouds and precipitation qualitatively and quantitatively using a numerical simulation.
Global warming may significantly increase the damage caused by mid-latitude convective events in the coming decades. An increase in average surface temperature could stimulate updraft, thereby increasing hail intensity [41]. IN is an important factor that affects the evolution of convective clouds such as severe storms. A severe storm can be an extremely disastrous weather event, which is often accompanied by severe convective weather such as thunderstorms and strong winds. Aerosols can affect the development of severe storms, and also affect the growth process of hail particles within the cloud. Because it is difficult to obtain information about microphysical factors from observational data, numerical models have become important tools to study the formation mechanism of hail. The results of one-dimensional model simulations showed that the formation of hail is very sensitive to the initial concentrations of CCN and IN [42]. If the aerosols strengthen the updrafts, the size of hail may increase. Observations have demonstrated that the concentration of IN that can be activated at −20 °C increased 15 times in the 32 years between 1963 and 1995 in Beijing [43]. Understanding the impacts of IN on mixed phase cloud precipitation over northern China has important implications for predicting the hydrology and local climate of the region. Understanding the key processes and factors that impact cloud phases is critical. Analysis of rainfall samples in combination with the meteorological environment can provide insight into the effects of IN on precipitation. What role does IN play in affecting cloud microphysics and precipitation? Many studies have focused on local artificial seeding for hail suppression and precipitation enhancement, but there are few background studies on the effects of an increase of the IN concentration on severe storms. The pollution in many regions of China is significant, and the background levels of the IN of aerosols have an overall increasing trend, making it necessary to perform research in this area. This study aims to (1) investigate the impact of IN on the formation and characteristics of hydrometeor particles, (2) quantify the response of precipitation to IN changes, and (3) understand the influence of IN on the dynamic structure and the thermal field of severe convective clouds.
A strong squall line occurred in northern China between 0700 to 1100 UTC on 23 June 2011. Cold, northwesterly winds occurred at the high altitudes and warm, moist southwesterly wind occurred at the low altitudes. The cold air moved southward and encountered with the warm moist airflow originating from the south, which provided unstable conditions for the generation of the squall line. The squall line occurred in the front of the upper level trough and moved from northwest to southeast. A detailed description of the weather conditions of this severe storm can be found in previous studies [44]. The model setup and experiment design are described in Section 2, the sensitive test results are analyzed in Section 3, the discussion is presented in Section 4 and the conclusions are provided in Section 5.

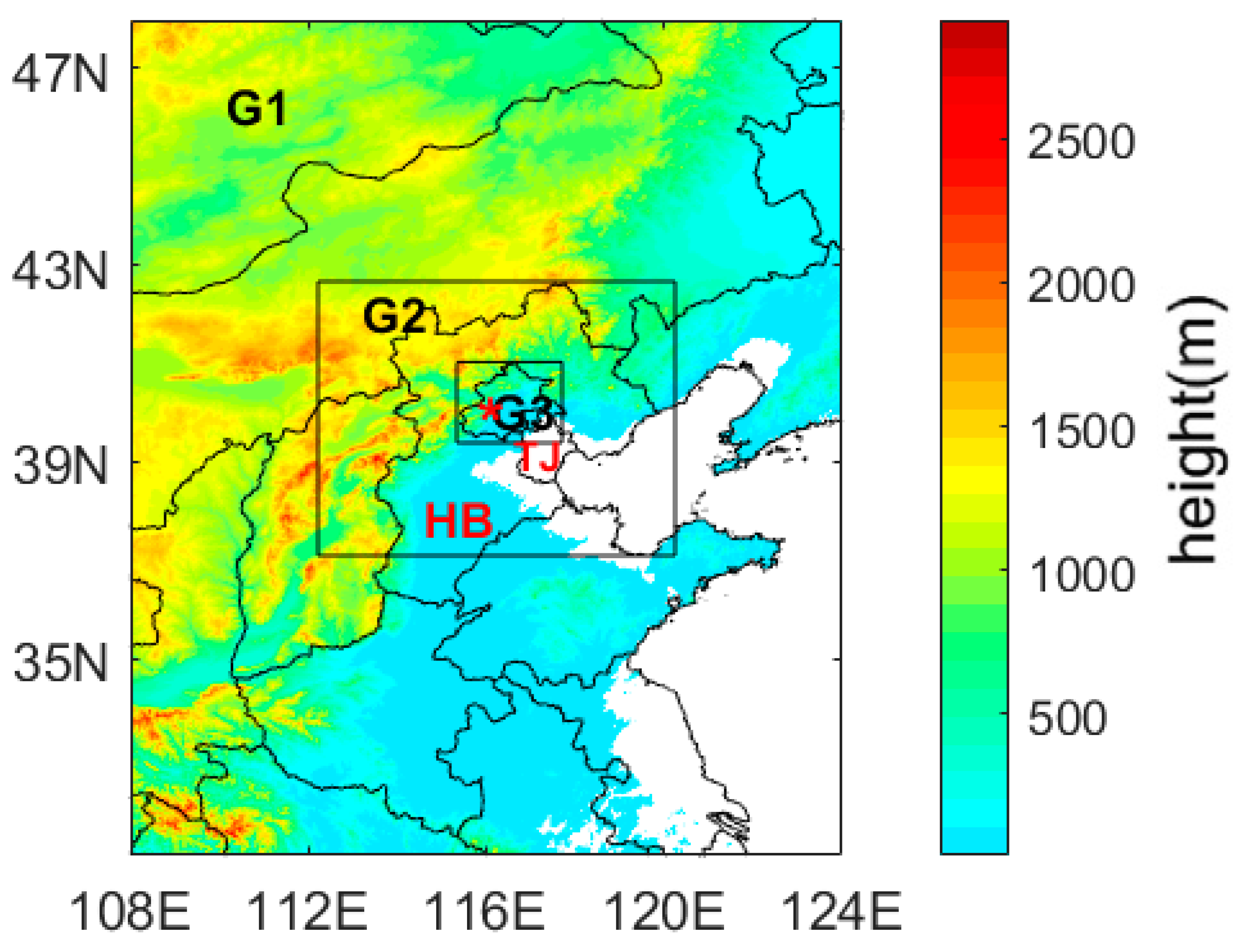
2. Model Setup and Experiment Design

The Regional Atmospheric Modeling System (RAMS) of Colorado State University was used in this study. The model uses fully elastic, compressible and non-static equilibrium equations, Standard C staggered grid and generalized terrain following coordinates. This model covers comprehensive physical processes. A two-moment bulk microphysics package was used to predict the mixing ratio and number concentration of cloud droplets, drizzle, rain, pristine ice, snow, aggregates, graupel, and hail. The model microphysics includes cloud nucleation, ice nucleation, vapor deposition, evaporation, collision-coalescence, melting, freezing, sedimentation and secondary ice production. The two-stream radiation model of Harrington takes into account the attenuation and scattering of hydrometeors [45]. RAMS microphysics is coupled to an advanced aerosol parameterization scheme that represents two ammonium sulfate modes, two dust modes, three sea salt modes, and two regenerated aerosol modes using a lognormal distribution. The model is fit for studying of aerosol effects on cloud systems across scales. More detailed descriptions of this model can be found in previous studies [46,47,48]. Three nested domains with horizontal grid spacing of 9 (178 × 224 grid points), 3 (208 × 201 grid points) and 1 km (250 × 242 grid points) were employed in this study, following a two-way nesting strategy. Figure 1 shows locations of the three nested domains. 42 unevenly spaced vertical levels extending from the surface to 20.5 km. The minimum grid spacing at the lowest level is 75 m, the vertical grid stretching ratio is 1.1 and the maximum grid spacing is 750 m.
The numerical simulation was driven by NCEP reanalysis data (1° × 1° spatial resolution and 6 h temporal resolution). The starting time of the simulation was 1800 UTC on 22 June and the model was simulated for 24 h. The region of major precipitation is defined as Area A (40°–41° N, 116°–117° E).
The CCN concentrations were initially horizontally homogeneous, with a vertical profile that linearly decreased with height up to an altitude of 4km. This CCN distribution is similar to several in situ observations [34,49]. The initial CCN concentrations were specified at 1000 cm−3. The IFN is displayed as a density-weighted decaying concentration profile with the maximum concentration of NIFN. The maximum number of nucleating IFN (ice forming nuclei) is dependent on supersaturation with respect to ice and is shown as follows:
N IN = N IFN × ρ 5.4 × exp ( 12.96 × ( S i − 0.40 ) ) × 10 ( − 4.077 × S i + 0.0975 )
This formula calculates the maximum number of ice crystals that nucleate via the freezing of deposited condensation upon IFN, where NIN is the predicted number of pristine ice crystals formed by the freezing of deposited condensation, NIFN is the concentration of IFN, Si is the ice supersaturation predicted by the model, and ρ represents the air density. Observations [42] have showed that the IN concentration during sandstorms is more than 100 times higher than that under normal weather conditions. DeMott et al. [17] found that long distance transport of dust aerosols can increase IN concentrations by 20–100 times. Due to the lack of atmospheric IN observation data for the same period, three tests were initialized with IFN concentrations of 1 times (C1), 10 times (C2) and 100 times (C3) that of the parametric concentration from the above formula, respectively.C1 is the base case.

3. Results Analysis

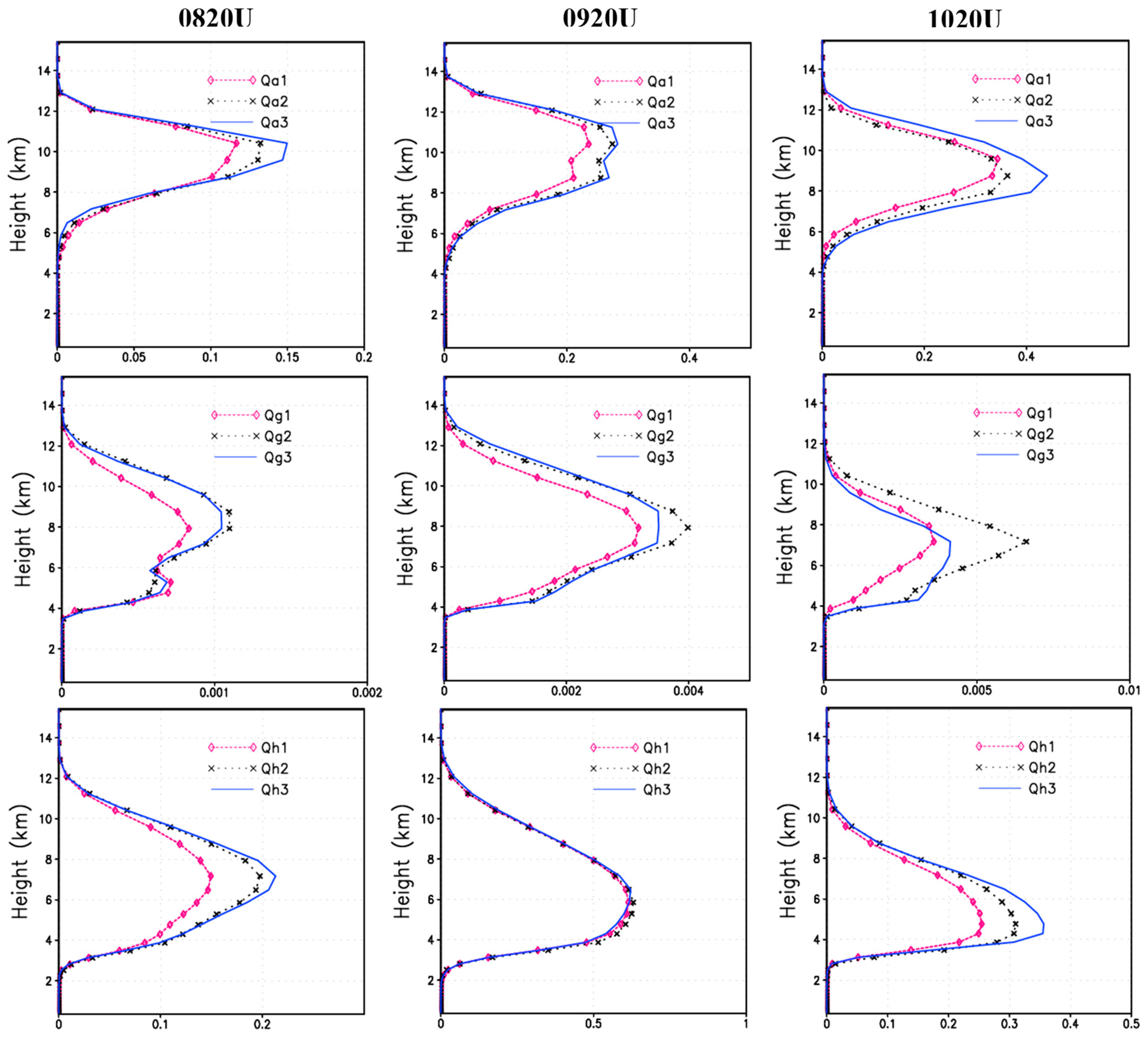
3.1. Effects on the Temporal and Spatial Distribution of Hydrometeor Particles

The vertically integrated liquid mixing ratios and ice mixing ratios are displayed in Figure 2 and Figure 3, respectively. The maximum vertically integrated liquid water content and area covered by liquid water decreases, but the clouds are better organized with an increase in the IN concentration. Therefore, the distribution of liquid water content in the clouds is more concentrated and clouds develop more vigorous with an increase in the IN concentration. Figure 3 shows that the coverage area and the maximum value of the ice mixing ratio both clearly increase with higher IN concentrations. Because ice phase condensate is the main component of the cloud anvil, the cloud anvil enhances with the increase of IN. This is mainly because ice crystal concentrations increase with increasing IN concentrations, ice crystals compete with each other for limited water vapor. Through the WBF process, large amounts of super-cooled water are converted into ice crystals, resulting in a decrease in the liquid water content.
A more detailed microphysical mechanism is described in the following section. In general, an increase in the IN concentration can affect the spatial distribution of liquid and ice condensate and has an important impact on the development of convection and cloud radiation. The vertical structures of the hydrometeor mixing ratios at each developmental stage of hailstorm clouds are shown in Figure 4. In the initial developing stage (Figure 4a,d,g), the total condensate mixing ratio and hail mixing ratio clearly increase with increasing IN concentrations. The maximum total condensate mixing ratios of C1, C2 and C3 are 4 g kg−1, 5 g kg−1 and 6 g kg−1, respectively. In addition, the maximum total hail mixing ratios of C1, C2 and C3 are 1 g kg−1, 2 g kg−1 and 3 g kg−1, respectively. During the mature stage (Figure 4b,e,h), the maximum total condensate mixing ratio is the largest in C3, and the strong convection center expands over a wide range and can develop to a height of 10 km. During the dissipation stage (Figure 4c,f,i), the C1stormweakens first, the storm clouds of C2 remain strong, and C3 is weaker than C2 but stronger than C1. Therefore, appropriately increasing the concentration of IN is beneficial for increasing the total water content, which enhances the storm. However, excessive IN concentrations will inhibit storm development.
The vertical profiles of regionally averaged hydrometeor particles within the convective area (Area A) are shown in Figure 5. After the increase in the IN concentration, the amounts of pristine ice, aggregates, graupel and hail clearly increase during each developmental stage of the storm. The variation trend of the amount of snow is less obvious. During the initial developing and mature stages, the supercooled cloud water and rain water show a decreasing trend after the increase in the IN concentration (above 4 km altitude), which is mainly related to the WBF process. Increasing IN leads to an increase in ice crystals and a decrease in supercooled water caused by excessive ice crystals competing for liquid water. During the dissipation stage, the ice particles grow large enough to fall and form precipitation, and the high cloud water mixing ratio is a result of the melting of the ice species such as ice crystals and aggregates with higher IN concentrations. The increase in rain water in the lower layer is mainly produced by the increase in hail melting.
The time series of the regionally averaged mixing ratios of hydrometeor particles are shown in Figure 6. With an increase in the IN concentration, both cloud water and rain water decrease in the developing and mature stages but increase in the dissipation stage. The decrease in liquid water in the early stage is mainly due to precipitation erosion while the increase in liquid water in the later stage in the cloud is caused by the gradual decrease in precipitation and the increase in hail melting. The pristine ice, snow, aggregates and graupel increase throughout the precipitation process, but the hail clearly decreases during the main precipitation period. Small ice particles increase and the large ice particles decrease with higher IN concentrations. This is mainly because the small ice crystals grow by vapor deposition, and a large number of ice crystal compete for water vapor, but limited water vapor inhibits the growth of ice particles. The larger is the concentration of IN, the smaller is size of ice crystals. The hail particles grow by riming process. The hail diameter decreases with the increase of IN number concentration, and the hail particles with smaller diameter melt more easily in the falling process. Thus, the amount of hail on the ground is reduced.

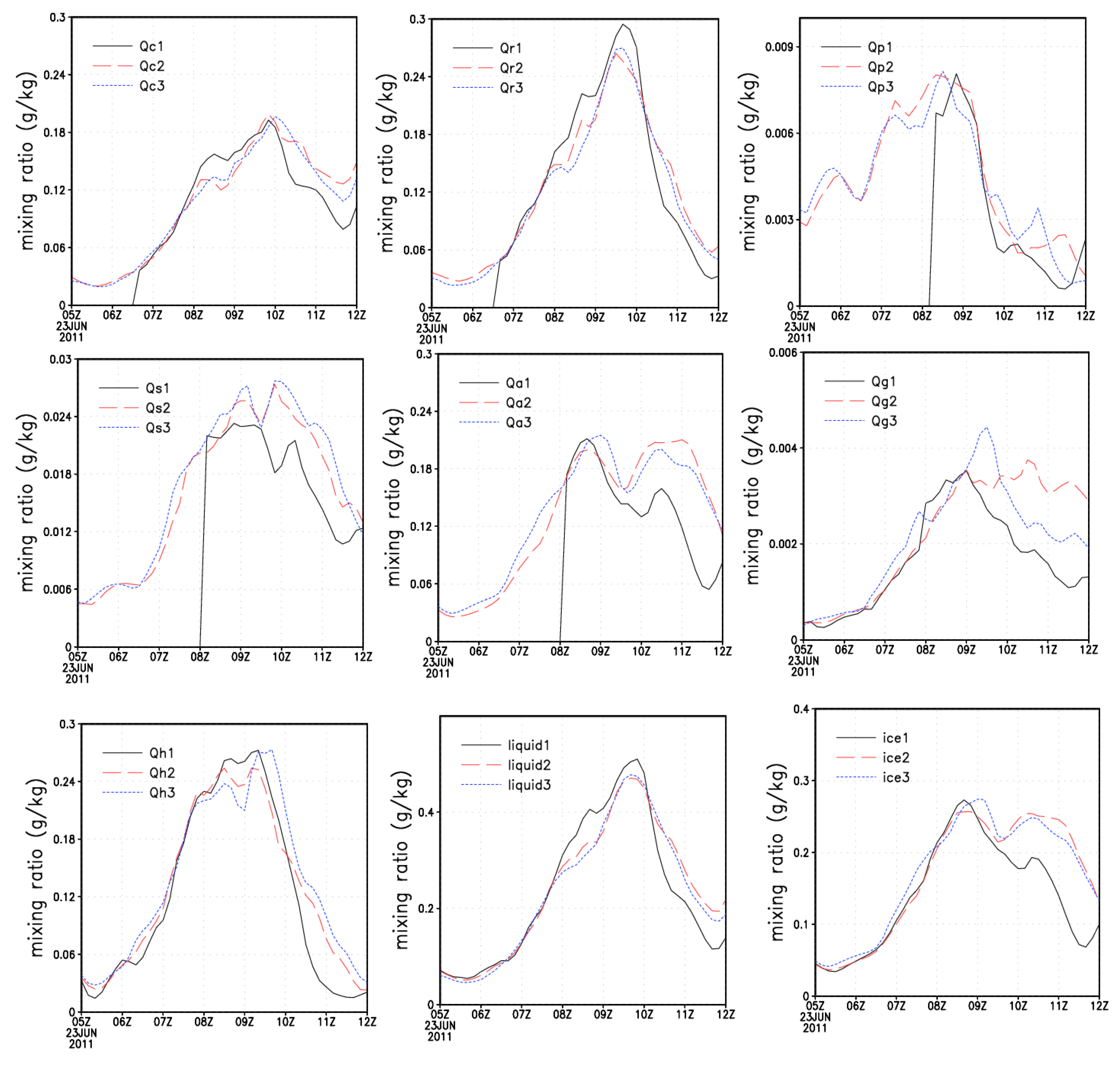
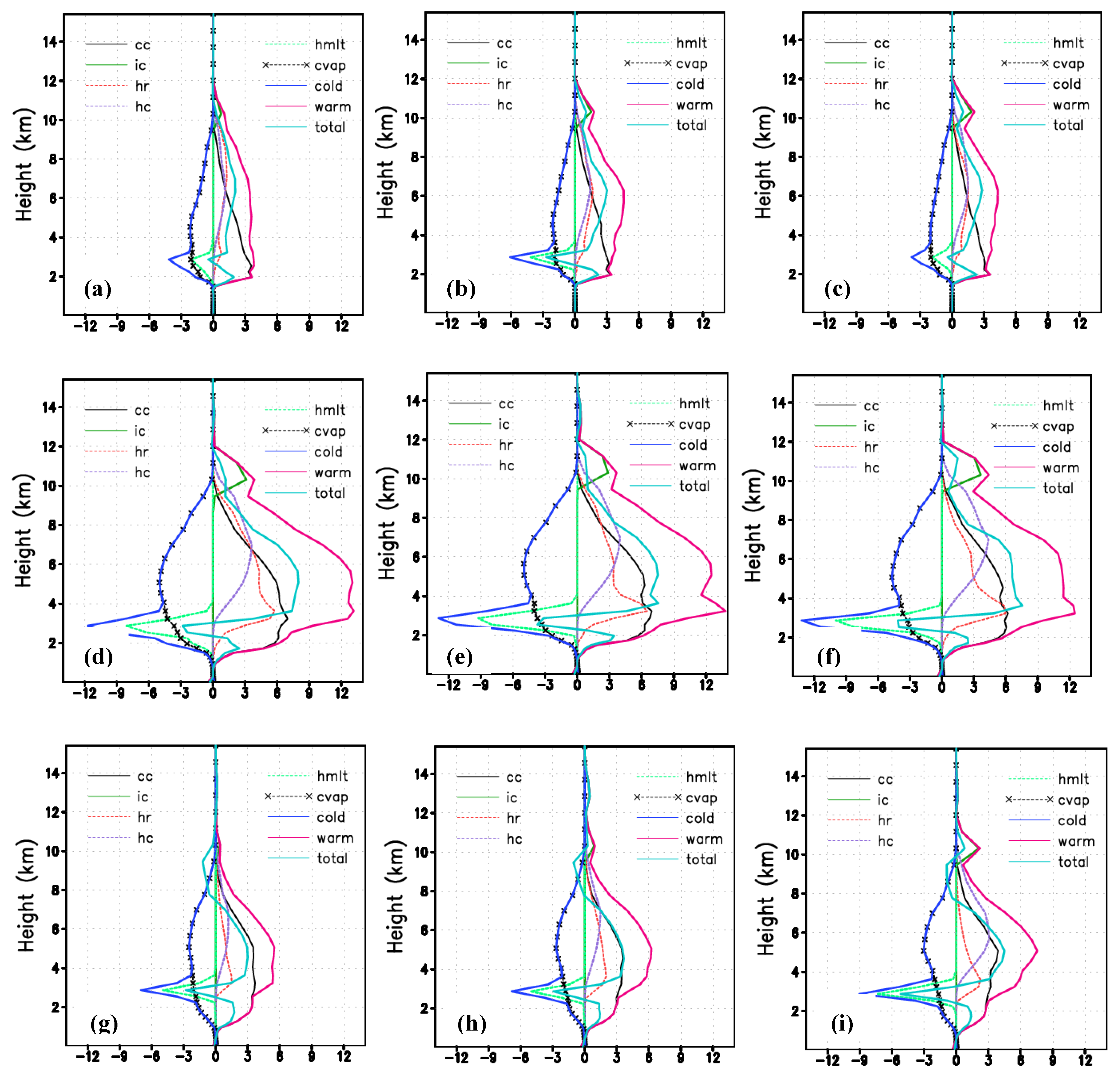
3.2. Effects of IN on Thehail Particle Characteristics and Microphysical Formation Processes of Hail, Rain and Pristine Ice

The formation and growth of hail particles in clouds are very complicated. Various hydrometeor particles are related to the formation of hail particles. To study the effects of IN on the microphysical processes of hail formation, the contributions of each hydrometeor particle to hail formation are shown in Table 1. The variable Chc1 (Chc2, Chr) represents the contributions of small cloud droplets (large cloud droplets, rain) to hail generation through the ice-liquid water collisions. The variable Cha (Chg, Chi, Chs) represents the relative contribution of aggregates (graupel, pristine ice, snow) to hail particle formation. Hail formation is achieved through two main microphysical processes: aggregation and accretion.
It can be seen from Table 1 that small cloud droplets (Chc1), aggregates (Cha), rain (Chr) and graupel (Chg) are the major contributors to hail formation, with rain droplets contributing the most to hail generation. The contribution rates of rain droplets to hail in C1, C2 and C3 are 46.4%, 48.2% and 46.6%, respectively. Contribution of small cloud droplets to hail formation in C1, C2 and C3 are 41.4%, 41.1% and 44.2%, respectively. Aggregates make a contribution of 7%, 6.1% and 5.4%to hail generation in C1, C2 and C3, respectively. Contribution of graupel to hail in C1, C2 and C3 are 2.5%, 2% and 1.7%, respectively. Comparing C1, C2 and C3, it can be seen that the addition of IN leads to the increase of the contribution rate of small cloud droplets to hail formation and a decrease in the contribution rate of aggregates and graupel to hail generation. Rain makes the largest contribution to hail formation in the C2 case.
Liquid water includes small cloud drops, large cloud drops and raindrops. The total contribution rates of liquid water to hail in C1, C2 and C3 are 89.1%, 90.5% and 91.7%, respectively. The remaining contributions to hail formation are from ice particles (aggregates, graupel, pristine ice and snow). The contribution rates of ice to hail formation in C1, C2 and C3 are 10.9%, 9.5% and 8.3%, respectively. Therefore, when the IN concentration increases, the contribution rate of liquid water to hail formation increases and the contribution rate of ice phase particles to hail formation decreases. In summary, small cloud droplets, aggregates, rain and graupel are the key contributors to hail generation, with rain droplets contributing the most. Increasing the IN concentration results in an increase in the contribution rate of liquid water to hail formation, and a decrease in the contribution rate of ice particles to hail formation.
The available hydrometeors within a cloud are considered to be transferrable from one hydrometeor category to another. Small cloud droplets (2–40 μm), large cloud droplets (40–80 μm) and snow all contribute to pristine ice generation. Table 2 shows the sum of the domain and time averaged relative contributions of each particle type to pristine ice generation. The values of Cic1 and Cic2 signify the relative contributions of small cloud droplets and large cloud droplets to pristine ice, which are achieved by two main processes: ice nucleation and ice crystal growth from sublimation. The variable of Cis represents the contributions of snow to pristine ice generation. The main process involved in pristine ice generation is snow rupture which produces ice crystals and is an ice crystal multiplication process.
It can be observed from Table 2 that the pristine ice production increases with an increase in the IN concentration. The contribution rates of small cloud droplets to pristine ice formation in C1, C2 and C3 are 46.6%, 46.7% and 48.2%, respectively. The contribution rates of large cloud droplets to pristine ice formation in C1, C2 and C3 are 44.7%, 44.9% and 45.2%, respectively. The contribution rates of snow to pristine ice formation in C1, C2 and C3 are 8.7%, 8.4% and 6.6%, respectively. The addition of IN leads to an increase in the contribution rates of small cloud droplets and large cloud droplets to pristine ice formation and a decrease in the contribution rate of snow to pristine ice generation.
The contributions of each hydrometeor particle to rain formation are shown in Table 3. The variable Crc1 (Crc2) represents the contributions of small cloud droplets (large cloud droplets) to rain generation through auto conversion and rain collection of cloud droplets. The variable Cra (Crg, Crh, Cri, and Crs) represents the relative contribution of aggregates (graupel, hail, pristine ice, and snow) to rain formation, which is achieved by the melting of the ice particles.
It can be seen from Table 3 that small cloud droplets (Crc1) and hail (Crh) are the major contributors to rain formation and that the contribution of small droplets to rain generation is the largest. The contribution rates of small cloud droplets to rain formation in C1, C2 and C3 are 65.8%, 64.1% and 59.5%, respectively. The contribution rates of hail to rain formation in C1, C2 and C3 are 33.7%, 35.4% and 39.9%, respectively. The total production of rain water is largest in the C2 experiment, implying that increasing the IN concentration by a certain amount is beneficial for the production of rainfall, but excessive IN inhibits the formation of rainfall. With an increase in IN concentration, the contribution of small cloud droplets to rain formation decreases and the contribution of hail melting to rain formation increases.
The temporally and spatially averaged hail characteristics (including the mixing ratio, concentration, and mean diameter) and the melting properties for the three sensitive experiments are shown in Table 4. The effect of the IN concentration on the overall characteristics of hail particles can be determined from this table. The hail mixing ratios and concentrations are the highest, but the hail diameter is the smallest both within the cloud and under the base of the cloud in the C3 experiment. These illustrate that the increase in IN favours the formation of small hail particles. On the other hand, the small hail particles in C3 melt more both within the cloud and under the base of the cloud during the falling process. Thus, increasing IN inhibits hailfall. Analysis of the effect of IN on hail particle characteristics is useful for better understanding the effects of IN on surface precipitation.

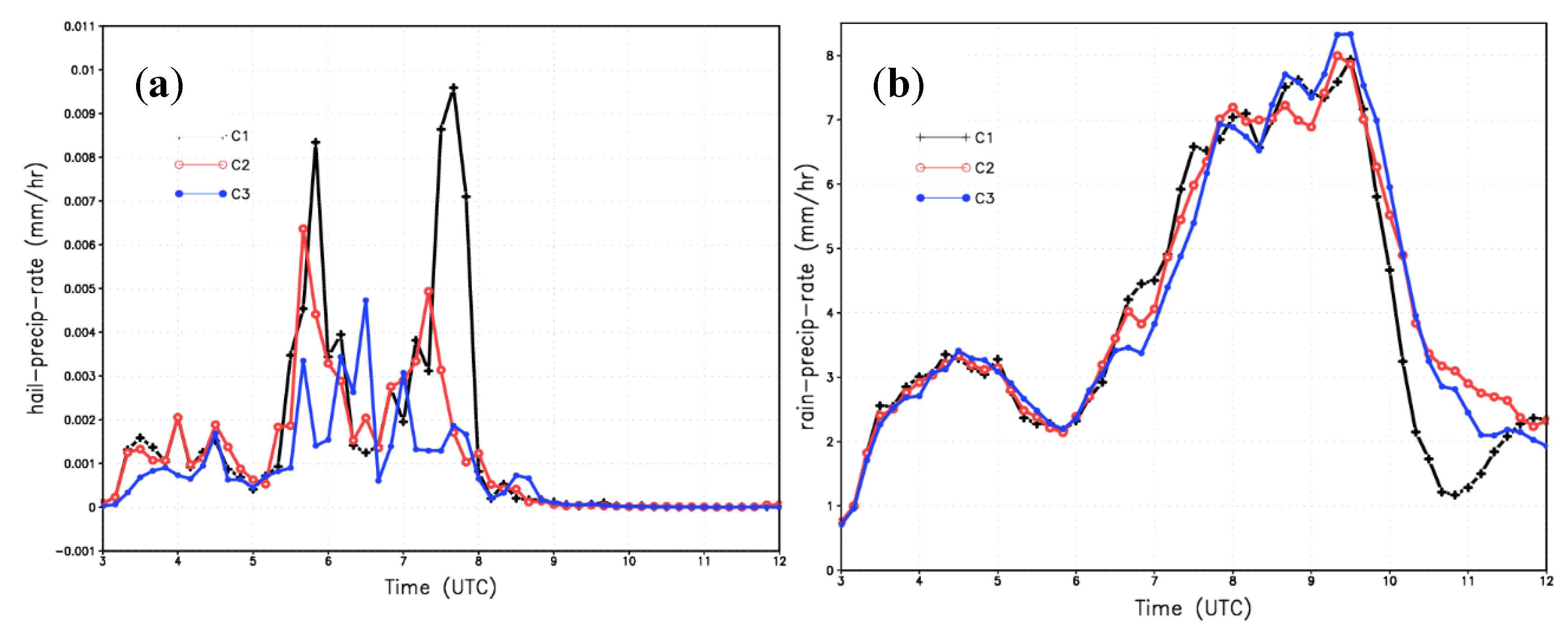
3.3. Effects of IN on the Temporal and Spatial Distribution of Precipitation

The distributions of surface precipitation and perturbation pressure are displayed in Figure 7. The change in IN has little effect on the distribution range of the precipitation belt. With the increase in the IN concentration, the moving speed of the precipitation belt slightly increases, while the distribution pattern of surface precipitation and perturbation pressure significantly change. The number of strong precipitation centers clearly increases, and both the intensity of precipitation and the coverage of strong precipitation centers increase. In summary, precipitation is more concentrated and its intensity is enhanced with a higher IN concentration. The distribution patterns of perturbation pressure are approximately the same for all three tests.
In the early development stage (Figure 7a,d,g), the low-pressure system occurs in the front of the rainfall region, while the high-pressure system appears in the back of the precipitation area. During the mature stage (Figure 7b,e,h), the high-pressure system occurs in the front of the precipitation region and the low pressure system appears in the back of the rainfall area. During the dissipation stage (Figure 7c,f,i), the high pressure system covers the entire precipitation area. However, the location of the pressure center is not completely consistent with varying IN concentrations, which leads to the location of the rainfall center being different in the three tests.
The time series of the domain-averaged hailfall rate and rainfall rate are shown in Figure 8. After an increase in the IN concentration, surface rainfall decreases at the beginning of the storm development, but the surface precipitation increases during the mature and extinction stages of the storm, indicating that the increased IN concentration has the effect of delaying precipitation. In the early developing stage, precipitation is mainly formed by the collision of cloud and rain droplets. Liquid water in the cloud is consumed by a large number of ice particles through the WBF process at higher IN concentrations, and the surface precipitation decreases. During the mature and dissipation stages, rainfall mainly originates from the melting of hail particles. Increasing IN concentrations produces many smaller hail particles and the melting precipitation increases.
Ground hailfall decreases at all developmental stages of the clouds with increasing IN, which mainly because the hail diameter decreases in clouds, the amount of melting increases during hail fall, and the amount of hail that reaches the ground decreases at higher IN concentrations.

3.4. Effects of IN on Latent Heat and Updrafts

The vertical profiles of the regionally averaged latent heat rate of the major storm region are given in Figure 9. Both latent heat release and absorption significantly increase with increasing IN. In the developing stage, cloud droplet evaporation plays a major role in latent heat absorption (cvap), while latent heat release mainly comes from cloud droplet condensation (cc). During the mature and dissipation stage, hail melting is the main source of the latent heat absorption (hmlt), while the latent heat release mainly comes from the collection of super-cooled water by hail (hc, hr). In the developing stage, the increase in latent heat release mainly occurs above 6km, which is mainly associated to accretion of cloud water and rain by hail. While during the mature stage, the latent heat release mainly appears at 4–6 km of altitude, which is mainly related to condensation of cloud water and accretion of rain by hail [50]. During the dissipation stage, falling precipitation is linked to hail melting and droplets evaporation, associated to latent heat absorption, causing cold downdrafts.
The vertical cross sections along the convective region for the airflow field are displayed in Figure 10. During the developing stage, the front-to-rear flow has not formed in the C1 and C3 tests, but has occurred in the C2 tests. During the mature stage, the front-to-rear flow is produced in all three tests and is strongest in C2. During the dissipation stage, due to the intrusion of the air flow at 4–6 km altitude, the front-to-rear flow has gradually dissipated in the C1 and C3 tests but is maintained in the C2 test. Many previous studies have focused on the effects of CCN on warm clouds, but relatively few studies have focused on the effects of IN on mixed clouds. During the developing stage, the 8–12 km updrafts in C2 and C3 are significantly stronger than the updraft in C1, which is similar to the previous studies [35]. The increase in updraft is closely related to the increase in latent heat release within the cloud (Figure 9). A previous study [35] tested the effects of IN using two different IN concentrations, while three different concentrations are used in this study. It can be seen that when the IN concentration is increased tenfold, the updraft is the strongest and lasts the longest. The downdraft associated to precipitation fall is stronger in C2 scenario, which is linked to a greater melting of smaller but more numerous hail hydrometeors. The updraft is weaker after a hundredfold increase in IN concentrations than it is after a tenfold increase in IN concentrations. Thus, appropriately increasing the concentration of IN strengthens the updraft, which is beneficial for the enhancement of the storm. However, an excessive IN concentration will inhibit the development of the storm. This appropriate amount of IN is important for guiding artificial hail suppression studies. In addition, a previous study [35] showed that the IN concentration has a strong effect on updraft during the mature and dissipation storm stages, while this study shows that the effect of the IN concentration on updraft is very clear throughout the entire development process. Variations in IN concentrations, therefore, not only affect microphysical properties but also have the potential to change the dynamics of the entire storm system.

4. Discussion

We ran three simulations to detect the effect of IN on hail storms. The effect of IN on microphysical transformation mechanism of hydrometeor particles is analyzed, which is of great significance for understanding the effect of IN on cloud microphysics [27]. Several authors [33,34] have claimed that the updraft and the latent heat release increase with increasing IN concentrations. Our results show that increasing appropriate concentration of IN is good for the enhancement of storm, but excessive IN will inhibit the development of storm. The increase of latent heat release with increasing IN concentrations is closely related to the condensation of cloud droplets and deposition of water vapor into pristine ice [33,34,35]. Detailed analysis of various latent heat related processes are presented in this study. The major latent heat release or absorption process varies with different development stages of the storm clouds [50]. For instance, in the developing stage, latent heat release mainly comes from cloud droplet condensation growth. While during the mature dissipation stage, the collection of super-cooled water by hail is the major sources for the latent heat release.
Previous studies have found that there is a great uncertainty about the effect of aerosols on precipitation [22,23,24,25,26,27,28,29,30]. The increase of IN may lead to an increase or decrease in precipitation [31,32,33,34,35]. Our results indicate that hail precipitation decreases with the increase of IN concentration, which is contrary to the previous study [34]. This indicates that the influences of IN on hail precipitation varies with different environmental conditions. The rainfall decreases in the early developing stage, while the rainfall increases during the mature and dissipation stage, indicating that precipitation delays with increasing IN [35]. Studies [48] found that the DeMott scheme reduced the precipitation of topographic clouds, while the snow accumulation was closer to the observation. Other studies [51] pointed out that it is necessary to add a correction factor cf to correct the deviation in the case of over-prediction of precipitation by DeMott scheme. The overestimation or underestimation of precipitation in different regions was closely related to the aerosol sampling error and the parameterization of various physical processes in the process of establishing the formula. In the future work, it is necessary to continue to improve the treatment of aerosols through more observations and simulations, so as to improve the simulation of their physical effects on clouds and climate systems.

5. Conclusions

The precipitation processes of a severe storm in northern China are simulated by using the RAMS meso-scale numerical model. Three sensitive tests are conducted to investigate the effects of IN on the microphysical characteristics, the formation mechanism of hydrometeor particles and precipitation. Figure 11 shows process flowchart for this study. It was found that variations in IN concentrations not only affect the microphysical properties but also have the potential to change the dynamics of the entire storm system. The main conclusions are as follows:
(1)
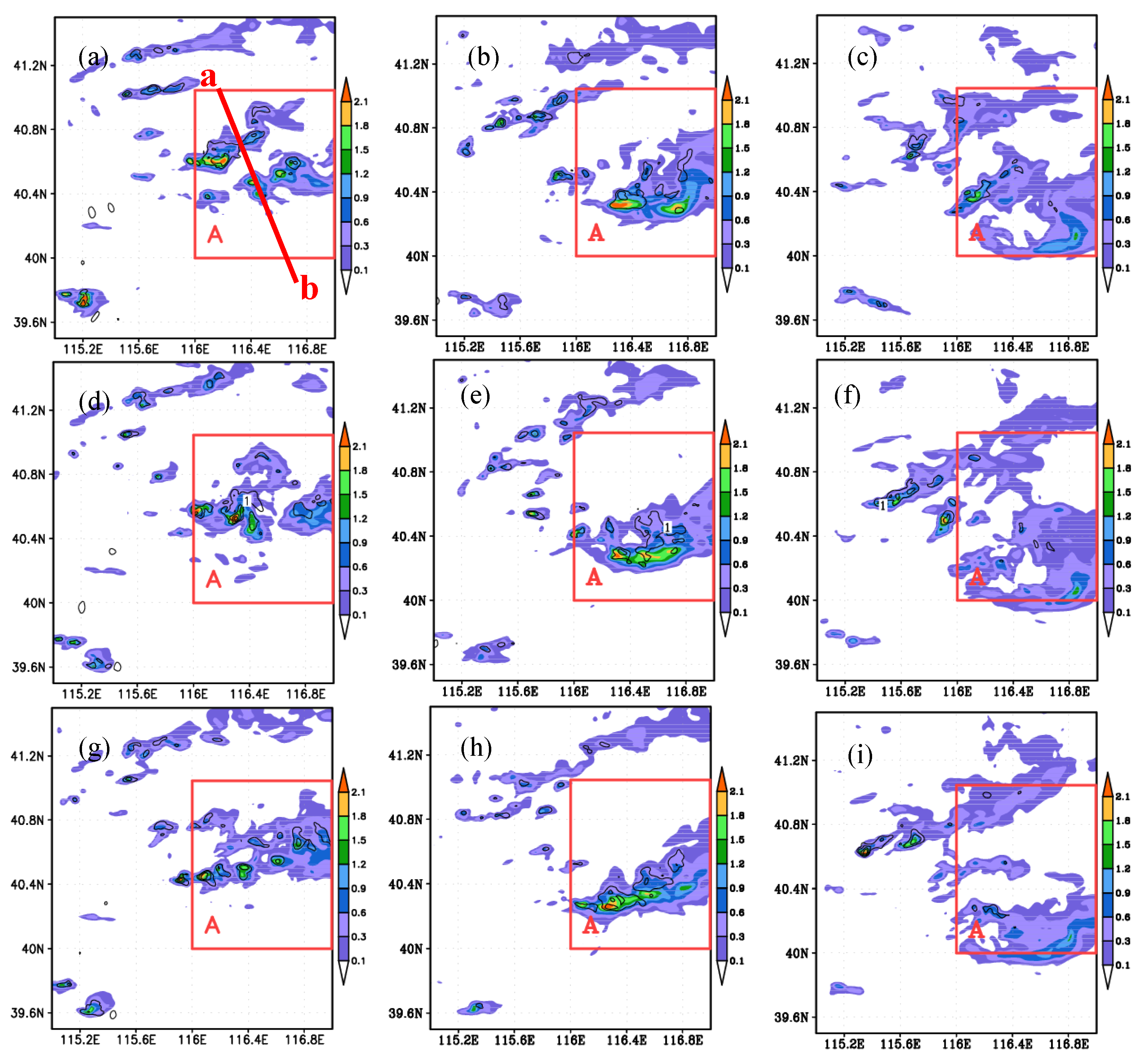
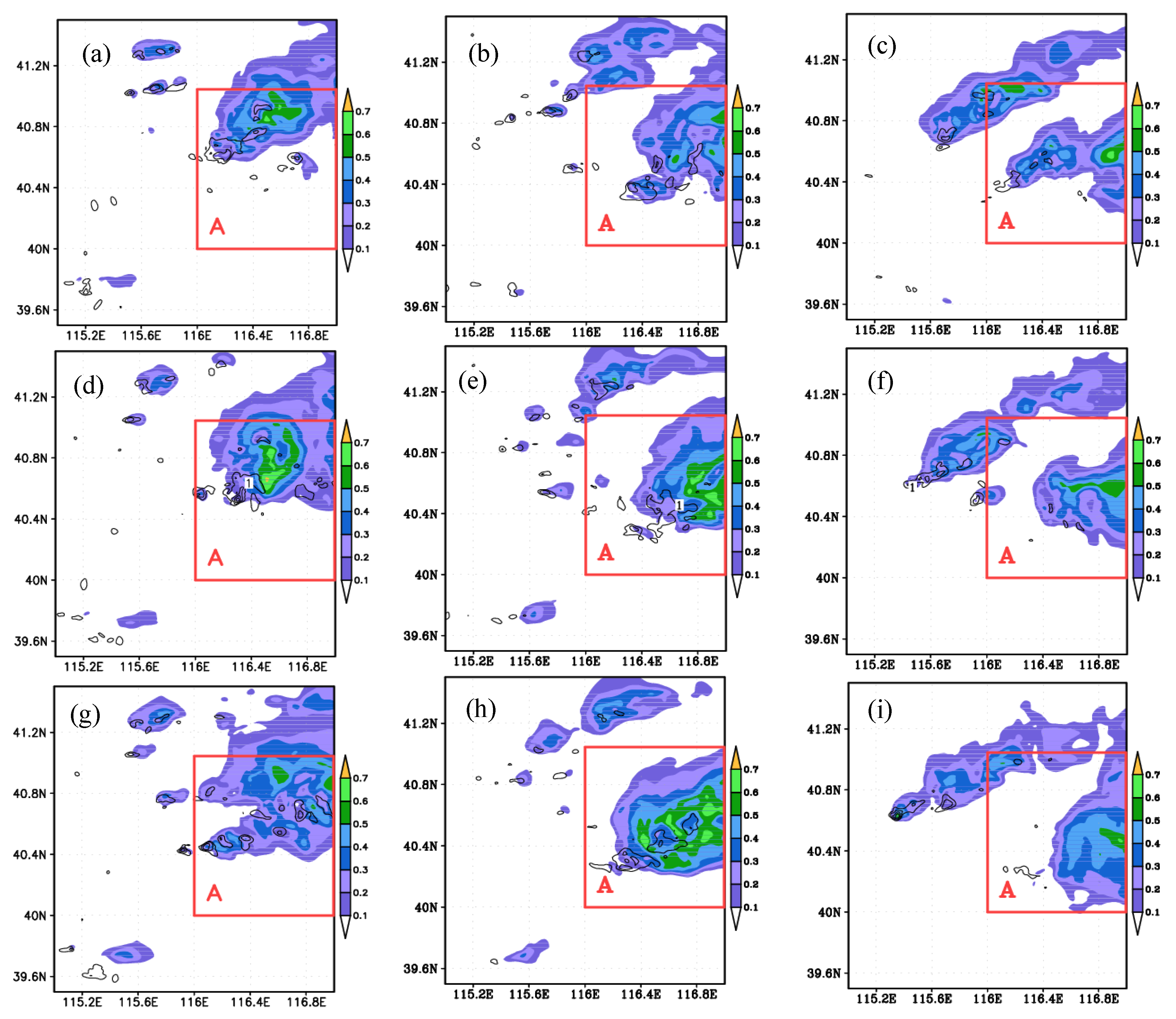
A change in the IN concentrations can affect the spatial distribution of vertically integrated liquid water mass and the ice condensate mixing ratio in the cloud. Liquid water covers a smaller area and has a lower maximum amount of vertically integrated liquid water, the ice mass covers a larger area and is better organized, and the cloud is more robust and has a higher maximum vertically integrated ice condensate mixing ratio in the cases with greater IN concentrations.
(2)
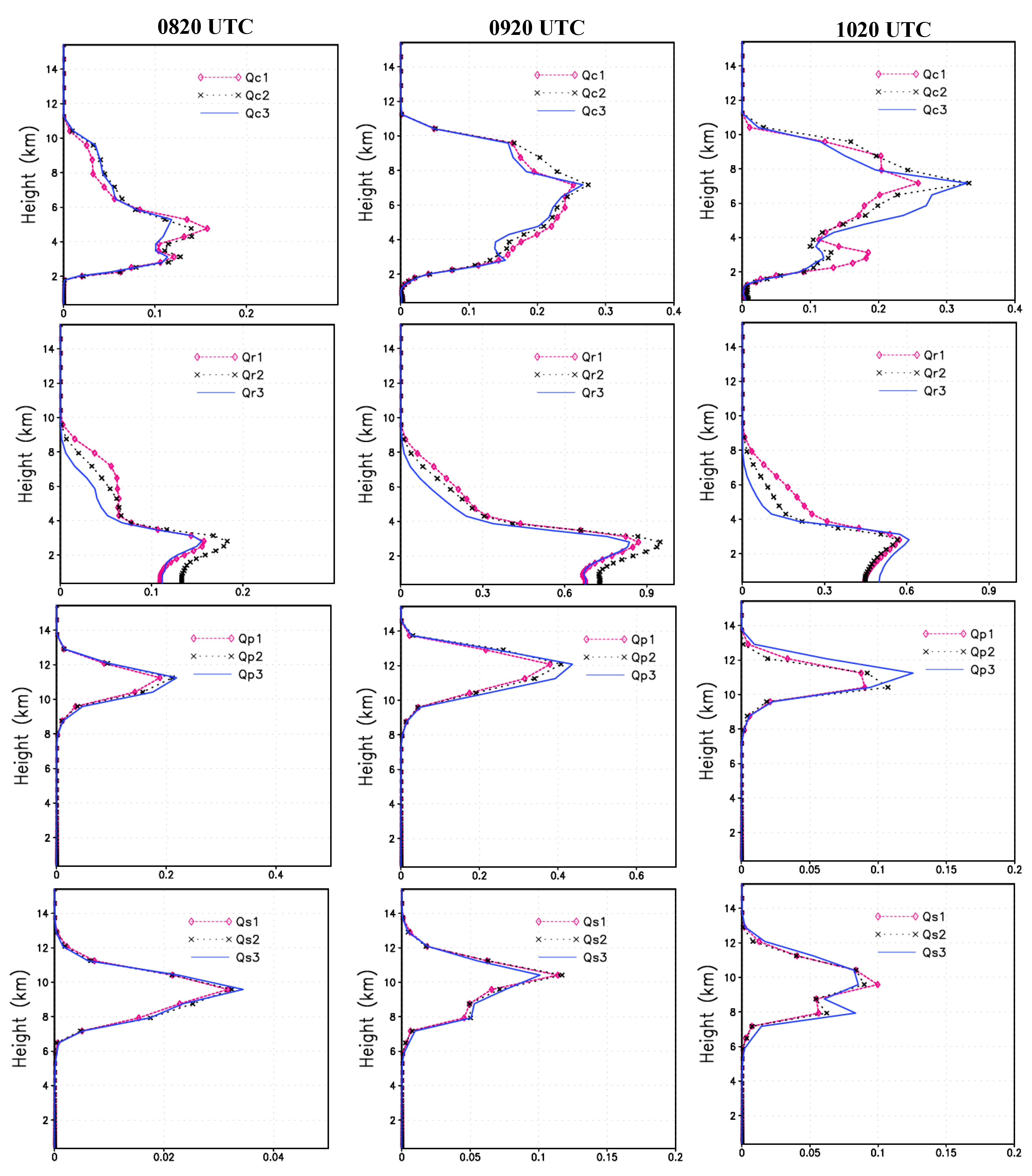
Most of the ice phase particles in the cloud (including pristine ice, snow, graupel and hail) increase with an increase in the IN concentration, while supercooled cloud water and rain water significantly decrease. The total amount of cloud and rain within the cloud decreases during the developing and mature stage, but increases in the dissipation stage. The hail concentration increases, the hail diameter clearly decreases, the amount of melting increases during hail particle fall, and the amount of hail reaching the ground decreases. Thus, increasing the IN concentration could reduce hailfall in this storm cloud.
(3)
The number of heavy precipitation centers increases and the coverage of heavy precipitation enhances with higher IN concentrations. Rainfall decreases in the early developing stage while rainfall increases during the mature and dissipation stages, indicating that the increase in IN has the effect of delaying precipitation. On the other hand, the hailfall decreases during all stages of the storm development, indicating that the increase of the IN can play the role of hail reduction.
(4)
Increasing IN leads to an increasing contribution rate of liquid water to hail formation but a decreasing contribution rate of ice particles to hail generation. The contribution of cloud droplets to pristine ice formation increases, while the contribution of snow to the formation of pristine ice decreases. The contribution of small cloud droplets to the formation of rain droplets decreases, while the contribution of hail melting to the formation of rain increases.
(5)
Both latent heat release and absorption significantly increase in all stages of storm development with increasing IN concentrations. In the developing stage, cloud droplets evaporation plays a major role in latent heat absorption, while latent heat release mainly comes from cloud droplet condensation. During the mature and dissipation stages, hail melting is the major sources of latent heat absorption, while the latent heat release mainly comes from the collection of supercooled water by hail.
(6)
An appropriate increase in IN is beneficial to the enhancement of the storm updraft, and excessive IN will inhibit an increase in the updraft. Therefore, an appropriate increase in IN is beneficial for the enhancement and maintenance of the storm, and excessive IN will inhibit the development of the storm.
The conclusions obtained in this study can only represent this case, and cannot be generalized to other regions of the world. More precipitation cases in different regions should be analyzed and summarized to get more extensive conclusions.

Author Contributions

H.Y. designed the experiments, analyzed the results and wrote the manuscript. H.X. supervised the work and provided critical comments. C.G. collected data and provided meaningful comments.

Funding

This work was partially supported by the National Key Research and Development Plan of China (Grant No. 2016YFE0201900-02), the National Natural Science Foundation of China (Grant Nos. 41575037, 41205099 and Grant No. 41605110), the National Grand Fundamental Research 973 Programs of China (Grant No. 2014CB441403), the Guizhou Province Scientific Research Joint Project (Grant No.G[2013]4001).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Tao, W.; Chen, J.; Li, Z.; Wang, C.; Zhang, C. Impact of aerosols on convective clouds and precipitation. Rev. Geophys. 2012, 50. [Google Scholar] [CrossRef] [Green Version]
  2. Liu, X.; Fu, Y.; Cao, Z.; Jin, S. Influence of Ice Nuclei Parameterization Schemes on the Hail Process. Adv. Meterol. 2018, 2018, 4204137. [Google Scholar] [CrossRef] [Green Version]
  3. Ramaswamy, V.; Boucher, O.; Haigh, J.; Hauglustaine, D.; Haywood, J.; Myhre, G.; Nakajima, T.; Shi, G.Y.; Solomon, S. Radiative Forcing of Climate Change. Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK, 2001; pp. 349–416. [Google Scholar]
  4. Li, R.; Dong, X.; Guo, J.; Fu, Y.; Zhao, C.; Wang, Y.; Min, Q. The implications of dust ice nuclei effect on cloud top temperature in a complex mesoscale convective system. Sci. Rep. 2017, 7, 13826. [Google Scholar] [CrossRef] [Green Version]
  5. Lau, K.; Wu, H. Warm rain processes over tropical oceans and climate implications. Geophys. Res. Lett. 2003, 30, 2290. [Google Scholar] [CrossRef]
  6. Tao, W.; Li, X.; Khain, A.; Matsui, T.; Lang, S.; Simpson, J. Role of atmospheric aerosol concentration on deep convective precipitation: Cloud-resolving model simulations. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
  7. Levin, Z.; Cotton, W. Aerosol Pollution Impact on Precipitation: A Scientific Review; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
  8. Guo, X.; Fu, D.; Guo, X.; Zhang, C. A case study of aerosol impacts on summer convective clouds and precipitation over northern China. Atmos. Res. 2014, 142, 142–157. [Google Scholar] [CrossRef]
  9. Guo, C.; Xiao, H.; Yang, H.; Wen, W. Effects of anthropogenic aerosols on a heavy rainstorm in Beijing. Atmosphere 2018, 10, 162. [Google Scholar] [CrossRef] [Green Version]
  10. Pitter, R.; Pruppacher, H. A wind tunnel investigation of freezing of small water drops falling at terminal velocity in air. Q. J. Roy. Meteorol. Soc. 1973, 99, 540–550. [Google Scholar] [CrossRef]
  11. Levin, Z.; Yankofsky, S. Contact Versus Immersion Freezing of Freely Suspended Droplets by Bacterial Ice Nuclei. J. Appl. Meteorol. 1983, 22, 1964–1966. [Google Scholar] [CrossRef] [Green Version]
  12. Diehl, K.; Quick, C.; Matthiasmaser, S.; Mitra, S.; Jaenicke, R. The ice nucleating ability of pollen: Part I: Laboratory studies in deposition and condensation freezing modes. Atmos. Res. 2001, 58, 75–87. [Google Scholar] [CrossRef]
  13. Gorbunov, B.; Baklanov, A.; Kakutkina, N.; Windsor, H.; Toumi, R. Ice nucleation on soot particles. J. Aerosol Sci. 1998, 32, 199–215. [Google Scholar] [CrossRef]
  14. Rosenfeld, D.; Yu, X.; Liu, G.; Xu, X.; Zhu, Y.; Yue, Z.; Dai, J.; Dong, Z.; Dong, Y.; Peng, Y. Glaciation temperatures of convective clouds ingesting desert dust, air pollution and smoke from forest fires. Geophys. Res. Lett. 2011, 38, L21804. [Google Scholar] [CrossRef]
  15. Morris, C.; Georgakopoulos, D.; Sands, D. Ice nucleation active bacteria and their potential role in precipitation. J. Phys. IV 2004, 121, 87–103. [Google Scholar] [CrossRef]
  16. Wiacek, A.; Peter, T.; Lohmann, U. The potential influence of Asian and African mineral dust on ice, mixed-phase and liquid water clouds. Atmos. Chem. Phys. 2010, 10, 8649–8667. [Google Scholar] [CrossRef] [Green Version]
  17. Demott, P.; Sassen, K.; Poellot, M.; Baumgardner, D.; Rogers, D.; Brooks, S.; Prenni, A.; Kreidenweis, S. African dust aerosols as atmospheric ice nuclei. Geophys. Res. Lett. 2003, 30, 1732. [Google Scholar] [CrossRef] [Green Version]
  18. Andreae, M.; Rosenfeld, D. Aerosol-cloud-precipitation interactions. Part 1. The nature and sources of cloud-active aerosols. Earth Sci. Rev. 2008, 89, 13–41. [Google Scholar] [CrossRef]
  19. Khain, A.; Rosenfeld, D.; Pokrovsky, A. Aerosol impact on the dynamics and microphysics of deep convective clouds. Q. J. Roy. Meteorol. Soc. 2005, 131, 2639–2663. [Google Scholar] [CrossRef] [Green Version]
  20. Hoose, C.; Kristjansson, J.; Burrows, S. How important is biological ice nucleation in clouds on a global scale. Environ. Res. Lett. 2010, 5, 024009. [Google Scholar] [CrossRef]
  21. Changnon, S. More on the La Porte Anomaly: A Review. Bull. Am. Meteorol. Soc. 1980, 61, 702–711. [Google Scholar] [CrossRef]
  22. Rosenfeld, D.; Chemke, R.; Demott, P.; Sullivan, R.; Rasmussen, R.; Mcdonough, F.; Comstock, J.; Schmid, B.; Tomlinson, J.; Jonsson, H.; et al. The Common Occurrence of Highly Supercooled Drizzle and Rain near the Coastal Regions of the Western United States. J. Geophys. Res. Atmos. 2013, 118, 9819–9833. [Google Scholar] [CrossRef]
  23. Ault, A.; Williams, C.; White, A.; Neiman, P.; Creamean, J.; Gaston, C.; Ralph, F.; Prather, K. Detection of Asian dust in California orographic precipitation. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
  24. Creamean, J.; Suski, K.; Rosenfeld, D.; Cazorla, A.; Demott, P.; Sullivan, R.; White, A.; Ralph, F.; Minnis, P.; Comstock, J.; et al. Dust and Biological Aerosols from the Sahara and Asia Influence Precipitation in the Western U.S. Science 2013, 339, 1572–1578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  25. Creamean, J.; Spackman, J.; Davis, S.; White, A. Climatology of long-range transported Asian dust along the West Coast of the United States. J. Geophys. Res. 2014, 119, 12171–12185. [Google Scholar] [CrossRef]
  26. Zipori, A.; Rosenfeld, D.; Tirosh, O.; Teutsch, N.; Erel, Y. Effects of aerosol sources and chemical compositions on cloud drop sizes and glaciation temperatures. J. Geophys. Res. 2015, 120, 9653–9669. [Google Scholar] [CrossRef]
  27. Fan, J.; Leung, L.; Demott, P.; Comstock, J.; Singh, B.; Rosenfeld, D.; Tomlinson, J.; White, A.; Prather, K.; Minnis, P.; et al. Aerosol impacts on California winter clouds and precipitation during CalWater 2011: Local pollution versus long-range transported dust. Atmos. Chem. Phys. 2013, 14, 81–101. [Google Scholar] [CrossRef] [Green Version]
  28. Bergeron, T. On the physics of cloud and precipitation. In Proceedings of the 5th Assembly of the U.G.G.I.; Paul Dupont: Paris, France, 1935. [Google Scholar]
  29. Hosler, C.; Jensen, D.; Goldshlak, L. On the Aggregation of Ice Crystals to form Snow. J. Meteorol. 1957, 14, 415–420. [Google Scholar] [CrossRef]
  30. Tobo, Y.; Prenni, A.; Demott, P.; Huffman, J.; Mccluskey, C.; Tian, G.; Pohlker, C.; Poschl, U.; Kreidenweis, S. Biological aerosol particles as a key determinant of ice nuclei populations in a forest ecosystem. J. Geophys. Res. Atmos. 2013, 118, 10100–10110. [Google Scholar] [CrossRef]
  31. Yuter, S.; Houze, R. Microphysical modes of precipitation growth determined by S-band vertically pointing radar in orographic precipitation during MAP. Q. J. Roy. Meteorol. Soc. 2003, 129, 455–476. [Google Scholar] [CrossRef]
  32. Pinsky, M.; Khain, A.; Rosenfeld, D.; Pokrovsky, A. Comparison of collision velocity differences of drops and graupel particles in a very turbulent cloud. Atmos. Res. 1998, 49, 99–113. [Google Scholar] [CrossRef]
  33. Khain, A.; Leung, L.; Lynn, B.; Ghan, S. Effects of aerosols on the dynamics and microphysics of squall lines simulated by spectral bin and bulk parameterization schemes. J. Geophys. Res. 2009, 114, D22203. [Google Scholar] [CrossRef] [Green Version]
  34. Fan, J.; Leung, L.; Rosenfeld, D.; Demott, P. Effects of cloud condensation nuclei and ice nucleating particles on precipitation processes and supercooled liquid in mixed-phase orographic clouds. Atmos. Chem. Phys. 2017, 17, 1017–1035. [Google Scholar] [CrossRef] [Green Version]
  35. van den Heever, S.; Carrió, G.; Cotton, W.; DeMott, P.; Prenni, A. Impacts of nucleating aerosol on Florida storms. Part I: Mesoscale simulations. J. Atmos. Sci. 2006, 63, 1752–1775. [Google Scholar] [CrossRef] [Green Version]
  36. Carrió, G.; van den Heever, S.; Cotton, W. Impacts of nucleating aerosol on anvil-cirrus clouds: A modeling study. Atmos. Res. 2007, 84, 111–131. [Google Scholar] [CrossRef]
  37. Colle, B.; Zeng, Y. Bulk Microphysical Sensitivities within the MM5 for Orographic Precipitation. Part I: The Sierra 1986 Event. Mon. Weather Rev. 2004, 132, 2780–2801. [Google Scholar] [CrossRef]
  38. Givati, A.; Rosenfeld, D. Quantifying Precipitation Suppression Due to Air Pollution. J. Appl. Meteorol. 2004, 43, 1038–1056. [Google Scholar] [CrossRef]
  39. Rosenfeld, D.; Givati, A. Evidence of Orographic Precipitation Suppression by Air Pollution–Induced Aerosols in the Western United States. J. Appl. Meteorol. Clim. 2006, 45, 893–911. [Google Scholar] [CrossRef]
  40. Muhlbauer, A.; Hashino, T.; Xue, L.; Teller, A.; Lohmann, U.; Rasmussen, R.; Geresdi, I.; Pan, Z. Intercomparison of aerosol-cloud-precipitation interactions in stratiform orographic mixed-phase clouds. Atmos. Chem. Phys. 2010, 10, 8173–8196. [Google Scholar] [CrossRef] [Green Version]
  41. Sanchez, J.; Merino, A.; Melcon, P.; Garciaorteqa, E.; Fernandezgonzalez, S.; Berthet, C.; Dessens, J. Are meteorological conditions favoring hail precipitation change in Southern Europe? Analysis of the period 1948–2015. Atmos. Res. 2017, 198, 1–10. [Google Scholar] [CrossRef]
  42. Danielsen, E. Inherent Difficulties in Hail Probability Prediction. In Hail: A Review of Hail Science and Hail Suppression; American Meteorological Society: Boston, MA, USA, 1977. [Google Scholar]
  43. You, L.; Yang, S.; Wang, X.; Pi, J. Study of ice nuclei concentration at Beijing in spring of 1995 and 1996, Acta. Meteorol. Sic. 2002, 60, 101–109. (In Chinese) [Google Scholar]
  44. Yang, H.; Xiao, H.; Guo, C. Structure and evolution of a squall line in northern China: A case study. Atmos. Res. 2015, 158–159, 139–157. [Google Scholar] [CrossRef]
  45. Walko, R.; Cotton, W.; Meyers, M.; Harrington, J. New RAMS cloud microphysics parameterization part I: The single-moment scheme. Atmos. Res. 1995, 38, 29–62. [Google Scholar] [CrossRef]
  46. Meyers, M.; Walko, R.; Harrington, J.; Cotton, W. New RAMS cloud microphysics parameterization. Part II. The two-moment scheme. Atmos. Res. 1997, 45, 3–39. [Google Scholar] [CrossRef] [Green Version]
  47. Saleeby, S.; Cotton, W. A large droplet mode and prognostic number concentration of cloud droplets in the Colorado State University Regional Atmospheric Modeling System (RAMS). Part I: Module descriptions and supercell test simulations. J. Appl. Meteorol. 2004, 43, 182–195. [Google Scholar] [CrossRef] [Green Version]
  48. Saleeby, S.; Van den Heever, S. Developments in the CSU-RAMS Aerosol Model: Emissions, Nucleation, Regeneration, Deposition, and Radiation. J. Appl. Meteor. Clim. 2013, 52, 2601–2622. [Google Scholar] [CrossRef]
  49. Yang, H.; Xiao, H.; Hong, Y. A numerical study of aerosol effects on cloud microphysical processes of hailstorm clouds. Atmos. Res. 2011, 102, 432–443. [Google Scholar] [CrossRef]
  50. Fernández-González, S.; Wang, P.; Gascón, E.; Valero, F.; Sánchez, J. Latent cooling and microphysics effects in deep convection. Atmos. Res. 2016, 180, 189–199. [Google Scholar] [CrossRef]
  51. Demott, P.; Prenni, A.; Mcmeeking, G.; Sullivan, R.; Petters, M.; Tobo, Y.; Niemand, M.; Mohler, O.; Snider, J.; Wang, Z.; et al. Integrating laboratory and field data to quantify the immersion freezing ice nucleation activity of mineral dust particles. Atmos. Chem. Phys. 2014, 15, 393–409. [Google Scholar] [CrossRef] [Green Version]
Atmosphere 10 00783 g001 550
Figure 1. Locations of the three nested domains. G1, G2, and G3 represent domain1, domain 2, and domain 3, respectively. The shaded area is the topography of the region. The characters represent: TJ, Tianjin; HB, Hebei Province; red star “*”, Beijing).
Figure 1. Locations of the three nested domains. G1, G2, and G3 represent domain1, domain 2, and domain 3, respectively. The shaded area is the topography of the region. The characters represent: TJ, Tianjin; HB, Hebei Province; red star “*”, Beijing).
Atmosphere 10 00783 g001
Atmosphere 10 00783 g002 550
Figure 2. Vertically integrated liquid mixing ratio in the major precipitation area A: at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3.
Figure 2. Vertically integrated liquid mixing ratio in the major precipitation area A: at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3.
Atmosphere 10 00783 g002
Atmosphere 10 00783 g003 550
Figure 3. Vertically integrated ice mixing ratio in the major precipitation area A: at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3.
Figure 3. Vertically integrated ice mixing ratio in the major precipitation area A: at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3.
Atmosphere 10 00783 g003
Atmosphere 10 00783 g004 550
Figure 4. Cross section along the line ‘a-b’ (Figure 2a) for hydrometeor mixing ratio (g kg−1) (shaded area shows total condensate mixing ratio; solid red lines represent the hail mixing ratio; dashed black lines are rain mixing ratio) at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3.
Figure 4. Cross section along the line ‘a-b’ (Figure 2a) for hydrometeor mixing ratio (g kg−1) (shaded area shows total condensate mixing ratio; solid red lines represent the hail mixing ratio; dashed black lines are rain mixing ratio) at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3.
Atmosphere 10 00783 g004
Atmosphere 10 00783 g005a 550Atmosphere 10 00783 g005b 550
Figure 5. Horizontally averaged mixing ratios of pristine ice (Qp), snow (Qs), aggregates (Qa), graupel (Qg), hail (Qh), cloud (Qc) and rain (Qr) at 0820 UTC, 0920 UTC and 1020UTC. The abscissa is mixing ratio (g kg−1) and the ordinate is height (km).
Figure 5. Horizontally averaged mixing ratios of pristine ice (Qp), snow (Qs), aggregates (Qa), graupel (Qg), hail (Qh), cloud (Qc) and rain (Qr) at 0820 UTC, 0920 UTC and 1020UTC. The abscissa is mixing ratio (g kg−1) and the ordinate is height (km).
Atmosphere 10 00783 g005aAtmosphere 10 00783 g005b
Atmosphere 10 00783 g006 550
Figure 6. Series of area averaged mixing ratios of pristine ice (Qp), snow (Qs), aggregates (Qa), graupel (Qg), hail (Qh), cloud (Qc), rain (Qr), liquid and ice at 0820 UTC, 0920 UTC and 1020UTC. The abscissa is time and the ordinate is mixing ratio (g kg−1).
Figure 6. Series of area averaged mixing ratios of pristine ice (Qp), snow (Qs), aggregates (Qa), graupel (Qg), hail (Qh), cloud (Qc), rain (Qr), liquid and ice at 0820 UTC, 0920 UTC and 1020UTC. The abscissa is time and the ordinate is mixing ratio (g kg−1).
Atmosphere 10 00783 g006
Atmosphere 10 00783 g007 550
Figure 7. Of surface precipitation and perturbation pressure at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3; Shading area shows the surface precipitation rate (units: mm h−1)and contour parts represents perturbation pressure (units: hPa), while the solid lines indicate positive values and dashed lines give negative values of perturbation pressure.
Figure 7. Of surface precipitation and perturbation pressure at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3; Shading area shows the surface precipitation rate (units: mm h−1)and contour parts represents perturbation pressure (units: hPa), while the solid lines indicate positive values and dashed lines give negative values of perturbation pressure.
Atmosphere 10 00783 g007
Atmosphere 10 00783 g008 550
Figure 8. Time series of domain averaged (Area A) hail precipitation rate (a) and rainfall rate (b) (units: mm h−1).
Figure 8. Time series of domain averaged (Area A) hail precipitation rate (a) and rainfall rate (b) (units: mm h−1).
Atmosphere 10 00783 g008
Atmosphere 10 00783 g009 550
Figure 9. Profiles of regionally averaged latent heating rate (units: °Ch−1) of the major storm region (Area A) at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3; The variables in the figures are: cc (condensation of cloud water); ic (deposition of water vapor into pristine ice); hr (accretion of rain by hail); hc (accretion of cloud water by hail); hmlt (melting of hail); cvap (evaporation of cloud); cold (total cooling rate); warm (total warming rate); total (net heating rate).
Figure 9. Profiles of regionally averaged latent heating rate (units: °Ch−1) of the major storm region (Area A) at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3; The variables in the figures are: cc (condensation of cloud water); ic (deposition of water vapor into pristine ice); hr (accretion of rain by hail); hc (accretion of cloud water by hail); hmlt (melting of hail); cvap (evaporation of cloud); cold (total cooling rate); warm (total warming rate); total (net heating rate).
Atmosphere 10 00783 g009
Atmosphere 10 00783 g010 550
Figure 10. Cross section along the line ‘a-b’ for airflow field at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3; Shading represents horizontal wind speed (m s−1), arrows represents the airflow speed field (m s−1).
Figure 10. Cross section along the line ‘a-b’ for airflow field at 0820 UTC, (a) C1; (b) C2; (c) C3; at 0920 UTC, (d) C1; (e) C2; (f) C3; at 1020 UTC, (g) C1; (h) C2; (i) C3; Shading represents horizontal wind speed (m s−1), arrows represents the airflow speed field (m s−1).
Atmosphere 10 00783 g010
Atmosphere 10 00783 g011 550
Figure 11. For thought.
Figure 11. For thought.
Atmosphere 10 00783 g011
Table
Table 1. Amount (g kg−1) averaged over time (0800–1100 UTC) and over area A of each particle in the cloud to hail in the four tests.
Table 1. Amount (g kg−1) averaged over time (0800–1100 UTC) and over area A of each particle in the cloud to hail in the four tests.
ExperimentChC1ChC2ChaChgChi (10−2)ChrChsTotal
C1141.64.224.08.63.6158.84.8342.0
C2157.34.023.77.84.1184.75.0382.5
C3223.63.927.68.76.4235.75.9505.4
Note: Ch = transfer amount (g kg−1) of each particle to hail. Subscript C1 = cloud1, C2 = cloud2, r = raindrop, I = pristine ice, s = snow, a = aggregate, g = graupel; Total = Cha+Chc1+Chc2+Chg+Chi+Chr+Chs.
Table
Table 2. Amount (g kg−1) averaged over time (0800–1100 UTC) and over area A of each particle in the cloud to pristine ice in the three experiments.
Table 2. Amount (g kg−1) averaged over time (0800–1100 UTC) and over area A of each particle in the cloud to pristine ice in the three experiments.
ExperimentCiC1CiC2CisTotal
C12.42.30.445.14
C22.52.40.455.35
C33.23.00.436.63
Note: Ci = transfer amount (g kg−1) of each particle to pristine ice. Subscript C1= cloud1, C2 = cloud2 and s = snow. Total = Cic1 + Cic2 + Cis.
Table
Table 3. Amount (g kg−1) averaged over time (0800–1100 UTC) and over area A of each particle in the cloud to rain in the three tests.
Table 3. Amount (g kg−1) averaged over time (0800–1100 UTC) and over area A of each particle in the cloud to rain in the three tests.
ExperimentCrC1CrC2 (10−2)Cra (10−4)Crg (10−2)Cri (10−7)CrhCrs (10−5)Total
C190.9654.74.33.746.64.4138.2
C292.8673.23.43.351.23.3144.7
C377.5601.93.91.1524.9130.1
Note: Cr = transfer amount (g kg−1) of each particle to rain. Subscript C1 = cloud1, C2 = cloud2, r = raindrop, I = pristine ice, s = snow, a = aggregate, g=graupel; Total = Cra+Crc1+Crc2+Crg+Cri+Crh+Crs.
Table
Table 4. Spatial-time (0800–1100 UTC, Area A) averaged values of hail particles parameter in cloud and on surface for SPR.
Table 4. Spatial-time (0800–1100 UTC, Area A) averaged values of hail particles parameter in cloud and on surface for SPR.
Experiment Q h ¯ ( 10 − 2   g   kg − 1 ) N h ¯ ( m − 3 ) D h ¯ ( mm ) Q m e l t ¯ ( 10 − 3   g   kg − 1 )
In Cloud/On SurfaceIn Cloud/On SurfaceIn Cloud/On SurfaceIn Cloud/Under Cloud Base
C117/0.244.2/0.026.49/8.431.5/1.99
C220.6/0.446.7/0.066.46/7.842.5/3.19
C325.9/0.555.0/0.076.38/7.661.3/3.21
Note: Q h ¯ : hail mixing ratio; N h ¯ : hail concentration; D h ¯ : hail mean diameter; Q m e l t ¯ : melting mixing ratio.

Share and Cite

MDPI and ACS Style

Yang, H.; Xiao, H.; Guo, C. Effects of Aerosols as Ice Nuclei on the Dynamics, Microphysics and Precipitation of Severe Storm Clouds. Atmosphere 2019, 10, 783. https://doi.org/10.3390/atmos10120783

AMA Style

Yang H, Xiao H, Guo C. Effects of Aerosols as Ice Nuclei on the Dynamics, Microphysics and Precipitation of Severe Storm Clouds. Atmosphere. 2019; 10(12):783. https://doi.org/10.3390/atmos10120783

Chicago/Turabian Style

Yang, Huiling, Hui Xiao, and Chunwei Guo. 2019. "Effects of Aerosols as Ice Nuclei on the Dynamics, Microphysics and Precipitation of Severe Storm Clouds" Atmosphere 10, no. 12: 783. https://doi.org/10.3390/atmos10120783

APA Style

Yang, H., Xiao, H., & Guo, C. (2019). Effects of Aerosols as Ice Nuclei on the Dynamics, Microphysics and Precipitation of Severe Storm Clouds. Atmosphere, 10(12), 783. https://doi.org/10.3390/atmos10120783

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop