1. Introduction
The cooling tower is a key component of a water-cooled air conditioning plant, which removes heat from the warm water in the condenser [
1]. However, evaporation loss in the cooling tower is high and difficult to recover. Meanwhile, when hot moist air emitted from the cooling tower is mixed with the ambient air, a visible plume is generated. In most cases, the plume is not considered as a pollutant; however, it can influence the visibility of the surrounding residential areas and road traffic. Moreover, it makes the pavement around the cooling tower wet and slippery, which affects the maintenance work.
In the past, the effect of visible plumes from cooling towers has always been neglected. Veldhuizen et al. [
2] considered several methods of alleviating plume generation and made cost estimates for the most promising methods. Other researchers have also focused on this problem, but have not reported any effective controlling measures [
3,
4,
5]. Until recently, plumes from cooling towers had become a major concern; therefore, a large number of studies are being conducted to find plume abatement methods. For example, Li et al. [
6] proposed that cooling tower plumes using coaxial plume structures have more advantages when compared with the traditional approach of cooling tower plume abatement. Tyagi et al. [
7] studied the principle of generating visible plumes, and presented a case study of the prediction, potential, and control of plumes from wet cooling towers of commercial buildings in Hong Kong, based on the weather data available for a particular year. Similarly, Xu et al. [
8] evaluated the plume potential and abatement of evaporative cooling towers in a subtropical region; the results showed that the control strategies had a significant effect on the plume potential and further impacted the system design and sizing of the plume abatement system. Hu et al. [
9] developed a thermodynamic coupling calculation model of hybrid cooling towers. They also proposed a novel scheme to combine the advantages of both dry and wet cooling subsystems to eliminate the plume problem inherent in wet cooling towers; moreover, this could also save a large amount of water. Further, application of renewable energy (such as heat pumps and solar collectors in heating systems) to control the visible plume from wet cooling towers is an environment-friendly method. The combined option is more economical than the heating alone option, especially in the case of heat pump systems [
10,
11].
In order to further solve the plume problem, it is necessary to investigate the prediction of a visible plume. The computational fluid dynamics (CFD) method is an effective way of research and widely used in many fields [
12,
13]; and it is also used to study the prediction of a visible plume. Meroney [
14] used the computational fluid dynamics (CFD) method to simulate the cooling tower plume dispersion and drift; the simulation replicated the experiments carried out in the Chalk Point natural draft cooling tower (MD, USA). Takata et al. [
15] used the CFD method to predict the generation and range of plume and analyze its mechanism of abatement. Ding et al. [
16] calculated the sensitivity analysis of plume rising height from cooling tower and results showed that the main factors affecting the plume rising height is the atmospheric stability. The experiment method is also an essential part of research and it can validate whether the numerical simulation results are correct. Michioka et al. [
17] developed a new method for a wind tunnel experiment to predict a visible plume region from a wet cooling tower, and the results revealed that the visible plume length and height were nearly in agreement with the observations. Guo [
18] also used a wind tunnel experiment to predict a visible plume from the cooling tower of a nuclear power plant, and the proposed wind tunnel experiment can simulate the visible plume region and plume rise with reasonable accuracy.
Evaporation loss is one of the important causes of plume generation, so solving the problem of cooling tower evaporation loss can not only save water, but also contribute to solve the plume problem. Lee et al. [
19] proposed a preliminary strategy involving a combination of dry and wet cooling methods, which could adequately conserve water without compromising on the performance. Other authors have further defined this approach, demonstrating that a satisfactory amount of water conservation could be achieved [
20,
21]. Askari et al. [
22] examined the effect of multi-walled carbon nanotubes (MWNTs) and nanoporous graphene nanoparticles on the thermal and rheological properties of water, as well as their impact on the performance of a mechanical wet cooling tower in terms of energy and water conservation. Chang et al. [
23] proposed a novel water and energy conservation method for a counterflow cooling tower using UV light disinfection and a variable speed fan. The authors reported that for 50% load tests, 76% energy savings and 23% water conservation were achieved. Marcia et al. [
24] proposed to use cooled porous media based on thermosiphons technology to recover the vapor from a cooling tower. Deziani et al. [
25] developed a laboratory model of a wet cooling tower with an air-to-air heat exchanger to study its potential for reducing water consumption, and 35% water conservation could be expected.
From the above literature, it can be seen that the existing studies mainly pay attention to plume generation, plume prevention, and water conservation. However, most of the researches have only considered plume abatement or water conservation, and little attention has been paid to couple water conservation with plume abatement. Based on the findings of these investigations, a novel coupling technology for water conservation and plume abatement is proposed in the present work, and a surface type heat exchanger is designed to realize this new coupling technology. The coupling technology combines the advantages of hot and cold channels comprising the heat exchanger to eliminate plume formation within the area surrounding the cooling tower. The vapor condenses into water and adheres to the channel surface to achieve the purpose of water conservation. The feasibility of this technology was verified by the predicted results of theoretical calculations. We believe that the results of the present study could prove beneficial to protect the environment and conserve water.
2. Research Methodology
2.1. Mechanism of Plume Formation
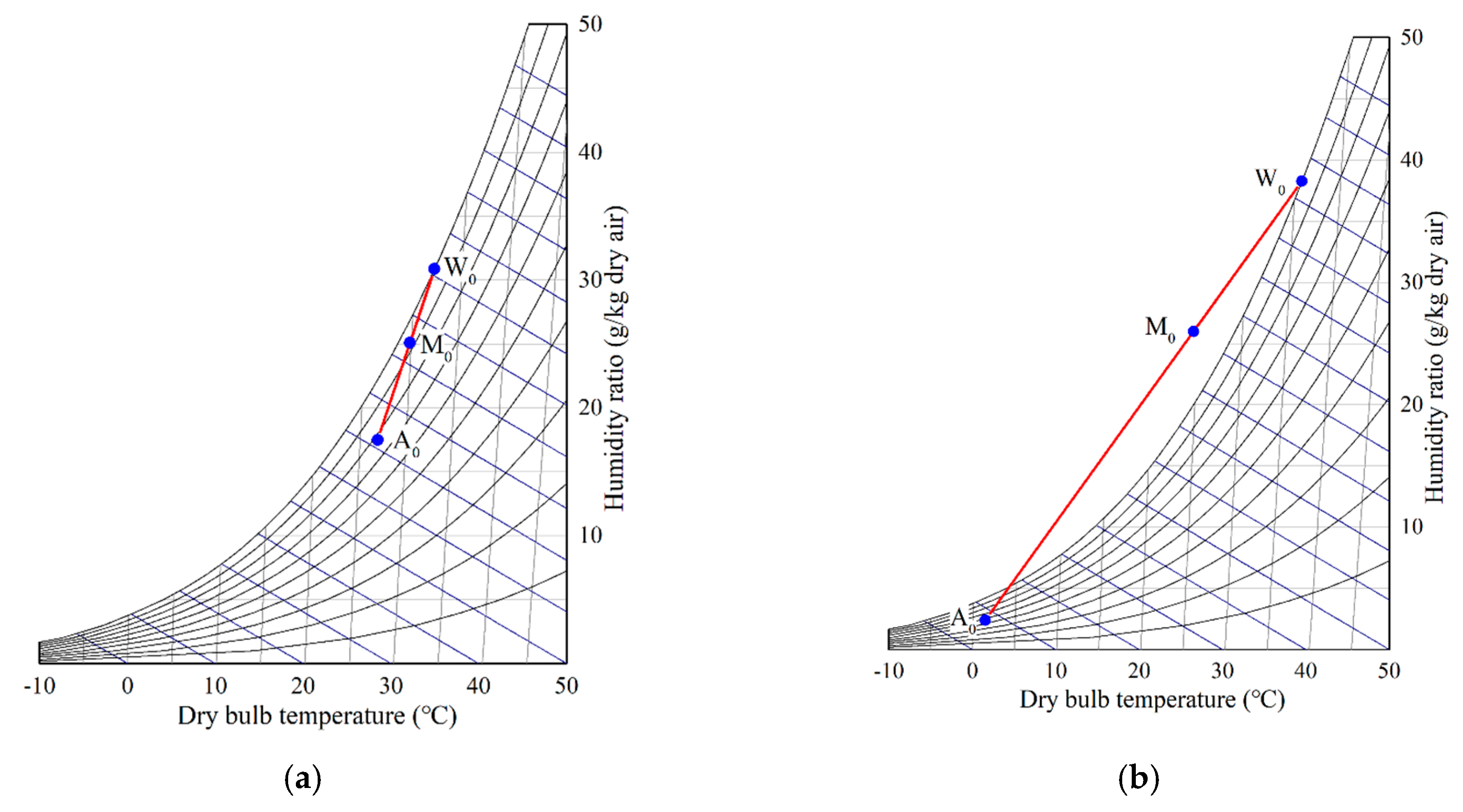
Moist air, commonly known as air, can be found in three states: Unsaturated, saturated, and supersaturated. As the saturated humidity ratio of moist air is closely related to temperature, when the constituent of moist air remains unchanged, the humidity ratio increases with temperature. Moreover, once relative humidity (RH) exceeds 1, unsaturated moist air transforms into supersaturated moist air. As water vapor in the moist air is unsustainable, the excess water vapor condenses into fine droplets that are suspended in the air to form fog, otherwise known as a visible plume.
During cooling tower operations, the ambient air introduced by the axial fan installed at the outlet of the cooling tower is warmed and humidified, owing to the high temperature of the circulating cooling water. Consequently, the tower outlet air and the ambient air are mixed, as indicated by the red line, A
0–B
0, in the enthalpy—Humidity chart shown in
Figure 1, where the symbols A
0, B
0, and M
0 denote ambient, tower outlet, and mixing air states, respectively. When the tower outlet air and ambient air are mixed, regardless of the changes induced in the mixing ratio, the mixing point will remain on the A
0–B
0 line. However, it is noteworthy that changes to the working conditions would shift the mixing line A
0–B
0 to a different region. As shown in
Figure 1a, under summer working conditions, the mixing line remains within the unsaturation region, whereas it would shift toward the supersaturation region during winter, as shown in
Figure 1b.
2.2. Technology of Plume Abatement
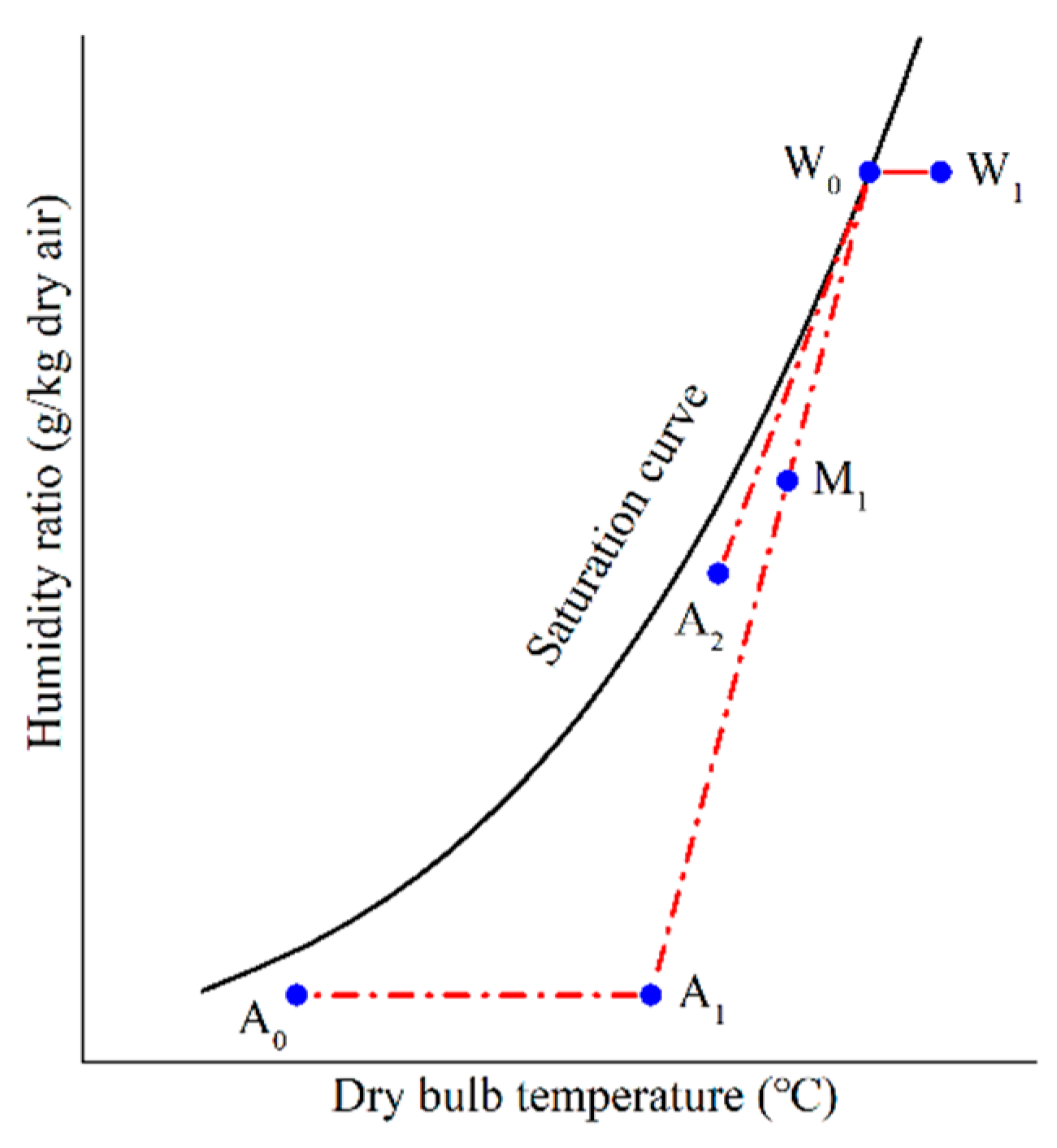
According to the mechanism of plume formation, as long as the mixing line does not pass through the supersaturation region during the mixing process, its mixing point will not be located in this region either, and visible plumes would form outside the cooling tower. Hence, by adjusting the temperature and humidity ratio of tower outlet air, the state of moist air could be modified to avoid plume formation.
At present, three plume abatement technologies are primarily used: (1) Heating plume abatement technology, (2) multi-air-volume plume abatement technology, and (3) air parallel plume abatement technology. As shown in
Figure 2, when the first approach is used, the tower outlet air moves horizontally from point W
0 to point W
1, owing to sensible heating, such as that involving dry, high-efficiency heat exchanger. When the second approach is adopted, as indicated in
Figure 2, the tower outlet air moves from point W
0 to point A
2 by increasing the air volume. This would reduce the humidity ratio of the cooling tower outlet air. Thus, it is necessary to ensure that the state point is located within the unsaturated region to avoid plume formation. The ambient air is forced into the cooling tower from both sides and mixed; one side of the air directly contacts with the circulating cooling water and forms hot moist air in the cooling tower, whereas the other side of the air A
0 moves to A
1 by sensible heating. Finally, the two streams of air are mixed in a parallel manner, and the tower outlet air point moves to M
1.
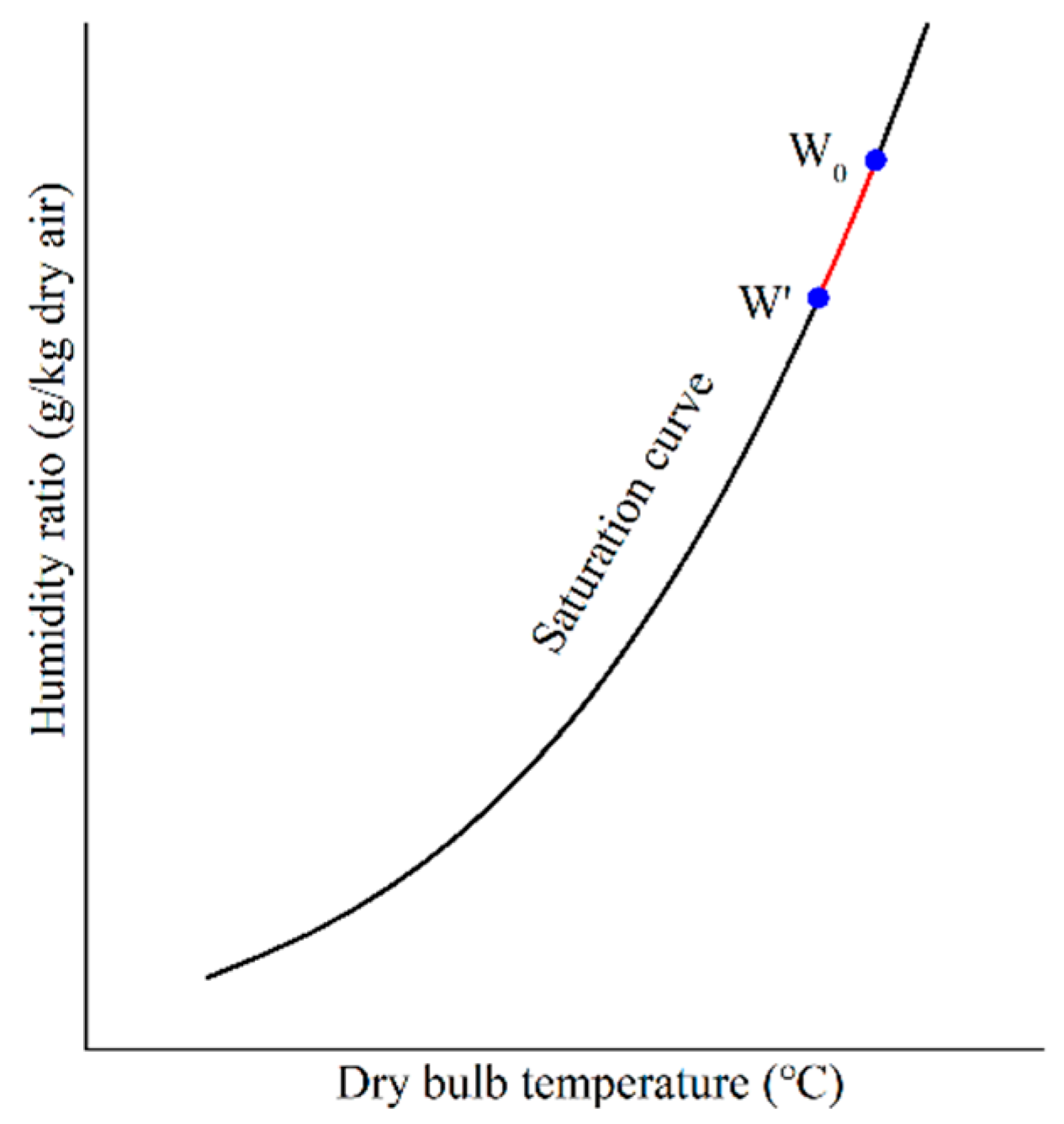
2.3. Technology of Water Conservation
There are two main methods employed to reduce the evaporation losses in a cooling tower: (1) Cooling the saturated moist air formed above the cooling tower after air-water heat exchange in the packing to cause some water to precipitate (which could then be recovered); and (2) reducing the temperature of the circulating cooling water before the air-water heat exchange occurs. This would ensure less formation of saturated moist air above the cooling tower. As indicated in
Figure 3, both these methods could be effective in conserving water by changing the condensation state of hot moist air from W
0 to W′.
2.4. New Coupling Technology of Water Conservation and Plume Abatement
Although the traditional plume abatement technology can effectively reduce the plume, the lost evaporated water cannot be easily recovered, which may negatively affect the long-term operation of the cooling tower. Thus, a novel coupling technology that can save water and eliminate the plume is proposed in the present study.
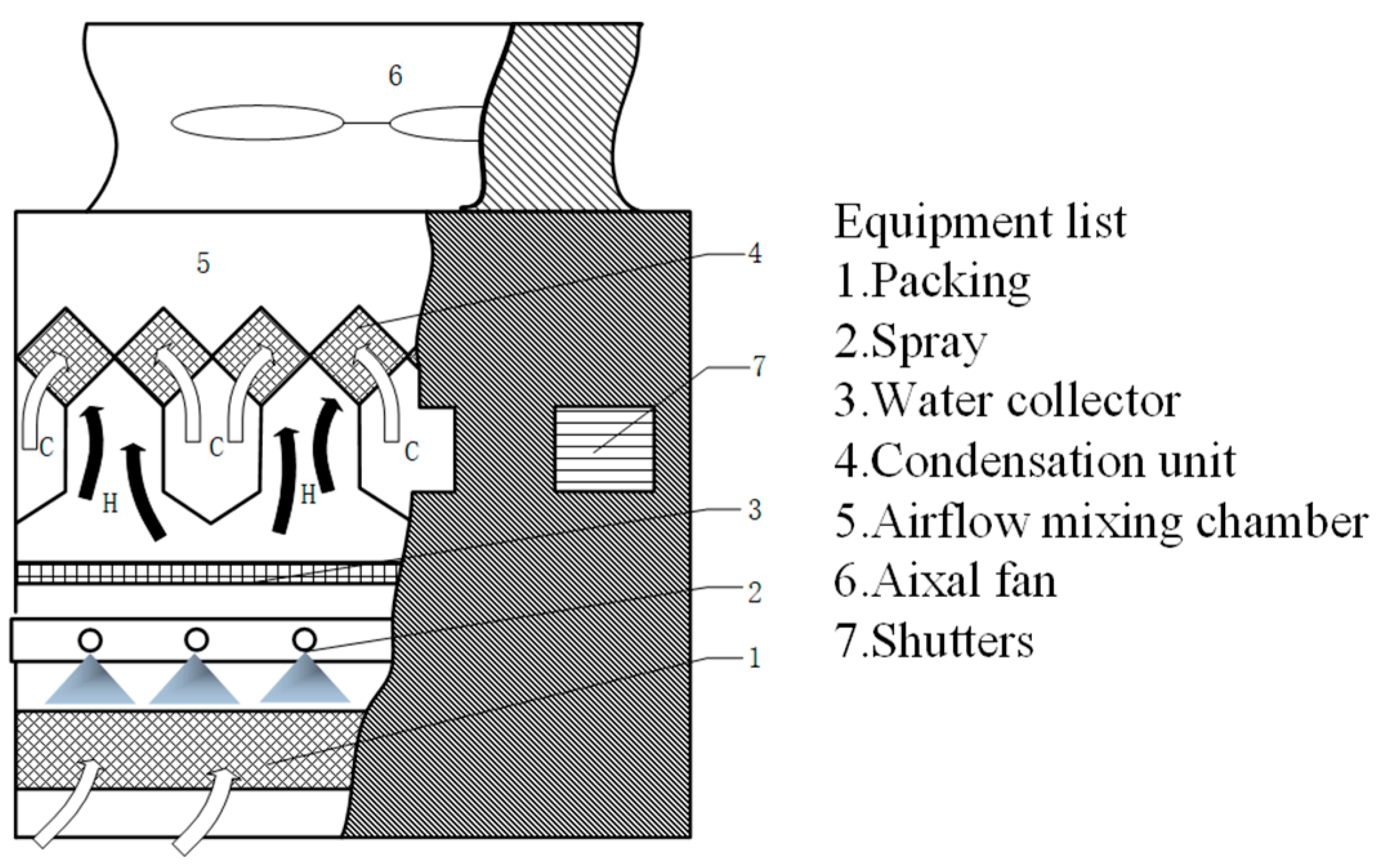
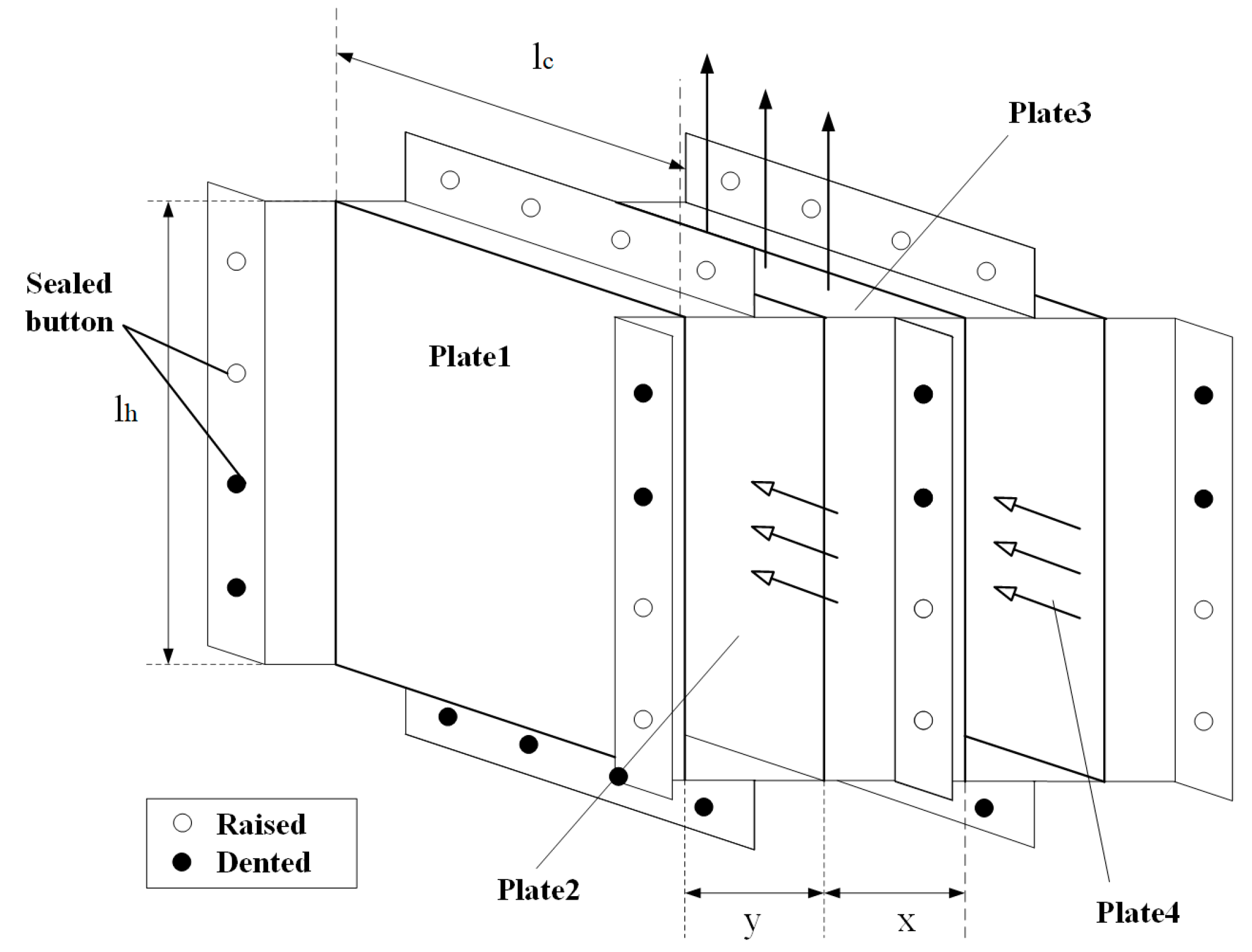
Figure 4 presents the schematic diagram of a cooling tower designed for the coupling technology. In the cooling tower, a surface-type heat exchanger is set above the water collector. The surface-type heat exchanger consists of an array of heat exchange components, each of which is composed of multiple cold and hot channels in an alternate manner.
Figure 5 shows the schematic diagram of a heat exchanger unit. Here, symbols
lh,
x,
lc, and
y refer to the length of hot channel, the width of single hot channel, the length of cold channel, and the width of single cold channel, respectively. Hollow and solid arrows indicate cold air flow and hot air flow, respectively. Each heat exchange channel consists of two heat exchange plates. The sealed heat exchange channel consists of four heat exchange plates, which can be straight or corrugated.
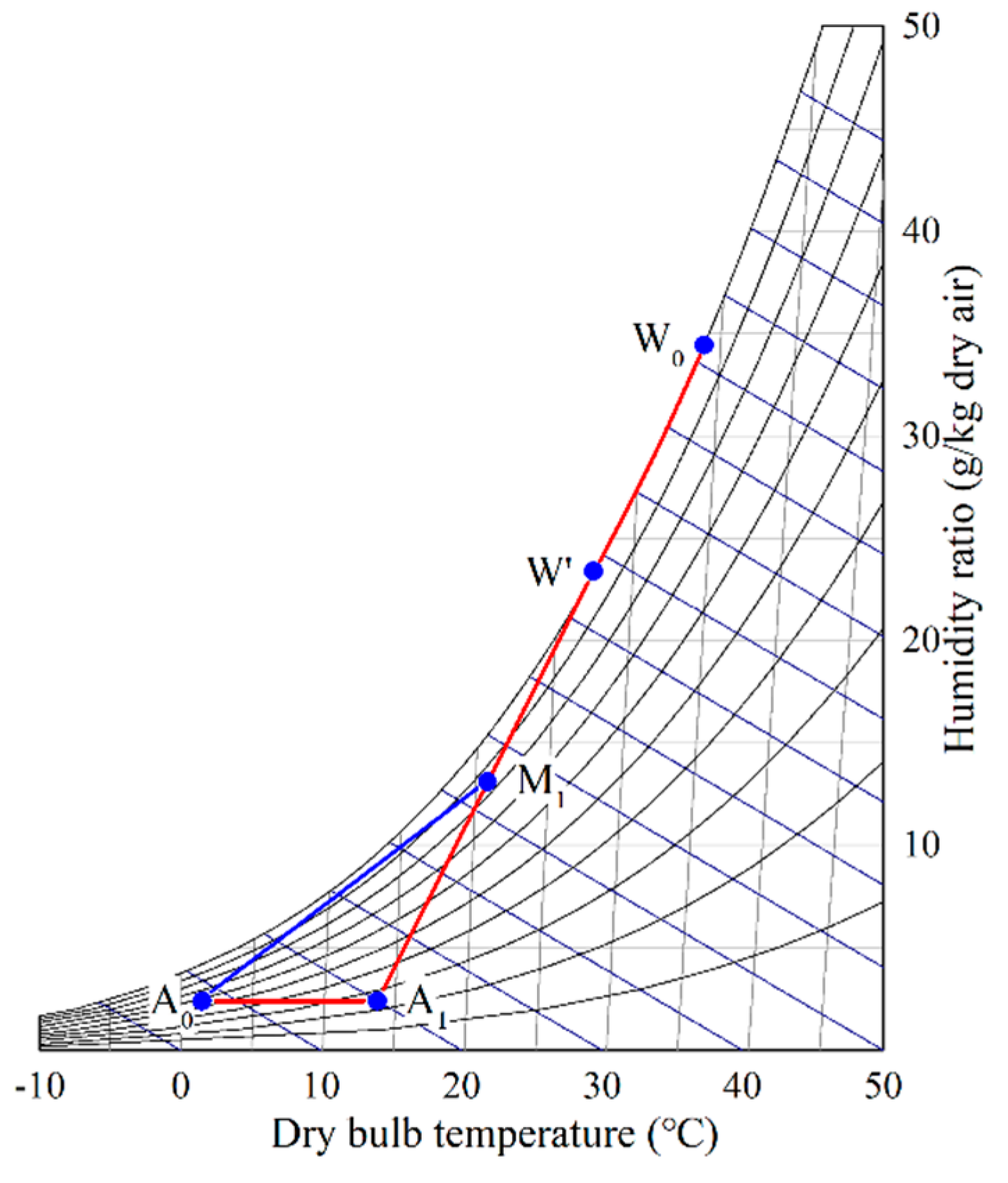
The principle of coupling technology is shown in
Figure 6. The ambient air outside the tower at A
0 flows into the cold channel, whereas the hot moist air at W
0 flows into the hot channel. Subsequently, their heat is exchanged using a surface-type heat exchanger, and therefore, the hot moist drops to W′ along the saturation curve. Simultaneously, the ambient air moves to A
1 by sensible heating. The condensed water is produced during the process of reducing humidity ratio, which is collected to save water. Next, the dry air at A
1 and moist air at W′ are mixed above the surface type heat exchanger; temperature and humidity ratio are further reduced, and the mixing point M
1 falls into the unsaturation region. In this manner, the formation of a plume at the outlet of the cooling tower could be avoided.
3. Thermodynamic Calculation Model
To realize the coupling technology of water conservation and plume abatement, the heat exchanger is considered the most important auxiliary equipment in the cooling tower. As mentioned in the above section, we designed a surface type heat exchanger whose flow mode was cross-flow.
The heat exchanger shown in
Figure 5 consists of an array of heat exchange components; its heat exchange plate is made up of superconducting carbon materials. We selected this plate as it has excellent corrosion resistance and lighter mass. The length of both the hot and cold channels was 1.45 m, whereas the width of the single hot channel and that of the single cold channel were 0.051 m and 0.017 m, respectively. The thickness of the heat exchange plate was 4 × 10
−4 m. We assumed that the width of the cooling tower was 17.062 m and the number of heat exchange plates was 495.
3.1. Condensation Calculation Model of Heat Exchanger
The surface-type heat exchanger is shown in
Figure 5, with saturated moist air in its inlet of the hot channel and dry air after heat exchange in the cold channel. Its state drops from W
0 to W′ along the saturation curve. During the condensation of moist air, the mass flow rate of dry air remains constant, owing to no mass transfer between moist and dry air. Only the mass of water vapor in the moist air changes; therefore, the amount of condensed water could be calculated using the change in the humidity ratio of moist air. The humidity ratio,
d, is expressed as:
where
is the water vapor mass flow rate,
mg is the dry air mass flow rate,
is the pressure of water vapor, and
is the pressure of dry air.
The amount of condensed water can be calculated using the following equation:
where
and
are humidity ratios corresponding to temperature
and
, respectively.
3.2. Thermodynamic Calculation Model of the Heat Exchanger
3.2.1. Heat Transfer Coefficient of the Cold Side
The heat exchange of the cold side is a single-phase flow, and can be calculated using the Dittus-Boelter Equation [
26]:
where 0.023, 0.8, and 0.4 are determined by experimental study,
is the Prandtl number of cold air and
is the Reynolds number of cold air, which can be expressed as:
where
is the density of cold air,
is the velocity of cold air,
is dynamic viscosity of cold air, and
y is the width of single cold channel.
Then, according to the definition of the Nusselt number, we can obtain the heat transfer coefficient of the cold side, which can be expressed as:
where
is the thermal conductivity of cold air, and 2
y is the characteristic length of the cold channel.
3.2.2. Heat Transfer Coefficient of the Hot Side
During the condensation of hot moist air, we can adopt a combined heat transfer correlation, which can be expressed as follows [
27]:
where 0.1823, 0.7707, 1/3, and 0.2615 are determined by experimental study, and
is a new criterion number for establishing the condensation process and can be expressed as:
where
is the temperature corresponding to water vapor partial pressure,
is the wall temperature,
is the mixed air temperature,
is the Prandtl number of hot air, and
is the Reynolds number of hot air, which can be expressed as:
where
is the density of cold air,
is the velocity of cold air,
is dynamic viscosity of cold air, and
x is the width of single hot channel.
Similarly, we can obtain the heat transfer coefficient of the hot side according to the definition of the Nusselt number, which can be expressed as:
where
is the thermal conductivity of hot air, and 2
x is the characteristic length of the hot channel.
3.2.3. Overall Heat Transfer Calculation Equation
The heat quality during the overall heat transfer process can be determined using the following equation:
where
is the logarithmic mean temperature difference, A is the overall heat transfer area, and
is the overall heat transfer coefficient, which can be expressed as:
where
and
are the heat transfer coefficients of the hot and cold sides, respectively,
is the wall thickness, and
is the thermal conductivity of the wall. It should be pointed that the overall heat transfer coefficient does not consider the thermal resistance resulting from impurities present on both sides of the heat exchanger wall, because in the process of heat transfer, condensed water is continuously formed and slides down to wash the heat exchange surface. Thus, it can be assumed that the exchange surface is relatively smooth and has no fouling resistance.
In the process of energy transfer, the total energy remains constant because of the energy conservation law. It can be expressed as:
and
can be expressed as:
and
3.3. Determination of the State Point and Plume Abatement Process
We first determined the state point, W
0, in the enthalpy-humidity chart, which is the inlet temperature of the hot channel and can be expressed as:
where
is the temperature of ambient air,
is the temperature of hot side air,
is the arithmetic mean of inlet and outlet water temperatures,
is the enthalpy of ambient air,
is the enthalpy of hot side air, and
is the enthalpy corresponding to the temperature
.
We next determined the state point, A
1. Because there is no mass transfer between the two flows, the absolute humidity at the cold channel outlet equals to that at the cold channel inlet. Using the heat balance equation, we can also calculate the specific value of W′, which is hot moist air after condensation. Hot moist air mixes with the heated dry air directly, and therefore, the state point, M
1, can be obtained as follows:
and
where
is the hot moist air mass flow rate,
is the cold air mass flow rate, and
is the overall air mass flow rate.
In comparison to the original straight line A0–W0, we connected the new line through the two points A0 and M1. This significantly avoided generation of the plume above the cooling tower. If the line still passes the supersaturation region, the number of the heat exchanger unit, N, is increased or decreased until the line does not pass this region. In this manner, the optimal number and dimensions of the heat exchanger unit could be obtained.
4. Results and Analysis
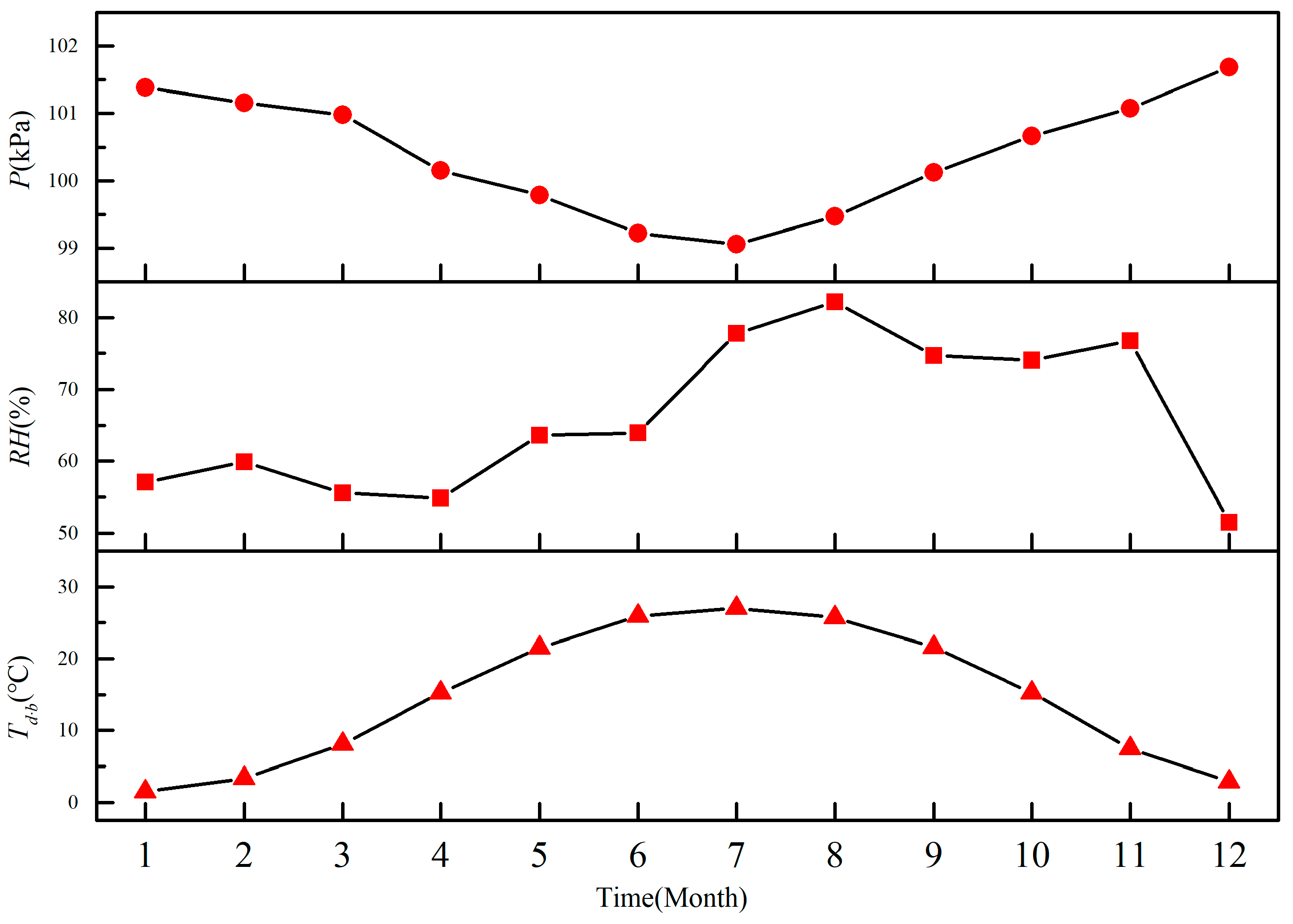
Figure 7 shows the parameters of a typical meteorological year, including atmospheric pressure (
), relative humidity (
), and dry bulb temperature (
). The meteorological parameters of Zhengzhou were obtained from the China standard weather database (CSWD).
First, the meteorological parameters at
°C (in January) were selected as the design condition, owing to its low temperatures and considerably high RH, which is the primary cause of plume generation. According to theoretical calculations, we could predict the optimal number and dimensions of the heat exchanger unit. Subsequently, these dimension parameters were used to predict the thermodynamic process in other typical months, as listed in
Table 1.
4.1. Thermodynamic Calculation at Design Condition
Under design conditions, the heat exchange area served as the core of the design. The value of thr heat exchange area could be determined using several other parameters, such as the amount of condensed water () and the cold air mass flow rate ().
We calculated the thermodynamic parameters of the heat exchanger unit. The inlet temperature of the hot channel, W0, can be calculated using Equation (15). We assumed that the heat exchange area was known, that is, assuming a different number of heat exchanger units, followed by solving Equations (10)–(15), we could obtain all the inlet and outlet air parameters, such as enthalpy, temperature, and humidity ratio. The amount of condensed water could be calculated using Equation (1).
Specific operation parameters, including hot moist air mass flow rate,
, hot moist air temperature difference,
, cold air mass flow rate,
, cold air temperature difference,
, amount of condensed water,
, and circulating water volume, G, are listed in
Table 2.
Table 2 shows certain operation parameters with different N values. Because cooling water volume remains constant, the hot moist air mass flow rate is also constant. The hot moist air temperature difference increases as N increases, because the heat exchange area increases. Decrease in the cold air temperature difference is attributed not only to the increase in the heat exchange area, but also to the gradual increase in the opening of shutters. The amount of condensed water increases as hot moist air temperature difference increases, because water vapor in the moist air reaches its limit at this temperature and pressure. Therefore, with the decrease in temperature, water vapor condenses into droplets.
4.2. Operation State Prediction
4.2.1. Influence of Different N
To ensure there is no visible plume above the cooling tower, it is important to select appropriate N values during the operation. We have already obtained some specific parameters that are listed in
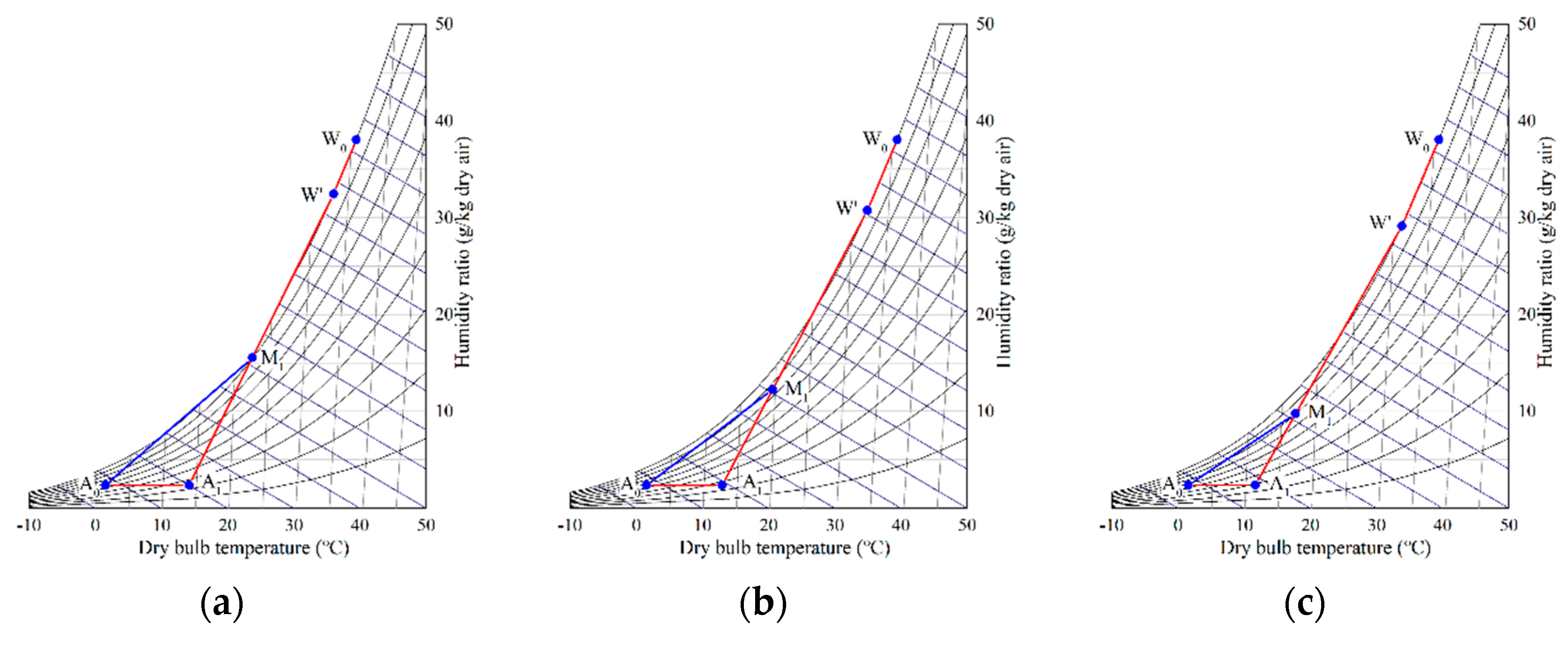
Table 2. The thermodynamic processes are illustrated in
Figure 8 with different numbers of heat exchanger units (N = 4, 6, and 8). The new mixing line A
0–M
1 falls into the supersaturation region; as N increases, M
1 tends to A
1 and the mixing line grows shorter and tends to fall into the unsaturation region, and the possibility of plume generation is gradually reduced.
When N = 4, the mixing line still passes the supersaturation region, and therefore, plume abatement cannot be achieved. At N = 6, although the mixing line no longer passes the supersaturation region, the possibility of the formation of plume still exists. When N = 8, the mixing line A0–M1 completely falls into the unsaturation region, thus avoiding plume generation to a large extent. A comparison of thermodynamic processes of the above three graphs reveals that as N increases, improved plume abatement is achieved.
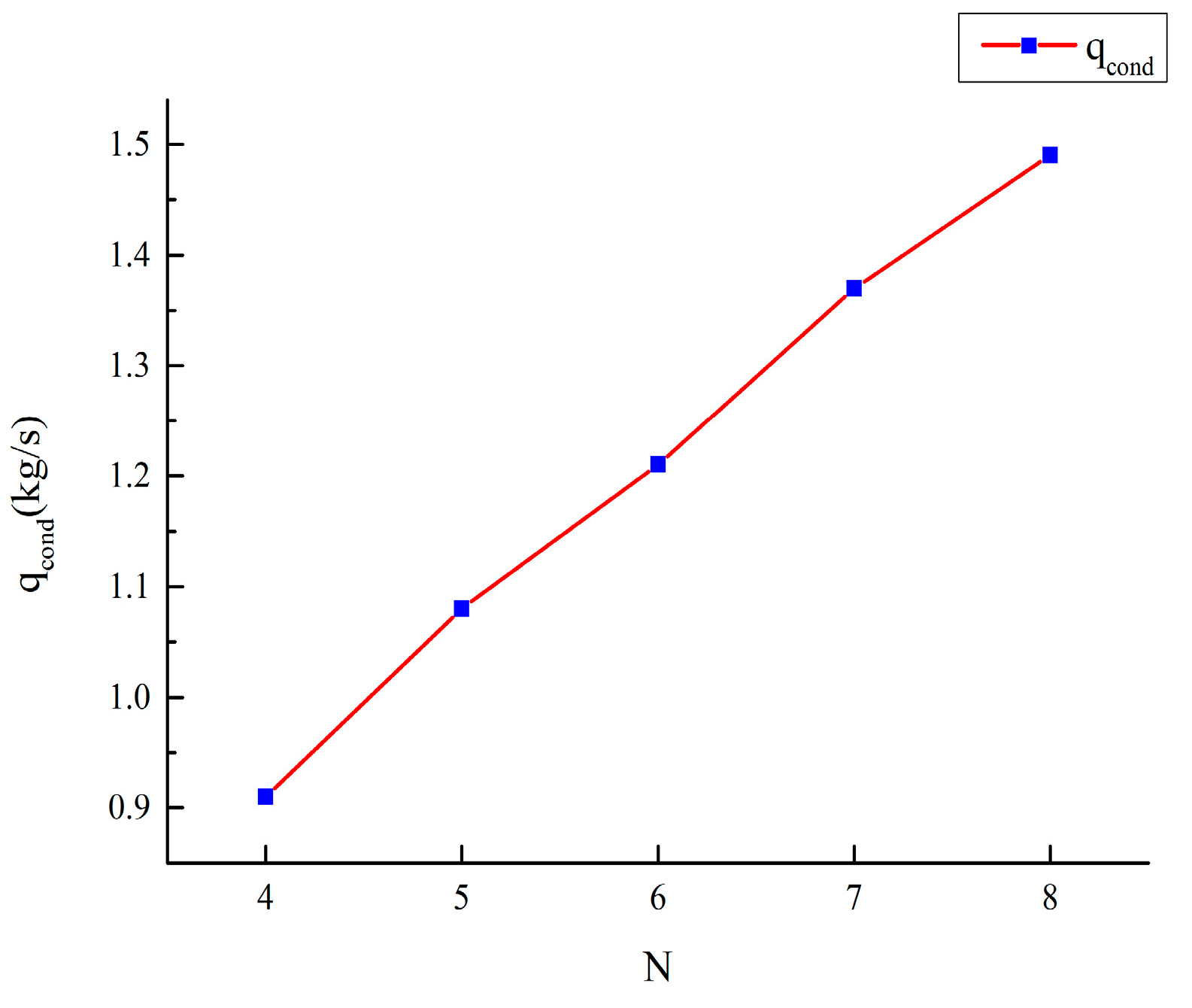
The relationship between N and
is shown in
Figure 9; it can be seen that the amount of condensed water increases with the increase of N value, and they are almost in direct proportion. Therefore, taking into consideration the cost-effectiveness and safety of the operation, N = 8 is recommended at
,
, and
.
4.2.2. Influence of Different G
We have already discussed the thermodynamic process with different values of N, and the results show that N = 8 is an optimal heat exchanger unit number. In this section, N is a constant value (8), with varying values of circulating water volume (G) of 800, 1500, 2000, and 3000 m
3/h.
Table 3 shows certain operation parameters with different G values.
With a gradual increase in the G values and keeping the cold air mass flow rate relatively stable, we can conclude from
Figure 10 that improved plume abatement is achieved when G is smaller; however, when G = 3000 m
3/h, there is a possibility of plume generation above the cooling tower.
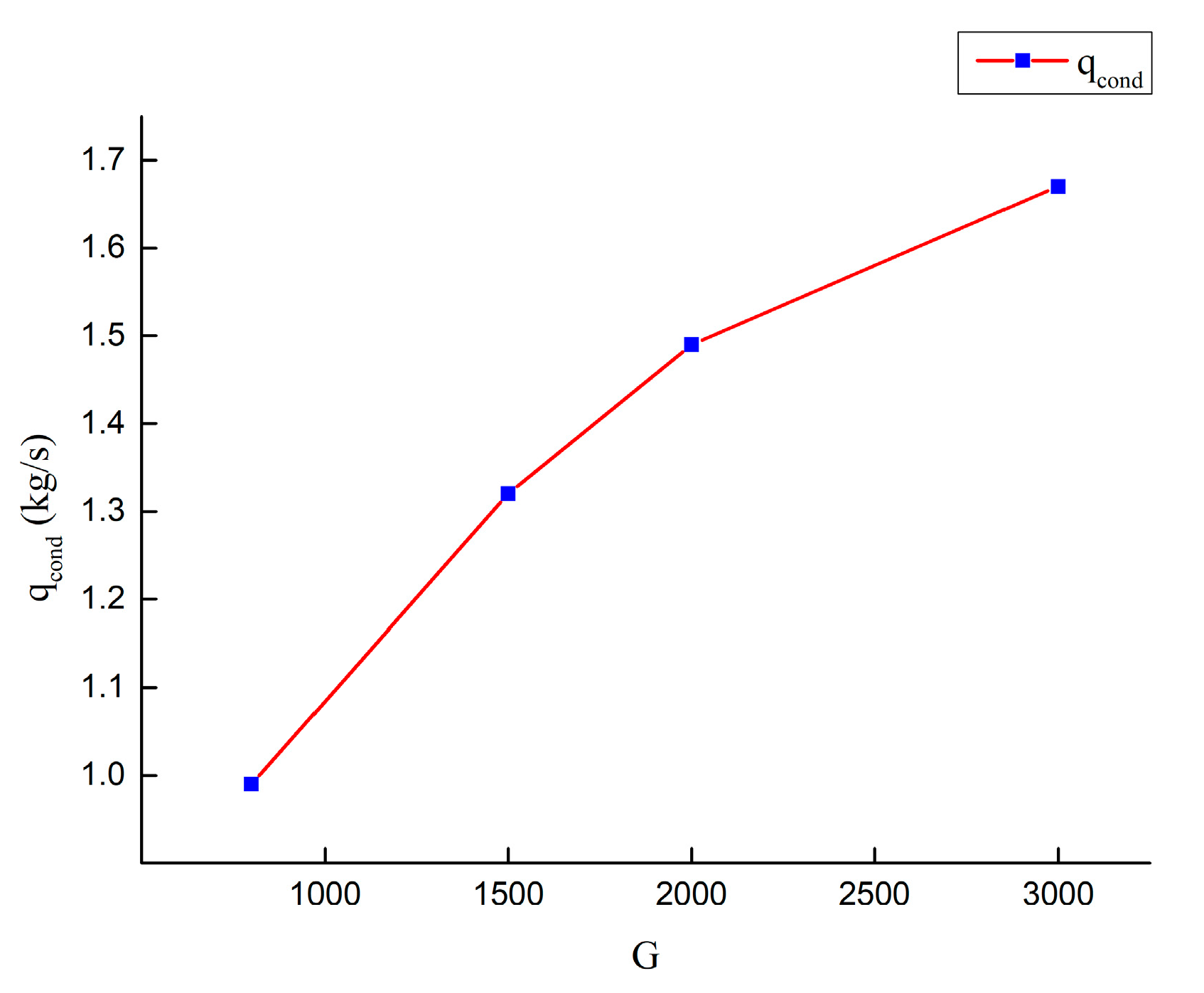
The relationship between G and
is shown in
Figure 11; it can be observed that
always increases with increasing G. However, the rate of increases of
slows as slower with G increases. Therefore, to achieve the optimal effect of plume abatement and water conservation, N = 8 and G < 3000 m
3/h are recommended.
4.3. Water Conservation Prediction
Compared with the traditional evaporative cooling tower, the cooling tower with a surface type heat exchanger provides an obvious advantage of reducing the evaporation losses and conserving water. Through the previous analysis, a large amount of condensed water could be saved at higher values of N and G. With N = 8 and G = 2000 m
3/h,
can reach up to 1.49 kg/s. The specific
values under various conditions are listed in
Table 4.
We estimated the amount of condensed water in several typical months. We found that water savings could be increased significantly at lower temperatures and higher RH. We selected January, April, July, and October as four seasons of the year, and the calculation results using certain specific operation parameters are shown in
Table 4. The average amount of condensed water was 1.105 kg/s. Assuming that the cooling tower runs 7200 h per year, the annual water savings amount reached 2.8641 × 107 kg.
5. Conclusions
The present study proposed a novel coupling technology for water conservation and plume abatement. Based on the analytical investigations presented in this study, the following preliminary conclusions could be drawn:
(1) A novel coupling technology for water conservation and plume abatement was proposed. The coupling technology combined the air parallel plume abatement technology with the condensation water conservatiofin technology. The feasibility of this technology was verified by thermodynamic analysis.
(2) A thermodynamic calculation model was established based on the designed surface type heat exchanger and its structural dimensions. According to the theoretical calculation, the parameters of each point in the thermodynamic process were determined. We found that compared with the original straight line A0–W0, a new line A0–M1 could avoid the generation of plumes above the cooling tower.
(3) To ensure that no plume was formed above the cooling tower, we first studied the operation parameters under the influence of different N values. The results revealed that the possibility of plume generation could be reduced by increasing the value of N. Taking into consideration both the cost-effectiveness and safety of the operation, N = 8 was recommended. Next, we studied the influence of different G values for N = 8. The results revealed that the smaller the G value, the better the plume abatement. However, G ≥ 3000 m3/h did not prove conducive for plume abatement; therefore, N = 8 and G < 3000 m3/h were recommended parameters for the operation of the cooling tower.
(4) Finally, we estimated water savings using the condensation calculation model. At lower temperatures and higher RH, water savings increased significantly, indicating that considerable water could be saved during winters. The average amount of condensed water was 1.105 kg/s and the amount of annual water savings reached 2.8641 × 107 kg.
Possible future research areas include using evaluation indexes and establishing a performance evaluation system.