Parameterization of The Single-Scattering Properties of Dust Aerosols in Radiative Flux Calculations
Abstract
1. Introduction
2. Methods
2.1. Single Scattering Properties
2.2. Radiative Transfer Model
3. Parameterization of the Single Scattering Properties of Dust Aerosols
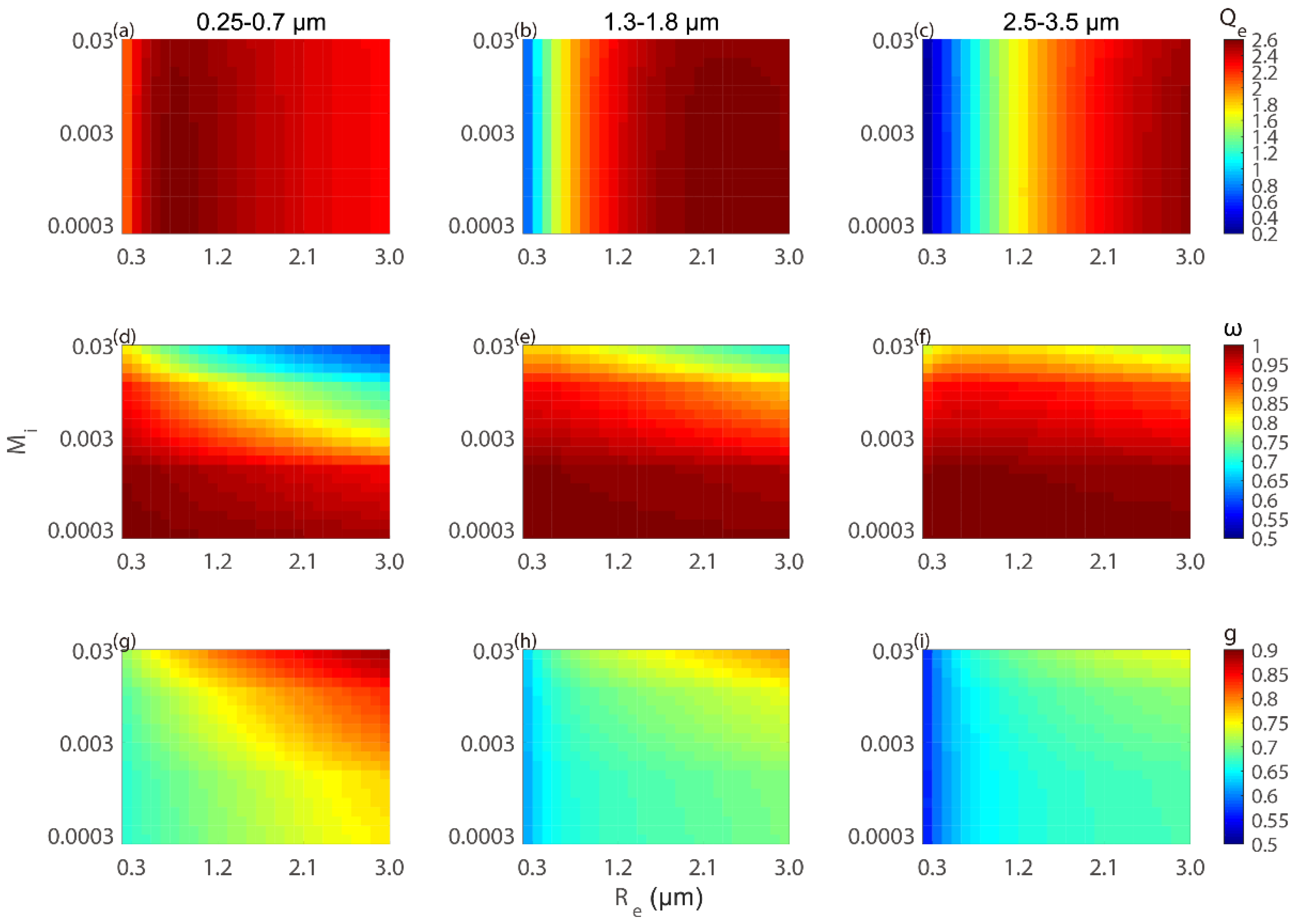
3.1. Description of Parameterization
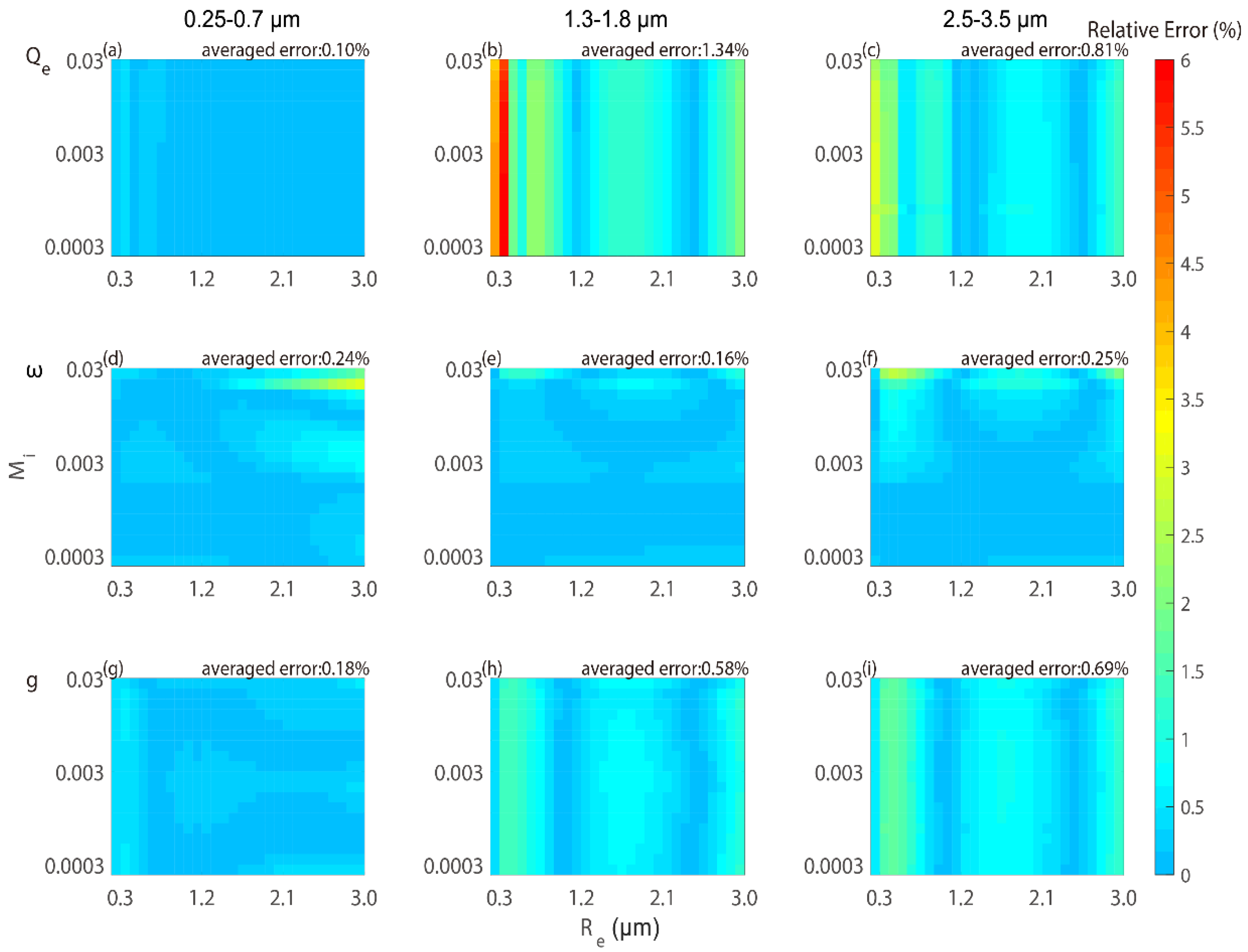
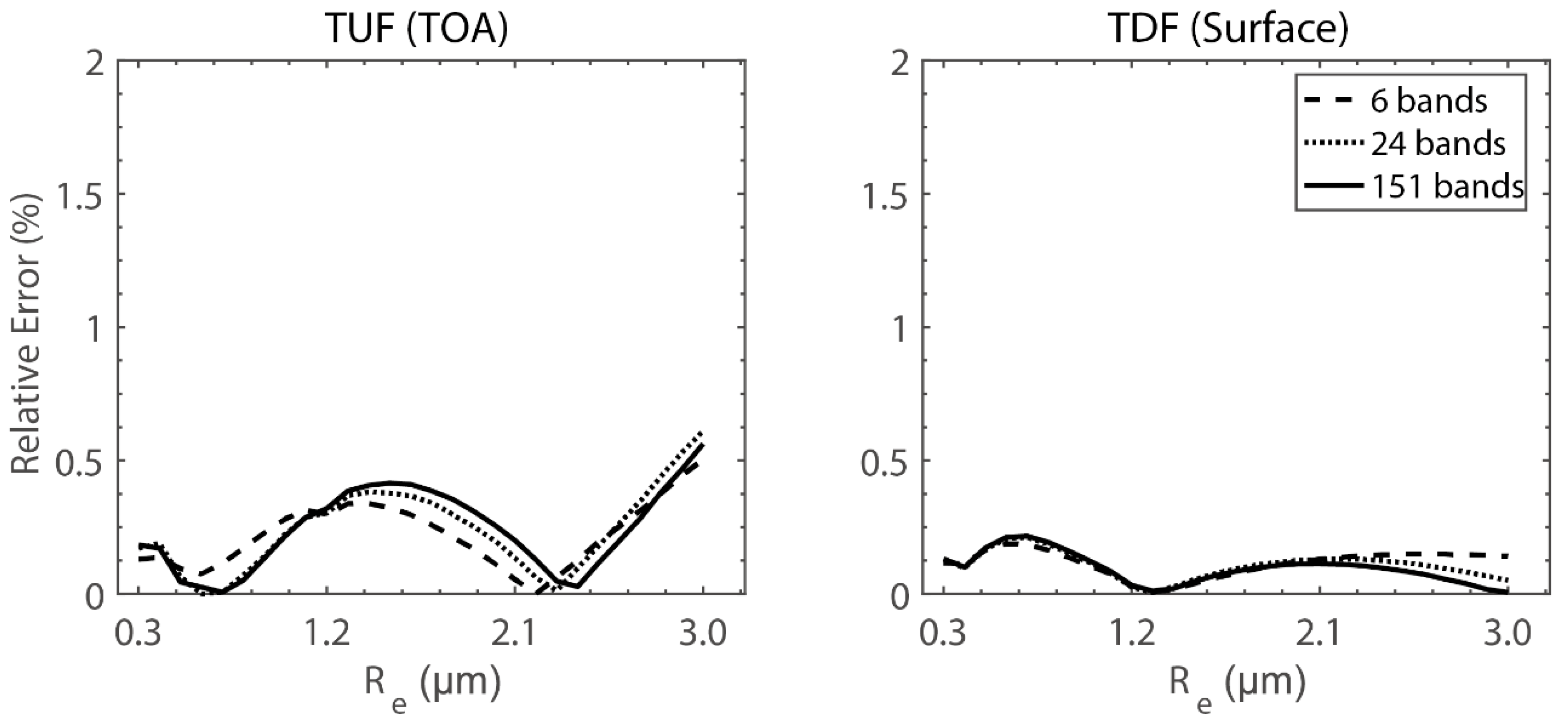
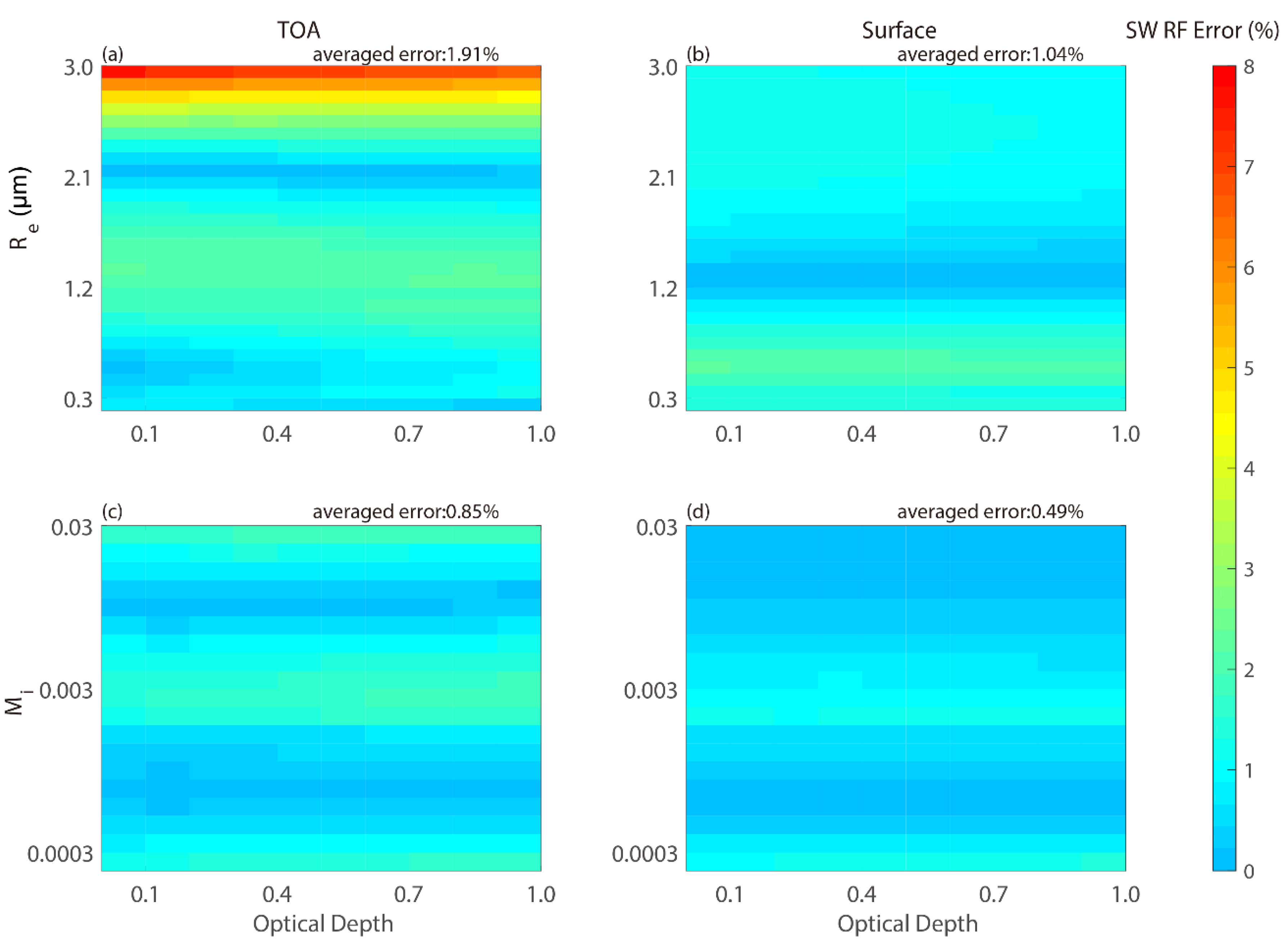
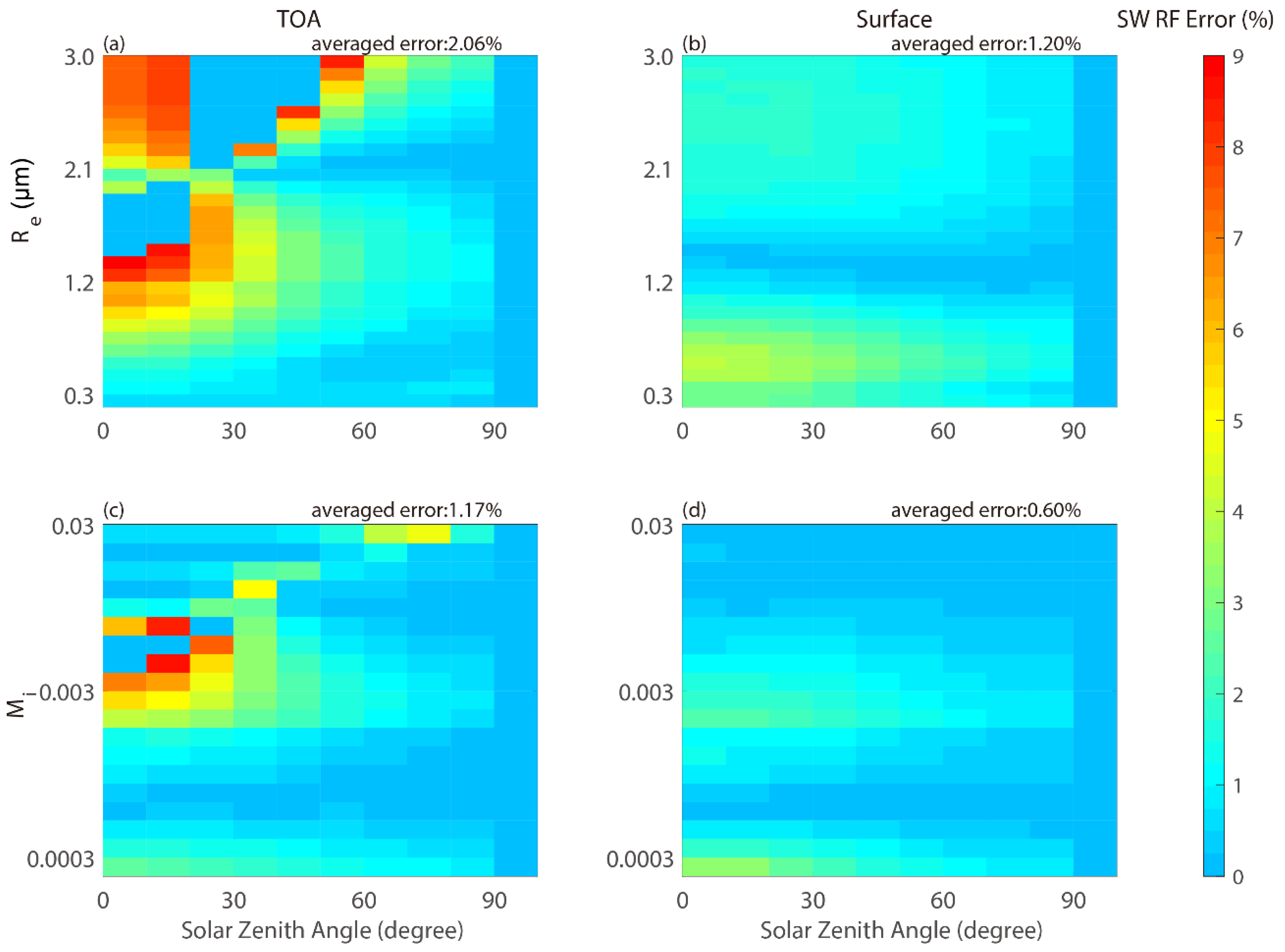
3.2. Evaluation of the Present Parameterization
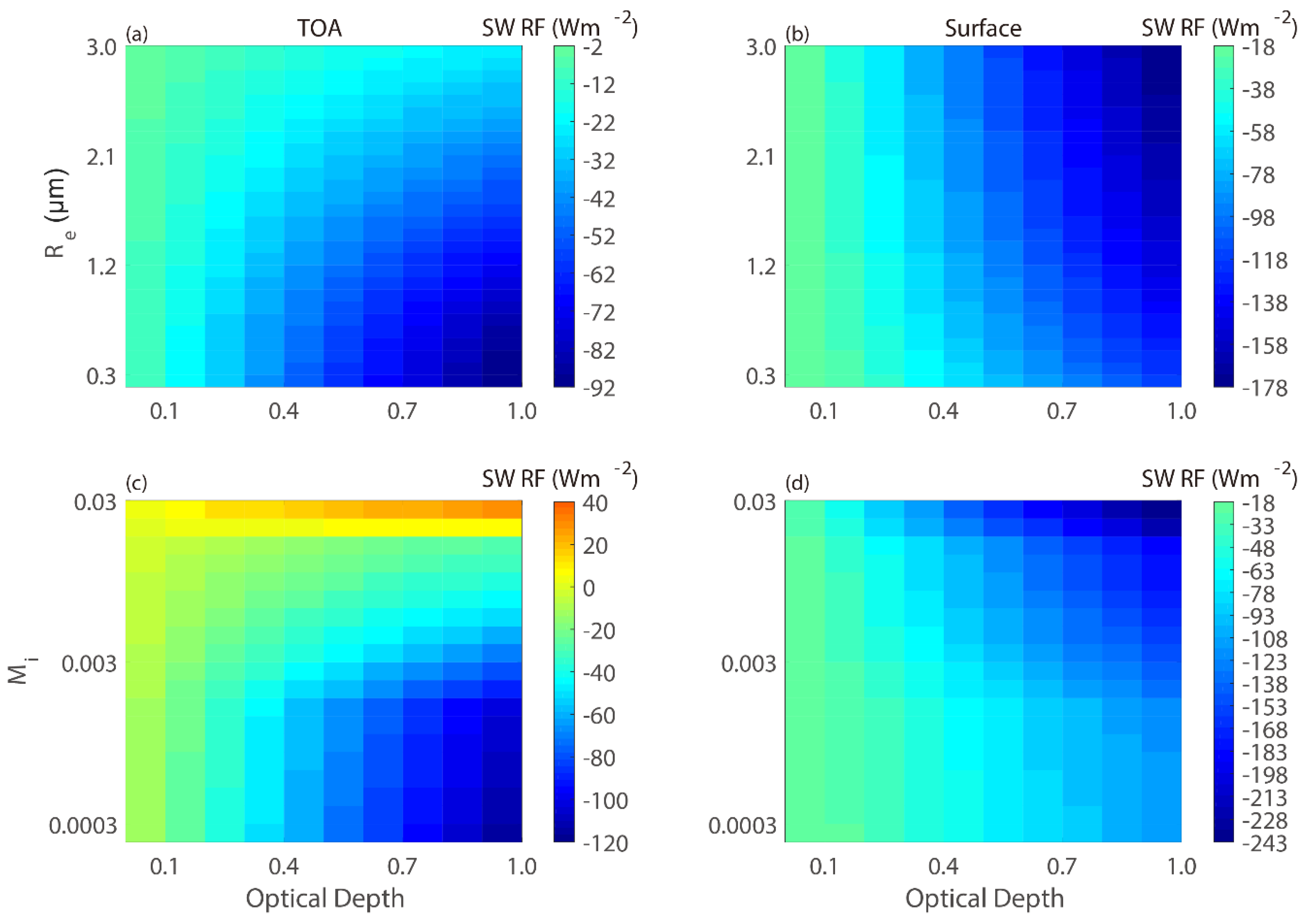
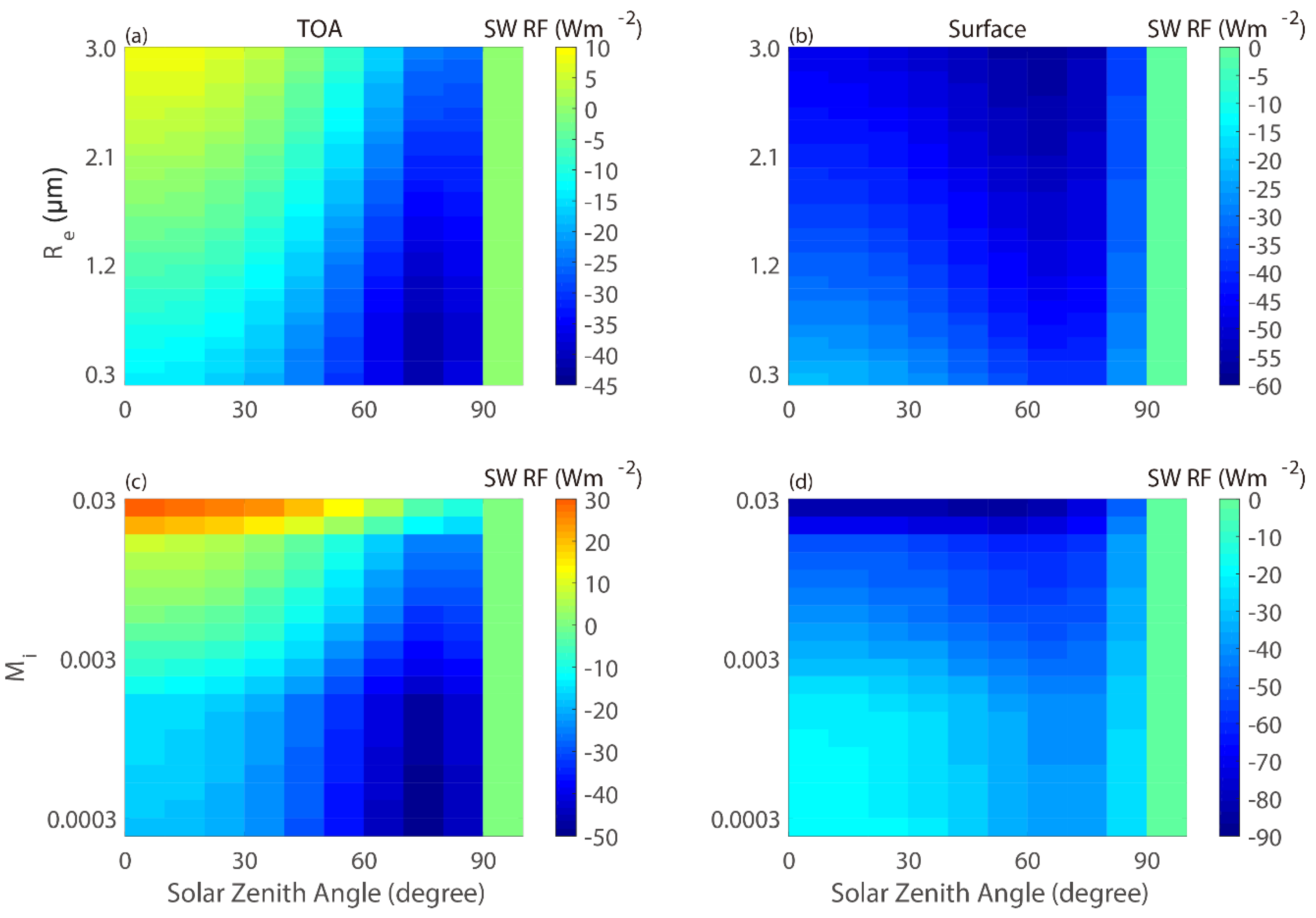
4. Physics of Dust Aerosol Radiative Forcing
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Charlson, R.J.; Heintzenberg, J. Aerosol Forcing of Climate; Wiley Chichester: New York, NY, USA, 1995. [Google Scholar]
- Houghton, J.T.; Meiro Filho, L.G.; Callander, B.A.; Harris, N.; Kattenburg, A.; Maske, K. Climate change 1995: The science of climate change. Clim. Chang. 1996, 584, 163–168. [Google Scholar]
- Ge, J.M.; Huang, J.P.; Xu, C.P.; Qi, Y.L.; Liu, H.Y. Characteristics of Taklimakan dust emission and distribution: A satellite and reanalysis field perspective. J. Geophys. Res. Atmos. 2014, 119, 11772–11783. [Google Scholar] [CrossRef]
- Tegen, I. Modeling the mineral dust aerosol cycle in the climate system. Sci. Rev. 2003, 22, 1821–1834. [Google Scholar] [CrossRef]
- Slingo, A.; Ackerman, T.P.; Allan, R.P.; Kassianov, E.I.; McFarlane, S.A. Observations of the impact of a major Saharan dust storm on the atmospheric radiation balance. Geophys. Res. Lett. 2006, 33, L24817. [Google Scholar] [CrossRef]
- Wu, L.; Su, H.; Jiang, J.H. Regional simulation of aerosol impacts on precipitation during the East Asian summer monsoon. J. Geophys. Res. Atmos. 2013, 118, 6454–6467. [Google Scholar] [CrossRef]
- Xu, X.; Wang, J. Retrieval of aerosol microphysical properties from AERONET photopolarimetric measurements: 1. Information content analysis. J. Geophys. Res. Atmos. 2015, 120, 7059–7078. [Google Scholar] [CrossRef]
- Sokolik, I.N.; Toon, O.B. Direct radiative forcing by anthropogenic airborne mineral aerosols. Nature 1996, 381, 681–683. [Google Scholar] [CrossRef]
- Tegen, I.; Hollrig, P.; Chin, M.; Fung, I.; Jacob, D.; Penner, J. Contribution of different aerosol species to the global aerosol extinction optical thickness: Estimates from model results. J. Geophys. Res. Atmos. 1997, 102, 23895–23915. [Google Scholar] [CrossRef]
- Miller, R.L.; Tegen, I. Climate response to soil dust aerosols. J. Climat. 1998, 11, 3247–3267. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Radiative forcing and climate response. J. Geophys. Res. Atmos. 1997, 102, 6831–6864. [Google Scholar] [CrossRef]
- Jacobson, M.Z. Global direct radiative forcing due to multicomponent anthropogenic and natural aerosols. J. Geophys. Res. Atmos. 2001, 106, 1551–1568. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Q.B.; Gu, Y.; Liou, K.N.; Meland, B. Dust vertical profile impact on global radiative forcing estimation using a coupled chemical-transport-radiative-transfer model. Atmos. Chem. Phys. 2013, 13, 7097–7114. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.N.; Lapyonok, T.; Sinyuk, A.; Mishchenko, M.I.; Yang, P.; Slutsker, I. Non-spherical aerosol retrieval method employing light scattering by spheroids. Geophys. Res. Lett. 2002, 29, 1415. [Google Scholar] [CrossRef]
- Okada, K.; Heintzenberg, J.; Kai, K.J.; Qin, Y. Shape of atmospheric mineral particles collected in three Chinese arid-regions. Geophys. Res. Lett. 2001, 28, 3123–3126. [Google Scholar] [CrossRef]
- Munoz, O.; Volten, H.; de Haan, J.F.; Vassen, W.; Hovenier, J.W. Experimental determination of scattering matrices of randomly oriented fly ash and clay particles at 442 and 633 nm. J. Geophys. Res. Atmos. 2001, 106, 22833–22844. [Google Scholar] [CrossRef]
- Kalashnikova, O.V.; Sokolik, I.N. Modeling the radiative properties of nonspherical soil-derived mineral aerosols. J. Quant. Spectrosc. Radiat. 2004, 87, 137–166. [Google Scholar] [CrossRef]
- Heintzenberg, J. Particle size distributions from scattering measurements of nonspherical particles via Mie-theory. Beitr. Phys. Atmos. 1998, 51, 91–99. [Google Scholar]
- Volten, H.; Munoz, O.; Rol, E.; de Haan, J.F.; Vassen, W. Scattering matrices of mineral aerosol particles at 441.6 nm and 632.8 nm. J. Geophys. Res. Atmos. 2001, 106, 17375–17401. [Google Scholar] [CrossRef]
- Herman, M.; Deuze, J.L.; Marchand, A.; Roger, B.; Lallart, P. Aerosol remote sensing from POLDER/ADEOS over the ocean: Improved retrieval using a nonspherical particle model. J. Geophys. Res. Atmos. 2005, 110, D10S02. [Google Scholar] [CrossRef]
- Kalashnikova, O.V.; Kahn, R.; Sokolik, I.N.; Li, W.H. Ability of multiangle remote sensing observations to identify and distinguish mineral dust types: Optical models and retrievals of optically thick plumes. J. Geophys. Res. Atmos. 2005, 110, D18S14. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Hovenier, J.W.; Travis, L.D. Light Scattering by Nonspherical Particles; Elsevier: New York, NY, USA, 2000. [Google Scholar]
- Kahn, R.; West, R.; McDonald, D.; Rheingans, B.; Mishchenko, M.I. Sensitivity of multiangle remote sensing observations to aerosol sphericity. J. Geophys. Res. Atmos. 1997, 102, 16861–16870. [Google Scholar] [CrossRef]
- Krotkov, N.A.; Flittner, D.E.; Krueger, A.J.; Kostinski, A.; Riley, C.; Rose, W.; Torres, O. Effect of particle non-sphericity on satellite monitoring of drifting volcanic ash clouds. J. Quant. Spectrosc. Radiat. 1999, 63, 613–630. [Google Scholar] [CrossRef]
- Liu, Y.G.; Arnott, W.P.; Hallett, J. Particle size distribution retrieval from multispectral optical depth: Influences of particle nonsphericity and refractive index. J. Geophys. Res. Atmos. 1999, 104, 31753–31762. [Google Scholar] [CrossRef]
- Dubovik, O.; Holben, B.; Eck, T.F.; Smirnov, A.; Kaufman, Y.J.; King, M.D.; Tanré, D.; Slutsker, I. Variability of absorption and optical properties of key aerosol types observed in worldwide locations. J. Atmos. Sci. 2002, 59, 590–608. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Geogdzhayev, I.V.; Liu, L.; Ogren, J.A.; Lacis, A.A.; Rossow, W.B.; Hovenier, J.W.; Volten, H.; Muñoz, O. Aerosol retrievals from AVHRR radiances: Effects of particle nonsphericity and absorption and an updated long-term global climatology of aerosol properties. J. Quant. Spectrosc. Radiat. 2003, 79, 953–972. [Google Scholar] [CrossRef]
- D’Almeida, G.A.; Koepke, P.; Shettle, E.P. Atmospheric Aerosols: Global Climatology and Radiative Characteristics; A Deepak Publishing: Hampton, VA, USA, 1991. [Google Scholar]
- Tegen, I.; Lacis, A.A. Modeling of particle size distribution and its influence on the radiative properties of mineral dust aerosol. J. Geophys. Res. Atmos. 1996, 101, 19237–19244. [Google Scholar] [CrossRef]
- Levoni, C.; Cervino, M.; Guzzi, R.; Torricella, F. Atmospheric aerosol optical properties: A database of radiative characteristics for different components and classes. Appl. Opt. 1997, 36, 8031–8041. [Google Scholar] [CrossRef] [PubMed]
- Collins, W.D.; Rasch, P.J.; Eaton, B.E.; Fillmore, D.W.; Kiehl, J.T.; Beck, C.T.; Zender, C.S. Simulation of aerosol distributions and radiative forcing for INDOEX: Regional climate impacts. J. Geophys. Res. Atmos. 2002, 107, 8028. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D.; Kahn, R.A.; West, R.A. Modeling phase functions for dustlike tropospheric aerosols using a shape mixture of randomly oriented polydisperse spheroids. J. Geophys. Res. Atmos. 1997, 102, 16831–16847. [Google Scholar] [CrossRef]
- Dubovik, O.; King, M.D. A flexible inversion algorithm for retrieval of aerosol optical properties from sun and sky radiance measurements. J. Geophys. Res. 2000, 105, 673–696. [Google Scholar] [CrossRef]
- Dubovik, O.; Sinyuk, A.; Lapyonok, T.; Holben, B.N.; Mishchenko, M. Application of spheroid models to account for aerosol particle nonsphericity in remote sensing of desert dust. J. Geophys. Res. Atmos. 2006, 111, D11208. [Google Scholar] [CrossRef]
- Feng, Q.; Yang, P.; Kattawar, G.W.; Hsu, C.N.; Tsay, S.-C.; Laszlo, I. Effects of particle nonsphericity and radiation polarization on retrieving dust properties from MODIS observations. J. Aerosol Sci. 2009, 40, 776–789. [Google Scholar] [CrossRef]
- Kanaya, Y.; Kajii, Y.; Akimoto, H. Solar actinic flux and photolysis frequency determinations by radiometers and a radiative transfer model at Rishiri Island: Comparisons, cloud effects, and detection of an aerosol plume from Russian forest fires. Atmos. Environ. 2003, 37, 2463–2475. [Google Scholar] [CrossRef]
- Mishchenko, M.I.; Travis, L.D. Light scattering by polydispersions of randomly oriented spheroids with sizes comparable to wavelengths of observatio. Appl. Opt. 1994, 33, 7206–7225. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, T.; Tanaka, M.; Yamano, M.; Shiobara, M.; Arao, K.; Nakanishi, Y. Aerosol optical characteristics in the yellow sand events observed in May, 1982 at Nagasaki-Part II Models. J. Meteorol. Soc. Jpn. Ser. 1989, 67, 279–291. [Google Scholar] [CrossRef]
- Yang, P.; Feng, Q.; Hong, G.; Kattawar, G.W.; Wiscombe, W.J. Modeling of the scattering and radiative properties of nonspherical dust-like aerosols. J. Aerosol Sci. 2007, 38, 995–1014. [Google Scholar] [CrossRef]
- Fu, Q.; Thorsen, T.J.; Su, J.; Ge, J.M.; Huang, J.P. Test of Mie-based single-scattering properties of non-spherical dust aerosols in radiative flux calculations. J. Quant. Spectrosc. Radiat. 2009, 110, 1640–1653. [Google Scholar] [CrossRef]
- Fu, Q.; Liou, K.N. Parameterization of the radiative properties of cirrus clouds. J. Atmos. Sci. 1993, 50, 2008–2025. [Google Scholar] [CrossRef]
- Fu, Q.A. An accurate parameterization of the solar radiative properties of cirrus clouds for climate models. J. Climat. 1996, 9, 2058–2082. [Google Scholar] [CrossRef]
- Vouk, V. Projected area of convex bodies. Nature 1948, 162, 330–331. [Google Scholar] [CrossRef]
- Neshyba, S.P.; Grenfell, T.C.; Warren, S.G. Representation of a nonspherical ice particle by a collection of independent spheres for scattering and absorption of radiation: 2. Hexagonal columns and plates. J. Geophys. Res. Atmos. 2003, 108, 4448. [Google Scholar] [CrossRef]
- Yi, B.; Hsu, C.N.; Yang, P.; Tsay, S.-C. Radiative transfer simulation of dust-like aerosols: Uncertainties from particle shape and refractive index. J. Aerosol Sci. 2011, 42, 631–644. [Google Scholar] [CrossRef]
- Haapanala, P.; Raisanen, P.; Kahnert, M.; Nousiainen, T. Sensitivity of the shortwave radiative effect of dust on particle shape: Comparison of spheres and spheroids. J. Geophys. Res. Atmos. 2012, 117, D08201. [Google Scholar] [CrossRef]
- Raisanen, P.; Haapanala, P.; Chung, C.E.; Kahnert, M.; Makkonen, R.; Tonttila, J.; Nousiainen, T. Impact of dust particle non-sphericity on climate simulations. Q. J. R. Meteorol. Soc. 2013, 139, 2222–2232. [Google Scholar] [CrossRef]
- Shettle, E.P.; Fenn, R.W. Models of aerosols of lower troposphere and the effect of humidity variations on their optical properties. AFCRL Tech. Rep. 1979, 79, 0214. [Google Scholar]
- WMO. Radiation commission of IAMAP meeting of experts on aerosol and their climatic effects. World Meteorol. Organ. Rep. 1983, WCP55, 28–30. [Google Scholar]
- Koepke, P.; Hess, M.; Schult, I.; Shettle, E.P. Global aerosol data set. MPI Meteorol. Hambg. Rep. 1997, 243, 44. [Google Scholar]
- Carlson, T.N.; Benjamin, S.G. Rradiative heating rates for saharan dust. J. Atmos. Sci. 1980, 37, 193–213. [Google Scholar] [CrossRef]
- Mogo, S.; Cachorro, V.E.; de Frutos, A.M. In situ UV-VIS-NIR absorbing properties of atmospheric aerosol particles: Estimates of the imaginary refractive index and comparison with columnar values. J. Environ. Manag. 2012, 111, 267–271. [Google Scholar] [CrossRef]
- Di Biagio, C.; Boucher, H.; Caquineau, S.; Chevaillier, S.; Cuesta, J.; Formenti, P. Variability of the infrared complex refractive index of African mineral dust: Experimental estimation and implications for radiative transfer and satellite remote sensing. Atmos. Chem. Phys. 2014, 14, 11093–11116. [Google Scholar] [CrossRef]
- Nakajima, T.; Tonna, G.; Rao, R.Z.; Boi, P.; Kaufman, Y.; Holben, B. Use of sky brightness measurements from ground for remote sensing of particulate polydispersions. Appl. Opt. 1996, 35, 2672–2686. [Google Scholar] [CrossRef] [PubMed]
- Hansen, J.E.; Travis, L.D. Light scattering in planetary atmospheres. Space Sci. Rev. 1974, 16, 527–610. [Google Scholar] [CrossRef]
- Ricchiazzi, P.; Yang, S.R.; Gautier, C.; Sowle, D. SBDART: A research and teaching software tool for plane-parallell radiative transfer in the Earth’s atmosphere. Bull. Am. Meteorol. Soc. 1998, 79, 2101–2114. [Google Scholar] [CrossRef]
- Liou, K.N. An Introduction to Atmospheric Radiation, 2nd ed.; China Meteorological Press: Beijing, China, 2004; Volume 10, p. 104. [Google Scholar]
- Slingo, A.; Schrecker, H.M. On the shortwave radiative properties of stratiform water clouds. Q. J. R. Meteorol. Soc. 1982, 108, 407–426. [Google Scholar] [CrossRef]
- Li, J.; Ma, X.; von Salzen, K.; Dobbie, S. Parameterization of sea-salt optical properties and physics of the associated radiative forcing. Atmos. Chem. Phys. 2008, 8, 4787–4798. [Google Scholar] [CrossRef]
- Alizadeh-Choobari, O.; Sturman, A.; Zawar-Reza, P. A global satellite view of the seasonal distribution of mineral dust and its correlation with atmospheric circulation. Dyn. Atmos. Ocean. 2014, 68, 20–34. [Google Scholar] [CrossRef]
- Shao, J.; Mao, J. Dust Particle Size Distributions during Spring in Yinchuan, China. Adv. Meteorol. 2016, 2016, 6940502. [Google Scholar] [CrossRef]
- Jeffrey, S.R.; Halflidi, H.J.; Hal, B.M.; Alexander, S. Comparison of size and morphological measurements of coarse mode dust particles from Africa. J. Geophys. Res. Atmos. 2003, 108, 8593. [Google Scholar]
| Band Limit (um) | A0 | A1 | A2 | A3 | A4 | Fraction of Sλ | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a00(×100) | a01(×10−2) | a10(×10−2) | a11(×10−1) | a20(×10−1) | a21(×10−3) | a30(×10−2) | a31(×10−3) | a40(×10−4) | a41(×10−3) | ||
| 0.25–0.3 | 2.001 | 5.605 | 54.63 | −2.060 | −1.405 | −495.0 | 1.150 | 184.5 | −1.652 | −17.70 | 0.0034 |
| 0.3–0.35 | 1.993 | 17.42 | 69.94 | −5.724 | −2.468 | −352.4 | 3.204 | 180.1 | −15.73 | −19.06 | 0.0215 |
| 0.35–0.375 | 1.983 | 24.31 | 79.84 | −8.669 | −3.251 | −183.5 | 4.925 | 152.0 | −28.83 | −17.55 | 0.0216 |
| 0.375–0.4 | 1.976 | 31.84 | 87.36 | −11.48 | −3.892 | −1.087 | 6.435 | 113.9 | −40.87 | −14.82 | 0.0188 |
| 0.4–0.425 | 1.970 | 35.51 | 94.65 | −14.19 | −4.553 | 195.9 | 8.057 | 69.16 | −54.19 | −11.38 | 0.0301 |
| 0.425–0.475 | 1.963 | 44.66 | 105.2 | −17.76 | −5.576 | 458.6 | 10.69 | 8.730 | −76.39 | −6.718 | 0.0701 |
| 0.475–0.5 | 1.958 | 52.84 | 114.5 | −22.62 | −6.552 | 851.3 | 13.30 | −93.00 | −99.03 | 1.984 | 0.0375 |
| 0.5–0.575 | 1.958 | 60.90 | 125.2 | −26.79 | −7.801 | 1214 | 16.81 | −188.6 | −130.3 | 10.15 | 0.1059 |
| 0.575–0.625 | 1.965 | 68.42 | 136.2 | −32.08 | −9.256 | 1711 | 21.10 | −327.4 | −169.4 | 22.52 | 0.0662 |
| 0.625–0.7 | 1.980 | 73.83 | 143.7 | −37.06 | −10.51 | 2217 | 25.04 | −476.2 | −206.4 | 36.24 | 0.0868 |
| 0.7–0.75 | 2.003 | 74.50 | 148.2 | −40.70 | −11.58 | 2641 | 28.58 | −607.5 | −240.7 | 48.66 | 0.0506 |
| 0.75–0.8 | 2.027 | 74.86 | 149.5 | −42.93 | −12.26 | 2926 | 31.01 | −698.9 | −264.8 | 57.48 | 0.0451 |
| 0.8–0.875 | 2.062 | 72.46 | 148.4 | −44.80 | −12.91 | 3215 | 33.51 | −796.6 | −290.5 | 67.12 | 0.0587 |
| 0.875–1 | 2.128 | 64.34 | 141.7 | −46.50 | −13.52 | 3586 | 36.42 | −931.4 | −322.2 | 80.89 | 0.0778 |
| 1–1.1 | 2.217 | 48.19 | 127.6 | −45.93 | −13.68 | 3813 | 38.34 | −1032 | −346.1 | 91.94 | 0.0505 |
| 1.1–1.2 | 2.301 | 29.66 | 110.6 | −43.73 | −13.39 | 3868 | 38.78 | −1081 | −355.7 | 98.02 | 0.0413 |
| 1.2–1.3 | 2.389 | 11.89 | 90.34 | −40.69 | −12.76 | 3827 | 38.23 | −1099 | −356.3 | 101.2 | 0.0347 |
| 1.3–1.55 | 2.538 | −24.49 | 51.53 | −33.04 | −11.12 | 3518 | 35.43 | −1058 | −339.1 | 99.80 | 0.0646 |
| 1.55–1.65 | 2.697 | −66.61 | 5.358 | −23.00 | −8.814 | 2999 | 30.74 | −955.5 | −304.4 | 92.60 | 0.0187 |
| 1.65–2.15 | 2.901 | −121.8 | −62.08 | −7.506 | −4.899 | 2033 | 21.68 | −726.2 | −230.4 | 73.73 | 0.0548 |
| 2.15–2.425 | 3.177 | −196.9 | −165.2 | 16.29 | 1.661 | 395.5 | 5.481 | −307.1 | −92.11 | 37.39 | 0.0136 |
| 2.425–2.925 | 3.347 | −244.2 | −242.9 | 33.46 | 7.082 | −911.0 | −8.691 | 49.76 | 33.21 | 5.116 | 0.0146 |
| 2.925–3.425 | 3.498 | −289.0 | −330.6 | 53.56 | 13.61 | −2541 | −26.36 | 511.2 | 192.8 | −37.53 | 0.0077 |
| 3.425–4 | 3.567 | −308.9 | −399.2 | 67.14 | 19.10 | −3763 | −41.78 | 874.5 | 334.8 | −72.00 | 0.0054 |
| 0.25–0.7 | 1.970 | 55.45 | 119.2 | −25.15 | −7.424 | 1142 | 16.12 | −182.1 | −125.9 | 10.32 | 0.4879 |
| 0.7–1.3 | 2.163 | 54.27 | 131.8 | −44.15 | −13.02 | 3469 | 35.46 | −910.0 | −315.5 | 79.56 | 0.3408 |
| 1.3–1.8 | 2.643 | −52.30 | 20.39 | −26.21 | −9.520 | 3152 | 32.10 | −982.7 | −313.9 | 94.28 | 0.1010 |
| 1.8–2.5 | 3.066 | −166.8 | −122.7 | 6.446 | −1.085 | 1085 | 12.33 | −485.4 | −150.9 | 52.96 | 0.0465 |
| 2.5–3.5 | 3.432 | −269.1 | −291.8 | 44.62 | 10.71 | −1814 | −18.52 | 305.1 | 121.8 | −18.46 | 0.0195 |
| 3.5–4.0 | 3.571 | −310.7 | −405.6 | 68.45 | 19.63 | −3885 | −43.29 | 911.1 | 348.8 | −75.50 | 0.0043 |
| Band Limit (um) | B0 | B1 | B2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| b00(×10−1) | b01(×10−2) | b02(×100) | b10(×10−4) | b11(×10−1) | b12(×10−2) | b20(×10−5) | b21(×10−2) | b22(×10−1) | |
| 0.25–0.3 | 10.01 | 91.27 | −35.22 | 181.7 | −120.0 | 10200 | −1127 | 204.4 | −103.7 |
| 0.3–0.35 | 10.00 | 78.23 | −30.72 | 177.4 | −103.1 | 8069 | −932.8 | 146.9 | −41.53 |
| 0.35–0.375 | 9.998 | 66.86 | −28.14 | 170.1 | −93.76 | 6977 | −824.9 | 117.2 | −12.29 |
| 0.375–0.4 | 9.997 | 57.32 | −26.34 | 163.1 | −87.30 | 6259 | −748.4 | 97.56 | 5.807 |
| 0.4–0.425 | 9.997 | 47.63 | −24.69 | 155.9 | −81.40 | 5628 | −682.2 | 80.35 | 20.67 |
| 0.425–0.475 | 9.997 | 32.74 | −22.44 | 145.8 | −73.26 | 4798 | −591.8 | 57.42 | 38.97 |
| 0.475–0.5 | 9.998 | 19.31 | −20.59 | 134.4 | −66.38 | 4130 | −510.7 | 38.88 | 52.51 |
| 0.5–0.575 | 10.00 | 1.886 | −18.48 | 121.9 | −58.37 | 3404 | −425.6 | 18.74 | 65.06 |
| 0.575–0.625 | 10.00 | −17.56 | −16.36 | 107.8 | −49.88 | 2687 | −337.5 | −1.253 | 75.23 |
| 0.625–0.7 | 10.01 | −35.09 | −14.72 | 93.92 | −42.85 | 2146 | −262.5 | −16.46 | 80.77 |
| 0.7–0.75 | 10.01 | −50.73 | −13.44 | 82.08 | −36.88 | 1726 | −202.9 | −28.29 | 83.15 |
| 0.75–0.8 | 10.01 | −61.90 | −12.64 | 73.91 | −32.83 | 1466 | −164.3 | −35.61 | 83.37 |
| 0.8–0.875 | 10.01 | −74.20 | −11.88 | 65.86 | −28.57 | 1220 | −126.5 | −42.65 | 82.14 |
| 0.875–1 | 10.02 | −91.49 | −11.00 | 53.78 | −22.92 | 932.8 | −75.40 | −50.95 | 78.54 |
| 1–1.1 | 10.02 | −108.9 | −10.36 | 42.36 | −17.59 | 710.4 | −31.99 | −57.59 | 72.78 |
| 1.1–1.2 | 10.02 | −122.4 | −10.02 | 33.79 | −13.78 | 585.0 | −2.662 | −61.59 | 67.19 |
| 1.2–1.3 | 10.02 | −134.6 | −9.846 | 27.19 | −10.59 | 506.7 | 20.05 | −64.50 | 61.54 |
| 1.3–1.55 | 10.03 | −152.7 | −9.738 | 17.58 | −6.260 | 435.3 | 47.68 | −67.73 | 52.59 |
| 1.55–1.65 | 10.03 | −172.0 | −9.575 | 8.219 | −2.074 | 393.8 | 71.92 | −71.08 | 43.88 |
| 1.65–2.15 | 10.04 | −196.2 | −9.910 | −1.750 | 2.486 | 388.5 | 95.07 | −74.40 | 33.79 |
| 2.15–2.425 | 10.05 | −238.5 | −10.09 | −16.98 | 9.642 | 376.1 | 130.8 | −83.22 | 22.47 |
| 2.425–2.925 | 10.05 | −275.8 | −10.03 | −28.86 | 15.27 | 347.4 | 157.5 | −92.14 | 16.78 |
| 2.925–3.425 | 10.07 | −333.6 | −9.417 | −45.70 | 23.50 | 232.8 | 198.7 | −108.8 | 14.30 |
| 3.425–4 | 10.08 | −402.0 | −7.957 | −64.57 | 32.87 | −4.109 | 247.7 | −131.0 | 17.72 |
| 0.25–0.7 | 10.00 | 3.893 | −19.54 | 127.2 | −62.92 | 3937 | −485.8 | 32.85 | 51.78 |
| 0.7–1.3 | 10.02 | −90.53 | −11.20 | 55.66 | −24.16 | 1043 | −89.09 | −46.75 | 75.92 |
| 1.3–1.8 | 10.03 | −161.8 | −9.754 | 13.20 | −4.347 | 422.9 | 58.42 | −68.55 | 47.80 |
| 1.8–2.5 | 10.04 | −216.3 | −10.03 | −9.221 | 5.944 | 389.5 | 111.9 | −77.79 | 27.26 |
| 2.5–3.5 | 10.06 | −300.1 | −9.862 | −36.01 | 18.71 | 314.6 | 173.9 | −98.24 | 14.67 |
| 3.5–4.0 | 10.08 | −408.4 | −7.783 | −66.29 | 33.75 | −31.61 | 252.4 | −133.2 | 18.31 |
| Band Limit (um) | C0 | C1 | C2 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| c00(×10−2) | c01(×10−1) | c02(×10−1) | c10(×10−1) | c11(×10−1) | c12(×100) | c20(×10−2) | c21(×10−2) | c22(×10−2) | |
| 0.25–0.3 | 48.27 | −2.478 | −13.47 | 3.234 | −3.580 | 6.749 | −11.56 | 93.71 | −476.6 |
| 0.3–0.35 | 58.35 | 5.591 | −27.10 | 1.597 | −18.26 | 8.272 | −4.240 | 136.3 | −462.8 |
| 0.35–0.375 | 58.83 | 5.872 | −27.04 | 1.432 | −18.38 | 8.026 | −3.345 | 131.9 | −436.2 |
| 0.375–0.4 | 59.13 | 5.948 | −26.65 | 1.323 | −18.19 | 7.782 | −2.760 | 127.6 | −414.5 |
| 0.4–0.425 | 59.46 | 5.873 | −25.94 | 1.214 | −17.71 | 7.487 | −2.212 | 122.3 | −391.9 |
| 0.425–0.475 | 59.58 | 5.875 | −25.11 | 1.140 | −17.28 | 7.116 | −1.818 | 116.0 | −362.5 |
| 0.475–0.5 | 59.80 | 5.573 | −23.76 | 1.047 | −16.24 | 6.661 | −1.364 | 107.6 | −331.6 |
| 0.5–0.575 | 59.51 | 5.412 | −22.52 | 1.057 | −15.46 | 6.210 | −1.407 | 99.85 | −299.6 |
| 0.575–0.625 | 58.95 | 5.081 | −20.87 | 1.116 | −14.29 | 5.661 | −1.707 | 90.14 | −263.0 |
| 0.625–0.7 | 58.15 | 4.696 | −19.26 | 1.227 | −13.07 | 5.154 | −2.253 | 80.99 | −230.8 |
| 0.7–0.75 | 57.09 | 4.368 | −17.90 | 1.396 | −12.04 | 4.727 | −3.080 | 73.35 | −204.1 |
| 0.75–0.8 | 56.09 | 4.164 | −17.02 | 1.561 | −11.37 | 4.444 | −3.867 | 68.21 | −186.3 |
| 0.8–0.875 | 54.78 | 3.929 | −16.04 | 1.784 | −10.62 | 4.134 | −4.919 | 62.61 | −167.3 |
| 0.875–1 | 52.62 | 3.564 | −14.66 | 2.151 | −9.510 | 3.704 | −6.639 | 54.77 | −141.8 |
| 1–1.1 | 49.93 | 3.245 | −13.43 | 2.613 | −8.515 | 3.316 | −8.766 | 47.71 | −119.0 |
| 1.1–1.2 | 47.58 | 3.004 | −12.55 | 3.013 | −7.778 | 3.036 | −10.58 | 42.63 | −103.1 |
| 1.2–1.3 | 45.25 | 2.814 | −11.84 | 3.406 | −7.176 | 2.806 | −12.33 | 38.39 | −90.01 |
| 1.3–1.55 | 41.66 | 2.552 | −10.89 | 4.005 | −6.362 | 2.500 | −14.96 | 32.85 | −73.35 |
| 1.55–1.65 | 37.69 | 2.338 | −10.11 | 4.657 | −5.676 | 2.239 | −17.76 | 28.20 | −59.40 |
| 1.65–2.15 | 33.12 | 2.098 | −9.267 | 5.383 | −4.927 | 1.965 | −20.77 | 23.28 | −45.59 |
| 2.15–2.425 | 25.79 | 1.829 | −8.328 | 6.512 | −4.051 | 1.638 | −25.31 | 17.54 | −29.51 |
| 2.425–2.925 | 20.73 | 1.627 | −7.677 | 7.254 | −3.465 | 1.431 | −28.15 | 14.02 | −20.30 |
| 2.925–3.425 | 14.35 | 1.480 | −7.114 | 8.155 | −2.943 | 1.230 | −31.47 | 10.76 | −11.64 |
| 3.425–4 | 8.668 | 1.328 | −6.576 | 8.917 | −2.477 | 1.057 | −34.15 | 8.070 | −4.767 |
| 0.25–0.7 | 59.65 | 5.260 | −21.99 | 1.071 | −15.32 | 6.217 | −1.513 | 101.1 | −306.5 |
| 0.7–1.3 | 53.28 | 3.461 | −14.28 | 2.039 | −9.331 | 3.667 | −6.139 | 54.29 | −141.9 |
| 1.3–1.8 | 39.97 | 2.421 | −10.42 | 4.281 | −5.969 | 2.358 | −16.14 | 30.29 | −66.06 |
| 1.8–2.5 | 29.61 | 1.944 | −8.733 | 5.923 | −4.440 | 1.787 | −22.95 | 20.12 | −36.96 |
| 2.5–3.5 | 18.13 | 1.529 | −7.351 | 7.612 | −3.169 | 1.329 | −29.45 | 12.26 | −16.08 |
| 3.5–4.0 | 8.180 | 1.316 | −6.535 | 8.983 | −2.442 | 1.043 | −34.38 | 7.867 | −4.240 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Su, J.; Li, X.; Wang, C.; Ge, J. Parameterization of The Single-Scattering Properties of Dust Aerosols in Radiative Flux Calculations. Atmosphere 2019, 10, 728. https://doi.org/10.3390/atmos10120728
Wang M, Su J, Li X, Wang C, Ge J. Parameterization of The Single-Scattering Properties of Dust Aerosols in Radiative Flux Calculations. Atmosphere. 2019; 10(12):728. https://doi.org/10.3390/atmos10120728
Chicago/Turabian StyleWang, Meihua, Jing Su, Xugang Li, Chen Wang, and Jinming Ge. 2019. "Parameterization of The Single-Scattering Properties of Dust Aerosols in Radiative Flux Calculations" Atmosphere 10, no. 12: 728. https://doi.org/10.3390/atmos10120728
APA StyleWang, M., Su, J., Li, X., Wang, C., & Ge, J. (2019). Parameterization of The Single-Scattering Properties of Dust Aerosols in Radiative Flux Calculations. Atmosphere, 10(12), 728. https://doi.org/10.3390/atmos10120728




