Analysis of the Diurnal, Weekly, and Seasonal Cycles and Annual Trends in Atmospheric CO2 and CH4 at Tower Network in Siberia from 2005 to 2016
Abstract
1. Introduction
2. Method
2.1. Data
2.2. The Prophet Model
3. Results and Discussion
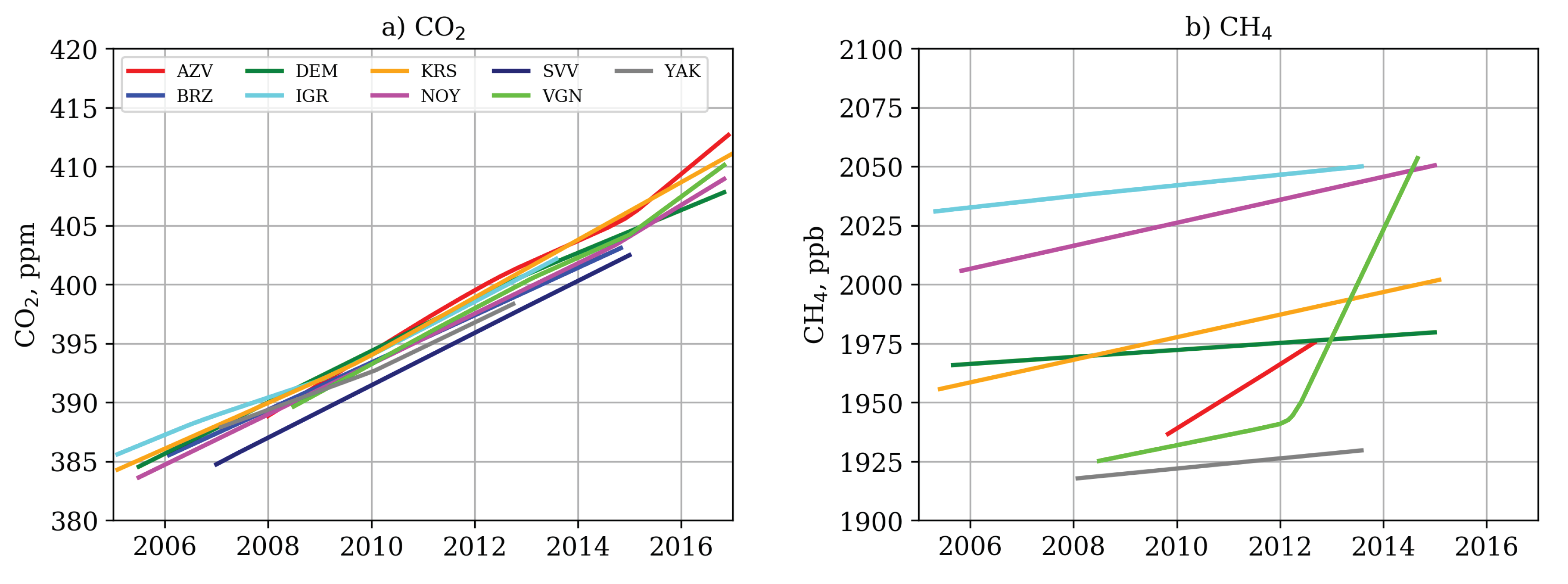
3.1. Trend
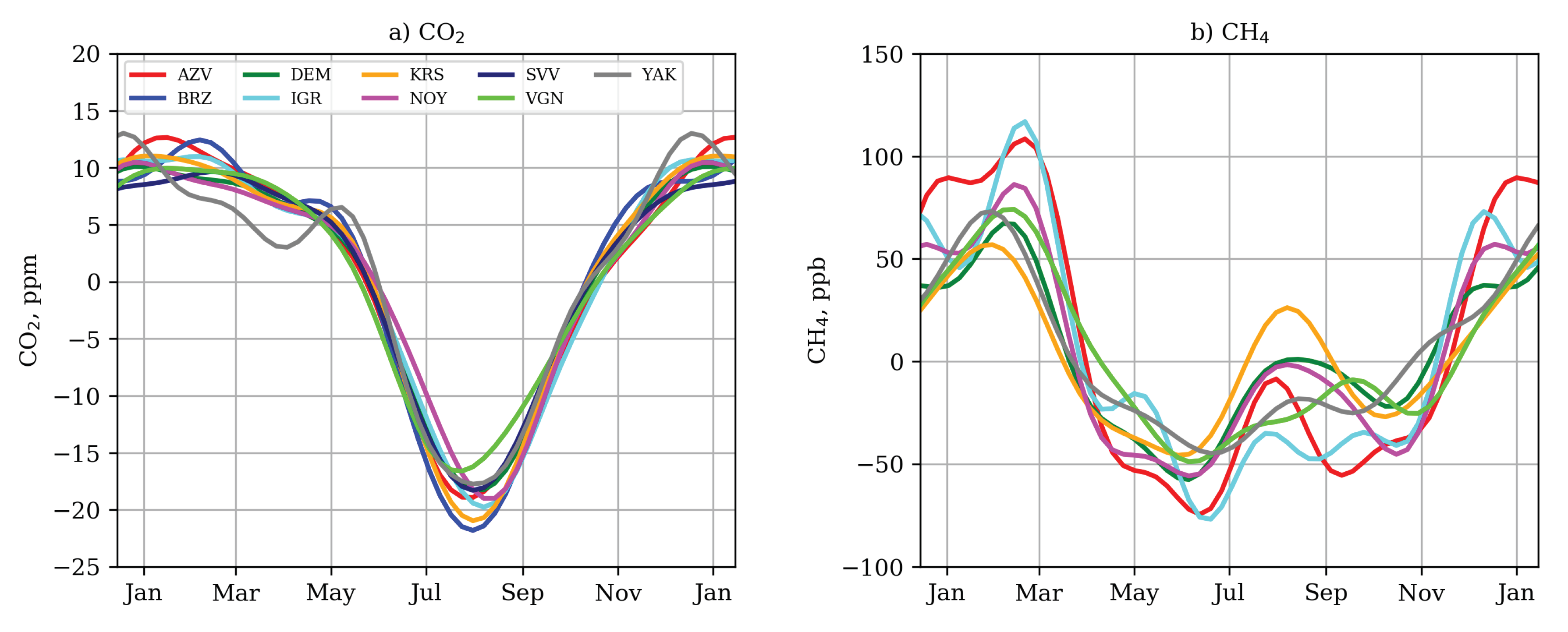
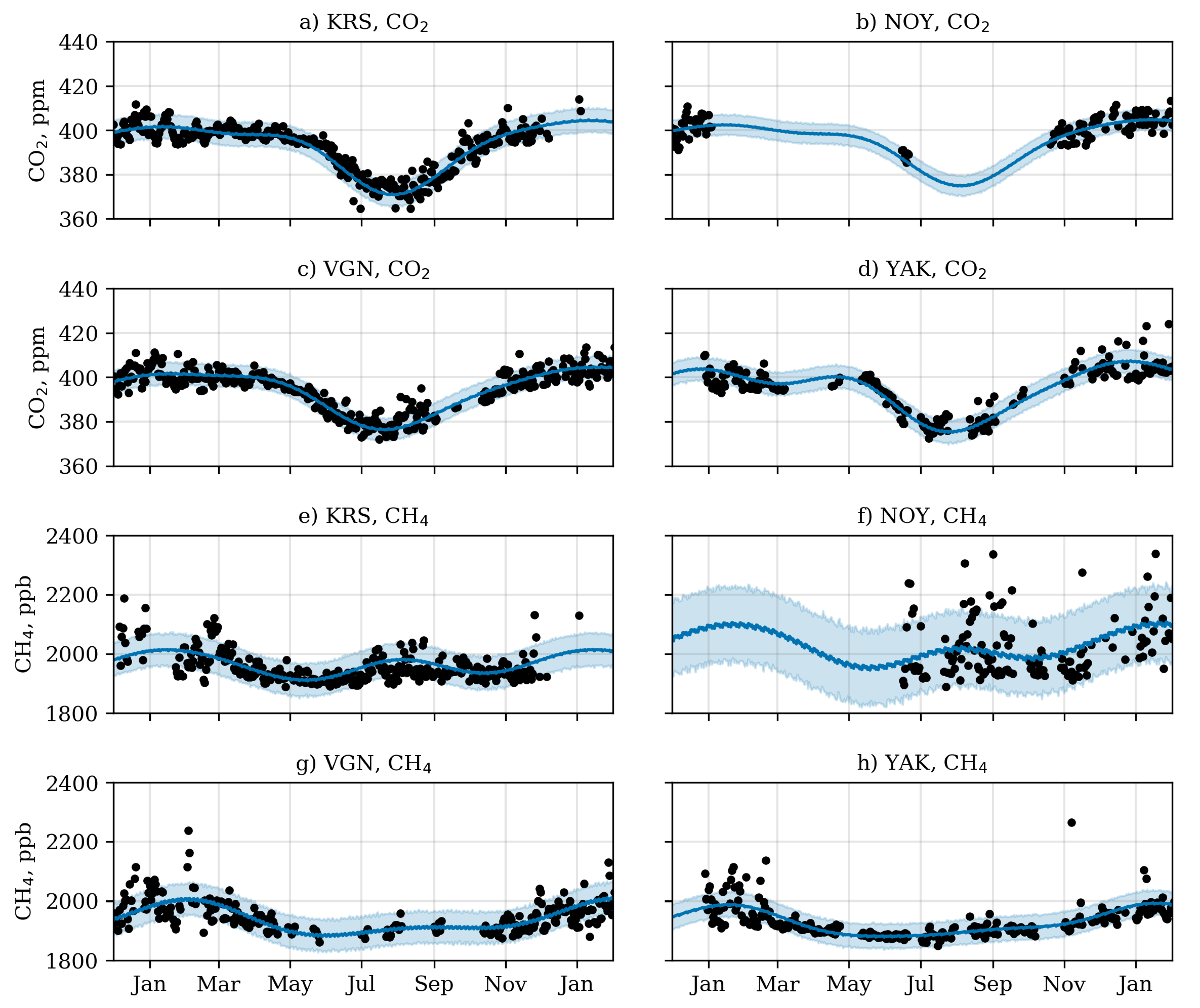
3.2. Seasonal Variation
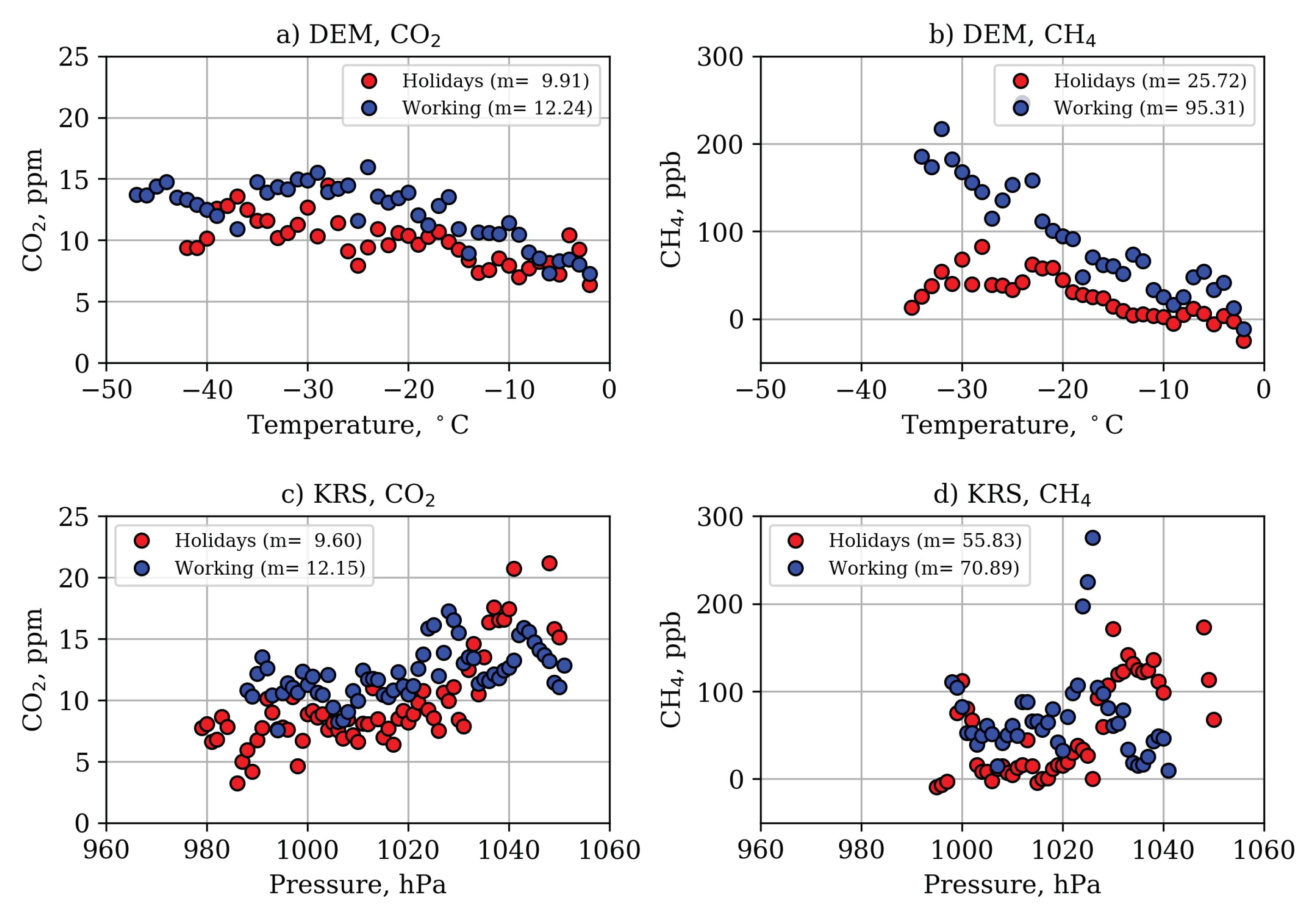
Case Study: Winter Vacation
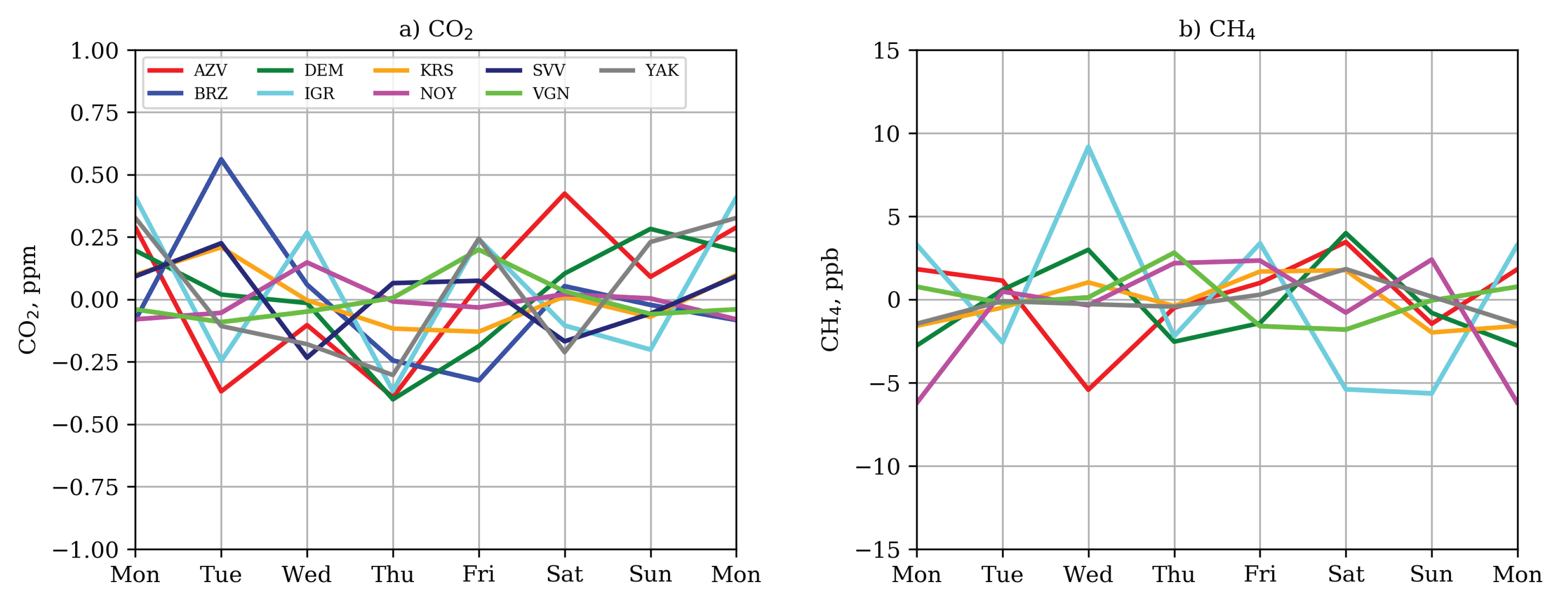
3.3. Weekly Variation
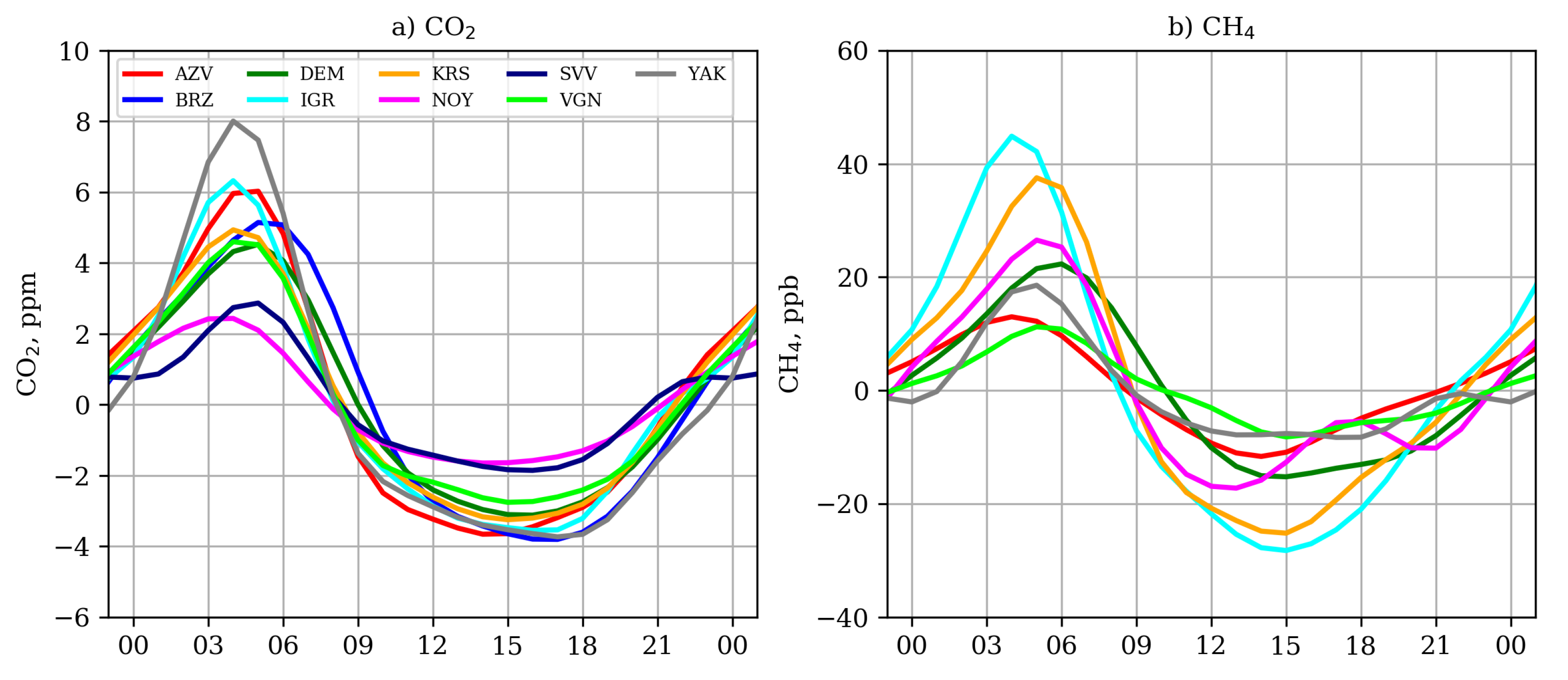
3.4. Daily Variation
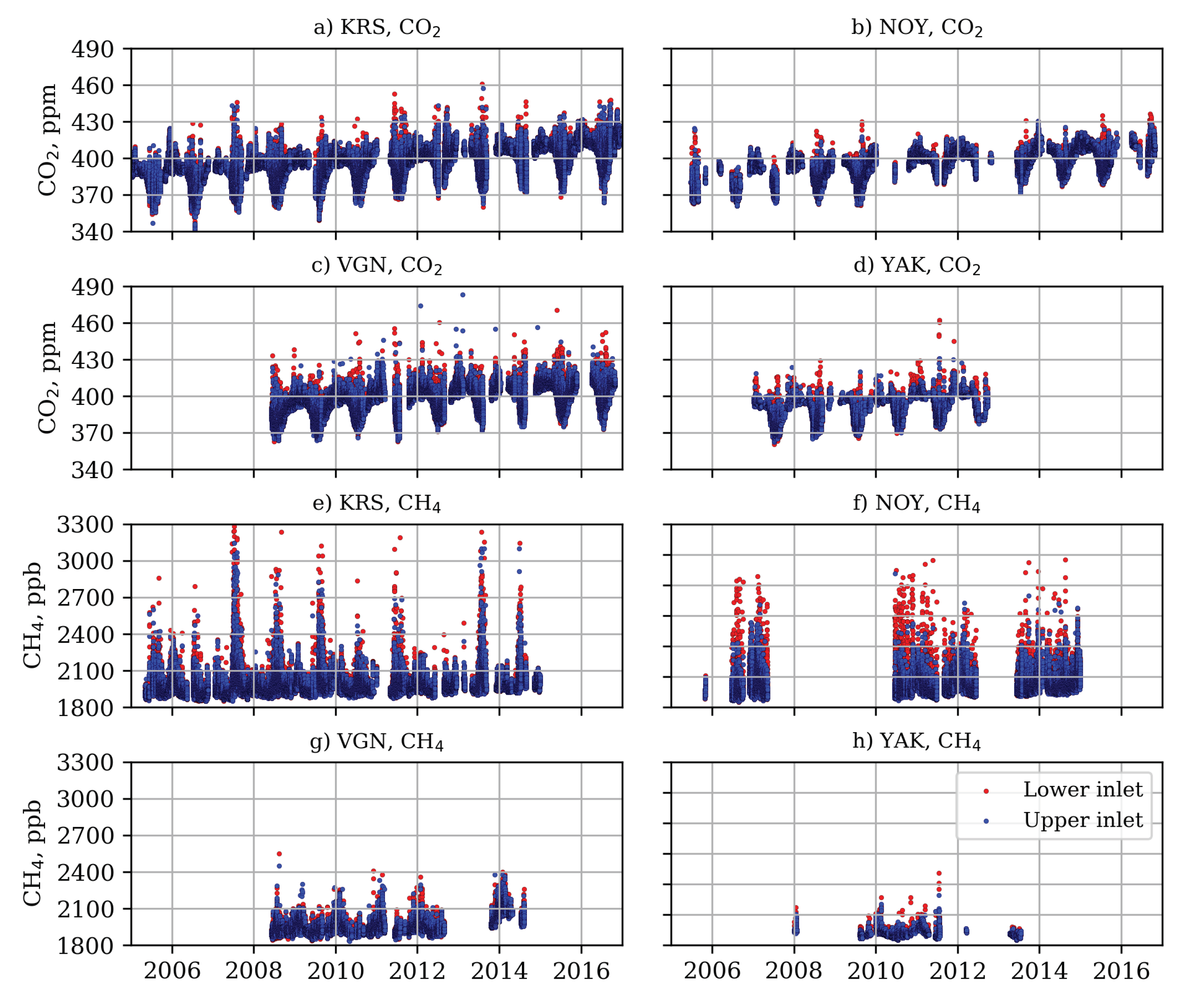
3.5. Diagnostic
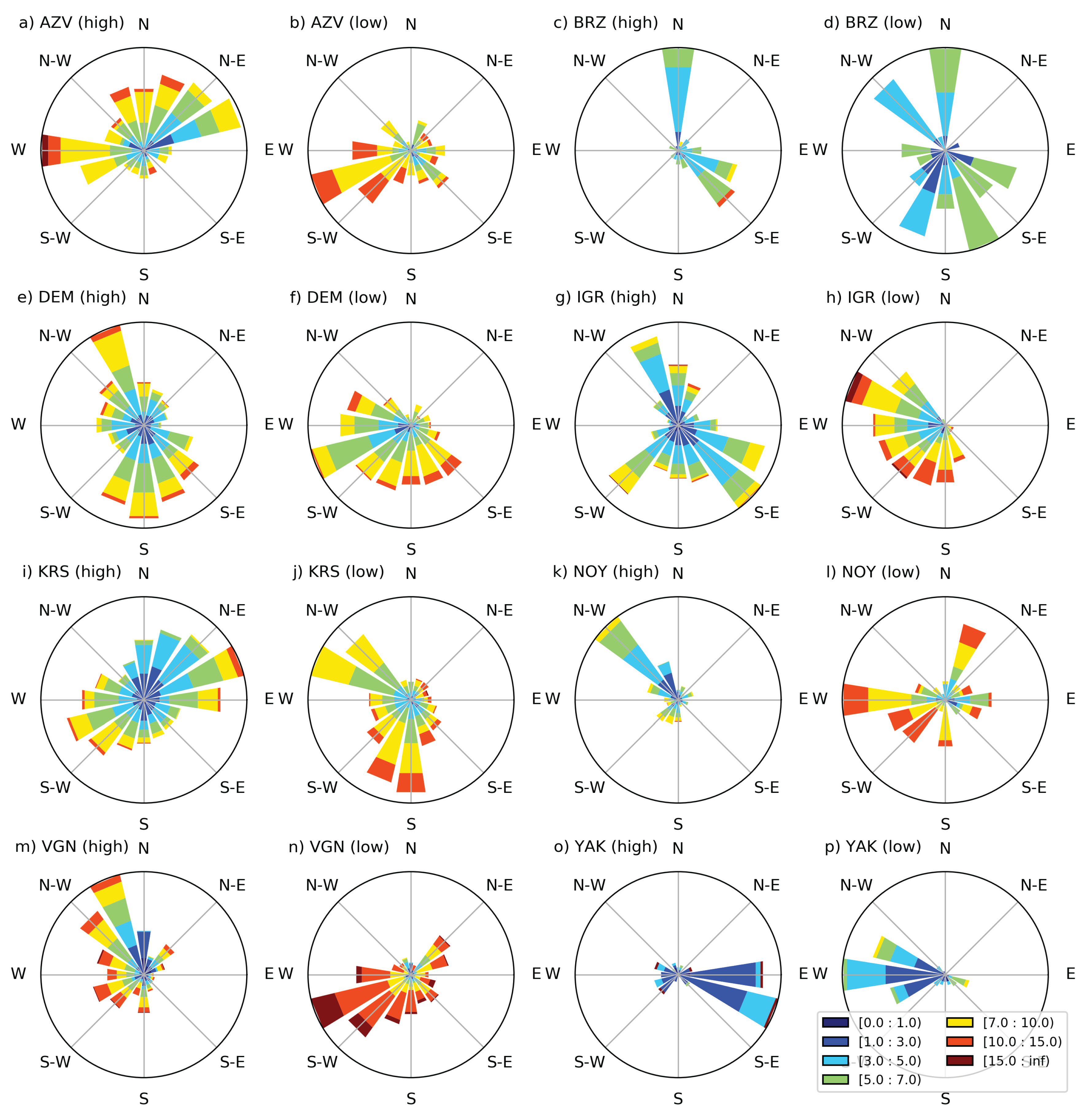
3.6. Temperature Inversion
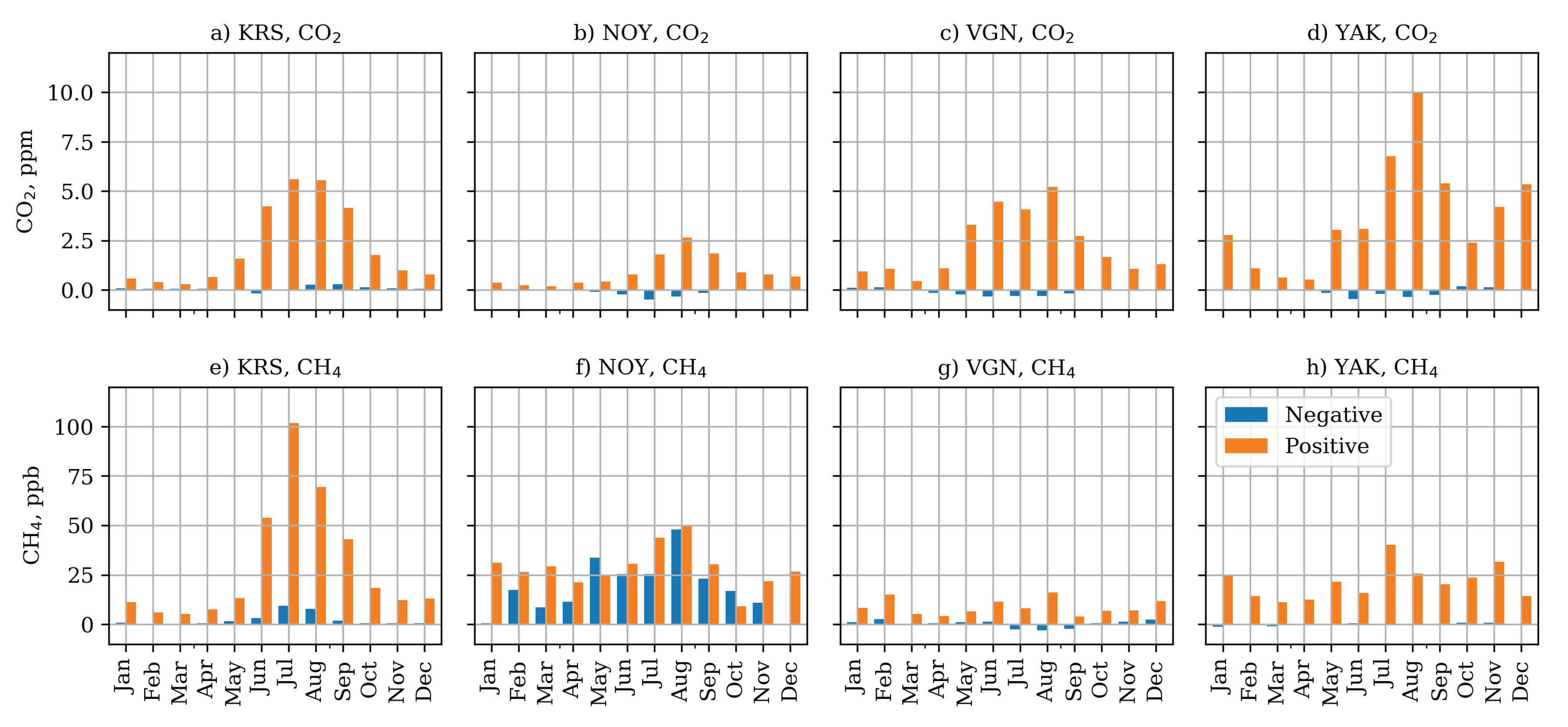
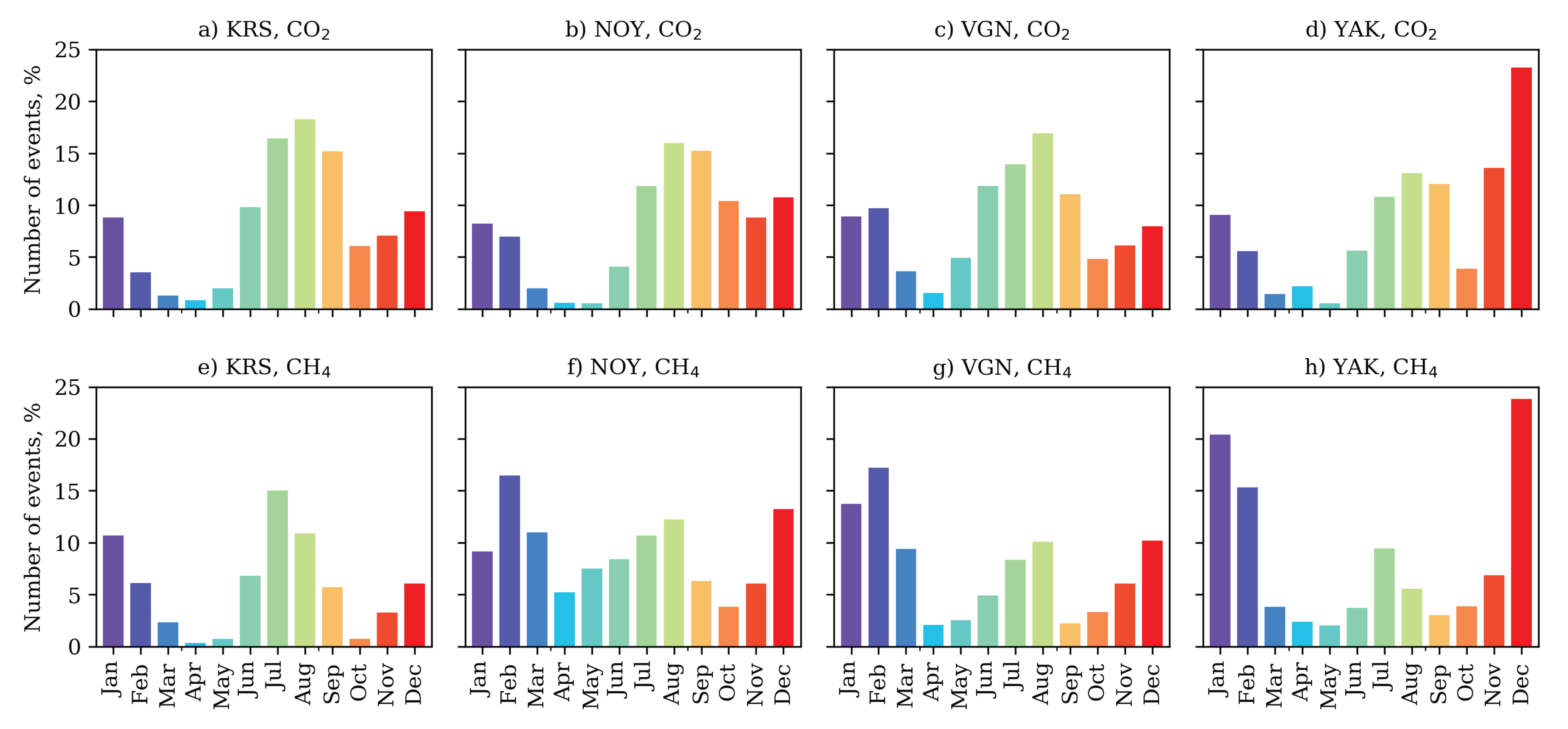
3.7. Elevated Concentration Events
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CO | carbon dioxide |
| CH | methane |
References
- Kurganova, I.; Kudeyarov, V.; Gerenyu, L.D. Updated estimate of carbon balance on Russian territory. Tellus Chem. Phys. Meteorol. 2010, 62, 497–505. [Google Scholar] [CrossRef]
- Le Quéré, C.; Andrew, R.M.; Friedlingstein, P.; Sitch, S.; Hauck, J.; Pongratz, J.; Pickers, P.A.; Korsbakken, J.I.; Peters, G.P.; Canadell, J.G.; et al. Global Carbon Budget 2018. Earth Syst. Sci. Data 2018, 10, 2141–2194. [Google Scholar] [CrossRef]
- Sasakawa, M.; Shimoyama, K.; Machida, T.; Tsuda, N.; Suto, H.; Arshinov, M.; Davydov, D.; Fofonov, A.; Krasnov, O.; Saeki, T.; et al. Continuous measurements of methane from a tower network over Siberia. Tellus Chem. Phys. Meteorol. 2010, 62, 403–416. [Google Scholar] [CrossRef]
- Lloyd, J.; Langenfelds, R.L.; Francey, R.J.; Gloor, M.; Tchebakova, N.M.; Zolotoukhine, D.; Brand, W.A.; Werner, R.A.; Jordan, A.; Allison, C.A.; et al. A trace-gas climatology above Zotino, central Siberia. Tellus Chem. Phys. Meteorol. 2002, 54, 749–767. [Google Scholar] [CrossRef]
- Arshinov, M.Y.; Belan, B.; Davydov, D.; Inoue, G. Spatio-temporal variability of CO2 and CH4 concentration in the surface atmospheric layer over West Siberia. Opt. Atmos. Okeana 2009, 22, 183–192. [Google Scholar]
- Arshinov, M.Y.; Belan, B.; Davydov, D.; Inouye, G.; Maksyutov, S.; Machida, T.; Fofonov, A. Vertical distribution of greenhouse gases above Western Siberia by the long-term measurement data. Atmos. Ocean. Opt. 2009, 22, 316–324. [Google Scholar] [CrossRef]
- Sasakawa, M.; Machida, T.; Tsuda, N.; Arshinov, M.; Davydov, D.; Fofonov, A.; Krasnov, O. Aircraft and tower measurements of CO2 concentration in the planetary boundary layer and the lower free troposphere over southern taiga in West Siberia: Long-term records from 2002 to 2011. J. Geophys. Res. Atmos. 2013, 118, 9489–9498. [Google Scholar] [CrossRef]
- Sasakawa, M.; Machida, T.; Ishijima, K.; Arshinov, M.; Patra, P.; Ito, A.; Aoki, S.; Petrov, V. Temporal Characteristics of CH4 Vertical Profiles Observed in the West Siberian Lowland Over Surgut From 1993 to 2015 and Novosibirsk From 1997 to 2015. J. Geophys. Res. Atmos. 2017, 122, 11–261. [Google Scholar] [CrossRef]
- Saeki, T.; Maksyutov, S.; Sasakawa, M.; Machida, T.; Arshinov, M.; Tans, P.; Conway, T.; Saito, M.; Valsala, V.; Oda, T.; et al. Carbon flux estimation for Siberia by inverse modeling constrained by aircraft and tower CO2 measurements. J. Geophys. Res. Atmos. 2013, 118, 1100–1122. [Google Scholar] [CrossRef]
- Berchet, A.; Pison, I.; Chevallier, F.; Paris, J.D.; Bousquet, P.; Bonne, J.L.; Arshinov, M.Y.; Belan, B.; Cressot, C.; Davydov, D.; et al. Natural and anthropogenic methane fluxes in Eurasia: A mesoscale quantification by generalized atmospheric inversion. Biogeosciences 2015, 12, 5393–5414. [Google Scholar] [CrossRef]
- Thompson, R.L.; Sasakawa, M.; Machida, T.; Aalto, T.; Worthy, D.; Lavric, J.V.; Lund Myhre, C.; Stohl, A. Methane fluxes in the high northern latitudes for 2005–2013 estimated using a Bayesian atmospheric inversion. Atmos. Chem. Phys. 2017, 17, 3553–3572. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Koutsoyiannis, D. Predictability of monthly temperature and precipitation using automatic time series forecasting methods. Acta Geophys. 2018, 66, 807–831. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, Y.; Vanos, J.K.; Cao, G. Day-of-week and seasonal patterns of PM2.5 concentrations over the United States: Time-series analyses using the Prophet procedure. Atmos. Environ. 2018, 192, 116–127. [Google Scholar] [CrossRef]
- Carbontracker-ch4. Available online: http://www.esrl.noaa.gov/gmd/ccgg/carbontracker-ch4/ (accessed on 1 November 2019).
- Peters, W.; Jacobson, A.R.; Sweeney, C.; Andrews, A.E.; Conway, T.J.; Masarie, K.; Miller, J.B.; Bruhwiler, L.M.; Pétron, G.; Hirsch, A.I.; et al. An atmospheric perspective on North American carbon dioxide exchange: CarbonTracker. Proc. Natl. Acad. Sci. USA 2007, 104, 18925–18930. [Google Scholar] [CrossRef]
- Watai, T.; Machida, T.; Shimoyama, K.; Krasnov, O.; Yamamoto, M.; Inoue, G. Development of an atmospheric carbon dioxide standard gas saving system and its application to a measurement at a site in the West Siberian forest. J. Atmos. Ocean. Technol. 2010, 27, 843–855. [Google Scholar] [CrossRef]
- Suto, H.; Inoue, G. A new portable instrument for in situ measurement of atmospheric methane mole fraction by applying an improved tin dioxide–based gas sensor. J. Atmos. Ocean. Technol. 2010, 27, 1175–1184. [Google Scholar] [CrossRef]
- Friborg, T.; Soegaard, H.; Christensen, T.R.; Lloyd, C.R.; Panikov, N.S. Siberian wetlands: Where a sink is a source. Geophys. Res. Lett. 2003, 30, 2129–2133. [Google Scholar] [CrossRef]
- Panikov, N.S.; Dedysh, S. Cold season CH4 and CO2 emission from boreal peat bogs (West Siberia): Winter fluxes and thaw activation dynamics. Glob. Biogeochem. Cycles 2000, 14, 1071–1080. [Google Scholar] [CrossRef]
- Bohn, T.J.; Melton, J.R.; Ito, A.; Kleinen, T.; Spahni, R.; Stocker, B.; Zhang, B.; Zhu, X.; Schroeder, R.; Glagolev, M.V.; et al. WETCHIMP-WSL: Intercomparison of wetland methane emissions models over West Siberia. Biogeosciences 2015, 12, 3321–3349. [Google Scholar] [CrossRef]
- Repo, E.; Huttunen, J.T.; Naumov, A.V.; Chichulin, A.V.; Lapshina, E.D.; Bleuten, W.; Martikainen, P.J. Release of CO2 and CH4 from small wetland lakes in western Siberia. Tellus Chem. Phys. Meteorol. 2007, 59, 788–796. [Google Scholar] [CrossRef]
- Harvey, A.C.; Peters, S. Estimation procedures for structural time series models. J. Forecast. 1990, 9, 89–108. [Google Scholar] [CrossRef]
- Harvey, A.C.; Shephard, N. 10 Structural time series models. In Econometrics; Handbook of Statistics; Elsevier: Amsterdam, The Netherlands, 1993; Volume 11, pp. 261–302. [Google Scholar] [CrossRef]
- The Prophet Package. Available online: https://facebook.github.io/prophet/ (accessed on 1 November 2019).
- Annual Mean Growth Rate for Mauna Loa, Hawaii. Available online: https://www.esrl.noaa.gov/gmd/ccgg/trends/gr.html (accessed on 1 November 2019).
- Dlugokencky, E.; Bruhwiler, L.; White, J.; Emmons, L.; Novelli, P.C.; Montzka, S.A.; Masarie, K.A.; Lang, P.M.; Crotwell, A.; Miller, J.B.; et al. Observational constraints on recent increases in the atmospheric CH4 burden. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Nisbet, E.; Dlugokencky, E.; Manning, M.; Lowry, D.; Fisher, R.; France, J.; Michel, S.; Miller, J.; White, J.; Vaughn, B.; et al. Rising atmospheric methane: 2007–2014 growth and isotopic shift. Glob. Biogeochem. Cycles 2016, 30, 1356–1370. [Google Scholar] [CrossRef]
- Arshinov, M.; Afonin, S.; Belan, B.; Belov, V.; Gridnev, Y.; Davydov, D.; Nedelec, P.; Paris, J.D.; Fofonov, A. Comparison between satellite spectrometric and aircraft measurements of the gaseous composition of the troposphere over Siberia during the forest fires of 2012. Izv. Atmos. Ocean. Phys. 2015, 50, 916–928. [Google Scholar] [CrossRef]
- Umezawa, T.; Machida, T.; Aoki, S.; Nakazawa, T. Contributions of natural and anthropogenic sources to atmospheric methane variations over western Siberia estimated from its carbon and hydrogen isotopes. Glob. Biogeochem. Cycles 2012, 26. [Google Scholar] [CrossRef]
- Worthy, D.; Levin, I.; Trivett, N.; Kuhlmann, A.; Hopper, J.; Ernst, M. Seven years of continuous methane observations at a remote boreal site in Ontario, Canada. J. Geophys. Res. Atmos. 1998, 103, 15995–16007. [Google Scholar] [CrossRef]
- Public Holidays in Russia. Available online: https://en.wikipedia.org/wiki/Public_holidays_in_Russia (accessed on 1 November 2019).
- Oberlander, E.A.; Brenninkmeijer, C.; Crutzen, P.; Elansky, N.; Golitsyn, G.; Granberg, I.; Scharffe, D.; Hofmann, R.; Belikov, I.; Paretzke, H.; et al. Trace gas measurements along the Trans-Siberian railroad: The TROICA 5 expedition. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Hollinger, D.; Kelliher, F.; Schulze, E.D.; Bauer, G.; Arneth, A.; Byers, J.; Hunt, J.; McSeveny, T.; Kobak, K.; Milukova, I.; et al. Forest–atmosphere carbon dioxide exchange in eastern Siberia. Agric. For. Meteorol. 1998, 90, 291–306. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2000, 16, 437–450. [Google Scholar] [CrossRef]
- Turnbull, J.; Miller, J.; Lehman, S.; Tans, P.; Sparks, R.; Southon, J. Comparison of 14CO2, CO, and SF6 as tracers for recently added fossil fuel CO2 in the atmosphere and implications for biological CO2 exchange. Geophys. Res. Lett. 2006, 33, L01817. [Google Scholar] [CrossRef]
- Zhang, F.; Zhou, L.; Conway, T.J.; Tans, P.P.; Wang, Y. Short-term variations of atmospheric CO2 and dominant causes in summer and winter: Analysis of 14-year continuous observational data at Waliguan, China. Atmos. Environ. 2013, 77, 140–148. [Google Scholar] [CrossRef]
- Basu, S.; Baker, D.F.; Chevallier, F.; Patra, P.K.; Liu, J.; Miller, J.B. The impact of transport model differences on CO2 surface flux estimates from OCO-2 retrievals of column average CO2. Atmos. Chem. Phys. 2018, 18, 7189–7215. [Google Scholar] [CrossRef]
- Baklanov, A.A.; Penenko, V.V.; Mahura, A.G.; Vinogradova, A.A.; Elansky, N.F.; Tsvetova, E.A.; Rigina, O.Y.; Maksimenkov, L.O.; Nuterman, R.B.; Pogarskii, F.A.; et al. Aspects of atmospheric pollution in Siberia. In Regional Environmental Changes in Siberia and Their Global Consequences; Springer: Berlin/Heidelberg, Germany, 2013; pp. 303–346. [Google Scholar]
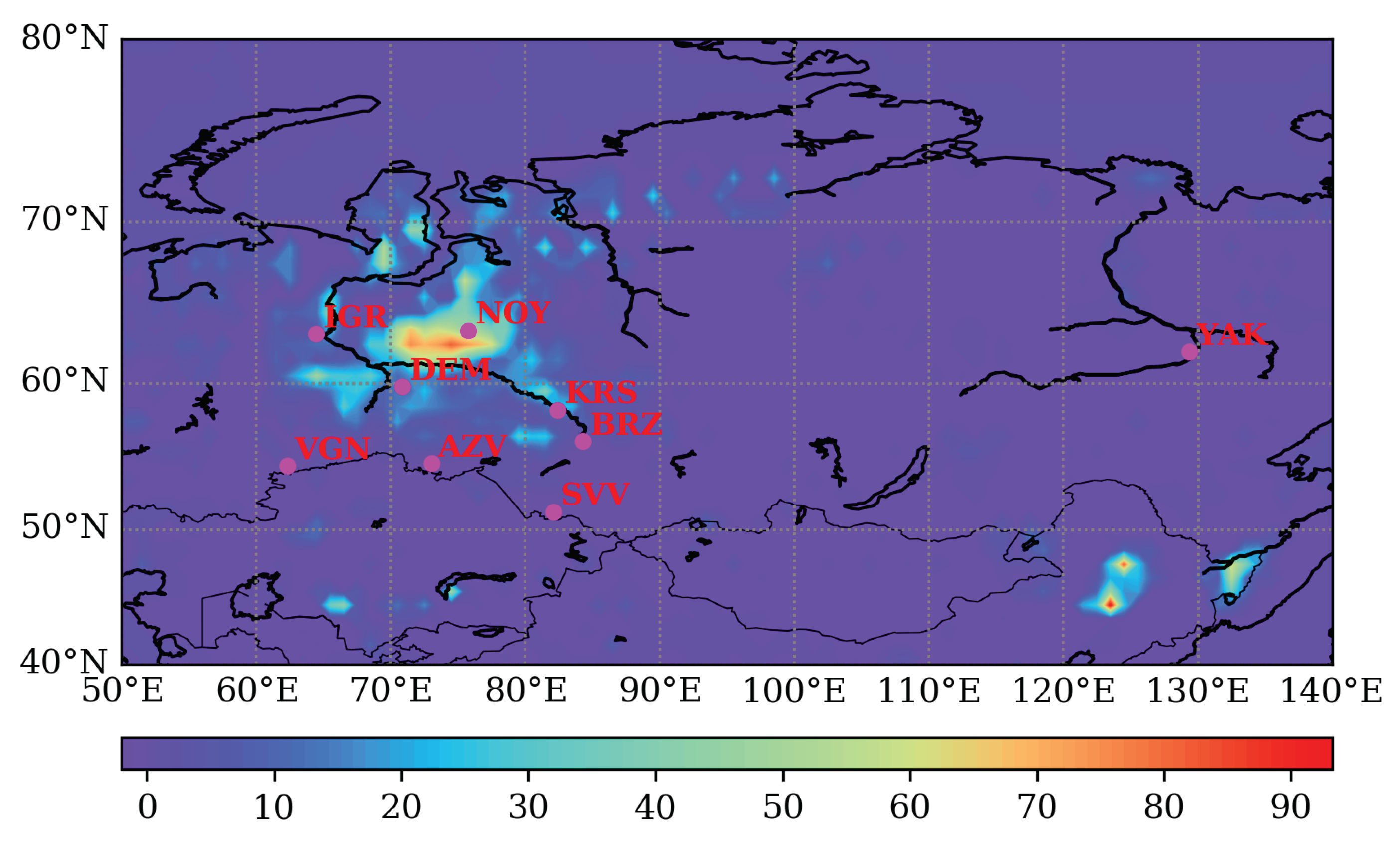
| # | Identifying Code | Location | Lat., | Lon., | Air Inlet Heights, m | Period of Observations, Years (Data Coverage %) | |
|---|---|---|---|---|---|---|---|
| CO | CH | ||||||
| 1 | AZV | Azovo | 54.71 | 73.03 | 29, 50 | 9 (79) | 4 (46) |
| 2 | BRZ | Berezorechka | 56.15 | 84.33 | 40, 80 | 7 (19) | 4 (10) |
| 3 | DEM | Demyanskoe | 59.79 | 70.87 | 45, 63 | 12 (68) | 10 (70) |
| 4 | IGR | Igrim | 63.19 | 64.41 | 24, 47 | 9 (85) | 10 (82) |
| 5 | KRS | Karasevoe | 58.25 | 82.42 | 35, 67 | 12 (70) | 10 (74) |
| 6 | NOY | Noyabrsk | 63.43 | 75.78 | 21, 43 | 12 (53) | 8 (37) |
| 7 | SVV | Savvushka | 51.33 | 82.13 | 27, 52 | 9 (58) | 1 (68) |
| 8 | VGN | Vaganovo | 54.50 | 62.32 | 42, 85 | 9 (75) | 7 (56) |
| 9 | YAK | Yakutsk | 62.09 | 129.36 | 11, 77 | 8 (58) | 6 (28) |
| # | Identifying Code | Mean CO, ppm | Mean CH, ppb | ||||
|---|---|---|---|---|---|---|---|
| Working | Holiday | Diff. (%) | Working | Holiday | Diff. (%) | ||
| 1 | AZV | 10.52 | 8.86 | 1.67 (15.85) | 113.84 | 120.09 | −6.25 (−5.49) |
| 2 | BRZ | 13.71 | 5.89 | 7.81 (57.00) | - | - | - ( - ) |
| 3 | DEM | 8.41 | 6.83 | 1.59 (18.87) | 60.76 | 10.76 | 50.00 (82.29) |
| 4 | IGR | 9.07 | 7.54 | 1.53 (16.91) | 31.91 | 21.45 | 10.47 (32.80) |
| 5 | KRS | 8.84 | 6.35 | 2.49 (28.14) | 42.90 | 6.60 | 36.29 (84.62) |
| 6 | NOY | 8.78 | 9.05 | −0.28 (−3.15) | 67.43 | 20.46 | 46.98 (69.66) |
| 7 | SVV | 6.87 | 7.27 | −0.39 (−5.76) | - | - | - ( - ) |
| 8 | VGN | 7.52 | 8.16 | −0.65 (−8.58) | 54.63 | 41.24 | 13.39 (24.51) |
| 9 | YAK | 8.17 | 6.71 | 1.46 (17.91) | 52.49 | 46.93 | 5.56 (10.59) |
| # | Identifying Code | Amplitude for CO, ppm | Amplitude for CH, ppb | ||||||
|---|---|---|---|---|---|---|---|---|---|
| DJF | MAM | JJA | SON | DJF | MAM | JJA | SON | ||
| 1 | AZV | 1.04 | 5.46 | 26.12 | 5.20 | 30.94 | 21.19 | 50.68 | 14.38 |
| 2 | BRZ | 1.24 | 4.76 | 23.37 | 4.54 | - | - | - | - |
| 3 | DEM | 0.61 | 3.31 | 20.45 | 6.63 | 10.73 | 22.53 | 109.42 | 33.89 |
| 4 | IGR | 1.01 | 3.66 | 17.90 | 9.74 | 31.27 | 36.46 | 146.79 | 54.20 |
| 5 | KRS | 0.55 | 3.29 | 22.07 | 7.09 | 11.11 | 20.06 | 182.98 | 41.89 |
| 6 | NOY | 0.24 | 1.48 | 10.53 | 3.48 | 31.12 | 37.47 | 92.62 | 39.76 |
| 7 | SVV | 0.95 | 4.12 | 11.89 | 3.48 | - | - | - | - |
| 8 | VGN | 0.29 | 5.45 | 17.56 | 3.87 | 6.39 | 17.68 | 52.76 | 16.75 |
| 9 | YAK | 6.73 | 6.25 | 12.46 | 17.92 | - | - | 35.04 | - |
| # | Identifying Code | CO | CH | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | MAPE (%) | RMSE | MAE | MAPE (%) | ||
| 1 | AZV | 4.97 | 3.84 | 0.96 | 48.67 | 39.96 | 2.03 |
| 2 | BRZ | 4.43 | 3.36 | 0.85 | - | - | - |
| 3 | DEM | 3.97 | 3.00 | 0.76 | 108.77 | 65.83 | 3.32 |
| 4 | IGR | 4.92 | 3.63 | 0.92 | 120.91 | 93.78 | 4.57 |
| 5 | KRS | 4.36 | 3.33 | 0.84 | 47.64 | 35.35 | 1.79 |
| 6 | NOY | 3.76 | 2.85 | 0.72 | 98.66 | 74.19 | 3.64 |
| 7 | SVV | 3.91 | 2.98 | 0.76 | - | - | - |
| 8 | VGN | 4.25 | 3.34 | 0.84 | 57.10 | 42.32 | 2.10 |
| 9 | YAK | 4.76 | 3.63 | 0.91 | 97.49 | 73.06 | 3.79 |
| # | Identifying Code | Threshold | |
|---|---|---|---|
| CO, ppm | CH, ppb | ||
| 1 | AZV | 9.33 | 45.00 |
| 2 | BRZ | 7.81 | - |
| 3 | DEM | 7.47 | 88.78 |
| 4 | IGR | 8.45 | 160.51 |
| 5 | KRS | 7.87 | 98.08 |
| 6 | NOY | 5.57 | 141.93 |
| 7 | SVV | 5.98 | - |
| 8 | VGN | 7.04 | 53.49 |
| 9 | YAK | 6.32 | 39.05 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belikov, D.; Arshinov, M.; Belan, B.; Davydov, D.; Fofonov, A.; Sasakawa, M.; Machida, T. Analysis of the Diurnal, Weekly, and Seasonal Cycles and Annual Trends in Atmospheric CO2 and CH4 at Tower Network in Siberia from 2005 to 2016. Atmosphere 2019, 10, 689. https://doi.org/10.3390/atmos10110689
Belikov D, Arshinov M, Belan B, Davydov D, Fofonov A, Sasakawa M, Machida T. Analysis of the Diurnal, Weekly, and Seasonal Cycles and Annual Trends in Atmospheric CO2 and CH4 at Tower Network in Siberia from 2005 to 2016. Atmosphere. 2019; 10(11):689. https://doi.org/10.3390/atmos10110689
Chicago/Turabian StyleBelikov, Dmitry, Mikhail Arshinov, Boris Belan, Denis Davydov, Aleksandr Fofonov, Motoki Sasakawa, and Toshinobu Machida. 2019. "Analysis of the Diurnal, Weekly, and Seasonal Cycles and Annual Trends in Atmospheric CO2 and CH4 at Tower Network in Siberia from 2005 to 2016" Atmosphere 10, no. 11: 689. https://doi.org/10.3390/atmos10110689
APA StyleBelikov, D., Arshinov, M., Belan, B., Davydov, D., Fofonov, A., Sasakawa, M., & Machida, T. (2019). Analysis of the Diurnal, Weekly, and Seasonal Cycles and Annual Trends in Atmospheric CO2 and CH4 at Tower Network in Siberia from 2005 to 2016. Atmosphere, 10(11), 689. https://doi.org/10.3390/atmos10110689







