Study on Wind Simulations Using Deep Learning Techniques during Typhoons: A Case Study of Northern Taiwan
Abstract
1. Introduction
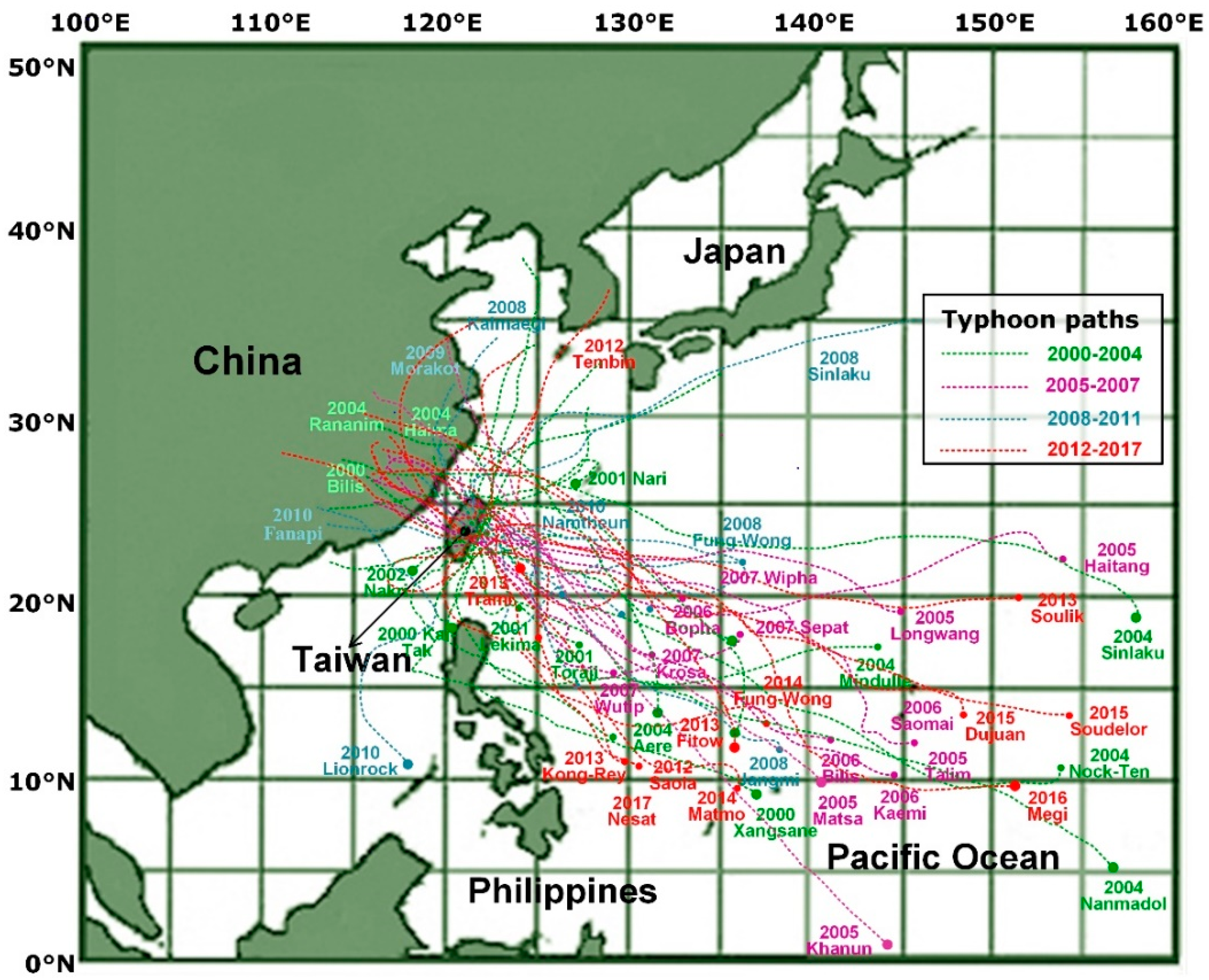
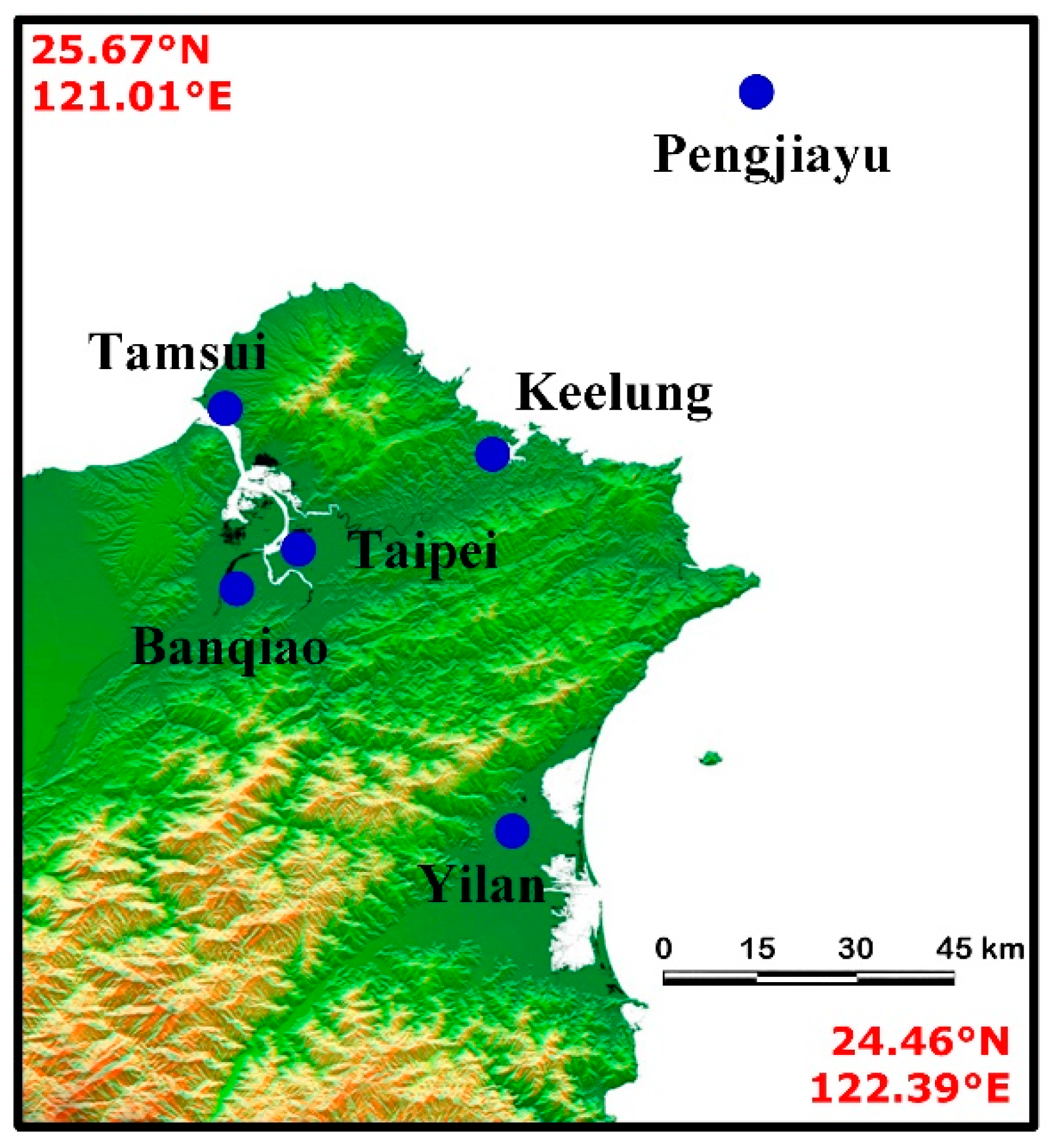
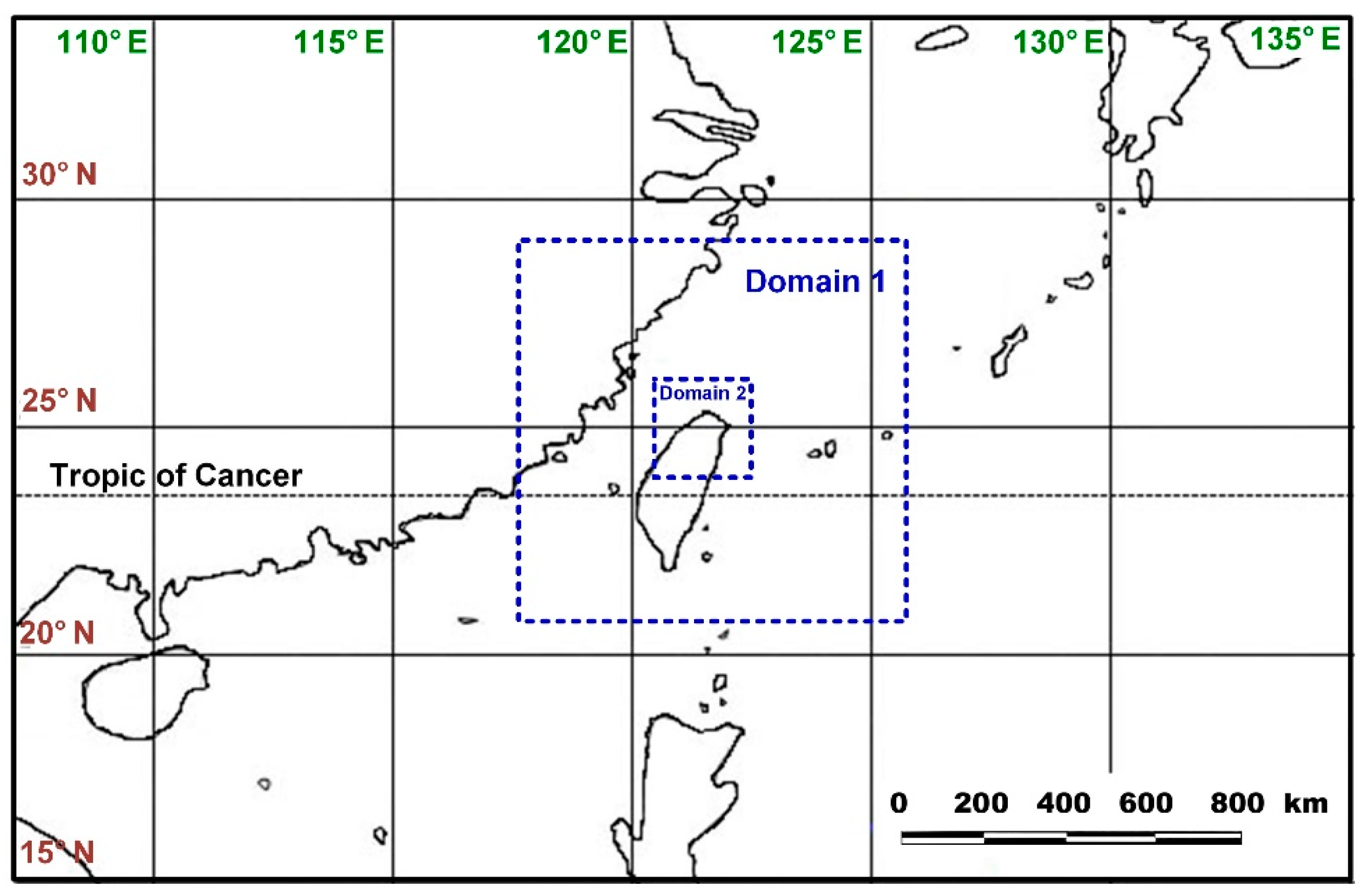
2. Study Region and Data
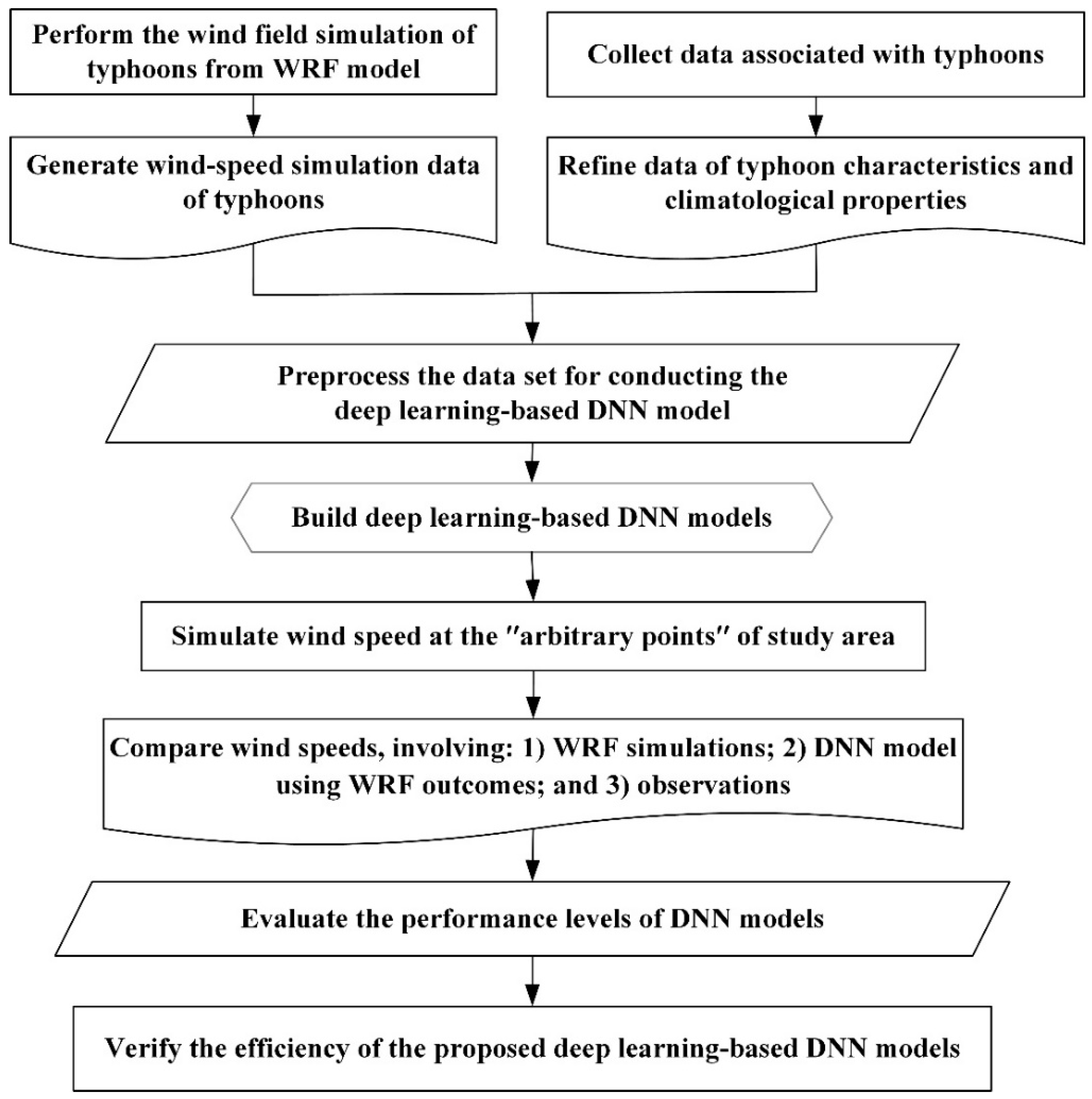
3. Methodology
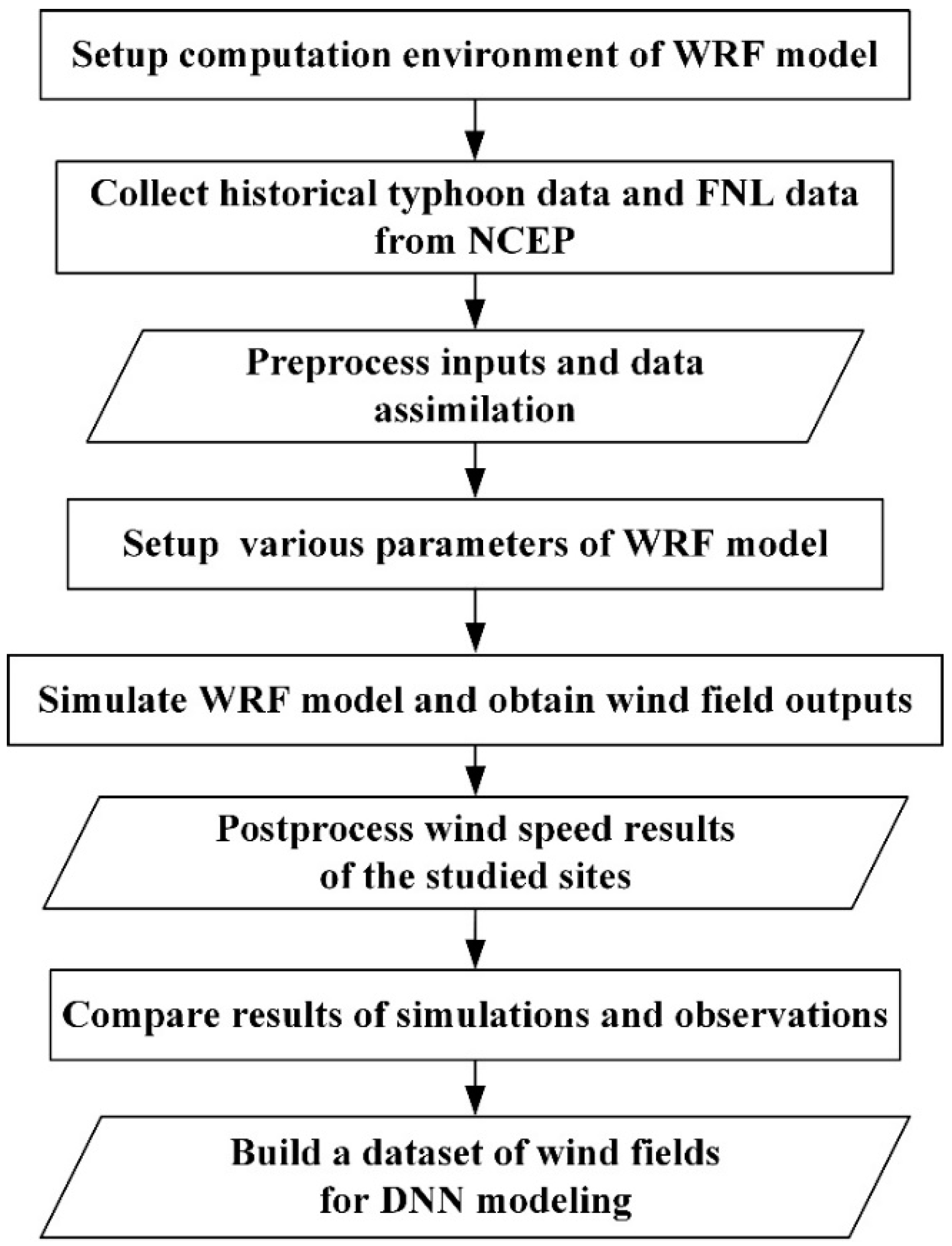
3.1. The WRF Model
3.2. The DNN Model
4. WRF Model and Analysis
4.1. WRF Settings and Calculations
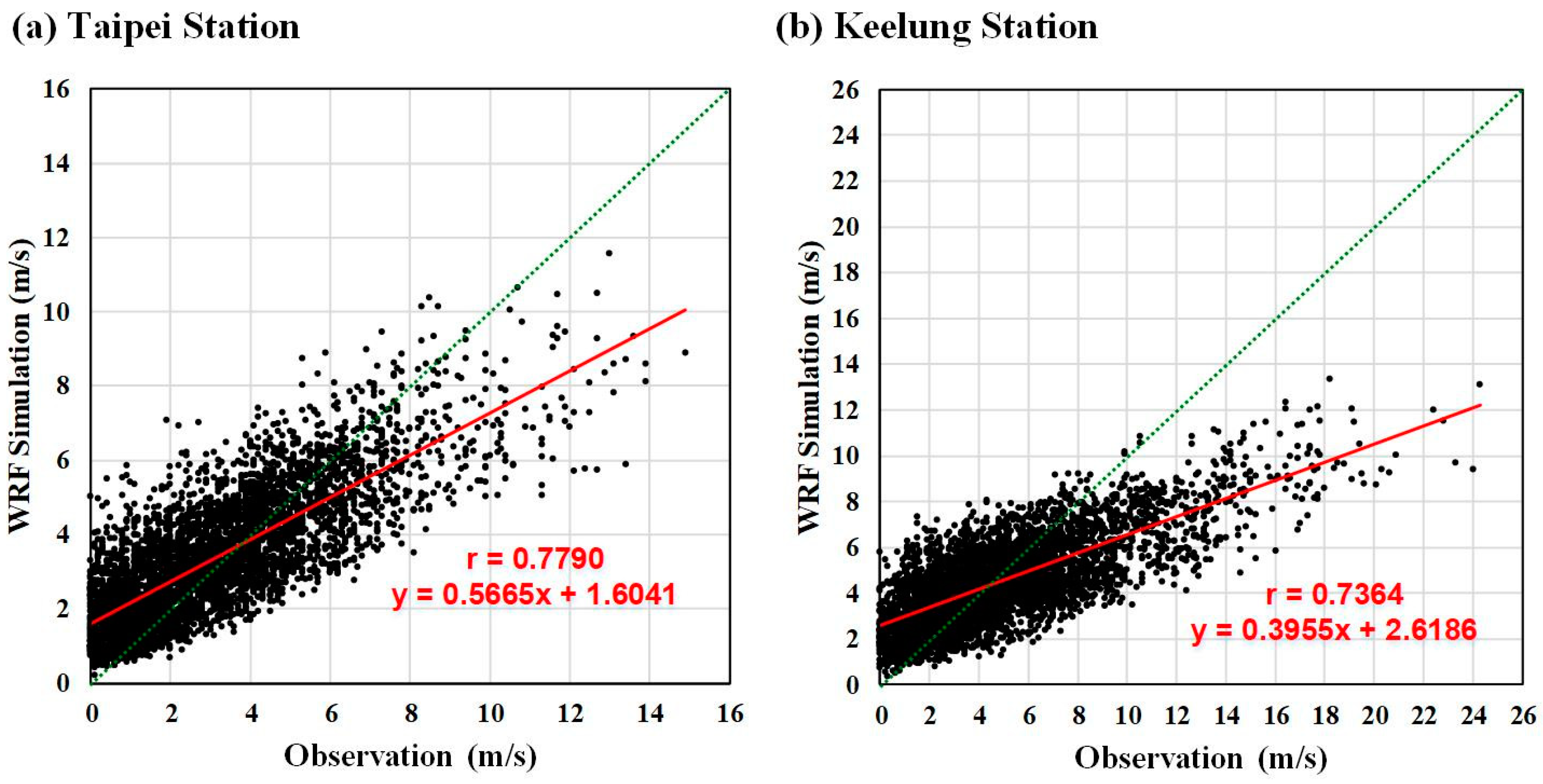
4.2. WRF Simulation Outcomes
5. DL Modeling using WRF Outcomes
5.1. Modeling and Feature Selection
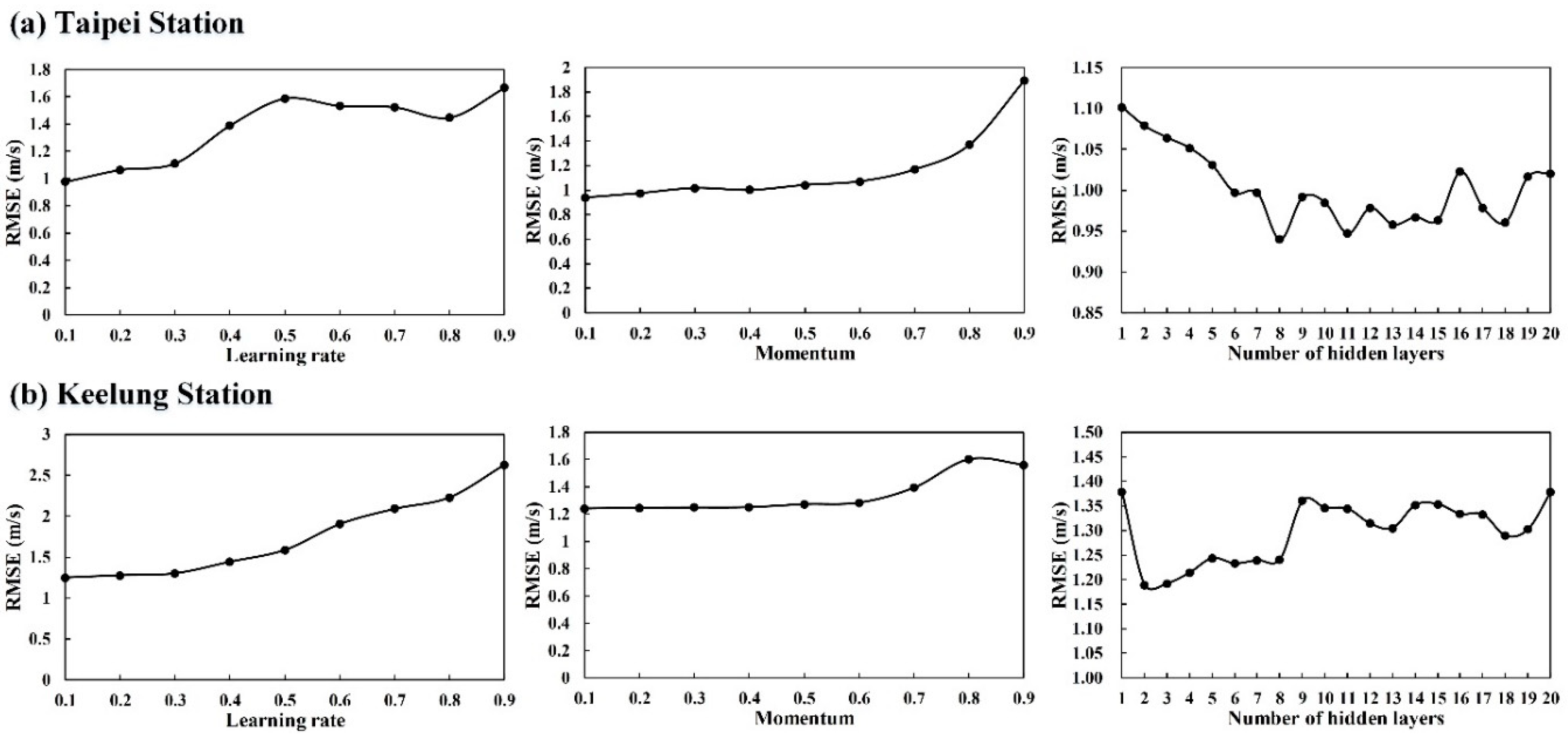
5.2. Data Splitting and Model Construction
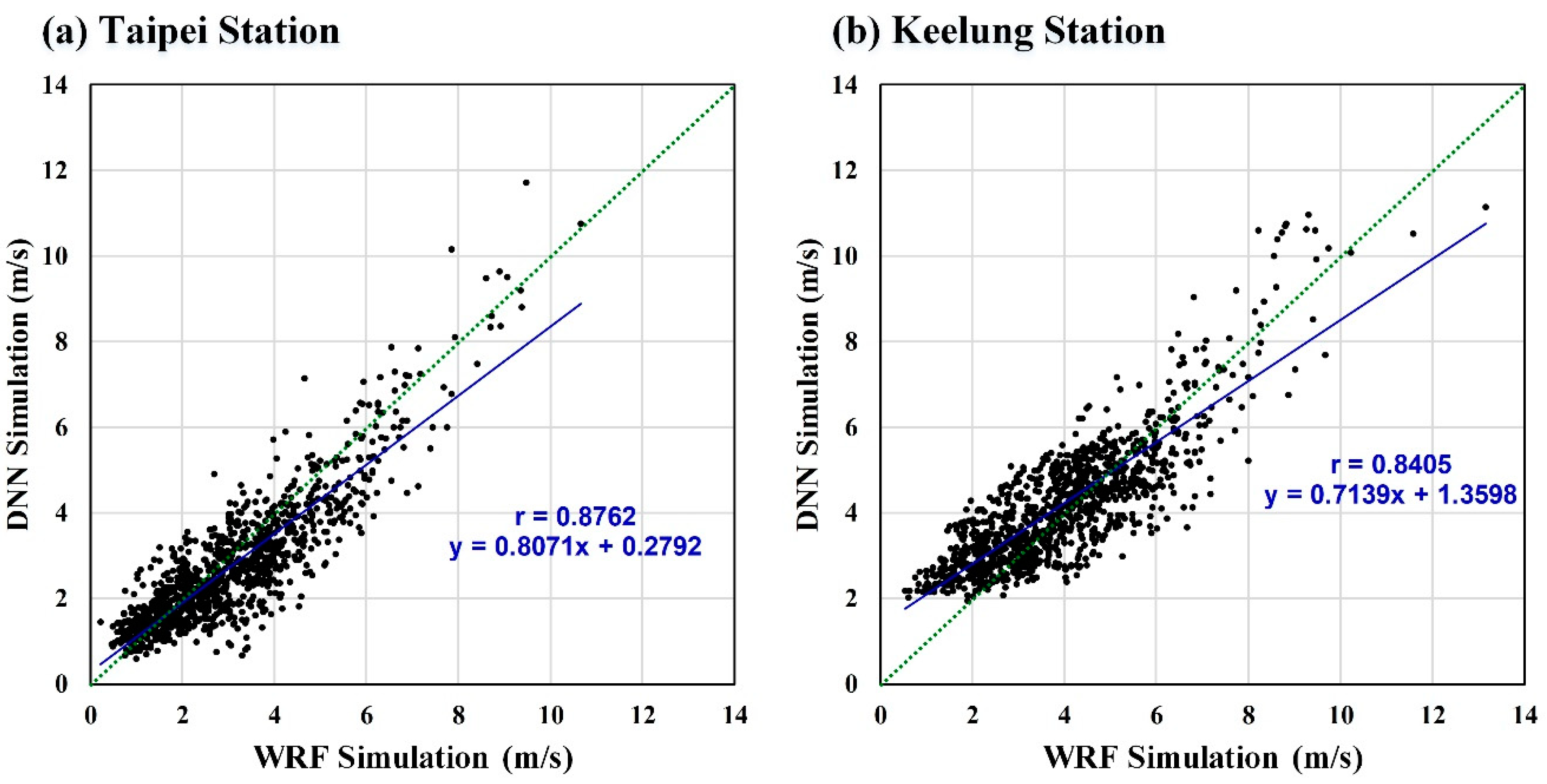
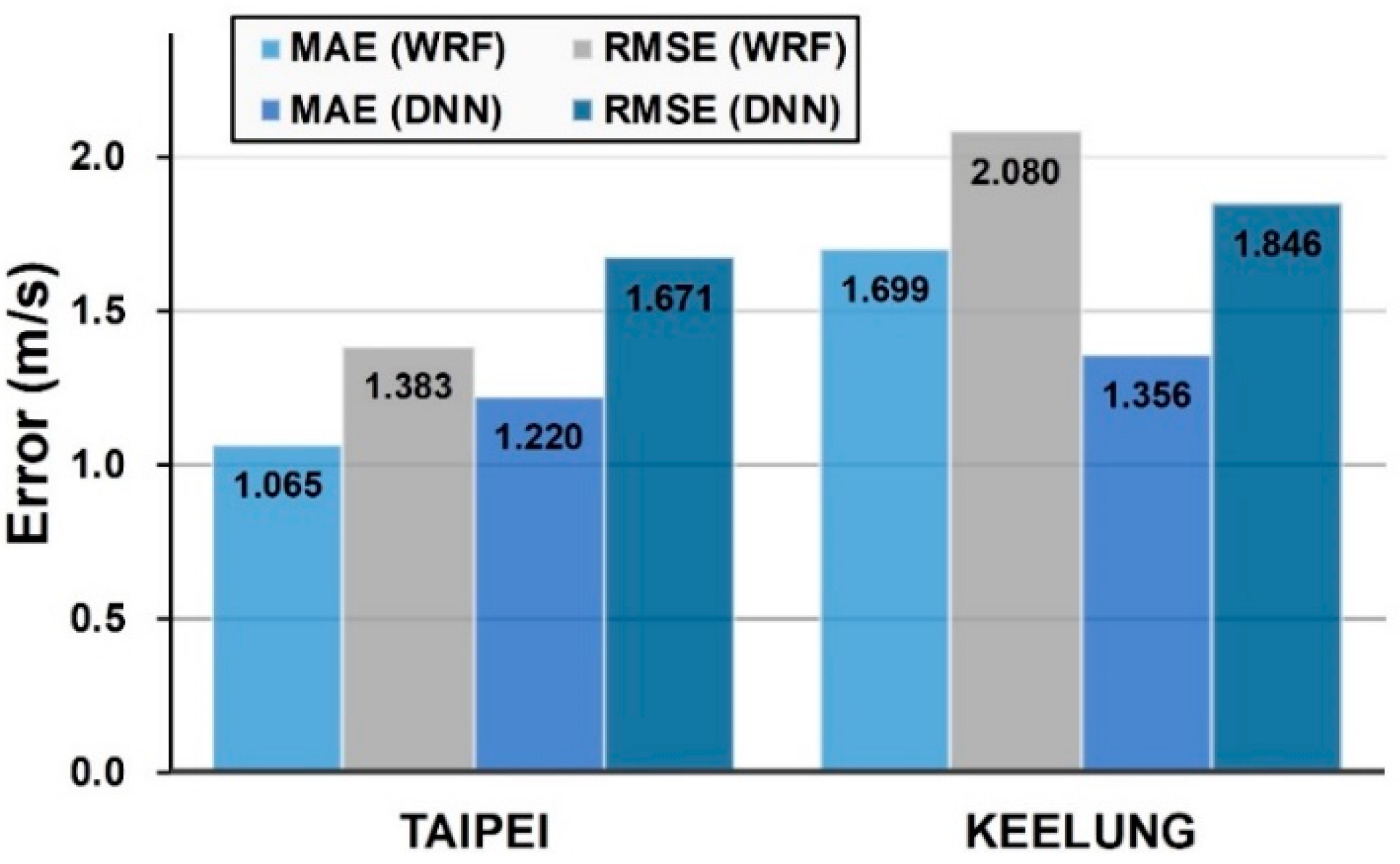
5.3. Model Performance
5.4. Computing Efficiency
6. Simulations of Testing Typhoons
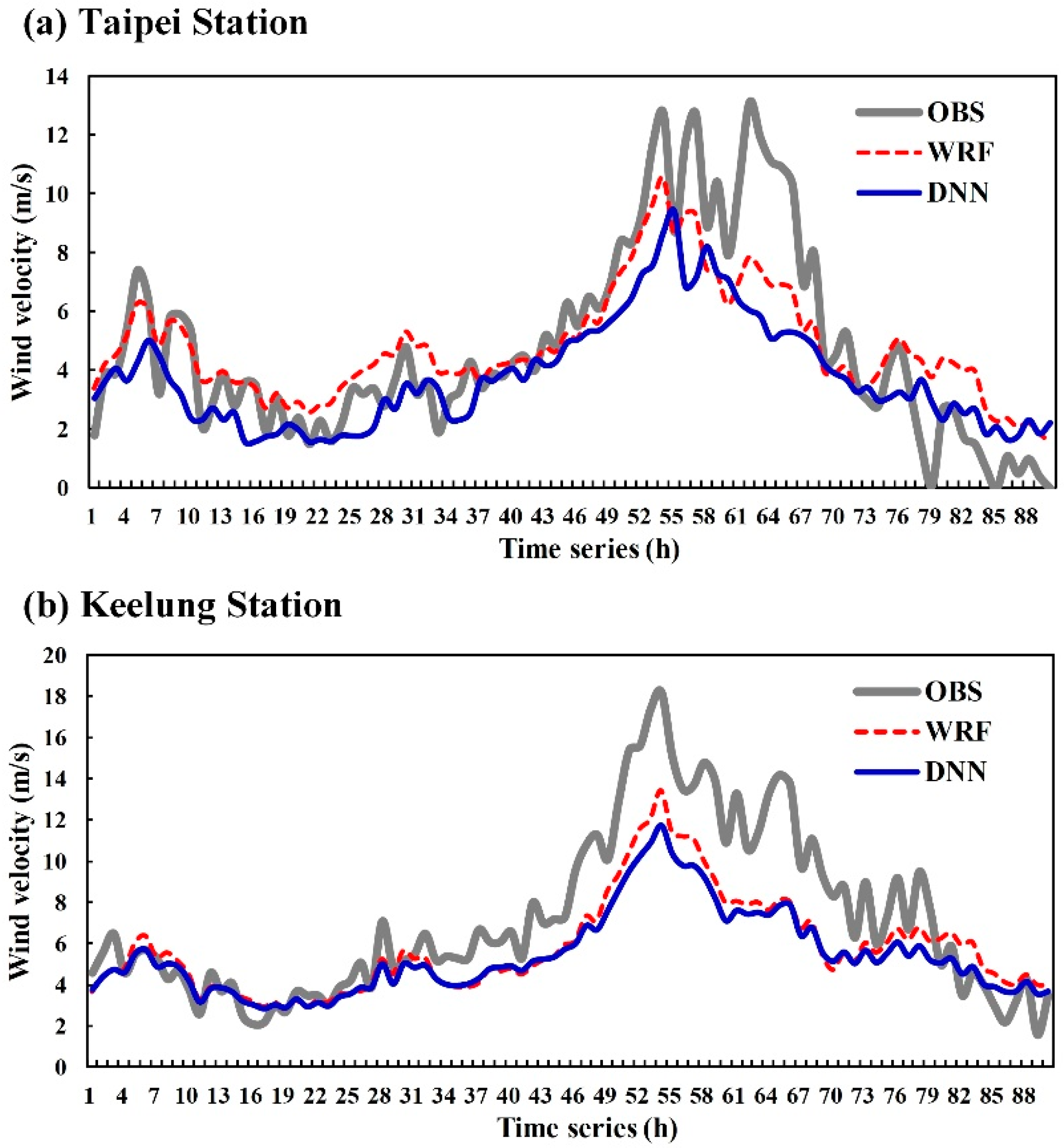
6.1. Simulation of Typhoon Megi
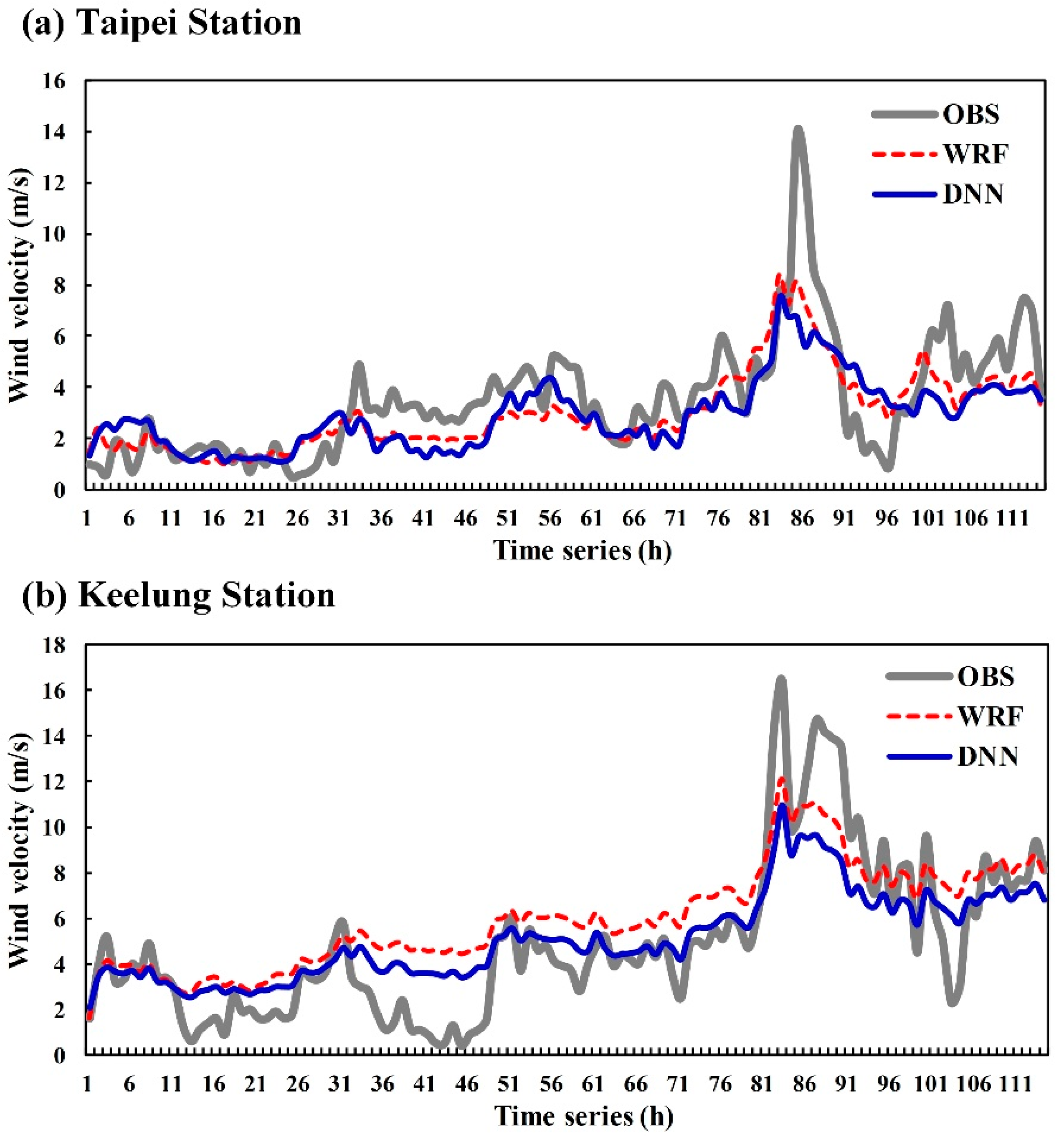
6.2. Simulation of Typhoon Nesat
7. Conclusions
- The observed wind speeds for all past typhoons recorded at Keelung station ranged from 0 to 25 m/s. The observed wind speeds at Taipei station ranged from 0 to 15 m/s. This result is primarily attributable to the effect of the terrain on typhoons; the effect on the wind speed at Taipei station, which is located in a basin area, was greater than the effect on Keelung station, which is located in a coastal area.
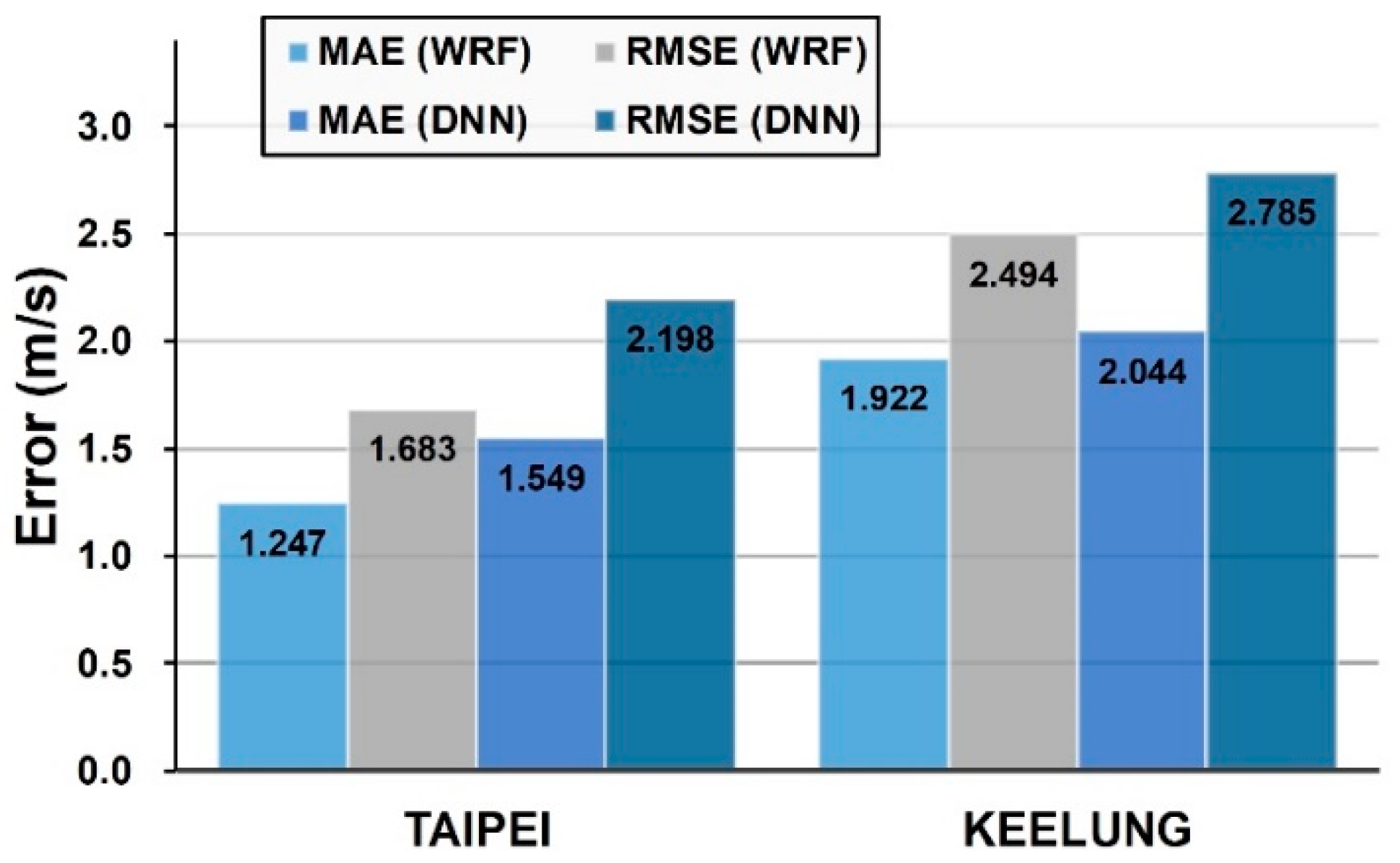
- In terms of WRF model performance, at both the Taipei and Keelung stations the WRF simulation values yielded an overestimation or underestimation when the wind speed was less than 9 m/s. However, the WRF simulation results produced an underestimation when the wind speed was greater than 9 m/s. The results for the two test typhoons, Megi and Nesat, indicated that the wind speed increased during the period between the typhoon landing and leaving land and was able to attain the maximum wind speed. Because the wind speed at this stage was approximately 9 m/s or greater, the WRF model still requires improvement with regard to simulating the period after typhoons land. Therefore, future studies can focus on the simulation process for this period of time. For example, studies can use sounding data from assimilation observation data or a combination of various physical parameters to improve the simulation results of wind speed.
- In terms of DNN model performance, both Keelung and Taipei stations underestimated the wind speed in comparison with the actual wind speed observations. Additionally, a comparison of the results of the two stations indicated that Keelung station exhibited a larger error and was more likely to underestimate the wind speed compared with Taipei station. This result is because the DNN model learns from the wind-speed simulation values of the WRF model. Therefore, when the simulation results of the WRF model underestimate the wind speed, the DNN model simulation results exhibit similar results (underestimation).
- In terms of overall model performance, both the WRF and DNN models tended to underestimate high wind speeds. However, both still could effectively demonstrate wind-speed trends. Thus, the conceptual model proposed in this study remains an effective method for simulating wind speed.
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Year | Typhoon | Period (UTC) | Year | Typhoon | Period (UTC) |
|---|---|---|---|---|---|
| 2000 | Kai-Tak | 6–10 Jul | 2007 | Sepat | 16–19 Aug |
| 2000 | Bilis | 21–23 Aug | 2007 | Wipha | 17–19 Sep |
| 2000 | Xangsane | 30 Oct–2 Nov | 2007 | Krosa | 5–8 Oct |
| 2001 | Toraji | 28–31 Jul | 2008 | Kalmaegi | 16–19 Jul |
| 2001 | Nari | 10–20 Sep | 2008 | Fung-Wong | 27–29 Jul |
| 2001 | Lekima | 24–29 Sep | 2008 | Sinlaku | 10–16 Sep |
| 2002 | Nakri | 9–11 Jul | 2008 | Jangmi | 27–30 Sep |
| 2002 | Sinlaku | 4–8 Sep | 2009 | Morakot | 6–9 Aug |
| 2004 | Mindulle | 29 Jun–3 Jul | 2010 | Namtheun | 30–31 Aug |
| 2004 | Rananim | 11–12 Aug | 2010 | Lionrock | 31 Aug–2 Sep |
| 2004 | Aere | 23–26 Aug | 2010 | Fanapi | 18–20 Sep |
| 2004 | Haima | 12–13 Sep | 2012 | Saola | 30 Jul–3 Aug |
| 2004 | Nock-Ten | 24–26 Oct | 2012 | Haikui | 4–8 Aug |
| 2004 | Nanmadol | 3–4 Dec | 2013 | Soulik | 10–14 Jul |
| 2005 | Haitang | 17–19 Jul | 2013 | Trami | 16–22 Aug |
| 2005 | Matsa | 3–6 Aug | 2013 | Kong-Rey | 27–30 Aug |
| 2005 | Talim | 31 Aug–1 Sep | 2013 | Fitow | 2–7 Oct |
| 2005 | Khanun | 10–11 Sep | 2014 | Matmo | 21–23 Jul |
| 2005 | Longwang | 1–2 Oct | 2014 | Fung-Wong | 19–22 Sep |
| 2006 | Bilis | 12–14 Jul | 2015 | Soudelor | 6–9 Aug |
| 2006 | Kaemi | 23–25 Jul | 2015 | Dujuan | 25–29 Sep |
| 2006 | Bopha | 8–9 Aug | 2016 | Megi | 25–28 Sep |
| 2006 | Saomai | 9–11 Aug | 2017 | Nesat | 26–30 Jul |
| 2006 | Shanshan | 14–16 Sep |
References
- Wei, C.C. Conceptual weather environmental forecasting system for identifying potential failure of under-construction structures during typhoons. J. Wind Eng. Ind. Aerodyn. 2017, 168, 48–59. [Google Scholar] [CrossRef]
- Al-Yahyai, S.; Charabi, Y.; Gastli, A. Review of the use of numerical weather prediction (NWP) models for wind energy assessment. Renew. Sustain. Energy Rev. 2010, 14, 3192–3198. [Google Scholar] [CrossRef]
- Pielke, R.A.; Cotton, W.R.; Walko, R.L.; Tremback, C.J.; Lyons, W.A.; Grasso, L.D.M.; Nicholls, E.; Moran, M.D.; Wesley, D.A.; Lee, T.J.; et al. A comprehensive meteorological modeling system—RAMS. Meteorol. Atmos. Phys. 1992, 49, 69–91. [Google Scholar] [CrossRef]
- Warner, T. Numerical Weather and Climate Prediction; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, J.; Xia, J.; Dai, Y.; Sheng, Y.; Yue, J. Performance evaluation and accuracy enhancement of a day-ahead wind power forecasting system in China. Renew. Energy 2012, 43, 234–241. [Google Scholar] [CrossRef]
- Yang, M.J.; Ching, L. A modeling study of Typhoon Toraji (2001): Physical parameterization sensitivity and topographic effect. Terr. Atmos. Ocean. Sci. 2005, 16, 177–213. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. A time-split nonhydrostatic atmospheric model for weather research and forecasting applications. J. Comput. Phys. 2008, 227, 3465–3485. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C. A sensitivity study of the WRF model in wind simulation for an area of high wind energy. Environ. Model. Softw. 2012, 33, 23–34. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.; Barker, D.; Duda, M.; Huang, X.Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; NCAR Technical Note NCAR/TN-475+STR; NCAR: Boulder, CO, USA, 2008.
- Huang, W.R.; Chang, Y.H.; Hsu, H.H.; Cheng, C.T.; Tu, C.Y. Dynamical downscaling simulation and future projection of summer rainfall in Taiwan: Contributions from different types of rain events. J. Geophys. Res. Atmos. 2016, 121, 13973–13988. [Google Scholar] [CrossRef]
- Di, Z.; Gong, W.; Gan, Y.; Shen, C.; Duan, Q. Combinatorial optimization for WRF physical parameterization schemes: A case study of three-day typhoon simulations over the Northwest Pacific Ocean. Atmosphere 2019, 10, 233. [Google Scholar] [CrossRef]
- Ming, F.C.; Jolivet, S.; Liou, Y.A.; Jégou, F.; Mekies, D.; Hong, J.S. Elliptical structures of gravity waves produced by Typhoon Soudelor in 2015 near Taiwan. Atmosphere 2019, 10, 260. [Google Scholar] [CrossRef]
- Mylonas, M.P.; Douvis, K.C.; Polychroni, I.D.; Politi, N.; Nastos, P.T. Analysis of a Mediterranean tropical-like cyclone: Sensitivity to WRF parameterizations and horizontal resolution. Atmosphere 2019, 10, 425. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Barbariol, F.; Benetazzo, A.; Bergamasco, A.; Bonaldo, D.; Cassardo, C.; Falcieri, F.M.; Modugno, G.; Russo, A.; et al. Sensitivity of a Mediterranean tropical-like cyclone to different model configurations and coupling strategies. Atmosphere 2017, 8, 92. [Google Scholar] [CrossRef]
- Wei, C.C. Wavelet support vector machines for forecasting precipitation in tropical cyclones: Comparisons with GSVM, regression, and MM5. Weather Forecast. 2012, 27, 438–450. [Google Scholar] [CrossRef]
- Tao, W.K.; Shi, J.J.; Lin, P.L.; Chen, J.; Lang, S.; Chang, M.Y.; Yang, M.J.; Wu, C.C.; Peters-Lidard, C.; Sui, C.H.; et al. High-resolution numerical simulation of the extreme rainfall associated with typhoon Morakot. Part I: Comparing the impact of microphysics and PBL parameterizations with observations. Terr. Atmos. Ocean. Sci. 2011, 22, 673–696. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Xu, H.; Chen, L. A possible mechanism responsible for exceptional rainfall over Taiwan from Typhoon Morakot. Atmos. Sci. Lett. 2011, 12, 294–299. [Google Scholar] [CrossRef]
- Hsiao, L.F.; Yang, M.J.; Lee, C.S.; Kuo, H.C.; Shih, D.S.; Tsai, C.C.; Wang, C.J.; Chang, L.Y.; Chen, D.Y.C.; Feng, L.; et al. Ensemble forecasting of typhoon rainfall and floods over a mountainous watershed in Taiwan. J. Hydrol. 2013, 506, 55–68. [Google Scholar] [CrossRef]
- Wu, Z.; Jiang, C.; Deng, B.; Chen, J.; Liu, X. Sensitivity of WRF simulated typhoon track and intensity over the South China Sea to horizontal and vertical resolutions. Acta Oceanol. Sin. 2019, 38, 74–83. [Google Scholar] [CrossRef]
- Smola, A.; Vishwanathan, S.V.N. Introduction to Machine Learning; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Wei, C.C. Meta-heuristic Bayesian networks retrieval combined polarization corrected temperature and scattering index for precipitations. Neurocomputing 2014, 136, 71–81. [Google Scholar] [CrossRef]
- Wei, C.C. Comparing lazy and eager learning models for water level forecasting in river-reservoir basins of inundation regions. Environ. Model. Softw. 2015, 63, 137–155. [Google Scholar] [CrossRef]
- Currie, J.J.; Goulet, P.J.; Ratsimandresy, A.W. Wind conditions in a Fjordlike Bay and predictions of wind speed using neighboring stations employing neural network models. J. Appl. Meteorol. Climatol. 2014, 53, 1525–1537. [Google Scholar] [CrossRef]
- Etienne, C.; Lehmann, A.; Goyette, S.; Lopez-Moreno, J.; Beniston, M. Spatial predictions of extreme wind speeds over Switzerland using generalized additive models. J. Appl. Meteorol. Climatol. 2010, 49, 1956–1970. [Google Scholar] [CrossRef]
- Kozar, M.E.; Misra, V.; Powell, M.D. Hindcasts of integrated kinetic energy in Atlantic tropical cyclones: A neural network prediction scheme. Mon. Weather Rev. 2016, 144, 4591–4603. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.; Li, Y. An EMD-recursive ARIMA method to predict wind speed for railway strong wind warning system. J. Wind Eng. Ind. Aerodyn. 2015, 141, 27–38. [Google Scholar] [CrossRef]
- Wei, C.C. Surface wind nowcasting in the Penghu Islands based on classified typhoon tracks and the effects of the Central Mountain Range of Taiwan. Weather Forecast. 2014, 29, 1425–1450. [Google Scholar] [CrossRef]
- Wei, C.C. Examining El Niño–Southern Oscillation effects in the subtropical zone to forecast long-distance total rainfall from typhoons: A case study in Taiwan. J. Atmos. Ocean. Technol. 2017, 34, 2141–2161. [Google Scholar] [CrossRef]
- Yang, J.; Astitha, M.; Anagnostou, E.N.; Hartman, B.M. Using a Bayesian regression approach on dual-model windstorm simulations to improve wind speed prediction. J. Appl. Meteorol. Climatol. 2017, 56, 1155–1174. [Google Scholar] [CrossRef]
- Li, L.; Xiao, Y.; Kareem, A.; Song, L.; Qin, P. Modeling typhoon wind power spectra near sea surface based on measurements in the South China sea. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 565–576. [Google Scholar] [CrossRef]
- Wei, C.C. Forecasting surface wind speeds over offshore islands near Taiwan during tropical cyclones: Comparisons of data-driven algorithms and parametric wind representations. J. Geophys. Res. Atmos. 2015, 120, 1826–1847. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, R.; Zhou, Y. Transfer learning for short-term wind speed prediction with deep neural networks. Renew. Energy 2016, 85, 83–95. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A fast learning algorithm for deep belief nets. Neural Comput. 2014, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Krinitskiy, M.; Verezemskaya, P.; Grashchenkov, K.; Tilinina, N.; Gulev, S.; Lazzara, M. Deep convolutional neural networks capabilities for binary classification of polar mesocyclones in satellite mosaics. Atmosphere 2018, 9, 426. [Google Scholar] [CrossRef]
- Wei, C.C.; Peng, P.C.; Tsai, C.H.; Huang, C.L. Regional forecasting of wind speeds during typhoon landfall in Taiwan: A case study of westward-moving typhoons. Atmosphere 2018, 9, 141. [Google Scholar] [CrossRef]
- Tsai, C.C.; Wei, C.C.; Hou, T.H.; Hsu, T.W. Artificial neural network for forecasting wave heights along a ship’s route during hurricanes. J. Waterw. Port Coast. Ocean Eng. 2018, 144, 04017042. [Google Scholar] [CrossRef]
- Wang, W.; Bruyère, C.; Duda, M.; Dudhia, J.; Gill, D.; Kavulich, M.; Keene, K.; Lin, H.-C.; Michalakes, J.; Rizvi, S.; et al. WRF Version 3 Modeling System User’s Guide; Mesoscale & Microscale Meteorology Division, National Center for Atmospheric Research: Boulder, CO, USA, 2016.
- Du, J.; Xu, Y. Hierarchical deep neural network for multivariate regression. Pattern Recognit. 2017, 63, 149–157. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, X.; Metallinou, A. Deep neural network acoustic models for spoken assessment applications. Speech Commun. 2015, 73, 14–27. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010; pp. 807–814. [Google Scholar]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 105, 2295–2329. [Google Scholar] [CrossRef]
- Yeh, T.C.; Chen, S.H.; Hong, J.S. The Forecast Technique Development Studies on the Typhoon Track, Rainfall and Winds Forecast over Taiwan Area: A Study on the Implementation of WRF Typhoon Forecasting Component in the Operational Environment of CWB; Funded by Ministry of Science and Technology of Taiwan, No. NSC96-2625-Z-052-003; MOST: Taipei, Taiwan, 2008. (In Chinese) [Google Scholar]
- Yeh, T.C.; Terng, C.T.; Lee, C.S.; Yang, M.J. The Forecast Technique Development Studies on the Typhoon Track, Rainfall and Winds Forecast over Taiwan Area: A Study on the Implementation of WRF Typhoon Forecasting Component in the Operational Environment of CWB (II); Funded by Ministry of Science and Technology of Taiwan, No. NSC97-2625-M-052-002; MOST: Taipei, Taiwan, 2009. (In Chinese) [Google Scholar]
- Yeh, T.C.; Terng, C.T.; Lee, C.S.; Yang, M.J. The Forecast Technique Development Studies on the Typhoon Track, Rainfall and Winds Forecast over Taiwan Area: A Study on the Implementation of WRF Typhoon Forecasting Component in the Operational Environment of CWB (III); Funded by Ministry of Science and Technology of Taiwan, No. NSC-98-2625-M-052-008; MOST: Taipei, Taiwan, 2010. (In Chinese) [Google Scholar]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Hong, S.Y.; Dudhia, J.; Chen, S.H. A revised approach to ice microphysical processes for the bulk parameterization of clouds and precipitation. Mon. Weather Rev. 2004, 132, 103–120. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. A one-dimensional entraining/detraining plume model and its application in convective parameterization. J. Atmos. Sci. 1990, 47, 2784–2802. [Google Scholar] [CrossRef]
- Kain, J.S.; Fritsch, J.M. Convective Parameterization for Mesoscale Models: The Kain-Fritsch Scheme; The Representation of Cumulus Convection in Numerical Models; Meteorological Monographs, No. 24; American Meteor Society: Geneseo, NY, USA, 1993; pp. 165–170.
- Mlawer, E.J.; Clough, S.A. On the extension of RRTM to the shortwave region. In Proceedings of the Sixth Atmospheric Measurement (ARM) Science Team Meeting, CONF-9603149, San Antonio, TX, USA, 4–7 March 1996; U.S. Department of Energy: Washington, DC, USA, 1997; pp. 223–226. [Google Scholar]
- Taylor, R. Interpretation of the correlation coefficient: A basic review. J. Diagn. Med. Sonogr. 1990, 1, 35–39. [Google Scholar] [CrossRef]
- Trenn, S. Multilayer perceptrons: Approximation order and necessary number of hidden units. IEEE Trans. Neural Netw. 2008, 19, 836–844. [Google Scholar] [CrossRef] [PubMed]
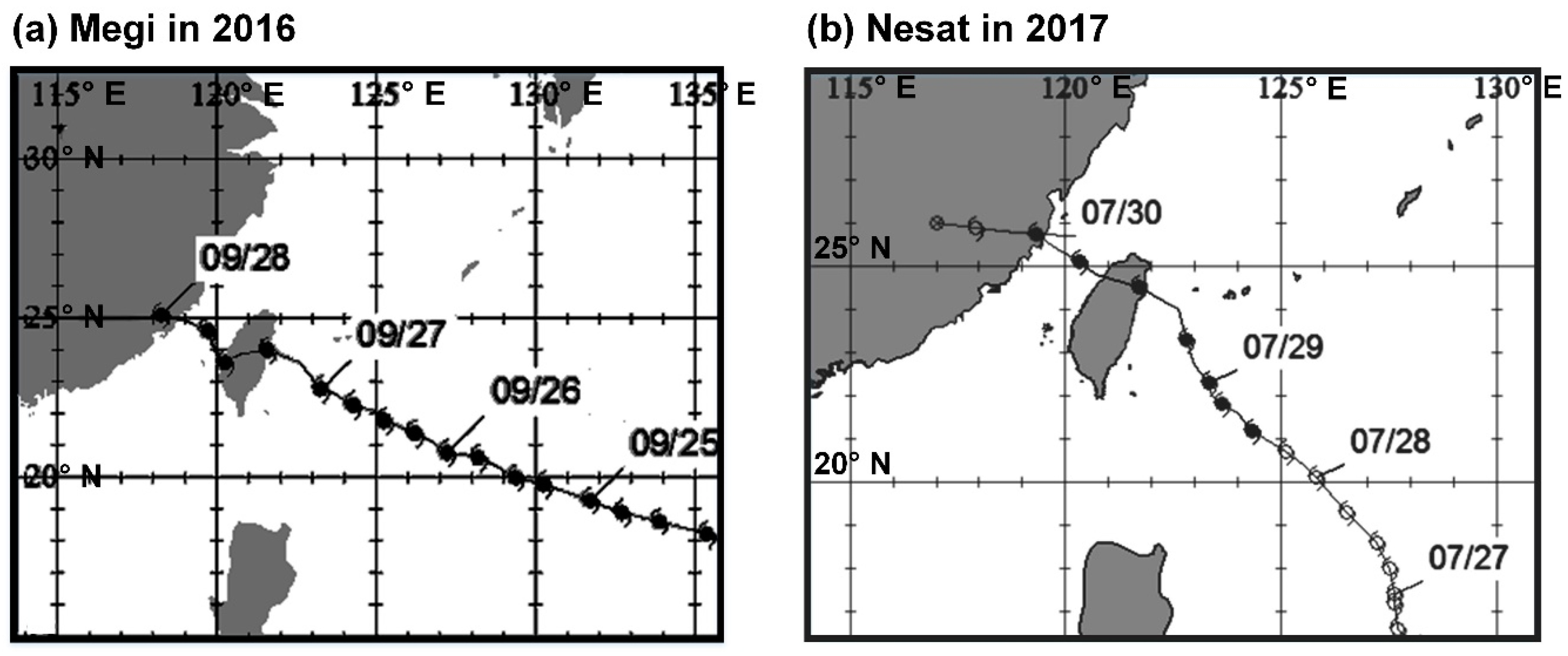
| Characteristics | Megi | Nesat |
|---|---|---|
| Duration of affecting periods | 90 h | 114 h |
| Average of pressure at typhoon center | 958.9 hPa | 972.4 hPa |
| Maximal typhoon radius of the winds over 15.5 m/s | 225.6 km | 159.5 km |
| Average moving speed of typhoon | 18.3 km/h | 16.6 km/h |
| Maximum wind speed of typhoon center | 45 m/s | 40 m/s |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, C.-C. Study on Wind Simulations Using Deep Learning Techniques during Typhoons: A Case Study of Northern Taiwan. Atmosphere 2019, 10, 684. https://doi.org/10.3390/atmos10110684
Wei C-C. Study on Wind Simulations Using Deep Learning Techniques during Typhoons: A Case Study of Northern Taiwan. Atmosphere. 2019; 10(11):684. https://doi.org/10.3390/atmos10110684
Chicago/Turabian StyleWei, Chih-Chiang. 2019. "Study on Wind Simulations Using Deep Learning Techniques during Typhoons: A Case Study of Northern Taiwan" Atmosphere 10, no. 11: 684. https://doi.org/10.3390/atmos10110684
APA StyleWei, C.-C. (2019). Study on Wind Simulations Using Deep Learning Techniques during Typhoons: A Case Study of Northern Taiwan. Atmosphere, 10(11), 684. https://doi.org/10.3390/atmos10110684





