Scaling Properties of Atmospheric Wind Speed in Mesoscale Range
Abstract
:1. Introduction
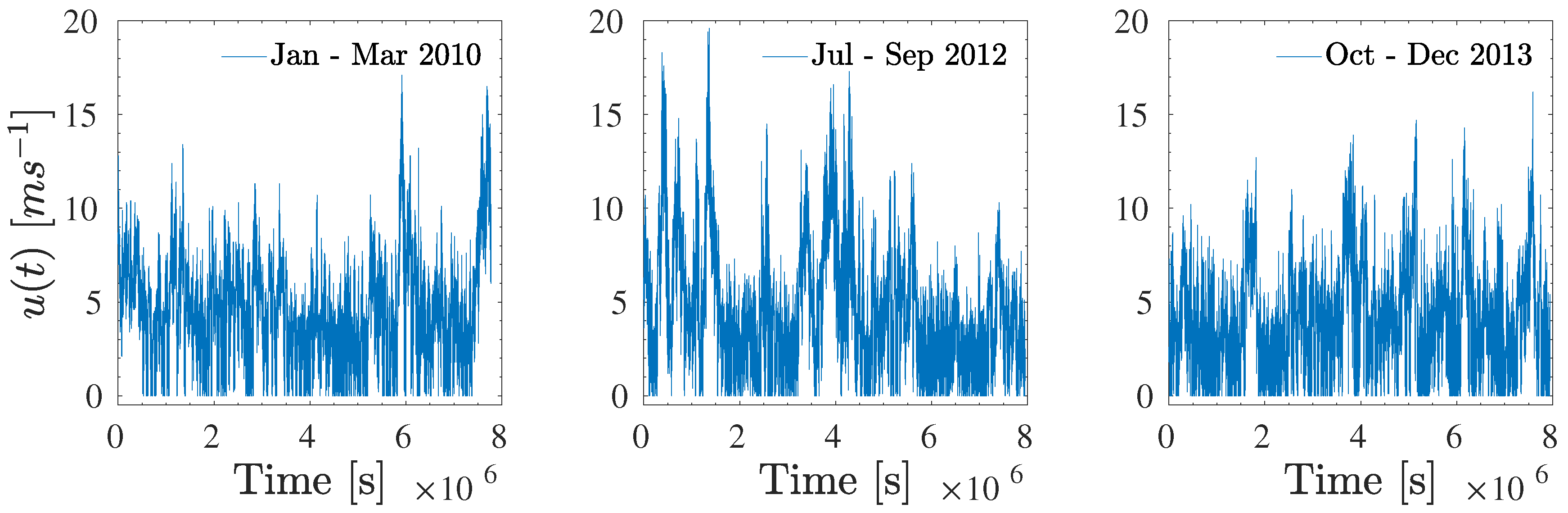
2. Analysis of Mesoscale Wind Velocity Data
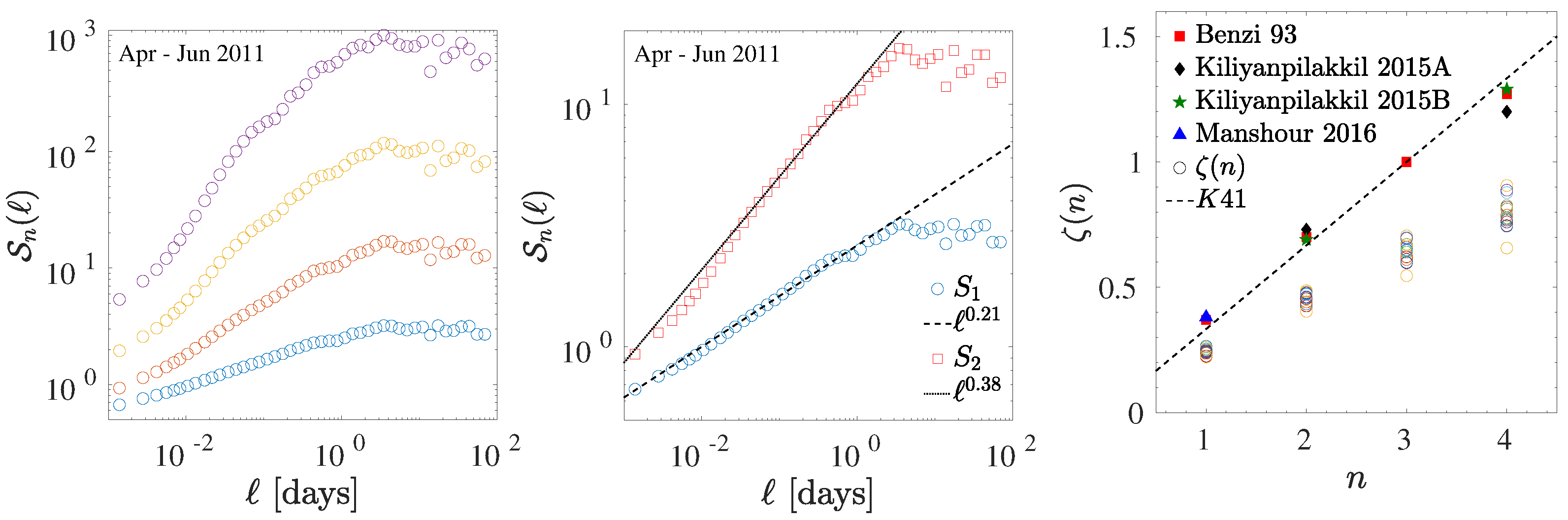
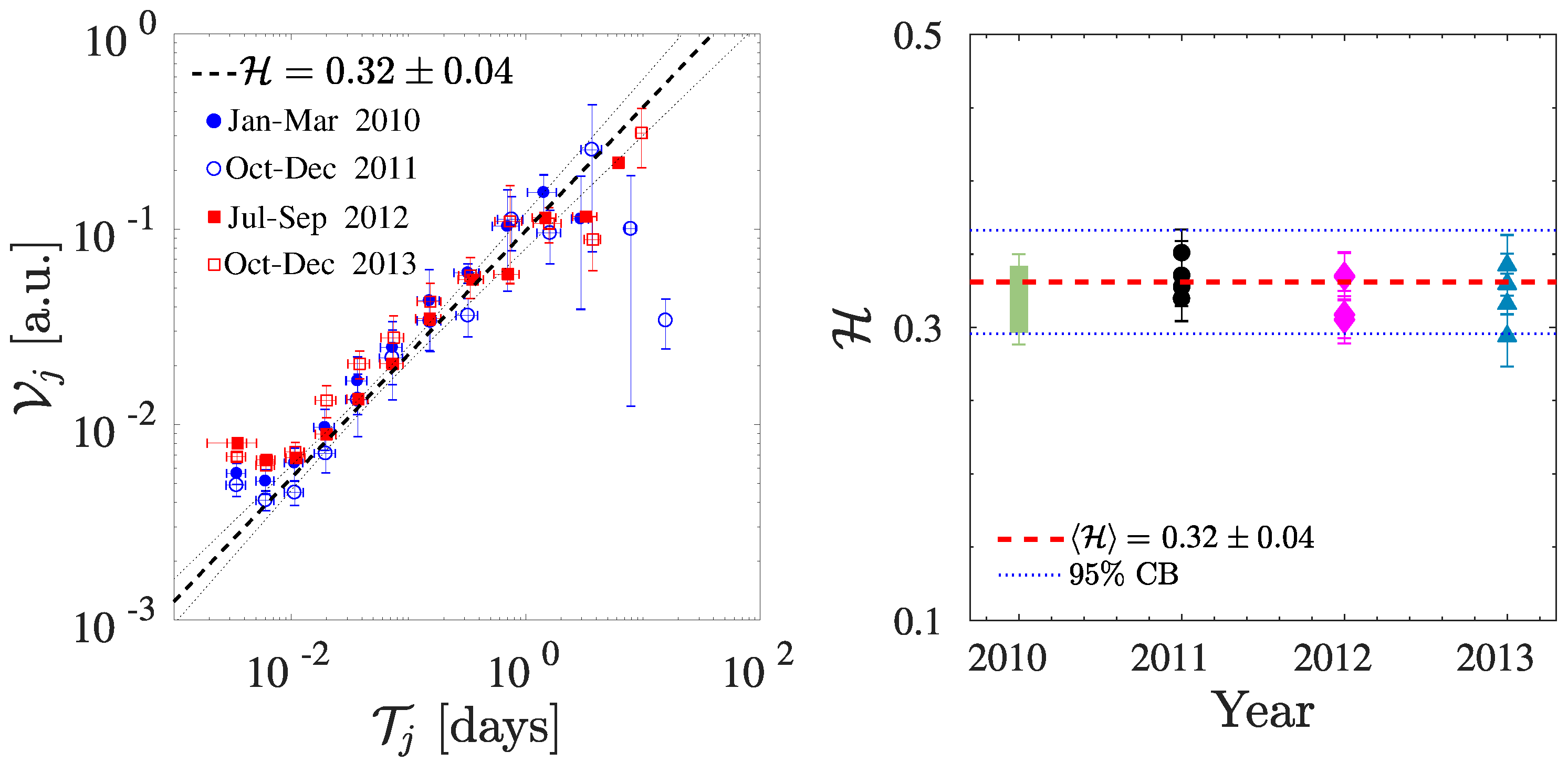
3. Structure Function Analysis and Hurst Exponent Estimation for Mesoscale Wind Speed
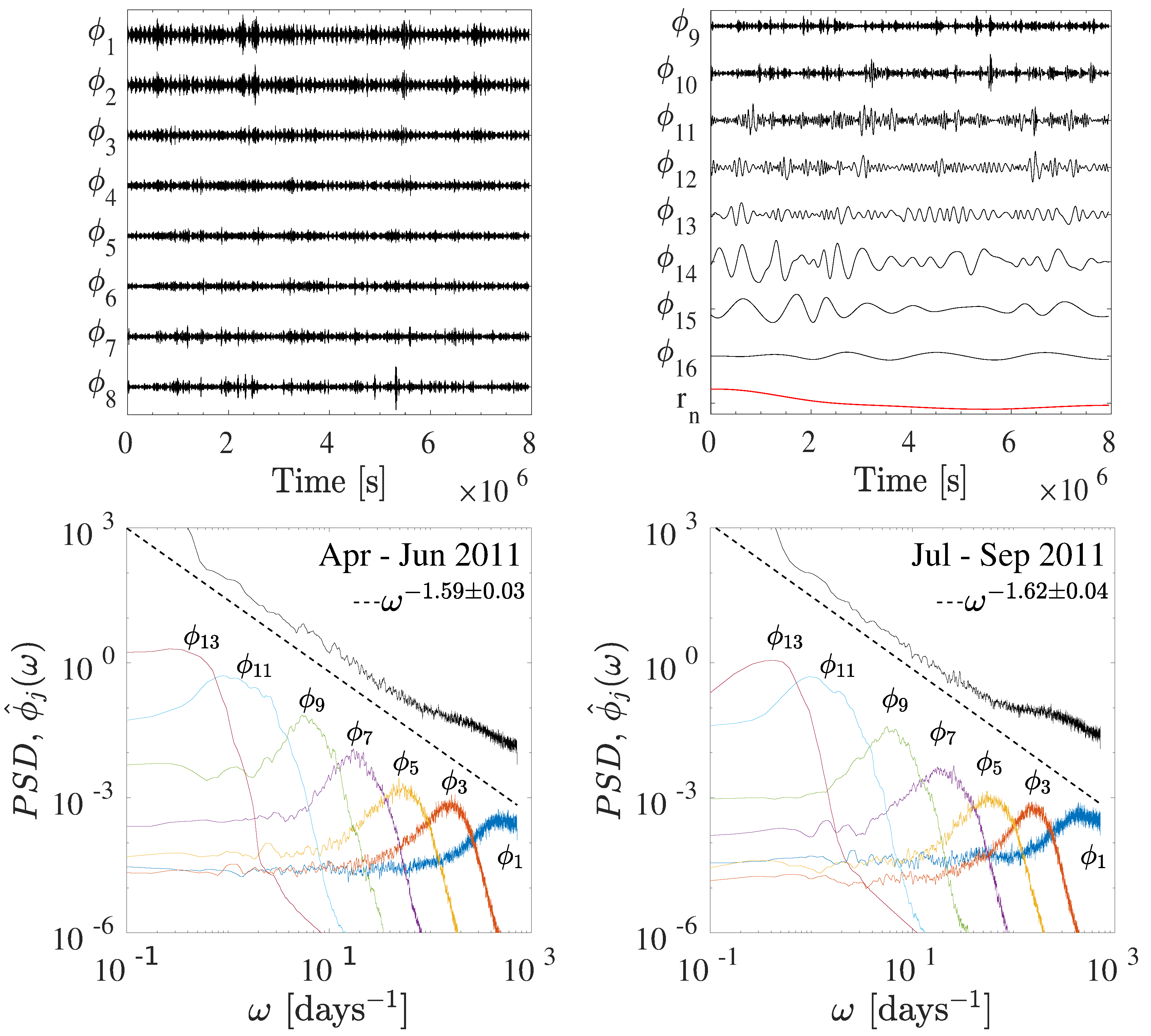
4. Hurst Exponent Estimation from the Empirical Mode Decomposition
Hurst Exponent Estimation from IMF Scaling Relations
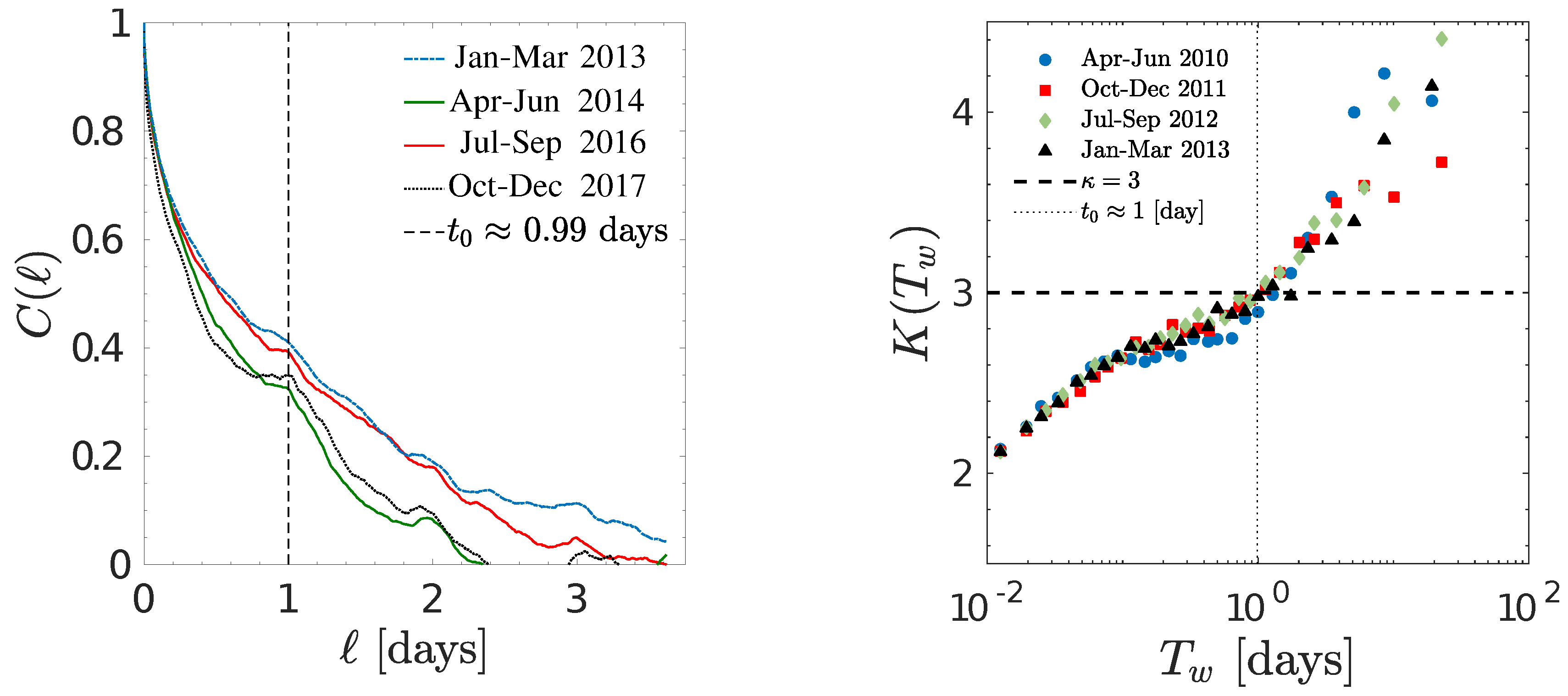
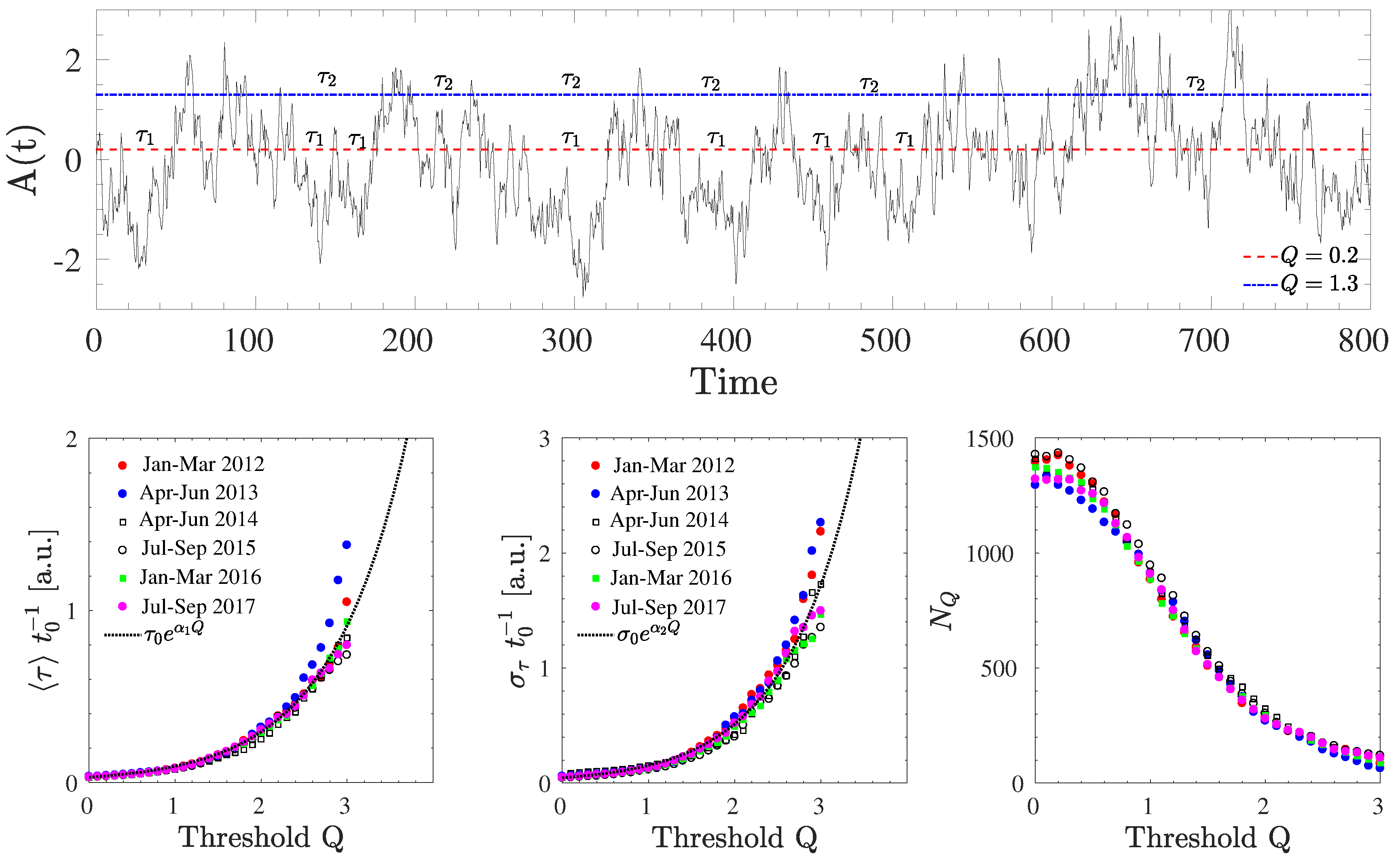
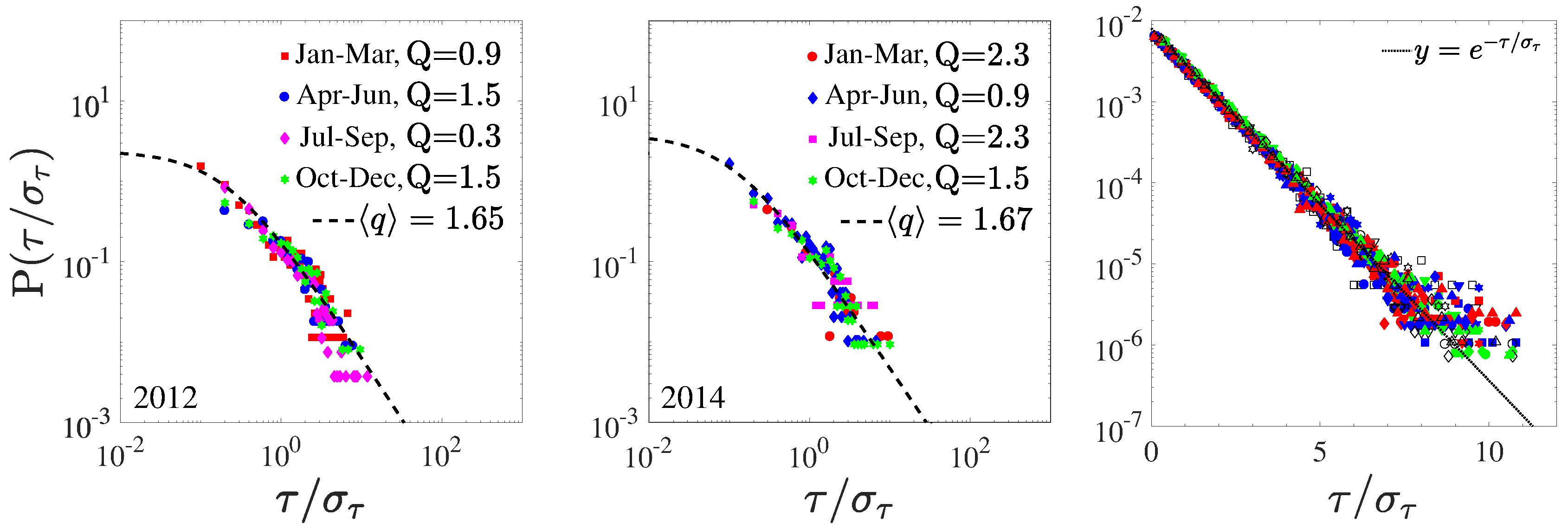
5. Interoccurrence Times Statistics in Mesoscale Wind
6. Scaling of High-Order Moments: Intermittency and Arbitrary Order Hilbert Spectral Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stull, R.B. An Introduction to Boundary Layer Meteorology, 1st ed.; Atmospheric and Oceanographic Sciences Library; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Garratt, J.R. The Atmospheric Boundary Layer; Cambridge Atmospheric and Space Science Series; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Rorai, C.; Mininni, P.D.; Pouquet, A. Turbulence comes in bursts in stably stratified flows. Phys. Rev. E 2014, 89, 043002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feraco, F.; Marino, R.; Pumir, A.; Primavera, L.; Mininni, P.D.; Pouquet, A.; Rosenberg, D. Vertical drafts and mixing in stratified turbulence: Sharp transition with Froude number. EPL 2018, 123, 44002. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Atmospheric Turbulence. Ann. Rev. Fluid Mech. 1992, 24, 205. [Google Scholar] [CrossRef]
- Lyons, T.J. Mesoscale wind spectra. Q. J. R. Meteorol. Soc. 1975, 101, 901–910. [Google Scholar] [CrossRef]
- Baïle, R.; Muzy, J.F.M.C. Spatial Intermittency of Surface Layer Wind Fluctuations at Mesoscale Range. Phys. Rev. Lett. 2010, 105, 254501. [Google Scholar] [CrossRef] [PubMed]
- Muzy, J.F.m.c.; Baïle, R.; Poggi, P. Intermittency of surface-layer wind velocity series in the mesoscale range. Phys. Rev. E 2010, 81, 056308. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Telesca, L.; Lovallo, M. Analysis of the time dynamics in wind records by means of multifractal detrended fluctuation analysis and the Fisher–Shannon information plane. J. Stat. Mech. Theory Exp. 2011, 2011, P07001. [Google Scholar] [CrossRef]
- Kiliyanpilakkil, V.P.; Basu, S.; Ruiz-Columbié, A.; Araya, G.; Castillo, L.; Hirth, B.; Burgett, W. Buoyancy effects on the scaling characteristics of atmospheric boundary-layer wind fields in the mesoscale range. Phys. Rev. E 2015, 92, 033005. [Google Scholar] [CrossRef] [Green Version]
- Bandi, M.M. Spectrum of Wind Power Fluctuations. Phys. Rev. Lett. 2017, 118, 028301. [Google Scholar] [CrossRef] [Green Version]
- McComb, W.D.; Yoffe, S.R.; Linkmann, M.F.; Berera, A. Spectral analysis of structure functions and their scaling exponents in forced isotropic turbulence. Phys. Rev. E 2014, 90, 053010. [Google Scholar] [CrossRef] [Green Version]
- McComb, W.D.; May, M.Q. The Effect of Kolmogorov (1962) Scaling on the Universality of Turbulence Energy Spectra. arXiv 2018, arXiv:1812.09174. [Google Scholar]
- Huang, Y.X.; Schmitt, F.G.; Hermand, J.P.; Gagne, Y.; Lu, Z.M.; Liu, Y.L. Arbitrary-order Hilbert spectral analysis for time series possessing scaling statistics: Comparison study with detrended fluctuation analysis and wavelet leaders. Phys. Rev. E 2011, 84, 016208. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.X.; Schmitt, F.G.; Lu, Z.M.; Fougairolles, P.; Gagne, Y.; Liu, Y.L. Second-order structure function in fully developed turbulence. Phys. Rev. E 2010, 82, 026319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carbone, F.; Gencarelli, C.N.; Hedgecock, I.M. Lagrangian statistics of mesoscale turbulence in a natural environment: The Agulhas return current. Phys. Rev. E 2016, 94, 063101. [Google Scholar] [CrossRef] [PubMed]
- Mendonca, B.G.; Iwaoka, W.T. The Trade Wind Inversion at the Slopes of Mauna Loa, Hawaii. J. Appl. Meteorol. 1969, 8, 213–219. [Google Scholar] [CrossRef] [Green Version]
- Mendonca, B.G. Local Wind Circulation on the Slopes of Mauna Loa. J. Appl. Meteorol. 1969, 8, 533–541. [Google Scholar] [CrossRef] [Green Version]
- Ryan, S. The wind field around Mauna Loa derived from surface and balloon observations. J. Geophys. Res. Atmos. 1997, 102, 10711–10725. [Google Scholar] [CrossRef]
- Ward, D.J.; Galewsky, J. Exploring landscape sensitivity to the Pacific Trade Wind Inversion on the subsiding island of Hawaii. J. Geophys. Res. Earth Surf. 2014, 119, 2048–2069. [Google Scholar] [CrossRef]
- Frisch, U. (Ed.) Turbulence: The Legacy of A. N. Kolmogorov; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Tomas, B.; Mogens, H.J.; Giovanni, P.; Vulpiani, A. Dynamical Systems Approach to Turbulence; Cambridge Nonlinear Science Series; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kiliyanpilakkil, V.P.; Basu, S. Extended self-similarity of atmospheric boundary layer wind fields in mesoscale regime: Is it real? EPL Europhys. Lett. 2015, 112, 64003. [Google Scholar] [CrossRef] [Green Version]
- Biferale, L.; Procaccia, I. Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 2005, 414, 43–164. [Google Scholar] [CrossRef] [Green Version]
- Mazzitelli, I.; Lanotte, A.S. Active and passive scalar intermittent statistics in turbulent atmospheric convection. Phys. D Nonlinear Phenom. 2012, 241, 251–259. [Google Scholar] [CrossRef]
- Antonelli, M.; Lanotte, A.; Mazzino, A. Anisotropies and Universality of Buoyancy-Dominated Turbulent Fluctuations: A Large-Eddy Simulation Study. J. Atmos. Sci. 2007, 64, 2642–2656. [Google Scholar] [CrossRef] [Green Version]
- Biferale, L.; Toschi, F. Anisotropic Homogeneous Turbulence: Hierarchy and Intermittency of Scaling Exponents in the Anisotropic Sectors. Phys. Rev. Lett. 2001, 86, 4831–4834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Biferale, L.; Daumont, I.; Lanotte, A.; Toschi, F. Theoretical and numerical study of highly anisotropic turbulent flows. Eur. J. Mech. B/Fluids 2004, 23, 401–414. [Google Scholar] [CrossRef]
- Stiperski, I.; Calaf, M. Dependence of near-surface similarity scaling on the anisotropy of atmospheric turbulence. Q. J. R. Meteorol. Soc. 2018, 144, 641–657. [Google Scholar] [CrossRef] [PubMed]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.S.P. (Eds.) The Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2005. [Google Scholar]
- Boudraa, A.O.; Cexus, J.C. EMD-Based Signal Filtering. IEEE Trans. Instrum. Meas. 2007, 56, 2196–2202. [Google Scholar] [CrossRef]
- Ludescher, J.; Tsallis, C.; Bunde, A. Universal Behaviour of Interoccurrence Times between Losses in Financial Markets: An Analytical Description. EPL Europhys. Lett. 2011, 95, 68002. [Google Scholar] [CrossRef]
- Ludescher, J.; Bunde, A. Universal Behavior of the Interoccurrence Times between Losses in Financial Markets: Independence of the Time Resolution. Phys. Rev. E 2014, 90, 062809. [Google Scholar] [CrossRef]
- Manshour, P.; Anvari, M.; Reinke, N.; Sahimi, M.; Tabar, M.R.R. Interoccurrence time statistics in fully-developed turbulence. Sci. Rep. 2016, 6, 27452. [Google Scholar] [CrossRef]
- Carbone, F.; Bruno, A.G.; Naccarato, A.; De Simone, F.; Gencarelli, C.N.; Sprovieri, F.; Hedgecock, I.M.; Landis, M.S.; Skov, H.; Pfaffhuber, K.A.; et al. The Superstatistical Nature and Interoccurrence Time of Atmospheric Mercury Concentration Fluctuations. J. Geophys. Res. Atmos. 2018, 123, 764–774. [Google Scholar] [CrossRef] [PubMed]
- Davis, A.; Marshak, A.; Wiscombe, W.; Cahalan, R. Multifractal characterizations of nonstationarity and intermittency in geophysical fields: Observed, retrieved, or simulated. J. Geophys. Res. Atmos. 1994, 99, 8055–8072. [Google Scholar] [CrossRef]
- Benzi, R.; Ciliberto, S.; Tripiccione, R.; Baudet, C.; Massaioli, F.; Succi, S. Extended self-similarity in turbulent flows. Phys. Rev. E 1993, 48, R29–R32. [Google Scholar] [CrossRef] [PubMed]
- Carbone, F.; Sorriso-Valvo, L.; Alberti, T.; Lepreti, F.; Chen, C.H.K.; Němeček, Z.; Šafránková, J. Arbitrary-order Hilbert Spectral Analysis and Intermittency in Solar Wind Density Fluctuations. Astrophys. J. 2018, 859, 27. [Google Scholar] [CrossRef]
- Sharma, N.C.; Barnes, J.E. Boundary Layer Characteristics over a High Altitude Station, Mauna Loa Observatory. Aerosol Air Qual. Res. 2016, 16, 729–737. [Google Scholar] [CrossRef] [Green Version]
- Mefford, T.K.; Bieniulis, M.; Halter, B.; Peterson, J. Meteorological Measurements. In CMDL Summary Report 1994–1995; U.S. Department of Commerce National Oceanic and Atmospheric Administration Oceanic and Atmospheric Research: Boulder, CO, USA, 1996; p. 17. [Google Scholar]
- Taguchi, S.; Murayama, S.; Higuchi, K. Sensitivity of inter-annual variation of CO2 seasonal cycle at Mauna Loa to atmospheric transport. Tellus B 2003, 55, 547–554. [Google Scholar] [CrossRef]
- Lintner, B.R.; Buermann, W.; Koven, C.D.; Fung, I.Y. Seasonal circulation and Mauna Loa CO2 variability. J. Geophys. Res. Atmos. 2006, 111, D13. [Google Scholar] [CrossRef]
- Yang, G.Y.; Slingo, J. The Diurnal Cycle in the Tropics. Mon. Weather Rev. 2001, 129, 784–801. [Google Scholar] [CrossRef]
- Beck, C.; Cohen, E.G.D.; Swinney, H.L. From time series to superstatistics. Phys. Rev. E 2005, 72, 056133. [Google Scholar] [CrossRef] [Green Version]
- Queirós, S.M.D. On new conditions for evaluate long-time scales in superstatistical time series. Phys. A Stat. Mech. Appl. 2007, 385, 191–198. [Google Scholar] [CrossRef]
- Jizba, P.; Korbel, J.; Lavička, H.; Prokš, M.; Svoboda, V.; Beck, C. Transitions between superstatistical regimes: Validity, breakdown and applications. Phys. A Stat. Mech. Appl. 2018, 493, 29–46. [Google Scholar] [CrossRef] [Green Version]
- Kolmogorov, A.N. The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. C. R. Acad. Sci. U. R. S. S. 1941, 30, 301. [Google Scholar] [CrossRef]
- Tarnopolski, M. On the relationship between the Hurst exponent, the ratio of the mean square successive difference to the variance, and the number of turning points. Phys. A Stat. Mech. Appl. 2016, 461, 662–673. [Google Scholar] [CrossRef] [Green Version]
- Stolovitzky, G.; Sreenivasan, K.R. Kolmogorov’s refined similarity hypotheses for turbulence and general stochastic processes. Rev. Mod. Phys. 1994, 66, 229–240. [Google Scholar] [CrossRef]
- Salisbury, J.I.; Wimbush, M. Using modern time series analysis techniques to predict ENSO events from the SOI time series. Nonlinear Process. Geophys. 2002, 9, 341–345. [Google Scholar] [CrossRef] [Green Version]
- Jánosi, I.M.; Müller, R. Empirical mode decomposition and correlation properties of long daily ozone records. Phys. Rev. E 2005, 71, 056126. [Google Scholar] [CrossRef] [Green Version]
- McDonald, A.J.; Baumgaertner, A.J.G.; Fraser, G.J.; George, S.E.; Marsh, S. Empirical Mode Decomposition of the atmospheric wave field. Ann. Geophys. 2007, 25, 375–384. [Google Scholar] [CrossRef]
- Vecchio, A.; Carbone, V. Amplitude-frequency fluctuations of the seasonal cycle, temperature anomalies, and long-range persistence of climate records. Phys. Rev. E 2010, 82, 066101. [Google Scholar] [CrossRef]
- Vecchio, A.; Capparelli, V.; Carbone, V. The complex dynamics of the seasonal component of USA’s surface temperature. Atmos. Chem. Phys. 2010, 10, 9657–9665. [Google Scholar] [CrossRef]
- Capparelli, V.; Vecchio, A.; Carbone, V. Long-range persistence of temperature records induced by long-term climatic phenomena. Phys. Rev. E 2011, 84, 046103. [Google Scholar] [CrossRef]
- Vecchio, A.; Anzidei, M.; Carbone, V. New insights on the tsunami recording of the May, 21, 2003, Mw 6.9 Boumerdès earthquake from tidal data analysis. J. Geodyn. 2014, 79, 39–49. [Google Scholar] [CrossRef]
- Carbone, F.; Landis, M.S.; Gencarelli, C.N.; Naccarato, A.; Sprovieri, F.; De Simone, F.; Hedgecock, I.M.; Pirrone, N. Sea surface temperature variation linked to elemental mercury concentrations measured on Mauna Loa. Geophys. Res. Lett. 2016, 43, 7751–7757. [Google Scholar] [CrossRef] [Green Version]
- Alberti, T.; Consolini, G.; Carbone, V.; Yordanova, E.; Marcucci, M.F.; De Michelis, P. Multifractal and Chaotic Properties of Solar Wind at MHD and Kinetic Domains: An Empirical Mode Decomposition Approach. Entropy 2019, 21, 320. [Google Scholar] [CrossRef]
- Xuan, Z.; Xie, S.; Sun, Q. The Empirical Mode Decomposition Process of Non-stationary Signals. In Proceedings of the 2010 International Conference on Measuring Technology and Mechatronics Automation, Changsha, China, 13–14 March 2010; Volume 3, pp. 866–869. [Google Scholar] [CrossRef]
- Liu, Q.; Fujita, T.; Watanabe, M.; Mitani, Y. Hilbert-Huang Transform and Wavelet Analysis of Oscillation Characteristics for Japan Western 60 Hz Power System Based on Campus WAMS. In IFAC Proceedings Volumes; Elsevier: Amsterdam, The Netherlands, 2012; Volume 45, pp. 144–149. [Google Scholar]
- Cummings, D.A.; Irizarry, R.A.; Huang, N.E.; Endy, T.P.; Nisalak, A.; Ungchusak, K.; Burke, D.S. Travelling waves in the occurrence of dengue haemorrhagic fever in Thailand. Nature 2004, 427, 344–347. [Google Scholar] [CrossRef] [PubMed]
- Rilling, G.; Flandrin, P.; Goncalves, P. On Empirical Mode Decomposition and Its Algorithms. In IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing; 2003; Available online: https://pdfs.semanticscholar.org/3f61/6db40f5da4446a039bb6ae5d801d4c616f2b.pdf?_ga=2.169233441.1820239345.1570677681-561144769.1570677681 (accessed on 20 September 2019).
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 460, 1597–1611. [Google Scholar] [CrossRef]
- Flandrin, P.; Rilling, G.; Goncalves, P. Empirical mode decomposition as a filter bank. IEEE Signal Process. Lett. 2004, 11, 112–114. [Google Scholar] [CrossRef]
- Flandrin, P.; Goncalves, P. Empirical mode decomposition as data-driven wavelet-like expansions. Int. J. Wavel. Multires. Inf. Process. 2004, 1, 477–496. [Google Scholar] [CrossRef]
- Huang, Y.X.; Schmitt, F.G.; Lu, Z.M.; Liu, Y.L. An amplitude-frequency study of turbulent scaling intermittency using Empirical Mode Decomposition and Hilbert Spectral Analysis. EPL Europhys. Lett. 2008, 84, 40010. [Google Scholar] [CrossRef]
- Thomas, W.G.; Dennis, N. Influence of the trade-wind inversion on the climate of a leeward mountain slope in Hawaii. Clim. Res. 1991, 1, 207–216. [Google Scholar]
- NCAR/HAO. Mauna Loa Seeing Study. 2006. Available online: https://archive.eol.ucar.edu/docs/isf/projects/mlo/report.shtml (accessed on 20 September 2019).
- He, P.; Basu, S. Extending a surface-layer Cn2 model for strongly stratified conditions utilizing a numerically generated turbulence dataset. Opt. Express 2016, 24, 9574–9582. [Google Scholar] [CrossRef]
- Nava, N.; Matteo, T.D.; Aste, T. Anomalous volatility scaling in high frequency financial data. Phys. A Stat. Mech. Appl. 2016, 447, 434–445. [Google Scholar] [CrossRef]
- Huang, Y.; Schmitt, F.G. Time dependent intrinsic correlation analysis of temperature and dissolved oxygen time series using empirical mode decomposition. J. Marine Syst. 2014, 130, 90–100. [Google Scholar] [CrossRef]
- Schmitt, F.; Schertzer, D.; Lovejoy, S. Estimation Of Universal Multifractal Indices For Atmospheric Turbulent Velocity Fields; 1994; pp. 274–281. Available online: https://www.worldscientific.com/doi/abs/10.1142/9789814503792_0025 (accessed on 20 September 2019).
- Lovejoy, S.; Schertzer, D.; Tuck, A.F. Fractal aircraft trajectories and nonclassical turbulent exponents. Phys. Rev. E 2004, 70, 036306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lovejoy, S.; Tuck, A.F.; Schertzer, D.; Hovde, S.J. Reinterpreting aircraft measurements in anisotropic scaling turbulence. Atmos. Chem. Phys. 2009, 9, 5007–5025. [Google Scholar] [CrossRef] [Green Version]
- Santhanam, M.; Kantz, H. Long-range correlations and rare events in boundary layer wind fields. Phys. A Stat. Mech. Appl. 2005, 345, 713–721. [Google Scholar] [CrossRef]
- Eichner, J.F.; Kantelhardt, J.W.; Bunde, A.; Havlin, S. Statistics of return intervals in long-term correlated records. Phys. Rev. E 2007, 75, 011128. [Google Scholar] [CrossRef] [Green Version]
- Bogachev, M.I.; Eichner, J.F.; Bunde, A. Effect of Nonlinear Correlations on the Statistics of Return Intervals in Multifractal Data Sets. Phys. Rev. Lett. 2007, 99, 240601. [Google Scholar] [CrossRef]
- Bogachev, M.I.; Bunde, A. Memory effects in the statistics of interoccurrence times between large returns in financial records. Phys. Rev. E 2008, 78, 036114. [Google Scholar] [CrossRef]
- Ferri, G.; Savio, M.R.; Plastino, A. Tsallis’ -triplet and the ozone layer. Phys. A Stat. Mech. Appl. 2010, 389, 1829–1833. [Google Scholar] [CrossRef]
- Ferri, G.L.; Figliola, A.; Rosso, O.A. Tsallis’ statistics in the variability of El Niño/Southern Oscillation during the Holocene epoch. Phys. A Stat. Mech. Appl. 2012, 391, 2154–2162. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Douglas, P.; Bergamini, S.; Renzoni, F. Tunable Tsallis Distributions in Dissipative Optical Lattices. Phys. Rev. Lett. 2006, 96, 110601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.; Wang, L. Cascade and intermittency of the sea surface temperature in the oceanic system. Phys. Scr. 2018, 94, 014009. [Google Scholar] [CrossRef] [Green Version]
- Cohen, L. Time-Frequency Analysis; Prentice Hall PTR: Englewood Cliffs, NJ, USA, 1995. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert Spectrum1. Ann. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Huang, N.E.; Chen, X.; Lo, M.T.; Wu, Z. On Hiblert spectral representation: A true time-frequency representation for nonlinear and nonstationary data. Adv. Adapt. Data Anal. 2011, 3, 63–93. [Google Scholar] [CrossRef]
- Arneodo, A.; Baudet, C.; Belin, F.; Benzi, R.; Castaing, B.; Chabaud, B.; Chavarria, R.; Ciliberto, S.; Camussi, R.; Chillà, F.; et al. Structure functions in turbulence, in various flow configurations, at Reynolds number between 30 and 5000, using extended self-similarity. EPL Europhys. Lett. 1996, 34, 411–416. [Google Scholar] [CrossRef]
- Schmitt, F.G. Linking Eulerian and Lagrangian structure functions’ scaling exponents in turbulence. Phys. A Stat. Mech. Appl. 2006, 368, 377–386. [Google Scholar] [CrossRef]
- Liu, L.; Hu, F.; Huang, S. A Multifractal Random-Walk Description of Atmospheric Turbulence: Small-Scale Multiscaling, Long-Tail Distribution, and Intermittency. Bound. Layer Meteorol. 2019, 172, 351–370. [Google Scholar] [CrossRef] [Green Version]
- Amati, G.; Benzi, R.; Succi, S. Extended self-similarity in boundary layer turbulence. Phys. Rev. E 1997, 55, 6985–6988. [Google Scholar] [CrossRef]
- Ruiz-Chavarria, G.; Ciliberto, S.; Baudet, C.; Lévêque, E. Scaling properties of the streamwise component of velocity in a turbulent boundary layer. Phys. D Nonlinear Phenom. 2000, 141, 183–198. [Google Scholar] [CrossRef]
- Schmitt, F.G. A causal multifractal stochastic equation and its statistical properties. Eur. Phys. J. B Condens. Matter Complex Syst. 2003, 34, 85–98. [Google Scholar] [CrossRef]
- Medina, O.D.; Schmitt, F.G.; Calif, R. Multiscale Analysis of Wind Velocity, Power Output and Rotation of a Windmill. Energy Proc. 2015, 76, 193–199. [Google Scholar] [CrossRef] [Green Version]

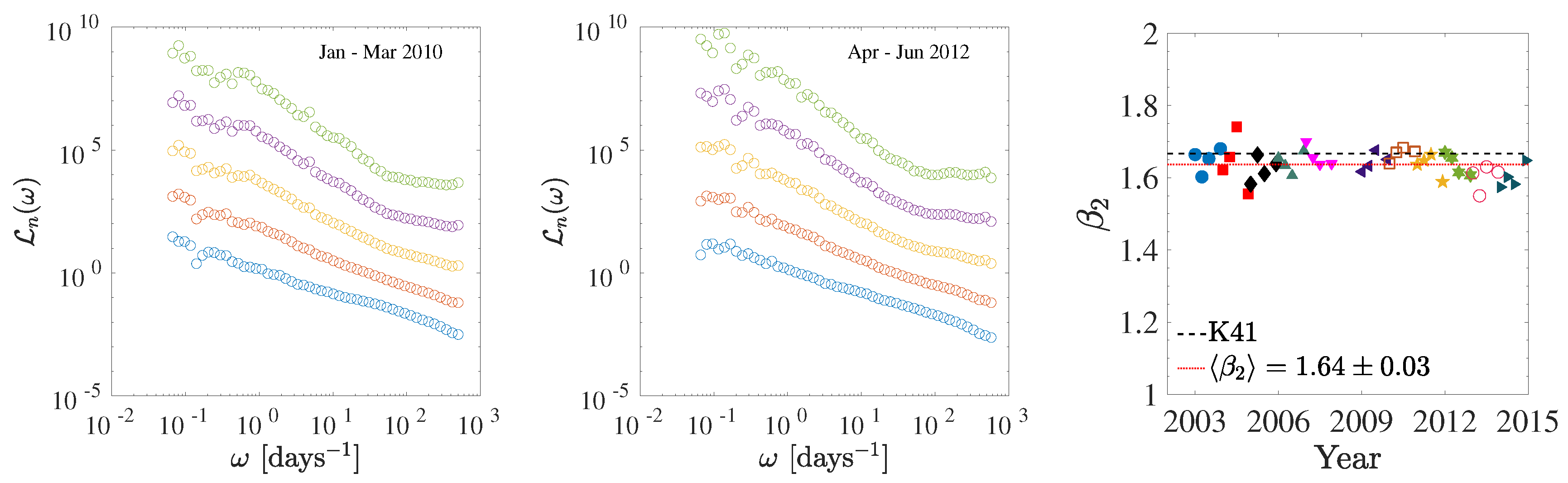

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carbone, F.; Telloni, D.; Bruno, A.G.; Hedgecock, I.M.; De Simone, F.; Sprovieri, F.; Sorriso-Valvo, L.; Pirrone, N. Scaling Properties of Atmospheric Wind Speed in Mesoscale Range. Atmosphere 2019, 10, 611. https://doi.org/10.3390/atmos10100611
Carbone F, Telloni D, Bruno AG, Hedgecock IM, De Simone F, Sprovieri F, Sorriso-Valvo L, Pirrone N. Scaling Properties of Atmospheric Wind Speed in Mesoscale Range. Atmosphere. 2019; 10(10):611. https://doi.org/10.3390/atmos10100611
Chicago/Turabian StyleCarbone, Francesco, Daniele Telloni, Antonio G. Bruno, Ian M. Hedgecock, Francesco De Simone, Francesca Sprovieri, Luca Sorriso-Valvo, and Nicola Pirrone. 2019. "Scaling Properties of Atmospheric Wind Speed in Mesoscale Range" Atmosphere 10, no. 10: 611. https://doi.org/10.3390/atmos10100611
APA StyleCarbone, F., Telloni, D., Bruno, A. G., Hedgecock, I. M., De Simone, F., Sprovieri, F., Sorriso-Valvo, L., & Pirrone, N. (2019). Scaling Properties of Atmospheric Wind Speed in Mesoscale Range. Atmosphere, 10(10), 611. https://doi.org/10.3390/atmos10100611





