1. Introduction
Supercell thunderstorms remain an active target of both observational and numerical study, as they are the source of most observed tornadoes, and are always associated with the most damaging, those rated EF4 and EF5 on the Enhanced Fujita scale. Since the 1970s, when computing technology had advanced enough, numerical models have been used to explore the three-dimensional structure and morphology of supercell thunderstorms. The earliest simulations (e.g., [
1,
2,
3]) were coarsely resolved and spanned a domain too small to hold the full storm, and yet captured important physical and morphological characteristics of supercells that have been found to be consistent with both theory and observations. Since this time, additional 3D cloud model simulations, e.g., [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13], containing tornadoes or tornado-like vortices have been conducted at increasingly higher resolutions over time; however, it is not clear that data is being saved at high enough spatial and temporal resolution to capture the relevant processes involving tornado genesis and maintenance in many of these simulations.
Despite advances in computing technology and numerical model sophistication, adequately resolved simulations of tornado producing supercells are lacking. Observational and numerical studies of tornado producing supercells have shown an abundance of subtornadic vortices along cold pool boundaries in supercells [
14,
15,
16,
17]. The smallest of these vortices exhibit diameters of tens of meters, and hence could not be present in supercell simulations run with O(100) meter resolution found in many recent studies, nor would even the most sophisticated subgrid turbulence closure be able to account for these unresolved features. Furthermore, many numerical studies of supercells use a stretched mesh focusing the most vertical resolution at the ground but decreasing with height. This configuration can result in improperly dissipating turbulent kinetic energy, piling up energy at high wave numbers [
18]. These choices of problem size and the use of a stretched mesh are chosen pragmatically to make the simulation less computationally intensive. While most, but not all, modern thunderstorm models are able to take advantage of distributed memory architectures such as those found on modern supercomputing hardware, scaling a simulation to run efficiently on hundreds of thousands to millions of processing cores is a nontrivial exercise. Without special attention to the underlying communication infrastructure, numerical models will scale poorly to large core counts to make such high resolution simulations unfeasible. In the United States, federally funded supercomputing systems such as Blue Waters [
19,
20] require a full NSF proposal process that includes evidence of reasonable scaling to large core counts. A model that scales poorly will likely not be granted access to run at large core counts, and even if it was, the amount of useful science produced would be minimal.
Further limiting scientists’ ability to run large simulations on distributed-memory supercomputers is the input/output (I/O) bottleneck. Typically, simulations of supercells are executed whereby floating-point data is saved periodically (typically on the order of once per model minute or more) for
post hoc analysis, which can take many months to years to complete due to the complexity of the simulation and the traditional methods for doing analysis (such as the use of Lagrangian tracers). A recent trend in large-scale modeling is the use of in situ visualization and analysis [
21] which enables investigators to visualize model output (and even manipulate the simulation) on the same supercomputing resources while the model’s state is held in core memory. The utility of in situ visualization and analysis for tornado research is questionable, however, considering that a scientifically interesting simulation may take months to years to analyze, and this analysis will be done from files saved to disk that are repeatedly accessed with analysis and visualization software, much of which may be written by investigators long after the simulation was executed. This typical analysis workflow does not benefit from the ability to visualize and/or analyze a simulation while it is in core memory of a supercomputer.
One of the limiting factors in conducting research on tornadic supercells is the ability to save significant amounts of data frequently to capture, at high resolution, the rapidly evolving flow associated with tornado behavior. Abundant visual evidence and radar observations indicate that the process of tornadogenesis often occurs rapidly, over periods of dozens of seconds, where surface flow quickly goes from nontornadic to producing visible debris from tornado strength damage. These observations further support the notion that to properly model tornado behavior in supercells, a small time step (associated with a small grid spacing) is required.
The well-known issue with increasing resolution in a three-dimensional model is that halving the grid spacing (doubling the resolution) requires (8) times more computer memory just to hold the arrays that define the model state. Furthermore, in order to maintain computational stability, a halving of the time step is required, resulting in (at least) 16 times more calculations than at twice the grid spacing. In reality, due to larger communication buffers for exchanging halo data between nodes and the increased latency and jitter inherent in larger simulations of this kind, performance is even worse than back-of-the-envelope calculations imply. If one considers a supercell simulation with 100m isotropic grid spacing, the same simulation run with 10m grid spacing would require more than 1000 times more memory and, owing to a halving of the time step to assure computational stability, more than 10,000 times more calculations. Such a simulation requires both supercomputing resources as well as a model that is able to efficiently use these resources, including the ability to save large amounts of data frequently to have scientific utility.
In this paper, the author describes the use of a modified version of the Bryan Cloud Model, version 1 (CM1) model [
22,
23] in executing an isotropic, ten-meter grid spacing, quarter-trillion grid volume simulation on the Blue Waters supercomputer. Modifications to CM1 were done exclusively on its I/O code with no modification to the model physics. The new I/O driver, dubbed Lack Of a File System (LOFS), uses the Hierarchical Data Format, Version 5 (HDF5) file format [
24] with the core driver (which buffers files to memory) and the lossy fixed-rate compression algorithm of [
25] (ZFP) on all 3D arrays. LOFS has enabled the author to save over 270 TB of total data in the simulation described below that includes a 42 min segment saved in 0.2 s intervals over a
subdomain, whereby I/O took up only 37% of total wallclock use. Post-processing code will also be described, with the main focus being a utility that converts LOFS data to individual Network Common Data Form (NetCDF) files. NetCDF [
26] is an open-source self-describing data format developed by Unidata that is commonly used in the atmospheric sciences. Visualization of the simulation data reveals a fascinating evolution of the storm’s low level vorticity field that includes formation and merging of dozens of vortices, some of which come together to form a powerful multiple-vortex tornado.
The paper is organized as follows: In
Section 2, the author’s use of the CM1 model is briefly described.
Section 3 describes LOFS and its objectives; how the author implemented LOFS in CM1; its file and directory layout; the internal structure of individual HDF5 files that comprise LOFS; and how data can be read back from LOFS and converted to NetCDF files. The performance of ZFP floating-point compression on saved 3D data is also described. In
Section 4, a primarily descriptive discussion of tornadogenesis is presented using output from 2D and 3D graphical software as support, revealing the benefit of saving high-resolution data at a very high temporal frequency to capture the rapid, fine-scale processes of tornadogenesis. The paper concludes with a brief summary and discussion of future work to be conducted.
2. The CM1 Model
The CM1 model [
22] was written to run efficiently on distributed-memory supercomputers, using non-blocking Message Passing Interface (MPI) communication that overlaps communication with calculation, resulting in a computational kernel that scales efficiently to hundreds of thousands of MPI ranks. As of this this writing, CM1 had been cited in over 220 peer-reviewed scientific studies published in 31 different scientific journals [
23]. CM1 offers several solver options and physics parameterizations, and the author finds CM1 especially suited for highly idealized, high-resolution thunderstorm modeling due to its parallel performance at large scale, high-order accurate numerics and sophisticated microphysics parameterization options. The model mechanics and governing equations are well documented, and its author makes the source code freely available.
CM1 is a hybrid-parallel model, offering both Open Multi-Processing (OpenMP) parallelization (via the parallelization of many triply nested for loops found throughout the code) and MPI for exchanging halo data between MPI ranks during model integration as well as executing occasional global communication operations. On the Blue Waters supercomputer, which contains 32 integer cores and 16 floating-point co-processors per node, the best performance was found running 2 OpenMP threads per MPI rank, with 16 MPI ranks per shared memory node, hence using all 32 cores per node. It is worth noting that ideally, one would prefer a single MPI rank to span a compute node with intranode parallelization being handled entirely by OpenMP across all cores such that halo data was not exchanged on a shared memory node; however, with CM1’s OpenMP implementation, this results in poor performance. It is also worth noting that the performant behavior of the author’s configuration on Blue Waters reflects the efforts of the MPI authors to optimize the code over the years, including its performance on shared memory hardware (e.g., [
27]).
CM1 by default contains output options that include unformatted binary output and NetCDF, with one uniquely named file being saved per MPI rank per save cycle. On distributed-memory multicore computers, the option of saving one NetCDF file per node per save cycle is also available, reducing the total number of files being saved by a factor of the number of ranks per node. However, the author was unable to achieve desired research goals with all available options. This led to experimentation with the HDF5 file format and ultimately resulted in the development of a file system called LOFS, described below.
3. LOFS: Lack of a File System
The LOFS abbreviation came about following the author’s realization that what was being achieved in his work was the creation of a file system, which can be loosely defined as a method for naming and storing files for storage and retrieval. LOFS is a “file-based file system” comprised of directories and files that lives on top of the actual file system of the operating system being used (on Blue Waters, the underlying file system is Lustre). The LOFS abbreviation was initially chosen from the author’s initials, but officially LOFS stands for Lack Of a File System, acknowledging that it is only a file system in the most basic sense, and should be discerned from the sophisticated code that underlies traditional file systems underpinning modern operating systems.
Following the acquisition of early access to the Blue Waters supercomputer in 2010, the author quickly found that I/O was be the major bottleneck with regards to wallclock use for large simulations on the machine with CM1. This marked the beginning of a process of trial and error with different I/O configurations with the HDF5 file format, so chosen due to its flexibility, extensibility, parallelization capability, and hierarchical storage model that enable saved data to be organized much like that found on the familiar Linux operating system.
LOFS uses the core HDF5 driver [
28] which allows HDF5 files to be entirely constructed in local memory and later flushed to disk. Multiple time levels are appended to individual files in memory, reducing the number of times files are written to the underlying file system. Writing files to memory, in addition to being faster due to higher available bandwidth, also involves less latency than doing frequent I/O to disk, which is often exacerbated by the fact that the underlying parallel file system is being concurrently used by other jobs running on the machine. Furthermore, Blue Waters XE nodes each contain 64 GB of memory, and, for large simulations, the memory footprint of CM1 on each node was only about 3% of that, allowing much headroom for the construction of multi-gigabyte files on each node. Of course, at some point data must be written to disk, but it was found that supercomputers such as Blue Waters actually perform quite well when hundreds to thousands of files on the order of several to dozens of GB each are written concurrently—and infrequently—to multiple directories.
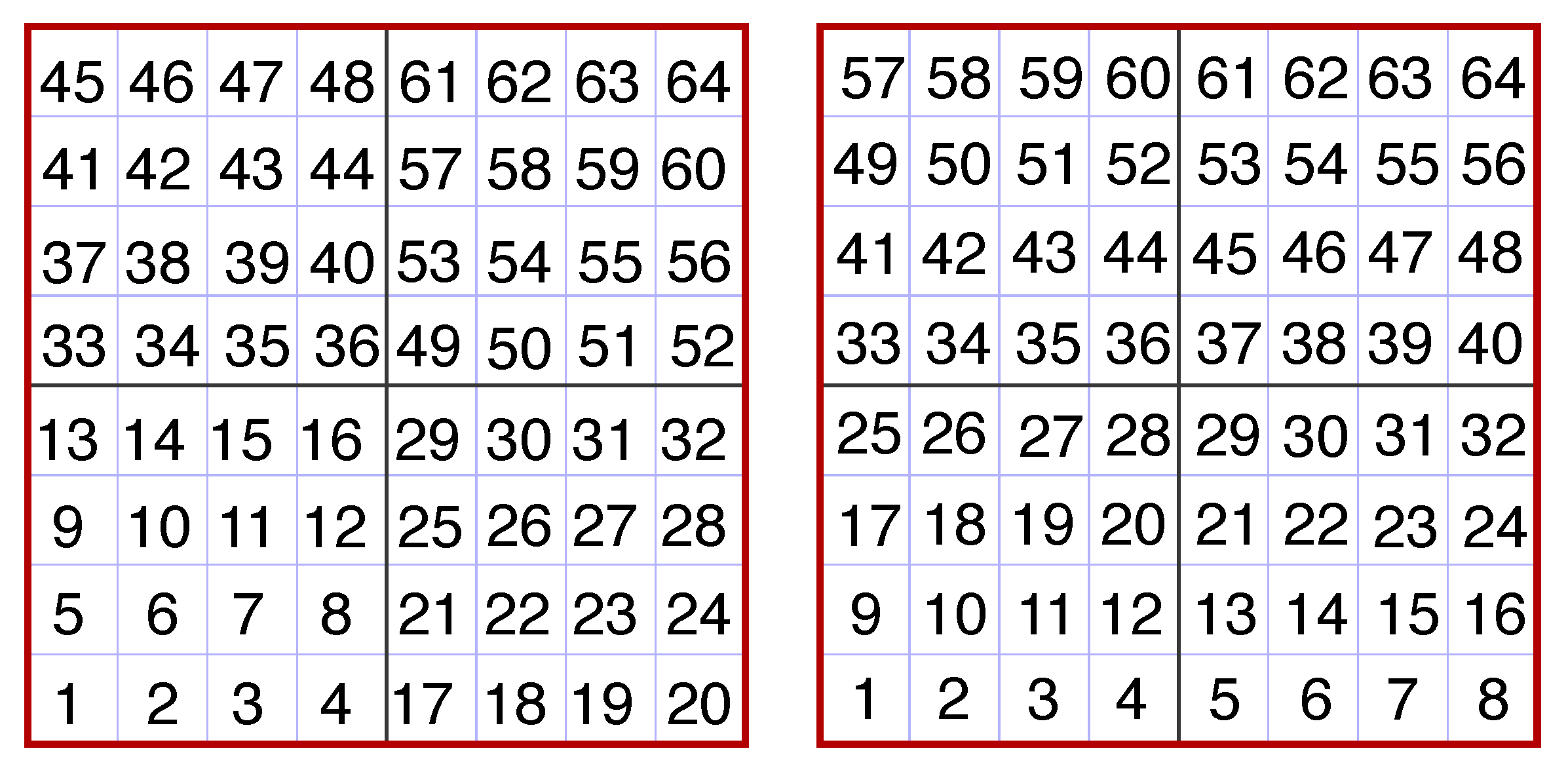
LOFS performs best when MPI ranks are reordered such that only intranode communication to a single core on each node occurs when assembling a continuous node-sized chunk of the domain (so that viewing any individual written file would be like looking at a tiny patch or column of the full physical domain). On multicore supercomputers, by default, MPI ranks are assigned in what Cray refers to as “SMP-style placement” [
29] where node 1 contains the first N ranks numbered consecutively, node 2 contains the next N consecutive ranks, etc., which for CM1’s 2D node decomposition, means each node contains a distorted piece of the actual physical model domain. Rank reordering can be achieved by using external tools provided by Cray that involved the construction a file containing the reordered rank numbers that was read at runtime, but LOFS uses an all-MPI hardware-agnostic approach in which a new global communicator is assembled whose rank numbers were assigned to match the 2D decomposition (see
Figure 1).
3.1. Objectives of the LOFS Approach
LOFS is a form of what has been called “poor man’s parallel I/O” [
30] or, using more modern terminology, a system of Multiple Independent Files (MIF) [
31]. LOFS uses serial HDF5, but from within CM1, files are written in parallel (concurrently) to disk. Supercomputers such as Blue Waters use a parallel file system that is writable from all nodes, and experience has shown that so long as not too many files are written concurrently to a single directory, but spread out among many different directories as is the case with LOFS, excellent I/O bandwidth is achieved. However, LOFS was designed such that “stitching together” files into one single file as an intermediate step is not required to read from a continuous region of stored data. One component of LOFS is a conversion program (
lofs2nc described below) that writes single Climate and Forecasting (CF) compliant NetCDF [
32] files which can be read by a variety of analysis and visualization software. In the case of the tornadic supercell simulation described below, the area surrounding the region of interest for studying tornado genesis and maintenance spans roughly
, or
gridpoints, which does not create too large a file size when several variables of that dimension are written to a NetCDF file.
The objectives of LOFS are as follows:
Reduce the number of files written to disk that would occur if each MPI rank wrote one file per save, as is traditionally done, to a reasonable number.
Minimize the number of times actual I/O is done to the underlying file system
Write files that are on the order of 1-10 GB in size.
Offer users the ability to use lossy floating-point compression to reduce the amount of written data.
Make it easy to save only a subdomain of the full model domain.
Make it easy to read in data for analysis and visualization after it is written.
These objectives are achieved as follows:
LOFS files each contain multiple time levels, as opposed to a single time per file, as well as having only one file per node (as opposed to one file per MPI rank per time) be. written to disk. If, for example, 50 times are buffered to memory per file and each multicore node contains 16 MPI ranks, the number of files saved is reduced by a factor of 800 under a typical one time per file and one file per MPI rank paradigm.
Similarly, by buffering many time levels to memory as the file is assembled, many “saves” occur without writing to disk.
This occurs naturally as a result of the prior two items. Files will never exceed the total memory available on a given node. For the 10-m simulation described below, a typical file size in an active area of the domain was only 2.5 GB when buffering 50 ZFP compressed times to memory and saving 15 3D arrays each of the 50 times.
This is achieved through the HDF5 plugin system that allows for external compression algorithms to be used.
Since hundreds to thousands of shared memory nodes are participating in the simulation, and each node independently writes LOFS data, namelist options are available that save over user-specified ranges in both the horizontal and vertical, resulting in only activating nodes that write “data of interest” over any continuous 3D subdomain. In the simulation described herein, the saved subdomain spanned 2080 by 2080 by 500 grid volumes (20.8km by 20.8km by 5km) in x, y and z respectively, centered on the low-level mesocyclone of the supercell.
This is achieved using reading and conversion code described in
Section 3.5.
3.2. CM1 Modifications
LOFS is written in Fortran95 and uses Fortran modules, and was written to minimize the amount of changes made to the default CM1 code for easier porting to new versions of CM1 and/or other distributed-memory MPI models. LOFS has been used with CM1 release 16 (the CM1 version that produced the simulation described below) as well as CM1 release 18. The process for adapting LOFS to CM1 can be summarized as follows:
Remove references to existing writeout code from CM1’s makefile (due to its scope, LOFS is not a “user-selectable” option like NetCDF).
Add appropriate references to LOFS source code files and compiler options for LOFS to the CM1 makefile.
Using the sed command, replace all instances of the communicator MPI_COMM_WORLD with MPI_COMM_CM1 in CM1 source code.
Insert rank reordering code, which initializes the MPI_COMM_CM1 communicator (this is done where CM1 initializes MPI).
Replace existing writeout subroutine with a new writeout subroutine that calls several other LOFS subroutines that exist in their own source code files.
Include the appropriate LOFS modules in existing CM1 source code that requires it.
In select parts of the code, insert subroutines that do tasks such as allocating LOFS-only variables, broadcasting LOFS-only namelist values, etc.
While LOFS has only been used with CM1, the process outlined above could is designed to be similar to any similar distributed-memory model that uses a 2D domain decomposition.
3.3. Writing Data
LOFS write-side code is provided as
supplementary material, and is referenced below. To provide an overview of how LOFS data is written within CM1, pseudocode is first presented. In the pseudocode below, the domain decomposition has already been done such that each node has been mapped to the 2D domain decomposition shown in
Figure 1, with each MPI rank containing the full vertical extent of the domain.
do while model_time .lt. total_integration_time
integrate_one_time_step !Run the solver to model_time +dt
if mod ( current_model_time , savefreq ) .eq. 0 !Time to do I/O
if i am an io core:
if first visit to this routine :
if iamroot: make directories
initialize_core_driver
initialize_compression_driver
open_hdf5_file !this creates an empty file on disk
create_hdf5_groups
else if this is a new write to disk cycle:
close_groups
close_file !This flushes the file to disk
if iamroot: make_directories
initialize_core_driver
initialize_compression_driver
open_hdf5_file !this creates an empty file on disk
create_hdf5_groups
else:
close_current_time_group
create_new_time_group
end if
write_metadata
for var in all 3D selected variables:
MPI_Gather 3D data to io core from other cores on shared memory module
Reassemble 3D data on I/O core to continuous subdomain chunk
write 3D data to time group
end for
end if !i am an io core
end if !mod( current_model_time , savefreq ) .eq. 0
end do
LOFS operates by first initializing the directory structure by calling the execute_command_line subroutine to call the Linux command mkdir -p to create directories that make up LOFS directory structure (subroutine h5_file_op in lofs-misc.F). Next, the HDF5 core driver and ZFP compression driver are initialized, and one core on each node that is participating in writing data opens its unique HDF5 file, which creates an empty HDF5 file on disk and in memory (subroutine h5_prelim in lofs-hdfprelim.F). Data to the disk file is written when the file in memory is closed. When it is time to write data, a single core on each participating node collects data (using MPI_Gather) from the remaining cores for each requested variable to be written and assembles it into a continuous block of model data that is then written to memory (subroutine h5_write_3d_float_scalar in lofs-hdfio.F). Following the first write, subsequent writes build the HDF5 files in memory with each new time resulting in a new base-level group. When the number of times buffered to memory reaches a user-selectable value (in this case, 50), all groups and files are closed, which flushes the files to disk. Then, new uniquely named directories are created to house new files, and the process repeats until the model finishes.
For simulations in which data is saved at a very small time interval, the best performance is achieved when many model times are buffered to memory. This is accomplished by creating a new base-level group that is a zero-padded integer corresponding to the time index (starting with 0) being written. Groups are a useful way to organize data in HDF5 files, and they are also used to organize metadata, mesh, and the base state sounding data. Because metadata is so small compared to the floating-point data that contains the model state, the author chose to write identical redundant metadata to all HDF5 files. Such redundant metadata includes the number of nodes and cores per node used in the simulation, Cartesian mesh coordinates and dimensions of the full model domain, and the model base state (from the CM1 input_sounding file) mapped to the vertical mesh. Routines for interrogating and reading in LOFS data exploit this redundancy as “any file will do” to retrieve enough metadata to describe and assemble any subdomain of the simulation. The /times dataset stored in each LOFS file contains the floating-point model time that corresponds to each saved time level within the file. Metadata that varies between files includes the grid indices and Cartesian location with respect to the full model domain that are contained in the file.
3.4. Directory Layout and File Naming Convention
A set of Fortran95 subroutines constructs the total path and filename for each HDF5 file based upon strict rules, with variations in the file and directories that are a function of the node number and time of the first saved time within the HDF5 file. In the simulation described below, a maximum of 1000 HDF5 files will be found in any node subdirectory. Spreading the many files that make up a simulation among many directories has been found to produce much better performance than placing them all in one directory.
On the read side, metadata is first extracted from the file and directory names themselves, then from selected LOFS files, to reconstruct the full-domain space such that the proper files can be accessed when users request data. Furthermore, because of the high temporal frequency of data saved in this simulation (in this case, every 0.2 s), the time string in seconds embedded within the HDF5 files is actually a floating-point representation of the time that is then converted to floating-point data in the read-side code. Because each HDF5 file contains 50 time levels in this simulation, the HDF5 time embedded within the file name descriptor refers to the first of 50 times contained within the file, with all saved times comprising the /times dataset (a 1D double precision array) stored in each file.
By enforcing strict file and directory naming conventions, read-side applications programmed with knowledge of these conventions (or using the existing LOFS read-side routines) can traverse the directory structure and extract metadata from directory names, file names, and finally the files themselves. Then, using HDF5 calls, a single floating point buffer is created for each requested variable from multiple files and is stored into an array for analysis, visualization, conversion, etc.
3.5. Reading Data from LOFS
For reading LOFS data, routines written in C have been created that provide a way to access any saved variable at any time spanning any arbitrary subdomain found within the LOFS data. To demonstrate, an example of the lofs2nc utility is described below, creating a NetCDF file containing all the 2D found within a subset the LOFS data as well as selected 3D data.
Consider a situation where a user wishes to make a NetCDF file that spans the region immediately surrounding the tornado in the simulation for visualization. This is achieved with
lofs2nc, a front end to a series of underlying routines that traverse the LOFS structure to extract metadata from directory names and file names, reads redundant metadata from one of the HDF5 files, and then loops across files, incrementally filling a buffer with user-requested data. An example command follows:
lofs2nc --time=5400.0 --offset --x0=800 --y0=750 --x1=1300 --y1=1250 --z1=300 \
--histpath=3D --base=torscale-10m --swaths --nthreads=4 \
thrhopert prespert uinterp vinterp winterp xvort yvort zvort qc qr qg ncg ncr dbz
Table 1 breaks down the different options to the above
lofs2nc command. The user has requested a 501 (in
x) by 501 (in
y) by 301 (in
z) volume of data whose indices are relative to the origin of the file corresponding to the lowest saved node number. The user has requested a list of variables, some of which are read directly from the LOFS data (
thrhopert,
prespert,
qc,
qr,
qg,
ncg,
ncr,
dbz) and some which require calculation based upon other saved data (
uinterp,
vinterp,
winterp,
xvort,
yvort,
zvort). Due to the large amount of data produced by simulations run at this scale, the author has chosen a save strategy that focuses on saving the minimum number of 3D arrays needed to calculate any possible other diagnostic/derived fields and calculating those fields from within
lofs2nc (with calculations parallelized using OpenMP on multicore machines). For instance, the LOFS data saved for this simulation saved the native
u,
v, and
w CM1 variables that lie on the staggered Arakawa C grid [
33] such that the velocity components interpolated to the scalar mesh, as well as the vorticity components interpolated to the scalar mesh, are calculated within the
lofs2nc code. This specific strategy ensures that the highest amount of accuracy is preserved for all calculations involving velocity variables in methods consistent with those done within the CM1 model.
The process by which the LOFS read-side code retrieves metadata involves an entire traversal of the saved directory structure as well as reading metadata from at least one of the HDF5 files in each time directory. These combined operations can take dozens of seconds to complete when hundreds to thousands of time levels are saved, but because the results of these operations always return identical information, the caching of this information is done the first time the command is run, and cache files are read for subsequent executions. This makes metadata acquisition essentially instantaneous (only requiring the formatted reading of several small text files), leaving the code to spend its time to read and write and, if requested, calculate derived variables.
Pseudocode for
lofs2nc is found below, and the LOFS read-side code is included as
supplemental material. The first four routines will first check for cache files and read from these if they exist; otherwise, the LOFS directory structure is traversed and, using routines of the
dirent C library, file names within directories are read, sorted, and a single HDF5 file is selected for internal metadata acquisition. Cache files are written if they do not exist, such that this process only occurs once, and does not need to be done again until the LOFS file structure is modified (for example, by adding more time levels as a simulation progresses through time).
get_num_time_dirs ! get number of top - level directories in 3D directory
get_sorted_time_dirs ! get the directory names and sort using quicksort
get_sorted_node_dirs ! get a sorted list of the zero - padded node directories
get_all_available_times ! get a list of every time level saved in all the data
get_available_3D_variable_names ! get a list of all 3D variable names
get_LOFS_metadata_from_a_HDF5_file ! get mesh , grid , and basestate information
initialize_netcdf ! Set dimensions , attributes , and define requested variables
if getswaths: get_all_swaths ; write_all_swaths ! All 2D fields read and written
get_data_to_buffer ! Buffer variables for diagnostic calculations , if requested
for each requested variable:
if exists_in_LOFS and not_already_buffered : read variable into buffer
if is_diagnostic: calculate diagnostic into buffer
write_requested_quantity_to_netcdf_file
Following metadata acquisition, the list of requested variables is checked against what is available, and, if diagnostic quantities (such as vorticity components) are requested, temporary arrays are allocated, and a flag is set to indicate which LOFS variable is needed for the diagnostic quantity for buffering to memory. As an example, if the vertical component of vorticity () was requested (called zvort in CM1/LOFS), u and v would be buffered to their own arrays such that zvort could be calculated. If u and v were also requested for writing to NetCDF files, these buffered values would be written without re-reading LOFS data. Hence, the code only allocates memory for what is needed and re-uses buffered variables when needed. The main loop over variable names contains code for calculating diagnostic quantities, and new quantities can be added at the end user’s leisure.
All LOFS HDF operations are serial, and this is also true with lofs2nc. However, because modern supercomputers use parallel file systems, excellent performance is found executing serial I/O operations in parallel by writing scripts that execute many instances of lofs2nc concurrently. This workflow is nearly always used since a main motivation for LOFS is doing analysis at very high temporal resolution. Running several instances of any code is easily achievable using shell scripting where jobs are forked into the background. A tremendous amount of data can be read and written quickly in this manner, exploiting the inherent parallelization of the operating system running on a multicore machine and reading (writing) from (to) a parallel file system such as Lustre or GPFS.
3.6. The Use of ZFP Compression
The primary motivation of the development of LOFS was to enable the saving of very high-resolution data at extremely high temporal resolution. This combination will, without care, result in unacceptably poor model I/O performance due to insufficient I/O bandwidth, as well producing as an overwhelmingly large amount of data. LOFS offers, using input parameters in the
namelist.input file that CM1 reads upon execution, the ability to save only a subset of the model domain, which is practical when one is interested in studying the region of the storm directly involved in tornado processes near the ground. In the simulation described below, a volume spanning 2080 by 2080 by 500 grid points (corresponding to 20.8 km by 20.8 km by 5 km in
x,
y and
z respectively) was saved in LOFS files from
through
, spanning 0.86% of the volume of the full model domain (see
Figure 2 to see the horizontal extent of saved data). However, this reduction still results in an unwieldy amount of uncompressed 32-bit floating-point data when saved in 0.2 s intervals over the life cycle of the tornado. In order to reduce the amount of data saved to disk to a reasonable value, ZFP [
25] floating-point compression was used.
ZFP uses a
lossy algorithm that results in three-dimensional floating-point data that contains less than the original 32 bits of precision after being uncompressed. However, the resulting data exhibits compression performance that (usually) far exceeds that of lossless compression algorithms. Furthermore, an attractive aspect of ZFP is that it offers a dynamic compression option whereby an accuracy parameter is specified for each value in each 3D array. The accuracy parameter specifies the maximum amount of deviation allowed from the original floating-point data, and this accuracy parameter is specified in the same units as the saved data. For instance, in the supercell simulation, simulated reflectivity, shown in
Figure 2, is saved in order to create plots that can be compared to real radar observations of supercells. This variable is used for plotting purposes only, and will never be differentiated or used in
post hoc analysis in equations where high amounts of accuracy are needed. A value of 1 dBZ was chosen as an accuracy parameter for the
dbz variable, which means following uncompression of the ZFP data, every value within the 3D
dbz arrays will never differ more than 1dBZ from the original 32 bit floating-point value. ZFP’s algorithm is conservative, and in reality, the accuracy of the data will typically far exceed this specified value throughout the 3D arrays.
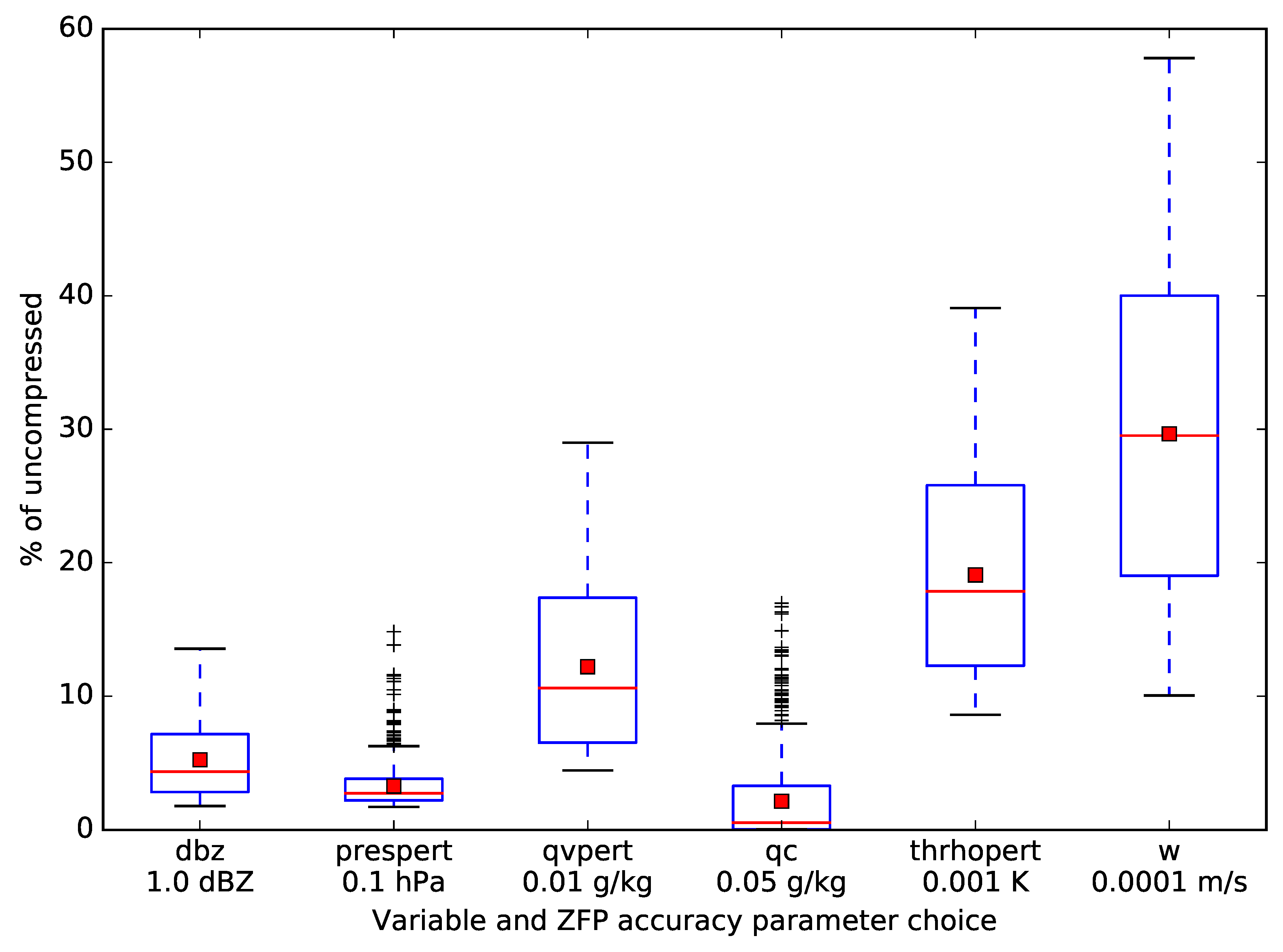
Figure 3 provides a box and whiskers plot of compression performance for several 3D variables at a snapshot in time when the tornado is mature and exhibiting a multiple vortex structure. These statistics were chosen from all 676 files spanning the saved subdomain. Data within this subdomain contains regions of both weak and sharp gradients, and the widely varying compression performance in this example reflects this. For the aforementioned
dbz variable, which was saved with 1.0 dBZ accuracy, the space taken by the 3D array was 5.2% of its uncompressed size, providing an average compression ratio for this variable of approximately 19:1. Had a larger accuracy parameter been chosen, compression performance would have increased accordingly.
Because future post hoc analysis will involve Lagrangian trajectory analysis and the effects of lossy compression on trajectory performance have yet to be determined by the author, a very small value (0.1 mm s−1) was chosen for each of the three components of velocity, each of which exhibited very similar compression performance. This resulted in an average reduction to 30% of uncompressed, or roughly a 3:1 average compression ratio, with values ranging from 10% to 58% of uncompressed across all saved files. This wide variation in compression performance across files is indicative of the dynamic nature of ZFP compression, where regions of large gradients result in less compression than regions of weaker gradients. The prespert variable (perturbation pressure in hPa) shows several outlier compression reductions that correspond to regions of abnormally large gradients that are found along the length of the tornado (which is tilted, spanning several files) and other weaker vortices. The cloud mixing ratio variable qc exhibits compression performance in some files where nearly no data is saved, corresponding to cloud free areas of the simulation, but also many outliers where large gradients are found within the cloud including along the periphery of the condensation funnel of the tornado.
So long as accuracy values are chosen carefully for each variable, one may be assured that post-processing and visualization will not result in artifacts or a substantial loss of accuracy that would result in faulty post hoc analysis. For work of this nature, the use of lossy compression is unfortunate but necessary and can be thought of as a trade-off between spatial accuracy and temporal accuracy; without lossy compression, to reduce the data load, data would need to be saved with significantly coarser temporal resolution, removing the ability to do the kind of visualization and analysis needed to achieve desired research goals.
4. The 10 m Resolution Tornadic Supercell Simulation
The simulation was run on an isotropic mesh with a grid spacing of 10 m, in a box spanning 112 km by 112 km by 20 km (using
, or 250,880,000,000, grid points). A model time step of 0.04 s was used to maintain stability, and a short time step of 0.01 s was used for the acoustic time step. The chosen time step is smaller than what was necessary for computational stability due to aliasing; however, a larger time step resulted in sporadic failure of CM1’s saturation adjustment scheme, which is iterative, to converge, causing the model to abort. The remaining model parameters were identical to those of [
17] with the exception that the TKE closure option of Deardorff et al. [
35] was used in place of that of Smagorinsky [
36], and the fully explicit pressure solver was used (
psolver=2).
4.1. Execution of the Simulation on Blue Waters
The supercell simulation was executed on the Blue Waters supercomputer in 22 segments between 19 April and 2 August 2019. Each segment of the simulation beyond the first was run from checkpoint files that were saved in HDF5 format with all 3D state variables compressed with lossless gzip compression. The simulation took approximately ten million node hours (320 million core hours) in total to run to a model time of 7490 s, a few minutes after the cyclonic tornado fully dissipated. This corresponds to just over 21 days of execution using 87% of all available XE nodes on Blue Waters.
Each segment of the simulation ran on 19,600 nodes (672,200 cores) when executing, with a maximum requested run time of 48 h per segment, the largest allowed on the machine. However, when running over such a large portion of the machine, node failures were common, occurring on average four times per 48 h block. These node failures were out of the author’s control and not due to model instability or any other failure of the CM1 model. When a node failure occurred, a message such as the following would appear in the CM1 standard output file: [NID 19080] Apid 78797135 killed. Received node event ec_node_failed for nid 19075.
Consultation with Blue Waters support staff indicated that these node failures occurred on the Opteron processors with a return value of COMPUTE_UNIT_DATA which indicates an uncorrectable error occurring on one of the node’s CPUs. Recognizing the regularity of these types of unavoidable errors, the author chose to save checkpoint files every 10 model seconds, and, via a loop within the PBS script file, restart the model from the most recent checkpoint file automatically such that the entire requested reservation time could be used. This required the allocation of a handful of extra nodes for each job submission as a reserve such that there were enough healthy nodes available for each execution, as the failed nodes would be removed from the pool. With these issues in mind, it is estimated that about a quarter of the used node hours on the machine were “wasted” due to these failures.
Because it was not known whether the simulation would produce a long-track EF5 tornado similar to [
17], full-domain data was saved only every 10 s until the beginning of tornado maintenance was observed. Then, using one of the saved checkpoint files, the model was restarted from a time approximately 10 min prior to tornadogenesis and subsequent data was saved over a smaller subdomain with a save interval of 0.2 s until tornado decay occurred. The 10 s full-domain data, saved between
and
comprised 83 TB of LOFS data, while the subdomain data saved every 0.2 s from
and
weighed in at 187 TB.
4.2. A First Look at Tornadogenesis
Here a description of the process of tornadogenesis is provided, focusing primarily on the growth of near-ground vorticity. The model times of the figures following in this section were chosen after creating a video animation of the 0.2 s data and stepping forwards and backwards through the video until key moments in the simulation were identified. It should be emphasized that only a topical analysis of tornadogenesis is provided in this section, and that a more exhaustive quantitative analysis is beyond the scope of this paper. The
supplemental video file SupV1 of the vorticity magnitude field and surface maximum vertical vorticity swaths from
through
is found at
https://doi.org/10.21231/rhja-kd44. This video sequence begins approximately three minutes prior to tornadogenesis and continues through about three minutes of tornado maintenance, with frames displayed every 0.2 s at 30 frames per second.
Figure 4,
Figure 5 and
Figure 6 provide an overview of cyclonic vortex paths, superimposed upon density potential temperature perturbation (
), to provide a context for the more information-dense three-dimensional images in subsequent figures (these images originated from the output of the
ncview [
37] utility, read from NetCDF files created with
lofs2nc). The bulk of surface vortices identified by swaths of maximum vertical vorticity (
) shown in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
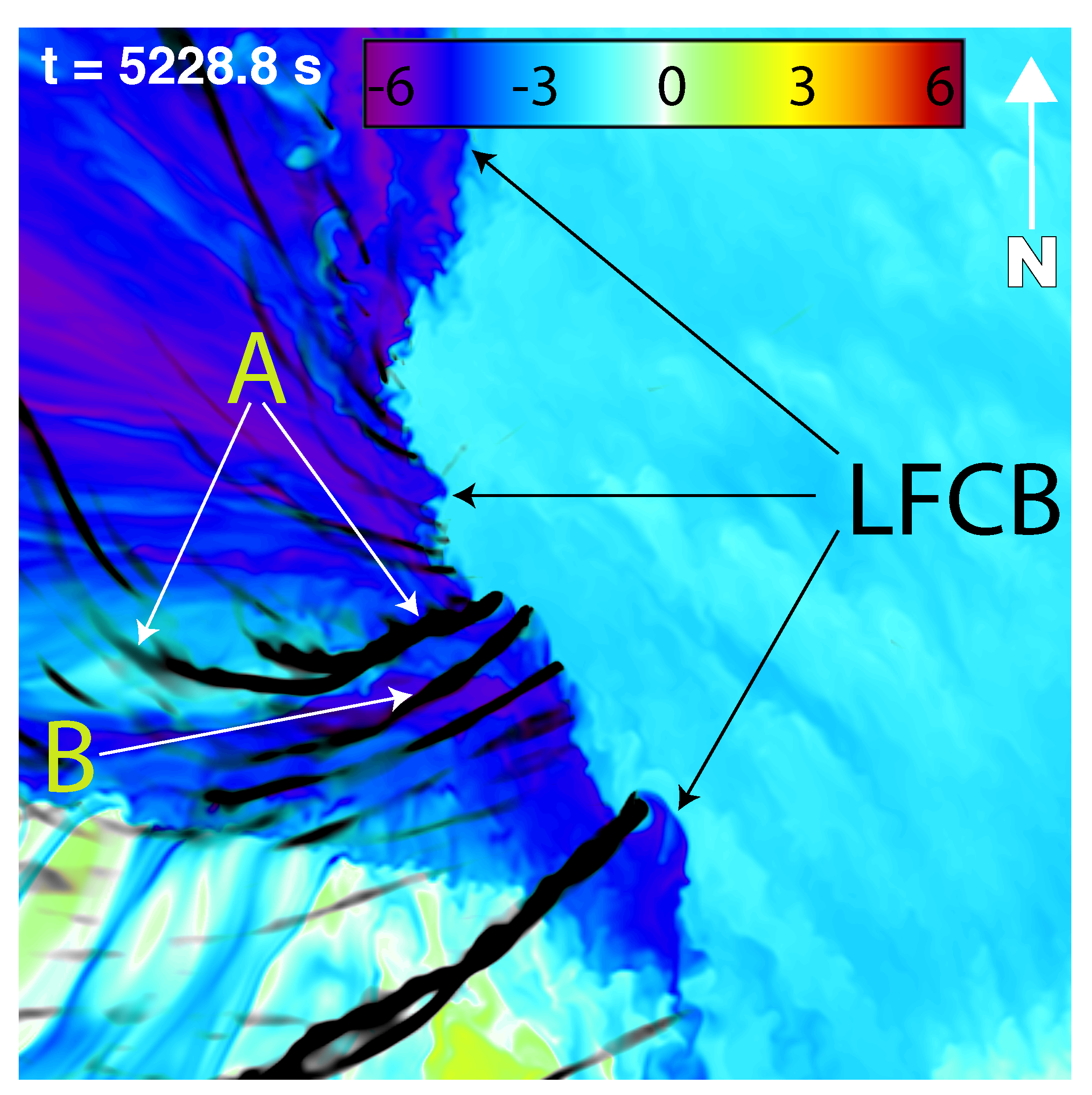
Figure 9 originate on the cold (west) side of what [
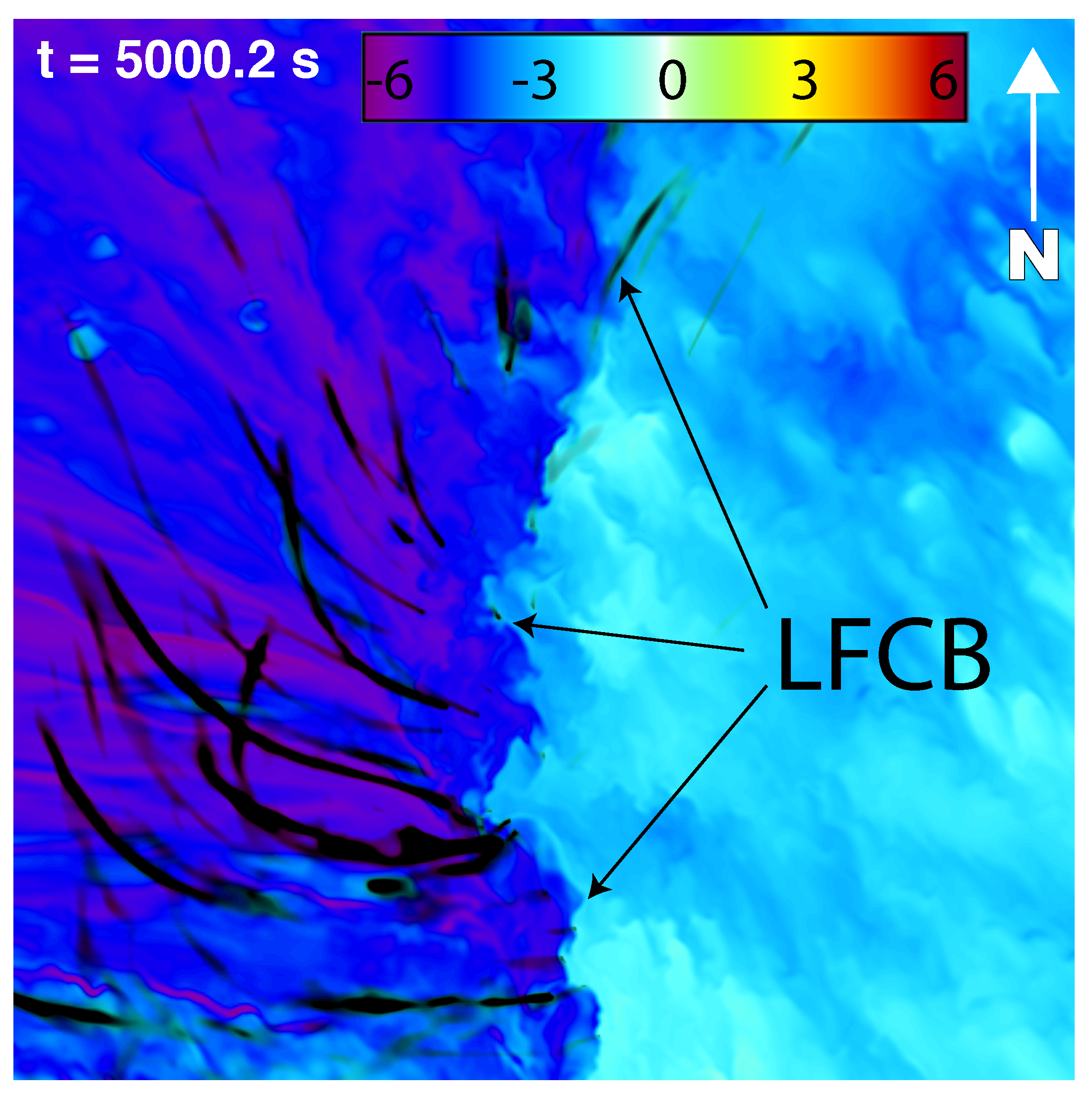
38] call the Left Flank Convergence Boundary (LFCB) (see their Figure 8). This boundary is clearly visible in both the surface horizontal wind and
fields, with its location along the sharp
gradient noted in
Figure 4,
Figure 5 and
Figure 6. At
, approximately three minutes prior to tornadogenesis, vortex path directions range from southward to eastward, with many paths abruptly turning from southward to eastward (see
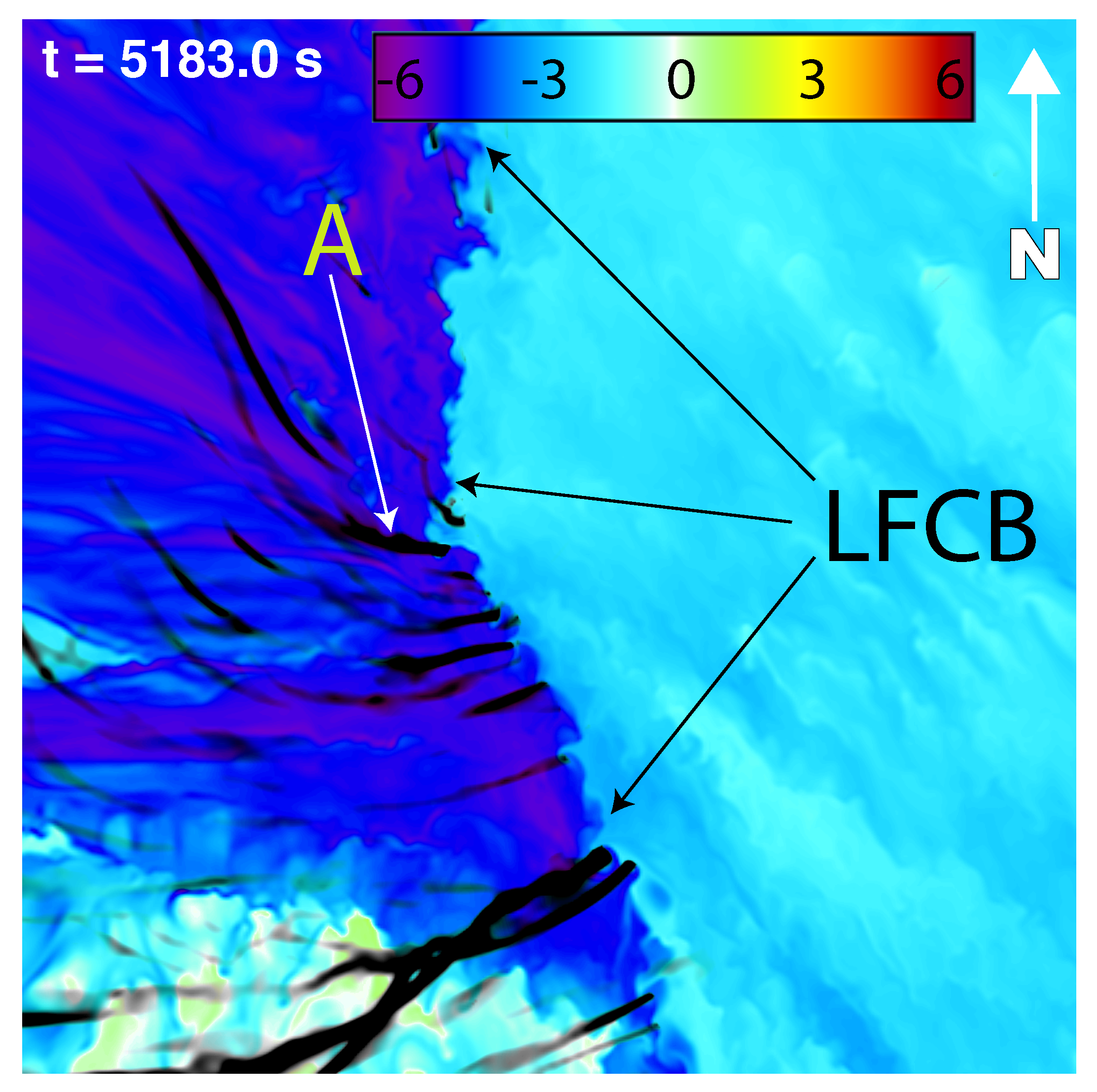
Figure 4). Three minutes later, at
, the incipient vortex that “becomes” the tornado (tagged to as vortex
A in subsequent figures) has turned from southeastward to eastward and has begun to produce a 20 m swath of instantaneous ground-relative winds just exceeding 39 m s
−1, the EF1 threshold. The direction of vortex paths to the south of vortex
A seen in
Figure 5 exhibit a slight to moderate northward component, indicating a convergence of vortices occurring in its direct vicinity. At this time, vortex
A is located along an inflection point in the LFCB, which is oriented directly north/south to its north, and towards the SSE to its south. The reorientation of the LFCB is seen to persist in
Figure 6, 46 s later, with the LFCB showing an eastward bulge consistent with an increase in eastward momentum to the south of vortex
A, which is now exhibiting a 40 m swath of EF2 strength winds (averaging 55 m s
−1). A second vortex, vortex
B noted in
Figure 6, follows a convergent path with vortex
A and is discussed below.
Figure 4.
Density potential temperature perturbation () in K at . Horizontal domain covers . Black swaths are the ground-relative paths of cyclonic vortices at the model’s lowest vertical level (motion is generally southward to eastward). The sharp boundary representing the Left Front Convergence Boundary (LFCB) is noted. The color map indicates values of in K.
Figure 4.
Density potential temperature perturbation () in K at . Horizontal domain covers . Black swaths are the ground-relative paths of cyclonic vortices at the model’s lowest vertical level (motion is generally southward to eastward). The sharp boundary representing the Left Front Convergence Boundary (LFCB) is noted. The color map indicates values of in K.
Figure 5.
As in
Figure 4 but at
. Vortex
A (shown in subsequent figures) is noted.
Figure 5.
As in
Figure 4 but at
. Vortex
A (shown in subsequent figures) is noted.
Figure 6.
As in
Figure 5 but at
, corresponding to the same time in
Figure 2.
Figure 6.
As in
Figure 5 but at
, corresponding to the same time in
Figure 2.
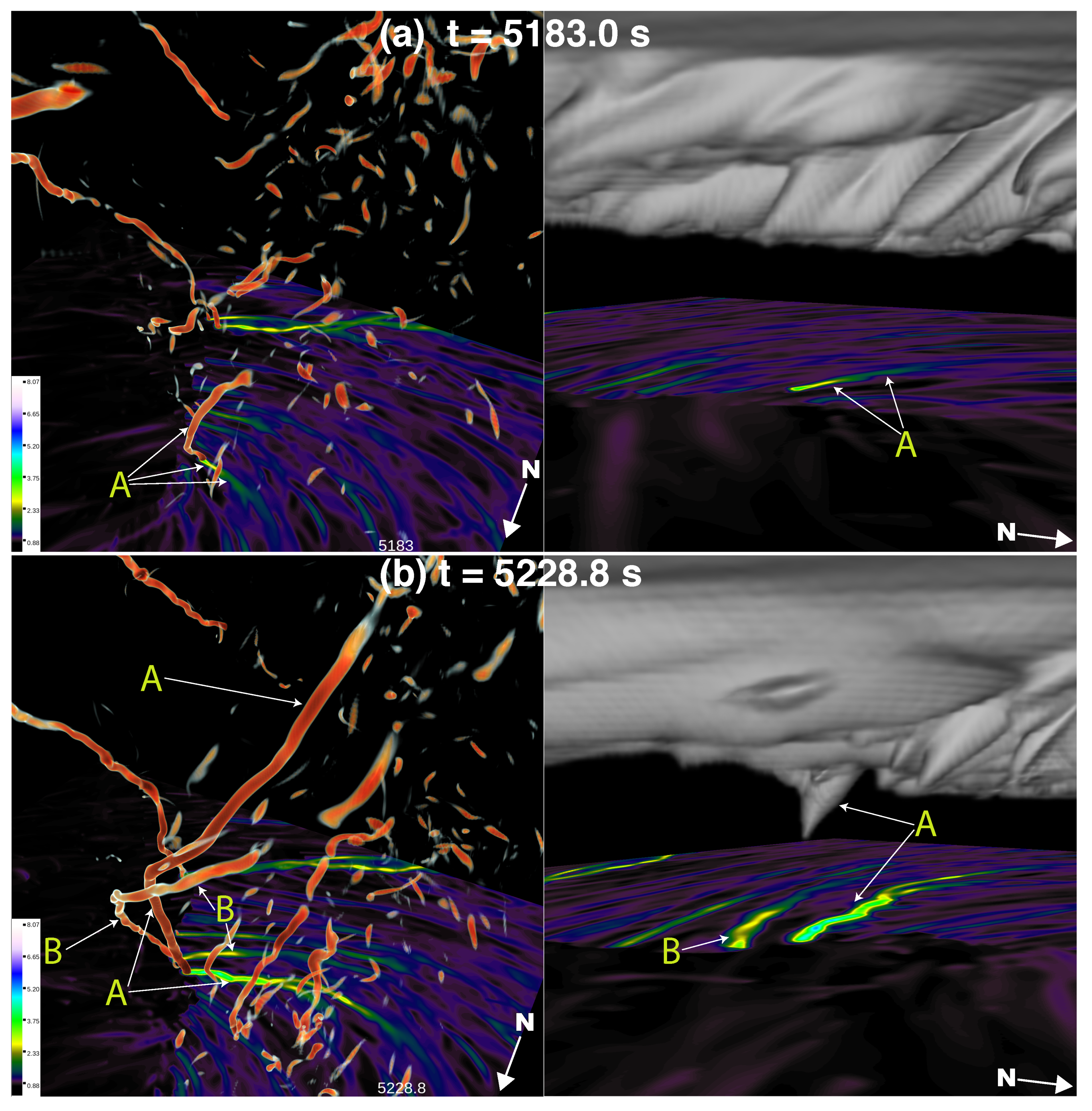
Figure 7,
Figure 8 and
Figure 9 provide six snapshots in time, the first two of which overlap with
Figure 5 and
Figure 6. These images were created with the NCAR’s VAPOR3 software [
39], which can read NetCDF files containing 2D and 3D floating-point data natively. The left panel of these images contains three-dimensional volume rendered vorticity magnitude with a visible threshold value of approximately 1.25 s
−1, along with surface maximum
swaths that can be matched with those in
Figure 5 and
Figure 6.
SupV1 corresponds to the left panels of these figures, while the right panels present a different viewing angle, and include, in addition to surface maximum
swaths, the liquid cloud water mixing ratio (
) field to show the behavior of the condensation funnels associated with strong rotation. In
Figure 7a, vortex
A can be seen extending upwards from the ground but is not associated with a visible condensation funnel at this time. In
Figure 7b, 45 s later, vortex
A has strengthened at the surface and extended upwards to a height of nearly 3 km. A second vortex, vortex
B, is also visible in the vorticity field, having formed in a similar “bottom-up” manner as vortex
A, and is in the process of being assimilated into the circulation of vortex
A. Vortex
A is also associated with a visible condensation funnel shown in
Figure 7a.
Figure 8a shows the same fields 44 s later, where vortex
A is exhibiting a 50 m wide swath of EF3 strength ground-relative surface winds (averaging 70 m s
−1) with another vortex, vortex
C, having just swept behind the path of vortex
A and extending upwards to a height of approximately 1 km. Vortex
A is now “the tornado” as is demonstrated by its co-location with a columnar condensation funnel that extends from the parent supercell cloud base to the ground. Over the next 12 s, vortex
C has grown upward to a height of exceeding 2 km and has begun a process of merging and wrapping into vortex
A (see
Figure 8b). This process is shown most clearly in
SupV1 where the two vortices wrap around one another in a “bottom-up” manner. While mergers of helical vortices in three dimensions have been observed and modeled [
40,
41], the author is unaware that this phenomenon has ever been seen in an observed supercell or in simulations of a supercell. By
, when the wrapping process has extended to a height of approximately 2.5 km, the tornado is exhibiting EF5 ground-relative surface winds exceeding 105 m s
−1 (see
Figure 9a). A minute later, the tornado’s diameter has widened, as is evident from the size of the visible condensation funnel and maximum
swath field, and has also assumed a more vertically erect position, and is moving in a linear fashion towards the northeast. Maximum instantaneous ground-relative surface winds exceeding 140 m s
−1 are found at this time, shortly before the tornado obtains a multiple-vortex structure.
Figure 7.
Left column: Three-dimensional vorticity magnitude (volume rendered field, visible threshold at about 1.2 s
−1) and surface maximum
swaths, representing the paths of cyclonic vortices at the model’s lowest vertical level. The domain of the 3D volume spans
in
. The color map references surface
values in s
−1. Right column: Cloud water mixing ratio (volume rendered field) and surface maximum
swaths. Vortex
A and vortex
B and their paths are annotated at (
a)
and (
b)
, which correspond to the times in
Figure 5 and
Figure 6. Images were created with VAPOR3 [
39].
Figure 7.
Left column: Three-dimensional vorticity magnitude (volume rendered field, visible threshold at about 1.2 s
−1) and surface maximum
swaths, representing the paths of cyclonic vortices at the model’s lowest vertical level. The domain of the 3D volume spans
in
. The color map references surface
values in s
−1. Right column: Cloud water mixing ratio (volume rendered field) and surface maximum
swaths. Vortex
A and vortex
B and their paths are annotated at (
a)
and (
b)
, which correspond to the times in
Figure 5 and
Figure 6. Images were created with VAPOR3 [
39].
Figure 8.
As in
Figure 7, but at (
a)
and (
b)
. Vortex
C, which has begun to wrap around vortex
A, is also noted.
Figure 8.
As in
Figure 7, but at (
a)
and (
b)
. Vortex
C, which has begun to wrap around vortex
A, is also noted.
Figure 9.
As in
Figure 8, but at (
a)
and (
b)
. The wrapping of vortex
C into vortex
A has reached a height of about 2.5 km by
, and at
, the tornado, exhibiting ground-relative instantaneous winds exceeding 140 m s
−1, is in the process of transitioning into a multiple-vortex structure and has become nearly vertically erect below 3 km, moving in a linear fashion towards the northeast.
Figure 9.
As in
Figure 8, but at (
a)
and (
b)
. The wrapping of vortex
C into vortex
A has reached a height of about 2.5 km by
, and at
, the tornado, exhibiting ground-relative instantaneous winds exceeding 140 m s
−1, is in the process of transitioning into a multiple-vortex structure and has become nearly vertically erect below 3 km, moving in a linear fashion towards the northeast.
5. Discussion and Future Work
In this paper, LOFS, a simple file system designed for saving large amounts of massively parallel cloud model data efficiently, was described, along with a use example of a the
lofs2nc utility for converting LOFS data to the widely read NetCDF format. NetCDF files created from
lofs2nc by the author were then read and displayed with
ncview [
37] (
Figure 2,
Figure 3,
Figure 4,
Figure 5 and
Figure 6) and VAPOR3 [
39] where 3D images were created (
Figure 7,
Figure 8 and
Figure 9) and saved to disk to be statically viewed as well as animated (
SupV1). The author’s experience with running the simulation on 19,600 Blue Waters nodes (672,200 cores), spanning 87% of the supercomputer’s XE nodes, was described, which included a process for recovering from node failures automatically by restarting the model from the most recent checkpoint files. The performance of dynamic ZFP lossy floating-point compression was described for six 3D fields saved by CM1, with each variable having an accuracy parameter set at runtime, specifying the largest amount of deviation allowed from the original floating-point data. The use of ZFP and the choice of saving a small subdomain, focused on the low-level mesocyclone, allowed data to be saved every 0.2 s, and this I/O approach took up a reasonable 37% of the model’s execution time. A total of 270 TB of data was saved, with 83 TB of full-domain data saved in 10 s intervals from
through
, and the remaining 187 TB of data saved from
and
over a 20.8 km by 20.8 km by 5 km subdomain every 0.2 s.
Visualizations of the vorticity and cloud field reveal a process of tornadogenesis characterized by the convergence, merging, and upward growth of several near-ground vortices, one of which wraps around the nascent tornado in a bottom-up fashion. The tornado forms along the Left Front Convergence Boundary [
38] which is prominently displayed as a sharp buoyancy gradient in the cold pool. A few minutes prior to tornadogenesis, vortices on the cold side of this boundary take a sharp turn towards their left (moving southward to eastward) and then begin to travel towards the north-east. Genesis occurs shortly thereafter, with the tornado forming along an inflection point in the LFCB, which has surged forward to the south of the developing tornado. While only a topical discussion of tornadogenesis, focusing on vorticity, has been presented, the value of using 3D volume rendering software such as VAPOR3 [
39] has been clearly demonstrated, with animations of vorticity at full 0.2 s frame spacing telling a compelling story. Only one aspect of the tornadogenesis process has been presented here, and only over a short span of time; the tornado, which transitions to a wide, multiple vortex tornado, lasts for 42 min before dissipating.
While the 10-m simulation has only been topically described, it bears many similarities to the 30-m simulation described in [
17] in which tornadogenesis was associated with the merging of several cyclonic vortices forming along a density gradient in the storm’s forward flank. Flow patterns evident in visualizations of vorticity in the 10-m simulation (not shown) are consistent with the streamwise vorticity current (SVC) identified in the 30-m simulation. The SVC in [
17] is associated with the development of a substantial (ranging from 10 hPa at the surface to 25 hPa 2.5 km AGL) pressure drop over the bottom 6 km of the domain in the heart of storm’s mesocyclone, resulting in an intense upward-directed nonhydrostatic vertical pressure gradient immediately above the ground. Tornado formation is associated with intense upward acceleration and attendant horizontal convergence centered over a region of concentrated surface cyclonic vorticity, similar to the most ideal configuration analyzed by [
42] in their idealized, dry simulations of supercell-like “pseudostorms.” Also consistent with [
42] is the presence of a comparatively weaker anticyclonic tornado that occurs in both simulations. The 10-m simulation indicates that aggregation of cyclonic vortices, found in abundance along and adjacent to the LFCB, occurs during tornadogenesis during a period where the updraft immediately above the ground is especially strong.
Much future work needs to be completed to quantify the complex morphology of the simulation. Such work will include:
The use of temporal averaging to “smooth out” the details of the simulation in order to focus on underlying, steady forcing prior to and during tornadogenesis.
Examining the momentum and pressure characteristics of the updraft prior to and during tornado formation.
Conducting Lagrangian parcel analysis to explore the forces acting on parcels in the vicinity of the tornado.
Exploring the sensitivity of the simulation to a turbulence kinetic energy closure by conducting a second run using the Smagorinsky. [
36] closure scheme, which was used in a 30m resolution simulation of the same storm [
17].
Work is already underway to develop Lagrangian parcel tracking code, using LOFS data as input, optimized for graphical processing units (GPUs) that will enable the tracking of millions of parcels throughout chosen segments of the simulation. Code has already been created to create the temporally averaged fields, the utility of which has been shown [
43] with the 30m resolution simulation of [
17].
LOFS read-side and write-side source code is available as
supplementary material to this paper. The write-side code is released in isolation from the CM1 model; it is the author’s intent to explore the possibility of releasing an LOFS-enabled branch of the latest version of the CM1 model on a repository such as GitHub such that other researchers can take advantage of LOFS. The LOFS read-side code is currently being refactored, and will be released on a public source code repository in the near future.