Horizontal Vortex Tubes near a Simulated Tornado: Three-Dimensional Structure and Kinematics
Abstract
1. Introduction
2. Numerical Experiments
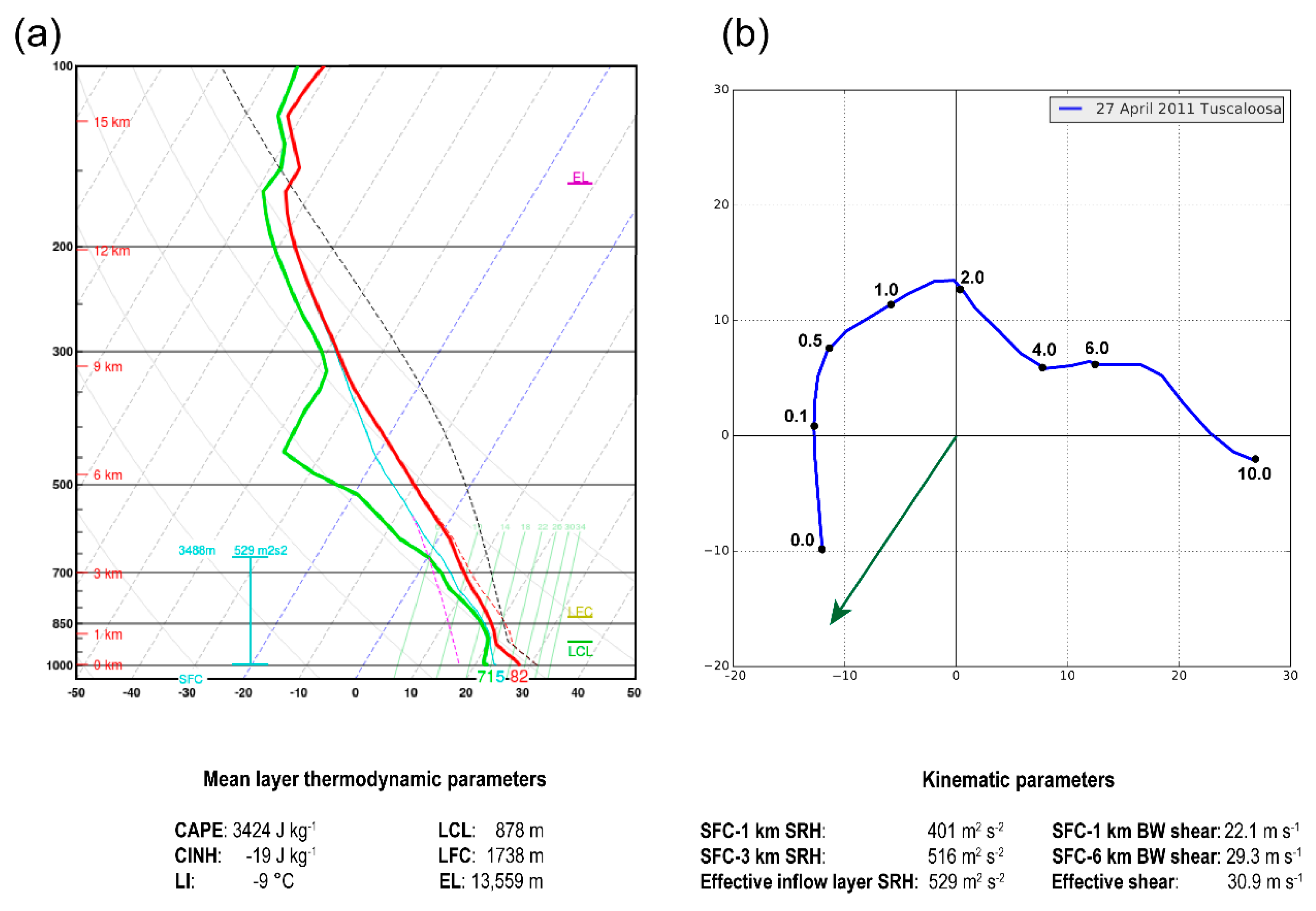
3. Simulated Storm Overview
4. Evolution and Kinematics of HVs near a Tornado
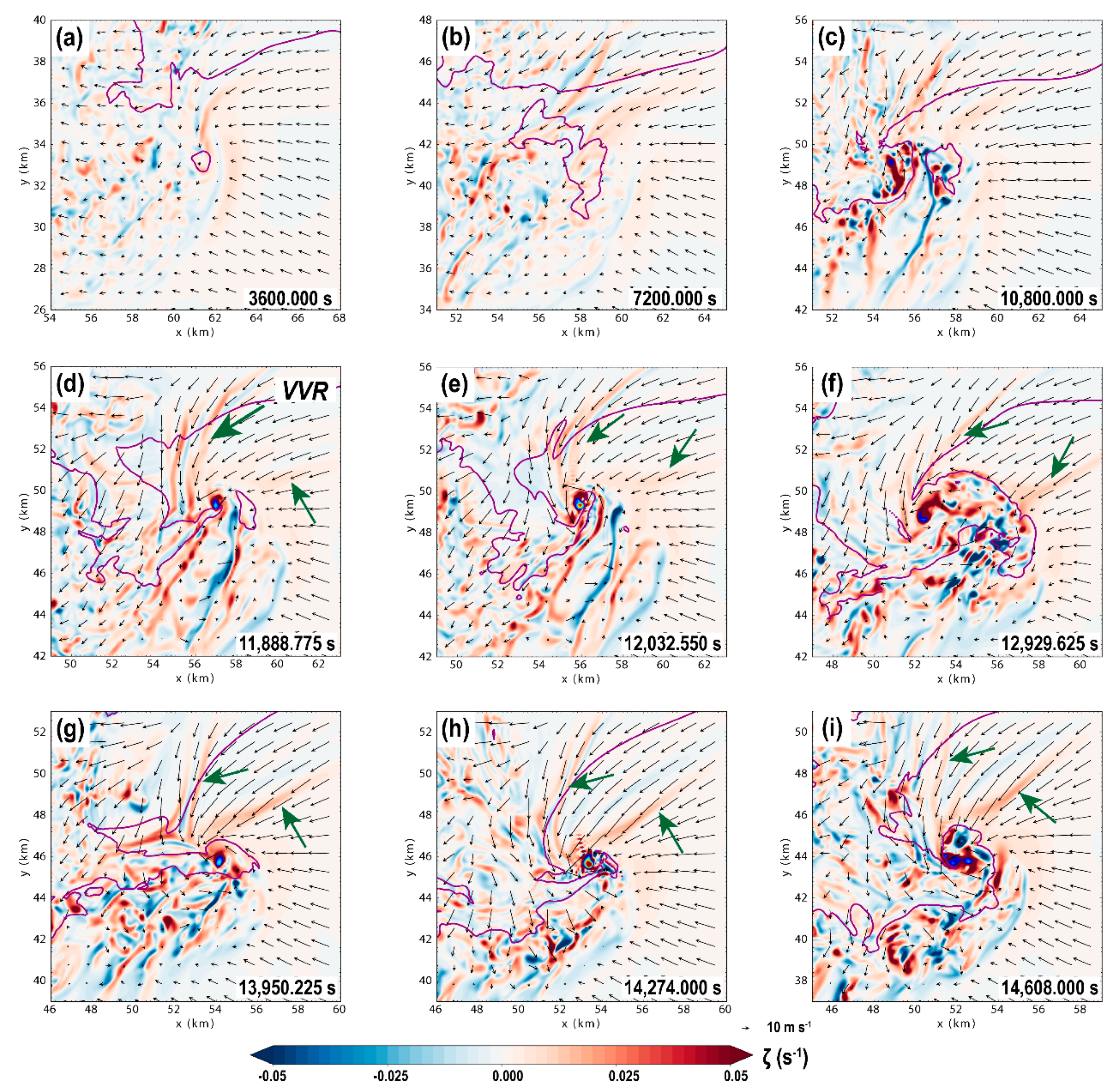
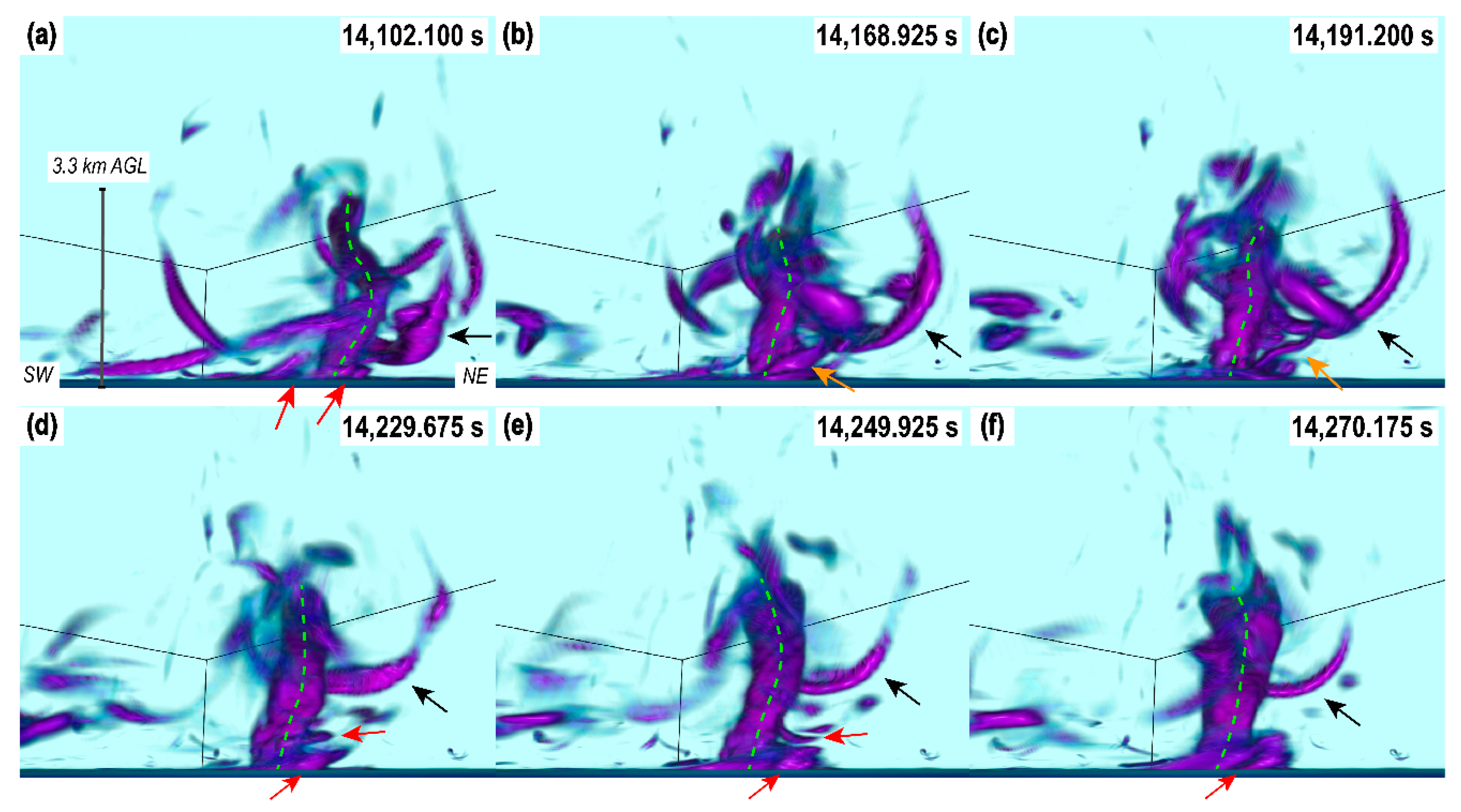
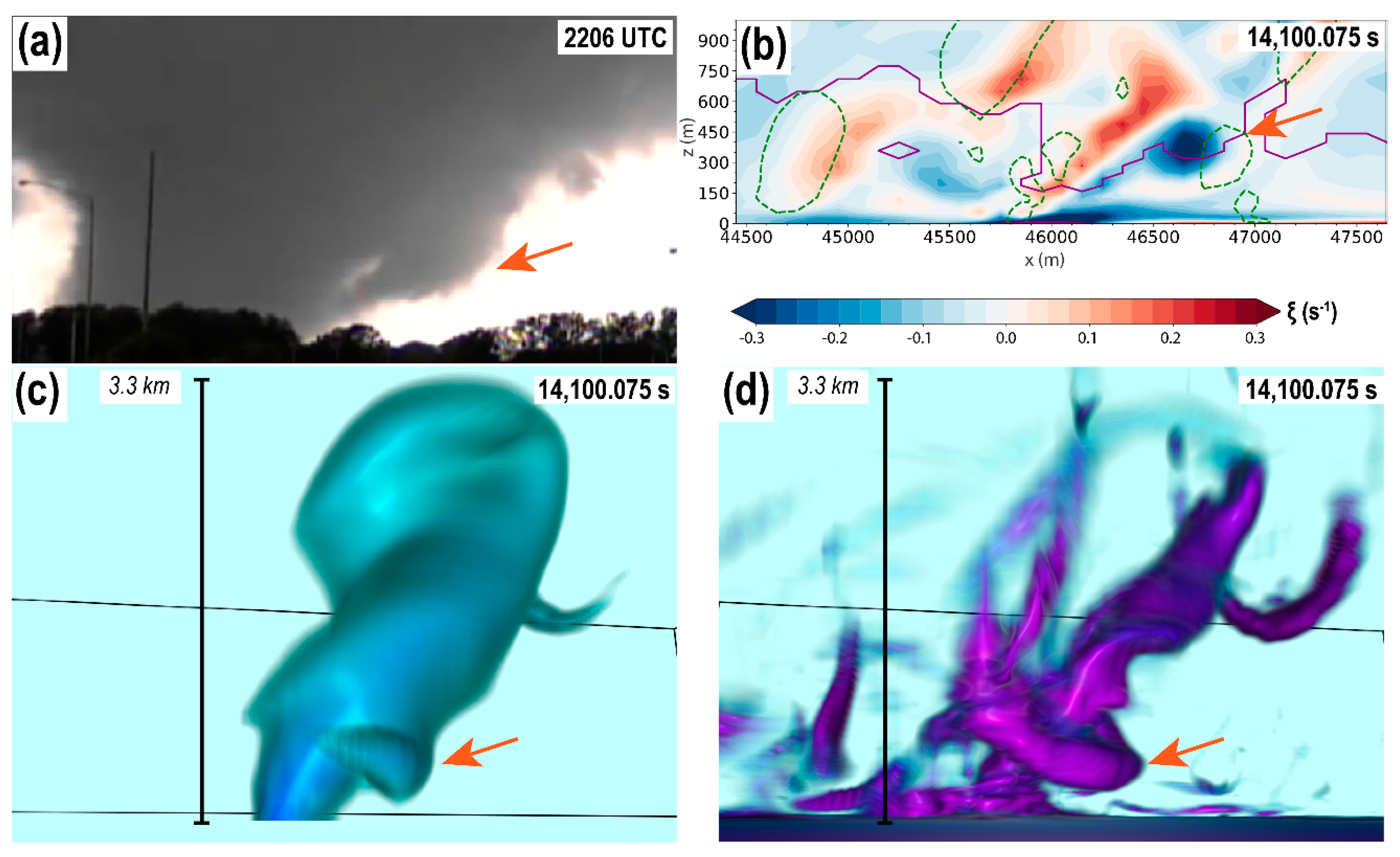
4.1. 3D vorticity Structure and Visual Observations
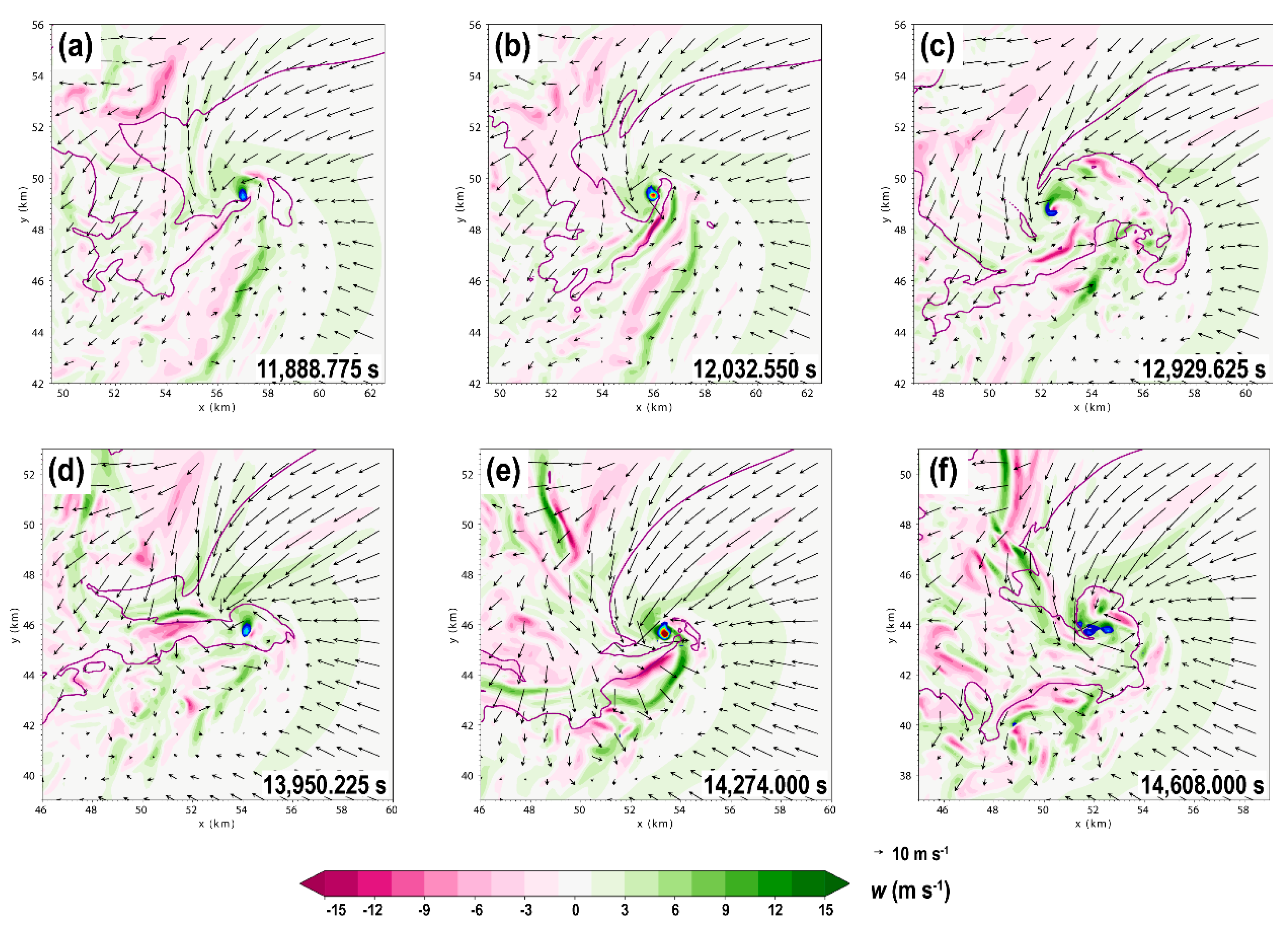
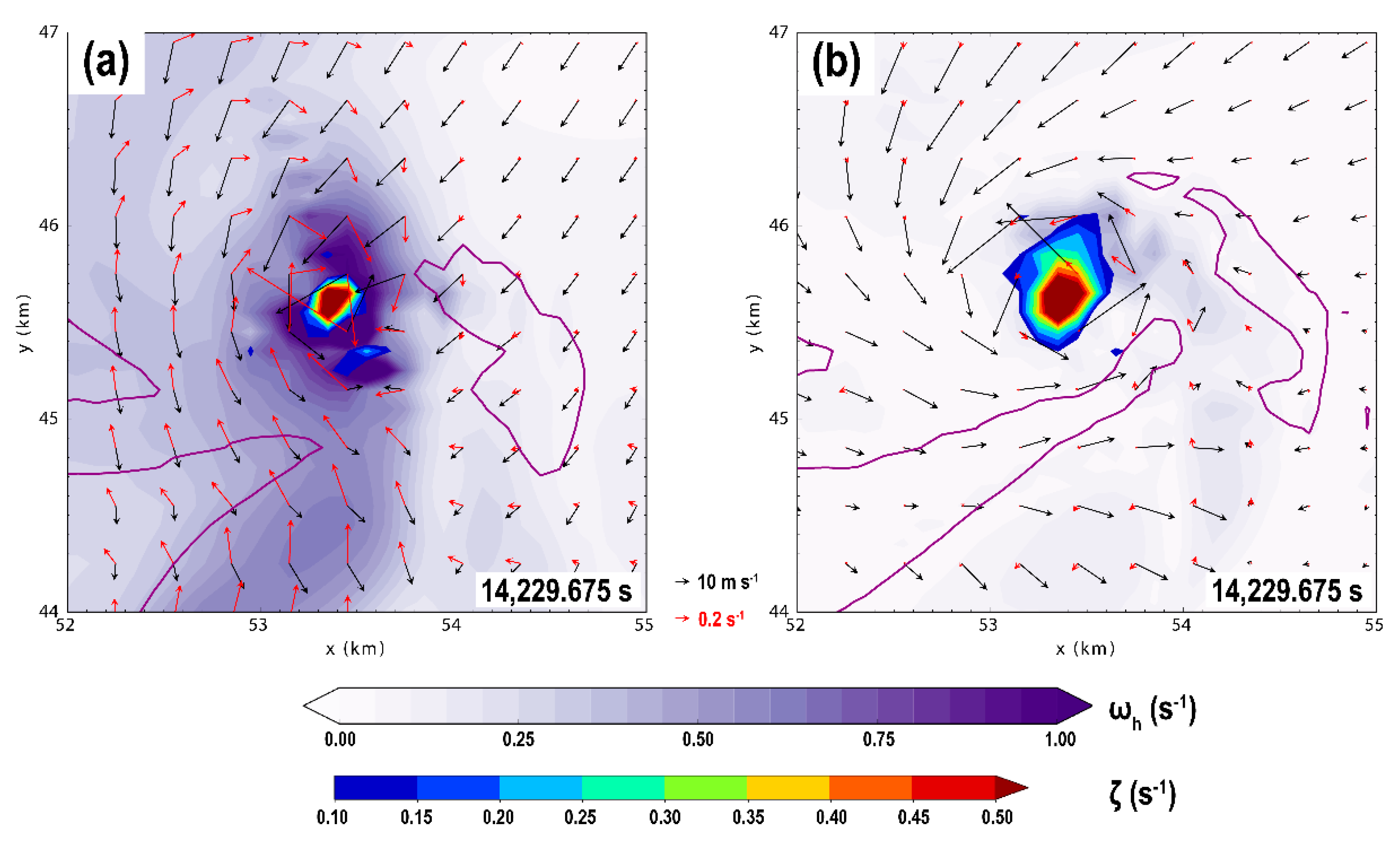
4.2. Near-Ground Flow Kinematics and Potential HV Formation Mechanisms
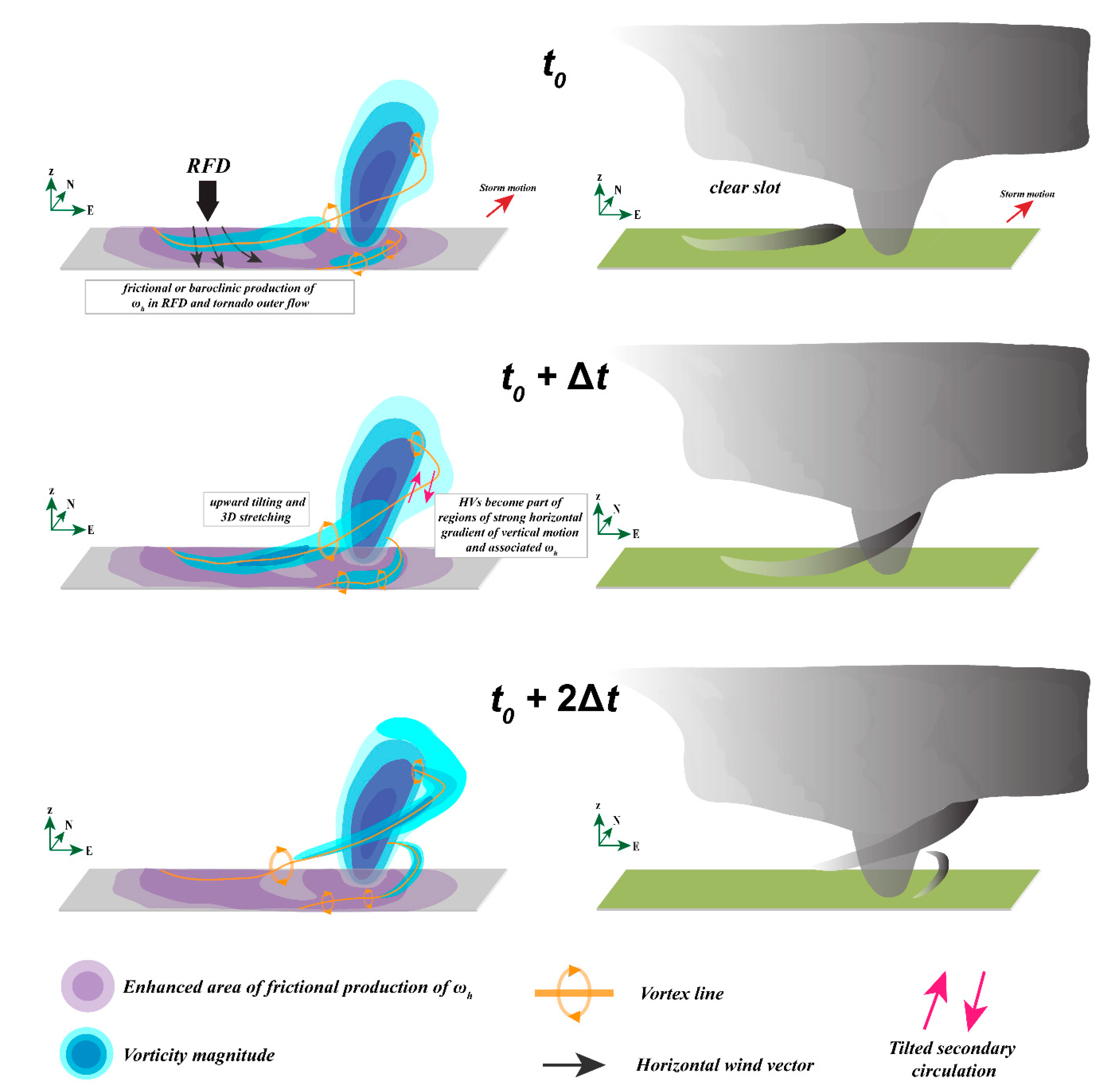
5. Discussion and Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Brandes, E.A. Vertical Vorticity Generation and Mesocyclone Sustenance in Tornadic Thunderstorms: The Observational Evidence. Mon. Weather Rev. 1984, 112, 2253–2269. [Google Scholar] [CrossRef]
- Wakimoto, R.M.; Cai, H.; Murphey, H.V. The Superior, Nebraska, Supercell During BAMEX. Bull. Am. Meteorol. Soc. 2004, 85, 1095–1106. [Google Scholar] [CrossRef]
- Fujita, T.T. Tornadoes and Downbursts in the Context of Generalized Planetary Scales. J. Atmos. Sci. 1981, 38, 1511–1534. [Google Scholar] [CrossRef]
- Fiedler, B. The suction vortices and spiral breakdown in numerical simulations of tornado-like vortices. Atmos. Sci. Let. 2009, 10, 109–114. [Google Scholar] [CrossRef]
- Wurman, J.; Kosiba, K. Finescale Radar Observations of Tornado and Mesocyclone Structures. Weather Forecast. 2013, 28, 1157–1174. [Google Scholar] [CrossRef]
- Bluestein, H.B.; Weiss, C.C.; French, M.M.; Holthaus, E.M.; Tanamachi, R.L.; Frasier, S.; Pazmany, A.L. The Structure of Tornadoes near Attica, Kansas, on 12 May 2004: High-Resolution, Mobile, Doppler Radar Observations. Mon. Weather Rev. 2007, 135, 475–506. [Google Scholar] [CrossRef]
- Knupp, K.R.; Murphy, T.A.; Coleman, T.A.; Wade, R.A.; Mullins, S.A.; Schultz, C.J.; Schultz, E.V.; Carey, E.; Sherrer, A.; McCaul, E.W., Jr.; et al. Meteorological Overview of the Devastating 27 April 2011 Tornado Outbreak. Bull. Amer. Meteorol. Soc. 2014, 95, 1041–1062. [Google Scholar] [CrossRef]
- Bai, L.; Meng, Z.; Huang, L.; Yan, L.; Li, Z.; Mai, X.; Huang, Y.; Yao, D.; Wang, X. An Integrated Damage, Visual, and Radar Analysis of the 2015 Foshan, Guangdong, EF3 Tornado in China Produced by the Landfalling Typhoon Mujigae (2015). Bull. Amer. Meteor. Soc. 2017, 98, 2619–2640. [Google Scholar] [CrossRef]
- Houser, J.L.; Bluestein, H.B.; Snyder, J.C. A Finescale Radar Examination of the Tornadic Debris Signature and Weak-Echo Reflectivity Band Associated with a Large, Violent Tornado. Mon. Weather Rev. 2016, 144, 4101–4130. [Google Scholar] [CrossRef]
- Orf, L.; Wilhelmson, R.; Lee, B.; Finley, C.; Houston, A. Evolution of a Long-Track Violent Tornado within a Simulated Supercell. Bull. Amer. Meteorol. Soc. 2017, 98, 45–68. [Google Scholar] [CrossRef]
- Schenkman, A.D.; Xue, M.; Hu, M. Tornadogenesis in a High-Resolution Simulation of the 8 May 2003 Oklahoma City Supercell. J. Atmos. Sci. 2014, 71, 130–154. [Google Scholar] [CrossRef]
- Xue, M.; Hu, M.; Schenkman, A.D. Numerical prediction of 8 May 2003 Oklahoma City Tornadic Supercell and Embedded Tornado using ARPS with the Assimilation of WSR-88D data. Weather Forecast. 2014, 29, 39–62. [Google Scholar] [CrossRef]
- Roberts, B.; Xue, M.; Schenkman, A.D.; Dawson, D.T. The Role of Surface Drag in Tornadogenesis within an Idealized Supercell Simulation. J. Atmos. Sci. 2016, 73, 3371–3395. [Google Scholar] [CrossRef]
- Roberts, B.; Xue, M. The Role of Surface Drag in Mesocyclone Intensification Leading to Tornadogenesis within an Idealized Supercell Simulation. J. Atmos. Sci. 2017, 74, 3055–3077. [Google Scholar] [CrossRef]
- Davies-Jones, R.; Trapp, R.J.; Bluestein, H.B. Tornadoes and tornadic storms. In Severe Convective Storms; Meteorological Monographs; American Meteorological Society: Boston, MA, US, 2001; pp. 167–221. [Google Scholar]
- Clyne, J.; Mininni, P.; Norton, A.; Rast, M. Interactive desktop analysis of high resolution simulations: Application to turbulent plume dynamics and current sheet formation. New J. Phys. 2007, 9, 301. [Google Scholar] [CrossRef]
- Li, S.; Jaroszynski, S.; Pearse, S.; Orf, L.; Clyne, J. VAPOR: A Visualization Package Tailored to Analyze Simulation Data in Earth System Science. Atmosphere 2019, 10, 488. [Google Scholar] [CrossRef]
- Xue, M.; Droegemeier, K.K.; Wong, V. The Advanced Regional Prediction System (ARPS)—A multiscale nonhydrostatic atmospheric simulation and prediction model. Part I: Model dynamics and verification. Meteor. Atmos. Phys. 2000, 75, 161–193. [Google Scholar] [CrossRef]
- Xue, M.; Droegemeier, K.K.; Wong, V.; Shapiro, A.; Brewster, K.; Carr, F.; Weber, D.; Liu, Y.; Wang, D. The Advanced Regional Prediction System (ARPS)—A multiscale nonhydrostatic atmospheric simulation and prediction tool. Part II: Model physics and applications. Meteor. Atmos. Phys. 2001, 76, 143–165. [Google Scholar] [CrossRef]
- Xue, M.; Wang, D.H.; Gao, J.D.; Brewster, K.; Droegemeier, K.K. The Advanced Regional Prediction System (ARPS), storm-scale numerical weather prediction and data assimilation. Meteor. Atmos. Phys. 2003, 82, 139–170. [Google Scholar] [CrossRef]
- Vande Guchte, A.; Dahl, J.M.L. Sensitivities of Parcels Trajectories beneath the Lowest Scalar Model Level of a Lorenz Vertical Grid. Mon. Weather Rev. 2018, 146, 1427–1435. [Google Scholar] [CrossRef]
- Lin, Y.L.; Farley, R.D.; Orville, H.D. Bulk Parameterization of the Snow Field in a Cloud Model. J. Appl. Clim. Meteor. 1983, 22, 1065–1092. [Google Scholar] [CrossRef]
- Snook, N.; Xue, M. Effects of microphysical drop size distribution on tornadogenesis in supercell thunderstorms. Geophys. Res. Lett. 2008, 35, 851–854. [Google Scholar] [CrossRef]
- Dawson, D.T.; Xue, M.; Milbrandt, J.A.; Yau, M.K. Comparison of Evaporation and Cold Pool Development between Single-Moment and Multimoment Bulk Microphysics Schemes in Idealized Simulations of Tornadic Thunderstorms. Mon. Weather Rev. 2010, 138, 1152–1171. [Google Scholar] [CrossRef]
- Moeng, C.H.; Wyngaard, J.C. Spectral Analysis of Large-Eddy Simulations of the Convective Boundary Layer. J. Atmos. Sci. 1988, 45, 3573–3587. [Google Scholar] [CrossRef]
- Yussouf, N.; Dowell, D.C.; Wicker, L.J.; Knopfmeier, K.H. Storm-Scale Data Assimilation and Ensemble Forecasts for the 27 April 2011 Severe Weather Outbreak in Alabama. Mon. Weather Rev. 2015, 143, 3044–3066. [Google Scholar] [CrossRef]
- Karstens, C.D.; Gallus, W.A., Jr.; Lee, B.D.; Finley, C.A. Analysis of Tornado-Induced Tree Fall Using Aerial Photography from the Joplin, Missouri, and Tuscaloosa–Birmingham, Alabama, Tornadoes of 2011. J. Appl. Clim. Meteor. 2013, 52, 1049–1068. [Google Scholar] [CrossRef]
- Potvin, C.K.; Elmore, K.L.; Weiss, S.J. Assessing the Impacts of Proximity Sounding Criteria on the Climatology of Significant Tornado Environments. Weather Forecast. 2010, 25, 921–930. [Google Scholar] [CrossRef]
- Blumberg, W.; Halbert, K.; Supinie, T.; Marsh, P.; Thompson, T.; Hart, J. SHARPpy: An Open Source Sounding Analysis Toolkit for the Atmospheric Sciences. Bull. Am. Meteorol. Soc. 2017, 98, 1625–1636. [Google Scholar] [CrossRef]
- Roberts, B.J. The Role of Surface Drag in Supercell Tornadogenesis and Mesocyclonegenesis: Studies Based on Idealized Numerical Simulations. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2017. [Google Scholar]
- Dawson, D.T.; Roberts, B.; Xue, M. A Method to Control the Environmental Wind Profile in Idealized Simulations of Deep Convection with Surface Friction. Mon. Weather Rev. 2019, 147, 3935–3954. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B. The Stability of Time-Split Numerical Methods for the Hydrostatic and the Nonhydrostatic Elastic Equations. Mon. Weather Rev. 1992, 147, 2109–2127. [Google Scholar] [CrossRef]
- Xue, M.; Droegemeier, K.K.; Wong, V.; Shapiro, A.; Brewster, K. ARPS user’s guide, version 4.0. Center for Analysis and Prediction of Storms. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 1995; p. 380. [Google Scholar]
- Adlerman, E.J.; Droegemeier, K.K. The Dependence of Numerically Simulated Cyclic Mesocyclonegenesis upon Environmental Vertical Wind Shear. Mon. Weather Rev. 2005, 133, 3595–3623. [Google Scholar] [CrossRef]
- Beck, J.; Weiss, C. An Assessment of Low-Level Baroclinicity and Vorticity within a Simulated Supercell. Mon. Weather Rev. 2013, 141, 649–669. [Google Scholar] [CrossRef]
- Dahl, J.M.L.; Parker, M.D.; Wicker, L.J. Imported and Storm-Generated Near-Ground Vertical Vorticity in a Simulated Supercell. J. Atmos. Sci. 2014, 71, 3027–3051. [Google Scholar] [CrossRef]
- Parker, M.D.; Dahl, J.M.L. Production of Near-Surface Vertical Vorticity by Idealized Downdrafts. Mon. Weather Rev. 2015, 143, 2795–2816. [Google Scholar] [CrossRef]
- Coffer, B.E.; Parker, M.D. Simulated Supercells in Nontornadic and Tornadic VORTEX2 Environments. Mon. Weather Rev. 2017, 145, 149–180. [Google Scholar] [CrossRef]
- Griffin, C.B.; Bodine, D.J.; Kurdzo, J.M.; Mahre, A.; Palmer, R.D. High-Temporal Resolution Observations of the 27 May 2015 Canadian, Texas, Tornado Using the Atmospheric Imaging Radar. Mon. Weather Rev. 2019, 147, 873–891. [Google Scholar] [CrossRef]
- Fujita, T.T.; Bradbury, D.L.; Van Thullenar, C.F. Palm Sunday Tornadoes of April 11, 1965. Mon. Weather Rev. 1970, 98, 29–69. [Google Scholar] [CrossRef]
- Dowell, D.C.; Bluestein, H.B. The 8 June 1995 McLean, Texas, storm. Part I: Observations of cyclic tornadogenesis. Mon. Weather Rev. 2002, 130, 2626–2648. [Google Scholar] [CrossRef]
- French, M.M.; Kingfield, D.M. Dissipation Characteristics of Tornadic Vortex Signatures Associated with Long-Duration Tornadoes. J. Appl. Clim. Meteor. 2019, 58, 317–339. [Google Scholar] [CrossRef]
- Markowski, P.M.; Richardson, Y.; Rasmussen, E.; Straka, J.; Davies-Jones, R.; Trapp, R.J. Vortex lines within low-level mesocyclones obtained from pseudo-dual-Doppler radar observations. Mon. Weather Rev. 2008, 136, 3513–3535. [Google Scholar] [CrossRef]
- Bluestein, H.B.; French, M.M.; Snyder, J.C.; Houser, J.B. Doppler radar observations of anticyclonic tornadoes in cyclonically rotating, right-moving supercells. Mon. Weather Rev. 2016, 144, 1591–1616. [Google Scholar] [CrossRef]
- Adlerman, E.J.; Droegemeier, K.K.; Davies-Jones, R. A numerical simulation of cyclic mesocyclogenesis. J. Atmos. Sci. 1999, 56, 2045–2069. [Google Scholar] [CrossRef]
- Lemon, L.R.; Doswell, C.A. Severe Thunderstorm Evolution and Mesocyclone Structure as Related to Tornadogenesis. Mon. Weather Rev. 1979, 107, 1184–1197. [Google Scholar] [CrossRef]
- Atkins, N.T.; Butler, K.M.; Flynn, K.R.; Wakimoto, R.M. 2014: An integrated damage, visual, and radar analysis of the 2013 Moore, Oklahoma, EF5 tornado. Bull. Amer. Meteor. Soc. 2014, 95, 1549–1561. [Google Scholar] [CrossRef]
- Jiménez, J.; Wray, A.A.; Saffman, P.G.; Rogallo, R.S. The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 1993, 255, 65–90. [Google Scholar] [CrossRef]
- Takahashi, N.; Ishii, H.; Miyazaki, T. The influence of turbulence on a columnar vortex. Phys. Fluids 2005, 17, 035105. [Google Scholar] [CrossRef]
- Leibovich, S.; Stewartson, K. A sufficient condition for the instability of columnar vortices. J. Fluid Mech. 1983, 126, 335–356. [Google Scholar] [CrossRef]
- Nolan, D.S. Three-dimensional instabilities in tornado-like vortices with secondary circulations. J. Fluid Mech. 2012, 711, 61–100. [Google Scholar] [CrossRef]
- Yokota, S.; Niino, H.; Seko, H.; Kunii, M.; Yamauchi, H. Important Factors for Tornadogenesis as Revealed by High-Resolution Ensemble Forecasts of the Tsukuba Supercell Tornado of 6 May 2012 in Japan. Mon. Weather Rev. 2018, 146, 1109–1132. [Google Scholar] [CrossRef]
- Orf, L. A Violently Tornadic Supercell Thunderstorm Simulation Spanning a Quarter-Trillion Grid Volumes: Computational Challenges, I/O Framework, and Visualizations of Tornadogenesis. Atmosphere 2019, 10, 578. [Google Scholar] [CrossRef]
- Chow, F.K.; Street, R.L.; Xue, M.; Ferziger, J.H. Explicit Filtering and Reconstruction of Turbulence Modeling for Large-Eddy Simulation of Neutral Boundary Layer Flow. J. Atmos. Sci. 2005, 62, 2058–2077. [Google Scholar] [CrossRef]
- Nishizawa, S.; Yashiro, H.; Sato, Y.; Miyamoto, Y.; Tomita, H. Influence of grid aspect ratio on planetary boundary layer turbulence in large-eddy simulations. Geosci. Model Dev. 2015, 8, 3393–3419. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, M.I.; Xue, M.; Roberts, B.J.; Wicker, L.J.; Yussouf, N. Horizontal Vortex Tubes near a Simulated Tornado: Three-Dimensional Structure and Kinematics. Atmosphere 2019, 10, 716. https://doi.org/10.3390/atmos10110716
Oliveira MI, Xue M, Roberts BJ, Wicker LJ, Yussouf N. Horizontal Vortex Tubes near a Simulated Tornado: Three-Dimensional Structure and Kinematics. Atmosphere. 2019; 10(11):716. https://doi.org/10.3390/atmos10110716
Chicago/Turabian StyleOliveira, Maurício I., Ming Xue, Brett J. Roberts, Louis J. Wicker, and Nusrat Yussouf. 2019. "Horizontal Vortex Tubes near a Simulated Tornado: Three-Dimensional Structure and Kinematics" Atmosphere 10, no. 11: 716. https://doi.org/10.3390/atmos10110716
APA StyleOliveira, M. I., Xue, M., Roberts, B. J., Wicker, L. J., & Yussouf, N. (2019). Horizontal Vortex Tubes near a Simulated Tornado: Three-Dimensional Structure and Kinematics. Atmosphere, 10(11), 716. https://doi.org/10.3390/atmos10110716




