Biological Prior Knowledge-Embedded Deep Neural Network for Plant Genomic Prediction
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Used for Genomic Prediction
2.2. Heritability Estimation
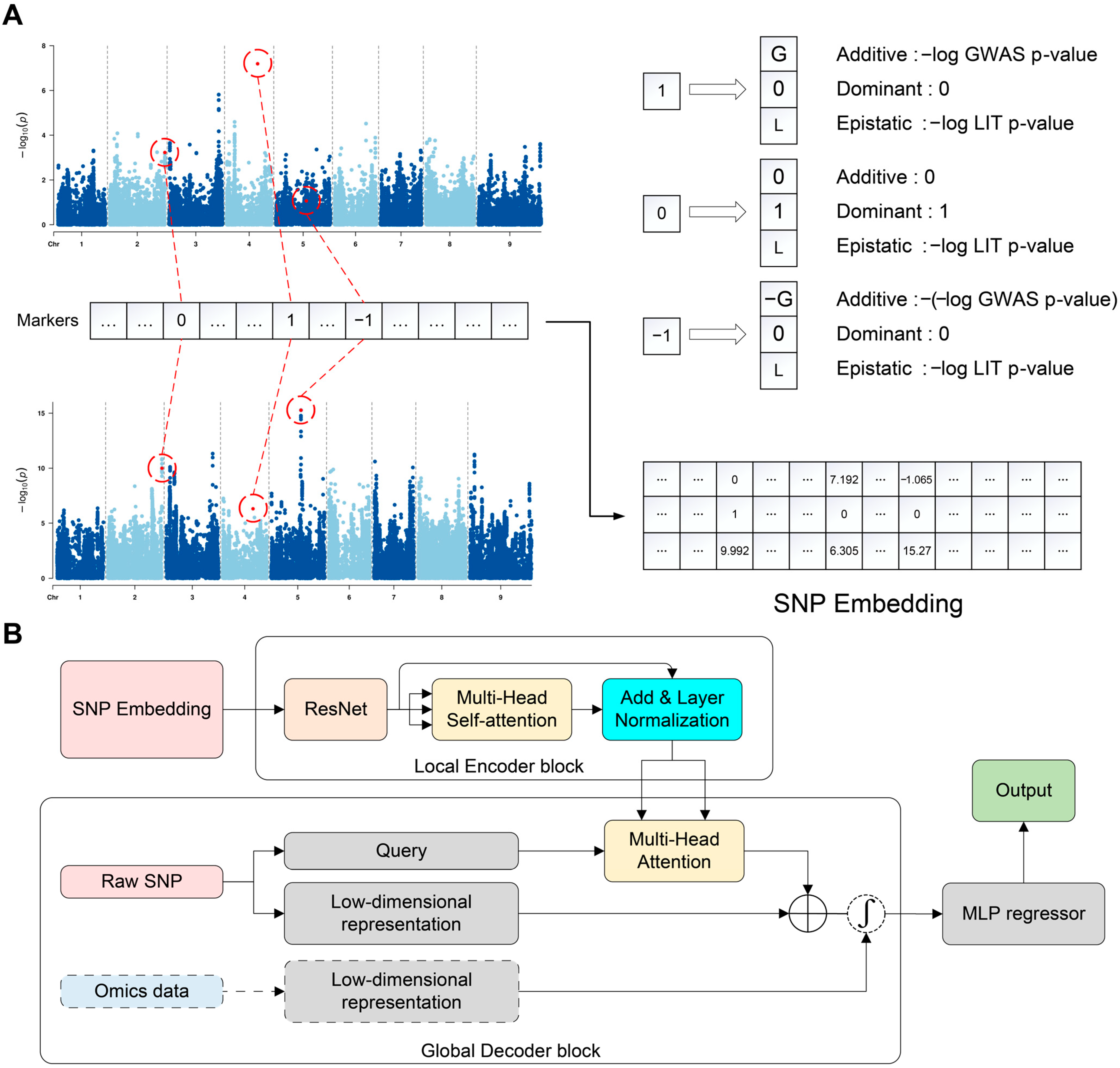
2.3. iADEP Algorithm
2.4. Model Construction of Existing Representative Methods
2.5. Model Evaluation
3. Results
3.1. Overview of iADEP Architecture
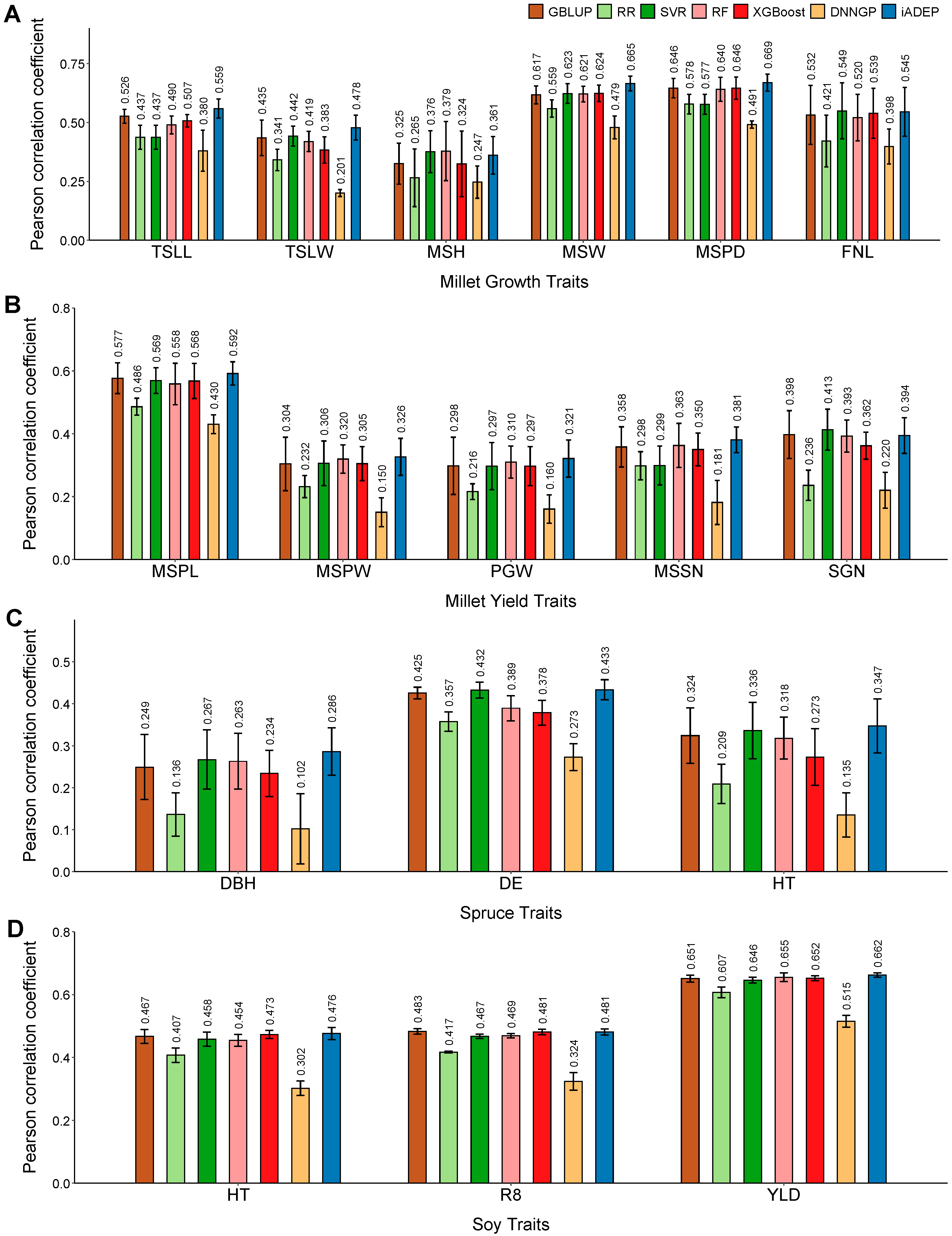
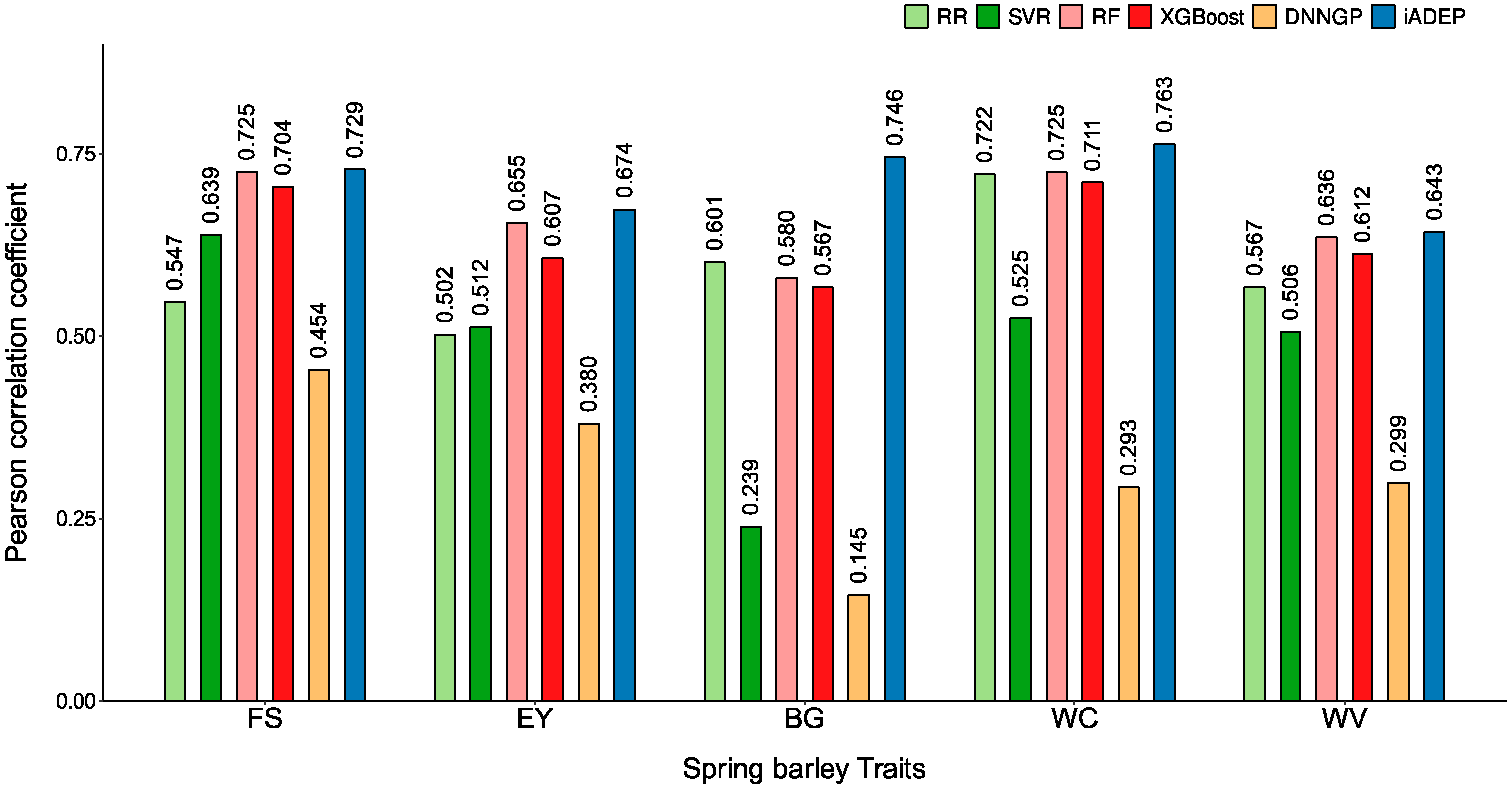
3.2. Prediction Performance of iADEP and Comparison with Other Methods
3.3. Ablation Experiments of SNP Embedding
3.4. Genomic Prediction Incorporating Other Omics Data
3.5. Effects of Feature Selection on iADEP
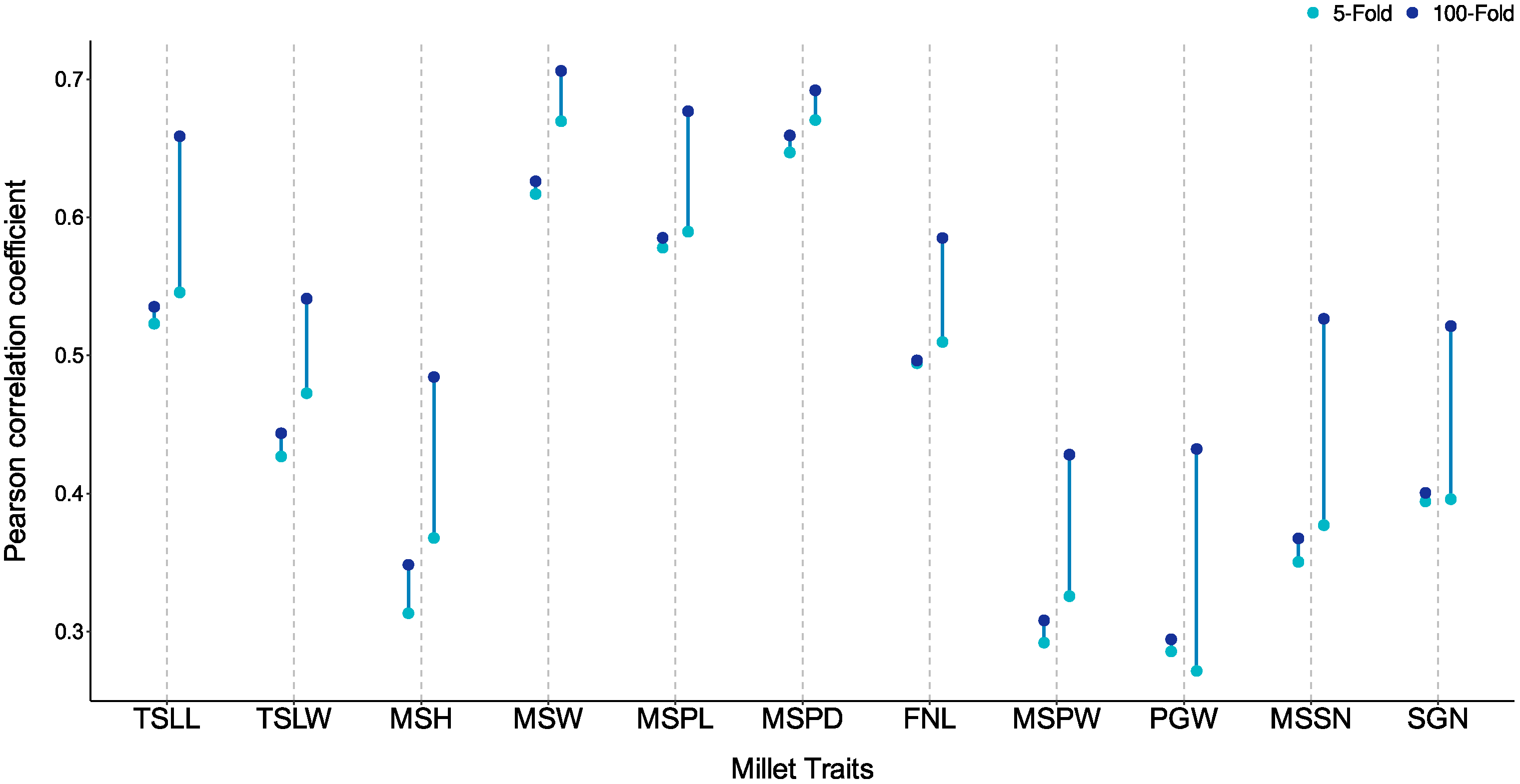
3.6. Impact of Transductive Learning and Inductive Learning on Genomic Prediction
4. Discussion
4.1. The Potential Role of SNP Embedding
4.2. Scalability of Multi-Omic Data Fusion
4.3. Differences Between Transductive Learning and Inductive Learning
4.4. Limitations of iADEP
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GP | Genomic prediction |
| GBLUP | Genomic best linear unbiased prediction |
| ML | Machine learning |
| RF | Random forest |
| RR | Ridge regression |
| SVR | Support vector regression |
| DL | Deep learning |
| DeepGS | Deep convolutional neural network |
| CNN | Convolutional neural networks |
| DArT | Diversity Array Technology |
| DNNGP | Deep neural network genomic prediction |
| SNP | Single nucleotide polymorphisms |
| GWAS | Genome-wide association study |
| iADEP | Integrated Additive, Dominant and Epistatic Prediction |
| MLP | Multilayer perceptrons |
| LIT | Latent Interaction Testing |
| XGBoost | eXtreme Gradient Boosting |
| PCC | Pearson correlation coefficient |
| iGEP | integrated genomic-enviromic prediction |
| GradCAM | Gradient-weighted Class Activation Mapping |
| MAF | Minor allele frequency |
| RIL | Recombinant lines |
| GCTA | Genetics complex trait analysis |
| GREML | Genome-based restricted maximum likelihood |
| MSE | Mean squared error |
| TSLL | Top second leaf length |
| TSLW | Top Second Leaf Width |
| MSH | Main Stem Height |
| MSW | Main Stem Width |
| MSPD | Panicle Diameter of Main Stem |
| FNL | Fringe Neck Length |
| MSPL | Panicle Length of Main Stem |
| MSPW | Main Stem Panicle Weight |
| PGW | Per Plant Grain Weight |
| MSSN | Spikelet Number of Main Stem |
| SGN | Grain Number per Spike |
| DBG | Diameter at Breast Height |
| DE | Wood Density |
| HT | Height |
| R8 | Time to R8 Developmental Stage |
| YLD | Yield |
| DTA | Days to Anther |
| DTS | Days to Silk |
| DTT | Days to Tassel |
| EH | Ear Height |
| ELL | Ear Leaf Length |
| ELW | Ear Leaf Width |
| PH | Plant Height |
| TBN | Tassel Branch Number |
| TL | Tassel Length |
| CW | Cob Weight |
| ED | Ear Diameter |
| EL | Ear Length |
| ERN | Ear Row Number |
| EW | Ear Weight |
| KNPE | Kernel Number per Ear |
| KNPR | Kernel Number per Row |
| KWPE | Kernel Weight per Ear |
| LBT | Length of Barren Tip |
| FS | Filtering Speed |
| EY | Extract Yield |
| WC | Wort Color |
| BG | Beta Glucan |
| WV | Wort Viscosity |
References
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M. Prediction of Total Genetic Value Using Genome-Wide Dense Marker Maps. Genetics 2001, 157, 1819–1829. [Google Scholar] [PubMed]
- Heffner, E.L.; Jannink, J.; Iwata, H.; Souza, E.; Sorrells, M.E. Genomic Selection Accuracy for Grain Quality Traits in Biparental Wheat Populations. Crop Sci. 2011, 51, 2597–2606. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, Y.; Ying, Z.; Li, L.; Wang, J.; Yu, H.; Zhang, M.; Feng, X.; Wei, X.; Xu, X. A Transformer-Based Genomic Prediction Method Fused with Knowledge-Guided Module. Brief. Bioinform. 2024, 25, bbad438. [Google Scholar]
- Zhang, Z.; Zhang, Q.; Ding, X. Advances in Genomic Selection in Domestic Animals. Chin. Sci. Bull. 2011, 56, 2655–2663. [Google Scholar] [CrossRef][Green Version]
- VanRaden, P.M. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar]
- Endelman, J.B. Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef]
- Kärkkäinen, H.P.; Sillanpää, M.J. Back to Basics for Bayesian Model Building in Genomic Selection. Genetics 2012, 191, 969–987. [Google Scholar]
- Yan, J.; Wang, X. Machine Learning Bridges Omics Sciences and Plant Breeding. Trends Plant Sci. 2023, 28, 199–210. [Google Scholar]
- González-Camacho, J.M.; Ornella, L.; Pérez-Rodríguez, P.; Gianola, D.; Dreisigacker, S.; Crossa, J. Applications of Machine Learning Methods to Genomic Selection in Breeding Wheat for Rust Resistance. Plant Genome 2018, 11, 170104. [Google Scholar] [CrossRef]
- Alves, A.A.C.; Espigolan, R.; Bresolin, T.; Costa, R.M.; Fernandes Júnior, G.A.; Ventura, R.V.; Carvalheiro, R.; Albuquerque, L.G. Genome-enabled Prediction of Reproductive Traits in Nellore Cattle Using Parametric Models and Machine Learning Methods. Anim. Genet. 2021, 52, 32–46. [Google Scholar] [CrossRef]
- Zhao, Z.; Gui, J.; Yao, A.; Le, N.Q.K.; Chua, M.C.H. Improved Prediction Model of Protein and Peptide Toxicity by Integrating Channel Attention into a Convolutional Neural Network and Gated Recurrent Units. ACS Omega 2022, 7, 40569–40577. [Google Scholar] [CrossRef]
- Le, N.Q.K. Predicting Emerging Drug Interactions Using GNNs. Nat. Comput. Sci. 2023, 3, 1007–1008. [Google Scholar]
- Ma, W.; Qiu, Z.; Song, J.; Li, J.; Cheng, Q.; Zhai, J.; Ma, C. A Deep Convolutional Neural Network Approach for Predicting Phenotypes from Genotypes. Planta 2018, 248, 1307–1318. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Abid, M.A.; Rasheed, A.; Crossa, J.; Hearne, S.; Li, H. DNNGP, a Deep Neural Network-Based Method for Genomic Prediction Using Multi-Omics Data in Plants. Mol. Plant 2023, 16, 279–293. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar] [CrossRef]
- Wu, H.; Xu, J.; Wang, J.; Long, M. Autoformer: Decomposition Transformers with Auto-Correlation for Long-Term Series Forecasting. Adv. Neural Inf. Process. Syst. 2021, 34, 22419–22430. [Google Scholar]
- Vitezica, Z.G.; Legarra, A.; Toro, M.A.; Varona, L. Orthogonal Estimates of Variances for Additive, Dominance, and Epistatic Effects in Populations. Genetics 2017, 206, 1297–1307. [Google Scholar] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Bass, A.J.; Bian, S.; Wingo, A.P.; Wingo, T.S.; Cutler, D.J.; Epstein, M.P. Identifying Latent Genetic Interactions in Genome-Wide Association Studies Using Multiple Traits. Genome Med. 2024, 16, 62. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Sun, S.; Jin, C.; Su, J.; Wei, J.; Luo, X.; Wen, J.; Wei, T.; Sahu, S.K. GWAS, MWAS and mGWAS Provide Insights into Precision Agriculture Based on Genotype-Dependent Microbial Effects in Foxtail Millet. Nat. Commun. 2022, 13, 5913. [Google Scholar]
- Chen, J.; Tan, C.; Zhu, M.; Zhang, C.; Wang, Z.; Ni, X.; Liu, Y.; Wei, T.; Wei, X.; Fang, X. CropGS-Hub: A Comprehensive Database of Genotype and Phenotype Resources for Genomic Prediction in Major Crops. Nucleic Acids Res. 2023, 52, D1519–D1529. [Google Scholar]
- Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-Generation PLINK: Rising to the Challenge of Larger and Richer Datasets. Gigascience 2015, 4, s13742-015. [Google Scholar]
- Beaulieu, J.; Doerksen, T.K.; MacKay, J.; Rainville, A.; Bousquet, J. Genomic Selection Accuracies within and between Environments and Small Breeding Groups in White Spruce. BMC Genom. 2014, 15, 1048. [Google Scholar] [CrossRef]
- Xavier, A.; Muir, W.M.; Rainey, K.M. Assessing Predictive Properties of Genome-Wide Selection in Soybeans. G3 Genes Genomes Genet. 2016, 6, 2611–2616. [Google Scholar]
- Heinrich, F.; Lange, T.M.; Kircher, M.; Ramzan, F.; Schmitt, A.O.; Gültas, M. Exploring the Potential of Incremental Feature Selection to Improve Genomic Prediction Accuracy. Genet. Sel. Evol. 2023, 55, 78. [Google Scholar] [CrossRef]
- Liu, H.-J.; Wang, X.; Xiao, Y.; Luo, J.; Qiao, F.; Yang, W.; Zhang, R.; Meng, Y.; Sun, J.; Yan, S.; et al. CUBIC: An Atlas of Genetic Architecture Promises Directed Maize Improvement. Genome Biol. 2020, 21, 20. [Google Scholar] [CrossRef]
- Yang, W.; Guo, T.; Luo, J.; Zhang, R.; Zhao, J.; Warburton, M.L.; Xiao, Y.; Yan, J. Target-Oriented Prioritization: Targeted Selection Strategy by Integrating Organismal and Molecular Traits through Predictive Analytics in Breeding. Genome Biol. 2022, 23, 80. [Google Scholar] [CrossRef]
- Guo, X. Data for Spring Barley from Nordic Seed A/S. Mendeley Data 2020. [Google Scholar] [CrossRef]
- Guo, X.; Sarup, P.; Jahoor, A.; Jensen, J.; Christensen, O.F. Metabolomic-Genomic Prediction Can Improve Prediction Accuracy of Breeding Values for Malting Quality Traits in Barley. Genet Sel. Evol. 2023, 55, 61. [Google Scholar] [CrossRef]
- Yang, J.; Benyamin, B.; McEvoy, B.P.; Gordon, S.; Henders, A.K.; Nyholt, D.R.; Madden, P.A.; Heath, A.C.; Martin, N.G.; Montgomery, G.W. Common SNPs Explain a Large Proportion of the Heritability for Human Height. Nat. Genet. 2010, 42, 565–569. [Google Scholar]
- Yang, J.; Lee, S.H.; Goddard, M.E.; Visscher, P.M. GCTA: A Tool for Genome-Wide Complex Trait Analysis. Am. J. Hum. Genet. 2011, 88, 76–82. [Google Scholar]
- Namkoong, G. Introduction to Quantitative Genetics in Forestry; Department of Agriculture, Forest Service: Washinton, DC, USA, 1979. [Google Scholar]
- Kang, H.M.; Sul, J.H.; Service, S.K.; Zaitlen, N.A.; Kong, S.; Freimer, N.B.; Sabatti, C.; Eskin, E. Variance Component Model to Account for Sample Structure in Genome-Wide Association Studies. Nat. Genet. 2010, 42, 348–354. [Google Scholar] [CrossRef]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network 2015. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Amit, Y.; Geman, D. Shape Quantization and Recognition with Randomized Trees. Neural Comput. 1997, 9, 1545–1588. [Google Scholar] [CrossRef]
- Maenhout, S.; De Baets, B.; Haesaert, G.; Van Bockstaele, E. Support Vector Machine Regression for the Prediction of Maize Hybrid Performance. Theor. Appl. Genet. 2007, 115, 1003–1013. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, San Francisco, CA, USA, 13 August 2016; pp. 785–794. [Google Scholar]
- Sandhu, K.S.; Lozada, D.N.; Zhang, Z.; Pumphrey, M.O.; Carter, A.H. Deep Learning for Predicting Complex Traits in Spring Wheat Breeding Program. Front. Plant Sci. 2021, 11, 613325. [Google Scholar]
- Yang, J.; Zeng, J.; Goddard, M.E.; Wray, N.R.; Visscher, P.M. Concepts, Estimation and Interpretation of SNP-Based Heritability. Nat. Genet. 2017, 49, 1304–1310. [Google Scholar]
- Zhu, H.; Zhou, X. Statistical Methods for SNP Heritability Estimation and Partition: A Review. Comput. Struct. Biotechnol. J. 2020, 18, 1557–1568. [Google Scholar] [CrossRef]
- Lee, H.-J.; Lee, J.H.; Gondro, C.; Koh, Y.J.; Lee, S.H. deepGBLUP: Joint Deep Learning Networks and GBLUP Framework for Accurate Genomic Prediction of Complex Traits in Korean Native Cattle. Genet. Sel. Evol. 2023, 55, 56. [Google Scholar] [CrossRef]
- Zhang, F.; Kang, J.; Long, R.; Li, M.; Sun, Y.; He, F.; Jiang, X.; Yang, C.; Yang, X.; Kong, J. Application of Machine Learning to Explore the Genomic Prediction Accuracy of Fall Dormancy in Autotetraploid Alfalfa. Hortic. Res. 2023, 10, uhac225. [Google Scholar] [PubMed]
- Lachaud, G.; Conde-Cespedes, P.; Trocan, M. Comparison between Inductive and Transductive Learning in a Real Citation Network Using Graph Neural Networks. In Proceedings of the 2022 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining (ASONAM), Istanbul, Turkey, 10–13 November 2022; IEEE: New York, NY, USA, 2022; pp. 534–540. [Google Scholar]
- Zingaretti, L.M.; Gezan, S.A.; Ferrão, L.F.V.; Osorio, L.F.; Monfort, A.; Muñoz, P.R.; Whitaker, V.M.; Pérez-Enciso, M. Exploring Deep Learning for Complex Trait Genomic Prediction in Polyploid Outcrossing Species. Front. Plant Sci. 2020, 11, 25. [Google Scholar] [CrossRef] [PubMed]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Xu, Y.; Zhang, X.; Li, H.; Zheng, H.; Zhang, J.; Olsen, M.S.; Varshney, R.K.; Prasanna, B.M.; Qian, Q. Smart Breeding Driven by Big Data, Artificial Intelligence, and Integrated Genomic-Enviromic Prediction. Mol. Plant 2022, 15, 1664–1695. [Google Scholar] [PubMed]
- Castro, J.; Gómez, D.; Tejada, J. Polynomial Calculation of the Shapley Value Based on Sampling. Comput. Oper. Res. 2009, 36, 1726–1730. [Google Scholar]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-Cam: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Heslot, N.; Jannink, J.; Sorrells, M.E. Perspectives for Genomic Selection Applications and Research in Plants. Crop Sci. 2015, 55, 1–12. [Google Scholar] [CrossRef]


| Dataset | Trait | SNP Embedding | One-Hot Encoding | Non-Encoding |
|---|---|---|---|---|
| millet827 | TSLL | 0.559 ± 0.040 | 0.535 ± 0.033 | 0.533 ± 0.024 |
| TSLW | 0.478 ± 0.053 | 0.438 ± 0.069 | 0.457 ± 0.048 | |
| MSH | 0.361 ± 0.080 | 0.348 ± 0.079 | 0.354 ± 0.089 | |
| MSW | 0.666 ± 0.031 | 0.639 ± 0.038 | 0.634 ± 0.042 | |
| MSPD | 0.669 ± 0.036 | 0.657 ± 0.030 | 0.649 ± 0.040 | |
| FNL | 0.545 ± 0.104 | 0.537 ± 0.112 | 0.544 ± 0.111 | |
| MSPL | 0.592 ± 0.037 | 0.582 ± 0.050 | 0.587 ± 0.039 | |
| MSPW | 0.326 ± 0.059 | 0.338 ± 0.062 | 0.291 ± 0.085 | |
| PGW | 0.321 ± 0.059 | 0.299 ± 0.061 | 0.281 ± 0.097 | |
| MSSN | 0.381 ± 0.041 | 0.351 ± 0.040 | 0.341 ± 0.035 | |
| SGN | 0.394 ± 0.057 | 0.393 ± 0.060 | 0.393 ± 0.059 | |
| spruce1722 | DBH | 0.286 ± 0.056 | 0.268 ± 0.078 | 0.225 ± 0.060 |
| DE | 0.433 ± 0.024 | 0.424 ± 0.028 | 0.417 ± 0.022 | |
| HT | 0.347 ± 0.064 | 0.334 ± 0.067 | 0.308 ± 0.041 | |
| soy5014 | HT | 0.476 ± 0.019 | 0.458 ± 0.026 | 0.453 ± 0.030 |
| R8 | 0.481 ± 0.010 | 0.437 ± 0.018 | 0.456 ± 0.024 | |
| YLD | 0.662 ± 0.007 | 0.659 ± 0.010 | 0.659 ± 0.008 | |
| maize5820 | DTA | 0.948 ± 0.001 | 0.940 ± 0.003 | 0.942 ± 0.003 |
| DTS | 0.946 ± 0.004 | 0.938 ± 0.005 | 0.941 ± 0.004 | |
| DTT | 0.948 ± 0.002 | 0.939 ± 0.003 | 0.944 ± 0.003 | |
| EH | 0.941 ± 0.002 | 0.921 ± 0.009 | 0.929 ± 0.001 | |
| ELL | 0.914 ± 0.003 | 0.884 ± 0.005 | 0.893 ± 0.004 | |
| ELW | 0.887 ± 0.007 | 0.883 ± 0.008 | 0.885 ± 0.008 | |
| PH | 0.941 ± 0.003 | 0.932 ± 0.004 | 0.931 ± 0.005 | |
| TBN | 0.927 ± 0.004 | 0.905 ± 0.004 | 0.913 ± 0.006 | |
| TL | 0.924 ± 0.002 | 0.902 ± 0.003 | 0.910 ± 0.004 | |
| CW | 0.852 ± 0.007 | 0.815 ± 0.007 | 0.826 ± 0.013 | |
| ED | 0.840 ± 0.013 | 0.552 ± 0.238 | 0.796 ± 0.094 | |
| EL | 0.831 ± 0.005 | 0.803 ± 0.008 | 0.807 ± 0.010 | |
| ERN | 0.914 ± 0.003 | 0.908 ± 0.004 | 0.908 ± 0.004 | |
| EW | 0.805 ± 0.014 | 0.776 ± 0.011 | 0.782 ± 0.014 | |
| KNPE | 0.847 ± 0.011 | 0.841 ± 0.010 | 0.842 ± 0.012 | |
| KNPR | 0.705 ± 0.016 | 0.686 ± 0.018 | 0.691 ± 0.019 | |
| KWPE | 0.778 ± 0.014 | 0.747 ± 0.022 | 0.756 ± 0.019 | |
| LBT | 0.683 ± 0.017 | 0.621 ± 0.106 | 0.678 ± 0.020 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, C.; Li, K.; Sun, W.; Jiang, Y.; Zhang, W.; Zhang, P.; Hu, Y.-J.; Han, Y.; Li, L. Biological Prior Knowledge-Embedded Deep Neural Network for Plant Genomic Prediction. Genes 2025, 16, 411. https://doi.org/10.3390/genes16040411
Ye C, Li K, Sun W, Jiang Y, Zhang W, Zhang P, Hu Y-J, Han Y, Li L. Biological Prior Knowledge-Embedded Deep Neural Network for Plant Genomic Prediction. Genes. 2025; 16(4):411. https://doi.org/10.3390/genes16040411
Chicago/Turabian StyleYe, Chonghang, Kai Li, Weicheng Sun, Yiwei Jiang, Weihan Zhang, Ping Zhang, Yi-Juan Hu, Yuepeng Han, and Li Li. 2025. "Biological Prior Knowledge-Embedded Deep Neural Network for Plant Genomic Prediction" Genes 16, no. 4: 411. https://doi.org/10.3390/genes16040411
APA StyleYe, C., Li, K., Sun, W., Jiang, Y., Zhang, W., Zhang, P., Hu, Y.-J., Han, Y., & Li, L. (2025). Biological Prior Knowledge-Embedded Deep Neural Network for Plant Genomic Prediction. Genes, 16(4), 411. https://doi.org/10.3390/genes16040411








