A Comprehensive Survey of Statistical Approaches for Differential Expression Analysis in Single-Cell RNA Sequencing Studies
Abstract
:1. Introduction
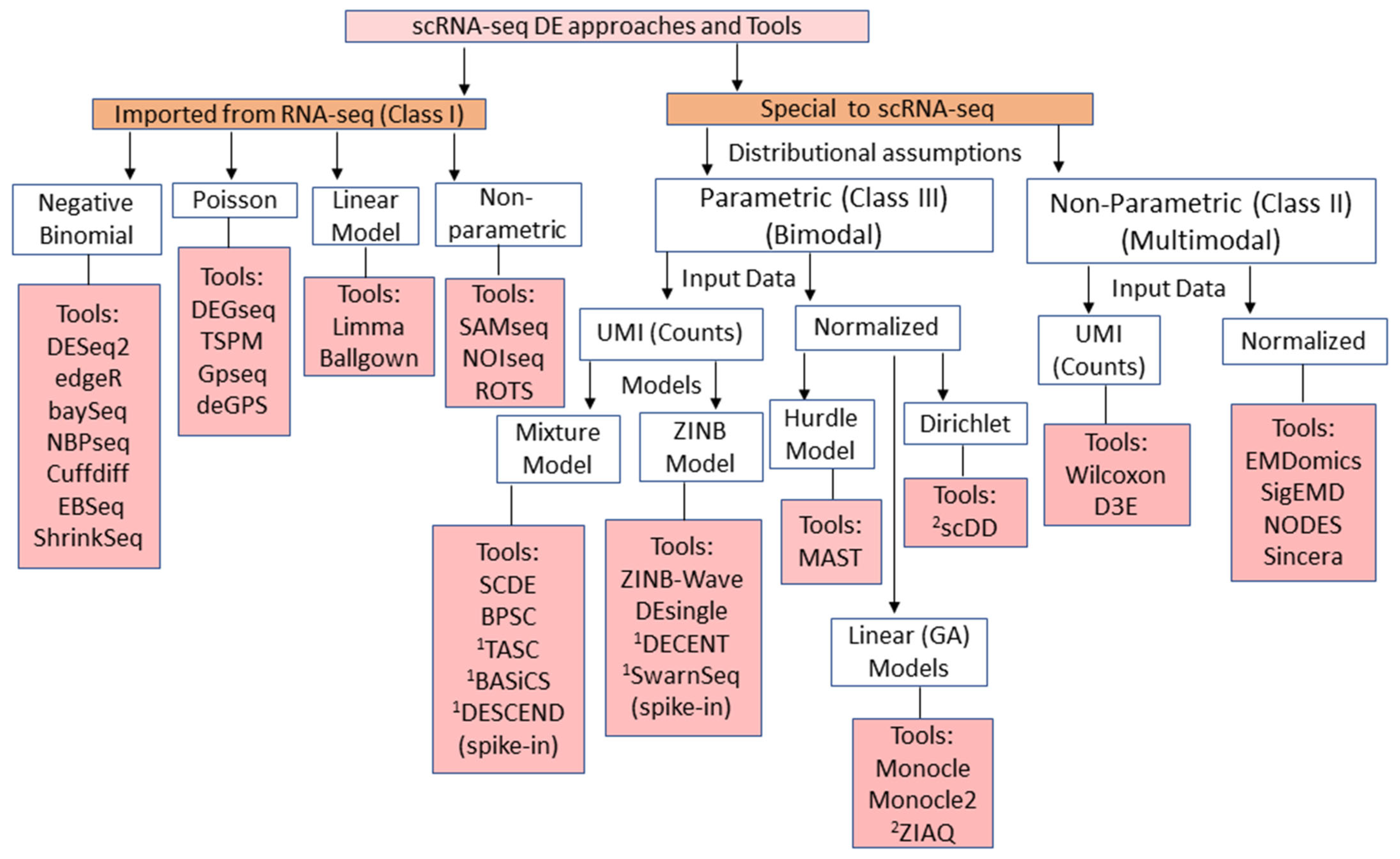
2. Overview and Classification of scRNA-seq DE Methods
3. Real scRNA-seq Datasets
4. Methods for scRNA-seq DE Analysis
4.1. Negative Binomial Model Based Methods
4.1.1. DESeq
4.1.2. edgeR
4.1.3. NBPSeq
4.1.4. EBSeq
4.2. Poisson Model
DEGseq
4.3. Zero Inflated Negative Binomial Model
4.3.1. DEsingle
4.3.2. DECENT
4.4. Mixed Model Based Methods
4.4.1. BPSC
4.4.2. scDD
4.5. Normal/Gaussian Based Methods
4.5.1. LIMMA
4.5.2. MAST
4.5.3. Monocle
4.5.4. T-Test
4.6. Non-Parametric Methods
4.6.1. EMDomics
4.6.2. NODES
4.6.3. Wilcoxon Signed Rank Test (Wilcox)
4.6.4. ROTS
5. Comparative Performance Evaluation
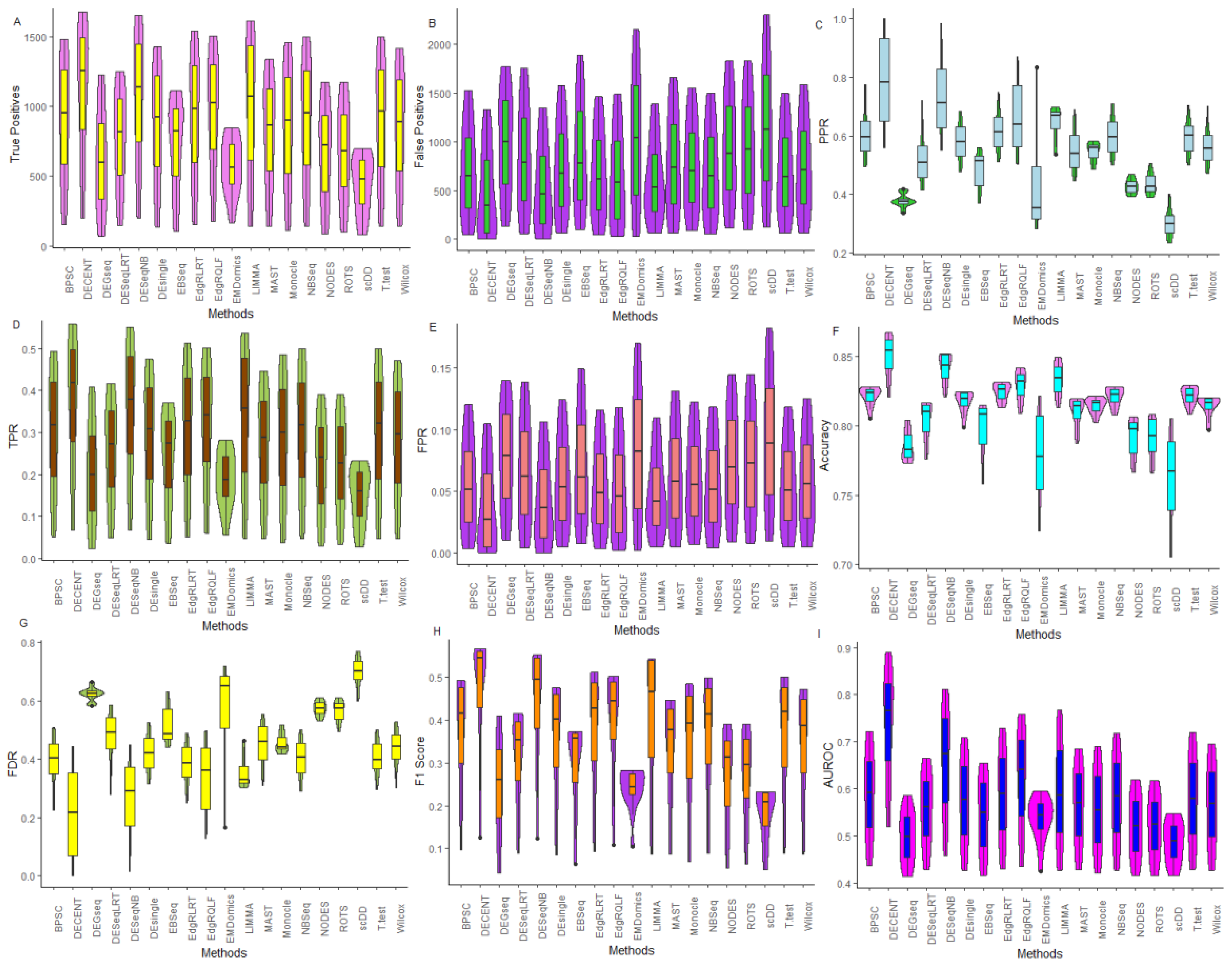
5.1. Performance Metrics
5.2. Performance Evaluation under Multiple Criteria Decision-Making setup
6. Results and Discussion
6.1. Count Models for Fitting of scRNA-seq Data
6.2. Comparative Performance Analysis of scRNA-seq DE Methods
6.2.1. Comparative Assessment Based on Performance Metrics
6.2.2. Performance Assessment Based on ROC
6.2.3. Performance Assessment Based on FDR Rates
6.2.4. Performance Assessment Based on Runtime
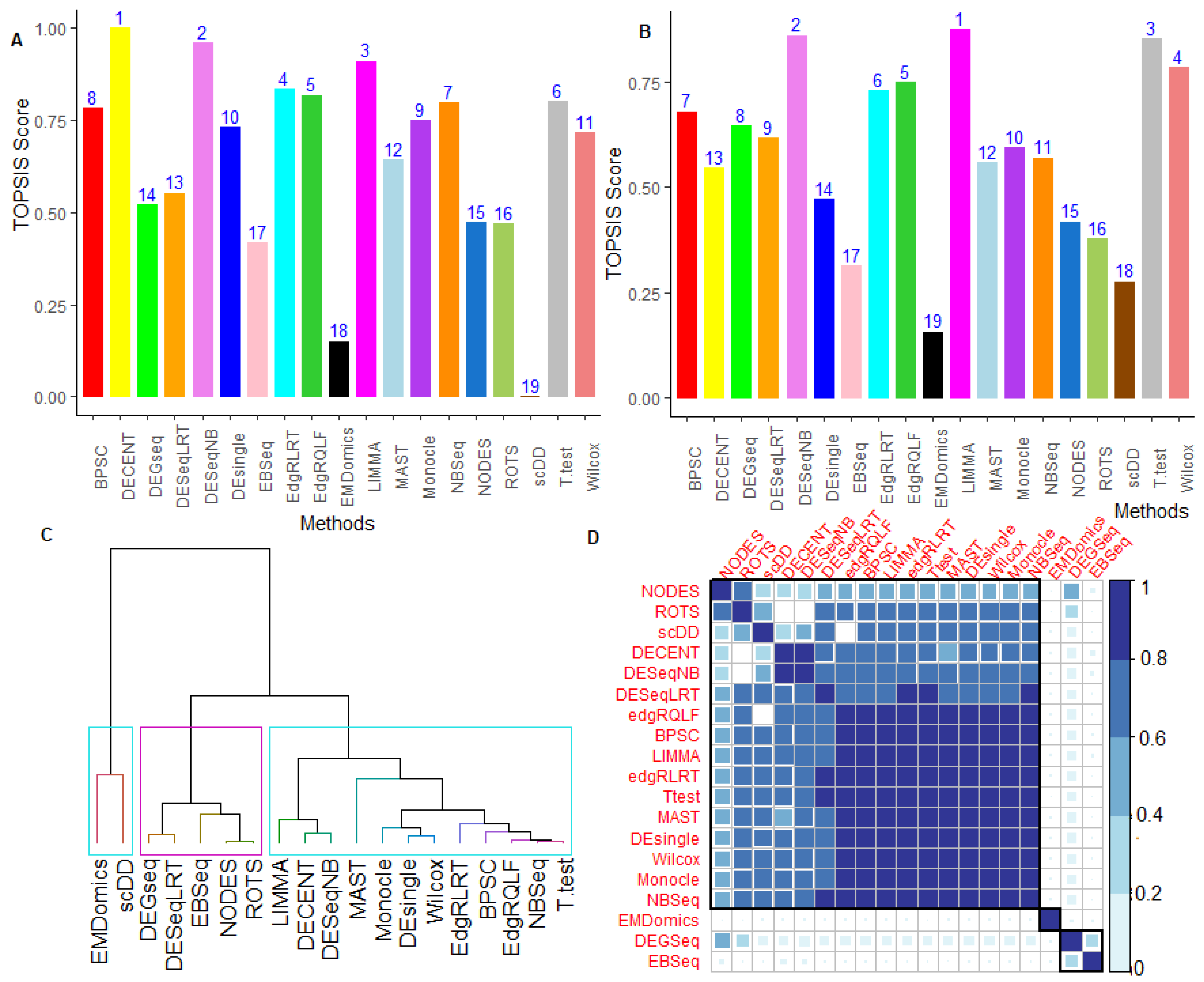
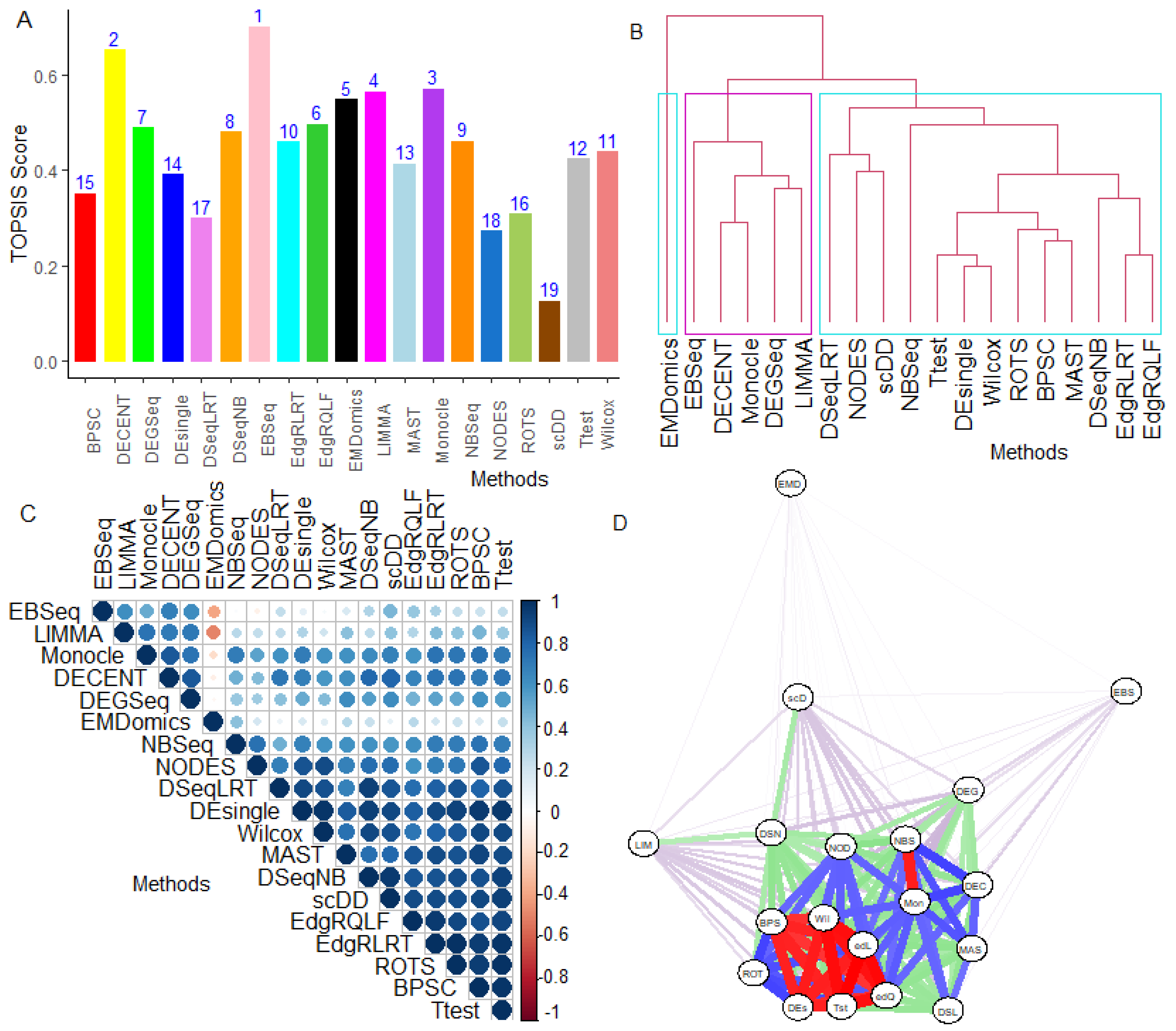
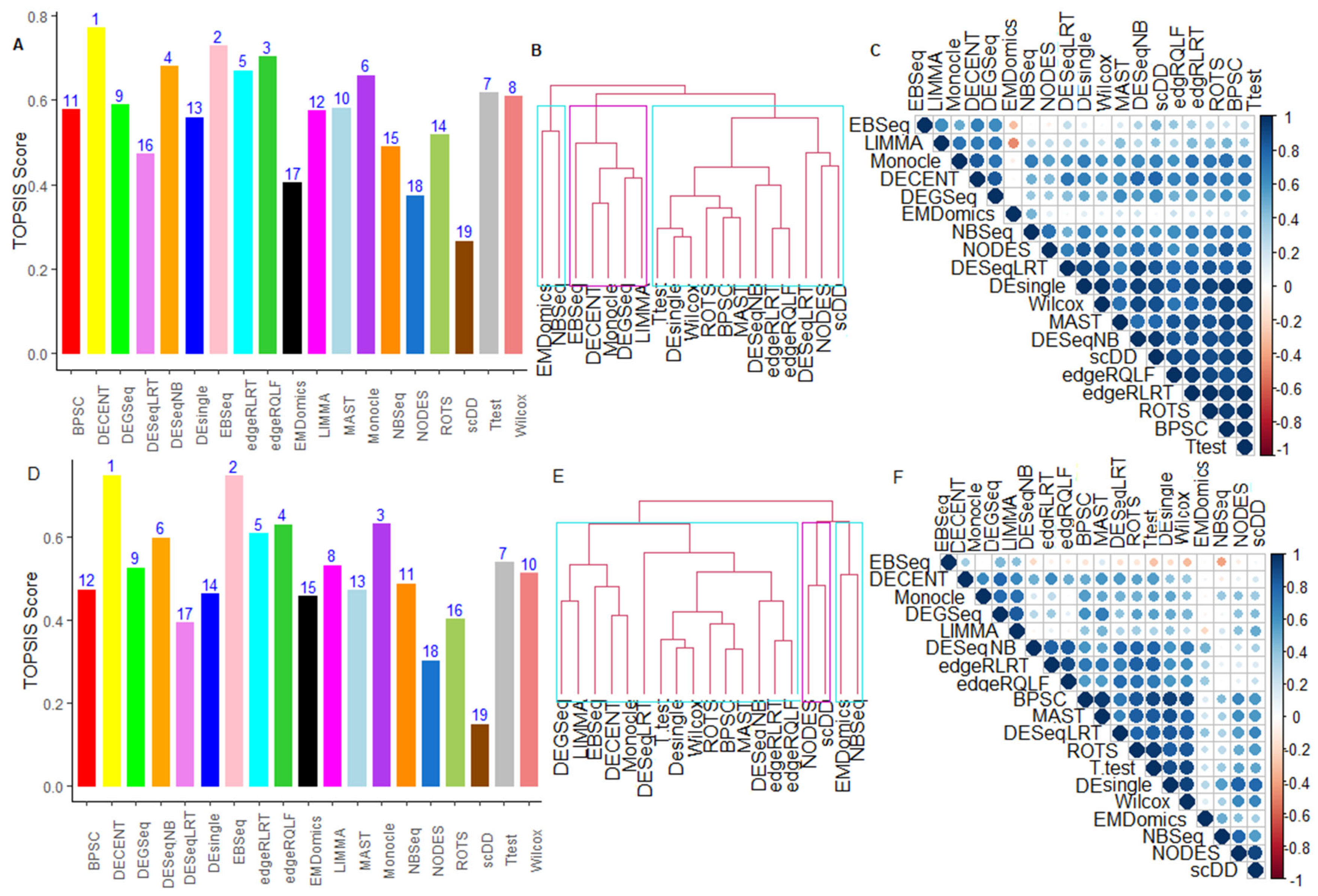
6.2.5. Performance Assessment Based on MCDM-TOPSIS Analysis
6.2.6. Between-Methods Similarity Analysis
6.2.7. Combined-Data Methods Analysis
7. Conclusions and Future Work
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miao, Z.; Zhang, X. Differential expression analyses for single-cell RNA-Seq: Old questions on new data. Quant. Biol. 2016, 4, 243–260. [Google Scholar] [CrossRef] [Green Version]
- Jaakkola, M.K.; Seyednasrollah, F.; Mehmood, A.; Elo, L. Comparison of methods to detect differentially expressed genes between single-cell populations. Brief. Bioinform. 2016, 18, 735–743. [Google Scholar] [CrossRef] [PubMed]
- Sandberg, R. Entering the era of single-cell transcriptomics in biology and medicine. Nat. Methods 2013, 11, 22–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trapnell, C. Defining cell types and states with single-cell genomics. Genome Res. 2015, 25, 1491–1498. [Google Scholar] [CrossRef] [Green Version]
- Islam, S.; Kjällquist, U.; Moliner, A.; Zajac, P.; Fan, J.-B.; Lönnerberg, P.; Linnarsson, S. Characterization of the single-cell transcriptional landscape by highly multiplex RNA-seq. Genome Res. 2011, 21, 1160–1167. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tung, P.-Y.; Blischak, J.; Hsiao, C.J.; Knowles, D.; Burnett, J.E.; Pritchard, J.K.; Gilad, Y. Batch effects and the effective design of single-cell gene expression studies. Sci. Rep. 2017, 7, 39921. [Google Scholar] [CrossRef] [Green Version]
- Bacher, R.; Kendziorski, C. Design and computational analysis of single-cell RNA-sequencing experiments. Genome Biol. 2016, 17, 63. [Google Scholar] [CrossRef] [Green Version]
- Kolodziejczyk, A.; Kim, J.K.; Svensson, V.; Marioni, J.; Teichmann, S.A. The Technology and Biology of Single-Cell RNA Sequencing. Mol. Cell 2015, 58, 610–620. [Google Scholar] [CrossRef] [Green Version]
- Stegle, O.; Teichmann, S.; Marioni, J.C. Computational and analytical challenges in single-cell transcriptomics. Nat. Rev. Genet. 2015, 16, 133–145. [Google Scholar] [CrossRef]
- Wang, T.; Li, B.; Nelson, C.E.; Nabavi, S. Comparative analysis of differential gene expression analysis tools for single-cell RNA sequencing data. BMC Bioinform. 2019, 20, 40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Finak, G.; McDavid, A.; Yajima, M.; Deng, J.; Gersuk, V.; Shalek, A.K.; Slichter, C.K.; Miller, H.W.; McElrath, M.J.; Prlic, M.; et al. MAST: A flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 2015, 16, 278. [Google Scholar] [CrossRef] [Green Version]
- Van den Berge, K.; Perraudeau, F.; Soneson, C.; Love, M.I.; Risso, D.; Vert, J.-P.; Robinson, M.D.; Dudoit, S.; Clement, L. Observation weights unlock bulk RNA-seq tools for zero inflation and single-cell applications. Genome Biol. 2018, 19, 24. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.D.; McCarthy, D.J.; Smyth, G.K. edgeR: A Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics 2010, 26, 139–140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anders, S.; Huber, W. Differential expression analysis for sequence count data. Nat. Preced. 2010, 11, R106. [Google Scholar] [CrossRef] [Green Version]
- Love, M.I.; Huber, W.; Anders, S. Differential analysis of count data—The DESeq2 package. Genome Biol. 2014, 15, 550. [Google Scholar] [CrossRef] [Green Version]
- Fujita, K.; Iwaki, M.; Yanagida, T. Transcriptional bursting is intrinsically caused by interplay between RNA polymerases on DNA. Nat. Commun. 2016, 7, 13788. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.; Huang, M.; Torre, E.; Dueck, H.; Shaffer, S.; Murray, J.; Raj, A.; Li, M.; Zhang, N.R. Gene expression distribution deconvolution in single-cell RNA sequencing. Proc. Natl. Acad. Sci. USA 2018, 115, E6437–E6446. [Google Scholar] [CrossRef] [Green Version]
- Ye, C.; Speed, T.P.; Salim, A. DECENT: Differential expression with capture efficiency adjustmeNT for single-cell RNA-seq data. Bioinformatics 2019, 35, 5155–5162. [Google Scholar] [CrossRef] [Green Version]
- Van den Berge, K.; Soneson, C.; Love, M.I.; Robinson, M.D.; Clement, L. zingeR: Unlocking RNA-seq tools for zero-inflation and single cell applications. bioRxiv 2017. [Google Scholar] [CrossRef] [Green Version]
- Miao, Z.; Deng, K.; Wang, X.; Zhang, X. DEsingle for detecting three types of differential expression in single-cell RNA-seq data. Bioinformatics 2018, 34, 3223–3224. [Google Scholar] [CrossRef] [Green Version]
- Trapnell, C.; Cacchiarelli, D.; Grimsby, J.; Pokharel, P.; Li, S.; Morse, M.A.; Lennon, N.J.; Livak, K.J.; Mikkelsen, T.S.; Rinn, J.L. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 2014, 32, 381–386. [Google Scholar] [CrossRef] [Green Version]
- Qiu, X.; Hill, A.; Packer, J.; Lin, D.; Ma, Y.-A.; Trapnell, C. Single-cell mRNA quantification and differential analysis with Census. Nat. Methods 2017, 14, 309–315. [Google Scholar] [CrossRef]
- Kharchenko, P.V.; Silberstein, L.; Scadden, D.T. Bayesian approach to single-cell differential expression analysis. Nat. Methods 2014, 11, 740–742. [Google Scholar] [CrossRef]
- Mou, T.; Deng, W.; Gu, F.; Pawitan, Y.; Vu, T.N. Reproducibility of Methods to Detect Differentially Expressed Genes from Single-Cell RNA Sequencing. Front. Genet. 2020, 10, 1331. [Google Scholar] [CrossRef] [PubMed]
- Soneson, C.; Robinson, M.D. Bias, robustness and scalability in single-cell differential expression analysis. Nat. Methods 2018, 15, 255–261. [Google Scholar] [CrossRef] [PubMed]
- Molin, A.D.; Baruzzo, G.; Di Camillo, B. Single-Cell RNA-Sequencing: Assessment of Differential Expression Analysis Methods. Front. Genet. 2017, 8, 62. [Google Scholar] [CrossRef]
- Wang, L.; Feng, Z.; Wang, X.; Wang, X.; Zhang, X. DEGseq: An R package for identifying differentially expressed genes from RNA-seq data. Bioinformatics 2009, 26, 136–138. [Google Scholar] [CrossRef]
- Ritchie, M.E.; Phipson, B.; Wu, D.; Hu, Y.; Law, C.W.; Shi, W.; Smyth, G.K. limma powers differential expression analyses for RNA-sequencing and microarray studies. Nucleic Acids Res. 2015, 43, e47. [Google Scholar] [CrossRef]
- Di, Y.; Schafer, D.W.; Cumbie, J.S.; Chang, J. The NBP Negative Binomial Model for Assessing Differential Gene Expression from RNA-Seq. Stat. Appl. Genet. Mol. Biol. 2011, 10, 24. [Google Scholar] [CrossRef]
- Leng, N.; Dawson, J.A.; Thomson, J.A.; Ruotti, V.; Rissman, A.I.; Smits, B.M.G.; Haag, J.D.; Gould, M.N.; Stewart, R.M.; Kendziorski, C. EBSeq: An empirical Bayes hierarchical model for inference in RNA-seq experiments. Bioinformatics 2013, 29, 1035–1043. [Google Scholar] [CrossRef] [Green Version]
- Vu, T.N.; Wills, Q.F.; Kalari, K.; Niu, N.; Wang, L.; Rantalainen, M.; Pawitan, Y. β-Poisson model for single-cell RNA-seq data analyses. Bioinformatics 2016, 32, 2128–2135. [Google Scholar] [CrossRef]
- Korthauer, K.D.; Chu, L.-F.; Newton, M.A.; Li, Y.; Thomson, J.; Stewart, R.; Kendziorski, C. A statistical approach for identifying differential distributions in single-cell RNA-seq experiments. Genome Biol. 2016, 17, 222. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sengupta, D.; Rayan, N.A.; Lim, M.; Lim, B.; Prabhakar, S. Fast, scalable and accurate differential expression analysis for single cells. bioRxiv 2016. [Google Scholar] [CrossRef]
- Welch, B.L. The Generalization of `Student’s’ Problem When Several Different Population Variances Are Involved. Biometrika 1947, 34, 28. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Seyednasrollah, F.; Rantanen, K.; Jaakkola, P.; Elo, L.L. ROTS: Reproducible RNA-seq biomarker detector—Prognostic markers for clear cell renal cell cancer. Nucleic Acids Res. 2016, 44, e1. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nabavi, S.; Schmolze, D.; Maitituoheti, M.; Malladi, S.; Beck, A.H. EMDomics: A robust and powerful method for the identification of genes differentially expressed between heterogeneous classes. Bioinformatics 2016, 32, 533–541. [Google Scholar] [CrossRef]
- Hardcastle, T.J.; Kelly, K.A. baySeq: Empirical Bayesian methods for identifying differential expression in sequence count data. BMC Bioinform. 2010, 11, 422. [Google Scholar] [CrossRef] [Green Version]
- Auer, P.L.; Doerge, R.W. A Two-Stage Poisson Model for Testing RNA-Seq Data. Stat. Appl. Genet. Mol. Biol. 2011, 10, 26. [Google Scholar] [CrossRef]
- Li, J.; Tibshirani, R. Finding consistent patterns: A nonparametric approach for identifying differential expression in RNA-Seq data. Stat. Methods Med. Res. 2013, 22, 519–536. [Google Scholar] [CrossRef] [Green Version]
- Elo, L.L.; Filén, S.; Lahesmaa, R.; Aittokallio, T. Reproducibility-Optimized Test Statistic for Ranking Genes in Microarray Studies. IEEE/ACM Trans. Comput. Biol. Bioinform. 2008, 5, 423–431. [Google Scholar] [CrossRef]
- Law, C.W.; Chen, Y.; Shi, W.; Smyth, G.K. voom: Precision weights unlock linear model analysis tools for RNA-seq read counts. Genome Biol. 2014, 15, R29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robinson, M.D.; Oshlack, A. A scaling normalization method for differential expression analysis of RNA-seq data. Genome Biol. 2013, 11, R25. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Trapnell, C.; Hendrickson, D.G.; Sauvageau, M.; Goff, L.; Rinn, J.L.; Pachter, L. Differential analysis of gene regulation at transcript resolution with RNA-seq. Nat. Biotechnol. 2012, 31, 46–53. [Google Scholar] [CrossRef] [PubMed]
- Frazee, A.; Pertea, G.; Jaffe, A.; Langmead, B.; Salzberg, S.; Leek, J. Flexible analysis of transcriptome assemblies with Ballgown. bioRxiv 2014. [Google Scholar] [CrossRef] [Green Version]
- Paulson, J.N.; Stine, O.C.; Bravo, H.C.; Pop, M. Differential abundance analysis for microbial marker-gene surveys. Nat. Methods 2013, 10, 1200–1202. [Google Scholar] [CrossRef] [Green Version]
- Delmans, M.; Hemberg, M. Discrete distributional differential expression (D3E)—A tool for gene expression analysis of single-cell RNA-seq data. BMC Bioinform. 2016, 17, 110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, X.; Mao, Q.; Tang, Y.; Wang, L.; Chawla, R.; Pliner, H.A.; Trapnell, C. Reversed graph embedding resolves complex single-cell trajectories. Nat. Methods 2017, 14, 979–982. [Google Scholar] [CrossRef] [Green Version]
- Guo, M.; Wang, H.; Potter, S.S.; Whitsett, J.A.; Xu, Y. SINCERA: A Pipeline for Single-Cell RNA-Seq Profiling Analysis. PLoS Comput. Biol. 2015, 11, e1004575. [Google Scholar] [CrossRef]
- Zhang, W.; Wei, Y.; Zhang, D.; Xu, E.Y. ZIAQ: A quantile regression method for differential expression analysis of single-cell RNA-seq data. Bioinformatics 2020, 36, 3124–3130. [Google Scholar] [CrossRef]
- Wang, T.; Nabavi, S. SigEMD: A powerful method for differential gene expression analysis in single-cell RNA sequencing data. Methods 2018, 145, 25–32. [Google Scholar] [CrossRef]
- Jia, C.; Hu, Y.; Kelly, D.; Kim, J.; Li, M.; Zhang, N.R. Accounting for technical noise in differential expression analysis of single-cell RNA sequencing data. Nucleic Acids Res. 2017, 45, 10978–10988. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Risso, D.; Perraudeau, F.; Gribkova, S.; Dudoit, S.; Vert, J.-P. A general and flexible method for signal extraction from single-cell RNA-seq data. Nat. Commun. 2018, 9, 284. [Google Scholar] [CrossRef] [Green Version]
- Das, S.; Rai, S.N. SwarnSeq: An improved statistical approach for differential expression analysis of single-cell RNA-seq data. Genomics 2021, 113, 1308–1324. [Google Scholar] [CrossRef]
- Das, S.; Rai, S.N. Statistical methods for analysis of single-cell RNA-sequencing data. MethodsX 2021, 8, 101580. [Google Scholar] [CrossRef]
- Vallejos, C.A.; Marioni, J.C.; Richardson, S. BASiCS: Bayesian Analysis of Single-Cell Sequencing Data. PLoS Comput. Biol. 2015, 11, e1004333. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Easton, J.; Finkelstein, D.; Wu, G.; Chen, X. UMI-count modeling and differential expression analysis for single-cell RNA sequencing. Genome Biol. 2018, 19, 70. [Google Scholar] [CrossRef] [Green Version]
- Van den Berge, K.; de Bézieux, H.R.; Street, K.; Saelens, W.; Cannoodt, R.; Saeys, Y.; Dudoit, S.; Clement, L. Trajectory-based differential expression analysis for single-cell sequencing data. Nat. Commun. 2020, 11, 1201. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Zhang, Y.; Stitzel, M.L.; Wu, H. Two-phase differential expression analysis for single cell RNA-seq. Bioinformatics 2018, 34, 3340–3348. [Google Scholar] [CrossRef] [PubMed]
- Tarazona, S.; García-Alcalde, F.; Dopazo, J.; Ferrer, A.; Conesa, A. Differential expression in RNA-seq: A matter of depth. Genome Res. 2011, 21, 2213–2223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van De Wiel, M.A.; Leday, G.G.; Pardo, L.; Rue, H.; Van Der Vaart, A.W.; Van Wieringen, W.N. Bayesian analysis of RNA sequencing data by estimating multiple shrinkage priors. Biostatistics 2013, 14, 113–128. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, S.; Chen, L. A two-parameter generalized Poisson model to improve the analysis of RNA-seq data. Nucleic Acids Res. 2010, 38, e170. [Google Scholar] [CrossRef]
- Chu, C.; Fang, Z.; Hua, X.; Yang, Y.; Chen, E.; Cowley, A.W.; Liang, M.; Liu, P.; Lu, Y. deGPS is a powerful tool for detecting differential expression in RNA-sequencing studies. BMC Genom. 2015, 16, 455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sekula, M.; Gaskins, J.; Datta, S. Detection of differentially expressed genes in discrete single-cell RNA sequencing data using a hurdle model with correlated random effects. Biometrics 2019, 75, 1051–1062. [Google Scholar] [CrossRef]
- Jiang, L.; Schlesinger, F.; Davis, C.A.; Zhang, Y.; Li, R.; Salit, M.; Gingeras, T.R.; Oliver, B. Synthetic spike-in standards for RNA-seq experiments. Genome Res. 2011, 21, 1543–1551. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moliner, A.; Ernfors, P.; Ibáñez, C.F.; Andäng, M. Mouse Embryonic Stem Cell-Derived Spheres with Distinct Neurogenic Potentials. Stem Cells Dev. 2008, 17, 233–243. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soumillon, M.; Cacchiarelli, D.; Semrau, S.; van Oudenaarden, A.; Mikkelsen, T.S. Characterization of directed differentiation by high-throughput single-cell RNA-Seq. bioRxiv 2014. [Google Scholar] [CrossRef] [Green Version]
- Klein, A.M.; Mazutis, L.; Akartuna, I.; Tallapragada, N.; Veres, A.; Li, V.; Peshkin, L.; Weitz, D.A.; Kirschner, M.W. Droplet Barcoding for Single-Cell Transcriptomics Applied to Embryonic Stem Cells. Cell 2015, 161, 1187–1201. [Google Scholar] [CrossRef] [Green Version]
- Gierahn, T.M.; Wadsworth, M.H.; Hughes, T.K.; Bryson, B.D.; Butler, A.; Satija, R.; Fortune, S.; Love, J.C.; Shalek, A.K. Seq-Well: Portable, low-cost RNA sequencing of single cells at high throughput. Nat. Methods 2017, 14, 395–398. [Google Scholar] [CrossRef]
- Savas, P.; Virassamy, B.; Ye, C.; Salim, A.; Mintoff, C.P.; Caramia, F.; Salgado, R.; Byrne, D.J.; Teo, Z.L.; Dushyanthen, S.; et al. Single-cell profiling of breast cancer T cells reveals a tissue-resident memory subset associated with improved prognosis. Nat. Med. 2018, 24, 986–993. [Google Scholar] [CrossRef] [PubMed]
- Grün, D.; Kester, L.; Van Oudenaarden, A. Validation of noise models for single-cell transcriptomics. Nat. Methods 2014, 11, 637–640. [Google Scholar] [CrossRef]
- Ziegenhain, C.; Vieth, B.; Parekh, S.; Reinius, B.; Guillaumet-Adkins, A.; Smets, M.; Leonhardt, H.; Heyn, H.; Hellmann, I.; Enard, W. Comparative Analysis of Single-Cell RNA Sequencing Methods. Mol. Cell 2017, 65, 631–643.e4. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.D.; Smyth, G.K. Moderated statistical tests for assessing differences in tag abundance. Bioinformatics 2007, 23, 2881–2887. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Robinson, M.D.; Smyth, G.K. Small-sample estimation of negative binomial dispersion, with applications to SAGE data. Biostatistics 2008, 9, 321–332. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, H.; Wong, W.H. Statistical inferences for isoform expression in RNA-Seq. Bioinformatics 2009, 25, 1026–1032. [Google Scholar] [CrossRef] [Green Version]
- Yoon, K.; Hwang, C.-L. Multiple Attribute Decision Making. In Multiple Attribute Decision Making; SAGE Publications, Inc.: Thousand Oaks, CA, USA, 1995. [Google Scholar] [CrossRef]
- Khezrian, M.; Jahan, A.; Kadir, W.M.N.W.; Ibrahim, S. An Approach for Web Service Selection Based on Confidence Level of Decision Maker. PLoS ONE 2014, 9, e97831. [Google Scholar] [CrossRef]
- Ahn, B.S. Compatible weighting method with rank order centroid: Maximum entropy ordered weighted averaging approach. Eur. J. Oper. Res. 2011, 212, 552–559. [Google Scholar] [CrossRef]
- Das, S.; Rai, A.; Mishra, D.; Rai, S.N. Statistical approach for selection of biologically informative genes. Gene 2018, 655, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Moriña, D.; Higueras, M.; Puig, P.; Oliveira, M. Generalized Hermite Distribution Modelling with the R Package hermite. R J. 2015, 7, 263–274. [Google Scholar] [CrossRef] [Green Version]
- Long, J.S.; Freese, J. Regression Models for Categorical Dependent Variables Using STATA. Sociol. J. Br. Sociol. Assoc. 2001, 2, 4. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
| SN. | Methods | Distribution | Utility | Input | DE Test Stat. | Runtime | Availability | Ref. |
|---|---|---|---|---|---|---|---|---|
| 01 | DESeq2 | NB | Bulk-cell | Counts | Wald | Low | Bioconductor | [15] |
| 02 | edgeR | NB | Bulk-cell | Counts | QLF, LRT | Low | Bioconductor | [13] |
| 03 | LIMMA | Linear Model | Bulk-cell | Norm. | Bayesian Wald | Low | Bioconductor | [28,42] |
| 04 | DEGseq | Poisson | Bulk-cell | Counts | Z-score | Low | Bioconductor | [27] |
| 05 | T-test | T-test | General | Norm. | t stat. | Low | CRAN | [34,43] |
| 06 | Wilcoxon | Wilcoxon test | General | Counts | Wilcox | Low | CRAN | [35,43] |
| 07 | baySeq | NB | Bulk-cell | Counts | Posterior prob. | Low | Bioconductor | [38] |
| 08 | NBseq | NB | Bulk-cell | Counts | Fisher’s stat. | Low | CRAN | [29] |
| 09 | EBSeq | NB | Bulk-cell | Counts | Bayesian | High | Bioconductor | [30] |
| 10 | Cuffdiff | Beta-NB | Bulk-cell | sam file | Low | Linux | [44] | |
| 11 | SAMseq | NP | Bulk-cell | Counts | Wilcox | Low | CRAN | [40] |
| 12 | Ballgown | Linear Model | Bulk-cell | Counts | Lin. Mod. test stat. | Medium | Bioconductor | [45] |
| 13 | TSPM | Poisson | Bulk-cell | Counts | Low | R code | [39] | |
| 14 | ROTS | NP | Bulk-cell | Norm. | Z-stat. (bootstrap) | Medium | Bioconductor | [36,41] |
| 15 | metagenomeSeq | Bulk-cell | Medium | [46] | ||||
| 16 | SCDE | Mixture Model | Single-cell | UMI | Bayesian Stat. | High | Bioconductor | [23] |
| 17 | scDD | Multi-Modal Bayesian | Single-cell | Norm. | Bayesian Stat. | High | Bioconductor | [32] |
| 18 | D3E | NP | Single-cell | UMI | Cramér-von Mises test/KS test | High | GitHub, Python | [47] |
| 19 | BPSC | Beta-Poisson | Single-cell | UMI | LRT | Medium | GitHub | [31] |
| 20 | MAST | Hurdle Model | Single-cell | Norm. | LRT | Medium | Bioconductor | [11] |
| 21 | Monocle2 | GAM | Single-cell | Norm. | LRT | Medium | Bioconductor | [21,48] |
| 22 | DEsingle | ZINB | Single-cell | UMI | LRT | High | Bioconductor, GitHub | [20] |
| 23 | DECENT | ZINB, Beta-Binomial | Single-cell | UMI | LRT | High | GitHub | [18] |
| 24 | DESCEND | Poisson | Single-cell | UMI | High | GitHub | [17] | |
| 25 | EMDomics | NP | Single-cell | Norm. | Euclidean distance | High | Bioconductor | [37] |
| 26 | Sincera | NP | Single-cell | Norm. | Welch’s t-stat. (LS) Wilcox (SS) | High | GitHub | [49] |
| 27 | ZIAQ | Logistic Regression | Single-cell | Norm. | Fisher’s stat. | Medium | GitHub | [50] |
| 28 | sigEMD | NP | Single-cell | Norm. | Distance measure | High | GitHub | [51] |
| 29 | TASC | Logistic, Poisson | Single-cell | UMI | LRT | High | GitHub | [52] |
| 30 | ZINB-Wave | ZINB | Single-cell | UMI | LRT | High | Bioconductor, GitHub | [12,53] |
| 31 | SwarnSeq | ZINB | Single-cell | UMI | LRT | High | GitHub | [54,55] |
| 32 | NODES | Wilcoxon test | Single-cell | Norm. | Wilcox | Medium | *Dropbox | [33] |
| 33 | BASiCS | Poisson-Gamma | Single-cell | Norm. | Posterior prob. | High | Bioconductor | [56] |
| 34 | NBID | NB | Single-cell | UMI | LRT | Medium | R code | [57] |
| 35 | tradeSeq | GAM | Single-cell | UMI | Wald | Medium | GitHub | [58] |
| 36 | SC2P | ZIP | Single-cell | UMI | Posterior prob. | High | GitHub | [59] |
| SN. | Classes | Descriptions |
|---|---|---|
| 01 | Class I | Underlying Models: Negative Binomial Model; Linear Model; Poisson Model; Bayesian Model |
| Features: Computationally simple; Requires less runtime; Applicable to both counts and normalized data | ||
| Limitations: Does not consider multi-modality of data; Ignores dropout events; Fails to consider zero-inflation; Overestimates dispersion parameter; Underestimates mean (difference in mean across cellular condition); Lesser statistical power; Does not consider higher technical and biological variations; Cannot handle long-tailed (skewed) distributions; Ignores high sparsity in data | ||
| Tools: DEseq2 [14,15], edgeR [13], Limma [28], SAMseq [40], DEGseq [27], baySeq [38], NBseq [29], Cuffdiff [44], Ballgown [45], TSPM [39], metagenomeSeq [46], ROTS [36,41], NOISeq [60] EBSeq [30], ShrinkSeq [61], GPseq [62], DeGPS [63] | ||
| 02 | Class II | Methods: NP methods |
| Features: Distribution-free approach; Considers multi-modality of data distribution; Computationally not cumbersome; Estimates parameters without fitting distributions; Computes test statistic through distance-like metrics across two conditions/cell groups; Performs well when lesser proportions of zeros in data | ||
| Limitations: Focuses on two cellular groups comparisons; Computationally complex for multi-groups; Performance severely affected due to high dropouts (some methods exclude dropouts); Cannot separate between true/biological and false/dropout zeros; Sensitive to sparsity; Methods like D3E and scDD fail to consider UMI count nature of data; Cannot separate technical from biological sources of variation; Cannot use cell-level auxiliary data | ||
| Tools: D3E [47], scDD [32], sigEMD [51], NODES [33], EMDomics [37], Sincera [49], ZIAQ [50], Wilcox [35,43] | ||
| 03 | Class III | Models: Zero inflated Models; Hurdle Models; Mixture Models; GLM; GAM |
| Features: Parametric approach; Captures only bi-modality distribution of data; Easily generalized to multi-cellular groups; Considers zero-inflations, dropout events; Methods like TASC, DECENT, SwarnSeq, etc. make use of external spike-ins to adjust distribution of observed data; Mostly uses GLM framework to compute DE statistics; Can accommodate cell-level auxiliary data while model building | ||
| Limitations: Cannot capture multi-modality (>2) of data distribution; Methods like MAST failed to consider UMI nature of data and exclude dropout events; Methods like SCDE and MAST do not differentiate between true and dropout zeros during the model building; Computationally complex; Most of methods do not distinguish biological from technical factors that are causing dropouts; Assumes dropout events to be linear (ignores non-linear dropouts, especially for genes with low to moderate expression) | ||
| Tools: SCDE [23], NBID [57], MAST [11], Monocle [21], Monocle2 [48], BPSC [31], ZINB-Wave [12], DEsingle [20], DECENT [18], DESCEND [17], TASC [52], BASiCS [56], Random Hurdle Model [64], SC2P [59], SwarnSeq [54,55] |
| SN. | Data | Description | Accession | #Genes | #Cells | Ref. |
|---|---|---|---|---|---|---|
| 01 | Tung | Human induced Pluripotent stem cell lines | GSE77288 | 18938 | 576 | [6] |
| 02 | Islam | single-cell (ES and MEF) transcriptional landscape by highly multiplex RNA-Seq | GSE29087 | 22928 | 92 | [5] |
| 03 | Soumillon1 | Differentiating adipose cells by scRNA-Seq (Day 1 vs. 2) | GSE53638 | 23895 | 1835 | [67] |
| 04 | Soumillon2 | Differentiating adipose cells by scRNA-Seq (Days 1 vs. 3) | GSE53638 | 23895 | 2268 | [67] |
| 05 | Soumillon3 | Differentiating adipose cells by scRNA-Seq (Days 2 vs. 3) | GSE53638 | 23895 | 1613 | [67] |
| 06 | Klein | Mouse ES cells | GSE65525 | 24174 | 1481 | [68] |
| 07 | Gierahn | Single-cell RNA sequencing experiments of HEK cells | GSE92495 | 24176 | 1453 | [69] |
| 08 | Chen | ScRNA-seq of Rh41 using 10x Genomics | GSE113660 | 33694 | 7261 | [57] |
| 09 | Savas | Breast cancer cells using 10x Genomics | GSE110686 | 33694 | 6311 | [70] |
| 10 | Grun | Mouse ES single cells using CEL-seq technique | GSE54695 | 12467 | 320 | [71] |
| 11 | Ziegenhain | Sc-RNA-seq of Mouse ES cells | GSE75790 | 39016 | 583 | [72] |
| TP | FP | TN | FN | TPR | FPR | FDR | PPR | NPV | ACC | F1 | AUROC | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| BPSC | 1478 | 1522 | 11113 | 1522 | 0.493 | 0.120 | 0.507 | 0.493 | 0.880 | 0.805 | 0.493 | 0.722 |
| DECENT | 1674 | 1326 | 11309 | 1326 | 0.558 | 0.105 | 0.442 | 0.558 | 0.895 | 0.830 | 0.558 | 0.857 |
| DEGseq | 1228 | 1772 | 10863 | 1772 | 0.409 | 0.140 | 0.591 | 0.409 | 0.860 | 0.773 | 0.409 | 0.585 |
| DESeqNB | 1653 | 1347 | 11288 | 1347 | 0.551 | 0.107 | 0.449 | 0.551 | 0.893 | 0.828 | 0.551 | 0.811 |
| DESeqLRT | 1247 | 1753 | 10882 | 1753 | 0.416 | 0.139 | 0.584 | 0.416 | 0.861 | 0.776 | 0.416 | 0.666 |
| DEsingle | 1428 | 1572 | 11063 | 1572 | 0.476 | 0.124 | 0.524 | 0.476 | 0.876 | 0.799 | 0.476 | 0.709 |
| EBSeq | 1110 | 1890 | 10745 | 1890 | 0.370 | 0.150 | 0.630 | 0.370 | 0.850 | 0.758 | 0.370 | 0.654 |
| edgeRLRT | 1537 | 1463 | 11172 | 1463 | 0.512 | 0.116 | 0.488 | 0.512 | 0.884 | 0.813 | 0.512 | 0.729 |
| edgeRQLF | 1506 | 1494 | 11141 | 1494 | 0.502 | 0.118 | 0.498 | 0.502 | 0.882 | 0.809 | 0.502 | 0.758 |
| EMDomics | 844 | 2156 | 10479 | 2156 | 0.281 | 0.171 | 0.719 | 0.281 | 0.829 | 0.724 | 0.281 | 0.594 |
| LIMMA | 1612 | 1388 | 11247 | 1388 | 0.537 | 0.110 | 0.463 | 0.537 | 0.890 | 0.822 | 0.537 | 0.768 |
| MAST | 1337 | 1663 | 10972 | 1663 | 0.446 | 0.132 | 0.554 | 0.446 | 0.868 | 0.787 | 0.446 | 0.685 |
| Monocle | 1454 | 1546 | 11089 | 1546 | 0.485 | 0.122 | 0.515 | 0.485 | 0.878 | 0.802 | 0.485 | 0.691 |
| NBSeq | 1497 | 1503 | 11132 | 1503 | 0.499 | 0.119 | 0.501 | 0.499 | 0.881 | 0.808 | 0.499 | 0.718 |
| NODES | 1173 | 1827 | 10808 | 1827 | 0.391 | 0.145 | 0.609 | 0.391 | 0.855 | 0.766 | 0.391 | 0.620 |
| ROTS | 1170 | 1830 | 10805 | 1830 | 0.390 | 0.145 | 0.610 | 0.390 | 0.855 | 0.766 | 0.390 | 0.618 |
| scDD | 697 | 2303 | 10332 | 2303 | 0.232 | 0.182 | 0.768 | 0.232 | 0.818 | 0.705 | 0.232 | 0.547 |
| T-test | 1501 | 1499 | 11136 | 1499 | 0.500 | 0.119 | 0.500 | 0.500 | 0.881 | 0.808 | 0.500 | 0.719 |
| Wilcox | 1413 | 1587 | 11048 | 1587 | 0.471 | 0.126 | 0.529 | 0.471 | 0.874 | 0.797 | 0.471 | 0.695 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.; Rai, A.; Merchant, M.L.; Cave, M.C.; Rai, S.N. A Comprehensive Survey of Statistical Approaches for Differential Expression Analysis in Single-Cell RNA Sequencing Studies. Genes 2021, 12, 1947. https://doi.org/10.3390/genes12121947
Das S, Rai A, Merchant ML, Cave MC, Rai SN. A Comprehensive Survey of Statistical Approaches for Differential Expression Analysis in Single-Cell RNA Sequencing Studies. Genes. 2021; 12(12):1947. https://doi.org/10.3390/genes12121947
Chicago/Turabian StyleDas, Samarendra, Anil Rai, Michael L. Merchant, Matthew C. Cave, and Shesh N. Rai. 2021. "A Comprehensive Survey of Statistical Approaches for Differential Expression Analysis in Single-Cell RNA Sequencing Studies" Genes 12, no. 12: 1947. https://doi.org/10.3390/genes12121947
APA StyleDas, S., Rai, A., Merchant, M. L., Cave, M. C., & Rai, S. N. (2021). A Comprehensive Survey of Statistical Approaches for Differential Expression Analysis in Single-Cell RNA Sequencing Studies. Genes, 12(12), 1947. https://doi.org/10.3390/genes12121947







