Next Article in Journal
MicroRNA Analysis of Human Stroke Brain Tissue Resected during Decompressive Craniectomy/Stroke-Ectomy Surgery
Next Article in Special Issue
Microarray Genotyping Identifies New Loci Associated with Dementia in Parkinson’s Disease
Previous Article in Journal
A Genome-Wide Identification Study Reveals That HmoCYP76AD1, HmoDODAα1 and HmocDOPA5GT Involved in Betalain Biosynthesis in Hylocereus
Previous Article in Special Issue
Gene Therapeutic Approaches for the Treatment of Mitochondrial Dysfunction in Parkinson’s Disease
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Genes
Volume 12
Issue 12
10.3390/genes12121859
genes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Validity and Prognostic Value of a Polygenic Risk Score for Parkinson’s Disease

by
Sebastian Koch
1,
Björn-Hergen Laabs
2,
Meike Kasten
3,4,
Eva-Juliane Vollstedt
4,
Jos Becktepe
5,
Norbert Brüggemann
4,6,
Andre Franke
7,
Ulrike M. Krämer
6,
Gregor Kuhlenbäumer
5,
Wolfgang Lieb
8,
Brit Mollenhauer
9,10,
Miriam Neis
6,11,
Claudia Trenkwalder
10,12,
Eva Schäffer
5,
Tatiana Usnich
4,
Michael Wittig
7,
Christine Klein
4,
Inke R. König
2,
Katja Lohmann
4,
Michael Krawczak
1 and
Amke Caliebe
1,*add Show full author list remove Hide full author list
1
Institute of Medical Informatics and Statistics, Kiel University, University Medical Center Schleswig-Holstein, Campus Kiel, 24105 Kiel, Germany
2
Institute of Medical Biometry and Statistics, University of Luebeck, University Medical Center Schleswig-Holstein, Campus Luebeck, 23562 Luebeck, Germany
3
Department of Psychiatry, University of Luebeck, 23538 Luebeck, Germany
4
Institute of Neurogenetics, University of Luebeck, University Medical Center Schleswig-Holstein, Campus Luebeck, 23538 Luebeck, Germany
5
Department of Neurology, Kiel University, 24105 Kiel, Germany
6
Department of Neurology, University of Luebeck, 23562 Luebeck, Germany
7
Institute of Clinical Molecular Biology, Kiel University, 24105 Kiel, Germany
8
Institute of Epidemiology and PopGen Biobank, Kiel University, University Medical Center Schleswig-Holstein, Campus Kiel, 24105 Kiel, Germany
9
Department of Neurology, University Medical Center Goettingen, 37075 Goettingen, Germany
10
Paracelsus-Elena-Klinik, 34128 Kassel, Germany
11
Department of Midwifery Science, University of Luebeck, 23562 Luebeck, Germany
12
Department of Neurosurgery, University Medical Center Goettingen, 37075 Goettingen, Germany
 
add Show full affiliation list
 
remove Hide full affiliation list
*
Author to whom correspondence should be addressed.
Genes 2021, 12(12), 1859; https://doi.org/10.3390/genes12121859
Submission received: 31 October 2021 / Accepted: 21 November 2021 / Published: 23 November 2021
(This article belongs to the Special Issue Parkinson's Disease: Genetics and Pathogenesis)
Browse Figures
Review Reports Versions Notes

Abstract

:
Idiopathic Parkinson’s disease (PD) is a complex multifactorial disorder caused by the interplay of both genetic and non-genetic risk factors. Polygenic risk scores (PRSs) are one way to aggregate the effects of a large number of genetic variants upon the risk for a disease like PD in a single quantity. However, reassessment of the performance of a given PRS in independent data sets is a precondition for establishing the PRS as a valid tool to this end. We studied a previously proposed PRS for PD in a separate genetic data set, comprising 1914 PD cases and 4464 controls, and were able to replicate its ability to differentiate between cases and controls. We also assessed theoretically the prognostic value of the PD-PRS, i.e., its ability to predict the development of PD in later life for healthy individuals. As it turned out, the PD-PRS alone can be expected to perform poorly in this regard. Therefore, we conclude that the PD-PRS could serve as an important research tool, but that meaningful PRS-based prognosis of PD at an individual level is not feasible.

1. Introduction

Parkinson’s disease (PD) is the second most common neurodegenerative disorder after Alzheimer’s disease, with a particularly high prevalence seen in Europe and North America [1]. PD has a complex multifactorial etiology in which both environmental and genetic factors play a prominent role. The main risk factor for PD hitherto identified, however, is age, and both prevalence and incidence increase exponentially in later life.
While some 3–5% of PD cases are monogenic, recent genome-wide association studies (GWAS) revealed that idiopathic PD is highly polygenic [2,3,4]. Therefore, the development of polygenic risk scores (PRSs) as a means to summarize the effect of the genetic background upon an individual’s disease risk in a single number appears meaningful for idiopathic PD. Several PRSs have been developed for PD affection status, age-at-onset and specific symptoms in studies of variable size and using different methodologies [2,5,6,7,8,9,10].
Although the construction of a PRS is rather straightforward using existing software, the validation of existing PRSs through an assessment of their performance in independent data sets has still been undertaken only rarely and, to our knowledge, not for PD. One aim of our study therefore was to investigate in more detail the discriminatory power of a PRS for PD previously published by Nalls et al. [2]. This PRS was developed based upon the largest meta-GWAS for the disease to date and comprises 1805 single nucleotide polymorphisms (SNPs). Our second aim was to assess the prognostic value of this PD-PRS. In fact, while PRSs usually differentiate well between cases and controls, their utility for disease prognostics has been a matter of intensive debate [11,12].

2. Materials and Methods

2.1. Samples

The samples analyzed in the present study originated from five German cohorts comprising a total of 1914 PD cases and 4464 controls after quality control (Table A1). The data sets were collated within the framework of DFG Research Unit ’ProtectMove’ (FOR2488). The samples of two PD patient and control cohorts (Kiel PD, Luebeck PD) were recruited locally in Schleswig-Holstein, the northernmost federal state of Germany. EPIPARK is an additional prospective and longitudinal observational single-center study from Luebeck, focused upon the non-motor symptoms of PD patients [13]. DeNoPa is a prospective and longitudinal observational single-center study from Kassel in central Germany, aimed specifically at improving early diagnosis and prognosis of PD. Participants include early untreated PD patients and matched healthy controls [14]. The PopGen biobank [15,16] is a central research infrastructure, maintained by Kiel University, for the recruitment of case-control cohorts for defined diseases [15,16]. For the present study, PopGen contributed 661 PD patients and 3093 unaffected individuals from the broader Kiel area.

2.2. Genotyping, Genotype Imputation and Quality Control

Genomic DNA was extracted from peripheral blood leukocytes and genotyped using the Infinium Global Screening Array with Custom Content (GSA; Illumina Inc., San Diego, CA, USA) which targets 645,896 variants. Quality control was performed with PLINK 1.9, PLINK 2.0 and R package plinkQC [17,18,19,20,21,22].
At the SNP level, quality control was carried out with thresholds of 0.01 for the minor allele frequency (MAF), of 0.98 for the SNP call rate and of 10−50 for the software-issued p value of the Hardy–Weinberg equilibrium test. Some 431,738 variants passed quality control and were used for imputation with SHAPEIT2 [23] and IMPUTE2 [24], based upon the public part of the HRC reference panel (release 1.1, The European Genome-Phenome Archive, EGAS00001001710) [25]. Imputation yielded genotype data for a total of 39,106,911 variants and after the exclusion of variants with MAF < 0.01 or an info score < 0.7, some 7,804,284 variants remained for further analyses.
At the participant level, 6794 individuals were initially available from the five cohorts. Individuals with a call rate < 0.98 or with a heterozygosity value > 3 standard deviations different from the mean on the non-imputed data were removed. To exclude potential relatives and population outliers, linkage disequilibrium pruning was performed using a window size of 50 variants, shifted by five variants, and an r2 threshold of 0.2, leaving 186,064 variants. Pairwise identity-by-descent (IBD) was then estimated and individuals were removed in a customized selection process (see Appendix A.1) until all pairwise IBD values were <0.1. For details on the identification of population outliers, see Appendix A.2 and Figure A1. In total, 416 individuals were removed leaving 6378 individuals (1914 cases, 4464 controls) for further analysis. Principal component analysis (PCA) plots of the samples from our study and from the 1000Genomes project can be found in Figure A2.

2.3. Analysis of Parkinson’s Disease Polygenic Risk Score (PD-PRS)

We evaluated a PRS for PD published by Nalls et al. [2]. The list of the 1805 SNPs included in this PD-PRS, together with reference alleles and effect sizes, was kindly provided to us by the first author. Matching the SNPs to our imputed SNPs was done by reference to their chromosomal positions. Some 1743 of the PD-PRS SNPs were represented in our data set, and all of these SNPs were imputed (the 62 omitted SNPs are listed in Table A2).
The PD-PRS values were standardized by subtraction of the mean and division by the standard deviation of the PD-PRS among controls. This standardized version of the PRS will henceforth be used and also referred to as ‘PD-PRS’ as well. Density plots were created with base-R function density. Logistic regression analysis was performed treating the case-control status as outcome and the PD-PRS value as influence variable, adjusted for the first three PCs, sex and age-at-sampling. An additional logistic regression analysis, excluding age-at-sampling, was performed among cases from the lowest and highest age-at-onset quartiles, treating quartile affiliation as outcome. A two-sided significance level of 0.05 was adopted for the Wald test embedded into the logistic regression analysis.
Receiver operating characteristic (ROC) curves and corresponding areas under curve (AUCs) were calculated with R package pROC [26] and 95% confidence intervals for odds ratios were constructed with the oddsratio.wald function from the epitools package [27].

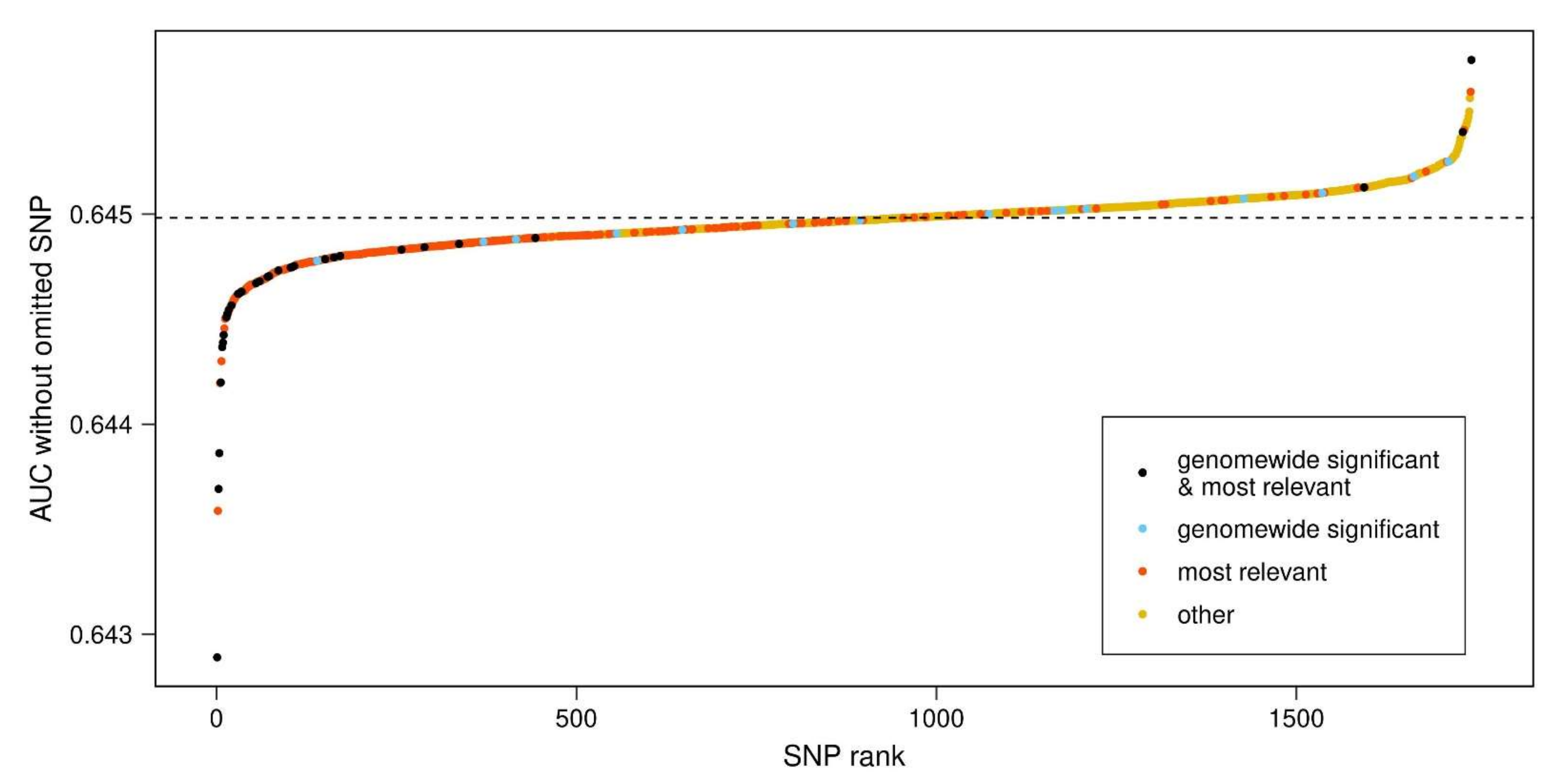
2.4. Identification of Most Relevant PD-PRS SNPs

We evaluated which SNPs of the PD-PRS were most relevant for distinguishing cases from controls by determining their influence upon the AUC. This was done in three steps.
  • The PD-PRS was repeatedly calculated, excluding one SNP each time, and determining the AUC of the PD-PRS without the SNP. These AUCs will be referred to as ‘AUC-SNP’ values.
  • SNPs were sequentially removed from the PD-PRS based upon the steepest decline of the AUC of the remaining SNPs, until the 95% confidence interval of the residual AUC included 0.5. This set of removed SNPs will be referred to as ‘most relevant SNPs’.
  • The results from step 1 and step 2 were combined in a single plot, relating the AUC-SNP values of SNPs (y axis) to their AUC-SNP-based rank (x axis) and color-coding the set of most relevant SNPs from step 2 together with the set of 47 genome-wide significant SNPs identified by Nalls et al. [2] and included in our PD-PRS.
R package biomaRt and the hsapiens_gene_ensembl data set from Ensembl were used to identify genes that included at least one of the most relevant SNPs [28,29,30]. Coding and functional information on individual SNPs were obtained from dbSNP [31].

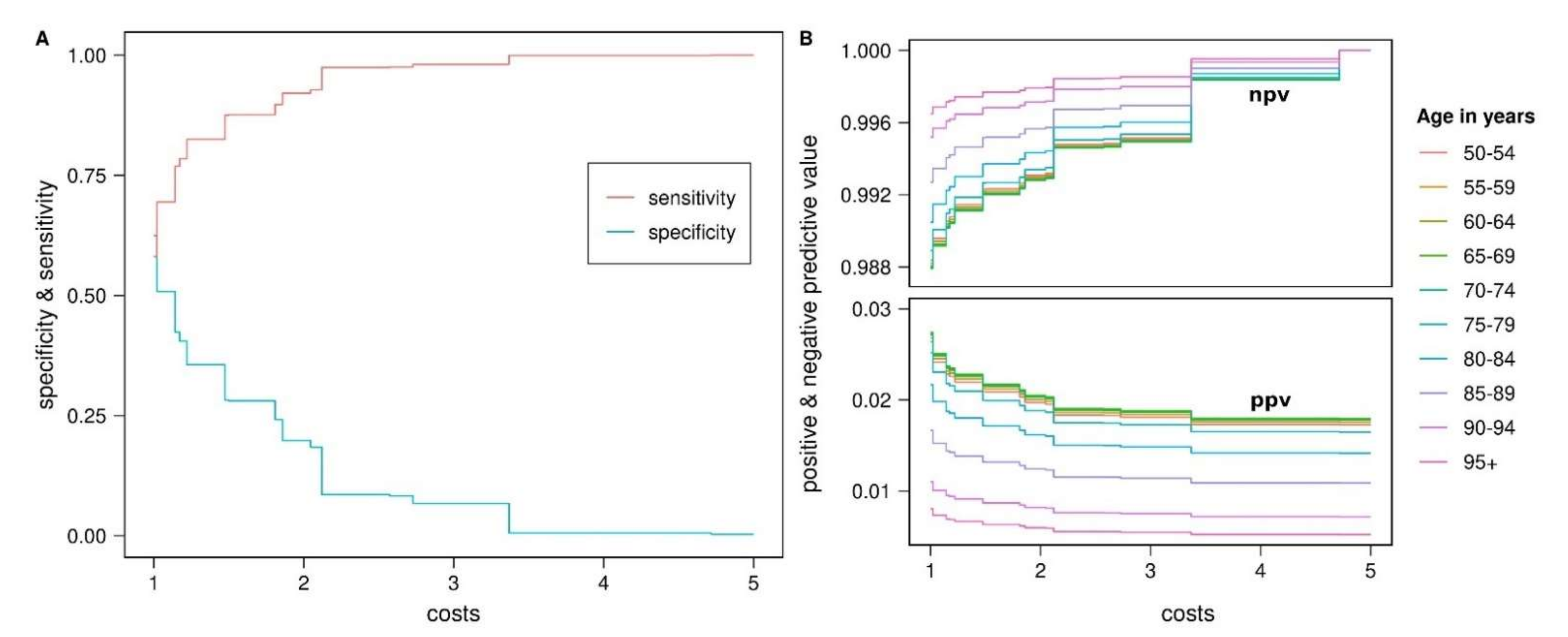
2.5. Prognostic Value of PD-PRS

The coords function from R package pROC [26] was used to derive appropriate PD-PRS thresholds from ROC curves, and to determine the corresponding values of sensitivity and specificity. Thresholds were calculated by maximizing a weighted Youden-Index:
max(costs ∙ sensitivity + specificity)
where ‘costs’ was defined as the relative severity of a false negative compared to a false positive result (i.e., classification or prediction as PD). Costs were varied from 1 to 5 in steps of 0.0001.
For fixed specificity and sensitivity, the positive and negative predictive values (ppv, npv) were computed with Bayes formula as
p p v = s e n s i t i v i t y ⋅ p r e v a l e n c e s e n s i t i v i t y ⋅ p r e v a l e n c e + 1 − s p e c i f i c i t y ⋅ 1 − p r e v a l e n c e
n p v = s p e c i f i c i t y ⋅ 1 − p r e v a l e n c e s p e c i f i c i t y ⋅ 1 − p r e v a l e n c e + 1 − s e n s i t i v i t y ⋅ p r e v a l e n c e
To evaluate the prognostic value of the PD-PRS, we had to include the residual lifetime incidence in the above formulae instead of the disease prevalence. To this end, we adopted the age-specific incidence and death rates I[interval] and D[interval] from the SIa strategy in [32]. The SIa strategy used only cases with at least two diagnoses of PD to avoid false positive diagnoses. I[interval] and D[interval] were given for 5-year age intervals, starting from [50–54] and ending with [95+]. Since the death rates were given as annual probabilities to die within a given interval, the probability to survive that interval can be approximated by S[interval] = (1 − D[interval])5. For individuals from a given age interval [d,d+5], the residual lifetime incidence can then be computed as
I[d, 95+] = I[d, d+5] + (I[d+6, d+11]∙S[d, d+5]∙(1 − I[d, d+5])) + … + (I[95+]∙S[d, d+5]∙…∙S[90, 94]∙(1 − I[d, d+5])∙ … ∙(1-I[90, 94])).
The resulting residual lifetime incidence values are listed in Table A3.

3. Results

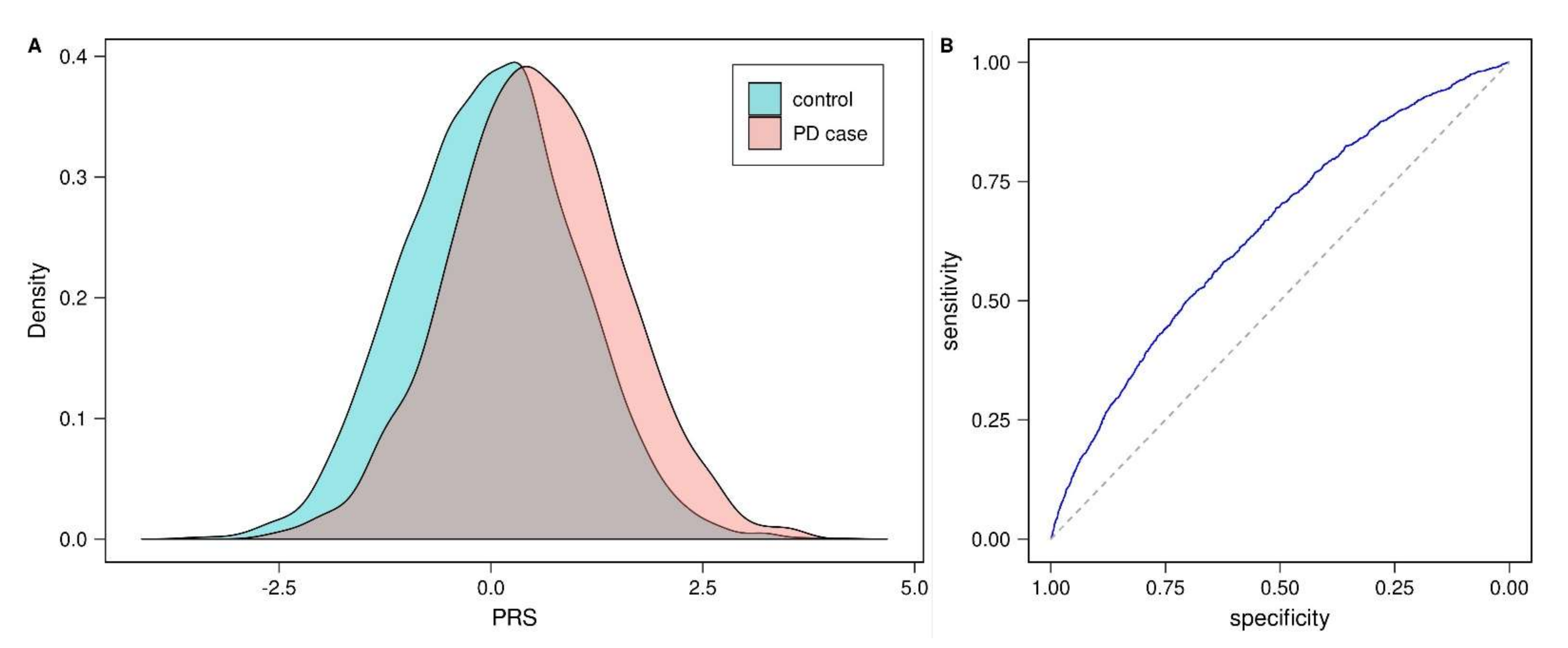
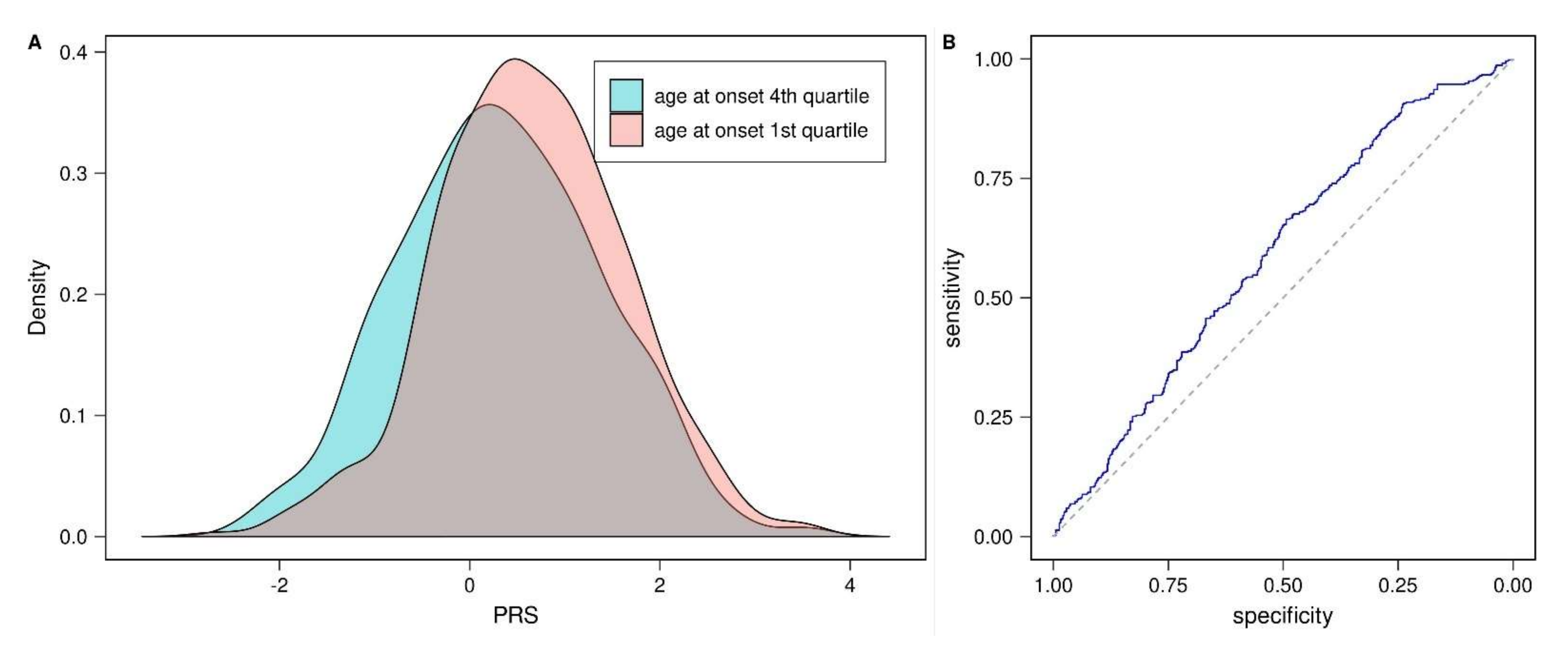
3.1. Validation of Published Parkinson’s Disease Polygenic Risk Score (PD-PRS)

To independently validate the (standardized) PD-PRS proposed by Nalls et al. [2], we investigated the performance of this PRS in a separate data set comprising 1914 PD cases and 4464 controls (Table A1). The distribution of the PD-PRS clearly differed between the two groups (Figure 1A; Wald test p < 10−5, Table 1). Nagelkerke’s pseudo-R2 from the logistic regression analysis equaled 0.35 when including PD-PRS, sex, age and the first three principal components (PCs), and 0.30 when the PD-PRS was not included (Table 1). The area under curve (AUC) for the receiver operating characteristic (ROC) curve (Figure 1B) was 0.65, which was comparable to the AUC obtained in the original study [2]. The disease odds ratios (ORs) for the 2nd to 10th deciles of the PRS distribution among controls ranged from 1.26 (2nd decile) to 6.10 (10th decile; 1st decile used as reference; Figure 2).
The PD-PRS was also able to distinguish well between cases from the 1st and 4th age-at-onset (AAO) quartile (≤54 years vs. >70 years, Figure 3A, p = 1.61 × 10−5, Table 1). Nagelkerke’s pseudo-R2 from the logistic regression was 0.039 including PD-PRS, sex and the first three PCs, and 0.009 when the PD-PRS was not included. The AUC of the ROC equaled 0.59 (Figure 3B, Table 1) and was hence considerably smaller than the AUC obtained for distinguishing cases from controls.

3.2. Most Relevant SNPs in PD-PRS

We identified 422 SNPs as being the most relevant for distinguishing cases from controls, judged by their influence upon the AUC in a backward-selection process (see Methods). Of these SNPs, 287 are located within a gene. Table 2 lists the top 20 most relevant SNPs inside genes (for a complete list, see Table A4). Of all 1743 SNPs analyzed, some 47 had been genome-wide significant in the meta-GWAS by Nalls et al. [2]. Thirty-two of these (68%) were among the 422 most relevant SNPs identified here, and 25 of them (78%) were intra-genic. When all 1743 SNPs were ranked according to the AUC obtained when a given SNP was removed (Figure 4), the 422 most relevant SNPs occurred mostly on the left side of the graph meaning that the AUC is strongly reduced upon the removal of the SNP. The 32 most relevant and genome-wide significant SNPs, in particular, were found to cluster at the far left of the graph.

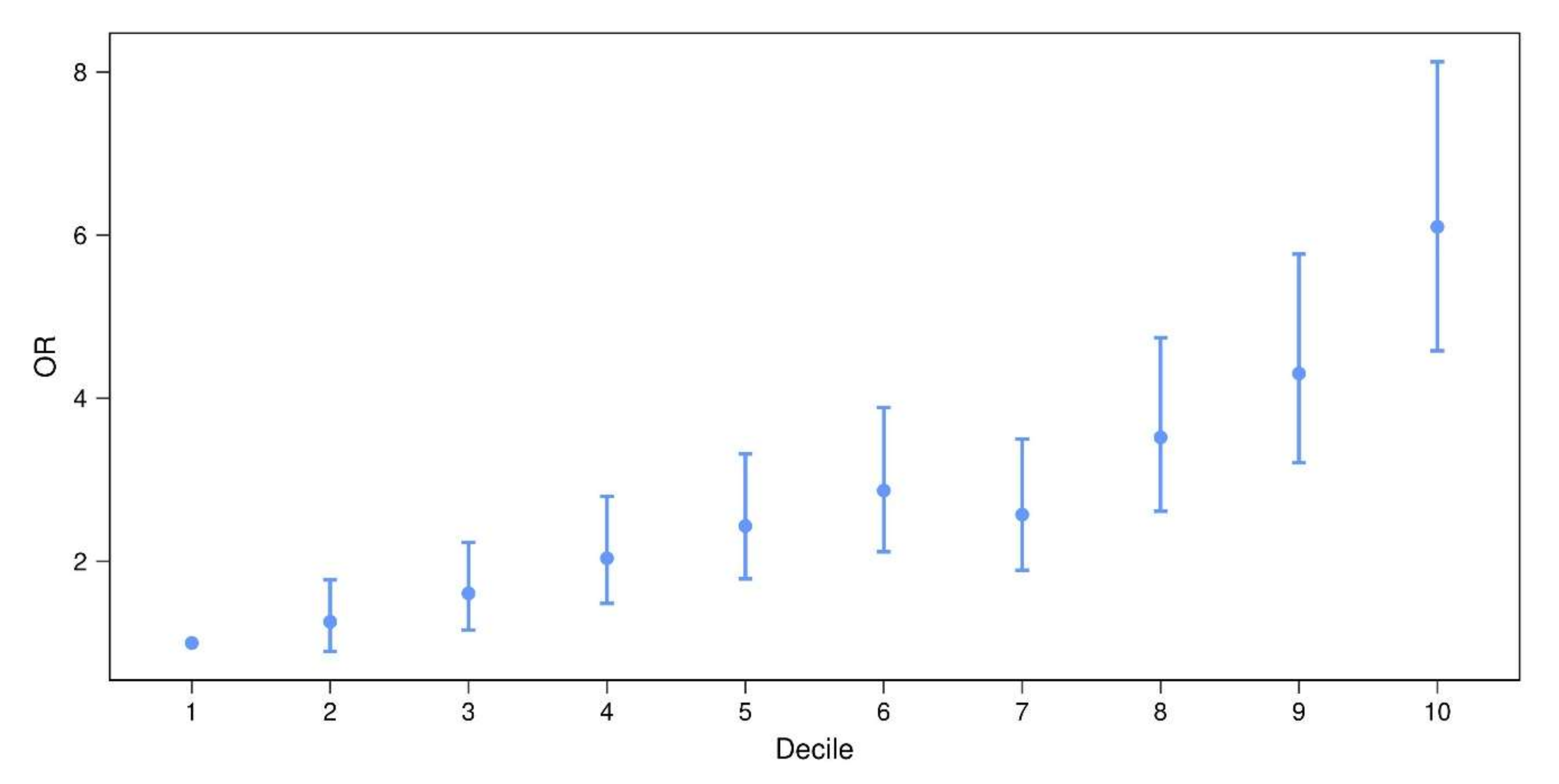
3.3. Prognostic Value of PD-PRS

To investigate the prognostic value of the PD-PRS, an individual was defined as ‘test-positive’ if their PRS exceeded a given threshold of the PRS and ‘test-negative’ if not. Thus, sensitivity in this context means the probability that a person who develops PD in later life has a PRS above the threshold while specificity is the probability that a person who will not develop PD during their lifetime is test-negative. Since sensitivity is generally more important than specificity for screening tests, we considered different relative costs of false negative vs false positive test results when maximizing a weighted Youden index to determine the optimal PD-PRS threshold (Table 3). For costs of 1, i.e., when false positives and false negatives are deemed equally serious, the optimal PD-PRS threshold equaled 0.33, yielding a sensitivity of 0.58 and a specificity of 0.63. For costs of 5, the sensitivity equaled 1 and the specificity equaled 0.003 at an optimal PD-PRS threshold of −2.667 (Table 3, Figure 5A).
For fixed costs, the age-specific predictive values of the PD-PRS differed only little up to age interval [70–74], after which the positive predictive value (ppv) declined and the negative predictive value (npv) increased (Table 4, Figure 5B). Across all age groups and costs levels, the ppv was very low with a maximum of 0.027 up to 74 years at costs of 1. The minimum ppv was 0.005 for the highest age group (90+) at costs of 5. The npv varied between 0.988 (≤74 years, costs 1) and 1 (all age groups, costs 5).

4. Discussion

In the present study, we replicated the performance of the PD-PRS developed by Nalls et al. [2] in an independent data set. It turned out that the PD-PRS was clearly able to distinguish between cases and controls and that it was increased in cases of early age-at-onset. Individuals in the 10th PRS decile had an OR of around 6 of having PD as compared to individuals in the lowest decile. This is in line with the results by Nalls et al. [2] who reported ORs of 3.74 and 6.25 for the highest quartiles in their two data sets. The most relevant PRS SNPs identified in our study included many genome-wide significant SNPs from the Nalls et al. study [2], as was to be expected. In fact, of the 47 genome-wide significant SNPs, some 32 (68%) were found to be most relevant in the sense of our study. However, this is still only a small fraction (7.5%) of the total number of 422 most relevant SNPs, which highlights the polygenic background of PD with several low-effect variants and justifies the fact that not only genome-wide significant SNPs were originally included in the PRS.
In the recent past, the research community has become increasingly aware of the problem of non-replicability of research findings in independent data sets or with different methods [33]. This has been termed the “replication crisis” or “reproducibility crisis” [34,35]. Studies aiming at validating existing PRSs are still rare and, usually, new data set-specific PRSs are developed instead because this is easy with existing software. Nevertheless, PRS replication should be mandatory [36] and our replication of the results reported by Nalls et al. [2], in an independent data set, is reassuring. It supports the idea that this PD-PRS can be used to capture the contribution of the genetic background of an individual to their PD risk. The PD-PRS could hence be a valid instrument to adjust for the genetic background component in statistical models for PD. Moreover, it may also facilitate studies of the genetic overlap between different diseases or disease subtypes and of the interaction between genetic and environmental factors.
It has to be kept in mind, however, that PRSs only capture the effect of common genetic variants. Highly-penetrant rare or private variants as well as other types of variations such as copy number variants or indels are not represented [37]. Another drawback of PRSs is their dependency on the ancestry of populations [38]. The PD-PRS analyzed in the present study was both constructed and validated in populations of European ancestry, and transferability of the results to other ancestries cannot be taken for granted but has to be investigated in future studies. On a related note, it must be kept in mind that all PD-PRS SNPs considered in our study were imputed. This does not seem to have impaired our replication of the results of Nalls et al. [2], probably due to our stringent quality control. For populations, where a good imputation reference is lacking, consistent PRS performance may not be taken for granted.
Quality control in our study led to the exclusion of 62 of the original 1805 PD-PRS SNPs. The omitted SNPs showed on average a larger effect size in the original meta-analysis than the SNPs included in our PRS (Table A2). The former were excluded mostly (79%) because of very low MAF and the rest because the info score was below 0.70. Despite the higher effect sizes, it is therefore not clear if the additional usage of the 62 SNPs would enhance the performance of the PD-PRS because of low MAF and perhaps difficult imputation. The loss of variants from the score due to difficulties in imputation is a good argument for the adoption of the development of standardized PRSs based on reference variants which are available in common genotyping arrays. This would reduce the imputation problem.
Whereas PRSs deserve a role in etiological research and statistical modelling of diseases, their prognostic value is dubious [11,12,36]. PRSs are developed to differentiate between cases and controls. Although the level of differentiation achieved is reasonable at a group level, the obtained AUCs are usually insufficient for individual diagnostic or prognostic testing, where an AUC > 0.90 is required [11]. In this study, we evaluated the prognostic value of a specific PD-PRS and calculated its sensitivity and specificity as well as its predictive values for various assumptions about the relative importance of mis-prognoses. Our results were in accordance with the generally held view that a prognostic application of PRSs alone is not meaningful. The negative predictive values were high which means that people with a low PRS can be reasonably sure not to develop PD, at least not of the type considered in this study. However, the positive predictive values were only of the order of a few percent which means that the probability of a person with a high PRS developing the disease is quite low. Here, the comparison to a hypothetical test which gives everybody a negative test result is helpful: Assuming a lifetime incidence of 5% [39], the negative predictive value of this (nonsense) test would be 95%, i.e., quite similar to a test based solely on the PD-PRS.
There are three ways in which a prognostic test for PD, or any other disease, could potentially help to reduce incidence or severity: change of lifestyle factors, enhanced surveillance or preventive treatment. Of these, a change towards a healthier lifestyle is always meaningful, both from an individual and a population health perspective, and only a test with a positive predictive value much higher, for example, than that of the PD-PRS would mean an additional individual incentive for change. Moreover, with a low incidence and positive predictive value, frequent medical screening of individuals with a high PRS would mean spending valuable resources for individuals who have only a probability of a few percent to actually develop the disease in question. The same holds true for possible preventive treatment if such treatment were available in the first place. Apart from economic constraints, side-effects might result in a negative benefit-risk balance when the incidence of the disease in question is as low as for PD.
A limitation of our study has been that the predictive values were only calculated from theoretical models and were not based directly upon empirical observations. This is a general drawback when evaluating the prognostic value of PRSs because adequate long-term studies would be time-consuming, require large sample sizes and would hence be rather expensive. This notwithstanding, PRSs have to be externally validated and compared to other (clinical) risk models in a clinically meaningful prospective set-up [12,36] because this is a conditio sine qua non for the applicability in practice of any prognostic marker. Only a few studies have taken first steps in this direction [40,41,42], and most have found none or only little additional prognostic value of PRSs over and above clinical and demographic predictors. To our knowledge, no such study has been performed yet for PD, where the combination of a PRS with established prodromal markers [43] might be specifically worth investigating in future prospective studies.

5. Conclusions

The PD-PRS proposed by Nalls et al. [2] could be validated independently in German patients and controls, suggesting that the PRS may be a meaningful research tool to investigate and adjust for the polygenic component of PD. Individual risk prediction using the PD-PRS alone is, however, not meaningful.

Author Contributions

Conceptualization, A.C., C.K., I.R.K., S.K., M.K. (Michael Krawczak) and K.L.; methodology, A.C., I.R.K., S.K. and M.K. (Michael Krawczak); formal analysis, S.K.; investigation, A.C.; resources, J.B., N.B., A.F., G.K., U.M.K., B.-H.L., K.L., W.L., B.M., M.N., E.S., C.T., T.U. and M.W.; data curation, M.K. (Meike Kasten) and E.-J.V.; writing—original draft preparation, A.C. and S.K.; writing—review and editing, A.C., C.K., I.R.K., S.K., M.K. (Michael Krawczak) and K.L.; visualization, S.K.; supervision, A.C. and M.K. (Michael Krawczak); project administration, C.K.; funding acquisition, A.C. and C.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the German Research Foundation (FOR2488 to N.B., A.C., M.K. (Meike Kasten), M.K. (Michael Krawczak), C.K., I.R.K., K.L. and TR-CRC134 to U.M.K., M.K. (Meike Kasten), C.K.).

Institutional Review Board Statement

The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Ethics Committees of the University of Lübeck, Germany (protocol code 16-039, date of approval 27 September 2019) and the P2N supervisory board, Kiel University, Germany (protocol code 2021-037, date of approval 16 September 2021).

Informed Consent Statement

Informed consent was obtained from all subjects involved in the study.

Data Availability Statement

The data that support the results of this study are available upon reasonable request from the corresponding author.

Acknowledgments

We thank Mike A. Nalls for providing us with the list of the 1805 SNPs included in their published PRS (together with reference alleles and effect sizes β).

Conflicts of Interest

C.K. serves as a medical advisor for genetic testing reports in the field of movement disorders and dementia, but excluding Parkinson’s disease, to Centogene and as a member of the Scientific Advisory Board of Retromer Therapeutics. N.B. has previously served as a consultant for Centogene GmbH. The other authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.

Appendix A

Appendix A.1. Removal of Related Individuals

Clusters of related individuals were generated such that each individual in a cluster had an IBD value ≥ 0.1 with at least one other individual in the cluster. Typical clusters were siblings or parent-child clusters but also larger clusters of extended families were found. A total of 238 disjunct clusters comprising 503 individuals were detected in our data set. For each cluster, the largest subset of unrelated individuals (all pairwise IBD values < 0.1) was next selected, and since cases were more valuable for our analysis than controls, the former were given double weight in the selection process. If two equally large subsets remained, the subset with the highest AAO for a case was selected because idiopathic PD typically has high AAO. If this was not possible, selection was in favor of the subset with the oldest control. Of the 503 individuals in clusters, 243 were kept for further analysis.

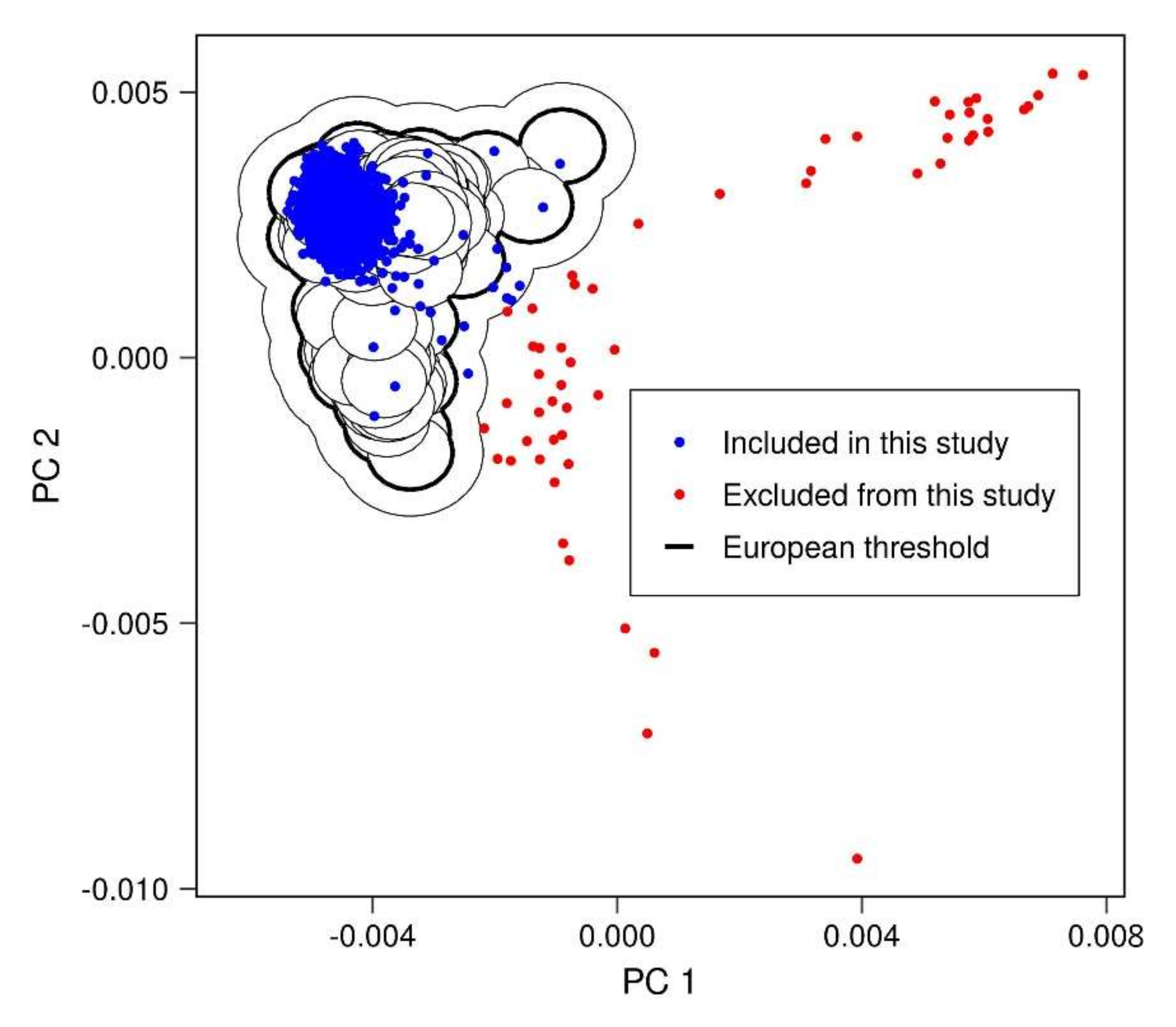
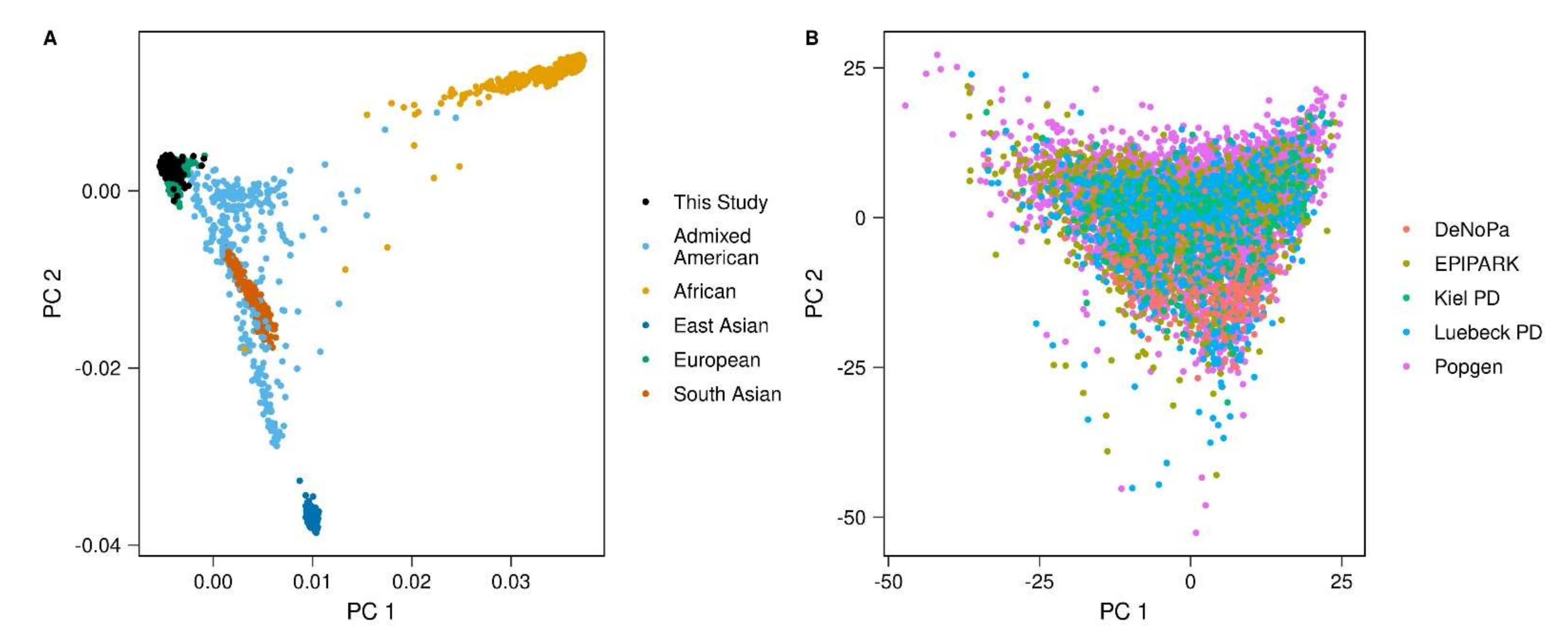
Appendix A.2. Removal of Population Outliers

Population outliers were removed in our study by two different approaches. In the first approach, our data set was merged with 2504 individuals from the 1000Genomes project (1000 Genomes Phase III, imputed). A PCA was then done with PLINK 1.9 [21] at the default setting of 20 PCs. Next, a polygon was constructed around the European populations of the 1000Genomes data (CEU, FIN, GBR, IBS and TSI) to identify population outliers in our own data by considering PC1 and PC2. In more detail, the polygon was generated by first transforming the PC1:PC2-coordinates of the European individuals from 1000Genomes and of our samples into spatial data, using R package sp [44,45]. Ideally, a circle around each European 1000Genomes data point (sample) would represent the genetic neighborhood of the respective individual, and the union of these circles would be the region of probable European ancestry. However, that is technically difficult and therefore R package rgeos was used to calculate 20-polygonal approximations of circles with a width of 0.0005 around each data point [46] (Figure A1). The width of these circle-polygons was chosen such that the union of all circle-polygons was connected. The width roughly equaled 1/8 of the mean of the first PC and 1/4 of the mean of the second PC of the 1000Genomes European data. As a boundary of the union of the circle-polygons, a polygon was then computed with an additional distance of 0.0005 to the circle-polygons to smooth indentations. Finally, we gauged the samples from our data set against this boundary and every sample outside the boundary was removed.
As a second approach to remove population outliers, we applied the K nearest neighbor (KNN) method suggested in [47] using R packages bigsnpr and bigparallelr [48,49]. Utilizing a scree plot, three PCs were considered important and a threshold of 0.15 was used for the KNN statistics.
Genes 12 01859 g0a1 550
Figure A1. Identification of population outliers by PCA drawing upon 1000Genomes data. White circles represent polygonal circle approximations around European samples of the 1000Genomes project. The thick black line marks the union set, the thinner line marks the final boundary. Dots representing our samples are colored according to their inclusion in or exclusion from the study. Samples were excluded if they were outside the boundary. PC: principal component, PCA: principal component analysis.
Figure A1. Identification of population outliers by PCA drawing upon 1000Genomes data. White circles represent polygonal circle approximations around European samples of the 1000Genomes project. The thick black line marks the union set, the thinner line marks the final boundary. Dots representing our samples are colored according to their inclusion in or exclusion from the study. Samples were excluded if they were outside the boundary. PC: principal component, PCA: principal component analysis.
Genes 12 01859 g0a1
Genes 12 01859 g0a2 550
Figure A2. PCA plots after quality control. (A) Plot of the first two PCs from the 1000Genomes supra populations and the samples of this study. Our study samples were plotted on top, therefore obscuring part of the European samples from the 1000Genomes project. (B) Plot of the first two PCs from the cohorts included in our study (Table A1). PC: principal component, PCA: principal component analysis.
Figure A2. PCA plots after quality control. (A) Plot of the first two PCs from the 1000Genomes supra populations and the samples of this study. Our study samples were plotted on top, therefore obscuring part of the European samples from the 1000Genomes project. (B) Plot of the first two PCs from the cohorts included in our study (Table A1). PC: principal component, PCA: principal component analysis.
Genes 12 01859 g0a2
Table
Table A1. Cohorts used in this study.
Table A1. Cohorts used in this study.
CohortN
N CasesN
Controls		N Female CasesN Female
Controls		Age-at-Sampling Cases 1Age-at-Sampling
Controls 1		Age-at-Onset Cases 1
Kiel PD184184059 (32%)068 [61–76]-58 [48–68]
Luebeck PD928395533139 (35%)323 (61%)68 [57–75]44 [35–48]60 [51–68]
EPIPARK [13]1271525746205 (39%)353 (47%)69 [60–76]67 [61–71]60 [52–70]
DeNoPa [14]2411499252 (35%)32 (35%)67 [59–73]67 [62–70]67 [59–73]
Popgen [15,16]37546613093262 (40%)1527 (49%)71 [66–77]54 [41–65]64 [56–71]
1 Median and interquartile-range. PD: Parkinson’s disease.
Table
Table A2. SNPs omitted from PD-PRS.
Table A2. SNPs omitted from PD-PRS.
SNP Location 1Beta 2GS 3MAF 4
1:1,186,833−0.4394no0.0178
1:145,716,7630.0448nonot imputed
1:154,837,9390.2467no0.0052
1:155,205,6340.7662yes0.0022
1:232,161,497−0.2638no0.0087
1:62,675,6730.317no0.0134
2:100,906,4270.1534no0.0098
2:102,368,8700.2332no0.0048
2:102,655,7730.2056no0.0046
2:136,388,639−0.0656no0.0513
2:191,364,8280.2497no0.0079
2:63,783,5070.173no0.0094
3:112,245,295−0.1391no0.9907
3:48,406,2860.0789no0.0398
3:96,921,3590.1607no0.0069
3:97,799,5410.1819no0.0062
4:133,792,8530.1797no0.0057
4:77,645,873−0.2104no0.0096
4:90,603,678−0.203no0.0087
4:90,673,143−0.3266no0.0032
4:90,810,3400.3754no0.0062
4:90,955,5530.2561no0.0052
4:90,967,3400.2829no0.0081
4:91,033,0470.3361no0.0078
4:91,278,5450.3511no0.0022
5:112,288,6170.2085no0.0076
5:141,311,8960.1052no0.0434
5:177,972,5600.1641no0.0080
5:60,150,8890.1637no0.0069
6:109,972,4530.1744no0.0071
6:27,483,3850.1698no0.0072
6:32,036,055−0.1716no0.0063
6:34,800,390−0.2314no0.0029
6:48,781,9380.2449no0.0087
7:6,070,1990.1652no0.0096
9:116,138,7700.2529no0.0042
9:139,566,889−0.0812no0.1093
10:102,056,7340.3817no0.0019
10:103,373,4630.1323no0.0099
10:103,941,8750.1667no0.0080
10:105,038,0080.1579no0.0076
10:27,198,1180.2103no0.0012
10:48,433,7200.0481no0.1562
11:93,561,1490.1769no0.0041
12:123,341,5000.2448no0.0064
12:123,923,6120.2771no0.0077
12:40,734,2022.4354yes0.0001
12:72,179,4460.2839no0.0156
14:103,351,7310.1973no0.0046
16:429,9260.2396no0.0077
16:71,451,5260.2423no0.0065
17:43,516,175−0.2917no0.0130
17:43,559,955−0.2548no0.0098
17:43,857,449−0.3906no0.0162
17:44,687,696−0.5875no0.0172
17:44,914,558−0.1824no0.0095
17:44,916,5330.2253no0.0095
17:8,209,654−0.1341no0.0131
19:11,084,4670.2043no0.0083
19:38,222,9140.1495no0.0085
19:39,756,425−0.1751no0.0092
20:31,687,4460.2054no0.0080
median [IQR]
omitted 62 SNPs		0.207
[0.166, 0.262] 5		 0.0080
[0.0062, 0.0098]
median [IQR]
1743 SNPs used in this study		0.056
[0.042, 0.091] 5		 0.1916
[0.0102, 0.4407]
1 Location of SNPs, given as chromosome:basepair position. 2 β from the meta-GWAS performed by Nalls et al. [2]. 3 Genome-wide significant (GS) in the meta-GWAS performed by Nalls et al. [2]. 4 MAF in our data set. 5 median and IQR of the absolute values of β. SNP: single nucleotide polymorphism, MAF: minor allele frequency, IQR: inter-quartile range, PRS: polygenic risk score, PD: Parkinson’s disease.
Table
Table A3. Incidence of PD in different age groups.
Table A3. Incidence of PD in different age groups.
Age Interval
in Years		Incidence 1Survival 2Residual Lifetime Incidence 3
50–540.00020.9940.017
55–590.00050.9920.017
60–640.00090.9870.018
65–690.00160.9830.018
70–740.00340.9740.018
75–790.00510.9580.016
80–840.00670.9290.014
85–890.00720.8740.011
90–940.00560.7820.007
95+0.00520.6540.005
1 Probability to develop PD during age interval (from [32]). 2 Probability to survive a year from the respective age interval (from [32]). 3 Probability to develop PD in later life (see Methods section). PD: Parkinson’s disease.
Table
Table A4. Most relevant SNPs located within genes.
Table A4. Most relevant SNPs located within genes.
HGNC Symbol 1ChrAUCStart 2End 3SNP Position 4A1 5A2 6GS 7
ENSG0000025109540.64390,472,50790,647,65490,626,111GAyes
SNCA40.6419,0645,25090,759,46690,684,278AGno
HIP1R120.640123,319,000123,347,507123,326,598GTyes
TMEM17540.639926,175952,444951,947TCyes
SNCA40.63890,645,25090,759,46690,757,294ACno
ASH1L10.637155,305,059155,532,598155,437,711GAno
UBQLN410.634156,005,092156,023,585156,007,988GAno
ENSG00000225342120.63340,579,81140,617,60540,614,434CTyes
LRRK2120.63340,590,54640,763,08740,614,434CTyes
STX1B160.63231,000,57731,021,94931,004,169TCno
INPP5F100.631121,485,609121,588,652121,536,327GAyes
CCSER140.63191,048,68692,523,06491,164,040CTno
SLC2A13120.63040,148,82340,499,89140,388,109CTno
FBXL19160.63030,934,37630,960,10430,943,096AGno
ENSG0000025109540.62990,472,50790,647,65490,619,032CTno
CAB39L130.62949,882,78650,018,26249,927,732TCyes
STK3920.628168,810,530169,104,651168,979,290CTno
CCT310.628156,278,759156,337,664156,300,731TCno
ENSG00000225342120.62740,579,81140,617,60540,614,656AGno
LRRK2120.62740,590,54640,763,08740,614,656AGno
SH3GL290.62717,579,08017,797,12717,726,888CTno
LRRK2120.62640,590,54640,763,08740,713,899TCno
ENSG0000025109540.62590,472,50790,647,65490,573,396GAno
ASXL3180.62531,158,57931,331,15631,304,318GTyes
SH3GL290.62417,579,08017,797,12717,579,690TGyes
ENSG00000259675150.62361,931,54862,007,37061,997,385TCyes
RGS10100.623121,259,340121,302,220121,260,786AGno
CASC16160.62252,586,00252,686,01752,636,242CAyes
EPRS10.621220,141,943220,220,000220,163,026CAno
BRIP1170.62159,758,62759,940,88259,918,091AGno
PCGF340.620699,537764,428758,444CTno
ENSG0000024959240.620756,175775,637758,444CTno
ENSG0000023379940.620758,275758,862758,444CTno
NDUFAF250.62060,240,95660,448,85360,297,500AGno
DLG2110.61983,166,05585,338,96683,488,901CTno
SEC16A90.618139,334,549139,372,141139,336,813TGno
FCGR2A10.617161,475,220161,493,803161,478,859TCno
SPTSSB30.617161,062,580161,090,668161,077,630AGyes
DSCAM210.61641,382,92642,219,06541,452,034CTno
GAK40.616843,064926,161893,712CTno
CTSB80.61511,700,03311,726,95711,707,174AGno
ASH1L10.615155,305,059155,532,598155,347,819ACno
DCST110.614155,006,300155,023,406155,014,968TGno
LRSAM190.614130,213,765130,265,780130,261,113GAno
UBAP290.61433,921,69134,048,94734,046,391CTyes
GCH1140.61355,308,72655,369,57055,348,869CTyes
PCGF2170.61336,890,15036,906,07036,896,751GAno
SETD530.6129,439,2999,520,9249,504,099GAno
LRRK2120.61140,590,54640,763,08740,753,796TCno
PRSS390.61133,750,51533,799,23033,778,399GAno
KANSL1170.61144,107,28244,302,73344,189,067AGno
ENSG0000021487170.61023,210,76023,234,50323,232,659TCno
NUPL270.61023,221,44623,240,63023,232,659TCno
SEC23IP100.610121,652,223121,702,014121,667,020TCno
ENSG0000025109540.61090,472,50790,647,65490,538,467AGno
SLC38A1120.60946,576,84646,663,80046,623,807GAno
MED12L30.609150,803,484151,154,860151,112,968CAno
NOD2160.60850,727,51450,766,98850,736,656AGyes
UBTF170.60842,282,40142,298,99442,294,462AGno
BTN2A260.60826,383,32426,395,10226,389,926CTno
PGS1170.60776,374,72176,421,19576,377,458AGno
MRVI1110.60710,594,63810,715,53510,660,840GTno
TMEM16320.607135,213,330135,476,570135,443,940AGno
ENSG00000264031170.60627,887,56528,034,10827,897,585TCno
TP53I13170.60627,893,07027,900,17527,897,585TCno
ZNF16560.60628,048,75328,057,34128,054,198AGno
PCGF340.606699,537764,428733,630GAno
PITPNM2120.605123,468,027123,634,562123,585,705CTno
PCGF340.605699,537764,428734,351AGno
C10orf32-ASMT100.605104,614,029104,661,656104,635,103GAno
AS3MT100.605104,629,273104,661,656104,635,103GAno
ENSG0000023266770.60479,959,50880,014,29579,998,372TCno
RNF141110.60410,533,22510,562,77710,558,777AGyes
STK3920.604168,810,530169,104,651169,023,263TCno
CCSER140.60391,048,68692,523,06491,057,794AGno
SEZ6L2160.60229,882,48029,910,86829,892,184GAno
VSTM5110.60293,551,39893,583,69793,576,556TCno
SPATA19110.602133,710,526133,715,433133,714,560ACno
ENSG0000025109540.60190,472,50790,647,65490,606,518TGno
H2AFX110.600118,964,564118,966,177118,965,479GAno
MSTO110.599155,579,979155,718,153155,698,425CTno
MSTO2P10.599155,581,011155,720,105155,698,425CTno
DAP310.599155,657,751155,708,801155,698,425CTno
GABRB140.59946,995,74047,428,46147,372,139ACno
TMEM16320.599135,213,330135,476,570135,464,616AGyes
MFSD620.598191,273,081191,373,931191,300,402AGno
AMPD3110.59810,329,86010,529,12610,525,791ACno
ADD140.5982,845,5842,931,8032,901,349AGno
NSF170.59744,668,03544,834,83044,808,902GAno
HCAR1120.597123,104,824123,215,390123,124,138TCno
NR1I310.597161,199,456161,208,092161,205,966GTno
GAK40.596843,064926,161903,249GAno
EIF3K190.59539,109,73539,127,59539,116,961AGno
BPTF170.59565,821,64065,980,49465,885,911CTno
FBRSL1120.595133,066,137133,161,774133,081,895CTno
ENSG00000260958160.59434,442,30834,518,51734,466,252TCno
RIT2180.59440,323,19240,695,65740,673,380AGyes
C10orf2100.594102,747,124102,754,158102,747,363GTno
MYOC10.593171,604,557171,621,823171,612,267GAno
XPO120.59261,704,98461,765,76161,763,207TCno
CRHR1170.59143,699,26743,913,19443,744,203CTyes
ENSG00000263715170.59143,699,27443,893,90943,744,203CTyes
PPP6R2220.59050,781,73350,883,51450,794,282CAno
NRG180.59031,496,90232,622,54831,942,557GAno
NRG1-IT180.59031,883,73531,996,99131,942,557GAno
LTK150.59041,795,83641,806,08541,798,614TCno
SAA1110.58918,287,72118,291,52418,290,067GTno
KCNIP320.58995,963,05296,051,82596,025,765AGno
PCGF340.588699,537764,428749,620TGno
ART340.58876,932,33777,033,95576,990,450CTno
ARL1550.58853,179,77553,606,41253,537,742GAno
ENSG0000027241440.58777,135,19377,204,93377,198,054CTyes
FAM47E40.58777,172,87477,232,28277,198,054CTyes
FAM47E-STBD140.58777,172,88677,232,75277,198,054CTyes
SCARB240.58777,079,89077,135,04677,100,807TCno
WNT3170.58744,839,87244,910,52044,868,187GAno
DSCR9210.58638,580,80438,594,03738,593,620GTno
MYLK3160.58646,740,89146,824,31946,778,070GAno
ENSG0000025109540.58690,472,50790,647,65490,513,701GAno
BST140.58515,704,57315,739,93615,737,348GAyes
C9orf12990.58596,080,48196,108,69696,087,807CTno
MMRN140.58490,800,68390,875,78090,804,532CTno
MAPT-AS1170.58443,921,01743,972,96643,935,838TCno
MCCC130.584182,733,006182,833,863182,760,073TGyes
MUC19120.58340,787,19740,964,63240,829,565GAno
ENSG00000258167120.58340,789,65540,837,64940,829,565GAno
CCNT2-AS120.583135,493,034135,676,280135,500,179GAno
XKR680.58310,753,55511,058,87510,999,583CTno
RCAN260.58246,188,47546,459,70946,229,444CTno
ITGA8100.58215,555,94815,762,12415,563,450CTno
RANBP960.58113,621,73013,711,79613,657,040GAno
IGF2BP370.58123,349,82823,510,08623,462,162CAno
FAM47E40.58077,135,19377,204,93377,202,861AGno
ENSG0000027241440.58077,172,87477,232,28277,202,861AGno
FAM47E-STBD140.58077,172,88677,232,75277,202,861AGno
ENSG0000025109540.57990,472,50790,647,65490,594,987GAno
SCARB240.57877,079,89077,135,04677,111,032CTno
ARHGAP27170.57843,471,27543,511,78743,472,507AGno
ZYG11B10.57853,192,12653,293,01453,233,374TCno
ENSG0000024412830.577164,924,748165,373,211165,020,212AGno
PER1170.5778,043,7908,059,8248,051,639AGno
KCNS320.57718,059,11418,542,88218,132,092CTno
HIBCH20.576191,054,461191,208,919191,071,057GAno
RN7SL416P70.576100,127,987100,128,282100,128,114GAno
YLPM1140.57575,230,06975,322,24475,234,329GAno
FGFRL140.5741,003,7241,020,6851,008,212CTno
CRHR1170.57443,699,26743,913,19443,798,308GAyes
ENSG00000263715170.57443,699,27443,893,90943,798,308GAyes
HIP1R120.574123,319,000123,347,507123,334,442CTno
MYO15B170.57373,584,13973,622,92973,587,257AGno
PITPNM2120.573123,468,027123,634,562123,525,280AGno
PREX280.57368,864,35369,149,26569,029,244CAno
ENSG00000255468110.57366,115,42166,132,27566,115,782GTno
SIPA1L210.572232,533,711232,697,304232,664,611CTyes
AMPD3110.57110,329,86010,529,12610,475,856GAno
PAM50.571102,089,685102,366,809102,363,402CTno
IFT140160.5711,560,4281,662,1111,593,645CTno
TMEM204160.5711,578,6891,605,5811,593,645CTno
CLIP1120.570122,755,979122,907,179122,891,863CTno
ABCB9120.570123,405,498123,466,196123,418,656GTno
ZC3H7B220.57041,697,52641,756,15141,755,105AGno
CRHR1170.56943,699,26743,913,19443,784,228TCno
ENSG00000263715170.56943,699,27443,893,90943,784,228TCno
LRRK2120.56940,590,54640,763,08740,730,463CTno
ENSG00000235423120.569123,736,577123,746,030123,744,082CAno
MSRA80.5689,911,77810,286,40110,280,818ACno
LYVE1110.56810,578,51310,633,23610,628,883GAno
MRVI1110.56810,594,63810,715,53510,628,883GAno
FAM162A30.568122,103,023122,131,181122,109,601TCno
MMRN140.56790,800,68390,875,78090,868,355TCno
ENSG0000023665610.567158,444,244158,464,676158,453,419ACno
ENSG0000023549520.56767,792,73667,911,20967,806,472AGno
DEFB119200.56629,964,96729,978,40629,971,435GAno
NGEF20.566233,743,396233,877,982233,864,457CTno
MGAT520.566134,877,554135,212,192135,202,455AGno
ASAH180.56517,913,93417,942,49417,927,609CTno
CPNE8120.56539,040,62439,301,23239,174,139TGno
SEMA3G30.56552,467,06952,479,10152,468,940TCno
PBRM130.56452,579,36852,719,93352,649,748AGno
HMBOX180.56428,747,9112892228128,809,951AGno
HMBOX1-IT180.56428,807,19328,813,47228,809,951AGno
SNCA40.56390,645,25090,759,46690,700,329TCno
MAPT170.56343,971,74844,105,70044,071,851GAno
ENSG0000025888120.56371,166,44871,222,46671,202,989TCno
ENSG0000025109540.56290,472,50790,647,65490,627,967GAno
CRHR1170.56243,699,26743,913,19443,901,665TCno
ARHGEF7130.562111,766,906111,958,084111,863,720CTno
GNPTAB120.561102,139,275102,224,716102,151,977CTno
FAM220A70.5616,369,0406,388,6126,369,946AGno
BRD260.56132,936,43732,949,28232,941,506CTno
ATG4D190.56110,654,57110,664,09410,663,997CTno
KRI1190.56110,663,76110,676,71310,663,997CTno
FBXO34140.56055,738,02155,828,63655,801,687ACno
ENSG00000258455140.56055,792,55255,806,21955,801,687ACno
CCDC101160.56028,565,23628,603,11128,566,158GTno
C14orf159140.56091,526,67791,691,97691,682,844TCno
KIF21A120.56039,687,03039,837,19239,738,666GAno
PRRC2C10.559171,454,651171,562,650171,471,672TCno
RNF141110.55910,533,22510,562,77710,560,447ACno
SOX2-OT30.559180,707,558181,554,668180,797,921TGno
SLC2A13120.55840,148,82340,499,89140,437,969AGno
RPP1430.55858,291,97458,310,42258,292,485GAno
DGKG30.557185,823,457186,080,026185,834,290TCno
ENSG00000251364110.5577,448,4977,533,7467,532,175TGno
OLFML1110.5577,506,6197,532,6087,532,175TGno
ADAM1510.557155,023,042155,035,252155,033,317TCno
TRHDE120.55672,481,04673,059,42272,714,601GTno
GAK40.556843,064926,161852,939GAno
CCDC134220.55542,196,68342,222,30342,216,326AGno
LZTS2100.55510,275,6375102,767,593102,764,511GAno
SLC44A2190.55510,713,13310,755,23510,730,352GAno
FYN60.554111,981,535112,194,655112,164,313GAno
RNF21240.5541,050,0381,107,3501,082,829TCno
CCSER140.55391,048,68692,523,06491,383,333GAno
ZNF58930.55348,282,59048,340,74348,333,546TCno
FGF14130.553102,372,134103,054,124102,996,713AGno
FGF14-IT1130.553102,944,677103,046,869102,996,713AGno
TFRC30.552195,754,054195,809,060195,775,449CTno
MAEA40.5521,283,6391,333,9351,312,394CTno
ANKRD11160.55189,334,03889,556,96989,369,869AGno
ZZZ310.55178,028,10178,149,10478,070,458CTno
DNM310.551171,810,621172,387,606171,845,192GTno
LARP1B40.550128,982,423129,144,086129,107,049TCno
STK3920.550168,810,530169,104,651169,071,190GTno
NEXN10.55078,354,19878,409,58078,392,446GAno
CD3840.55015,779,89815,854,85315,829,612AGno
HAVCR150.549156,456,424156,486,130156,479,424ACno
SCAND360.54928,539,40728,583,98928,547,283TCno
APOM60.54831,620,19331,625,98731,622,606CAno
TRIM37170.54857,059,99957,184,28257,111,269ACno
OR9Q1110.54857,791,35357,949,08857,870,219GAno
KIAA184120.54761,293,00661,391,96061,347,469CTno
TATDN230.54710,289,70710,322,90210,300,941AGno
ENSG0000027241030.54710,291,05610,327,48010,300,941AGno
ZNF320190.54753,367,04353,400,94653,399,832CTno
ENSG00000272657210.54635,445,89235,732,33235,677,897GAno
ENSG00000214955210.54635,577,35635,697,33435,677,897GAno
ITGAL160.54630,483,97930,534,50630,520,856CTno
UNKL160.5461,413,2061,464,7521,436,510GAno
FYN60.545111,981,535112,194,655112,122,373CTno
SYBU80.545110,586,207110,704,020110,644,774TCno
AGMO70.54515,239,94315,601,64015,262,499GTno
MED12L30.544150,803,484151,154,860151,133,211GAno
SYNDIG1200.54424,449,83524,647,25224,645,939GAno
MYO7A110.54476,839,31076,926,28476,920,983AGno
CAPRIN2120.54330,862,48630,907,88530,895,251TCno
BRSK2110.5431,411,1291,483,9191,478,565TCno
ARID2120.54246,123,44846,301,82346,134,812TCno
RALYL80.54285,095,02285,834,07985,772,129AGno
HCAR1120.542123,104,824123,215,390123,189,794TCno
ENSG00000256249120.542123,171,672123,200,526123,189,794TCno
SPPL2B190.5412,328,6142,355,0992,341,047CTyes
RNF165180.54143,906,77244,043,10344,040,660TCno
HSF5170.54156,497,52856,565,74556,507,063CTno
ENO3170.5404,851,3874,860,4264,858,206AGno
WBP1L100.539104,503,727104,576,021104,562,212CTno
ERC230.53855,542,33656,502,39156,014,781AGno
MYO1H120.538109,785,708109,893,328109,846,466GTno
MAEA40.5381,283,6391,333,9351,311,933GTno
ENSG0000024403670.538129,593,074129,666,391129,663,496CTno
ZC3HC170.538129,658,126129,691,291129,663,496CTno
CSMD180.5372,792,8754,852,4943,078,351AGno
ENSG0000025984820.53795,533,23195,613,08695,555,581TCno
POU2F3110.536120,107,349120,190,653120,178,753TGno
HLA-DOA60.53632,971,95532,977,38932,973,303TCno
TMPO120.53698,909,29098,944,15798,939,838CAno
MTF210.53693,544,79293,604,63893,570,368GAno
SLC16A1060.535111,408,781111,552,397111,489,059GTno
ENSG0000025000350.53538,025,79938,184,03438,046,354GAno
ENSG0000022598170.5341,499,5731,503,6441,502,497CTno
LRRK2120.5344,059,054640,763,08740,707,861CTno
TRAPPC1350.53364,920,54364,962,06064,952,500CTno
METTL1310.533171,750,788171,783,163171,772,453TGno
ENSG00000259675150.53361,931,54862,007,37062,005,917CAno
AIRE210.53245,705,72145,718,53145,708,277CTno
ENSG0000027230530.53253,003,13553,133,46953,087,621AGno
C6orf1060.53132,256,30332,339,68432,303,848GAno
HLA-DQA260.53032,709,11932,714,99232,712,666CTno
XPO120.53061,704,98461,765,76161,763,170CTno
HLA-DQB160.52932,627,24432,636,16032,634,646TCno
LRRK2120.52940,579,81140,617,60540,607,566GAno
ENSG00000225342120.52940,590,54640,763,08740,607,566GAno
C1orf16710.52911,821,84411,849,64211,827,776AGno
ENSG0000024998840.52814,166,07914,244,43714,167,196AGno
LAMA260.528129,204,342129,837,714129,537,858GAno
SOX6110.52815,987,99516,761,13816,158,420GAno
CCDC6950.527150,560,613150,603,706150,566,196CTno
ENSG0000022334330.52749,022,48249,027,42149,025,101ACno
MAP4K420.527102,313,312102,511,149102,468,624AGno
KLHL770.52623,145,35323,217,53323,208,043GAno
ENSG0000025319460.526119,255,950119,352,706119,322,992CTno
FAM184A60.526119,280,928119,470,552119,322,992CTno
QRICH130.52549,067,14049,131,79649,083,566GAno
SYT17160.52519,179,29319,279,65219,279,380TCno
CCDC62120.524123,258,874123,312,075123,296,204GAno
SHC4150.52449,115,93249,255,64149,174,661CTno
PNKD20.523219,135,115219,211,516219,142,491CTno
TMBIM120.523219,138,915219,157,309219,142,491CTno
DIP2C100.523320,130735,683570,172TCno
SCCPDH10.523246,887,349246,931,439246,893,948CTno
IP6K130.52249,761,72749,823,97549,808,007AGno
FAM167A80.52211,278,97211,332,22411,309,780GAno
ADCY530.521123,001,143123,168,605123,143,272GAno
PCGF340.521699,537764,428701,896AGno
RPRD210.520150,335,567150,449,042150,438,362ACno
CARM1190.52010,982,18911,033,45311,025,817GAno
ENSG0000025124610.519155,036,224155,059,283155,055,863GAno
EFNA310.519155,036,224155,060,014155,055,863GAno
MMS22L60.51997,590,03797,731,09397,662,784GAno
C12orf40120.51940,019,96940,302,10240,042,940CTno
C3orf8430.51849,215,06549,229,29149,220,504ACno
MMRN140.51890,800,68390,875,78090,859,279GAno
RILPL2120.517123,899,936123,921,264123,912,213TCno
CHAT100.51750,817,14150,901,92550,821,191GTno
TMEM161B50.51787,485,45087,565,29387,513,775CTno
BIN380.51722,477,93122,526,66122,525,980TCyes
TRPM4190.51649,660,99849,715,09349,695,007AGno
USP8150.51650,716,57750,793,28050,741,068ACno
BCAR310.51694,027,34794,312,70694,038,847GAno
TNXB60.51632,008,93132,083,11132,062,687GAno
1 HGNC symbol or Ensemble gene ID if there is no HGNC symbol available. 2 Base pair position of start of gene. 3 Base pair position of end of gene. 4 Genomic position of SNP. 5 Major SNP allele. 6 Minor SNP allele. 7 Genome-wide significant in the meta-GWAS by Nalls et al. [2]. HGNC: HUGO Gene Nomenclature Committee, Chr: Chromosome, AUC: area under ROC curve, ROC: receiver operating characteristic, PRS: polygenic risk score, PD: Parkinson’s disease, n.a.: not available.

References

  1. Kalia, L.V.; Lang, A.E. Parkinson’s disease. Lancet 2015, 386, 896–912. [Google Scholar] [CrossRef]
  2. Nalls, M.A.; Blauwendraat, C.; Vallerga, C.L.; Heilbron, K.; Bandres-Ciga, S.; Chang, D.; Tan, M.; Kia, D.A.; Noyce, A.J.; Xue, A.; et al. Identification of novel risk loci, causal insights, and heritable risk for Parkinson’s disease: A meta-analysis of genome-wide association studies. Lancet Neurol. 2019, 18, 1091–1102. [Google Scholar] [CrossRef]
  3. Chang, D.; Nalls, M.A.; Hallgrimsdottir, I.B.; Hunkapiller, J.; van der Brug, M.; Cai, F.; International Parkinson’s Disease Genomics Consortium; 23andMe Research Team; Kerchner, G.A.; Ayalon, G.; et al. A meta-analysis of genome-wide association studies identifies 17 new Parkinson’s disease risk loci. Nat. Genet. 2017, 49, 1511–1516. [Google Scholar] [CrossRef] [PubMed]
  4. Bloem, B.R.; Okun, M.S.; Klein, C. Parkinson’s disease. Lancet 2021, 397, 2284–2303. [Google Scholar] [CrossRef]
  5. Nalls, M.A.; Pankratz, N.; Lill, C.M.; Do, C.B.; Hernandez, D.G.; Saad, M.; DeStefano, A.L.; Kara, E.; Bras, J.; Sharma, M.; et al. Large-scale meta-analysis of genome-wide association data identifies six new risk loci for Parkinson’s disease. Nat. Genet. 2014, 46, 989–993. [Google Scholar] [CrossRef] [PubMed]
  6. Ibanez, L.; Dube, U.; Saef, B.; Budde, J.; Black, K.; Medvedeva, A.; Del-Aguila, J.L.; Davis, A.A.; Perlmutter, J.S.; Harari, O.; et al. Parkinson disease polygenic risk score is associated with Parkinson disease status and age at onset but not with α-synuclein cerebrospinal fluid levels. BMC Neurol. 2017, 17, 198. [Google Scholar] [CrossRef]
  7. Li, W.W.; Fan, D.Y.; Shen, Y.Y.; Zhou, F.Y.; Chen, Y.; Wang, Y.R.; Yang, H.; Mei, J.; Li, L.; Xu, Z.Q.; et al. Association of the polygenic risk score with the incidence risk of Parkinson’s disease and cerebrospinal fluid α-synuclein in a Chinese cohort. Neurotox. Res. 2019, 36, 515–522. [Google Scholar] [CrossRef]
  8. Escott-Price, V.; Sims, R.; Bannister, C.; Harold, D.; Vronskaya, M.; Majounie, E.; Badarinarayan, N.; Morgan, K.; Passmore, P.; Holmes, C.; et al. Common polygenic variation enhances risk prediction for Alzheimer’s disease. Brain 2015, 138, 3673–3684. [Google Scholar] [CrossRef]
  9. Jacobs, B.M.; Belete, D.; Bestwick, J.; Blauwendraat, C.; Bandres-Ciga, S.; Heilbron, K.; Dobson, R.; Nalls, M.A.; Singleton, A.; Hardy, J.; et al. Parkinson’s disease determinants, prediction and gene-environment interactions in the UK Biobank. J. Neurol. Neurosurg. Psychiatry 2020, 91, 1046–1054. [Google Scholar] [CrossRef] [PubMed]
  10. Paul, K.C.; Schulz, J.; Bronstein, J.M.; Lill, C.M.; Ritz, B.R. Association of polygenic risk score with cognitive decline and motor progression in Parkinson disease. JAMA Neurol. 2018, 75, 360–366. [Google Scholar] [CrossRef]
  11. Wald, N.J.; Old, R. The illusion of polygenic disease risk prediction. Genet. Med. 2019. [Google Scholar] [CrossRef] [PubMed]
  12. Caliebe, A.; Heinzel, S.; Schmidtke, J.; Krawczak, M. Genorakel polygene Risikoscores: Möglichkeiten und Grenzen. Dtsch. Arztebl. Int. 2021, 118, A410. [Google Scholar]
  13. Kasten, M.; Hagenah, J.; Graf, J.; Lorwin, A.; Vollstedt, E.J.; Peters, E.; Katalinic, A.; Raspe, H.; Klein, C. Cohort Profile: A population-based cohort to study non-motor symptoms in parkinsonism (EPIPARK). Int. J. Epidemiol. 2013, 42, 128–128k. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  14. Mollenhauer, B.; Trautmann, E.; Sixel-Doring, F.; Wicke, T.; Ebentheuer, J.; Schaumburg, M.; Lang, E.; Focke, N.K.; Kumar, K.R.; Lohmann, K.; et al. Nonmotor and diagnostic findings in subjects with de novo Parkinson disease of the DeNoPa cohort. Neurology 2013, 81, 1226–1234. [Google Scholar] [CrossRef]
  15. Lieb, W.; Jacobs, G.; Wolf, A.; Richter, G.; Gaede, K.I.; Schwarz, J.; Arnold, N.; Bohm, R.; Buyx, A.; Cascorbi, I.; et al. Linking pre-existing biorepositories for medical research: The PopGen 2.0 Network. J. Community Genet. 2019, 10, 523–530. [Google Scholar] [CrossRef] [Green Version]
  16. Krawczak, M.; Nikolaus, S.; von Eberstein, H.; Croucher, P.J.; El Mokhtari, N.E.; Schreiber, S. PopGen: Population-based recruitment of patients and controls for the analysis of complex genotype-phenotype relationships. Community Genet. 2006, 9, 55–61. [Google Scholar] [CrossRef]
  17. Meyer, H. plinkQC: Genotype Quality Control with ‘PLINK’. R Package Version 0.3.4. 2021. Available online: https://cran.r-project.org/web/packages/plinkQC/index.html (accessed on 15 October 2021).
  18. Chang, C.C.; Chow, C.C.; Tellier, L.C.; Vattikuti, S.; Purcell, S.M.; Lee, J.J. Second-generation PLINK: Rising to the challenge of larger and richer datasets. Gigascience 2015, 4, 7. [Google Scholar] [CrossRef]
  19. Wigginton, J.E.; Cutler, D.J.; Abecasis, G.R. A note on exact tests of Hardy-Weinberg equilibrium. Am. J. Hum. Genet. 2005, 76, 887–893. [Google Scholar] [CrossRef] [Green Version]
  20. Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.; Daly, M.J.; et al. PLINK: A tool set for whole-genome association and population-based linkage analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef] [Green Version]
  21. Purcell, S.; Chang, C. PLINK 1.9. Available online: https://www.cog-genomics.org/plink (accessed on 22 November 2021).
  22. Purcell, S.; Chang, C. PLINK 2.0. Available online: https://www.cog-genomics.org/plink/2.0 (accessed on 22 November 2021).
  23. O’Connell, J.; Gurdasani, D.; Delaneau, O.; Pirastu, N.; Ulivi, S.; Cocca, M.; Traglia, M.; Huang, J.; Huffman, J.E.; Rudan, I.; et al. A general approach for haplotype phasing across the full spectrum of relatedness. PLoS Genet. 2014, 10, e1004234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Howie, B.N.; Donnelly, P.; Marchini, J. A flexible and accurate genotype imputation method for the next generation of genome-wide association studies. PLoS Genet. 2009, 5, e1000529. [Google Scholar] [CrossRef] [Green Version]
  25. McCarthy, S.; Das, S.; Kretzschmar, W.; Delaneau, O.; Wood, A.R.; Teumer, A.; Kang, H.M.; Fuchsberger, C.; Danecek, P.; Sharp, K.; et al. A reference panel of 64,976 haplotypes for genotype imputation. Nat. Genet. 2016, 48, 1279–1283. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  26. Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.C.; Muller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef]
  27. Aragon, T. Epitools: Epidemiology Tools. R Package Version 0.5-10.1. 2012. Available online: https://cran.r-project.org/web/packages/epitools/index.html (accessed on 22 November 2021).
  28. Durinck, S.; Moreau, Y.; Kasprzyk, A.; Davis, S.; De Moor, B.; Brazma, A.; Huber, W. BioMart and Bioconductor: A powerful link between biological databases and microarray data analysis. Bioinformatics 2005, 21, 3439–3440. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  29. Durinck, S.; Spellman, P.T.; Birney, E.; Huber, W. Mapping identifiers for the integration of genomic datasets with the R/Bioconductor package biomaRt. Nat. Protoc. 2009, 4, 1184–1191. [Google Scholar] [CrossRef] [Green Version]
  30. Howe, K.L.; Achuthan, P.; Allen, J.; Allen, J.; Alvarez-Jarreta, J.; Amode, M.R.; Armean, I.M.; Azov, A.G.; Bennett, R.; Bhai, J.; et al. Ensembl 2021. Nucleic Acids Res. 2021, 49, D884–D891. [Google Scholar] [CrossRef]
  31. Sherry, S.T.; Ward, M.H.; Kholodov, M.; Baker, J.; Phan, L.; Smigielski, E.M.; Sirotkin, K. dbSNP: The NCBI database of genetic variation. Nucleic Acids Res. 2001, 29, 308–311. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  32. Nerius, M.; Fink, A.; Doblhammer, G. Parkinson’s disease in Germany: Prevalence and incidence based on health claims data. Acta Neurol. Scand. 2017, 136, 386–392. [Google Scholar] [CrossRef]
  33. Hoffmann, S.; Schonbrodt, F.; Elsas, R.; Wilson, R.; Strasser, U.; Boulesteix, A.L. The multiplicity of analysis strategies jeopardizes replicability: Lessons learned across disciplines. R. Soc. Open Sci. 2021, 8, 201925. [Google Scholar] [CrossRef]
  34. Baker, M. 1500 scientists lift the lid on reproducibility. Nature 2016, 533, 452–454. [Google Scholar] [CrossRef] [Green Version]
  35. Loken, E.; Gelman, A. Measurement error and the replication crisis. Science 2017, 355, 584–585. [Google Scholar] [CrossRef] [PubMed]
  36. Janssens, A. Validity of polygenic risk scores: Are we measuring what we think we are? Hum. Mol. Genet. 2019, 28, R143–R150. [Google Scholar] [CrossRef]
  37. Fullerton, J.M.; Nurnberger, J.I. Polygenic risk scores in psychiatry: Will they be useful for clinicians? F1000Research 2019, 8. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  38. Martin, A.R.; Kanai, M.; Kamatani, Y.; Okada, Y.; Neale, B.M.; Daly, M.J. Clinical use of current polygenic risk scores may exacerbate health disparities. Nat. Genet. 2019, 51, 584–591. [Google Scholar] [CrossRef]
  39. Altenbuchinger, M.; Weihs, A.; Quackenbush, J.; Grabe, H.J.; Zacharias, H.U. Gaussian and Mixed Graphical Models as (multi-)omics data analysis tools. Biochim. Biophys. Acta Gene Regul. Mech. 2020, 1863, 194418. [Google Scholar] [CrossRef]
  40. Elliott, J.; Bodinier, B.; Bond, T.A.; Chadeau-Hyam, M.; Evangelou, E.; Moons, K.G.M.; Dehghan, A.; Muller, D.C.; Elliott, P.; Tzoulaki, I. Predictive accuracy of a polygenic risk score-enhanced prediction model vs a clinical risk score for coronary artery disease. JAMA 2020, 323, 636–645. [Google Scholar] [CrossRef]
  41. Landi, I.; Kaji, D.A.; Cotter, L.; Van Vleck, T.; Belbin, G.; Preuss, M.; Loos, R.J.F.; Kenny, E.; Glicksberg, B.S.; Beckmann, N.D.; et al. Prognostic value of polygenic risk scores for adults with psychosis. Nat. Med. 2021, 27, 1576–1581. [Google Scholar] [CrossRef]
  42. Yanes, T.; Young, M.A.; Meiser, B.; James, P.A. Clinical applications of polygenic breast cancer risk: A critical review and perspectives of an emerging field. Breast Cancer Res. 2020, 22, 21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  43. Heinzel, S.; Berg, D.; Gasser, T.; Chen, H.; Yao, C.; Postuma, R.B.; Disease, M.D.S.T.F.o.t.D.o.P.s. Update of the MDS research criteria for prodromal Parkinson’s disease. Mov. Disord. 2019, 34, 1464–1470. [Google Scholar] [CrossRef]
  44. Pebesma, E.; Bivand, R. Classes and Methods for Spatial Data in R. R. News 2005, 5, 9–13. [Google Scholar]
  45. Bivand, R.; Pebesma, E.; Gómez Rubio, V. Applied Spatial Data Analysis With R; Springer: New York, NY, USA, 2013. [Google Scholar]
  46. Bivand, R.; Rundel, C. Rgeos: Interface to Geometry Engine-Open Source (GEOS). R Package Version 0.5-8. 2021. Available online: https://cran.r-project.org/web/packages/rgeos/index.html (accessed on 22 November 2021).
  47. Prive, F.; Luu, K.; Blum, M.G.B.; McGrath, J.J.; Vilhjalmsson, B.J. Efficient toolkit implementing best practices for principal component analysis of population genetic data. Bioinformatics 2020, 36, 4449–4457. [Google Scholar] [CrossRef] [PubMed]
  48. Prive, F.; Aschard, H.; Ziyatdinov, A.; Blum, M.G.B. Efficient analysis of large-scale genome-wide data with two R packages: Bigstatsr and bigsnpr. Bioinformatics 2018, 34, 2781–2787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  49. Privé, F. Bigparallelr: Easy Parallel Tools. R Package Version 0.3.1. 2021. Available online: https://rdrr.io/cran/bigparallelr/man/bigparallelr-package.html (accessed on 22 November 2021).
Genes 12 01859 g001 550
Figure 1. PD-PRS in PD cases and controls. (A) Density of PD-PRS in cases and controls. (B) ROC curve for PD-PRS as a predictor of case-control status. PRS: polygenic risk score, PD: Parkinson’s disease, ROC: receiver operating characteristic.
Figure 1. PD-PRS in PD cases and controls. (A) Density of PD-PRS in cases and controls. (B) ROC curve for PD-PRS as a predictor of case-control status. PRS: polygenic risk score, PD: Parkinson’s disease, ROC: receiver operating characteristic.
Genes 12 01859 g001
Genes 12 01859 g002 550
Figure 2. Disease OR for the 2nd to 10th deciles of the PD-PRS distribution among controls. (1st decile used as reference). Vertical bars demarcate 95% confidence intervals. OR: odds ratio, PD: Parkinson’s disease, PRS: polygenic risk score.
Figure 2. Disease OR for the 2nd to 10th deciles of the PD-PRS distribution among controls. (1st decile used as reference). Vertical bars demarcate 95% confidence intervals. OR: odds ratio, PD: Parkinson’s disease, PRS: polygenic risk score.
Genes 12 01859 g002
Genes 12 01859 g003 550
Figure 3. PD-PRS in early and late onset cases. (A) Density of PD-PRS in the 1st and 4th AAO quartile of cases. (B) ROC curve for PD-PRS as a predictor of 1st vs 4th AAO quartile. AAO: age-at-onset, PRS: polygenic risk score, PD: Parkinson’s disease, ROC: receiver operating characteristic.
Figure 3. PD-PRS in early and late onset cases. (A) Density of PD-PRS in the 1st and 4th AAO quartile of cases. (B) ROC curve for PD-PRS as a predictor of 1st vs 4th AAO quartile. AAO: age-at-onset, PRS: polygenic risk score, PD: Parkinson’s disease, ROC: receiver operating characteristic.
Genes 12 01859 g003
Genes 12 01859 g004 550
Figure 4. Influence of individual SNPs upon PD-PRS performance. For each of the 1743 PD-PRS SNPs, the AUC was calculated after removing the SNP from the PRS. SNPs were color-coded as either genome-wide significant in a meta-GWAS [2] (blue), as ‘most relevant’ in the present study (red), both of the former (black) or none of the former (yellow). SNP: single nucleotide polymorphism, PD: Parkinson’s disease, PRS: polygenic risk score, AUC: area under ROC curve, ROC: receiver operating characteristic, GWAS: genome-wide association study.
Figure 4. Influence of individual SNPs upon PD-PRS performance. For each of the 1743 PD-PRS SNPs, the AUC was calculated after removing the SNP from the PRS. SNPs were color-coded as either genome-wide significant in a meta-GWAS [2] (blue), as ‘most relevant’ in the present study (red), both of the former (black) or none of the former (yellow). SNP: single nucleotide polymorphism, PD: Parkinson’s disease, PRS: polygenic risk score, AUC: area under ROC curve, ROC: receiver operating characteristic, GWAS: genome-wide association study.
Genes 12 01859 g004
Genes 12 01859 g005 550
Figure 5. Prognostic value of PD-PRS. (A) Sensitivity and specificity of PD-PRS for the optimal threshold were determined by maximizing a weighted Youden index. The relative costs of false negative vs false positive results varied from 1 to 5. (B) ppv and npv were calculated from the costs-based sensitivity and specificity and the residual lifetime incidence (see Methods and Table A3) in 10 age groups. PRS: polygenic risk score, PD: Parkinson’s disease, ppv: positive predictive value, npv: negative predictive value.
Figure 5. Prognostic value of PD-PRS. (A) Sensitivity and specificity of PD-PRS for the optimal threshold were determined by maximizing a weighted Youden index. The relative costs of false negative vs false positive results varied from 1 to 5. (B) ppv and npv were calculated from the costs-based sensitivity and specificity and the residual lifetime incidence (see Methods and Table A3) in 10 age groups. PRS: polygenic risk score, PD: Parkinson’s disease, ppv: positive predictive value, npv: negative predictive value.
Genes 12 01859 g005
Table
Table 1. Comparative validation of PD-PRS.
Table 1. Comparative validation of PD-PRS.
Data SetSamples
(N)		SNPs
(N)		AUC
[95% CI]		Nagelkerke’s
Pseudo-R2 a		p Value bNagelkerke’s
Pseudo-R2 c
This study
(case/control)		637817430.645 [0.630, 0.660]0.348<10−50.298
Nalls training d
(case/control)		11,24318090.640 [0.630, 0.650]n.a.<10−5n.a.
Nalls validation e
(case/control)		99918050.692 [0.660, 0.725]n.a.<10−5n.a.
This study
(AAO) f		83617430.590 [0.551, 0.629]0.0391.6 × 10−50.009
a From logistic regression analysis of PD case-control status (first line) and AAO 1st vs 4th quartile (fourth line), each time including PD-PRS, sex, age (only for the analysis of case-control status) and the first three PCs as independent variables. Nalls et al. [2] used a different approach to evaluate logistic regression models, hence a comparison of pseudo-R2 is not meaningful. b p value for PD-PRS as an independent variable in the logistic regression analysis (Wald test). c Same logistic regression model as before, but without PD-PRS as an independent variable. d NeuroX-dbGaP data set (5851 cases, 5866 controls). e Harvard Biomarker Study (527 cases, 472 controls). f Samples belonging to the 1st and 4th AAO quartile among cases analyzed in this study. PD: Parkinson’s disease, PRS: polygenic risk score, SNP: single nucleotide polymorphism, AUC: area under ROC curve, CI: confidence interval, AAO: age-at-onset, ROC: receiver operating characteristic, n.a.: not available.
Table
Table 2. Top 20 most relevant SNPs located within genes.
Table 2. Top 20 most relevant SNPs located within genes.
HGNC Symbol 1ChrAUCStart 2End 3SNP Position 4A1 5A2 6GS 7SNP Type
ENSG0000025109540.64390,472,50790,647,65490,626,111GAyesintron
SNCA40.64190,645,25090,759,46690,684,278AGnointron
HIP1R120.640123,319,000123,347,507123,326,598GTyesintron
TMEM17540.639926,175952,444951,947TCyesmissense
SNCA40.63890,645,25090,759,46690,757,294ACnointron
ASH1L10.637155,305,059155,532,598155,437,711GAnointron
UBQLN410.634156,005,092156,023,585156,007,988GAnointron
ENSG00000225342120.63340,579,81140,617,60540,614,434CTyesn.a.
LRRK2120.63340,590,54640,763,08740,614,434CTyesn.a.
STX1B160.63231,000,57731,021,94931,004,169TCnosynonymous
INPP5F100.631121,485,609121,588,652121,536,327GAyesintron
CCSER140.63191,048,68692,523,06491,164,040CTnointron
SLC2A13120.63040,148,82340,499,89140,388,109CTnointron
FBXL19160.63030,934,37630,960,10430,943,096AGnointron
ENSG0000025109540.62990,472,50790,647,65490,619,032CTnointron
CAB39L130.62949,882,78650,018,26249,927,732TCyesintron
STK3920.628168,810,530169,104,651168,979,290CTnointron
CCT310.628156,278,759156,337,664156,300,731TCnointron
ENSG00000225342120.62740,579,81140,617,60540,614,656AGnon.a.
LRRK2120.62740,590,54640,763,08740,614,656AGnon.a.
1 HGNC symbol or Ensemble gene ID if there is no HGNC symbol available. 2 Base pair position of start of gene. 3 Base pair position of end of gene. 4 Genomic position of SNP. 5 Major SNP allele. 6 Minor SNP allele. 7 Genome-wide significant (GS) in the meta-GWAS by Nalls et al. [2]. HGNC: HUGO Gene Nomenclature Committee, Chr: Chromosome, AUC: area under ROC curve, ROC: receiver operating characteristic, PRS: polygenic risk score, PD: Parkinson’s disease, n.a.: not available.
Table
Table 3. Prognostic value of PD-PRS.
Table 3. Prognostic value of PD-PRS.
Costs
12345
Sensitivity
[95% CI]		0.581
[0.479, 0.733]		0.921
[0.880, 0.981]		0.981
[0.973, 1]		0.999
[0.983, 1]		1
[0.996, 1]
Specificity
[95% CI]		0.625
[0.472, 0.725]		0.198
[0.075, 0.289]		0.067
[0.004, 0.096]		0.006
[0.002, 0.082]		0.003
[0.002, 0.034]
Threshold 10.330−0.868−1.507−2.533−2.667
1 Optimal threshold for PD-PRS as determined by maximizing a weighed Youden index. PD: Parkinson’s disease, PRS: polygenic risk score, CI: confidence interval.
Table
Table 4. Costs- and age-dependent PD-PRS predictive values.
Table 4. Costs- and age-dependent PD-PRS predictive values.
Costs
12345
ppvnpvppvnpvppvnpvppvnpvppvnpv
Age group (Years)50–540.0260.9880.0200.9930.0180.9950.0170.9980.0171
55–590.0270.9880.0200.9930.0180.9950.0180.9980.0181
60–640.0270.9880.0200.9930.0190.9950.0180.9980.0181
65–690.0270.9880.0210.9930.0190.9950.0180.9980.0181
70–740.0270.9880.0200.9930.0190.9950.0180.9980.0181
75–790.0250.9890.0190.9930.0170.9950.0170.9990.0161
80–840.0220.9900.0160.9940.0150.9960.0140.9990.0141
85–890.0170.9930.0120.9960.0110.9970.0110.9990.0111
90–940.0110.9950.0080.9970.0080.9980.0070.9990.0071
95+0.0080.9960.0060.9980.0050.9990.0051.0000.0051
PRS: polygenic risk score, PD: Parkinson’s disease, ppv: positive predictive value, npv: negative predictive value.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Koch, S.; Laabs, B.-H.; Kasten, M.; Vollstedt, E.-J.; Becktepe, J.; Brüggemann, N.; Franke, A.; Krämer, U.M.; Kuhlenbäumer, G.; Lieb, W.; et al. Validity and Prognostic Value of a Polygenic Risk Score for Parkinson’s Disease. Genes 2021, 12, 1859. https://doi.org/10.3390/genes12121859

AMA Style

Koch S, Laabs B-H, Kasten M, Vollstedt E-J, Becktepe J, Brüggemann N, Franke A, Krämer UM, Kuhlenbäumer G, Lieb W, et al. Validity and Prognostic Value of a Polygenic Risk Score for Parkinson’s Disease. Genes. 2021; 12(12):1859. https://doi.org/10.3390/genes12121859

Chicago/Turabian Style

Koch, Sebastian, Björn-Hergen Laabs, Meike Kasten, Eva-Juliane Vollstedt, Jos Becktepe, Norbert Brüggemann, Andre Franke, Ulrike M. Krämer, Gregor Kuhlenbäumer, Wolfgang Lieb, and et al. 2021. "Validity and Prognostic Value of a Polygenic Risk Score for Parkinson’s Disease" Genes 12, no. 12: 1859. https://doi.org/10.3390/genes12121859

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop