Evolution of Codon Usage Bias in Diatoms
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Codon Usage Analysis
2.3. Analysis of Divergence within Genera
2.4. Species Delimitation
2.5. Estimation of the Strength of Selection for Optimal Codons
3. Results
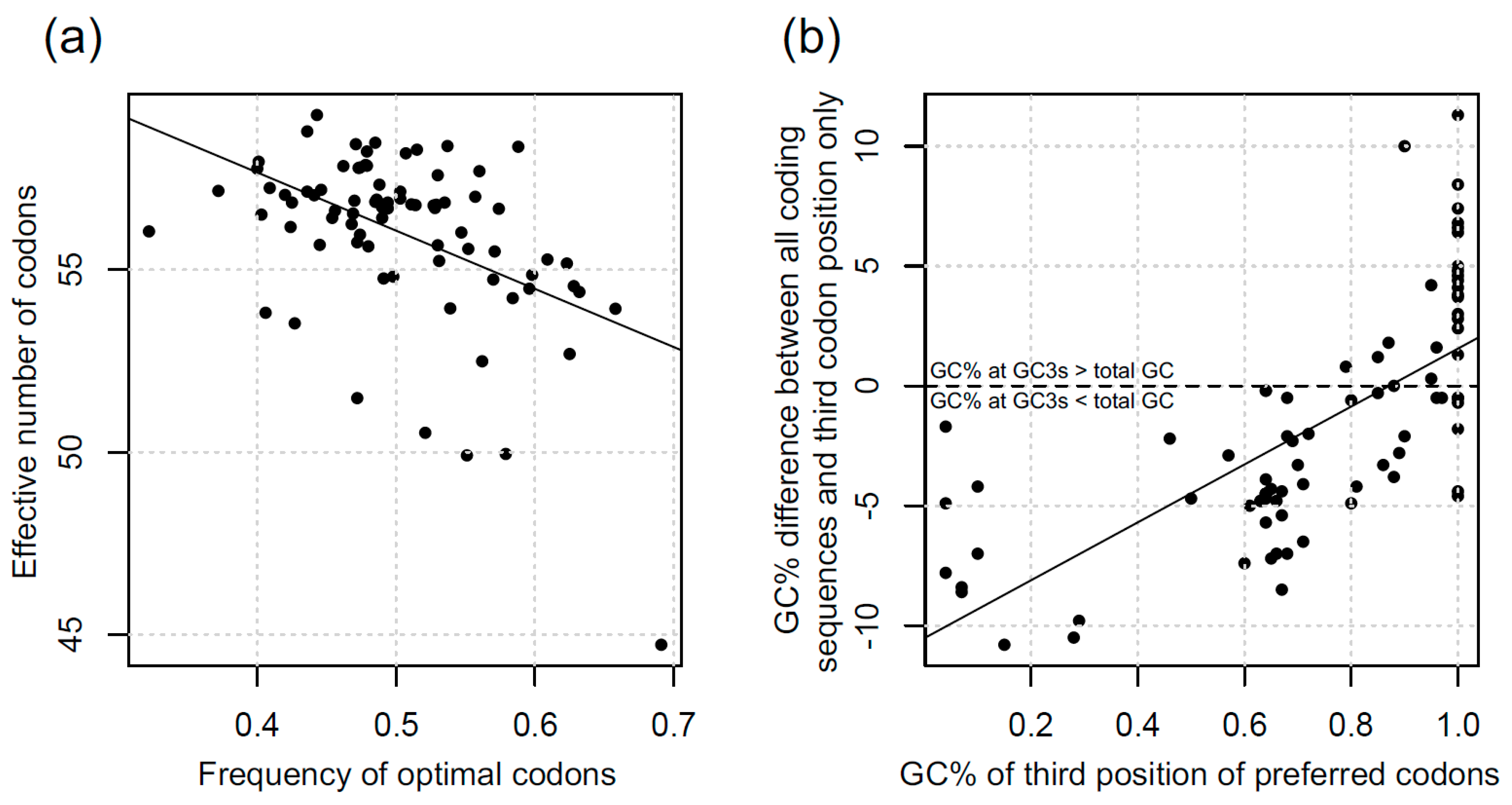
3.1. Codon Bias in Diatoms
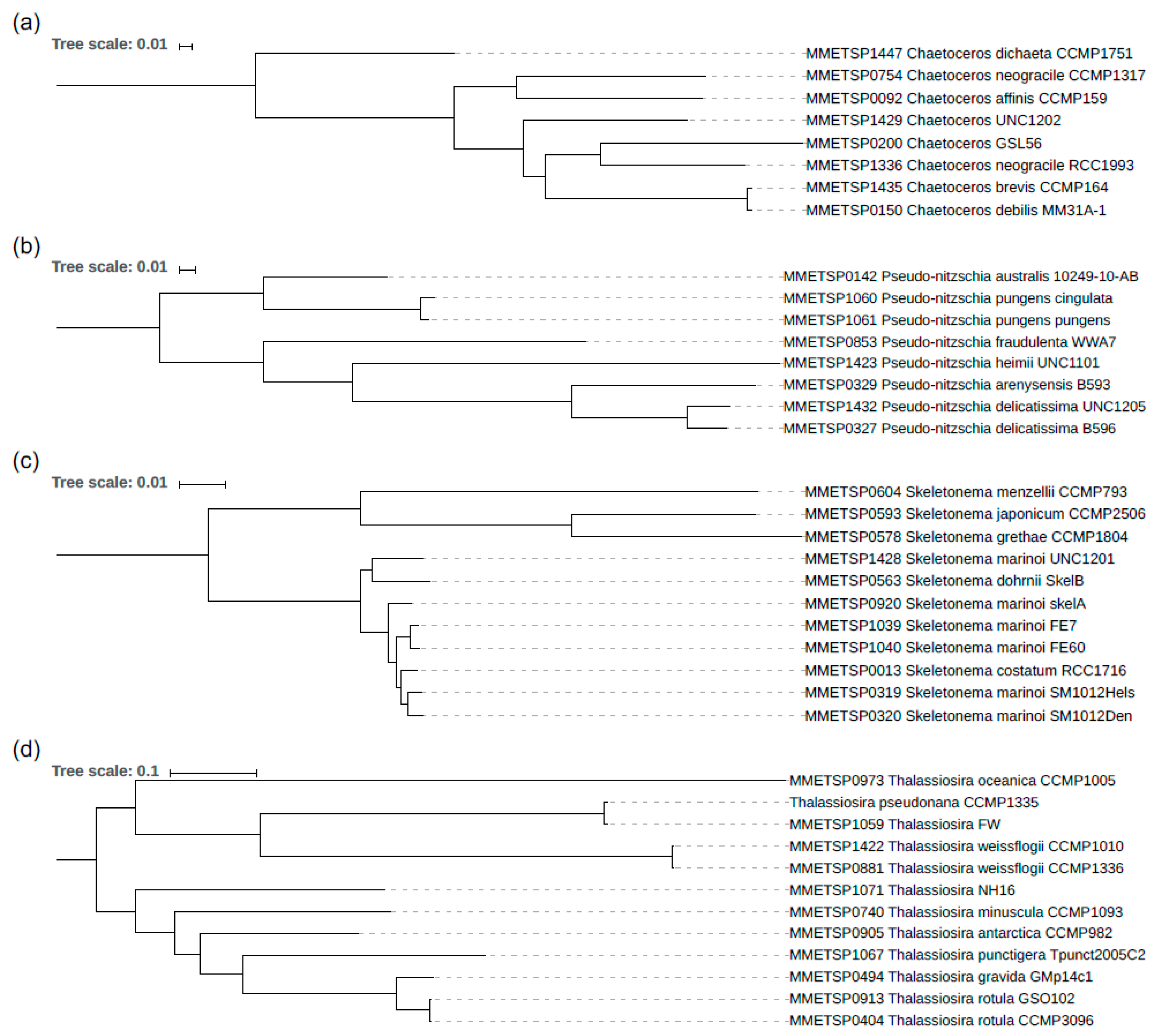
3.2. The Phylogeny of the Diatom Species Analysed
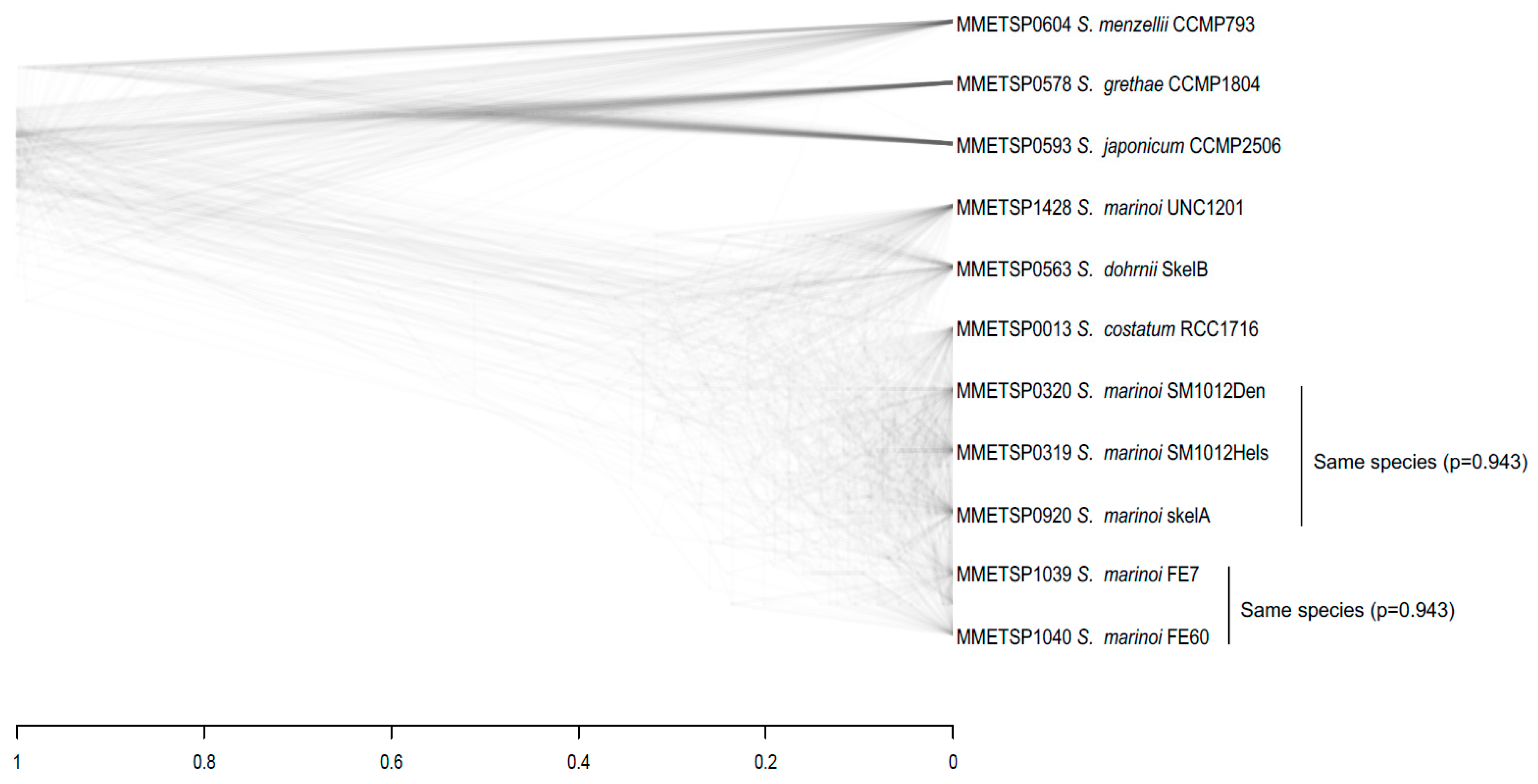
3.3. Species Assignments and Delimitations for the Diatom Strains Analysed
3.4. Effective Population Size in Marine Plankton Species
3.5. Estimating the Strength of Selection for Optimal Codons in Diatoms
3.6. Evolution of Codon Bias within Diatom Genera
4. Discussion
4.1. Variation in CUB in Diatoms
4.2. What are the Causes of CUB Variation in Diatoms?
4.3. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Hershberg, R.; Petrov, D.A. Selection on Codon Bias. Annu. Rev. Genet. 2008, 42, 287–299. [Google Scholar] [CrossRef] [PubMed]
- Bulmer, M. The selection-mutation-drift theory of synonymous codon usage. Genetics 1991, 129, 897–907. [Google Scholar] [PubMed]
- Gouy, M.; Gautier, C. Codon usage in bacteria: Correlation with gene expressivity. Nucleic Acids Res. 1982, 10, 7055–7074. [Google Scholar] [CrossRef] [PubMed]
- Shields, D.C.; Sharp, P.M.; Higgins, D.G.; Wright, F. “Silent” sites in Drosophila genes are not neutral: Evidence of selection among synonymous codons. Mol. Biol. Evol. 1988, 5, 704–716. [Google Scholar] [PubMed]
- Akashi, H. Synonymous codon usage in Drosophila melanogaster: Natural selection and translational accuracy. Genetics 1994, 136, 927–935. [Google Scholar]
- Stoletzki, N.; Eyre-Walker, A. Synonymous codon usage in Escherichia coli: Selection for translational accuracy. Mol. Biol. Evol. 2007, 24, 374–381. [Google Scholar] [CrossRef]
- Drummond, D.A.; Wilke, C.O. Mistranslation-induced protein misfolding as a dominant constraint on coding-sequence evolution. Cell 2008, 134, 341–352. [Google Scholar] [CrossRef]
- Sørensen, M.A.; Pedersen, S. Absolute in vivo translation rates of individual codons in Escherichia coli. The two glutamic acid codons GAA and GAG are translated with a threefold difference in rate. J. Mol. Biol. 1991, 222, 265–280. [Google Scholar] [CrossRef]
- Ehrenberg, M.; Kurland, C.G. Costs of accuracy determined by a maximal growth rate constraint. Q. Rev. Biophys. 1984, 17, 45–82. [Google Scholar] [CrossRef]
- Sharp, P.M.; Bailes, E.; Grocock, R.J.; Peden, J.F.; Sockett, R.E. Variation in the strength of selected codon usage bias among bacteria. Nucleic Acids Res. 2005, 33, 1141–1153. [Google Scholar] [CrossRef]
- Ikemura, T. Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes: A proposal for a synonymous codon choice that is optimal for the E. coli translational system. J. Mol. Biol. 1981, 151, 389–409. [Google Scholar] [CrossRef]
- Sharp, P.M.; Cowe, E.; Higgins, D.G.; Shields, D.C.; Wolfe, K.H.; Wright, F. Codon usage patterns in Escherichia coli, Bacillus subtilis, Saccharomyces cerevisiae, Schizosaccharomyces pombe, Drosophila melanogaster and Homo sapiens; a review of the considerable within-species diversity. Nucleic Acids Res. 1988, 16, 8207–8211. [Google Scholar] [CrossRef] [PubMed]
- Vicario, S.; Moriyama, E.N.; Powell, J.R. Codon usage in twelve species of Drosophila. BMC Evol. Biol. 2007, 7, 226. [Google Scholar] [CrossRef] [PubMed]
- Krasovec, M.; Eyre-Walker, A.; Sanchez-Ferandin, S.; Piganeau, G. Spontaneous Mutation Rate in the Smallest Photosynthetic Eukaryotes. Mol. Biol. Evol. 2017, 34, 1770–1779. [Google Scholar] [CrossRef] [PubMed]
- Katju, V.; Bergthorsson, U. Old Trade, New Tricks: Insights into the Spontaneous Mutation Process from the Partnering of Classical Mutation Accumulation Experiments with High-Throughput Genomic Approaches. Genome Biol. Evol. 2019, 11, 136–165. [Google Scholar] [CrossRef] [PubMed]
- Ossowski, S.; Schneeberger, K.; Lucas-Lledó, J.I.; Warthmann, N.; Clark, R.M.; Shaw, R.G.; Weigel, D.; Lynch, M. The rate and molecular spectrum of spontaneous mutations in Arabidopsis thaliana. Science 2010, 327, 92–94. [Google Scholar] [CrossRef]
- Denver, D.R.; Dolan, P.C.; Wilhelm, L.J.; Sung, W.; Lucas-Lledó, J.I.; Howe, D.K.; Lewis, S.C.; Okamoto, K.; Thomas, W.K.; Lynch, M.; et al. A genome-wide view of Caenorhabditis elegans base-substitution mutation processes. Proc. Natl. Acad. Sci. USA 2009, 106, 16310–16314. [Google Scholar] [CrossRef]
- Lynch, M.; Sung, W.; Morris, K.; Coffey, N.; Landry, C.R.; Dopman, E.B.; Dickinson, W.J.; Okamoto, K.; Kulkarni, S.; Hartl, D.L.; et al. A genome-wide view of the spectrum of spontaneous mutations in yeast. PNAS 2008, 105, 9272–9277. [Google Scholar] [CrossRef]
- Duret, L. Evolution of synonymous codon usage in metazoans. Curr. Opin. Genet. Dev. 2002, 12, 640–649. [Google Scholar] [CrossRef]
- Yang, Z.; Nielsen, R. Mutation-selection models of codon substitution and their use to estimate selective strengths on codon usage. Mol. Biol. Evol. 2008, 25, 568–579. [Google Scholar] [CrossRef]
- De, S.P.; Zeng, K.; Betancourt, A.J.; Charlesworth, B. Selection on codon usage and base composition in Drosophila americana. Biol. Lett. 2012, 8, 82–85. [Google Scholar]
- de Vargas, C.; Audic, S.; Henry, N.; Decelle, J.; Mahé, F.; Logares, R.; Lara, E.; Berney, C.; Le Bescot, N.; Probert, I.; et al. Ocean plankton. Eukaryotic plankton diversity in the sunlit ocean. Science 2015, 348, 1261605. [Google Scholar] [CrossRef] [PubMed]
- Malviya, S.; Scalco, E.; Audic, S.; Vincent, F.; Veluchamy, A.; Poulain, J.; Wincker, P.; Iudicone, D.; de Vargas, C.; Bittner, L.; et al. Insights into global diatom distribution and diversity in the world’s ocean. PNAS 2016, 113, E1516–E1525. [Google Scholar] [CrossRef]
- Bowler, C.; Vardi, A.; Allen, A.E. Oceanographic and biogeochemical insights from diatom genomes. Ann. Rev. Mar. Sci. 2010, 2, 333–365. [Google Scholar] [CrossRef] [PubMed]
- Bowler, C.; Allen, A.E.; Badger, J.H.; Grimwood, J.; Jabbari, K.; Kuo, A.; Maheswari, U.; Martens, C.; Maumus, F.; Otillar, R.P.; et al. The Phaeodactylum genome reveals the evolutionary history of diatom genomes. Nature 2008, 456, 239–244. [Google Scholar] [CrossRef]
- Armbrust, E.V.; Berges, J.A.; Bowler, C.; Green, B.R.; Martinez, D.; Putnam, N.H.; Zhou, S.; Allen, A.E.; Apt, K.E.; Bechner, M.; et al. The Genome of the Diatom Thalassiosira Pseudonana: Ecology, Evolution, and Metabolism. Science 2004, 306, 79–86. [Google Scholar] [CrossRef]
- Keeling, P.J.; Burki, F.; Wilcox, H.M.; Allam, B.; Allen, E.E.; Amaral-Zettler, L.A.; Armbrust, E.V.; Archibald, J.M.; Bharti, A.K.; Bell, C.J.; et al. The Marine Microbial Eukaryote Transcriptome Sequencing Project (MMETSP): Illuminating the Functional Diversity of Eukaryotic Life in the Oceans through Transcriptome Sequencing. PLOS Biol. 2014, 12, e1001889. [Google Scholar] [CrossRef]
- Huang, R.; Ding, J.; Gao, K.; Cruz de Carvalho, M.H.; Tirichine, L.; Bowler, C.; Lin, X. A Potential Role for Epigenetic Processes in the Acclimation Response to Elevated pCO2 in the Model Diatom Phaeodactylum tricornutum. Front. Microbiol. 2019, 9. [Google Scholar] [CrossRef]
- Li, B.; Dewey, C.N. RSEM: Accurate transcript quantification from RNA-Seq data with or without a reference genome. BMC Bioinform. 2011, 12, 323. [Google Scholar] [CrossRef]
- The R Project for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 2 July 2018).
- Emms, D.M.; Kelly, S. OrthoFinder: Solving fundamental biases in whole genome comparisons dramatically improves orthogroup inference accuracy. Genome Biol. 2015, 16, 157. [Google Scholar] [CrossRef]
- Löytynoja, A. Phylogeny-aware alignment with PRANK. Methods Mol. Biol. 2014, 1079, 155–170. [Google Scholar] [PubMed]
- Korber-Irrgang, B. HIV Signature and Sequence Variation Analysis. Comput. Anal. HIV Mol. Seq. 2000, 4, 55–72. [Google Scholar]
- Dutheil, J.; Boussau, B. Non-homogeneous models of sequence evolution in the Bio++ suite of libraries and programs. BMC Evol. Biol. 2008, 8, 255. [Google Scholar] [CrossRef] [PubMed]
- Stamatakis, A. RAxML-VI-HPC: Maximum likelihood-based phylogenetic analyses with thousands of taxa and mixed models. Bioinformatics 2006, 22, 2688–2690. [Google Scholar] [CrossRef]
- Emms, D.M.; Kelly, S. STAG: Species Tree Inference from All Genes. BioRxiv 2018, 267914. [Google Scholar]
- Emms, D.M.; Kelly, S. STRIDE: Species Tree Root Inference from Gene Duplication Events. Mol. Biol. Evol. 2017, 34, 3267–3278. [Google Scholar] [CrossRef]
- Katoh, K.; Standley, D.M. MAFFT multiple sequence alignment software version 7: Improvements in performance and usability. Mol. Biol. Evol. 2013, 30, 772–780. [Google Scholar] [CrossRef]
- Nguyen, L.-T.; Schmidt, H.A.; von Haeseler, A.; Minh, B.Q. IQ-TREE: A Fast and Effective Stochastic Algorithm for Estimating Maximum-Likelihood Phylogenies. Mol. Biol. Evol. 2015, 32, 268–274. [Google Scholar] [CrossRef]
- Flouri, T.; Jiao, X.; Rannala, B.; Yang, Z. Species Tree Inference with BPP Using Genomic Sequences and the Multispecies Coalescent. Mol. Biol. Evol. 2018, 35, 2585–2593. [Google Scholar] [CrossRef]
- Yang, Z. The BPP program for species tree estimation and species delimitation. Curr. Zool. 2015, 61, 854–865. [Google Scholar] [CrossRef]
- Krasovec, M.; Sanchez-Brosseau, S.; Piganeau, G. First Estimation of the Spontaneous Mutation Rate in Diatoms. Genome Biol. Evol. 2019, 11, 1829–1837. [Google Scholar] [CrossRef] [PubMed]
- Wright, F. The “effective number of codons” used in a gene. Gene 1990, 87, 23–29. [Google Scholar] [CrossRef]
- Alverson, A.J.; Beszteri, B.; Julius, M.L.; Theriot, E.C. The model marine diatom Thalassiosira pseudonana likely descended from a freshwater ancestor in the genus Cyclotella. BMC Evol. Biol. 2011, 11, 125. [Google Scholar] [CrossRef] [PubMed]
- Alverson, A.J. Timing marine–freshwater transitions in the diatom order Thalassiosirales. Paleobiology 2014, 40, 91–101. [Google Scholar] [CrossRef]
- Filatov, D.A. Extreme Lewontin’s Paradox in Ubiquitous Marine Phytoplankton Species. Mol. Biol. Evol. 2019, 36, 4–14. [Google Scholar] [CrossRef] [PubMed]
- Blanc-Mathieu, R.; Krasovec, M.; Hebrard, M.; Yau, S.; Desgranges, E.; Martin, J.; Schackwitz, W.; Kuo, A.; Salin, G.; Donnadieu, C.; et al. Population genomics of picophytoplankton unveils novel chromosome hypervariability. Sci. Adv. 2017, 3, e1700239. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, R.; Bauer DuMont, V.L.; Hubisz, M.J.; Aquadro, C.F. Maximum likelihood estimation of ancestral codon usage bias parameters in Drosophila. Mol. Biol. Evol. 2007, 24, 228–235. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zaslavskaia, L.A.; Lippmeier, J.C.; Kroth, P.G.; Grossman, A.R.; Apt, K.E. Transformation of the diatom Phaeodactylum tricornutum (Bacillariophyceae) with a variety of selectable marker and reporter genes. J. Phycol. 2000, 36, 379–386. [Google Scholar] [CrossRef]
- Sims, P.A.; Mann, D.G.; Medlin, L. Evolution of the diatoms: Insights from fossil, biological and molecular data. Phycologia 2006, 45, 361–402. [Google Scholar] [CrossRef]
- Makałowski, W.; Boguski, M.S. Evolutionary parameters of the transcribed mammalian genome: An analysis of 2,820 orthologous rodent and human sequences. PNAS 1998, 95, 9407–9412. [Google Scholar] [CrossRef]
- Eyre-Walker, A. The genomic rate of adaptive evolution. Trends Ecol. Evol. (Amst.) 2006, 21, 569–575. [Google Scholar] [CrossRef] [PubMed]
- Gladenkov, A.Y. First finds of Eocene diatoms in the marine Paleogene reference section in the Il’pinskii Peninsula, northeastern Kamchatka. Stratigr. Geol. Correl. 2013, 21, 96–106. [Google Scholar] [CrossRef]
- Suto, I. The explosive diversification of the diatom genus Chaetoceros across the Eocene/Oligocene and Oligocene/Miocene boundaries in the Norwegian Sea. Mar. Micropaleontol. 2006, 58, 259–269. [Google Scholar] [CrossRef]
- Bendif, E.M.; Nevado, B.; Wong, E.L.Y.; Hagino, K.; Probert, I.; Young, J.R.; Rickaby, R.E.M.; Filatov, D.A. Repeated species radiations in the recent evolution of the key marine phytoplankton lineage Gephyrocapsa. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Finkel, Z.V.; Katz, M.E.; Wright, J.D.; Schofield, O.M.E.; Falkowski, P.G. Climatically driven macroevolutionary patterns in the size of marine diatoms over the Cenozoic. Proc. Natl. Acad. Sci. USA 2005, 102, 8927–8932. [Google Scholar] [CrossRef]
- Finkel, Z.V.; Sebbo, J.; Feist-Burkhardt, S.; Irwin, A.J.; Katz, M.E.; Schofield, O.M.E.; Young, J.R.; Falkowski, P.G. A universal driver of macroevolutionary change in the size of marine phytoplankton over the Cenozoic. Proc. Natl. Acad. Sci. USA 2007, 104, 20416–20420. [Google Scholar] [CrossRef]
- Schmidt, D.N.; Thierstein, H.R.; Bollmann, J.; Schiebel, R. Abiotic Forcing of Plankton Evolution in the Cenozoic. Science 2004, 303, 207–210. [Google Scholar] [CrossRef]
- Krasovec, M.; Chester, M.; Ridout, K.; Filatov, D.A. The Mutation Rate and the Age of the Sex Chromosomes in Silene latifolia. Curr. Biol. 2018, 28, 1832–1838.e4. [Google Scholar] [CrossRef]
- Schrider, D.R.; Houle, D.; Lynch, M.; Hahn, M.W. Rates and genomic consequences of spontaneous mutational events in Drosophila melanogaster. Genetics 2013, 194, 937–954. [Google Scholar] [CrossRef]
- Oppold, A.-M.; Pfenninger, M. Direct estimation of the spontaneous mutation rate by short-term mutation accumulation lines in Chironomus riparius. Evol. Lett. 2017, 1, 86–92. [Google Scholar] [CrossRef]
- Liu, H.; Jia, Y.; Sun, X.; Tian, D.; Hurst, L.D.; Yang, S. Direct Determination of the Mutation Rate in the Bumblebee Reveals Evidence for Weak Recombination-Associated Mutation and an Approximate Rate Constancy in Insects. Mol. Biol. Evol. 2017, 34, 119–130. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhang, J. Yeast Spontaneous Mutation Rate and Spectrum Vary with Environment. Curr. Biol. 2019, 29, 1584–1591.e3. [Google Scholar] [CrossRef] [PubMed]
- Ness, R.W.; Morgan, A.D.; Vasanthakrishnan, R.B.; Colegrave, N.; Keightley, P.D. Extensive de novo mutation rate variation between individuals and across the genome of Chlamydomonas reinhardtii. Genome Res. 2015, 25, 1739–1749. [Google Scholar] [CrossRef] [PubMed]
- Krasovec, M.; Sanchez-Brosseau, S.; Grimsley, N.; Piganeau, G. Spontaneous mutation rate as a source of diversity for improving desirable traits in cultured microalgae. Algal Res. 2018, 35, 85–90. [Google Scholar] [CrossRef]
- Ness, R.W.; Morgan, A.D.; Colegrave, N.; Keightley, P.D.; Ness, R.W.; Morgan, A.D.; Colegrave, N.; Keightley, P.D. Estimate of the Spontaneous Mutation Rate in Chlamydomonas reinhardtii. Genetics 2012, 192, 1447–1454. [Google Scholar] [CrossRef] [PubMed]
- Sung, W.; Ackerman, M.S.; Miller, S.F.; Doak, T.G.; Lynch, M. Drift-barrier hypothesis and mutation-rate evolution. Proc. Natl. Acad. Sci. USA 2012, 109, 18488–18492. [Google Scholar] [CrossRef]
- Shields, D.C. Switches in species-specific codon preferences: The influence of mutation biases. J. Mol. Evol. 1990, 31, 71–80. [Google Scholar] [CrossRef]
- Zeng, K.; Charlesworth, B. Estimating Selection Intensity on Synonymous Codon Usage in a Nonequilibrium Population. Genetics 2009, 183, 651–662. [Google Scholar] [CrossRef]
- Chepurnov, V.A.; Mann, D.G.; Sabbe, K.; Vyverman, W. Experimental studies on sexual reproduction in diatoms. Int. Rev. Cytol. 2004, 237, 91–154. [Google Scholar]
- Falciatore, A.; Bowler, C. Revealing the Molecular Secrets of Marine Diatoms. Annu. Rev. Plant Biol. 2002, 53, 109–130. [Google Scholar] [CrossRef]
- Kliman, R.M.; Hey, J. Reduced natural selection associated with low recombination in Drosophila melanogaster. Mol. Biol. Evol. 1993, 10, 1239–1258. [Google Scholar] [PubMed]
- Rengefors, K.; Kremp, A.; Reusch, T.B.H.; Wood, A.M. Genetic diversity and evolution in eukaryotic phytoplankton: Revelations from population genetic studies. J. Plankton Res. 2017, 39, 165–179. [Google Scholar] [CrossRef]
| Pseudo-nitschia | S |
|---|---|
| MMETSP0327_P.delicatissima_B596 | 0.3224 *** |
| MMETSP0329_P.arenysensis_B593 | 0.5128 *** |
| MMETSP0853_P.fraudulenta_WWA7 | 0.1069 *** |
| MMETSP1060_P.pungens_cingulata | 0.1282 *** |
| MMETSP1061_P.pungens_pungens | 0.2265 *** |
| MMETSP1423_P.heimii_UNC1101 | 0.0491 *** |
| MMETSP1432_P.delicatissima_UNC1205 | 0.3986 *** |
| Minutocellus | |
| MMETSP1070_M.polymorphus_NH13 | 0.4625 *** |
| MMETSP1322_M.polymorphus_RCC2270 | 0.5208 *** |
| MMETSP1434_M.polymorphus_CCMP3303 | −0.1424 ns |
| Leptocylindrus | |
| MMETSP0321_D.danicus_B650 | 0.4990 *** |
| MMETSP0322_D.danicus_apora_B651 | 0.5163 *** |
| MMETSP1362_D.danicus_CCMP1856 | 0.7312 *** |
| Thalassiosira | |
| MMETSP0404_T.rotula_CCMP3096 | 0.5433 *** |
| MMETSP0494_T.gravida_GMp14c1 | 0.2919 *** |
| MMETSP0740_T.minuscula_CCMP1093 | 0.2284 *** |
| MMETSP0881_T.weissflogii_CCMP1336 | 0.7675 *** |
| MMETSP0905_T.antarctica_CCMP982 | 0.7422 *** |
| MMETSP0913_T.rotula_GSO102 | 0.6406 *** |
| MMETSP0973_T.oceanica_CCMP1005 | 0.4032 *** |
| MMETSP1059_T._FW | 0.5631 *** |
| MMETSP1067_T.punctigera_Tpunct2005C2 | 0.5752 *** |
| MMETSP1071_T._NH16 | 0.6420 *** |
| MMETSP1422_T.weissflogii_CCMP1010 | 0.6491 *** |
| Skeletonema | |
| MMETSP0013_S.costatum_RCC1716 | 0.4699 *** |
| MMETSP0319_S.marinoi_SM1012Hels | 0.5485 *** |
| MMETSP0320_S.marinoi_SM1012Den | 0.5096 *** |
| MMETSP0563_S.dohrnii_SkelB | 0.4569 *** |
| MMETSP0578_S.grethae_CCMP1804 | 0.3390 *** |
| MMETSP0593_S.japonicum_CCMP2506 | 0.3625 *** |
| MMETSP0604_S.menzellii_CCMP793 | 0.4057 *** |
| MMETSP0920_S.marinoi_SkelA | 0.4275 *** |
| MMETSP1039_S.marinoi_FE7 | 0.3182 *** |
| MMETSP1040_S.marinoi_FE60 | 0.2763 *** |
| MMETSP1428_S.marinoi_UNC1201 | 0.5165 *** |
| Genus | Species | GC3 of Preferred Codons | To Preferred | To Unpreferred | Total SUBSTITUTIONS | GC Ancestral | GC Current | 2 × 2 χ2 Test |
|---|---|---|---|---|---|---|---|---|
| Chaetoceros (53 genes; total length 77,214 nucleotides) | MMETSP0092_C.affinis_CCMP159 | 0.80 | 1524 | 2348 | 3872 | 36.39 | 52.22 | 0.0001 |
| MMETSP0150_C.debilis_MM31A | 0.64 | 1906 | 745 | 2651 | 26.10 | 68.73 | 0.0001 | |
| MMETSP0200_C.GSL56 | 0.65 | 4609 | 2745 | 7354 | 27.89 | 55.22 | 0.0001 | |
| MMETSP0754_C.neogracile_CCMP1317 | 0.15 | 2713 | 2257 | 4970 | 50.99 | 33.02 | 0.0001 | |
| MMETSP1336_C.neogracile_RCC1993 | 0.61 | 4727 | 2302 | 7029 | 24.58 | 57.01 | 0.0001 | |
| MMETSP1429_C.UNC1202 | 0.68 | 4671 | 1957 | 6628 | 21.23 | 70.70 | 0.0001 | |
| MMETSP1435_C.brevis_CCMP164 | 0.70 | 1099 | 531 | 1630 | 22.09 | 75.28 | 0.0001 | |
| MMETSP1447_C.dichaeta_CCMP1751 | 0.10 | 3795 | 3405 | 7200 | 46.01 | 48.17 | 0.0001 | |
| Pseudo-nitzschia (1094 genes; total length 2,006,448 nucleotides) | MMETSP0142_P.australis_10249 | 1.00 | 58,578 | 74,556 | 133,134 | 59.37 | 47.40 | 0.0001 |
| MMETSP0327_P.delicatissima_B596 | 0.85 | 34,900 | 25,100 | 60,000 | 45.42 | 60.73 | 0.0001 | |
| MMETSP0329_P.arenysensis_B593 | 0.80 | 46,274 | 50,697 | 96,971 | 55.36 | 48.87 | 0.0001 | |
| MMETSP0853_P.fraudulenta_WWA7 | 1.00 | 46,621 | 29,852 | 76,473 | 44.89 | 62.85 | 0.0001 | |
| MMETSP1060_P.pungens_cingulata | 1.00 | 58,723 | 16,794 | 75,517 | 25.02 | 83.10 | 0.0001 | |
| MMETSP1061_P.pungens_pungens | 1.00 | 58,414 | 16,385 | 74,799 | 24.72 | 83.46 | 0.0001 | |
| MMETSP1423_P.heimii_UNC1101 | 1.00 | 76,249 | 75,362 | 151,611 | 50.88 | 52.37 | 0.0013 | |
| MMETSP1432_P.delicatissima_UNC1205 | 0.87 | 23,380 | 27,853 | 51,233 | 46.63 | 60.20 | 0.0001 | |
| Skeletonema (125 genes; total length 140,730 nucleotides) | MMETSP0563_S.dohrnii_SkelB | 0.64 | 493 | 463 | 956 | 44.56 | 49.27 | 0.0185 |
| MMETSP0578_S.grethae_CCMP1804 | 0.67 | 1704 | 861 | 2565 | 26.82 | 65.50 | 0.0001 | |
| MMETSP0593_S.japonicum_CCMP2506 | 0.64 | 1466 | 688 | 2154 | 24.56 | 72.93 | 0.0001 | |
| MMETSP0604_S.menzellii_CCMP793 | 0.64 | 2935 | 2354 | 5289 | 41.96 | 51.35 | 0.0001 | |
| MMETSP1040_S.marinoi_FE60 | 0.64 | 1220 | 907 | 2127 | 38.81 | 61.64 | 0.0001 | |
| MMETSP1428_S.marinoi_UNC1201 | 0.64 | 2122 | 1728 | 3850 | 40.44 | 54.10 | 0.0001 | |
| Thalassiosira (204 genes; total length 398,550 nucleotides) | MMETSP0404_T.rotula_CCMP3096 | 1.00 | 4506 | 2778 | 7284 | 58.83 | 61.86 | 0.0001 |
| MMETSP0494_T.gravida_GMp14c1 | 1.00 | 3225 | 3036 | 6261 | 64.29 | 54.72 | 0.0008 | |
| MMETSP0740_T.minuscula_CCMP1093 | 0.96 | 6697 | 7244 | 13,941 | 49.11 | 55.70 | 0.0001 | |
| MMETSP0905_T.antarctica_CCMP982 | 0.97 | 5058 | 8047 | 13,105 | 70.67 | 38.99 | 0.0001 | |
| MMETSP0973_T.oceanica_CCMP1005 | 1.00 | 17,637 | 11,133 | 28,770 | 50.84 | 63.00 | 0.0001 | |
| MMETSP1067_T.punctigera_Tpunct2005C2 | 1.00 | 13,348 | 5128 | 18476 | 39.15 | 73.28 | 0.0001 | |
| MMETSP1071_T.NH16 | 1.00 | 10,106 | 7236 | 17,342 | 52.98 | 59.81 | 0.0001 | |
| MMETSP0881_T.weissflogii_CCMP1336 | 1.00 | 10,543 | 10,658 | 21,201 | 55.92 | 51.45 | 0.2682 | |
| MMETSP1059_T. FW | 0.68 | 11,369 | 10,174 | 21,543 | 65.27 | 38.67 | 0.0001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krasovec, M.; Filatov, D.A. Evolution of Codon Usage Bias in Diatoms. Genes 2019, 10, 894. https://doi.org/10.3390/genes10110894
Krasovec M, Filatov DA. Evolution of Codon Usage Bias in Diatoms. Genes. 2019; 10(11):894. https://doi.org/10.3390/genes10110894
Chicago/Turabian StyleKrasovec, Marc, and Dmitry A. Filatov. 2019. "Evolution of Codon Usage Bias in Diatoms" Genes 10, no. 11: 894. https://doi.org/10.3390/genes10110894
APA StyleKrasovec, M., & Filatov, D. A. (2019). Evolution of Codon Usage Bias in Diatoms. Genes, 10(11), 894. https://doi.org/10.3390/genes10110894




