Quantifying the Role of Stochasticity in the Development of Autoimmune Disease
Abstract
:1. Introduction
2. Materials and Methods
2.1. Deterministic Mathematical Model
2.2. Stochastic Model
2.3. Experimental Set-Up
3. Results
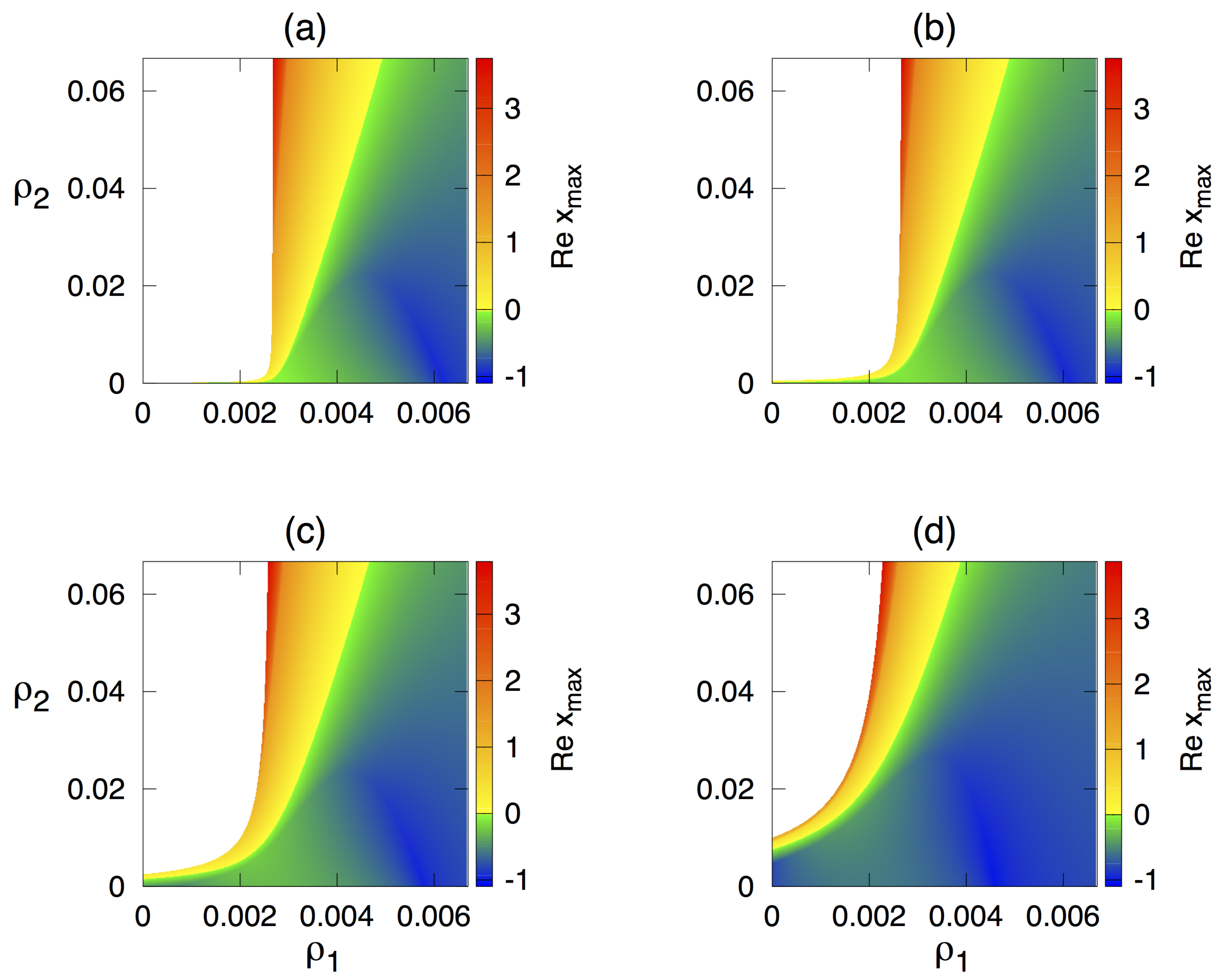
3.1. Stability Analysis of the Deterministic Model
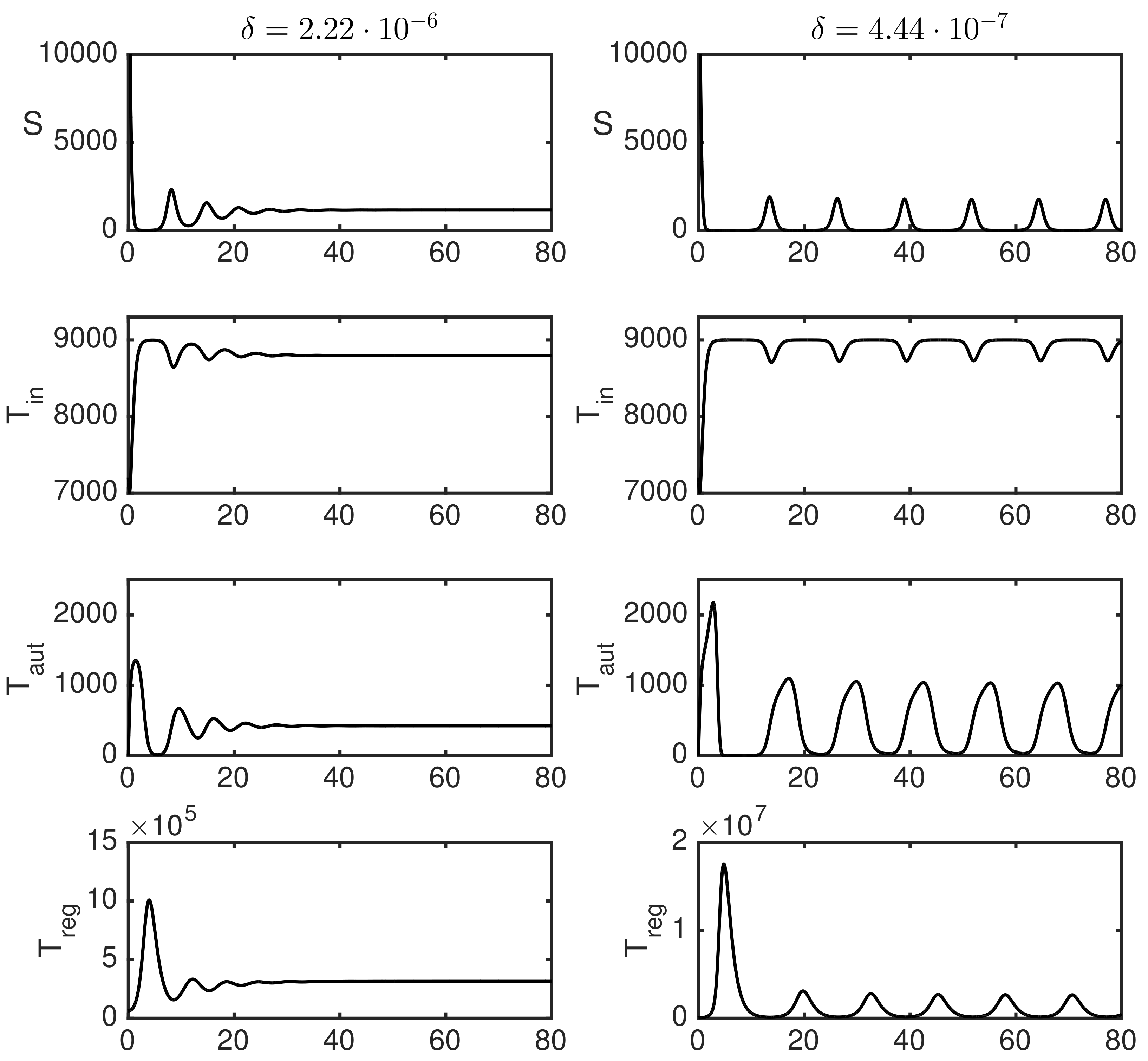
3.2. Numerical Simulations
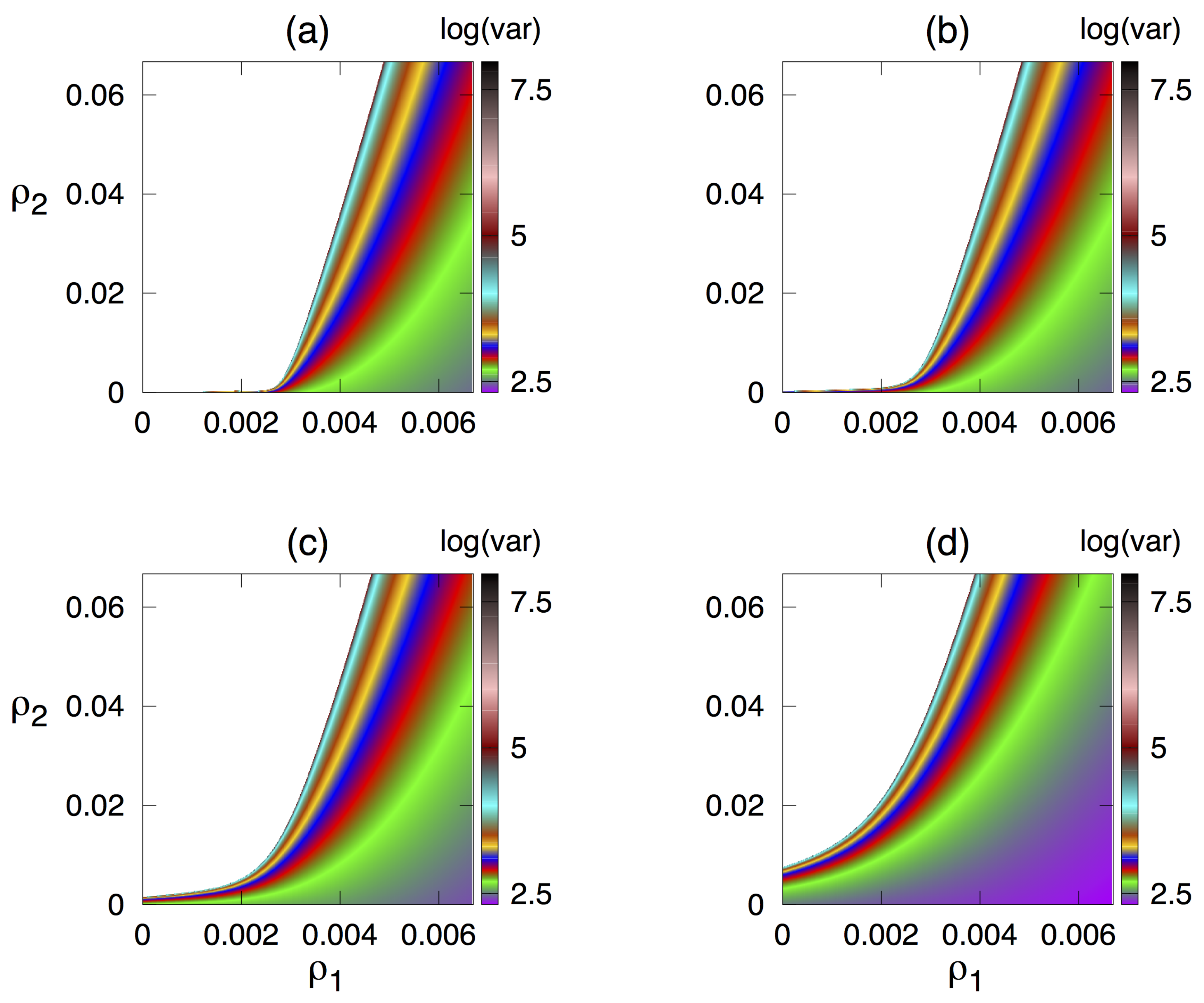
3.3. Dependence of Variance of Oscillations on Parameters
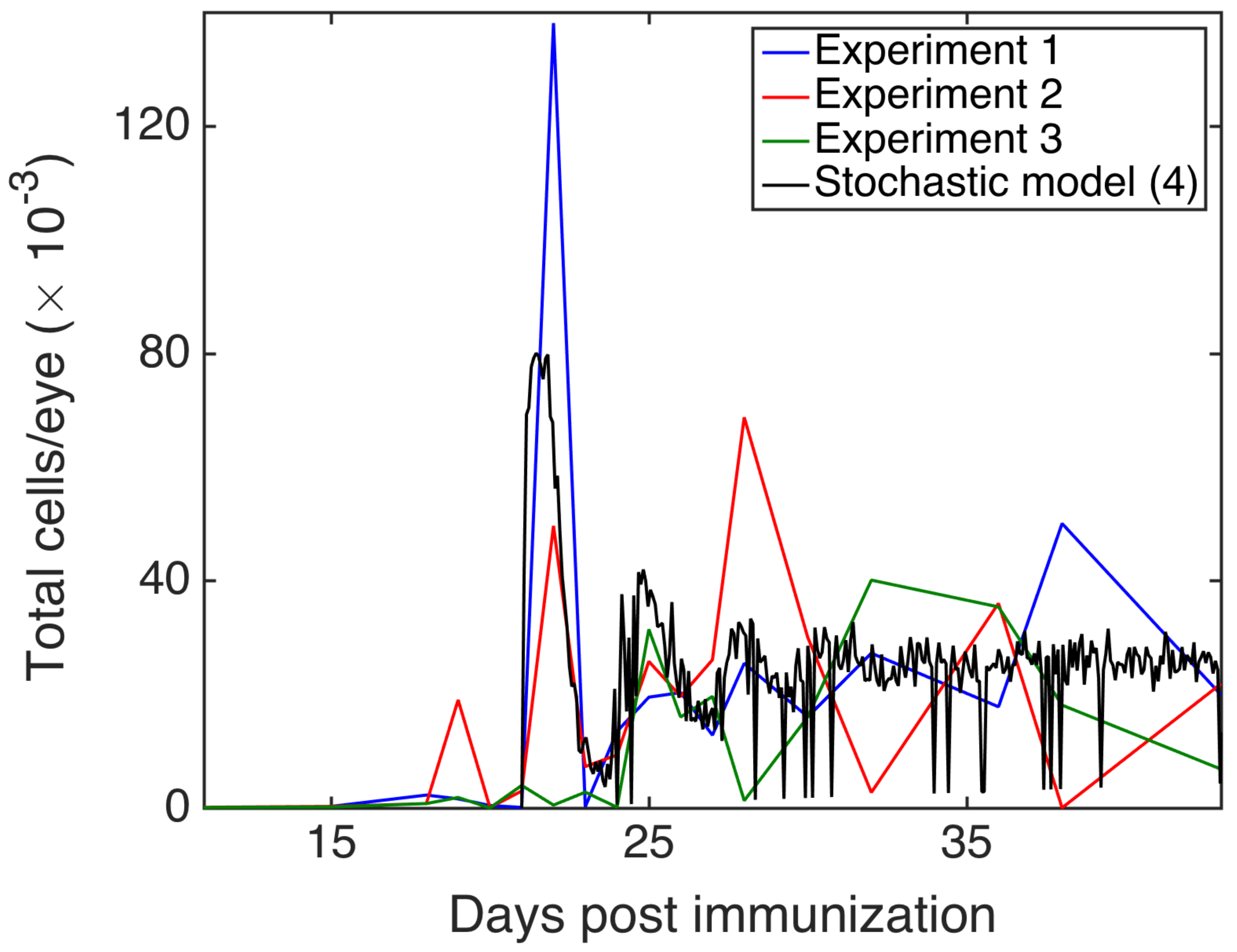
3.4. Comparison with Experiments
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A. System-Size Expansion and Fluctuations
Appendix B. State Changes and Their Probabilities
| i | Probability | |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 |
Appendix C. Derivation of Itô SDE Model
References
- Davidson, A.; Diamond, B. Autoimmune diseases. N. Engl. J. Med. 2001, 345, 340–350. [Google Scholar] [CrossRef] [PubMed]
- Ercolini, A.M.; Miller, S.D. The role of infections in autoimmune disease. Clin. Exp. Immunol. 2009, 155, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Marrack, P.; Kappler, J.; Kotzin, B.L. Autoimmune disease: Why and where it occurs. Nat. Med. 2001, 7, 899–905. [Google Scholar] [CrossRef]
- Segel, L.A.; Jäger, E.; Elias, D.; Cohen, I.R. A quantitative model of autoimmune disease and T-cell vaccination: Does more mean less? Immunol. Today 1995, 16, 80–84. [Google Scholar] [CrossRef]
- Borghans, J.A.M.; De Boer, R.J. A minimal model for T-cell vaccination. Proc. R. Soc. Lond. B 1995, 259, 173–178. [Google Scholar]
- Borghans, J.A.M.; De Boer, R.J.; Sercarz, E.; Kumar, V. T cell vaccination in experimental autoimmune encephalomyelitis: A mathematical model. J. Immunol. 1998, 161, 1087–1093. [Google Scholar] [PubMed]
- León, K.; Perez, R.; Lage, A.; Carneiro, J. Modelling T-cell-mediated suppression dependent on interactions in multicellular conjugates. J. Theor. Biol. 2000, 207, 231–254. [Google Scholar] [CrossRef]
- León, K.; Lage, A.; Carneiro, J. Tolerance and immunity in a mathematical model of T-cell mediated suppression. J. Theor. Biol. 2003, 225, 107–126. [Google Scholar] [CrossRef]
- León, K.; Faro, J.; Lage, A.; Carneiro, J. Inverse correlation between the incidences of autoimmune disease and infection predicted by a model of T cell mediated tolerance. J. Autoimmun. 2004, 22, 31–42. [Google Scholar] [CrossRef]
- Iwami, S.; Takeuchi, Y.; Miura, Y.; Sasaki, T.; Kajiwara, T. Dynamical properties of autoimmune disease models: Tolerance, flare-up, dormancy. J. Theor. Biol. 2007, 246, 646–659. [Google Scholar] [CrossRef]
- Iwami, S.; Takeuchi, Y.; Iwamoto, K.; Naruo, Y.; Yasukawa, M. A mathematical design of vector vaccine against autoimmune disease. J. Theor. Biol. 2009, 256, 382–392. [Google Scholar] [CrossRef] [PubMed]
- Burroughs, N.J.; de Oliveira, B.M.P.M.; Pinto, A.A. Regulatory T cell adjustment of quorum growth thresholds and the control of local immune responses. J. Theor. Biol. 2006, 241, 134–141. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burroughs, N.J.; Ferreira, M.; Oliveira, B.M.P.M.; Pinto, A.A. Autoimmunity arising from bystander proliferation of T cells in an immune response model. Math. Comput. Model. 2011, 53, 1389–1393. [Google Scholar] [CrossRef]
- Burroughs, N.J.; Ferreira, M.; Oliveira, B.M.P.M.; Pinto, A.A. A transcritical bifurcation in an immune response model. J. Differ. Equ. Appl. 2011, 17, 1101–1106. [Google Scholar] [CrossRef]
- Oliveira, B.M.P.M.; Trinchet, R.; Espinar, M.V.O.; Pinto, A.; Burroughs, N. Modelling the suppression of autoimmunity after pathogen infection. Math. Meth. Appl. Sci. 2018, 41, 8565–8570. [Google Scholar] [CrossRef]
- Root-Bernstein, R. Theories and Modeling of Autoimmunity. J. Theor. Biol. 2015, 375, 1–124. [Google Scholar] [CrossRef] [PubMed]
- Eftimie, R.; Gillard, J.J.; Cantrell, D.A. Mathematical models for immunology: Current state of the art and future research directions. Bull. Math. Biol. 2016, 78, 2091–2134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bocharov, G.; Volpert, V.; Ludewig, B.; Meyerhans, A. Mathematical modeling of the immune system in homeostasis, infection and disease. Front. Immunol. 2019, 10, 2944. [Google Scholar] [CrossRef]
- Corthay, A. How do regulatory T cells work? Scand. J. Immunol. 2009, 70, 326–336. [Google Scholar] [CrossRef]
- Josefowicz, S.Z.; Lu, L.F.; Rudensky, A.Y. Regulatory T cells: Mechanisms of differentiation and function. Ann. Rev. Immunol. 2012, 30, 531–564. [Google Scholar] [CrossRef]
- Khattri, R.; Cox, T.; Yasayko, S.A.; Ramsdell, F. An essential role for Scurfin in CD4+CD25+ T regulatory cells. Nat. Immunol. 2003, 4, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, S. Naturally arising CD4+ regulatory T cells for immunologic self-tolerance and negative control of immune responses. Ann. Rev. Immunol. 2004, 22, 531–562. [Google Scholar] [CrossRef]
- Alexander, H.K.; Wahl, L.M. Self-tolerance and autoimmunity in a regulatory T cell model. Bull. Math. Biol. 2011, 73, 33–71. [Google Scholar] [CrossRef] [PubMed]
- Grossman, Z.; Paul, W.E. Adaptive cellular interactions in the immune system: The tunable activation threshold and the significance of subthreshold responses. Proc. Natl. Acad. Sci. USA 1992, 89, 10365–10369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grossman, Z.; Singer, A. Tuning of activation thresholds explains flexibility in the selection and development of T cells in the thymus. Proc. Natl. Acad. Sci. USA 1996, 93, 14747–14752. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grossman, Z.; Paul, W.E. Self-tolerance: Context dependent tuning of T cell antigen recognition. Sem. Immunol. 2000, 12, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Grossman, Z.; Paul, W.E. Dynamic tuning of lymphocytes: physiological basis, mechanisms, and function. Annu. Rev. Immunol. 2015, 33, 677–713. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grossman, Z. Immunological paradigms, mechanisms, and models: Conceptual understanding is a prerequisite to effective modeling. Front. Immunol. 2019, 10, 2522. [Google Scholar] [CrossRef] [Green Version]
- Bitmansour, A.D.; Douek, D.C.; Maino, V.C.; Picker, L.J. Direct ex vivo analysis of human CD4+ memory T cell activation requirements at the single clonotype level. J. Immunol. 2002, 169, 1207–1218. [Google Scholar] [CrossRef] [Green Version]
- Nicholson, L.B.; Anderson, A.C.; Kuchroo, V.K. Tuning T cell activation threshold and effector function with cross-reactive peptide ligands. Int. Immunol. 2000, 12, 205–213. [Google Scholar] [CrossRef]
- Römer, P.S.; Berr, S.; Avota, E.; Na, S.Y.; Battaglia, M.; ten Berge, I.; Einsele, H.; Hunig, T. Preculture of PBMC at high cell density increases sensitivity of T-cell responses, revealing cytokine release by CD28 superagonist TGN1412. Blood 2011, 118, 6772–6782. [Google Scholar]
- Stefanová, I.; Dorfman, J.R.; Germain, R.N. Self-recognition promotes the foreign antigen sensitivity of naive T lymphocytes. Nature 2002, 420, 429–434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carneiro, J.; Paixão, T.; Milutinovic, D.; Sousa, J.; Leon, K.; Gardner, R.; Faro, J. Immunological self-tolerance: Lessons from mathematical modeling. J. Comput. Appl. Math. 2005, 184, 77–100. [Google Scholar] [CrossRef] [Green Version]
- Blyuss, K.B.; Nicholson, L.B. The role of tunable activation thresholds in the dynamics of autoimmunity. J. Theor. Biol. 2012, 308, 45–55. [Google Scholar] [CrossRef] [Green Version]
- Blyuss, K.B.; Nicholson, L.B. Understanding the roles of activation threshold and infections in the dynamics of autoimmune disease. J. Theor. Biol. 2015, 375, 13–20. [Google Scholar] [CrossRef]
- Fatehi, F.; Kyrychko, S.N.; Ross, A.; Kyrychko, Y.N.; Blyuss, K.B. Stochastic effects in autoimmune dynamics. Front. Physiol. 2018, 9, 45. [Google Scholar] [CrossRef] [Green Version]
- Fatehi, F.; Kyrychko, Y.N.; Blyuss, K.B. Effects of viral and cytokine delays on dynamics of autoimmunity. Mathematics 2018, 6, 66. [Google Scholar] [CrossRef] [Green Version]
- Fatehi, F.; Kyrychko, Y.N.; Molchanov, R.; Blyuss, K.B. Bifurcations and multi-stability in a model of cytokine-mediated autoimmunity. Int. J. Bifurc. Chaos 2019, 29, 1950034. [Google Scholar] [CrossRef]
- Fatehi, F.; Kyrychko, Y.N.; Blyuss, K.B. Time-delayed model of autoimmune dynamics. Math. Biosci. Eng. 2019, 16, 5613–5639. [Google Scholar] [CrossRef]
- Fatehi, F.; Kyrychko, Y.N.; Blyuss, K.B. Stochastic time-delayed model of autoimmunity. Math. Biosci. 2020, 322, 108323. [Google Scholar] [CrossRef]
- Perelson, A.S.; Weisbuch, G. Immunology for physicists. Rev. Mod. Phys. 1997, 69, 1219–1267. [Google Scholar] [CrossRef]
- Lythe, G.; Molina-París, C. Some deterministic and stochastic mathematical models of naïve T-cell homeostasis. Immunol. Rev. 2018, 285, 206–217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stirk, E.R.; Lythe, G.; van den Berg, H.A.; Hurst, G.A.D.; Molina-París, C. The limiting conditional probability distribution in a stochastic model of T cell repertoire maintenance. Math. Biosci. 2010, 224, 74–86. [Google Scholar] [CrossRef] [PubMed]
- Stirk, E.R.; Lythe, G.; van den Berg, H.A.; Molina-París, C. Stochastic competitive exclusion in the maintenance of the naïve T cell repertoire. J. Theor. Biol. 2010, 265, 396–410. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scherer, A.; Noest, A.; de Boer, R.J. Activation-threshold tuning in an affinity model for the T-cell repertoire. Proc. R. Soc. B 2004, 271, 609–616. [Google Scholar] [CrossRef] [Green Version]
- Van den Berg, H.A.; Rand, D.A. Dynamics of T cell activation threshold tuning. J. Theor. Biol. 2004, 228, 397–416. [Google Scholar] [CrossRef]
- Mayer, H.; Bovier, A. Stochastic modelling of T-cell activation. J. Math. Biol. 2015, 70, 99–132. [Google Scholar] [CrossRef] [Green Version]
- Deenick, E.K.; Gett, A.V.; Hodgkin, P.D. Stochastic model of T cell proliferation: A calculus revealing IL-2 regulation of precursor frequencies, cell cycle time, and survival. J. Immunol. 2003, 170, 4963–4972. [Google Scholar] [CrossRef] [Green Version]
- Heinzel, S.; Marchingo, J.M.; Horton, M.B.; Hodgkin, P.D. The regulation of lymphocyte activation and proliferation. Curr. Opin. Immunol. 2018, 51, 32–38. [Google Scholar] [CrossRef] [Green Version]
- Chao, D.L.; Davenport, M.P.; Forrest, S.; Perelson, A.S. A stochastic model of cytotoxic T cell responses. J. Theor. Biol. 2004, 228, 227–240. [Google Scholar] [CrossRef] [Green Version]
- Detours, V.; Perelson, A.S. The paradox of alloreactivity and self MHC restriction: Quantitative analysis and statistics. Proc. Natl. Acad. Sci. USA 2000, 97, 8479–8483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wolf, S.D.; Dittel, B.N.; Hardardottir, F.; Janeway, C.A. Experimental autoimmune encephalomyelitis induction in genetically B cell-deficient mice. J. Exp. Med. 1996, 184, 2271–2278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, H.J.; Ivanov, I.I.; Darce, J.; Hattori, K.; Shima, T.; Umesaki, Y.; Littman, D.R.; Benoist, C.; Mathis, D. Gut-residing segmented filamentous bacteria drive autoimmune arthritis via T helper 17 cells. Immunity 2010, 32, 815–827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nicholson, L.B.; Wraith, D.C. T-cell receptor degeneracy: The dog that did not bark; Adaptation of the self-reactive T-cell response to limit autoimmune disease. Mol. Immunol. 2004, 40, 997–1002. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J.S. An Introduction to Stochastic Processes with Applications to Biology; Chapman and Hall/CRC: New York, NY, USA, 2010. [Google Scholar]
- Allen, L.J.S.; Allen, E.J. A comparison of three different stochastic population models with regard to persistence times. Theor. Popul. Biol. 2003, 64, 439–449. [Google Scholar] [CrossRef]
- Wang, X.; Gautam, R.; Pinedo, P.J.; Allen, L.J.S.; Ivanek, R. A stochastic model for transmission, extinction and outbreak of Escherichia coli O157:H7 in cattle as affected by ambient temperature and cleaning practices. J. Math. Biol. 2014, 69, 501–532. [Google Scholar] [CrossRef]
- Allen, E.J.; Allen, L.J.S.; Arciniega, A.; Greenwood, P.E. Construction of equivalent stochastic differential equation models. Stoch. Anal. Appl. 2008, 26, 274–297. [Google Scholar] [CrossRef]
- Mandal, P.S.; Allen, L.J.S.; Banerjee, M. Stochastic modeling of phytoplankton allelopathy. Appl. Math. Model. 2014, 38, 1583–1596. [Google Scholar] [CrossRef]
- Allen, E.J. Modeling with Itô Stochastic Differential Equations; Springer: Berlin, Germany, 2014. [Google Scholar]
- Caspi, R.R. A look at autoimmunity and inflammation in the eye. J. Clin. Investig. 2010, 120, 3073–3083. [Google Scholar] [CrossRef] [Green Version]
- Silver, P.B.; Chan, C.C.; Wiggert, B.; Caspi, R.R. The requirement for pertussis to induce EAU is strain-dependent: B10.RIII, but not B10.A mice, develop EAU and Th1 responses to IRBP without pertussis treatment. Investig. Ophthalmol. Vis. Sci. 1999, 40, 2898–2905. [Google Scholar]
- Avichezer, D.; Silver, P.B.; Chan, C.C.; Wiggert, B.; Caspi, R.R. Identification of a new epitope of human IRBP that induces autoimmune uveoretinitis in mice of the H-2b haplotype. Investig. Ophthalmol. Vis. Sci. 2001, 41, 127–131. [Google Scholar]
- Guyver, C.J.; Copland, D.A.; Calder, C.J.; Sette, A.; Sidney, J.; Dick, A.D.; Nicholson, L.B. Mapping immune responses to mRBP-3 1-16 peptide with altered peptide ligands. Investig. Ophthalmol. Vis. Sci. 2006, 47, 2027–2035. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kerr, E.C.; Copland, D.A.; Dick, A.D.; Nicholson, L.B. The dynamics of leukocyte infiltration in experimental autoimmune uveoretinitis. Prog. Retin. Eye Res. 2008, 27, 527–535. [Google Scholar] [CrossRef] [PubMed]
- Kerr, E.C.; Raveney, B.J.E.; Copland, D.A.; Dick, A.D.; Nicholson, L.B. Analysis of retinal cellular infiltrate in experimental autoimmune uveoretinitis reveals multiple regulatory cell populations. J. Autoimm. 2008, 31, 354–361. [Google Scholar] [CrossRef]
- Epps, S.J.; Boldison, J.; Stimpson, M.L.; Khera, T.K.; Lait, P.J.P.; Copland, D.A.; Dick, A.D.; Nicholson, L.B. Re-programming immunosurveillance in persistent non-infectious ocular inflammation. Progr. Retinal Eye Res. 2018, 93, 93–106. [Google Scholar] [CrossRef]
- Alonso, D.; McKane, A.J.; Pascual, M. Stochastic amplification in epidemics. J. R. Soc. Interface 2007, 4, 575–582. [Google Scholar] [CrossRef] [Green Version]
- Kuske, R.; Gordillo, L.F.; Greenwood, P.E. Sustained oscillations via coherence resonance in SIR. J. Theor. Biol. 2007, 245, 459–469. [Google Scholar] [CrossRef]
- Flugel, A.; Berkowicz, T.; Ritter, T.; Labeur, M.; Jenne, D.E.; Li, Z.; Ellwart, J.W.; Willem, M.; Lassmann, H.; Wekerle, H. Migratory activity and functional changes of green fluorescent effector cells before and during experimental autoimmune encephalomyelitis. Immunity 2001, 14, 547–560. [Google Scholar] [CrossRef] [Green Version]
- Silver, P.; Horai, R.; Chen, J.; Jittayasothorn, Y.; Chan, C.C.; Villasmil, R.; Kesen, M.R.; Caspi, R.R. Retina-specific T regulatory cells bring about resolution and maintain remission of autoimmune uveitis. J. Immunol. 2015, 194, 3011–3019. [Google Scholar] [CrossRef] [Green Version]
- Raveney, B.J.E.; Copland, D.A.; Dick, A.D.; B, N.L. TNFR1-dependent regulation of myeloid cell function in experimental autoimmune uveoretinis. J. Immunol. 2009, 183, 2321–2329. [Google Scholar] [CrossRef] [Green Version]
- Yaari, G.; Flajnik, M.; Hershberg, U. Questions of stochasticity and control in immune repertoires. Trends Immunol. 2018, 39, 859–861. [Google Scholar] [CrossRef] [PubMed]
- Derbinski, J.; Pinto, S.; Rösch, S.; Hexel, K.; Kyewski, B. Promiscuous gene expression patterns in single medullary thymic epithelial cells argue for a stochastic mechanism. Proc. Natl. Acad. Sci. USA 2008, 105, 657–662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meredith, M.; Zemmour, D.; Mathis, D.; Benoist, C. Aire controls gene expression in the thymic epithelium with ordered stochasticity. Nat. Immunol. 2015, 16, 942–952. [Google Scholar] [CrossRef] [Green Version]
- Abadi, K.; Pease, N.A.; Wither, M.J.; Kueh, H.Y. Order by chance: Origins and benefits of stochasticity in immune cell fate control. Curr. Opin. Syst. Biol. 2019, 18, 95–103. [Google Scholar] [CrossRef]
- Macfarlane, F.R.; Chaplain, M.A.J.; Eftimie, R. Quantitative predictive modelling approaches to aunderstanding rheumatoid arthritis: A brief review. Cells 2020, 9, 74. [Google Scholar] [CrossRef] [Green Version]
- Dobrovolny, H.M.; Reddy, M.B.; Kamal, M.A.; Rayner, C.R.; Beauchemin, C.A.A. Assessing mathematical models of influenza infections using features of the immune response. PLoS ONE 2013, 8, e57088. [Google Scholar] [CrossRef]
- Miao, H.; Hollenbaugh, J.A.; Zand, M.S.; Holden-Wiltse, J.; Mosmann, T.R.; Perelson, A.S.; Wu, H.; Topham, D.J. Stochastic modelling of T-cell activation. J. Virol. 2010, 84, 6687–6698. [Google Scholar] [CrossRef] [Green Version]
- Pawelek, K.A.; Huynh, G.T.; Quinlivan, M.; Cullinane, A.; Rong, L.; Perelson, A.S. Modeling within-host dynamics of influenza virus infection including immune responses. PLoS Comput. Biol. 2012, 8, e1002588. [Google Scholar] [CrossRef] [Green Version]
- Chowell, G.; Sattenspiel, L.; Bansal, S.; Viboud, C. Mathematical models to characterize early epidemic growth: A review. Phys. Life Rev. 2016, 18, 66–97. [Google Scholar] [CrossRef] [Green Version]
- Viboud, C.; Simonsen, L.; Chowell, G. A generalized-growth model to characterize the early ascending phase of infectious disease outbreaks. Epidemics 2016, 15, 27–37. [Google Scholar] [CrossRef] [Green Version]
- Burić, N.; Mudrinic, M.; Vasović, N. Time delay in a basic model of the immune response. Chaos Sol. Fract. 2001, 12, 483–489. [Google Scholar] [CrossRef] [Green Version]
- Holder, B.P.; Beauchemin, C.A.A. Exploring the effect of biological delays in kinetic models of influenza within a host or cell culture. BMC Public Health 2012, 11 (Suppl. S1), S10. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M.; McCullers, J.A.; Adler, F.R. Mathematical model of a three-stage innate immune response to a pneumococcal lung infection. J. Theor. Biol. 2011, 276, 106–116. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Kumar, A.; Miao, H.; Holden-Wiltse, J.; Mosmann, T.R.; Livingstong, A.M.; Belz, G.T.; Perelson, A.S.; Zand, D.J.; Topham, D.J. Modeling of influenza-specific CD8+ T cells during the primary response indicates that the spleen is a major source of effectors. J. Immunol. 2011, 187, 4474–4482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cappuccio, A.; Tieri, P.; Castiglione, F. Multiscale modelling in immunology: A review. Brief. Bioinf. 2016, 17, 408–418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Quintela, B.M.; Weber dos Santos, R.; Lobosco, M. On the coupling of two models of the human immune response to an antigen. BioMed Res. Int. 2014, 2014, 410457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bandyopadhyay, M.; Chattopadhyay, J. Ratio-dependent predator-prey model: Effect of environmental fluctuation and stability. Nonlinearity 2005, 18, 913–936. [Google Scholar] [CrossRef]
- Samanta, G.P. The effects of random fluctuating environment on interacting species with time delay. Int. J. Math. Ed. Sci. Technol. 1996, 27, 13–21. [Google Scholar] [CrossRef]
- Tapaswi, P.K.; Mukhopadhyay, A. Effects of environmental fluctuation on plankton allelopathy. J. Math. Biol. 1999, 39, 39–58. [Google Scholar] [CrossRef]
- Gray, A.; Greenhalgh, D.; Hu, L.; Mao, X.; Pan, J. A stochastic differential equation SIS epidemic model. SIAM J. Appl. Math. 2011, 71, 876–902. [Google Scholar] [CrossRef] [Green Version]
- Mukandavire, Z.; Das, P.; Chiyaka, C.; Gazi, N.H.; Das, K.; Shiri, T. Stochastic modelling of T-cell activation. J. Math. Mod. Alg. 2010, 10, 181–191. [Google Scholar] [CrossRef]
- Keino, H.; Horie, S.; Sugita, S. Immune privilege and eye-derived T-regulatory cells. J. Immunol. Res. 2018, 2018, 1679197. [Google Scholar] [CrossRef] [PubMed]
- Taylor, A.W. Ocular immune privilege. Eye 2009, 23, 1885–1889. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Taylor, A.W. Ocular immune privilege and transplantation. Front. Immunol. 2016, 7, 37. [Google Scholar] [CrossRef] [Green Version]
- Zhou, R.; Caspi, R.R. Ocular immune privilege. F1000 Biol. Rep. 2010, 2, 3. [Google Scholar] [CrossRef]
- Damico, F.M.; Kiss, S.; Young, L.H. Sympathetic ophthalmia. Sem. Ophthalm. 2005, 20, 191–197. [Google Scholar] [CrossRef]
- Ung, C.; Young, L.H. Sympathetic ophthalmia. In Inflammatory and Infectious Ocular Disorders; Yu, H.G., Ed.; Springer: New York, NY, USA, 2020; pp. 59–65. [Google Scholar]
- Van Kampen, N.G. Stochastic Processes in Physics and Chemistry; Elsevier: New York, NY, USA, 1992. [Google Scholar]
- Wallace, E.W.J.; Gillespie, D.T.; Sanft, K.R.; Petzold, L.R. Linear noise approximation is valid over limited times for any chemical system that is sufficiently large. IET Syst. Biol. 2012, 6, 102–115. [Google Scholar] [CrossRef]
- Hayot, F.; Jayaprakash, C. The linear noise approximation for molecular fluctuations within cells. Phys. Biol. 2004, 1, 205–210. [Google Scholar] [CrossRef]
- Pahle, J.; Challenger, J.D.; Mendes, P.; McKane, A.J. Biochemical fluctuations, optimisation and the linear noise approximation. BMC Syst. Biol. 2012, 6, 86. [Google Scholar] [CrossRef] [Green Version]
- Black, A.J.; McKane, J.A.; Nunes, A.; Parisi, A. Realistic distributions of infectious periods in epidemic models: Changing patterns of persistence and dynamics. Phys. Rev. E 2009, 80, 021922. [Google Scholar] [CrossRef] [Green Version]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| r | 2 | N | 20,000 |
| 0.0044 | |||
| 18,000 | 2 | ||
| 54,000 | 0.8 | ||
| p | 0.4 | ||
| 0.8 | 0.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nicholson, L.B.; Blyuss, K.B.; Fatehi, F. Quantifying the Role of Stochasticity in the Development of Autoimmune Disease. Cells 2020, 9, 860. https://doi.org/10.3390/cells9040860
Nicholson LB, Blyuss KB, Fatehi F. Quantifying the Role of Stochasticity in the Development of Autoimmune Disease. Cells. 2020; 9(4):860. https://doi.org/10.3390/cells9040860
Chicago/Turabian StyleNicholson, Lindsay B., Konstantin B. Blyuss, and Farzad Fatehi. 2020. "Quantifying the Role of Stochasticity in the Development of Autoimmune Disease" Cells 9, no. 4: 860. https://doi.org/10.3390/cells9040860
APA StyleNicholson, L. B., Blyuss, K. B., & Fatehi, F. (2020). Quantifying the Role of Stochasticity in the Development of Autoimmune Disease. Cells, 9(4), 860. https://doi.org/10.3390/cells9040860





