Mechanistic Modeling of the Relative Biological Effectiveness of Boron Neutron Capture Therapy
Abstract
1. Introduction
2. Materials and Methods
2.1. Conceptual Aspects of a Multiscale Radiobiological Model
2.2. MCDS + MCNP Model for a Mixed Radiation Field
2.3. RMF Model for a Mixed Radiation Field
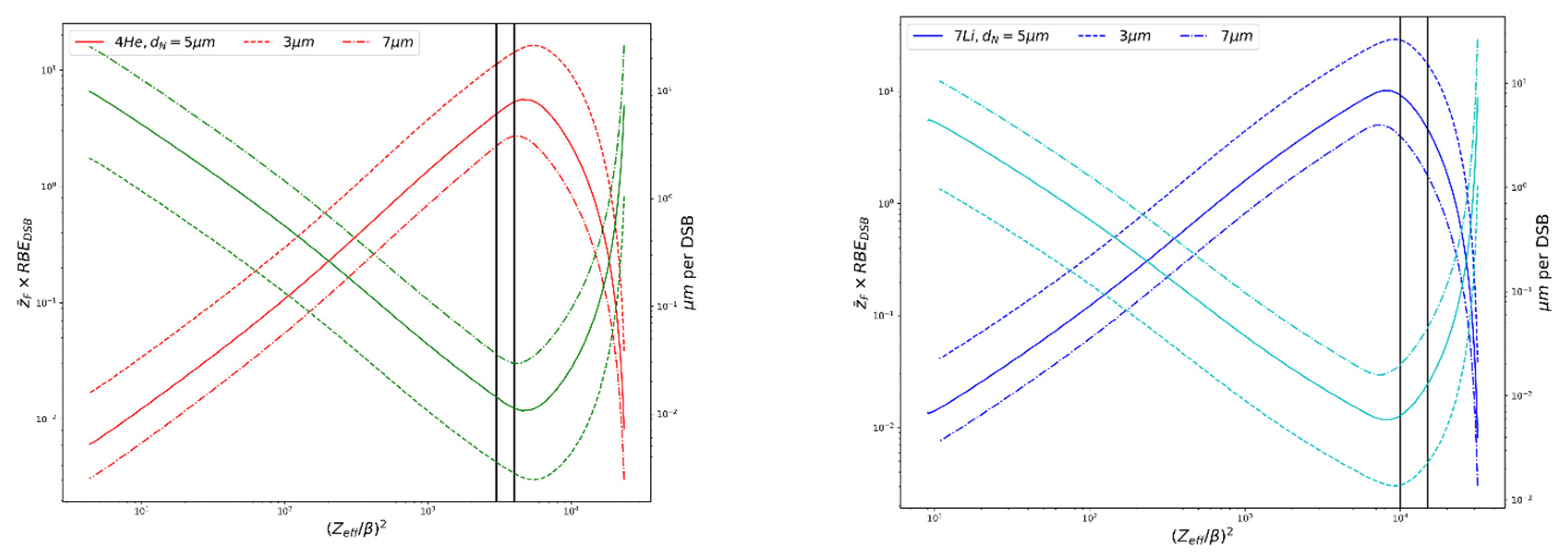
2.4. Simulation of the Secondary Charged-Particle Spectrum
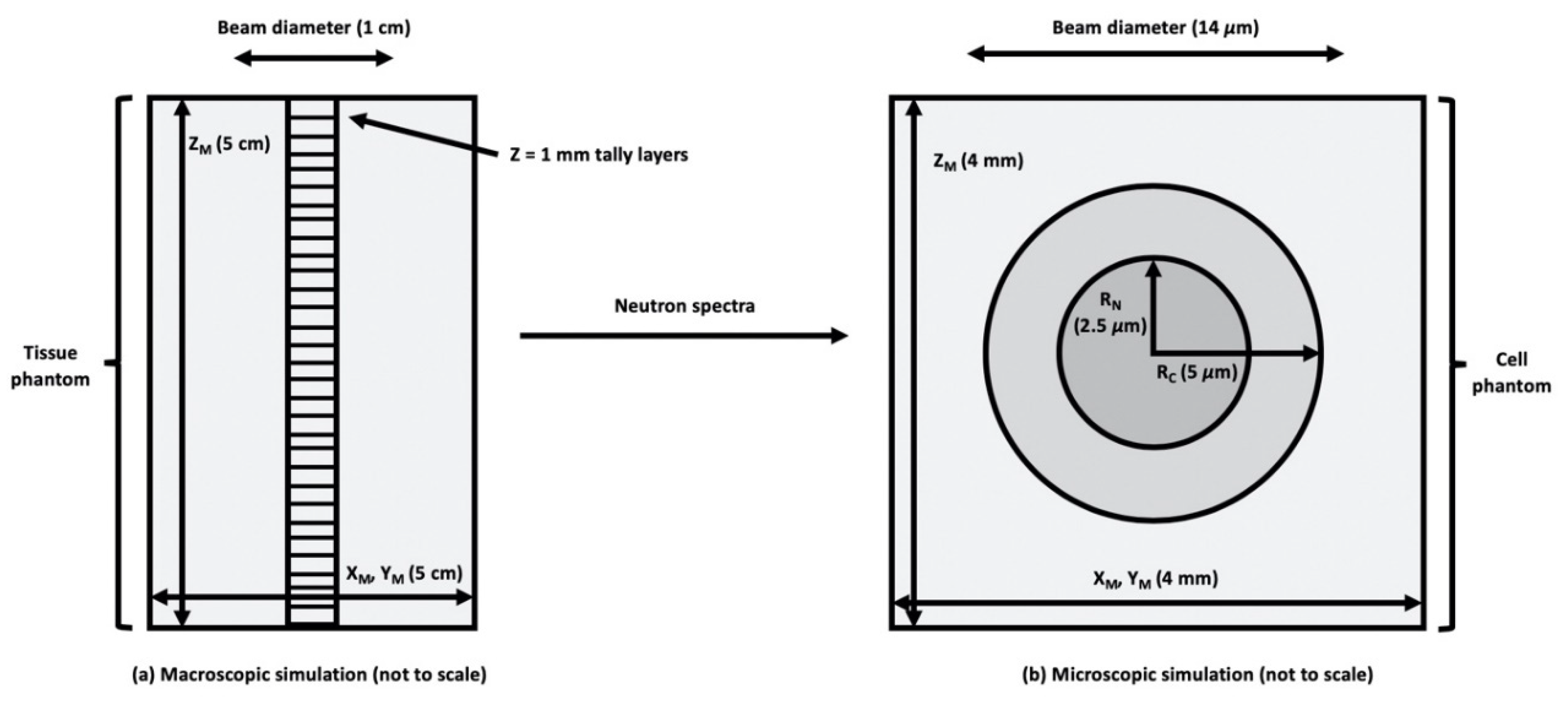
2.5. Model for Cellular Dosimetry
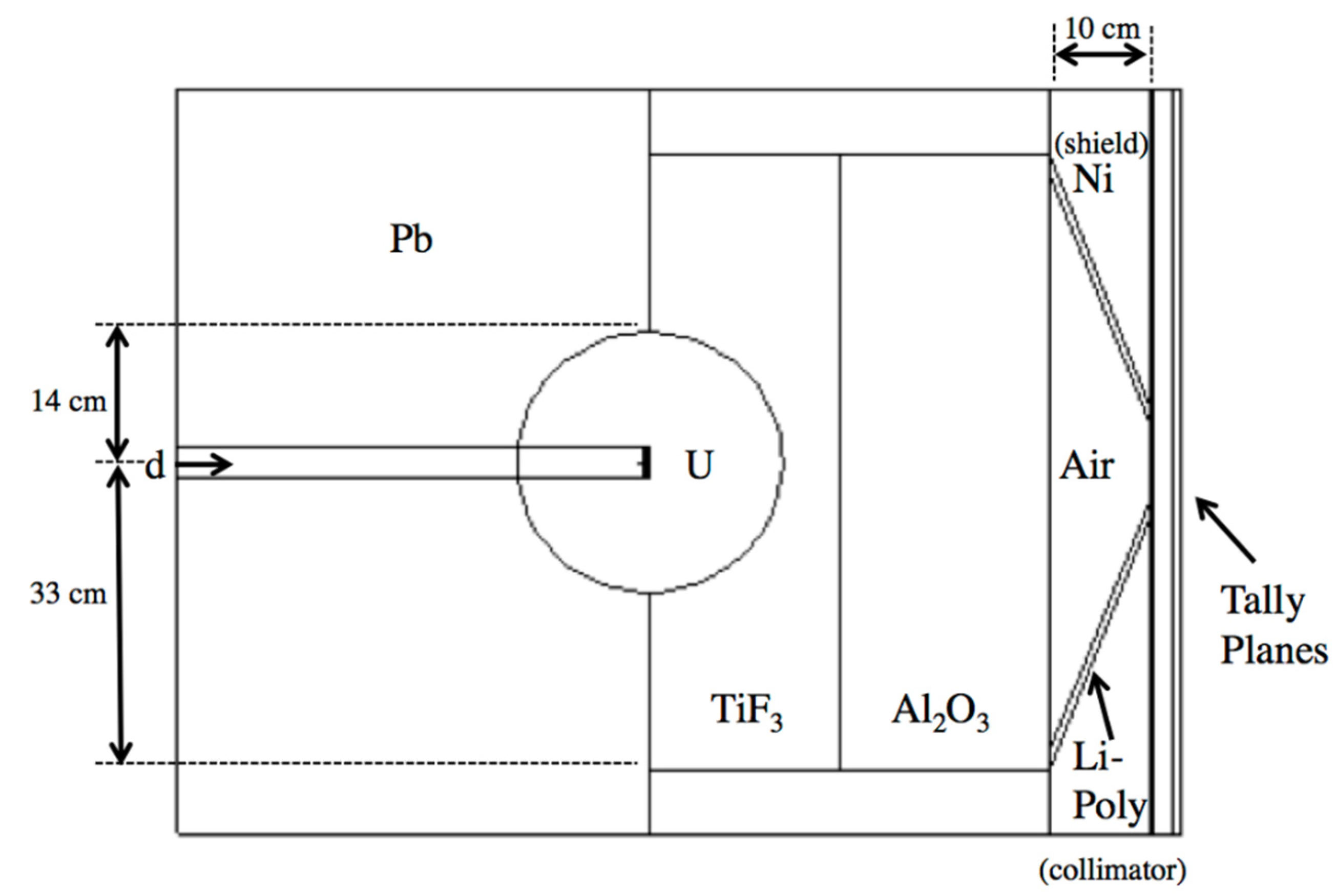
2.6. Neutron Source Models for BNCT
- The Massachusetts Institute of Technology Fission Convertor Beam (MIT-FCB) [10]. The MIT-FCB is a commonly used source for analyzing BNCT because of the purity and intensity of epithermal neutrons [9]. It has a very similar neutron spectrum and microdosimetric properties to the Brookhaven Medical Research Reactor (BMRR) [41,42].
- A new CN source derived from the NM by removing the uranium sphere from the NM source.
MCNP6 Model of the Clinical Neutron Therapy System (CNTS)
3. Results
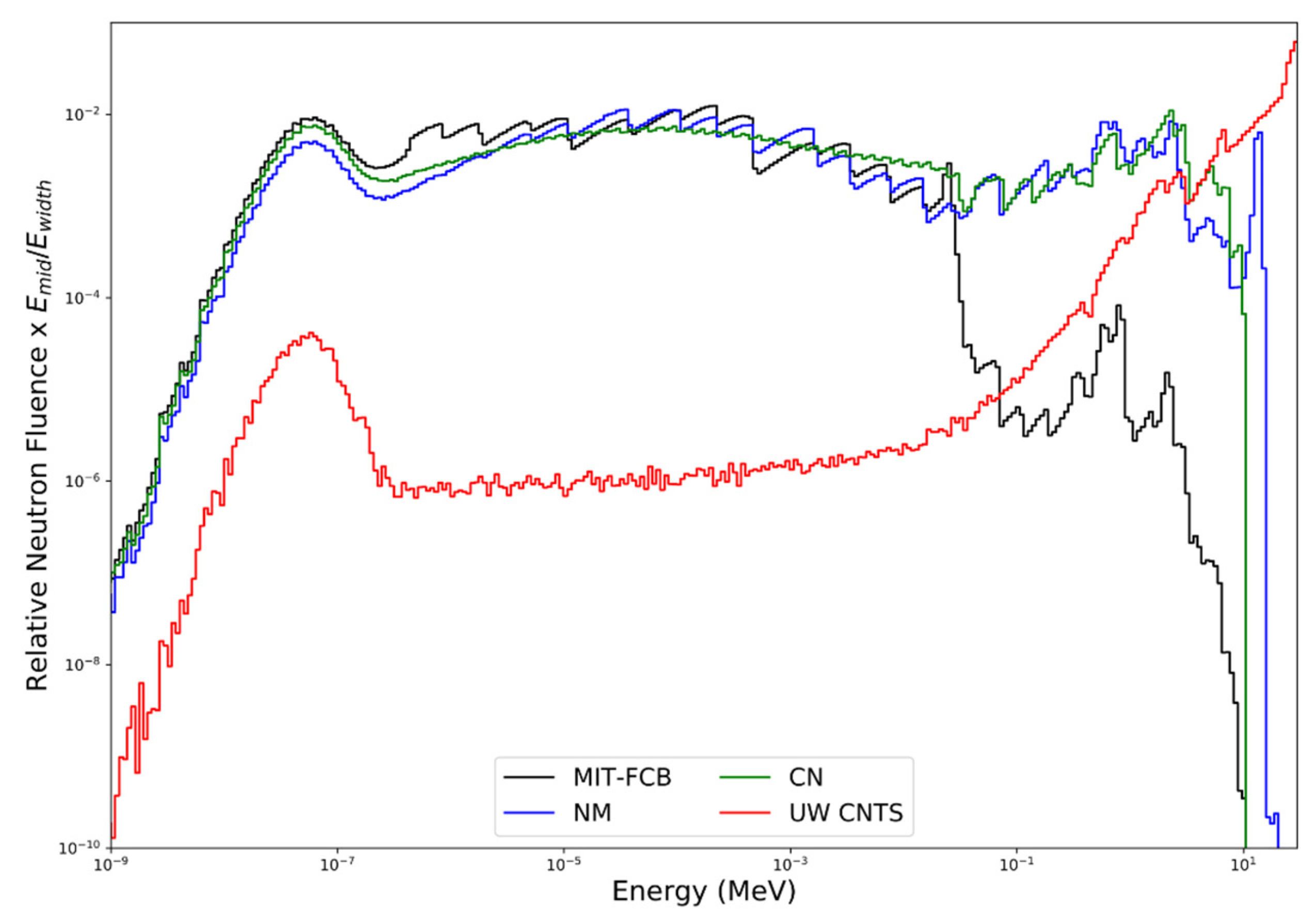
3.1. Energy Fluence of the MIT-FCB, NM, CN and UW CNTS Neutron Sources
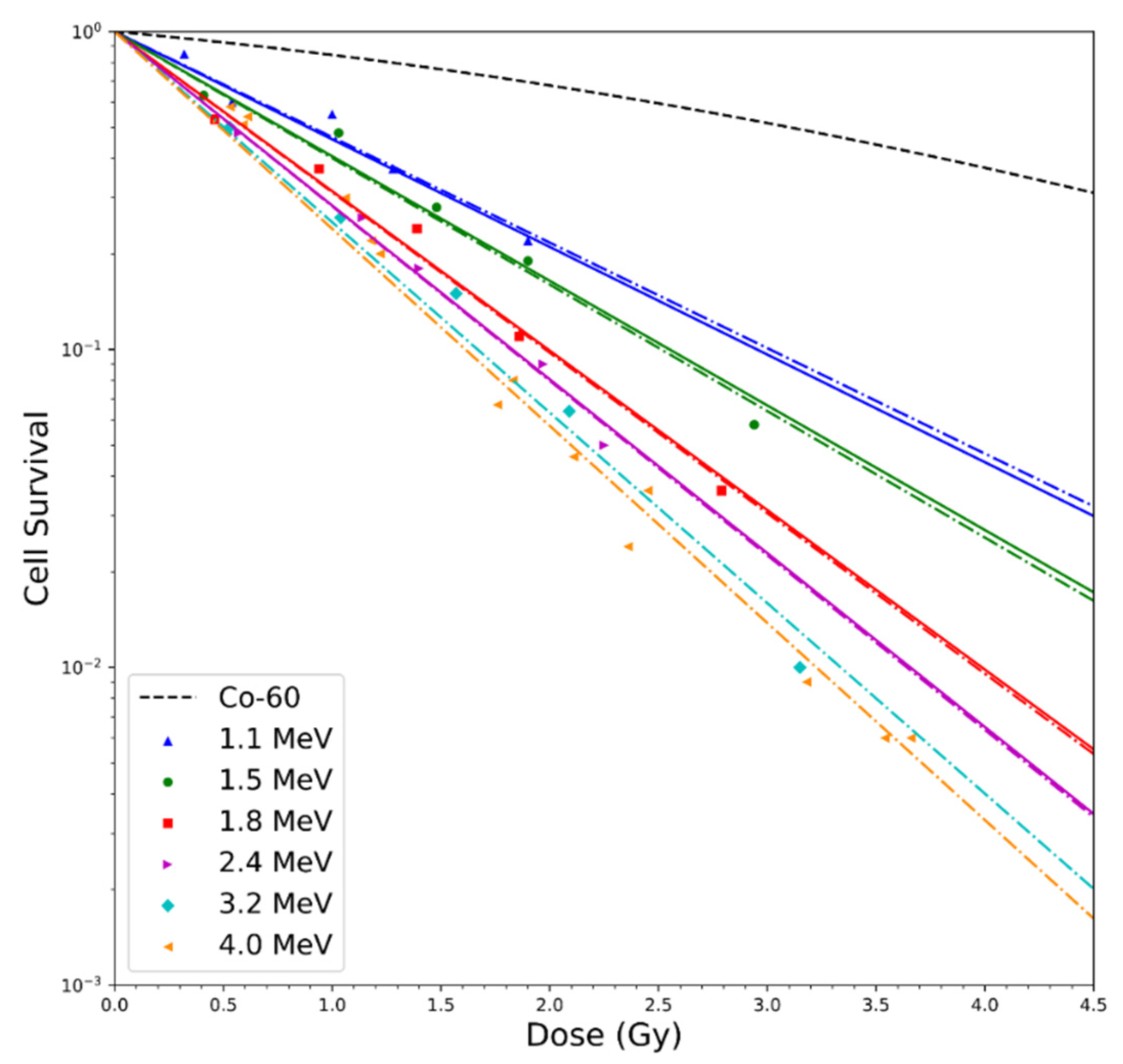
3.2. Proton and Alpha Particle Cell Survival Benchmarks
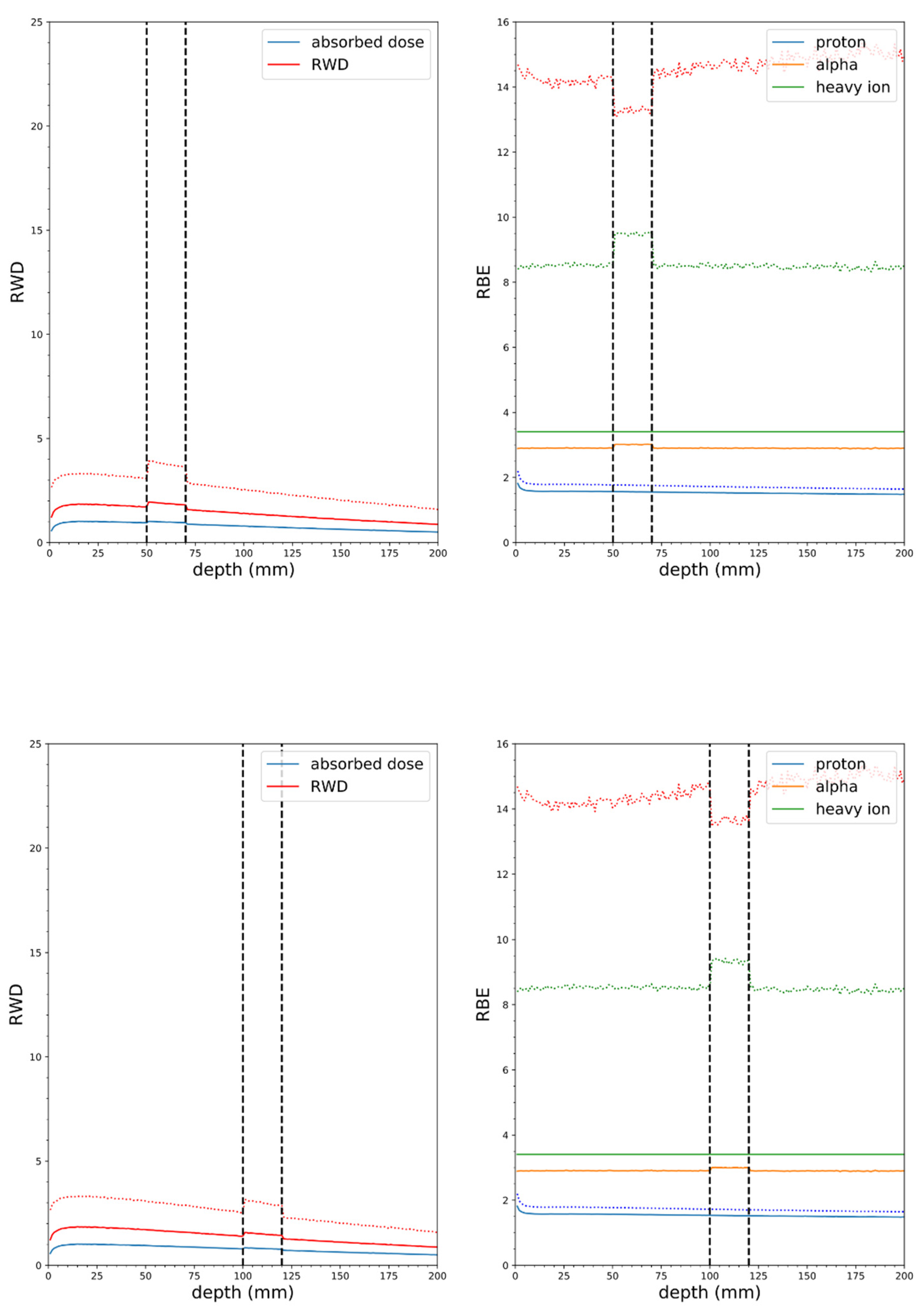
3.3. RBE of Selected Ions Produced in BNCT Reactions
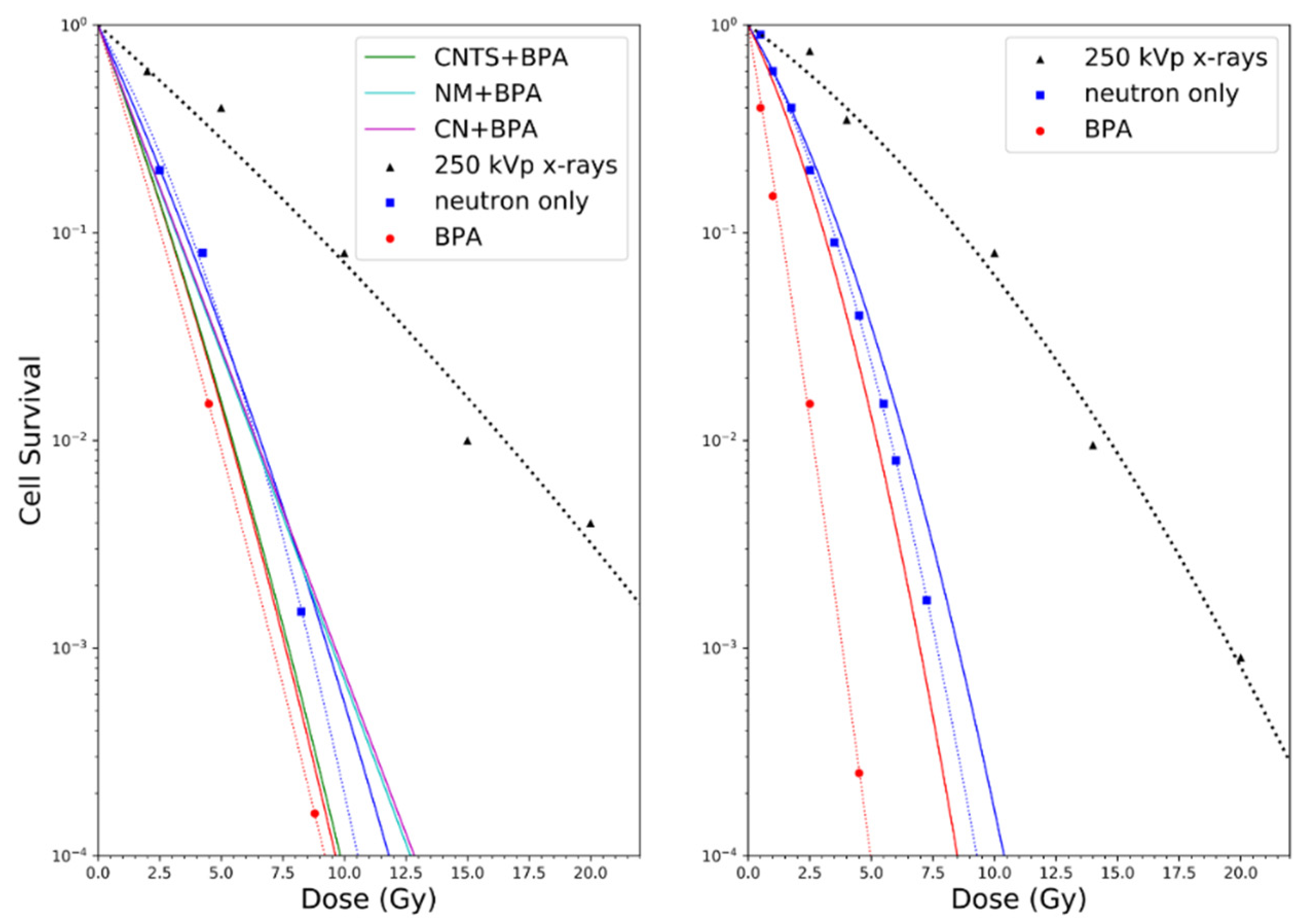
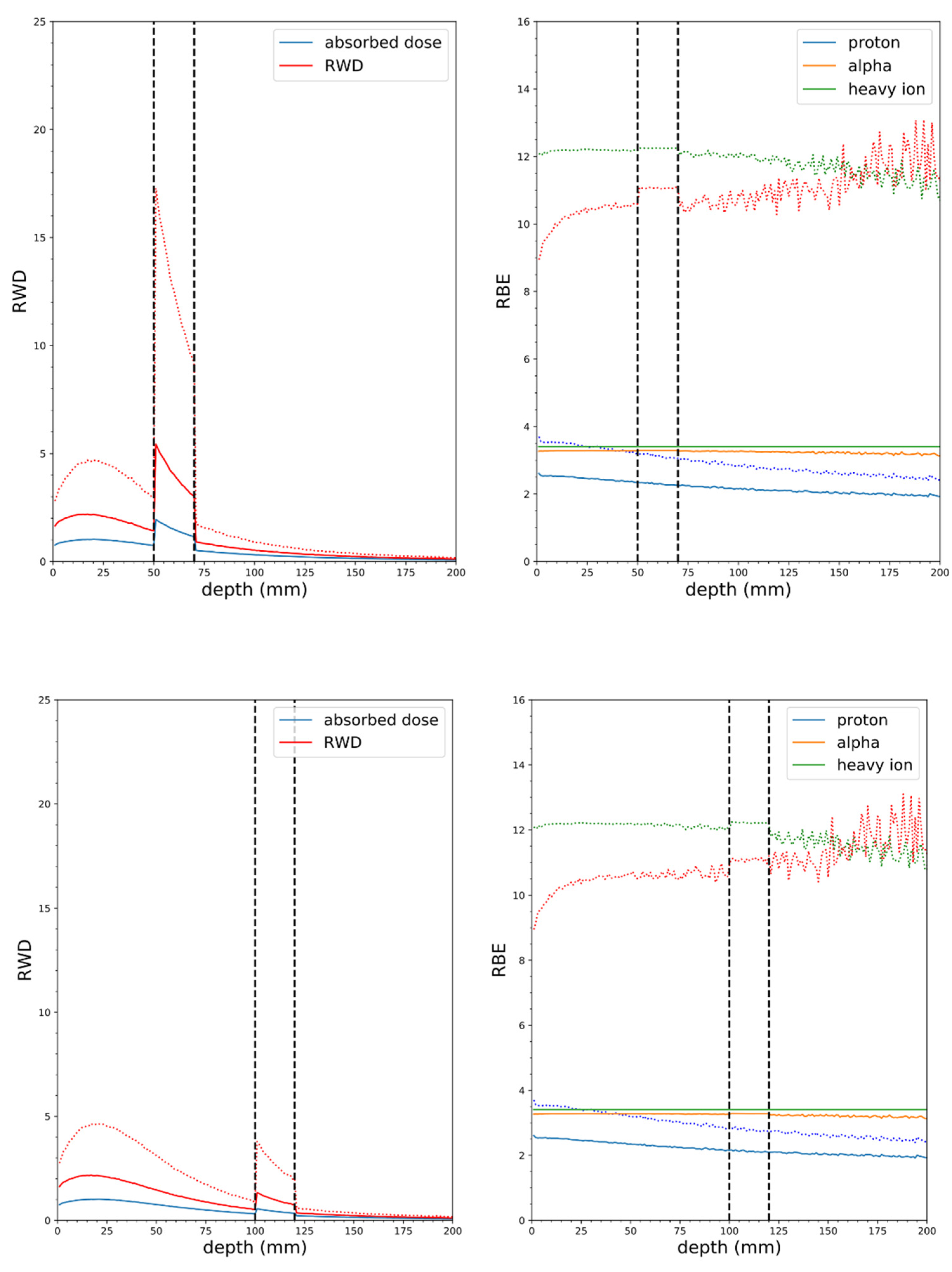
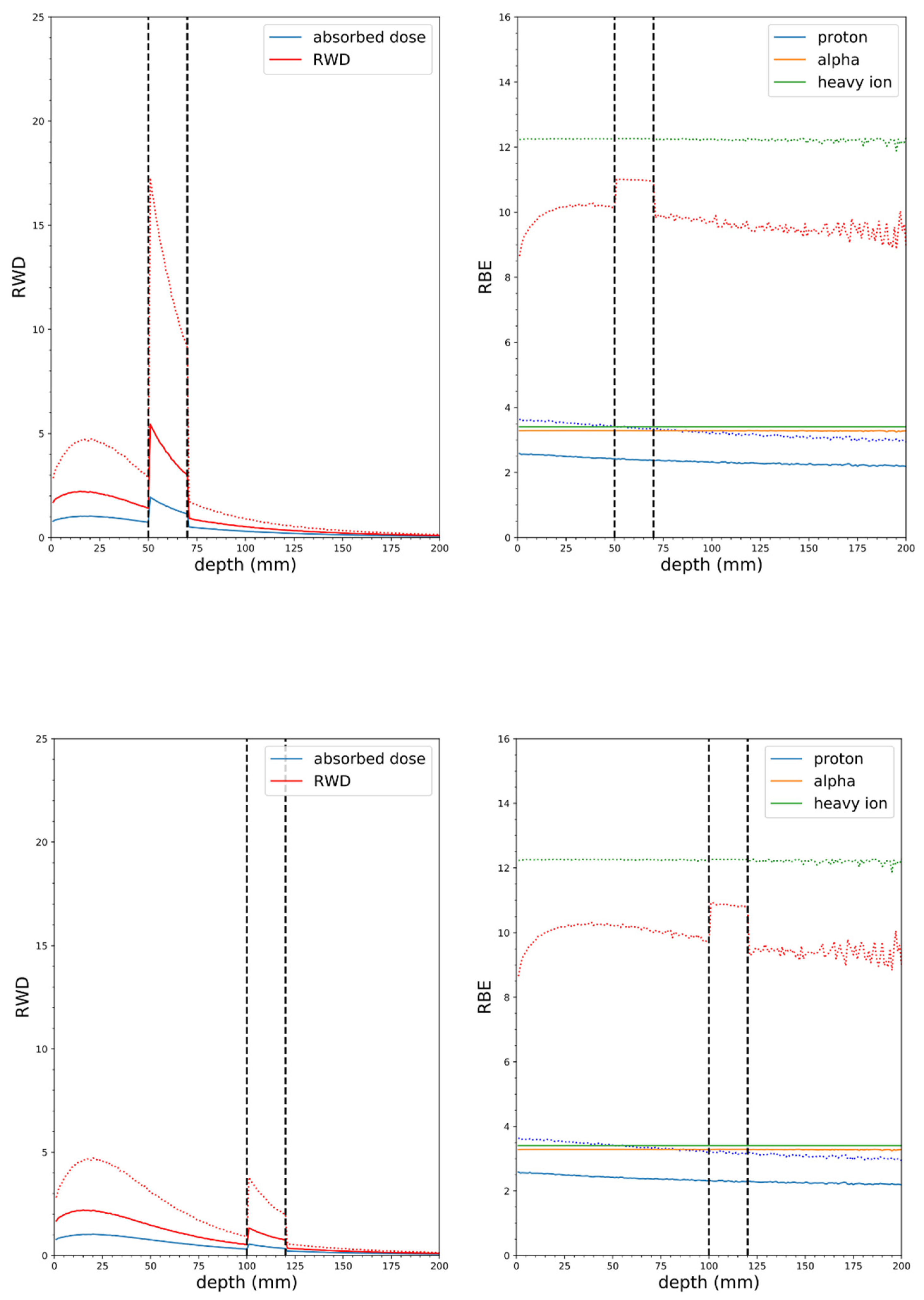
3.4. In Vitro and In Vivo Testing of the Dosimetry and CBE Models
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Barth, R.F. Boron neutron capture therapy at the crossroads: Challenges and opportunities. Appl. Radiat. Isot. 2009, 67, S3–S6. [Google Scholar] [CrossRef] [PubMed]
- Hopewell, J.W.; Morris, G.M.; Schwint, A.; Coderre, J.A.; Sauerwein, W.; Wittig, A.; Moss, R.L.; Nakagawa, Y. Boron neutron capture therapy: Application of radiobiological principles. In Textbook of Neutron Capture Therapy; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Coderre, J.A.; Elowitz, E.H.; Chadha, M.; Bergland, R.; Capala, J.; Joel, D.D.; Liu, H.B.; Slatkin, D.N.; Chanana, A.D. Boron neutron capture therapy for glioblastoma multiforme using p-boronophenylalanine and epithermal neutrons: Trial design and early clinical results. J. Neurooncol. 1997, 33, 141–152. [Google Scholar] [CrossRef] [PubMed]
- Laramore, G.E.; Spence, A.M. Boron neutron capture therapy (BNCT) for high-grade gliomas of the brain: A cautionary note. Radiat. Oncol. Biol. 1996, 36, 241–246. [Google Scholar] [CrossRef]
- Hawthorne, M.F.; Lee, M.W. A critical assessment of boron target compounds for boron neutron capture therapy. J. Neurooncol. 2003, 62, 33–45. [Google Scholar] [CrossRef] [PubMed]
- Coderre, J.A.; Morris, G.M. The radiation biology of boron neutron capture therapy. Radiat. Res. 1999, 151, 1–18. [Google Scholar] [CrossRef]
- Laramore, G.E.; Risler, R.; Griffin, T.W.; Wootton, P. Fast neutron radiotherapy and boron neutron capture therapy: Application to a human melanoma test system. Bull. Cancer Radiother. 1996. [Google Scholar] [CrossRef]
- Menéndez, P.R.; Roth, B.M.C.; Pereira, M.D.; Casal, M.R.; González, S.J.; Feld, D.B.; Santa Cruz, G.A.; Kessler, J.; Longhino, J.; Blaumann, H.; et al. BNCT for skin melanoma in extremities: Updated Argentine clinical results. Appl. Radiat. Isot. 2009, 67, S50–S53. [Google Scholar] [CrossRef]
- Riley, K.J.; Binns, P.J.; Harling, O.K. Performance characteristics of the MIT fission converter based epithermal neutron beam. Phys. Med. Biol. 2003, 48, 943–958. [Google Scholar] [CrossRef]
- Riley, K.J.; Binns, P.J.; Harling, O.K. A state-of-the-art epithermal neutron irradiation facility for neutron capture therapy. Phys. Med. Biol. 2004, 49, 3725–3735. [Google Scholar] [CrossRef]
- Mundy, D.W.; Harb, W.; Jevremovic, T. Radiation binary targeted therapy for HER-2 positive breast cancers: Assumptions, theoretical assessment and future directions. Phys. Med. Biol. 2006, 51, 1377–1391. [Google Scholar] [CrossRef]
- Sztejnberg Gonçalves-Carralves, M.L.; Jevremovic, T. Numerical assessment of radiation binary targeted therapy for HER-2 positive breast cancers: Advanced calculations and radiation dosimetry. Phys. Med. Biol. 2007, 52, 4245–4264. [Google Scholar] [CrossRef] [PubMed]
- Mitri, Z.; Constantine, T.; O’Regan, R. The HER2 Receptor in Breast Cancer: Pathophysiology, Clinical Use, and New Advances in Therapy. Chemother. Res. Pract. 2012, 2012, 743193. [Google Scholar] [CrossRef] [PubMed]
- Dijkers, E.C.; Oude Munnink, T.H.; Kosterink, J.G.; Brouwers, A.H.; Jager, P.L.; de Jong, J.R.; van Dongen, G.A.; Schröder, C.P.; Lub-de Hooge, M.N.; de Vries, E.G. Biodistribution of 89Zr-trastuzumab and PET imaging of HER2-positive lesions in patients with metastatic breast cancer. Clin. Pharmacol. Ther. 2010, 87, 586–592. [Google Scholar] [CrossRef] [PubMed]
- Nigg, D.W.; Wemple, C.A.; Risler, R.; Hartwell, J.K.; Harker, Y.D.; Laramore, G.E. Modification of the University of Washington Neutron Radiotherapy Facility for optimization of neutron capture enhanced fast-neutron therapy. Med. Phys. 2000, 27, 359–367. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, D.L.; Einck, J.; Bellon, J.; Laramore, G.E. Fast neutron radiotherapy for soft tissue and cartilaginous sarcomas at high risk for local recurrence. Radiat. Oncol. Biol. 2001, 50, 449–456. [Google Scholar] [CrossRef]
- Kalet, I.; Jacky, J.; Risler, R.; Rohlin, S.; Wootton, P. Integration of radiotherapy planning systems and radiotherapy treatment equipment: 11 years experience. Int. J. Radiat. Oncol. Biol. Phys. 1997, 38, 213–221. [Google Scholar] [CrossRef]
- Kalet, A.M.; Sandison, G.A.; Phillips, M.H.; Parvathaneni, U. Validation of the Pinnacle™ photon convolution-superposition algorithm applied to fast neutron beams. J. Appl. Clin. Med. Phys. 2013, 14, 133–154. [Google Scholar] [CrossRef]
- Moffitt, G.B.; Stewart, R.D.; Sandison, G.A.; Goorley, J.T.; Argento, D.C.; Jevremovic, T. MCNP6 model of the University of Washington clinical neutron therapy system (CNTS). Phys. Med. Biol. 2016, 61, 937–957. [Google Scholar] [CrossRef]
- Stewart, R.D.; Streitmatter, S.W.; Argento, D.C.; Kirkby, C.; Goorley, J.T.; Moffitt, G.; Jevremovic, T.; Sandison, G.A. Rapid MCNP simulation of DNA double strand break (DSB) relative biological effectiveness (RBE) for photons, neutrons, and light ions. Phys. Med. Biol. 2015, 60, 8249–8274. [Google Scholar] [CrossRef]
- Carlson, D.; Stewart, R.; Semenenko, V.; Sandison, G. Combined use of Monte Carlo DNA damage Simulations and deterministic repair models to examine putative mechanisms of cell killing. Radiat. Res. 2008, 169, 447–459. [Google Scholar] [CrossRef]
- Stewart, R.D.; Carlson, D.J.; Butkus, M.P.; Hawkins, R.; Friedrich, T.; Scholz, M. A comparison of mechanism-inspired models for particle relative biological effectiveness (RBE). Med. Phys. 2018, 45, e925–e952. [Google Scholar] [CrossRef]
- ICRU. Microdosimetry. Report 36; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1983. [Google Scholar]
- Georgakilas, A.G. Role of the immune system and inflammation in ionizing radiation effects. Cancer Lett. 2015, 368, 154–155. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; O’Neill, P.; Goodhead, D.T.; Terrissol, M. Computational modelling of low-energy electron-induced DNA damage by early physical and chemical events. Int. J. Radiat. Biol. 1997, 71, 467–483. [Google Scholar] [CrossRef] [PubMed]
- Nikjoo, H.; O’Neill, P.; Terrissol, M.; Goodhead, D.T. Quantitative modelling of DNA damage using Monte Carlo track structure method. Radiat. Environ. Biophys. 1999, 38, 31–38. [Google Scholar] [CrossRef]
- Nikjoo, H.; Bolton, C.E.; Watanabe, R.; Terrissol, M.; O’Neill, P.; Goodhead, D.T. Modelling of DNA damage induced by energetic electrons (100 eV to 100 keV). Radiat. Prot. Dosim. 2002, 99, 77–80. [Google Scholar] [CrossRef]
- Friedland, W.; Jacob, P.; Bernhardt, P.; Paretzke, H.G.; Dingfelder, M. Simulation of DNA damage after proton irradiation. Radiat. Res. 2003, 159, 401–410. [Google Scholar] [CrossRef]
- Campa, A.; Alloni, D.; Antonelli, F.; Ballarini, F.; Belli, M.; Dini, V.; Esposito, G.; Facoetti, A.; Friedland, W.; Furusawa, Y.; et al. DNA fragmentation induced in human fibroblasts by 56Fe ions: Experimental data and Monte Carlo simulations. Radiat. Res. 2009, 171, 438–445. [Google Scholar] [CrossRef]
- Alloni, D.; Campa, A.; Belli, M.; Esposito, G.; Facoetti, A.; Friedland, W.; Liotta, M.; Mariotti, L.; Paretzke, H.G.; Ottolenghi, A. A Monte Carlo study of the radiation quality dependence of DNA fragmentation spectra. Radiat. Res. 2010, 173, 263–271. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.; Stewart, R. Monte Carlo simulation of DNA damage induction by x-rays and selected radioisotopes. Phys. Med. Biol. 2008, 53, 233. [Google Scholar] [CrossRef]
- Stewart, R.D.; Yu, V.K.; Georgakilas, A.G.; Koumenis, C.; Park, J.H.; Carlson, D.J. Effects of Radiation Quality and Oxygen on Clustered DNA Lesions and Cell Death. Radiat. Res. 2011, 176, 587–602. [Google Scholar] [CrossRef]
- Streitmatter, S.W.; Stewart, R.D.; Jenkins, P.A.; Jevremovic, T. DNA double strand break (DSB) induction and cell survival in iodine-enhanced computed tomography (CT). Phys. Med. Biol. 2017, 62, 6164–6184. [Google Scholar] [CrossRef] [PubMed]
- Mairani, A.; Dokic, I.; Magro, G.; Tessonnier, T.; Kamp, F.; Carlson, D.J.; Ciocca, M.; Cerutti, F.; Sala, P.R.; Ferrari, A.; et al. Biologically optimized helium ion plans: Calculation approach and its in vitro validation. Phys. Med. Biol. 2016, 4283–4299. [Google Scholar] [CrossRef] [PubMed]
- Kamp, F.; Cabal, G.; Mairani, A.; Parodi, K.; Wilkens, J.J.; Carlson, D.J. Fast Biological Modeling for Voxel-based Heavy Ion Treatment Planning Using the Mechanistic Repair-Misrepair-Fixation Model and Nuclear Fragment Spectra. Int. J. Radiat. Oncol. Biol. Phys. 2015, 93, 557–568. [Google Scholar] [CrossRef] [PubMed]
- Frese, M.; Yu, V.; Stewart, R.; Carlson, D. A Mechanism-Based Approach to Predict the Relative Biological Effectiveness of Protons and Carbon Ions in Radiation Therapy. Radiat. Oncol. Biol. 2012, 83, 442–450. [Google Scholar] [CrossRef] [PubMed]
- Pelowitz, D.B. (Ed.) MCNPX Users Manual Version 2.7.0; LA-CP-11-00438; Los Alamos National Laboratory: Los Alamos, NM, USA, 2011. [Google Scholar]
- Elbast, M.; Saudo, A.; Franck, D.; Petitot, F.; Desbree, A. Microdosimetry of alpha particles for simple and 3D voxelised geometries using MCNPX and Geant4 Monte Carlo codes. Radiat. Prot. Dosim. 2012, 150, 342–349. [Google Scholar] [CrossRef]
- Nguyen, T.; Brownell, G.L.; Holden, S.A.; Kahl, S.; Miura, M.; Teicher, B.A. Subcellular distribution of various boron compounds and implications for their efficacy in boron neutron capture therapy by Monte Carlo simulations. Radiat. Res. 1993, 133, 33–40. [Google Scholar] [CrossRef] [PubMed]
- ICRU. Photon, Electron, Proton and Neutron Interaction Data for Body Tissues; Report 46; International Commission on Radiation Units and Measurements: Bethesda, MD, USA, 1992. [Google Scholar]
- Burmeister, J.; Riley, K.; Coderre, J.A.; Harling, O.K.; Ma, R.; Wielopolski, L.; Kota, C.; Maughan, R.L. Microdosimetric intercomparison of BNCT beams at BNL and MIT. Med. Phys. 2003, 30, 2131. [Google Scholar] [CrossRef]
- Binns, P.J.; Riley, K.J.; Harling, O.K. Epithermal neutron beams for clinical studies of boron neutron capture therapy: A dosimetric comparison of seven beams. Radiat. Res. 2005, 164, 212–220. [Google Scholar] [CrossRef]
- Rasouli, F.S.; Masoudi, S.F. Design and optimization of a beam shaping assembly for BNCT based on D–T neutron generator and dose evaluation using a simulated head phantom. Appl. Radiat. Isot. 2012, 70, 2755–2762. [Google Scholar] [CrossRef]
- Bichsel, H.; Eenmaa, J.; Weaver, K.; Williams, D.L.; Wootton, P.; Wyckoff, W.G. A physics cyclotron adapted for fast neutron beam therapy. Phys. Med. Biol. 1974, 19, 236. [Google Scholar] [CrossRef]
- Stelzer, K.J.; Laramore, G.E.; Griffin, T.W.; Koh, W.J.; Austin-Seymour, M.; Russell, K.J.; Buchholz, T.A. Fast neutron radiotherapy. The University of Washington experience. Acta Oncol. 1994, 33, 275–280. [Google Scholar] [CrossRef] [PubMed]
- Douglas, J.G.; Koh, W.-J.; Austin-Seymour, M.; Laramore, G.E. Treatment of salivary gland neoplasms with fast neutron radiotherapy. Arch. Otolaryngol. Head Neck Surg. 2003, 129, 944–948. [Google Scholar] [CrossRef] [PubMed]
- Auterinen, I.; Serén, T.; Anttila, K.; Kosunen, A.; Savolainen, S. Measurement of free beam neutron spectra at eight BNCT facilities worldwide. Appl. Radiat. Isot. 2004, 61, 1021–1026. [Google Scholar] [CrossRef]
- Verbeke, J.M.; Vujic, J.L.; Leung, K.N. Neutron beam optimization for boron neutron capture therapy using the DD and DT high-energy neutron sources. Nucl. Technol. 2000, 129, 257–278. [Google Scholar] [CrossRef]
- Maughan, R.L.; Kota, C.; Yudelev, M. A microdosimetric study of the dose enhancement in a fast neutron beam due to boron neutron capture. Phys. Med. Biol. 1993, 38, 1957–1961. [Google Scholar] [CrossRef]
- Buchholz, T.A.; Laramore, G.E.; Stelzer, K.J.; Risler, R.; Wootton, P.; Griffin, T.W. Boron neutron capture enhanced fast neutron radiotherapy for malignant gliomas and other tumors. J. Neurooncol. 1997, 33, 171–178. [Google Scholar] [CrossRef]
- Laramore, G.E.; Wootton, P.; Livesey, J.C.; Wilbur, D.S.; Risler, R.; Phillips, M.; Jacky, J.; Buchholz, T.A.; Griffin, T.W.; Brossard, S. Boron neutron capture therapy: A mechanism for achieving a concomitant tumor boost in fast neutron radiotherapy. Radiat. Oncol. Biol. 1994, 28, 1135–1142. [Google Scholar] [CrossRef]
- Goodhead, D.T.; Belli, M.; Mill, A.J.; Bance, D.A. Direct comparison between protons and alpha-particles of the same LET: I. Irradiation methods and inactivation of asynchronous V79, HeLa and C3H 10T½ cells. Int. J. Radiat. Biol. 1992, 61, 611–624. [Google Scholar] [CrossRef]
- Tracy, B.L.; Stevens, D.L.; Goodhead, D.T.; Hill, M.A. Variation in RBE for Survival of V79-4 Cells as a Function of Alpha-Particle (Helium Ion) Energy. Radiat. Res. 2015, 184, 33–45. [Google Scholar] [CrossRef]
- Coderre, J.A.; Makar, M.S.; MICCA, P.L.; Nawrocky, M.M.; Liu, H.B.; Joel, D.D.; Slatkin, D.N.; Amols, H.I. Derivations of relative biological effectiveness for the high-let radiations produced during boron neutron capture irradiations of the 9l rat gliosarcoma in vitro and in vivo. Radiat. Oncol. Biol. 1993, 27, 1121–1129. [Google Scholar] [CrossRef]
- Bennett, B.D.; Mumford-Zisk, J.; Coderre, J.A.; Morrison, G.H. Subcellular localization of p-boronophenylalanine-delivered boron-10 in the rat 9L gliosarcoma: Cryogenic preparation in vitro and in vivo. Radiat. Res. 1994, 140, 72–78. [Google Scholar] [CrossRef]
- Van Dongen, G.A.M.S.; Visser, G.W.M.; Lub-de Hooge, M.N.; de Vries, E.G.; Perk, L.R. Immuno-PET: A navigator in monoclonal antibody development and applications. Oncologist 2007, 12, 1379–1389. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.H.; Yoon, S.M.; Park, S.H.; Choi, I.S.; Kim, J.K.; Choi, E.K.; Ahn, S.D.; Lee, S.-W.; Song, S.Y.; Kim, J.H. A treatment planning study on glioblastoma with different techniques using boron neutron capture therapy, 3-dimensional conformal radiotherapy, and intensity modulated radiotherapy. Appl. Radiat. Isot. 2009, 67, 1180–1184. [Google Scholar] [CrossRef]
- Mairani, A.; Böhlen, T.T.; Schiavi, A.; Tessonnier, T.; Molinelli, S.; Brons, S.; Battistoni, G.; Parodi, K.; Patera, V. A Monte Carlo-based treatment planning tool for proton therapy. Phys. Med. Biol. 2013, 58, 2471–2490. [Google Scholar] [CrossRef]
- Horiguchi, H.; Sato, T.; Kumada, H.; Yamamoto, T.; Sakae, T. Estimation of relative biological effectiveness for boron neutron capture therapy using the PHITS code coupled with a microdosimetric kinetic model. J. Radiat. Res. 2014, 56, 382–390. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Kase, Y.; Watanabe, R.; Niita, K.; Sihver, L. Biological Dose Estimation for Charged-Particle Therapy Using an Improved PHITS Code Coupled with a Microdosimetric Kinetic Model. Radiat. Res. 2009, 171, 107–117. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Furusawa, Y. Cell survival fraction estimation based on the probability densities of domain and cell nucleus specific energies using improved microdosimetric kinetic models. Radiat. Res. 2012, 178, 341–356. [Google Scholar] [CrossRef]
- González, S.J.; Cruz, G.A.S. The Photon-Isoeffective Dose in Boron Neutron Capture Therapy. Radiat. Res. 2012, 178, 609–621. [Google Scholar] [CrossRef]


| Particle | E (MeV) | LET (keV/μm) | CSDA Range (μm) | ||
|---|---|---|---|---|---|
| 1H1+ | 0.59 | 38.03 | 11.09 | 0.34 | 0.31 |
| 4He2+ | 1.47 | 186.5 | 8.28 | 1.69 | 1.52 |
| 4He2+ | 1.78 | 170.4 | 10.02 | 1.54 | 1.39 |
| 7Li3+ | 0.84 | 369.1 | 4.18 | 1.79 | 3.01 |
| 7Li3+ | 1.01 | 386.1 | 4.63 | 2.07 | 3.15 |
| Particle | LET (keV/μm) | α (Gy−1) | RBEDSB | ||
|---|---|---|---|---|---|
| Goodhead et al. | MCDS * | Goodhead et al. | MCDS + RMF * | MCDS * | |
| 1.2 MeV +H | 22.02 | 23.65 | 0.30 | 0.29 | 1.80 |
| 1.4 MeV +H | 19.67 | 21.13 | 0.42 | 0.27 | 1.71 |
| 30 MeV α | 23.00 | 22.72 | 0.21 | 0.25 | 1.56 |
| 35 MeV α | 20.45 | 20.07 | 0.25 | 0.23 | 1.50 |
| Dose-Weighted LET (keV/μm) | RBEDSB | |||||
|---|---|---|---|---|---|---|
| α Energy (MeV) | Tracy et al. | MCDS + MCNP | MCDS + MCNP | RMF Fit | MCDS + MCNP | |
| 5 µm | 3–6 µm | |||||
| 1.1 | 181 | 203 | 1.09 | 3.76–0.67 | 1.03 | 3.30 |
| 1.5 | 201 | 213 | 1.60 | 5.33–1.16 | 1.66 | 3.24 |
| 1.8 | 190 | 195 | 1.69 | 4.67–1.16 | 2.68 | 3.19 |
| 2.4 | 161 | 161 | 1.44 | 3.84–1.02 | 3.32 | 3.09 |
| 3.2 | 131 | 130 | 1.13 | 3.06–0.79 | 4.21 | 2.96 |
| 4.0 | 112 | 110 | 0.94 | 2.56–0.66 | 4.90 | 2.84 |
| Protons | Alphas | Lithium | Heavy Ions | |||||
|---|---|---|---|---|---|---|---|---|
| Neutron source | RBEHD = RBEDSB | RBELD (α/β = 3 Gy) | RBEHD = RBEDSB | RBELD (α/β = 3 Gy) | RBEHD = RBEDSB | RBELD (α/β = 3 Gy) | RBEHD = RBEDSB | RBELD (α/β = 3 Gy) |
| MIT-FCB | 2.85 | 3.42 | 3.06 | 8.79 | 3.39 | 7.05 | 3.15 | 6.39 |
| NM | 2.57 | 3.47 | 3.02 | 8.74 | 3.39 | 7.08 | 3.15 | 6.55 |
| CN | 2.54 | 3.38 | 3.04 | 9.06 | 3.39 | 6.82 | 3.15 | 5.59 |
| UW CNTS | 2.22 | 3.01 | 2.79 | 7.86 | 3.39 | 7.05 | 3.15 | 11.2 |
| RBEHD = RBEDSB | RBELD (α/β = 87) | RBELD (α/β = 3) | RBELD (α/β = 10) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Neutron source | no 10B | BPA | mAb | no 10B | BPA | mAb | no 10B | BPA | mAb | no 10B |
| MIT-FCB | 2.87 | 2.97 | 3.04 | 2.89 | 3.06 | 3.17 | 3.46 | 5.78 | 6.99 | 3.09 |
| NM | 2.63 | 2.66 | 2.69 | 2.68 | 2.71 | 2.75 | 3.99 | 4.08 | 4.34 | 3.02 |
| CN | 2.62 | 2.63 | 2.69 | 2.66 | 2.68 | 2.75 | 3.71 | 3.94 | 4.47 | 2.94 |
| UW CNTS | 2.66 | 2.66 | 2.72 | 2.80 | 2.81 | 2.88 | 6.86 | 6.88 | 7.40 | 4.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Streitmatter, S.W.; Stewart, R.D.; Moffitt, G.; Jevremovic, T. Mechanistic Modeling of the Relative Biological Effectiveness of Boron Neutron Capture Therapy. Cells 2020, 9, 2302. https://doi.org/10.3390/cells9102302
Streitmatter SW, Stewart RD, Moffitt G, Jevremovic T. Mechanistic Modeling of the Relative Biological Effectiveness of Boron Neutron Capture Therapy. Cells. 2020; 9(10):2302. https://doi.org/10.3390/cells9102302
Chicago/Turabian StyleStreitmatter, Seth W., Robert D. Stewart, Gregory Moffitt, and Tatjana Jevremovic. 2020. "Mechanistic Modeling of the Relative Biological Effectiveness of Boron Neutron Capture Therapy" Cells 9, no. 10: 2302. https://doi.org/10.3390/cells9102302
APA StyleStreitmatter, S. W., Stewart, R. D., Moffitt, G., & Jevremovic, T. (2020). Mechanistic Modeling of the Relative Biological Effectiveness of Boron Neutron Capture Therapy. Cells, 9(10), 2302. https://doi.org/10.3390/cells9102302





