Ensemble of Deep Recurrent Neural Networks for Identifying Enhancers via Dinucleotide Physicochemical Properties
Abstract
1. Introduction
2. Materials and Methods
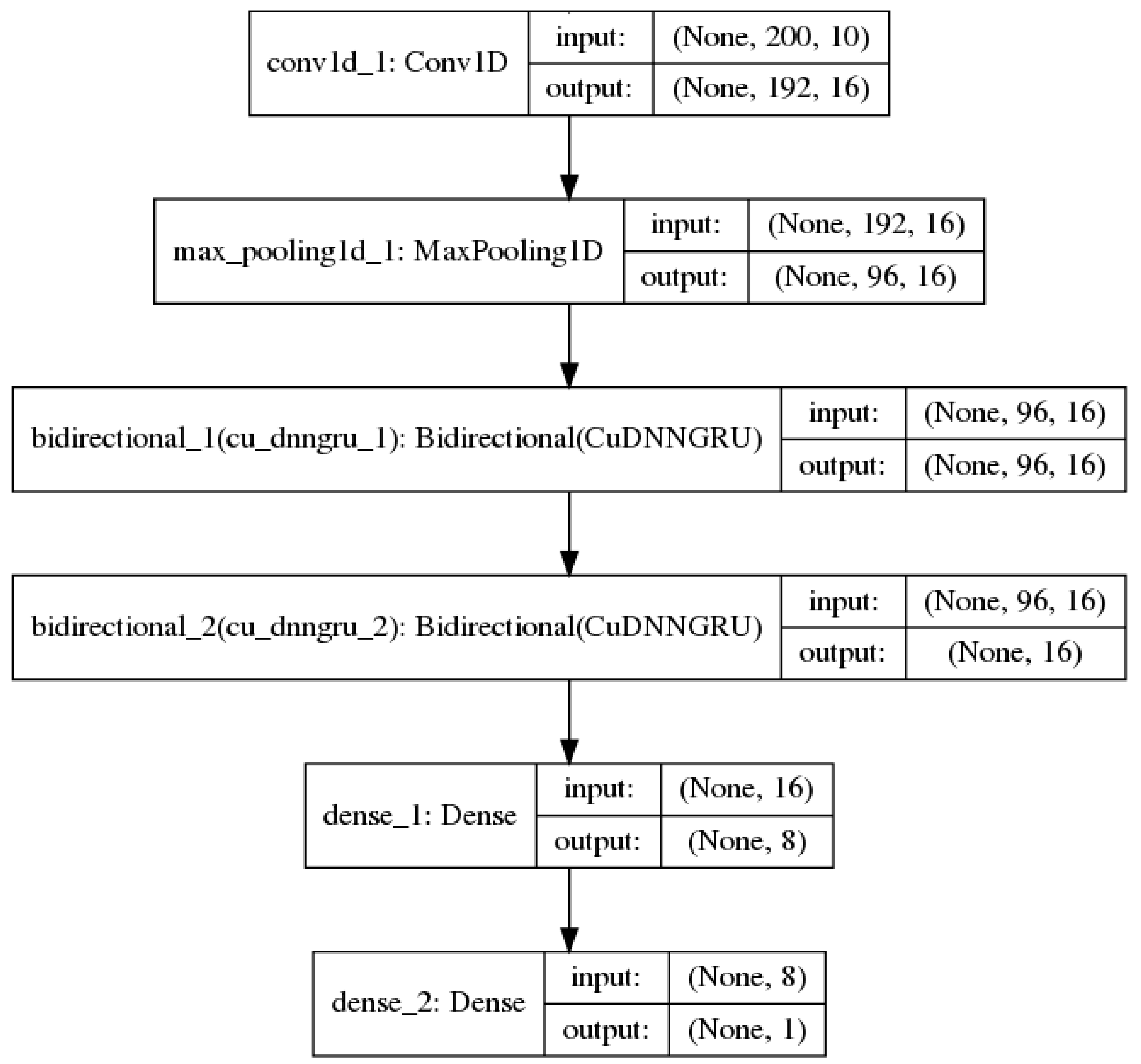
2.1. Convolutional Neural Networks
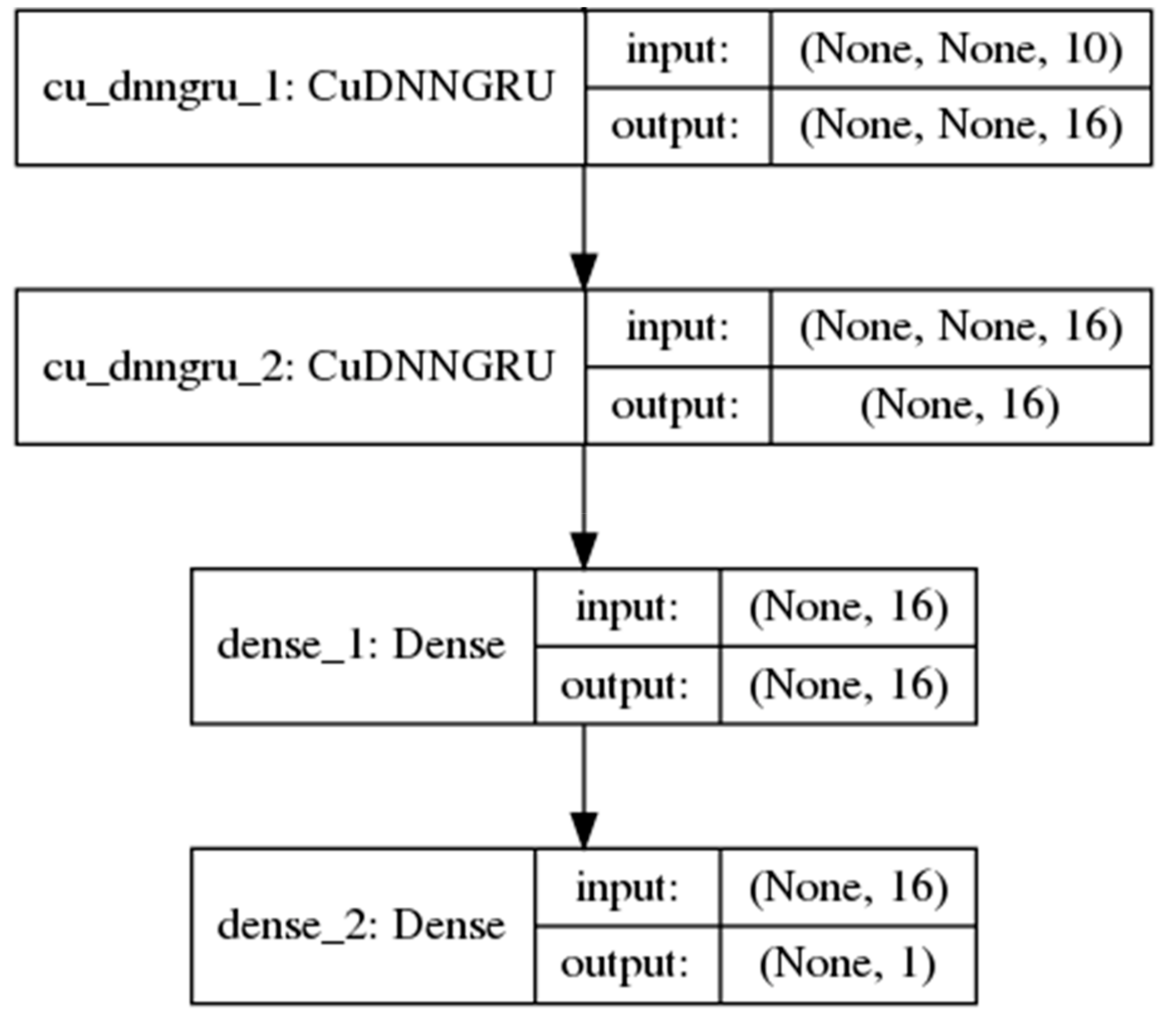
2.2. Recurrent Neural Networks
2.3. Model Ensembles
3. Experiment
3.1. Dataset and Machine Learning Task
3.2. Assessment of Predictive Ability
3.3. Model Training Setup
3.4. Feature Extraction
4. Results
4.1. Base Models
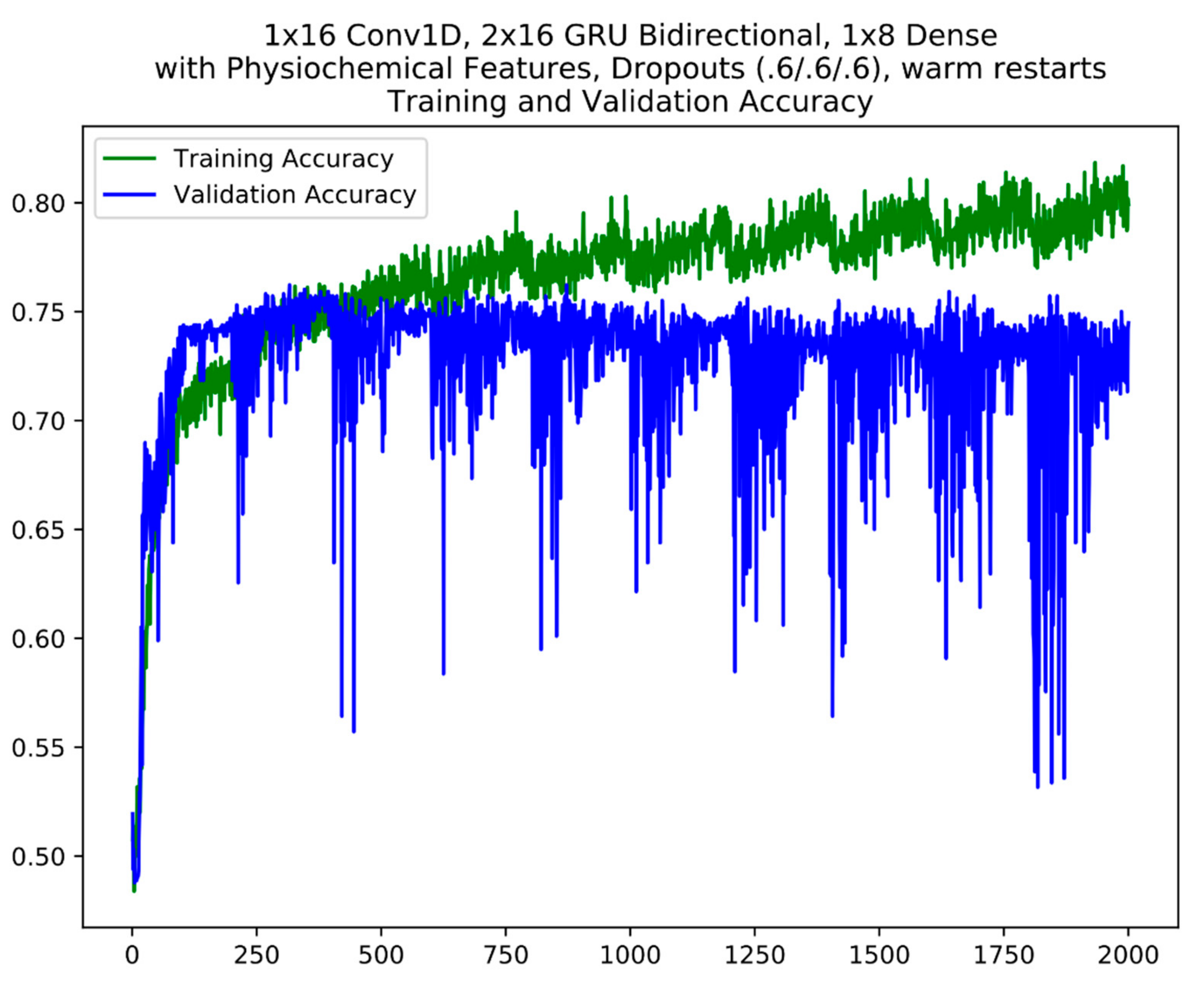
4.2. Model Fine-Tuning
4.3. Model Ensembles
4.4. Cross-Validation Results
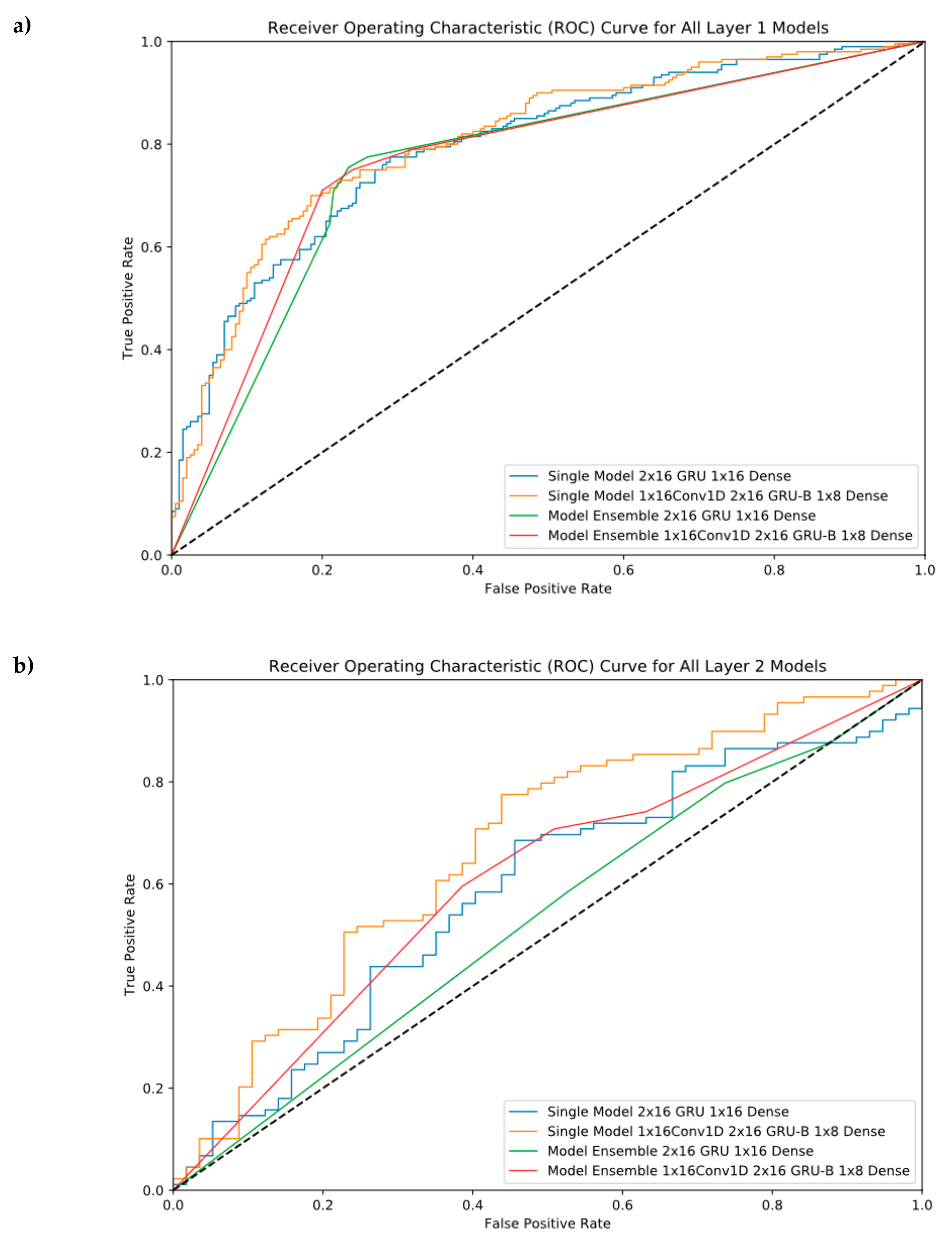
4.5. Independent Test Results
5. Discussion
5.1. General
5.2. Model Ensembles
5.3. Biological Discussion
5.4. Source Codes and Web Application for Reproducing the Results
- (1)
- Step 1: git clone this repository to your local machine using the command below:
- (2)
- Install all the required python package dependencies using the command below:“pip install -r requirements.txt”
- (3)
- Run the web server and Flask application using the command below:“python3 manage.py runserver”
- (4)
- Open a web browser and enter the following url: localhost:5000. The users should see our web application.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blackwood, E.M.; Kadonaga, J.T. Going the Distance: A Current View of Enhancer Action. Science 1998, 281, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Pennacchio, L.A.; Bickmore, W.; Dean, A.; Nobrega, M.A.; Bejerano, G. Enhancers: Five essential questions. Nat. Rev. Genet. 2013, 14, 288–295. [Google Scholar] [CrossRef] [PubMed]
- Boyle, A.P.; Song, L.; Lee, B.K.; London, D.; Keefe, D.; Birney, E.; Iyer, V.R.; Crawford, G.E.; Furey, T.S. High-resolution genome-wide in vivo footprinting of diverse transcription factors in human cells. Genome Res. 2011, 21, 456–464. [Google Scholar] [CrossRef] [PubMed]
- Rhie, S.K.; Tak, Y.G.; Guo, Y.; Yao, L.; Shen, H.; Coetzee, G.A.; Laird, P.W.; Farnham, P.J. Identification of activated enhancers and linked transcription factors in breast, prostate, and kidney tumors by tracing enhancer networks using epigenetic traits. Epigenetics Chromatin 2016, 9, 50. [Google Scholar] [CrossRef] [PubMed]
- Blinka, S.; Reimer, M.H.; Pulakanti, K.; Pinello, L.; Yuan, G.C.; Rao, S. Identification of Transcribed Enhancers by Genome-Wide Chromatin Immunoprecipitation Sequencing. In Enhancer RNAs: Methods and Protocols; Ørom, U.A., Ed.; Humana Press: New York, NY, USA, 2017; pp. 91–109. [Google Scholar]
- Xiong, L.; Kang, R.; Ding, R.; Kang, W.; Zhang, Y.; Liu, W.; Huang, Q.; Meng, J.; Guo, Z. Genome-wide Identification and Characterization of Enhancers Across 10 Human Tissues. Int. J. Biol. Sci. 2018, 14, 1321–1332. [Google Scholar] [CrossRef]
- Arbel, H.; Basu, S.; Fisher, W.W.; Hammonds, A.S.; Wan, K.H.; Park, S.; Weiszmann, R.; Booth, B.W.; Keranen, S.V.; Henriquez, C.; et al. Exploiting regulatory heterogeneity to systematically identify enhancers with high accuracy. Proc. Natl. Acad. Sci. USA 2019, 116, 900–908. [Google Scholar] [CrossRef] [PubMed]
- Huerta, M.; Downing, G.; Haseltine, F.; Seto, B.; Liu, Y. NIH Working Definition of Bioinformatics and Computational Biology; US National Institute of Health: Bethesda, MD, USA, 2000.
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Liu, B.; Li, K.; Huang, D.-S.; Chou, K.-C. iEnhancer-EL: Identifying enhancers and their strength with ensemble learning approach. Bioinformatics 2018, 34, 3835–3842. [Google Scholar] [CrossRef]
- Liu, B.; Fang, L.; Long, R.; Lan, X.; Chou, K.-C. iEnhancer-2L: A two-layer predictor for identifying enhancers and their strength by pseudo k-tuple nucleotide composition. Bioinformatics 2015, 32, 362–369. [Google Scholar] [CrossRef]
- Jia, C.; He, W. EnhancerPred: A predictor for discovering enhancers based on the combination and selection of multiple features. Sci. Rep. 2016, 6, 38741. [Google Scholar] [CrossRef]
- Liu, B. iEnhancer-PsedeKNC: Identification of enhancers and their subgroups based on Pseudo degenerate kmer nucleotide composition. Neurocomputing 2016, 217, 46–52. [Google Scholar] [CrossRef]
- He, W.; Jia, C. EnhancerPred2.0: Predicting enhancers and their strength based on position-specific trinucleotide propensity and electron–ion interaction potential feature selection. Mol. BioSyst. 2017, 13, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Firpi, H.A.; Ucar, D.; Tan, K. Discover regulatory DNA elements using chromatin signatures and artificial neural network. Bioinformatics 2010, 26, 1579–1586. [Google Scholar] [CrossRef] [PubMed]
- Rajagopal, N.; Xie, W.; Li, Y.; Wagner, U.; Wang, W.; Stamatoyannopoulos, J.; Ernst, J.; Kellis, M.; Ren, B. RFECS: A Random-Forest Based Algorithm for Enhancer Identification from Chromatin State. PLoS Comput. Biol. 2013, 9, e1002968. [Google Scholar] [CrossRef] [PubMed]
- Erwin, G.D.; Oksenberg, N.; Truty, R.M.; Kostka, D.; Murphy, K.K.; Ahituv, N.; Pollard, K.S.; Capra, J.A. Integrating Diverse Datasets Improves Developmental Enhancer Prediction. PLoS Comput. Biol. 2014, 10, e1003677. [Google Scholar] [CrossRef] [PubMed]
- Bu, H.; Gan, Y.; Wang, Y.; Zhou, S.; Guan, J. A new method for enhancer prediction based on deep belief network. BMC Bioinform. 2017, 18, 418. [Google Scholar] [CrossRef] [PubMed]
- Le, N.Q.K.; Yapp, E.K.Y.; Ho, Q.T.; Nagasundaram, N.; Ou, Y.Y.; Yeh, H.Y. iEnhancer-5Step: Identifying enhancers using hidden information of DNA sequences via Chou’s 5-step rule and word embedding. Anal. Biochem. 2019, 571, 53–61. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Min, X.; Zeng, W.; Chen, S.; Chen, N.; Chen, T.; Jiang, R. Predicting enhancers with deep convolutional neural networks. BMC Bioinform. 2017, 18, 478. [Google Scholar] [CrossRef]
- Yang, B.; Liu, F.; Ren, C.; Ouyang, Z.; Xie, Z.; Bo, X.; Shu, W. BiRen: Predicting enhancers with a deep-learning-based model using the DNA sequence alone. Bioinformatics 2017, 33, 1930–1936. [Google Scholar] [CrossRef]
- LeCun, Y. Generalization and Network Design Strategies, in Connectionism in Perspective; Elsevier: Amsterdam, The Netherlands, 1989; Volume 19. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning Publications Company: Shelter Island, NY, USA, 2017. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. LSTM can solve hard long time lag problems. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Cho, K.; Van Merrienboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning Phrase Representations Using RNN Encoder–Decoder for Statistical Machine Translation. arXiv 2014, arXiv:1406.1078, 1724–1734. [Google Scholar]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Jozefowicz, R.; Zaremba, W.; Sutskever, I. An empirical exploration of recurrent network architectures. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015. [Google Scholar]
- Dietterich, T.G. Ensemble methods in machine learning. In International Workshop on Multiple Classifier Systems; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Loshchilov, I.; Hutter, F. SGDR: Stochastic Gradient Descent with Warm Restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Huang, G.; Li, Y.; Pleiss, G.; Liu, Z.; Hopcroft, J.E.; Weinberger, K.Q. Snapshot Ensembles: Train 1, Get M for Free. arXiv 2017, arXiv:1704.00109. [Google Scholar]
- Wei, L.; Su, R.; Luan, S.; Liao, Z.; Manavalan, B.; Zou, Q.; Shi, X. Iterative feature representations improve N4-methylcytosine site prediction. Bioinformatics 2019. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Zhou, C.; Su, R.; Zou, Q. PEPred-Suite: Improved and robust prediction of therapeutic peptides using adaptive feature representation learning. Bioinformatics 2019. [Google Scholar] [CrossRef] [PubMed]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognition. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Chollet, F. Keras; 2015. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A system for large-scale machine learning. In Proceedings of the 12th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 16), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Carneiro, T.; Da Nobrega, R.V.M.; Nepomuceno, T.; Bian, G.-B.; De Albuquerque, V.H.C.; Filho, P.P.R. Performance Analysis of Google Colaboratory as a Tool for Accelerating Deep Learning Applications. IEEE Access 2018, 6, 61677–61685. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Chetlur, S.; Woolley, C.; Vandermersch, P.; Cohen, J.; Tran, J.; Catanzaro, B.; Shelhamer, E. Cudnn: Efficient Primitives for Deep Learning. arXiv 2014, arXiv:1410.0759. [Google Scholar]
- Chen, W.; Lei, T.-Y.; Jin, D.-C.; Lin, H.; Chou, K.-C. PseKNC: A flexible web server for generating pseudo K-tuple nucleotide composition. Anal. Biochem. 2014, 456, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Jia, C.; Yang, Q.; Zou, Q. NucPosPred: Predicting species-specific genomic nucleosome positioning via four different modes of general PseKNC. J. Theor. Biol. 2018, 450, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Tieleman, T.; Hinton, G. Divide the Gradient by a Running Average of Its Recent Magnitude. COURSERA Neural Networks for Machine Learning 6; 2012. [Google Scholar]
- Russell, S.J.; Norvig, P. Artificial Intelligence: A Modern Approach; Pearson Education Limited: Kuala Lumpur, Malaysia, 2016. [Google Scholar]
- Singh, A.P.; Mishra, S.; Jabin, S. Sequence based prediction of enhancer regions from DNA random walk. Sci. Rep. 2018, 8, 15912. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Breiman, L. Bias, Variance, and Arcing Classifiers; Tech. Rep. 460; Statistics Department, University of California: Berkeley, CA, USA, 1996. [Google Scholar]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Moretti, F.; Pizzuti, S.; Panzieri, S.; Annunziato, M. Urban traffic flow forecasting through statistical and neural network bagging ensemble hybrid modeling. Neurocomputing 2015, 167, 3–7. [Google Scholar] [CrossRef]
- Khwaja, A.; Naeem, M.; Anpalagan, A.; Venetsanopoulos, A.; Venkatesh, B. Improved short-term load forecasting using bagged neural networks. Electr. Power Syst. Res. 2015, 125, 109–115. [Google Scholar] [CrossRef]
- Schwenk, H.; Bengio, Y. Boosting neural networks. Neural Comput. 2000, 12, 1869–1887. [Google Scholar] [CrossRef]
- Zheng, J. Cost-sensitive boosting neural networks for software defect prediction. Expert Syst. Appl. 2010, 37, 4537–4543. [Google Scholar] [CrossRef]
- Kim, M.-J.; Kang, D.-K. Ensemble with neural networks for bankruptcy prediction. Expert Syst. Appl. 2010, 37, 3373–3379. [Google Scholar] [CrossRef]
- Mao, J. A case study on bagging, boosting and basic ensembles of neural networks for OCR. In Proceedings of the 1998 IEEE International Joint Conference on Neural Networks Proceedings IEEE World Congress on Computational Intelligence (Cat. No. 98CH36227), Anchorage, AK, USA, 4–9 May 1998; IEEE: New York, NY, USA, 1998. [Google Scholar]
- Assaad, M.; Boné, R.; Cardot, H. A new boosting algorithm for improved time-series forecasting with recurrent neural networks. Inf. Fusion 2008, 9, 41–55. [Google Scholar] [CrossRef]
| Rise | Roll | Shift | Slide | Tilt | Twist | |
|---|---|---|---|---|---|---|
| AA | 0.430303 | 0.403042 | 1.000000 | 0.545455 | 0.4 | 0.833333 |
| AC | 0.818182 | 0.695817 | 0.618557 | 1.000000 | 0.7 | 0.833333 |
| AG | 0.257576 | 0.315589 | 0.762887 | 0.772727 | 0.3 | 0.791667 |
| AT | 0.860606 | 1.000000 | 0.319588 | 0.863636 | 0.6 | 0.750000 |
| CA | 0.045455 | 0.220532 | 0.360825 | 0.090909 | 0.1 | 0.291667 |
| CC | 0.548485 | 0.171103 | 0.731959 | 0.545455 | 0.3 | 1.000000 |
| CG | 0.000000 | 0.304183 | 0.371134 | 0.000000 | 0.0 | 0.333333 |
| CT | 0.257576 | 0.315589 | 0.762887 | 0.772727 | 0.3 | 0.791667 |
| GA | 0.706061 | 0.277567 | 0.618557 | 0.500000 | 0.4 | 0.833333 |
| GC | 1.000000 | 0.536122 | 0.494845 | 0.500000 | 1.0 | 0.750000 |
| GG | 0.548485 | 0.171103 | 0.731959 | 0.545455 | 0.3 | 1.000000 |
| GT | 0.818182 | 0.695817 | 0.618557 | 1.000000 | 0.7 | 0.833333 |
| TA | 0.000000 | 0.000000 | 0.000000 | 0.136364 | 0.0 | 0.000000 |
| TC | 0.706061 | 0.277567 | 0.618557 | 0.500000 | 0.4 | 0.833333 |
| TG | 0.045455 | 0.220532 | 0.360825 | 0.090909 | 0.1 | 0.291667 |
| TT | 0.430303 | 0.403042 | 1.000000 | 0.545455 | 0.4 | 0.833333 |
| S/N | Conv1D/Maxpool | GRU | Dense | Acc (%) | @Epoch |
|---|---|---|---|---|---|
| Layer 1 | |||||
| #1 | - | 1 × 8 | - | 75.61 | 586 |
| #2 | - | 1 × 16 | - | 75.20 | 252 |
| #3 | - | 2 × 16 | - | 75.51 | 232 |
| #4 | - | 2 × 16 | 1 × 16 | 75.41 | 392 |
| #5 | - | 1 × 16b | 1 × 16 | 74.82 | 206 |
| #6 | 1 × 16(9)/2 | 2 × 8 | 1 × 8 | 74.49 | 44 |
| #7 | 1 × 16(9)/2 | 2 × 8b | 1 × 8 | 75.00 | 161 |
| Layer 2 | |||||
| #8 | - | 2 × 16 | 1 × 16 | 62.29 | 61 |
| #9 | 1 × 16(9)/2 | 2 × 8b | 1 × 8 | 60.27 | 68 |
| S/N | Conv1D/Maxpool | GRU | Dense | Regularization | Acc (%) | @Epoch |
|---|---|---|---|---|---|---|
| Layer 1 | ||||||
| #1 | - | 2 × 16 | 1 × 16 | dp 0.1 | 77.65 | 865 |
| #2 | - | 2 × 16 | 1 × 16 | dp 0.2 | 76.22 | 1044 |
| #3 | - | 2 × 16 | 1 × 16 | dp 0.3 | 76.12 | 3744 |
| #4 | - | 2 × 16 | 1 × 16 | dp 0.4 | 75.10 | 1104 |
| #5 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | dp 0.6 | 77.24 | 693 |
| #6 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | dp 0.6; l1l2 3 × 10−5 | 77.14 | 604 |
| Layer 2 | ||||||
| #7 | - | 2 × 16 | 1 × 16 | dp 0.1 | 62.96 | 547 |
| #8 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | dp 0.6 | 61.28 | 2081 |
| S/N | Conv1D/Maxpool | GRU | Dense | Warm Restarts | Acc (%) | @Epoch |
|---|---|---|---|---|---|---|
| Layer 1 | ||||||
| #1 | - | 2 × 16 | 1 × 16 | dp 0.1; cyc 200; max_lr 0.003 | 76.73 | 1283 |
| #2 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | dp 0.6; cyc 200; max_lr 0.001 | 76.22 | 871 |
| Layer 2 | ||||||
| #3 | - | 2 × 16 | 1 × 16 | dp 0.1; cyc 200; max_lr 0.003 | 63.30 | 228 |
| #4 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | dp 0.6; cyc 200; max_lr 0.001 | 59.60 | 1224 |
| S/N | Conv1D/Maxpool | GRU | Dense | # of Models | Acc (%) |
|---|---|---|---|---|---|
| Layer 1 | |||||
| #1 | - | 2 × 16 | 1 × 16 | 5 | 77.45 |
| #2 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | 3 | 76.43 |
| Layer 2 | |||||
| #3 | - | 2 × 16 | 1 × 16 | 3 | 63.64 |
| #4 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | 3 | 59.60 |
| Acc (%) | MCC | Sn (%) | Sp (%) | AUC (%) |
|---|---|---|---|---|
| Layer 1 | ||||
| 74.83 | 0.498 | 73.25 | 76.42 | 76.94 |
| Layer 2 | ||||
| 58.96 | 0.197 | 79.65 | 38.28 | 60.68 |
| S/N | Conv1D/Maxpool | GRU | Dense | Type | Acc (%) | MCC | Sn (%) | Sp (%) | AUC (%) |
|---|---|---|---|---|---|---|---|---|---|
| Layer 1 | |||||||||
| #1 | - | 2 × 16 | 1 × 16 | Single | 74 | 0.48 | 75.00 | 73.00 | 79.63 |
| #2 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | Single | 73.75 | 0.475 | 75.00 | 72.50 | 80.86 |
| #3 | - | 2 × 16 | 1 × 16 | Ensemble | 75.25 | 0.506 | 73.00 | 77.50 | 76.16 |
| #4 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | Ensemble | 75.5 | 0.51 | 75.50 | 76.00 | 77.04 |
| Layer 2 | |||||||||
| #5 | - | 2 × 16 | 1 × 16 | Single | 60.96 | 0.100 | 86.52 | 21.05 | 58.57 |
| #6 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | Single | 68.49 | 0.312 | 83.15 | 45.61 | 67.14 |
| #7 | - | 2 × 16 | 1 × 16 | Ensemble | 58.90 | 0.071 | 79.78 | 26.32 | 53.19 |
| #8 | 1 × 16(9)/2 | 2 × 16b | 1 × 8 | Ensemble | 62.33 | 0.201 | 70.79 | 49.12 | 60.48 |
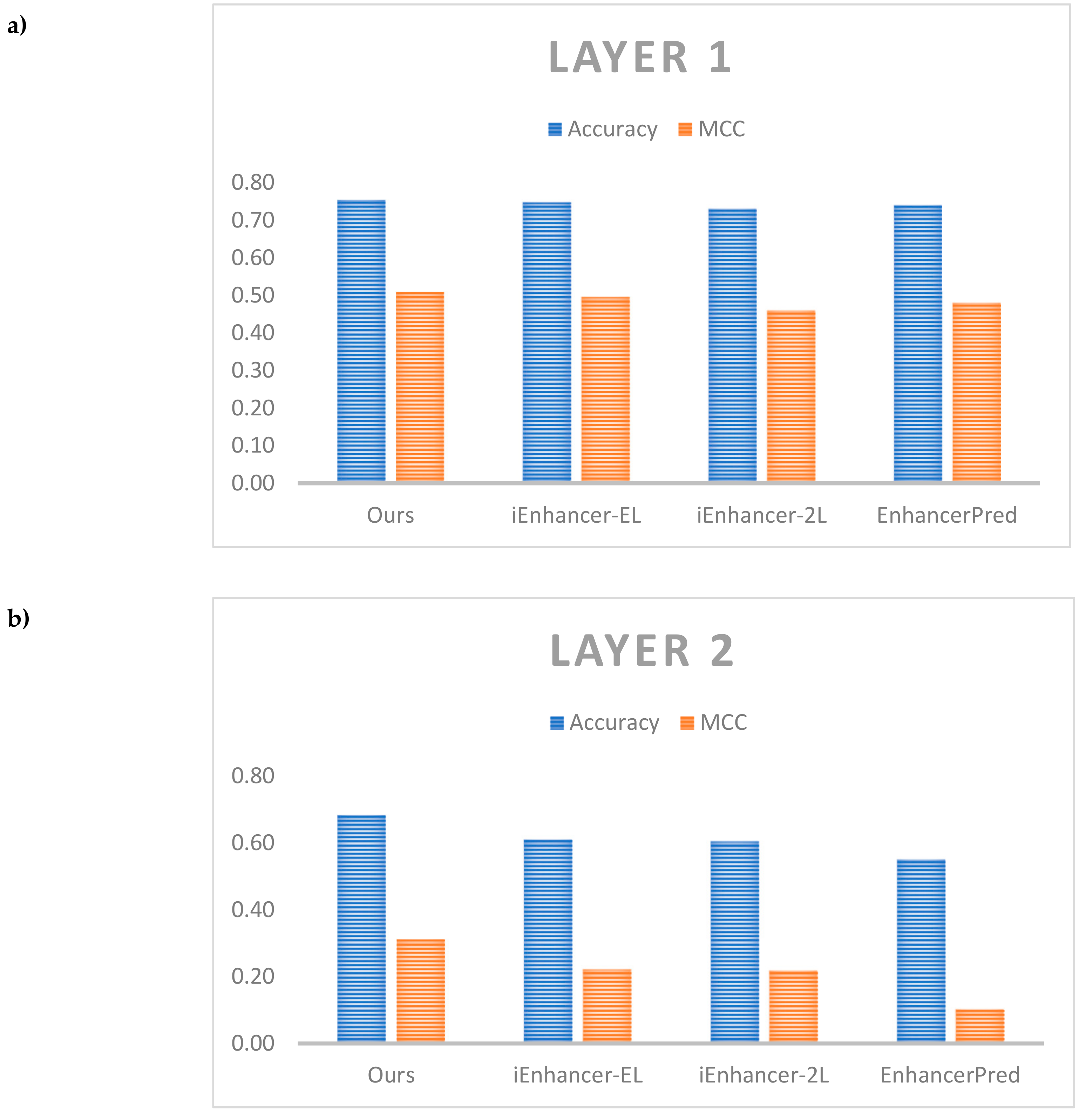
| Predictors | Acc (%) | MCC | Sn (%) | Sp (%) | AUC (%) |
|---|---|---|---|---|---|
| Layer 1 | |||||
| Ours | 75.50 | 0.510 | 75.5 | 76.0 | 77.04 |
| iEnhancer-EL | 74.75 | 0.496 | 71.0 | 78.5 | 81.73 |
| iEnhancer-2L | 73.00 | 0.460 | 71.0 | 75.0 | 80.62 |
| EnhancerPred | 74.00 | 0.480 | 73.5 | 74.5 | 80.13 |
| Layer 2 | |||||
| Ours | 68.49 | 0.312 | 83.15 | 45.61 | 67.14 |
| iEnhancer-EL | 61.00 | 0.222 | 54.00 | 68.00 | 68.01 |
| iEnhancer-2L | 60.50 | 0.218 | 47.00 | 74.00 | 66.78 |
| EnhancerPred | 55.00 | 0.102 | 45.00 | 65.00 | 57.90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, K.K.; Le, N.Q.K.; Yeh, H.-Y.; Chua, M.C.H. Ensemble of Deep Recurrent Neural Networks for Identifying Enhancers via Dinucleotide Physicochemical Properties. Cells 2019, 8, 767. https://doi.org/10.3390/cells8070767
Tan KK, Le NQK, Yeh H-Y, Chua MCH. Ensemble of Deep Recurrent Neural Networks for Identifying Enhancers via Dinucleotide Physicochemical Properties. Cells. 2019; 8(7):767. https://doi.org/10.3390/cells8070767
Chicago/Turabian StyleTan, Kok Keng, Nguyen Quoc Khanh Le, Hui-Yuan Yeh, and Matthew Chin Heng Chua. 2019. "Ensemble of Deep Recurrent Neural Networks for Identifying Enhancers via Dinucleotide Physicochemical Properties" Cells 8, no. 7: 767. https://doi.org/10.3390/cells8070767
APA StyleTan, K. K., Le, N. Q. K., Yeh, H.-Y., & Chua, M. C. H. (2019). Ensemble of Deep Recurrent Neural Networks for Identifying Enhancers via Dinucleotide Physicochemical Properties. Cells, 8(7), 767. https://doi.org/10.3390/cells8070767







