Mathematical Modeling of Mucociliary Clearance: A Mini-Review
Abstract
1. Introduction
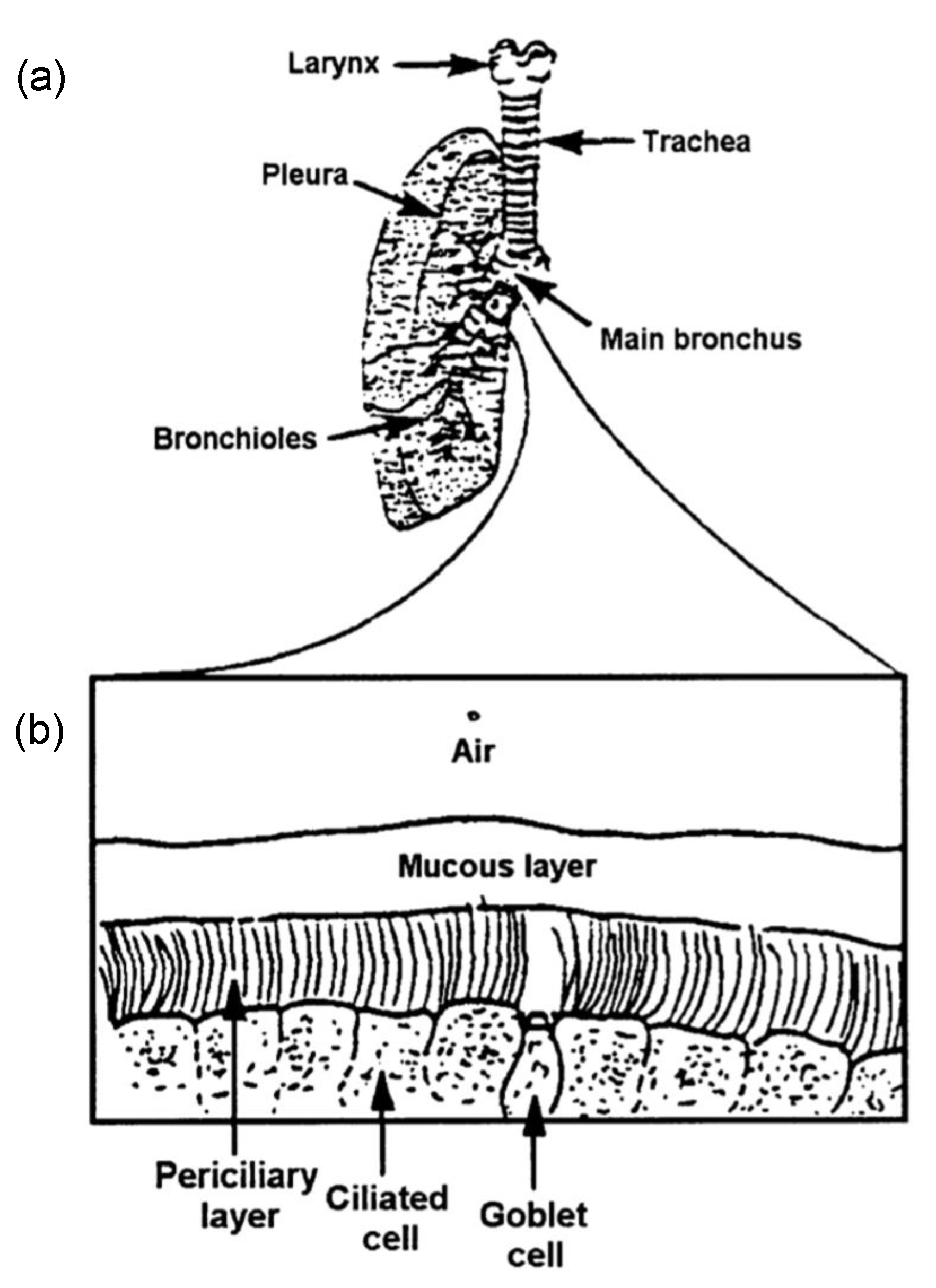
2. Cilia and Mucus
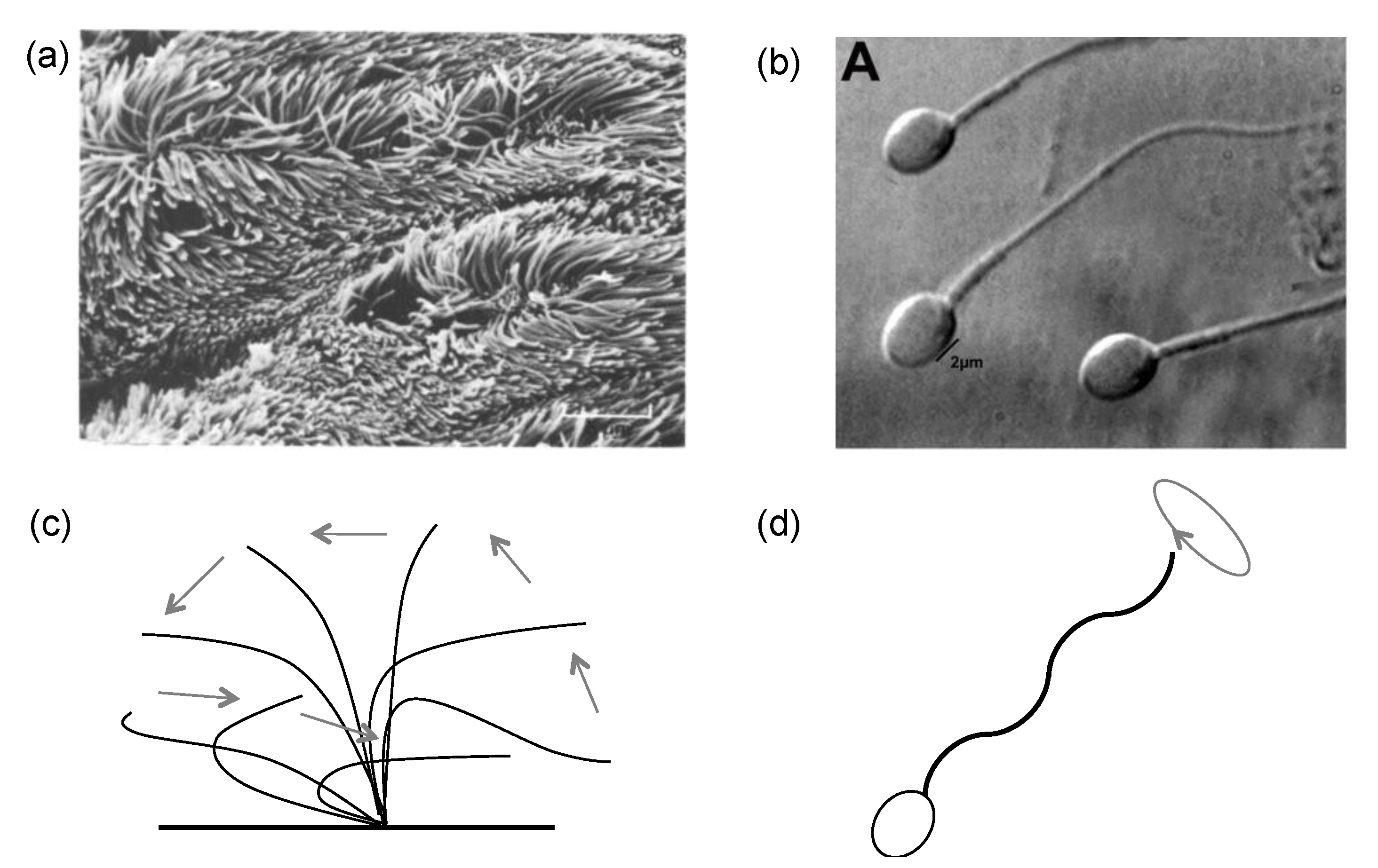
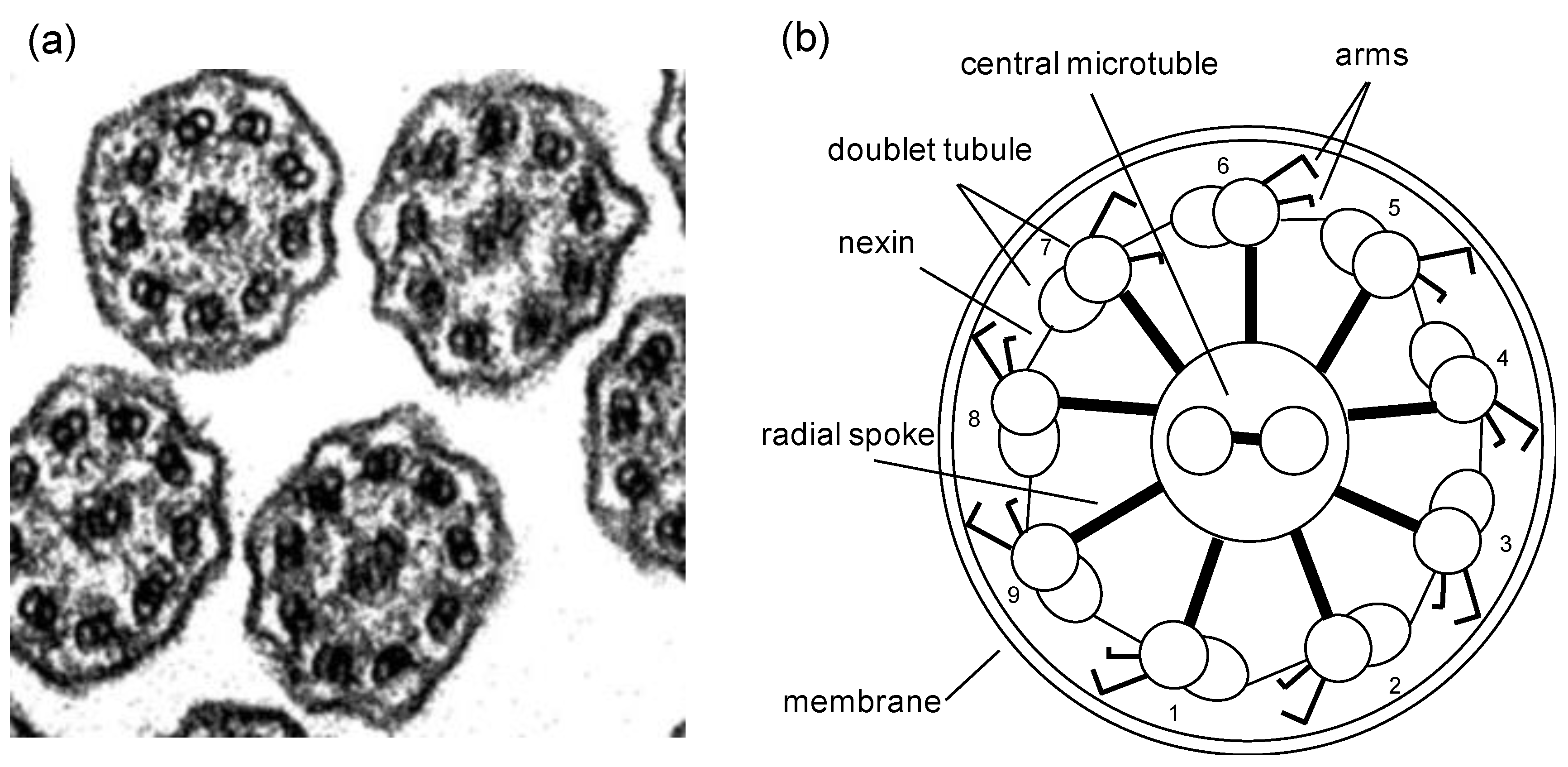
2.1. Cilia and Flagella Structure
2.2. Mucus and Periciliary Layer
3. Phylogeny of Mathematical Models of Mucociliary System
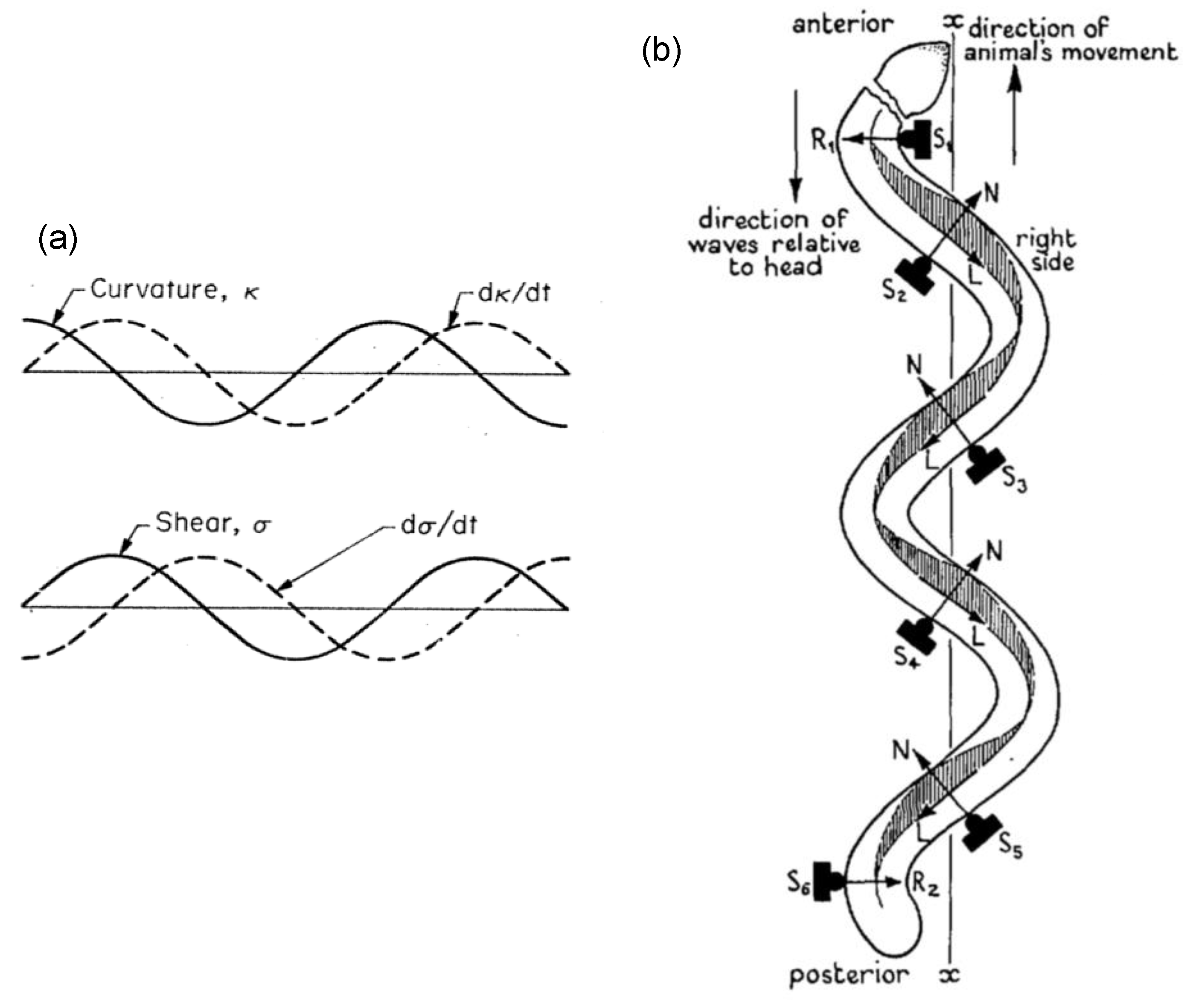
3.1. G1: Analytic Mathematical Formulation for Cilium/Flagellum Morphology and Motion
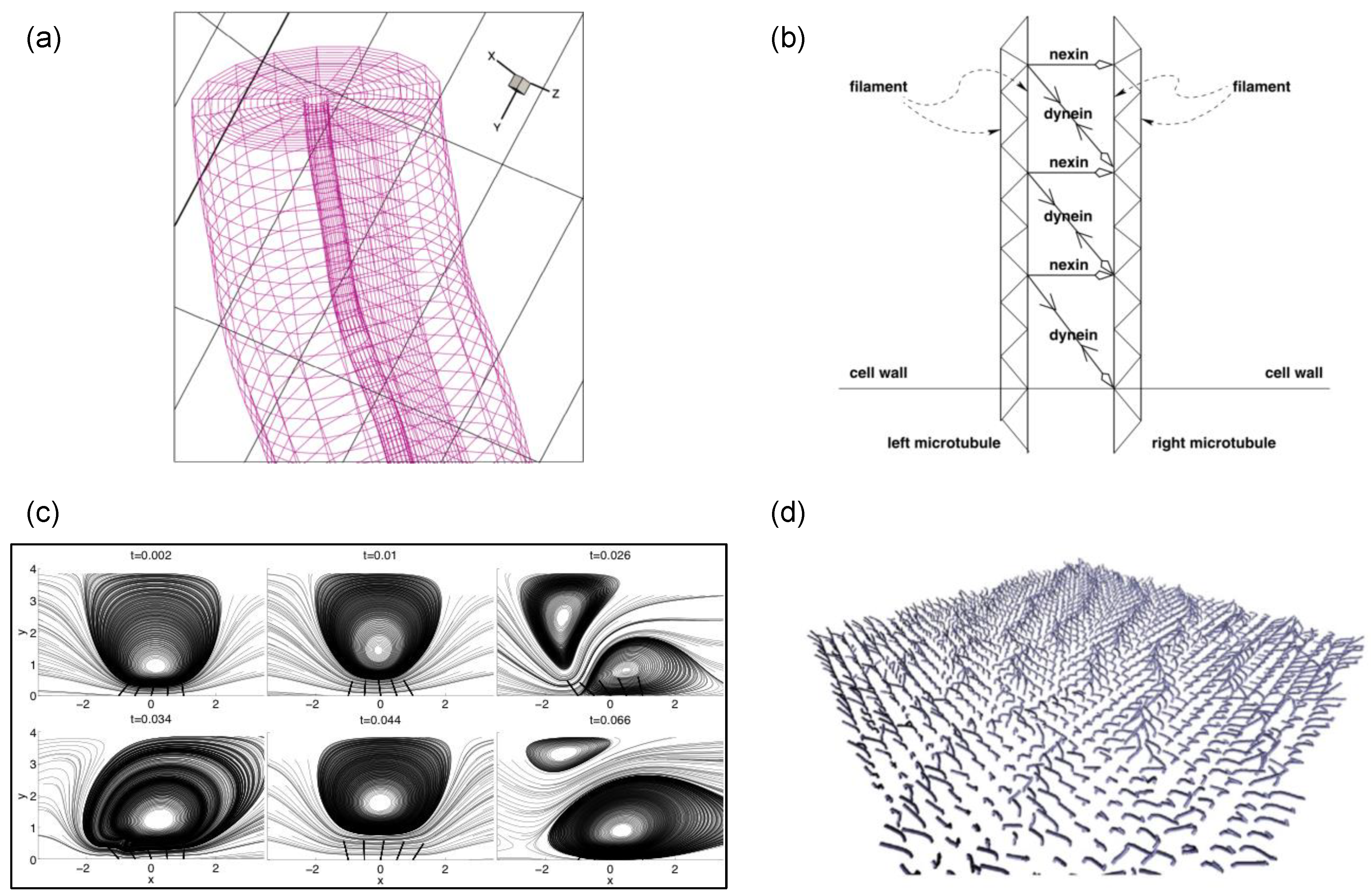
3.2. G2: Computer-Assisted Modeling for Mechanisms of Wave Propagation
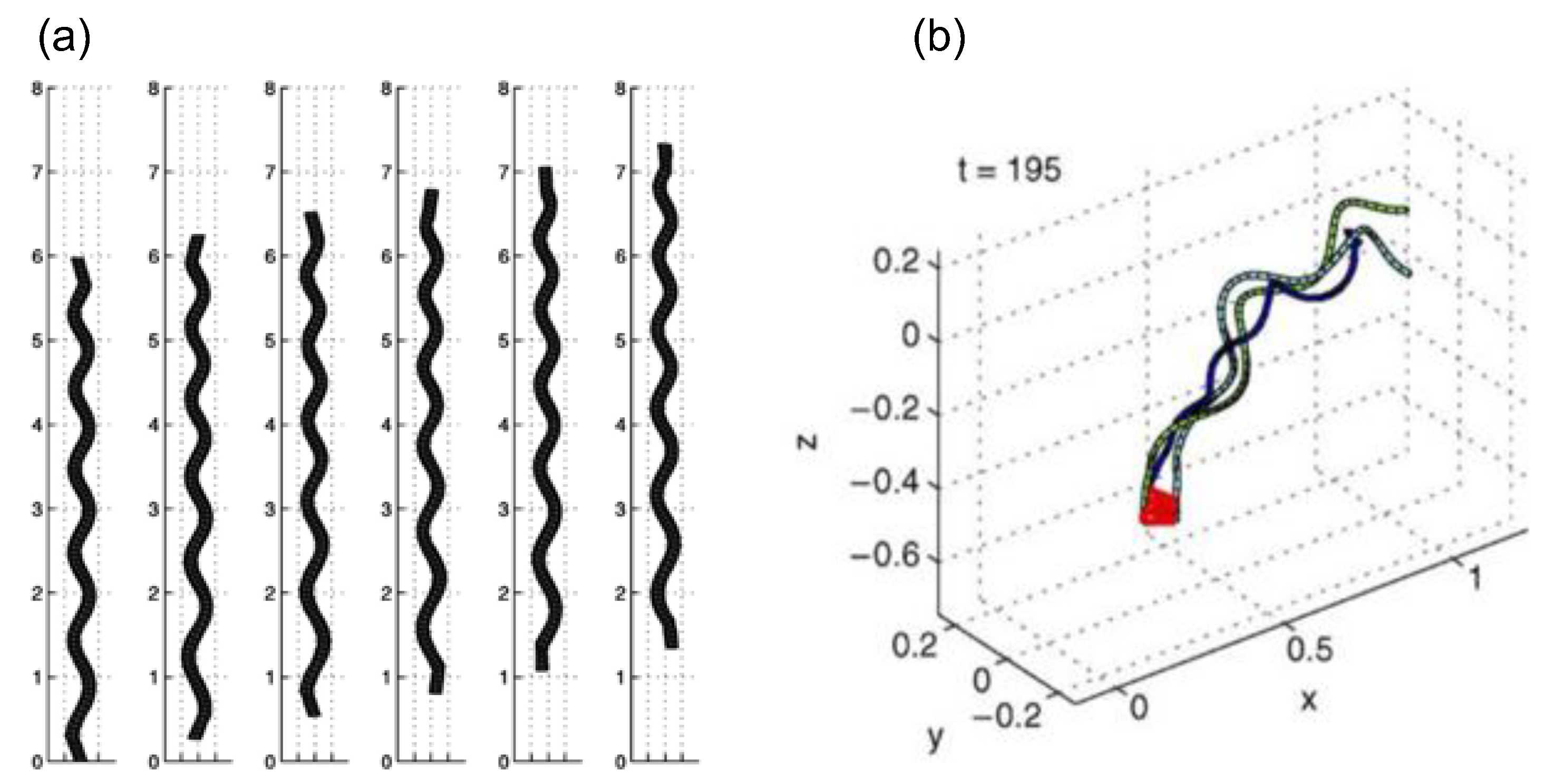
3.3. G3: Hydrodynamic Coupling between Cilium and Fluids
3.3.1. Viscous Force Alone ()
3.3.2. Viscous and Inertial Forces ()
4. Models of Force Generation Mechanisms
5. Summary and Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- Brooks, E.R.; Wallingford, J.B. Multiciliated cells. Curr. Biol. 2014, 24, 973–982. [Google Scholar] [CrossRef] [PubMed]
- Hines, M.; Blum, J.J. Bend propagation in flagella. I. Derivation of equations of motion and their simulation. Biophys. J. 1978, 23, 41–57. [Google Scholar] [CrossRef]
- Houtmeyers, E.; Gosselink, R.; Ramirez, G.G.; Decramer, M. Regulation of mucociliary clearance in health and disease. Eur. Respir. J. 1999, 13, 1177–1188. [Google Scholar] [CrossRef] [PubMed]
- Satir, P. Studies on cilia: II. examination of the distal region of the ciliary shaft and the role of the filaments in motility. J. Cell Biol. 1965, 26, 805–834. [Google Scholar] [CrossRef] [PubMed]
- Fauci, L.J.; Dillon, R. Biofluidmechanics of reproduction. Annu. Rev. Fluid Mech. 2006, 38, 371–394. [Google Scholar] [CrossRef]
- Lauga, E.; Powers, T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009, 72, 096601. [Google Scholar] [CrossRef]
- Chaitin, M.H.; Schneider, B.G.; Hall, M.O.; Papermaster, D.S. Actin in the photoreceptor connecting cilium: Immunocytochemical localization to the site of outer segment disk formation. J. Cell Biol. 1984, 99, 239–247. [Google Scholar] [CrossRef]
- Papermaster, D.S.; Schneider, B.G. Biosynthesis and morphogenesis of outer segment membranes in vertebrate photoreceptor cells. In Cell Biology of the Eye; McDebitt, D.S., Ed.; Academic Press: New York, NY, USA, 1982; pp. 475–531. [Google Scholar]
- Creeth, J.M. Constituents of mucus and their separation. British medical bulletin 1978, 34, 17–24. [Google Scholar] [CrossRef]
- Dillon, R.H.; Fauci, L.; Omoto, C.; Yang, X. Fluid dynamic models of flagellar and ciliary beating. Ann. N Y Acad. Sci. 2007, 1101, 497–505. [Google Scholar] [CrossRef]
- Snyder, S.H.; Sklar, P.B.; Pevsner, J. Molecular mechanisms of olfaction. J. Biol. Chem. 1988, 263, 13971–13974. [Google Scholar] [CrossRef]
- Hollenberg, M.D. Mechanisms of receptor-mediated transmembrane signaling. Experientia 1986, 42, 718–727. [Google Scholar] [CrossRef] [PubMed]
- Horridge, G.A. Macrocilia with numerous shafts from the lips of the ctenophore Beroe. Proc. Roy. Soc. Ser. B 1965, 162, 351–364. [Google Scholar]
- Blake, J.R. Fluid mechanics of ciliary propulsion. In Computational Modeling in Biological Fluid Dynamics; Fauci, L.J., Gueron, S., Eds.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Morris, R.L.; Scholey, J.M. Heterotrimeric kinesin-II is required for the assembly of motile 9+2 ciliary axonemes on sea urchin embryos. J. Cell Biol. 1997, 138, 1009–1022. [Google Scholar] [CrossRef] [PubMed]
- Kozminski, K.G.; Beech, P.L.; Rosenbaum, J.L. The Chlamydomonas kinesin-like protein FLA10 is involved in motility associated with the flagellar membrane. J. Cell Biol. 1995, 131, 1517–1527. [Google Scholar] [CrossRef] [PubMed]
- Marshall, W.F.; Nonaka, S. Cilia: Tuning in to the cell’s antenna. Cur. Biol. 2006, 16, R604–R614. [Google Scholar] [CrossRef] [PubMed]
- Matsui, H.; Randell, S.H.; Peretti, S.W.; Davis, C.W.; Boucher, R.C. Coordinated clearance of periciliary liquid and mucus from airway surfaces. J. Clin. Invest. 1998, 102, 1125–1131. [Google Scholar] [CrossRef] [PubMed]
- Bockman, D.E.; Buchler, M.; Beger, H.G. Structure and function of specialized cilia in the exocrine pancreas. Int. J. Pancreatol. 1986, 1, 21–28. [Google Scholar] [PubMed]
- Pazour, G.J.; Dickert, B.L.; Vucica, Y.; Seeley, E.S.; Rosenbaum, J.L.; Witman, G.B.; Cole, D.G. Chlamydomonas IFT88 and its mouse homologue, polycystic kidney disease gene Tg737, are required for assembly of cilia and flagella. J. Cell Biol. 2000, 151, 709–718. [Google Scholar] [CrossRef]
- Ivel, R.; Holstein, A.F. The fate of the male germ cell. In Advances in Experimental Medicine and Biology; Springer: New York, NY, USA, 1997. [Google Scholar]
- Villalon, M.; Vergudo, P. Hormonal regulation of ciliary function in the oviduct: The effect of beta-adrenergic agonists. Cell motilityt. 1982, 1, 59–65. [Google Scholar] [CrossRef]
- Sleigh, M.A. Ciliary function in transport of mucus. Eur. J. Respir Dis. Suppl. 1983, 128, 287–292. [Google Scholar]
- Svartegren, M.; Ericsson, C.H.; Philipson, K.; Mossberg, B.; Camner, P. Tracheobronchial clearance in asthma-discordant monozygotic twins. Respiration 1989, 56, 70–79. [Google Scholar] [CrossRef] [PubMed]
- Sorokin, S.P. Reconstructions of centriole formation and ciliogenesis in mammalian lungs. J. Cell Sci. 1968, 3, 207–230. [Google Scholar] [PubMed]
- Satir, P. How cilia move. Scientific American 1974, 231, 44–54. [Google Scholar] [PubMed]
- Satir, P.; Pedersen, L.B.; Christensen, S.T. The primary cilium at a glance. J. Cell Sci. 2010, 123, 499–503. [Google Scholar] [CrossRef] [PubMed]
- Rosenbaum, J.L.; Witman, G.B. Intraflagellar transport. Nat. Reviews 2002, 3, 813–825. [Google Scholar] [CrossRef] [PubMed]
- Eshel, D.; Priel, Z. Characterization of metachronal wave of beating cilia on frog’s palate epithelium in tissue culture. J. Physiol. 1987, 388, 1–8. [Google Scholar] [CrossRef]
- Gheber, L.; Korngreen, A.; Priel, Z. Effect of viscosity on metachrony in mucus propelling cilia. Cell Motil. Cytoskeleton 1998, 39, 9–20. [Google Scholar] [CrossRef]
- Sanderson, M.J.; Sleigh, M.A. Ciliary activity of cultured rabbit tracheal epithelium: Beat pattern and metachrony. J. Cell Sci. 1981, 47, 331–347. [Google Scholar]
- Oliveira, J.B.; Petersen, C.G.; Massaro, F.C.; Baruffi, R.L.; Mauri, A.L.; Silva, L.F.; Ricci, J.; Franco, J.G. Motile sperm organelle morphology examination (MSOME): Intervariation study of normal sperm and sperm with large nuclear vacuoles. Reprod. Biol. Endocrinol. 2010, 8, 20529256. [Google Scholar] [CrossRef]
- Sleigh, M.A. Patterns of movement of cilia and flagella. In Cilia and Flagella; Sleigh, M.A., Ed.; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Xu, L.; Jiang, Y. Cilium height difference between strokes is more effective in driving fluid transport in mucociliary clearance: A numerical study. Math. Biosci. Eng. 2015, 12, 1107–1126. [Google Scholar] [CrossRef][Green Version]
- Low, P.M.; Luk, C.L.; Dulfano, M.J.; Finch, R.J. Ciliary beat frequency of human respiratory tract by different sampling techniques. Am. Rev. Respir. Dis. 1984, 130, 497–498. [Google Scholar] [PubMed]
- Marino, M.R.; Aiello, E. Cinemicrographic analysis of beat dynamics of human respiratory cilia. Cell Motility 1982, 2, 35–39. [Google Scholar] [CrossRef]
- Chilvers, M.A.; O’Callaghan, C. Analysis of ciliary beat pattern and beat frequency using digital high-speed imaging: Comparison with the photomultiplier and photodiode methods. Thorax 2000, 55, 314–317. [Google Scholar] [CrossRef] [PubMed]
- Foster, W.M.; Langenback, E.; Bergofsky, E.H. Measurement to tracheal and bronchial mucus velocities in man: Relation to lung clearance. J. Appl. Physiol. Respir Env. Exerc. Physiol. 1980, 48, 965–971. [Google Scholar] [CrossRef] [PubMed]
- Friedman, M.; Dougherty, R.; Nelson, S.R.; White, R.P.; Sackner, M.A.; Wanner, A. Acute effects of an aerosol hair spray on tracheal mucociliary transport. Am. Rev. Respir Dis. 1977, 116, 281–286. [Google Scholar] [PubMed]
- Afzelius, B.A. Ultrastructural basis for ciliary motility. Eur. J. Respir Dis. Suppl. 1983, 128, 280–286. [Google Scholar] [PubMed]
- Clamp, J.R. Chemical aspects of mucus. General considerations. Br Med Bull. 1978, 34, 25–27. [Google Scholar] [CrossRef]
- Sale, W.S.; Satir, P. Direction of active sliding of microtubules in Tetrahymena cilia. Proc. Natl. Acad. Sci. USA 1977, 74, 2045–2049. [Google Scholar] [CrossRef]
- Sears, P.R.; Thompson, K.; Knowles, M.R.; Davis, C.W. Human airway ciliary dynamics. Am. J. Physiol. Lung Cell Mol. Phyiol. 2013, 304, L170–L183. [Google Scholar] [CrossRef]
- Chilvers, M.A.; Rutman, A.; O’Callaghan, C. Ciliary beat pattern is associated with specific ultrastructural defects in primary ciliary dyskinesia. J Allergy Clin Immunol. 2003, 112, 518–524. [Google Scholar] [CrossRef]
- Knowles, M.R.; Boucher, R.C. Mucus clearance as a primary innate defense mechanism for mammalian airways. J Clin Invest. 2002, 109, 571–577. [Google Scholar] [CrossRef] [PubMed]
- Tuomanen, E. The surface of mammalian respiratory cilia: Interactions between cilia and respiratory pathogens. In Ciliary and Flagellar Membranes; Bloodgood, R.A., Ed.; Plenum Press: New York, NY, USA, 1990. [Google Scholar]
- Liu, W.; Murcia, N.S.; Duan, Y.; Weinbaum, S.; Yoder, B.K.; Schwiebert, E.; Satlin, L.M. Mechanoregulation of intracellular Ca2+ concentration is attenuated in collecting duct of monocilium-impaired orpk mice. Am. J. Physiol. Ren. Physiol. 2005, 289, F978–F988. [Google Scholar] [CrossRef] [PubMed]
- Noone, P.G.; Leigh, M.W.; Sannuti, A.; Minnix, S.L.; Carson, J.L.; Hazucha, M.; Zariwala, M.A.; Knowles, M.R. Primary ciliary dyskinesia: Diagnostic and phenotypic features. Am. J. Respir Crit. Care Med. 2004, 169, 459–467. [Google Scholar] [CrossRef] [PubMed]
- Dirksen, E.R.; Satir, P. Ciliary activity in the mouse oviduct as studied by transmission and scanning electron microscopy. Tissue & Cell 1972, 4, 389–404. [Google Scholar]
- Thornton, D.J.; Sheehan, J.K. From mucins to mucus: Toward a more coherent understanding of this essential barrier. Proc. Am. Thorac Soc. 2004, 1, 54–61. [Google Scholar] [CrossRef]
- Linden, S.K.; Sutton, P.; Karlsson, N.G.; Korolik, V.; McGuckin, M.A. Mucins in the mucosal barrier to infection. Mucosal Immunol. 2008, 1, 183–197. [Google Scholar] [CrossRef]
- Thornton, D.J.; Rousseau, K.; McGuckin, M.A. Structure and function of the polymeric mucins in airways mucus. Annu. Rev. Physiol. 2008, 70, 459–486. [Google Scholar] [CrossRef]
- King, M.; Rubin, B.K. Rheology of airway mucus: Relationship with clearance function. Lung Biol. Health Dis. 1994, 72, 283–314. [Google Scholar]
- Fung, Y.C. First course in continuum mechanics. In Englewood Cliffs, N.J.; Prentice-Hall: Upper Saddle River, NJ, USA, 1969. [Google Scholar]
- Button, B.; Cai, L.H.; Ehre, C.; Kesimer, M.; Hill, D.B.; Sheehan, J.K.; Boucher, R.C.; Rubinstein, M.A. periciliary brush promotes the lung health by separating the mucus layer from airway epithelia. Science 2012, 337, 937–941. [Google Scholar] [CrossRef]
- Livraghi, A.; Randell, S.H. Cystic fibrosis and other respiratory diseases of impaired mucus clearance. Toxicol. Pathol. 2007, 35, 116–129. [Google Scholar] [CrossRef]
- Bateman, J.R.; Pavia, D.; Sheahan, N.F.; Agnew, J.E.; Clarke, S.W. Impaired tracheobronchial clearance in patients with mild stable asthma. Thorax 1983, 38, 463–467. [Google Scholar] [CrossRef] [PubMed]
- Faty, J.V.; Dickey, B.F. Airway mucus function and dysfunction. N. Engl. J. Med. 2010, 363, 2233–2247. [Google Scholar]
- Gray, J. Studies in animal locomotion: VIII. The kinetics of locomotion of Nereis diversicolor. J. Exp. Biol. 1939, 16, 9–17. [Google Scholar]
- Gray, J.; Hancock, G.J. The propulsion of sea-urchin spermatozoa. Exp. Biol. 1955, 32, 802–814. [Google Scholar]
- Gueron, S.; Liron, N. Ciliary motion modeling, and dynamic multicilia interactions. Biophys. J. 1992, 63, 1045–1058. [Google Scholar] [CrossRef]
- Brokaw, C.J. Non-sinusoidal bending waves of sperm flagella. J. Exp. Biol. 1965, 43, 155–169. [Google Scholar] [PubMed]
- Brokaw, C.J. Microtubule sliding in swimming sperm flagella: Direct and indirect measurements on sea urchin and tunicate spermatozoa. J. Cell Biol. 1991, 114, 1201–1215. [Google Scholar] [CrossRef]
- Machin, K.E. Wave propagation along flagella. J. Exp. Biol. 1958, 35, 796–806. [Google Scholar]
- Brokaw, C.J. Bend propagation by a sliding filament model for flagella. J. Exp. Biol. 1971, 55, 289–304. [Google Scholar]
- Gray, J. Undulatory propulsion. J. Cell Sci. 1953, 94, 551–578. [Google Scholar]
- Taylor, G.I. The action of waving cylindrical tails in propelling microscopic organisms. Proc. Roy. Soc. A 1951, 211, 225–239. [Google Scholar]
- Barton, C.; Raynor, S. Analytical investigation of cilia induced mucous flow. Bull Math Biophys. 1967, 29, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Lighthill, M.J. On waves generated in dispersive systems by travelling forcing effects, with applications to the dynamics of rotating fluids. J. Fluid Mech. 1967, part 4, part–752. [Google Scholar] [CrossRef]
- Blake, J.R. A spherical envelope approach to ciliary propulsion. J. Fluid Mech. 1971, 46, 46,199–208. [Google Scholar] [CrossRef]
- Blake, J.R. A model for the micro-structure in ciliated organisms. J. Fluid Mech. 1972, 55, 1–23. [Google Scholar] [CrossRef]
- Osterman, N.; Vilfan, A. Finding the ciliary beating pattern with optimal efficiency. Proc. Natl. Acad. Sci. USA 2011, 108, 15727–15732. [Google Scholar] [CrossRef]
- Eloy, E. and Lauga, E. Kinematics of the most efficient cilium. Phys. Rev. Lett. 2012, 109, 038101. [Google Scholar] [CrossRef] [PubMed]
- Batchelor, C.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 1967. [Google Scholar]
- Dusenbery, D.B. Living at Micro Scale: The Unexpected Physics of Being Small; Harvard University Press: Cambridge, MA, USA.
- Cortez, R. The method of regularized Stokeslets. Siam J. Sci. Comput. 2001, 23, 1204–1225. [Google Scholar] [CrossRef]
- Cortez, R.; Fauci, L.; Medovikov, A. The method of regularized Stokeslets in three dimensions: Analysis, validation, and application to helical swimming. Phys. Fluids 2005, 17, 031504. [Google Scholar] [CrossRef]
- Flores, H.; Lobaton, E.; Mendez-Diez, S.; Tlupova, S.; Cortez, R. A study of bacterial flagellar bundling. Bull. Math. Biol. 2005, 67, 67,137–168. [Google Scholar] [CrossRef]
- Guo, H.; Fauci, L.; Shelley, M.; Kanso, E. Bistability in the synchronization of actuated microfilaments. J. Fluid Mech. 2018, 836, 304–323. [Google Scholar] [CrossRef]
- Lighthill, M.J. Flagellar hydrodynamics. Siam Rev. 1976, 18, 161–230. [Google Scholar] [CrossRef]
- Lindemann, C.B. A ’geometric clutch’ hypothesis to explain oscillations of the axoneme of cilia and flagella. J. Theor. Biol. 1994, 168, 175–189. [Google Scholar] [CrossRef]
- Ling, F.; Guo, H.; Kanso, E. Instability-driven oscillations of elastic microfilaments. J. R. Soc. Interface 2018, 15, 20180594. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.Q.; Chwang, A.T. Unsteady free-surface waves due to a submerged body moving in a viscous fluid. Phys. Rev. E 2005, 71, 066303. [Google Scholar] [CrossRef]
- Price, W.G.; Tan, M. Fundamental viscous solitons or ‘transient oseenlets; associated with a body manoeuvring in a viscous fluid. Proc. R. Soc. Lond. A. 1992, 438, 447–466. [Google Scholar] [CrossRef]
- Mitran, S.M. Metachronal wave formation in a model of pulmonary cilia. Comput. Struct. 2007, 85, 763–774. [Google Scholar] [CrossRef]
- Eymard, R.; Gallouët, T.; Herbin, R. Finite volume method. Handbook Numer. Anal. 2000, 7, 713–1018. [Google Scholar]
- Yang, X.; Dillon, R.H.; Fauci, L.J. An integrative computational model of multiciliary beating. Bull Math Biol. 2008, 70, 1192–1215. [Google Scholar] [CrossRef]
- Elgeti, J.; Gompper, G. Emergence of metachronal waves in cilia arrays. Proc. Natl. Acad. Sci. USA 2013, 110, 4470–4475. [Google Scholar] [CrossRef]
- Lai, M.C.; Peskin, C.S. An immersed boundary method with formal second-order accuracy and reduced numerical viscosity. J. Comput. Phys. 2000, 160, 705–719. [Google Scholar] [CrossRef]
- Donaldson, S.H.; Bennett, W.D.; Zeman, K.L.; Knowles, M.R.; Tarran, R.; Boucher, R.C. Mucus clearance and lung function in cystic fibrosis with hypertonic saline. N. Engl. J. Med. 2006, 354, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Drescher, K.; Dunkel, J.; Cisneros, L.H.; Ganguly, S.; Goldstein, R.E. Fluid dynamics and noise in bacterial cell-cell and cell-surface scattering. Proc. Natl. Acad. Sci. USA 2011, 108, 10940–10945. [Google Scholar] [CrossRef] [PubMed]
- Machin, K.E. The control and synchronization of flagellar movement. Proc. R. Soc. Lond. B 1963, 158, 88–104. [Google Scholar]
- Gueron, S.; Gurevich, K.L.; Liron, N.; Blum, J.J. Cilia internal mechanism and metachronal coordination as the result of hydrodynamical coupling. Proc. Natl. Acad. Sci. USA 1997, 94, 6001–6006. [Google Scholar] [CrossRef] [PubMed]
- Gueron, S.; Gurevich, K.L. Computation of the internal forces in cilia: Application to ciliary motion, the effects of viscosity, and cilia interactions. Biophys. J. 1998, 74, 1658–1676. [Google Scholar] [CrossRef]
- Brokaw, C.J. Simulating the effects of fluid viscosity on the behaviour of sperm flagella. Math. Meth. Appl. Sci. 2001, 24, 1351–1365. [Google Scholar] [CrossRef]
- Hill, D.B.; Swaminathan, V.; Estes, A.; Cribb, J.; O’Brien, E.T.; Davis, C.W.; Superfine, R. Force generation and dynamics of individual cilia under external loading. Biophys. J. 2010, 98, 57–66. [Google Scholar] [CrossRef]
- Lindemann, C.B. A model of flagellar and ciliary functioning which uses the forces transverse to the axoneme as the regulator of dynein activation. Cell Motil. Cytoskelet. 1994, 29, 141–154. [Google Scholar] [CrossRef]
- Lindemann, C.B. Testing the geometric clutch hypothesis. Biol. Cell 2004, 96, 681–690. [Google Scholar] [CrossRef]
- Han, J.; Peskin, C.S. Spontaneous oscillation and fluid–structure interaction of cilia. Proc. Natl. Acad. Sci. USA 2018, 115, 4417–4422. [Google Scholar] [CrossRef] [PubMed]
- Oriola, D.; Gadelha, H.; Casademunt, J. Nonlinear amplitude dynamics in flagellar beating. R. Soc. Open Sci. 2017, 4, 160698. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, B.; Saintillan, D. Spontaneous oscillations, beating patterns, and hydrodynamics of active microfilaments. Phys. Rev. Fluids 2019, 4, 043102. [Google Scholar] [CrossRef]
- Gauger, E.M.; Downton, M.T.; Stark, H. Fluid transport at low Reynolds number with magnetically actuated artificial cilia. Eur. Phys. J. E. 2009, 28, 231–242. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Matsunaga, D.; Yeomans, J.M.; Golestanian, R. Magnetically-actuated artificial cilium: A simple theoretical model. Soft Matter 2019, 15, 3864–3871. [Google Scholar] [CrossRef] [PubMed]
- Orbay, S.; Ozcelik, A.; Bachman, H.; Huang, T.J. Acoustic actuation of in situ fabricated artificial cilia. J. Micromech. Microeng. 2018, 28, 025012. [Google Scholar] [CrossRef]
- Segre, G.; Silberberg, A. Behaviour of macroscopic rigid spheres in Poiseuille flow Part 1. J. Fluid Mech. 1962, 14, 115–135. [Google Scholar] [CrossRef]
- Segre, G.; Silberberg, A. Behaviour of macroscopic rigid spheres in Poiseuille flow Part 2. J. Fluid Mech. 1962, 14, 136–157. [Google Scholar] [CrossRef]
- Branscomb, J.; Alexeev, A. Designing ciliated surfaces that regulate deposition of solid particles. Soft Matter 2010, 6, 4066–4069. [Google Scholar] [CrossRef]
| Parameter | Values | References |
|---|---|---|
| Cilium length | 5–7 | Sanderson & Sleigh [31] |
| Cilium density | 6–8 −2 | Sleigh et al. [23] |
| Beating frequency | 13–29 Hz | Sanderson & Sleigh [31] |
| 14 Hz | Low et al. [35] | |
| 15.6 Hz | Marino & Aiello [36] | |
| 11–1-5 Hz (human nasal cilia without mucus) | Chilvers & Challaghan [37] | |
| Tracheal mucus velocity | 5.5 mm/min−1 | Foster et al. [38] |
| 6.7–11.4mm/min−1 | Friedman et al. [39] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Jiang, Y. Mathematical Modeling of Mucociliary Clearance: A Mini-Review. Cells 2019, 8, 736. https://doi.org/10.3390/cells8070736
Xu L, Jiang Y. Mathematical Modeling of Mucociliary Clearance: A Mini-Review. Cells. 2019; 8(7):736. https://doi.org/10.3390/cells8070736
Chicago/Turabian StyleXu, Ling, and Yi Jiang. 2019. "Mathematical Modeling of Mucociliary Clearance: A Mini-Review" Cells 8, no. 7: 736. https://doi.org/10.3390/cells8070736
APA StyleXu, L., & Jiang, Y. (2019). Mathematical Modeling of Mucociliary Clearance: A Mini-Review. Cells, 8(7), 736. https://doi.org/10.3390/cells8070736




