2.2. The Proposed Model
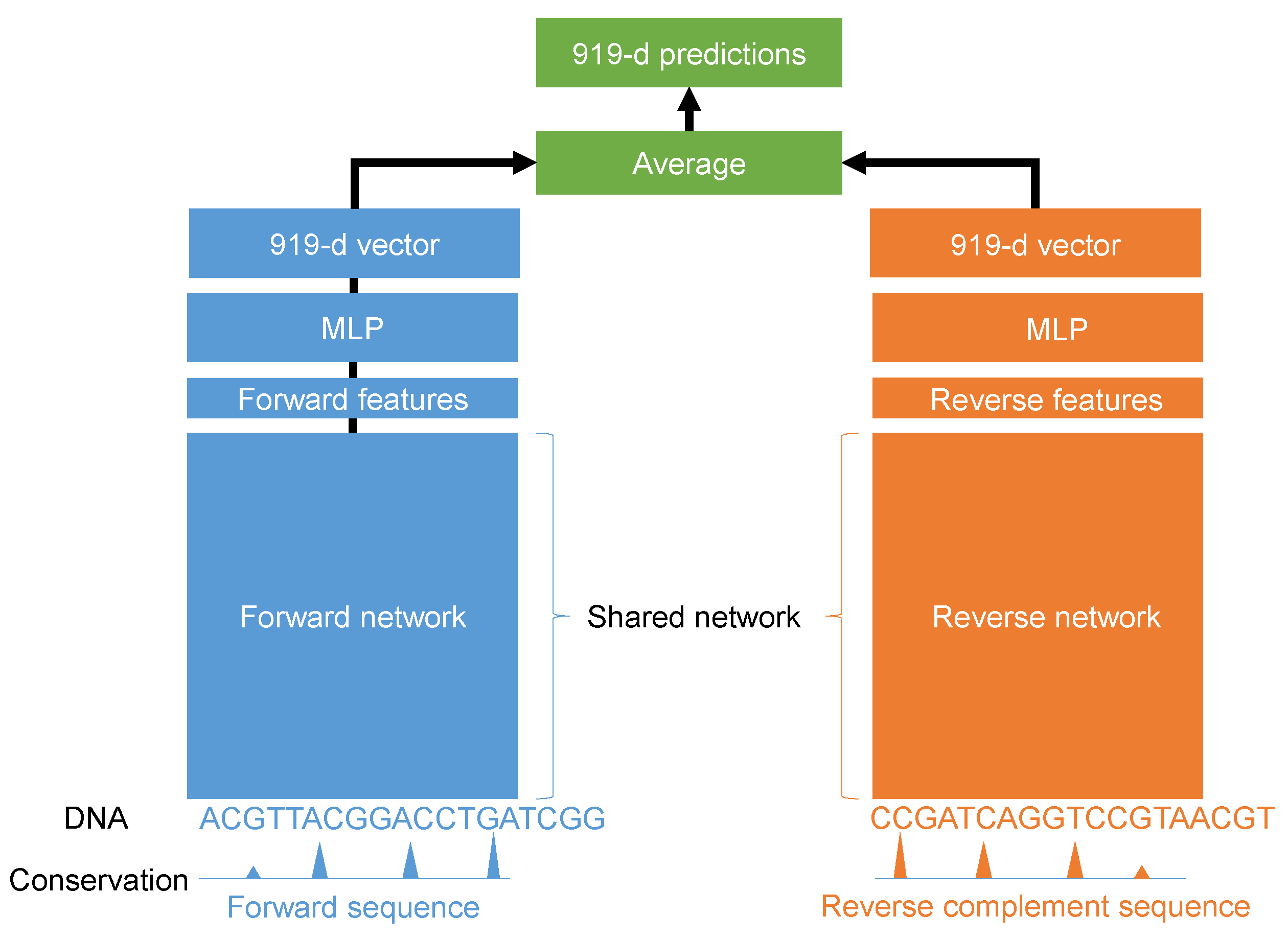
In this paper, we propose a deep learning model for the quantification of non-coding DNA regions. Instead of treating forward and reverse complement sequences independently, we considered using both sequences together as the input. The proposed model is illustrated in
Figure 1. It was a Siamese architecture in which the weights of the forward and reverse complement networks were shared. Different architectures were tested using the grid search algorithm. For every input sequence S with L nucleotide, we encoded A, G, C, and T using the one-hot method such as A being represented by [1 0 0 0], G being represented by [0 1 0 0], C being represented by [0 0 1 0], and T being represented by [0 0 0 1]. In this work, L is 1000 nucleotides. In addition, we added the evolution score for every nucleotide in the input sequence. Therefore, the final input would have a shape of
such that four channels were for one-hot encoding and the last channel was for the evolution scores.
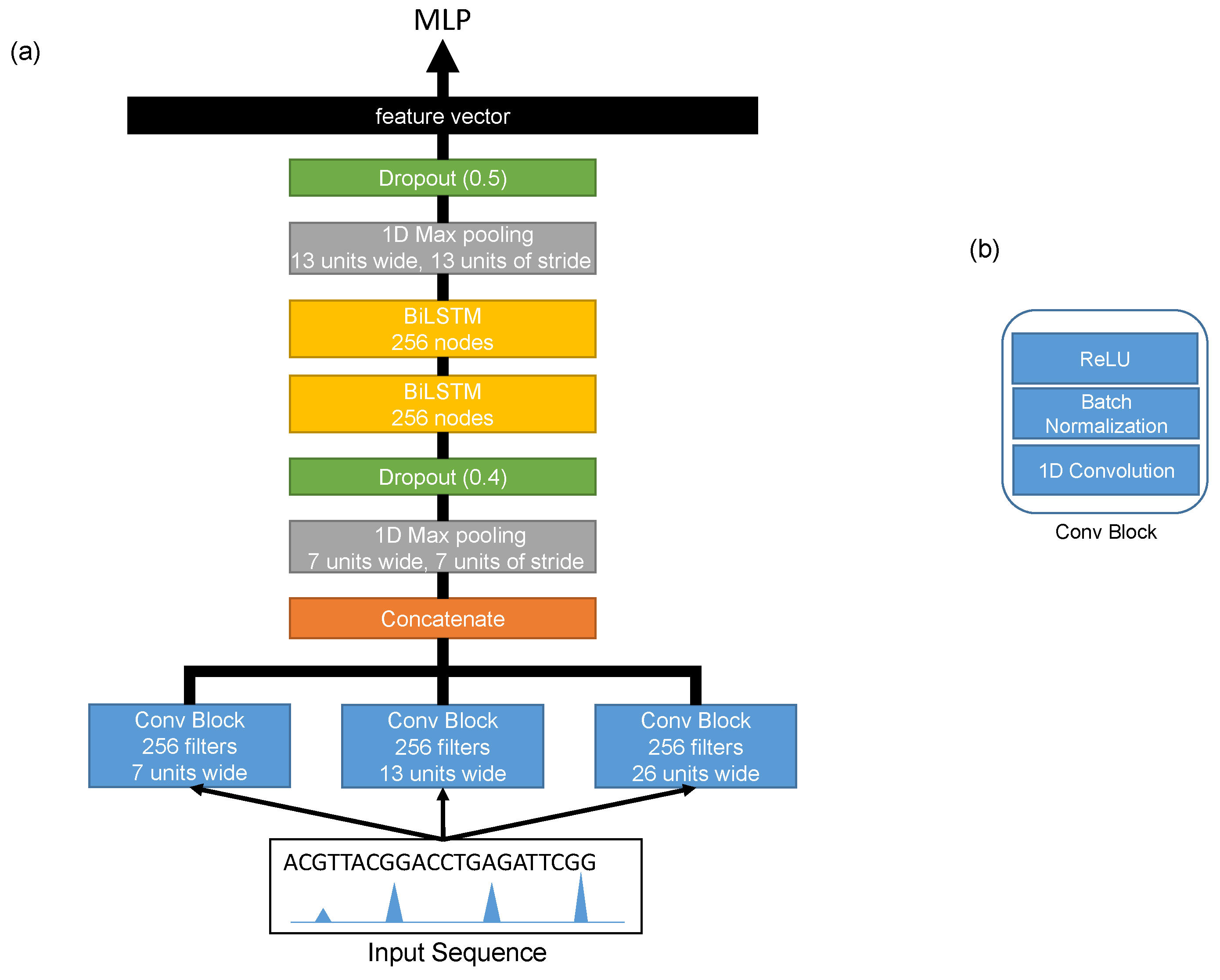
The architecture of the shared network is shown in
Figure 2. It consisted of three convolution layers running in parallel in order to extract different features (motifs) at different scales from the input sequences. Each convolution layer was a one-dimensional convolution layer [
18] with 256 filters, and the sizes of the filters of these layers were 26, 13, and 7. Each convolution layer was followed by a batch normalization layer [
19] and a rectified linear unit (ReLU) [
20]. The outputs of these convolution layers were then concatenated and passed threw a max-pooling layer with a window size of 7 and a stride of 7. Then, a dropout layer [
21] was added with a probability of 0.4. After that, we added two bidirectional LSTM layers [
22] with 256 nodes in order to extract the long term relationships between the extracted features from the first convolution layers. The output of the second bidirectional LSTM layer went through a max-pooling layer with a window size of 13 and a stride of 13 and a dropout layer with a probability of 0.5. The final output was flattened into a feature vector representing the learned features of the input sequence. The detailed configurations are shown in
Table 1.
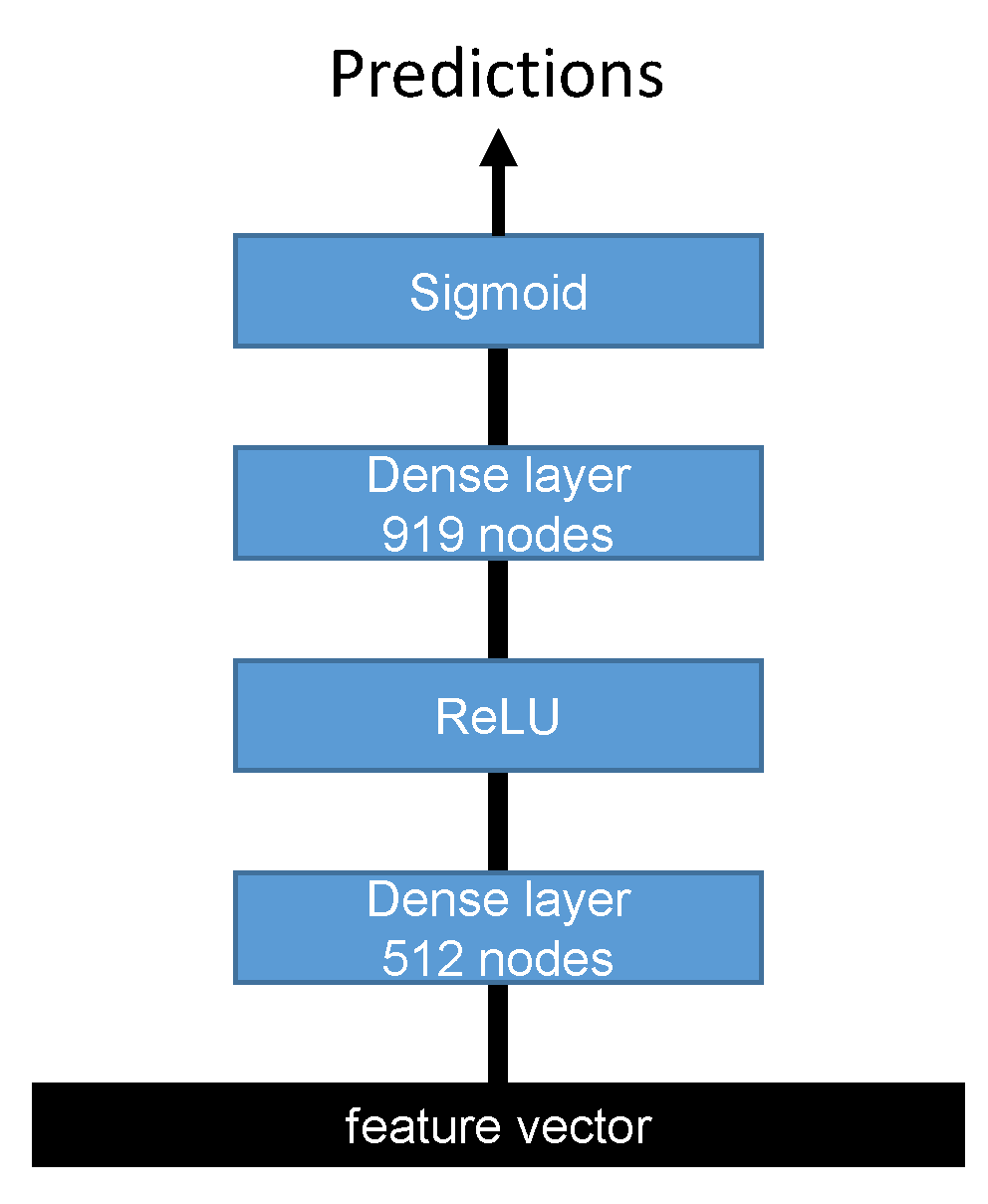
Two feature vectors were extracted from forward and reverse complement networks, and each one was passed to a multi-layer perceptron (MLP) network with two dense layers, as shown in
Figure 3.
The first dense layer had 512 nodes followed by the ReLU activation function, while the second dense layer had 919 nodes with a sigmoid activation function. Finally, the outputs of the second fully connected layer of the forward and reverse complement inputs were averaged to output the final predictions. The detailed configurations of the MLP classifier are shown in
Table 2.
In
Table 1, the operation Conv1D(
) is a one-dimensional convolution layer with
f filters of size
s and stride
t. It can be expressed mathematically by Equation (
1) where
X is the input feature map and
i and
k are the indices of the output position and the kernels, respectively.
is a convolution kernel with an
weight matrix of a window size of
M and a number of input channels of
N.
The operation “Concatenate” links together all outputs from the three convolution layers. The operation Max_pooling_1D(
) is a pooling function that selects the maximum value within a window
W and stride
t. It is expressed mathematically in Equation (
2), where
X is the input and
i and
k represent the indices for output position and the kernels, respectively.
The Dropout(
) operator drops some nodes with a probability of
at training time in order to avoid over fitting. The operator BiLSTM is a bidirectional long short term memory that helps in capturing the dependencies among the learned motifs of the first layers. Thus, considering an input sequence {
x}
, the LSTM has cell states {
C}
and hidden states {
h}
and outputs a sequence {
o}
. This can be expressed mathematically by Equation (
3) where
,
,
,
,
, and
are the weight matrices and
,
,
, and
are the biases. Sigmoid and Tanh are the activation functions.
The Flatten operator converts the learned features from a 2D vector to a 1D vector to be used in the fully connected layers. In
Table 2, Dense(
n) is a fully connected layer with
n nodes, and the output of each node is described mathematically as:
where
z is the incoming 1D vector,
is the weight of
’s contribution to the output, and
is the additive bias term. ReLU and Sigmoid are nonlinear activation functions and described in Equations (
5) and (
6), respectively, where
z represents the input to these functions.
The proposed model was designed and implemented by the Keras deep learning framework (
https://keras.io/). The Adam optimizer [
23,
24] was used with a learning rate of 0.001 and a batch size of 1000 divided on 4 TitanXP GPUs. The number of training epochs was set to 60. The evolutionary information was obtained from
http://hgdownload.cse.ucsc.edu/goldenpath/hg19/phyloP100way/, where we used the conservation scores of multiple alignments of 99 vertebrate genomes to the human genome. These scores were obtained from the Phylogenetic Analysis with Space/Time Models (PHAST) package (
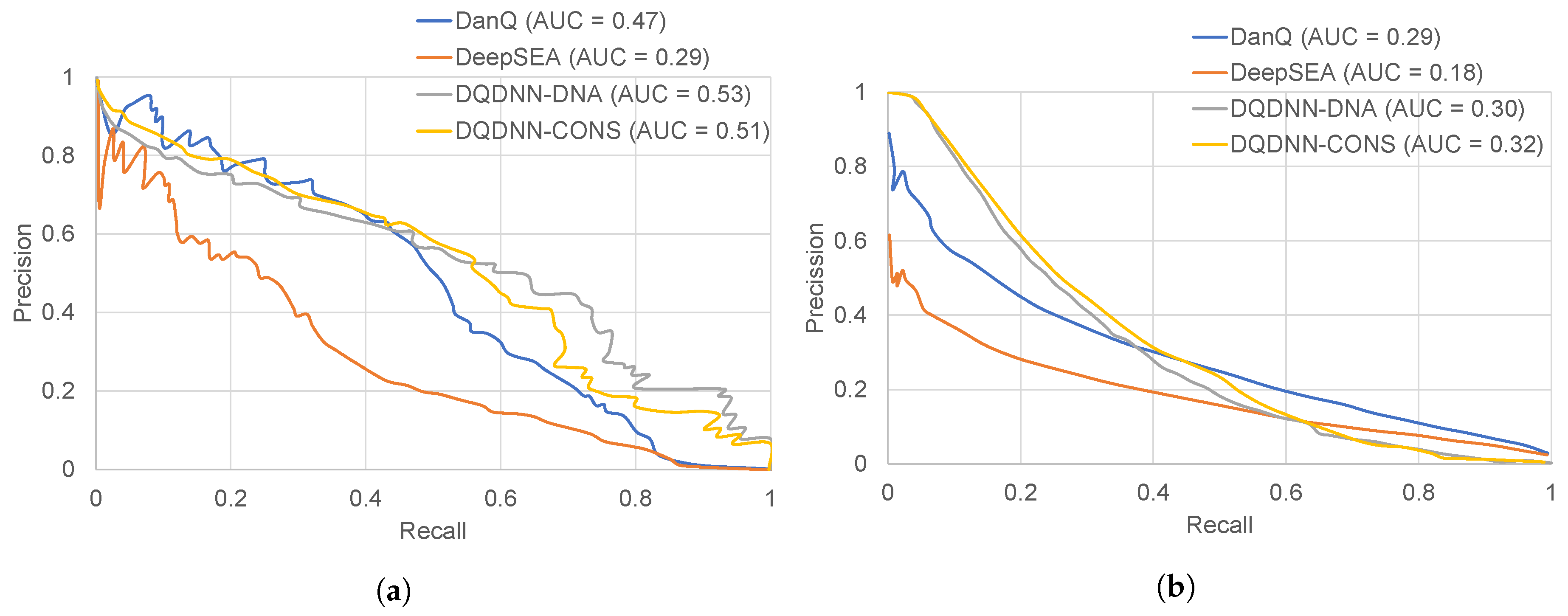
http://compgen.bscb.cornell.edu/phast/). For performance evaluation, we followed [
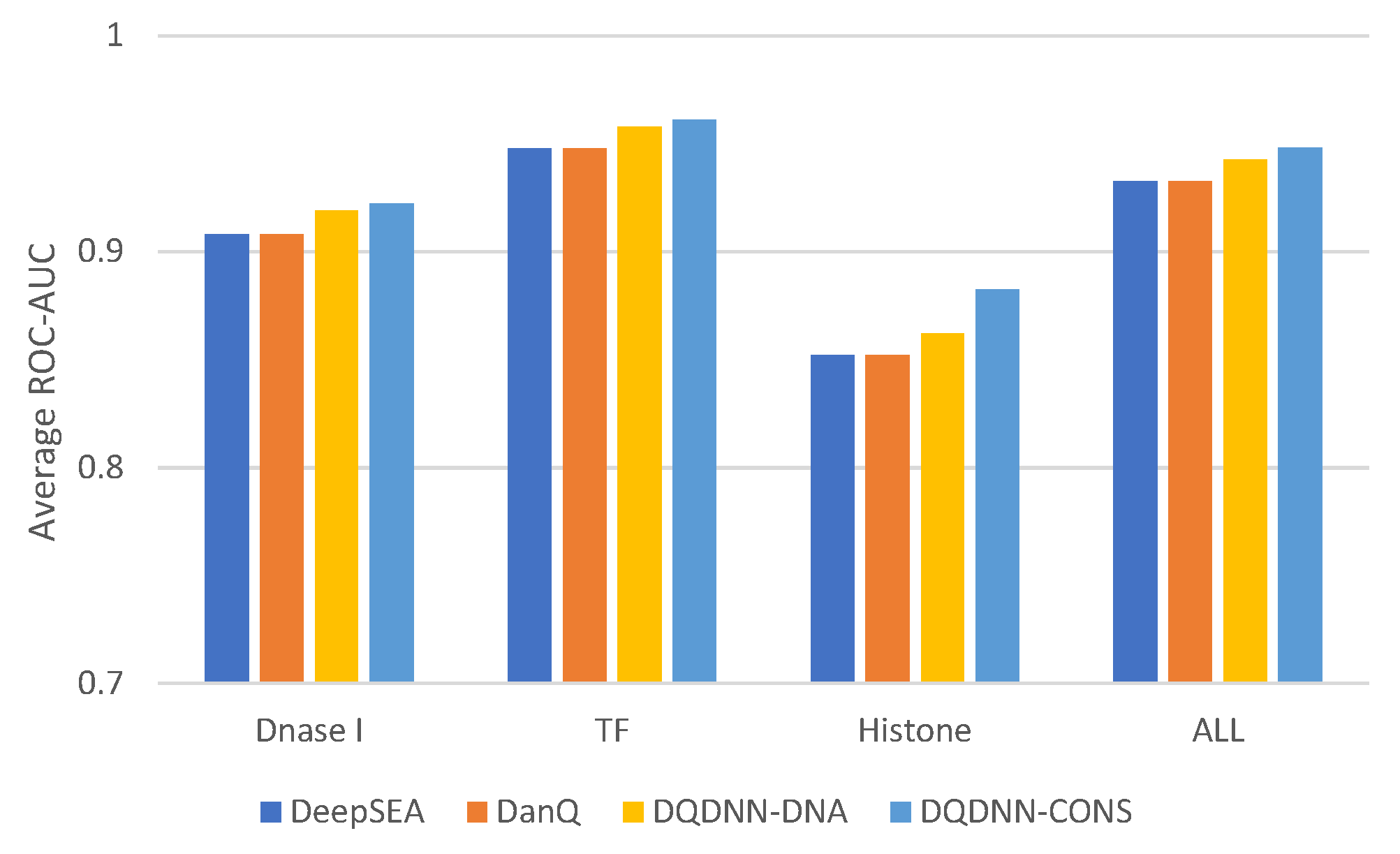
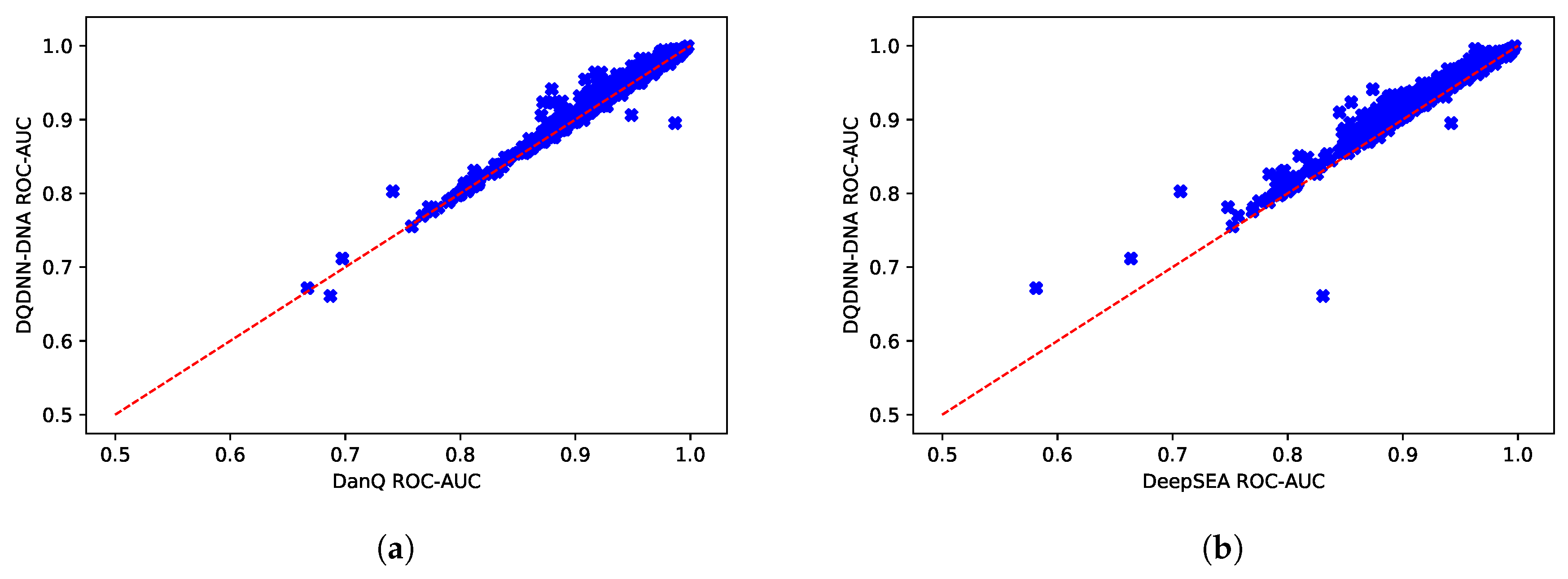
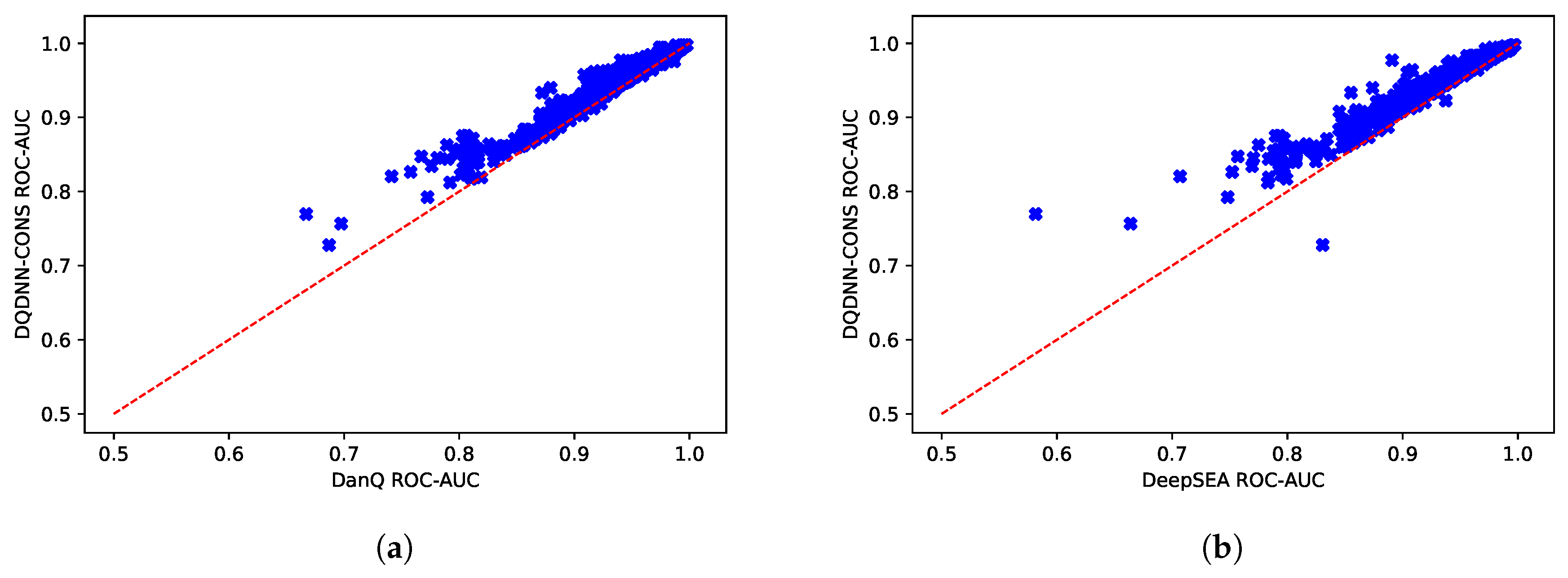
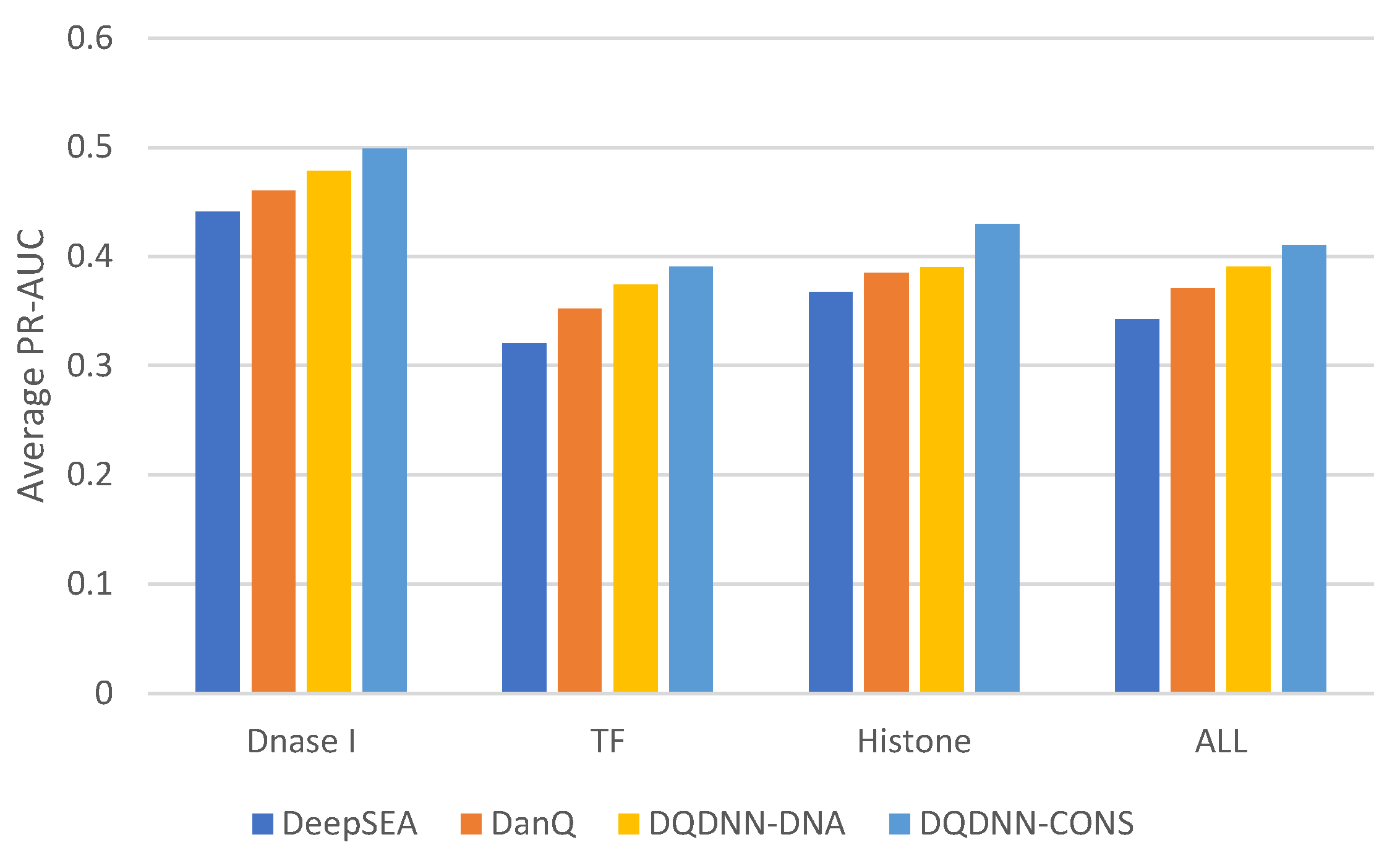
16,
17] by using the area under the operating receiver curve (ROC-AUC) and the area under the precision-recall curve (PR-AUC). The PR-AUC was more important than ROC-AUC as the dataset we used for evaluation was imbalanced [
25].
2.3. Functional SNP Prioritization
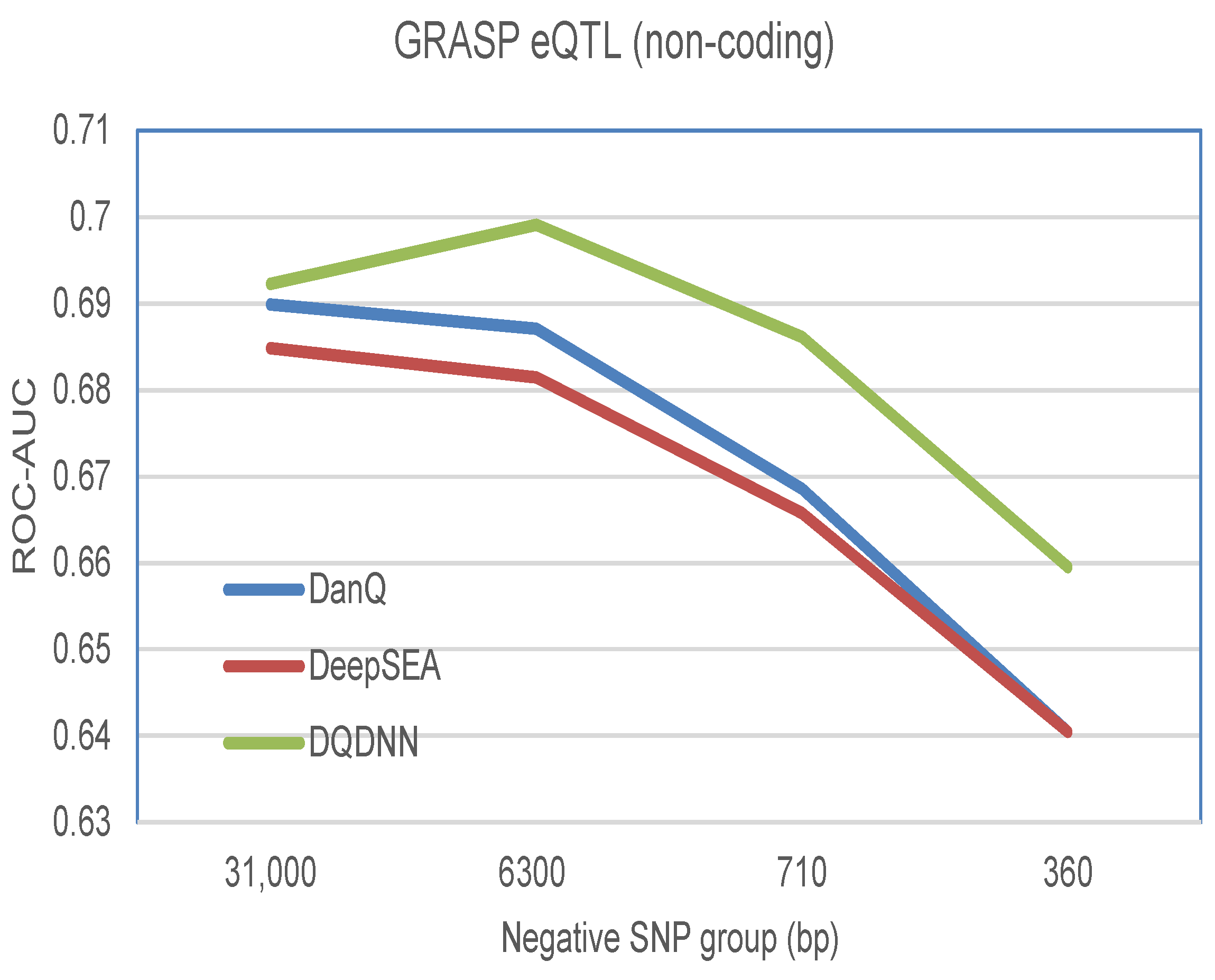
The proposed DQDNN model could be used to study the functional SNP prioritization. Here, we used the positive and negative datasets provided by DeepSEA. The positive dataset was obtained from the genome-wide repository of associations between SNPs and phenotypes (GRASP) database, and it includes the expression quantitative trait loci (eQTLs) [
26]. For the negative dataset, we used 1000 Genomes Project SNPs [
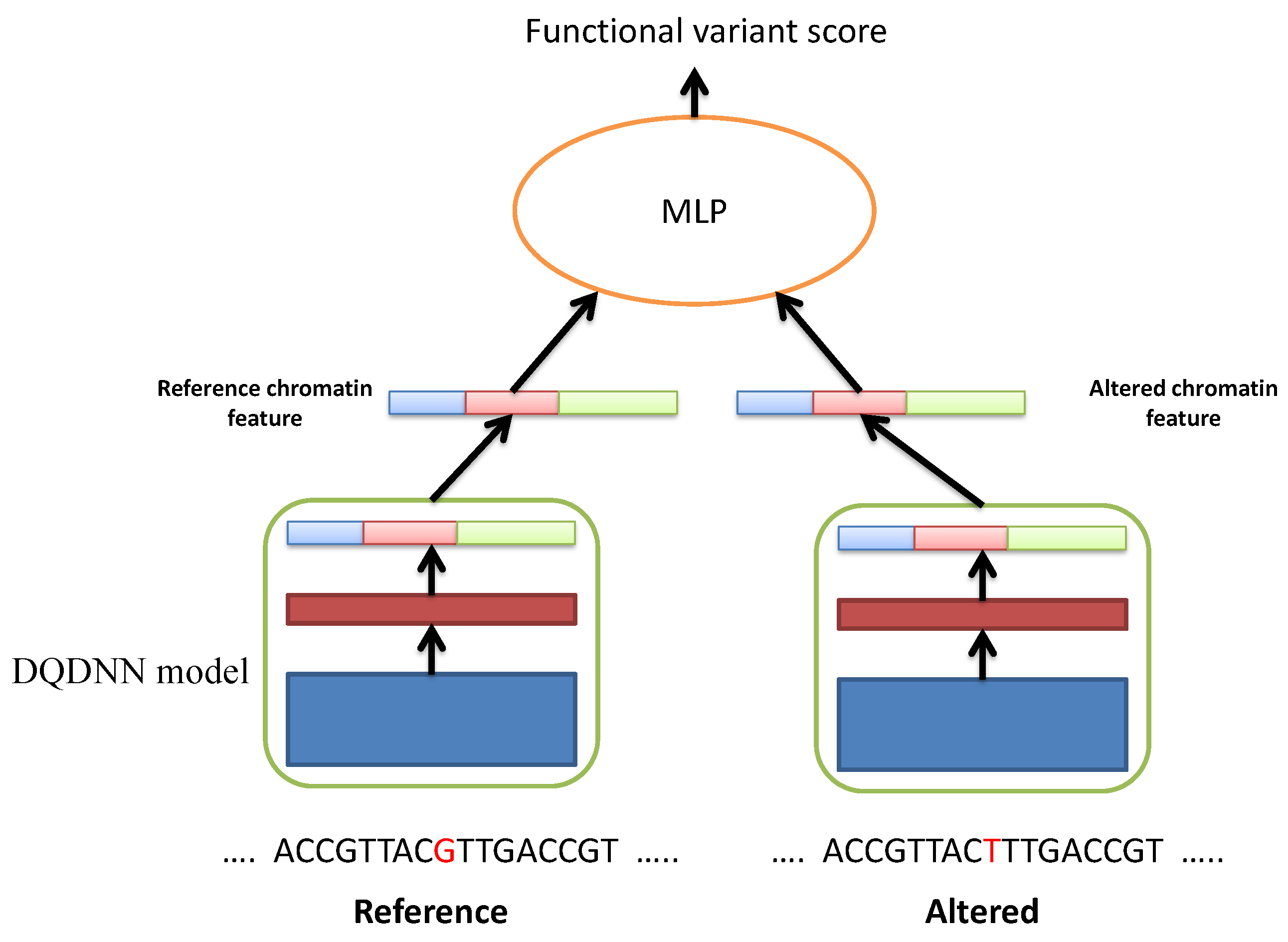
27]. The negative SNPs dataset was divided into different groups based on their distances to the positive standard SNPs such as 360 bp, 710 bp, 6.3 kbp, and 31 kbp. By following DeepSEA and DanQ, the features for the positive and negative SNP sequences were extracted using the proposed model DQDNN. Then, these features were passed to a multi-layer perceptron (MLP) neural network to learn the functional SNP prioritization as shown in
Figure 4.
In more detail, we extracted the chromatin features using DQDNN for the reference sequence, and we call it
; and the altered sequence we call
. From these two chromatin features vectors, we calculated
chromatin effect features that were the concatenation of the absolute differences:
and the relative log fold changes of odds:
In our design, we calculated the chromatin effect features from DQDNN-DNA and DQDNN-CONS. Thus, we had
chromatin effect features to be used in the MLP model. The MLP model was a two layer fully connected network, and the detailed configurations of the MLP model are given in
Table 3.