The Relationship between Turgor Pressure Change and Cell Hydraulics of Midrib Parenchyma Cells in the Leaves of Zea mays
Abstract
1. Introduction
2. Materials and Methods
2.1. Plant Material
2.2. Experimental Setup Using a Cell Pressure Probe
2.3. Pressurization Experiment
3. Results
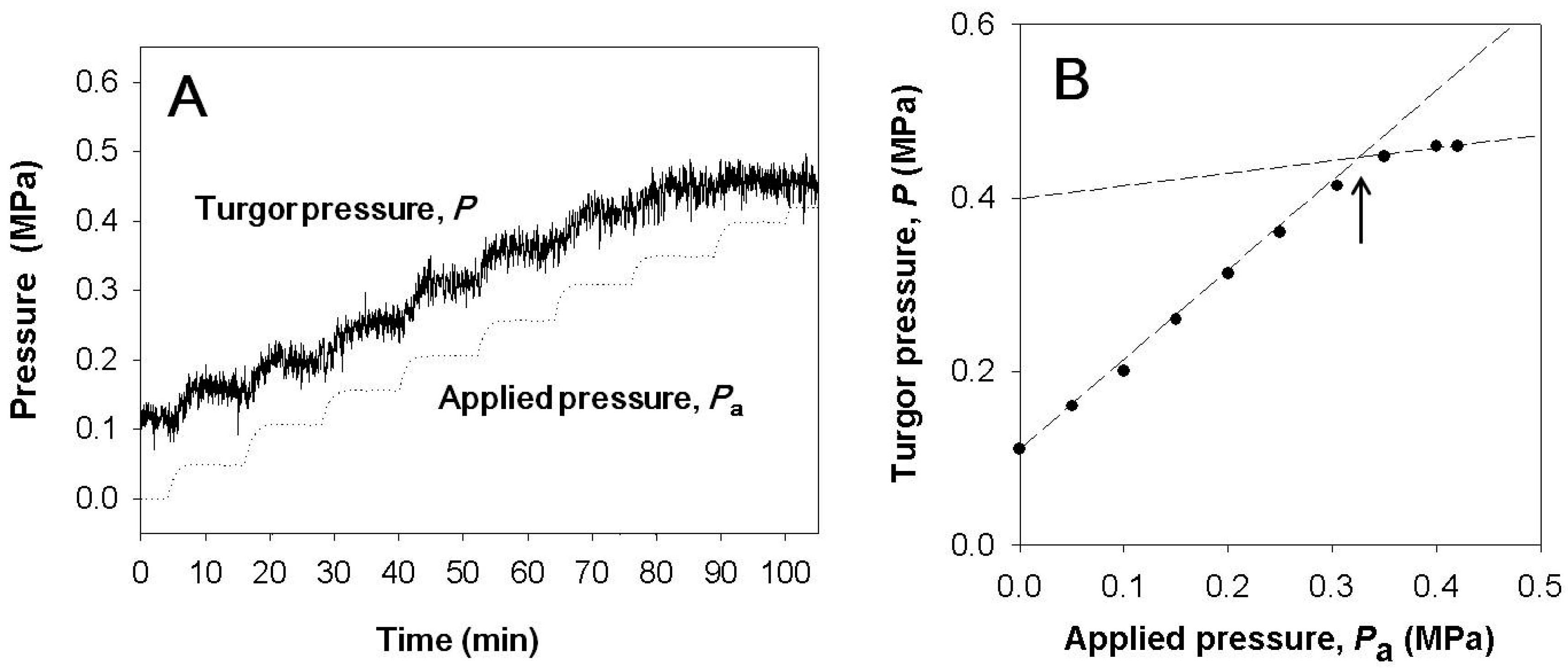
3.1. Pressure Chamber Pressure vs. Cell Turgor Pressure
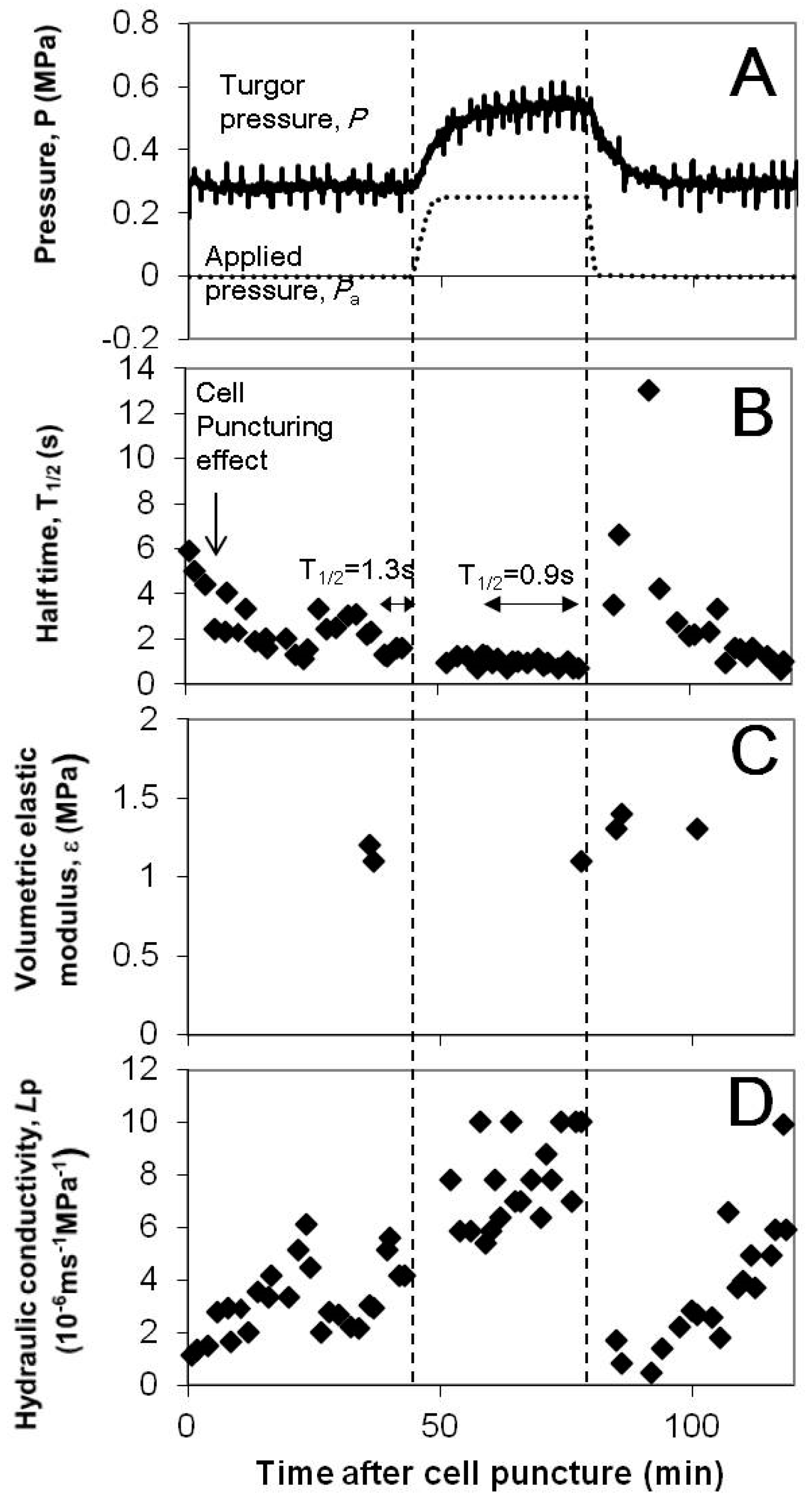
3.2. Cell Hydraulic Conductivity, Lp and the Half Time of Hydrostatic Relaxation,
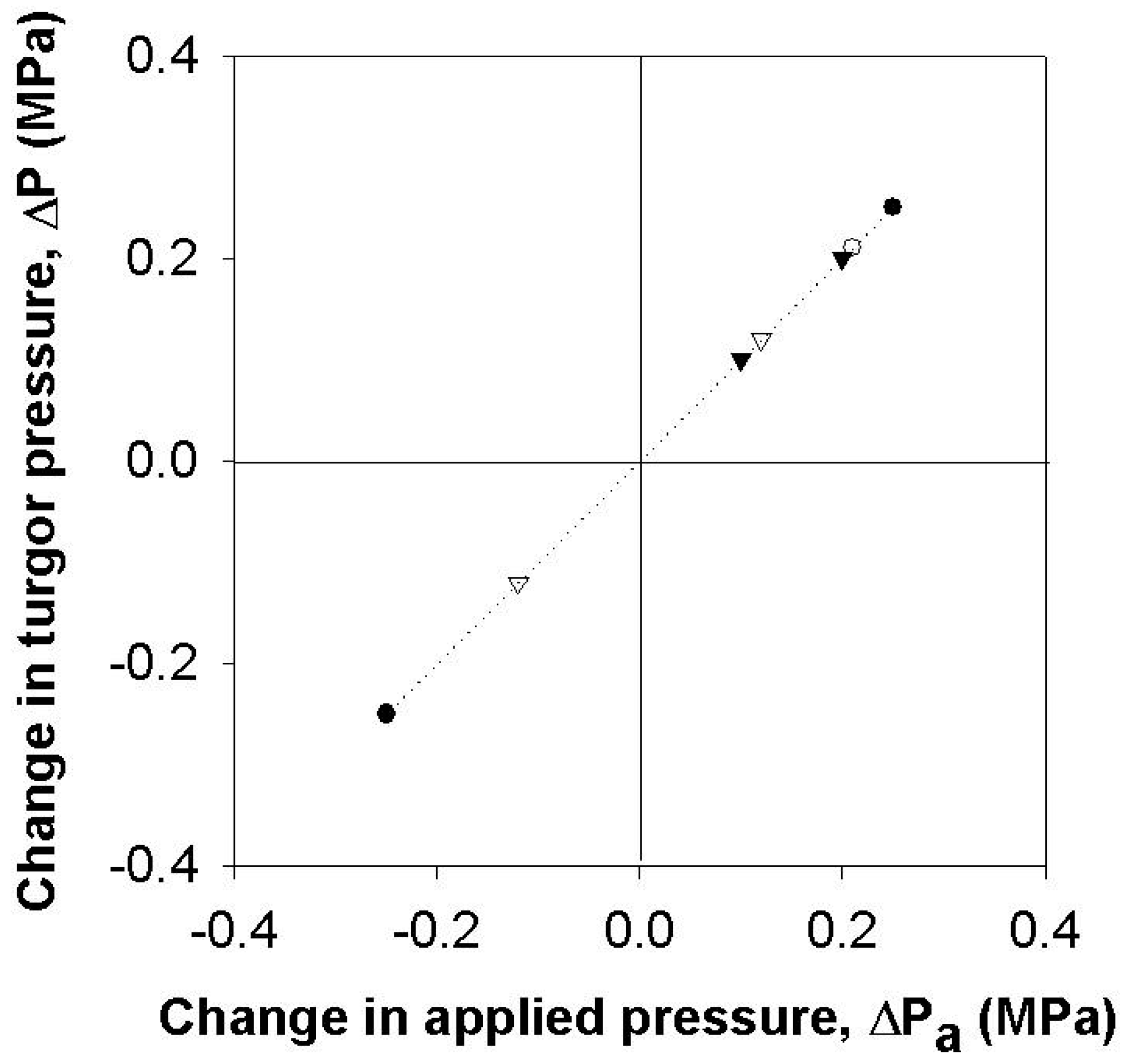
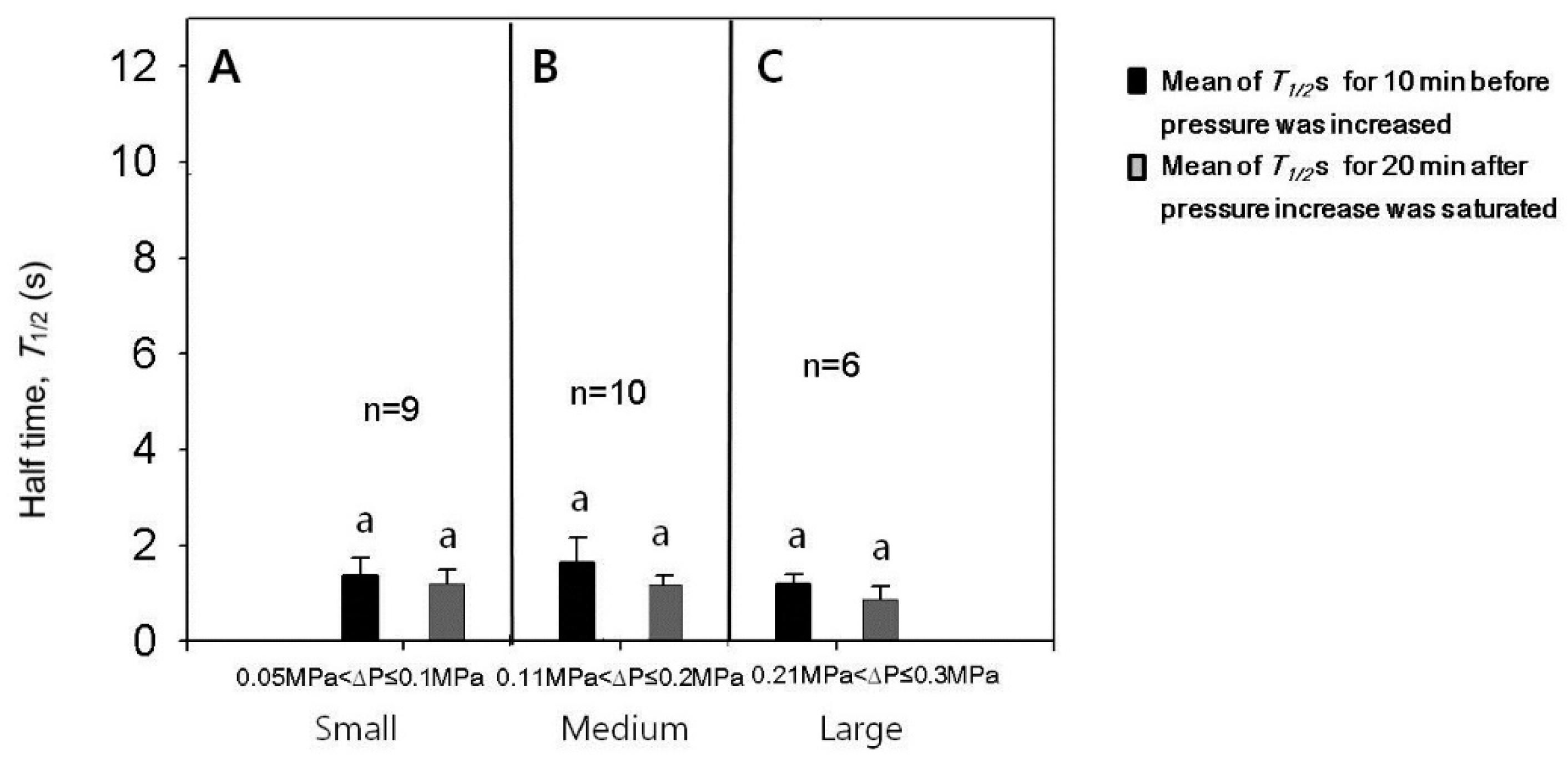
3.3. Effect of Turgor Pressure Alterations on
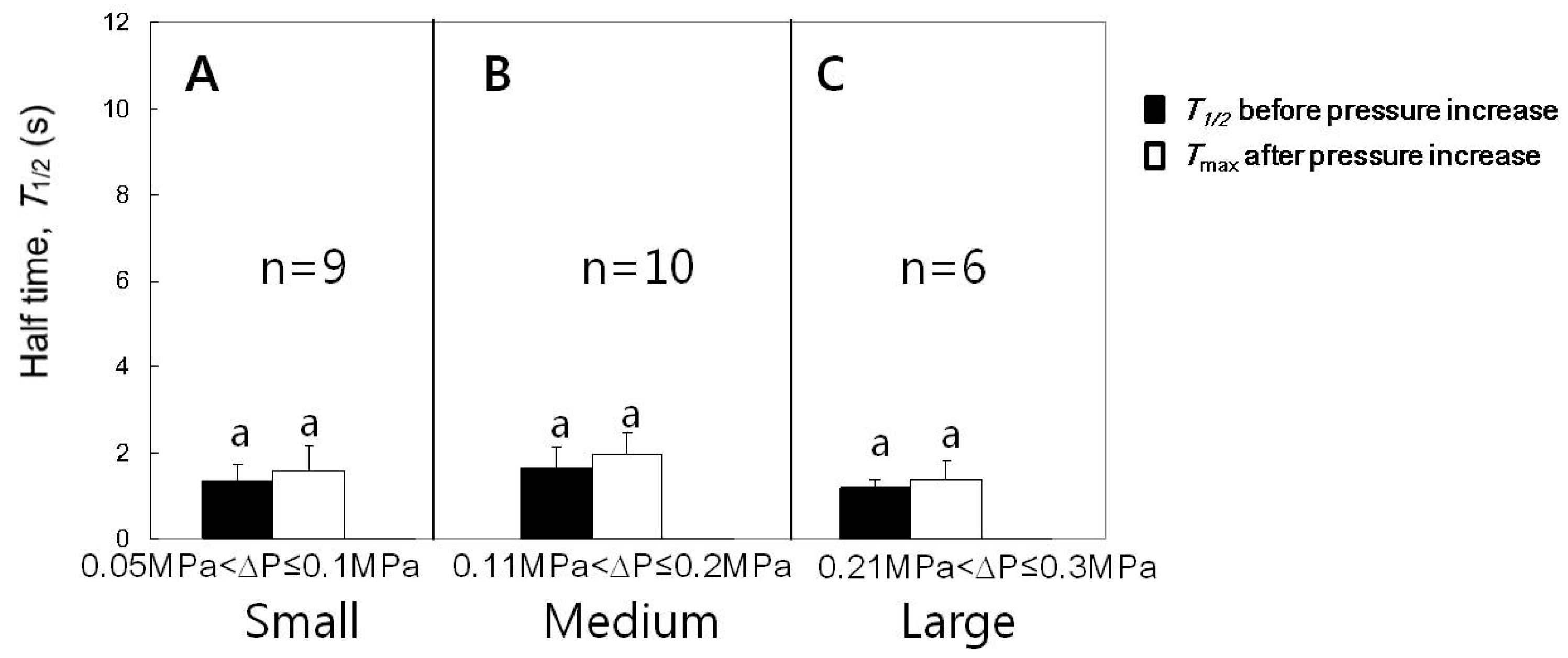
3.4. Effect of Turgor Pressure Increase on
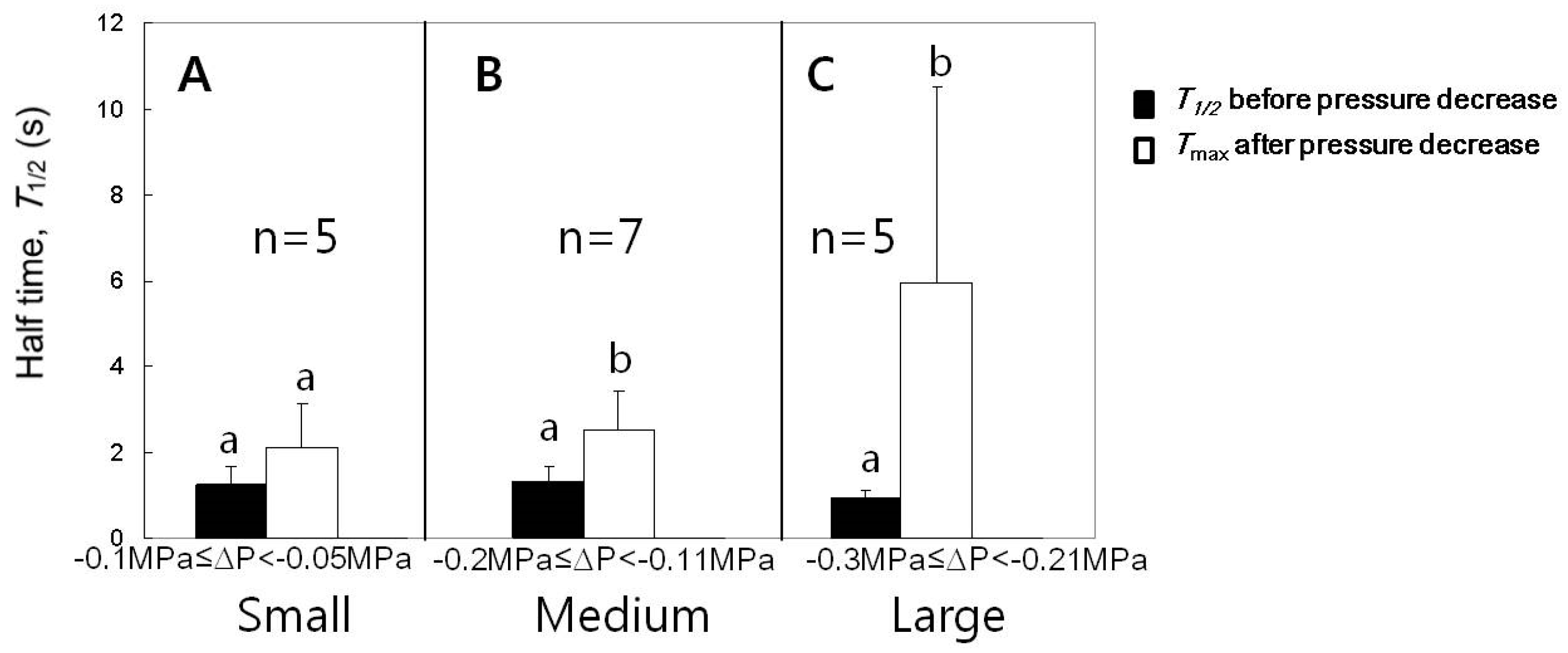
3.5. Effect of Decreases in Turgor Pressure Back to the Original Value on
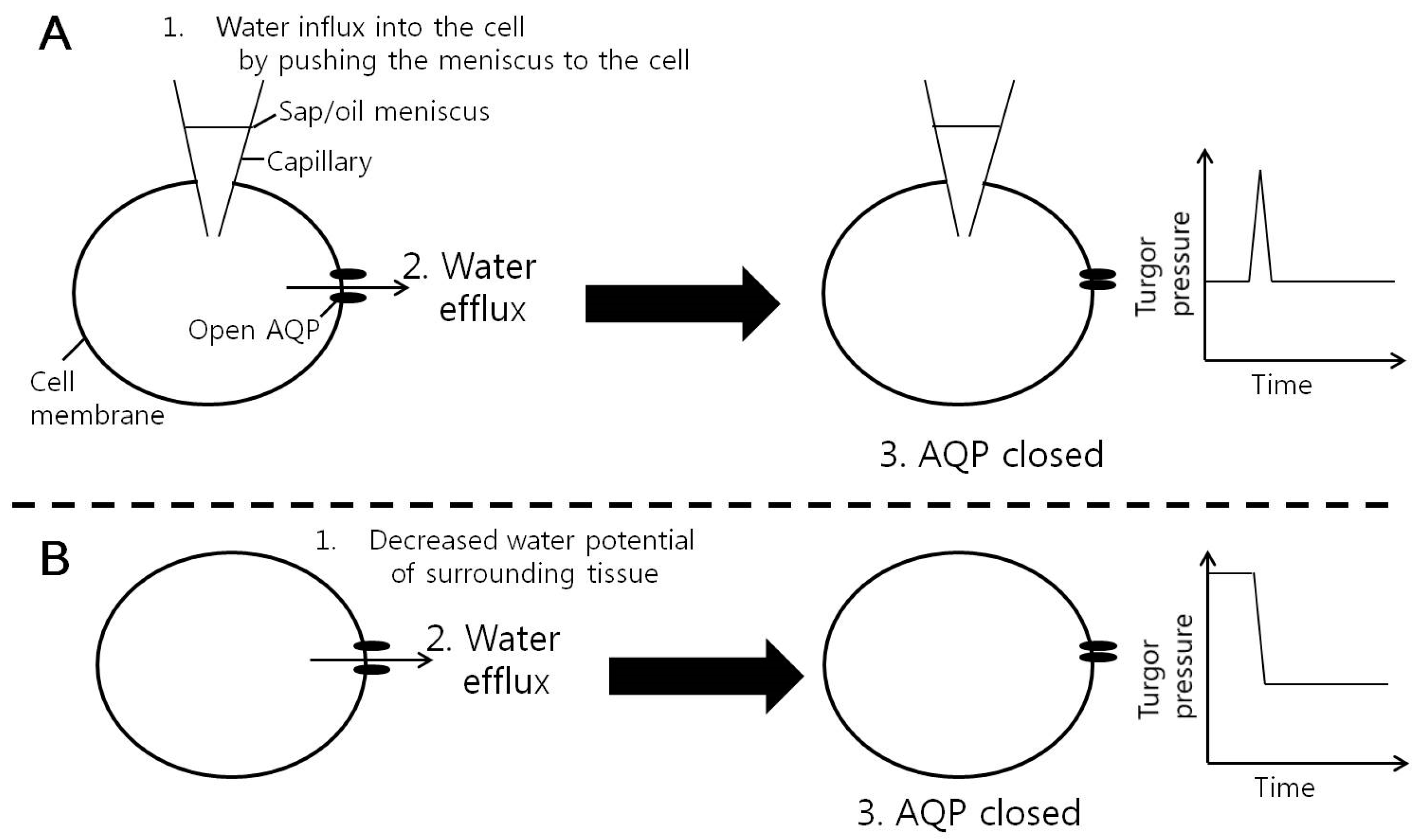
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sack, L.; Holbrook, N.M. Leaf hydraulics. Annu. Rev. Plant Biol. 2006, 57, 361–381. [Google Scholar] [CrossRef] [PubMed]
- Guyot, G.; Scoffoni, C.; Sack, L. Combined impacts of irradiance and dehydration on leaf hydraulic conductance: Insights into vulnerability and stomatal control. Plant Cell Environ. 2012, 35, 857–871. [Google Scholar] [CrossRef] [PubMed]
- Pou, A.; Medrano, H.; Flexas, J.; Tyerman, S.D. A putative role for TIP and PIP aquaporins in dynamics of leaf hydraulic and stomatal conductances in grapevine under water stress and re-watering. Plant Cell Environ. 2013, 36, 828–843. [Google Scholar] [CrossRef] [PubMed]
- Scoffoni, C.; Vuong, C.; Diep, S.; Cochard, H.; Sack, L. Leaf shrinkage with dehydration: Coordination with hydraulic vulnerability and drought tolerance. Plant Physiol. 2014, 164, 1772–1788. [Google Scholar] [CrossRef] [PubMed]
- Hachez, C.; Heinen, R.B.; Draye, X.; Chaumont, F. The expression pattern of plasma membrane aquaporins in maize leaf highlights their role in hydraulic regulation. Plant Mol. Biol. 2008, 68, 337–353. [Google Scholar] [CrossRef] [PubMed]
- Shatil-Cohen, A.; Attia, Z.; Moshelion, M. Bundle-sheath cell regulation of xylem-mesophyll water transport via aquaporins under drought stress: A target of xylem-borne ABA? Plant J. 2011, 67, 72–80. [Google Scholar] [CrossRef] [PubMed]
- Prado, K.; Maurel, C. Regulation of leaf hydraulics: From molecular to whole plant levels. Front. Plant Sci. 2013, 4, 255. [Google Scholar] [CrossRef] [PubMed]
- Scoffoni, C. Modelling the outside-xylem hydraulic conductance: Towards a new understanding of leaf water relations. Plant Cell Environ. 2015, 38, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.X.; Steudle, E. Light and turgor affect the water permeability (aquaporins) of parenchyma cells in the midrib of leaves of Zea mays. J. Exp. Bot. 2007, 58, 4119–4129. [Google Scholar] [CrossRef] [PubMed]
- Steudle, E.; Henzler, T. Water channels in plants: Do basic concepts of water transport change? J. Exp. Bot. 1995, 46, 1067–1076. [Google Scholar] [CrossRef]
- Maurel, C. Aquaporins and water permeability of plant membranes. Ann. Rev. Plant Physiol. Plant Mol. Biol. 1997, 48, 399–429. [Google Scholar] [CrossRef] [PubMed]
- Kjellbom, P.; Larsson, C.; Johansson, I.; Karlsson, M.; Johanson, U. Aquaporins and water homeostasis in plants. Trends Plant Sci. 1999, 4, 308–314. [Google Scholar] [CrossRef]
- Tyerman, S.D.; Bohnert, H.J.; Maurel, C.; Steudle, E.; Smith, J.A.C. Plant aquaporins: Their molecular biology, biophysics and significance for plant water relations. J. Exp. Bot. 1999, 50, 1055–1071. [Google Scholar] [CrossRef]
- Steudle, E. Water uptake by roots: Effects of water deficit. J. Exp. Bot. 2000, 51, 1531–1542. [Google Scholar] [CrossRef] [PubMed]
- Steudle, E. The cohesion–tension mechanism and the acquisition of water by plant roots. Ann. Rev. Plant Physiol. Plant Mol. Biol. 2001, 52, 847–875. [Google Scholar] [CrossRef] [PubMed]
- Maurel, C.; Chrispeels, M.J. Aquaporins. A molecular entry into plant water relations. Plant Physiol. 2001, 125, 135–138. [Google Scholar] [CrossRef] [PubMed]
- Chaumont, F.; Tyerman, S.D. Aquaporins: Highly regulated channels controlling plant water relations. Plant Physiol. 2014, 164, 1600–1618. [Google Scholar] [CrossRef] [PubMed]
- Maurel, C.; Boursiac, Y.; Luu, D.T.; Santoni, V.; Shahzad, Z.; Verdoucq, L. Aquaporins in plants. Physiol. Rev. 2015, 95, 1321–1358. [Google Scholar] [CrossRef] [PubMed]
- Henzler, T.; Waterhouse, R.N.; Smyth, A.J.; Carvajal, M.; Cooke, D.T.; Schäffner, A.R.; Steudle, E.; Clarkson, D.T. Diurnal variations in hydraulic conductivity and root pressure can be correlated with the expression of putative aquaporins in the root of Lotus japonicus. Planta 1999, 210, 50–60. [Google Scholar] [CrossRef] [PubMed]
- Moshelion, M.; Becker, D.; Biela, A.; Uehlein, N.; Hedrich, R.; Otto, B.; Levi, H.; Moran, N.; Kaldenhoff, R. Plasma membrane aquaporins in the motor cells of Samanea saman: Diurnal and circadian regulation. Plant Cell 2002, 14, 727–739. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.X.; Ranathunge, K.; Lee, S.; Lee, Y.; Lee, D.; Sung, J. Composite transport model and water and solute transport across plant roots: An update. Front. Plant Sci. 2018, 9, 193. [Google Scholar] [CrossRef] [PubMed]
- Johansson, I.; Karlsson, M.; Shukla, V.K.; Chrispeels, M.J.; Larsson, C.; Kjellbom, P. Water transport activity of the plasma membrane aquaporin PM28A is regulated by phosphorylation. Plant Cell 1998, 10, 451–459. [Google Scholar] [CrossRef] [PubMed]
- Brodribb, T.J.; Holbrook, N.M. Declining hydraulic efficiency as transpiring leaves desiccate: Two types of response. Plant Cell Environ. 2006, 29, 2205–2215. [Google Scholar] [CrossRef] [PubMed]
- Wan, X.C.; Steudle, E.; Hartung, W. Gating of water channels (aquaporins) in cortical cells of young corn roots by mechanical stimuli (pressure pulses): Effects of ABA and of HgCl2. J. Exp. Bot. 2004, 55, 411–422. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Chung, G.C.; Steudle, E. Low temperature and mechanical stresses differently gate aquaporins of root cortical cells of chilling-sensitive cucumber and -resistant figleaf gourd. Plant Cell Environ. 2005, 28, 1191–1202. [Google Scholar] [CrossRef]
- Kim, Y.X.; Steudle, E. Gating of aquaporins by light and reactive oxygen species in leaf parenchyma cells of the midrib of Zea mays. J. Exp. Bot. 2009, 60, 547–556. [Google Scholar] [CrossRef] [PubMed]
- Westgate, M.E.; Steudle, E. Water transport in the midrib tissue of maize leaves. Plant Physiol. 1985, 78, 183–191. [Google Scholar] [CrossRef] [PubMed]
- Wei, C.; Tyree, M.T.; Steudle, E. Direct measurement of xylem pressure in leaves of intact maize plants. A test of the cohesion-tension theory taking hydraulic architecture into consideration. Plant Physiol. 1999, 121, 1191–1205. [Google Scholar] [CrossRef] [PubMed]
- Steudle, E. Pressure probe techniques: Basic principles and application to studies of water and solute relations at the cell, tissue and organ level. In Water Deficits: Plant Responses from Cell to Community; Smith, J.A.C., Griffiths, H., Eds.; Bios Scientific Publishers: Oxford, UK, 1993; pp. 5–36. [Google Scholar]
- Henzler, T.; Steudle, E. Reversible closing of water channels in Chara internodes provides evidence for a composite transport model of the plasma membrane. J. Exp. Bot. 1995, 46, 199–209. [Google Scholar] [CrossRef]
- Ye, Q.; Steudle, E. Oxidative gating of water channels (aquaporins) in corn roots. Plant Cell Environ. 2006, 29, 459–470. [Google Scholar] [CrossRef] [PubMed]
- Johansson, I.; Larsson, C.; Ek, B.; Kjellbom, P. The major integral proteins of spinach leaf plasma membranes are putative aquaporins and are phoshorylated in response to Ca2+ and apoplastic water potential. Plant Cell 1996, 8, 1181–1191. [Google Scholar] [PubMed]
- Alleva, K.; Niemietz, C.M.; Sutka, M.; Maurel, C.; Parisi, M.; Tyerman, S.D.; Amodeo, G. Plasma membrane of Β. vulgaris storage root shows high water channel activity regulated by cytoplasmic pH and a dual range of calcium concentrations. J. Exp. Bot. 2006, 57, 609–621. [Google Scholar] [CrossRef] [PubMed]
- Tournaire-Roux, C.; Sutka, M.; Javot, H.; Gout, E.; Gerbeau, P.; Luu, D.T.; Bligny, R.; Maurel, C. Cytosolic pH regulates root water transport during anoxic stress through gating of aquaporins. Nature 2003, 425, 393–397. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.X.; Stumpf, B.; Sung, J.; Lee, S.J. The Relationship between Turgor Pressure Change and Cell Hydraulics of Midrib Parenchyma Cells in the Leaves of Zea mays. Cells 2018, 7, 180. https://doi.org/10.3390/cells7100180
Kim YX, Stumpf B, Sung J, Lee SJ. The Relationship between Turgor Pressure Change and Cell Hydraulics of Midrib Parenchyma Cells in the Leaves of Zea mays. Cells. 2018; 7(10):180. https://doi.org/10.3390/cells7100180
Chicago/Turabian StyleKim, Yangmin X., Burkhard Stumpf, Jwakyung Sung, and Sang Joon Lee. 2018. "The Relationship between Turgor Pressure Change and Cell Hydraulics of Midrib Parenchyma Cells in the Leaves of Zea mays" Cells 7, no. 10: 180. https://doi.org/10.3390/cells7100180
APA StyleKim, Y. X., Stumpf, B., Sung, J., & Lee, S. J. (2018). The Relationship between Turgor Pressure Change and Cell Hydraulics of Midrib Parenchyma Cells in the Leaves of Zea mays. Cells, 7(10), 180. https://doi.org/10.3390/cells7100180





