Numerical Modelling of Keratinocyte Behaviour: A Comprehensive Review of Biochemical and Mechanical Frameworks
Abstract
1. Introduction
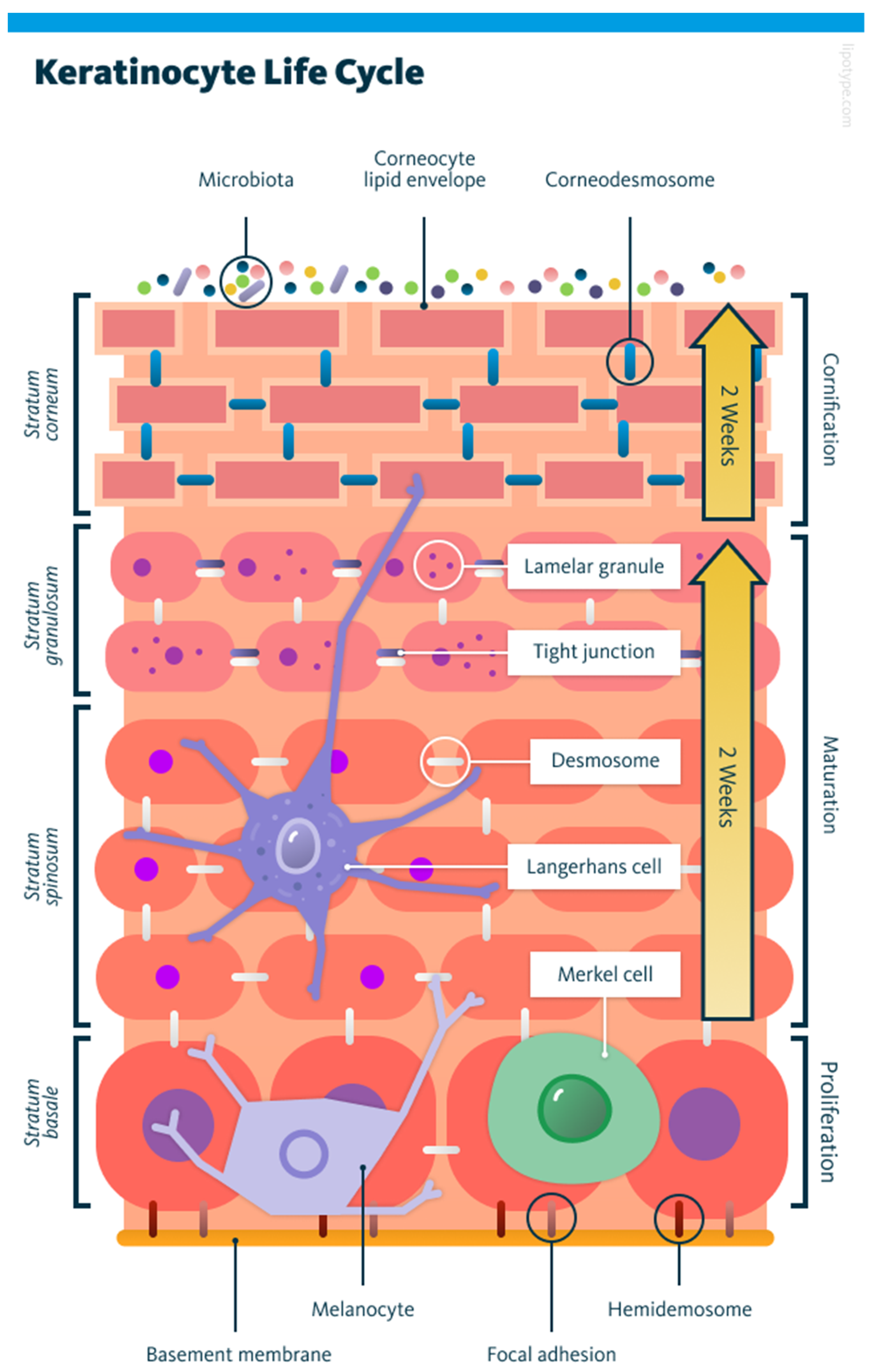
1.1. Basics of Keratinocyte Biology
1.2. Motivation for Modelling Keratinocyte Behaviour
2. An Overview of Modelling Techniques
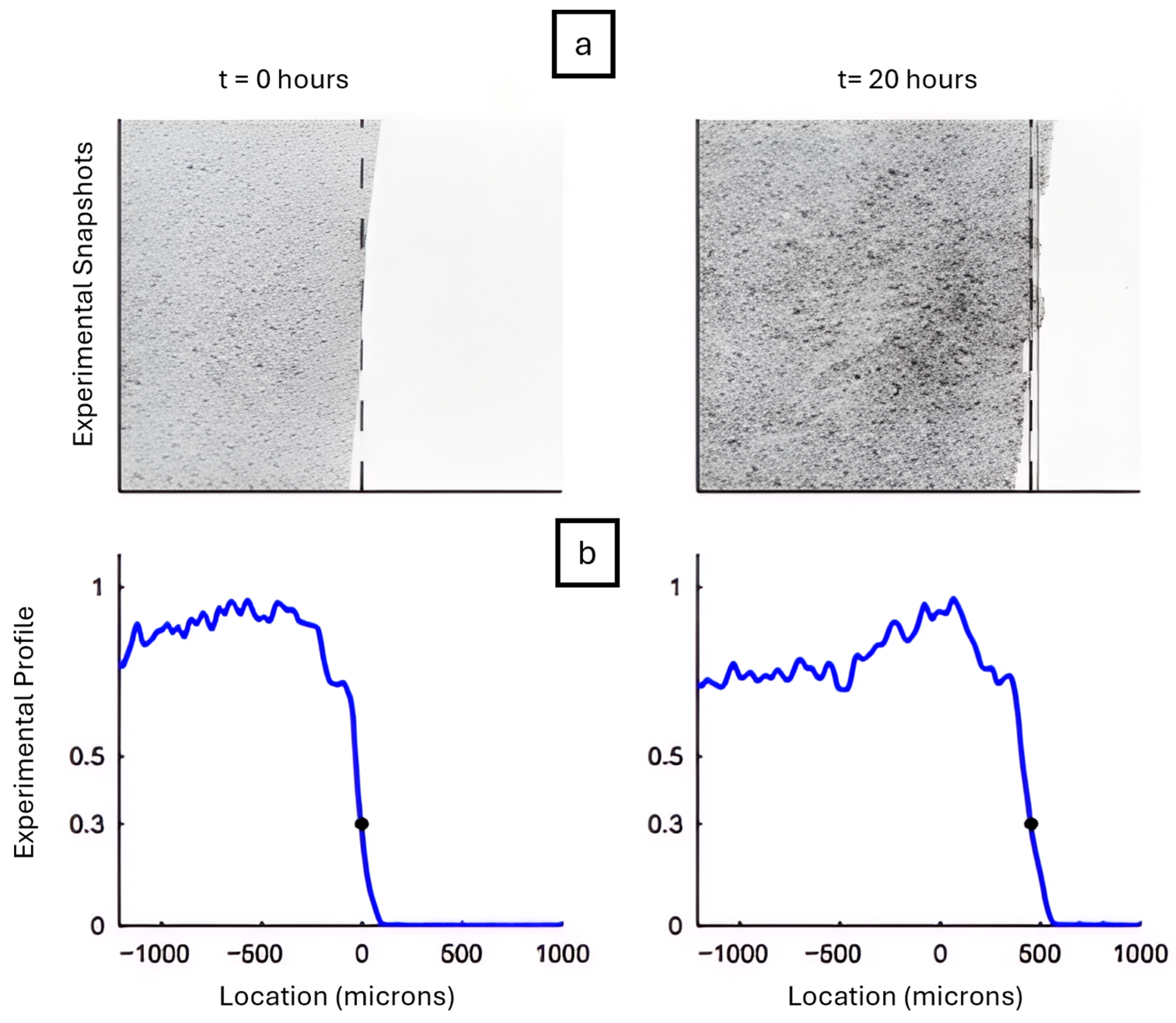
2.1. Reaction Diffusion Frameworks
- Cellular Potts Model: a technique where cell behaviour is simulated using a lattice structure.
- Partial Differential Equations (PDEs): used to define concentrations of various chemicals using continuous fields.
2.2. Stochastic and Kinetic Modelling Approaches
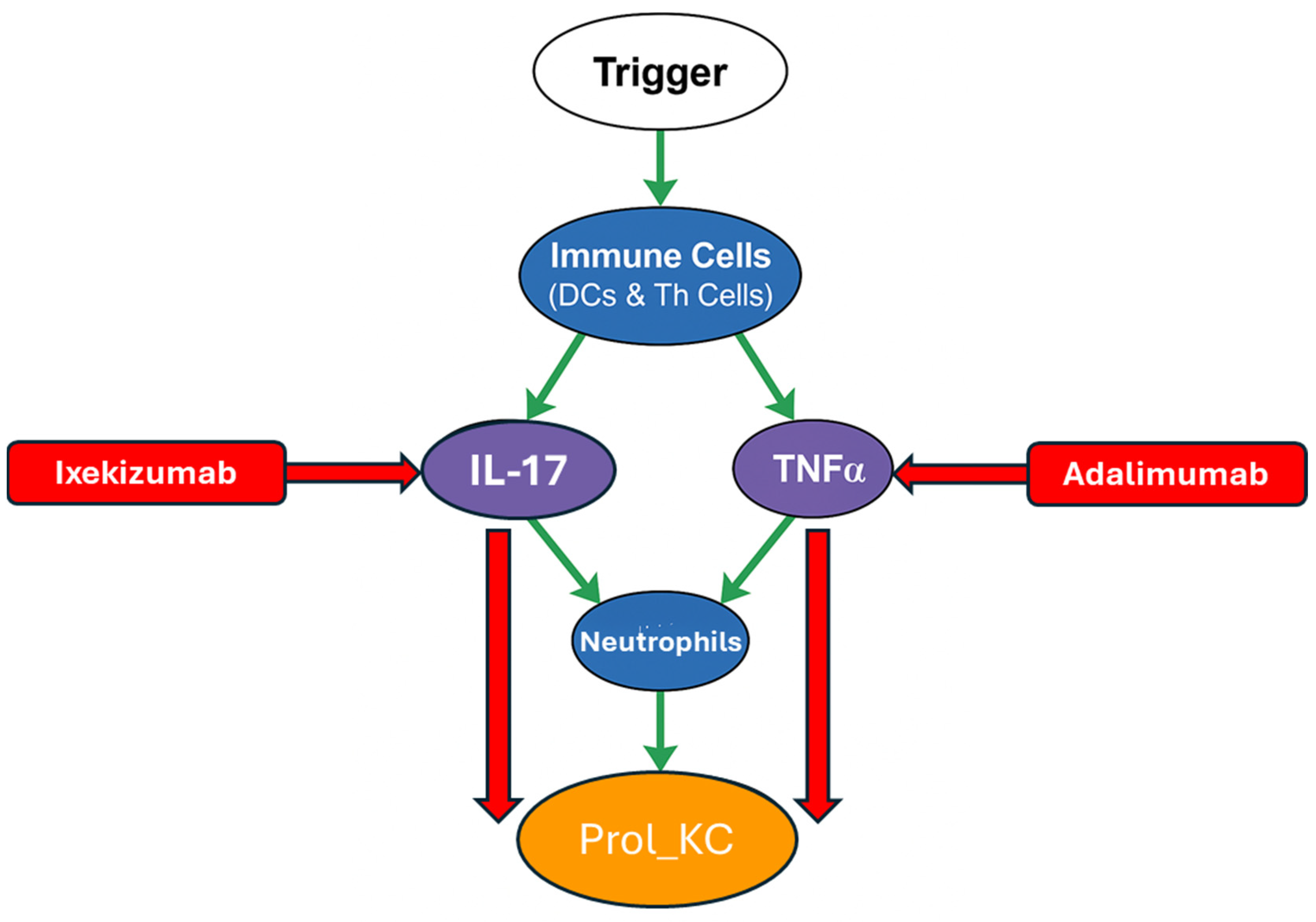
2.3. Agent-Based Modelling (ABM)
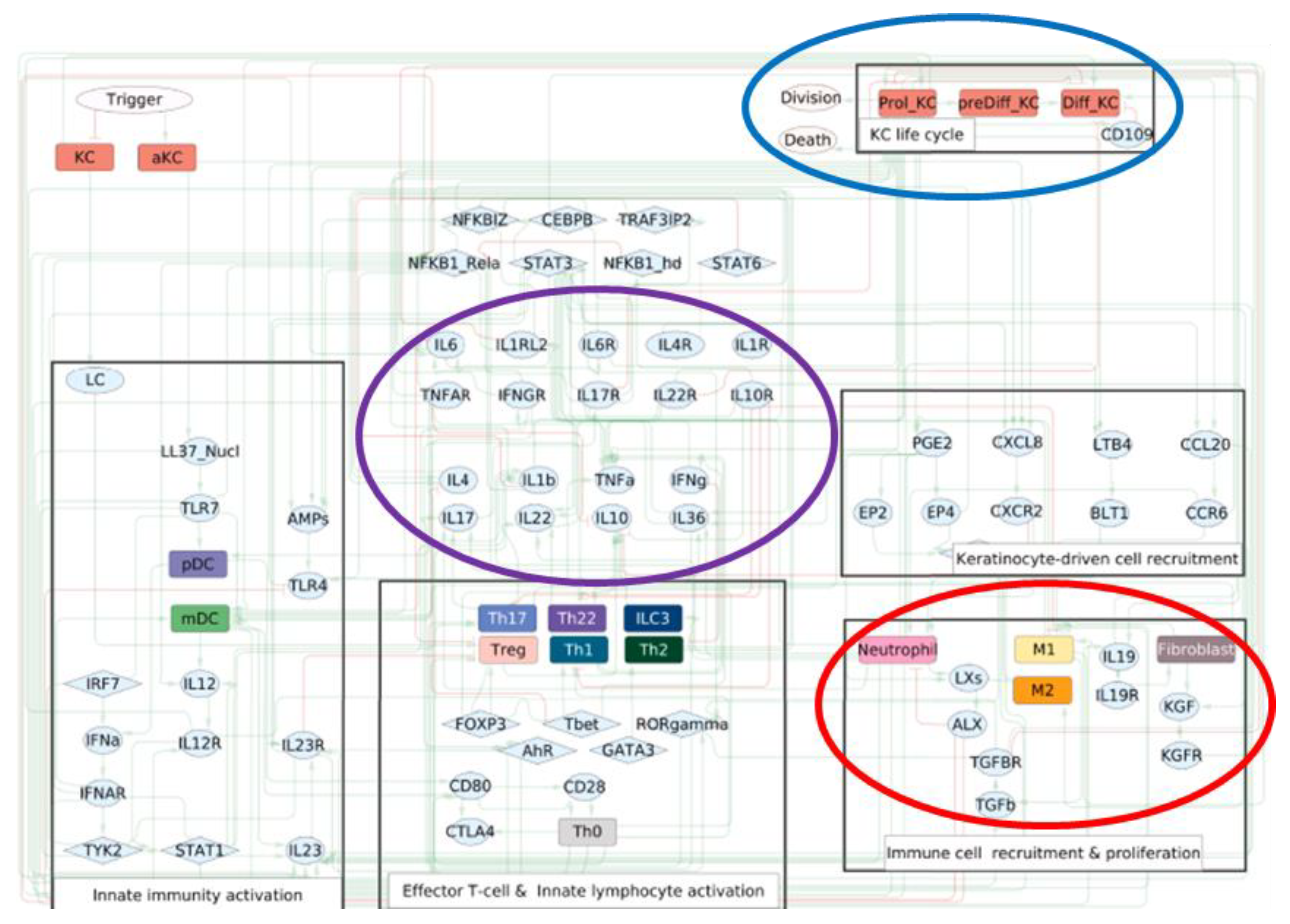
- Trigger: Represents the initial external or internal events that kick off psoriasis (e.g., skin injury, infections, stress).
- Immune cell types are shown in a blue circle. For example, neutrophils, Dendritic Cells and T-helper subtypes (Th).
- Keratinocyte state shown in an orange circle (e.g., proliferating keratinocytes (Prol_KC)). This is linked to uncontrolled growth and a key measure of disease activity in the model.
- Major cytokines shown in a purple circle (e.g., Interleukin 17 (IL-17), Tumour Necrosis Factor Alpha (TNFα). These are inflammatory responses and are the key drivers of psoriasis.
- Therapeutic and Regulatory Drugs/Agents shown in a red rectangle (e.g., Ixekizumab, Adalimumab).
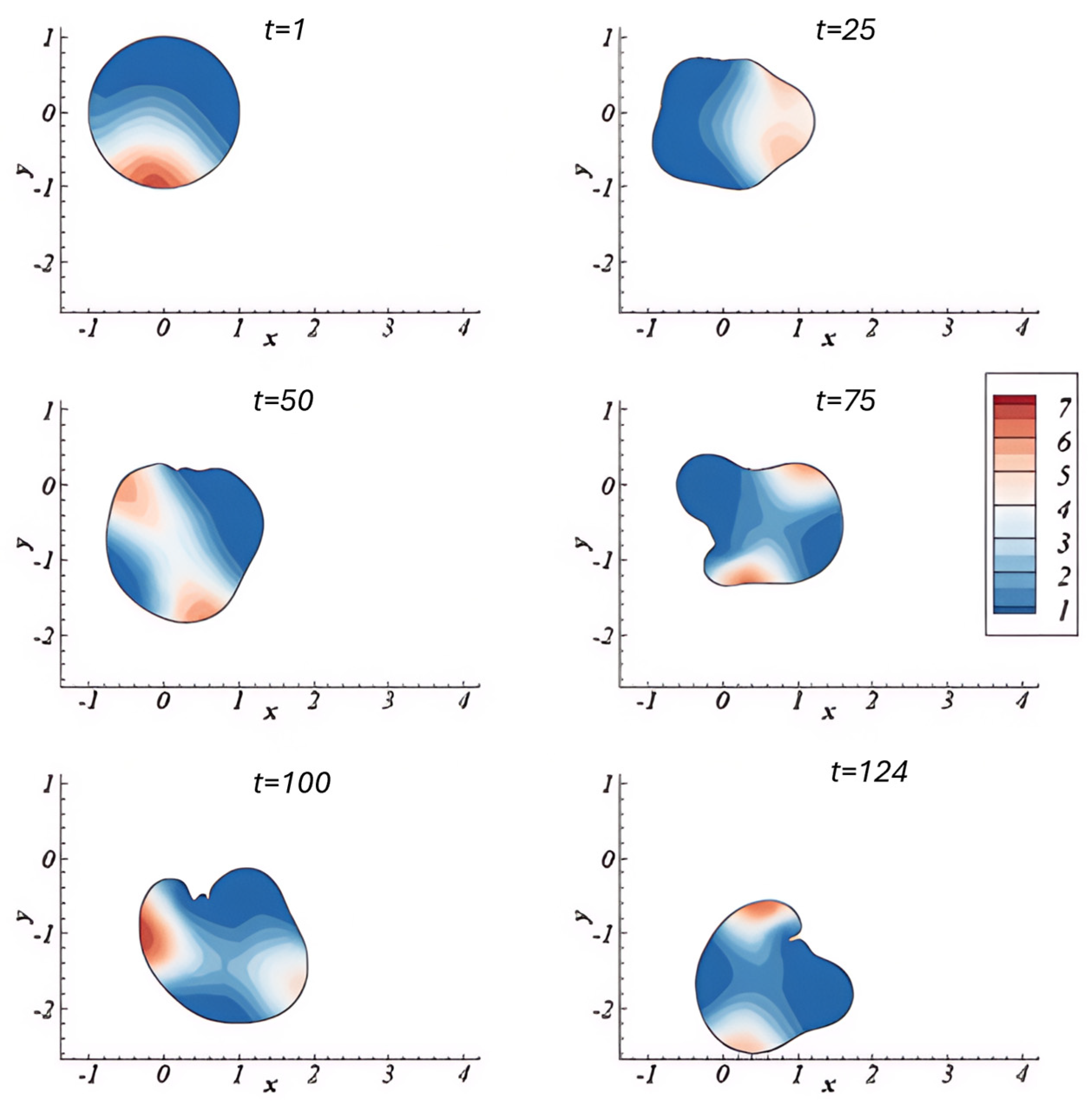
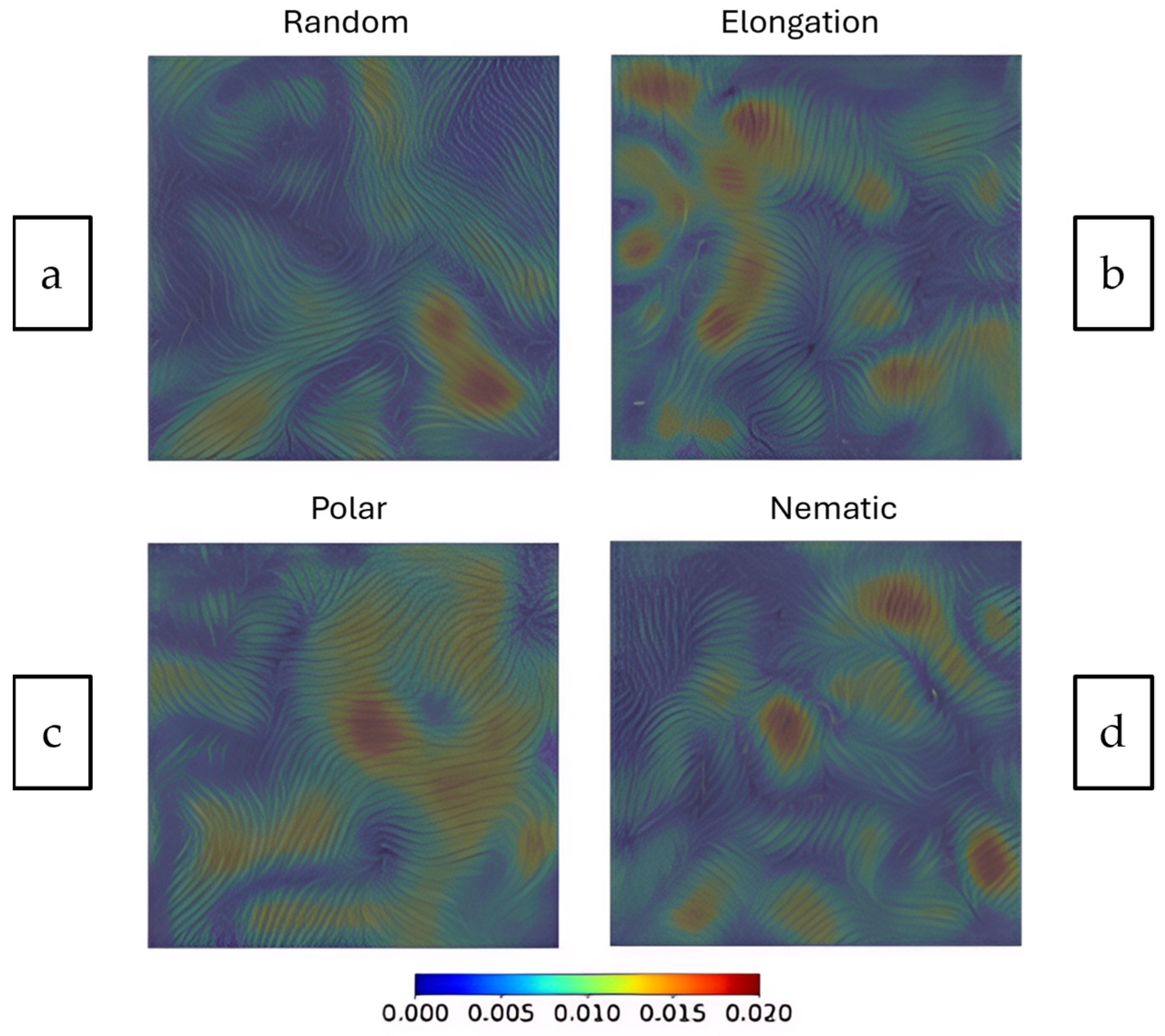
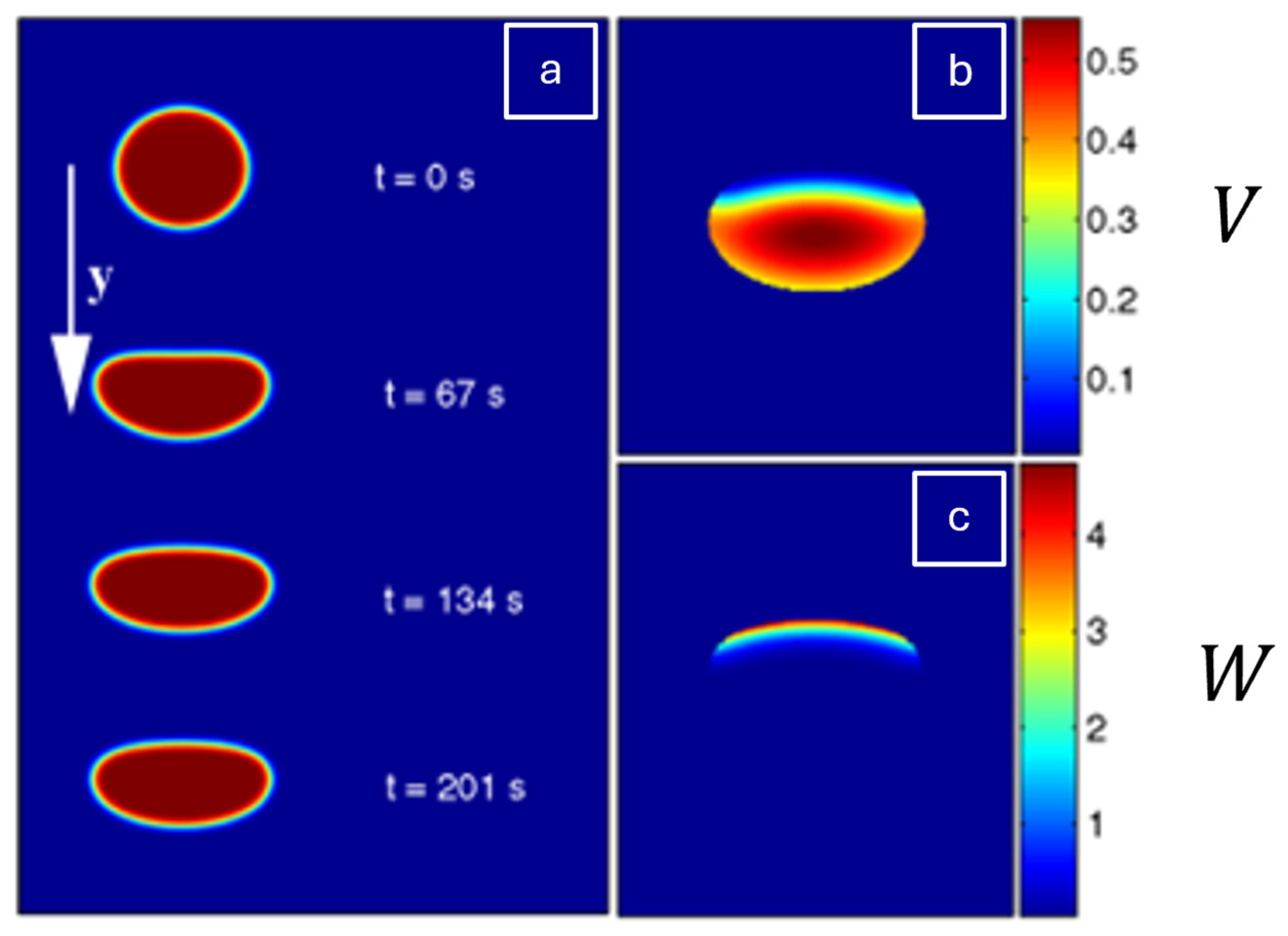
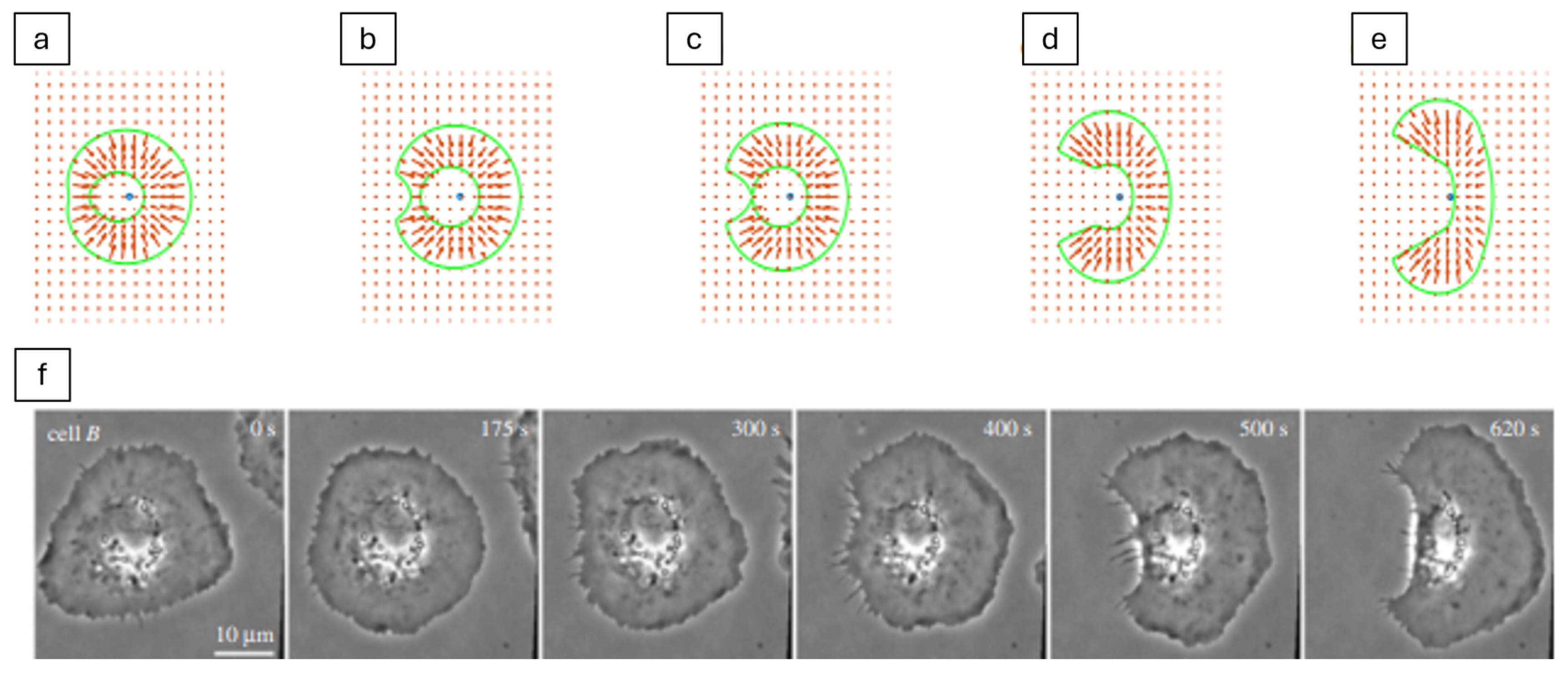
2.4. Continuum and Multiphase Modelling
- Random: Uncoordinated movement.
- Elongation: Cells stretch in a particular direction.
- Polar: Cells having a defined front-to-back direction.
- Nematic: Cells aligning without a specific directional bias (like liquid crystals).
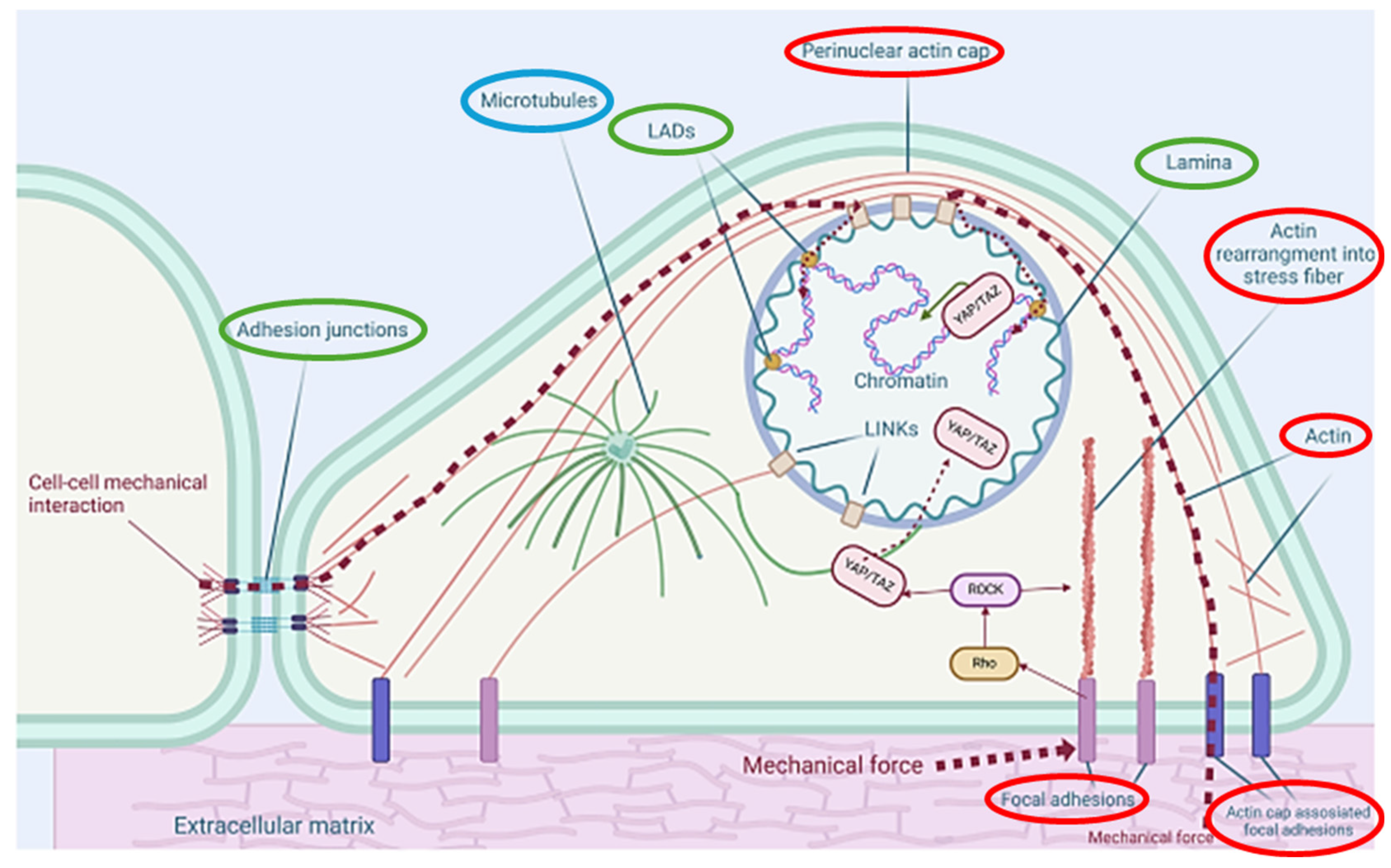
3. Mechanobiology of Keratinocytes
3.1. Substrate Stiffness
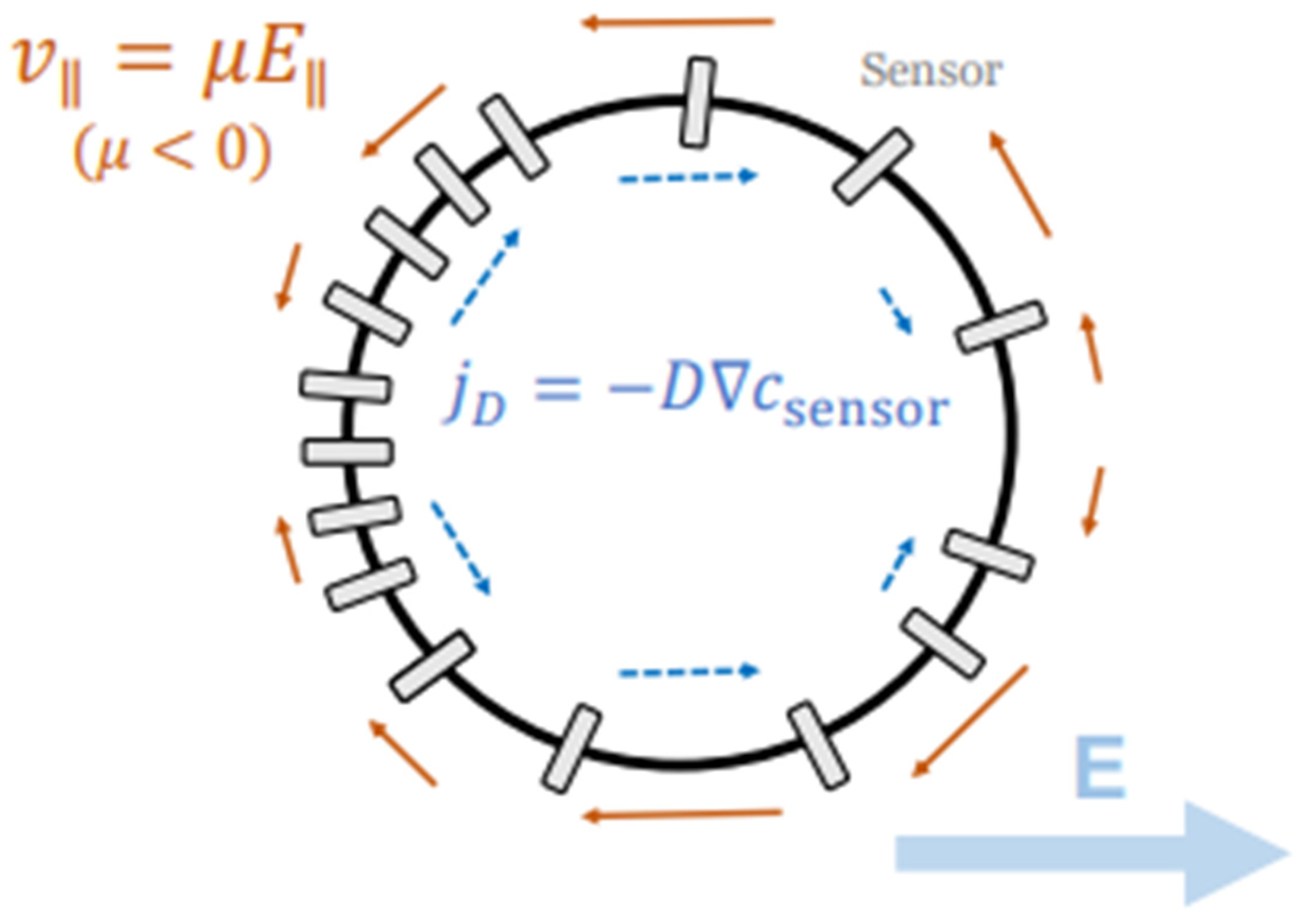
3.2. Electric Fields (EFs)
3.3. Extracellular Matrix (ECM) Effects
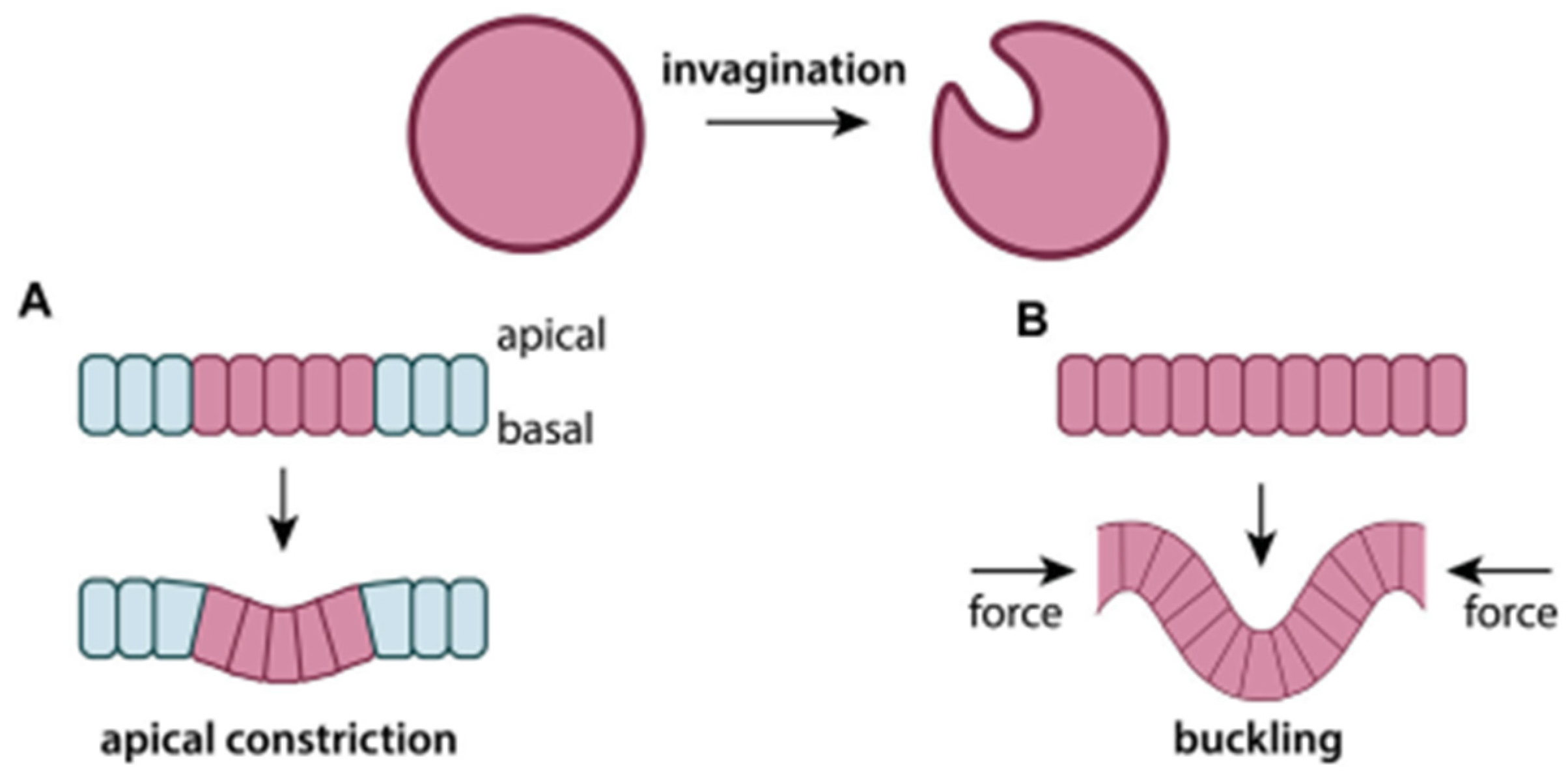
4. Finite Element (FE) Modelling of Keratinocytes
4.1. Instantaneous Elastic Modulus
4.2. Internal Stress Distribution and Focal Adhesion (FA) Loading
4.3. Viscoelastic Response and Active Contraction Dynamics
- Stress-relaxation tests, using experimental force–time curves to tune model parameters [158].
- Laser ablation recoil, where a laser is used to cut part of a cell or tissue, and the subsequent retraction or recoil of the remaining material is measured [159].
- Time-lapse wound healing, comparing simulated and real closure rates [160].
- Bioprinted phantoms, which are 3D-printed materials acting as biological substitutes. They test inverse modelling solutions in controlled conditions [161].
5. Discussion
5.1. Summary of Insights and Limitations
5.2. Machine Learning (ML) and Artificial Intelligence (AI)
6. Future Work and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FBP1 | Fructose-1,6-Bisphosphatase 1 |
| REG3A | Regenerating Islet-Derived Protein 3 Alpha |
| ML | Machine Learning |
| IF | Intermediate Filaments |
| LAD | Lamina-Associated Domains |
| ABM | Agent-Based Models |
| SCC | Squamous Cell Carcinoma |
| FEA | Finite Element Analysis |
| LED | Light Emitting Diode |
| micro-PIV | micro-Particle Image Velocimetry |
| ATP | Adenosine Triphosphate |
| EGF | Epidermal Growth Factor |
| EGFR | Epidermal Growth Factor Receptor |
| PDE | Partial Differential Equations |
| CPM | Cellular Potts Model |
| PDMP | Piecewise Deterministic Markov Processes |
| DC | Direct Current |
| PBC | Particle-Based Compass |
| ERK | Extracellular Signal-Regulated Kinase |
| LIC | Line Integral Convolution |
| PA | Polyacrylamide |
| PDMS | Polydimethylsiloxane |
| EFs | Electric Fields |
| AMPK | Adenosine Monophosphate-Activated Protein Kinase |
| RNA-seq | Single-Cell RNA Sequencing |
| CNN | Convolutional Neural Networks |
| AI | Artificial Intelligence |
| NHEK | Normal Human Epidermal Keratinocytes |
| GPU | Graphics Processing Unit |
| SPNs | Stochastic Petri Nets |
| MuTrans | Multiscale Stochastic Dynamics |
| MAPK | Mitogen-Activated Protein Kinase |
| FAK | Focal Adhesion Kinase |
| PI3K | Phosphoinositide 3-Kinase |
| KFs | Keratin Filaments |
| CARE | Content-Aware Image Restoration |
| TV | Transcriptomic Variation |
| NN | Neural networks |
| ODEs | Ordinary Differential Equations |
| KMC | Kinetic Monte Carlo |
| CLE | Chemical Langevin Equation |
| R-D | Reaction–Diffusion |
| ECM | Extracellular Matrix |
| Prol_KC | Proliferating Keratinocyte |
| Th | T-helper |
| IL-17 | Interleukin 17 |
| TNFα | Tumour Necrosis Factor Alpha |
| HaCaT | Human Adult Low Calcium Temperature |
| AFM | Atomic Force Microscopy |
| FE | Finite Element |
| TFM | Traction Force Microscopy |
| FTTC | Fourier Transform Traction Cytometry |
| FA | Focal Adhesion |
| HD | Hemidesmosome |
| QLV | Quasi-Linear Viscoelastic |
| MPFL | Medial Patellofemoral Ligament |
| SLS | Standard Linear Solid |
Appendix A
References
- Swift, A.; James, S. Taking the pain out of wound healing with microcurrent electrical stimulation therapy. Wounds UK 2024, 20, 56–62. [Google Scholar]
- Public Policy Projects. Time to Tackle the Burden of Woundcare. accexxe2023. Available online: https://publicpolicyprojects.com/wound-care (accessed on 4 April 2025).
- Semmeling, S.; Saatchi, A. Assessing Unmet Needs and Proposing Transformational Reform of UK Wound Management Going Further for Wound Healing. 2023. Available online: https://publicpolicyprojects.com/new-ppp-report-calls-on-icbs-to-prioritise-wound-care-as-annual-cost-nears-10-billion (accessed on 1 July 2025).
- Zhang, P.; Yang, J.; Liu, X.; Huang, C.; Tao, Y.; Shen, P.; Bai, Z.; Xiao, C.; Zhou, L.; Li, G.; et al. FBP1 orchestrates keratinocyte proliferation/differentiation and suppresses psoriasis through metabolic control of histone acetylation. Cell Death Dis. 2024, 15, 6. [Google Scholar] [CrossRef]
- Lai, Y.; Li, D.; Li, C.; Muehleisen, B.; Radek, K.A.; Park, H.J.; Jiang, Z.; Li, Z.; Lei, H.; Quan, Y.; et al. The Antimicrobial Protein REG3A Regulates Keratinocyte Proliferation and Differentiation after Skin Injury. Immunity 2012, 37, 74–84. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Weström, S.; Kappelin, P.; Virtanen, M.; Vahlquist, A.; Törmä, H. Exploration of novel candidate genes involved in epidermal keratinocyte differentiation and skin barrier repair in man. Differentiation 2021, 119, 19–27. [Google Scholar] [CrossRef]
- (Olya) Vvedenskaya, O. Lipidomics of Keratinocyte Differentiation0 Lipotype. Available online: https://www.lipotype.com/lipidomics-applications/lipidomics-of-keratinocyte-differentiation/ (accessed on 1 July 2025).
- Versey, Z.; Nizer, W.S.d.C.; Russell, E.; Zigic, S.; DeZeeuw, K.G.; Marek, J.E.; Overhage, J.; Cassol, E. Biofilm-Innate Immune Interface: Contribution to Chronic Wound Formation. Front. Immunol. 2021, 12, 648554. [Google Scholar] [CrossRef]
- Larouche, J.; Sheoran, S.; Maruyama, K.; Martino, M.M. Immune Regulation of Skin Wound Healing: Mechanisms and Novel Therapeutic Targets. Adv. Wound Care 2018, 7, 209–231. [Google Scholar] [CrossRef]
- Almeida, B.M.; Evans, R.; Kayssi, A. Fundamentals of wound care for amputation prevention. Semin. Vasc. Surg. 2025, 38, 54–63. [Google Scholar] [CrossRef] [PubMed]
- Oota, S.R.; Rahman, N.; Mohammed, S.S.; Galitz, J.; Liu, M. Wound and Episode Level Readmission Risk or Weeks to Readmit: Why do patients get readmitted? How long does it take for a patient to get readmitted? In Proceedings of the 3rd ACM India Joint International Conference on Data Science & Management of Data (8th ACM IKDD CODS & 26th COMAD), Bangalore India, 2–4 January 2021; pp. 359–365. [Google Scholar]
- Szondi, D.-C.; Cruickshank, S.; Vardy, L.; Wong, J. P11 A role for keratinocyte arginase in skin wound healing and barrier function. Br. J. Dermatol. 2024, 190, 6. [Google Scholar] [CrossRef]
- Momotyuk, E.; Ebrahim, N.; Shakirova, K.; Dashinimaev, E. Role of the cytoskeleton in cellular reprogramming: Effects of biophysical and biochemical factors. Front. Mol. Biosci. 2025, 12, 1538806. [Google Scholar] [CrossRef]
- Svitkina, T. The Actin Cytoskeleton and Actin-Based Motility. Cold Spring Harb. Perspect. Biol. 2018, 10, a018267. [Google Scholar] [CrossRef]
- Zhang, J.; Li, L.; Zhang, Q.; Wang, W.; Zhang, D.; Jia, J.; Lv, Y.; Yuan, H.; Song, H.; Xiang, F.; et al. Microtubule-associated protein 4 phosphorylation regulates epidermal keratinocyte migration and proliferation. Int. J. Biol. Sci. 2019, 15, 1962–1976. [Google Scholar] [CrossRef]
- Laly, A.C.; Sliogeryte, K.; Pundel, O.J.; Ross, R.; Keeling, M.C.; Avisetti, D.; Waseem, A.; Gavara, N.; Connelly, J.T. The keratin network of intermediate filaments regulates keratinocyte rigidity sensing and nuclear mechanotransduction. Sci. Adv. 2021, 7, eabd6187. [Google Scholar] [CrossRef]
- Castellano-Pellicena, I.; Thornton, M.J. Isolation of Epidermal Keratinocytes from Human Skin: The Scratch-Wound Assay for Assessment of Epidermal Keratinocyte Migration. In Methods in Molecular Biology; Springer: New York, NY, USA, 2020; Volume 2154. [Google Scholar] [CrossRef]
- Main, K.A.; Mikelis, C.M.; Doçi, C.L. In Vitro Wound Healing Assays to Investigate Epidermal Migration. In Epidermal Cells; Methods in Molecular Biology; Humana Press: New York, NY, USA, 2019; Volume 2109, pp. 147–154. [Google Scholar] [CrossRef]
- Chen, S.; Rahim, A.A.b.A.; Mok, P.; Liu, D. An effective device to enable consistent scratches for in vitro scratch assays. BMC Biotechnol. 2023, 23, 32. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.O.Y.; Sampath, D.; Bosykh, D.A.; Wang, C.; Wang, X.; Subramaniam, T.; Han, W.; Hong, W.; Chakraborty, S. YAP/TAZ Drive Agrin–Matrix Metalloproteinase 12–Mediated Diabetic Skin Wound Healing. J. Investig. Dermatol. 2024, 145, 155–170.e2. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Chen, X.; Huang, W.; Yang, J.; Zhang, Z.; Liu, J.; Liu, L.; Chen, Y.; Jiang, X.; Zhang, J. Electric fields reverse the differentiation of keratinocyte monolayer by down-regulating E-cadherin through PI3K/AKT/Snail pathway. Heliyon 2024, 10, e33069. [Google Scholar] [CrossRef] [PubMed]
- Cwycyshyn, J.; Stansbury, C.; Meixner, W.; Hoying, J.B.; Muir, L.A.; Rajapakse, I. Automated In Vitro Wound Healing Assay. bioRxiv 2023. [Google Scholar] [CrossRef]
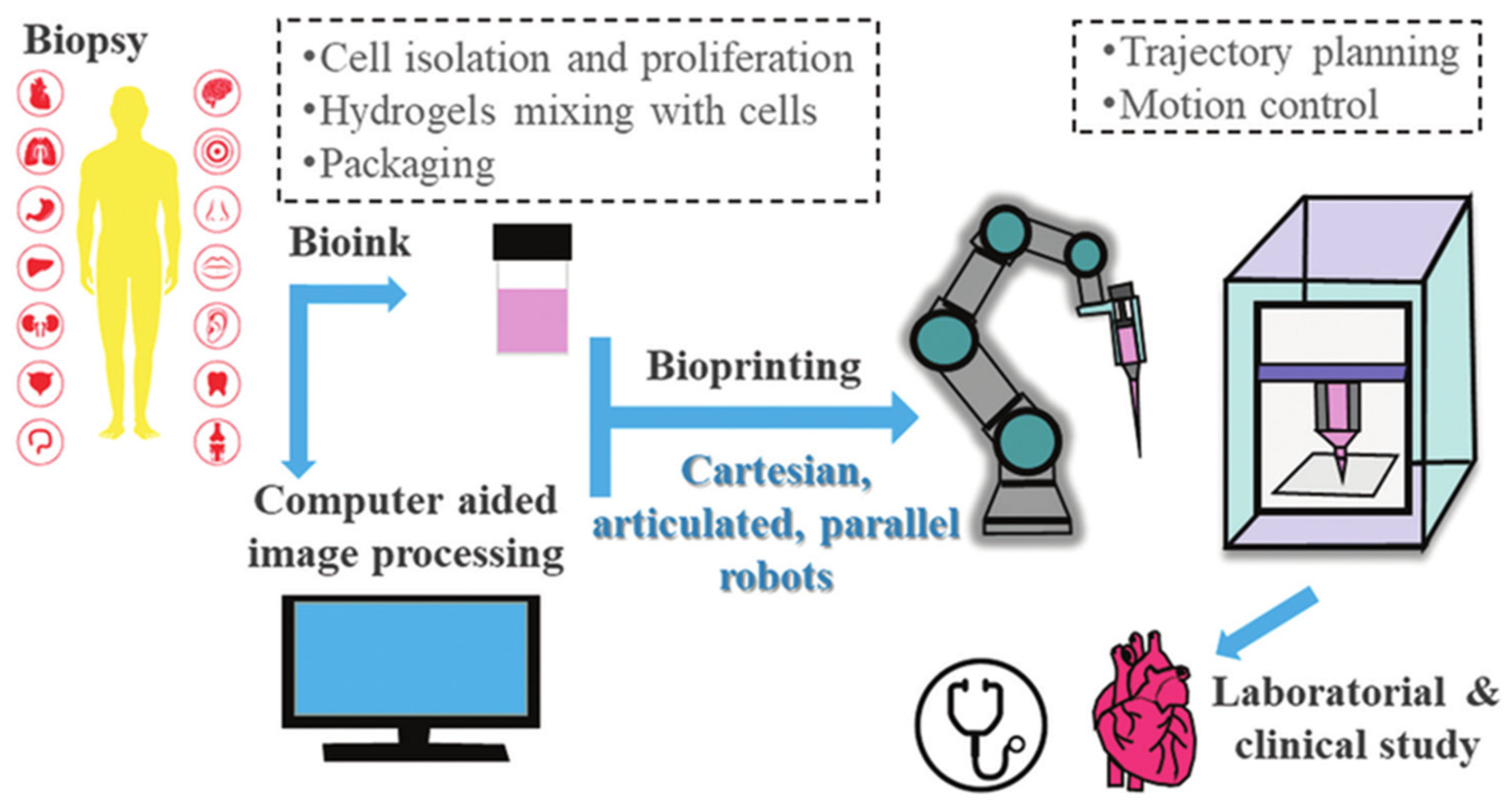
- Dong, H.; Hu, B.; Zhang, W.; Xie, W.; Mo, J.; Sun, H.; Shang, J. Robotic-assisted automated in situ bioprinting. Int. J. Bioprinting 2022, 9, 98–108. [Google Scholar] [CrossRef]
- Li, X.; Upadhyay, A.K.; Bullock, A.J.; Dicolandrea, T.; Xu, J.; Binder, R.L.; Robinson, M.K.; Finlay, D.R.; Mills, K.J.; Bascom, C.C.; et al. Skin Stem Cell Hypotheses and Long Term Clone Survival—Explored Using Agent-based Modelling. Sci. Rep. 2013, 3, srep01904. [Google Scholar] [CrossRef]
- Wenzel, D.; Voigt, A. Multiphase field models for collective cell migration. Phys. Rev. E 2021, 104, 054410. [Google Scholar] [CrossRef]
- Yadav, P.R.; Han, T.; Olatunji, O.; Pattanayek, S.K.; Das, D.B. Mathematical Modelling, Simulation and Optimisation of Microneedles for Transdermal Drug Delivery: Trends and Progress. Pharmaceutics 2020, 12, 693. [Google Scholar] [CrossRef]
- Holt, J.R.; Zeng, W.-Z.; Evans, E.L.; Woo, S.-H.; Ma, S.; Abuwarda, H.; Loud, M.; Patapoutian, A.; Pathak, M.M. Spatiotemporal dynamics of PIEZO1 localization controls keratinocyte migration during wound healing. eLife 2021, 10, e65415. [Google Scholar] [CrossRef]
- Garcia-Gonzalez, D.; Muñoz-Barrutia, A. Computational insights into the influence of substrate stiffness on collective cell migration. Extreme Mech. Lett. 2020, 40, 100928. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sampath, D.; Lin, M.O.Y.; Bilton, M.; Huang, C.-K.; Nai, M.H.; Njah, K.; Goy, P.-A.; Wang, C.-C.; Guccione, E.; et al. Agrin-Matrix Metalloproteinase-12 axis confers a mechanically competent microenvironment in skin wound healing. Nat. Commun. 2021, 12, 6349. [Google Scholar] [CrossRef]
- Ren, X.; Sun, H.; Liu, J.; Guo, X.; Huang, J.; Jiang, X.; Zhang, Y.; Huang, Y.; Fan, D.; Zhang, J. Keratinocyte electrotaxis induced by physiological pulsed direct current electric fields. Bioelectrochemistry 2019, 127, 113–124. [Google Scholar] [CrossRef]
- Terri, M.; Mancianti, N.; Trionfetti, F.; Casciaro, B.; de Turris, V.; Raponi, G.; Bontempi, G.; Montaldo, C.; Domenici, A.; Menè, P.; et al. Exposure to b-LED Light While Exerting Antimicrobial Activity on Gram-Negative and -Positive Bacteria Promotes Transient EMT-like Changes and Growth Arrest in Keratinocytes. Int. J. Mol. Sci. 2022, 23, 1896. [Google Scholar] [CrossRef]
- Domíguez-Hüttinger, E.; Flores-Garza, E.; Caldú-Primo, J.L.; Day, H.; Ramírez, A.R.; Tanaka, R.J.; Martinez-Garcia, R. History-dependent switch-like differentiation of keratinocytes in response to skin barrier damage. PLOS Comput. Biol. 2025, 21, e1013162. [Google Scholar] [CrossRef] [PubMed]
- Sree, V.D.; Rausch, M.K.; Tepole, A.B. Towards understanding pressure ulcer formation: Coupling an inflammation regulatory network to a tissue scale finite element model. Mech. Res. Commun. 2019, 97, 80–88. [Google Scholar] [CrossRef]
- Odagiri, K.; Fujisaki, H. Mathematical model for wound healing caused by exogeneous mechanical forces. In Proceedings of the International Conference of Computational Methods in Sciences and Engineering ICCMSE, Crete, Greece, 29 April–3 May 2020; p. 020017. [Google Scholar]
- Odagiri, K.; Fujisaki, H.; Takada, H.; Ogawa, R. Numerical simulation using cellular Potts model for wound closure with ATP release and the mechanobioligical effects. arXiv 2022, arXiv:2209.01354. [Google Scholar] [CrossRef]
- Shi, J.; Barakat, M.; Chen, D.; Chen, L. Bicellular Tight Junctions and Wound Healing. Int. J. Mol. Sci. 2018, 19, 3862. [Google Scholar] [CrossRef]
- Nardini, J.T.; Chapnick, D.A.; Liu, X.; Bortz, D.M. Modeling keratinocyte wound healing dynamics: Cell–cell adhesion promotes sustained collective migration. J. Theor. Biol. 2016, 400, 103–117. [Google Scholar] [CrossRef] [PubMed]
- Andasari, V.; Lü, D.; Swat, M.; Feng, S.; Spill, F.; Chen, L.; Luo, X.; Zaman, M.; Long, M. Computational model of wound healing: EGF secreted by fibroblasts promotes delayed re-epithelialization of epithelial keratinocytes. Integr. Biol. 2018, 10, 605–634. [Google Scholar] [CrossRef]
- Madzvamuse, A.; Hernandez–Aristizabal, D.; Garzon–Alvarado, D.A.; Duque–Daza, C.A. A bulk-surface moving-mesh finite element method for modelling cell migration pathways. bioRxiv 2023. [Google Scholar] [CrossRef]
- Murphy, L.; Madzvamuse, A. A moving grid finite element method applied to a mechanobiochemical model for 3D cell migration. Appl. Numer. Math. 2020, 158, 336–359. [Google Scholar] [CrossRef]
- Asakura, Y.; Kondo, Y.; Aoki, K.; Naoki, H. Hierarchical modeling of mechano-chemical dynamics of epithelial sheets across cells and tissue. Sci. Rep. 2021, 11, 4069. [Google Scholar] [CrossRef]
- Zhao, T.; Sun, Y.; Zhu, Q.; Li, X.; Baghaee, M.; Wang, Y.; Yuan, H. A contraction-reaction-diffusion model for circular pattern formation in embryogenesis. J. Mech. Phys. Solids 2021, 157, 104630. [Google Scholar] [CrossRef]
- Cao, Y.; Ghabache, E.; Rappel, W.-J. Plasticity of cell migration resulting from mechanochemical coupling. eLife 2019, 8, e48478. [Google Scholar] [CrossRef] [PubMed]
- Uatay, A. Dissertation Multiscale Mathematical Modeling of Cell Migration: From Single Cells to Populations. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2019. [Google Scholar]
- Hahl, S.K.; Kremling, A. A Comparison of Deterministic and Stochastic Modeling Approaches for Biochemical Reaction Systems: On Fixed Points, Means, and Modes. Front. Genet. 2016, 7, 157. [Google Scholar] [CrossRef] [PubMed]
- Akçay, N.I.; Bashirov, R. Comparison of modelling approaches demonstrated for p16-mediated signalling pathway in higher eukaryotes. Biosystems 2021, 210, 104562. [Google Scholar] [CrossRef]
- Safaeifard, F.; Shariatpanahi, S.P.; Goliaei, B. A survey on random walk-based stochastic modeling in eukaryotic cell migration with emphasis on its application in cancer. Multidiscip. Cancer Investig. 2018, 2, 1–12. [Google Scholar] [CrossRef]
- Simoni, G.; Reali, F.; Priami, C.; Marchetti, L. Stochastic simulation algorithms for computational systems biology: Exact, approximate, and hybrid methods. Wiley Interdiscip. Rev. Syst. Biol. Med. 2019, 11, e1459. [Google Scholar] [CrossRef]
- Pahle, J. Biochemical simulations: Stochastic, approximate stochastic and hybrid approaches. Briefings Bioinform. 2008, 10, 53–64. [Google Scholar] [CrossRef]
- Gouveia, M.; Zemljič-Jokhadar, Š.; Vidak, M.; Stojkovič, B.; Derganc, J.; Travasso, R.; Liovic, M. Keratin Dynamics and Spatial Distribution in Wild-Type and K14 R125P Mutant Cells—A Computational Model. Int. J. Mol. Sci. 2020, 21, 2596. [Google Scholar] [CrossRef]
- Huang, Y.; Rüdiger, S.; Shuai, J. Accurate Langevin approaches to simulate Markovian channel dynamics. Phys. Biol. 2015, 12, 061001. [Google Scholar] [CrossRef] [PubMed]
- Roberto, Y. Computational Models of Signaling Processes in Cells with Applications: Influence of Stochastic and Spatial Effects; Rice University: Houston, TX, USA, 2011; Available online: https://hdl.handle.net/1911/70209 (accessed on 16 May 2025).
- Zhou, P.; Wang, S.; Li, T.; Nie, Q. Dissecting transition cells from single-cell transcriptome data through multiscale stochastic dynamics. Nat. Commun. 2021, 12, 5609. [Google Scholar] [CrossRef] [PubMed]
- Alarcón, T.; Briñas-Pascual, N.; Calvo, J.; Guerrero, P.; Stepanova, D. Hybrid methods in reaction-diffusion equations. arXiv 2024, arXiv:2409.13911. [Google Scholar]
- Ham, L.; Coomer, M.A.; Stumpf, M.P.H. The chemical Langevin equation for biochemical systems in dynamic environments. J. Chem. Phys. 2022, 157, 094105. [Google Scholar] [CrossRef]
- Ditlevsen, S.; Samson, A. Introduction to stochastic models in biology. In Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2058. [Google Scholar] [CrossRef]
- Schnoerr, D.; Sanguinetti, G.; Grima, R. Corrigendum: Approximation and inference methods for stochastic biochemical kinetics—A tutorial review. J. Phys. A Math. Theor. 2017, 50, 093001, Erratum in: J. Phys. A Math. Theor. 2018, 51, 169501. [Google Scholar] [CrossRef]
- Sequeiros, C.; Otero-Muras, I.; Vázquez, C.; Banga, J.R. Global Optimization Approach for Parameter Estimation in Stochastic Dynamic Models of Biosystems. IEEE/ACM Trans. Comput. Biol. Bioinform. 2022, 20, 1971–1982. [Google Scholar] [CrossRef] [PubMed]
- Hsu, I.S.; Moses, A.M. Stochastic models for single-cell data: Current challenges and the way forward. FEBS J. 2021, 289, 647–658. [Google Scholar] [CrossRef]
- Paramalingam, D.; Li, B.; Reynolds, N.; Zuliani, P. ESDR089-3D Computational Modelling of Immune Interaction and Epidermal Homeostasis in Psoriasis. J. Investig. Dermatol. 2022, 142, S195. [Google Scholar] [CrossRef]
- Tsirvouli, E.; Noël, V.; Flobak, Å.; Calzone, L.; Kuiper, M. Dynamic Boolean modeling of molecular and cellular interactions in psoriasis predicts drug target candidates. iScience 2024, 27, 108859. [Google Scholar] [CrossRef] [PubMed]
- Arciero, J.; Swigon, D. Equation-based models of wound healing and collective cell migration. In Complex Systems and Computational Biology Approaches to Acute Inflammation; Springer: New York, NY, USA, 2013; Volume 9781461480082, pp. 185–207. [Google Scholar] [CrossRef]
- Sun, T.; McMinn, P.; Coakley, S.; Holcombe, M.; Smallwood, R.; MacNeil, S. An integrated systems biology approach to understanding the rules of keratinocyte colony formation. J. R. Soc. Interface 2007, 4, 1077–1092. [Google Scholar] [CrossRef]
- Hu, B.; Leow, W.R.; Amini, S.; Nai, B.; Zhang, X.; Liu, Z.; Cai, P.; Li, Z.; Wu, Y.; Miserez, A.; et al. Orientational Coupling Locally Orchestrates a Cell Migration Pattern for Re-Epithelialization. Adv. Mater. 2017, 29, 1700145. [Google Scholar] [CrossRef]
- Fuhr, M.J.; Meyer, M.; Fehr, E.; Ponzio, G.; Werner, S.; Herrmann, H.J.; Brandner, J.M. A Modeling Approach to Study the Effect of Cell Polarization on Keratinocyte Migration. PLoS ONE 2015, 10, e0117676. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, G.; Wu, J.; Lee, R.M.; Zhu, Z.; Sun, Y.; Zhu, K.; Losert, W.; Liao, S.; Zhang, G.; et al. Propagation dynamics of electrotactic motility in large epithelial cell sheets. iScience 2022, 25, 105136. [Google Scholar] [CrossRef]
- Kadelka, C.; Butrie, T.-M.; Hilton, E.; Kinseth, J.; Schmidt, A.; Serdarevic, H. A meta-analysis of Boolean net-work models reveals design principles of gene regulatory networks. Sci. Adv. 2024, 10, eadj0822. [Google Scholar] [CrossRef]
- Feess, S.; Kurfiss, K.; Michels, D.L. Accurate Simulation of Wound Healing and Skin Deformation. In Proceedings of the Symposium on Computer Animation, Zurich, Switzerland, 11–13 July 2016. [Google Scholar]
- Kobayashi, Y.; Sanno, Y.; Sakai, A.; Sawabu, Y.; Tsutsumi, M.; Goto, M.; Kitahata, H.; Nakata, S.; Kumamoto, J.; Denda, M.; et al. Mathematical Modeling of Calcium Waves Induced by Mechanical Stimulation in Keratinocytes. PLoS ONE 2014, 9, e92650. [Google Scholar] [CrossRef][Green Version]
- Hamed, M.A.; Nepomnyashchy, A.A. Three-dimensional phase field model for actin-based cell membrane dynamics. arXiv 2021, arXiv:2106.01938. [Google Scholar] [CrossRef]
- Shao, D.; Rappel, W.-J.; Levine, H. Computational Model for Cell Morphodynamics. Phys. Rev. Lett. 2010, 105, 108104. [Google Scholar] [CrossRef] [PubMed]
- Najem, S.; Grant, M. Phase-field model for collective cell migration. Phys. Rev. E 2016, 93, 052405. [Google Scholar] [CrossRef]
- Espath, L. A continuum framework for phase field with bulk-surface dynamics. SN Partial. Differ. Equ. Appl. 2022, 4, 1. [Google Scholar] [CrossRef]
- Brückner, D.B.; Broedersz, C.P. Learning dynamical models of single and collective cell migration: A review. Rep. Prog. Phys. 2024, 87, 056601. [Google Scholar] [CrossRef]
- Skamrahl, M. Mechanics and Motility of Epithelial Cells: From Single Cell Behavior to Collective Migration. Ph.D. Thesis, Georg-August-Universität Göttingen, Göttingen, Germany, 2023. [Google Scholar] [CrossRef]
- Polito, M.P.; Marini, G.; Palamenghi, M.; Enzo, E. Decoding the Human Epidermal Complexity at Single-Cell Resolution. Int. J. Mol. Sci. 2023, 24, 8544. [Google Scholar] [CrossRef]
- Liu, Z.; Bian, X.; Luo, L.; Björklund, Å.K.; Li, L.; Zhang, L.; Chen, Y.; Guo, L.; Gao, J.; Cao, C.; et al. Spatiotemporal single-cell roadmap of human skin wound healing. Cell Stem Cell 2024, 32, 479–498.e8. [Google Scholar] [CrossRef] [PubMed]
- Martino, F.; Perestrelo, A.R.; Vinarsky, V.; Pagliari, S.; Forte, G. Cellular Mechanotransduction: From Tension to Function. Front. Physiol. 2018, 9, 824. [Google Scholar] [CrossRef]
- Shutova, M.S.; Boehncke, W.-H. Mechanotransduction in Skin Inflammation. Cells 2022, 11, 2026. [Google Scholar] [CrossRef] [PubMed]
- Fu, S.; Fan, J. Research progress of signaling channels of mechanotransduction on keratinocytes. Zhongguo Xiu Fu Chong Jian Wai Ke Za Zhi = Zhongguo Xiufu Chongjian Waike Zazhi = Chin. J. Reparative Reconstr. Surg. 2013, 27, 500–506. [Google Scholar]
- Gupta, P.; Hari Narayana S. N., G.; Kasiviswanathan, U.; Agarwal, T.; K., S.; Mukhopadhyay, D.; Pal, K.; Giri, S.; Maiti, T.K.; Banerjee, I. Substrate stiffness does affect the fate of human keratinocytes. RSC Adv. 2015, 6, 3539–3551. [Google Scholar] [CrossRef]
- Wagner, R.M.; Maiti, R.; Carré, M.J.; Perrault, C.M.; Evans, P.C.; Lewis, R. Bio-tribology of Vascular Devices: A Review of Tissue/Device Friction Research. Biotribology 2021, 25, 100169. [Google Scholar] [CrossRef]
- Zarkoob, H.; Bodduluri, S.; Ponnaluri, S.V.; Selby, J.C.; Sander, E.A. Substrate Stiffness Affects Human Keratinocyte Colony Formation. Cell. Mol. Bioeng. 2015, 8, 32–50. [Google Scholar] [CrossRef] [PubMed]
- Pora, A.; Yoon, S.; Dreissen, G.; Hoffmann, B.; Merkel, R.; Windoffer, R.; Leube, R.E. Regulation of keratin network dynamics by the mechanical properties of the environment in migrating cells. Sci. Rep. 2020, 10, 4574. [Google Scholar] [CrossRef]
- Romano, D.J.; Gomez-Salinero, J.M.; Šunić, Z.; Checco, A.; Rabbany, S.Y. Tracking of Endothelial Cell Migration and Stiffness Measurements Reveal the Role of Cytoskeletal Dynamics. Int. J. Mol. Sci. 2022, 23, 568. [Google Scholar] [CrossRef]
- Zhang, Z.; Rosakis, P.; Hou, T.Y.; Ravichandran, G. A minimal mechanosensing model predicts keratocyte evolution on flexible substrates. J. R. Soc. Interface 2020, 17, 20200175. [Google Scholar] [CrossRef]
- Nwogbaga, I.; Camley, B.A. Coupling cell shape and velocity leads to oscillation and circling in keratocyte galvanotaxis. Biophys. J. 2022, 122, 130–142. [Google Scholar] [CrossRef]
- Kozyrska, K.; Pilia, G.; Vishwakarma, M.; Wagstaff, L.; Goschorska, M.; Cirillo, S.; Mohamad, S.; Gallacher, K.; Salas, R.E.C.; Piddini, E. p53 directs leader cell behavior, migration, and clearance during epithelial repair. Science 2022, 375, eabl8876. [Google Scholar] [CrossRef] [PubMed]
- Charbonier, F.; Zhu, J.; Slyman, R.; Allan, C.; Chaudhuri, O. Substrate stress relaxation regulates monolayer fluidity and leader cell formation for collectively migrating epithelia. Proc. Natl. Acad. Sci. USA 2025, 122, e2417290122. [Google Scholar] [CrossRef]
- Hu, A.; Pickup, M.E.; Lawal, M.A.; Patel, H.J.; Ahmed, M.I.; Han, J. The involvement of Elf5 in regulating keratinocyte proliferation and differentiation processes in skin. PLoS ONE 2025, 20, e0316134. [Google Scholar] [CrossRef]
- Zhao, M. Electrical fields in wound healing—An overriding signal that directs cell migration. Semin. Cell Dev. Biol. 2009, 20, 674–682. [Google Scholar] [CrossRef] [PubMed]
- Hart, F.X.; Laird, M.; Riding, A.; Pullar, C.E. Keratinocyte galvanotaxis in combined DC and AC electric fields supports an electromechanical transduction sensing mechanism. Bioelectromagnetics 2012, 34, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Ji, R.; Teng, M.; Zhang, Z.; Wang, W.; Zhang, Q.; Lv, Y.; Zhang, J.; Jiang, X. Electric field down-regulates CD9 to promote keratinocytes migration through AMPK pathway. Int. J. Med Sci. 2020, 17, 865–873. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Jin, X.; A, C.; Gong, P.; Zhao, S. The Electric Field Guided HaCaT Cell Migration Through the EGFR/p38 MAPK/Akt Pathway. Curr. Issues Mol. Biol. 2024, 47, 16. [Google Scholar] [CrossRef]
- Gruler, H.; Nuccitelli, R. The Galvanotaxis Response Mechanism of Keratinocytes Can Be Modeled as a Proportional Controller. Cell. Biochem. Biophys. 2000, 33, 33–51. [Google Scholar] [CrossRef] [PubMed]
- Nwogbaga, I.; Belliveau, N.M.; Singh, A.R.; Sun, D.; Mulenga, N.; Theriot, J.A.; Camley, B.A. Protein diffusion controls how single cells respond to electric fields. bioRxiv 2025. [Google Scholar] [CrossRef] [PubMed]
- Nwogbaga, I.; Kim, A.H.; Camley, B.A. Physical limits on galvanotaxis. Phys. Rev. E 2023, 108, 064411. [Google Scholar] [CrossRef]
- Yang, H.-Y.; Charles, R.-P.; Hummler, E.; Baines, D.L.; Isseroff, R.R. The epithelial sodium channel mediates the directionality of galvanotaxis in human keratinocytes. J. Cell Sci. 2013, 126, 1942–1951. [Google Scholar] [CrossRef]
- Shaner, S.; Savelyeva, A.; Kvartuh, A.; Jedrusik, N.; Matter, L.; Leal, J.; Asplund, M. Bioelectronic microfluidic wound healing: A platform for investigating direct current stimulation of injured cell collectives. Lab Chip 2023, 23, 1531–1546. [Google Scholar] [CrossRef]
- Ly, A.T.; Tyagi, V.; Bertaccini, G.A.; Evans, E.L.; Freites, J.A.; Tobias, D.J.; Pathak, M.M. Probing Piezo1 diffusion heterogeneity via single particle tracking and machine learning. Biophys. J. 2022, 121, 436a. [Google Scholar] [CrossRef]
- Rennekampff, H.-O.; Tenenhaus, M.; Rennekampff, I.; Alharbi, Z. Roles of Mechanosensitive Channel Piezo1 in Wound Healing and Scar Formation. Life 2024, 14, 377. [Google Scholar] [CrossRef]
- Mikesell, A.R.; Isaeva, O.; Moehring, F.; Sadler, K.E.; Menzel, A.D.; Stucky, C.L. PIEZO1-induced cellular retraction controls keratinocyte migration in wound healing. eLife 2020, 11, e65987. [Google Scholar] [CrossRef]
- Martina-Perez, S.F.; Breinyn, I.B.; Cohen, D.J.; Baker, R.E. Optimal Control of Collective Electrotaxis in Epithelial Monolayers. Bull. Math. Biol. 2024, 86, 95. [Google Scholar] [CrossRef]
- Yang, Q.; Miao, Y.; Campanello, L.J.; Hourwitz, M.J.; Abubaker-Sharif, B.; Bull, A.L.; Devreotes, P.N.; Fourkas, J.T.; Losert, W. Cortical waves mediate the cellular response to electric fields. eLife 2022, 11, e73198. [Google Scholar] [CrossRef]
- Copos, C.; Sun, Y.-H.; Zhu, K.; Zhang, Y.; Reid, B.; Draper, B.; Lin, F.; Yue, H.; Bernadskaya, Y.; Zhao, M.; et al. Galvanotactic directionality of cell groups depends on group size. Proc. Natl. Acad. Sci. USA 2025, 122, e2416440122. [Google Scholar] [CrossRef]
- Dawson, R.; Goberdhan, N.; Freedlander, E.; MacNeil, S. Influence of extracellular matrix proteins on human keratinocyte attachment, proliferation and transfer to a dermal wound model. Burns 1996, 22, 93–100. [Google Scholar] [CrossRef]
- O’Toole, E.A. Extracellular matrix and keratinocyte migration. Clin. Exp. Dermatol. 2001, 26, 525–530. [Google Scholar] [CrossRef] [PubMed]
- Schlie-Wolter, S.; Ngezahayo, A.; Chichkov, B.N. The selective role of ECM components on cell adhesion, morphology, proliferation and communication in vitro. Exp. Cell Res. 2013, 319, 1553–1561. [Google Scholar] [CrossRef] [PubMed]
- Crossley, R.M.; Johnson, S.; Tsingos, E.; Bell, Z.; Berardi, M.; Botticelli, M.; Braat, Q.J.S.; Metzcar, J.; Ruscone, M.; Yin, Y.; et al. Modeling the extracellular matrix in cell migration and morphogenesis: A guide for the curious biologist. Front. Cell Dev. Biol. 2024, 12, 1354132. [Google Scholar] [CrossRef] [PubMed]
- Suveges, S.; Chamseddine, I.; Rejniak, K.A.; Eftimie, R.; Trucu, D. Collective Cell Migration in a Fibrous Environment: A Hybrid Multiscale Modelling Approach. Front. Appl. Math. Stat. 2021, 7, 680029. [Google Scholar] [CrossRef]
- Di Russo, J.; Young, J.L.; Wegner, J.W.; Steins, T.; Kessler, H.; Spatz, J.P. Integrin α5β1 nano-presentation regulates collective keratinocyte migration independent of substrate rigidity. eLife 2021, 10, e69861. [Google Scholar] [CrossRef]
- Taufalele, P.V.; VanderBurgh, J.A.; Muñoz, A.; Zanotelli, M.R.; Reinhart-King, C.A.; O’COnnell, G. Fiber alignment drives changes in architectural and mechanical features in collagen matrices. PLoS ONE 2019, 14, e0216537. [Google Scholar] [CrossRef]
- Jetta, D.; Shireen, T.; Prabhu, R.D.; Hua, S.Z. Contribution of Piezo1 in ECM Stiffness Incited Epithelial Cell Remodeling. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Columbus, OH, USA, 30 October–3 November 2022. [Google Scholar]
- Wang, Y.; Wang, Y.; Zhu, Y.; Yu, P.; Zhou, F.; Zhang, A.; Gu, Y.; Jin, R.; Li, J.; Zheng, F.; et al. Angiomotin cleavage promotes leader formation and collective cell migration. Dev. Cell 2024, 60, 101–118.e7. [Google Scholar] [CrossRef]
- Xue, M.; Jackson, C.J. Extracellular Matrix Reorganization During Wound Healing and Its Impact on Abnormal Scarring. Adv. Wound Care 2015, 4, 119–136. [Google Scholar] [CrossRef]
- Dibus, M.; Joshi, O.; Ivaska, J. Novel tools to study cell-ECM interactions, cell adhesion dynamics and migration. Curr. Opin. Cell Biol. 2024, 88, 102355. [Google Scholar] [CrossRef]
- Pak, B.A.; Kelleci, K.; Ozer, S. Investigation of nanoparticles on cell elasticity using the nanoindentation method. Int. J. Comput. Methods Eng. Sci. Mech. 2023, 25, 152–164. [Google Scholar] [CrossRef]
- Milner, J.S.; Grol, M.W.; Beaucage, K.L.; Dixon, S.J.; Holdsworth, D.W. Finite-Element Modeling of Viscoelastic Cells During High-Frequency Cyclic Strain. J. Funct. Biomater. 2012, 3, 209–224. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Shelley, M.J. Modeling epithelial tissue and cell deformation dynamics using a viscoelastic slab sculpted by surface forces. Phys. Rev. Res. 2023, 5, 023190. [Google Scholar] [CrossRef]
- Bai, J.; Zeng, X. Computational modeling and simulation of epithelial wound closure. Sci. Rep. 2023, 13, 6265. [Google Scholar] [CrossRef] [PubMed]
- Bornschlögl, T.; Bildstein, L.; Thibaut, S.; Santoprete, R.; Fiat, F.; Luengo, G.S.; Doucet, J.; Bernard, B.A.; Baghdadli, N. Keratin network modifications lead to the mechanical stiffening of the hair follicle fiber. Proc. Natl. Acad. Sci. USA 2016, 113, 5940–5945. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press (CUP): Cambridge, UK, 1985. [Google Scholar]
- Ding, Y.; Xu, G.-K.; Wang, G.-F. On the determination of elastic moduli of cells by AFM based indentation. Sci. Rep. 2017, 7, 45575. [Google Scholar] [CrossRef]
- Greenwood, J.A. Formulas for Moderately Elliptical Hertzian Contacts. J. Tribol. 1985, 107, 501–504. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Kojic, M.; Zivkovic, M.; Fabry, B.; Fredberg, J.J. A finite element model of cell deformation during magnetic bead twisting. J. Appl. Physiol. 2002, 93, 1429–1436. [Google Scholar] [CrossRef]
- Limbert, G.; Kuhl, E. On skin microrelief and the emergence of expression micro-wrinkles. Soft Matter 2018, 14, 1292–1300. [Google Scholar] [CrossRef]
- Imam, S.A.; Hughes, A.C.; Carré, M.J.; Driscoll, H.; Winwood, K.; Venkatraman, P.; Allen, T. Finite element model to simulate impact on a soft tissue simulant. Sports Eng. 2023, 26, 16. [Google Scholar] [CrossRef]
- Estermann, S.-J.; Pahr, D.H.; Reisinger, A. Material design of soft biological tissue replicas using viscoelastic micromechanical modelling. J. Mech. Behav. Biomed. Mater. 2022, 125, 104875. [Google Scholar] [CrossRef]
- Kobiela, T.; Lelen-Kaminska, K.; Stepulak, M.; Lekka, M.; Malejczyk, M.; Arct, J.; Majewski, S. The influence of surfactants and hydrolyzed proteins on keratinocytes viability and elasticity. Ski. Res. Technol. 2012, 19, e200–e208. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Irianto, J.; Inamdar, S.; Pravincumar, P.; Lee, D.; Bader, D.; Knight, M. Cell Mechanics, Structure, and Function Are Regulated by the Stiffness of the Three-Dimensional Microenvironment. Biophys. J. 2012, 103, 1188–1197. [Google Scholar] [CrossRef]
- Shigemura, K.; Kuribayashi-Shigetomi, K.; Tanaka, R.; Yamasaki, H.; Okajima, T. Mechanical properties of epithelial cells in domes investigated using atomic force microscopy. Front. Cell Dev. Biol. 2023, 11, 1245296. [Google Scholar] [CrossRef]
- Fung, C.K.M.; Xi, N.; Yang, R.; Seiffert-Sinha, K.; Lai, K.W.C.; A Sinha, A. Quantitative Analysis of Human Keratinocyte Cell Elasticity Using Atomic Force Microscopy (AFM). IEEE Trans. NanoBioscience 2011, 10, 9–15. [Google Scholar] [CrossRef]
- Rheinlaender, J.; Dimitracopoulos, A.; Wallmeyer, B.; Kronenberg, N.M.; Chalut, K.J.; Gather, M.C.; Betz, T.; Charras, G.; Franze, K. Cortical cell stiffness is independent of substrate mechanics. Nat. Mater. 2020, 19, 1019–1025. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Vidal, L.; Murdica, V.; Venegoni, C.; Pederzoli, F.; Bandini, M.; Necchi, A.; Salonia, A.; Alfano, M. Causal contributors to tissue stiffness and clinical relevance in urology. Commun. Biol. 2021, 4, 1011. [Google Scholar] [CrossRef]
- Polak-Kraśna, K.; Mazgajczyk, E.; Heikkilä, P.; Georgiadis, A. Parametric Finite Element Model and Mechanical Characterisation of Electrospun Materials for Biomedical Applications. Materials 2021, 14, 278. [Google Scholar] [CrossRef]
- Santoro, L.; Vaiani, L.; Boccaccio, A.; Lamberti, L.; Muzio, L.L.; Ballini, A.; Cantore, S. Finite Element Modeling of Cells Adhering to a Substrate: An Overview. Appl. Sci. 2024, 14, 2596. [Google Scholar] [CrossRef]
- Soon, C.F.; Tee, K.S.; Youseffi, M. Compressive Forces of Cell Induced Longitudinal Deformation to the Liquid Crystal Surface. Available online: https://www.researchgate.net/publication/284163694 (accessed on 1 September 2025).
- Akhmanova, M.A.; Ratheesh, A.; Siekhaus, D.E. Modeling of Epithelial Sheet Deformation Under External Force Applied by a Migrating Cell. COMSOL Technical Papers and Presentations. 2017. Available online: https://www.comsol.com/paper/modeling-of-epithelial-sheet-deformation-under-external-force-applied-by-a-migrating-cell-50691 (accessed on 15 June 2025).
- Han, Y.L.; Ronceray, P.; Xu, G.; Malandrino, A.; Kamm, R.D.; Lenz, M.; Broedersz, C.P.; Guo, M. Cell contraction induces long-ranged stress stiffening in the extracellular matrix. Proc. Natl. Acad. Sci. USA 2018, 115, 4075–4080. [Google Scholar] [CrossRef] [PubMed]
- Zielinski, R.; Mihai, C.; Kniss, D.; Ghadiali, S.N. Finite Element Analysis of Traction Force Microscopy: Influence of Cell Mechanics, Adhesion, and Morphology. J. Biomech. Eng. 2013, 135, 071009–0710099. [Google Scholar] [CrossRef] [PubMed]
- Stolarska, M.A.; Rammohan, A.R.; Lee, J.W. Center or periphery? Modeling the effects of focal adhesion placement during cell spreading. PLoS ONE 2017, 12, e0171430. [Google Scholar] [CrossRef]
- Fhong, S. Investigation of Traction Patterns and Forces of Single Quiescent and Migratory Keratinocytes Using a Novel Cell Traction Force Microscopy Technique; Universiti Tun Hussein Onn Malaysia: Johor, Malaysia, 2012. [Google Scholar]
- Wang, W.; Zuidema, A.; te Molder, L.; Nahidiazar, L.; Hoekman, L.; Schmidt, T.; Coppola, S.; Sonnenberg, A. Hemidesmosomes modulate force generation via focal adhesions. J. Cell Biol. 2020, 219, e201904137. [Google Scholar] [CrossRef]
- Morin, T.R.; Ghassem-Zadeh, S.A.; Lee, J. Traction force microscopy in rapidly moving cells reveals separate roles for ROCK and MLCK in the mechanics of retraction. Exp. Cell Res. 2014, 326, 280–294. [Google Scholar] [CrossRef] [PubMed]
- Soon, C.F.; Youseffi, M.; Twigg, P.; Blagden, N.; Denyer, M.C.T. Finite Element Quantification of the Compressive Forces Induced by Keratinocyte on a Liquid Crystal Substrate. In Analysis and Design of Biological Materials and Structures; Springer: Berlin/Heidelberg, Germany, 2012; pp. 79–99. [Google Scholar] [CrossRef]
- Zancla, A.; Mozetic, P.; Orsini, M.; Forte, G.; Rainer, A. A primer to traction force microscopy. J. Biol. Chem. 2022, 298, 101867. [Google Scholar] [CrossRef]
- Wiegold, T.; Klinge, S.; Aygün, S.; Gilbert, R.P.; Holzapfel, G.A. Viscoelasticity of cross-linked actin network embedded in cytosol. PAMM 2018, 18, e201800151. [Google Scholar] [CrossRef]
- Hutson, M.S.; Veldhuis, J.; Ma, X.; Lynch, H.E.; Cranston, P.G.; Brodland, G.W. Combining Laser Microsurgery and Finite Element Modeling to Assess Cell-Level Epithelial Mechanics. Biophys. J. 2009, 97, 3075–3085. [Google Scholar] [CrossRef]
- Kaouri, K.; Christodoulou, N.; Chakraborty, A.; Méndez, P.E.; Skourides, P.; Ruiz-Baier, R. A new mechanochemical model for apical constriction: Coupling calcium signalling and viscoelasticity. Front. Syst. Biol. 2022, 2, 962790. [Google Scholar] [CrossRef]
- Karimi, A.; Haghighatnama, M.; Shojaei, A.; Navidbakhsh, M.; Haghi, A.M.; Sadati, S.J.A. Measurement of the viscoelastic mechanical properties of the skin tissue under uniaxial loading. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 230, 418–425. [Google Scholar] [CrossRef]
- Kaouri, K.; Méndez, P.E.; Ruiz-Baier, R. Mechanochemical Models for Calcium Waves in Embryonic Epithelia. Vietnam. J. Math. 2022, 50, 947–975. [Google Scholar] [CrossRef]
- Cóndor, M.; García-Aznar, J.M. A phenomenological cohesive model for the macroscopic simulation of cell–matrix adhesions. Biomech. Model. Mechanobiol. 2017, 16, 1207–1224. [Google Scholar] [CrossRef]
- Anjum, S.; Vijayraghavan, D.; Fernandez-Gonzalez, R.; Sutherland, A.; Davidson, L. Inferring active and passive mechanical drivers of epithelial convergent extension. bioRxiv 2025. [Google Scholar] [CrossRef]
- Safshekan, F.; Tafazzoli-Shadpour, M.; Abdouss, M.; Shadmehr, M.B. Viscoelastic Properties of Human Tracheal Tissues. J. Biomech. Eng. 2016, 139, 011007. [Google Scholar] [CrossRef] [PubMed]
- Anon, E.; Serra-Picamal, X.; Hersen, P.; Gauthier, N.C.; Sheetz, M.P.; Trepat, X.; Ladoux, B. Cell crawling mediates collective cell migration to close undamaged epithelial gaps. Proc. Natl. Acad. Sci. USA 2012, 109, 10891–10896. [Google Scholar] [CrossRef]
- Brugués, A.; Anon, E.; Conte, V.; Veldhuis, J.H.; Gupta, M.; Colombelli, J.; Muñoz, J.J.; Brodland, G.W.; Ladoux, B.; Trepat, X. Forces driving epithelial wound healing. Nat. Phys. 2014, 10, 683–690. [Google Scholar] [CrossRef]
- Kim, D.; Kwon, S.; Bajpai, V.K. Vibrational stress affects extracellular signal-regulated kinases activation and cytoskeleton structure in human keratinocytes. PLoS ONE 2020, 15, e0231174. [Google Scholar] [CrossRef]
- Wei, F.; Zhou, P.; Li, G.; Liu, L. Finite element simulation of stress relaxation process in living cells. In Proceedings of the 10th IEEE International Conference on Nano/Micro Engineered and Molecular Systems, Xi’an, China, 7–11 April 2015; pp. 67–71. [Google Scholar]
- Ma, X.; E Lynch, H.; Scully, P.C.; Hutson, M.S. Probing embryonic tissue mechanics with laser hole drilling. Phys. Biol. 2009, 6, 036004. [Google Scholar] [CrossRef] [PubMed]
- Vermolen, F.; Javierre, E. Computer simulations from a finite-element model for wound contraction and closure. J. Tissue Viability 2010, 19, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Verga, A.S.; Tucker, S.J.; Gao, Y.; Plaskett, A.M.; Hollister, S.J. Nonlinear Viscoelastic Properties of 3D-Printed Tissue Mimicking Materials and Metrics to Determine the Best Printed Material Match to Tissue Mechanical Behavior. Front. Mech. Eng. 2022, 8, 862375. [Google Scholar] [CrossRef]
- Corominas-Murtra, B.; Petridou, N.I. Viscoelastic Networks: Forming Cells and Tissues. Front. Phys. 2021, 9, 666916. [Google Scholar] [CrossRef]
- Mierke, C.T. Viscoelasticity, Like Forces, Plays a Role in Mechanotransduction. Front. Cell Dev. Biol. 2022, 10, 789841. [Google Scholar] [CrossRef] [PubMed]
- Gorfinkiel, N.; Blanchard, G.B. Dynamics of actomyosin contractile activity during epithelial morphogenesis. Curr. Opin. Cell Biol. 2011, 23, 531–539. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X. Biomechanical Study on Elastic and Viscoelastic Properties of Osteoblasts Using Atomic Force Microscopy. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 1377–1381. [Google Scholar]
- Wang, X.-H.; Yang, F.; Pan, J.-B.; Kang, B.; Xu, J.-J.; Chen, H.-Y. Quantitative Imaging of pN Intercellular Force and Energetic Costs during Collective Cell Migration in Epithelial Wound Healing. Anal. Chem. 2020, 92, 16180–16187. [Google Scholar] [CrossRef]
- Dai, L.-G.; Dai, N.-T.; Chen, T.-Y.; Kang, L.-Y.; Hsu, S.-H. A bioprinted vascularized skin substitute with fibroblasts, keratinocytes, and endothelial progenitor cells for skin wound healing. Bioprinting 2022, 28, e00237. [Google Scholar] [CrossRef]
- Lin, C.-Y.; Lin, S.-R. Investigating the accuracy of ultrasound viscoelastic creep imaging for measuring the viscoelastic properties of a single-inclusion phantom. Int. J. Mech. Sci. 2021, 199. [Google Scholar] [CrossRef]
- Yoon, S.; Windoffer, R.; Kozyrina, A.N.; Piskova, T.; Di Russo, J.; Leube, R.E. Combining Image Restoration and Traction Force Microscopy to Study Extracellular Matrix-Dependent Keratin Filament Network Plasticity. Front. Cell Dev. Biol. 2022, 10, 901038. [Google Scholar] [CrossRef]
- Horiuchi, R.; Kamimura, A.; Hanaki, Y.; Matsumoto, H.; Ueda, M.; Higaki, T. Deep learning-based cytoskeleton segmentation for accurate high-throughput measurement of cytoskeleton density. Protoplasma 2024, 262, 739–751. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Caplan, J.; Kambhamettu, C. Extraction and Quantification of Actin Cytoskeleton in Microscopic Images Using a Deep Learning Based Framework and a Curve Clustering Model. In Proceedings of the 2022 26th International Conference on Pattern Recognition (ICPR), Montreal, QC, Canada, 21–25 August 2022; pp. 4270–4276. [Google Scholar]
- Sargent, B.; Jafari, M.; Marquez, G.; Mehta, A.S.; Sun, Y.-H.; Yang, H.-Y.; Zhu, K.; Isseroff, R.R.; Zhao, M.; Gomez, M. A machine learning based model accurately predicts cellular response to electric fields in multiple cell types. Sci. Rep. 2022, 12, 9912. [Google Scholar] [CrossRef] [PubMed]
- Kratz, F.S.; Moellerherm, L.; Kierfeld, J. Enhancing Robustness, Precision and Speed of Traction Force Microscopy with Machine Learning. bioRxiv 2022. [Google Scholar] [CrossRef]
- Serener, A.; Serte, S. Keratinocyte Carcinoma Detection via Convolutional Neural Networks. In Proceedings of the 2019 3rd International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Ankara, Turkey, 11–13 October 2019; pp. 1–5. [Google Scholar]
- Alheejawi, S.; Berendt, R.; Jha, N.; Mandal, M. Melanoma Detection in Histopathological Images using Deep Learning. In Proceedings of the 8th International Conference of Security, Privacy and Trust Management (SPTM 2020), Helsinki, Finland, 13–14 June 2020. [Google Scholar]
- Parajuli, M.; Shaban, M.; Phung, T.L. Automated differentiation of skin melanocytes from keratinocytes in high-resolution histopathology images using a weakly-supervised deep-learning framework. Int. J. Imaging Syst. Technol. 2022, 33, 262–275. [Google Scholar] [CrossRef]
- Ghose, S.; Ju, Y.; McDonough, E.; Ho, J.; Karunamurthy, A.; Chadwick, C.; Cho, S.; Rose, R.; Corwin, A.; Surrette, C.; et al. Human Digital Twin: Automated Cell Type Distance Computation and 3D Atlas Construction in Multiplexed Skin Biopsies. Commun. Biol. 2023, 6, 718. [Google Scholar] [CrossRef]
- Akbarialiabad, H.; Pasdar, A.; Murrell, D.F. Digital twins in dermatology, current status, and the road ahead. npj Digit. Med. 2024, 7, 228. [Google Scholar] [CrossRef] [PubMed]
- Windoffer, R.; Schwarz, N.; Yoon, S.; Piskova, T.; Scholkemper, M.; Stegmaier, J.; Bönsch, A.; Di Russo, J.; E Leube, R. Quantitative mapping of keratin networks in 3D. eLife 2022, 11, e75894. [Google Scholar] [CrossRef] [PubMed]
- Holle, A.W.; Kalafat, M.; Ramos, A.S.; Seufferlein, T.; Kemkemer, R.; Spatz, J.P. Intermediate filament reorganization dynamically influences cancer cell alignment and migration. Sci. Rep. 2017, 7, srep45152. [Google Scholar] [CrossRef] [PubMed]

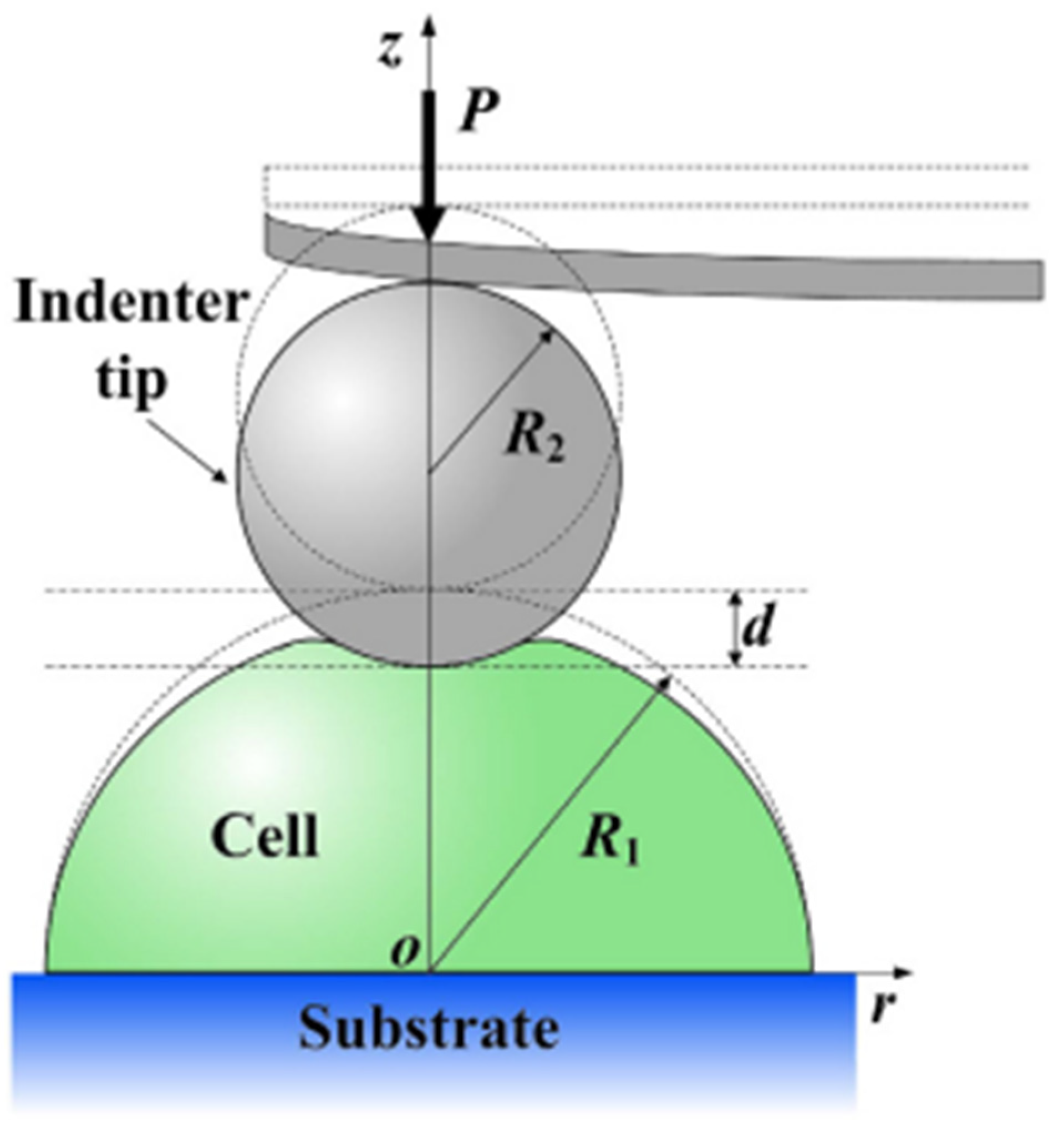
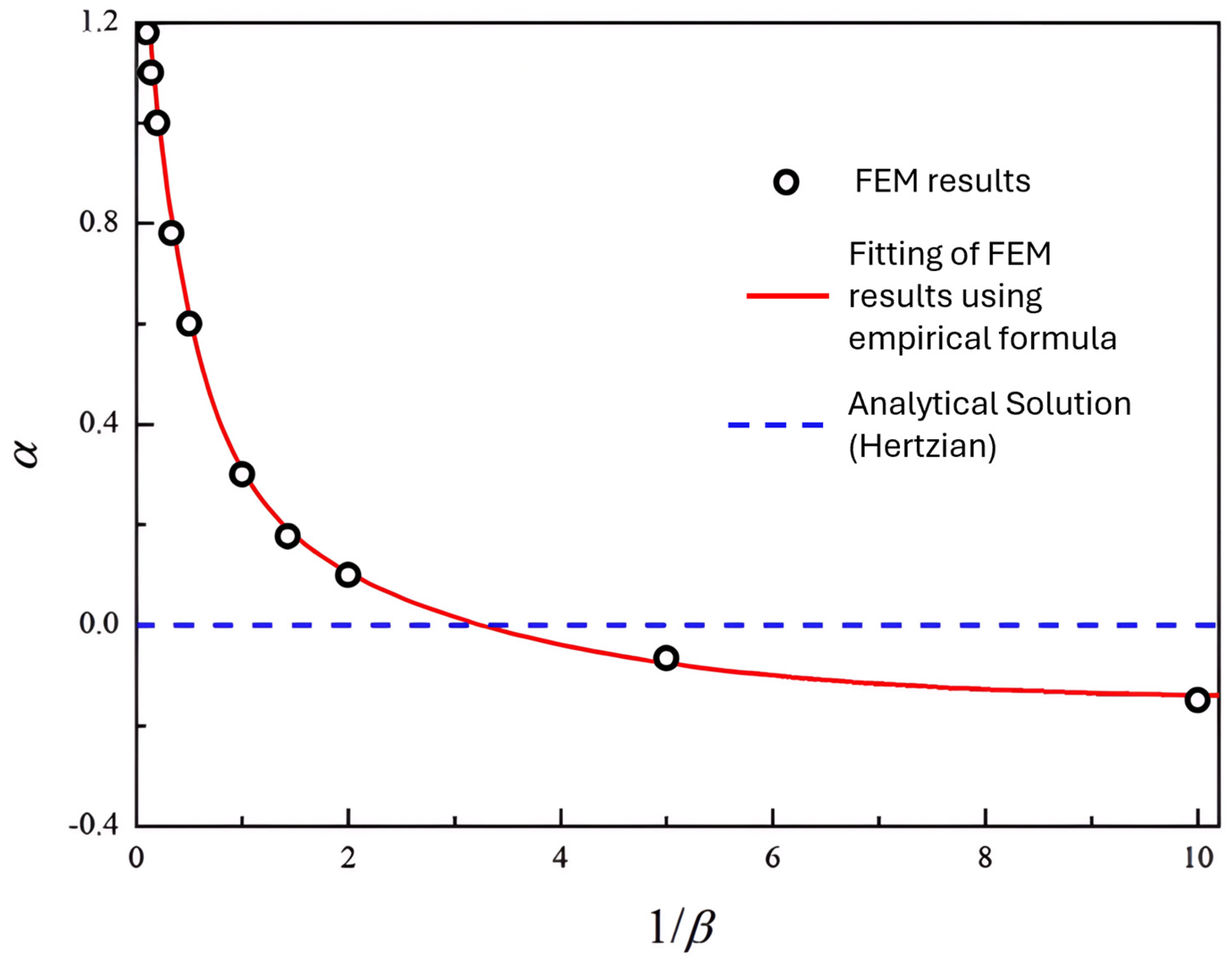
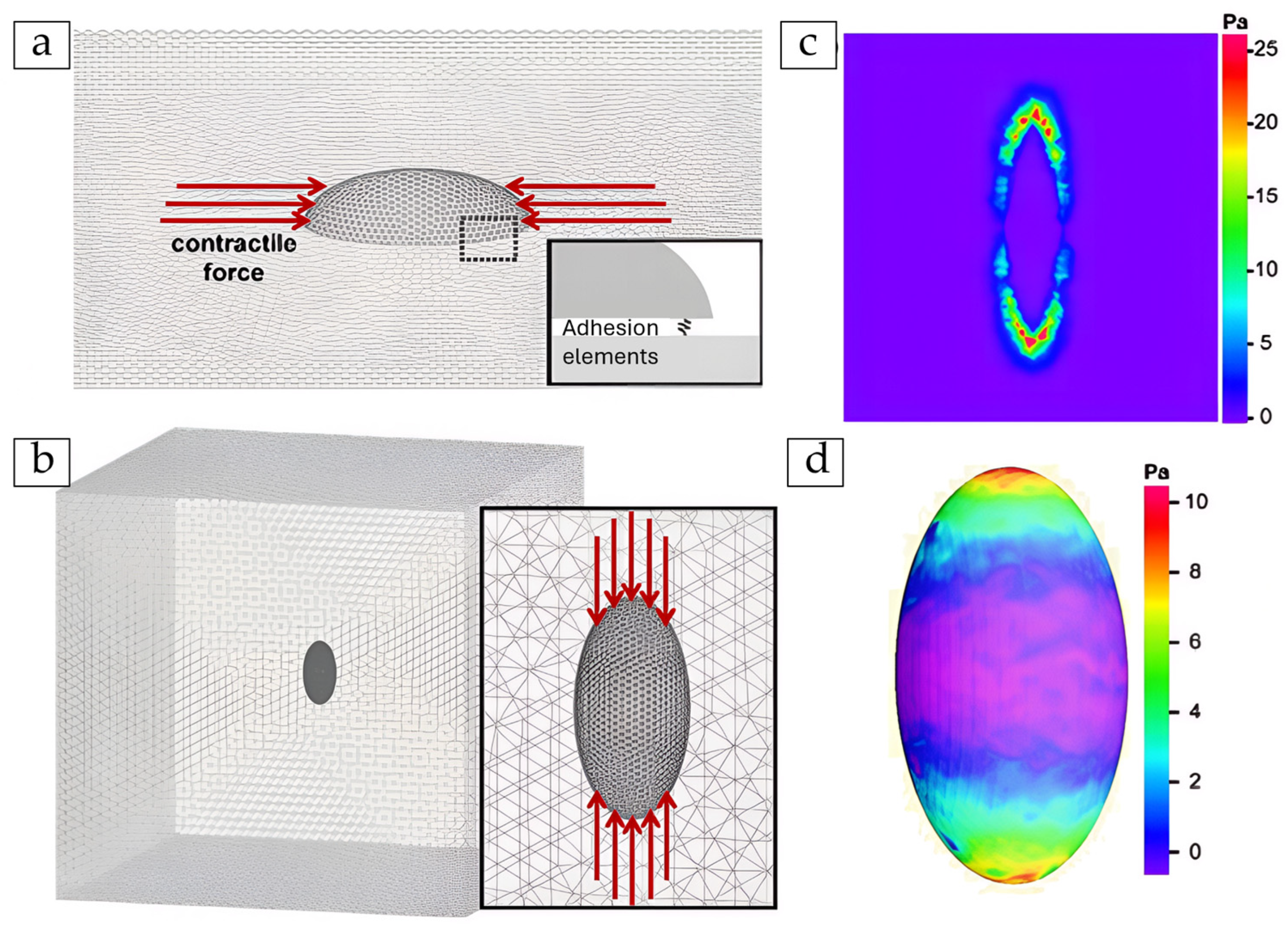

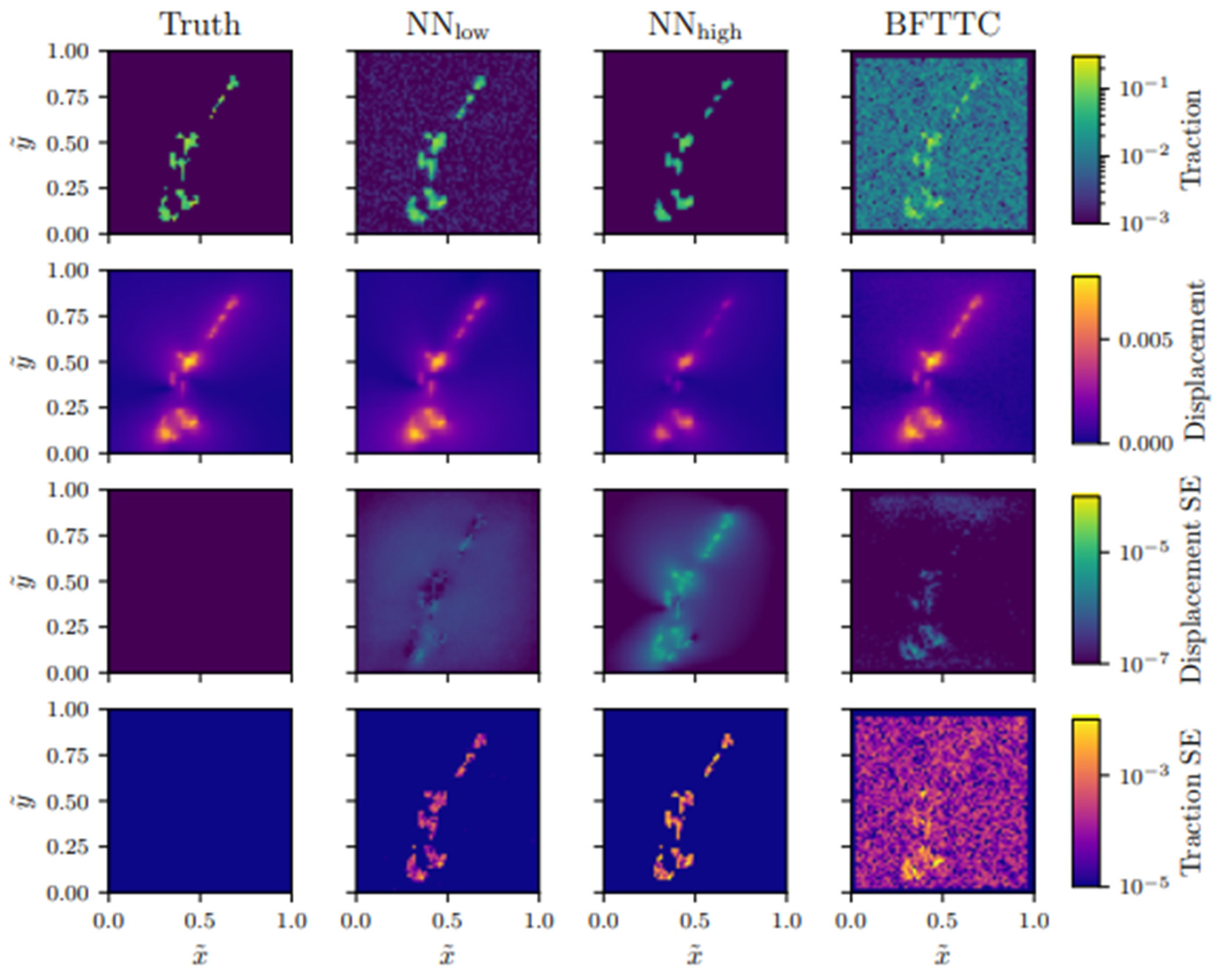
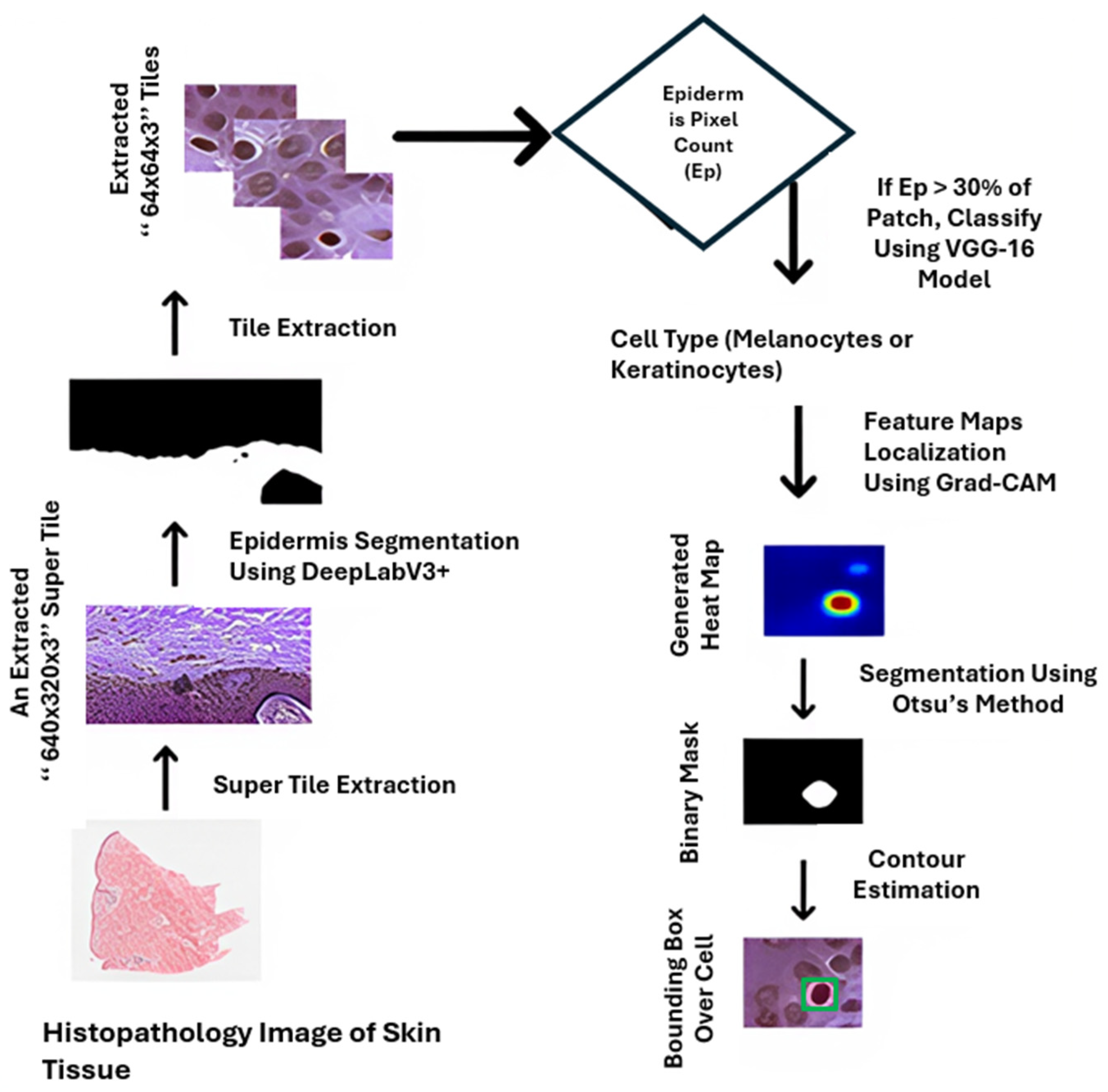
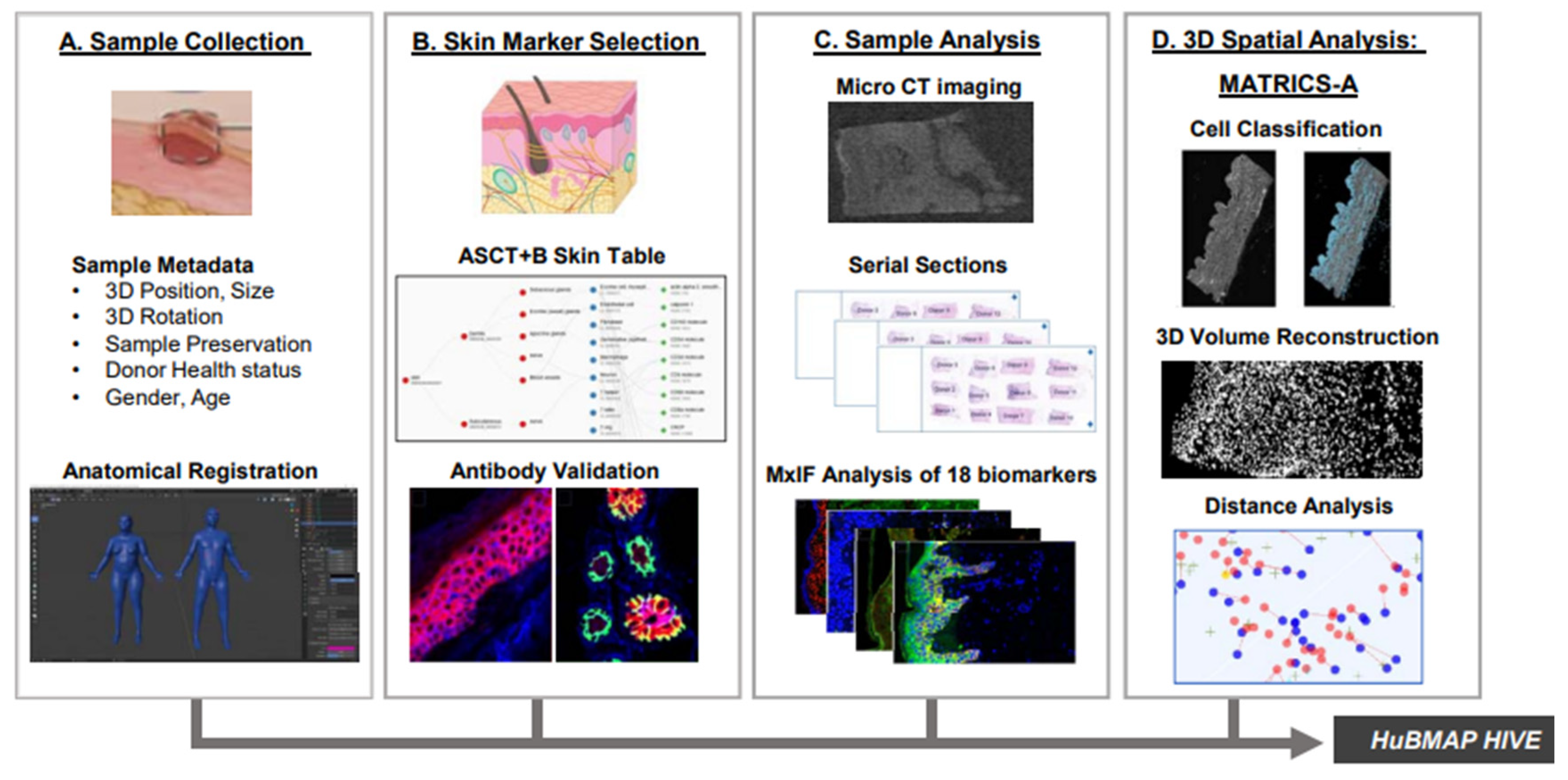
| Formalism | Strength | Limitation |
|---|---|---|
| ODEs | Computationally efficient, suitable for large systems | Fails to capture stochastic effects, unsuitable for small systems with noise |
| KMC Methods | Accurate, captures rare events and transitions | Computationally intensive, unsuitable for large systems |
| Langevin Noise | Computationally efficient, captures intrinsic and extrinsic noise | Less accurate than KMC methods, assumes continuous concentrations |
| Framework | Linked Core Formalism(s) | Key Uses | Strengths | Limitations |
|---|---|---|---|---|
| Cellular Potts Model (CPM) [48] | KMC/ODE | Cell shape, adhesion, migration | Captures cell behaviour, polarity, ECM effects | Computationally heavy; overfitting risk |
| Stochastic Petri Nets (SPNs) [46,52] | KMC/ODE/Langevin | Signalling pathways, fuzzy timing | Structured, handles uncertainty, scalable | Approximate moments only; scaling challenges |
| Multiscale Stochastic Dynamics (MuTrans) [53] | Langevin/KMC | Cell fate transitions from transcriptomics | Visualises stability landscape; multiscale resolution | Needs large datasets; assumes steady state |
| Hybrid Methods [54,55] | ODE + KMC/Chemical Langevin Equation (CLE) | Spatial RD systems with variable copy numbers | Efficient multiscale handling; dynamic switching | Complex interfaces; R-D master equation has issues in 2D+ |
| Piecewise Deterministic Markov Processes (PDMPs) [56,57] | ODE + KMC (jumps) | Gene networks, rare-event dynamics | Combines flow and stochasticity; tractable dynamics | Limited analytical solutions; poor fit for continuous noise |
| Type of Cell | Experimental Method Used | Estimated Elastic Modulus | Insights |
|---|---|---|---|
| Hair follicle keratinocytes [121] | AFM indentation | 30 ± 23 kPa → 11 ± 10 MPa | Large stiffening during differentiation |
| Epithelial monolayers [120] | Wound closure modelling | approx. 0.2 kPa | Soft phenotype; stress concentration at wound edge |
| HaCaT (immortalised Human Keratinocytes [129] | AFM nanoindentation with surfactants/peptides | 50% decrease with Sodium Lauryl Sulphate; However, the modulus was restored/increased with hydrolysed collagen included | Softening with Sodium Lauryl Sulphate, stiffening with hydrolysed collagen; cytoskeletal protection implied |
| Cytoplasm of osteoblasts [118] | Cell geometry obtained from confocal microscopy | 6.5 kPa | Maxwell model; frequency dependent behaviour |
| Chondrocytes in hydrogels [130] | Inverse FE fitting to 3D hydrogel deformation | approx. 5 → −20 kPa | Modulus increases with gel stiffness; actin-dependent |
| Madin–Darby Canine Kidney epithelial domes [131] | AFM force–indentation microscopy | Significantly increased | Stiffer than surrounding monolayers; linked to actomyosin |
| General cell model [125] | FE model simulating Magnetic twisting cytometry | 1 kPa (shear modulus) | Elastic modulus estimation based on bead displacement under applied torque. |
| Type of Cell | Experimental Method Used | Estimated Stress/Force Output | Insights |
|---|---|---|---|
| Keratinocyte (focal contacts) [137] | Lateral displacement inputs applied along the substrate | 14.93 ± 1.9 nN/µm2 per FA; Total: 25–90 nN | Stress/displacement decreases quadratically from the force plane |
| Epithelial cells (monolayer) [120] | FE wound healing simulation | normal > shear stress at localised wound edge. | Captures progressive weakening of a cell–cell junction. |
| Invasive and non-invasive breast cancer cells. [140] | Traction-force microscopy | Traction stress maps (visualisation of stress) | Cell stiffness and adhesion energy affect force outputs independent of contractility |
| Keratinocyte + carcinoma [143] | BioID assays, super-resolution imaging | HD’s alter traction and tension | Mechanical coupling exists between HDs and FAs, indicating coordinated force transmission. |
| FA model [145] | Liquid crystal deformation | Forces distributed around the cells: 25–90 nN | Modulus increases with gel stiffness; actin-dependent |
| General cell model [141] | TFM-based FE simulation | Intracellular stress distributions; FA loading profiles | Hypoelastic model coupled with linear elastic substrate |
| Single cell [146] | Fourier Transform Traction Cytometry (FTTC) + particle image velocimetry | Traction stress maps | FA proteins (e.g., talin) essential for cytoskeletal force transmission |
| Constitutive Model Type | Purpose/Mechanism | Application |
|---|---|---|
| Generalised Maxwell [118] | Captures linear time-dependent stress in viscoelastic cytoplasm. | Osteoblast cytoplasmic response |
| Kelvin–Voigt [149] | Models long-term elasticity with rapid damping | Embryonic tissue stiffness |
| QLV + Prony series [127,150] | Describes nonlinear relaxation over short and long timescales | Skin and ligament mechanics |
| Calcium-dependent contraction [151] | Links Ca2+ concentration to active mechanical stress generation and viscoelasticity | Embryonic epithelial contraction |
| Cohesive zone [152] | Simulates adhesion dynamics at junctions under time-varying forces | Accurately predicts initiation, growth, and rupture of adhesions under cyclic stresses |
| Type of Cell | Experimental Method Used | Estimated Viscoelastic/Active Parameters | Insights |
|---|---|---|---|
| Murine MC3T3-E1 osteoblasts [165] | AFM | Creep equilibrium times: almost instant at the edge, approx. 3–4 s at cytoplasm, approx. 4–5 s at nucleus Instantaneous elastic modulus (E0): edge 8 kPa, nucleus 1.7 kPa, cytoplasm 2.5 kPa | Nucleus is softest with slowest creep. Cytoskeletal remodelling likely causes delayed viscoelastic recovery. |
| Embryonic epithelial tissue [31,149] | Area contraction + Ca2+ modulation | Shear viscosity: 3790 Pa s Bulk Viscosity: 550 Pa s | Active contraction tied to intracellular calcium concentration. |
| Skin tissue (rat) [48,150] | Stress-relaxation test | QLV + Prony Parameters (back skin): ≈ 12.7 MPa, g1 = 0.3, g2 = 0.25 τ = 0.062s | approx. 70% relaxation Highly viscoelastic; stronger relaxation in back skin than abdomen. |
| Epithelial monolayer [166] | Wound healing experiments | Edge protrusion force ≈ 2 pN; Protrusion force elsewhere ≈ 0–0.3 pN | Promotes faster wound closure; active tug-of-war at boundary. |
| Epithelial embryos of fruit fly embryos (Drosophila melanogaster) [148] | Laser ablation (microsurgery) | Viscosity ≈ 10 Pa·s; Tension ≈ 1.9 nN; Stress ≈ 100 Pa | Adding viscoelastic rods improves the model’s accuracy in simulating recoil behaviour after wounding. |
| Bioprinted skin substitute with keratinocytes, fibroblasts etc. [167] | Water-based process to create hydrogel bioink. Variable shear rates with a range of 0.1–1000 s were then applied | increased from 7.2 ± 0.6 kPa to 14.7 ± 1.3 kPa after 24 h at 37 °C | In vivo, the bi-layer constructs achieved significant wound healing and tissue integration after 28 days. |
| Heterogeneous materials (single inclusion phantom) [168] | Ultrasound via excitation through compressional waves to assess tissue characteristics | = 0.1–11.5 s. Maxwell SLS model used to fit creep curves from FE simulations. | of inclusion material differs >10% from background. Boundary zones show greatest error. |
| 3D-Printed Tissue-like Materials (J750 Shore) [166] | uniaxial tensile stress–relaxation tests | = 0.87 ± 0.02 MPa, g1 = 3.00, τ1 = 0.49 s; g2 = 0.23, τ2 = 11.0 s; g3 = 0.12, τ3 = 49.2 ± 4.67 s; | 3D-printed materials show Neo-Hookean behaviour, lacking the anisotropy and strain stiffening of real tissues. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, S.; Maiti, R.; Roy, A. Numerical Modelling of Keratinocyte Behaviour: A Comprehensive Review of Biochemical and Mechanical Frameworks. Cells 2025, 14, 1382. https://doi.org/10.3390/cells14171382
Rashid S, Maiti R, Roy A. Numerical Modelling of Keratinocyte Behaviour: A Comprehensive Review of Biochemical and Mechanical Frameworks. Cells. 2025; 14(17):1382. https://doi.org/10.3390/cells14171382
Chicago/Turabian StyleRashid, Sarjeel, Raman Maiti, and Anish Roy. 2025. "Numerical Modelling of Keratinocyte Behaviour: A Comprehensive Review of Biochemical and Mechanical Frameworks" Cells 14, no. 17: 1382. https://doi.org/10.3390/cells14171382
APA StyleRashid, S., Maiti, R., & Roy, A. (2025). Numerical Modelling of Keratinocyte Behaviour: A Comprehensive Review of Biochemical and Mechanical Frameworks. Cells, 14(17), 1382. https://doi.org/10.3390/cells14171382





