Identification of Distinct, Quantitative Pattern Classes from Emergent Tissue-Scale hiPSC Bioelectric Properties
Abstract
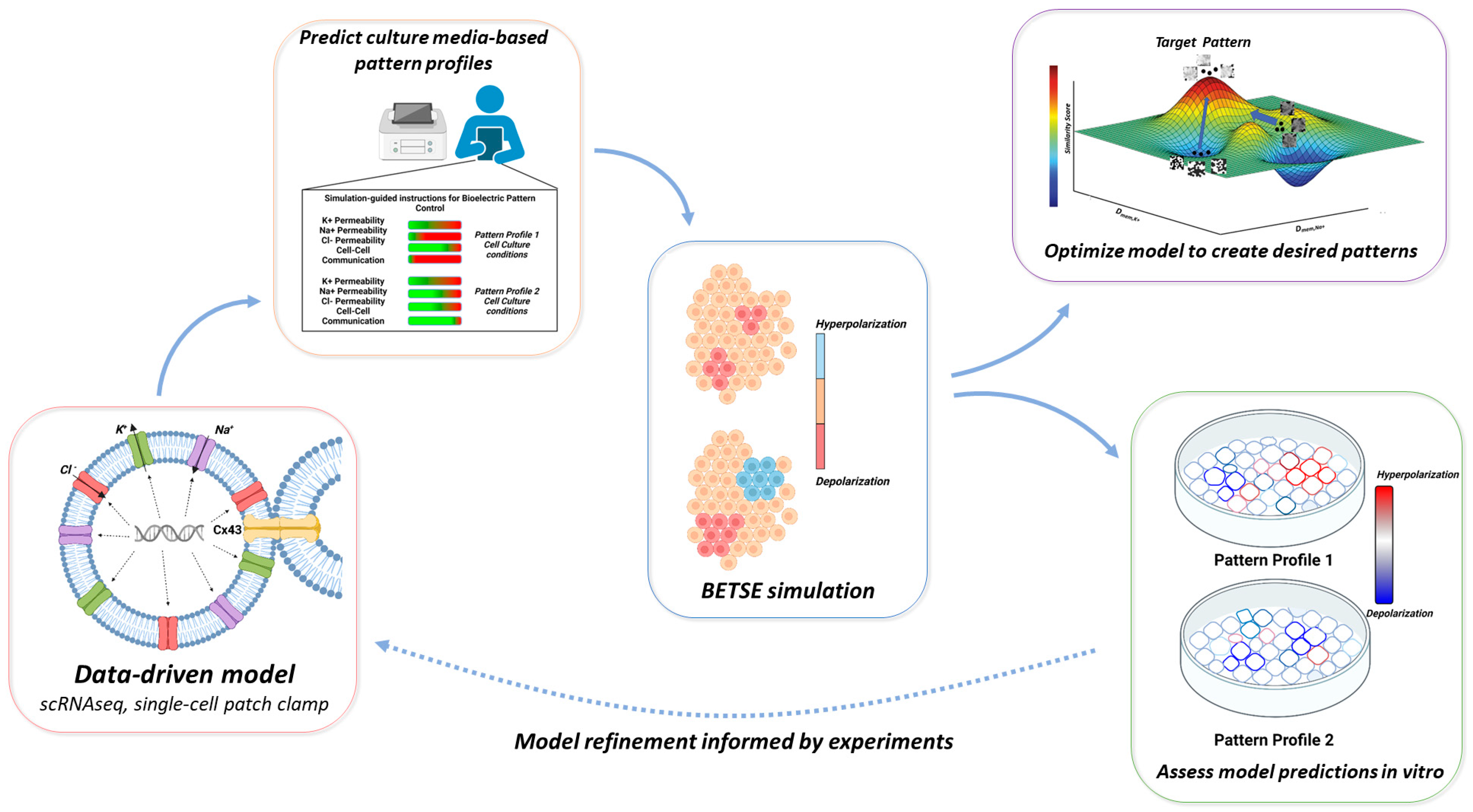
1. Introduction
2. Materials and Methods
2.1. Contribution of Active Ionic Transport to Steady-State Vmem Maintenance
2.2. WTC11 hiPSC Cell Culture
2.3. Calibration of DiBAC to Cellular Vmem
2.4. Whole-Cell Electrophysiological Patch Clamp of WTC11 hiPSCs
2.5. GJA1-Modified hiPSC Cell Culture and Experiment Preparation
2.6. Gap Junction Pharmacological Molecule Inhibition
2.7. K+ Supplementation DiBAC Experiment
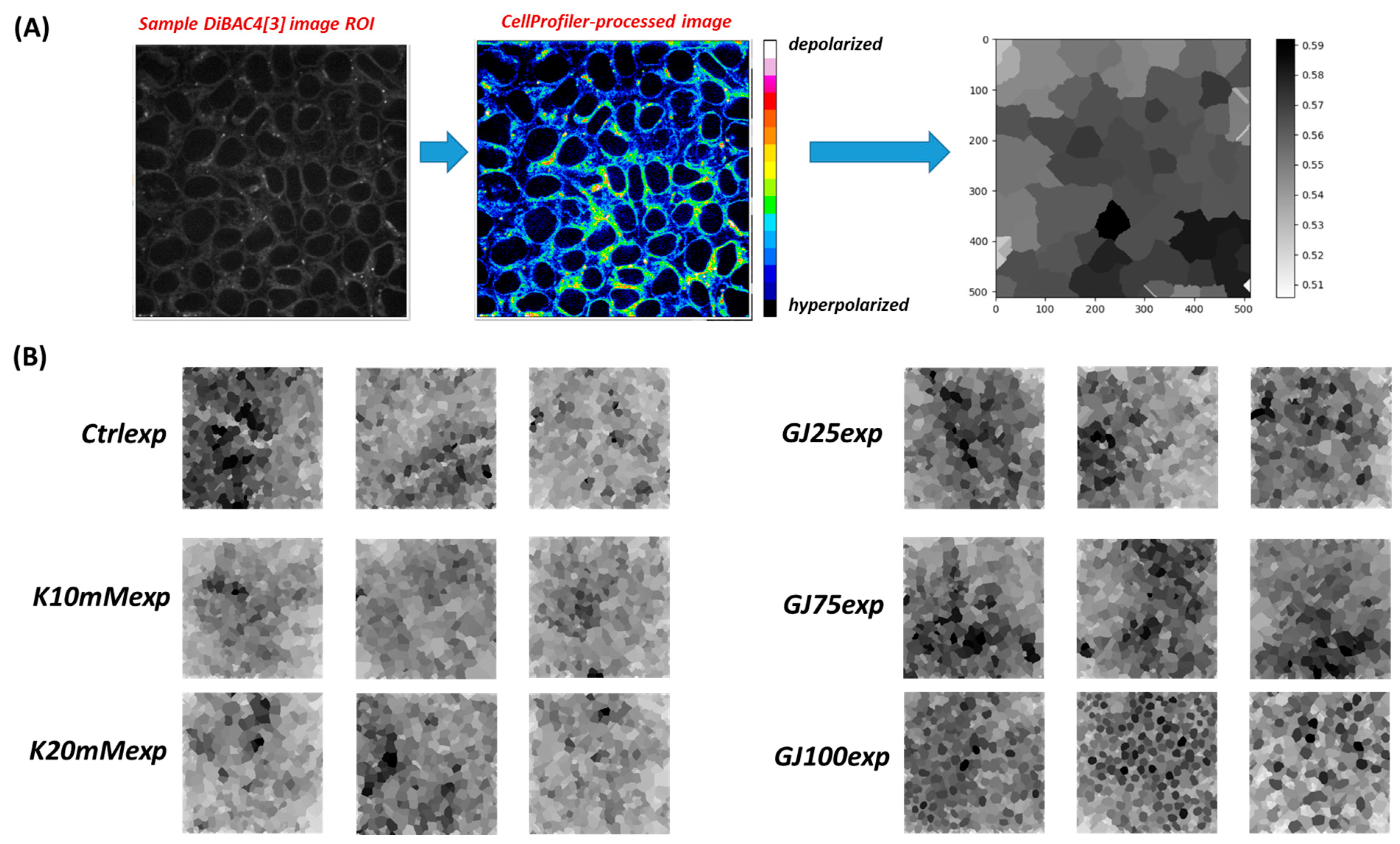
2.8. Experimental Image Transformation, Segmentation, and Analysis
2.9. Immunocytohistochemistry and Imaging
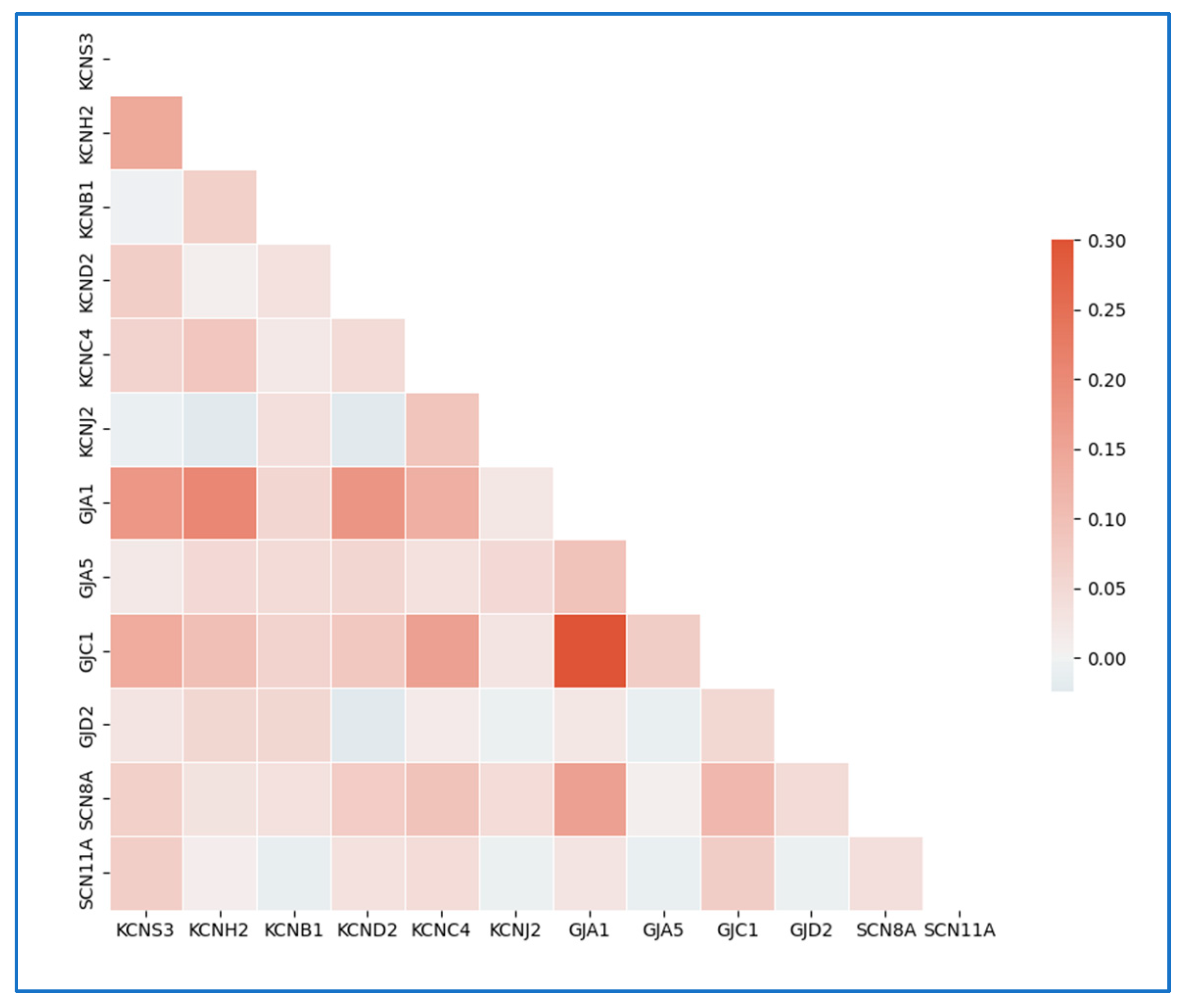
2.10. Single-Cell RNA Sequencing of hiPSCs
2.11. Processing Raw Single-Cell RNA Sequencing Data
2.12. Computational Model (BETSE)
2.13. Computational Image Analysis
2.14. Quad-Tree Image Representation and Tree Spatial Superposition Logic
2.15. Particle Swarm Optimization
2.16. Software Availability
3. Results
3.1. Electrophysiologic and Bioinformatic Data Enable hiPSC-Specific Bioelectric Modeling
3.2. Single-Cell Bioelectric Dynamics Enable hiPSC Multicellular Pattern Prediction under Varying Cell Culture Conditions
3.3. A Pipeline for Comparing Multicellular Bioelectric Patterns
3.4. Particle Swarm Optimization Highlights Parameters That Potentially Lead to Desired Bioelectric Patterns
3.5. Disruption of Intrinsic Gap Junction Connectivity in iPSC Colonies Leads to Novel Pattern Formation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Estimated Single-Ion Flux Contribution
Appendix A.2. Model Core Mathematical Strategy
Appendix A.3. BETSE Parameter and WTC11 Parameter Values and Derivation
Appendix A.3.1. GJ Ion Flux parameters
Appendix A.3.2. -GA Effect Estimation
Appendix A.3.3. Single-Ion Flux Parameters
Appendix A.3.4. Na+/K+-ATPase Parameters
Appendix A.3.5. WTC11-Specific Voltage Gated K+ Ion Channel Parameters
Appendix A.4. Main Model Parameters
| Parameter | Description | Typical Value | Units |
|---|---|---|---|
| Ion index (i = Na, K, Cl, Ca, H, M) | |||
| Free diffusion coefficient for ion i | |||
| Time | 1–10 | s | |
| Spatial coordinates | 500 | m | |
| System height | 10 | m | |
| Standard free energy of ATP hydrolysis | 37 | kJ/mol | |
| Temperature | 310 | K | |
| Faraday’s constant | 96,485 | C/mol | |
| Ideal gas constant | 8.3145 | J/K mol | |
| Electron charge constant | C/ion | ||
| Boltzmann constant | J/K | ||
| Cell and extracellular | |||
| Cell membrane and extracellular surface area | |||
| Membrane capacitance | 0.022 | F/ | |
| Electrolyte-induced self-capacitance | 0.86 | F/ | |
| Max rate constant for pump | 1/s | ||
| GJ voltage-gating half-closed parameter | 50 | mV | |
| Cell membrane thickness | m | ||
| Intercellular spacing | m | ||
| Water viscosity | Pas | ||
| Variable | Description | Typical value | Units |
| Extracellular concentration | 1–150 | ||
| Intracellular concentration | 1–150 | ||
| Membrane diffusion coefficient for ion i | |||
| Membrane permeability for ion i | 0.13 | nm/s | |
| Voltage in cell and environment | −10 to −80 | mV | |
| Cell transmembrane voltage potential | −10 to −80 | mV | |
| Mass flux of ion i | 1.0 | ||
| Ionic charge density | 600 | ||
| Ionic current density | 10–500 | ||
| GJ diffusion scaling-coefficient | |||
| TJ diffusion scaling-coefficient | |||
| Max membrane diffusion for voltage-gated channel | |||
| Electric field | V/m |
Appendix B
Appendix B.1. Quad-Tree Analysis
Appendix B.2. QTS/TSSL Formula and Pattern Classification
Appendix B.3. Similarity Score Calculations
References
- Arnold, S.J.; Robertson, E.J. Making a commitment: Cell lineage allocation and axis patterning in the early mouse embryo. Nat. Rev. Mol. Cell Biol. 2009, 10, 91–103. [Google Scholar] [CrossRef] [PubMed]
- Warmflash, A.; Sorre, B.; Etoc, F.; Siggia, E.D.; Brivanlou, A.H. A method to recapitulate early embryonic spatial patterning in human embryonic stem cells. Nat. Methods 2014, 11, 847–854. [Google Scholar] [CrossRef] [PubMed]
- Kamm, R.D.; Bashir, R.; Arora, N.; Dar, R.D.; Gillette, M.U.; Griffith, L.G.; Kemp, M.L.; Kinlaw, K.; Levin, M.; Martin, A.C.; et al. Perspective: The promise of multi-cellular engineered living systems. APL Bioeng. 2018, 2, 040901. [Google Scholar] [CrossRef] [PubMed]
- Cervera, J.; Levin, M.; Mafe, S. Morphology changes induced by intercellular gap junction blocking: A reaction-diffusion mechanism. Biosystems 2021, 209, 104511. [Google Scholar] [CrossRef] [PubMed]
- Glen, C.M.; McDevitt, T.C.; Kemp, M.L. Dynamic intercellular transport modulates the spatial patterning of differentiation during early neural commitment. Nat. Commun. 2018, 9, 4111. [Google Scholar] [CrossRef]
- Libby, A.R.G.; Briers, D.; Haghighi, I.; Joy, D.A.; Conklin, B.R.; Belta, C.; McDevitt, T.C. Automated Design of Pluripotent Stem Cell Self-Organization. Cell Syst. 2019, 9, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Tewary, M.; Ostblom, J.; Prochazka, L.; Zulueta-Coarasa, T.; Shakiba, N.; Fernandez-Gonzalez, R.; Zandstra, P.W. A stepwise model of reaction-diffusion and positional information governs self-organized human peri-gastrulation-like patterning. Development 2017, 144, 4298–4312. [Google Scholar] [CrossRef] [PubMed]
- Okuda, S.; Takata, N.; Hasegawa, Y.; Kawada, M.; Inoue, Y.; Adachi, T.; Sasai, Y.; Eiraku, M. Strain-triggered mechanical feedback in self-organizing optic-cup morphogenesis. Sci. Adv. 2018, 4, eaau1354. [Google Scholar] [CrossRef] [PubMed]
- Chhabra, S.; Liu, L.; Goh, R.; Kong, X.; Warmflash, A. Dissecting the dynamics of signaling events in the BMP, WNT, and NODAL cascade during self-organized fate patterning in human gastruloids. PLoS Biol. 2019, 17, e3000498. [Google Scholar] [CrossRef]
- Toda, S.; Blauch, L.R.; Tang, S.K.Y.; Morsut, L.; Lim, W.A. Programming self-organizing multicellular structures with synthetic cell-cell signaling. Science 2018, 361, 156–162. [Google Scholar] [CrossRef]
- Molitoris, J.M.; Paliwal, S.; Sekar, R.B.; Blake, R.; Park, J.; Trayanova, N.A.; Tung, L.; Levchenko, A. Precisely parameterized experimental and computational models of tissue organization. Integr. Biol. 2016, 8, 230–242. [Google Scholar] [CrossRef]
- George, L.F.; Bates, E.A. Mechanisms Underlying Influence of Bioelectricity in Development. Front. Cell Dev. Biol. 2022, 10, 772230. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, P.; Kane, A.; Harrison, C.; Levin, M. A Meta-Analysis of Bioelectric Data in Cancer, Embryogenesis, and Regeneration. Bioelectricity 2021, 3, 42–67. [Google Scholar] [CrossRef]
- Pai, V.P.; Pietak, A.; Willocq, V.; Ye, B.; Shi, N.-Q.; Levin, M. HCN2 Rescues brain defects by enforcing endogenous voltage pre-patterns. Nat. Commun. 2018, 9, 998. [Google Scholar] [CrossRef]
- Cervera, J.; Pai, V.P.; Levin, M.; Mafe, S. From non-excitable single-cell to multicellular bioelectrical states supported by ion channels and gap junction proteins: Electrical potentials as distributed controllers. Prog. Biophys. Mol. Biol. 2019, 149, 39–53. [Google Scholar] [CrossRef] [PubMed]
- Riol, A.; Cervera, J.; Levin, M.; Mafe, S. Cell Systems Bioelectricity: How Different Intercellular Gap Junctions Could Regionalize a Multicellular Aggregate. Cancers 2021, 13, 5300. [Google Scholar] [CrossRef]
- Emmons-Bell, M.; Durant, F.; Hammelman, J.; Bessonov, N.; Volpert, V.; Morokuma, J.; Pinet, K.; Adams, D.S.; Pietak, A.; Lobo, D.; et al. Gap Junctional Blockade Stochastically Induces Different Species-Specific Head Anatomies in Genetically Wild-Type Girardia dorotocephala Flatworms. Int. J. Mol. Sci. 2015, 16, 27865–27896. [Google Scholar] [CrossRef] [PubMed]
- Zamir, A.; Li, G.; Chase, K.; Moskovitch, R.; Sun, B.; Zaritsky, A. Emergence of synchronized multicellular mechanosensing from spatiotemporal integration of heterogeneous single-cell information transfer. Cell Syst. 2022, 13, 711–723.e7. [Google Scholar] [CrossRef]
- Jiang, P.; Rushing, S.N.; Kong, C.-W.; Fu, J.; Lieu, D.K.-T.; Chan, C.W.; Deng, W.; Li, R.A. Electrophysiological properties of human induced pluripotent stem cells. Am. J. Physiol.-Cell Physiol. 2010, 298, C486–C495. [Google Scholar] [CrossRef]
- Wang, K.; Xue, T.; Tsang, S.Y.; Van Huizen, R.; Wong, C.W.; Lai, K.W.; Ye, Z.; Cheng, L.; Au, K.W.; Zhang, J.; et al. Electrophysiological properties of pluripotent human and mouse embryonic stem cells. Stem Cells 2005, 23, 1526–1534. [Google Scholar] [CrossRef]
- Pietak, A.; Levin, M. Exploring Instructive Physiological Signaling with the Bioelectric Tissue Simulation Engine. Front. Bioeng. Biotechnol. 2016, 4, 55. [Google Scholar] [CrossRef] [PubMed]
- Pietak, A.; Levin, M. Bioelectric gene and reaction networks: Computational modelling of genetic, biochemical and bioelectrical dynamics in pattern regulation. J. R. Soc. Interface 2017, 14, 20170425. [Google Scholar] [CrossRef] [PubMed]
- Krasznai, Z.; Márián, T.; Balkay, L.; Emri, M.; Trón, L. Flow cytometric determination of absolute membrane potential of cells. J. Photochem. Photobiol. B Biol. 1995, 28, 93–99. [Google Scholar] [CrossRef]
- Huettner, J.E.; Lu, A.; Qu, Y.; Wu, Y.; Kim, M.; McDonald III, J.W. Gap Junctions and Connexon Hemichannels in Human Embryonic Stem Cells. Stem Cells 2006, 24, 1654–1667. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.S.; Levin, M. Measuring resting membrane potential using the fluorescent voltage reporters DiBAC4(3) and CC2-DMPE. Cold Spring Harb. Protoc. 2012, 2012, 459–464. [Google Scholar] [CrossRef] [PubMed]
- Dobin, A.; Davis, C.A.; Schlesinger, F.; Drenkow, J.; Zaleski, C.; Jha, S.; Batut, P.; Chaisson, M.; Gingeras, T.R. STAR: Ultrafast universal RNA-seq aligner. Bioinformatics 2013, 29, 15–21. [Google Scholar] [CrossRef] [PubMed]
- Hao, Y.; Hao, S.; Andersen-Nissen, E.; Mauck, W.M., III; Zheng, S.; Butler, A.; Lee, M.J.; Wilk, A.J.; Darby, C.; Zager, M.; et al. Integrated analysis of multimodal single-cell data. Cell 2021, 184, 3573–3587.e29. [Google Scholar] [CrossRef] [PubMed]
- Gemel, J.; Valiunas, V.; Brink, P.R.; Beyer, E.C. Connexin43 and connexin26 form gap junctions, but not heteromeric channels in co-expressing cells. J. Cell Sci. 2004, 117, 2469. [Google Scholar] [CrossRef]
- Vrbjar, N.; Dzurba, A.; Ziegelhöffer, A. Enzyme kinetics and the activation energy of (Na,K)-ATPase in ischaemic hearts: Influence of the duration of ischaemia. Gen. Physiol. Biophys. 1994, 13, 405–411. [Google Scholar]
- Costa, P.F.; Emilio, M.G.; Fernandes, P.L.; Ferreira, H.G.; Ferreira, K.G. Determination of ionic permeability coefficients of the plasma membrane of Xenopus laevis oocytes under voltage clamp. J. Physiol. 1989, 413, 199–211. [Google Scholar] [CrossRef]
- Haghighi, I.; Jones, A.; Kong, Z.; Bartocci, E.; Gros, R.; Belta, C. SpaTeL: A novel spatial-temporal logic and its applications to networked systems. In Proceedings of the 18th International Conference on Hybrid Systems: Computation and Control, Seattle, WA, USA, 14–16 April 2015; pp. 189–198. [Google Scholar]
- Silver, B.B.; Wolf, A.E.; Lee, J.; Pang, M.F.; Nelson, C.M. Epithelial tissue geometry directs emergence of bioelectric field and pattern of proliferation. Mol. Biol. Cell 2020, 31, 1691–1702. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.S.; Levin, M. Inverse drug screens: A rapid and inexpensive method for implicating molecular targets. Genesis 2006, 44, 530–540. [Google Scholar] [CrossRef]
- Bhavsar, M.B.; Leppik, L.; Costa Oliveira, K.M.; Barker, J.H. Role of Bioelectricity During Cell Proliferation in Different Cell Types. Front. Bioeng. Biotechnol. 2020, 8, 603. [Google Scholar] [CrossRef]
- McNamara, H.M.; Salegame, R.; Al Tanoury, Z.; Xu, H.; Begum, S.; Ortiz, G.; Pourquie, O.; Cohen, A.E. Bioelectrical domain walls in homogeneous tissues. Nat. Phys. 2020, 16, 357–364. [Google Scholar] [CrossRef] [PubMed]
- Webb, S.E.; Miller, A.L. Ca2+ signalling and early embryonic patterning during zebrafish development. Clin. Exp. Pharmacol. Physiol. 2007, 34, 897–904. [Google Scholar] [CrossRef]
- Adams, D.S.; Uzel, S.G.M.; Akagi, J.; Wlodkowic, D.; Andreeva, V.; Yelick, P.C.; Devitt-Lee, A.; Pare, J.-F.; Levin, M. Bioelectric signalling via potassium channels: A mechanism for craniofacial dysmorphogenesis in KCNJ2-associated Andersen–Tawil Syndrome. J. Physiol. 2016, 594, 3245–3270. [Google Scholar] [CrossRef]
- Levin, M. Large-scale biophysics: Ion flows and regeneration. Trends Cell Biol. 2007, 17, 261–270. [Google Scholar] [CrossRef]
- Pai, V.P.; Aw, S.; Shomrat, T.; Lemire, J.M.; Levin, M. Transmembrane voltage potential controls embryonic eye patterning in Xenopus laevis. Development 2012, 139, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Kirichok, Y.; Navarro, B.; Clapham, D.E. Whole-cell patch-clamp measurements of spermatozoa reveal an alkaline-activated Ca2+ channel. Nature 2006, 439, 737–740. [Google Scholar] [CrossRef]
- Picoli, C.; Soleilhac, E.; Journet, A.; Barette, C.; Comte, M.; Giaume, C.; Mouthon, F.; Fauvarque, M.O.; Charvériat, M. High-Content Screening Identifies New Inhibitors of Connexin 43 Gap Junctions. Assay. Drug Dev. Technol. 2019, 17, 240–248. [Google Scholar] [CrossRef]
- Otsu, K.; Kuruma, A.; Yanagida, E.; Shoji, S.; Inoue, T.; Hirayama, Y.; Uematsu, H.; Hara, Y.; Kawano, S. Na+/K+ ATPase and its functional coupling with Na+/Ca2+ exchanger in mouse embryonic stem cells during differentiation into cardiomyocytes. Cell Calcium 2005, 37, 137–151. [Google Scholar] [CrossRef] [PubMed]
- Takeda, Y.; Ward, S.M.; Sanders, K.M.; Koh, S.D. Effects of the gap junction blocker glycyrrhetinic acid on gastrointestinal smooth muscle cells. Am. J. Physiol. Gastrointest. Liver Physiol. 2005, 288, G832–G841. [Google Scholar] [CrossRef] [PubMed]
- Matchkov, V.V.; Rahman, A.; Peng, H.; Nilsson, H.; Aalkjaer, C. Junctional and nonjunctional effects of heptanol and glycyrrhetinic acid derivates in rat mesenteric small arteries. Br. J. Pharmacol. 2004, 142, 961–972. [Google Scholar] [CrossRef] [PubMed]
- Davidson, J.S.; Baumgarten, I.M.; Harley, E.H. Reversible inhibition of intercellular junctional communication by glycyrrhetinic acid. Biochem. Biophys. Res. Commun. 1986, 134, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Hille, B. Ion Channels of Excitable Membranes; Oxford University Press: Oxford, UK, 2001; Volume 18, pp. 1–814. [Google Scholar]
- Bartocci, E.; Gol, E.A.; Haghighi, I.; Belta, C. A Formal Methods Approach to Pattern Recognition and Synthesis in Reaction Diffusion Networks. IEEE Trans. Control Netw. Syst. 2018, 5, 308–320. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the MHS’95, Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Schwindt, P.C.; Crill, W.E. Amplification of synaptic current by persistent sodium conductance in apical dendrite of neocortical neurons. J. Neurophysiol. 1995, 74, 2220–2224. [Google Scholar] [CrossRef]
- Salas, P.J.; López, E.M. Validity of the Goldman-Hodgkin-Katz equation in paracellular ionic pathways of gallbladder epithelium. Biochim. Biophys. Acta 1982, 691, 178–182. [Google Scholar] [CrossRef] [PubMed]
- Bonzanni, M.; Payne, S.L.; Adelfio, M.; Kaplan, D.L.; Levin, M.; Oudin, M.J. Defined extracellular ionic solutions to study and manipulate the cellular resting membrane potential. Biol. Open 2020, 9, bio048553. [Google Scholar] [CrossRef]
- Gallacher, D.V.; Morris, A.P. A patch-clamp study of potassium currents in resting and acetylcholine-stimulated mouse submandibular acinar cells. J. Physiol. 1986, 373, 379–395. [Google Scholar] [CrossRef]
- Palacios-Prado, N.; Bukauskas, F.F. Heterotypic gap junction channels as voltage-sensitive valves for intercellular signaling. Proc. Natl. Acad. Sci. USA 2009, 106, 14855–14860. [Google Scholar] [CrossRef]
- Belus, M.T.; Rogers, M.A.; Elzubeir, A.; Josey, M.; Rose, S.; Andreeva, V.; Yelick, P.C.; Bates, E.A. Kir2.1 is important for efficient BMP signaling in mammalian face development. Dev. Biol. 2018, 444 (Suppl. S1), S297–S307. [Google Scholar] [CrossRef] [PubMed]
- Dahal, G.R.; Rawson, J.; Gassaway, B.; Kwok, B.; Tong, Y.; Ptácek, L.J.; Bates, E. An inwardly rectifying K+ channel is required for patterning. Development 2012, 139, 3653–3664. [Google Scholar] [CrossRef] [PubMed]
- Voit, E.O. A First Course in Systems Biology; Garland Science: New York, NY, USA, 2018. [Google Scholar]
- Sun, Y.H.; Kao, H.K.J.; Chang, C.W.; Merleev, A.; Overton, J.L.; Pretto, D.; Yechikov, S.; Maverakis, E.; Chiamvimonvat, N.; Chan, J.W.; et al. Human induced pluripotent stem cell line with genetically encoded fluorescent voltage indicator generated via CRISPR for action potential assessment post-cardiogenesis. Stem Cells 2020, 38, 90–101. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Du, L.; Peng, G.-H. Optogenetic stimulation inhibits the self-renewal of mouse embryonic stem cells. Cell Biosci. 2019, 9, 73. [Google Scholar] [CrossRef]
- Weir, M.P.; Lo, C.W. Gap junctional communication compartments in the Drosophila wing disk. Proc. Natl. Acad. Sci. USA 1982, 79, 3232–3235. [Google Scholar] [CrossRef] [PubMed]
- Krüger, J.; Bohrmann, J. Bioelectric patterning during oogenesis: Stage-specific distribution of membrane potentials, intracellular pH and ion-transport mechanisms in Drosophila ovarian follicles. BMC Dev. Biol. 2015, 15, 1. [Google Scholar] [CrossRef] [PubMed]
- Jayaram, D.T.; Luo, Q.; Thourson, S.B.; Finlay, A.H.; Payne, C.K. Controlling the Resting Membrane Potential of Cells with Conducting Polymer Microwires. Small 2017, 13, 1700789. [Google Scholar] [CrossRef] [PubMed]
- Paoletti, P.; Ellis-Davies, G.C.R.; Mourot, A. Optical control of neuronal ion channels and receptors. Nat. Rev. Neurosci. 2019, 20, 514–532. [Google Scholar] [CrossRef] [PubMed]
- Schafer, M. Chapter 4: Finite volume methods. In Computational Engineering–Introduction to Numerical Methods; Springer: Berlin/Heidelberg, Germany, 2006; pp. 77–105. [Google Scholar]
- Andreev, V.P.; Lisin, E.E. Investigation of the electroosmotic flow effect on the efficiency of capillary electrophoresis. Electrophoresis 1992, 13, 832–837. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Katz, B. The effect of sodium ions on the electrical activity of giant axon of the squid. J. Physiol. 1949, 108, 37–77. [Google Scholar] [CrossRef]
- Harris, A.L.; Spray, D.C.; Bennett, M.V. Control of intercellular communication by voltage dependence of gap junctional conductance. J. Neurosci. Off. J. Soc. Neurosci. 1983, 3, 79–100. [Google Scholar] [CrossRef] [PubMed]
- Cohen, W.W. Fast Effective Rule Induction. In Machine Learning Proceedings 1995; Prieditis, A., Russell, S., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 115–123. [Google Scholar]
- Clarke, E.M.; Emerson, E.A. Design and synthesis of synchronization skeletons using branching time temporal logic. In Logics of Programs; Springer: Berlin/Heidelberg, Germany, 1982; pp. 52–71. [Google Scholar]


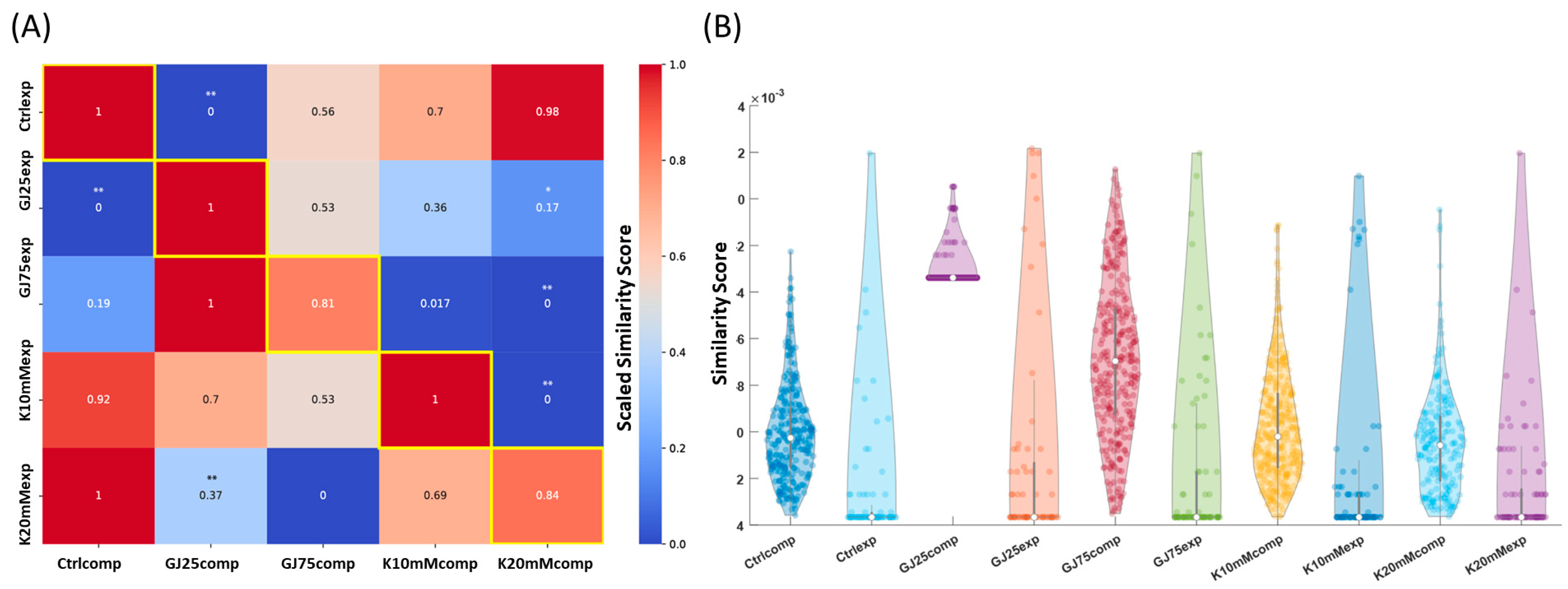
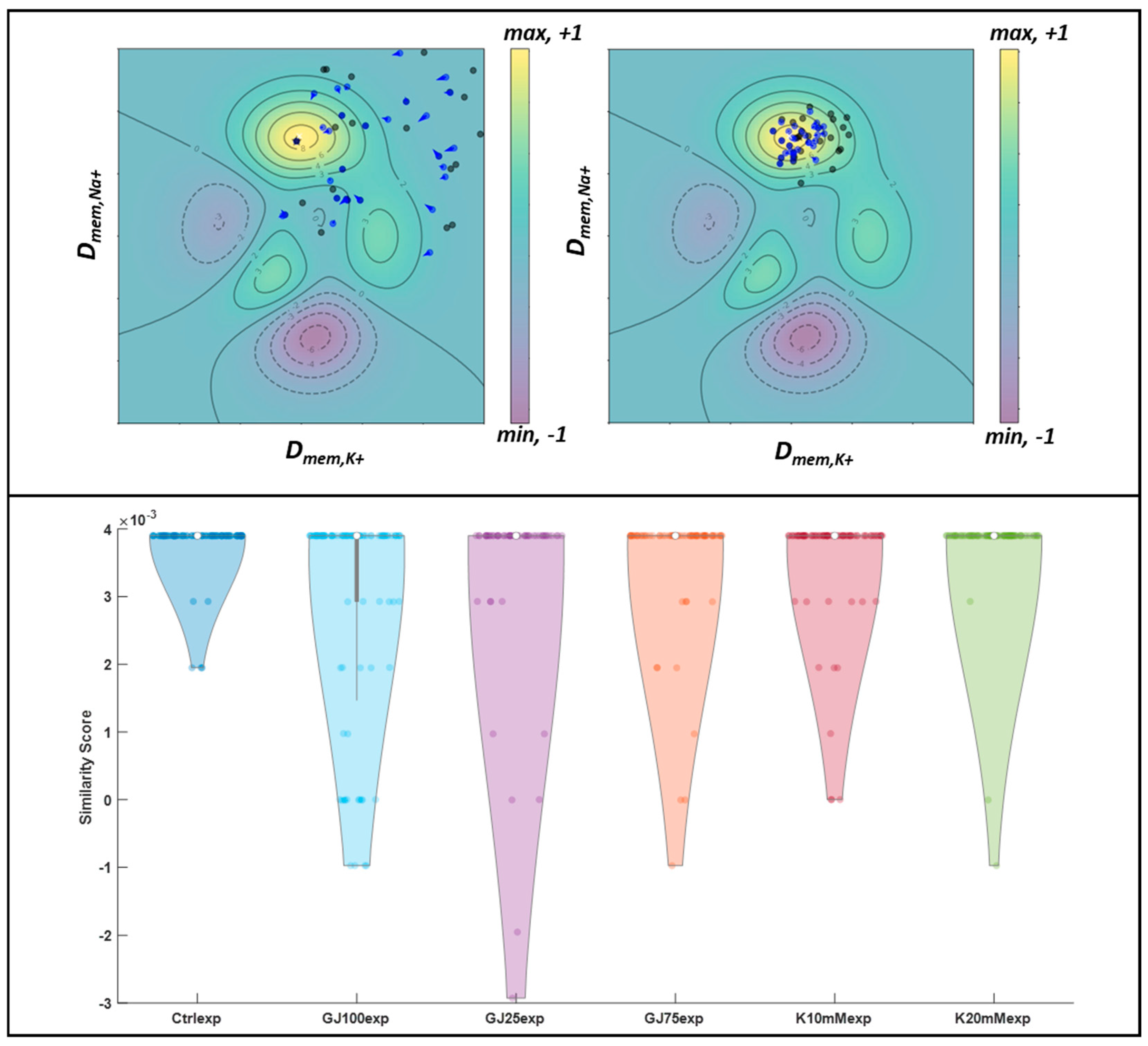

| Simulated Condition | # of Images | Correct Pattern ID % (Training Set) | F-Measure | Precision | Recall | Experimental Condition | # of Images | Normalized Similarity Score |
|---|---|---|---|---|---|---|---|---|
| Control (Ctrlcomp) | 282 | 90.63% | 0.686 | 0.836 | 0.645 | Control (Ctrlexp) | 89 | 1 |
| 25% GJC inhibition (GJ25comp) | 393 | 75.2% | 0.681 | 0.672 | 0.726 | βGA 10 μM (GJ25exp) | 95 | 1 |
| 75% GJC inhibition (GJ75comp) | 298 | 98.9% | 0.969 | 0.969 | 0.968 | βGA 60 μM (GJ75exp) | 85 | 0.81 |
| K+ 10 mM (K10mMcomp) | 377 | 72% | 0.688 | 0.678 | 0.737 | K+ 10 mM (K10mMexp) | 86 | 1 |
| K+ 20 mM (K20mMcomp) | 199 | 89.7% | 0.828 | 0.818 | 0.842 | K+ 20 mM (K20mMexp) | 93 | 0.84 |
| 95% GJC block (GJ95comp) | 199 | 99.5% | 0.929 | 0.951 | 0.922 | 100% Cx43 KD, GJA1 CRISPRi cells (GJ100exp) | 90 | 0.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Norfleet, D.A.; Melendez, A.J.; Alting, C.; Kannan, S.; Nikitina, A.A.; Caldeira Botelho, R.; Yang, B.; Kemp, M.L. Identification of Distinct, Quantitative Pattern Classes from Emergent Tissue-Scale hiPSC Bioelectric Properties. Cells 2024, 13, 1136. https://doi.org/10.3390/cells13131136
Norfleet DA, Melendez AJ, Alting C, Kannan S, Nikitina AA, Caldeira Botelho R, Yang B, Kemp ML. Identification of Distinct, Quantitative Pattern Classes from Emergent Tissue-Scale hiPSC Bioelectric Properties. Cells. 2024; 13(13):1136. https://doi.org/10.3390/cells13131136
Chicago/Turabian StyleNorfleet, Dennis Andre, Anja J. Melendez, Caroline Alting, Siya Kannan, Arina A. Nikitina, Raquel Caldeira Botelho, Bo Yang, and Melissa L. Kemp. 2024. "Identification of Distinct, Quantitative Pattern Classes from Emergent Tissue-Scale hiPSC Bioelectric Properties" Cells 13, no. 13: 1136. https://doi.org/10.3390/cells13131136
APA StyleNorfleet, D. A., Melendez, A. J., Alting, C., Kannan, S., Nikitina, A. A., Caldeira Botelho, R., Yang, B., & Kemp, M. L. (2024). Identification of Distinct, Quantitative Pattern Classes from Emergent Tissue-Scale hiPSC Bioelectric Properties. Cells, 13(13), 1136. https://doi.org/10.3390/cells13131136






