Large-Scale, Wavelet-Based Analysis of Lysosomal Trajectories and Co-Movements of Lysosomes with Nanoparticle Cargos
Abstract
1. Introduction
2. Materials and Methods
2.1. Cell Culture, Nanoparticle Treatments, and Confocal Microscopy
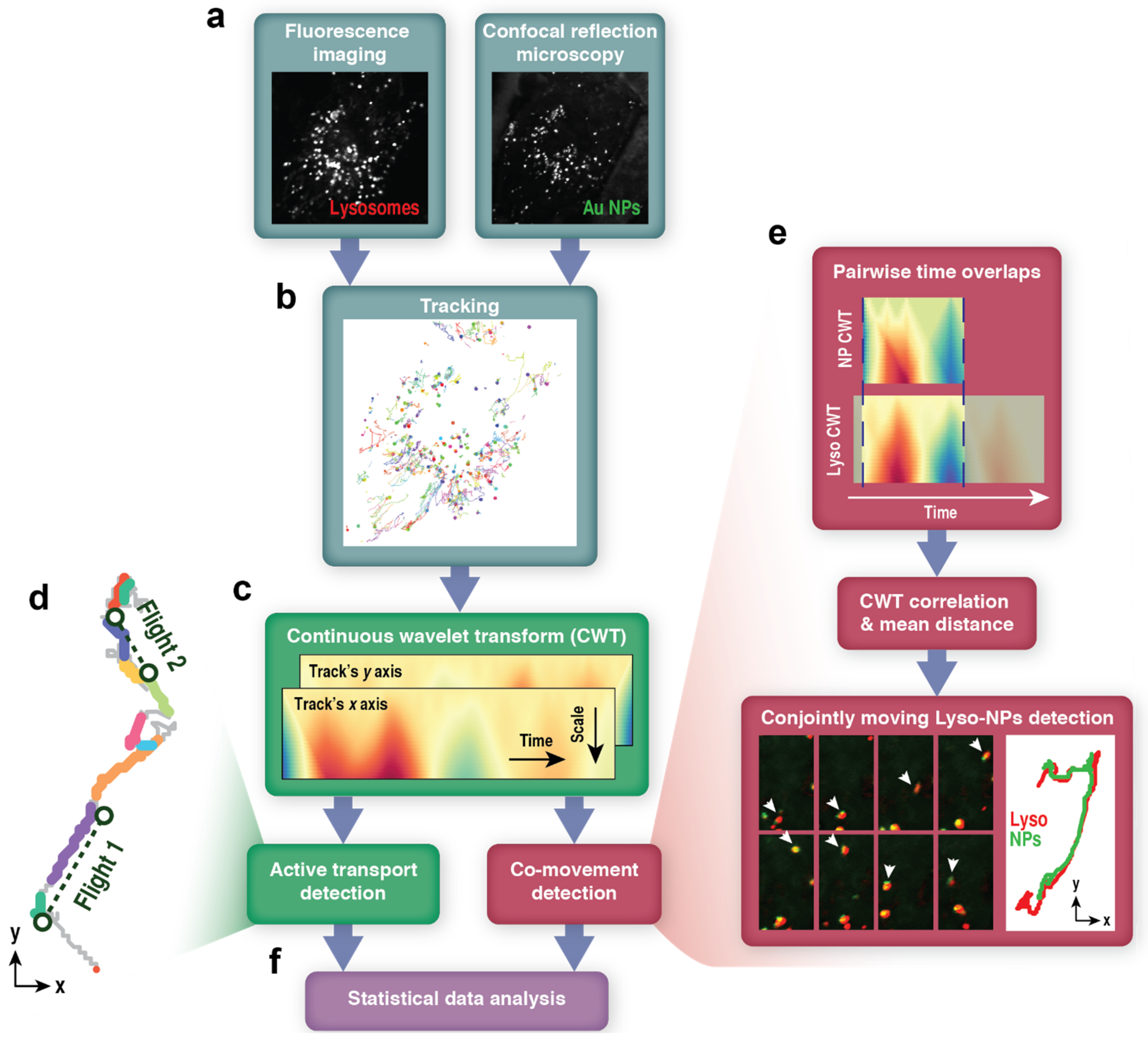
2.2. Image Processing and Tracking
2.3. Movement Analysis
2.3.1. Continuous Wavelet Transform
2.3.2. Active Transport Detection
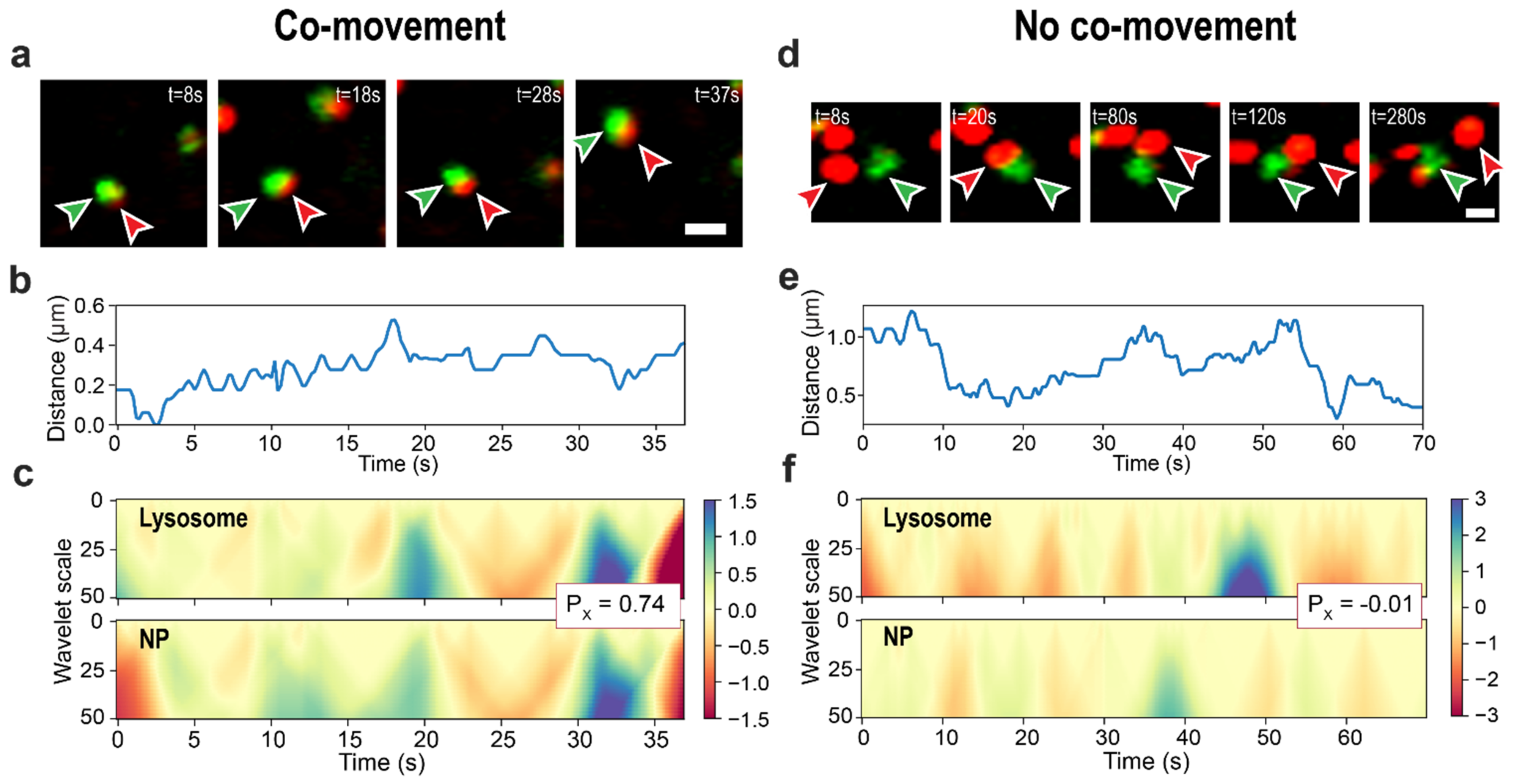
2.3.3. Co-Movement Detection
2.4. Statistical Data Analysis
3. Results
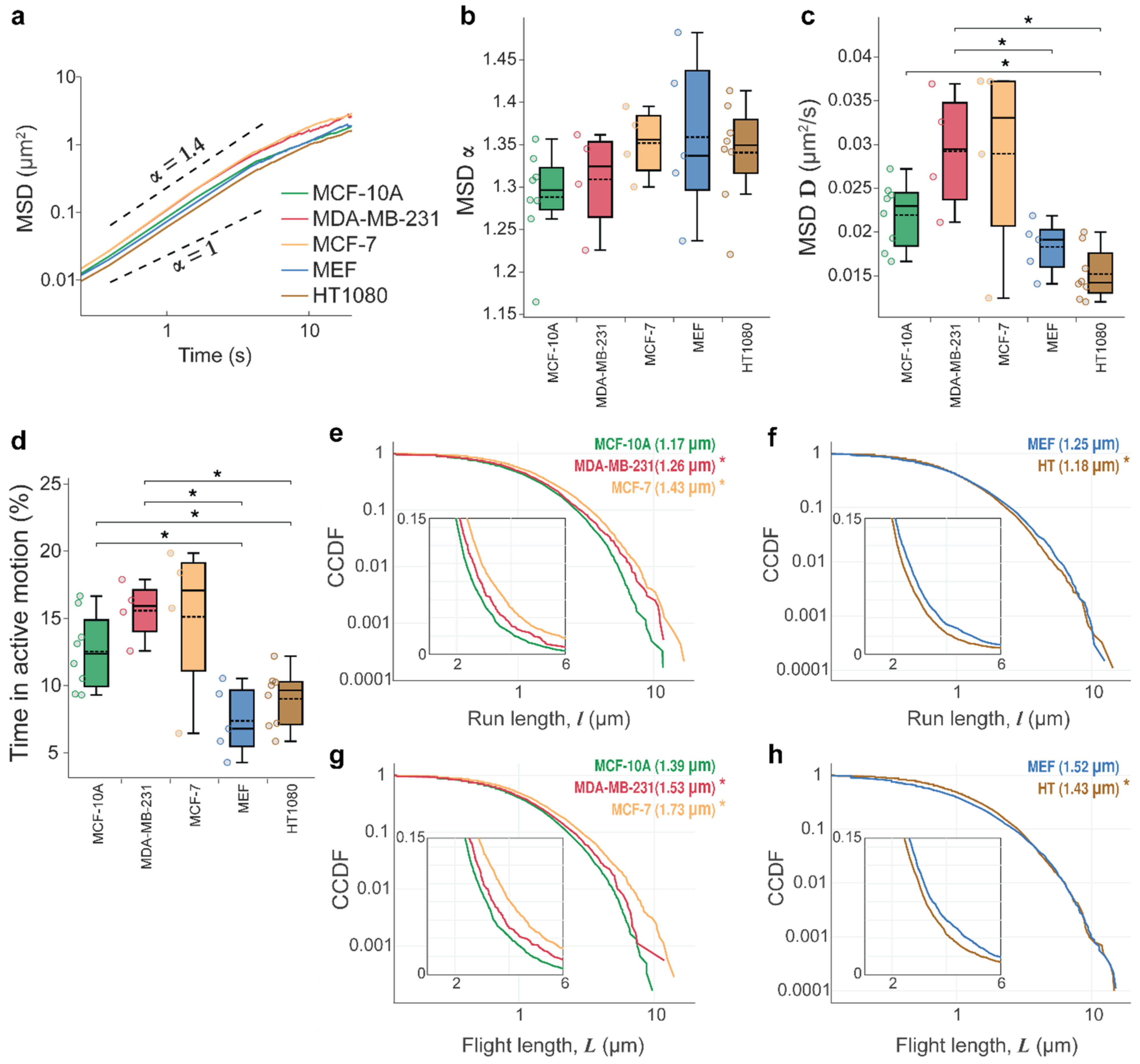
3.1. Lysosomal Movements Are Characterized by a Heavy-Tailed, Lognormal Distribution of Run/Flight Lengths
3.2. Tissue Origin and Cancer-Specific Differences in Lysosomal Dynamics
3.3. Wavelet-Based Approach for Detection of Lysosome-Nanoparticle Co-Movement
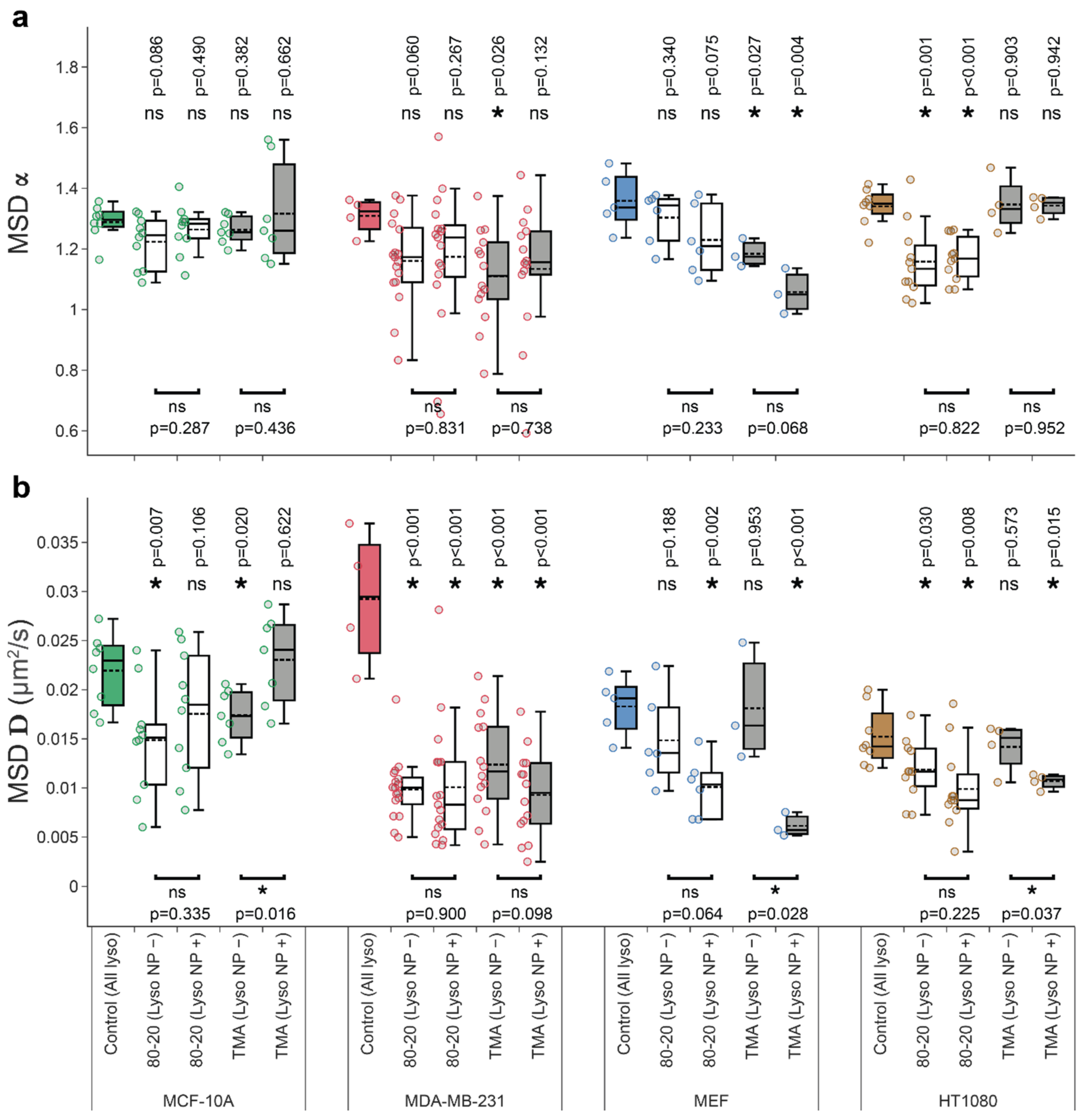
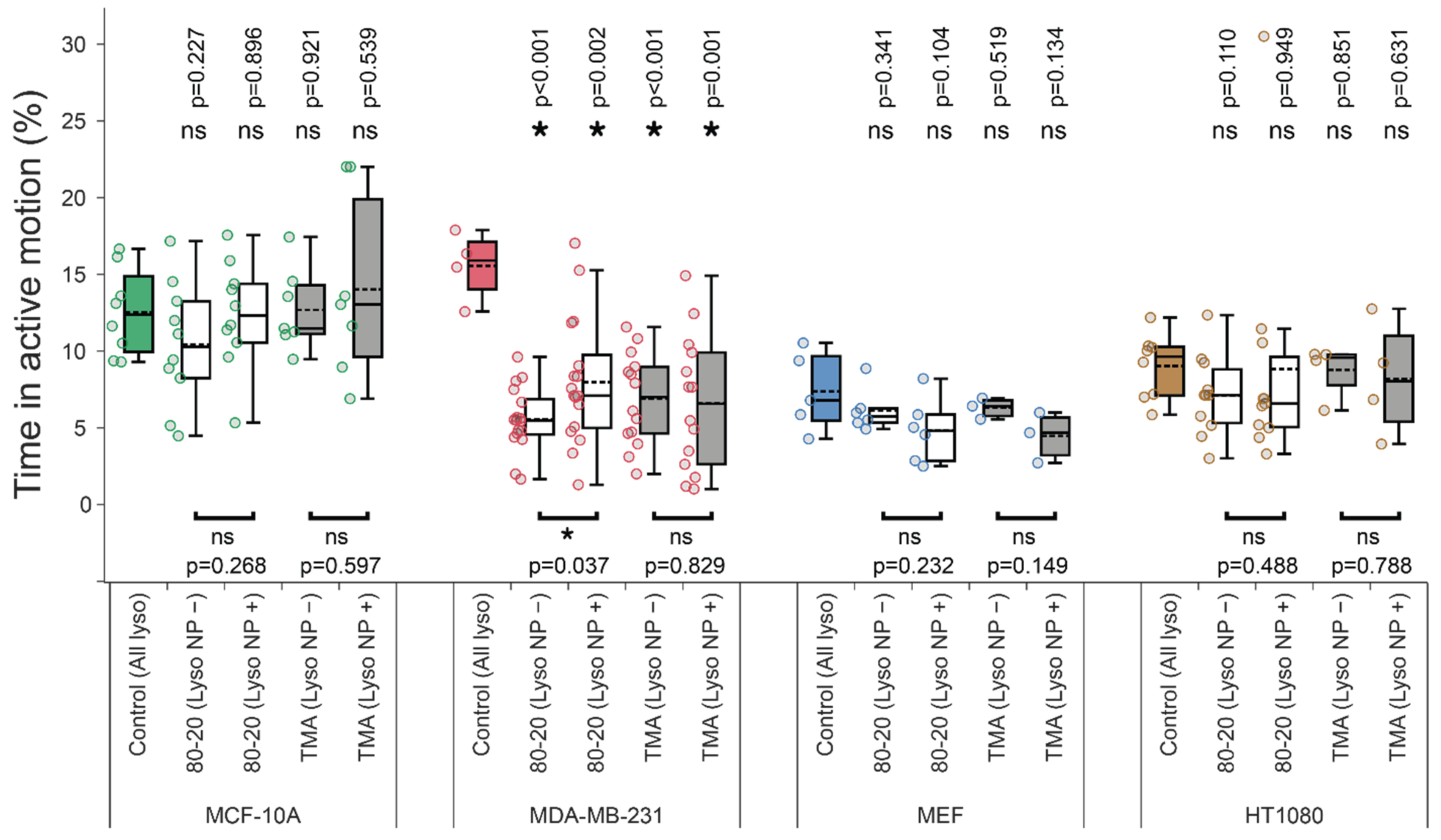
3.4. Mixed-Charge Gold Nanoparticles Selectively Disrupt Lysosomal Transport in Cancer Cells
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
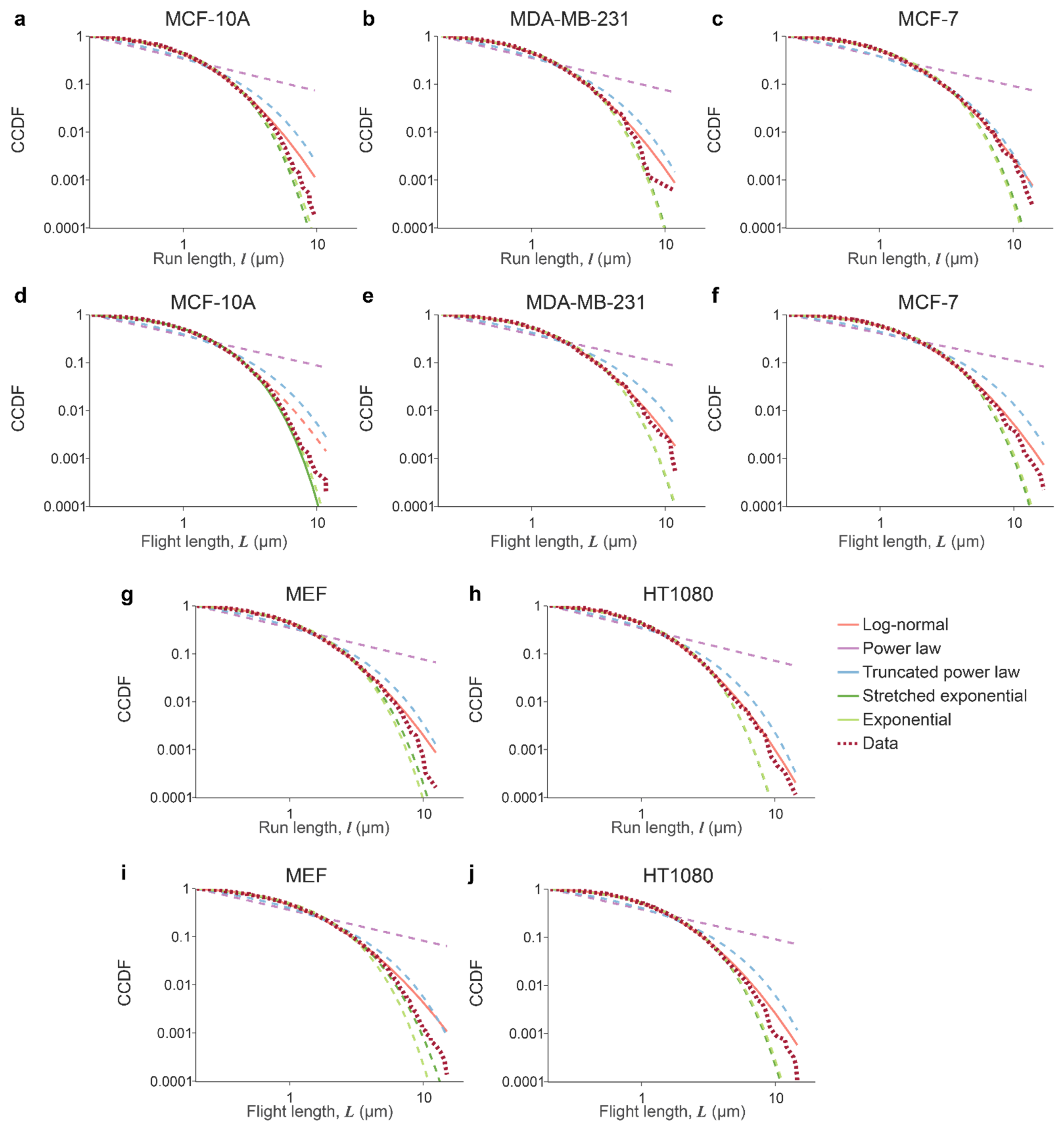
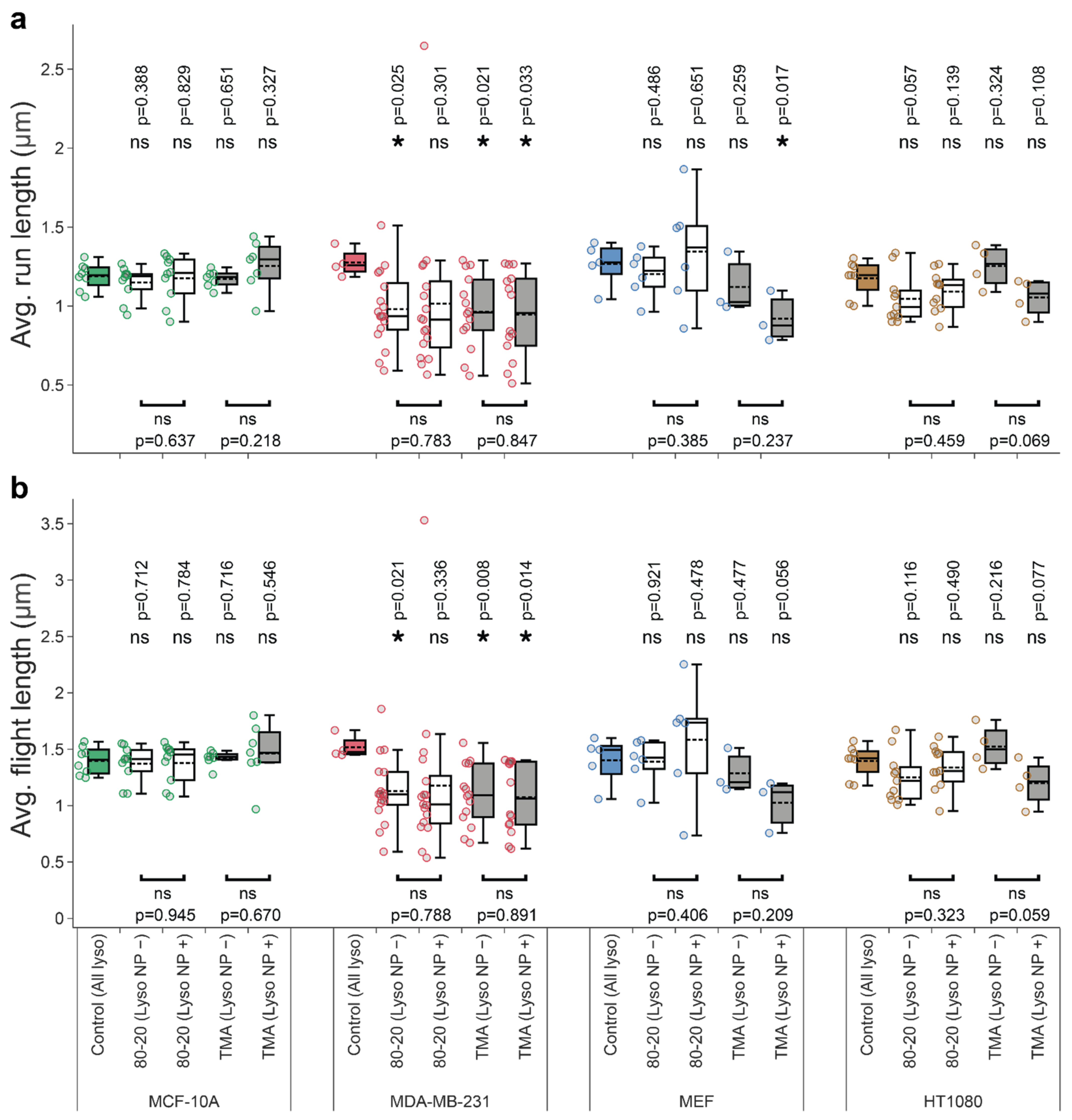
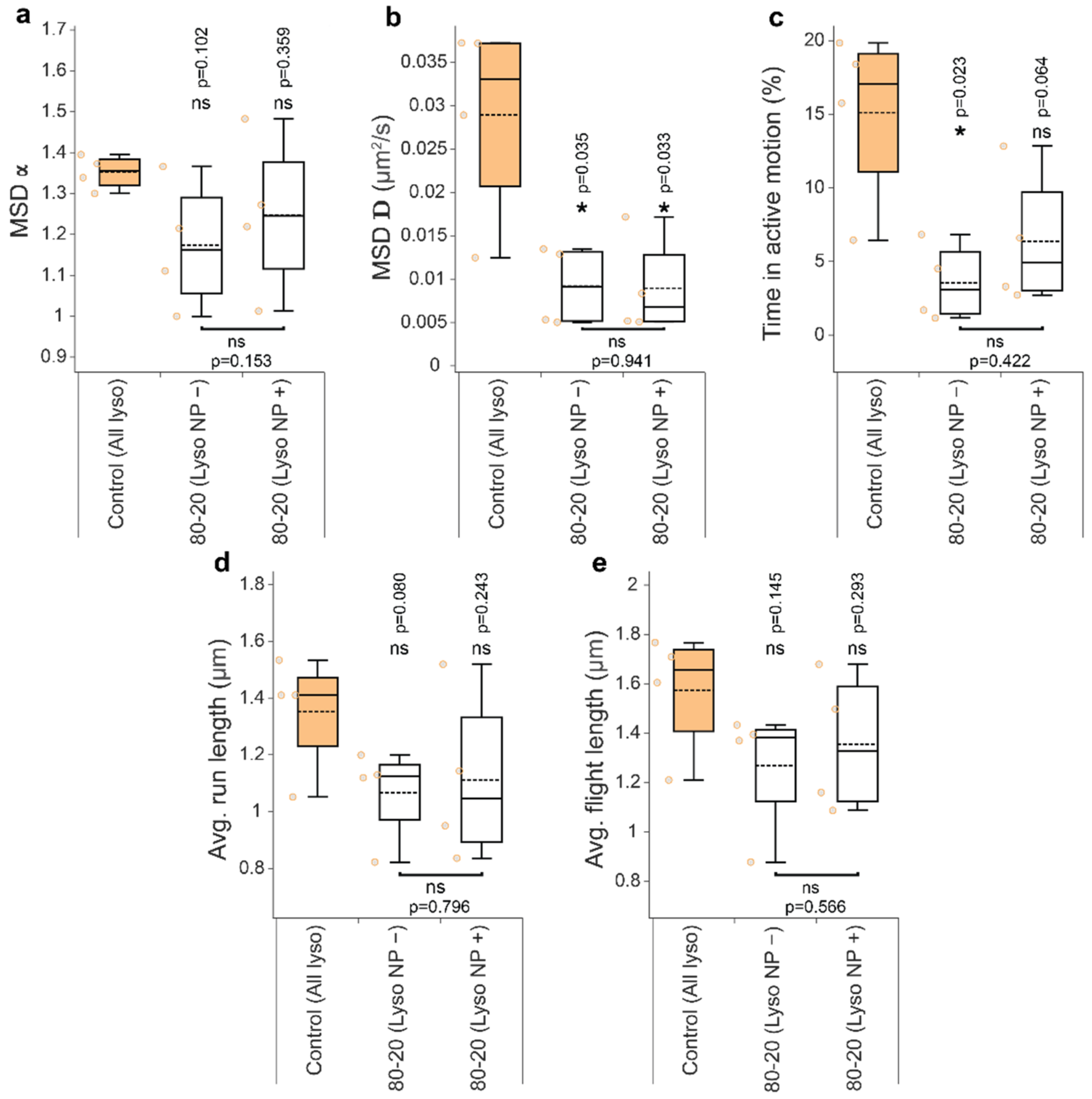
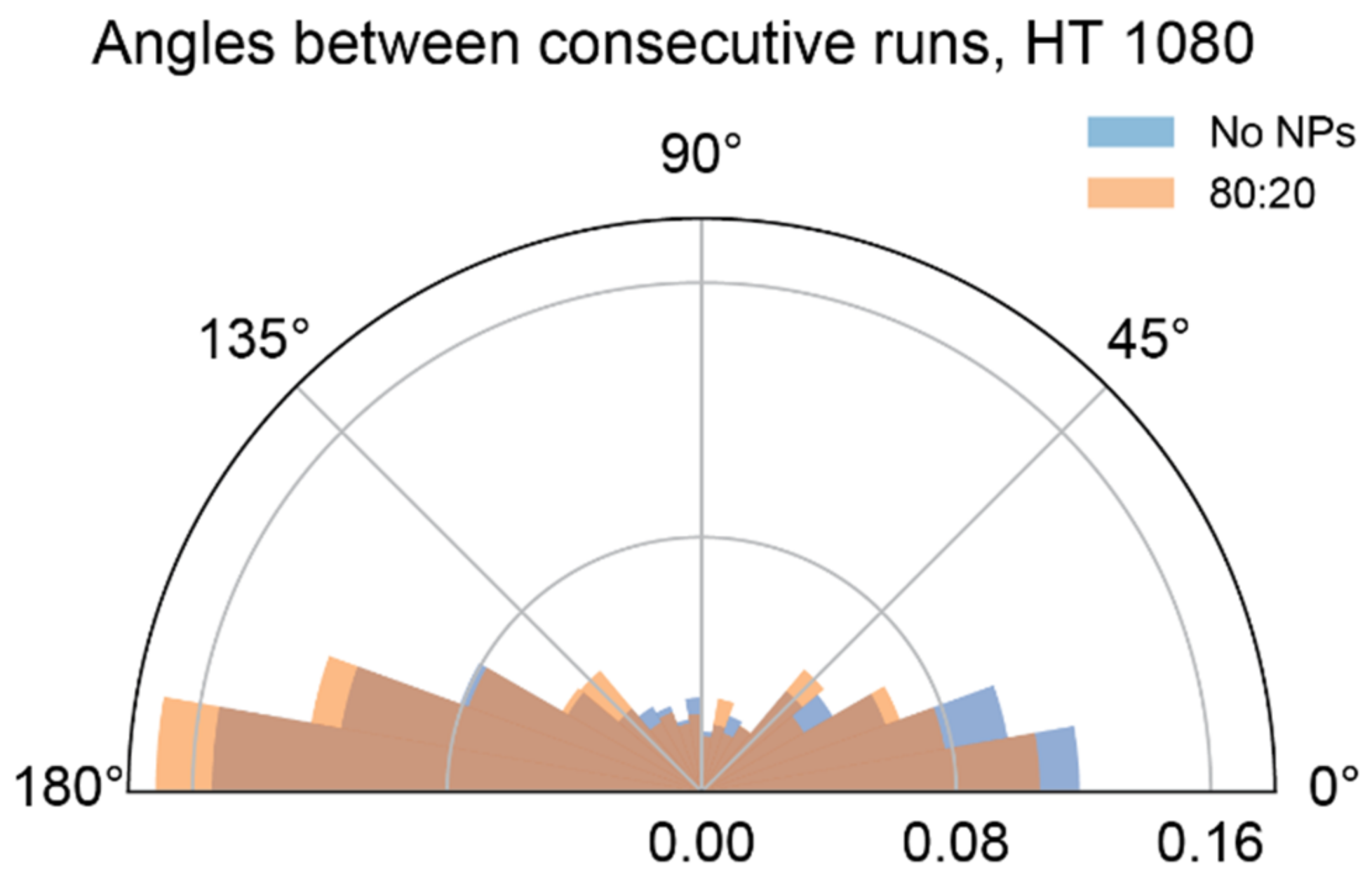
Appendix B
| Distribution Name | Probability Density Function p(x) |
|---|---|
| Power law | |
| Truncated power law | |
| Log-normal | |
| Stretched exponential | |
| Exponential |
| Cell Type/Treatment | Lysosomal Diameter [μm] | Lysosomes, l | Cells, n |
|---|---|---|---|
| MEF | 0.65 ± 0.23 | 525 | 7 |
| MEF + 80:20 NPs | 0.71 ± 0.25 * | 759 | 6 |
| HT-1080 | 0.67 ± 0.24 | 707 | 6 |
| HT-1080 + 80:20 NPs | 0.99 ± 0.34 * | 539 | 11 |
| MCF-10A | 0.54 ± 0.20 | 316 | 10 |
| MCF-10A + 80:20 NPs | 0.57 ± 0.22 ns | 340 | 12 |
| MDA-MB-231 | 0.67 ± 0.30 | 418 | 16 |
| MDA-MB-231 + 80:20 NPs | 1.00 ± 0.49 * | 235 | 10 |
| MCF-7 | 0.80 ± 0.35 | 250 | 11 |
| MCF-7 + 80:20 NPs | 1.42 ± 0.92 * | 239 | 11 |
References
- Saftig, P.; Klumperman, J. Lysosome biogenesis and lysosomal membrane proteins: Trafficking meets function. Nat. Rev. Mol. Cell Biol. 2009, 10, 623–635. [Google Scholar] [CrossRef]
- Ballabio, A.; Bonifacino, J.S. Lysosomes as dynamic regulators of cell and organismal homeostasis. Nat. Rev. Mol. Cell Biol. 2020, 21, 101–118. [Google Scholar] [CrossRef] [PubMed]
- Lawrence, R.E.; Zoncu, R. The lysosome as a cellular centre for signalling, metabolism and quality control. Nat. Cell Biol. 2019, 21, 133–142. [Google Scholar] [CrossRef] [PubMed]
- Ba, Q.; Raghavan, G.; Kiselyov, K.; Yang, G. Whole-Cell Scale Dynamic Organization of Lysosomes Revealed by Spatial Statistical Analysis. Cell Rep. 2018, 23, 3591–3606. [Google Scholar] [CrossRef] [PubMed]
- Tancini, B.; Buratta, S.; Delo, F.; Sagini, K.; Chiaradia, E.; Pellegrino, R.M.; Emiliani, C.; Urbanelli, L. Lysosomal Exocytosis: The Extracellular Role of an Intracellular Organelle. Membranes 2020, 10, 406. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Haka; Abigail, S. Lyosome exocytosis and membrane repair. In Lysosomes: Biology, Diseases, and Therapeutics; Maxfield, F.R., Willard, J.M., Lu, S., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 63–85. [Google Scholar]
- Glunde, K.; Guggino, S.E.; Solaiyappan, M.; Pathak, A.P.; Ichikawa, Y.; Bhujwalla, Z.M. Extracellular acidification alters lysosomal trafficking in human breast cancer cells. Neoplasia 2003, 5, 533–545. [Google Scholar] [CrossRef]
- Webb, B.A.; Aloisio, F.M.; Charafeddine, R.A.; Cook, J.; Wittmann, T.; Barber, D.L. pHLARE: A new biosensor reveals decreased lysosome pH in cancer cells. Mol. Biol. Cell 2021, 32, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Hamalisto, S.; Jaattela, M. Lysosomes in cancer-living on the edge (of the cell). Curr. Opin. Cell Biol. 2016, 39, 69–76. [Google Scholar] [CrossRef] [PubMed]
- Machado, E.R.; Annunziata, I.; van de Vlekkert, D.; Grosveld, G.C.; d’Azzo, A. Lysosomes and Cancer Progression: A Malignant Liaison. Front. Cell Dev. Biol. 2021, 9, 642494. [Google Scholar] [CrossRef]
- Kallunki, T.; Olsen, O.D.; Jaattela, M. Cancer-associated lysosomal changes: Friends or foes? Oncogene 2013, 32, 1995–2004. [Google Scholar] [CrossRef]
- Zhitomirsky, B.; Assaraf, Y.G. Lysosomal accumulation of anticancer drugs triggers lysosomal exocytosis. Oncotarget 2017, 8, 45117–45132. [Google Scholar] [CrossRef]
- Wang, B.; Kuo, J.; Granick, S. Bursts of active transport in living cells. Phys. Rev. Lett. 2013, 111, 208102. [Google Scholar] [CrossRef]
- Cabukusta, B.; Neefjes, J. Mechanisms of lysosomal positioning and movement. Traffic 2018, 19, 761–769. [Google Scholar] [CrossRef]
- Cordonnier, M.N.; Dauzonne, D.; Louvard, D.; Coudrier, E. Actin filaments and myosin I alpha cooperate with microtubules for the movement of lysosomes. Mol. Biol. Cell 2001, 12, 4013–4029. [Google Scholar] [CrossRef]
- Balint, S.; Verdeny Vilanova, I.; Sandoval Alvarez, A.; Lakadamyali, M. Correlative live-cell and superresolution microscopy reveals cargo transport dynamics at microtubule intersections. Proc. Natl. Acad. Sci. USA 2013, 110, 3375–3380. [Google Scholar] [CrossRef]
- Caspi, A.; Granek, R.; Elbaum, M. Enhanced diffusion in active intracellular transport. Phys. Rev. Lett. 2000, 85, 5655–5658. [Google Scholar] [CrossRef]
- Mohan, N.; Sorokina, E.M.; Verdeny, I.V.; Alvarez, A.S.; Lakadamyali, M. Detyrosinated microtubules spatially constrain lysosomes facilitating lysosome-autophagosome fusion. J. Cell Biol. 2019, 218, 632–643. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Qian, H.; Sheetz, M.P.; Elson, E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991, 60, 910–921. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Huda, S.; Weigelin, B.; Wolf, K.; Tretiakov, K.V.; Polev, K.; Wilk, G.; Iwasa, M.; Emami, F.S.; Narojczyk, J.W.; Banaszak, M.; et al. Levy-like movement patterns of metastatic cancer cells revealed in microfabricated systems and implicated in vivo. Nat. Commun. 2018, 9, 4539. [Google Scholar] [CrossRef] [PubMed]
- Reynolds, A. Liberating Levy walk research from the shackles of optimal foraging. Phys. Life Rev. 2015, 14, 59–83. [Google Scholar] [CrossRef] [PubMed]
- Chen, K.; Wang, B.; Granick, S. Memoryless self-reinforcing directionality in endosomal active transport within living cells. Nat. Mater. 2015, 14, 589–593. [Google Scholar] [CrossRef] [PubMed]
- Fricke, G.M.; Letendre, K.A.; Moses, M.E.; Cannon, J.L. Persistence and Adaptation in Immunity: T Cells Balance the Extent and Thoroughness of Search. PLoS Comput. Biol. 2016, 12, e1004818. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Cyphersmith, A.; Zapata, J.A.; Kim, Y.J.; Payne, C.K. Lysosome transport as a function of lysosome diameter. PLoS ONE 2014, 9, e86847. [Google Scholar] [CrossRef]
- Bouzigues, C.; Dahan, M. Transient directed motions of GABA(A) receptors in growth cones detected by a speed correlation index. Biophys. J. 2007, 92, 654–660. [Google Scholar] [CrossRef]
- Huet, S.; Karatekin, E.; Tran, V.S.; Fanget, I.; Cribier, S.; Henry, J.P. Analysis of transient behavior in complex trajectories: Application to secretory vesicle dynamics. Biophys. J. 2006, 91, 3542–3559. [Google Scholar] [CrossRef]
- Arcizet, D.; Meier, B.; Sackmann, E.; Radler, J.O.; Heinrich, D. Temporal analysis of active and passive transport in living cells. Phys. Rev. Lett. 2008, 101, 248103. [Google Scholar] [CrossRef]
- Ahmed, W.W.; Williams, B.J.; Silver, A.M.; Saif, T.A. Measuring nonequilibrium vesicle dynamics in neurons under tension. Lab Chip 2013, 13, 570–578. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, Q.; Xia, M.; Feng, J.; Chen, Y.; Zhang, S.; Zhang, X. Characterize Collective Lysosome Heterogeneous Dynamics in Live Cell with a Space- and Time-Resolved Method. Anal. Chem. 2018, 90, 9138–9147. [Google Scholar] [CrossRef]
- Durso, W.; Martins, M.; Marchetti, L.; Cremisi, F.; Luin, S.; Cardarelli, F. Lysosome Dynamic Properties during Neuronal Stem Cell Differentiation Studied by Spatiotemporal Fluctuation Spectroscopy and Organelle Tracking. Int. J. Mol. Sci. 2020, 21, 3397. [Google Scholar] [CrossRef]
- Marchetti, L.; Callegari, A.; Luin, S.; Signore, G.; Viegi, A.; Beltram, F.; Cattaneo, A. Ligand signature in the membrane dynamics of single TrkA receptor molecules. J. Cell Sci. 2013, 126, 4445–4456. [Google Scholar] [CrossRef]
- Han, D.; Korabel, N.; Chen, R.; Johnston, M.; Gavrilova, A.; Allan, V.J.; Fedotov, S.; Waigh, T.A. Deciphering anomalous heterogeneous intracellular transport with neural networks. eLife 2020, 9, e52224. [Google Scholar] [CrossRef]
- Chen, K.; Wang, B.; Guan, J.; Granick, S. Diagnosing heterogeneous dynamics in single-molecule/particle trajectories with multiscale wavelets. ACS Nano 2013, 7, 8634–8644. [Google Scholar] [CrossRef]
- Koslover, E.F.; Chan, C.K.; Theriot, J.A. Disentangling Random Motion and Flow in a Complex Medium. Biophys. J. 2016, 110, 700–709. [Google Scholar] [CrossRef][Green Version]
- Borkowska, M.; Siek, M.; Kolygina, D.V.; Sobolev, Y.I.; Lach, S.; Kumar, S.; Cho, Y.K.; Kandere-Grzybowska, K.; Grzybowski, B.A. Targeted crystallization of mixed-charge nanoparticles in lysosomes induces selective death of cancer cells. Nat. Nanotechnol. 2020, 15, 331–341. [Google Scholar] [CrossRef]
- Siek, M.; Kandere-Grzybowska, K.; Grzybowski, B.A. Mixed-Charge, pH-Responsive Nanoparticles for Selective Interactions with Cells, Organelles, and Bacteria. Acc. Mater. Res. 2020, 1, 188–200. [Google Scholar] [CrossRef]
- Rebecca, V.W.; Nicastri, M.C.; McLaughlin, N.; Fennelly, C.; McAfee, Q.; Ronghe, A.; Nofal, M.; Lim, C.Y.; Witze, E.; Chude, C.I.; et al. A Unified Approach to Targeting the Lysosome’s Degradative and Growth Signaling Roles. Cancer Discov. 2017, 7, 1266–1283. [Google Scholar] [CrossRef]
- Petersen, N.H.; Olsen, O.D.; Groth-Pedersen, L.; Ellegaard, A.M.; Bilgin, M.; Redmer, S.; Ostenfeld, M.S.; Ulanet, D.; Dovmark, T.H.; Lonborg, A.; et al. Transformation-associated changes in sphingolipid metabolism sensitize cells to lysosomal cell death induced by inhibitors of acid sphingomyelinase. Cancer Cell 2013, 24, 379–393. [Google Scholar] [CrossRef]
- Pillai, P.P.; Kowalczyk, B.; Kandere-Grzybowska, K.; Borkowska, M.; Grzybowski, B.A. Engineering Gram Selectivity of Mixed-Charge Gold Nanoparticles by Tuning the Balance of Surface Charges. Angew. Chem. Int. Ed. Engl. 2016, 55, 8610–8614. [Google Scholar] [CrossRef]
- Pillai, P.P.; Huda, S.; Kowalczyk, B.; Grzybowski, B.A. Controlled pH stability and adjustable cellular uptake of mixed-charge nanoparticles. J. Am. Chem. Soc. 2013, 135, 6392–6395. [Google Scholar] [CrossRef]
- Maier, O.; Marvin, S.A.; Wodrich, H.; Campbell, E.M.; Wiethoff, C.M. Spatiotemporal dynamics of adenovirus membrane rupture and endosomal escape. J. Virol. 2012, 86, 10821–10828. [Google Scholar] [CrossRef]
- Guo, Y.; Li, D.; Zhang, S.; Yang, Y.; Liu, J.J.; Wang, X.; Liu, C.; Milkie, D.E.; Moore, R.P.; Tulu, U.S.; et al. Visualizing Intracellular Organelle and Cytoskeletal Interactions at Nanoscale Resolution on Millisecond Timescales. Cell 2018, 175, 1430–1442. [Google Scholar] [CrossRef]
- Liao, Y.C.; Fernandopulle, M.S.; Wang, G.; Choi, H.; Hao, L.; Drerup, C.M.; Patel, R.; Qamar, S.; Nixon-Abell, J.; Shen, Y.; et al. RNA granules hitchhike on lysosomes for long-distance transport, using annexin A11 as a molecular tether. Cell 2019, 179, 147–164. [Google Scholar] [CrossRef]
- Mogre, S.S.; Christensen, J.R.; Niman, C.S.; Reck-Peterson, S.L.; Koslover, E.F. Hitching a Ride: Mechanics of Transport Initiation through Linker-Mediated Hitchhiking. Biophys. J. 2020, 118, 1357–1369. [Google Scholar] [CrossRef]
- Kolygina, D.V.; Siek, M.; Borkowska, M.; Ahumada, G.; Barski, P.; Witt, D.; Jee, A.Y.; Miao, H.; Ahumada, J.C.; Granick, S.; et al. Mixed-Charge Nanocarriers Allow for Selective Targeting of Mitochondria by Otherwise Nonselective Dyes. ACS Nano 2021, 15, 11470–11490. [Google Scholar] [CrossRef]
- de Jager, M.; Weissing, F.J.; Herman, P.M.; Nolet, B.A.; van de Koppel, J. Levy walks evolve through interaction between movement and environmental complexity. Science 2011, 332, 1551–1553. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- Alstott, J.; Bullmore, E.; Plenz, D. Powerlaw: A Python package for analysis of heavy-tailed distributions. PLoS ONE 2014, 9, e85777. [Google Scholar] [CrossRef]
- Mrass, P.; Oruganti, S.R.; Fricke, G.M.; Tafoya, J.; Byrum, J.R.; Yang, L.; Hamilton, S.L.; Miller, M.J.; Moses, M.E.; Cannon, J.L. ROCK regulates the intermittent mode of interstitial T cell migration in inflamed lungs. Nat. Commun. 2017, 8, 1010. [Google Scholar] [CrossRef]
- Davidson, S.M.; Vander Heiden, M.G. Critical Functions of the Lysosome in Cancer Biology. Annu. Rev. Pharm. Toxicol. 2017, 57, 481–507. [Google Scholar] [CrossRef]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal distributions across the sciences: Keys and clues. Bioscience 2001, 51, 341–352. [Google Scholar] [CrossRef]
- Gunning, C.E.; Wearing, H.J. Probabilistic measures of persistence and extinction in measles (meta)populations. Ecol. Lett. 2013, 16, 985–994. [Google Scholar] [CrossRef]
- Klafter, J.; Blumen, A.; Shlesinger, M.F. Stochastic pathway to anomalous diffusion. Phys. Rev. A Gen. Phys. 1987, 35, 3081–3085. [Google Scholar] [CrossRef]
- Hao, H.; Niu, J.; Xue, B.; Su, Q.P.; Liu, M.; Yang, J.; Qin, J.; Zhao, S.; Wu, C.; Sun, Y. Golgi-associated microtubules are fast cargo tracks and required for persistent cell migration. EMBO Rep. 2020, 21, e48385. [Google Scholar] [CrossRef]
- Wadsworth, P.; McGrail, M. Interphase microtubule dynamics are cell type-specific. J. Cell Sci. 1990, 95, 23–32. [Google Scholar] [CrossRef]
- Shelden, E.; Wadsworth, P. Observation and quantification of individual microtubule behavior in vivo: Microtubule dynamics are cell-type specific. J. Cell Biol. 1993, 120, 935–945. [Google Scholar] [CrossRef]
- Schulze, E.; Kirschner, M. New features of microtubule behaviour observed in vivo. Nature 1988, 334, 356–359. [Google Scholar] [CrossRef]
- Cai, D.W.; McEwen, D.P.; Martens, J.R.; Meyhofer, E.; Verhey, K.J. Single Molecule Imaging Reveals Differences in Microtubule Track Selection Between Kinesin Motors. PLoS Biol. 2009, 7, e1000216. [Google Scholar] [CrossRef]
- De Pace, R.; Britt, D.J.; Mercurio, J.; Foster, A.M.; Djavaherian, L.; Hoffmann, V.; Abebe, D.; Bonifacino, J.S. Synaptic Vesicle Precursors and Lysosomes Are Transported by Different Mechanisms in the Axon of Mammalian Neurons. Cell Rep. 2020, 31, 107775. [Google Scholar] [CrossRef]
- Verdeny-Vilanova, I.; Wehnekamp, F.; Mohan, N.; Sandoval Alvarez, A.; Borbely, J.S.; Otterstrom, J.J.; Lamb, D.C.; Lakadamyali, M. 3D motion of vesicles along microtubules helps them to circumvent obstacles in cells. J. Cell Sci. 2017, 130, 1904–1916. [Google Scholar] [CrossRef]
- Kamata, H.; Tsukasaki, Y.; Sakai, T.; Ikebe, R.; Wang, J.; Jeffers, A.; Boren, J.; Owens, S.; Suzuki, T.; Higashihara, M.; et al. KIF5A transports collagen vesicles of myofibroblasts during pleural fibrosis. Sci. Rep. 2017, 7, 4556. [Google Scholar] [CrossRef]
- Varela, J.A.; Aberg, C.; Simpson, J.C.; Dawson, K.A. Trajectory-based co-localization measures for nanoparticle-cell interaction studies. Small 2015, 11, 2026–2031. [Google Scholar] [CrossRef]
- Kang, K.A.; Wang, J.; Jasinski, J.B.; Achilefu, S. Fluorescence manipulation by gold nanoparticles: From complete quenching to extensive enhancement. J. Nanobiotechnol. 2011, 9, 16. [Google Scholar] [CrossRef]
- Quiroga, R.Q.; Nadasdy, Z.; Ben-Shaul, Y. Unsupervised spike detection and sorting with wavelets and superparamagnetic clustering. Neural Comput. 2004, 16, 1661–1687. [Google Scholar] [CrossRef]
- Clemson, P.; Lancaster, G.; Stefanovska, A. Reconstructing Time-Dependent Dynamics. Proc. IEEE 2016, 104, 223–241. [Google Scholar] [CrossRef]
- Ivanov, P.C.; Rosenblum, M.G.; Peng, C.K.; Mietus, J.; Havlin, S.; Stanley, H.E.; Goldberger, A.L. Scaling behaviour of heartbeat intervals obtained by wavelet-based time-series analysis. Nature 1996, 383, 323–327. [Google Scholar] [CrossRef]
- Yang, H. Detection and characterization of dynamical heterogeneity in an event series using wavelet correlation. J. Chem. Phys. 2008, 129, 074701. [Google Scholar] [CrossRef]
- Chavez, M.; Cazelles, B. Detecting dynamic spatial correlation patterns with generalized wavelet coherence and non-stationary surrogate data. Sci. Rep. 2019, 9, 7389. [Google Scholar] [CrossRef]
- Skidmore, F.; Korenkevych, D.; Liu, Y.; He, G.; Bullmore, E.; Pardalos, P.M. Connectivity brain networks based on wavelet correlation analysis in Parkinson fMRI data. NeuroSci. Lett. 2011, 499, 47–51. [Google Scholar] [CrossRef]
- Vacha, L.; Barunik, J. Co-movement of energy commodities revisited: Evidence from wavelet coherence analysis. Energy Econ. 2012, 34, 241–247. [Google Scholar] [CrossRef]
- Huang, S.P.; An, H.Z.; Gao, X.Y.; Huang, X. Time-frequency featured co-movement between the stock and prices of crude oil and gold. Phys. A 2016, 444, 985–995. [Google Scholar] [CrossRef]
- Shang, S.; Ding, R.; Zheng, K.; Jensen, C.S.; Kalnis, P.; Zhou, X. Personalized trajectory matching in spatial networks. VLDB J. 2013, 23, 449–468. [Google Scholar] [CrossRef]
- Guggenheim, E.J.; Khan, A.; Pike, J.; Chang, L.; Lynch, I.; Rappoport, J.Z. Comparison of Confocal and Super-Resolution Reflectance Imaging of Metal Oxide Nanoparticles. PLoS ONE 2016, 11, e0159980. [Google Scholar] [CrossRef]
- Liu, M.; Wang, F.; Zhang, X.; Mao, X.; Wang, L.; Tian, Y.; Fan, C.; Li, Q. Tracking endocytosis and intracellular distribution of spherical nucleic acids with correlative single-cell imaging. Nat. Protoc. 2021, 16, 383–404. [Google Scholar] [CrossRef]
- Korolchuk, V.I.; Saiki, S.; Lichtenberg, M.; Siddiqi, F.H.; Roberts, E.A.; Imarisio, S.; Jahreiss, L.; Sarkar, S.; Futter, M.; Menzies, F.M.; et al. Lysosomal positioning coordinates cellular nutrient responses. Nat. Cell Biol. 2011, 13, 453–460. [Google Scholar] [CrossRef]
| Cell Type | MSD (a) | D (μm2/s) | Fit Parameters | Akaike Weights | ||||
|---|---|---|---|---|---|---|---|---|
| LN | P | TP | SE | E | ||||
| MCF-10A | 1.29 ± 0.05 | 0.022 ± 0.004 | Runs: μ = −0.193; σ = 0.804 Flights: λ = 0.840; β = 1.037 | 1 0 | 0 <0.01 | <0.01 <0.01 | <0.01 0.83 | <0.01 0.17 |
| MDA-MB-231 | 1.31 ± 0.05 | 0.029 ± 0.006 | Runs: μ = −0.147; σ = 0.833 Flights: μ = 0.028; σ = 0.838 | 0.99 1 | <0.01 <0.01 | <0.01 <0.01 | <0.01 <0.01 | <0.01 <0.01 |
| MCF-7 | 1.35 ± 0.04 | 0.029 ± 0.010 | Runs: μ = −0.013; σ = 0.834 Flights: μ = 0.151; σ = 0.838 | 1 1 | 0 0 | 0 <0.01 | <0.01 <0.01 | <0.01 <0.01 |
| MEF | 1.36 ± 0.09 | 0.018 ± 0.003 | Runs: μ = −0.175; σ = 0.856 Flights: μ = −0.155; σ = 0.929 | 1 0.99 | 0 0 | <0.01 <0.01 | <0.01 <0.01 | <0.01 <0.01 |
| HT-1080 | 1.34 ± 0.06 | 0.015 ± 0.003 | Runs: μ = −0.183; σ = 0.802 Flights: μ = −0.019; σ = 0.829 | 1 1 | 0 0 | 0 0 | <0.01 <0.01 | <0.01 <0.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polev, K.; Kolygina, D.V.; Kandere-Grzybowska, K.; Grzybowski, B.A. Large-Scale, Wavelet-Based Analysis of Lysosomal Trajectories and Co-Movements of Lysosomes with Nanoparticle Cargos. Cells 2022, 11, 270. https://doi.org/10.3390/cells11020270
Polev K, Kolygina DV, Kandere-Grzybowska K, Grzybowski BA. Large-Scale, Wavelet-Based Analysis of Lysosomal Trajectories and Co-Movements of Lysosomes with Nanoparticle Cargos. Cells. 2022; 11(2):270. https://doi.org/10.3390/cells11020270
Chicago/Turabian StylePolev, Konstantin, Diana V. Kolygina, Kristiana Kandere-Grzybowska, and Bartosz A. Grzybowski. 2022. "Large-Scale, Wavelet-Based Analysis of Lysosomal Trajectories and Co-Movements of Lysosomes with Nanoparticle Cargos" Cells 11, no. 2: 270. https://doi.org/10.3390/cells11020270
APA StylePolev, K., Kolygina, D. V., Kandere-Grzybowska, K., & Grzybowski, B. A. (2022). Large-Scale, Wavelet-Based Analysis of Lysosomal Trajectories and Co-Movements of Lysosomes with Nanoparticle Cargos. Cells, 11(2), 270. https://doi.org/10.3390/cells11020270







