Skin under Strain: From Epithelial Model Tissues to Adult Epithelia
Abstract
1. Introduction
2. Materials and Methods
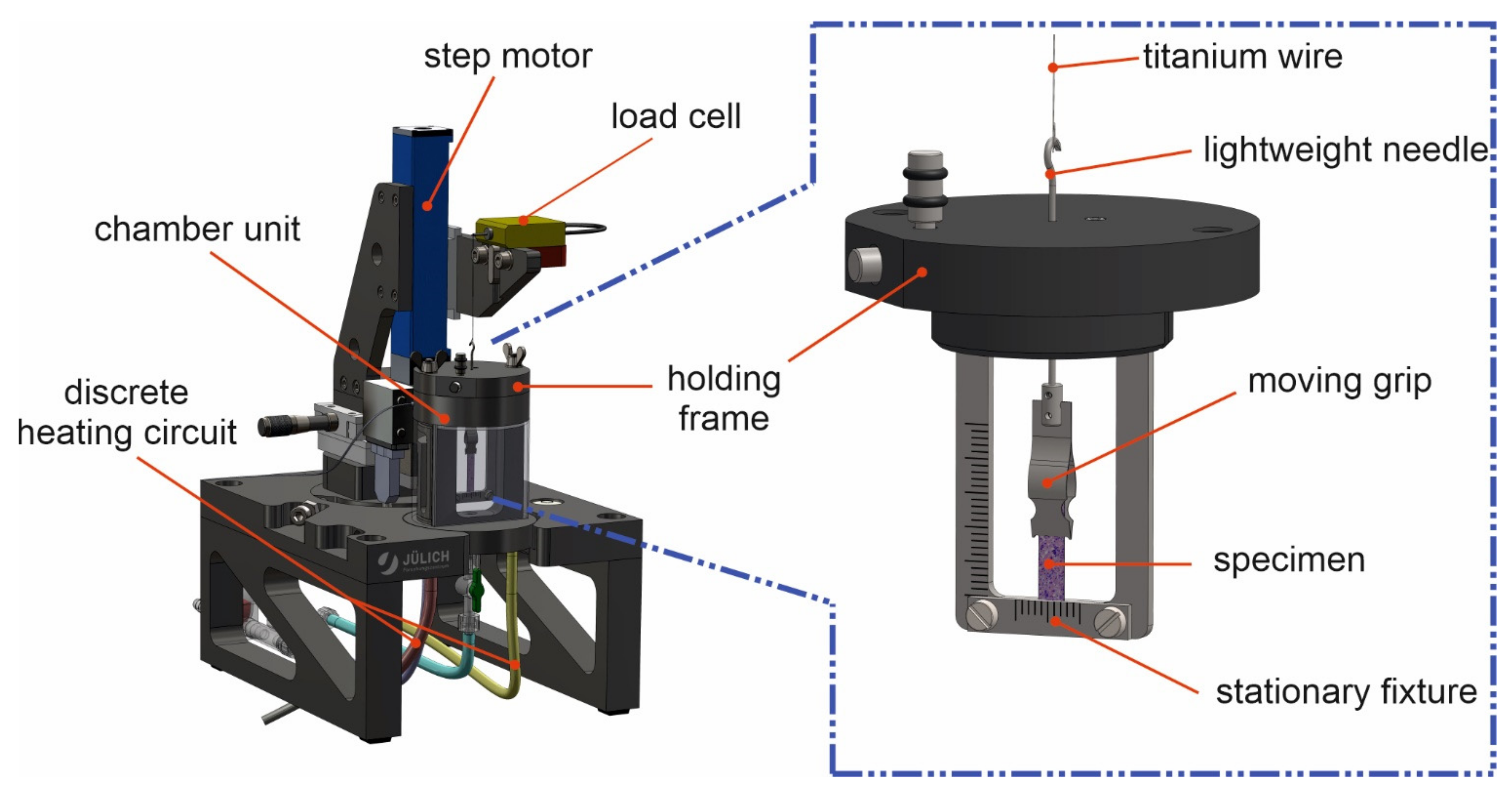
2.1. Tissue Stretcher Design
2.2. Tissue Stretcher Calibration
2.3. Tissue Stretcher Noise Characterization
2.4. Generation of a Simplified Epidermis Equivalent (SEEs) as Multilayered Model System
2.5. Preparation of Ex Vivo Full-Thickness Back Skin Explants from Fetal and Adult Rats
2.6. Tissue Thickness Determination
2.7. Tissue Stretch Protocol and Data Analysis
2.8. Viability Assays of Fetal Rat Skin and SEEs
2.9. Data Analysis
3. Results
3.1. Experimental Setup Development for Sensitive Tensile Measurements of Living Samples
3.2. Tested Tissues Differ in Complexity, Maturation and Composition
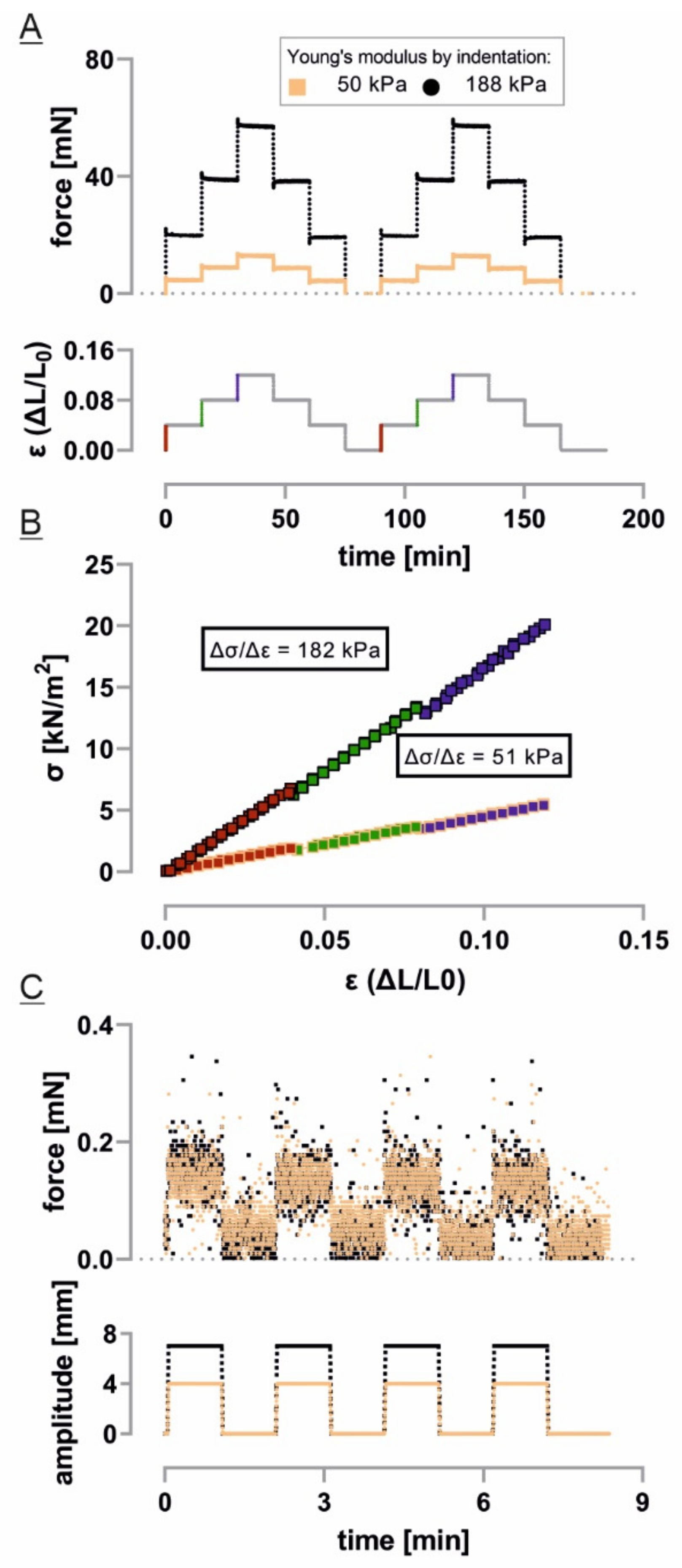
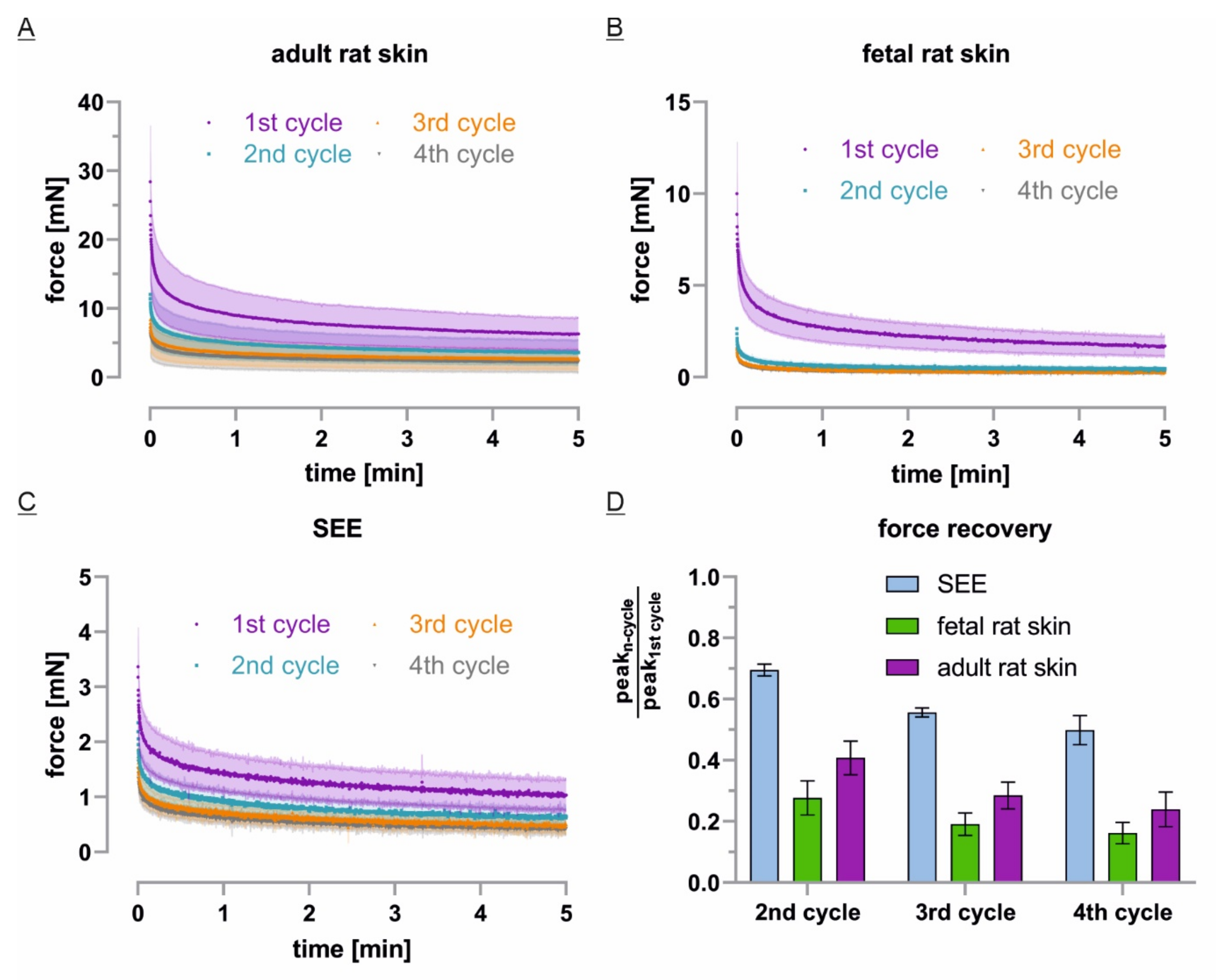
3.3. Static Stretch Shows Viscoelastic and Plastic Properties and Indicates Partial Recovery
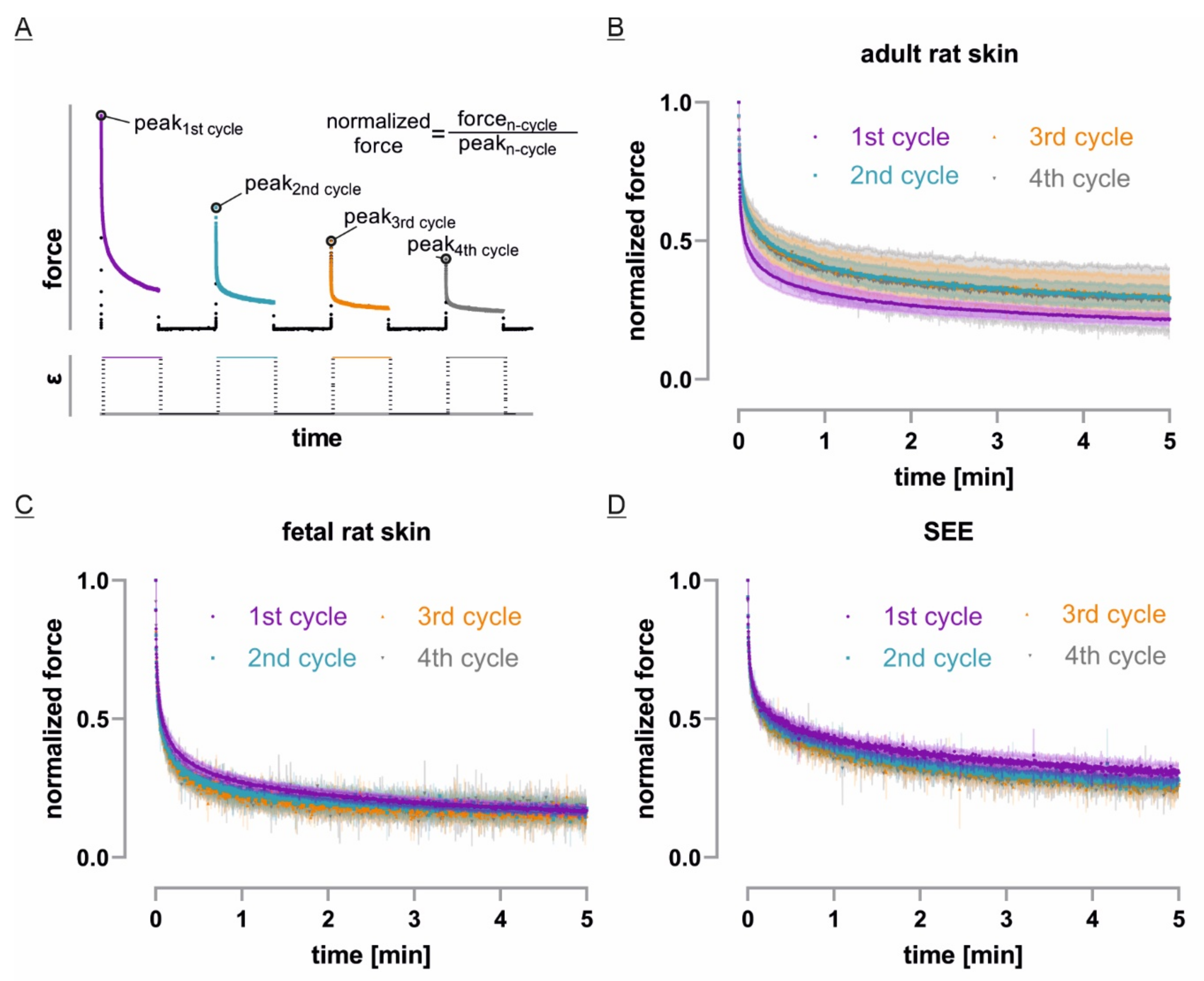
3.4. Only Adult Skin Differs in Relaxation Behavior between Initial and Repetitive Cycles
3.5. ECM-Free Epidermis Equivalents Recover Like Previously Stretched Tissue
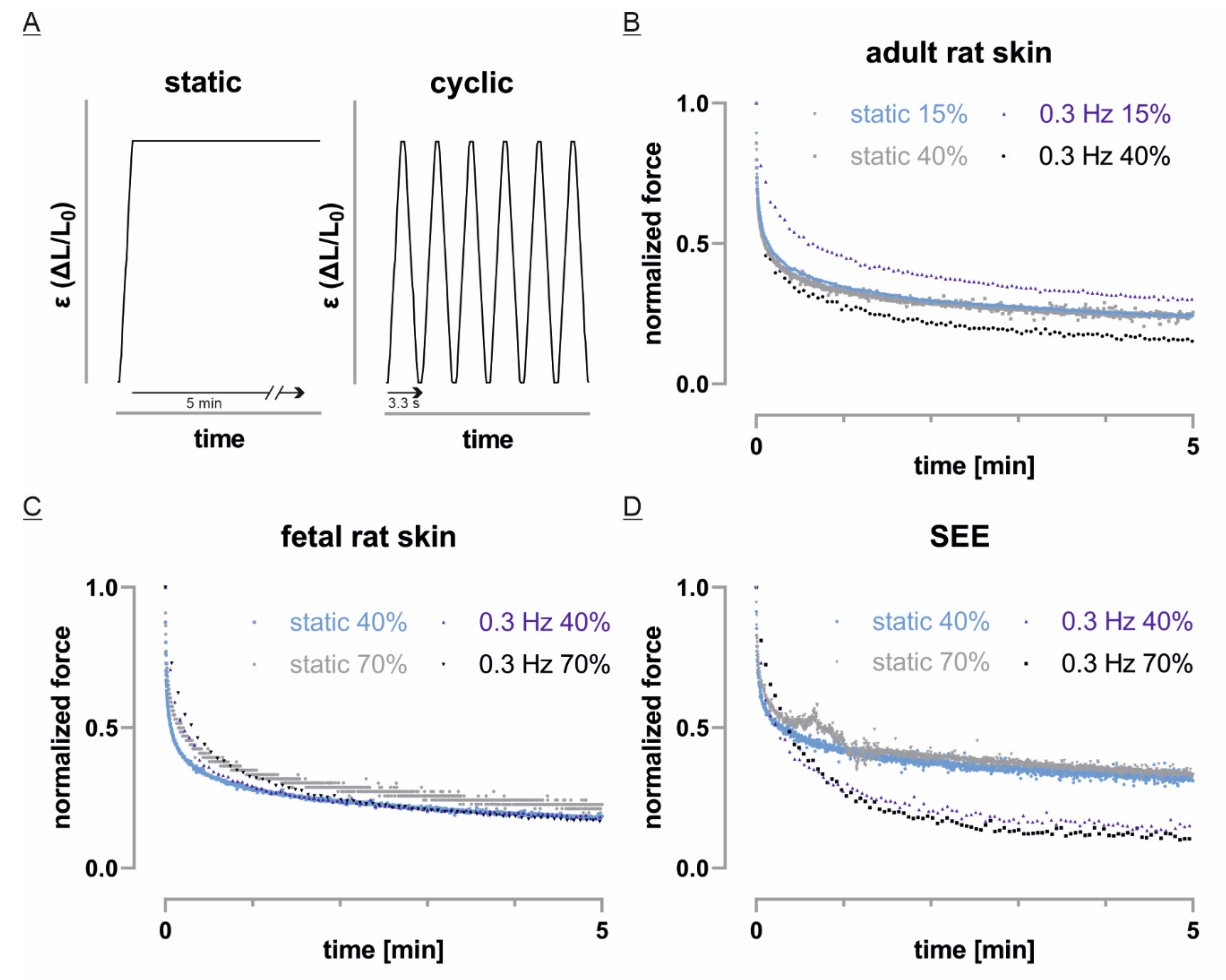
3.6. Fast Cyclic Strain Has a Tissue Dependent Impact on Force Relaxation
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wong, V.W.; Akaishi, S.; Longaker, M.T.; Gurtner, G.C. Pushing back: Wound mechanotransduction in repair and regeneration. J. Investig. Dermatol. 2011, 131, 2186–2196. [Google Scholar] [CrossRef]
- Simpson, C.L.; Patel, D.M.; Green, K.J. Deconstructing the skin: Cytoarchitectural determinants of epidermal morphogenesis. Nat. Rev. Mol. Cell Biol. 2011, 12, 565–580. [Google Scholar] [CrossRef]
- Wei, J.C.J.; Edwards, G.A.; Martin, D.J.; Huang, H.; Crichton, M.L.; Kendall, M.A.F. Allometric scaling of skin thickness, elasticity, viscoelasticity to mass for micro-medical device translation: From mice, rats, rabbits, pigs to humans. Sci. Rep. 2017, 7, 15885. [Google Scholar] [CrossRef]
- Fenske, N.A.; Lober, C.W. Structural and functional changes of normal aging skin. J. Am. Acad. Dermatol. 1986, 15, 571–585. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics: Mechanical Properties of Living Tissues; Online Resource (568 pages); Springer: New York, NY, USA, 1993; p. 1. [Google Scholar]
- Joodaki, H.; Panzer, M.B. Skin mechanical properties and modeling: A review. Proc. Inst. Mech. Eng. Part H 2018, 232, 323–343. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Yeung, K. The preconditioning and stress relaxation of skin tissue. J. Biomed. Eng. 2008, 2, 22–28. [Google Scholar]
- Ottenio, M.; Tran, D.; Ni Annaidh, A.; Gilchrist, M.D.; Bruyere, K. Strain rate and anisotropy effects on the tensile failure characteristics of human skin. J. Mech. Behav. Biomed. Mater. 2015, 41, 241–250. [Google Scholar] [CrossRef]
- Wong, W.L.; Joyce, T.J.; Goh, K.L. Resolving the viscoelasticity and anisotropy dependence of the mechanical properties of skin from a porcine model. Biomech. Model. Mechanobiol. 2016, 15, 433–446. [Google Scholar] [CrossRef]
- Ní Annaidh, A.; Bruyère, K.; Destrade, M.; Gilchrist, M.D.; Otténio, M. Characterization of the anisotropic mechanical properties of excised human skin. J. Mech. Behav. Biomed. Mater. 2012, 5, 139–148. [Google Scholar] [CrossRef]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Schaible, E.; Stewart, P.; Ritchie, R.O.; Meyers, M.A. On the tear resistance of skin. Nat. Commun. 2015, 6, 6649. [Google Scholar] [CrossRef]
- Ni Annaidh, A.; Bruyere, K.; Destrade, M.; Gilchrist, M.D.; Maurini, C.; Ottenio, M.; Saccomandi, G. Automated estimation of collagen fibre dispersion in the dermis and its contribution to the anisotropic behaviour of skin. Ann. Biomed. Eng. 2012, 40, 1666–1678. [Google Scholar] [CrossRef]
- Purslow, P.P.; Wess, T.J.; Hukins, D.W. Collagen orientation and molecular spacing during creep and stress-relaxation in soft connective tissues. J. Exp. Biol. 1998, 201, 135–142. [Google Scholar] [CrossRef] [PubMed]
- Eshel, H.; Lanir, Y. Effects of strain level and proteoglycan depletion on preconditioning and viscoelastic responses of rat dorsal skin. Ann. Biomed. Eng. 2001, 29, 164–172. [Google Scholar] [CrossRef] [PubMed]
- Coolen, N.A.; Schouten, K.C.; Middelkoop, E.; Ulrich, M.M. Comparison between human fetal and adult skin. Arch. Dermatol. Res. 2010, 302, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Chin, M.S.; Lancerotto, L.; Helm, D.L.; Dastouri, P.; Prsa, M.J.; Ottensmeyer, M.; Akaishi, S.; Orgill, D.P.; Ogawa, R. Analysis of neuropeptides in stretched skin. Plast. Reconstr. Surg. 2009, 124, 102–113. [Google Scholar] [CrossRef] [PubMed]
- Kumaraswamy, N.; Khatam, H.; Reece, G.P.; Fingeret, M.C.; Markey, M.K.; Ravi-Chandar, K. Mechanical response of human female breast skin under uniaxial stretching. J. Mech. Behav. Biomed. Mater. 2017, 74, 164–175. [Google Scholar] [CrossRef] [PubMed]
- Vogel, H.G.; Denkel, K. In vivo recovery of mechanical properties in rat skin after repeated strain. Arch. Dermatol. Res. 1985, 277, 484–488. [Google Scholar] [CrossRef] [PubMed]
- Kang, G.; Wu, X. Ratchetting of porcine skin under uniaxial cyclic loading. J. Mech. Behav. Biomed. Mater. 2011, 4, 498–506. [Google Scholar] [CrossRef]
- Munoz, M.J.; Bea, J.A.; Rodriguez, J.F.; Ochoa, I.; Grasa, J.; del Palomar, A.P.; Zaragoza, P.; Osta, R.; Doblare, M. An experimental study of the mouse skin behaviour: Damage and inelastic aspects. J. Biomech. 2008, 41, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Afsar-Kazerooni, N.; Srinivasa, A.R.; Criscione, J.C. Experimental Investigation of the Inelastic Response of Pig and Rat Skin Under Uniaxial Cyclic Mechanical Loading. Exp. Mech. 2020, 60, 535–551. [Google Scholar] [CrossRef]
- Jemec, G.B.; Serup, J. Epidermal hydration and skin mechanics. The relationship between electrical capacitance and the mechanical properties of human skin in vivo. Acta Derm. Venereol. 1990, 70, 245–247. [Google Scholar] [CrossRef]
- Hsu, C.K.; Lin, H.H.; Harn, H.I.; Hughes, M.W.; Tang, M.J.; Yang, C.C. Mechanical forces in skin disorders. J. Dermatol. Sci. 2018, 90, 232–240. [Google Scholar] [CrossRef] [PubMed]
- Werner, N.S.; Windoffer, R.; Strnad, P.; Grund, C.; Leube, R.E.; Magin, T.M. Epidermolysis bullosa simplex-type mutations alter the dynamics of the keratin cytoskeleton and reveal a contribution of actin to the transport of keratin subunits. Mol. Biol. Cell 2004, 15, 990–1002. [Google Scholar] [CrossRef] [PubMed]
- Cavanaugh, K.J., Jr.; Oswari, J.; Margulies, S.S. Role of stretch on tight junction structure in alveolar epithelial cells. Am. J. Respir. Cell Mol. Biol. 2001, 25, 584–591. [Google Scholar] [CrossRef]
- Rodrigues Neves, C.; Gibbs, S. Progress on Reconstructed Human Skin Models for Allergy Research and Identifying Contact Sensitizers. Curr. Top. Microbiol. Immunol. 2018. [Google Scholar] [CrossRef]
- Frankart, A.; Malaisse, J.; De Vuyst, E.; Minner, F.; de Rouvroit, C.L.; Poumay, Y. Epidermal morphogenesis during progressive in vitro 3D reconstruction at the air-liquid interface. Exp. Dermatol. 2012, 21, 871–875. [Google Scholar] [CrossRef]
- Monemian Esfahani, A.; Rosenbohm, J.; Reddy, K.; Jin, X.; Bouzid, T.; Riehl, B.; Kim, E.; Lim, J.Y.; Yang, R. Tissue Regeneration from Mechanical Stretching of Cell-Cell Adhesion. Tissue Eng. Part C Methods 2019, 25, 631–640. [Google Scholar] [CrossRef]
- Noethel, B.; Ramms, L.; Dreissen, G.; Hoffmann, M.; Springer, R.; Rubsam, M.; Ziegler, W.H.; Niessen, C.M.; Merkel, R.; Hoffmann, B. Transition of responsive mechanosensitive elements from focal adhesions to adherens junctions on epithelial differentiation. Mol. Biol. Cell 2018, 29, 2317–2325. [Google Scholar] [CrossRef]
- Faust, U.; Hampe, N.; Rubner, W.; Kirchgessner, N.; Safran, S.; Hoffmann, B.; Merkel, R. Cyclic stress at mHz frequencies aligns fibroblasts in direction of zero strain. PLoS ONE 2011, 6, e28963. [Google Scholar] [CrossRef] [PubMed]
- Merkel, R.; Kirchgessner, N.; Cesa, C.M.; Hoffmann, B. Cell force microscopy on elastic layers of finite thickness. Biophys. J. 2007, 93, 3314–3323. [Google Scholar] [CrossRef] [PubMed]
- Ulbricht, A.; Eppler, F.J.; Tapia, V.E.; van der Ven, P.F.; Hampe, N.; Hersch, N.; Vakeel, P.; Stadel, D.; Haas, A.; Saftig, P.; et al. Cellular mechanotransduction relies on tension-induced and chaperone-assisted autophagy. Curr. Biol. 2013, 23, 430–435. [Google Scholar] [CrossRef]
- Rubsam, M.; Mertz, A.F.; Kubo, A.; Marg, S.; Jungst, C.; Goranci-Buzhala, G.; Schauss, A.C.; Horsley, V.; Dufresne, E.R.; Moser, M.; et al. E-cadherin integrates mechanotransduction and EGFR signaling to control junctional tissue polarization and tight junction positioning. Nat. Commun. 2017, 8, 1250. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat Methods 2012, 9, 676–682. [Google Scholar] [CrossRef]
- Yap, A.S.; Duszyc, K.; Viasnoff, V. Mechanosensing and Mechanotransduction at Cell-Cell Junctions. Cold Spring Harb. Perspect. Biol. 2018, 10. [Google Scholar] [CrossRef] [PubMed]
- Pinheiro, D.; Bellaiche, Y. Mechanical Force-Driven Adherens Junction Remodeling and Epithelial Dynamics. Dev. Cell 2018, 47, 3–19. [Google Scholar] [CrossRef] [PubMed]
- Griffin, M.; Premakumar, Y.; Seifalian, A.; Butler, P.E.; Szarko, M. Biomechanical Characterization of Human Soft Tissues Using Indentation and Tensile Testing. J. Vis. Exp. 2016. [Google Scholar] [CrossRef]
- Cowin, S.C.; Doty, S.B. SpringerLink. Tissue Mechanics; 682 Online Resource; Springer: New York, NY, USA, 2007; p. XVI. [Google Scholar]
- Ehret, A.E.; Bircher, K.; Stracuzzi, A.; Marina, V.; Zundel, M.; Mazza, E. Inverse poroelasticity as a fundamental mechanism in biomechanics and mechanobiology. Nat. Commun. 2017, 8, 1002. [Google Scholar] [CrossRef] [PubMed]
- Bircher, K.; Zundel, M.; Pensalfini, M.; Ehret, A.E.; Mazza, E. Tear resistance of soft collagenous tissues. Nat. Commun. 2019, 10, 792. [Google Scholar] [CrossRef]
- Lokshin, O.; Lanir, Y. Viscoelasticity and preconditioning of rat skin under uniaxial stretch: Microstructural constitutive characterization. J. Biomech. Eng. 2009, 131, 031009. [Google Scholar] [CrossRef]
- Harada, K.; Enosawa, S.; Zhang, B.; Yuan, W.; Chiba, T.; Fujie, M.G. Evaluation of fetal tissue viscoelastic characteristics for robotic fetal surgery. Int. J. Comput. Assist. Radiol. Surg. 2011, 6, 797–802. [Google Scholar] [CrossRef] [PubMed]
- Tsubouchi, K.; Enosawa, S.; Harada, K.; Okamoto, J.; Fujie, M.G.; Chiba, T. Evaluation of the relationship between the viscoelastic stress and strain of fetal rat skin as a guide for designing the structure and dynamic performance of a manipulator for fetal surgery. Surg. Today 2006, 36, 701–706. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Moeendarbary, E.; Valon, L.; Fritzsche, M.; Harris, A.R.; Moulding, D.A.; Thrasher, A.J.; Stride, E.; Mahadevan, L.; Charras, G.T. The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 2013, 12, 253–261. [Google Scholar] [CrossRef]
- Lanir, Y.; Fung, Y.C. Two-dimensional mechanical properties of rabbit skin. II. Experimental results. J. Biomech. 1974, 7, 171–182. [Google Scholar] [CrossRef]
- Wyatt, T.P.J.; Fouchard, J.; Lisica, A.; Khalilgharibi, N.; Baum, B.; Recho, P.; Kabla, A.J.; Charras, G.T. Actomyosin controls planarity and folding of epithelia in response to compression. Nat. Mater. 2020, 19, 109–117. [Google Scholar] [CrossRef]
- Khalilgharibi, N.; Fouchard, J.; Asadipour, N.; Barrientos, R.; Duda, M.; Bonfanti, A.; Yonis, A.; Harris, A.; Mosaffa, P.; Fujita, Y.; et al. Stress relaxation in epithelial monolayers is controlled by the actomyosin cortex. Nat. Phys. 2019, 15, 839–847. [Google Scholar] [CrossRef] [PubMed]
- Remache, D.; Caliez, M.; Gratton, M.; Dos Santos, S. The effects of cyclic tensile and stress-relaxation tests on porcine skin. J. Mech. Behav. Biomed. Mater. 2018, 77, 242–249. [Google Scholar] [CrossRef]
- Zielinski, A.; Linnartz, C.; Pleschka, C.; Dreissen, G.; Springer, R.; Merkel, R.; Hoffmann, B. Reorientation dynamics and structural interdependencies of actin, microtubules and intermediate filaments upon cyclic stretch application. Cytoskeleton 2018, 75, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Harris, A.R.; Peter, L.; Bellis, J.; Baum, B.; Kabla, A.J.; Charras, G.T. Characterizing the mechanics of cultured cell monolayers. Proc. Natl. Acad. Sci. USA 2012, 109, 16449–16454. [Google Scholar] [CrossRef]
- Springer, R.; Zielinski, A.; Pleschka, C.; Hoffmann, B.; Merkel, R. Unbiased pattern analysis reveals highly diverse responses of cytoskeletal systems to cyclic straining. PLoS ONE 2019, 14, e0210570. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Püllen, R.; Konrad, J.; Merkel, R.; Hoffmann, B. Skin under Strain: From Epithelial Model Tissues to Adult Epithelia. Cells 2021, 10, 1834. https://doi.org/10.3390/cells10071834
Püllen R, Konrad J, Merkel R, Hoffmann B. Skin under Strain: From Epithelial Model Tissues to Adult Epithelia. Cells. 2021; 10(7):1834. https://doi.org/10.3390/cells10071834
Chicago/Turabian StylePüllen, Robin, Jens Konrad, Rudolf Merkel, and Bernd Hoffmann. 2021. "Skin under Strain: From Epithelial Model Tissues to Adult Epithelia" Cells 10, no. 7: 1834. https://doi.org/10.3390/cells10071834
APA StylePüllen, R., Konrad, J., Merkel, R., & Hoffmann, B. (2021). Skin under Strain: From Epithelial Model Tissues to Adult Epithelia. Cells, 10(7), 1834. https://doi.org/10.3390/cells10071834





