Deciphering the Genetic Architecture of Plant Virus Resistance by GWAS, State of the Art and Potential Advances
Abstract
1. Introduction
2. Mapping QTLs via GWAS Using Historical Recombinations
3. The Pre-GWAS Step: Assembled Diversity Panel That Is Genetically and Phenotypically Diverse
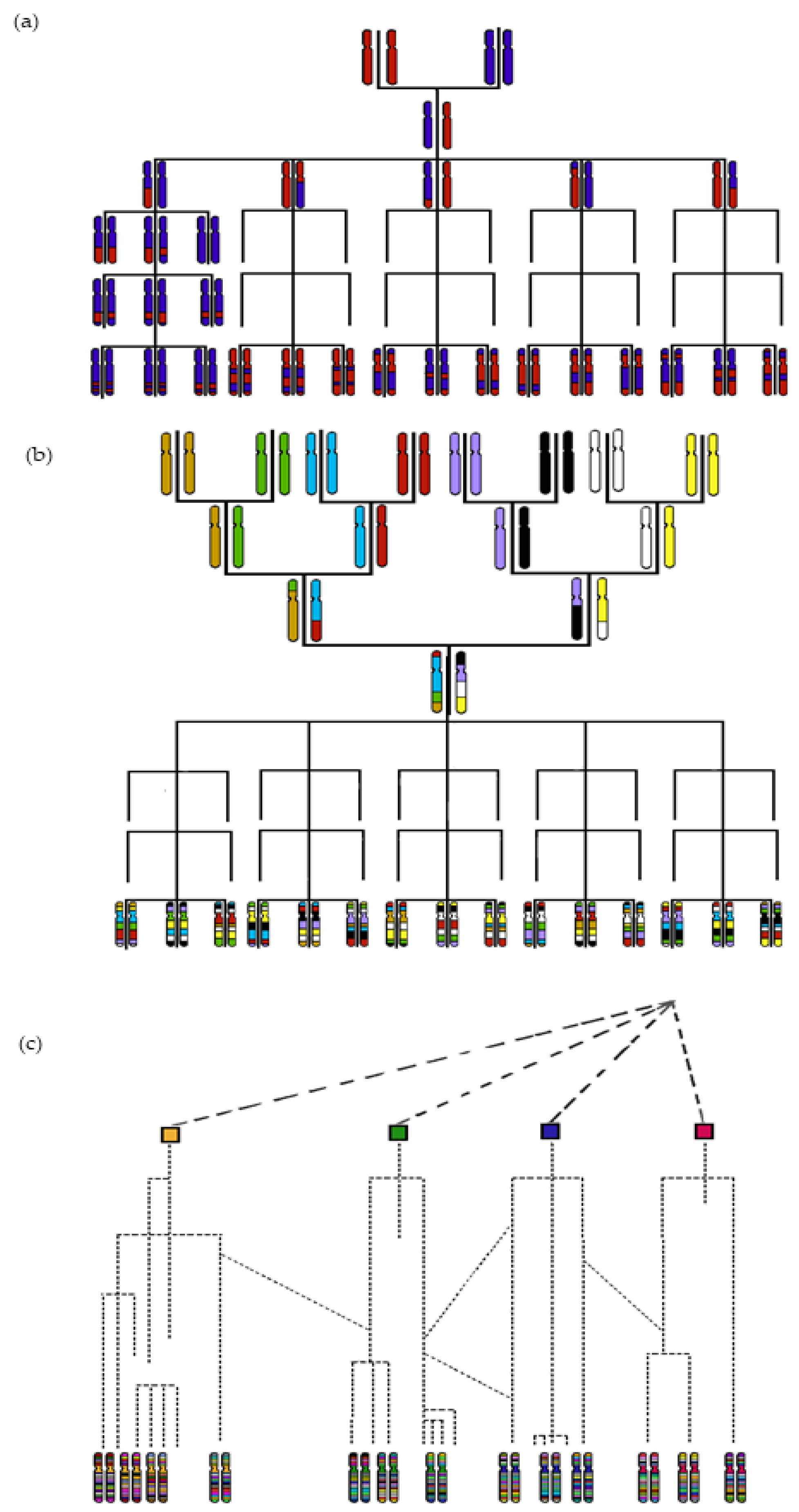
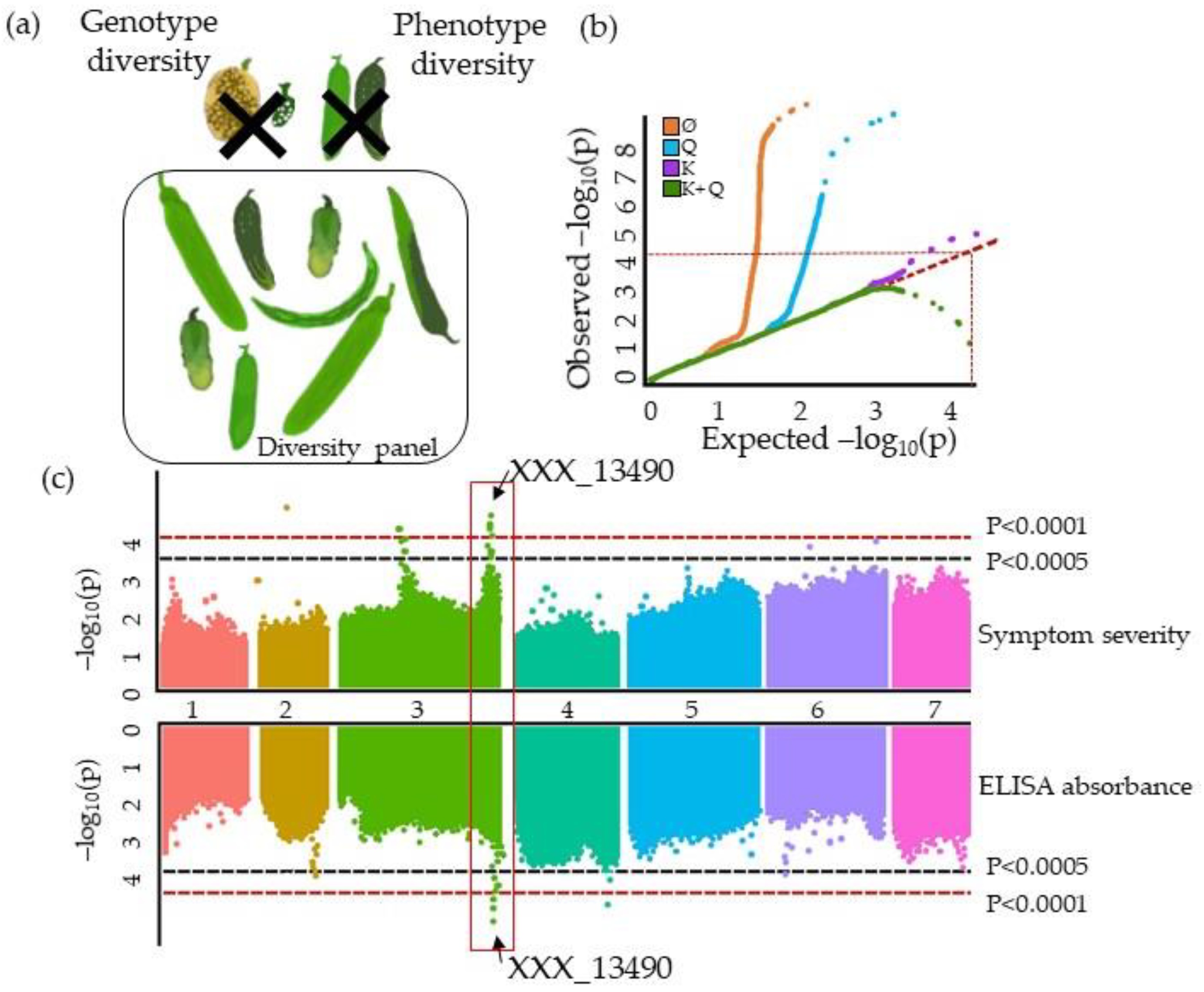
3.1. The GWAS Panel Composition Plays a Major Role in GWAS
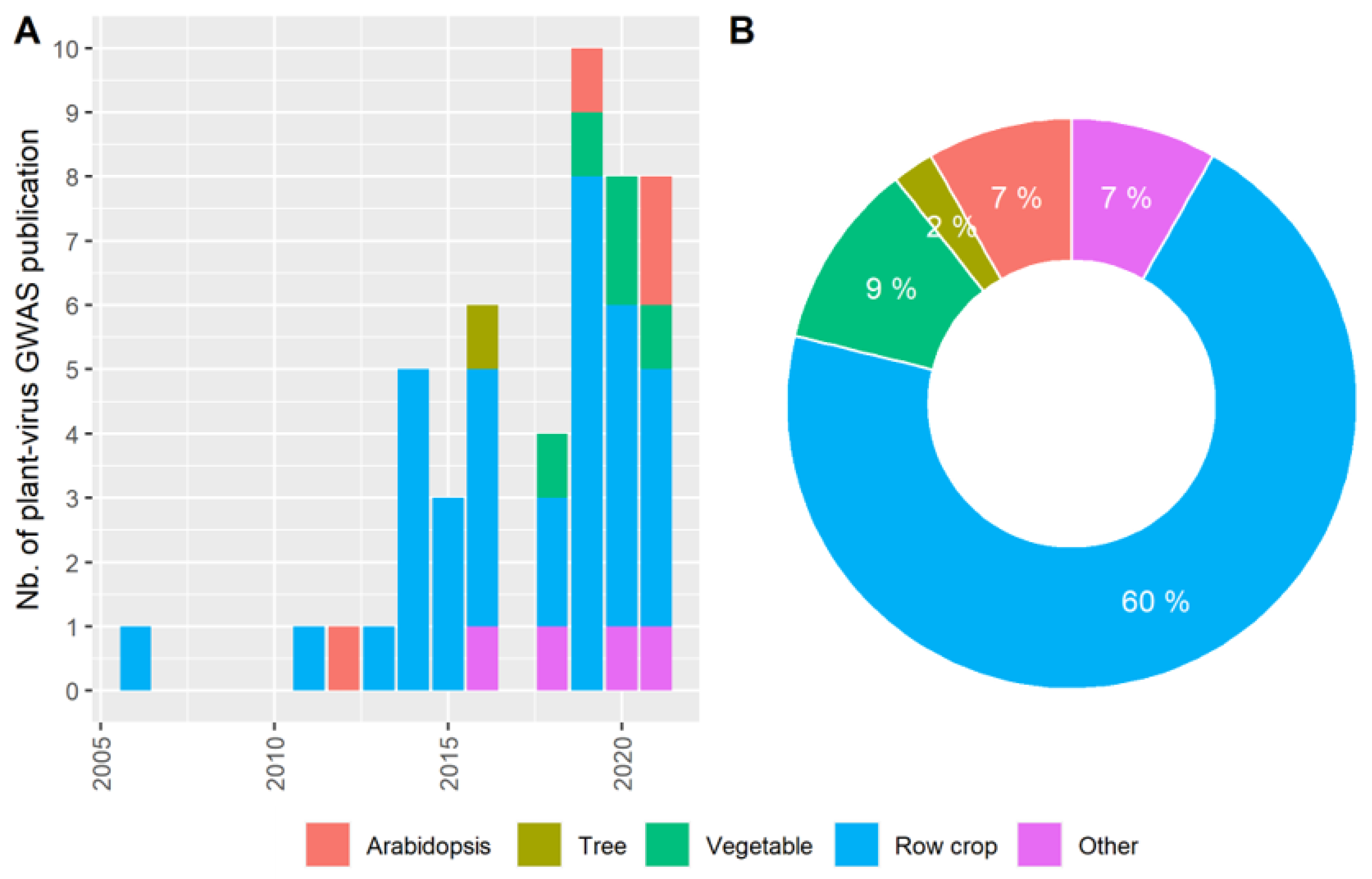
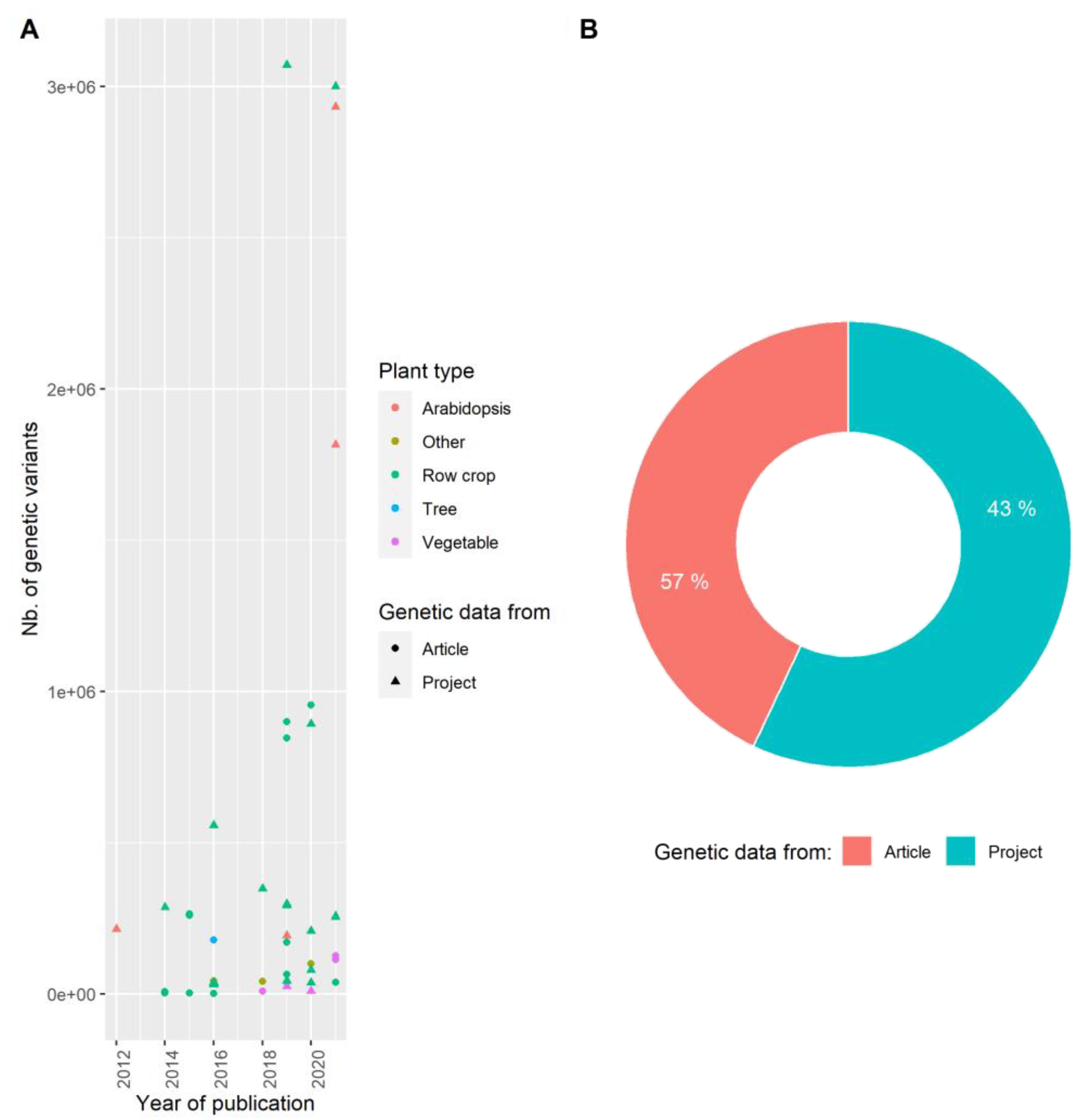
3.2. Producing Genetic Variant Array to Enhance Positive Association Detection: A New Deal for GWAS
3.3. Examining Resistance Distributions among Genetic Groups of the Panel
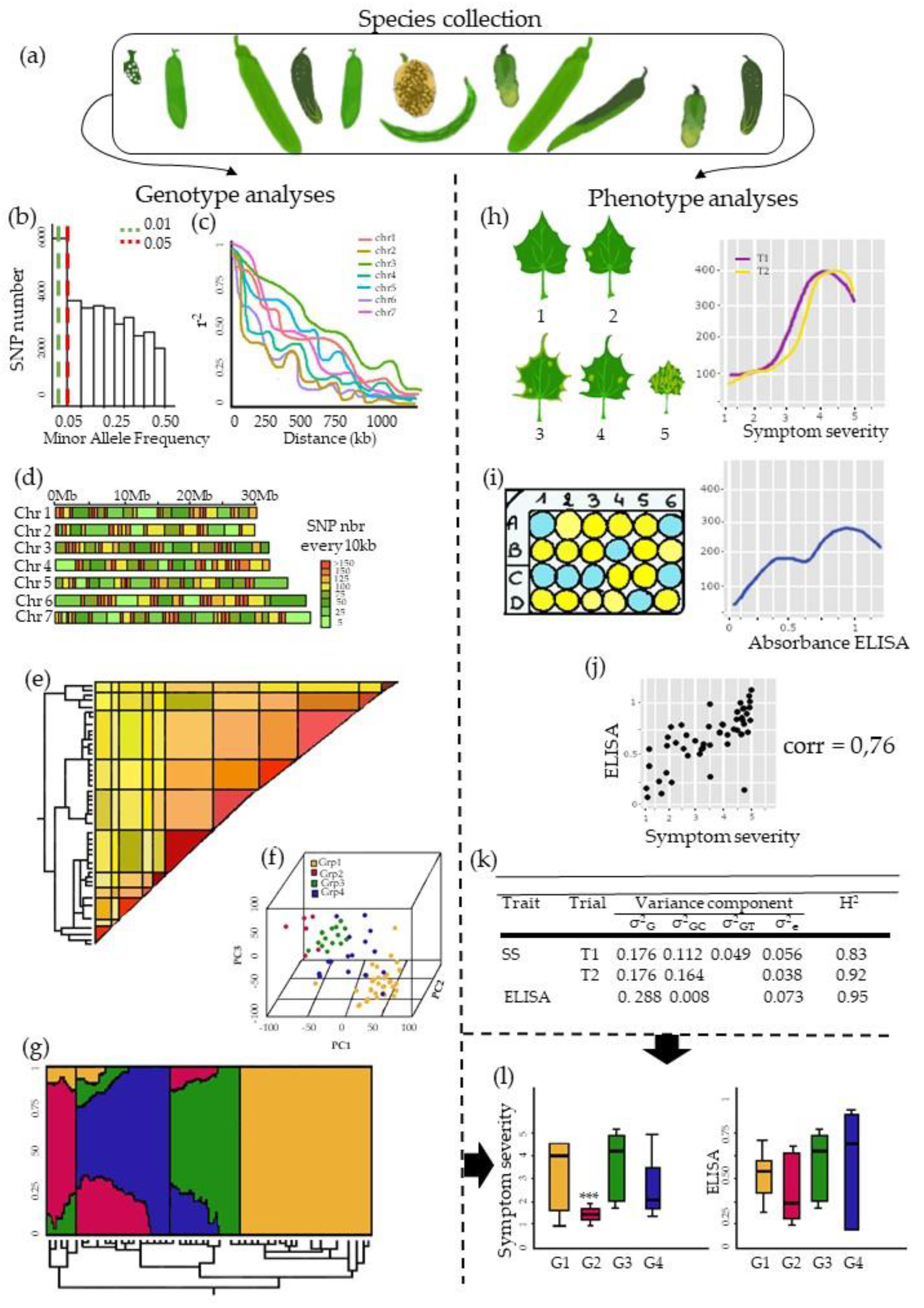
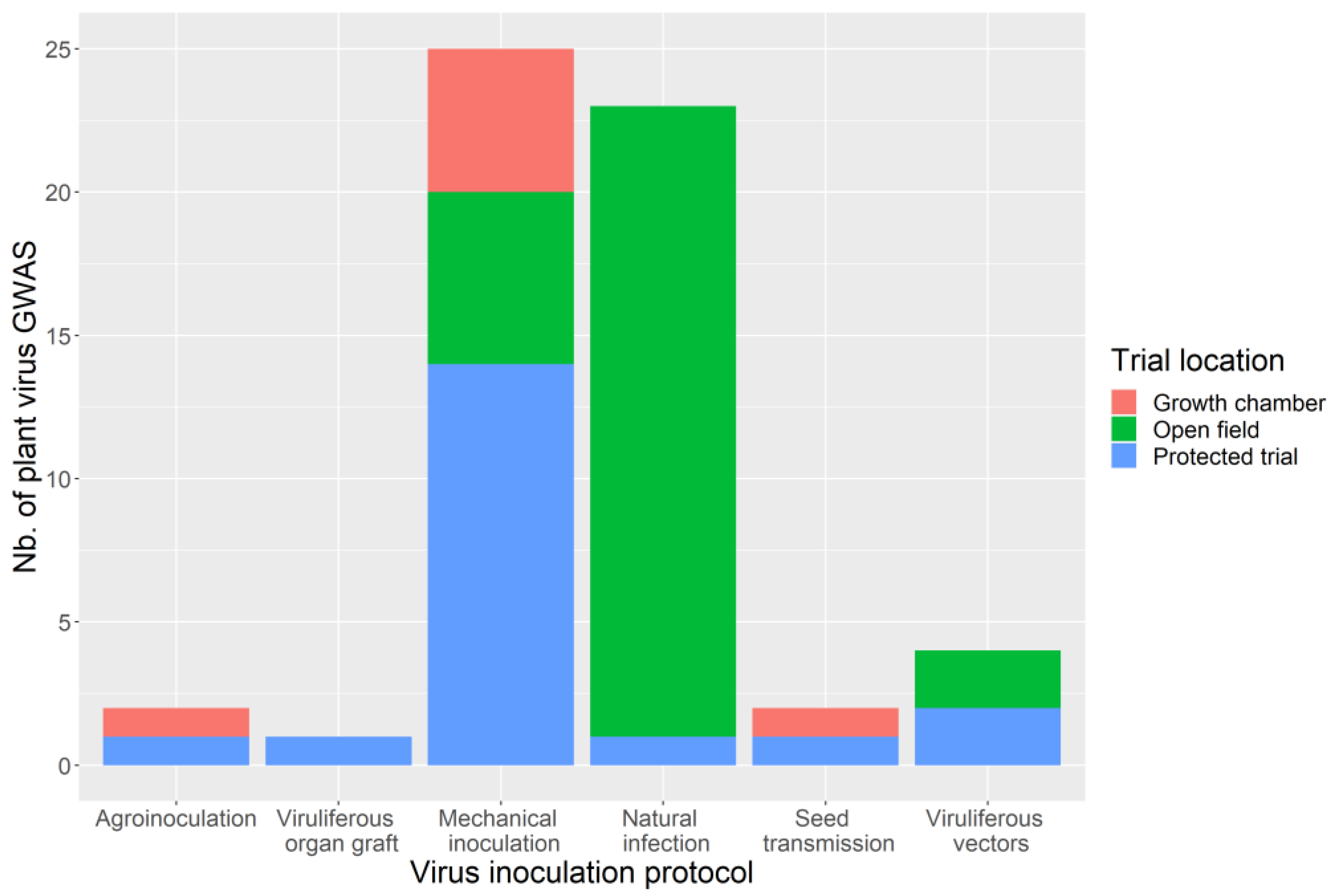
3.4. Phenotyping: Tricky Steps for a Powerful GWAS
4. The GWAS Step: Choosing a Model Tailored for the Datasets
4.1. Linear Mixed Models (LMM) Are the Most Used in GWAS
4.2. Multilocus Models in GWAS: Detecting Markers Hidden by Major Effect QTLs
4.3. Other Models That Are More Tailored to Virus Phenotype Distributions
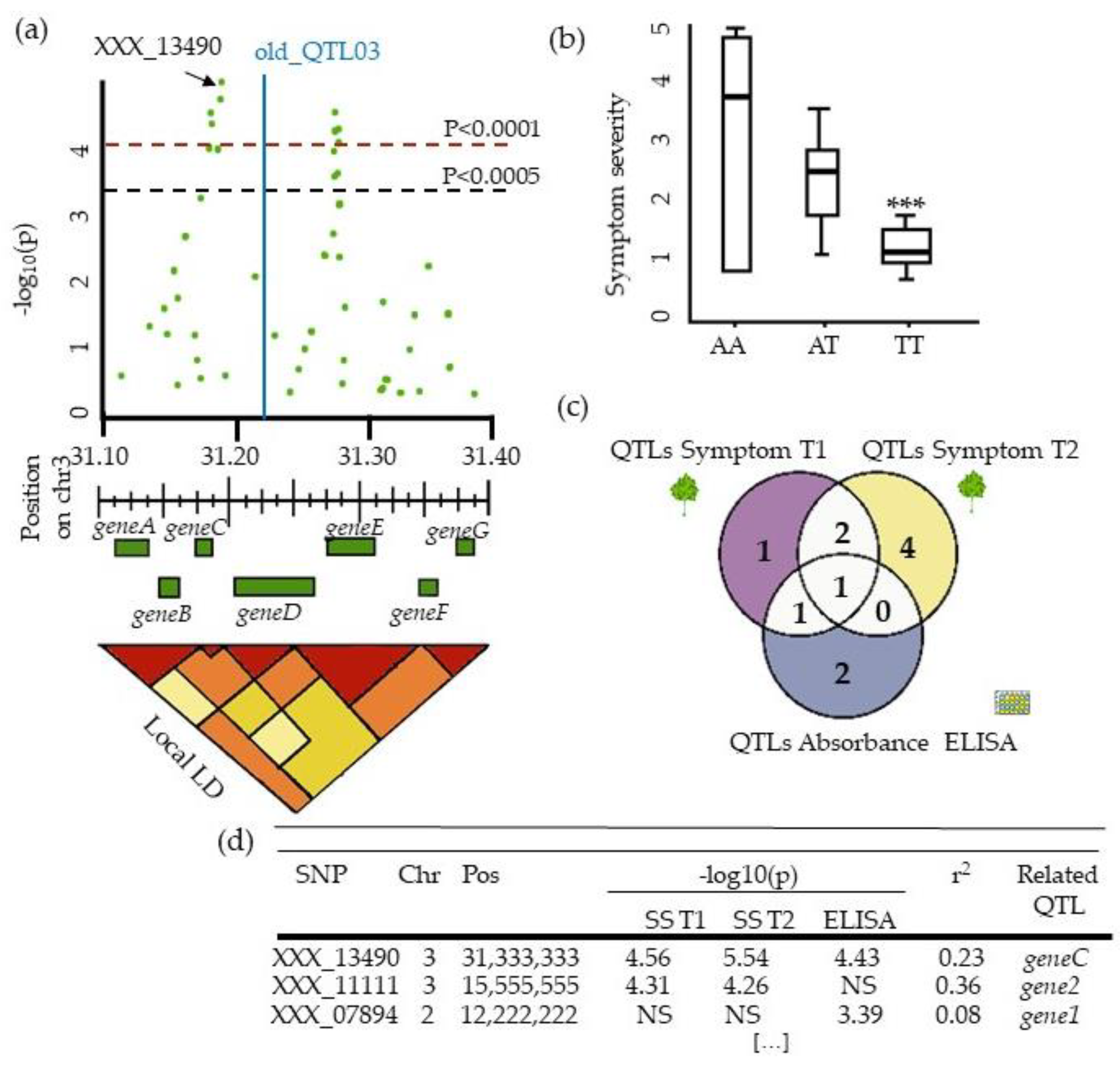
4.4. Describing QTLs: Significance, Number, Precision, and Allele Frequency
5. The Post-GWAS Step: From QTL Validation for Breeding to Candidate Gene Research
5.1. Inferring QTL Effects and Identifying Favorable Alleles… A Complex Issue
5.2. Inviting QTLs in Breeding Programs
5.3. From QTLs to Causal Genes, a Budding Approach
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anderson, P.K.; Cunningham, A.A.; Patel, N.G.; Morales, F.J.; Epstein, P.R.; Daszak, P. Emerging Infectious Diseases of Plants: Pathogen Pollution, Climate Change and Agrotechnology Drivers. Trends Ecol. Evol. 2004, 19, 535–544. [Google Scholar] [CrossRef]
- Chauhan, P.; Singla, K.; Rajbhar, M.; Singh, A.; Das, N.; Kumar, K. A Systematic Review of Conventional and Advanced Approaches for the Control of Plant Viruses. J. Appl. Biol. Biotechnol. 2019, 7, 89–98. [Google Scholar] [CrossRef]
- France: France’s Sugar Beet Crop Devastated by Disease-Sugar Industry’s Viability Threatened; U.S. Department of Agriculture, Foreign Agricultural Service, 2020.
- Martín-Hernández, A.M.; Picó, B. Natural Resistances to Viruses in Cucurbits. Agronomy 2021, 11, 23. [Google Scholar] [CrossRef]
- Hao, D.; Cheng, Y.; Chen, G.; Lu, H.; Shi, M.; Zhang, Z.; Huang, X.; Mao, Y.; Xue, L. Identification of Significant Single Nucleotide Polymorphisms for Resistance to Maize Rough Dwarf Disease in Elite Maize (Zea Mays L.) Inbred Lines. Euphytica 2015, 203, 109–120. [Google Scholar] [CrossRef]
- Feng, Z.; Kang, H.; Li, M.; Zou, L.; Wang, X.; Zhao, J.; Wei, L.; Zhou, N.; Li, Q.; Lan, Y.; et al. Identification of New Rice Cultivars and Resistance Loci against Rice Black-Streaked Dwarf Virus Disease through Genome-Wide Association Study. Rice 2019, 12, 49. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, M.; Chirco, E.M.; Gonsalves, D. Movement of Coat Protein Genes from a Commercial Virus-Resistant Transgenic Squash into a Wild Relative. Environ. Biosaf. Res. 2004, 3, 5–16. [Google Scholar] [CrossRef][Green Version]
- Gonsalves, D.; Gonsalves, C.; Ferreira, S.; Pitz, K.; Fitch, M.; Manshardt, R.; Slightom, J. Transgenic Virus Resistant Papaya: From Hope to Reality for Controlling Papaya Ringspot Virus in Hawaii. APSnet Features 2004. [Google Scholar] [CrossRef]
- Zamir, D. Improving plant breeding with exotic genetic libraries. Nat. Rev. Genet. 2001, 2, 983–989. [Google Scholar] [CrossRef]
- Lebeda, A.; Křístková, E.; Kitner, M.; Mieslerová, B.; Jemelková, M.; Pink, D.A.C. Wild Lactuca Species, Their Genetic Diversity, Resistance to Diseases and Pests, and Exploitation in Lettuce Breeding. Eur. J. Plant Pathol. 2014, 138, 597–640. [Google Scholar] [CrossRef]
- Chen, J.-F.; Staub, J.E.; Tashiro, Y.; Isshiki, S.; Miyazaki, S. Successful Interspecific Hybridization between Cucumis sativus L. and C. Hystrix Chakr. Euphytica 1997, 96, 413–419. [Google Scholar] [CrossRef]
- Bedinger, P.A.; Chetelat, R.T.; McClure, B.; Moyle, L.C.; Rose, J.K.C.; Stack, S.M.; van der Knaap, E.; Baek, Y.S.; Lopez-Casado, G.; Covey, P.A.; et al. Interspecific Reproductive Barriers in the Tomato Clade: Opportunities to Decipher Mechanisms of Reproductive Isolation. Sex. Plant Reprod. 2011, 24, 171–187. [Google Scholar] [CrossRef]
- Boissot, N.; Urbino, C.; Dintinger, J.; Pavis, C. Vector and Graft Inoculations of Potato Yellow Mosaic Virus Reveal Recessive Resistance in Solanum Pimpinellifolium. Ann. Appl. Biol. 2008, 152, 263–269. [Google Scholar] [CrossRef]
- Schoeny, A.; Desbiez, C.; Millot, P.; Wipf-Scheibel, C.; Nozeran, K.; Gognalons, P.; Lecoq, H.; Boissot, N. Impact of Vat Resistance in Melon on Viral Epidemics and Genetic Structure of Virus Populations. Virus Res. 2017, 241, 105–115. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Lee, K.C.; Gaba, V.; Wong, S.M.; Palukaitis, P.; Gal-On, A. Breakage of resistance to Cucumber mosaic virus by co-infection with Zucchini yellow mosaic virus: Enhancement of CMV accumulation independent of symptom expression. Arch. Virol. 2004, 149, 379–396. [Google Scholar] [CrossRef] [PubMed]
- Palloix, A.; Ayme, V.; Moury, B. Durability of Plant Major Resistance Genes to Pathogens Depends on the Genetic Background, Experimental Evidence and Consequences for Breeding Strategies. New Phytol. 2009, 183, 190–199. [Google Scholar] [CrossRef]
- Schneider, D.J.; Collmer, A. Studying Plant-Pathogen Interactions in the Genomics Era: Beyond Molecular Koch’s Postulates to Systems Biology. Annu. Rev. Phytopathol. 2010, 48, 457–479. [Google Scholar] [CrossRef]
- Sun, X.; Fernando, R.; Dekkers, J. Contributions of Linkage Disequilibrium and Co-Segregation Information to the Accuracy of Genomic Prediction. Genet. Sel. Evol. 2016, 48, 77. [Google Scholar] [CrossRef] [PubMed]
- Michelmore, R.W.; Paran, I.; Kesseli, R.V. Identification of markers linked to disease-resistance genes by bulked segregant analysis: A rapid method to detect markers in specific genomic regions by using segregating populations. Proc. Natl. Acad. Sci. USA 1991, 88, 9828–9832. [Google Scholar] [CrossRef]
- Gmitter, F.; Xiao, S.; Huang, S.; Hu, X.; Garnsey, S.; Deng, Z. A localized linkage map of the citrus tristeza virus resistance gene region. Theor. Appl. Genet. 1996, 92, 688–695. [Google Scholar] [CrossRef]
- Strausbaugh, C.; Myers, J.; Forster, R.; McClean, P. Bc-1 and Bc-u—Two Loci Controlling Bean Common Mosaic Virus Resistance in Common Bean Are Linked. J. Am. Soc. Hortic. Sci. 1999, 124, 644–648. [Google Scholar] [CrossRef]
- Ramírez-Madera, A.O.; Havey, M.J. Different Haplotypes Encode the Same Protein for Independent Sources of Zucchini Yellow Mosaic Virus Resistance in Cucumber. Hortscience 2017, 52, 1040–1042. [Google Scholar] [CrossRef]
- Kover, P.X.; Valdar, W.; Trakalo, J.; Scarcelli, N.; Ehrenreich, I.M.; Purugganan, M.D.; Durrant, C.; Mott, R. A Multiparent Advanced Generation Inter-Cross to Fine-Map Quantitative Traits in Arabidopsis Thaliana. PLoS Genet. 2009, 5, e1000551. [Google Scholar] [CrossRef] [PubMed]
- Poque, S.; Pagny, G.; Ouibrahim, L.; Chague, A.; Eyquard, J.-P.; Caballero, M.; Candresse, T.; Caranta, C.; Mariette, S.; Decroocq, V. Allelic Variation at the Rpv1 Locus Controls Partial Resistance to Plum Pox Virus Infection in Arabidopsis Thaliana. BMC Plant Biol. 2015, 15, 159. [Google Scholar] [CrossRef]
- Weigel, D. Natural Variation in Arabidopsis: From Molecular Genetics to Ecological Genomics. Plant Physiol. 2012, 158, 2–22. [Google Scholar] [CrossRef]
- Korte, A.; Farlow, A. The Advantages and Limitations of Trait Analysis with GWAS: A Review. Plant Methods 2013, 9, 29. [Google Scholar] [CrossRef]
- Rey, M.-D.; Martín, A.C.; Smedley, M.; Hayta, S.; Harwood, W.; Shaw, P.; Moore, G. Magnesium Increases Homoeologous Crossover Frequency During Meiosis in ZIP4 (Ph1 Gene) Mutant Wheat-Wild Relative Hybrids. Front. Plant Sci. 2018, 9, 509. [Google Scholar] [CrossRef] [PubMed]
- Pagny, G.; Paulstephenraj, P.S.; Poque, S.; Sicard, O.; Cosson, P.; Eyquard, J.-P.; Caballero, M.; Chague, A.; Gourdon, G.; Negrel, L.; et al. Family-based linkage and association mapping reveals novel genes affecting Plum pox virus infection in Arabidopsis thaliana. New Phytol. 2012, 196, 873–886. [Google Scholar] [CrossRef]
- Sitonik, C.; Suresh, L.M.; Beyene, Y.; Olsen, M.S.; Makumbi, D.; Oliver, K.; Das, B.; Bright, J.M.; Mugo, S.; Crossa, J.; et al. Genetic Architecture of Maize Chlorotic Mottle Virus and Maize Lethal Necrosis through GWAS, Linkage Analysis and Genomic Prediction in Tropical Maize Germplasm. Appl. Genet. 2019, 132, 2381–2399. [Google Scholar] [CrossRef]
- Choudhury, S.; Larkin, P.; Xu, R.; Hayden, M.; Forrest, K.; Meinke, H.; Hu, H.; Zhou, M.; Fan, Y. Genome Wide Association Study Reveals Novel QTL for Barley Yellow Dwarf Virus Resistance in Wheat. BMC Genom. 2019, 20, 891. [Google Scholar] [CrossRef]
- Ozaki, K.; Ohnishi, Y.; Iida, A.; Sekine, A.; Yamada, R.; Tsunoda, T.; Sato, H.; Sato, H.; Hori, M.; Nakamura, Y.; et al. Functional SNPs in the Lymphotoxin-α Gene That Are Associated with Susceptibility to Myocardial Infarction. Nat. Genet. 2002, 32, 650–654. [Google Scholar] [CrossRef]
- Aranzana, M.J.; Kim, S.; Zhao, K.; Bakker, E.; Horton, M.; Jakob, K.; Lister, C.; Molitor, J.; Shindo, C.; Tang, C.; et al. Genome-Wide Association Mapping in Arabidopsis Identifies Previously Known Flowering Time and Pathogen Resistance Genes. PLoS Genet. 2005, 1, e60. [Google Scholar] [CrossRef]
- Chang, H.-X.; Brown, P.J.; Lipka, A.E.; Domier, L.L.; Hartman, G.L. Genome-Wide Association and Genomic Prediction Identifies Associated Loci and Predicts the Sensitivity of Tobacco Ringspot Virus in Soybean Plant Introductions. BMC Genom. 2016, 17, 153. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, B.; Liu, Y.; Miao, T.; Zhang, H.; Wen, P.; He, J.; Huang, J.; Liu, D.; Qiu, Z.; et al. Genome-Wide Association Study and Linkage Analysis on Resistance to Rice Black-Streaked Dwarf Virus Disease. Mol. Breed. 2019, 39, 73. [Google Scholar] [CrossRef]
- Yang, X.; Sood, S.; Luo, Z.; Todd, J.; Wang, J. Genome-Wide Association Studies Identified Resistance Loci to Orange Rust and Yellow Leaf Virus Diseases in Sugarcane (Saccharum spp.). Phytopathology 2018, 109, 623–631. [Google Scholar] [CrossRef]
- Wu, S.; Wang, X.; Reddy, U.; Sun, H.; Bao, K.; Gao, L.; Mao, L.; Patel, T.; Ortiz, C.; Abburi, V.L.; et al. Genome of ‘Charleston Gray’, the principal American watermelon cultivar, and genetic characterization of 1,365 accessions in the U.S. National Plant Germplasm System watermelon collection. Plant Biotechnol. J. 2019, 17, 2246–2258. [Google Scholar] [CrossRef] [PubMed]
- Rubio, B.; Cosson, P.; Caballero, M.; Revers, F.; Bergelson, J.; Roux, F.; Schurdi-Levraud, V. Genome-wide association study reveals new loci involved in Arabidopsis thaliana and Turnip mosaic virus (TuMV) interactions in the field. New Phytol. 2019, 221, 2026–2038. [Google Scholar] [CrossRef] [PubMed]
- Butković, A.; González, R.; Rivarez, M.P.S.; Elena, S.F. Arabidopsis Thaliana Genes Contributing to Differences in the Outcome of Infection with Generalist and Specialist Strains of Turnip Mosaic Virus Identified by Genome-Wide Association Studies. bioRxiv 2020. [Google Scholar] [CrossRef]
- Montes, N.; Cobos, A.; Gil-Valle, M.; Caro, E.; Pagán, I. Arabidopsis Thaliana Genes Associated with Cucumber Mosaic Virus Virulence and Their Link to Virus Seed Transmission. Microorganisms 2021, 9, 692. [Google Scholar] [CrossRef]
- Mariette, S.; Wong Jun Tai, F.; Roch, G.; Barre, A.; Chague, A.; Decroocq, S.; Groppi, A.; Laizet, Y.; Lambert, P.; Tricon, D.; et al. Genome-wide association links candidate genes to resistance to Plum Pox Virus in apricot (Prunus armeniaca). New Phytol. 2016, 209, 773–784. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Liu, C.; Song, X.; Sun, F.; Xiao, D.; Wei, Y.; Hou, X.; Zhang, C. Genome-Wide Association Study of Turnip Mosaic Virus Resistance in Non-Heading Chinese Cabbage. 3 Biotech 2020, 10, 363. [Google Scholar] [CrossRef]
- Tamisier, L.; Rousseau, E.; Barraillé, S.; Nemouchi, G.; Szadkowski, M.; Mailleret, L.; Grognard, F.; Fabre, F.; Moury, B.; Palloix, A. Quantitative Trait Loci in Pepper Control the Effective Population Size of Two RNA Viruses at Inoculation. J. Gen. Virol. 2017, 98, 1923–1931. [Google Scholar] [CrossRef]
- Tamisier, L.; Szadkowski, M.; Nemouchi, G.; Lefebvre, V.; Szadkowski, E.; Duboscq, R.; Santoni, S.; Sarah, G.; Sauvage, C.; Palloix, A.; et al. Genome-wide association mapping of QTLs implied in potato virus Y population sizes in pepper: Evidence for widespread resistance QTL pyramiding. Mol. Plant Pathol. 2020, 21, 3–16. [Google Scholar] [CrossRef] [PubMed]
- Soler-Garzón, A.; Oladzad, A.; Beaver, J.; Beebe, S.; Lee, R.; Lobaton, J.D.; Macea, E.; McClean, P.; Raatz, B.; Rosas, J.C.; et al. NAC Candidate Gene Marker for bgm-1 and Interaction With QTL for Resistance to Bean Golden Yellow Mosaic Virus in Common Bean. Front. Plant Sci. 2021, 12, 477. [Google Scholar]
- Gowda, M.; Das, B.; Makumbi, D.; Babu, R.; Semagn, K.; Mahuku, G.; Olsen, M.S.; Bright, J.M.; Beyene, Y.; Prasanna, B.M. Genome-wide association and genomic prediction of resistance to maize lethal necrosis disease in tropical maize germplasm. Theor. Appl. Genet. 2015, 128, 1957–1968. [Google Scholar] [CrossRef] [PubMed]
- Nyaga, C.; Gowda, M.; Beyene, Y.; Muriithi, W.T.; Makumbi, D.; Olsen, M.S.; Suresh, L.M.; Bright, J.M.; Das, B.; Prasanna, B.M. Genome-Wide Analyses and Prediction of Resistance to MLN in Large Tropical Maize Germplasm. Genes 2020, 11, 16. [Google Scholar] [CrossRef] [PubMed]
- Tao, Y.; Jiang, L.; Liu, Q.; Zhang, Y.; Zhang, R.; Ingvardsen, C.R.; Frei, U.K.; Wang, B.; Lai, J.; Lübberstedt, T.; et al. Combined Linkage and Association Mapping Reveals Candidates for Scmv1, a Major Locus Involved in Resistance to Sugarcane Mosaic Virus (SCMV) in Maize. BMC Plant Biol. 2013, 13, 162. [Google Scholar] [CrossRef]
- Horn, F.; Habekuß, A.; Stich, B. Genes Involved in Barley Yellow Dwarf Virus Resistance of Maize. Theor. Appl. Genet. 2014, 127, 2575–2584. [Google Scholar] [CrossRef]
- Leng, P.; Ji, Q.; Tao, Y.; Ibrahim, R.; Pan, G.; Xu, M.; Lübberstedt, T. Characterization of Sugarcane Mosaic Virus Scmv1 and Scmv2 Resistance Regions by Regional Association Analysis in Maize. PLoS ONE 2015, 10, e0140617. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Han, L.; Wen, J.; Chen, G.; Li, H.; Wang, Y.; Zhao, R.; Zhang, X.; Xia, Z.; et al. Association Mapping Resolving the Major Loci Scmv2 Conferring Resistance to Sugarcane Mosaic Virus in Maize. Eur. J. Plant Pathol. 2016, 145, 385–391. [Google Scholar] [CrossRef]
- Gustafson, T.J.; de Leon, N.; Kaeppler, S.M.; Tracy, W.F. Genetic Analysis of Sugarcane Mosaic Virus Resistance in the Wisconsin Diversity Panel of Maize. Crop Sci. 2018, 58, 1853–1865. [Google Scholar] [CrossRef]
- Rossi, E.A.; Ruiz, M.; Bonamico, N.C.; Balzarini, M.G. Genome-Wide Association Study of Resistance to Mal de Río Cuarto Disease in Maize. Agron. J. 2020, 112, 4624–4633. [Google Scholar] [CrossRef]
- Gage, J.L.; Vaillancourt, B.; Hamilton, J.P.; Manrique-Carpintero, N.C.; Gustafson, T.J.; Barry, K.; Lipzen, A.; Tracy, W.F.; Mikel, M.A.; Kaeppler, S.M.; et al. Multiple Maize Reference Genomes Impact the Identification of Variants by Genome-Wide Association Study in a Diverse Inbred Panel. Plant Genome 2019, 12. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Wang, X.; Hao, J.; Yan, J.; Ding, J. Genome-Wide Association Implicates Candidate Genes Conferring Resistance to Maize Rough Dwarf Disease in Maize. PLoS ONE 2015, 10, e0142001. [Google Scholar] [CrossRef] [PubMed]
- Foresman, B.J.; Oliver, R.E.; Jackson, E.W.; Chao, S.; Arruda, M.P.; Kolb, F.L. Genome-Wide Association Mapping of Barley Yellow Dwarf Virus Tolerance in Spring Oat (Avena Sativa L.). PLoS ONE 2016, 11, e0155376. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Bai, G.; Hunger, R.M.; Bockus, W.W.; Yu, J.; Carver, B.F.; Brown-Guedira, G. Association Study of Resistance to Soilborne wheat mosaic virus in U.S. Winter Wheat. Phytopathology 2011, 101, 1322–1329. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Yang, X.; Zhang, D.; Bai, G.; Chao, S.; Bockus, W. Genome-wide association analysis identified SNPs closely linked to a gene resistant to Soil-borne wheat mosaic virus. Theor. Appl. Genet. 2014, 127, 1039–1047. [Google Scholar] [CrossRef]
- Hourcade, D.; Bogard, M.; Bonnefoy, M.; Savignard, F.; Mohamadi, F.; Lafarge, S.; Du Cheyron, P.; Mangel, N.; Cohan, J.P. Genome-Wide Association Analysis of Resistance to Wheat Spindle Streak Mosaic Virus in Bread Wheat. Plant Pathol. 2019, 68, 609–616. [Google Scholar] [CrossRef]
- Milner, S.G.; Jost, M.; Taketa, S.; Mazón, E.R.; Himmelbach, A.; Oppermann, M.; Weise, S.; Knüpffer, H.; Basterrechea, M.; König, P.; et al. Genebank Genomics Highlights the Diversity of a Global Barley Collection. Nat. Genet. 2019, 51, 319–326. [Google Scholar] [CrossRef]
- Gonzalez, M.Y.; Zhao, Y.; Jiang, Y.; Stein, N.; Habekuss, A.; Reif, J.C.; Schulthess, A.W. Genomic prediction models trained with historical records enable populating the German ex situ genebank bio-digital resource center of barley (Hordeum sp.) with information on resistances to soilborne barley mosaic viruses. Theor. Appl. Genet. 2021, 134, 2181–2196. [Google Scholar] [CrossRef]
- Cubry, P.; Pidon, H.; Ta, K.N.; Tranchant-Dubreuil, C.; Thuillet, A.-C.; Holzinger, M.; Adam, H.; Kam, H.; Chrestin, H.; Ghesquière, A.; et al. Genome Wide Association Study Pinpoints Key Agronomic QTLs in African Rice Oryza Glaberrima. Rice 2020, 13, 66. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.Q.; Lan, G.; Zhu, Y.; Chen, K.; Shen, C.; Zhao, X.; Zhang, F.; Xu, J.; Li, Z. Genome-Wide Association Study on Resistance to Rice Black-Streaked Dwarf Disease Caused by Rice black-streaked dwarf virus. Plant Dis. 2020, 105, 607–615. [Google Scholar] [CrossRef] [PubMed]
- Wei, X.; Jackson, P.A.; McIntyre, C.L.; Aitken, K.S.; Croft, B. Associations between DNA Markers and Resistance to Diseases in Sugarcane and Effects of Population Substructure. Theor. Appl. Genet. 2006, 114, 155–164. [Google Scholar] [CrossRef] [PubMed]
- Debibakas, S.; Rocher, S.; Garsmeur, O.; Toubi, L.; Roques, D.; D’Hont, A.; Hoarau, J.-Y.; Daugrois, J.H. Prospecting Sugarcane Resistance to Sugarcane Yellow Leaf Virus by Genome-Wide Association. Theor. Appl. Genet. 2014, 127, 1719–1732. [Google Scholar] [CrossRef]
- Pimenta, R.J.G.; Aono, A.H.; Villavicencio, R.C.B.; da Silva, C.C.; dos Anjos, I.A.; de Andrade Landell, M.G.; Gonçalves, M.C.; Pinto, L.R.; de Souza, A.P. Genome-Wide Association Mapping of Sugarcane Yellow Leaf Virus Resistance. bioRxiv 2020. [Google Scholar] [CrossRef]
- Gouy, M.; Rousselle, Y.; Thong Chane, A.; Anglade, A.; Royaert, S.; Nibouche, S.; Costet, L. Genome wide association mapping of agro-morphological and disease resistance traits in sugarcane. Euphytica 2015, 202, 269–284. [Google Scholar] [CrossRef]
- Chang, H.-X.; Lipka, A.E.; Domier, L.L.; Hartman, G.L. Characterization of Disease Resistance Loci in the USDA Soybean Germplasm Collection Using Genome-Wide Association Studies. Phytopathology 2016, 106, 1139–1151. [Google Scholar] [CrossRef]
- Liu, Q.; Hobbs, H.A.; Domier, L.L. Genome-Wide Association Study of the Seed Transmission Rate of Soybean Mosaic Virus and Associated Traits Using Two Diverse Population Panels. Theor. Appl. Genet. 2019, 132, 3413–3424. [Google Scholar] [CrossRef]
- Che, Z.; Yan, H.; Liu, H.; Yang, H.; Du, H.; Yang, Y.; Liu, B.; Yu, D. Genome-Wide Association Study for Soybean Mosaic Virus SC3 Resistance in Soybean. Mol. Breed. 2020, 40, 69. [Google Scholar] [CrossRef]
- Li, J.; Tang, Y.; Jacobson, A.L.; Dang, P.M.; Li, X.; Wang, M.L.; Hagan, A.; Chen, C.Y. Population Structure and Association Mapping to Detect QTL Controlling Tomato Spotted Wilt Virus Resistance in Cultivated Peanuts. Crop J. 2018, 6, 516–526. [Google Scholar] [CrossRef]
- Rabbi, I.Y.; Kayondo, S.I.; Bauchet, G.; Yusuf, M.; Aghogho, C.I.; Ogunpaimo, K.; Uwugiaren, R.; Smith, I.A.; Peteti, P.; Agbona, A.; et al. Genome-wide association analysis reveals new insights into the genetic architecture of defensive, agro-morphological and quality-related traits in cassava. Plant Mol. Biol. 2020, 1–19. [Google Scholar] [CrossRef]
- Wolfe, M.D.; Rabbi, I.Y.; Egesi, C.; Hamblin, M.; Kawuki, R.; Kulakow, P.; Lozano, R.; Carpio, D.P.D.; Ramu, P.; Jannink, J.-L. Genome-Wide Association and Prediction Reveals Genetic Architecture of Cassava Mosaic Disease Resistance and Prospects for Rapid Genetic Improvement. Plant Genome 2016, 9. [Google Scholar] [CrossRef]
- Kayondo, S.I.; Pino Del Carpio, D.; Lozano, R.; Ozimati, A.; Wolfe, M.; Baguma, Y.; Gracen, V.; Offei, S.; Ferguson, M.; Kawuki, R.; et al. Genome-Wide Association Mapping and Genomic Prediction for CBSD Resistance in Manihot Esculenta. Sci. Rep. 2018, 8, 1549. [Google Scholar] [CrossRef] [PubMed]
- Norman, P.; Asiedu, R.; Asfaw, A. Identification of Quantitative Trait Nucleotides and Candidate Genes for Tuber Yield and Mosaic Virus Tolerance in an Elite Population of White Guinea Yam (Dioscorea Rotundata) Using Genome-Wide Association Scan. BMC Plant Biol. 2021, 20, 404. [Google Scholar]
- Bartoli, C.; Roux, F. Genome-Wide Association Studies in Plant Pathosystems: Toward an Ecological Genomics Approach. Front. Plant Sci. 2017, 8, 763. [Google Scholar] [CrossRef]
- Tomás, D.M.; Cañizares, M.C.; Abad, J.; Fernández-Muñoz, R.; Moriones, E. Resistance to Tomato Yellow Leaf Curl Virus Accumulation in the Tomato Wild Relative Solanum Habrochaites Associated with the C4 Viral Protein. Mol. Plant Microbe Interact. 2011, 24, 849–861. [Google Scholar] [CrossRef]
- Fraile, A.; García-Arenal, F. Chapter 1-The Coevolution of Plants and Viruses: Resistance and Pathogenicity. In Advances in Virus Research; Carr, J.P., Loebenstein, G., Eds.; Academic Press: London, UK, 2010; Volume 76, pp. 1–32. ISBN 0065-3527. [Google Scholar]
- Lin, T.; Zhu, G.; Zhang, J.; Xu, X.; Yu, Q.; Zheng, Z.; Zhang, Z.; Lun, Y.; Li, S.; Wang, X.; et al. Genomic Analyses Provide Insights into the History of Tomato Breeding. Nat. Genet. 2014, 46, 1220–1226. [Google Scholar] [CrossRef] [PubMed]
- Kitsios, G.D.; Zintzaras, E. Genome-wide association studies: Hypothesis-“free” or “engaged”? Transl. Res. 2009, 154, 161–164. [Google Scholar] [CrossRef]
- Brachi, B.; Faure, N.; Horton, M.; Flahauw, E.; Vazquez, A.; Nordborg, M.; Bergelson, J.; Cuguen, J.; Roux, F. Linkage and Association Mapping of Arabidopsis Thaliana Flowering Time in Nature. PLoS Genet. 2010, 6, e1000940. [Google Scholar] [CrossRef]
- Zuk, O.; Schaffner, S.F.; Samocha, K.; Do, R.; Hechter, E.; Kathiresan, S.; Daly, M.J.; Neale, B.M.; Sunyaev, S.R.; Lander, E.S. Searching for Missing Heritability: Designing Rare Variant Association Studies. Proc. Natl. Acad. Sci. USA 2014, 111, E455–E464. [Google Scholar] [CrossRef]
- Marouli, E.; Graff, M.; Medina-Gomez, C.; Lo, K.S.; Wood, A.R.; Kjaer, T.R.; Fine, R.S.; Lu, Y.; Schurmann, C.; Highland, H.M.; et al. Rare and Low-Frequency Coding Variants Alter Human Adult Height. Nature 2017, 542, 186–190. [Google Scholar] [CrossRef]
- Bandyopadhyay, B.; Chanda, V.; Wang, Y. Finding the Sources of Missing Heritability within Rare Variants through Simulation. Bioinform. Biol. Insights 2017, 11, 1177932217735096. [Google Scholar] [CrossRef]
- Claussnitzer, M.; Cho, J.H.; Collins, R.; Cox, N.J.; Dermitzakis, E.T.; Hurles, M.E.; Kathiresan, S.; Kenny, E.E.; Lindgren, C.M.; MacArthur, D.G.; et al. A Brief History of Human Disease Genetics. Nature 2020, 577, 179–189. [Google Scholar] [CrossRef]
- Frachon, L.; Libourel, C.; Villoutreix, R.; Carrère, S.; Glorieux, C.; Huard-Chauveau, C.; Navascués, M.; Gay, L.; Vitalis, R.; Baron, E.; et al. Intermediate degrees of synergistic pleiotropy drive adaptive evolution in ecological time. Nat. Ecol. Evol. 2017, 1, 1551–1561. [Google Scholar] [CrossRef] [PubMed]
- Ranc, N.; Muños, S.; Xu, J.; Le Paslier, M.-C.; Chauveau, A.; Bounon, R.; Rolland, S.; Bouchet, J.-P.; Brunel, D.; Causse, M. Genome-Wide Association Mapping in Tomato (Solanum Lycopersicum) Is Possible Using Genome Admixture of Solanum Lycopersicum Var. Cerasiforme. G3 2012, 2, 853–864. [Google Scholar] [CrossRef]
- Huang, X.; Han, B. Natural Variations and Genome-Wide Association Studies in Crop Plants. Annu. Rev. Plant Biol. 2014, 65, 531–551. [Google Scholar] [CrossRef]
- Gupta, P.K.; Kulwal, P.L.; Jaiswal, V. Chapter Two-Association mapping in plants in the post-GWAS genomics era. In Advances in Genetics; Kumar, D., Ed.; Academic Press: London, UK, 2019; Volume 104, pp. 75–154. ISBN 0065-2660. [Google Scholar]
- Bayer, P.E.; Golicz, A.A.; Scheben, A.; Batley, J.; Edwards, D. Plant Pan-Genomes Are the New Reference. Nat. Plants 2020, 6, 914–920. [Google Scholar] [CrossRef]
- Chovelon, V.; Feriche-Linares, R.; Barreau, G.; Chadoeuf, J.; Callot, C.; Gautier, V.; Le Paslier, M.-C.; Berad, A.; Faivre-Rampant, P.; Lagnel, J.; et al. Building a Cluster of NLR Genes Conferring Resistance to Pests and Pathogens: The Story of the Vat Gene Cluster in Cucurbits. Hortic. Res. 2021, 8, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Jayakodi, M.; Schreiber, M.; Stein, N.; Mascher, M. Building pan-genome infrastructures for crop plants and their use in association genetics. DNA Res. 2021, 28, dsaa030. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Li, R.; Zhang, Z.; Li, L.; Gu, X.; Fan, W.; Lucas, W.J.; Wang, X.; Xie, B.; Ni, P.; et al. The Genome of the Cucumber, Cucumis sativus L. Nat. Genet. 2009, 41, 1275–1281. [Google Scholar] [CrossRef]
- Li, Q.; Li, H.; Huang, W.; Xu, Y.; Zhou, Q.; Wang, S.; Ruan, J.; Huang, S.; Zhang, Z. A Chromosome-Scale Genome Assembly of Cucumber (Cucumis sativus L.). GigaScience 2019, 8, giz072. [Google Scholar] [CrossRef] [PubMed]
- Porter, R.H. The Reaction of Cucumbers to Types of Mosaic; Iowa State University: Ames, IA, USA, 1932. [Google Scholar]
- Jiao, W.-B.; Schneeberger, K. Chromosome-Level Assemblies of Multiple Arabidopsis Genomes Reveal Hotspots of Rearrangements with Altered Evolutionary Dynamics. Nat. Commun. 2020, 11, 989. [Google Scholar] [CrossRef]
- Van de Weyer, A.-L.; Monteiro, F.; Furzer, O.J.; Nishimura, M.T.; Cevik, V.; Witek, K.; Jones, J.D.; Dangl, J.L.; Weigel, D.; Bemm, F. The Arabidopsis thaliana pan-NLRome. bioRxiv 2019. [Google Scholar] [CrossRef]
- Gabur, I.; Chawla, H.S.; Snowdon, R.J.; Parkin, I.A.P. Connecting Genome Structural Variation with Complex Traits in Crop Plants. Theor. Appl. Genet. 2019, 132, 733–750. [Google Scholar] [CrossRef]
- Arora, S.; Steuernagel, B.; Gaurav, K.; Chandramohan, S.; Long, Y.; Matny, O.; Johnson, R.; Enk, J.; Periyannan, S.; Singh, N.; et al. Resistance Gene Cloning from a Wild Crop Relative by Sequence Capture and Association Genetics. Nat. Biotechnol. 2019, 37, 139–143. [Google Scholar] [CrossRef] [PubMed]
- VanRaden, P.M. Efficient Methods to Compute Genomic Predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef] [PubMed]
- Moury, B.; Fabre, F.; Senoussi, R. Estimation of the Number of Virus Particles Transmitted by an Insect Vector. Proc. Natl. Acad. Sci. USA 2007, 104, 17891–17896. [Google Scholar] [CrossRef]
- Poland, J.A.; Nelson, R.J. In the Eye of the Beholder: The Effect of Rater Variability and Different Rating Scales on QTL Mapping. Phytopathology 2011, 101, 290–298. [Google Scholar] [CrossRef] [PubMed]
- Clark, M.F.; Adams, A.N.; Graham, F.L.; Smiley, J.; Russell, W.C.; Nairn, R. Characteristics of the Microplate Method of Enzyme-Linked Immunosorbent Assay for the Detection of Plant Viruses. J. Gen. Virol. 1977, 34, 475–483. [Google Scholar] [CrossRef]
- Henson, J.M.; French, R. The Polymerase Chain Reaction and Plant Disease Diagnosis. Annu. Rev. Phytopathol. 1993, 31, 81–109. [Google Scholar] [CrossRef]
- Jeger, M.J.; Viljanen-Rollinson, S.L.H. The Use of the Area under the Disease-Progress Curve (AUDPC) to Assess Quantitative Disease Resistance in Crop Cultivars. Theor. Appl. Genet. 2001, 102, 32–40. [Google Scholar] [CrossRef]
- Simko, I.; Piepho, H.-P. The Area Under the Disease Progress Stairs: Calculation, Advantage, and Application. Phytopathology 2011, 102, 381–389. [Google Scholar] [CrossRef]
- Jombart, T.; Devillard, S.; Balloux, F. Discriminant Analysis of Principal Components: A New Method for the Analysis of Genetically Structured Populations. BMC Genet. 2010, 11, 94. [Google Scholar] [CrossRef]
- Pritchard, J.K.; Stephens, M.; Donnelly, P. Inference of Population Structure Using Multilocus Genotype Data. Genetics 2000, 155, 945–959. [Google Scholar] [CrossRef] [PubMed]
- Frichot, E.; Mathieu, F.; Trouillon, T.; Bouchard, G.; François, O. Fast and Efficient Estimation of Individual Ancestry Coefficients. Genetics 2014, 196, 973. [Google Scholar] [CrossRef]
- Alexander, D.H.; Novembre, J.; Lange, K. Fast Model-Based Estimation of Ancestry in Unrelated Individuals. Genome Res. 2009, 19, 1655–1664. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Pressoir, G.; Briggs, W.H.; Bi, I.V.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B.; et al. A Unified Mixed-Model Method for Association Mapping That Accounts for Multiple Levels of Relatedness. Nat. Genet. 2006, 38, 203–208. [Google Scholar] [CrossRef]
- Rincent, R.; Moreau, L.; Monod, H.; Kuhn, E.; Melchinger, A.E.; Malvar, R.A.; Moreno-Gonzalez, J.; Nicolas, S.; Madur, D.; Combes, V.; et al. Recovering Power in Association Mapping Panels with Variable Levels of Linkage Disequilibrium. Genetics 2014, 197, 375–387. [Google Scholar] [CrossRef] [PubMed]
- Segura, V.; Vilhjálmsson, B.J.; Platt, A.; Korte, A.; Seren, Ü.; Long, Q.; Nordborg, M. An Efficient Multi-Locus Mixed-Model Approach for Genome-Wide Association Studies in Structured Populations. Nat. Genet. 2012, 44, 825–830. [Google Scholar] [CrossRef]
- Wang, S.-B.; Feng, J.-Y.; Ren, W.-L.; Huang, B.; Zhou, L.; Wen, Y.-J.; Zhang, J.; Dunwell, J.M.; Xu, S.; Zhang, Y.-M. Improving Power and Accuracy of Genome-Wide Association Studies via a Multi-Locus Mixed Linear Model Methodology. Sci. Rep. 2016, 6, 19444. [Google Scholar] [CrossRef] [PubMed]
- Zeng, P.; Zhao, Y.; Qian, C.; Zhang, L.; Zhang, R.; Gou, J.; Liu, J.; Liu, L.; Chen, F. Statistical Analysis for Genome-Wide Association Study. J. Biomed. Res. 2015, 29, 285–297. [Google Scholar]
- Chen, H.; Wang, C.; Conomos, M.P.; Stilp, A.M.; Li, Z.; Sofer, T.; Szpiro, A.A.; Chen, W.; Brehm, J.M.; Celedón, J.C.; et al. Control for Population Structure and Relatedness for Binary Traits in Genetic Association Studies via Logistic Mixed Models. Am. J. Hum. Genet. 2016, 98, 653–666. [Google Scholar] [CrossRef]
- Fraser, R.S.S. The Genetics of Resistance to Plant Viruses. Annu. Rev. Phytopathol. 1990, 28, 179–200. [Google Scholar] [CrossRef]
- Bonnafous, F.; Fievet, G.; Blanchet, N.; Boniface, M.-C.; Carrère, S.; Gouzy, J.; Legrand, L.; Marage, G.; Bret-Mestries, E.; Munos, S.; et al. Comparison of GWAS Models to Identify Non-Additive Genetic Control of Flowering Time in Sunflower Hybrids. Theor. Appl. Genet. 2018, 131, 319–332. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Storey, J.D. The Positive False Discovery Rate: A Bayesian Interpretation and the q-Value. Ann. Stat. 2003, 31, 2013–2035. [Google Scholar] [CrossRef]
- Bonferroni, C.E. Il Calcolo Delle Assicurazioni Su Gruppi Di Teste. In Studi in onore del Professore Salvatore Ortu Carboni; Bardi: Roma, Italy, 1935; pp. 13–60. [Google Scholar]
- Sorić, B. Statistical “Discoveries” and Effect-Size Estimation. J. Am. Stat. Assoc. 1989, 84, 608–610. [Google Scholar] [CrossRef]
- Gao, X.; Starmer, J.; Martin, E.R. A Multiple Testing Correction Method for Genetic Association Studies Using Correlated Single Nucleotide Polymorphisms. Genet. Epidemiol. 2008, 32, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Becker, L.C.; Becker, D.M.; Starmer, J.D.; Province, M.A. Avoiding the High Bonferroni Penalty in Genome-Wide Association Studies. Genet. Epidemiol. 2010, 34, 100–105. [Google Scholar] [CrossRef]
- Gao, X. Multiple Testing Corrections for Imputed SNPs. Genet. Epidemiol. 2011, 35, 154–158. [Google Scholar] [CrossRef] [PubMed]
- Hancock, A.M.; Brachi, B.; Faure, N.; Horton, M.W.; Jarymowycz, L.B.; Sperone, F.G.; Toomajian, C.; Roux, F.; Bergelson, J. Adaptation to Climate across the Arabidopsis Thaliana Genome. Science 2011, 334, 83–86. [Google Scholar] [CrossRef]
- Meijón, M.; Satbhai, S.B.; Tsuchimatsu, T.; Busch, W. Genome-Wide Association Study Using Cellular Traits Identifies a New Regulator of Root Development in Arabidopsis. Nat. Genet. 2014, 46, 77–81. [Google Scholar] [CrossRef]
- Josephs, E.B.; Stinchcombe, J.R.; Wright, S.I. What Can Genome-wide Association Studies Tell Us about the Evolutionary Forces Maintaining Genetic Variation for Quantitative Traits? New Phytol. 2017, 214, 21–33. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, J.; He, X.; Wang, Y.; Ma, X.; Yin, D. Genome-Wide Association Study of Major Agronomic Traits Related to Domestication in Peanut. Front. Plant Sci. 2017, 8, 1611. [Google Scholar] [CrossRef]
- Aoun, N.; Desaint, H.; Boyrie, L.; Bonhomme, M.; Deslandes, L.; Berthomé, R.; Roux, F. A Complex Network of Additive and Epistatic Quantitative Trait Loci Underlies Natural Variation of Arabidopsis Thaliana Quantitative Disease Resistance to Ralstonia Solanacearum under Heat Stress. Mol. Plant Pathol. 2020, 21, 1405–1420. [Google Scholar] [CrossRef] [PubMed]
- Manolio, T.A.; Collins, F.S.; Cox, N.J.; Goldstein, D.B.; Hindorff, L.A.; Hunter, D.J.; McCarthy, M.I.; Ramos, E.M.; Cardon, L.R.; Chakravarti, A.; et al. Finding the Missing Heritability of Complex Diseases. Nature 2009, 461, 747–753. [Google Scholar] [CrossRef] [PubMed]
- Visscher, P.M.; Brown, M.A.; McCarthy, M.I.; Yang, J. Five Years of GWAS Discovery. Am. J. Hum. Genet. 2012, 90, 7–24. [Google Scholar] [CrossRef] [PubMed]
- Slatkin, M. Epigenetic Inheritance and the Missing Heritability Problem. Genetics 2009, 182, 845–850. [Google Scholar] [CrossRef]
- Platt, A.; Vilhjálmsson, B.J.; Nordborg, M. Conditions under Which Genome-Wide Association Studies Will Be Positively Misleading. Genetics 2010, 186, 1045–1052. [Google Scholar] [CrossRef]
- Brachi, B.; Morris, G.P.; Borevitz, J.O. Genome-Wide Association Studies in Plants: The Missing Heritability Is in the Field. Genome Biol. 2011, 12, 232. [Google Scholar] [CrossRef]
- Bonhomme, M.; Fariello, M.I.; Navier, H.; Hajri, A.; Badis, Y.; Miteul, H.; Samac, D.A.; Dumas, B.; Baranger, A.; Jacquet, C.A.; et al. Local Score Approach Improves GWAS Resolution and Detects Minor QTL: Application to Medicago Truncatula Quantitative Disease Resistance to Multiple Aphanomyces Euteiches Isolates. Heredity 2019, 123, 517–531. [Google Scholar] [CrossRef]
- Fariello, M.I.; Boitard, S.; Mercier, S.; Robelin, D.; Faraut, T.; Arnould, C.; Recoquillay, J.; Bouchez, O.; Salin, G.; Dehais, P.; et al. Accounting for Linkage Disequilibrium in Genome Scans for Selection without Individual Genotypes: The Local Score Approach. Mol. Ecol. 2017, 26, 3700–3714. [Google Scholar] [CrossRef] [PubMed]
- McElroy, M.S.; Navarro, A.J.R.; Mustiga, G.; Stack, C.; Gezan, S.; Peña, G.; Sarabia, W.; Saquicela, D.; Sotomayor, I.; Douglas, G.M.; et al. Prediction of Cacao (Theobroma Cacao) Resistance to Moniliophthora Spp. Diseases via Genome-Wide Association Analysis and Genomic Selection. Front. Plant Sci. 2018, 9, 343. [Google Scholar] [CrossRef]
- Maurano, M.T.; Humbert, R.; Rynes, E.; Thurman, R.E.; Haugen, R.; Wang, H.; Reynolds, A.P.; Sandstrom, R.; Qu, H.; Brody, J.; et al. Systematic Localization of Common Disease-Associated Variation in Regulatory DNA. Science 2012, 337, 1190–1195. [Google Scholar] [CrossRef] [PubMed]
- Chisholm, S.T.; Parra, M.A.; Anderberg, R.J.; Carrington, J.C. Arabidopsis RTM1 and RTM2 Genes Function in Phloem to Restrict Long-Distance Movement of Tobacco Etch Virus. Plant Physiol. 2001, 127, 1667–1675. [Google Scholar] [CrossRef]
- Bastet, A.; Lederer, B.; Giovinazzo, N.; Arnoux, X.; German-Retana, S.; Reinbold, C.; Brault, V.; Garcia, D.; Djennane, S.; Gersch, S.; et al. Trans-Species Synthetic Gene Design Allows Resistance Pyramiding and Broad-Spectrum Engineering of Virus Resistance in Plants. Plant Biotechnol. J. 2018, 16, 1569–1581. [Google Scholar] [CrossRef]
- Zhao, K.; Aranzana, M.J.; Kim, S.; Lister, C.; Shindo, C.; Tang, C.; Toomajian, C.; Zheng, H.; Dean, C.; Marjoram, P.; et al. An Arabidopsis Example of Association Mapping in Structured Samples. PLoS Genet. 2007, 3, e4. [Google Scholar] [CrossRef]
- Wang, M.; Roux, F.; Bartoli, C.; Huard-Chauveau, C.; Meyer, C.; Lee, H.; Roby, D.; McPeek, M.S.; Bergelson, J. Two-Way Mixed-Effects Methods for Joint Association Analysis Using Both Host and Pathogen Genomes. Proc. Natl. Acad. Sci. USA 2018, 115, E5440–E5449. [Google Scholar] [CrossRef] [PubMed]

| Species | Latin Name | Virus | Article |
|---|---|---|---|
| Arabidopsis thaliana | Cucumber mosaic virus (CMV) Turnip mosaic virus (TuMV) (×2) Plum pox virus (PPV) | [28,37,38,39] | |
| Apricot | Prunus armeniaca | PPV | [40] |
| Chinese cabbage | Brassica rapa | TuMV | [41] |
| Pepper | Capsicum annuum | Potato virus Y (PVY) | [42,43] |
| Common bean | Phaseolus vulgaris | Bean golden yellow mosaic virus (BGYMV) | [44] |
| Watermelon | Citrullus lanatus | Papaya ringspot virus (PRSV) | [36] |
| Maize | Zea maize spp Mays | Sugarcane mosaic virus (SCMV) (×5) Maize chlorotic mottle vírus (MCMV) SCMV + MCMV (MCMD) (×3) Mal de Rio cuarto virus (MRCV) Rice black-streaked dwarf virus (RBSDV) (×2) Barley yellow dwarf virus (BYDV) | [5,29,45,46,47,48,49,50,51,52,53,54] |
| Oat | Avena sativa L. | BYDV | [55] |
| Wheat | Triticum aestivum | BYDV Soil-borne wheat mosaic virus (SBWMV) (×2) Wheat spindle streak mosaic virus (WSSMV) | [30,56,57,58] |
| Barley | Hordeum sp. | Barley mild mosaic virus (BaMMV) (×2) Barley yellow mosaic virus (BaYMV) (×2) | [59,60] |
| Rice | Oryza sativa L. Oryza glaberrima | Rice yellow mottle vírus (RYMV) RBSDV (×3) | [6,34,61,62] |
| Sugarcane | Saccharum officinarum Saccharum spontaneum | Fiji disease virus Sugarcane yellow leaf virus (SCYLV) (×4) | [35,63,64,65,66] |
| Soybean | Glycine max | Tomato ringspot virus (TRSV) Peanut mottle virus (PMV) Bean pod mosaic virus (BPMV) Soybean mosaic virus (SMV) (×3) | [33,67,68,69] |
| Peanut | Arachis hypogaea L. | Tomato spotted wilt virus (TSWV) | [70] |
| Cassava | Manihot esculenta | Cassava mosaic disease (CMD) (×2) Cassava brown streak virus (CBSV) | [71,72,73] |
| Yam | Dioscorea rotundata | Yam mosaic virus (YMV) | [74] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monnot, S.; Desaint, H.; Mary-Huard, T.; Moreau, L.; Schurdi-Levraud, V.; Boissot, N. Deciphering the Genetic Architecture of Plant Virus Resistance by GWAS, State of the Art and Potential Advances. Cells 2021, 10, 3080. https://doi.org/10.3390/cells10113080
Monnot S, Desaint H, Mary-Huard T, Moreau L, Schurdi-Levraud V, Boissot N. Deciphering the Genetic Architecture of Plant Virus Resistance by GWAS, State of the Art and Potential Advances. Cells. 2021; 10(11):3080. https://doi.org/10.3390/cells10113080
Chicago/Turabian StyleMonnot, Severine, Henri Desaint, Tristan Mary-Huard, Laurence Moreau, Valerie Schurdi-Levraud, and Nathalie Boissot. 2021. "Deciphering the Genetic Architecture of Plant Virus Resistance by GWAS, State of the Art and Potential Advances" Cells 10, no. 11: 3080. https://doi.org/10.3390/cells10113080
APA StyleMonnot, S., Desaint, H., Mary-Huard, T., Moreau, L., Schurdi-Levraud, V., & Boissot, N. (2021). Deciphering the Genetic Architecture of Plant Virus Resistance by GWAS, State of the Art and Potential Advances. Cells, 10(11), 3080. https://doi.org/10.3390/cells10113080






