Classification of Varieties of Grain Species by Artificial Neural Networks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Properties
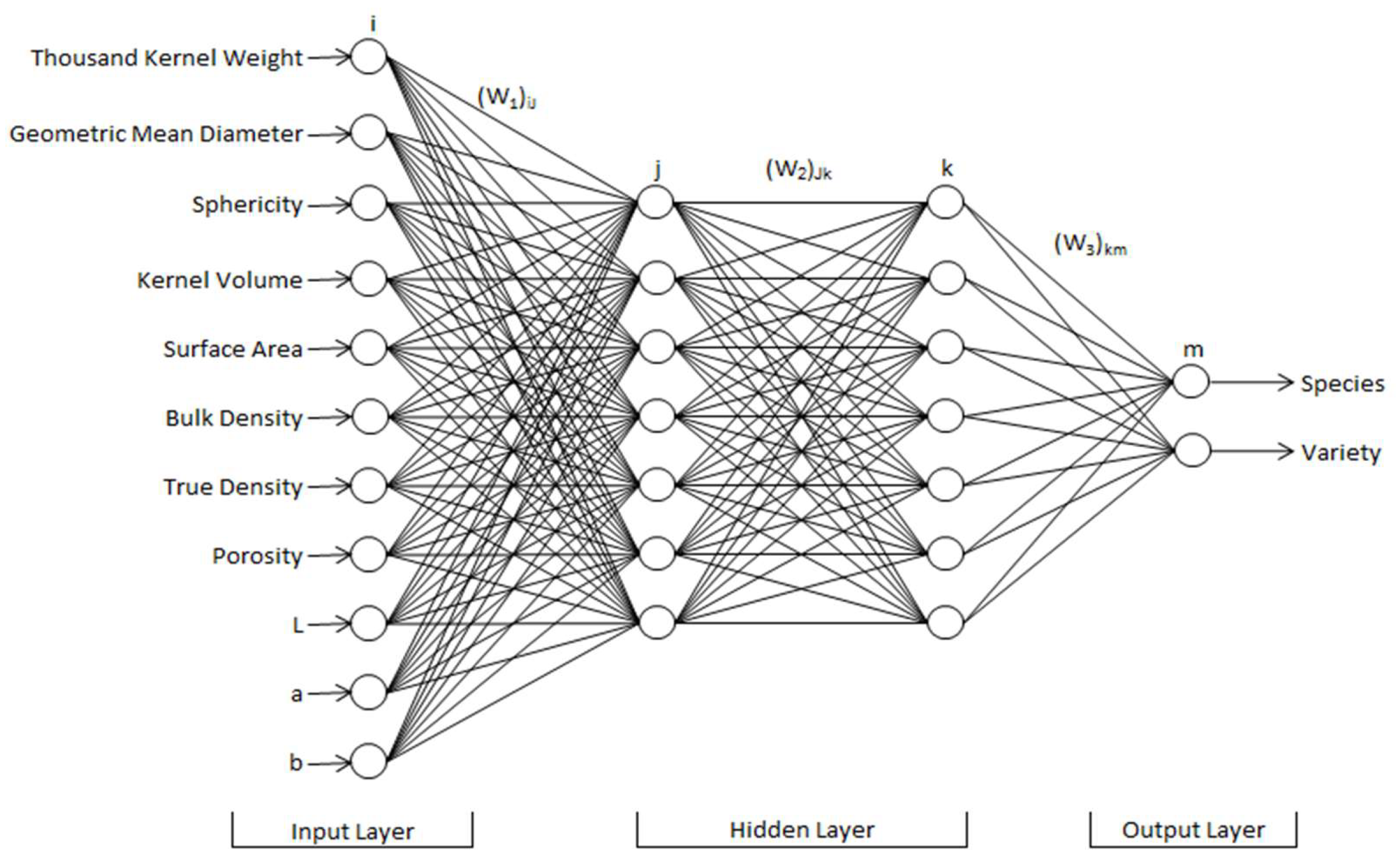
2.2. Artificial Neural Networks
3. Results and Discussion
3.1. Physical Properties
3.2. Thousand Kernel Weight
3.3. Geometric Mean Diameter
3.4. Sphericity
3.5. Kernel Volume
3.6. Surface Area
3.7. Bulk Density
3.8. True Density
3.9. Porosity
3.10. Colour
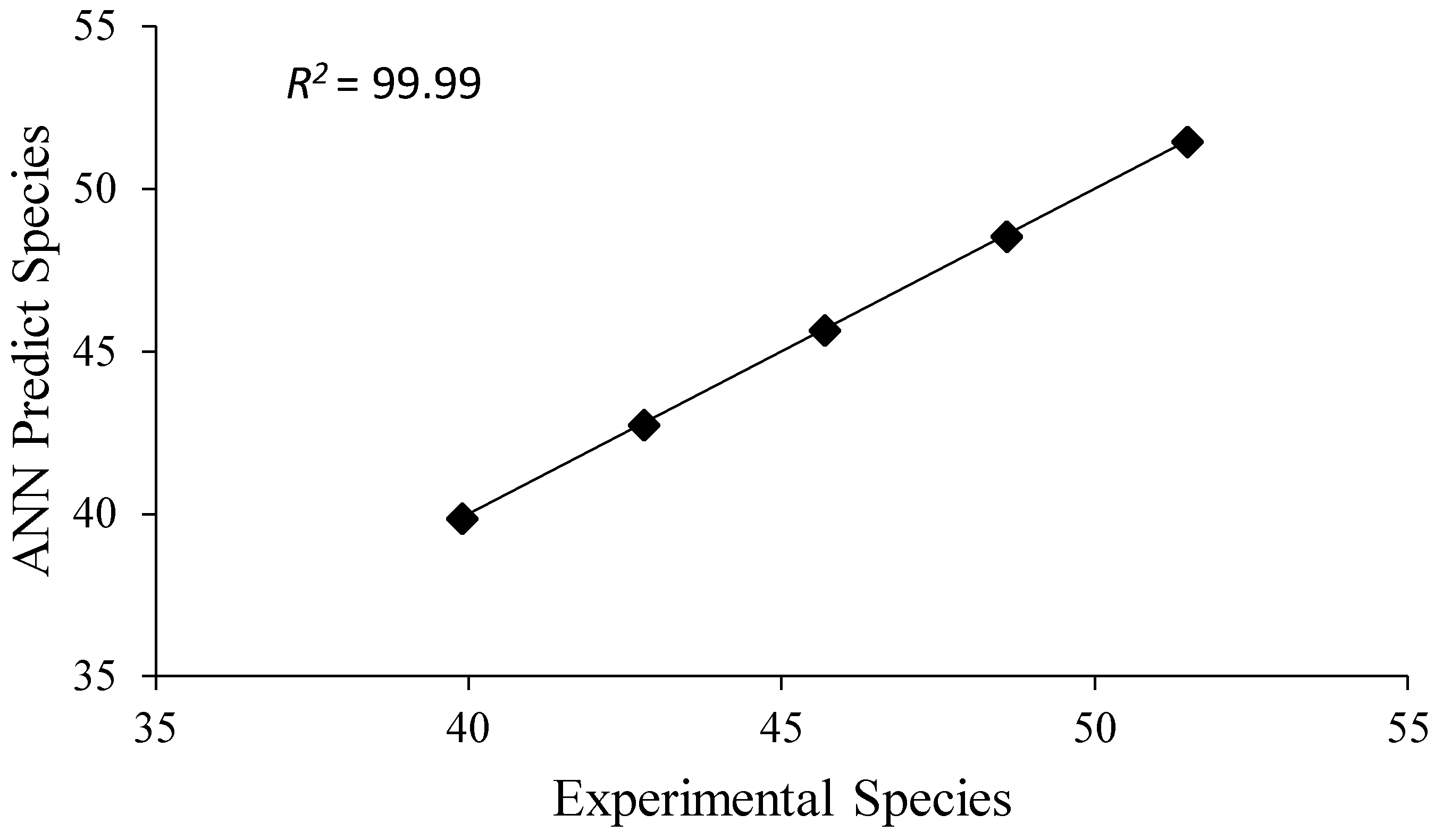
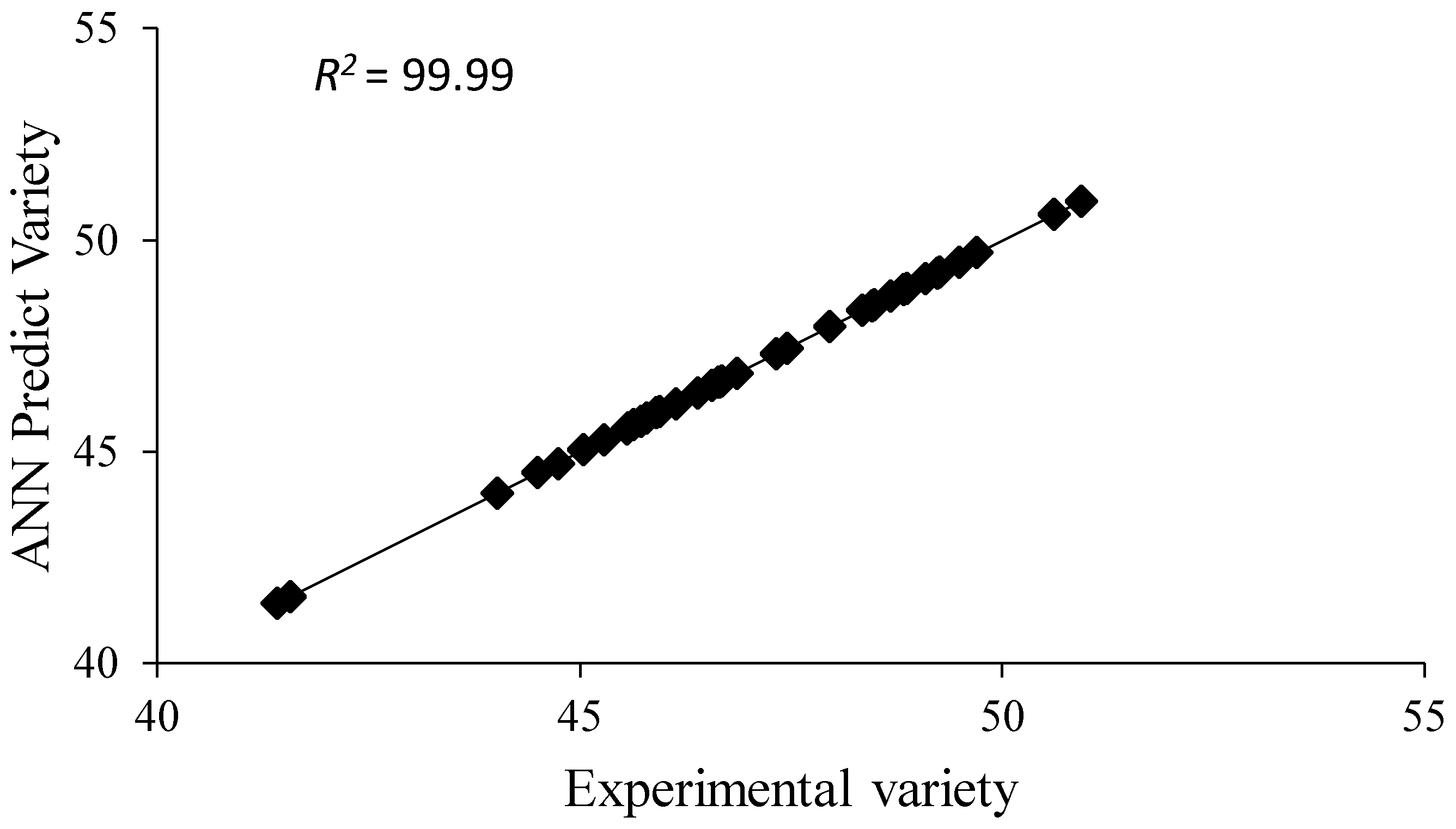
3.11. Artificial Neural Networks
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| RMSE | root mean square error |
| B | diameter of the spherical part of the kernel (mm) |
| Dg | geometric mean diameter (mm) |
| L | length (mm) |
| S | kernel surface area (mm2) |
| T | thickness (mm) |
| V | kernel volume (mm3) |
| W | width (mm) |
| sphericity (%) | |
| Pt | porosity (%) |
| ρb | bulk density (kg/m3) |
| ρt | true density (kg/m3) |
| m | thousand kernel weight (g) |
References
- Neuman, M.; Sapirstein, H.D.; Shwedyk, E.; Bushuk, W. Discrimination of wheat class and variety by digital image analysis of whole grain samples. J. Cereal Sci. 1987, 6, 125–132. [Google Scholar] [CrossRef]
- Barker, D.A.; Vouri, T.A.; Hegedus, M.R.; Myers, D.G. The use of ray parameters for the discrimination of Australian wheat varieties. Plant Var. Seeds 1992, 5, 35–45. [Google Scholar]
- Chen, X.; Xun, Y.; Li, W.; Zhang, J. Combining discriminant analysis and neural networks for corn variety identification. Comput. Electron. Agric. 2010, 71, 48–53. [Google Scholar] [CrossRef]
- Pourreza, A.; Pourreza, H.R.; Abbaspour-Fard, M.H.; Sadrnia, H. Identification of nine Iranian wheat seed varieties by textural analysis with image processing. Comput. Electron. Agric. 2012, 83, 102–108. [Google Scholar] [CrossRef]
- Mohsenin, N.N. Physical Properties of Plant and Animal Materials; Gordon and Breach Science Publishers Inc.: New York, NY, USA, 1970. [Google Scholar]
- Tabatabaeefar, A. Moisture-dependent physical properties of wheat. Int. Agrophys. 2003, 17, 207–211. [Google Scholar]
- Kalogirou, S.A. Applications of artificial neural networks in energy systems. Comput. Electron. Agric. 1999, 40, 1073–1087. [Google Scholar] [CrossRef]
- Aydogan, H.; Altun, A.A.; Ozcelik, A.E. Performance analysis of a turbo charged diesel engine using biodiesel with back propagation artificial neural network. Energy Educ. Sci. Technol-A. 2011, 28, 459–468. [Google Scholar]
- Visen, N.S.; Paliwal, J.; Jayas, D.S.; White, N.D.G. Specialist neural networks for cereal grain classification. Biosyst. Eng. 2002, 82, 151–159. [Google Scholar] [CrossRef]
- Dubey, B.P.; Bhagwat, S.G.; Shouche, S.P.; Sainis, J.K. Potential of artificial neural networks in varietal identification using morphometry of wheat grains. Biosyst. Eng. 2006, 95, 61–67. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial neural networks in the renewable energy systems applications: A review. Renew. Sustain. Energy Rev. 2001, 5, 373–401. [Google Scholar] [CrossRef]
- Paliwal, J.; Visen, N.S.; Jayas, D.S. Evaluation of neural network architectures for cereal grain classification using morphological features. J. Agric. Eng. Res. 2001, 79, 361–370. [Google Scholar] [CrossRef]
- Wang, N.; Dowell, F.; Zhang, N. Determining wheat vitreousness using image processing and a neural network. Presented at the 2002 ASAE Annual International Meeting/CIGR XVth World Congress, Chicago, IL, USA, 28–31 July 2002. [Google Scholar]
- Visen, N.S.; Jayas, D.S.; Paliwal, J.; White, N.D.G. Comparison of two neural network architectures for classification of singulated cereal grains. Can. Biosyst. Eng. 2004, 46, 7–14. [Google Scholar]
- Baykan, Ö.K.; Babalık, A.; Botsalı, F.M. Recognition of wheat type using artificial neural network. Presented at the 4th International Advanced Technologies Symposium, Konya, Turkey, 28–30 September 2005. [Google Scholar]
- Babalık, A.; Baykan, Ö.K.; Botsalı, F.M. Determination of wheat kernel type by using image processing techniques and ANN. Presented at the International Conference on Modelling and Simulating, Konya, Turkey, 28–30 August 2006. [Google Scholar]
- Pazoki, A.R.; Pazoki, Z. Classification system for rain fed wheat grain cultivars using artificial neural network. Afr. J. Biotechnol. 2011, 10, 8031–8038. [Google Scholar]
- Taner, A.; Tekgüler, A.; Sauk, H.; Demirel, B. Classification of oat varieties by using artificial neural networks. Presented at the 27th National Congress of Agricultural Mechanization, Samsun, Turkey, 5–7 September 2012. [Google Scholar]
- Liao, K.; Paulsen, M.R.; Reid, J.F.; Ni, B.C.; Bonifacio-Maghirang, E.P. Corn kernel breakage classification by machine vision using a neural network classifier. Trans. ASAE 1993, 36, 1949–1953. [Google Scholar] [CrossRef]
- Romaniuk, M.D.; Sokhansanj, S.; Wood, H.C. Barley seed recognition using a multi-layer neural network. Presented at the 1993 International ASAE Winter Meeting, Chicago, IL, USA, 14–17 December 1993. [Google Scholar]
- Jayas, D.S.; Paliwal, J.; Visen, N.S. Multi-layer neural networks for image analysis of agricultural products. J. Agric. Eng. Res. 2000, 77, 119–128. [Google Scholar] [CrossRef]
- Federico, M.; Remo, B.; Antonio, L.M.; Andrea, D.M.; Rita, A.; Roberta, F. Classification of 6 durum wheat cultivars from Sicily (Italy) using artificial neural networks. Chemometr. Intell. Lab. Syst. 2008, 90, 1–7. [Google Scholar]
- Wang, Z.; Cong, P.; Zhou, J.; Zhu, Z. Method for identification of external quality of wheat grain based on image processing and artificial neural network. Trans. CSAE 2007, 23, 158–161. [Google Scholar]
- Zapotoczny, P. Discrimination of wheat grain varieties using image analysis and neural networks. Part I. Single kernel texture. J. Cereal Sci. 2011, 54, 60–68. [Google Scholar]
- Jain, R.K.; Bal, S. Properties of pearl millet. J. Agric. Eng. Res. 1997, 66, 85–91. [Google Scholar] [CrossRef]
- Hacıseferogulları, H.; Özcan, M.; Demir, F.; Çalışır, S. Some nutritional and technological properties of garlic (Allium sativum L.). J. Food Eng. 2005, 68, 463–469. [Google Scholar] [CrossRef]
- Bell, M.; Fischer, R.A. Guide to Plant and Crop Sampling: Measurement and Observations for Agronomic and Physiological Research in Small Grain Cereals; Wheat Special Report No. 32; CIMMYT: Veracruz, Mexico, 1994. [Google Scholar]
- Cölkesen, M.; Öktem, A.; Eren, N.; Akıncı, C. Determination of suitable durum wheat varieties on dry and irrigated conditions in şanliurfa. Presented at the Symposium of Durum Wheat and Products, Ankara, Turkey, 30 November–3 December 1993. [Google Scholar]
- Aviara, N.A.; Gwandzang, M.I.; Haque, M.A. Physical properties of guna seeds. J. Agric. Eng. Res. 1999, 73, 105–111. [Google Scholar] [CrossRef]
- Sacilik, K.; Oztürk, R.; Keskin, R. Some physical properties of hemp seed. Biosyst. Eng. 2003, 86, 191–198. [Google Scholar] [CrossRef]
- Ogunjimi, L.O.; Aviara, N.A.; Aregbesola, O.A. Some engineering properties of locust bean seed. J. Food Eng. 2002, 55, 95–99. [Google Scholar] [CrossRef]
- Smedley, S.M. Discrimination between beers with small colour differences using the CIELAB colour space. J. Inst. Brew. 1995, 101, 195–201. [Google Scholar] [CrossRef]
- Connolly, C.; Fleiss, T. A study of efficiency and accuracy in the transformation from RGB to CIELAB colour space. IEEE Trans. Image Process. 1997, 6, 1046–1048. [Google Scholar] [CrossRef] [PubMed]
- Purushothaman, S.; Srinivasa, Y.G. A back-propagation algorithm applied to tool wear monitoring. Int. J. Mach. Tool Manuf. 1994, 34, 625–631. [Google Scholar] [CrossRef]
- Jacobs, R.A. Increased rate of convergence through learning rate adaptation. Neural Netw. 1988, 1, 295–307. [Google Scholar] [CrossRef]
- Minai, A.A.; Williams, R.D. Back-propagation heuristics: A study of the extended delta-bar-delta algorithm. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990. [Google Scholar]
- Levenberg, K. A method for the solution of certain nonlinear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquart, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Bechtler, H.; Browne, M.W.; Bansal, P.K.; Kecman, V. New approach to dynamic modelling of vapour-compression liquid chillers: Artificial neural networks. Appl. Therm. Eng. 2001, 21, 941–953. [Google Scholar] [CrossRef]
- Taner, A.; Tekgüler, A.; Sauk, H. Classification of durum wheat varieties by artificial neural networks. Anadolu J. Agric. Sci. 2015, 30, 51–59. [Google Scholar] [CrossRef]
- Yurtsever, N. Experimental Statistical Methods; Soil and Fertilizer Research Institute, The Global Forum on Agricultural Research and Innovation: Ankara, Turkey, 1984. [Google Scholar]
- Babi´c, L.; Babi´c, M.; Turan, J.; Mati´c-Keki´c, S.; Radojˇcin, M.; Mehandˇzi´c-Staniˇsi´c, S.; Pavkov, I.; Zoranovi´c, M. Physical and stress-strain properties of wheat (Triticum aestivum) kernel. J. Sci. Food Agric. 2011, 91, 1236–1243. [Google Scholar] [CrossRef] [PubMed]
- Topal, A.; Aydın, C.; Akgün, N.; Babaoglu, M. Diallel cross analysis in durum wheat (Triticum durum Desf.): Identification of best parents for some kernel physical features. Field Crop Res. 2004, 87, 1–12. [Google Scholar] [CrossRef]
- Güner, M. Pneumatic conveying characteristics of some agricultural seeds. J. Food Eng. 2007, 80, 904–913. [Google Scholar] [CrossRef]
- Dursun, E.; Güner, M. Determination of mechanical behaviour of wheat and barley under compression loading. J. Agric. Sci. 2003, 9, 415–420. [Google Scholar]
- Molenda, M.; Horabik, J. Part1: Characterization of mechanical properties of particulate solids for storage and handling. In Mechanical Properties of Granular Agro-Materials and Food Powders for Industrial Practice; Molenda, M., Horabik, J., Eds.; Institute of Agrophysics Polish Academy of Sciences: Lublin, Poland, 2005. [Google Scholar]
- Nelson, S.O. Dimensional and density data for seeds of cereal grain and other crops. Trans. ASAE 2002, 45, 165–170. [Google Scholar] [CrossRef]
- Markowski, M.; Zuk-Golaszewska, K.; Kwiatkowski, D. Influence of variety on selected physical and mechanical properties of wheat. Ind. Crop Prod. 2013, 47, 113–117. [Google Scholar] [CrossRef]
- Tavakoli, M.; Tavakoli, H.; Rajabipour, A.; Ahmadi, H.; Gharib-Zahedi, S.M.T. Moisture-dependent physical properties of barley grains. Int. J. Agric. Biol. Eng. 2009, 2, 84–91. [Google Scholar] [CrossRef]
- Song, H.; Litchfield, J.B. Predicting method of terminal velocity for grains. Trans. ASAE 1991, 34, 225–231. [Google Scholar] [CrossRef]
- Sokhansanj, S.; Lang, W. Prediction of kernel and bulk volüme of wheat and canola during adsorption and desorption. J. Agric. Eng. Res. 1996, 63, 129–136. [Google Scholar] [CrossRef]
| Bread Wheat | Durum Wheat | Barley | Oat | Triticale | |
|---|---|---|---|---|---|
| Ahmetağa | Karahan-99 | Altın | Avcı-2002 | Argentina | Karma 2000 |
| Alpu 2001 | Kınacı-97 | Altıntaç-95 | Aydanhanım | Checota | Melez-2001 |
| Atay-85 | Konya-2002 | Çeşit-1252 | Beyşehir | Faikbey | Mikham-2002 |
| Bağcı-2002 | Kutluk 94 | Dumlupınar | Çetin 2000 | Seydişehir | Samur Sortu |
| Bayraktar 2000 | Müfitbey | Kızıltan-91 | Karatay 94 | Y-1779 | |
| Bezostaja 1 | Pehlivan | Kümbet-2000 | Kıral-97 | Y-330 | |
| Dağdaş-94 | Soyer 02 | Meram-2002 | Konevi | ||
| Ekiz | Sönmez 2001 | Mirzabey-2000 | Larende | ||
| Eser | Sultan 95 | Selçuklu-97 | |||
| Gerek 79 | Süzen 97 | Yelken-2000 | |||
| Göksu-99 | Tosunbey | Yılmaz-98 | |||
| Gün-91 | Yakar-99 | ||||
| İkizce 96 | Yektay 406 | ||||
| İzgi 2001 | Yıldız 98 | ||||
| Species | Thousand Kernel Weight (g) | Geometric Mean Diameter (mm) | Sphericity (%) | Kernel Volume (mm3) | Surface Area (mm2) | Bulk Density (kg/m3) | True Density (kg/m3) | Porosity (%) | L | a | b |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bread Wheat | 42.23 ± 0.036 c | 3.93 ± 0.004 d | 60.85 ± 0.062 a | 21.04 ± 0.081 c | 40.96 ± 0.119 d | 773.17 ± 0.40 a | 1271.88 ± 1.78 a | 39.18 ± 0.096 d | 49.11 ± 0.026 c | 8.33 ± 0.01 b | 17.84 ± 0.013 c |
| Durum Wheat | 48.47 ± 0.057 a | 4.16 ± 0.007 c | 54.05 ± 0.098 b | 23.73 ± 0.129 b | 46.29 ± 0.190 c | 745.56 ± 0.64 b | 1270.65 ± 2.83 a | 41.30 ± 0.153 c | 48.66 ± 0.041 d | 0.86 ± 0.016 a | 17.65 ± 0.021 d |
| Barley | 48.49 ± 0.067 a | 4.44 ± 0.008 a | 50.78 ± 0.116 d | 28.11 ± 0.151 a | 53.19 ± 0.223 b | 679.43 ± 0.76 d | 1202.84 ± 3.33 c | 43.48 ± 0.179 b | 58.43 ± 0.049 a | 4.48 ± 0.019 e | 18.71 ± 0.025 b |
| Oat | 33.83 ± 0.078 d | 4.30 ± 0.010 b | 34.76 ± 0.134e | 23.45 ± 0.175 b | 55.22 ± 0.258 a | 482.80 ± 0.87 e | 997.36 ± 3.84 d | 51.54 ± 0.207 a | 55.36 ± 0.056 b | 6.82 ± 0.022 d | 19.00 ± 0.028 a |
| Triticale | 44.60 ± 0.095 b | 4.15 ± 0.012 c | 52.71 ± 0.164 c | 23.28 ± 0.214 b | 46.22 ± 0.316 c | 717.44 ± 1.07 c | 1228.01 ± 4.70 b | 41.58 ± 0.254 c | 45.59 ± 0.069 e | 7.29 ± 0.027 c | 15.06 ± 0.035 e |
| Mean | 43.59 | 4.10 | 54.81 | 22.96 | 45.57 | 720.21 | 1229.98 | 41.66 | 50.74 | 7.61 | 17.85 |
| CV (%) | 1.42 | 2.43 | 1.74 | 7.31 | 5.02 | 0.68 | 2.17 | 3.16 | 0.71 | 1.72 | 1.07 |
| LSD(0.05) | 0.25 | 0.03 | 0.42 | 0.56 | 0.82 | 2.81 | 12.33 | 0.66 | 0.18 | 0.07 | 0.09 |
| (J) | (W1)i1 | (W1)i2 | (W1)i3 | (W1)i4 | (W1)i5 | (W1)i6 | (W1)i7 | (W1)i8 | (W1)i9 | (W1)i10 | (W1)i11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5722 | −0.1842 | 0.2088 | −0.4904 | 0.8882 | 0.0004 | 0.1553 | −0.2154 | 0.0294 | 0.2401 | 0.0727 |
| 2 | 0.1007 | 0.7627 | −0.2897 | 0.4454 | −1.485 | −1.0178 | 0.7479 | −0.7256 | −0.3673 | 0.0447 | −0.4264 |
| 3 | −0.0103 | 0.0607 | −0.0985 | 0.0191 | −0.0794 | −0.0455 | −0.0053 | −0.0056 | −0.0095 | −0.0704 | −0.0183 |
| 4 | −3.8002 | 7.4396 | 2.5305 | −15.66 | 10.0015 | −39.2805 | 26.9969 | −27.0111 | 2.3286 | −4.7543 | −3.5571 |
| 5 | 3.1613 | 10.7492 | −8.5456 | 7.0885 | −22.8294 | 7.962 | −8.0335 | 7.4794 | 0.9506 | 0.1078 | −1.782 |
| 6 | −0.0105 | 0.0993 | −0.1542 | 0.0196 | −0.1033 | −0.0662 | −0.0115 | −0.0028 | −0.0117 | −0.1014 | −0.0257 |
| 7 | −0.0855 | −0.7741 | 0.1382 | −0.4588 | 1.6941 | −0.0753 | −0.0859 | 0.1043 | 0.1076 | 1.8165 | 0.1336 |
| (k) | (W2)j1 | (W2)j2 | (W2)j3 | (W2)j4 | (W2)j5 | (W2)j6 | (W2)j7 |
|---|---|---|---|---|---|---|---|
| 1 | −5.1431 | 70.406 | −4.5058 | −18.016 | −11.9865 | −7.7543 | 15.8411 |
| 2 | −0.1415 | 0.0677 | −40.336 | −0.0007 | −0.0007 | 19.4536 | −0.0737 |
| 3 | 51.1274 | 85.4875 | −25.997 | 66.2967 | 50.4012 | −36.0585 | −67.172 |
| 4 | −32.12 | −63.85 | −4.2685 | 15.3922 | 5.191 | 1.8093 | 29.4206 |
| 5 | 0.3936 | −0.2782 | 18.4034 | 0.1364 | 0.1275 | −13.0859 | −4.0637 |
| 6 | 6.5031 | −57.464 | −8.112 | −13.945 | 78.3948 | −9.5059 | 81.1453 |
| 7 | −14.722 | −56.893 | 17.9144 | −18.052 | −13.727 | 13.933 | 8.3927 |
| (m) | (W3)k1 | (W3)k2 | (W3)k3 | (W3)k4 | (W3)k5 | (W3)k6 | (W3)k7 |
|---|---|---|---|---|---|---|---|
| 1 | −0.007 | 32.1518 | −0.0078 | −0.0003 | 10.3896 | 0.0001 | −0.0089 |
| 2 | 0.25 | −0.0002 | 0.75 | 1 | 0.0006 | 0.25 | 0 |
| Number of Neurons | bi | bj | bk |
|---|---|---|---|
| 1 | −1.2269 | 2.1839 | −15.7802 |
| 2 | 1.4557 | 13.8917 | −0.2506 |
| 3 | 0.8503 | −63.862 | |
| 4 | 23.8469 | −23.8218 | |
| 5 | 2.7217 | 2.2416 | |
| 6 | 0.7096 | −32.6007 | |
| 7 | −1.2706 | 30.4023 |
| Output | Training Set | Test Set | ||
|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | |
| Species | 0.000027 | 0.99 | 0.000184 | 0.99 |
| Variety | 0.000318 | 0.99 | 0.000624 | 0.99 |
| Variety | Variety | Species | ||||
|---|---|---|---|---|---|---|
| Experimental Data | Test Data | Error (%) | Experimental Data | Test Data | Error (%) | |
| Sultan 95 | 49.26 | 49.26 | 0.004 | 39.89 | 39.89 | 0.000 |
| Süzen 97 | 46.65 | 46.65 | 0.004 | 39.89 | 39.89 | 0.000 |
| Tosunbey | 47.96 | 47.96 | 0.001 | 39.89 | 39.89 | 0.000 |
| Gerek 79 | 45.79 | 45.79 | 0.001 | 39.89 | 39.89 | 0.000 |
| Alpu 2001 | 49.70 | 49.70 | 0.003 | 39.89 | 39.89 | 0.000 |
| İkizce 96 | 45.05 | 45.06 | 0.016 | 39.89 | 39.89 | 0.000 |
| Göksu-99 | 45.57 | 45.57 | 0.002 | 39.89 | 39.89 | 0.000 |
| Konya-2002 | 46.57 | 46.57 | 0.004 | 39.89 | 39.89 | 0.000 |
| Müfitbey | 45.73 | 45.72 | 0.006 | 39.89 | 39.89 | 0.000 |
| Kınacı-97 | 48.83 | 48.83 | 0.016 | 39.89 | 39.89 | 0.000 |
| Bağcı-2002 | 46.68 | 46.68 | 0.001 | 39.89 | 39.89 | 0.000 |
| Bayraktar 2000 | 45.91 | 45.92 | 0.008 | 39.89 | 39.89 | 0.000 |
| Ahmetağa | 45.64 | 45.64 | 0.006 | 39.89 | 39.89 | 0.000 |
| Ekiz | 47.45 | 47.45 | 0.001 | 39.89 | 39.89 | 0.000 |
| Pehlivan | 49.49 | 49.49 | 0.002 | 39.89 | 39.90 | 0.031 |
| Altıntaç-95 | 46.64 | 46.64 | 0.001 | 42.78 | 42.78 | 0.008 |
| Çeşit-1252 | 50.93 | 50.93 | 0.001 | 42.78 | 42.78 | 0.000 |
| Mirzabey-2000 | 48.67 | 48.67 | 0.004 | 42.78 | 42.78 | 0.000 |
| Meram-2002 | 50.61 | 50.61 | 0.003 | 42.78 | 42.78 | 0.000 |
| Yılmaz-98 | 48.87 | 48.87 | 0.009 | 42.78 | 42.78 | 0.000 |
| Kızıltan-91 | 48.34 | 48.34 | 0.008 | 42.78 | 42.78 | 0.000 |
| Karatay 94 | 45.28 | 45.29 | 0.009 | 45.67 | 45.67 | 0.000 |
| Çetin 2000 | 47.32 | 47.31 | 0.024 | 45.67 | 45.67 | 0.000 |
| Larende | 48.49 | 48.49 | 0.005 | 45.67 | 45.67 | 0.000 |
| Avcı-2002 | 48.46 | 48.45 | 0.009 | 45.67 | 45.67 | 0.000 |
| Kıral-97 | 44.75 | 44.72 | 0.069 | 45.67 | 45.67 | 0.000 |
| Beyşehir | 49.23 | 49.23 | 0.006 | 45.67 | 45.67 | 0.000 |
| Aydanhanım | 49.09 | 49.08 | 0.005 | 45.67 | 45.67 | 0.000 |
| Karma 2000 | 46.40 | 46.39 | 0.005 | 48.57 | 48.57 | 0.000 |
| Melez-2001 | 45.94 | 45.95 | 0.012 | 48.57 | 48.57 | 0.000 |
| Mikham-2002 | 46.14 | 46.13 | 0.007 | 48.57 | 48.57 | 0.000 |
| Samur Sortu | 44.02 | 44.02 | 0.002 | 48.57 | 48.57 | 0.002 |
| Y-1779 | 45.55 | 45.54 | 0.034 | 51.46 | 51.46 | 0.000 |
| Checota | 44.50 | 44.50 | 0.010 | 51.46 | 51.46 | 0.000 |
| Argentina | 41.43 | 41.43 | 0.002 | 51.46 | 51.46 | 0.000 |
| Seydişehir | 46.86 | 46.85 | 0.035 | 51.46 | 51.46 | 0.000 |
| Faikbey | 41.58 | 41.57 | 0.011 | 51.46 | 51.46 | 0.000 |
| Mean Error | 0.009 | 0.001 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taner, A.; Öztekin, Y.B.; Tekgüler, A.; Sauk, H.; Duran, H. Classification of Varieties of Grain Species by Artificial Neural Networks. Agronomy 2018, 8, 123. https://doi.org/10.3390/agronomy8070123
Taner A, Öztekin YB, Tekgüler A, Sauk H, Duran H. Classification of Varieties of Grain Species by Artificial Neural Networks. Agronomy. 2018; 8(7):123. https://doi.org/10.3390/agronomy8070123
Chicago/Turabian StyleTaner, Alper, Yeşim Benal Öztekin, Ali Tekgüler, Hüseyin Sauk, and Hüseyin Duran. 2018. "Classification of Varieties of Grain Species by Artificial Neural Networks" Agronomy 8, no. 7: 123. https://doi.org/10.3390/agronomy8070123
APA StyleTaner, A., Öztekin, Y. B., Tekgüler, A., Sauk, H., & Duran, H. (2018). Classification of Varieties of Grain Species by Artificial Neural Networks. Agronomy, 8(7), 123. https://doi.org/10.3390/agronomy8070123





