Assessing Olive Evapotranspiration Partitioning from Soil Water Balance and Radiometric Soil and Canopy Temperatures
Abstract
1. Introduction
2. Material and Methods
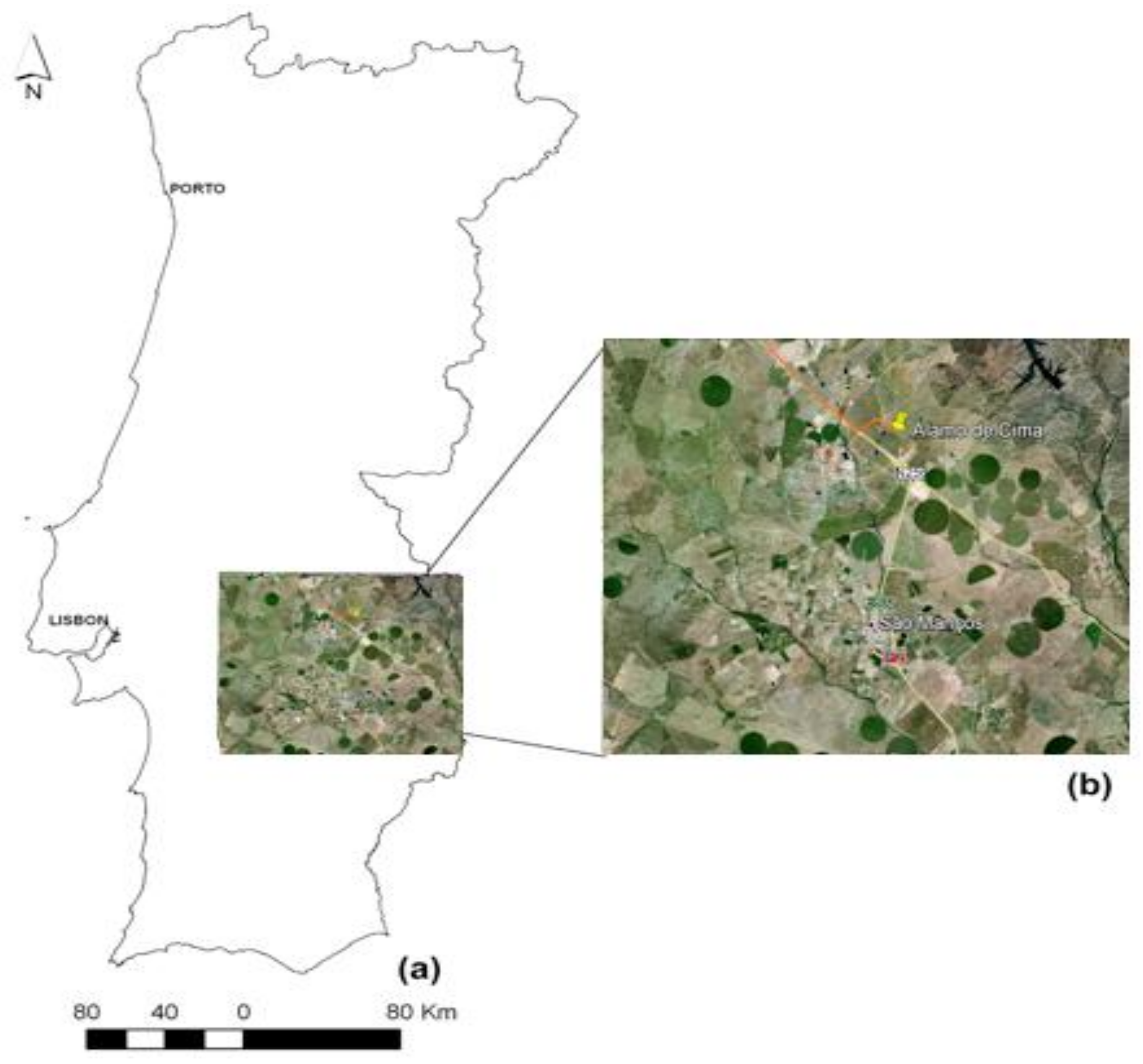
2.1. Study Site and Measurements
2.2. Field Data
2.3. The STSEB Simplified Energy Balance Model
2.4. The SIMDualKc Water Balance Model
2.5. Statistical Analysis
3. Results and Discussion
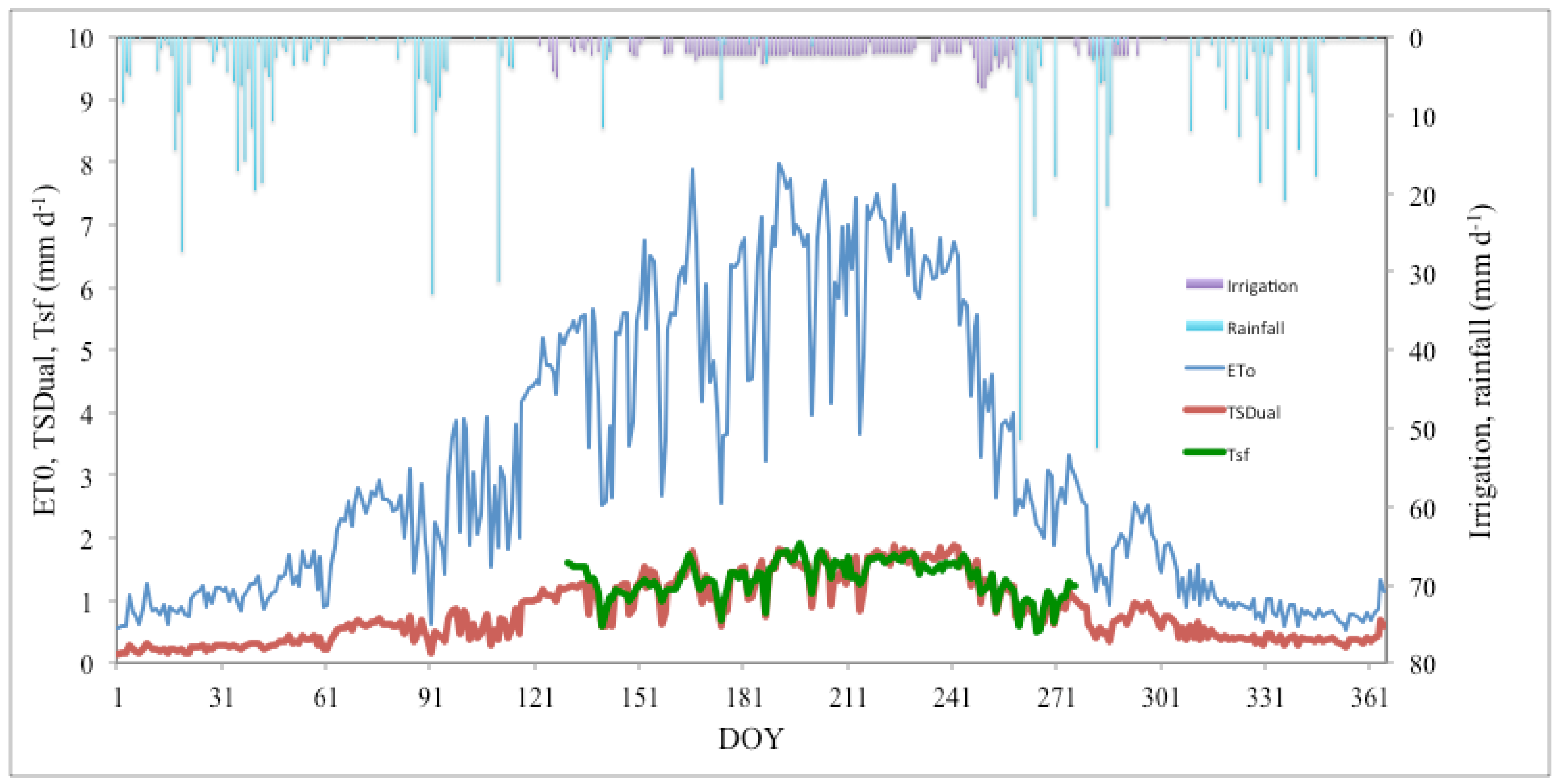
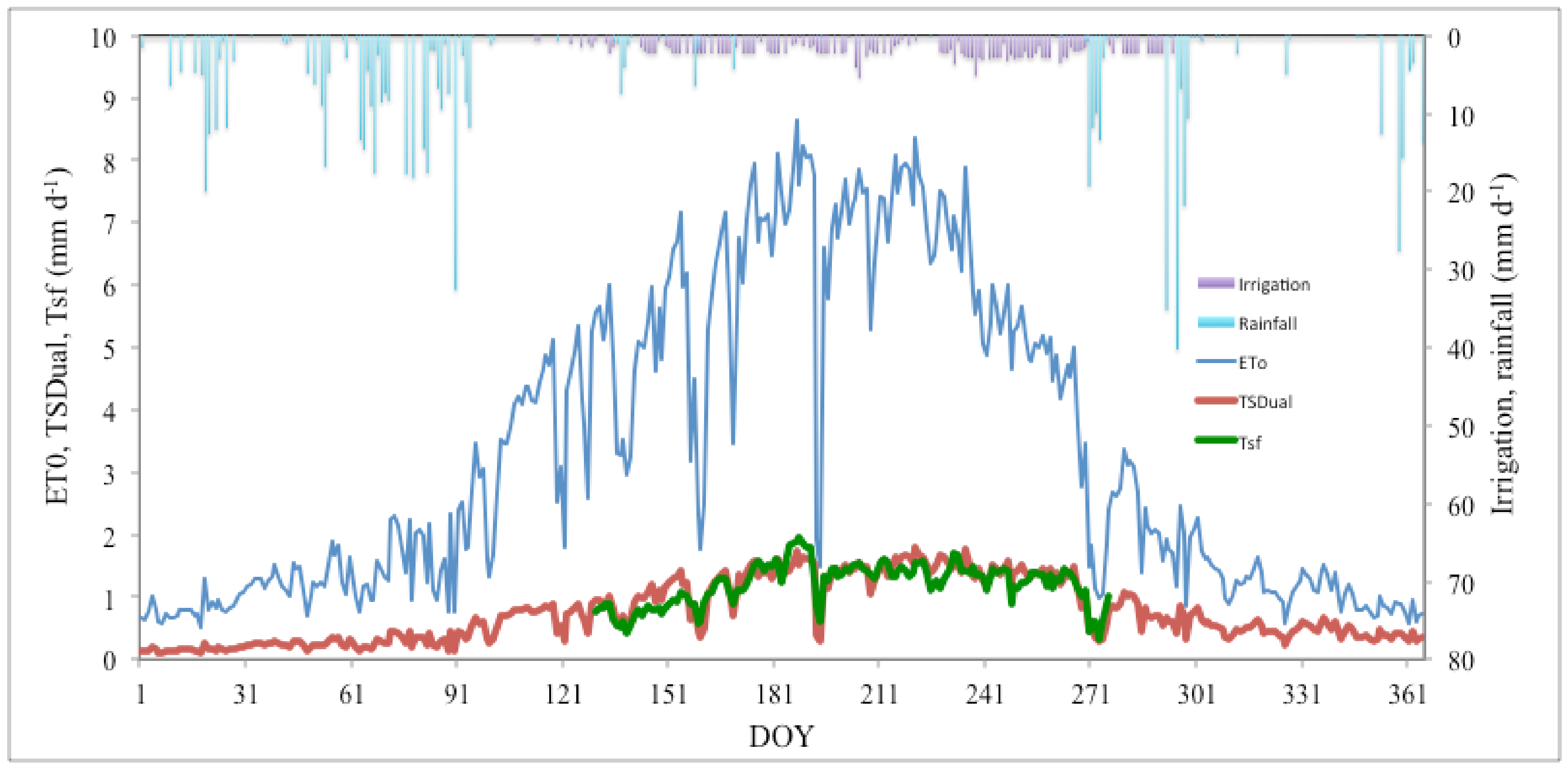
3.1. Validation of the SIMDualKc Model
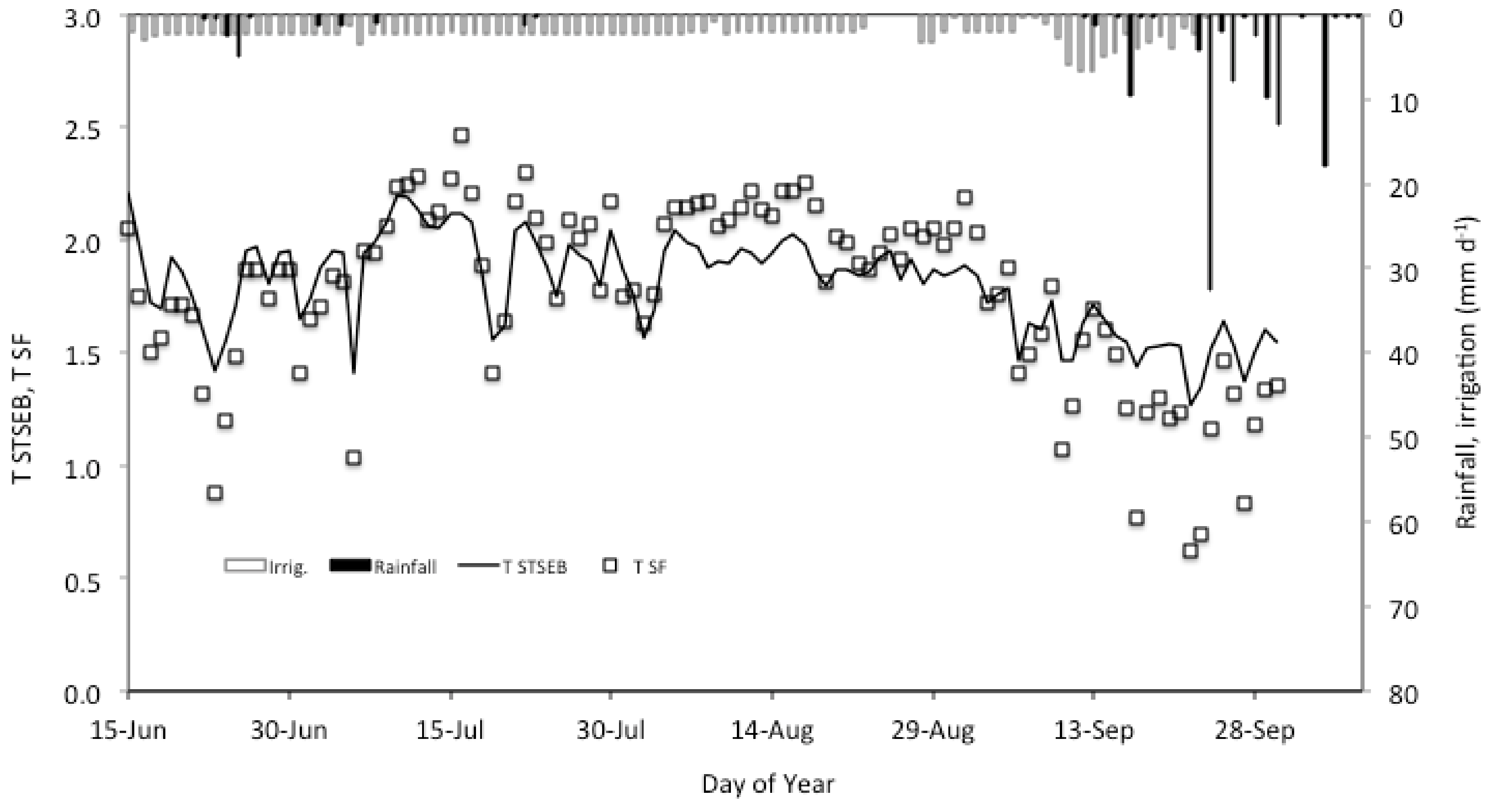
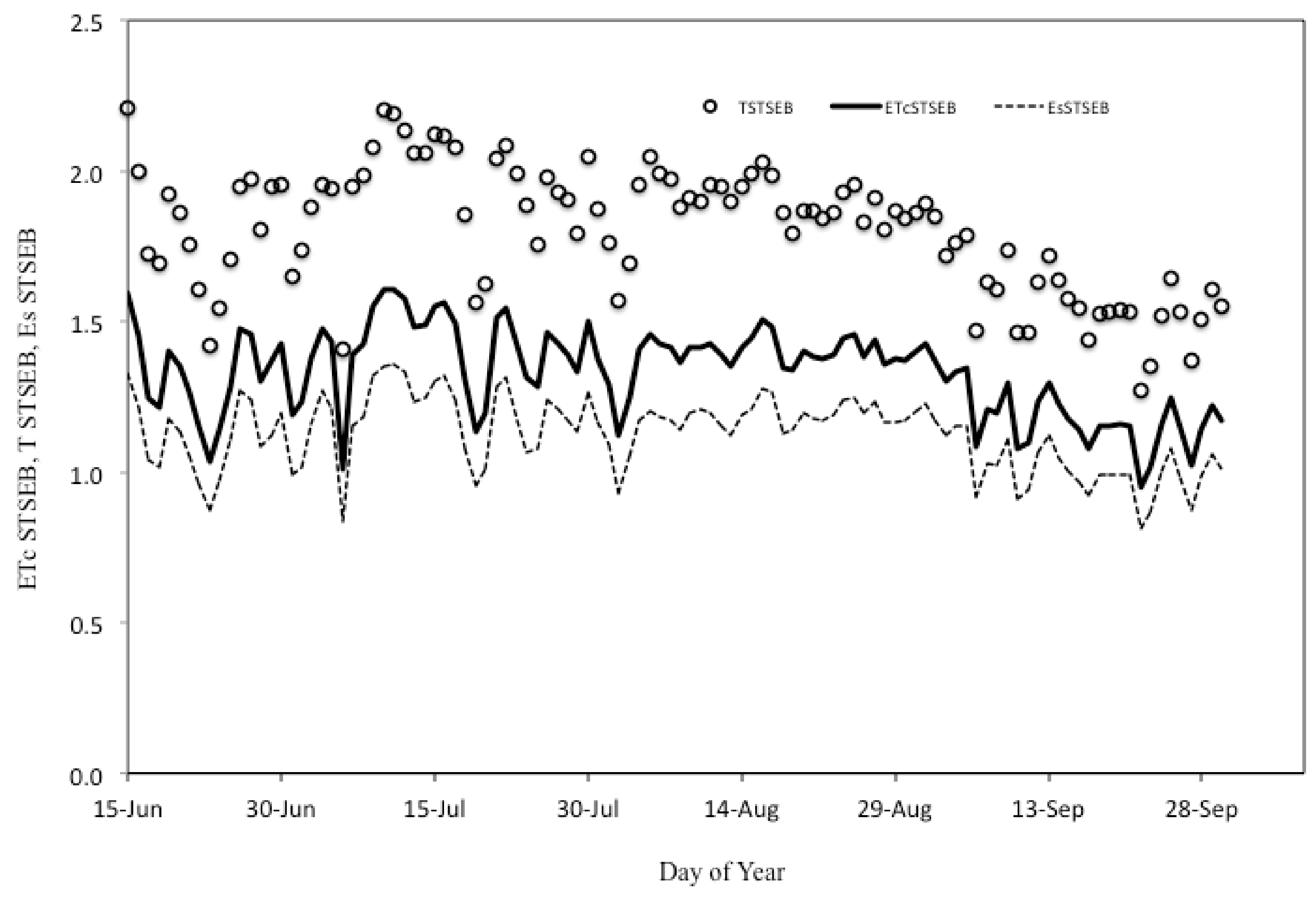
3.2. Validation TSTSEB with Field Sap Flow Transpiration Rates
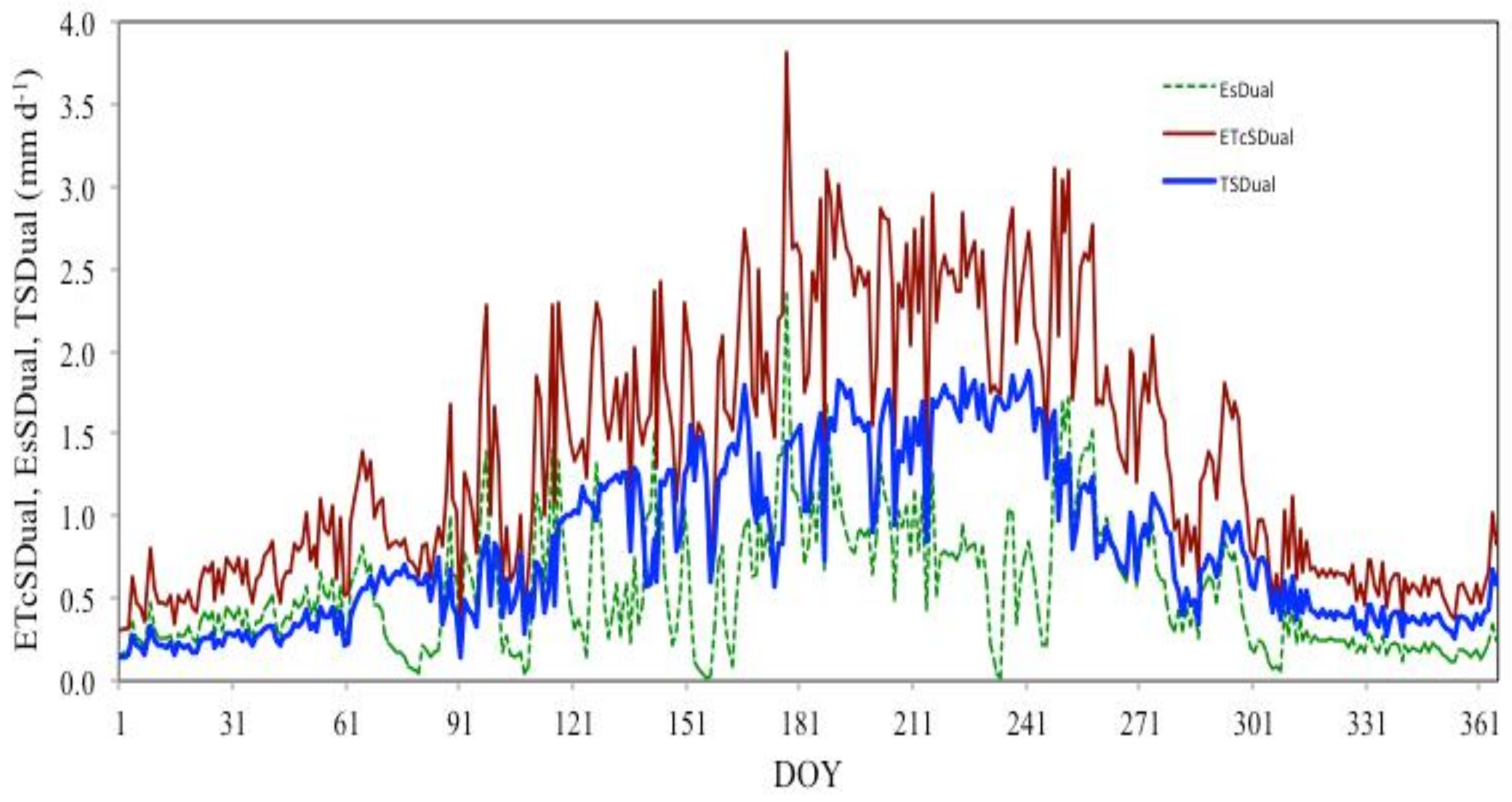
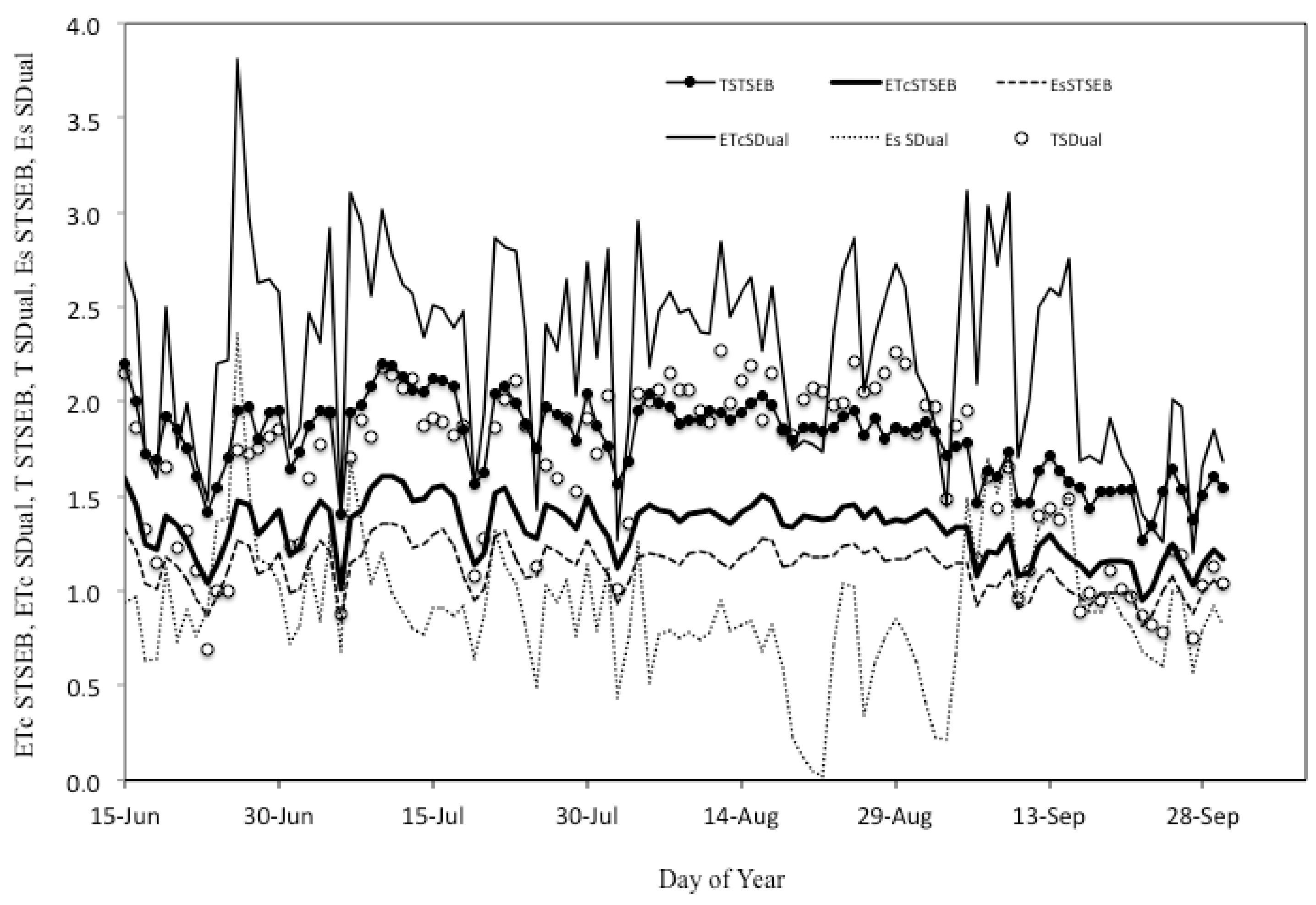
3.3. Assessing ETc with the SIMDualKc and STSEB Models
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Fereres, E.; Soriano, M. Deficit Irrigation for Reducing Agricultural Water Use. J. Exp. Bot. 2007, 58, 147–159. [Google Scholar] [CrossRef] [PubMed]
- Fernández, J.E.; Perez-Martin, A.; Torres-Ruiz, J.M.; Cuevas, M.V.; Rodriguez-Dominguez, C.M.; Elsayed-Farag, S.; Morales-Sillero, A.; García, J.M.; Hernandez-Santana, V.; Diaz-Espejo, A. A regulated deficit irrigation strategy for hedgerow olive orchards with high plant density. Plant Soil 2013, 372, 279–295. [Google Scholar] [CrossRef]
- Palese, A.M.; Nuzzo, V.; Favati, F.; Pietrafesa, A.; Celano, G.; Xiloyannisa, C. Effects of water deficit on the vegetative response, yield and oil quality of olive trees (Olea europaea L., cv Coratina) grown under intensive cultivation. Sci. Hortic. 2010, 125, 222–229. [Google Scholar] [CrossRef]
- Iniesta, F.; Testi, L.; Orgaz, F.; Villalobos, F.J. The effects of regulated and continuous deficit irrigation on the water use, growth and yield of olive trees. Eur. J. Agron. 2009, 30, 258–265. [Google Scholar] [CrossRef]
- Moriana, A.; Orgaz, F.; Pastor, M.; Fereres, E. Yield responses of a mature olive orchard to water deficits. J. Am. Soc. Hortic. Sci. 2003, 128, 425–431. [Google Scholar]
- Connor, D.J. Adaptation of olive (Olea europaea L.) to water-limited environments. Aust. J. Agric. Res. 2005, 56, 1181–1189. [Google Scholar] [CrossRef]
- Girona, J.; Mata, M.; Arbonès, A.; Alegre, S.; Rufat, J.; Marsal, J. Peach tree response to single and combined regulated deficit irrigation regimes under swallow soils. J. Am. Soc. Hortic. Sci. 2003, 128, 432–440. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guide-Lines for Computing Crop Water Requirements; Irrigation and Drainage Paper; FAO: Rome, Italy, 1998; p. 56. [Google Scholar]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Paredes, P.; Rodrigues, G.C.; Alves, I.; Pereira, L.S. Partitioning evapotranspiration, yield prediction and economic returns of maize under various irrigation management strategies. Agric. Water Manag. 2014, 135, 27–39. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Smith, M.; Raes, D.; Wright, J. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Rodrigues, G.C.; Neves, M. Modeling malt barley water use and evapotranspiration partitioning in two contrasting rainfall years. Assessing AquaCrop and SIMDualKc models. Agric. Water Manag. 2015, 159, 239–254. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Alves, I.; Fernando, R.M.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software. 1. Background and computational strategy. Agric. Water Manag. 2012, 103, 8–24. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Fernando, R.M.; Alves, I.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software: 2. Model testing. Agric. Water Manag. 2012, 103, 62–77. [Google Scholar] [CrossRef]
- Paço, T.A.; Pôças, I.; Cunha, M.; Silvestre, J.C.; Santos, F.L.; Paredes, P.; Pereira, L.S. Evapotranspiration and crop coefficients for a super intensive olive orchard. An application of SIMDualKc and METRIC models using ground and satellite observations. J. Hydrol. 2014, 519, 2067–2080. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.; Paredes, P.; Cunha, M.; Pereira, L. Estimation of actual crop coefficients using remotely sensed vegetation indices and soil water balance modelled data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef]
- Pôças, I.; Paço, T.A.; Cunha, M.; Andrade, J.A.; Silvestre, J.; Sousa, A.; Santos, F.L.; Pereira, L.S.; Allen, R.G. Satellite based evapotranspiration of a super-intensive olive orchard: Application of METRIC algorithms. Biosyst. Eng. 2014, 126, 69–81. [Google Scholar] [CrossRef]
- Wei, Z.; Paredes, P.; Liu, Y.; Chi, W.-W.; Pereira, L.S. Modelling transpiration, soil evaporation and yield prediction of soybean in North China Plain. Agric. Water Manag. 2015, 147, 43–53. [Google Scholar] [CrossRef]
- Zhao, N.; Liu, Y.; Cai, J.; Paredes, P.; Rosa, R.D.; Pereira, L.S. Dual crop coefficient modeling applied to the winter wheat—Summer maize crop sequence in North China Plain: Basal crop coefficients and soil evaporation component. Agric. Water Manag. 2013, 117, 93–105. [Google Scholar] [CrossRef]
- Fandiño, M.; Cancela, J.J.; Rey, B.J.; Martínez, E.M.; Rosa, R.G.; Pereira, L.S. Using the dual-Kc approach to model evapotranspiration of albariño vineyards (Vitis vinifera L. cv. albariño) with consideration of active ground cover. Agric. Water Manag. 2012, 112, 75–87. [Google Scholar] [CrossRef]
- Flumignan, D.L.; de Faria, R.T.; Prete, C.E.C. Evapotranspiration components and dual crop coefficients of coffee trees during crop production. Agric. Water Manag. 2011, 98, 791–800. [Google Scholar] [CrossRef]
- Paço, T.; Ferreira, M.; Rosa, R.; Paredes, P.; Rodrigues, G.; Conceição, N.; Pacheco, C.; Pereira, L. The dual crop coefficient approach using a density factor to simulate the evapotranspiration of a peach orchard: SIMDualKc model versus eddy covariance measurements. Irrig. Sci. 2012, 30, 115–126. [Google Scholar] [CrossRef]
- Diarra, A.; Jarlan, L.; Er-Raki, S.; Le Page, M.; Khabba, S.; Bigeard, G.; Tavernier, A.; Chirouze, J.; Fanise, P.; Moutammani, A.; et al. Characterization of evapotranspiration over irrigated crops in a semi-arid area (Marrakech, Marocco). Procedia Environ. Sci. 2013, 19, 504–513. [Google Scholar] [CrossRef][Green Version]
- Minacapilli, M.; Agnese, C.; Blanda, F.; Cammalleri, C.; Ciraolo, G.; D’Urso, G.; Iovino, M.; Pumo, D.; Provenzano, G.; Rallo, G. Estimation of actual evapotranspiration of Mediterranean perennial crops by means of remote-sensing based surface energy balance models. Hydrol. Earth Syst. Sci. 2009, 13, 1061–1074. [Google Scholar] [CrossRef]
- Neale, C.; Geli, H.; Kustas, W.P.; Alfieri, J.G.; Gowda, P.; Evett, S.R.; Prueger, J.H.; Hipps, L.E.; Dulaney, W.P.; Chavez, J.; et al. Soil water content estimation using a remote sensing based hybrid evapotranspiration modeling approach. Adv. Water Res. 2012, 50, 152–161. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Ciraolo, G.; D’Urso, G.; Kustas, W.P.; La Loggia, G.; Minacapilli, M. Applications of a remote sensing-based two-source energy balance algorithm for mapping surface fluxes without in situ air temperature observations. Remote Sens. Environ. 2012, 124, 502–515. [Google Scholar] [CrossRef]
- Liu, S.; Lu, L.; Mao, D.; Jia, L. Evaluating parameterizations of aerodynamic resistance to heat transfer using field measurements. Hydrol. Earth Syst. Sci. 2007, 11, 769–783. [Google Scholar] [CrossRef]
- Yunusa, I.A.M.; Walker, R.R.; Lu, P. Evapotranspiration components from energy balance, sap flow and microlysimetry techniques for an irrigated vineyard in inland Australia. Agric. For. Meteorol. 2004, 127, 93–107. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops—An energy combination theory. Quart. J. Roy. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M. Modelling surface energy fluxes over maize using a two-source patch model and radiometric soil and canopy temperature observations. Remote Sens. Environ. 2008, 112, 1130–1143. [Google Scholar] [CrossRef]
- Sánchez, J.M.; López-Urrea, R.; Rubio, E.; González-Piqueras, J.; Caselles, V. Assessing crop coefficients of sunflower and canola using two-source energy balance and thermal radiometry. Agric. Water Manag. 2014, 137, 23–29. [Google Scholar] [CrossRef]
- Sánchez, J.M.; López-Urrea, R.; Rubio, E.; Caselles, V. Determining water use of sorghum from two-source energy balance and radiometric temperatures. Hydrol. Earth Syst. Sci. 2011, 15, 3061–3070. [Google Scholar] [CrossRef]
- World Reference Base (WRB). World Reference Base for Soil Resources; World Soil Resources Report 84; FAO: Rome, Italy, 2006. [Google Scholar]
- Green, S.R.; Clothier, B.E.; Jardine, B. Theory and practical application of heat pulse to measure sap flow. Agron. J. 2003, 95, 1371–1379. [Google Scholar] [CrossRef]
- Santos, F.L.; Valverde, P.C.; Ramos, A.F.; Reis, J.L.; Castanheira, N.L. Water use and response of a dry-farmed olive orchard recently converted to irrigation. Biosyst. Eng. 2007, 98, 102–114. [Google Scholar] [CrossRef]
- Fernández, J.E.; Palomo, M.J.; Díaz-Espejo, A.; Clothier, B.E.; Green, S.R.; Girón, I.F.; Moreno, F. Heat-pulse measurements of sap flow in olives for automating irrigation: Tests, root flow and diagnostics of water stress. Agric. Water Manag. 2001, 51, 99–123. [Google Scholar] [CrossRef]
- Villalobos, F.J.; Orgaz, F.; Mateos, L. Non-destructive measurement of leaf area in olive (Olea europaea L.) trees using a gap inversion method. Agric. For. Meteorol. 1995, 73, 29–42. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar]
- Ortega Farías, S.; Antonioletti, R.; Olioso, A. Net radiation model evolution at an hourly time step for Mediterranean conditions. Agronomie 2000, 20, 157–164. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Monteith, J.L. A four-layer model for the heat budget of homogeneous land surfaces. Quart. J. R. Meteorol. Soc. 1998, 114, 373–398. [Google Scholar] [CrossRef]
- Kalma, J.D. A Comparison of Expressions for the Aerodynamic Resistance to Sensible Heat Transfer; Technical Memorandum 89/6; CSIRO, Institute of Natural Resources and Energy, Division of Water Resources: Canberra, Australia, 1989. [Google Scholar]
- Ezzahar, J.; Er-Raki, S.; Marah, H.; Khabba, S.; Amenzou, N.; Chehbouni, G. Coupling soil-vegetationatmosphere-transfer model with energy balance model for estimating energy and water vapor fluxes over an olive grove in a semi-arid region. Glob. Meteorol. 2012, 1. [Google Scholar] [CrossRef]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef]
| Mean Maximum Temperature (°C) | Mean Mimimum Temperature (°C) | Rainfall (mm Month−1) | ETo (mm Month−1) | |||||
|---|---|---|---|---|---|---|---|---|
| Month | 2013 | 2014 | 2013 | 2014 | 2013 | 2014 | 2013 | 2014 |
| January | 15.2 | 14.9 | 6.3 | 6.8 | 89.9 | 102.2 | 28.4 | 31.9 |
| February | 14.8 | 14.5 | 3.8 | 5.6 | 48.9 | 148.0 | 42.5 | 35.0 |
| March | 16.2 | 18.5 | 7.9 | 5.9 | 240 | 40.1 | 51.5 | 80.9 |
| April | 20.8 | 21.3 | 7.7 | 9.7 | 26.2 | 119.1 | 99.9 | 82.3 |
| May | 24.6 | 25.7 | 8.2 | 9.9 | 15.2 | 16.7 | 134.6 | 144.1 |
| June | 29.8 | 28.5 | 12.3 | 13.1 | 13.0 | 9.4 | 167.6 | 150.7 |
| July | 33.1 | 31.5 | 15.3 | 14.3 | 0.1 | 5.5 | 175.3 | 173.8 |
| August | 35.0 | 31.7 | 15.0 | 14.6 | 0.1 | 0.0 | 176.0 | 175.2 |
| September | 31.0 | 27.7 | 14.4 | 15.6 | 55.9 | 124.1 | 125.4 | 97.8 |
| October | 24.3 | 24.8 | 12.8 | 13.9 | 159.9 | 106.3 | 83.5 | 80.1 |
| November | 16.9 | 16.8 | 5.9 | 7.7 | 8.2 | 172.8 | 52.8 | 53.5 |
| December | 15.6 | 14.3 | 4.4 | 3.7 | 79.7 | 9.0 | 43.0 | 35.0 |
| Parameters | Initial | Calibrated |
|---|---|---|
| KcbSDual ini | 0.5 | 0.4 |
| KcbSDual mid | 0.55 | 0.3 |
| KcbSDual end | 0.5 | 0.5 |
| pini, pmid, pend | 0.5 | 0.4; 0.4; 0.5 |
| Soil evaporation parameters | ||
| REW (mm) | 9.0 | 8.0 |
| TEW (mm) | 22.0 | 22.0 |
| Ze (mm) | 0.10 | 0.10 |
| Runoff and deep percolation parameters | ||
| CN | 68 | 68 |
| aD | 235 | 235 |
| bD | 0.02 | 0.02 |
| TSDual vs. Tsf | n | b | R2 | RMSE (mm d−1) | Emax (mm d−1) | AAE (mm d−1) | ARE (%) | EF | WIA |
|---|---|---|---|---|---|---|---|---|---|
| Calibration, 2013 | 146 | 1.02 | 0.72 | 0.20 | 0.52 | 0.215 | 20.3 | 0.67 | 0.92 |
| Validation, 2014 | 146 | 0.97 | 0.81 | 0.20 | 0.55 | 0.201 | 16.0 | 0.62 | 0.92 |
| DOY 130 to 276 | TSDual (mm d−1) | Tsf (mm d−1) |
|---|---|---|
| Calibration year (2013) | ||
| Mean | 1.25 | 1.21 |
| Maximum | 1.79 | 1.94 |
| Minimum | 1.29 | 1.31 |
| Validation year (2014) | ||
| Mean | 1.31 | 1.35 |
| Maximum | 1.89 | 1.92 |
| Minimum | 0.58 | 0.49 |
| TSTSEB vs. Tsf | n | b | R2 | RMSE (mm d−1) | Emax (mm d−1) | AAE (mm d−1) | ARE (%) | EF | WIA |
|---|---|---|---|---|---|---|---|---|---|
| 2014 | 107 | 0.99 | 0.86 | 0.20 | 0.68 | 0.169 | 12.4 | 0.70 | 0.87 |
| DOY 166 to 273 (2014) | SIMDualKc | Total (mm) | STSEB | Total (mm) |
|---|---|---|---|---|
| Mean (mm d−1) | ||||
| ETc | 2.37 | 245.1 | 1.33 | 143.4 |
| T | 1.48 | 147.2 | 1.80 | 194.8 |
| Es | 0.89 | 98.0 | 1.12 | 121.4 |
| Maximum (mm d−1) | ||||
| ETc | 3.81 | 1.61 | ||
| T | 1.89 | 2.21 | ||
| Es | 2.36 | 1.36 | ||
| Minimum (mm d−1) | ||||
| ETc | 1.20 | 0.95 | ||
| T | 0.58 | 1.27 | ||
| Es | 0.02 | 0.81 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, F.L. Assessing Olive Evapotranspiration Partitioning from Soil Water Balance and Radiometric Soil and Canopy Temperatures. Agronomy 2018, 8, 43. https://doi.org/10.3390/agronomy8040043
Santos FL. Assessing Olive Evapotranspiration Partitioning from Soil Water Balance and Radiometric Soil and Canopy Temperatures. Agronomy. 2018; 8(4):43. https://doi.org/10.3390/agronomy8040043
Chicago/Turabian StyleSantos, Francisco L. 2018. "Assessing Olive Evapotranspiration Partitioning from Soil Water Balance and Radiometric Soil and Canopy Temperatures" Agronomy 8, no. 4: 43. https://doi.org/10.3390/agronomy8040043
APA StyleSantos, F. L. (2018). Assessing Olive Evapotranspiration Partitioning from Soil Water Balance and Radiometric Soil and Canopy Temperatures. Agronomy, 8(4), 43. https://doi.org/10.3390/agronomy8040043




