Construction of a CFD Simulation and Prediction Model for Pesticide Droplet Drift in Agricultural UAV Spraying

Abstract

This study employed a combined approach of computational fluid dynamics (CFD), numerical simulations, and wind tunnel tests to investigate droplet drift characteristics and develop prediction models in order to address the issues of low pesticide utilization rates and high drift risk, associated with droplet drift during agricultural unmanned aerial vehicle (UAV) spraying, as well as the unreliable results of field experiments. Firstly, a numerical model of the rotor wind field was established using the multiple reference frame (MRF) method, while the realizable k-ε turbulence model was employed to analyze the flow field. The model’s reliability was verified through wind field tests. Next, the Euler–Lagrange method was used to couple the wind field with droplet movement. The drift characteristics of two flat-fan nozzles (FP90-02 and F80-02) were then compared and analyzed. The results showed that the relative error between the simulated and wind tunnel test values was within 20%. Centrifugal nozzle experiments were carried out using single-factor and orthogonal designs to analyze the effects of flight height, rotor wind speed, flight speed, and droplet size on drift. The priority order of influence was found to be “rotor wind speed > flight height > flight speed”, while droplet size (D_V50 = 100–300 µm) was found to have no significant effect. Based on the simulation data, a multiple linear regression drift prediction model was constructed with a goodness of fit R² value of 0.9704. Under the verification condition, the relative error between the predicted and simulated values was approximately 10%. These results can provide a theoretical basis and practical guidance for assessing drift risk and optimizing operational parameters for agricultural UAVs.

1. Introduction

Unmanned aerial vehicles (UAVs) are rapidly expanding their role in agriculture for crop protection, enabling effective disease and pest management across large areas and complex landscapes. Their advantages—including low labor input, low pesticide consumption, and high operational efficiency—are key drivers of this increasing adoption [1,2]. However, agricultural UAV spraying operations are characterized by high flight height, fine droplet size, and fast flight speed. This makes droplet drift a key issue that restricts the effectiveness of spraying. Not only does it reduce the utilization rate of pesticides, but it may also have an adverse effect on the surrounding environment and crops [3].

Previous studies have demonstrated that the effectiveness of droplet deposition is influenced by various factors, such as UAV flight height and speed, nozzle type, droplet size, and environmental wind speed. Optimizing these parameters can improve the amount and uniformity of droplet deposition [4]. However, the transient variability of the field environment makes it difficult to repeat deposition experiments, and it is hard to systematically reveal the drift law by relying solely on field experiments [5]. Currently, the most common methods of detecting droplet deposition include model simulation calculation and analysis, wind tunnel testing, drift test platforms, as well as field experiment [6,7,8]. Model simulation and wind tunnel testing in particular have become important technical approaches to compensate for the limitations of field experiments, due to their high level of controllability.

Experimental studies on the characteristics of rotor wind fields have shown that the width and speed of the wind field when agricultural UAVs are hovering are affected by factors such as the type of rotor, the height of the rotor above the ground, the direction of rotation and the rotor speed. These changes impact droplet size and deposition distribution [9,10]. During flight, excessively high speeds reduce the intensity of the downwash airflow. This alters the disturbance characteristics of the crop canopy and generates horseshoe-shaped vortices in the downwash flow field. These vortices entrain droplets, resulting in uneven deposition and drift [11,12]. Furthermore, the deposition characteristics of droplets are influenced by the natural environment, the properties of the pesticide, the characteristics of the crop canopy and the operational parameters of the agricultural UAV, thereby complicating the research process [13,14,15].

A variety of droplet deposition and drift models have been developed internationally in order to predict the effects of such deposition and drift risks [16]. One such model is the AGDISP (Agricultural DISPersion) model, which uses the Lagrangian method to take into account factors such as aircraft wake, meteorological conditions and spray characteristics. It tracks the movement of droplets by solving the motion equation. Initially, the model was used to analyze and predict droplet deposition during spraying by large fixed-wing aircraft and helicopters [17]. Subsequently, by combining it with the Comprehensive Hierarchical Aeromechanics Rotorcraft Model (CHARM) for helicopters, its application was extended to predict the spray trajectory and deposition of multi-rotor UAVs [18,19]. However, this model relies on empirical formulas and cannot fully simulate the details of the flow field. In contrast, the CFD method can effectively simulate the coupled motion of UAV wake vortices and droplets, clearly revealing the influence of crosswind on vortex evolution and droplet drift. This makes up for the shortcomings of traditional models [20]. The Lattice Boltzmann Method (LBM) is advantageous in capturing vortex structures due to its fourth-order accuracy [21]. Zhang et al. [22] constructed a single-rotor agricultural UAV deposition and drift model based on the LBM, integrating an intelligent monitoring system for spraying deposition and drift. The system judges the pesticide deposition area by monitoring the spatial movement trajectory of the pesticide droplets. Other studies have established a central drift model for the deposition of droplets from manned helicopters, providing a methodological reference for UAV drift research [23].

Although previous research into the deposition of droplets by agricultural UAVs has identified some influencing factors and areas for optimization, related issues persist. These include poor experimental repeatability caused by transient changes in the field environment, and the difficulty of accurately controlling the influence of wind field characteristics and operational parameters on droplet drift [24]. Therefore, this study used CFD numerical simulation in conjunction with wind tunnel testing to validate the simulation results. Single-factor analysis and orthogonal experiments were employed to systematically investigate the primary and interactive effects of flight height, rotor speed, flight speed, and droplet diameter on droplet drift. Multiple linear regression analysis was then employed to determine the functional relationship between drift rate and the experimental factors. This resulted in the development of a droplet drift prediction model under ideal meteorological conditions. The aim was to clarify the correlation between agricultural UAV operating parameters and drift risk, thereby providing a theoretical basis and practical guidance for formulating drift control strategies.

2. Materials and Methods

2.1. Numerical Simulation and Verification of the Rotor Wind Field

2.1.1. Numerical Simulation of the Rotor Wind Field

The MRF method was used to simulate the rotor’s rotational motion. A 3D model of the rotor was constructed with the following dimensions: a diameter of 580 mm; a tip chord length of 25 mm; and a distance of 1100 mm between the front and rear rotors. The rotating domain of the rotor had a thickness of 168 mm and a diameter of 610 mm, while the static domain was a cube. The distance from the bottom of the static domain to the rotating domain was equal to the UAV’s flight height. The distance from the top of the static domain to the rotating domain was 1 m; the width was 4 m; and the distance from the outlet of the static domain to the rotating domain was 8 m.

Mesh refinement was performed in areas of the rotating domain with significant geometric changes, as well as in areas below the rotating domain with substantial gradient variations. The static and rotating domains shared the topology [25]. Meshing was carried out in Workbench Meshing, with “curvature capture” and “proximity capture” selected for size control. The flow field region was divided into two grids. The coarse grid comprised 718,000 elements, while the fine grid contained 1,790,969 elements. Upon convergence, the average rotor lift forces were 13.38 N and 13.60 N for the coarse and fine grids, respectively, with a relative error of 1.62%. The maximum rotor wind speeds were 11 m/s and 11.5 m/s for the coarse and fine grids, respectively, with a relative error of 4.35%. Due to the small difference in computational error between the two mesh configurations, the coarse mesh was ultimately selected to conserve memory and accelerate convergence. Its mesh parameter configuration is as follows: the overall element size was set to 200 mm, and the mesh element size in the local refined area was set to 40 mm; the rotor wall boundary layer was set to 15 layers with a growth rate of 1.1, and the outer wall boundary layer was set to 5 layers with a growth rate of 1.2. After conversion to polyhedral mesh (as shown in Figure 1), with a minimum orthogonal quality of 0.18.

The fluid material is air, with properties set to default values. The boundary conditions were defined as follows: The rotating domain was set as a moving reference frame with a specified rotation speed. When viewed from the top of the rotor, the rotation direction was anticlockwise and the rotor speed was 2500 rpm. The top was set as a pressure inlet, the ground as a wall boundary, and the upper part and circumferential direction of the computational domain as pressure outlet boundaries. The rotor was set as a rotating, no-slip wall boundary with a rotation speed of 0.

The control equations were discretized using the finite volume method and a double-precision coupling algorithm was adopted. The realizable k-ε model with expandable wall functions was employed for turbulence modeling, while the standard wall function method was used to calculate near-wall turbulence. The flow field was initialized using hybrid initialization method. The calculation was considered to have converged when the residual was less than the required accuracy of 0.001.

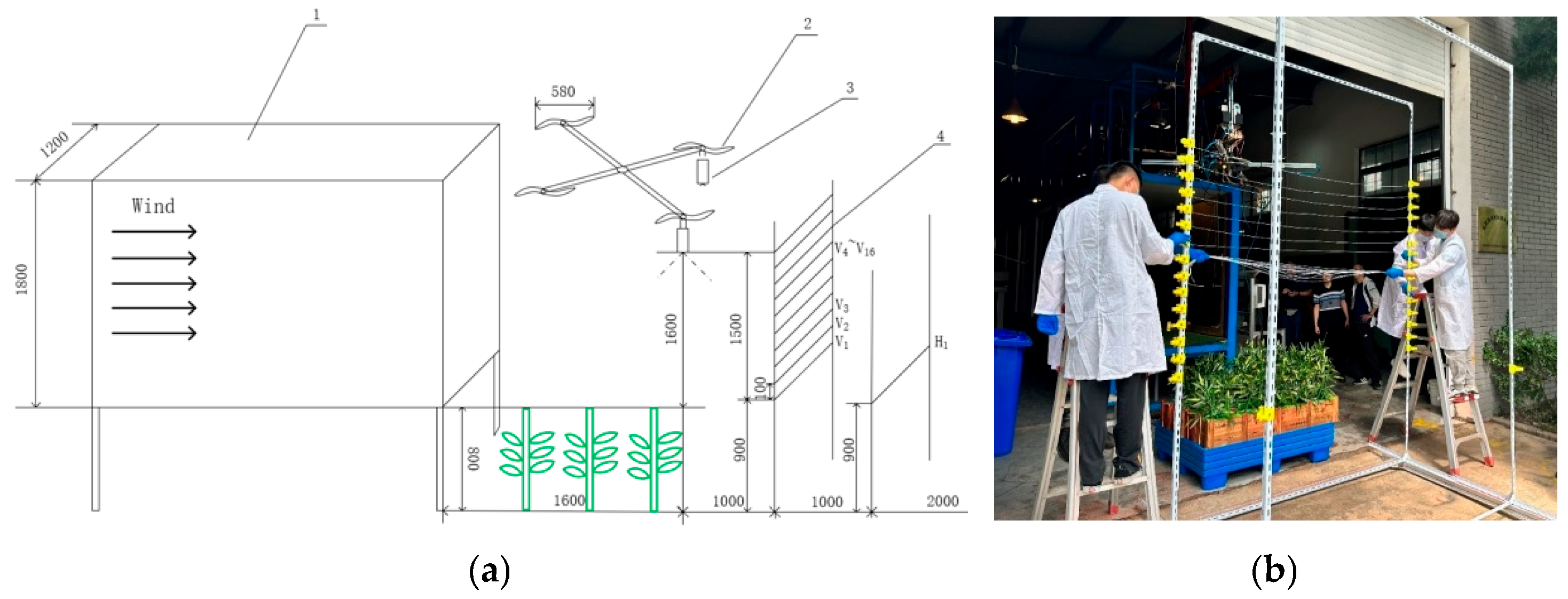
2.1.2. Intensity Test of the Rotor Wind Field

A rotor wind field test platform was built, incorporating a motor and blades, a speed control system, a flight control system and a handheld ground station. The platform can control the motor speed in real time to generate the target wind field and monitor the platform’s dynamic parameters while saving test data [26]. The rotor speed was set to 2500 rpm.

A portable NK4500 weather station (Nielsen-Kellerman Co., Ltd., Boothwyn, PA, USA) with a wind speed measurement range of 0.4–40 m/s, an accuracy of ±3% and a resolution of 0.1 m/s was used to test the wind field intensity. The test height was 0.5 m below the rotor and 25 test points were arranged at 4 directions and 5 cm radial intervals within a radius of 30 cm (as shown in Figure 2). Wind speed data were collected at each test point.

2.2. Droplet Drift Simulation and Wind Tunnel Test Under Coupled Wind Field

2.2.1. Droplet Drift Simulation Under a Coupled Wind Field

Given that the downwash flow field generated by the rotation of the rotor during the spraying of pesticides by agricultural drones interacts strongly with external wind fields and influences the distribution of droplets [27], this study coupled the rotor wind fields with the wind tunnel wind fields in order to simulate the motion patterns of droplets during drone operations.

The Euler–Lagrange method was used to simulate the Gas–Liquid two-phase flow: the continuous-phase fluid was treated as a continuous medium to solve the Navier–Stokes (NS) equations. Meanwhile, the discrete phase was solved by tracking a large number of dispersed droplets. The discrete phase could exchange momentum, mass, and energy with the continuous phase [28,29]. The calculation parameters were set as follows: a rotor speed of 2000 rpm, incoming wind speed of 5 m/s, and a rotor height of 1.5 m. The ground was set as a droplet capture (trap) wall boundary and the rest were set as pressure outlet boundaries.

Considering the actual spraying characteristics of UAVs, the flight speed disturbs the downwash airflow of the front rotor; therefore, the spray position is typically set below the rear rotor [12]. The droplet dispersion phase of the nozzle adopted a flat-fan atomizer and the atomization breakup model used a linearized unstable liquid film atomization model [30].

The parameters of the discrete-phase injection source were set as follows: the discrete-phase material was water-liquid, and the release position was 0.3 m below the rear rotor; the nozzle injection direction was vertical downwards, the fan surface was perpendicular to the incoming wind speed; the droplet mass flow rate was 0.013 kg/s; the spray half-angle of the FP90-02 nozzle was 45° and that of the F80-02 nozzle was 40°; and the spray diffusion angle was 6° for both nozzles. Unsteady particle tracking was enabled, and the discrete random walk model was used, with a particle release timescale of 0.01 s.

At the plane 1 m downwind from the nozzle spray position, the flow rate of droplet mass concentration was counted. The percentage of droplet flow rate passing through this plane relative to the total flow was considered the droplet drift rate for that distance.

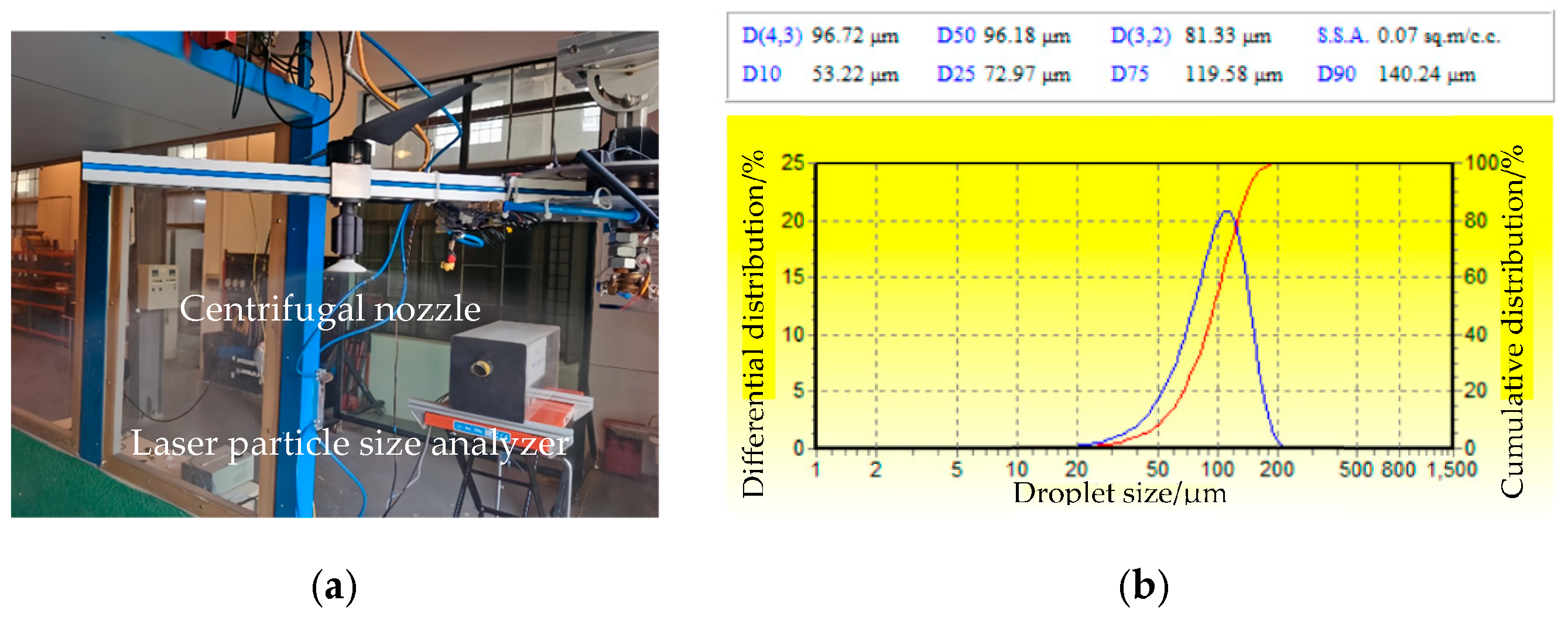
2.2.2. Wind Tunnel Test for Droplet Drift Performance Under a Coupled Wind Field

The test system comprised the NJS-1 agricultural low-speed wind tunnel (developed by Nanjing Institute of Agricultural Mechanization, Ministry of Agriculture and Rural Affairs). It has a test section size of 7.5 m × 1.2 m × 1.8 m, a wind speed range of 0.5~10 m/s, and an airflow turbulence degree of less than 1%. The system also included a rotor wind field testing platform and a spray control system consisting of a water pump, a pressure-regulating valve and a solenoid valve.

The connecting line between the front and rear rotors was perpendicular to the wind tunnel outlet plane and located in the middle of the wind tunnel outlet plane. The nozzle was placed 0.3 m directly below the rear rotor.

The test parameters were set as follows: rotor speed of 2000 rpm, wind tunnel wind speed of 5 m/s. The nozzle types were an anti-drift flat-fan nozzle FP90-02 (Suzhou Lanao Precision Plastic Co., Ltd., Suzhou, China) and an ordinary flat-fan nozzle F80-02 (Spraying Systems Co. Teejet Technologies, Wheaton, IL, USA). The spray pressure was 0.3 MPa. The particle sizes of nozzles FP90-02 and F80-02 were measured using the DP-02 laser particle size analyzer (OMEC Instrument Co., Ltd., Zhuhai, China), with respective D_V50 values of 574.88 μm and 203.28 μm. The spray time was set to 4 s; the spray solution was a 2500 mg/L Allura Red tracer solution.

In accordance with the ISO standard [31], 2 mm diameter polyethylene plastic wires were used to collect drifting droplets. To minimize wind tunnel attenuation interference, the first collection frame was positioned 1 m behind the rotor and had a width of 2 m. The sampling height began at the virtual ground above the canopy. Collection wires were arranged at 10 cm intervals up to the height at which the nozzle releases droplets is reached (1.5 m), totaling 16 wires (as shown in Figure 3).

After sampling, ultrasonic oscillation elution was performed. The droplet drift volume T and drift rate d were calculated by integrating Equations (1)–(4) [32,33] using the n-order polynomial curve $\dot{t\left(z\right)}$ of the droplet drift volume distribution with respect to height in the vertical plane.

$$T_i={\displaystyle \frac{A_i\times V}{C}}\times 10^3$$

(1)

$$t_i={\displaystyle \frac{T_i}{2\mathrm{mm}}}$$

(2)

$$T={\int }_0^{h_n}\dot{t\left(z\right)}dz$$

(3)

$$d={\displaystyle \frac{T\times 60}{Q\times t}}\times {10}^{-6}\times 100\%$$

(4)

where

T_i: Droplet drift amount on the i-th collection wire, μL;

A_i: Deposition concentration of tracer on the i-th collection wire, mg/L;

V: Volume of elution water, mL;

C: Concentration of tracer solution, mg/L

t_i: Drift volume per unit cross-sectional width of the sampler on the i-th collection wire, μL/mm;

T: Droplet drift flux in the vertical sampling direction, μL;

h_n: Maximum distance from the virtual ground in the vertical sampling direction, mm;

$\dot{t\left(z\right)}$: Fitting formula of drift deposition per unit cross-sectional width of the sampler in the vertical sampling direction, μL/mm;

Q: Nozzle flow rate, L/min;

t: Spray time, s.

2.3. Construction of Droplet Drift Model for a Centrifugal Nozzle

2.3.1. Influence of UAV Operation Parameters on Droplet Drift Characteristics

Based on the actual operation scenario and parameter sensitivity [34], 4 influencing factors and their respective levels were identified (

Table 1. Factor levels of agricultural UAV operation parameters.

	Factor	Flight Height (m)	Rotor Wind Speed (m/s)	Flight Speed (m/s)	DV50 (μm)
Level
1		1.5	10	3	100
2		2	15	5	200
3		2.5	20	7	300

): flight height of 1.5~2.5 m, rotor wind speed of 10~20 m/s, flight speed of 3~7 m/s, and droplet size (D_V50) of 100~300 μm.

Single-factor experiments were conducted. 3 factors were fixed at the median level, while 1 factor was changed. Each experiment was repeated 3 times, and analysis of variance (ANOVA) was used to evaluate the significance of each factor’s influence. Orthogonal experiments were designed for the three significantly influential factors (flight height, rotor wind speed and flight speed) using the L9(3⁴) orthogonal table, and each experiment was repeated 3 times.

2.3.2. Numerical Simulation of Droplet Drift for Centrifugal Nozzles Under Different Operating Parameters

Centrifugal nozzles disperse liquid into fine droplets through high-speed rotation, thereby enhancing pesticide coverage and uniformity, and are widely used in agricultural UAVs [35]. Based on the convergence of the coupled wind field calculations, discrete-phase injection source were defined according to the atomization characteristics (spray angle, droplet distribution range) of centrifugal nozzles.

The centrifugal nozzle model adopted a hollow-cone atomizer model. The parameters of the discrete-phase injection source were set as follows: the material was water, and the release position was 0.3 m below the rear rotor; the nozzle injection direction was vertically downward, the droplet speed was 15 m/s, and the droplet mass flow rate was 0.013 kg/s; the spray half-angle of the centrifugal nozzle was 75°, and the nozzle radius was 0.03 m; the droplet size was set according to the Rosin-Rammler distribution. The droplet size settings were based on the actual measurement results from the DP-02 laser particle size analyzer (see Figure 4a). Figure 4b shows the droplet size distribution range for D_V50 = 100 μm, with minor adjustments possible within the upper and lower limits. When the D_V50 was 100 μm, 200 μm, and 300 μm, the corresponding [maximum droplet size, minimum droplet size] were [55 μm, 150 μm], [105 μm, 310 μm], and [150 μm, 430 μm], respectively. Unsteady particle tracking was enabled, and the discrete random walk model was used, with a particle release time scale of 0.01 s.

2.3.3. Droplet Drift Prediction Model for Agricultural UAVs

Multiple linear regression analysis was performed based on the results of single-factor and orthogonal experiments. Variables were selected using the CP criterion to construct a drift rate regression model. The model’s accuracy was evaluated by comparing its predicted results with numerical simulation outcomes.

3. Results

3.1. Rotor Wind Field Intensity

Figure 5 shows that the simulation and test results of the flow field speed at 0.5 m below the rotor. The numerical simulation contour (Figure 5a) shows that the area of high wind speed generated by rotor rotation is concentrated in the central area, with the wind speed decreasing gradually as the radial distance increases. The wind field test results (Figure 5b) further verify that the maximum wind speed generated by the rotor can exceed 10.5 m/s. The diameter of the wind field with a wind speed of >9 m/s is approximately 30 cm, the diameter of the wind field with a wind speed of >7 m/s is approximately 40 cm, and the diameter of the wind field with a wind speed of >3 m/s extends to 50–60 cm. The trend of wind speed distribution between the simulated results and test results is highly consistent, which proves the reliability of the rotor rotating domain simulation calculation and lays the groundwork for the subsequent coupled wind field simulations.

3.2. Droplet Drift Performance Under Coupled Wind Field

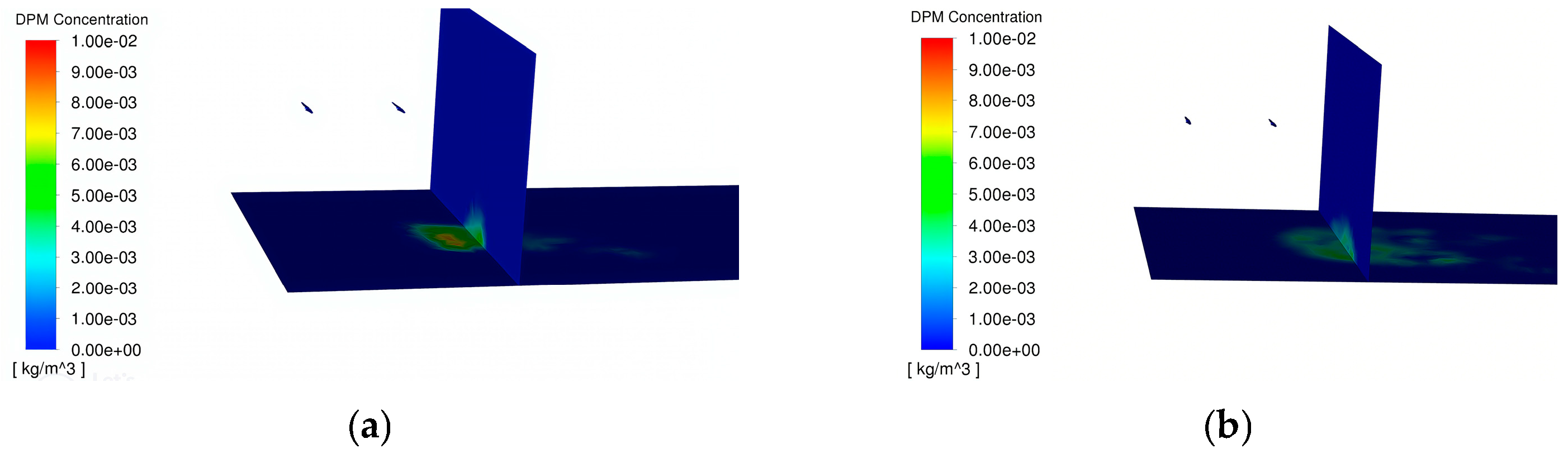
3.2.1. Characteristics of Coupled Wind Field

Figure 6 shows the coupled wind field of the wind tunnel wind field and rotor wind fields. As can be seen, the wind field of the first rotor (on the windward side) is significantly disturbed by the incoming wind from the wind tunnel, resulting in a chaotic airflow. Meanwhile, the second rotor (the rear rotor) still maintains a stable downward pressure wind field. This explains why UAVs typically activate the nozzle beneath the rear rotor during spraying operations.

3.2.2. The Atomization and Drift Characteristics of Flat-Fan Nozzles

Figure 7 shows the atomization effects of the two flat-fan nozzles (FP90-02 and F80-02) and the droplet movement trajectories in the coupled wind field. The comparison shows that the FP90-02 nozzle d generates larger droplets than the F80-02 nozzle. Under the action of the wind tunnel wind field, the droplet fan surfaces of both nozzles drift backwards. However, the F80-02 nozzle exhibits a more significant degree of drift, indicating that fine droplets are more susceptible to airflow disturbance.

Figure 8 shows the distribution of droplet mass concentration on the plane 1 m downwind from the nozzle and on the ground. The droplet deposition area of the FP90-02 nozzle is concentrated within 1.5 m behind the rotor (Figure 8a); while the droplet deposition of the F80-02 nozzle is relatively scattered, with low concentration and obvious downwind deviation (Figure 8b). This further confirms the influence of droplet size on the concentration of droplet deposition.

Figure 9 shows the distribution and fitting results of drift deposition per unit cross-sectional width of the two nozzles in the vertical sampling direction. When the height is greater than 900 mm, the drift volume fitting value becomes negative (without any practical physical significance), so the maximum distance h_n from the virtual ground in the vertical sampling direction is set to 900 mm.

The test values of the drift rate at 1 m downwind from the nozzle for the FP90-02 and F80-02 nozzles were calculated by Equations (1)–(4). The results are 9.49% and 42.54%, respectively, and the simulated values are 11.77% and 50.05%, respectively. The relative error between the simulated values and test values for both nozzles is controlled within 20%, which verifies the effectiveness of the droplet drift simulation method under the coupled wind field.

3.3. Droplet Drift Model for Centrifugal Nozzles

3.3.1. Analysis of Single-Factor Influence

Table 2. Drift rate under different levels of each factor (%).

	Factor	Flight Height (m)	Rotor Wind Speed (m/s)	Flight Speed (m/s)	DV50 (μm)
Level
1		24.43 ± 1.34 (b)	46.28 ± 1.66 (a)	19.07 ± 0.72 (c)	30.20 ± 1.74 (a)
2		27.39 ± 1.07 (b)	27.39 ± 1.07 (b)	27.39 ± 1.07 (b)	27.39 ± 1.07 (a)
3		65.94 ± 2.35 (a)	13.48 ± 0.54 (c)	33.94 ± 0.61 (a)	29.98 ± 0.84 (a)

Note: The letters a, b, and c in the table represent the results of the LSD multiple comparison test.

shows the statistical results of the drift rate at different levels of each factor. At rotor wind speed of 15 m/s and flight speed of 5 m/s, the drift rates at flight heights of 1.5 m and 2 m are 24.43% ± 1.34% and 27.39% ± 1.07%, respectively, with no significant difference. However, when the flight height increases to 2.5 m, the drift rate rises sharply to 65.94% ± 2.35%. This indicates that when the flight height exceeds 2.5 m, the air retention time of droplets increases, thereby significantly increasing the drift risk.

The drift rate shows a significant downward trend with the increase in rotor wind speed: the drift rate reaches 46.28% ± 1.66% when the wind speed is 10 m/s, and decreases to 13.48% ± 0.54% when the wind speed is 20 m/s. This indicates that the strong downward airflow pressure formed by the high rotor wind speed can effectively inhibit the droplets drift.

The drift rate increases with the increase in flight speed: the drift rate is 19.07% ± 0.72% when the speed at 3 m/s, and increases to 33.94% ± 0.61% when the speed at 7 m/s. It is inferred that high flight speed weakens the intensity of the downwash airflow, causing droplets to be entrained within the vortex.

When the D_V50 is between 100 μm and 300 μm, the drift rates are 30.20% ± 1.74%, 27.39% ± 1.07%, and 29.98% ± 0.84%, respectively, with no significant difference. This suggests that airflow dominates the movement of droplets in this size range, and that the influence of droplet size can be ignored.

3.3.2. Results of Orthogonal Experiment and Factor Significance

The L9(3⁴) orthogonal experiment scheme and drift rate results for flight height, rotor wind speed, and flight speed are shown in

Table 3. Droplet drift rate under different operation parameters.

Experiment No.	Flight Height (m)	Rotor Wind Speed (m/s)	Flight Speed (m/s)	Drift Rate (%)
				Repeat 1	Repeat 2	Repeat 3
1	1.5	10	3	33.23	32.59	29.32
2	1.5	15	5	23.61	23.72	25.98
3	1.5	20	7	0	0	0
4	2	10	5	45.44	44.36	43.71
5	2	15	7	30.14	36.23	33.93
6	2	20	3	3.02	3.38	3.35
7	2.5	10	7	82.97	86.98	86.80
8	2.5	15	3	37.13	38.31	36.39
9	2.5	20	5	14.21	14.62	14.48

. The drift rate varies significantly depending on the parameter combinations. For example, in Experiment 3 (flight height of 1.5 m, rotor wind speed of 20 m/s, flight speed of 7 m/s), the drift rate is 0%; while in Experiment 7 (flight height of 2.5 m, rotor wind speed of 10 m/s, flight speed of 7 m/s), the drift rate is as high as 82.97%~86.98%. This highlights the importance of parameter combination optimization.

ANOVA was performed on the drift rate (

Table 4. ANOVA of drift rate.

Source of Variance	Degrees of Freedom	Sum of Squares	Mean Square	F-Value	Pr > F
Flight height	2	3453.5	1726.75	45.71	<0.0001
Rotor wind speed	2	10,404.29	5202.15	137.72	<0.0001
Flight speed	2	1194.17	597.08	15.81	<0.0001
Error	20	755.45	37.77

). The results show that flight height, rotor wind speed, and flight speed all have extremely significant effects on the drift rate (p < 0.0001). In terms of F-value, rotor wind speed has the largest F-value (137.72), followed by flight height (45.71); flight speed has the smallest F-value (15.81). This indicates that the priority order of the three factors on droplet drift is: rotor wind speed > flight height > flight speed.

3.3.3. Droplet Drift Prediction Model and Verification

Parameter estimating test for drift are shown in

Table 5. Parameter estimating test for drift.

Variable	Estimated Value	t Value	Pr > |t|
Flight height	38.641	13.01	<0.0001
Rotor wind speed	2.514	1.56	0.1242
Flight speed	−13.473	−2.82	0.0069
Flight height * Rotor wind speed	−3.177	−4.36	<0.0001
Flight height * Flight speed	7.909	3.56	0.0008

Note: * indicates interaction between variables.

. A prediction model was constructed through multiple linear regression analysis (variable selected by CP criterion) using flight height (h), rotor wind speed (r), and flight speed (v) as independent variables, and drift rate (d) as the dependent variable. The significance test of the regression equation shows p < 0.0001, indicating the model is extremely significant with a goodness of fit R² of 0.9704. The final regression equation is shown in Equation (5):

d = 38.641h + 2.514r − 13.473v − 3.177hr + 7.909hv

(5)

where

d: Drift rate, %;

h: Flight height, m;

r: Rotor wind speed, m/s;

v: Flight speed, m/s.

To verify the model’s accuracy, a verification condition was set: flight height of 2 m, rotor wind speed of 11.8 m/s, flight speed of 6 m/s, and droplet size range of 55~430 μm (D_V50 = 250 μm). Figure 10 shows the simulation results of the coupled wind field and droplet movement trajectory. After 3 repeated calculations, the average drift rate was found to be 51.186%; the drift rate predicted by the model is 46.04%, resulting in a relative error of 10.05%. This proves that the model has high prediction accuracy under ideal meteorological conditions.

4. Discussion

This study systematically explored the droplet drift characteristics of agricultural UAVs and constructed a prediction model by combining CFD numerical simulation with wind tunnel testing. The core findings align with those of existing studies and provide additional information. However, there are certain limitations that need to be addressed in the context of practical application scenarios.

In terms of method reliability, the rotor wind field model constructed based on the MRF method in this study was verified by wind tunnel tests. The distribution trend of wind field intensity between the simulated and test results was found to be highly consistent. This is consistent with the conclusion of Divazi et al. [25], who verified the reliability of the model by simulating the downwash flow field of multi-rotor UAVs using CFD, proving that this method can effectively restore the rotor’s aerodynamic characteristics. In the coupled wind field drift simulation for flat-fan nozzles, the relative error between the simulated values and test values of the FP90-02 and F80-02 nozzles was kept to under 20%. This level of accuracy is comparable to that reported by Hong et al. [36] in their study of orchard air-assisted sprayers, where the overall relative errors of the spray concentration inside canopies and off-target losses were found to be 22.1% and 40.6%, respectively. The errors originate from two main aspects: Firstly, in the wind tunnel test, the collection frame is located outside the tunnel, resulting in deviations in the actual drift amount due to airflow attenuation and interference from external natural winds. Secondly, in the discrete-phase simulation of flat-fan nozzles, there is a slight difference between the droplet size distribution and the actual measurement results (e.g., the measured D_V50 value of the FP90-02 nozzle under 0.3 MPa is 574.88 μm, whereas the simulated value is 516 μm). Multi-injector technology [29] can be used in future to further optimize the atomization model parameters, thereby reducing the discrepancy between the simulated and actual droplet size distributions.

In terms of the mechanism of influencing factors, ANOVA of orthogonal experiments shows that rotor wind speed, flight height, and flight speed have extremely significant effects on droplet drift, with the priority order of influence being “rotor wind speed > flight height > flight speed”, while the droplet size (D_V50 = 100~300 μm) has no significant effect. This result is consistent with the observations made by Yang et al. [29] that “the influence of incoming wind speed on drift distance is greater than that of droplet size”. Specifically, high rotor wind speed (e.g., 20 m/s) can form a stronger downward pressure airflow, which stably transports droplets to the crop canopy and reduces drift—this also explains why rotor wind speed becomes the core parameter for drift control [37]. When the flight height exceeds 2.5 m, the air retention time of droplets is prolonged, and the drift risk rises sharply; an increase in flight speed weakens the downwash airflow and even generates vortices to entrain droplets [11,12]. The combined effect of height and speed amplifies the drift impact, requiring coordinated control measures.

The insignificant influence of droplet size is presumably because under the analyzed droplet size range, the initial speed of droplets generated by the high-speed rotation of centrifugal nozzles attenuates rapidly under the action of air drag [38]. At this point, the rotor downwash flow field becomes the main driving force for droplet movement.

As UAV payload capacity has improved continuously, increasing from 12 kg to 90 kg [39], their rotor wind speeds also rise accordingly. For agricultural UAVs with a low rotor wind speed of ≤15 m/s, flight speed has a significant impact on droplet drift [9,29]. It is therefore recommended that the flight speed is reduced to ≤5 m/s and the flight height to ≤2 m. However, for agricultural UAVs with a large payload and a high rotor wind speed (≥20 m/s), the flight height and speed can be increased slightly. Nevertheless, excessive flight speed (e.g., the DJI AGRAS T40 agricultural UAV with a 40 L payload (T40—SZ DJI Technology Co., Shenzhen, China)) reduces the coverage rate when the flight speed exceeds 10 m/s [40].

This study examined how operating parameters affect the drift characteristics of droplets for multi-rotor agricultural UAVs with nozzles positioned beneath the rear rotor. However, there are certain limitations.

Firstly, the coupled effect of multiple natural environmental factors was not considered; the analysis focused solely on ideal meteorological conditions, ignoring the effects of temperature and humidity on droplet evaporation, as well as the disturbances caused by natural wind fields. Existing studies have shown that, at a wind speed of 2 m/s, droplets with a diameter of less than 75 μm are the main source of spray drift [30]. Based on field experiments investigating the influence of droplet size on the deposition characteristics and drift of aerial spray droplets from agricultural UAVs, Chen S [41] recommended setting the droplet size at no less than 160 μm. Therefore, in actual operations, the droplet size should be increased appropriately to reduce the risk of drift caused by evaporation.

Secondly, the effect of crop canopies on the interception of droplets was not simulated. However, canopy structure changes the distribution of downwash airflow, thereby affecting the final deposition position of droplets [13,14,15]. In future, it will be necessary to combine 3D models of typical crop canopies (such as rice and wheat) to supplement the coupled simulation of canopies, airflow and droplets, in order to improve the model’s adaptability in field scenarios.

Thirdly, the scope of the research is relatively narrow, focusing solely on specific rotor sizes (580 mm in diameter) and a limited number of nozzle types. In future, expanding the research to include different rotor airfoils, speed ranges and new nozzles could help to make the conclusions more universal.

5. Conclusions

This study focuses on spray drift from agricultural USVs. A “CFD numerical simulation + wind tunnel validation” approach was employed to investigate the influencing factors and construct predictive models. The conclusions are as follows: (1) The MRF rotor wind field model at 0.5 m shows consistent simulation results compared to experimental data. In the Euler–Lagrange coupled simulation, the drift rates of the FP90-02 and F80-02 nozzles exhibit simulation errors of ≤20% compared to the experimental values, which demonstrates the reliability of this method. (2) Centrifugal nozzle tests revealed that rotor wind speed, flight height, and flight speed have a highly significant effect on drift (p < 0.0001), with the following order of priority: “rotor wind speed > flight height > flight speed.” Particle sizes within the D_V50 = 100~300 μm range had no effect. The drift rate decreased with increasing rotor wind speed, while it increased with rising flight height and flight speed. (3) A regression prediction model based on flight height, rotor wind speed, and flight speed was established, yielding an R² value of 0.9704 (p < 0.0001). The validation error under operational conditions was only 10.05%, enabling precise prediction of drift risks under ideal conditions. (4) Parameter recommendations: For small-to-medium UAVs with rotor wind speeds ≤ 15 m/s, we recommend flight altitude ≤ 2 m and speed ≤ 5 m/s. For heavy-payload UAVs with rotor wind speeds ≥ 20 m/s, parameters can be moderately increased, but excessive flight speeds should be avoided to prevent reduce coverage.