Machine Learning-Based Estimation of Tractor Performance in Tillage Operations Using Soil Physical Properties
Abstract
1. Introduction
- (1)
- To establish an experimental environment and a data acquisition (DAQ) capable of evaluating soil physical properties and tractor performance and collecting data under various field conditions.
- (2)
- To analyze the influence of SMC, CI, and sand proportion on ET, EP, SR, and AP.
- (3)
- To develop and validate a machine-learning-based model that estimates tractor performance for diverse soil physical characteristics using field-collected data.
2. Materials and Methods
2.1. Tractor-Implement System
2.1.1. Agricultural Tractor
2.1.2. Data Measurement System
2.2. Data Collection
2.2.1. Field Experiment
2.2.2. Field-Data-Based Analysis of Soil Physical Properties and Tractor Performance
2.3. Data Analysis
2.3.1. Combination of Input Variables
- (1)
- Model A estimated the tractor performance using only SMC because SMC more significantly influences the tractor performance compared to other soil physical properties [18].
- (2)
- Model B used only CI as the input variable. Since models with a few input variables simplify data collection, models A and B were designed to study the effects of SMC and CI, which are measured in real time using portable sensors [10].
- (3)
- Model C incorporated SMC and CI as input variables, aiming to improve the estimation accuracy by accurately reflecting soil physical characteristics and tractor performance.
- (4)
- Model D included all available input variables—SMC, CI, and sand proportion—based on the premise that incorporating more variables enhances the estimation performance.
2.3.2. Tractor Performance Analysis
2.3.3. Model Accuracy Evaluation Metric
- Train-to-test loss ratio (TTLR): This variable represents the ratio of the mean squared errors (MSE) of the test and training datasets. A TTLR of <1.5 indicates underfitting, while a TTLR of >1.5 indicates overfitting.
- R2 Gap: This measures the difference between the R2 values of the training and test datasets. A large R2 Gap value suggests a strong likelihood of overfitting, implying the model performs significantly better on training data than test data.
2.3.4. Software
2.3.5. Overall Process
3. Results
3.1. Effect of Soil Physical Properties on Tractor Performance
3.2. Machine Learning Model-Based Estimation of Tractor Performance
3.2.1. Engine Torque
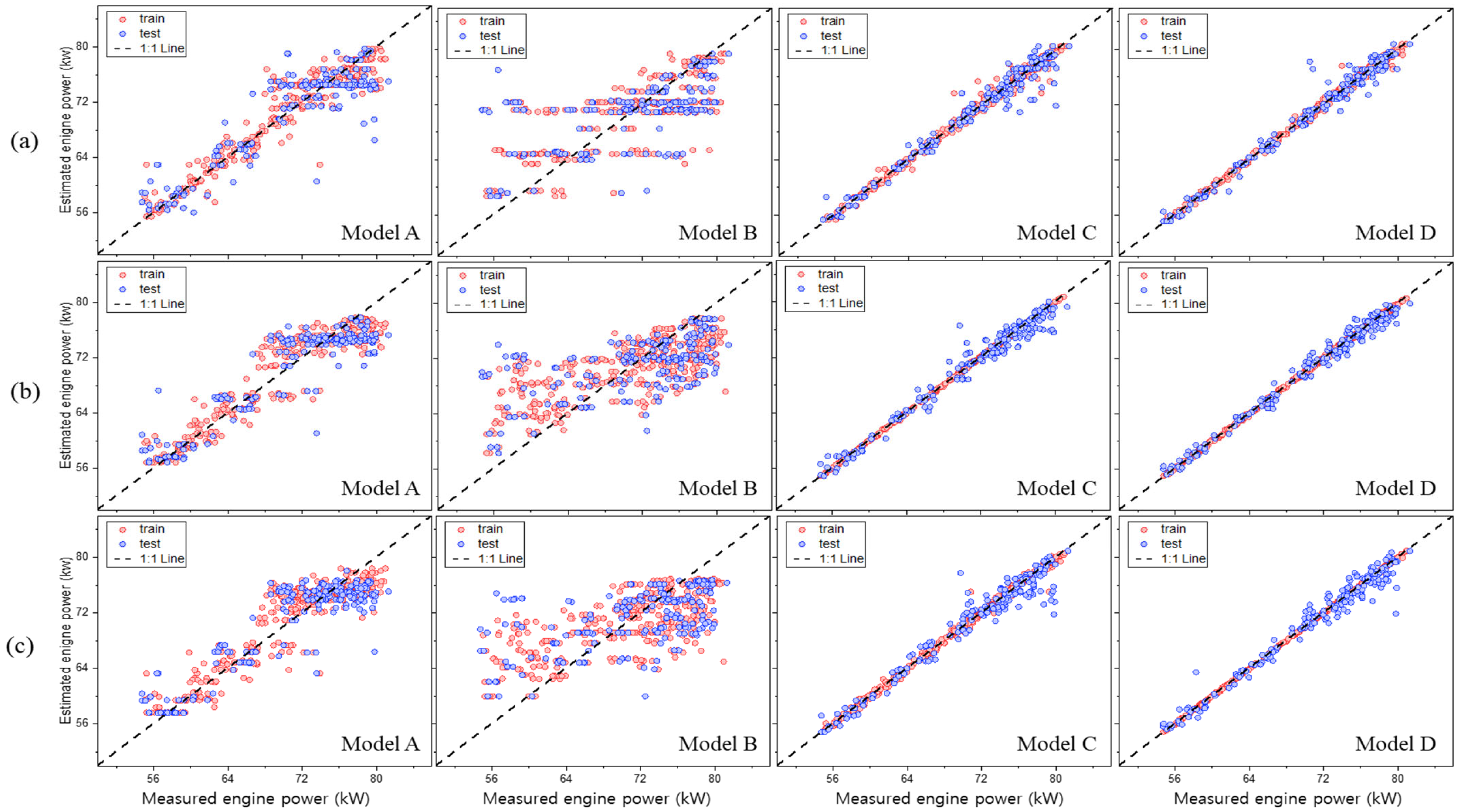
3.2.2. Engine Power
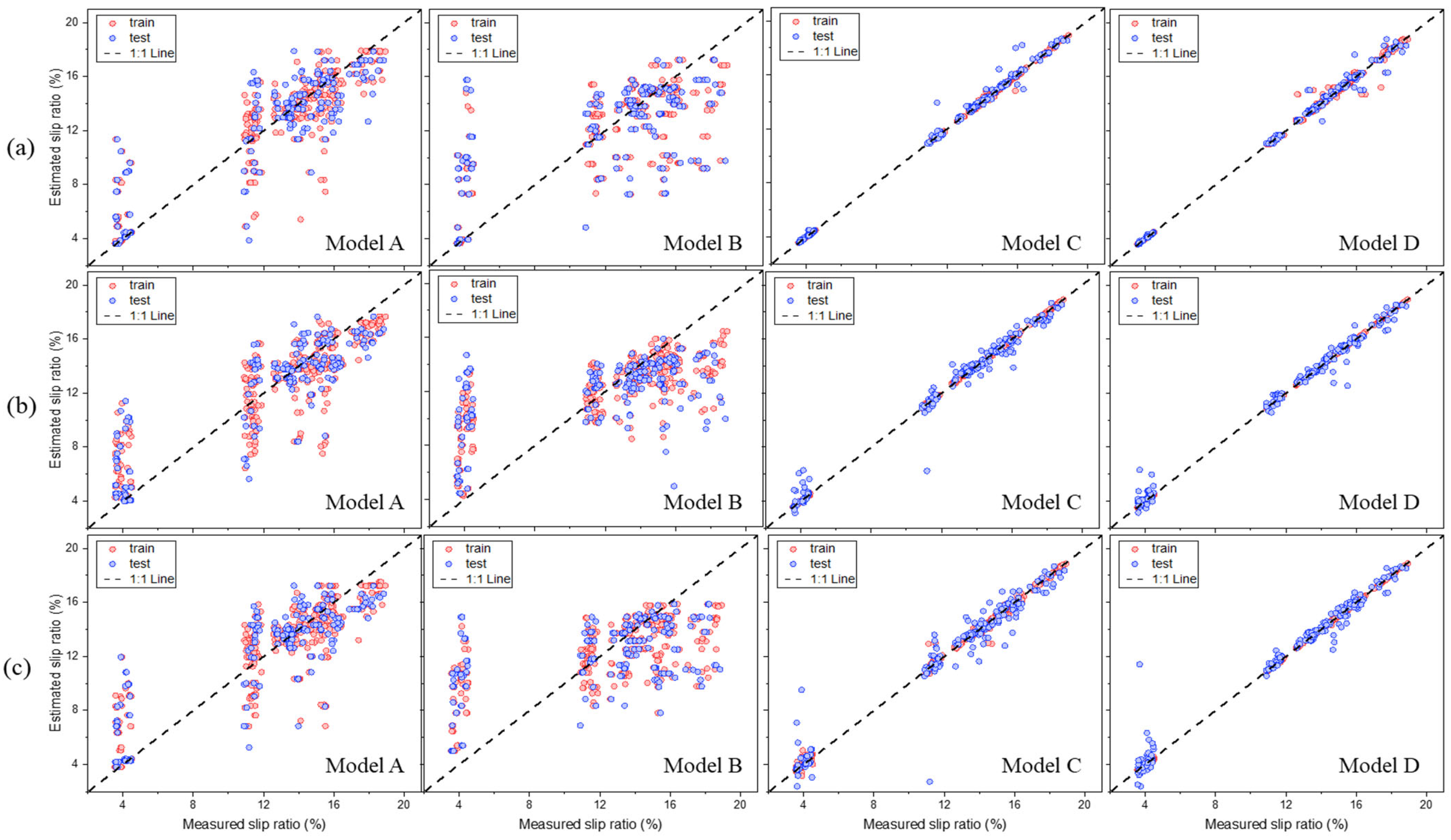
3.2.3. Slip Ratio
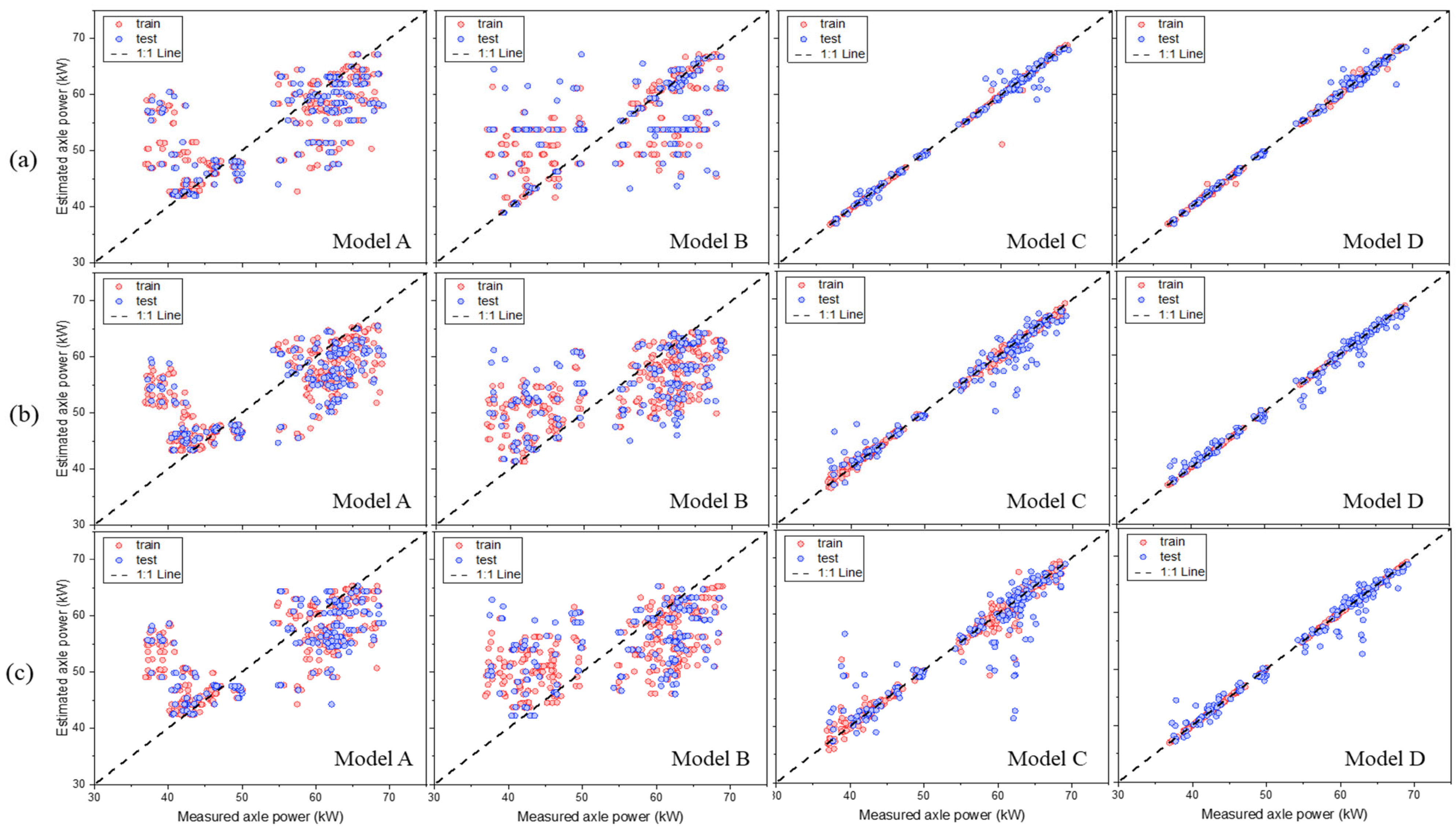
3.2.4. Axle Power
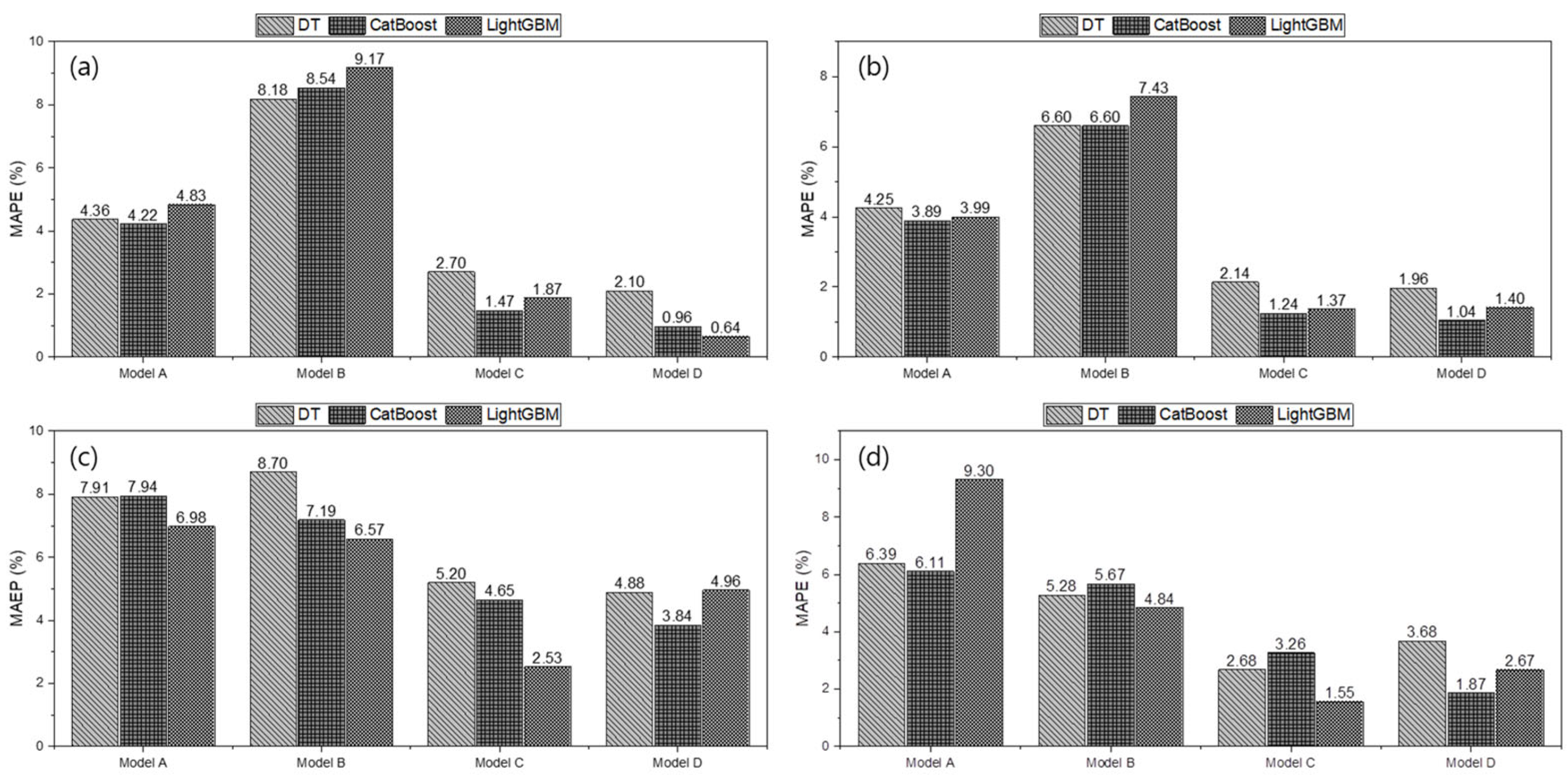
3.3. Combination and Evaluation of the Machine Learning-Based Estimation Models
3.4. Hyperparameter Optimization Results
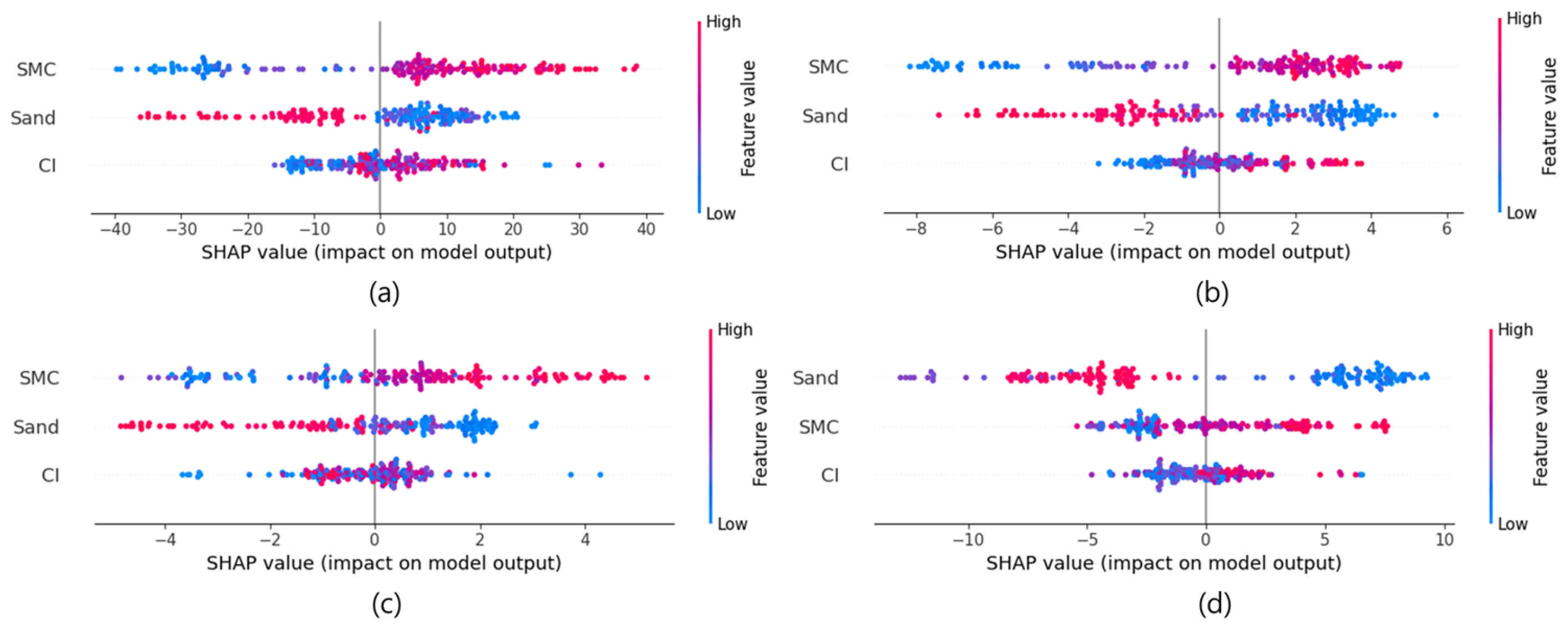
3.5. Shap Interpretation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, J.-H.; Lee, C.-Y.; Cho, Y.-H.; Yu, Z.; Kim, K.-M.; Yang, Y.-J.; Nam, J.-S. Potato Farming in the United States and South Korea: Status Comparison of Cultivation Patterns and Agricultural Machinery Use. J. Biosyst. Eng. 2024, 49, 252–269. [Google Scholar] [CrossRef]
- Raikwar, S.; Tewari, V.K. Development of Transmission Control Algorithm for Power Shuttle Transmission System for an Agricultural Tractor. J. Biosyst. Eng. 2022, 48, 136–151. [Google Scholar] [CrossRef]
- Simikić, M.; Dedović, N.; Savin, L.; Tomić, M.; Ponjičan, O. Power Delivery Efficiency of a Wheeled Tractor at Oblique Drawbar Force. Soil Tillage Res. 2014, 141, 32–43. [Google Scholar] [CrossRef]
- Ahn, D.-V.; Kim, K.; Choi, K.; Lee, J.W.; Kim, J.-G.; Yu, J.; Kim, H.-S.; Seo, J.; Park, Y.-J. Effect of Clutch Control to Improve Launch Quality for a Power Shuttle Tractor during Launching. Comput. Electron. Agric. 2024, 224, 109235. [Google Scholar] [CrossRef]
- Kwon, D.; Ahn, D.-V.; Kim, J.-G.; Park, Y.-J. Effect Analysis of Motor Power Characteristics on the Energy Consumption of Dual Motor Driven Powertrain for Electric Tractor. J. Biosyst. Eng. 2024, 49, 465–475. [Google Scholar] [CrossRef]
- Rajabi-Vandecchali, M.; Abbaspour-Fard, M.H.; Rohani, A. Development of a Prediction Model for Estimating Tractor Engine Torque Based on Soft Computing and Low Cost Sensors. Measurement 2018, 121, 83–95. [Google Scholar] [CrossRef]
- Janulevičius, A.; Juostas, A.; Pupinis, G. Tractor’s Engine Performance and Emission Characteristics in the Process of Ploughing. Energy Convers. Manag. 2013, 75, 498–508. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, L.; Zhu, Z.; Mao, E.; Chen, Y.; Liu, Y.; Du, X. Measuring Method of Slip Ratio for Tractor Driving Wheels Based on Machine Vision. Agriculture 2022, 12, 292. [Google Scholar] [CrossRef]
- Kara, S.; Karadirek, I.E.; Muhammetoglu, A.; Muhammetoglu, H. Real Time Monitoring and Control in Water Distribution Systems for Improving Operational Efficiency. Desalination Water Treat. 2016, 57, 11506–11519. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Kim, D.; Choi, C.; Lee, M.; Kim, H.S. Developing a Prediction Model (Heavy Rain Damage Occurrence Probability) Based on Machine Learning. J. Korean Soc. Hazard Mitig. 2019, 19, 115–127. [Google Scholar] [CrossRef]
- Kumari, A.; Reheman, H. Tillage Operation with a Tractor Drawn Rotavator Using an Embedded Advisory System for Minimizing Fuel Consumption. J. Biosyst. Eng. 2023, 48, 487–502. [Google Scholar] [CrossRef]
- Oduma, O.; Oluka, S.I.; Eze, P.C. Effect of Soil Physical Properties on Performance of Agricultural Field Machinery in South Eastern Nigeria. Agric. Eng. Int. CIGR J. 2018, 20, 25–31. [Google Scholar]
- Al-Shammary, A.A.G.; Caballero-Calvo, A.; Fernández-Gálvez, J. Evaluating the Performance of a Novel Digital Slippage System for Tractor Wheels Across Varied Tillage Methods and Soil Textures. Agriculture 2024, 14, 1597. [Google Scholar] [CrossRef]
- Siddique, A.A.; Baek, S.-M.; Baek, S.-Y.; Jeon, H.-H.; Park, J.-D.; Park, M.-J.; Yang, C.-W.; Park, M.J.; Kim, Y.-S.; Kim, W.-S.; et al. Effect of Motor Speeds on Traction Performance of a Single-Motor Electric Tractor at Various Gear Stages during Plow Tillage. Sci. Rep. 2023, 13, 56590. [Google Scholar] [CrossRef]
- Janulevičius, A.; Damanauskas, V. Prediction of Tractor Drive Tire Slippage under Different Inflation Pressures. J. Terramech. 2022, 101, 23–31. [Google Scholar] [CrossRef]
- Ge, J.; Peng, S.; Cao, C.; Fang, L.; Qin, K. Numerical Prediction of Tractive Performance of Track–Soil Interaction System through Different Grouser Heights. Eng. Agrícola 2022, 42, 19–24. [Google Scholar]
- Min, Y.-S.; Kim, Y.-S.; Lim, R.-G.; Kim, T.-J.; Kim, Y.-J.; Kim, W.-S. The Influence of Soil Physical Properties on the Load Factor for Agricultural Tractors in Different Paddy Fields. Agriculture 2023, 13, 2073. [Google Scholar] [CrossRef]
- Alhassan, E.A.; Olaoye, J.O.; Lukman, A.F.; Adekanye, T.A.; Abioye, O.M. Statistical Modelling of a Tractor Tractive Performance during Ploughing Operation on a Tropical Alfisol. Open Agric. 2024, 9, 20220282. [Google Scholar] [CrossRef]
- Al-Dosary, N.M.N.; Alnajjar, F.M.; Aboukarima, A.E.W.M. Estimation of Wheel Slip in 2WD Mode for an Agricultural Tractor during Plowing Operation Using an Artificial Neural Network. Sci. Rep. 2023, 13, 59975. [Google Scholar] [CrossRef]
- Angelucci, L.; Varani, M.; Pinet, F.; Martin, V.; Vertua, A.; Molari, G.; Mattetti, M. The Role of Tyres and Soil Conditions in Enhancing the Efficiency of Agricultural Tractors. Soil Tillage Res. 2025, 251, 106570. [Google Scholar] [CrossRef]
- Almaliki, S.A.; Himoud, M.S.; Muhsin, S.J. Mathematical Model for Evaluating Slippage of Tractor under Various Field Conditions. Basrah J. Agric. Sci. 2021, 34, 49–59. [Google Scholar] [CrossRef]
- Seifu, Y.; Hiresamhir, S.; Tole, S.; Yilak, A. Evaluation of Tractor Field Performance Using Visual Basics Programming for Agricultural Farm Lands. Am. J. Agric. Sci. Eng. Technol. 2023, 7, 25–35. [Google Scholar] [CrossRef]
- Al-Mastawi, K.E.; Dahham, G.A.; Yahya, L.M. Effects of Soil Moisture Content, Tire Inflation Pressure, and Tillage Speed on Tractive Performance of 2WD Tractor in Northern Iraq. Trans. Chin. Soc. Agric. Mach. 2022, 53, 409–418. [Google Scholar]
- Kim, W.S.; Kim, Y.J.; Baek, S.Y.; Baek, S.M.; Kim, Y.S.; Kim, Y.K.; Choi, I.S. Traction Performance Evaluation of a 78-kW-Class Agricultural Tractor Using Cone Index Map in a Korean Paddy Field. J. Terramech. 2020, 91, 285–296. [Google Scholar] [CrossRef]
- Shafaei, S.M.; Loghavi, M.; Kamgar, S. Feasibility of Implementation of Intelligent Simulation Configurations Based on Data Mining Methodologies for Prediction of Tractor Wheel Slip. Inf. Process. Agric. 2019, 6, 183–199. [Google Scholar] [CrossRef]
- Najafi, G.; Ghobadian, B.; Tavakoli, T.; Buttsworth, D.R.; Yusaf, T.F.; Faizollahnejad, M. Performance and Exhaust Emissions of a Gasoline Engine with Ethanol Blended Gasoline Fuels Using Artificial Neural Network. Appl. Energy 2009, 86, 630–639. [Google Scholar] [CrossRef]
- Al-Sager, S.M.; Almady, S.S.; Marey, S.A.; Al-Hamed, S.A.; Aboukarima, A.M. Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method. Agronomy 2024, 14, 492. [Google Scholar] [CrossRef]
- TYM Co. TYM Tractors Official Website. TYM Official Website. Available online: https://tym.world (accessed on 15 September 2025).
- Spectrum Technologies Inc. FieldScout TDR 350 Soil Moisture Meter (Case Included). Spectrum Technologies Official Website. Available online: https://www.specmeters.com/FieldScout-TDR350-Soil-Moisture-Meter (accessed on 15 September 2025).
- Spectrum Technologies Inc. FieldScout SC900 Soil Compaction Meter. Spectrum Technologies Official Website. Available online: https://www.specmeters.com/FieldScout-SC900-Soil-Compaction-Meter (accessed on 15 September 2025).
- ASABE Standards EP542; Procedure for Using and Reporting Data Obtained with the Soil Cone Penetrometer. American Society of Agricultural and Biological Engineers: St. Joseph, MO, USA, 2019.
- Sima, N.Q.; Harmel, R.D.; Fang, Q.X.; Ma, L.; Andales, A.A. A modified F-test for evaluating model performance by including both experimental and simulation uncertainties. Environ. Model. Softw. 2018, 104, 236–248. [Google Scholar] [CrossRef]
- Tadić, V.; Radočaj, D.; Jurišić, M. Machine Learning Methods for Evaluation of Technical Factors of Spraying in Permanent Plantations. Agronomy 2024, 14, 1977. [Google Scholar] [CrossRef]
- Dhanka, S.; Maini, S. A Hybridization of XGBoost Machine Learning Model by Optuna Hyperparameter Tuning Suite for Cardiovascular Disease Classification with Significant Effect of Outliers and Heterogeneous Training Datasets. Int. J. Cardiol. 2024, 420, 132757. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Ahn, J.M.; Kim, J.; Kim, K. Ensemble Machine Learning of Gradient Boosting (XGBoost, LightGBM, CatBoost) and Attention-Based CNN-LSTM for Harmful Algal Blooms Forecasting. Toxins 2023, 15, 608. [Google Scholar] [CrossRef]
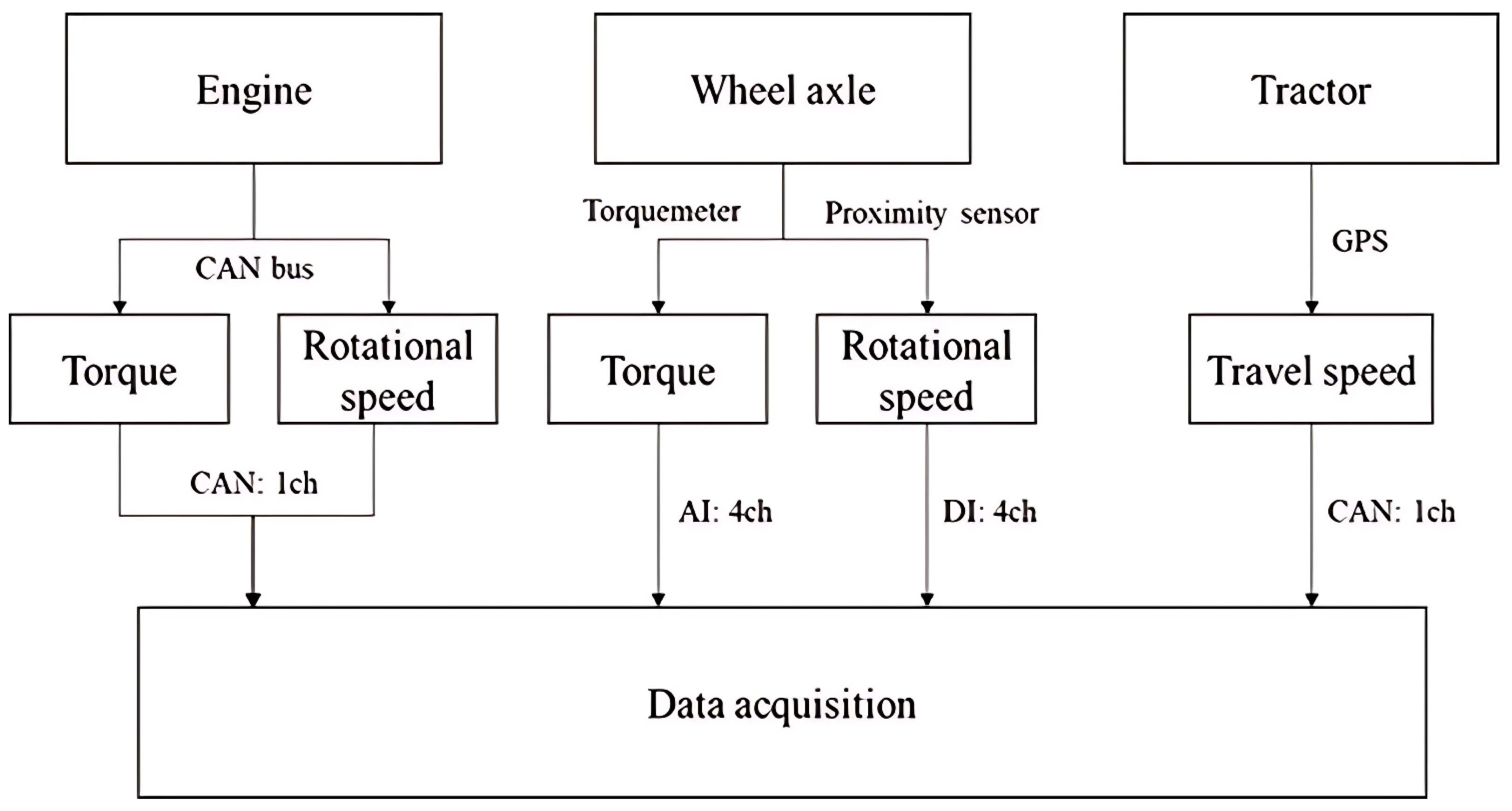



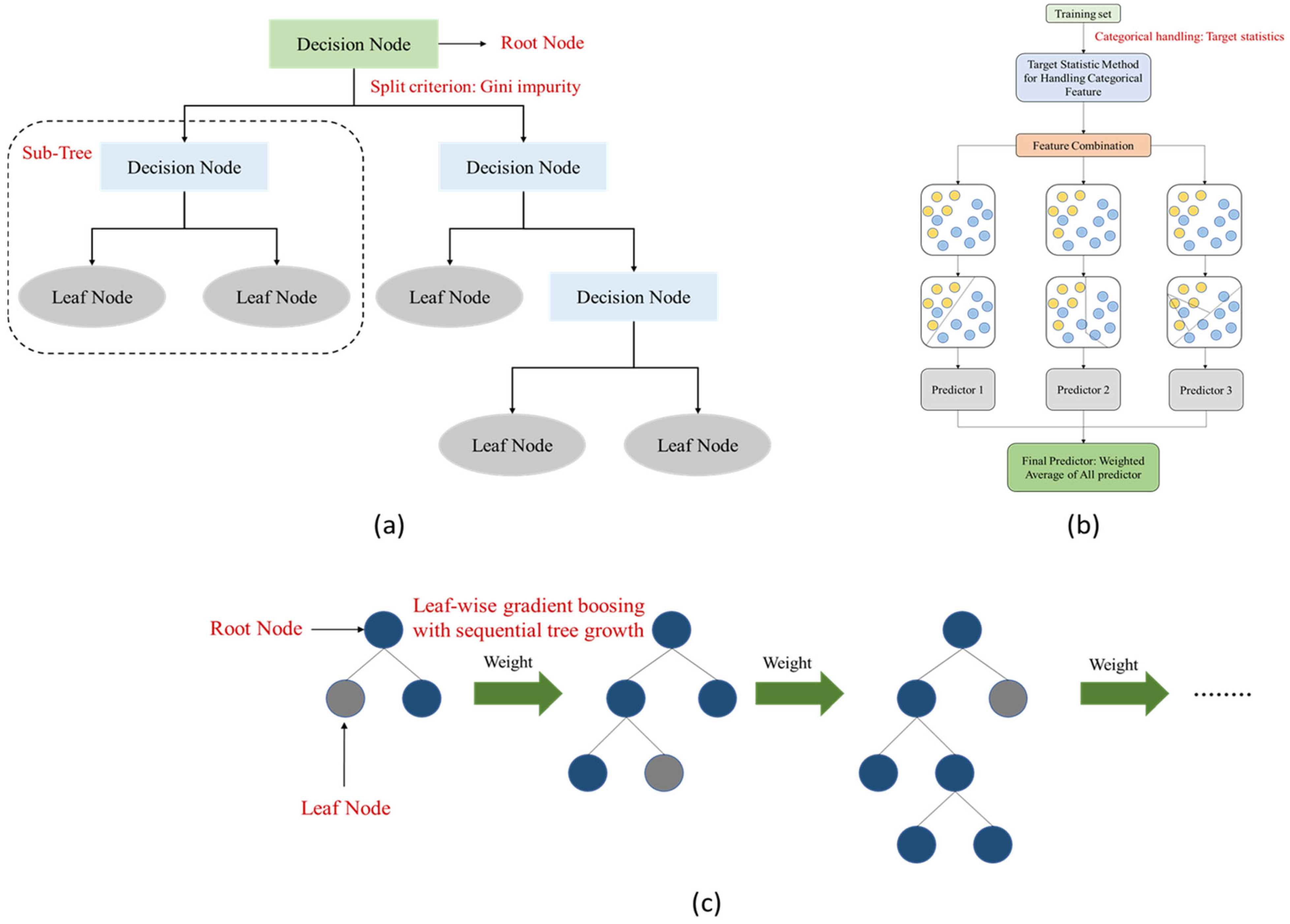

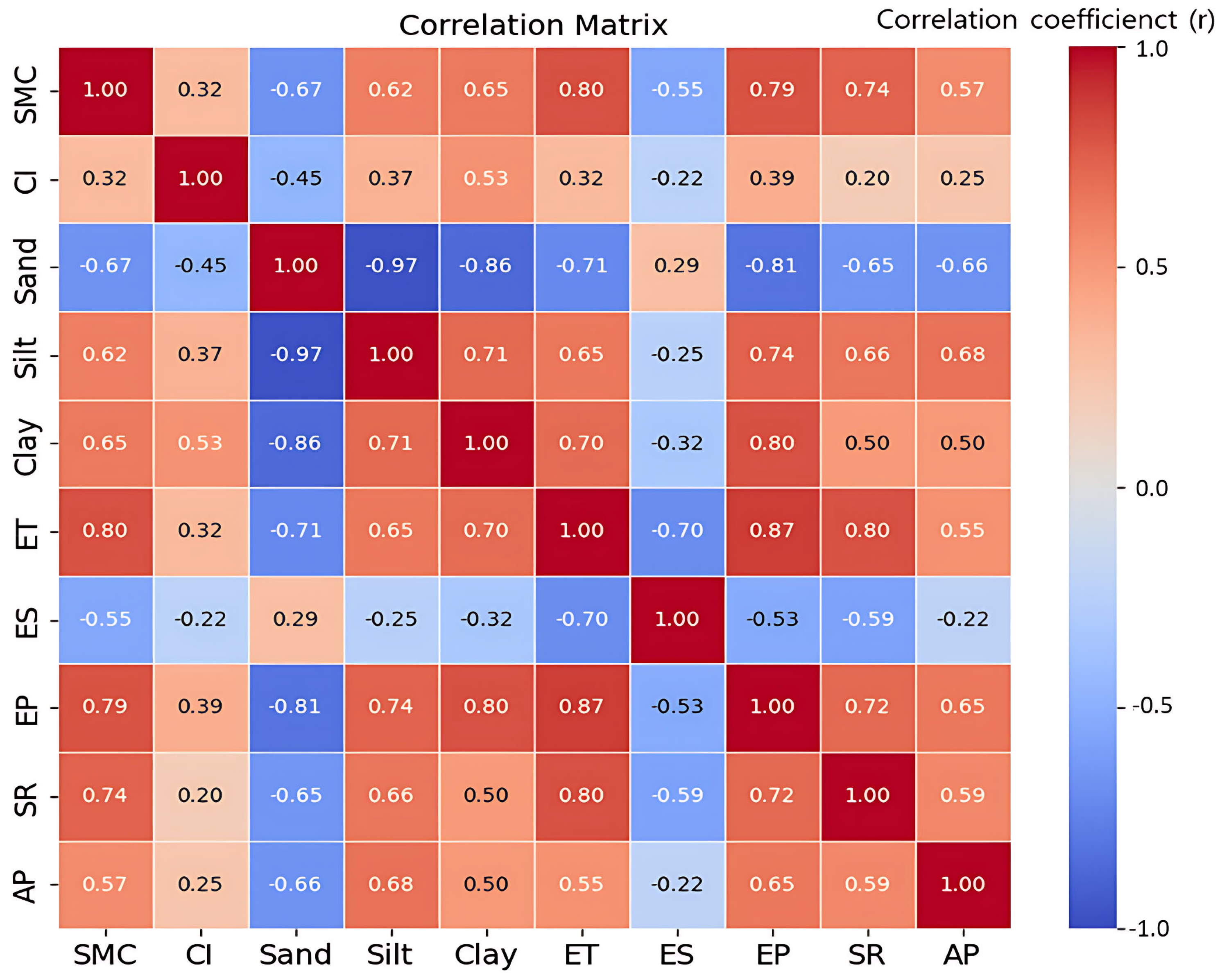
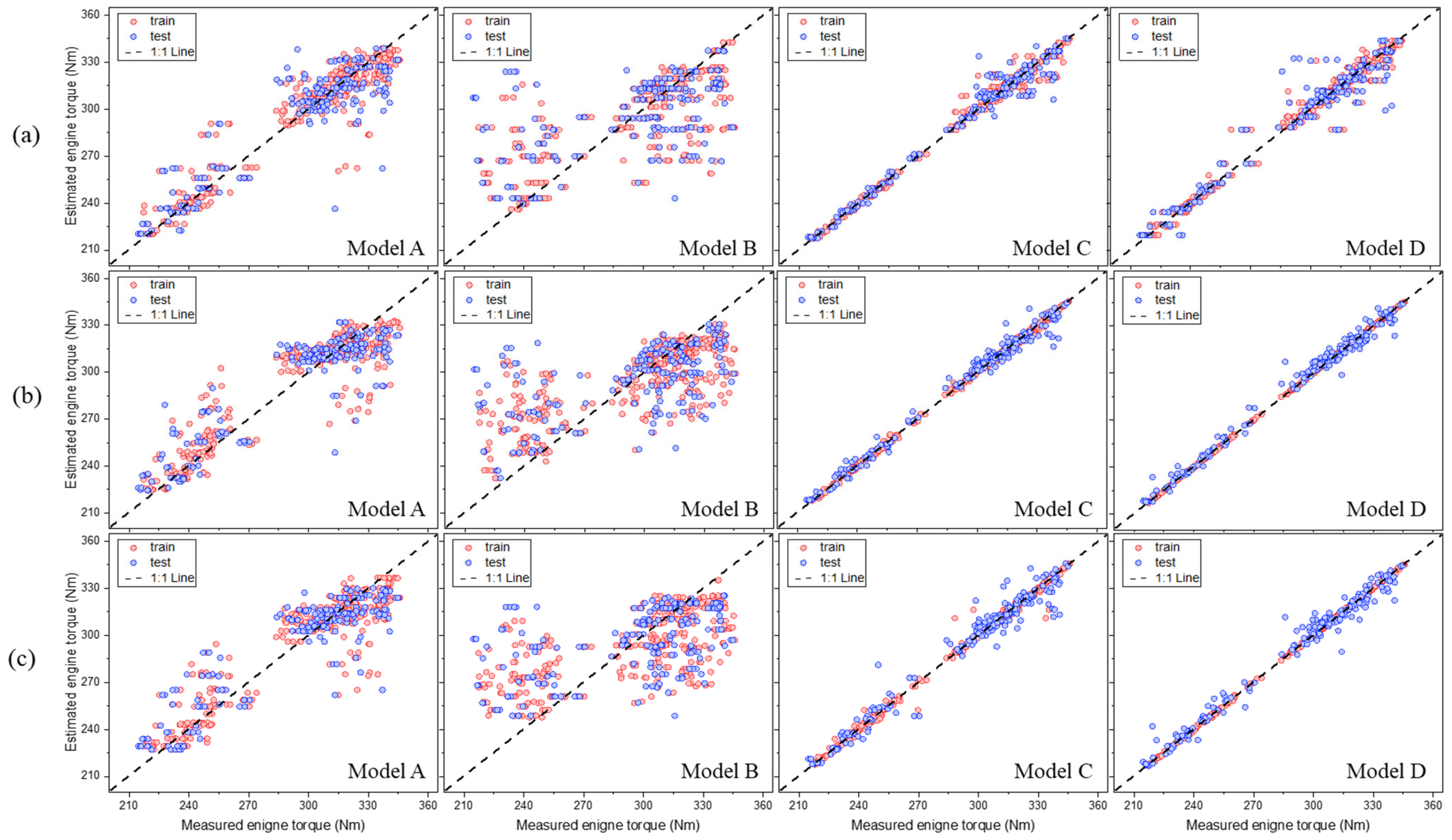


| Items | Specification |
|---|---|
| Soil moisture sensor | Measurement unit: percentage of volumetric water content (VWC) |
| Range: 0% VWC to saturation | |
| Accuracy: ±3.0% VWC | |
| Cone penetrometer | Measurement unit: cone index (kPa) |
| Range: 0–45 cm, 0–7000 kPa | |
| Accuracy: ±1.25 cm and ±103 ka |
| Site | Field Size (m2) | Province | City |
|---|---|---|---|
| S1 | 6000 | Chungcheongnam-do | Seosan |
| S2 | 6000 | Chungcheongnam-do | Seosan |
| S3 | 4000 | Chungcheongnam-do | Cheongyang |
| S4 | 4000 | Chungcheongnam-do | Cheongyang |
| S5 | 3000 | Gyeonggi-do | Anseong |
| S6 | 4000 | Gyeonggi-do | Anseong |
| S7 | 6000 | Chungcheongnam-do | Dangjin |
| S8 | 4000 | Chungcheongnam-do | Dangjin |
| S9 | 4000 | Chungcheongnam-do | Dangjin |
| S10 | 4000 | Chungcheongnam-do | Dangjin |
| Items | Max. | Avg. | Std. | CV (%) | |
|---|---|---|---|---|---|
| Soil physical property | SMC | 46.24 | 31.32 | 5.64 | 18 |
| CI | 2104 | 891 | 383 | 43 | |
| Sand | 88.18 | 51.9 | 24.26 | 46.7 | |
| Silt | 62.76 | 34.59 | 17.45 | 50.4 | |
| Clay | 34.11 | 13.5 | 8.48 | 62.8 | |
| Engine performance indicators | ET | 345.8 | 293.8 | 37 | 12.6 |
| ES | 2567.5 | 2303.7 | 122.3 | 5.3 | |
| EP | 81.32 | 70.87 | 7.03 | 9.9 | |
| SR | 18.94 | 12.17 | 4.52 | 37.1 | |
| AP | 69.1 | 54.6 | 9.97 | 18.3 | |
| Site | Field Size (m2) | Location |
|---|---|---|
| S1 | 6000 | Chungcheongnam-do |
| S2 | 6000 | Chungcheongnam-do |
| S3 | 4000 | Chungcheongnam-do |
| S4 | 4000 | Chungcheongnam-do |
| S5 | 3000 | Gyeonggi-do |
| S6 | 4000 | Gyeonggi-do |
| S7 | 6000 | Chungcheongnam-do |
| S8 | 4000 | Chungcheongnam-do |
| S9 | 4000 | Chungcheongnam-do |
| S10 | 4000 | Chungcheongnam-do |
| Output | Model | Regression Model | R2 | R2 Adj | S.E. |
|---|---|---|---|---|---|
| Engine torque | A | ET = 5.23SMC + 129.7339 | 0.637 | 0.636 | 22.3 |
| B | ET = 0.0313CI + 265.8501 | 0.105 | 0.104 | 35.1 | |
| C | ET = 5.07SMC + 0.00768CI + 128.0591 | 0.643 | 0.642 | 22.2 | |
| D | ET = 3.82SMC − 0.000800CI − 0.499Sp + 200.8467 | 0.695 | 0.693 | 20.5 | |
| Engine power | A | EP = 0.987SMC + 39.9625 | 0.627 | 0.627 | 4.30 |
| B | EP = 0.00724CI + 64.4265 | 0.155 | 0.154 | 6.47 | |
| C | EP = 0.924SMC + 0.00292CI + 39.3251 | 0.650 | 0.649 | 4.17 | |
| D | EP = 0.558SMC + 0.000451CI − 0.145Sp + 60.5472 | 0.773 | 0.771 | 4.17 | |
| Slip ratio | A | SR = 0.590SMC − 6.3114 | 0.542 | 0.542 | 3.06 |
| B | SR = 0.00238CI + 10.0487 | 0.041 | 0.039 | 4.43 | |
| C | SR = 0.599SMC − 0.000415CI − 6.2210 | 0.544 | 0.542 | 3.06 | |
| D | SR = 0.441SMC − 0.00148CI − 0.0627Sp + 2.9293 | 0.599 | 0.597 | 2.87 | |
| Axle power | A | AP = 1.000SMC + 23.1241 | 0.323 | 0.322 | 8.21 |
| B | AP = 0.00658CI + 48.7421 | 0.064 | 0.062 | 9.66 | |
| C | AP = 0.960SMC + 0.00210CI + 22.6669 | 0.329 | 0.327 | 8.19 | |
| D | AP = 0.402SMC − 0.00168CI − 0.221Sp + 54.9721 | 0.470 | 0.468 | 7.28 |
| Output | Model | Degrees of Freedom (Df) | Sum of Squares (SS) | Mean Squares (MS) | F-Value | p-Value | Variable | Tolerance | Variance Inflation Factor (VIF) | |
|---|---|---|---|---|---|---|---|---|---|---|
| Engine torque | A | Regression | 1 | 523,869.8 | 523,869.8 | 1049.7 | 0.000 * | SMC | ||
| Residual | 9 | 298,450.1 | 499.1 | |||||||
| B | Regression | 1 | 86,400.7 | 86,400.7 | 70.2 | 0.000 * | CI | |||
| Residual | 9 | 735,919.1 | 1230.6 | |||||||
| C | Regression | 2 | 528,537.6 | 264,268.8 | 537.0 | 0.000 * | SMC | 0.990 | 1.111 | |
| Residual | 8 | 293,782.3 | 492.1 | CI | 0.990 | 1.111 | ||||
| D | Regression | 3 | 571,231.4 | 190,410.5 | 452.000 | 0.000 * | SMC CI Sand | 0.550 0.794 0.486 | 1.817 1.260 2.059 | |
| Residual | 7 | 251,088.4 | 421.3 | |||||||
| Engine power | A | Regression | 1 | 18,598.7 | 18,598.7 | 1006.500 | 0.000 * | SMC | ||
| Residual | 9 | 11,049.7 | 18.5 | |||||||
| B | Regression | 1 | 4602.0 | 4602.0 | 109.900 | 0.000 * | CI | |||
| Residual | 9 | 25,046.3 | 41.9 | |||||||
| C | Regression | 2 | 19,274.8 | 9637.4 | 554.600 | 0.000 * | SMC | 0.900 | 1.111 | |
| Residual | 8 | 10,373.6 | 17.4 | CI | 0.900 | 1.111 | ||||
| D | Regression | 3 | 22,904.1 | 7634.7 | 674.700 | 0.000 * | SMC CI Sand | 0.550 0.794 0.486 | 1.817 1.260 2.059 | |
| Residual | 7 | 6744.2 | 11.3 | |||||||
| Slip ratio | A | Regression | 1 | 6648.4 | 6648.4 | 708.900 | 0.000 * | SMC | ||
| Residual | 9 | 5608.6 | 9.4 | |||||||
| B | Regression | 1 | 497.9 | 497.9 | 25.300 | 0.000 * | CI | |||
| Residual | 9 | 11,759.1 | 19.7 | |||||||
| C | Regression | 2 | 6662.0 | 3331.0 | 355.429 | 0.000 * | SMC | 0.900 | 1.111 | |
| Residual | 8 | 5594.9 | 9.4 | CI | 0.900 | 1.111 | ||||
| D | Regression | 3 | 7336.7 | 2445.6 | 296.200 | 0.000 * | SMC CI Sand | 0.550 0.794 0.486 | 1.817 1.260 2.059 | |
| Residual | 7 | 4920.3 | 8.3 | |||||||
| Axle power | A | Regression | 1 | 19,287.0 | 19,287.0 | 285.828 | 0.000 * | SMC | ||
| Residual | 9 | 40,351.7 | 67.5 | |||||||
| B | Regression | 1 | 3801.7 | 3801.7 | 40.715 | 0.000 * | CI | |||
| Residual | 9 | 55,837.0 | 93.4 | |||||||
| C | Regression | 2 | 19,634.9 | 9817.5 | 146.512 | 0.000 * | SMC | 0.900 | 1.111 | |
| Residual | 8 | 40,003.8 | 67.0 | CI | 0.900 | 1.111 | ||||
| D | Regression | 3 | 28,044.9 | 9348.3 | 176.400 | 0.000 * | SMC CI Sand | 0.550 0.794 0.486 | 1.817 1.260 2.059 | |
| Residual | 7 | 31,593.8 | 53.0 | |||||||
| Items | R2 | R2 Gap | RMSE (Nm) | TTLR | MAE (Nm) | MAPE (%) | RD (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||||
| A | DT | 0.834 | 0.747 | 0.088 | 5.17 | 6.31 | 1.49 | 5.82 | 6.96 | 3.69 | 4.36 | 5.17 | 6.22 |
| CatBoost | 0.883 | 0.780 | 0.103 | 5.54 | 6.78 | 1.50 | 8.70 | 9.46 | 2.98 | 4.22 | 4.27 | 6.04 | |
| LightGBM | 0.822 | 0.703 | 0.119 | 5.73 | 7.82 | 1.86 | 6.47 | 7.33 | 3.95 | 4.83 | 5.36 | 6.73 | |
| B | DT | 0.411 | 0.220 | 0.192 | 8.60 | 9.15 | 1.13 | 5.55 | 6.67 | 7.44 | 8.18 | 9.74 | 10.92 |
| CatBoost | 0.532 | 0.347 | 0.185 | 5.51 | 6.59 | 1.43 | 5.90 | 6.71 | 7.21 | 8.54 | 8.69 | 10.73 | |
| LightGBM | 0.424 | 0.300 | 0.124 | 4.30 | 5.55 | 1.66 | 6.40 | 6.43 | 8.10 | 9.17 | 9.64 | 11.06 | |
| C | DT | 0.963 | 0.848 | 0.115 | 7.18 | 8.20 | 1.31 | 4.67 | 8.00 | 1.60 | 2.70 | 2.45 | 4.82 |
| CatBoost | 0.999 | 0.972 | 0.027 | 1.15 | 1.34 | 1.37 | 0.93 | 1.34 | 1.32 | 1.47 | 1.39 | 2.15 | |
| LightGBM | 0.991 | 0.949 | 0.043 | 3.45 | 4.23 | 1.50 | 2.06 | 2.51 | 0.72 | 1.87 | 1.17 | 2.80 | |
| D | DT | 0.961 | 0.915 | 0.046 | 7.28 | 8.06 | 1.23 | 3.85 | 6.23 | 1.32 | 2.10 | 2.48 | 3.76 |
| CatBoost | 0.999 | 0.990 | 0.009 | 3.30 | 3.65 | 1.22 | 2.25 | 2.80 | 0.86 | 0.96 | 1.10 | 1.24 | |
| LightGBM | 0.999 | 0.968 | 0.031 | 5.32 | 5.65 | 1.13 | 3.72 | 4.68 | 0.26 | 0.64 | 1.45 | 2.27 | |
| Items | R2 | R2 Gap | RMSE (kW) | TTLR | MAE (kW) | MAPE (%) | RD (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Train | Test | Test | Train | Test | ||||
| A | DT | 0.867 | 0.728 | 0.139 | 2.50 | 2.87 | 1.32 | 1.82 | 3.01 | 2.54 | 4.25 | 3.53 | 5.45 |
| CatBoost | 0.851 | 0.749 | 0.102 | 2.71 | 3.53 | 1.70 | 2.16 | 2.77 | 3.06 | 3.89 | 3.83 | 4.97 | |
| LightGBM | 0.819 | 0.737 | 0.082 | 2.99 | 3.61 | 1.46 | 2.34 | 2.84 | 3.32 | 3.99 | 4.22 | 5.08 | |
| B | DT | 0.591 | 0.410 | 0.181 | 4.46 | 5.34 | 1.43 | 2.88 | 4.51 | 4.23 | 6.60 | 6.29 | 8.98 |
| CatBoost | 0.562 | 0.394 | 0.168 | 4.53 | 5.78 | 1.63 | 3.50 | 4.50 | 5.15 | 6.60 | 6.40 | 8.14 | |
| LightGBM | 0.499 | 0.377 | 0.123 | 4.94 | 6.47 | 1.72 | 3.74 | 5.12 | 5.47 | 7.43 | 6.96 | 9.17 | |
| C | DT | 0.950 | 0.877 | 0.073 | 1.62 | 2.25 | 1.94 | 1.02 | 1.57 | 1.42 | 2.14 | 2.30 | 3.13 |
| CatBoost | 0.999 | 0.967 | 0.032 | 1.09 | 1.28 | 1.39 | 0.68 | 0.89 | 0.97 | 1.24 | 0.13 | 1.80 | |
| LightGBM | 0.996 | 0.952 | 0.045 | 1.43 | 1.49 | 1.08 | 0.29 | 0.98 | 0.42 | 1.37 | 1.61 | 2.10 | |
| D | DT | 0.962 | 0.898 | 0.064 | 1.34 | 1.49 | 1.23 | 0.85 | 1.37 | 1.17 | 1.96 | 1.88 | 3.27 |
| CatBoost | 0.999 | 0.980 | 0.019 | 0.99 | 1.00 | 1.01 | 0.77 | 0.72 | 0.91 | 1.04 | 1.13 | 1.41 | |
| LightGBM | 0.999 | 0.965 | 0.034 | 1.21 | 1.38 | 1.30 | 1.16 | 1.99 | 1.23 | 1.40 | 1.30 | 1.95 | |
| Items | R2 | R2 Gap | RMSE (%) | TTLR | MAE (%) | MAPE (%) | RD (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Train | Test | Test | Train | Test | ||||
| A | DT | 0.702 | 0.562 | 0.140 | 2.48 | 2.96 | 1.42 | 1.79 | 2.30 | 6.72 | 7.91 | 6.50 | 6.94 |
| CatBoost | 0.781 | 0.642 | 0.139 | 2.12 | 2.67 | 1.58 | 1.59 | 2.08 | 7.61 | 7.94 | 7.58 | 7.64 | |
| LightGBM | 0.808 | 0.635 | 0.173 | 1.99 | 2.70 | 1.84 | 1.37 | 2.01 | 6.53 | 6.98 | 6.47 | 6.85 | |
| B | DT | 0.534 | 0.462 | 0.072 | 3.11 | 4.04 | 1.69 | 2.07 | 2.77 | 8.18 | 8.70 | 6.88 | 7.29 |
| CatBoost | 0.583 | 0.327 | 0.257 | 2.94 | 3.62 | 1.52 | 2.10 | 2.59 | 6.78 | 7.19 | 5.47 | 6.94 | |
| LightGBM | 0.485 | 0.296 | 0.189 | 3.27 | 3.70 | 1.28 | 2.40 | 2.71 | 6.78 | 6.57 | 7.20 | 9.59 | |
| C | DT | 0.938 | 0.822 | 0.116 | 1.11 | 1.34 | 1.45 | 0.42 | 0.76 | 4.86 | 5.20 | 3.09 | 5.24 |
| CatBoost | 0.999 | 0.977 | 0.022 | 0.57 | 0.70 | 1.53 | 0.36 | 0.38 | 4.47 | 4.65 | 4.46 | 5.87 | |
| LightGBM | 0.997 | 0.928 | 0.069 | 1.24 | 1.24 | 1.00 | 0.54 | 0.63 | 1.66 | 2.53 | 1.96 | 2.54 | |
| D | DT | 0.997 | 0.919 | 0.078 | 1.25 | 1.34 | 1.14 | 0.11 | 0.46 | 3.92 | 4.88 | 2.06 | 3.95 |
| CatBoost | 0.999 | 0.983 | 0.016 | 0.52 | 0.61 | 1.38 | 0.22 | 0.35 | 3.08 | 3.84 | 2.18 | 2.97 | |
| LightGBM | 0.998 | 0.955 | 0.044 | 0.98 | 1.00 | 1.04 | 0.51 | 0.54 | 4.46 | 4.96 | 1.45 | 2.18 | |
| Items | R2 | R2 Gap | RMSE (kW) | TTLR | MAE (kW) | MAPE (%) | RD (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Train | Test | Test | Train | Test | ||||
| A | DT | 0.424 | 0.388 | 0.036 | 7.61 | 7.69 | 1.02 | 5.56 | 5.73 | 6.24 | 6.39 | 3.98 | 3.98 |
| CatBoost | 0.537 | 0.410 | 0.127 | 6.82 | 7.55 | 1.23 | 4.99 | 5.62 | 6.08 | 6.11 | 4.53 | 4.72 | |
| LightGBM | 0.621 | 0.502 | 0.120 | 6.17 | 8.21 | 1.77 | 4.30 | 5.76 | 8.63 | 9.30 | 4.34 | 4.93 | |
| B | DT | 0.240 | 0.120 | 0.120 | 8.71 | 9.28 | 1.14 | 7.48 | 7.98 | 4.81 | 5.28 | 6.03 | 6.81 |
| CatBoost | 0.535 | 0.310 | 0.224 | 6.82 | 8.84 | 1.68 | 5.66 | 7.11 | 5.19 | 5.67 | 4.54 | 6.01 | |
| LightGBM | 0.423 | 0.386 | 0.036 | 7.59 | 9.46 | 1.55 | 6.26 | 7.69 | 4.39 | 4.84 | 3.97 | 4.13 | |
| C | DT | 0.849 | 0.743 | 0.106 | 3.88 | 4.73 | 1.48 | 1.68 | 3.00 | 3.39 | 2.68 | 5.07 | 5.46 |
| CatBoost | 0.999 | 0.889 | 0.110 | 3.21 | 3.31 | 1.07 | 0.17 | 1.52 | 0.31 | 3.26 | 2.38 | 3.13 | |
| LightGBM | 0.989 | 0.831 | 0.158 | 4.07 | 4.09 | 1.01 | 1.57 | 2.29 | 1.11 | 1.55 | 1.95 | 2.57 | |
| D | DT | 0.958 | 0.840 | 0.118 | 2.06 | 2.28 | 1.23 | 0.93 | 1.67 | 1.87 | 3.68 | 3.76 | 4.13 |
| CatBoost | 0.999 | 0.959 | 0.040 | 1.11 | 1.27 | 1.32 | 0.79 | 0.88 | 1.17 | 1.87 | 3.20 | 3.63 | |
| LightGBM | 0.999 | 0.924 | 0.075 | 2.21 | 2.68 | 1.47 | 0.14 | 1.28 | 2.28 | 2.67 | 0.38 | 0.92 | |
| DT | CatBoost | LightGBM |
|---|---|---|
| max_depth: 8 | number of iterations: 609 | num_leaves: 75 |
| min_samples_split: 8 | learning_rate: 0.160 | learning_rate: 0.108 |
| min_samples_leaf: 2 | depth: 10 | n_estimators: 746 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, S.-Y.; Baek, S.-M.; Baek, S.-Y.; Kim, Y.-J.; Kim, W.-S. Machine Learning-Based Estimation of Tractor Performance in Tillage Operations Using Soil Physical Properties. Agronomy 2025, 15, 2228. https://doi.org/10.3390/agronomy15092228
Gong S-Y, Baek S-M, Baek S-Y, Kim Y-J, Kim W-S. Machine Learning-Based Estimation of Tractor Performance in Tillage Operations Using Soil Physical Properties. Agronomy. 2025; 15(9):2228. https://doi.org/10.3390/agronomy15092228
Chicago/Turabian StyleGong, So-Yun, Seung-Min Baek, Seung-Yun Baek, Yong-Joo Kim, and Wan-Soo Kim. 2025. "Machine Learning-Based Estimation of Tractor Performance in Tillage Operations Using Soil Physical Properties" Agronomy 15, no. 9: 2228. https://doi.org/10.3390/agronomy15092228
APA StyleGong, S.-Y., Baek, S.-M., Baek, S.-Y., Kim, Y.-J., & Kim, W.-S. (2025). Machine Learning-Based Estimation of Tractor Performance in Tillage Operations Using Soil Physical Properties. Agronomy, 15(9), 2228. https://doi.org/10.3390/agronomy15092228







