Practical Test and Inference on the Inheritance of Dual Multi-Factors and Tri-Normal Distributions of Quantitative Characters

Abstract

The multi-factorial hypothesis of quantitative trait inheritance originated from Nilson’s wheat hybridization experiments. It takes unit traits as the object and is based on the binomial distribution mathematically. Due to the requirement of the same distribution, it cannot include genes of other distributions. This is its limitation. Moreover, it does not incorporate the environmental effects that constitute the phenotype, so it is not comprehensive enough. This article started from the overallness of quantitative traits, was based on the central limit theorem, and was analyzed from both the genotype and the environment and proposed the assumption on the inheritance of dual multi-factors and tri-normal distributions of quantitative traits. This genetic model was tested with practical examples, and three inferences were made. Method and Results: Firstly, the overallness of quantitative traits was discussed, thus the above assumption was proposed. Next, using many examples of normal distribution of quantitative characters in the homogeneous populations, the research on the identification of the environments without GEI was carried out. Then, the examples of normal distribution of the same quantitative characters in the homogeneous populations and in the segregated populations of the same family were used. By means of normal distribution of quantitative characters in the homogeneous populations, it was indicated that the test locations were the environments without GEI. By utilizing the properties of normal distribution and variance, it was proven that normal distribution of phenotypic value for quantitative traits in a segregated population was formed by adding normal distribution of genotypic value and environmental effect, which enables the genetic model to be tested in practice. Three types of normal distribution of quantitative traits were inferred, indicating that the quantitative characters of a considerable number of organisms in nature obey a normal distribution, expressing continuous variation.

1. Introduction

Mendel read Experiments in plant hybridization at the Meetings of the Brünn Natural History Society in 1865 [1]. This is a classic work of genetic research on qualitative characters. It opened the door of genetics and made people clearly understand the role of heredity in character performance. He also first proposed the law of segregation and the law of independent assortment. In 1910, Morgan, through his research on fruit flies, put forward the law of linkage inheritance [2]. Thus, the three major laws of qualitative trait inheritance were formed. The fourth major discovery in genetics is the Hardy–Weinberg law about population genetics. It was developed by British mathematician Hardy and German physician Weinberg in 1908 [3]. These four laws are relatively complete and have been widely recognized. The most intense debate has been over the inheritance of quantitative traits, which has continued from the beginning until now. As early as 1831 and 1884, Quetelet and Galton began to collect data, respectively, to fit people’s body weight, body height, and chest circumference with a normal distribution curve, which involved the inheritance of quantitative characters [4,5]. In 1900, Nilsson-Ehle found a wheat variety with three pairs of red alleles and old red seed coat in northern Sweden and hybridized it with white grain variety to produce different red grain offspring [6,7]. On this basis, in 1906, Bateson and Yule put forward the multi-factorial hypothesis of quantitative character inheritance, by use of which they explained the continuity of quantitative character [8]. However, like Galton, these experts only paid attention to the role of heredity and denied or ignored environmental effects. In 1903, Johannsen published the pure line theory based on the research of haricot beans [9]. The results showed that the average seed weight of offspring between lines was significantly different, and the average seed weight of offspring in a line was almost the same, but there was a fluctuating variation between individuals, which could not be inherited. He pointed out emphatically that it is the genotype of the line working in intimate conjunction with the external environment of a specific locality at a particular time that determines the average characteristics of an individual [9]. This is the original textual description of the later universal inheritance model, as follows: phenotype = genotype + environment. While recognizing the role of genotype, Fisher (1918) clearly pointed out that the variation affected by environmental factors is very important and first elaborated on the idea of analysis of variance [10]. Later, geneticists decomposed environmental variance from organisms, and environmental factors were applied in the genetic practice of quantitative characters [11]. However, in the genetic analysis of quantitative characters, some people still favor one over the other for genotype and environment. In 1901, Lyapunov perfected the central limit theorem with more common random variables as the content [12]. Applying this, later mathematicians were able to explain the common normal distribution phenomenon of biological inheritance. Unfortunately, they regarded genotype, that parallels environment in biological inheritance, as only small factors like light, water, and carbon dioxide and underestimated or ignored the large component of genotype [13,14,15]. At the beginning of the 20th century, Nelson’s article on hybridization experiments in wheat was officially published, and the multi-factorial hypothesis was all the rage. Later, it was regarded as a classical theory of quantitative character inheritance and has been widely popular in the world [16]. In fact, Nelson’s hybridization experiments in wheat only involve three pairs of alleles on chromosomes 3D, 3A, and 3B, while grain color variation is the additive effect of three pairs of alleles [17,18]. This hypothesis is based on a binomial distribution in mathematics. Due to the requirement of the same distribution, it cannot include genes from other distributions. Moreover, in mathematical analysis, the hypothesis does not theoretically include the environmental effect that plays an important role in determining phenotype. It is also impossible to solve the continuity of quantitative character phenotype in the homogeneous population of living things, genotypes of which are identical. Therefore, it is neither practical nor complete and cannot satisfactorily solve the continuity problem of quantitative character [18]. Recently, Chinese scholar Xu (2016) proposed the concept of environmental type for the first time, believing that environmental type identification, genotype identification, and phenotype identification are expected to become the three pillars of efficient crop breeding and production in the future [19]. After Johnson and Fisher, he again emphasized the role of environment in inheritance. On the basis of ten years of investigation and research on nursery production, the authors juxtaposed environmental effect with genotypic value, incorporated them into the genetic analysis of quantitative characters, and explored the inheritance of dual multi-factors and tri-normal distributions of quantitative characters [18,20,21], which has been recognized by many geneticists and mathematicians. Yan et al. (2007) divided macro-environment into two major categories and three target environments [22]. Based on this, the authors tested the genetic model using practical scientific examples that they collected and studied and made three inferences. Thereby, the problem of continuity of quantitative characters was solved more effectively.

2. The Overallness and the Assumption of the Inheritance of Dual Multi-Factors and Tri-Normal Distributions of Quantitative Characters

2.1. The Overallness of Quantitative Character

Mendel was a founder of modern genetics. When studying the inheritance of characters in plants such as peas, he divided the overall set of characters exhibited by plants into unit characters as the research object [23]. Later, genetic studies, including the current popular quantitative genetics theory, the multi-factorial hypothesis, have continued to use this method. However, quantitative characters, especially many quantitative characters with economic value, such as crop yield, meat yield of beef cattle, milk yield of dairy cows, and volume of trees, etc., are characterized by increases in quantity and enlargement in volume. They are produced through a series of physiological and biochemical processes. If, like physiological characteristics, the main biochemical characteristics are also attributed to characters, a quantitative character may contain many unit characters specific to that organism. This is true even for simple quantitative characters. For example, a piece of green leaf, its weight, and its size are related to the length, width, and thickness of the blade and petiole, the development of leaf veins, leaf margins and stomata, the proportion of palisade tissue and spongy tissue, the content of water, chlorophyll, sugar, starch, and other inclusions, as well as to the epiphytic materials of leaf surface, such as hairs and waxes. Their formation involves a considerable number of unit characters; therefore, a piece of green leaf is the overall set of these characters. As for plant biomass and animal body weight, they contain all the unit characters and organs associated with growth and development and are the overall set of all the characters or the products of their metabolic activities. Thus, quantitative characters possess an inherent overallness [18,20,21].

Quantitative traits characterized by overallness, whether large or small, contain many unit traits, which inevitably involve many genes with different properties at different loci. These genes come from the father and mother, respectively, and are contained in the fertilized egg cells, starting to work in a coordinated manner. A quantitative character is controlled by its genotype value, which is the result of the cumulative actions of dominant and additive effects of a series of genes, focusing on their contributions to the same quantitative character. These genes are located on different loci; for example, genes at least 50 different loci are related to the chlorophyll variation in maize (Zea mays), and genes at least 34 different loci affect the wing size in fruit fly (Drosophila melanogaster) [24,25]. Their properties are not completely identical and their effects are not equal. They do not have the same distribution; instead, genes with different dominant effects have different distributions, those with different additive effects have different distributions, and these two types of genes have a more distinct distributions. In this way, only the central limit theorem can unify them together. In contrast, qualitative characters emphasize the role of individual genes in different qualitative characters. The genetic basis of forming these characters is segregation of allelic genes and free combination of non-allelic genes. Thus, qualitative character takes the unit character as the object and is studied using a binomial distribution model. The research methods for the two characters are completely different.

Unlike qualitative characters, quantitative characters are significantly influenced by environmental factors in their variation. The function of environmental factors, i.e., environmental effect, is the result of the comprehensive action of many factors, such as light, heat, water, and so on. Ultimately, they construct the quantitative character and organism body. In terms of the distribution, each environmental factor has its own characteristics and needs to be studied using the central limit theorem.

It is precisely due to this overallness and the combination of polygenic inheritance with multi-factor environmental effects that quantitative characters, such as leaf size and plant biomass, can be inherited in a normal distribution. For example, the leaf size among plants of 3–4-year-old seedlings in the reciprocal cross of Fuji and Qinguan in apple (Malus pumila) varies greatly, and average leaf area per plant shows a continuously normal distribution [26]. Similarly, biomass per plant of Leymus chinensis, Stipa grandis, Agropyron michnoi, and Artemisia frigida is normally distributed or approaches normal distribution [27]. How are genetic and environmental factors integrated in the inheritance of quantitative characters?

2.2. The Assumption on the Inheritance of Dual Multi-Factors and Tri-Normal Distributions of Quantitative Characters

The inheritance of dual multi-factors and tri-normal distributions takes the overallness of quantitative character as the object, and the dual multi-factors, many genes controlling the character and numerous factors forming environmental effect, as the content. It uses the Lyapunov central limit theorem for mathematical analysis, to form the normal distribution of the genotypic value and the environmental effect. When the two are independent of each other, according to the additivity of the normal distribution, the phenotypic value also presents a normal distribution. In this way, the assumption can be expressed as follows:

$$P=G+E~N({\mu }_G,{\sigma }_G^2+{\sigma }_E^2)$$

where P is the phenotypic value, and G is the genotypic value, which is the sum of additive effects and dominant effects of many genes with different properties at every gene locus that control the quantitative character. These two effects play a decisive role in character inheritance, like other quantitative trait studies, the additive–dominant genotype model is also applied here in quantitative inheritance research [28,29,30]. ${\mu }_G$ is the mean genotypic value, and ${{\sigma }_G}^2$ is the genotypic variance. E is the environmental effect, ${\mu }_E$ is the mean environmental effect, and ${{\sigma }_E}^2$ is the environmental variance. In a population as a whole ${\mu }_E=0$, and the mean phenotypic value ${\mu }_P={\mu }_G$ [31]. The important condition for dual multi-factors to form the tri- normal distributions is that G and E are independent of each other [18,21]. The formula has been thoroughly demonstrated [18,20,21] and is presented in a graphical way, which is very intuitive and clear at a glance (see Figure 1 in reference [20]).

3. Identification of the Environment Without GEI

The selection and utilization of the test location depend on the test purpose. The macro-environment must be considered first. Wang (2017) believed that the macro-environment is a set of non-genetic factors that affect the performance of individuals of organisms. It can be a single cultivation method, location, or year or a combination of different cultivation methods, different locations, and different years [32]. Yan et al. (2007) ivided the macro-environment into two categories with three types of target environment, one of which is the environment without genotype-by-environmental interaction (GEI), which is repeatable across years. The other two are the environments with GEI, one of which can be repeatable across years and the other can be not. In addition, he believed that the appropriate test environment for excellent genotype selection should be the environment with GEI, so as to make full use of the contribution of environment [22]. The authors believe that the research on biological natural attributes should minimize the performance and interference of the environment. The inheritance of dual multi-factors and tri-normal distributions of quantitative characters is finally implemented in the addition of two normal distributions, so the environment without GEI is an ideal environment.

Xu (2016) believed that phenotypes collected for homogeneous, identical genotypes under large-scale experiments can be used to reveal within-site variation and environmental variability [19]. This is just as geneticists have previously shown that phenotypes in the homogeneous population of organisms can provide unbiased estimates of the environment in the test location, which are often used in genetic analysis [23,31] and QTL mapping of modern crop breeding [33,34]. The following environments without GEI are identified by the normal distribution of quantitative characters in the homogeneous populations with identical genotypes, such as clones.

3.1. Practical Examples for the Quantitative Characters of Living Things with Identical Genotype to Yield to the Normal Distribution

A total of four examples are presented, including five quantitative characters in four homogeneous populations of four species (as shown in the

Table 1. Normal distribution of quantitative traits in four homogeneous populations.

Clones and Experimental Locations	Normal Distribution Characters and Normality Test			Researchers and Time
① Populus tomentosa, annual seedlings of clone No. 105 (Poplar seedling experimental site, Huxian central nursery, Xi’an)	Plant height, Ground diameter (S-W test, histograms) H: p = 0.098, D: p = 0.251(R 4.2.2 software)			Zhang et al., 2016 [20], 2019 [21]
② Euramerican poplar 107 (P. × euramericana cv. ‘74/76’), Clonal annual seedlings (107 Poplar seedling experimental site, Beijing forestry University nursery)	Ground diameter (S-W test) p = 0.456 (SPSS 25.0 software)			Feng Dan 2017 * [35]
③ Italy 1-101 (P.alba) × 84k poplar (P. alba × P. glandulasa),Clone Qinbai No.3, 7-year-old forest [36] (Qinbai No.3 poplar experimental forest, Weihe experimental station, Northwest A&F University)	DBH (S-W test) p = 0.200 (SPSS 25.0 software)			Supplementary Materials **
④ Eucalyptus urophyllo × E. grandis, DH32-29 Clonal 2 and 3-year-old pure forest-DH is the first letter of the Dongmen-Chinese pinyin and Hybrid-English of Dongmen Hybrid (DH32-29 forest site, jijia forest farm, Leizhou peninsula, Guangdong province)		DBH (K-S test)		Xu Xiaodong et al., 2019 [37]
		in 2-year-old forest p > 0.05	in 3-year-old forest p > 0.05
	Kurtosis	−0.5721	−0.2656
	Skewness	−0.1373	0.0121

Note: * The authors conducted an S-W test on the data of Dan Feng; ** The clonal forest of Qinbai No. 3 is an experimental forest of Fan Junfeng’s team. Jianshe Gao and Yongxue Zhou conducted a special investigation for this study in 2023, and the authors conducted a normality test on the measurement data. The sample sizes: ① 147 Populus totentosa plants, ② 164 poplar 107, ③ 60 poplar Qinbai No. 3, ④ 30 plots of Eucalyptus urophylla.

).

3.2. Derivation of an Independent Normal Distribution of Environmental Effect (E) of Organisms with Identical Genotype

It is known that the genotype of each individual of organisms in Table 1 is identical, and the phenotypic value of quantitative character follows a normal distribution. Let the phenotypic value of quantitative character of a certain organism be denoted as ${}_{c}P$, the genotypic value as ${}_{c}G$, and the environmental effect as ${}_{c}E$. Here, the subscript c represents a homogeneous population of clones with identical genotype. The distribution of the phenotypic value of quantitative character of the organism can be expressed by the following formula:

$${}_{c}P={}_{c}G+{}_{c}E~N({\mu }_{{}_{c}P},{{\sigma }_{{}_{c}P}}^2)$$

Its graph is a normal distribution curve with ${\mu }_{{}_{c}P}$ as the mean phenotypic value and with ${{\sigma }_{{}_{c}P}}^2$ as the phenotypic variance.

According to Section 2.2, in this homogeneous population, ${\mu }_{{}_{c}P}={\mu }_{{}_{c}G}$. Then,

$${}_{c}P={}_{c}G+{}_{c}E~N({\mu }_{{}_{c}G},{{\sigma }_{{}_{c}P}}^2)$$

where the genotype of each individual of the organism is identical, its genotypic value, ${}_{c}G$, is equal to the mean genotypic value in the population, ${\mu }_{{}_{c}G}$; both are a constant. Let it be denoted as C. Its variance is 0, then the phenotypic variance, ${{\sigma }_{{}_{c}P}}^2$, is produced by the environmental effects, that is, ${{\sigma }_{{}_{c}P}}^2={{\sigma }_{{}_{c}E}}^2$. Thus,

$${}_{c}P=C+{}_{c}E~N(C,{{\sigma }_{{}_{c}E}}^2)$$

It shows that the phenotype of quantitative character of the organism can essentially be represented as a normal distribution curve, where C is the mean genotypic value, and ${{\sigma }_{{}_{c}E}}^2$ is the environmental variance. As far as the seedling height and ground diameter of Popolus tomentosa N.105 clone are concerned, the C values are 1.87 m and 1.46 cm, and ${{\sigma }_{{}_{c}E}}^2$ values are 0.198 and 0.134, respectively [20,21]. It indicates that the environmental effect is involved in the performance of quantitative character. This is beyond the reach of the multi-factorial hypothesis.

From the given formula and the properties of the normal distribution, it is easy to conclude that the environmental effect, ${}_{c}E$, also follows a normal distribution. That is,

$${}_{c}E~N(0,{{\sigma }_{{}_{c}E}}^2)$$

It is an independent normal distribution. This can be more clearly understood from the following examples:

① When discussing univariate regression and correlation analysis, Wang (2017) [32] pointed out that the phenotypic value of the clone, $X_i=G_i+\epsilon$, $\epsilon \text{~}N(0,{{\sigma }_{\epsilon }}^2)$, $\epsilon$, and $G_i$ are independent of each other; that is, $\epsilon$ obeys an independent normal distribution. Among them, $X_i$ is the phenotypic value of the ith individual of the clone, $G_i$ is the mean genotypic value, and $\epsilon$ is the random error effect, which is equivalent to the environmental effect, ${}_{c}E$, and ${{\sigma }_{\epsilon }}^2$ is the random error variance, which is equivalent to the environmental variance, ${{\sigma }_{{}_{c}E}}^2$. If the mean genotypic value, $G_i$, is regarded as a constant, then $X_i=G_i+\epsilon$ also follows a normal distribution. This is completely consistent with the normal distribution of the phenotypic value of quantitative characters in the homogeneous population discussed above. This indicates that the independent normal distribution of the random error effect, i.e., environmental effect, is the origin of the normal distribution of the characters in clones. ② Yan et al. (2007) also applied $\overline{e_{ij}}$ obeying $NID(0,{\sigma }^2/r)$ when analyzing genotypic and environmental data with GGE biplot; here, NID is normally and independently distributed, and $r$ is the number of repetitions [22].

The graph of ${}_{c}E$ is a normal distribution curve that translates the normal distribution curve of the phenotypic value to the vertical axis by C units.

3.3. Summary of This Section

Through the above derivation, it has been proven that the environmental effect ${}_{c}E$ of the above four cases exhibits independent normal distribution, indicating that ${}_{c}E$ and ${}_{c}G$ are independent of each other, and the test locations are environments without GEI, which can be repeated between different years [22]. Therefore, researchers can use the normal distribution of quantitative characters in the homogeneous populations, with the help of independent normal distribution of environmental effects, to evaluate and make use of the environments without GEI and to carry out some fruitful research.

The environments without GEI exist objectively in nature [22,32]. In such environments, the environmental effects are independently and normally distributed, and the quantitative characters in the homogeneous populations of organisms growing under these conditions are also normally distributed. In this section and the next section, the authors illustrated the concept with practical examples. Shi et al. (2008) also saw this clue in a study on cotton [38]. However, in some research, variations in quantitative traits in homogeneous populations caused by the environments were misinterpreted as the genetic segregation of organisms [39]. The figuring out of these issues and the correct understanding and utilization of the role of environmental effects will further advance the development of modern breeding and cultivation industries.

4. Practical Testing on the Inheritance of Dual Multi-Factors and Tri-Normal Distributions of Quantitative Characters

4.1. Practical Examples for the Same Quantitative Characters in the Homogeneous Populations and in the Segregated Populations of Families to Show the Normal Distribution Within Certain Time Limit

A total of five examples are presented, including 26 quantitative traits in 15 homogeneous populations and 28 quantitative traits in 9 segregated populations from six families of three species (rape, cucumber, cotton) (as shown in the

Table 2. Normal distribution of the same quantitative characters in the homogeneous and in the segregated populations of five families.

Varieties and Cross Combinations (Experimental Locations)	Normal Distribution Characters and Normality Test					Researchers and Times
① Brassica napus P1 (H155) × P2 (Qva) → F1 (both P1 and P2 were self- crossed by multiple generations) F1 × F1 → F2 (experimental field, Henan academy of agricultural sciences)	Cracking angle resistance character (cracking angle resistance index SSRI)					Wen Yancheng 2012 [40]
		Kurtosis		Skewness
	P1	0.1684		0.9376
	P2	0.2787		0.7898
	F1	0.2633		0.7128
	F2	0.3211		0.4336
② Cucumber (Cucumiss ativus), (cross combinations of the same parents were tested at two locations) P1 (DE843) × P2 (EP326) → F1 (the two parents were self-crossed by multiple generations) F1 × F1 → F2 (cucumber experimental site and greenhouse, the vegetable experimental base, college of horticulture and plant protection, Yangzhou University)	Fruit tannin content (S-W test, p value)					Xu Qiang et al., 2014 * [41]
		In the field		In the greenhouse
	P1	0.281		0.637
	P2	0.694		0.107
	F1	0.230		0.350
	F2	0.384		0.339
③ Cotton (Gossypium), land cotton variety P1 (Xinluzhong 37) × P2 (Xinluzhong 51) → F1 F1 × F1 → F2 (experimental field, Twelfth Regiment, Tarim University, Alar City, Xinjiang)	Single boll weight(g) (k-s test, p value)					Ma Xiaoman et al., 2024 [42]
	P1	0.200
	P2	0.200
	F1	0.200
	F2	0.200
④ Cotton (two backcross combinations using variety CCRI36, Zhong221 and Hai1)	Five traits of 2 BC2F1 self-crossing bolls (homogeneous populations), 2 BC2F1 self-crossing bolls and 2 BC3F0 inter-crossing bolls (segregated populations): (1) Fiber length, (2) fiber specific strength, (3) micronaire value, (4) fiber uniformity, and (5) fiber elongation (histograms—there were 30 normal distribution graphs of 5 characters in 2 homogeneous populations and 4 segregated populations)					Shi Yuzhen et al., 2008 [38]
⑤ Cotton (complete diallelhybrid variety Nongza 62) F1 self-crossing bolls (homogeneous population) and F2 self-crossing bolls (segregated population) (Field, Mingshantou town, Nan County, Hunan province)		F1 self-crossing bolls		F2 self-crossing bolls		Chen Jinxiang et al., 2004 [39]
		Kurtosis	Skewness	Kurtosis	Skewness
	Fiber specific strength	−0.4787	−0.1755	−0.0813	0.1359
	Micronaire Value	−0.0616	−0.4090	0.9176	0.2557
	Reflectivity	−0.1047	−0.0971	−0.2476	−0.3179
	Yellowness	−0.6710	−0.0723	−0.4670	−0.3194

Note: * The authors conducted an S-W test on data of Xu Qiang and others. The sample sizes: ① 240 Brassica napus plants. ② Cucumber: In the field, 60 P₁ plants, 58 P₂ plants, 59 F₁ plants, and 143 F₂ plants. In the greenhouse, 52 P₁ plants, 55 P₂ plants, 58 F₁ plants, and 144 F₂ plants. ③ 25 plants of upland cotton P₁, P₂, and F₁, with 133 F₂ plants. Other sample sizes. ④ 30 backcrossed cotton plants. ⑤ 100 cotton plants were tested in the field.

).

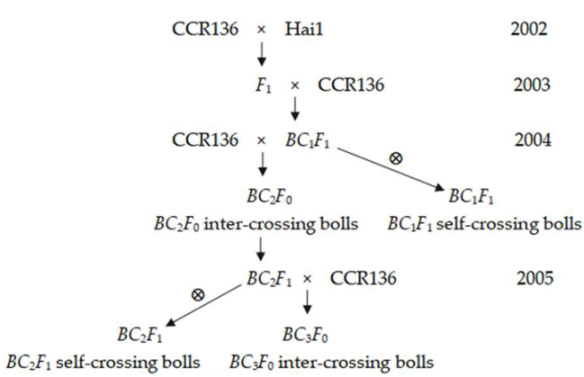
The comparative populations in Examples ① and ③ are studied in the same place and year, and the quantitative traits of populations P₁, P₂, F₁, and F₂ of each family are normally distributed, which are easy to analyze. In Examples ④ and ⑤, cotton varieties are studied. Cotton is mainly self-pollinated; its fibers are developed from the integuments in the mother’s body [23], and the fiber characters are determined by the genotype of the mother’s body. In Example ④, the homogeneous populations, BC₂F₀ inter-crossing bolls, were obtained in 2004, and the segregated populations, BC₂F₁ self-crossing bolls and BC₃F₀ inter-crossing bolls, were obtained in 2005 [38]. Example ⑤ is a large area experimental field with 0.4 hectares (F₁ plants) and 0.3 hectares (F₂ plants) of cotton variety Nongza 62. In 2001 and 2002, the homogenous population F₁ self-crossing bolls and the segregated population F₂ self-crossing bolls were obtained [39]. These two examples are, respectively, made with the same cotton variety and cultivated in the same place using the same cultivation method for two years. Moreover, the fiber traits of the homogeneous and the segregated populations are normally distributed in both years. Wang (2017) believed that macro-environment effects generally have a certain degree of repeatability [32]. Zobel et al. (1984) discovered that the results caused by macro-environment effects in the nursery can persist for a number of years [43]. Yan et al. (2007) pointed out that the environment without GEI can repeat across years [22]. Based on the repeatability across years of the macro-environment effects and the realistic performance of the experiments, the studies in Example ④ and Example ⑤ in two years each have the same macro-environment background, and normal distributions of quantitative characters in their homogeneous and segregated populations have comparability, respectively.

4.2. Derivation for the Genetic Composition of Normal Distribution of Phenotypic Value of Quantitative Characters in the Segregated Population

Five examples in Table 2 contain six different families, of which the homogeneous populations have P₁, P₂, F₁, BC₂F₀ inter-crossing bolls and F₁ self-crossing bolls, and the segregated populations have F₂, BC₂F₁ self-crossing bolls, BC₃F₀ inter-crossing bolls, and F₂ self-crossing bolls. Quantitative characters in two populations are normally distributed in the same place and within a certain time limit. Let the phenotypic value of quantitative character in the segregated population of a certain family be denoted as ${}_{f}P$, the genotypic value as ${}_{f}G$, and the environmental effect as ${}_{f}E$. Here, the subscript f represents the different populations of the family. Then, normal distribution of the phenotypic value of quantitative character can be expressed by the following formula:

$${}_{f}P={}_{f}G+{}_{f}E~N({\mu }_{{}_{f}P},{{\sigma }_{{}_{f}p}}^2)$$

(1)

Its graph is a normal distribution curve with ${\mu }_{{}_{f}P}$ as the mean phenotypic value and with ${{\sigma }_{{}_{f}P}}^2$ as the phenotypic variance.

(1) According to the results of Section 3, if the phenotypic value of quantitative traits in the homogeneous population follows a normal distribution, then the test location (containing a segregated population) represents the environment without GEI. In this case, its environmental effect, ${}_{f}E$, follows an independent normal distribution, as follows:

$${}_{f}E~N(0,{{\sigma }_{{}_{f}E}}^2)$$

(2)

When calculating the broad sense heritability, many researchers have used the phenotype of the homogeneous population, F₁, to estimate the environmental variance of the segregated population, F₂ [23,31]. The same is true for multi-generation joint analysis using maximum likelihood ratio in crop genetic research [33,34].

The graph of environmental effect, ${}_{f}E$, in the segregated populations is as described in Section 3.2. Its independent normal distribution implies that the normal distribution of the environmental effect in the segregated population is formed by the comprehensive action of many environmental factors in accordance with Lyapunov’s central limit theorem.

(2) Falconer (1989) believed that the mean environmental effect in the population as a whole is taken to be zero, so that the mean phenotypic value is equal to the mean genotypic value [31]. According to (1), the environment here is the environment without GEI, and its mean environmental effect is zero. Undoubtedly, the mean phenotypic value in the population and its mean genotypic value are in such a relationship, as follows:

$${\mu }_{{}_{f}P}={\mu }_{{}_{f}G}$$

(3)

(3) Since ${}_{f}P={}_{f}G+{}_{f}E$, and ${}_{f}G$ and ${}_{f}E$ are independent of each other, the phenotype variance ${{\sigma }_{{}_{f}P}}^2$ in Formula (1) should be composed of the genotypic variance, ${{\sigma }_{{}_{f}G}}^2$, and the environmental variance, ${{\sigma }_{{}_{f}E}}^2$, as follows:

$${{\sigma }_{{}_{f}P}}^2={{\sigma }_{{}_{f}G}}^2+{{\sigma }_{{}_{f}E}}^2$$

(4)

(4) Substituting ${\mu }_{{}_{f}G}$ of Formula (3) and ${{\sigma }_{{}_{f}G}}^2+{{\sigma }_{{}_{f}E}}^2$ of Formula (4) into ${\mu }_{{}_{f}P}$ and ${{\sigma }_{{}_{f}P}}^2$ of Formula (1), the genetic composition of normal distribution of the phenotypic value of quantitative character in the segregated population is as follows:

$${}_{f}P={}_{f}G+{}_{f}E~N({\mu }_{{}_{f}G},{{\sigma }_{{}_{f}G}}^2+{{\sigma }_{{}_{f}E}}^2)$$

(5)

Since Formula (2), ${}_{f}E~N(0,{{\sigma }_{{}_{f}E}}^2)$

Formula (6) is easily derived from Formulas (5) and (2),

$${}_{f}G~N({\mu }_{{}_{f}G},{{\sigma }_{{}_{f}G}}^2)$$

(6)

That is, the genotypic value, ${}_{f}G$, in the segregated population also shows an independent normal distribution. The graph is a normal distribution curve with ${\mu }_{{}_{f}G}$ as the mean genotypic value and with ${{\sigma }_{{}_{f}G}}^2$ as the genotypic variance. This is extremely important, as it implies that normal distribution of the genotypic value in the segregated population is formed by the cumulative action of mutually independent additive effects and dominant effects produced by many genes in accordance with Lyapunov’s central limit theorem [20].

4.3. Summary of Section Four

The research above demonstrated that the test locations in the above five cases are the environments without GEI, and the normal distributions of the phenotypic value, ${}_{f}P$, of quantitative character in the segregated population (Formula (5)) are essentially a new normal distribution resulting from the addition of two normal distributions of genotypic value, ${}_{f}G$, (Formula (6)) and environmental effect, ${}_{f}E$ (Formula (2)). Thus, the inheritance of dual multi-factors and tri-normal distributions of quantitative characters has been validated by the above practices.

5. Inference

From the inheritance of dual multi-factors and tri-normal distributions of quantitative characters, as tested in Section 4, it can be inferred that the normal distribution of the phenotypic values of quantitative characters in living organisms in nature can also be categorized into the following three types.

5.1. The Normal Distribution Dominated by the Environmental Effect

In the environment without GEI, due to the independent normal distribution of environmental effects, according to the relationship between normal distribution and the constant, it is easy to obtain that the phenotypic value of quantitative characters of clones, inbred lines, pure line varieties, and homogeneous heterozygous varieties, which are genotype-identical populations, follows a normal distribution (such as Formula (7)).

$${}_{e}P={}_{e}G+{}_{e}E=C+{}_{e}E~N(C,{{\sigma }_{{}_{e}E}}^2)$$

(7)

where the subscript e represents the populations dominated by the environmental effect, such as the various clones in Table 1 and P₁, P₂, F₁, BC₂F₀ inter-crossing bolls and F₁ self-crossing bolls in Table 2, in which some quantitative traits exhibit a normal distribution.

5.2. The Normal Distribution Composed of Genotypic Value and Environmental Effect—The Normal Distribution of Quantitative Characters in Mendelian Population of Randomly Mating

Many organisms in nature, including animals and plants, form one Mendelian population after another through random mating. For certain traits, humans are also random-mating Mendelian populations. These populations are the result of long-term adaptation of genotype and environments. Their quantitative traits, such as the height and diameter of forest trees and the body weight, body height, and chest circumference of different human populations, have not been artificially selected and bred like those of crops, and their heritability is generally not very high. For instance, according to the research by Zheng et al. (2003), the heritability of tree height in the free-pollinated progeny forest of Yunna pine (Pinus yunnanensis) ranges from 28.0% to 57.5%, and that of ground diameter ranges from 16.0% to 66.6% [44]. Additionally, Malina et al. (1976) estimated the heritability of body height to be 37% for Blacks and 49% for Whites [45]. Unlike the crop populations discussed in the next section, the normal distribution of the phenotypic values in Mendelian populations is not solely determined by genotypic value.

In a Mendelian population of randomly mating, there are various individuals with different genotypes. The quantitative trait of each individual is controlled by its genotypic value, which involves a considerable number of loci, respectively. When the linkage equilibrium is reached, the contribution of each gene locus is independent of that of the others, whether or not the loci are linked [46]. According to the Lyapunov central limit theorem, the genotypic value follows a normal distribution [30].

Random mating produces individuals with diverse genotypes, which are randomly distributed in a randomized environment. Falconer (1989) believed that the randomization of the environments can ignore the interaction between genotype and environment [31]. Bulmer (1985) advocates that an independent normal distribution of the environmental effect is an important condition for genotypic and environmental independence in Mendelian populations of random mating [30]. More precisely, in an environment without GEI, environmental effects follow a normal distributions, according to the additivity of normal distribution, and it is added to the normal distribution of genotypic values, so that the phenotypic value follows a normal distribution (as shown in Formula (8)).

$${}_{m}P={}_{m}G+{}_{m}E~N({\mu }_{{}_{m}G},{{\sigma }_{{}_{m}G}}^2+{{\sigma }_{{}_{m}E}}^2)$$

(8)

where the subscript m represents the Mendelian population, such as different tree species in the forest and different human population, in which their quantitative traits are normally distributed (see

Table 3. Examples of normal distribution of quantitative characters in Mendelian populations.

Living Things and Population	Normal Distribution Characters	Researcher and Time
① Picea schrenkiana vrt. tishanica and Betula tanschanica, mixed forest	Diameter grade of two species (K-S test)	Zhang Zhen et al., 2010 [47]
② Scottish and French, soldier	Chest circumference, body height (5738 and 100,000, respectively)	Quetelet, 1846 (see [4])
③ Britisher	Body weight, body height (9337)	Galton, 1890 (see [5])
④ Italian, two groups of 20-year-old men born in 1874 and 1916	Body height (the number of the two samples includes more than 200,000, respectively)	W. F. Bodmer et al., 1976 (see [48])

).

Due to the independent contribution of linked genes by linkage equilibrium, organisms that mate randomly have a high probability of normal distribution of genotypic values regardless of chromosome number. When it is combined with the normal distribution of the environmental effect, the phenotypic value is normally distributed. This type of organism constitutes a large biological community, which is the reason why the quantitative traits of organisms in nature are continuously distributed in relatively large quantities.

5.3. The Normal Distribution Dominated by Genotypic Value

Crop breeding practice is to cultivate excellent new varieties through different breeding methods. Consequently, many superior genes with significant effects are concentrated in the new varieties and the materials used to develop them. As a result, the genotypes of these varieties have been improved from generation to generation. In terms of their contribution to phenotype, these genotypic values often have a greater impact than environmental effects and genotype-by-environment interaction (GEI). That is, in the environments with GEI, the following occurs:

$P=G+E+GEI$, and $G>E+GEI$

Xu (2016) pointed out that if the contribution from E and GEI to P is relatively small, P can be predicted largely by G alone [19].

According to this point of view, in terms of the normal distribution in the segregated populations for crop breeding, the formula above becomes:

$${}_{g}P={}_{g}G+{}_{g}e+{}_{g}G{}_{g}eI~N({\mu }_{{}_{g}G},{{\sigma }_{{}_{g}G}}^2)$$

(9)

where the subscript g represents the populations dominated by genotypic value, ${}_{g}G$ is the genotypic value. ${}_{g}e$ is the environmental effect, and ${}_{g}G{}_{g}eI$ represents the interaction between these two. Their role (${}_{g}e+{}_{g}G{}_{g}eI$) is relatively smaller than that of the genotypic value, ${}_{g}G$, where ${}_{g}G$ follows a normal distribution. Because for crops and their breeding materials, the quantitative trait of individuals is controlled by many gene loci, and the genotypic value of segregated populations is normally distributed, the following occurs:

$${}_{g}G~N({\mu }_{{}_{g}G},{{\sigma }_{{}_{g}G}}^2)$$

Normal distributions such as Formula (9) are innumerable, examples of which are given in

Table 4. Examples of normal distribution of quantitative characters dominated by the genotype value.

Living Things and Population	Normal Distribution Characters	Researcher and Time
① Cucumber, population of F2	Plant height (kurtosis and skewness test, histogram)	Xin Ming 2007 [49]
② Maize, population of F2 from a four-way cross	Kernel thickness (kurtosis and skewness test)	Huang Rongrong 2012 [50]
③ Maize, population of F2:3	Plant height, ear height, coefficient of ear height (P-P diagram test, histogram)	Li Haochuan et al., 2019 [51]

The heritability of these characters is generally high, with genotypic variance often exceeding 70%.

.

6. Conclusions and Discussion

The multi-factorial hypothesis of quantitative trait inheritance originated from Nelsson’s wheat hybridization experiment, which takes unit characters as the object and binomial distribution as the mathematical basis [18]. This is because wheat is an allohexaploid, and the three pairs of red genes in red grain varieties are located on chromosomes 3D, 3A, and 3B. They are independent allelomorphs or polymorphic genes [6,7,17], with equal gene effects at each locus. Segregated genes have the same distribution and can be added together. The hybridization of red and white grain varieties results in that grain color variation in the offspring exhibiting the expansion of a binomial (1/2 red + 1/2 white)^2×3. Formally, it is a continuous variation in quantitative traits, but in reality, like the inheritance of pumpkin (Cucurbita pepo) fruit shape, it is the adding effect of three pairs of genes. Theoretically, only when the number of gene pairs is quite large, can the binomial distribution transform into a normal distribution, showing continuous variation. The advocates of the multi-factorial hypothesis look forward to an increase in the number of gene pairs [8], but to date, the number of additive gene pairs is 3 [52], the variation in grain color is still discretely distributed, and the environmental effect is not involved. Essentially, grain color variation still belongs to the category of qualitative trait inheritance [17,18].

Most organisms in nature are diploid, and almost all animals are diploid [23]. There are many gene loci that control the same quantitative trait. For example, the genotypic value that controls the size of fruit fly wings includes at least 34 different loci. Drosophila has only eight chromosomes, but it is a randomly mating organism. When linkage equilibrium is reached, each gene locus contributes independently to the genotypic value [46]. Humans have 46 chromosomes, and in terms of body weight, body height, and chest circumference, they mate randomly. There may be more independent loci that determine these traits. According to Lyapunov’s central limit theorem, the contribution of each gene locus accumulates, and the genotypic value can follow a normal distribution. Different from wheat, the gene effects here are not equal, and the gene distributions are different. The contribution of each gene locus may not be analyzed by binomial distribution and can only rely on the central limit theorem. The factors that affect the environmental effect are very large, and many of them are independent and also require analysis using the central limit theorem [18,20]. The normal distribution of the environmental effect, E, discussed by Bulmer in his “Mathematical Theory of Quantitative Genetics” should be derived in this way [30].

The multi-factorial hypothesis, influenced by the inheritance of qualitative characters, takes unit traits as its object and the binomial distribution as its mathematical foundation. Due to the requirement of the same distribution, the genotypic values cannot include the genic effects of other distributions, not even other binomial distributions with different parameters. This significantly reduces the number of genes involved in the genotypic values. This is its limitation. Its even greater drawback is that it does not involve environmental effects. It is well known that environmental effects have a significant impact on phenotypes and are an important part of them. The multi-factorial hypothesis excludes environmental effects, thus causing phenotypes to lose almost half of their territory. Over the past century, due to the influence of the hypothesis, there has been a tendency in animal and plant breeding to emphasize genotypes, while neglecting the utilization of environmental conditions. For example, the double hybridization of rice developed by the renowned breeder Yuan Longping requires specific light and temperature environments, and he also attaches great importance to the prevention and control of pests and diseases as well as water and fertilizer management [53]. This is a normal procedure in breeding work to strengthen environmental effects, but it has been criticized by some people as being overly complicated.

Despite the shortcomings of the multi-factorial hypothesis, we still agree with the idea of polygenic inheritance proposed by William Bateson and G. Udney Yule, which is a great contribution. The inheritance of dual multi-factors and tri-normal distributions are developments of the multi-factorial hypothesis.

The inheritance of dual multi-factors and tri-normal distributions of quantitative characters takes the overallness as the object. When genotype and environment are independent of each other, the Lyapunov central limit theorem is used to analyze the environmental effect and genotypic value, forming tri-normal distributions of the environmental effect, genotypic value, and phenotypic value. This genetic model has been tested through many biological examples in environments without GEI, and three inferences have been drawn from it, which not only solve the continuity of quantitative traits in homogeneous populations but also solve the continuity of quantitative traits in Mendelian populations of randomly mating in environments without GEI; it also addresses the continuity of quantitative traits of crop varieties and highly intensive breeding materials in environments with GEI.

In practical investigations, there are also instances of non-normal distribution of quantitative traits in the above situations. For example, in the study of Brassica napus by Guan et al. (2009), after the authors’ normality test, the oleic acid content of homogeneous population P₁ did not follow a normal distribution [54]. Li et al. (1998) found that the diameter of Larix olgensis followed a Weibull distribution [55]. Wang et al. (1990) used histograms, skewness, and kurtosis test, D’Agostino test, and so on to prove that the specific gravity of seeds, the content of aspartic acid, proline, and histidine in wheat did not follow a normal distribution [56]. Furthermore, under the same conditions, not all quantitative characters are normally distributed. For example, Zhang et al. (2021) conducted a K-S test on the 3-year-old seedling characters of the reciprocal cross of New Red Star and Miyazaki Nagasaki Fujiinin apple and found that the internode length, germination rate, and branch base thickness showed a normal distribution, while the branch length and total number of buds did not follow a normal distribution [57]. In the study of quantitative traits in wheat F_2:3 segregated population, Li (2008) found that plant height and spike length exhibited a normal distribution, while flag leaf width and length exhibited a non-normal distribution [58]. The appearance of non-normal distribution of quantitative traits is related to many reasons, including the number of loci that determine genotypic values. Only when the number of gene loci or genes is quite large, does the genotypic value become normally distributed. So the phenotype of quantitative character can be normally distributed or approximate to a normal distribution. Otherwise, they do not show normal distribution. Moreover, this may be due to the interaction between genotype and environment, the probability of a certain addend being high, too many interacting genes, or human intervention, etc.