Effects of Groundwater Depth on Soil Water and Salinity Dynamics in the Hetao Irrigation District: Insights from Laboratory Experiments and HYDRUS-1D Simulations
Abstract
1. Introduction
2. Materials and Methods
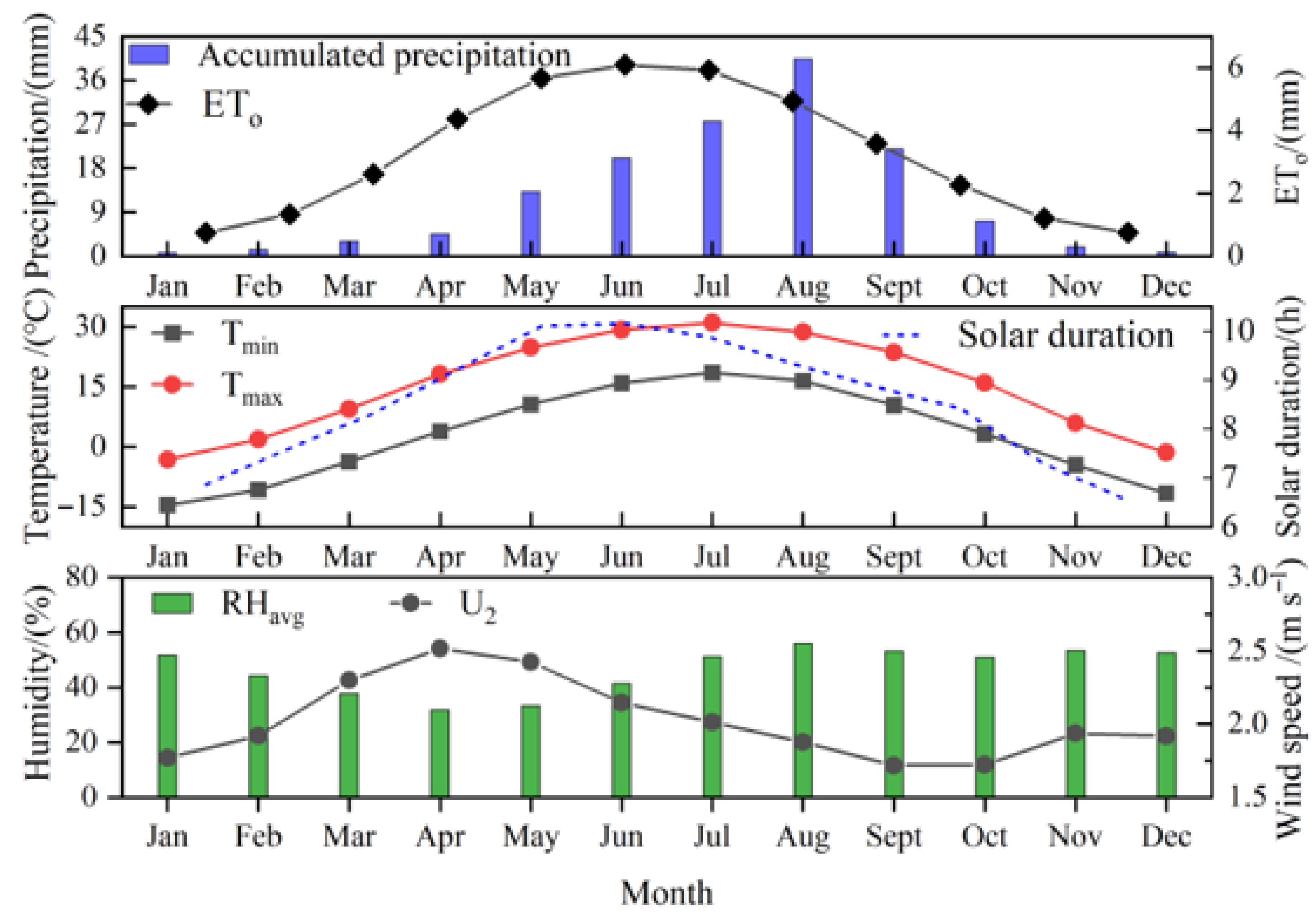
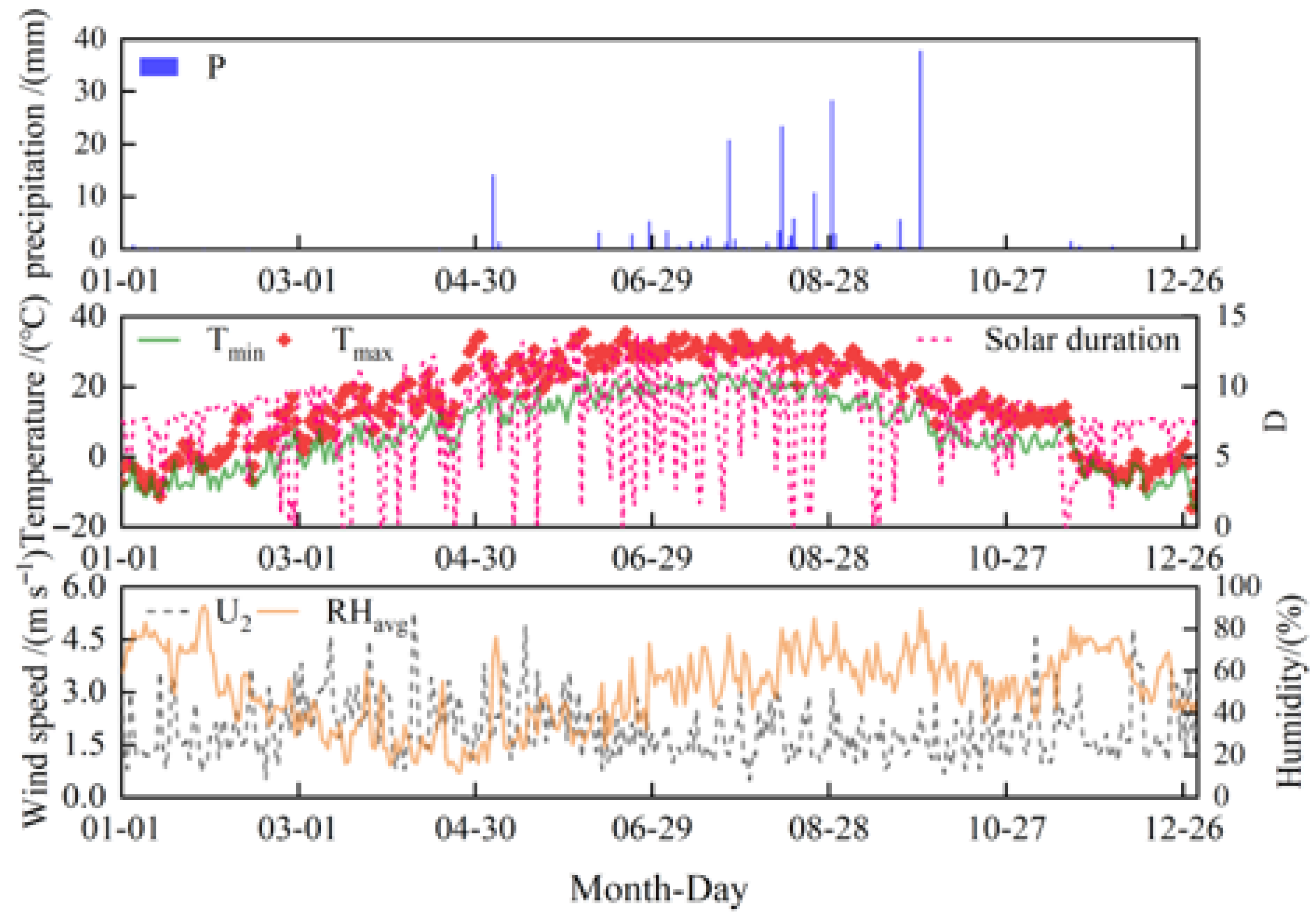
2.1. Study Area
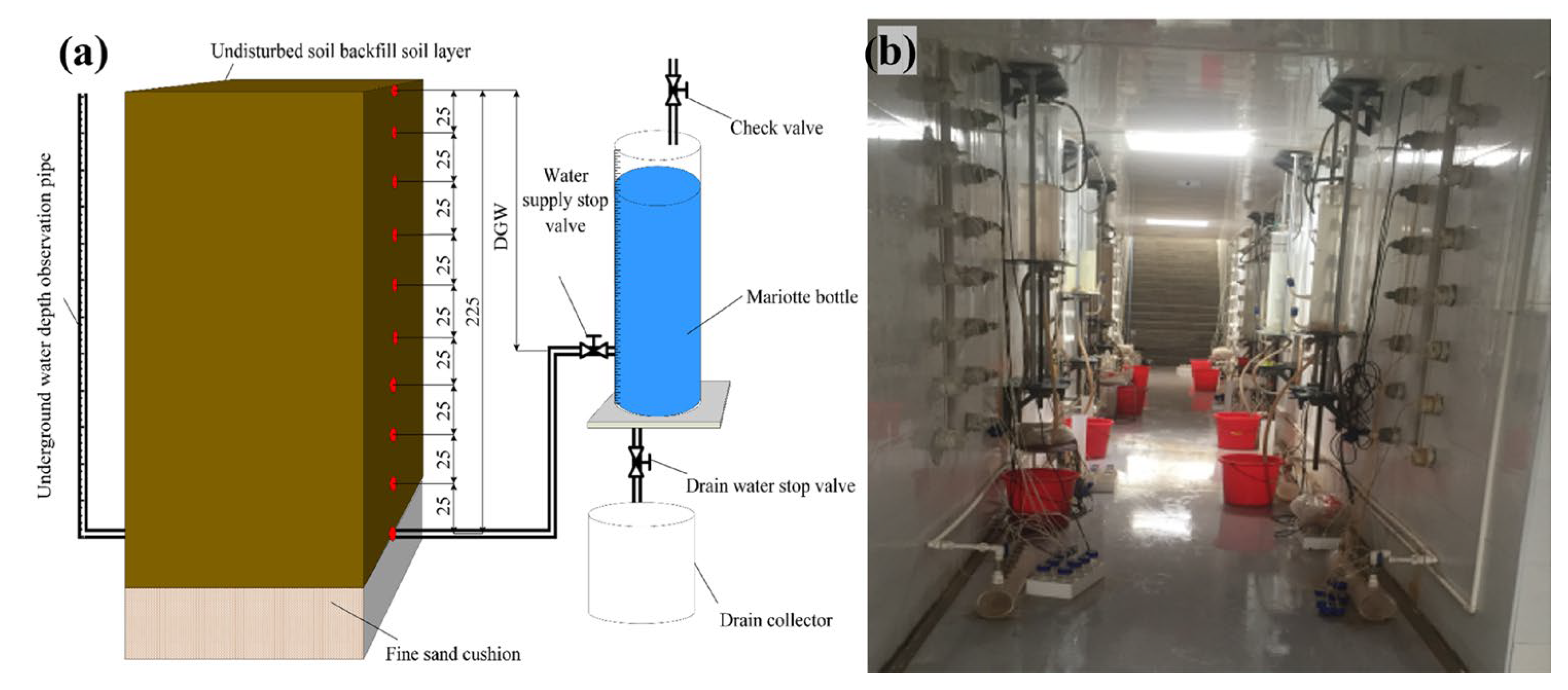
2.2. Experimental Methods
2.3. Measurement Items
2.4. Model Setup
2.4.1. HYDRUS-1D Model Description
2.4.2. Soil Solute Transport Model
2.4.3. Root Water Uptake Module
2.4.4. The Evapotranspiration Module
2.4.5. Statistical Evaluation
3. Results
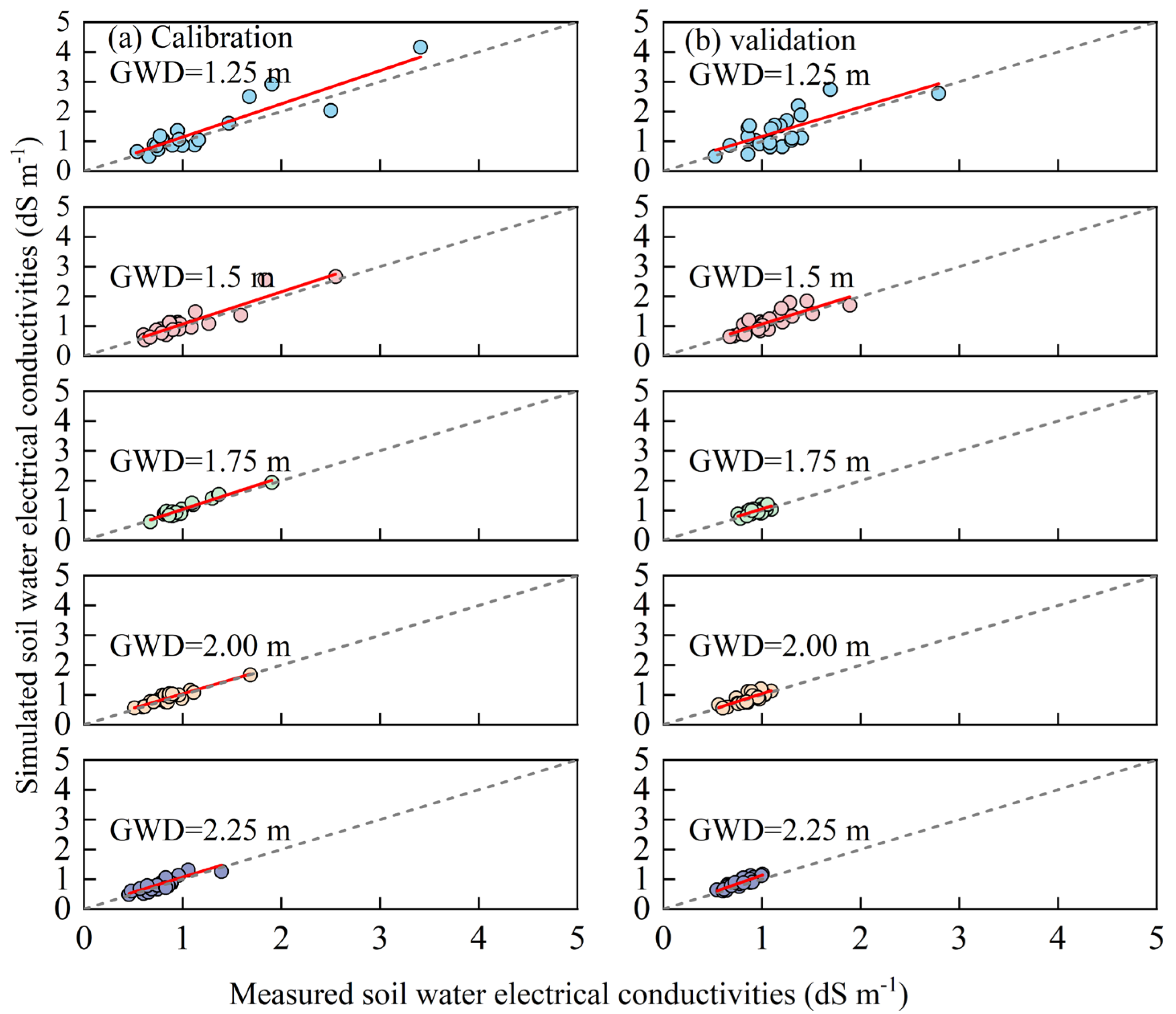
3.1. Calibration and Validation of Hydraulic Parameters
3.2. Influence of Different GWDs on Crop Evapotranspiration Patterns
3.3. Effects on Root Water Uptake Rate Patterns
3.4. Impacts of Groundwater Depth on Soil Salinity Dynamics and Salt Migration
3.5. Effects of Groundwater Depth on Soil Water and Salt Storage in the Maize Root Zone
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qu, Z.; Yang, X.; Huang, Y. Analysis and assessment of water-saving project of Hetao Irrigation District in Inner Mongolia. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2015, 46, 70–76, 112. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Sun, C.; Pereira, L.S.; Ramos, T.B.; Huang, Q.; Hao, Y. Assessing the effects of water table depth on water use, soil salinity and wheat yield: Searching for a target depth for irrigated areas in the upper Yellow River basin. Agric. Water Manag. 2013, 125, 46–60. [Google Scholar] [CrossRef]
- Shao, W.; Yang, D.; Hu, H.; Sanbongi, K. Water Resources Allocation Considering the Water Use Flexible Limit to Water Shortage—A Case Study in the Yellow River Basin of China. Water Resour. Manag. 2009, 23, 869–880. [Google Scholar] [CrossRef]
- Xiong, L.; Xu, X.; Engel, B.; Huang, Q.; Huo, Z.; Xiong, Y.; Han, W.; Huang, G. Modeling agro-hydrological processes and analyzing water use in a super-large irrigation district (Hetao) of arid upper Yellow River basin. J. Hydrol. 2021, 603, 127014. [Google Scholar] [CrossRef]
- Feng, Z.-Z.; Wang, X.-K.; Feng, Z.-W. Soil N and salinity leaching after the autumn irrigation and its impact on groundwater in Hetao Irrigation District, China. Agric. Water Manag. 2005, 71, 131–143. [Google Scholar] [CrossRef]
- Cao, Z.; Zhu, T.; Cai, X. Hydro-agro-economic optimization for irrigated farming in an arid region: The Hetao Irrigation District, Inner Mongolia. Agric. Water Manag. 2023, 277, 108095. [Google Scholar] [CrossRef]
- Xu, X.; Huang, G.; Qu, Z.; Pereira, L.S. Assessing the groundwater dynamics and impacts of water saving in the Hetao Irrigation District, Yellow River basin. Agric. Water Manag. 2010, 98, 301–313. [Google Scholar] [CrossRef]
- Chen, S.; Mao, X.; Shukla, M.K. Influence of coarse-textured soil layers under crop root zone on soil water and salt dynamics and crop yield in shallow groundwater areas. Soil Sci. Soc. Am. J. 2021, 85, 1479–1495. [Google Scholar] [CrossRef]
- Zheng, N.Z.; Guo, M.S.; Yue, W.F.; Teng, Y.G.; Zhai, Y.Z.; Yang, J.; Zuo, R. Evaluating the impact of flood irrigation on spatial variabilities of soil salinity and groundwater quality in an arid irrigated region. Hydrol. Res. 2021, 52, 229–240. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, J.W.; Yang, Y.; Peng, X.; Li, C.S.; Zhao, Q. A method to determine optimum ecological groundwater table depth in semi-arid areas. Ecol. Indic. 2022, 139, 108915. [Google Scholar] [CrossRef]
- Yuan, C.F.; Pan, Y.X.; Jing, S.Y. Simulation soil water-salt dynamic and groundwater depth of spring maize based on SWAP model in salinized irrigation district. Comput. Electron. Agric. 2025, 231, 109992. [Google Scholar] [CrossRef]
- Hou, L.; Zhou, Y.; Bao, H.; Wenninger, J. Simulation of maize (Zea mays L.) water use with the HYDRUS-1D model in the semi-arid Hailiutu River catchment, Northwest China. Hydrol. Sci. J. 2017, 62, 93–103. [Google Scholar] [CrossRef]
- Zhang, T.; Zou, Y.; Kisekka, I.; Biswas, A.; Cai, H. Comparison of different irrigation methods to synergistically improve maize’s yield, water productivity and economic benefits in an arid irrigation area. Agric. Water Manag. 2021, 243, 106497. [Google Scholar] [CrossRef]
- Min, L.; Shen, Y.; Pei, H. Estimating groundwater recharge using deep vadose zone data under typical irrigated cropland in the piedmont region of the North China Plain. J. Hydrol. 2015, 527, 305–315. [Google Scholar] [CrossRef]
- Xu, X.; Sun, C.; Neng, F.; Fu, J.; Huang, G. AHC: An integrated numerical model for simulating agroecosystem processes—Model description and application. Ecol. Model. 2018, 390, 23–39. [Google Scholar] [CrossRef]
- Šimůnek, J.; Genuchten, M.T.; Šejna, M. Recent Developments and Applications of the HYDRUS Computer Software Packages. Vadose Zone J. 2016, 15, e20310. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W.z. Modeling soil water balance and irrigation strategies in a flood-irrigated wheat-maize rotation system. A case in dry climate, China. Agric. Water Manag. 2019, 221, 286–302. [Google Scholar] [CrossRef]
- Dai, L.; Miao, Q.; Shi, H.; Feng, Z.; Li, Y.; Liu, Y.; Xu, Y.; Xu, R.; Feng, W. Influence of Groundwater Depth on Salt Migration and Maize Growth in the Typical Irrigation Area. Agronomy 2025, 15, 1021. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Lebeau, M.; Konrad, J.-M. A new capillary and thin film flow model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 2010, 46, W12554. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and Applications of the HYDRUS and STANMOD Software Packages and Related Codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef]
- Feddes, R.A.; Kowalik, P.J.; Zaradny, H. Simulation of Field Water Use and Crop Yield; Wageningen Centre for Agricultural Publishing and Documentation: Wageningen, The Netherlands, 1978. [Google Scholar]
- Yu, J.; Wu, Y.; Xu, L.; Peng, J.; Chen, G.; Shen, X.; Lan, R.; Zhao, C.; Zhangzhong, L. Evaluating the Hydrus-1D Model Optimized by Remote Sensing Data for Soil Moisture Simulations in the Maize Root Zone. Remote Sens 2022, 14, 6079. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: Guidelines for computing crop water requirements. Fao Rome 1998, 300, D05109. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Liu, M.; Shi, H.; Paredes, P.; Ramos, T.B.; Dai, L.; Feng, Z.; Pereira, L.S. Estimating and partitioning maize evapotranspiration as affected by salinity using weighing lysimeters and the SIMDualKc model. Agric. Water Manag. 2022, 261, 107362. [Google Scholar] [CrossRef]
- Ramos, T.B.; Liu, M.; Paredes, P.; Shi, H.; Feng, Z.; Lei, H.; Pereira, L.S. Salts dynamics in maize irrigation in the Hetao plateau using static water table lysimeters and HYDRUS-1D with focus on the autumn leaching irrigation. Agric. Water Manag. 2023, 283, 108306. [Google Scholar] [CrossRef]
- Li, X.; Zhang, C.; Huo, Z.; Adeloye, A.J. A sustainable irrigation water management framework coupling water-salt processes simulation and uncertain optimization in an arid area. Agric. Water Manag. 2020, 231, 105594. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Gong, S.; Xu, D.; Sui, J.; Wu, Z.; Mo, Y. Effects of film mulching on evapotranspiration, yield and water use efficiency of a maize field with drip irrigation in Northeastern China. Agric. Water Manag. 2018, 205, 90–99. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, F.; Wang, Y.; Jiang, R. Evaluating the Effect of Groundwater Table on Summer Maize Growth Using the AquaCrop Model. Environ. Model. Assess. 2020, 25, 343–353. [Google Scholar] [CrossRef]
- Huo, Z.; Feng, S.; Huang, G.; Zheng, Y.; Wang, Y.; Guo, P. Effect of groundwater level depth and irrigation amount on water fluxes at the groundwater table and water use of wheat. Irrig. Drain. 2012, 61, 348–356. [Google Scholar] [CrossRef]
- Soylu, M.E.; Istanbulluoglu, E.; Lenters, J.D.; Wang, T. Quantifying the impact of groundwater depth on evapotranspiration in a semi-arid grassland region. Hydrol. Earth Syst. Sci. 2011, 15, 787–806. [Google Scholar] [CrossRef]
- Luo, Y.; Sophocleous, M. Seasonal groundwater contribution to crop-water use assessed with lysimeter observations and model simulations. J. Hydrol. 2010, 389, 325–335. [Google Scholar] [CrossRef]
- Chang, X.; Gao, Z.; Wang, S.; Chen, H. Modelling long-term soil salinity dynamics using SaltMod in Hetao Irrigation District, China. Comput. Electron. Agric. 2019, 156, 447–458. [Google Scholar] [CrossRef]
- Wang, G.S.; Shi, H.B.; Li, X.Y.; Yan, J.W.; Miao, Q.F.; Li, Z.; Akae, T. A Study on Water and Salt Transport, and Balance Analysis in Sand Dune-Wasteland-Lake Systems of Hetao Oases, Upper Reaches of the Yellow River Basin. Water 2020, 12, 3454. [Google Scholar] [CrossRef]



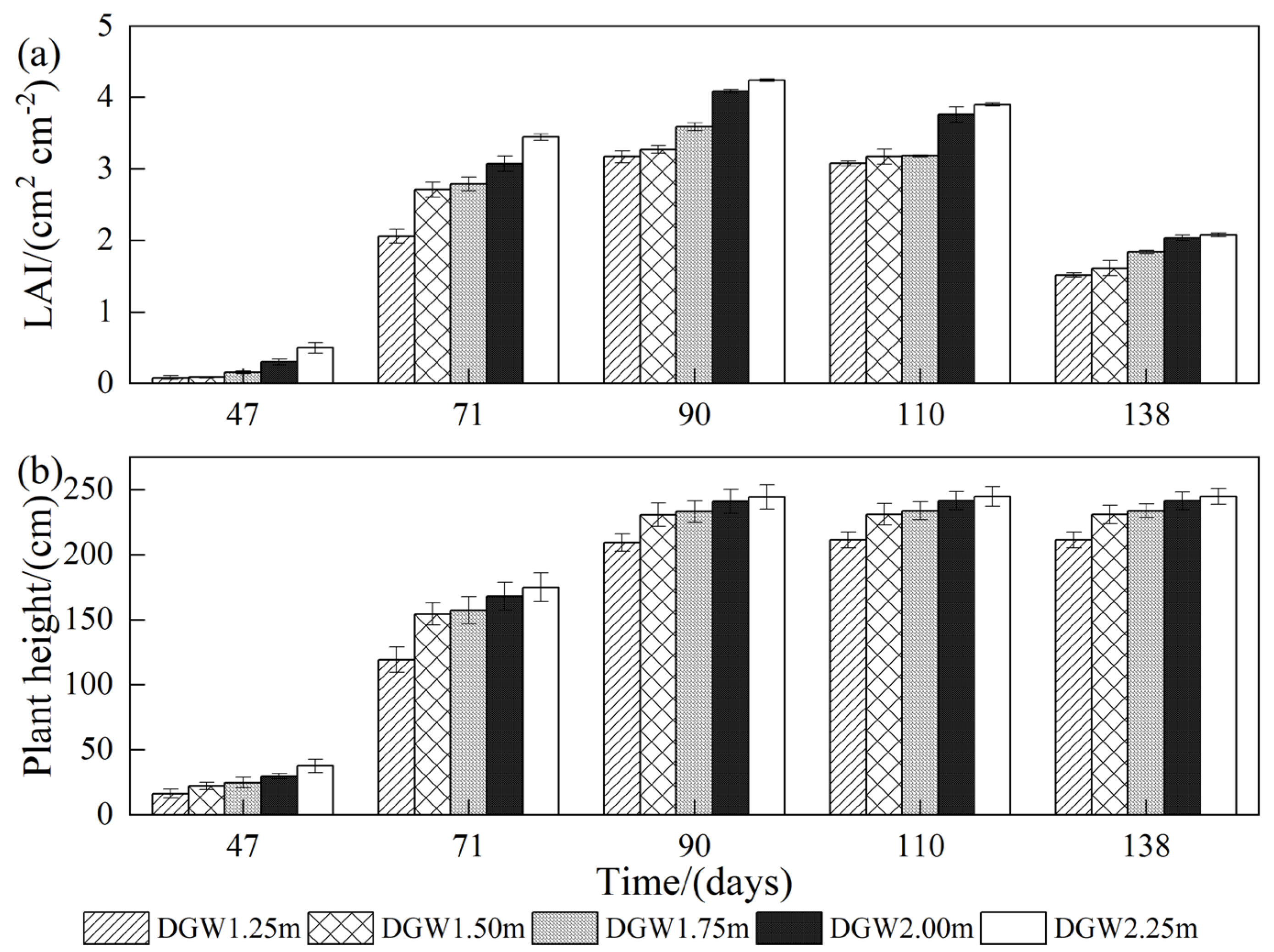
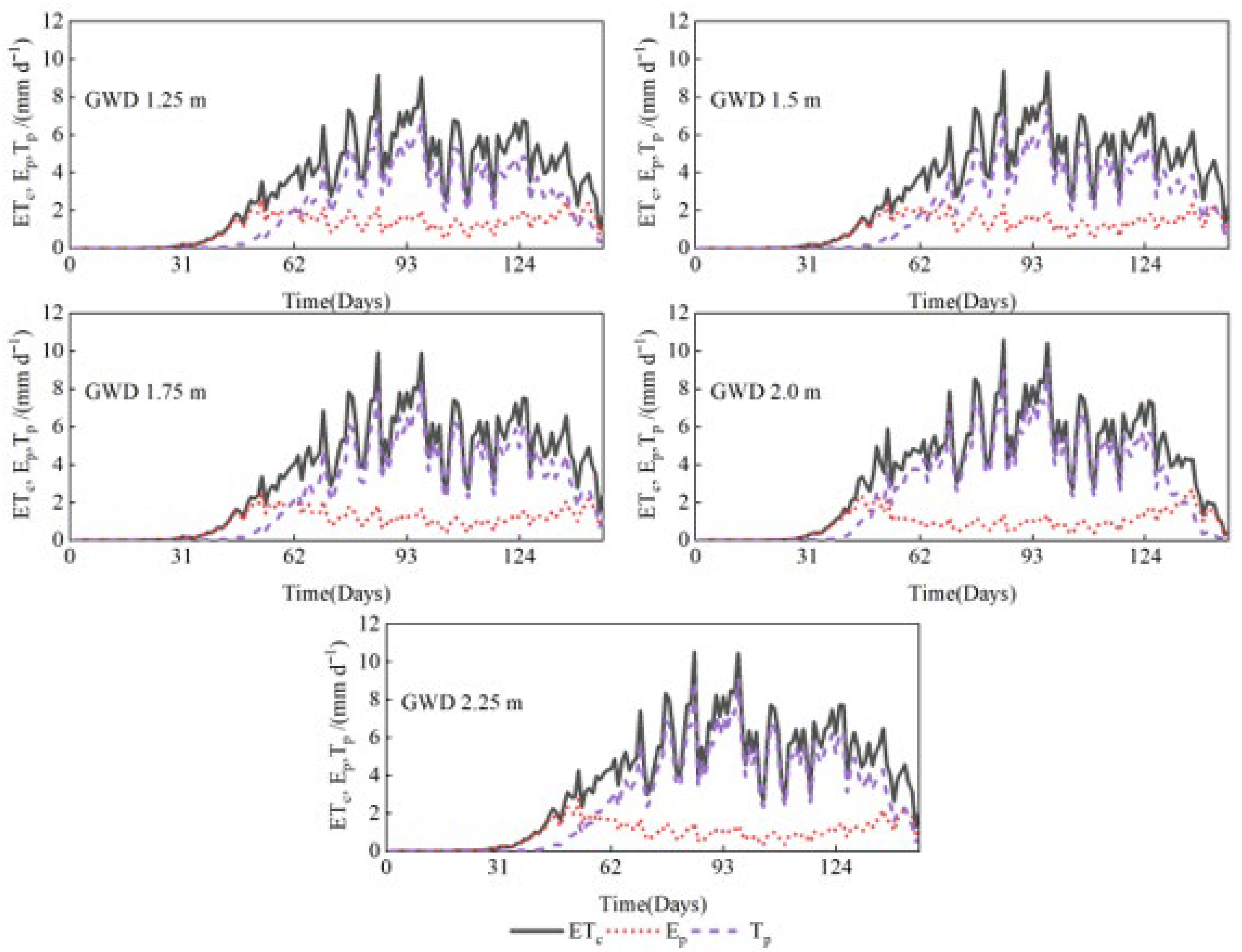
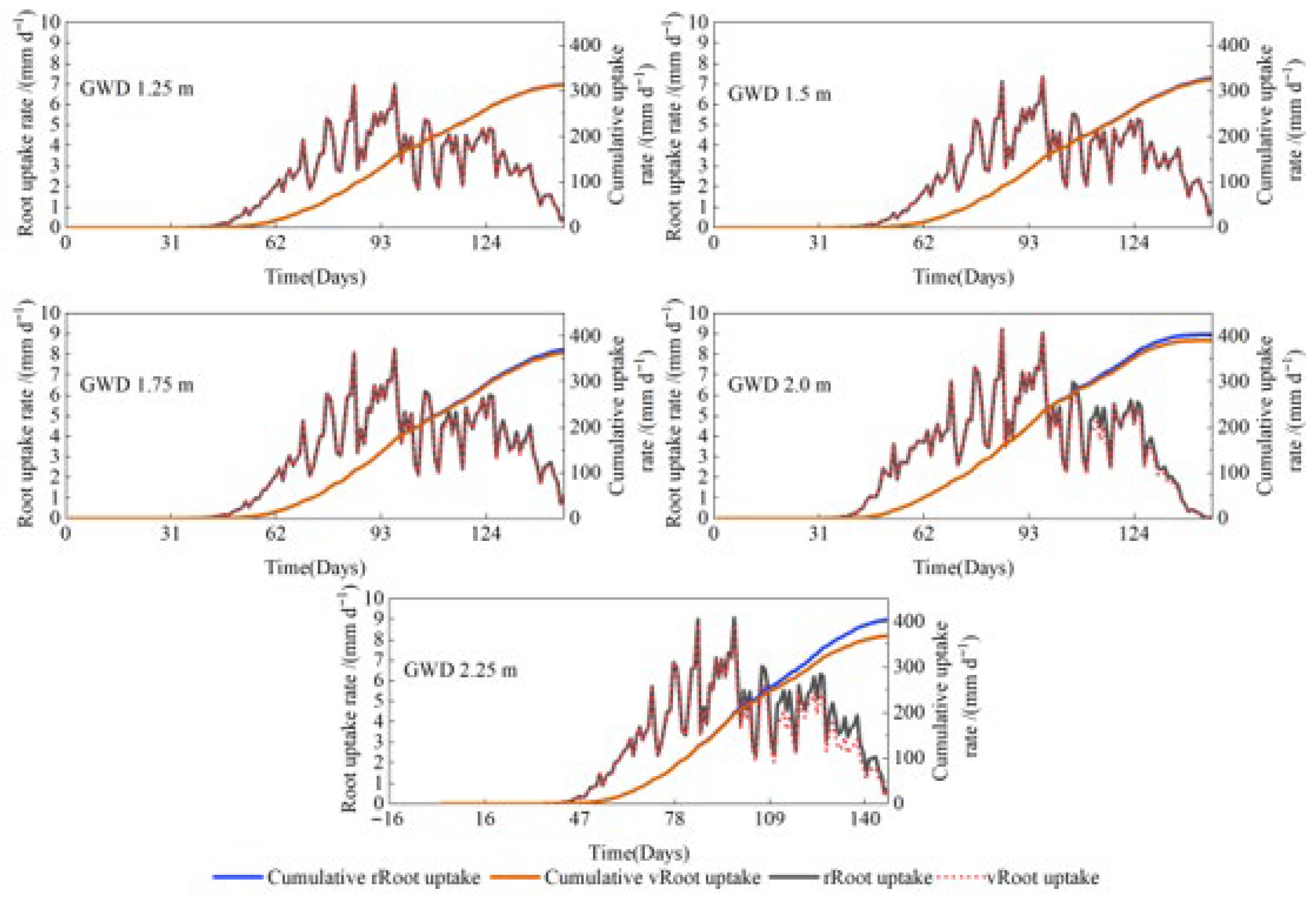


| Soil Layer (cm) | Bulk Density (g/cm3) | Particle Size Distribution % | Soil Texture | ||
|---|---|---|---|---|---|
| >0.05 mm | 0.002–0.05 mm | <0.002 mm | |||
| 0–10 | 1.46 | 17.27 | 75.15 | 7.58 | Silty loam |
| 10–20 | 1.44 | 15.03 | 76.20 | 8.77 | Silty loam |
| 20–40 | 1.52 | 20.60 | 73.23 | 6.17 | Silty loam |
| 40–60 | 1.56 | 26.04 | 66.44 | 7.52 | Silty loam |
| 60–80 | 1.53 | 22.41 | 70.72 | 6.87 | Silty loam |
| 80–100 | 1.53 | 22.51 | 70.67 | 6.82 | Silty loam |
| 100–120 | 1.55 | 24.45 | 67.48 | 8.07 | Silty loam |
| Irrigation Depth/(mm) | Total Irrigation Depth/(mm) | |||
|---|---|---|---|---|
| 26 June 2020 | 17 July 2020 | 1 August 2020 | 30 August 2020 | |
| 54 | 72 | 72 | 54 | 252 |
| Initial | Crop Development | Mid-Season | Late Season |
|---|---|---|---|
| 6 May–29 May | 30 May–9 July | 10 July–22 August | 23 August–29 September |
| Groundwater Depth | Depth (m) | θr (cm3 cm−3) | θs (cm3 cm−3) | α (cm−1) | η (−) | Ks (−) | l (−) | λ (−) |
|---|---|---|---|---|---|---|---|---|
| GWD 1.25 m | 0.0–0.4 | 0.067 | 0.435 | 0.013 | 2.51 | 400 | 0.5 | 50 |
| 0.4–2.35 | 0.067 | 0.435 | 0.013 | 1.2 | 60 | 0.5 | 150 | |
| 2.35–2.6 | 0.045 | 0.43 | 0.145 | 2.68 | 712.8 | 0.5 | 30 | |
| GWD 1.50 m | 0.0–0.4 | 0.067 | 0.435 | 0.009 | 3 | 400 | 0.5 | 50 |
| 0.4–2.35 | 0.067 | 0.435 | 0.013 | 1.2 | 60 | 0.5 | 150 | |
| 2.35–2.6 | 0.045 | 0.435 | 0.145 | 2.68 | 712.8 | 0.5 | 30 | |
| GWD 1.75 m | 0.0–04 | 0.067 | 0.435 | 0.009 | 3 | 400 | 0.5 | 50 |
| 0.4–2.35 | 0.067 | 0.435 | 0.013 | 1.2 | 70 | 0.5 | 150 | |
| 2.35–2.6 | 0.045 | 0.435 | 0.145 | 2.68 | 712.8 | 0.5 | 30 | |
| GWD 2.00 m | 0.0–0.4 | 0.067 | 0.435 | 0.008 | 2.54 | 400 | 0.5 | 50 |
| 0.4–2.35 | 0.067 | 0.435 | 0.019 | 1.35 | 60 | 0.5 | 150 | |
| 2.35–2.6 | 0.045 | 0.435 | 0.145 | 2.68 | 712.8 | 0.5 | 30 | |
| GWD 2.25 m | 0.0–0.4 | 0.067 | 0.435 | 0.007 | 2.54 | 400 | 0.5 | 50 |
| 0.4–2.35 | 0.067 | 0.435 | 0.013 | 1.2 | 60 | 0.5 | 150 | |
| 2.35–2.6 | 0.045 | 0.435 | 0.145 | 2.68 | 712.8 | 0.5 | 30 |
| Stage | Project | Statistic | GWD 1.25 | GWD 1.5 | GWD1.75 | GWD 2.0 | GWD 2.25 |
|---|---|---|---|---|---|---|---|
| Calibration | Soil water contents | R2 | 0.69 | 0.82 | 0.88 | 0.93 | 0.89 |
| RMSE | 0.03 | 0.02 | 0.02 | 0.01 | 0.02 | ||
| NRMSE | 0.11 | 0.06 | 0.07 | 0.91 | 0.03 | ||
| NSE | 0.46 | 0.14 | 0.65 | 0.76 | 0.84 | ||
| b0 | 0.98 | 0.96 | 1.03 | 1.02 | 0.82 | ||
| Bottom flux | R2 | 0.72 | 0.69 | 0.67 | 0.72 | 0.59 | |
| RMSE | 0.21 | 0.11 | 0.17 | 0.05 | 0.03 | ||
| NRMSE | 3.56 | 2.93 | 2.56 | 2.02 | 1.21 | ||
| NSE | 0.42 | 0.30 | 0.15 | 0.11 | 0.32 | ||
| b0 | 0.91 | 0.60 | 0.71 | 0.96 | 0.71 | ||
| Soil bulk electrical conductivity | R2 | 0.74 | 0.81 | 0.87 | 0.78 | 0.75 | |
| RMSE | 0.09 | 0.15 | 0.12 | 0.09 | 0.09 | ||
| NRMSE | 0.34 | 0.08 | 0.11 | 0.12 | 0.09 | ||
| NSE | 0.21 | 0.32 | 0.79 | 0.82 | 0.58 | ||
| b0 | 0.99 | 1.12 | 0.99 | 1.10 | 1.05 | ||
| Validation | Soil water contents | R2 | 0.69 | 0.78 | 0.86 | 0.98 | 0.98 |
| RMSE | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | ||
| NRMSE | 0.05 | 0.08 | 0.04 | 1.66 | 0.02 | ||
| NSE | −0.13 | −0.16 | 0.78 | 0.97 | 0.97 | ||
| b0 | 1.02 | 1.05 | 1.01 | 0.99 | 0.99 | ||
| Bottom flux | R2 | 0.62 | 0.68 | 0.36 | 0.42 | 0.29 | |
| RMSE | 0.19 | 0.13 | 0.14 | 0.08 | 0.09 | ||
| NRMSE | 4.07 | 3.04 | 2.29 | 1.72 | 1.95 | ||
| NSE | 0.6 | 0.49 | 0.12 | −0.09 | −0.25 | ||
| b0 | 0.88 | 0.8 | 0.69 | 0.92 | 0.6 | ||
| Soil bulk electrical conductivity | R2 | 0.62 | 0.73 | 0.61 | 0.63 | 0.79 | |
| RMSE | 0.01 | 0.22 | 0.06 | 0.11 | 0.12 | ||
| NRMSE | 0.35 | 0.2 | 0.06 | 0.13 | 0.16 | ||
| NSE | −0.01 | 0.77 | 0.92 | 0.74 | 0.63 | ||
| b0 | 1.14 | 1.08 | 1.01 | 1.04 | 1.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Z.; Dai, L.; Miao, Q.; Gonçalves, J.M.; Shi, H.; Li, Y.; Feng, W. Effects of Groundwater Depth on Soil Water and Salinity Dynamics in the Hetao Irrigation District: Insights from Laboratory Experiments and HYDRUS-1D Simulations. Agronomy 2025, 15, 2025. https://doi.org/10.3390/agronomy15092025
Feng Z, Dai L, Miao Q, Gonçalves JM, Shi H, Li Y, Feng W. Effects of Groundwater Depth on Soil Water and Salinity Dynamics in the Hetao Irrigation District: Insights from Laboratory Experiments and HYDRUS-1D Simulations. Agronomy. 2025; 15(9):2025. https://doi.org/10.3390/agronomy15092025
Chicago/Turabian StyleFeng, Zhuangzhuang, Liping Dai, Qingfeng Miao, José Manuel Gonçalves, Haibin Shi, Yuxin Li, and Weiying Feng. 2025. "Effects of Groundwater Depth on Soil Water and Salinity Dynamics in the Hetao Irrigation District: Insights from Laboratory Experiments and HYDRUS-1D Simulations" Agronomy 15, no. 9: 2025. https://doi.org/10.3390/agronomy15092025
APA StyleFeng, Z., Dai, L., Miao, Q., Gonçalves, J. M., Shi, H., Li, Y., & Feng, W. (2025). Effects of Groundwater Depth on Soil Water and Salinity Dynamics in the Hetao Irrigation District: Insights from Laboratory Experiments and HYDRUS-1D Simulations. Agronomy, 15(9), 2025. https://doi.org/10.3390/agronomy15092025









