A Simplified Model for Substrate-Cultivated Pepper in a Hexi Corridor Greenhouse
Abstract
1. Introduction
2. Materials and Methods
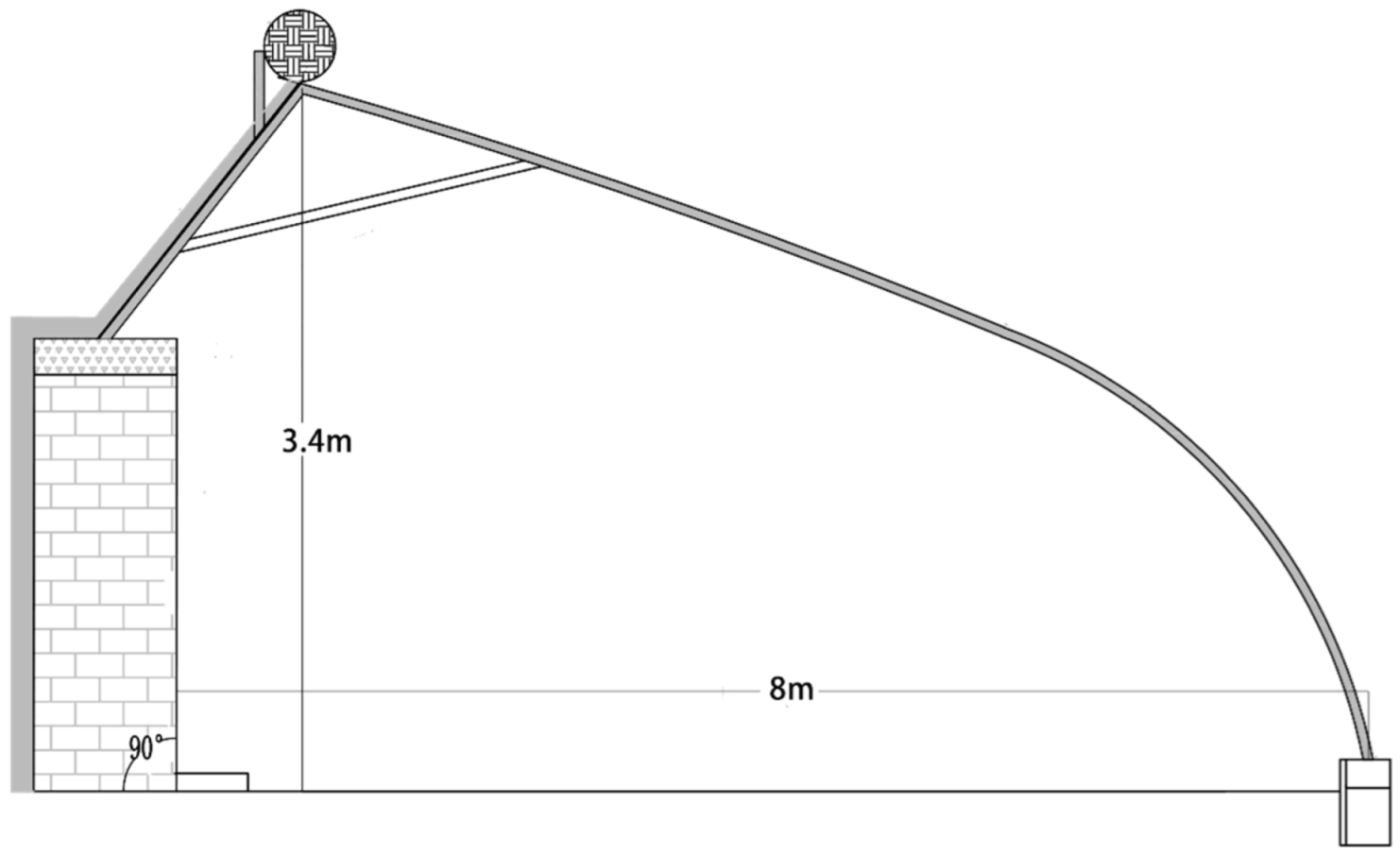
2.1. Study Area
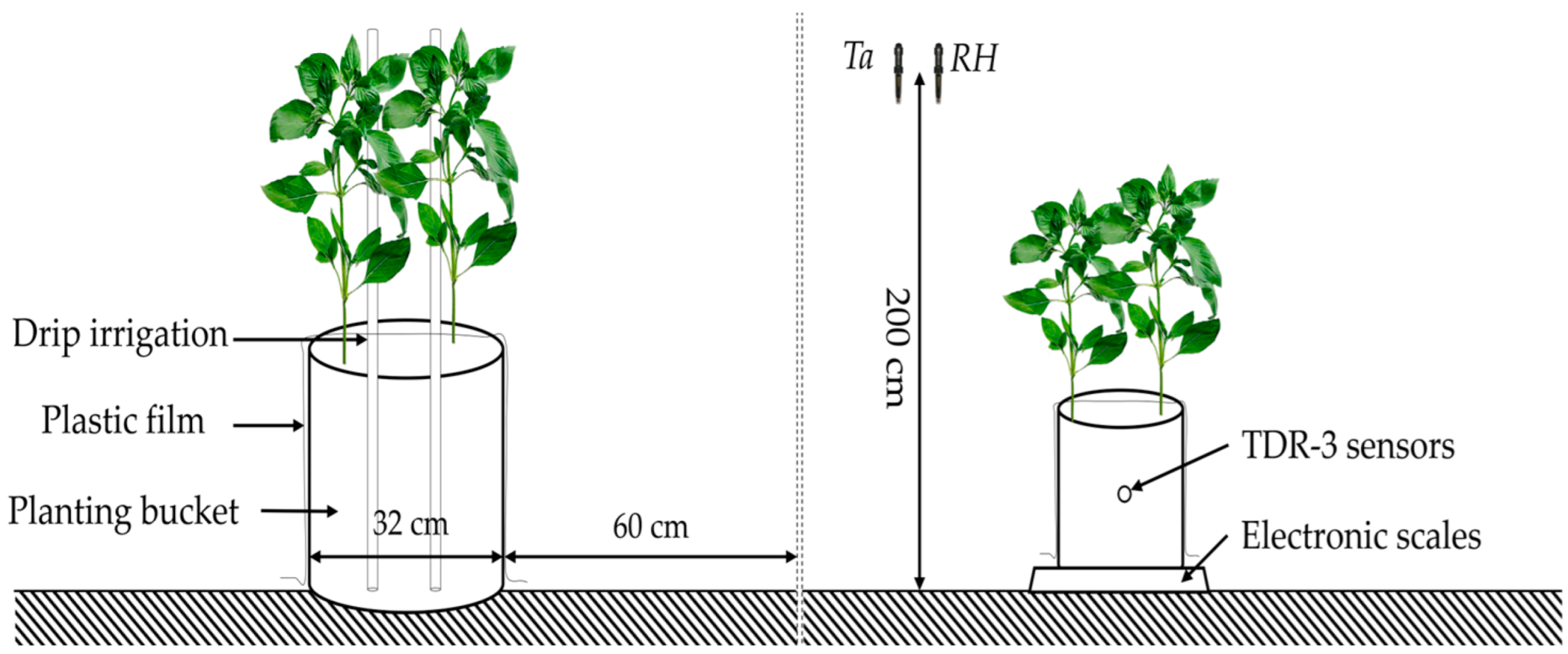
2.2. Growing Conditions
2.3. Measurement Items
2.4. Estimation, Calculation, and Validation of Transpiration
2.4.1. FAO 56 PM Model
2.4.2. Solar Radiation Estimation Model
2.4.3. Forecasting Incoming and Greenhouse Solar Radiation
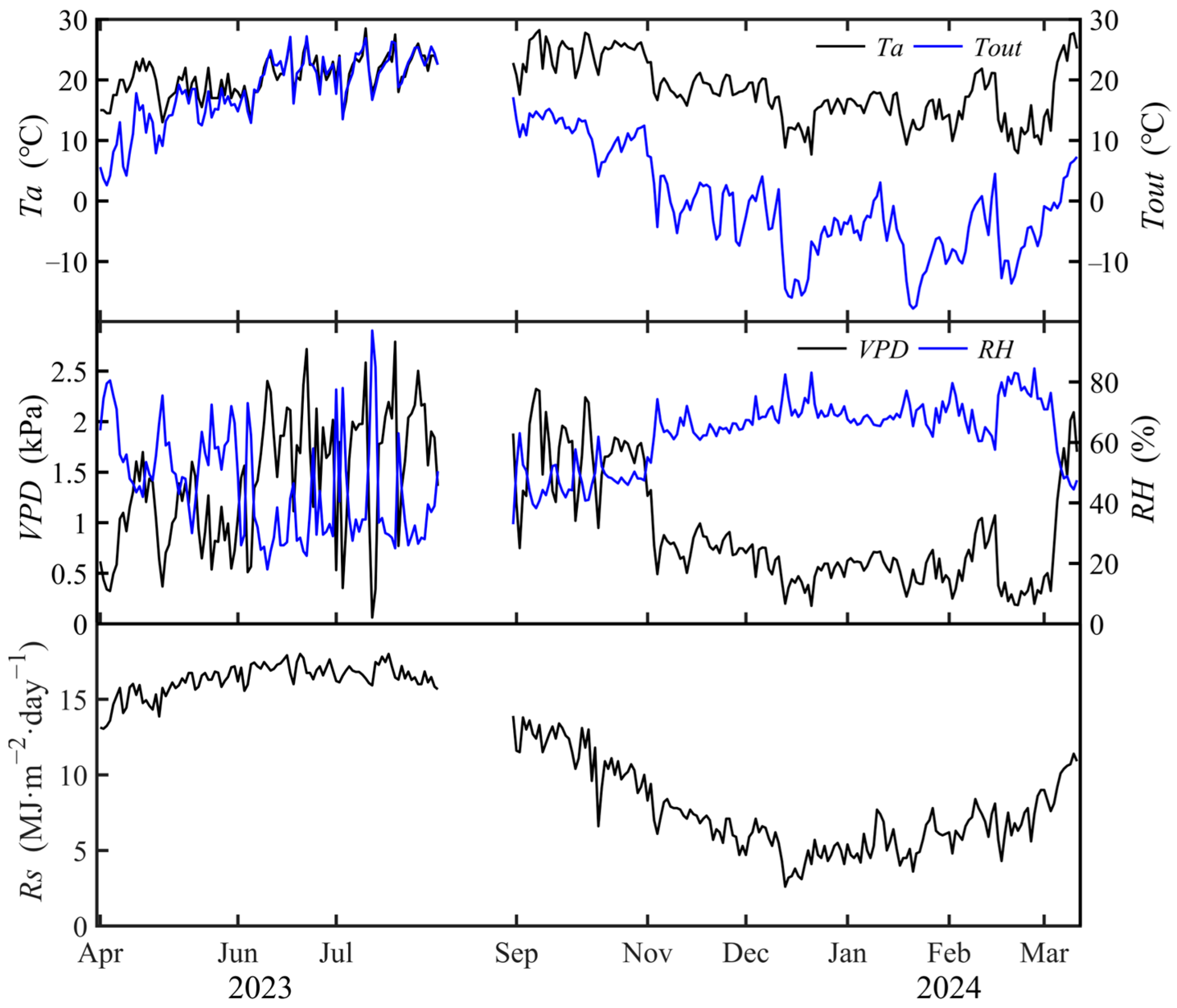
2.5. Meteorological Data Collection and Description
2.6. Evaluation of Model Performance
3. Results
3.1. Variation in Environmental Factors
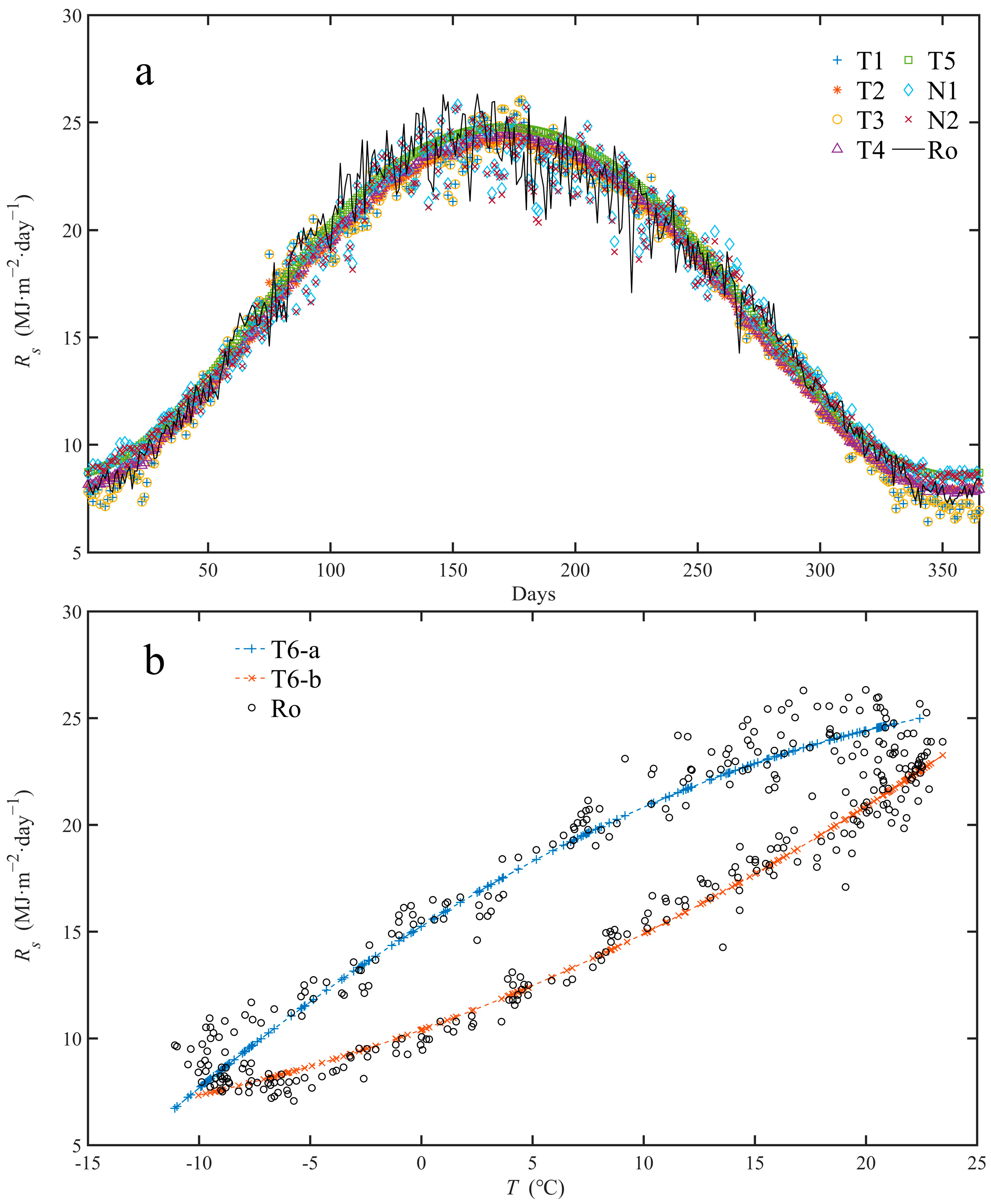
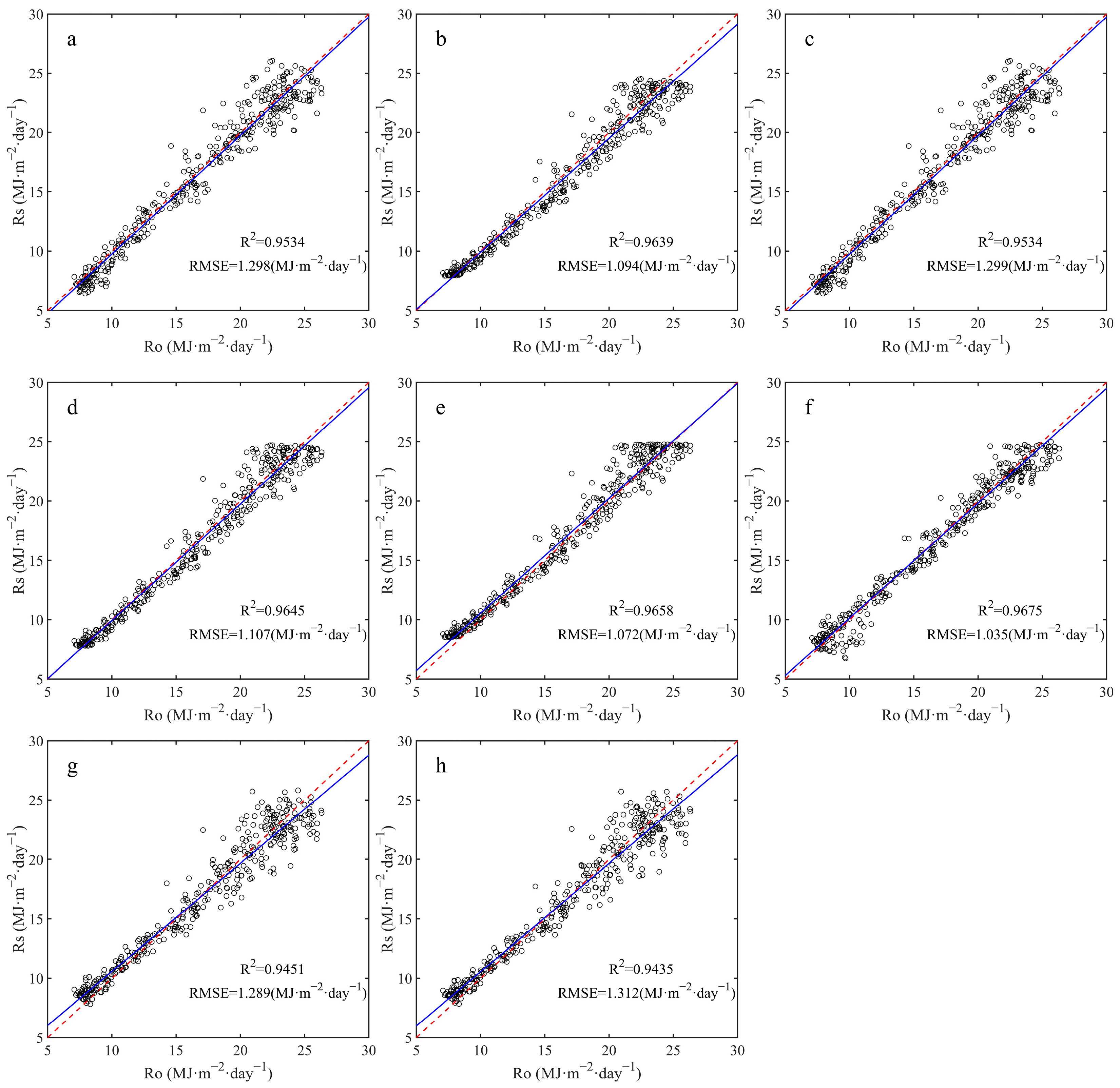
3.2. Comparison of Estimation Accuracy of Different Rs Models
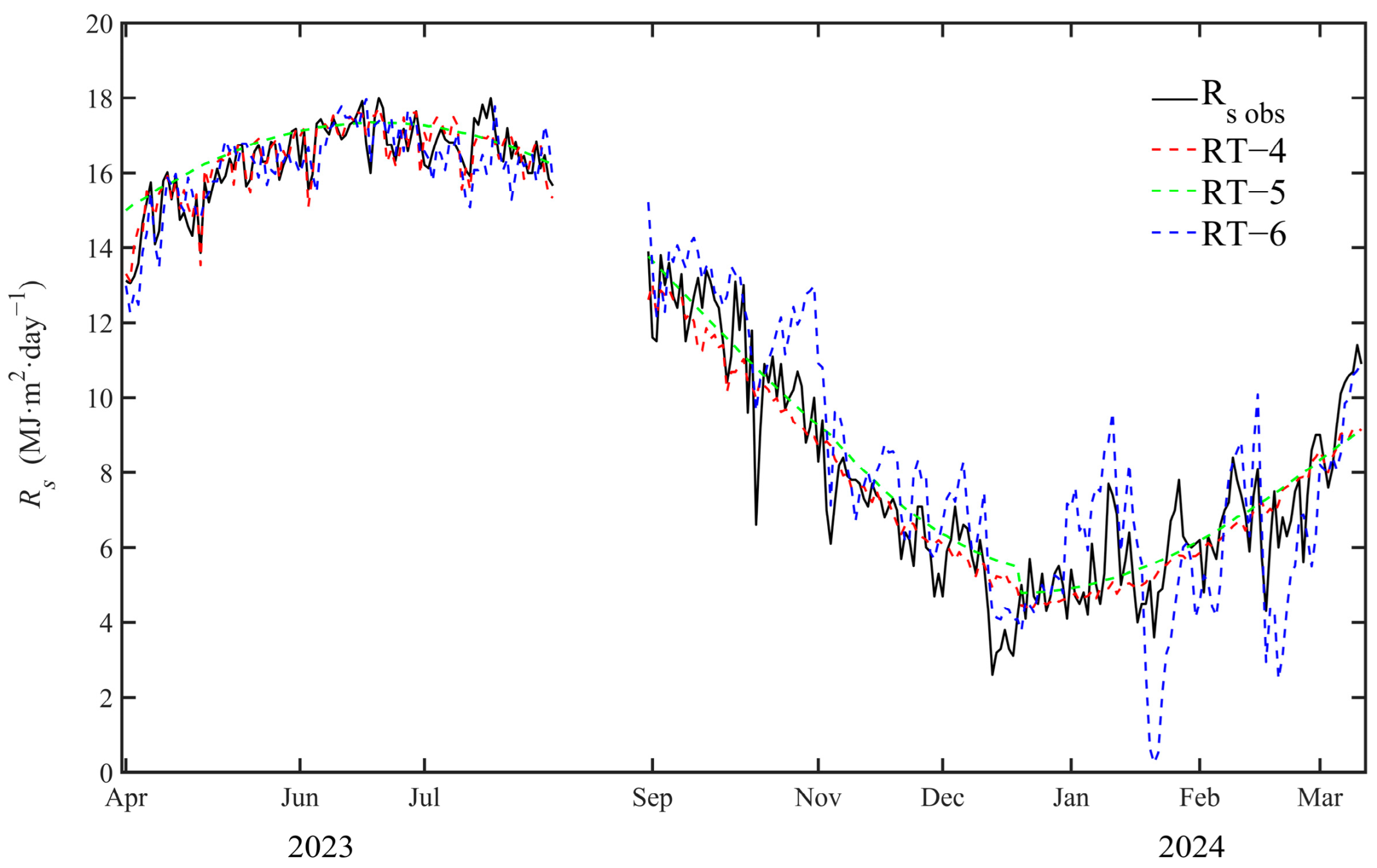
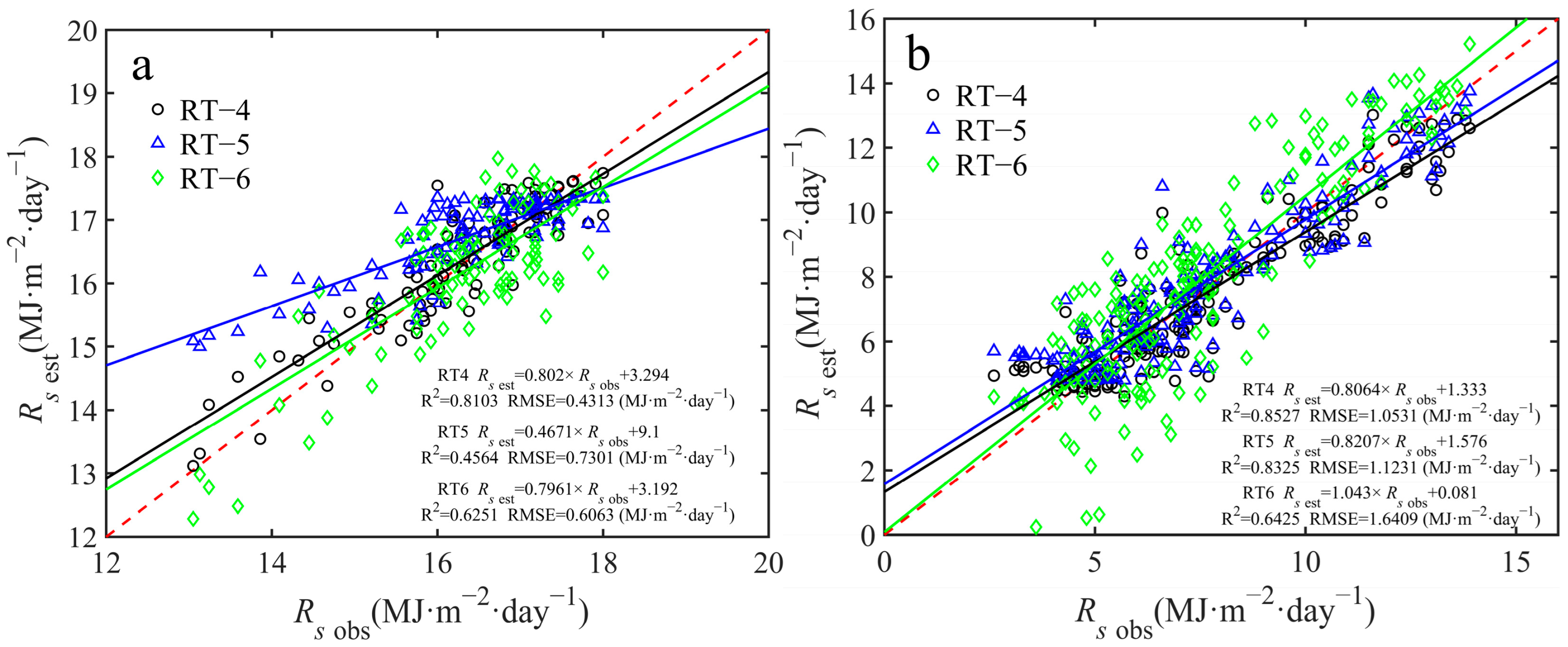
3.3. Forecasting Incoming and GSGs Solar Radiation
3.4. Crop Coefficient and Transpiration
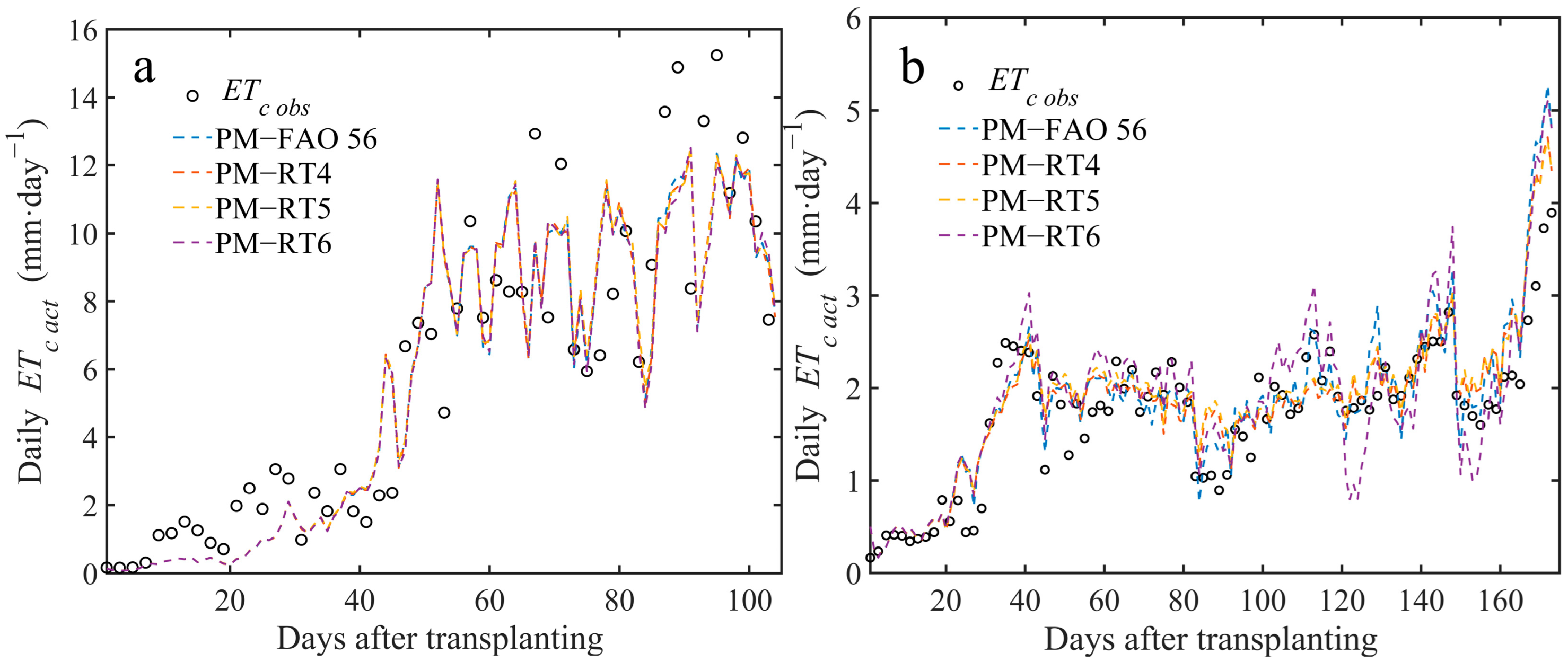
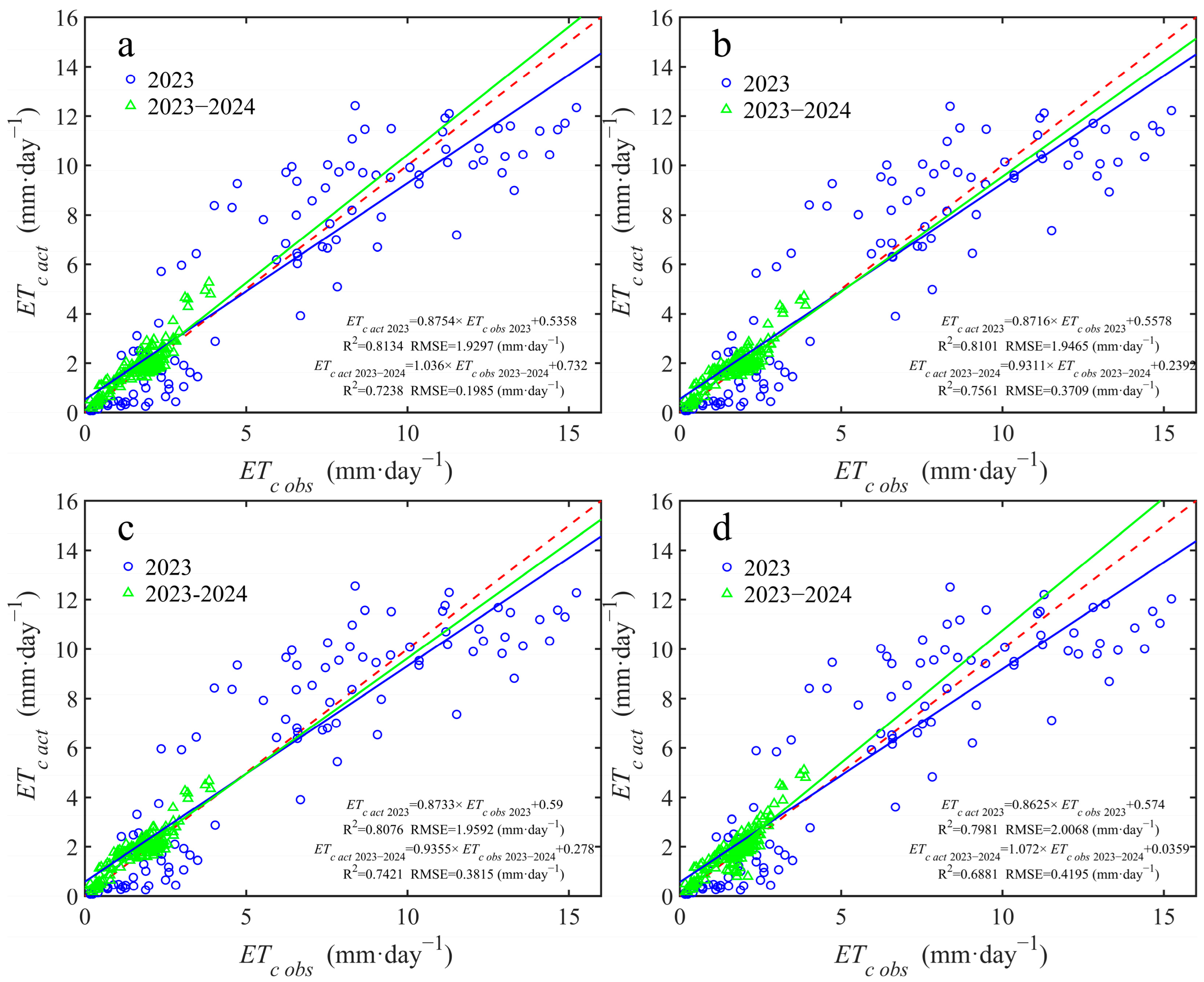
3.5. Comparison of the Accuracy of Estimating ETc act Based on Different Rs Models
4. Discussion
4.1. The Solar Radiation Estimation Models
4.2. Estimation of Incident Solar Radiation in GSGs
4.3. Estimation of Kcb
4.4. The Performance of the PM–RT Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Yang, Y.; Li, Y.; Li, J. Conversion from rural settlements and arable land under rapid urbanization in Beijing during 1985–2010. J. Rural Stud. 2017, 51, 141–150. [Google Scholar] [CrossRef]
- Mueller, N.D.; Gerber, J.S.; Johnston, M.; Ray, D.K.; Ramankutty, N.; Foley, J.A. Closing yield gaps through nutrient and water management. Nature 2012, 490, 254–257. [Google Scholar] [CrossRef]
- Panwar, N.; Kaushik, S.; Kothari, S. Solar greenhouse an option for renewable and sustainable farming. Renew. Sustain. Energy Rev. 2011, 15, 3934–3945. [Google Scholar] [CrossRef]
- Xie, J.; Yu, J.; Chen, B.; Feng, Z.; Lyu, J.; Hu, L.; Gan, Y.; Siddique, K.H.M. Gobi agriculture: An innovative farming system that increases energy and water use efficiencies. A review. Agron. Sustain. Dev. 2018, 38, 62. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Z.; Xu, X.; Kuang, W.; Zhou, W.; Zhang, S.; Li, R.; Yan, C.; Yu, D.; Wu, S. Spatial patterns and driving forces of land use change in China during the early 21st century. J. Geogr. Sci. 2010, 20, 483–494. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.; Wang, L.; Sun, G.; Zhao, J.; Zhang, H.; Du, N. The influence of facility agriculture production on phthalate esters distribution in black soils of northeast China. Sci. Total Environ. 2015, 506, 118–125. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Yu, J.; Chen, B.; Feng, Z.; Li, J.; Zhao, C.; Lyu, J.; Hu, L.; Gan, Y.; Siddique, K.H. Facility cultivation systems “设施农业”: A Chinese model for the planet. Adv. Agron. 2017, 145, 1–42. [Google Scholar]
- Gong, X.; Liu, H.; Sun, J.; Gao, Y.; Zhang, H. Comparison of Shuttleworth-Wallace model and dual crop coefficient method for estimating evapotranspiration of tomato cultivated in a solar greenhouse. Agric. Water Manag. 2019, 217, 141–153. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; Irrigation and Drainage Paper No 56; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 1998. [Google Scholar]
- Paredes, P.; Martins, D.S.; Pereira, L.S.; Cadima, J.; Pires, C. Accuracy of daily estimation of grass reference evapotranspiration using ERA-interim reanalysis products with assessment of alternative bias correction schemes. Agric. Water Manag. 2018, 210, 340–353. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Djaman, K.; O’Neill, M.; Diop, L.; Bodian, A.; Allen, S.; Koudahe, K.; Lombard, K. Evaluation of the Penman-Monteith and other 34 reference evapotranspiration equations under limited data in a semiarid dry climate. Theor. Appl. Climatol. 2019, 137, 729–743. [Google Scholar] [CrossRef]
- Song, X.; Lu, F.; Xiao, W.; Zhu, K.; Zhou, Y.; Xie, Z. Performance of 12 reference evapotranspiration estimation methods compared with the Penman–Monteith method and the potential influences in northeast China. Meteorol. Appl. 2019, 26, 83–96. [Google Scholar] [CrossRef]
- Fernández, M.; Bonachela, S.; Orgaz, F.; Thompson, R.; López, J.; Granados, M.; Gallardo, M.; Fereres, E. Measurement and estimation of plastic greenhouse reference evapotranspiration in a Mediterranean climate. Irrig. Sci. 2010, 28, 497–509. [Google Scholar] [CrossRef]
- Morille, B.; Migeon, C.; Bournet, P.E. Is the Penman–Monteith model adapted to predict crop transpiration under greenhouse conditions? Application to a new guinea impatiens crop. Sci. Hortic. 2013, 152, 80–91. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Priestley, C.; Taylor, R. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weather Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Almorox, J.; Hontoria, C.; Benito, M. Models for obtaining daily global solar radiation with measured air temperature data in Madrid (Spain). Appl. Energy 2011, 88, 1703–1709. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Ibrakhimov, M.; Saito, L. Estimating daily global solar radiation by day of the year in six cities located in the Yucatán Peninsula, Mexico. J. Clean. Prod. 2016, 141, 75–82. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Anisi, M.H.; Alam, K.A.; Petković, D. Support vector regression based prediction of global solar radiation on a horizontal surface. Energy Convers. Manag. 2015, 91, 433–441. [Google Scholar] [CrossRef]
- Kumar, R.; Aggarwal, R.K.; Sharma, J.D. Comparison of regression and artificial neural network models for estimation of global solar radiations. Renew. Sustain. Energy Rev. 2015, 52, 1294–1299. [Google Scholar] [CrossRef]
- Alonso-Montesinos, J.; Batlles, F.J.; Bosch, J.L. Beam, diffuse and global solar irradiance estimation with satellite imagery. Energy Convers. Manag. 2015, 105, 1205–1212. [Google Scholar] [CrossRef]
- Pawlak, D.T.; Clothiaux, E.E.; Modest, M.F.; Cole, J.N.S. Full-spectrum correlated-k distribution for shortwave atmospheric radiative transfer. J. Atmos. Sci. 2004, 61, 2588–2601. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Review and statistical analysis of different global solar radiation sunshine models. Renew. Sustain. Energy Rev. 2015, 52, 1869–1880. [Google Scholar] [CrossRef]
- Besharat, F.; Dehghan, A.A.; Faghih, A.R. Empirical models for estimating global solar radiation: A review and case study. Renew. Sustain. Energy Rev. 2013, 21, 798–821. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Ye, B. Improving estimation of hourly, daily, and monthly solar radiation by importing global data sets. Agric. For. Meteorol. 2006, 137, 43–55. [Google Scholar] [CrossRef]
- Annandale, J.; Jovanovic, N.; Benadé, N.; Allen, R. Software for missing data error analysis of Penman-Monteith reference evapotranspiration. Irrig. Sci. 2002, 21, 57–67. [Google Scholar] [CrossRef]
- Samani, Z. Estimating solar radiation and evapotranspiration using minimum climatological data. J. Irrig. Drain. Eng.-ASCE 2000, 126, 265–267. [Google Scholar] [CrossRef]
- Chen, R.; Ersi, K.; Yang, J.; Lu, S.; Zhao, W. Validation of five global radiation models with measured daily data in China. Energy Convers. Manag. 2004, 45, 1759–1769. [Google Scholar] [CrossRef]
- Hassan, G.E.; Youssef, M.E.; Mohamed, Z.E.; Ali, M.A.; Hanafy, A.A. New temperature-based models for predicting global solar radiation. Appl. Energy 2016, 179, 437–450. [Google Scholar] [CrossRef]
- Rooij, G.H.d. Methods of soil analysis: Part 4. Physical methods. Vadose Zone J. 2004, 3, 722–723. [Google Scholar] [CrossRef]
- Reatto, A.; Silva, E.M.D.; Bruand, A.; Martins, E.S.; Lima, J.E.F.W. Validity of the centrifuge method for determining the water retention properties of tropical soils. Soil Sci. Soc. Am. J. 2008, 72, 1547–1553. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef]
- Ding, R.; Kang, S.; Zhang, Y.; Hao, X.; Tong, L.; Du, T. Partitioning evapotranspiration into soil evaporation and transpiration using a modified dual crop coefficient model in irrigated maize field with ground-mulching. Agric. Water Manag. 2013, 127, 85–96. [Google Scholar] [CrossRef]
- Katsoulas, N.; Stanghellini, C. Modelling crop transpiration in greenhouses: Different models for different applications. Agronomy 2019, 9, 392. [Google Scholar] [CrossRef]
- Bontsema, J.; Hemming, J.; Stanghellini, C.; De Visser, P.; Van Henten, E.; Budding, J.; Rieswijk, T.; Nieboer, S. On-line estimation of the transpiration in greenhouse horticulture. In Proceedings of the Agricontrol 2007 2nd IFAC International Conference on Modeling and Design of Control Systems in Agriculture, Osijek, Croatia, 3–5 September 2007; Volume 2008, pp. 29–34. [Google Scholar]
- Jahani, B.; Dinpashoh, Y.; Nafchi, R.A. Evaluation and development of empirical models for estimating daily solar radiation. Renew. Sustain. Energy Rev. 2017, 73, 878–891. [Google Scholar] [CrossRef]
- Angstrom, A. Solar and terrestrial radiation. Report to the international commission for solar research on actinometric investigations of solar and atmospheric radiation. Q. J. R. Meteorol. Soc. 1924, 50, 121–126. [Google Scholar] [CrossRef]
- Bahel, V.; Bakhsh, H.; Srinivasan, R. A correlation for estimation of global solar radiation. Energy 1987, 12, 131–135. [Google Scholar] [CrossRef]
- Ayodele, T.R.; Ogunjuyigbe, A.S.O. Prediction of monthly average global solar radiation based on statistical distribution of clearness index. Energy 2015, 90, 1733–1742. [Google Scholar] [CrossRef]
- ASHRAE. ASHRAE Handbook of Fundamentals; American Society of Heating, Refrigerating and Air Conditioning Engineers: Atlanta, GA, USA, 1972. [Google Scholar]
- Zhang, X.; Lv, J.; Xie, J.; Yu, J.; Zhang, J.; Tang, C.; Li, J.; He, Z.; Wang, C. Solar radiation allocation and spatial distribution in Chinese solar greenhouses: Model development and application. Energies 2020, 13, 1108. [Google Scholar] [CrossRef]
- TPDC. China Meteorological Forcing Dataset (1979–2018). Available online: https://data.tpdc.ac.cn/home (accessed on 9 September 2024).
- He, J.; Yang, K.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. The first high-resolution meteorological forcing dataset for land process studies over China. Sci. Data 2020, 7, 25. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C.C.K. On downward shortwave and longwave radiations over high altitude regions: Observation and modeling in the Tibetan Plateau. Agric. For. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Trnka, M.; Žalud, Z.; Eitzinger, J.; Dubrovský, M. Global solar radiation in Central European lowlands estimated by various empirical formulae. Agric. For. Meteorol. 2005, 131, 54–76. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Lopez-Urrea, R.; Hunsaker, D.J.; Mota, M.; Shad, Z.M. Standard single and basal crop coefficients for vegetable crops, an update of FAO56 crop water requirements approach. Agric. Water Manag. 2020, 243, 106196. [Google Scholar] [CrossRef]
- Tong, X.; Sun, Z.; Sigrimis, N.; Li, T.; Yu, X. Energy sustainability performance of a sliding cover solar greenhouse: Solar energy capture aspects. Biosyst. Eng. 2018, 176, 88–102. [Google Scholar] [CrossRef]
- Qiu, R.; Du, T.; Wu, L.; Chen, R.; Kang, S. Assessing the SIMDualKc model for estimating evapotranspiration of hot pepper grown in a solar greenhouse in Northwest China. Agric. Syst. 2015, 138, 1–9. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Alves, I.; Fernando, R.M.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software. 1. Background and computational strategy. Agric. Water Manag. 2012, 103, 8–24. [Google Scholar] [CrossRef]
- Alemayehu, Y.A.; Steyn, J.M.; Annandale, J.G. FAO-type crop factor determination for irrigation scheduling of hot pepper (Capsicum annuum L.) cultivars. S. Afr. J. Plant Soil 2009, 26, 186–194. [Google Scholar] [CrossRef]
- Shukla, S.; Jaber, F.H.; Goswami, D.; Srivastava, S. Evapotranspiration losses for pepper under plastic mulch and shallow water table conditions. Irrig. Sci. 2013, 31, 523–536. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef]
- Dobon-Suarez, A.; Gimenez, M.J.; Castillo, S.; Garcia-Pastor, M.E.; Zapata, P.J. Influence of the phenological stage and harvest date on the bioactive compounds content of green pepper fruit. Molecules 2021, 26, 3099. [Google Scholar] [CrossRef]
- Rajametov, S.; Lee, K.; Jeong, H.B.; Cho, M.C.; Nam, C.W.; Yang, E.Y. The effect of night low temperature on agronomical traits of thirty-nine pepper accessions (Capsicum annuum L.). Agronomy 2021, 11, 1986. [Google Scholar] [CrossRef]
- Qiu, R.; Kang, S.; Li, F.; Du, T.; Tong, L.; Wang, F.; Chen, R.; Liu, J.; Li, S. Energy partitioning and evapotranspiration of hot pepper grown in greenhouse with furrow and drip irrigation methods. Sci. Hortic. 2011, 129, 790–797. [Google Scholar] [CrossRef]



| Parameter | Value | Unit | Source |
|---|---|---|---|
| Soil evaporation coefficient (Ke) | 0 | - | measured |
| Water stress coefficient (Ks) | 1 | - | measured |
| Leaf senescence factor (fs) | 0 | - | measured |
| Field capacity (θFC) | 0.459 | cm3·cm−3 | measured |
| Wilting point (θWP) | 0.08 | cm3·cm−3 | measured |
| Effective rooting depth (Zr) | 0.25 | m | measured |
| Depletion fractions (pini) | 0.3 | - | [9] |
| Depletion fractions (pdev) | 0.3 | - | [9] |
| Depletion fractions (pmid) | 0.3 | - | [9] |
| Minimum basal crop coefficient (Kcb,min) | 0.1 | - | [34] |
| Soil heat flux (G) | 0 | W·m−2 | [8] |
| Extinction coefficient of light attenuation (kx) | 0.7 | - | [36] |
| Reflection coefficient of light attenuation (a) | 0.86 | - | [36] |
| Model class | Model Name | ID | Model Formulae |
|---|---|---|---|
| Temperature-based | Allen [9] | T1 | |
| Samani [27] | T2 | ||
| Annandale [26] | T3 | ||
| Chen [28] | T4 | ||
| Hassan [29] | T5 | ||
| Present study | T6 | ||
| Sunshine-based | Angstrom [38] | N1 | |
| Bahel [39] | N2 |
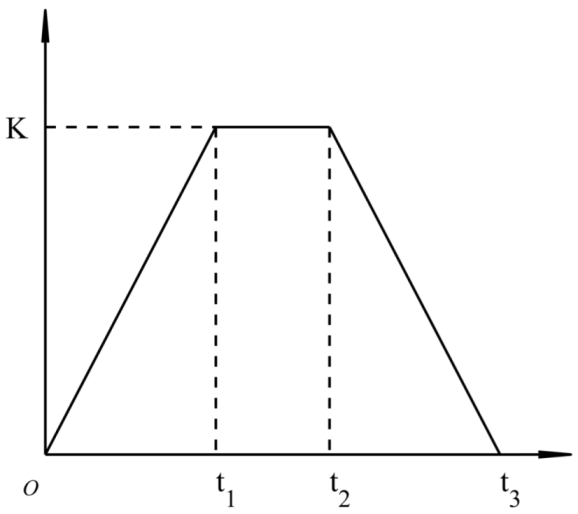
| o | t1 | t2 | t3 | |
|---|---|---|---|---|
| Date | 1 November | 1 December | 1 February | 1 March |
| N | 305 | 335 | 32 | 60 |
| Model Class | ID | Model Empirical Coefficients | R2 | MAE (MJ·m−2·day−1) | MBE (MJ·m−2·day−1) | RMSE (MJ·m−2·day−1) | NRMSE % | Rank | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | ||||||||
| Temperature-based | T1 | 0.1856 | 0.9492 | 0.0616 | −0.2547 | 1.3208 | 6.86 | 5 | |||
| T2 | 0.001 | −0.0273 | 0.3641 | 0.9599 | 0.0531 | −0.3661 | 1.1731 | 6.09 | 4 | ||
| T3 | 0.169 | 0.9492 | 0.0617 | −0.2585 | 1.3213 | 6.86 | 6 | ||||
| T4 | 0.441 | 0.0577 | 0.9631 | 0.0506 | −0.1913 | 1.1255 | 5.85 | 2 | |||
| T5 | −0.001 | 0.0404 | 0.6296 | 0.9625 | 0.0559 | 0.3371 | 1.1357 | 5.9 | 3 | ||
| T6 | −0.001 | 0.6577 | 15.25 | 0.9774 | 0.0666 | −0.3293 | 1.2501 | 6.49 | 1 | ||
| 0.0073 | 0.378 | 10.4 | 0.9892 | 0.0456 | −0.0129 | 0.8562 | 4.45 | ||||
| Sunshine-based | N1 | 0.2761 | 0.4512 | 0.9437 | 0.0649 | −0.0384 | 1.3908 | 7.22 | 8 | ||
| N2 | 0.2508 | 0.1339 | 1.1086 | −0.8537 | 0.9425 | 0.0639 | −0.0459 | 1. 406 | 7.3 | 7 | |
| Season | Model | Rs est (MJ·m−2·Day−1) | Rs obs (MJ·m−2·Day−1) | R2 | MAE (MJ·m−2·Day−1) | MBE (MJ·m−2·Day−1) | RMSE (MJ·m−2·Day−1) | NRMSE % |
|---|---|---|---|---|---|---|---|---|
| 2023 | RT-4 | 16.37 | 16.19 | 0.8103 | 0.0205 | −0.0838 | 0.4313 | 2.45 |
| RT-5 | 16.71 | 0.4564 | 0.0356 | −0.4299 | 0.7301 | 4.14 | ||
| RT-6 | 15.98 | 0.6251 | 0.032 | 0.0919 | 0.6063 | 3.44 | ||
| 2023–2024 | RT-4 | 7.43 | 7.55 | 0.8527 | 0.125 | 0.1293 | 1.0531 | 9.32 |
| RT-5 | 7.78 | 0.8325 | 0.1385 | −0.2214 | 1.1231 | 9.94 | ||
| RT-6 | 7.96 | 0.6425 | 0.2051 | −0.4031 | 1.6409 | 14.52 |
| Standard | Calibrated | ||
|---|---|---|---|
| 2023 Growing Season | 2023–2024 Growing Season | ||
| Kcb ini | 0.15 | 0.15 | 0.17 |
| Kcb mid | 1.10 | 1.01 | 0.82 |
| Season | Model | ETc act (mm·Day−1) | ETc obs (mm·Day−1) | R2 | MAE (mm·Day−1) | MBE (mm·Day−1) | RMSE (mm·Day−1) | NRMSE % |
|---|---|---|---|---|---|---|---|---|
| 2023 | PM–FAO-56 | 5.6921 | 5.8901 | 0.8134 | 0.3807 | 0.1981 | 1.9297 | 12.8 |
| PM–RT4 | 5.6920 | 0.8101 | 0.3812 | 0.1984 | 1.9465 | 12.91 | ||
| PM–RT5 | 5.7336 | 0.8076 | 0.3859 | 0.1565 | 1.9592 | 13 | ||
| PM–RT6 | 5.6547 | 0.7981 | 0.3851 | 0.2354 | 2.0068 | 13.31 | ||
| 2023–2024 | PM–FAO-56 | 3.0932 | 1.7243 | 0.7238 | 0.1985 | −0.1353 | 0.3948 | 10.58 |
| PM–RT4 | 3.0686 | 0.7561 | 0.2184 | −0.1204 | 0.3709 | 9.94 | ||
| PM–RT5 | 3.1462 | 0.7421 | 0.2290 | −0.1671 | 0.3815 | 10.23 | ||
| PM–RT6 | 3.1341 | 0.6881 | 0.2274 | −0.1598 | 0.4195 | 11.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, N.; Xie, J.; Zhang, X.; Zhang, J.; Chang, Y. A Simplified Model for Substrate-Cultivated Pepper in a Hexi Corridor Greenhouse. Agronomy 2025, 15, 1921. https://doi.org/10.3390/agronomy15081921
Ma N, Xie J, Zhang X, Zhang J, Chang Y. A Simplified Model for Substrate-Cultivated Pepper in a Hexi Corridor Greenhouse. Agronomy. 2025; 15(8):1921. https://doi.org/10.3390/agronomy15081921
Chicago/Turabian StyleMa, Ning, Jianming Xie, Xiaodan Zhang, Jing Zhang, and Youlin Chang. 2025. "A Simplified Model for Substrate-Cultivated Pepper in a Hexi Corridor Greenhouse" Agronomy 15, no. 8: 1921. https://doi.org/10.3390/agronomy15081921
APA StyleMa, N., Xie, J., Zhang, X., Zhang, J., & Chang, Y. (2025). A Simplified Model for Substrate-Cultivated Pepper in a Hexi Corridor Greenhouse. Agronomy, 15(8), 1921. https://doi.org/10.3390/agronomy15081921




