Management Zones for Irrigated and Rainfed Grain Crops Based on Data Layer Integration
Abstract
1. Introduction
2. Materials and Methods
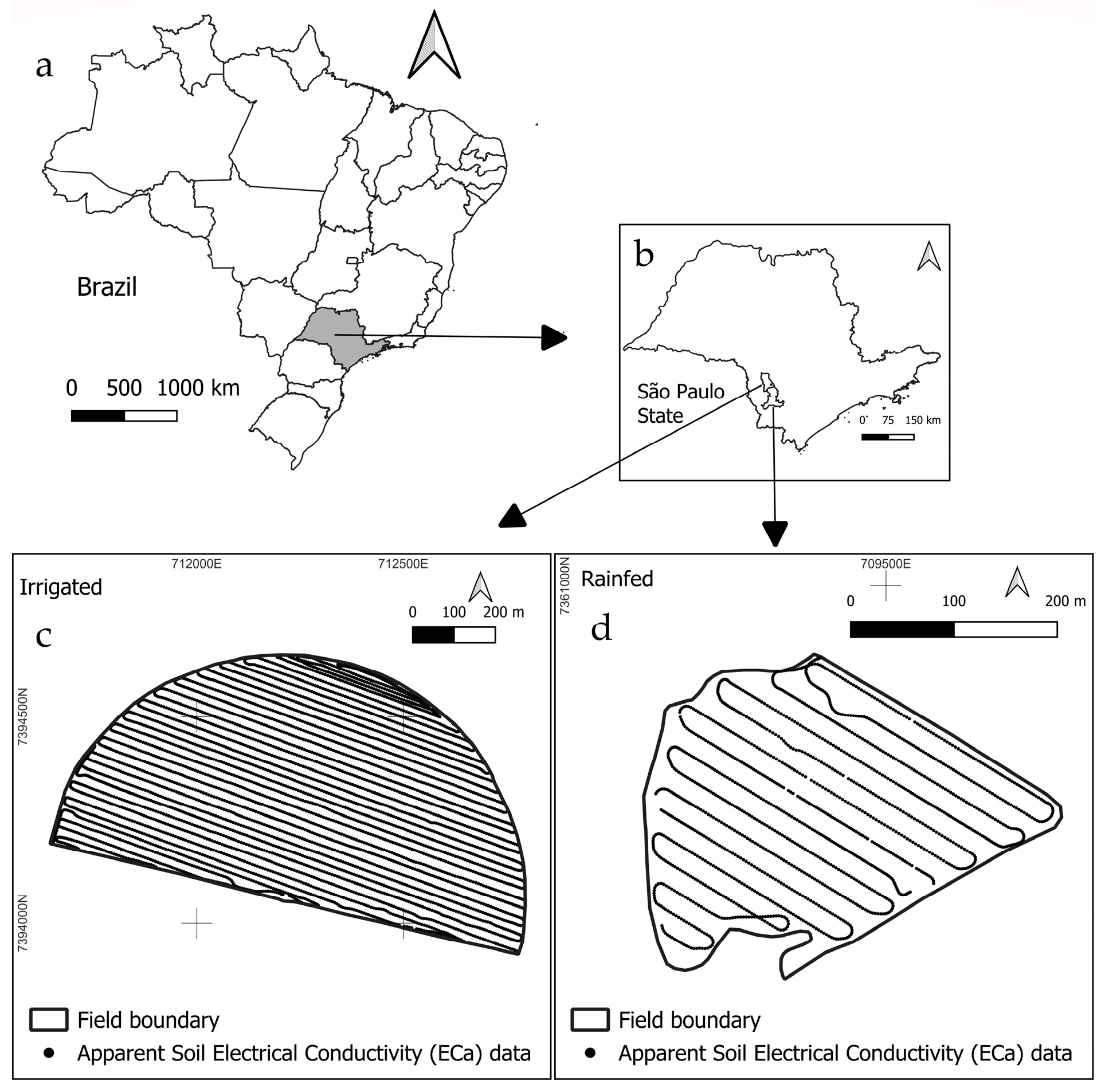
2.1. Study Areas
2.2. Data Characterization
2.3. Data Filtering, Statistical and Geostatistical Analysis
2.4. Multivariate Statistics and MZs Delineation Methods
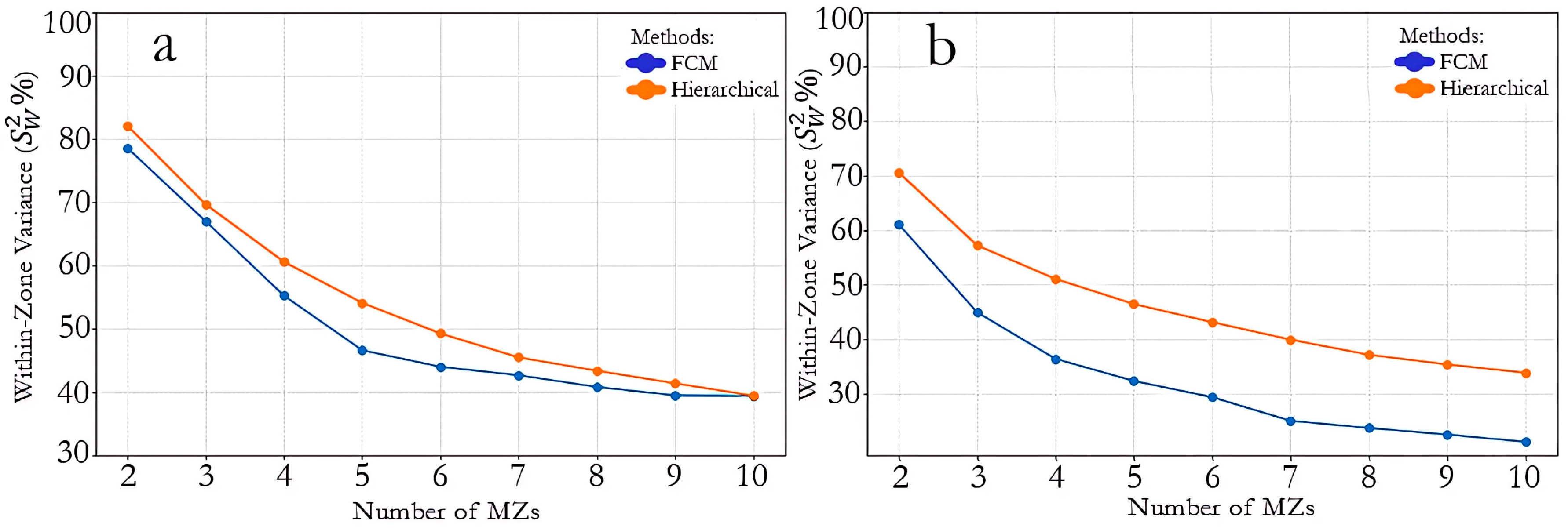
2.5. Evaluation of MZs Separation
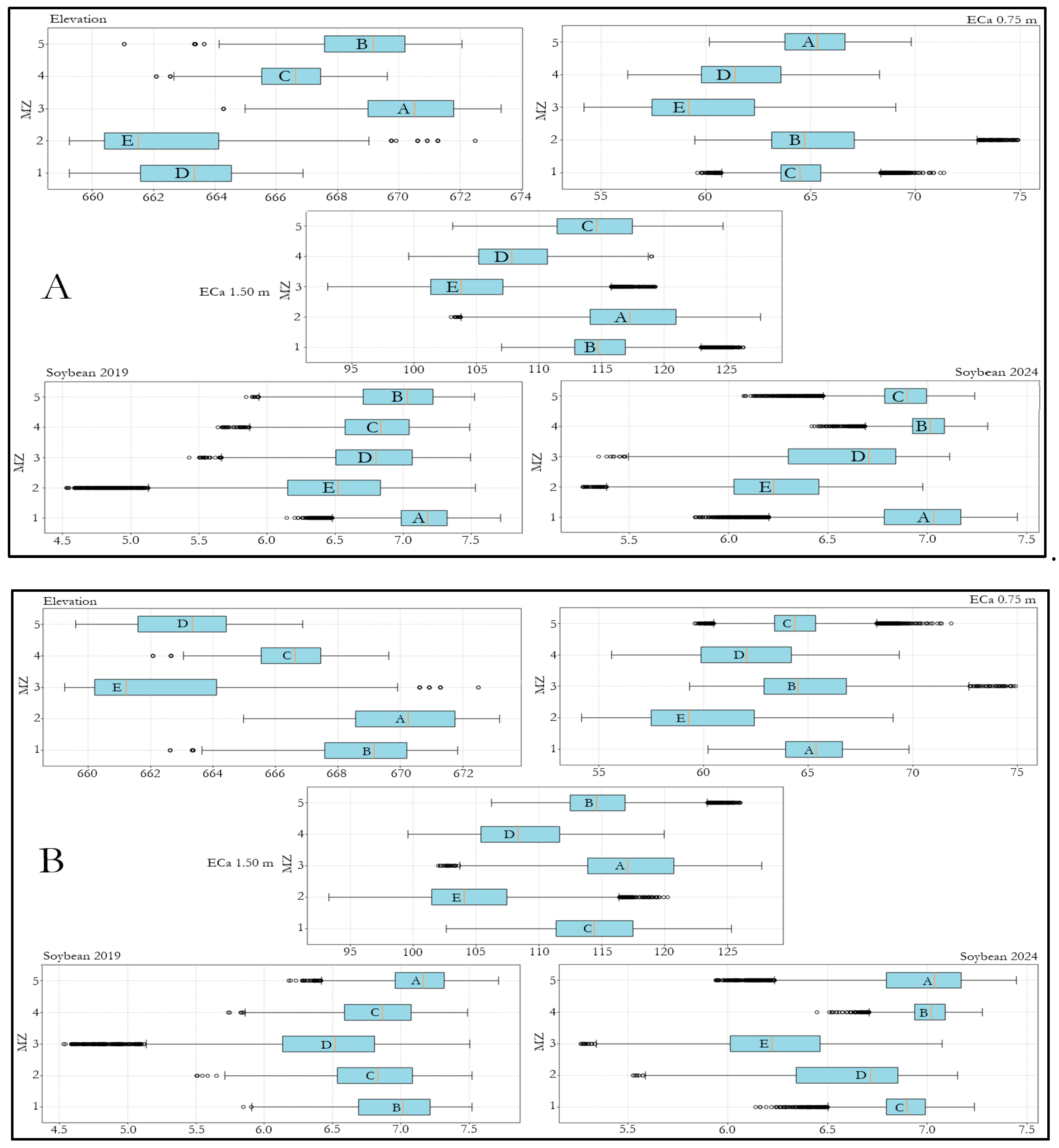
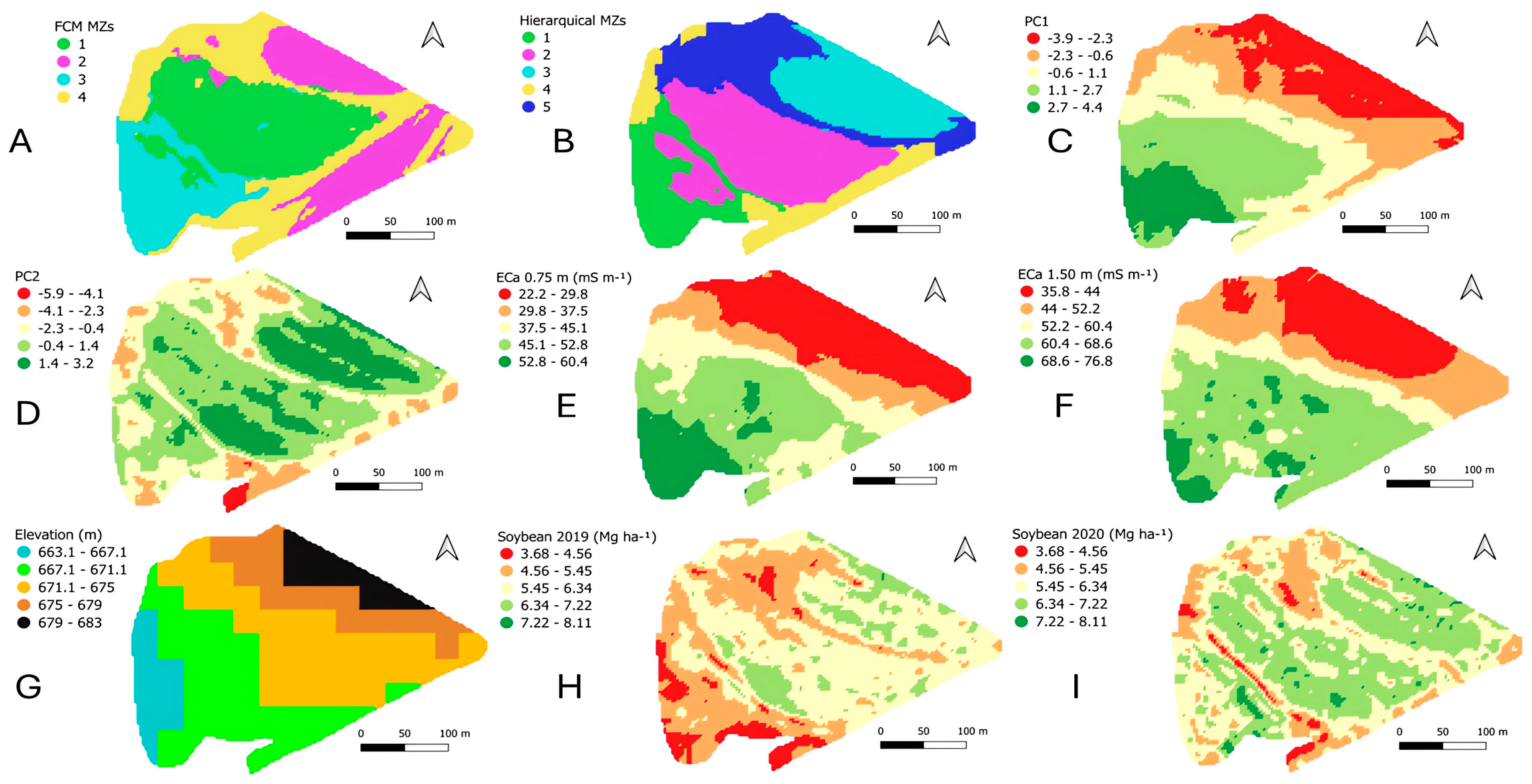
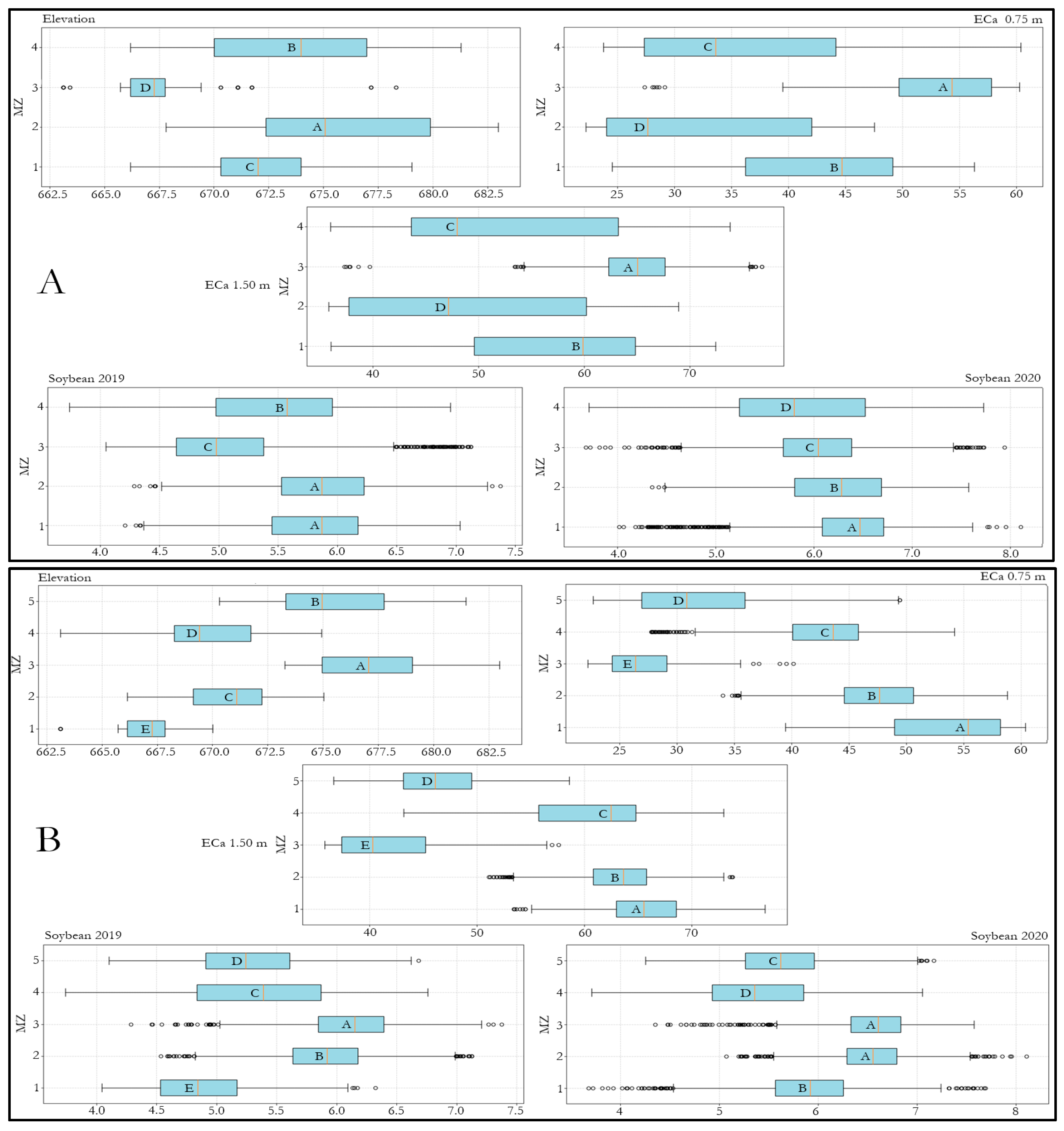
3. Results and Discussion
3.1. Data Filtering
3.2. Geostatistic
3.3. Descriptive Statistics of the Attributes
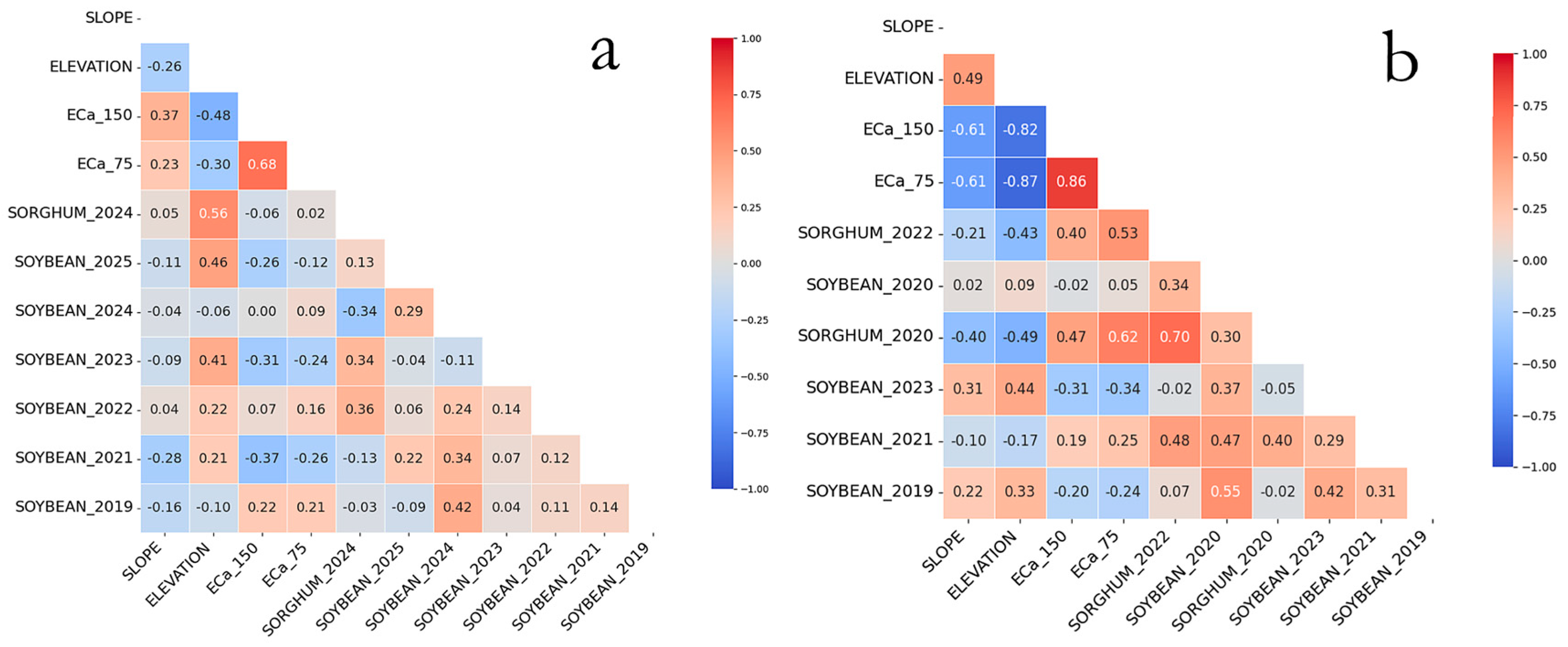
3.4. Spearman Correlation
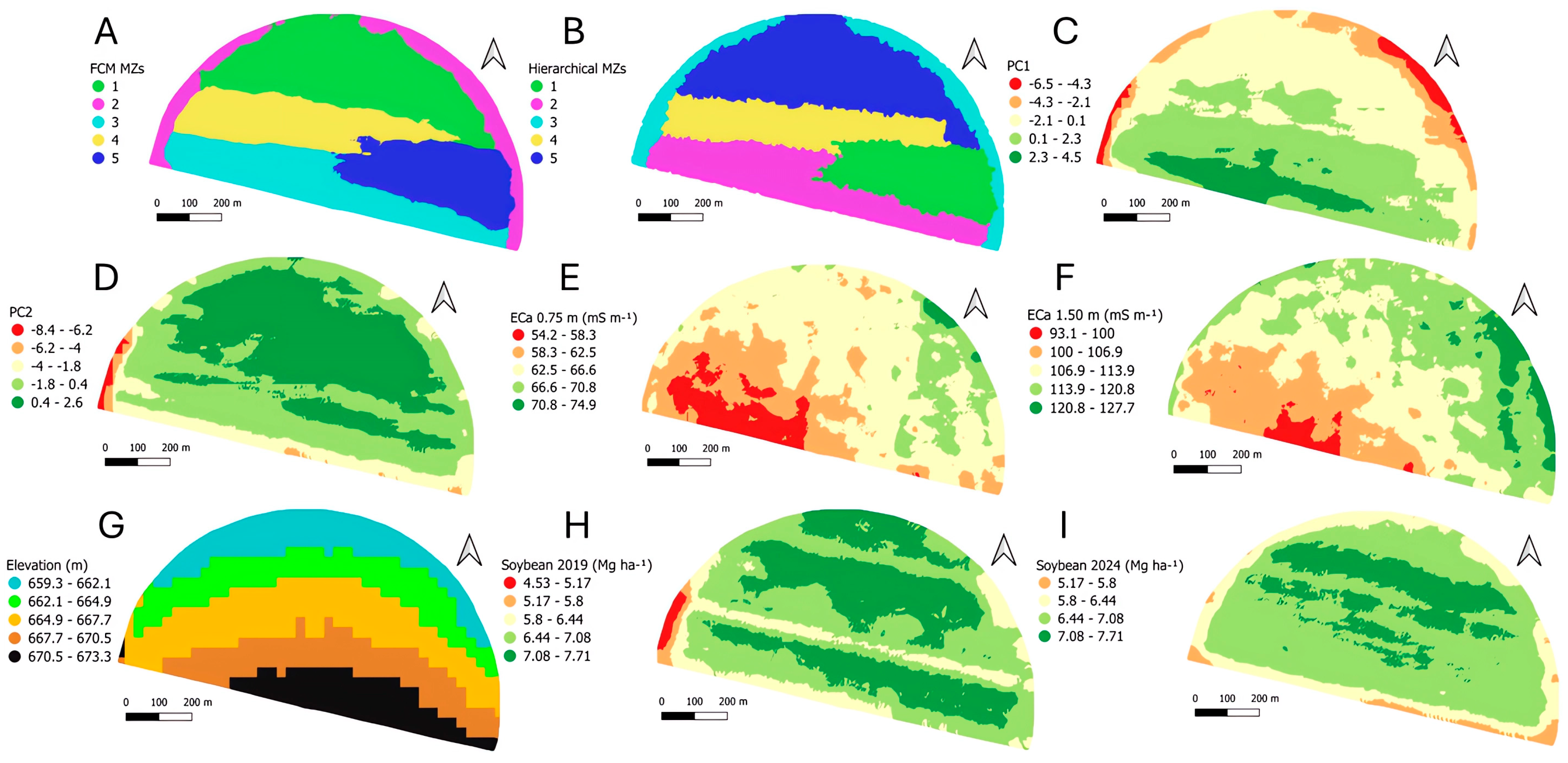
3.5. Principal Component Analysis (PCA)
3.6. MZs Delineation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bottega, E.L.; Queiroz, D.M.; Pinto, F.A.C.; Valente, D.S.M.; Souza, C.M.A. Precision agriculture applied to soybean crop: Part II—Temporal stability of management zones. Aust. J. Crop Sci. 2017, 11, 676–682. [Google Scholar] [CrossRef]
- ISPA. International Society of Precision Agriculture. 2024. Available online: https://ispag.org/about/definition (accessed on 20 April 2025).
- Mulla, D.J. Using geostatistics and GIS to manage spatial patterns in soil fertility. In Automated Agriculture for the 21st Century; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1991. [Google Scholar]
- Molin, J.P.; Amaral, L.R.; Colaço, A.F. Agricultura de precisão; Oficina de Textos: São Paulo, Brazil, 2015. [Google Scholar]
- McBratney, A.G.; Webster, A.G. Choosing functions for semi-variograms and fitting them to sampling estimates. J. Soil Sci. 1986, 37, 617–639. [Google Scholar] [CrossRef]
- Franzen, D.W.; Halvorson, A.D.; Krupinsky, J.; Hofman, V.L.; Cihacek, L.J. Directed sampling using topography as a logical basis. In Proceedings of the 4th International Conference on Precision Agriculture, St. Paul, MN, USA, 19–22 July 1998; ASA: Madison, WI, USA, 1998; pp. 1559–1568. [Google Scholar] [CrossRef]
- Sudduth, K.A.; Drummond, S.T.; Birrell, S.J.; Kitchen, N.R. Spatial modeling of crop yield using soil and topographic data. In Proceedings of the 1st European Conference on Precision Agriculture, Warwick, UK, 7–10 September 1997; Bios Scientific Publishers: Oxford, UK, 1997; pp. 439–447. [Google Scholar]
- Moral, F.; Terrón, J.M.; da Silva, J.M. Delineation of management zones using mobile measurements of soil apparent electrical conductivity and multivariate geostatistical techniques. Soil Tillage Res. 2010, 106, 335–343. [Google Scholar] [CrossRef]
- Fraisse, C.W.; Sudduth, K.A.; Kitchen, N.R. Delineation of site-specific management zones by unsupervised classification of topographic attributes and soil electrical conductivity. Trans. ASABE 2001, 44, 155–166. [Google Scholar] [CrossRef]
- Oldoni, H.; Silva Terra, V.S.; Timm, L.C.; Junior, C.R.; Monteiro, A.B. Delineation of management zones in a peach orchard using multivariate and geostatistical analyses. Soil Tillage Res. 2019, 191, 1–10. [Google Scholar] [CrossRef]
- Damian, J.M.; Pias, O.H.C.; Cherubin, M.R.; Fonseca, A.Z.D.; Fornari, E.Z.; Santi, A.L. Applying the NDVI from satellite images in delimiting management zones for annual crops. Sci. Agric. 2020, 77, e20180055. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Application of soil electrical conductivity to precision agriculture: Theory, principles, and guidelines. Agron. J. 2003, 95, 455–471. [Google Scholar] [CrossRef]
- James, I.T.; Waine, T.W.; Bradley, R.I.; Taylor, J.C.; Godwin, R.J. Determination of soil type boundaries using electromagnetic induction scanning techniques. Biosyst. Eng. 2003, 86, 421–430. [Google Scholar] [CrossRef]
- Brevik, E.C.; Fenton, T.E. Influence of soil water content, clay, temperature, and carbonate minerals on electrical conductivity readings taken with an EM-38. Soil Surv. Horiz. 2002, 43, 9–13. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Martínez, G.; Ramos, M.; Mateos, L. Relevance of NDVI, soil apparent electrical conductivity and topography for variable rate irrigation zoning in an olive grove. Precis. Agric. 2024, 25, 3086–3108. [Google Scholar] [CrossRef]
- Fortes, R.; Millán, S.; Prieto, M.H.; Campillo, C. A methodology based on apparent electrical conductivity and guided soil samples to improve irrigation zoning. Precis. Agric. 2015, 16, 441–454. [Google Scholar] [CrossRef]
- Moharana, P.C.; Jena, R.K.; Pradhan, U.K.; Nogiya, M.; Tailor, B.L.; Singh, R.S.; Singh, S.K. Geostatistical and fuzzy clustering approach for delineation of site-specific management zones and yield-limiting factors in irrigated hot arid environment of India. Precis. Agric. 2019, 21, 426–448. [Google Scholar] [CrossRef]
- Gavioli, A.; de Souza, E.G.; Bazzi, C.L.; Guedes, L.P.C.; Schenatto, K. Optimization of management zone delineation by using spatial principal components. Comput. Electron. Agric. 2016, 127, 302–310. [Google Scholar] [CrossRef]
- Hongyu, K.; Sandanielo, V.L.M.; Oliveira Junior, G.J. Análise de componentes principais: Resumo teórico, aplicação e interpretação. Eng. Sci. 2016, 5, 83–98. [Google Scholar] [CrossRef]
- Kitchen, N.R.; Sudduth, K.A.; Myers, D.B.; Drummond, S.T.; Hong, S.Y. Delineating yield zones on claypan soil fields using apparent soil electrical conductivity. Comput. Electron. Agric. 2005, 46, 285–308. [Google Scholar] [CrossRef]
- Fridgen, J.J.; Kitchen, N.R.; Sudduth, K.A.; Drummond, S.T.; Wiebold, W.J.; Fraisse, C.W. Management zone analyst (MZA): Software for subfield Management zone delineation. Agron. J. 2004, 96, 100–108. [Google Scholar] [CrossRef]
- Guastaferro, F.; Castrignanò, A.; De Benedetto, D.; Sollitto, D.; Troccoli, A.; Cafarelli, B. A comparison of different algorithms for the delineation of management zones. Precis. Agric. 2010, 11, 600–620. [Google Scholar] [CrossRef]
- Ward, J.H. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Russ, G.; Kruse, R. Exploratory hierarchical clustering for management zone delineation in precision agriculture. In Advances in Data Mining; Springer: Berlin/Heidelberg, Germany, 2011; pp. 161–173. [Google Scholar] [CrossRef]
- Haghverdi, A.; Leib, B.G.; Washington-Allen, R.A.; Ayers, P.D.; Buschermohle, M.J. Perspectives on delineating management zones for variable rate irrigation. Comput. Electron. Agric. 2015, 117, 154–167. [Google Scholar] [CrossRef]
- Lajili, A.; Cambouris, A.N.; Chokmani, K.; Duchemin, M.; Perron, I.; Zebarth, B.J.; Biswas, A.; Adamchuk, V.I. Analysis of four delineation methods to identify potential management zones in a commercial potato field in Eastern Canada. Agronomy 2021, 11, 432. [Google Scholar] [CrossRef]
- Bottega, E.L.; Safanelli, J.L.; Zeraatpisheh, M.; Amado, T.J.C.; Queiroz, D.M.; Oliveira, Z.B. Site-specific management zones delineation based on apparent soil electrical conductivity in two contrasting fields of Southern Brazil. Agronomy 2022, 12, 1390. [Google Scholar] [CrossRef]
- Climate-data.org. Climate Data for Cities Worldwide. Available online: https://en.climate-data.org/ (accessed on 10 March 2025).
- Köppen, W.; Geiger, R. Klimate der Erde; Justus Perthes: Gotha, Germany, 1928. [Google Scholar]
- EMBRAPA. Súmula da 10. reunião Técnica de Levantamento de Solos; Serviço Nacional de Levantamento e Conservação de Solos: Rio de Janeiro, Brazil, 1979. [Google Scholar]
- Win, K.N. OpenTopography DEM Downloader (Version 3.0) [Plugin]. QGIS. 2024. Available online: https://plugins.qgis.org/plugins/OpenTopography-DEM-Downloader/ (accessed on 30 March 2025).
- Maldaner, L.F.; Molin, J.P.; Spekken, M. Map Filter 2.0. 2021. Available online: https://www.agriculturadeprecisao.org.br/softwares/ (accessed on 27 March 2025).
- Pereira, G.W.; Valente, D.S.M.; Queiroz, D.M.; Coelho, A.L.F.; Costa, M.M.; Grift, T. Smart-Map: An Open-Source QGIS Plugin for Digital Mapping Using Machine Learning Techniques and Ordinary Kriging. Agronomy 2022, 12, 1350. [Google Scholar] [CrossRef]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-scale variability of soil properties in Central Iowa soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Wilding, L.P. Spatial variability: Its documentation, accommodation and implication to soil surveys. In Soil Spatial Variability; Nielsen, D.R., Bouma, J., Eds.; International Soil Science Society: Wageningen, The Netherlands, 1985; pp. 166–194. [Google Scholar]
- Sousa, Á. Coeficiente de Correlação de Pearson e Coeficiente de Correlação de Spearman: O que Medem e em que Situações Devem ser Utilizados? Correio dos Açores—Matemática. 21 March 2019, p. 19. Available online: https://repositorio.uac.pt/entities/publication/48103d09-4406-4176-b520-41bce0b65345 (accessed on 15 March 2025).
- Rumsey, D.J. What Is r Value Correlation? Dummies. 2023. Available online: https://www.dummies.com/article/academics-the-arts/math/statistics/how-to-interpret-a-correlation-coefficient-r-169792/ (accessed on 16 April 2025).
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- González Perea, R.; Daccache, A.; Rodríguez Díaz, J.A.; Camacho Poyato, E.; Knox, J.W. Modelling impacts of precision irrigation on crop yield and in-field water management. Precis. Agric. 2018, 19, 497–512. [Google Scholar] [CrossRef]

| Irrigated | ||||||||||
| Attribute | Model | Max_dist (m) | Lag (m) | C0 | C0 + C1 | Range (m) | RMSE | R2 | DSD (%) | DSD Class |
| ECa 0.75 m | Linear with Sill | 694.7 | 6.6 | 8.15 | 26.75 | 691.1 | 37.42 | 0.99 | 30.45 | Moderate |
| ECa 1.50 m | Linear with Sill | 694.7 | 6.6 | 26.89 | 87.74 | 605.5 | 353.48 | 0.99 | 30.65 | Moderate |
| Soybean 2019 | Linear with Sill | 750.0 | 12.8 | 0.38 | 0.60 | 746.7 | 0.02 | 0.91 | 63.71 | Moderate |
| Soybean 2021 | Gaussian | 696.6 | 12.7 | 0.19 | 0.31 | 691.5 | 0.01 | 0.94 | 62.21 | Moderate |
| Soybean 2022 | Linear with Sill | 696.2 | 12.7 | 0.18 | 0.26 | 691.1 | 0.00 | 0.91 | 69.96 | Moderate |
| Soybean 2023 | Exponential | 697.5 | 12.7 | 0.09 | 0.31 | 397.3 | 0.01 | 0.93 | 28.80 | Moderate |
| Soybean 2024 | Spherical | 692.9 | 12.7 | 0.17 | 0.36 | 639.3 | 0.00 | 0.99 | 45.88 | Moderate |
| Sorghum 2024 | Exponential | 696.1 | 12.7 | 0.04 | 2.65 | 585.9 | 0.17 | 0.99 | 1.36 | Strong |
| Soybean 2025 | Spherical | 696.7 | 12.7 | 0.27 | 0.63 | 592.3 | 0.02 | 0.97 | 43.35 | Moderate |
| Rainfed | ||||||||||
| Attribute | Model | Max_dist (m) | Lag (m) | C0 | C0 + C1 | Range (m) | RMSE | R2 | DSD (%) | DSD Class |
| ECa 0.75 m | Linear | 150.0 | 15.0 | 0.00 | 74.04 | 101.8 | 1601.95 | 0.90 | 0.00 | Strong |
| ECa 1.50 m | Spherical | 140.0 | 10.0 | 2.42 | 66.75 | 135.5 | 37.48 | 0.99 | 3.63 | Strong |
| Soybean 2019 | Exponential | 200.0 | 2.4 | 0.34 | 0.79 | 130.1 | 0.08 | 0.93 | 43.04 | Moderate |
| Soybean 2020 | Exponential | 200.0 | 2.0 | 0.14 | 0.65 | 53.3 | 0.09 | 0.91 | 20.71 | Strong |
| Sorghum 2020 | Linear | 170.0 | 6.7 | 0.93 | 1.36 | 98.0 | 0.06 | 0.95 | 68.39 | Moderate |
| Soybean 2021 | Linear | 241.4 | 2.0 | 0.63 | 1.00 | 127.8 | 0.68 | 0.88 | 62.70 | Moderate |
| Sorghum 2022 | Spherical | 160.0 | 6.9 | 0.18 | 0.38 | 158.6 | 0.00 | 0.98 | 46.19 | Moderate |
| Soybean 2023 | Exponential | 240.8 | 2.3 | 0.46 | 1.22 | 240.3 | 0.54 | 0.88 | 37.35 | Moderate |
| Irrigated | ||||||||
| Min | Mean | Max | SD | CV (%) | S | K | Var | |
| Slope | 0.7 | 2.6 | 17.2 | 1.2 | 47.3 | 3.95 | 30.55 | high |
| Elevation | 659.2 | 666.1 | 673.3 | 3.5 | 0.5 | −0.01 | −1.02 | low |
| ECa 1.50 m | 93.1 | 111.7 | 127.7 | 6.1 | 5.4 | −0.26 | −0.43 | low |
| ECa 0.75 m | 54.2 | 63.3 | 74.9 | 3.1 | 5.0 | −0.39 | 0.09 | low |
| Sorghum 2024 | 3.8 | 6.7 | 9.1 | 1.4 | 21.0 | 0.25 | −1.42 | moderate |
| Soybean 2025 | 6.4 | 8.1 | 9.4 | 0.5 | 6.3 | −0.11 | −0.17 | low |
| Soybean 2024 | 5.3 | 6.8 | 7.4 | 0.4 | 5.4 | −1.15 | 0.94 | low |
| Soybean 2023 | 5.2 | 6.5 | 7.7 | 0.4 | 6.5 | 0.33 | −0.13 | low |
| Soybean 2022 | 6.3 | 7.5 | 8.1 | 0.2 | 3.2 | −0.45 | 1.09 | low |
| Soybean 2021 | 6.7 | 7.9 | 8.6 | 0.3 | 3.5 | −0.89 | 0.86 | low |
| Soybean 2019 | 4.5 | 6.9 | 7.7 | 0.4 | 6.3 | −1.48 | 3.98 | low |
| Rainfed | ||||||||
| Min | Mean | Max | SD | CV (%) | S | K | Var | |
| Slope | 0.7 | 5.9 | 11.9 | 2.4 | 40.0 | −0.09 | −0.71 | high |
| Elevation | 663.1 | 672.4 | 683.0 | 4.2 | 0.6 | 0.28 | −0.88 | low |
| ECa 1.50 m | 35.8 | 55.3 | 76.8 | 10.8 | 19.5 | −0.29 | −1.28 | moderate |
| ECa 0.75 m | 22.2 | 40.4 | 60.4 | 10.9 | 26.9 | −0.10 | −1.23 | moderate |
| Sorghum 2022 | 2.5 | 3.6 | 4.7 | 0.4 | 12.0 | −0.12 | −0.45 | low |
| Sorghum 2020 | 5.6 | 8.2 | 10.9 | 0.9 | 10.7 | −0.14 | −0.08 | low |
| Soybean 2023 | 4.8 | 6.8 | 9.3 | 0.8 | 11.5 | 0.29 | −0.57 | low |
| Soybean 2021 | 4.6 | 8.1 | 10.1 | 0.8 | 9.4 | −0.96 | 1.09 | low |
| Soybean 2020 | 3.7 | 6.1 | 8.1 | 0.7 | 11.1 | −0.58 | −0.02 | low |
| Soybean 2019 | 3.7 | 5.6 | 7.4 | 0.6 | 11.6 | −0.24 | −0.61 | low |
| Variable | PC1—Irrigated (%) | PC2—Irrigated (%) | PC1—Rainfed (%) | PC2—Rainfed (%) |
|---|---|---|---|---|
| Elevation | 19.9 | 3.4 | 19.0 | 1.3 |
| ECa 1.50 m | 17.3 | 4.0 | 19.2 | 0.5 |
| ECa 0.75 m | 11.3 | 6.2 | 22.0 | 0.1 |
| Soybean 2024 | - | 29.2 | - | - |
| Soybean 2019 | - | 24.7 | - | 18.7 |
| Soybean 2020 | - | - | - | 26.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sterle, L.G.d.G.; Molin, J.P. Management Zones for Irrigated and Rainfed Grain Crops Based on Data Layer Integration. Agronomy 2025, 15, 1864. https://doi.org/10.3390/agronomy15081864
Sterle LGdG, Molin JP. Management Zones for Irrigated and Rainfed Grain Crops Based on Data Layer Integration. Agronomy. 2025; 15(8):1864. https://doi.org/10.3390/agronomy15081864
Chicago/Turabian StyleSterle, Luiz Gustavo de Góes, and José Paulo Molin. 2025. "Management Zones for Irrigated and Rainfed Grain Crops Based on Data Layer Integration" Agronomy 15, no. 8: 1864. https://doi.org/10.3390/agronomy15081864
APA StyleSterle, L. G. d. G., & Molin, J. P. (2025). Management Zones for Irrigated and Rainfed Grain Crops Based on Data Layer Integration. Agronomy, 15(8), 1864. https://doi.org/10.3390/agronomy15081864










