Soil Water-Soluble Ion Inversion via Hyperspectral Data Reconstruction and Multi-Scale Attention Mechanism: A Remote Sensing Case Study of Farmland Saline–Alkali Lands
Abstract
1. Introduction
1.1. Significance of Soil Salinization Monitoring
1.2. Overview of Existing Monitoring Methods
1.3. Capabilities and Limitations of Remote Sensing and Ground-Based Hyperspectral Data
1.4. Hyperspectral Reconstruction and Deep Learning Advances
1.5. Research Objectives and Framework
- Reconstructing ground-based hyperspectral data from existing Landsat 8 multispectral data to improve the accuracy and reduce the cost of high-precision soil salinity monitoring;
- The multi-scale fusion mechanism of the MSATransformer model is used to optimize the processing of hyperspectral data and further improve the accuracy of soil water-soluble ion concentration inversion. It is expected to provide a low-cost and high-precision technical solution for soil salinization monitoring and help precision agriculture and environmental management.
2. Materials and Methods
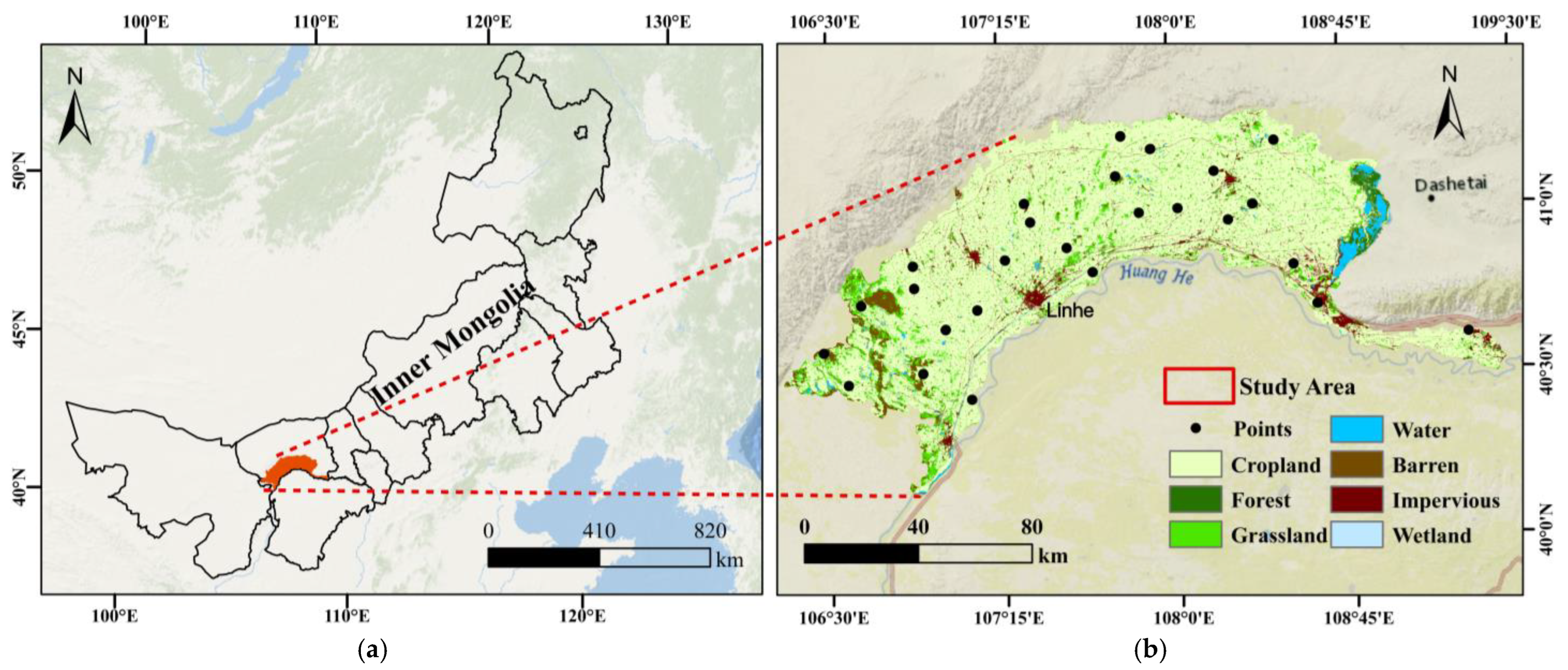
2.1. Research Area Overview
2.2. Data Collection and Processing
2.2.1. On-Site Hyperspectral Data and Soil Sample Collection
2.2.2. Landsat 8 Multispectral Data Preprocessing
2.2.3. Data Collection of Soil Water-Soluble Ions
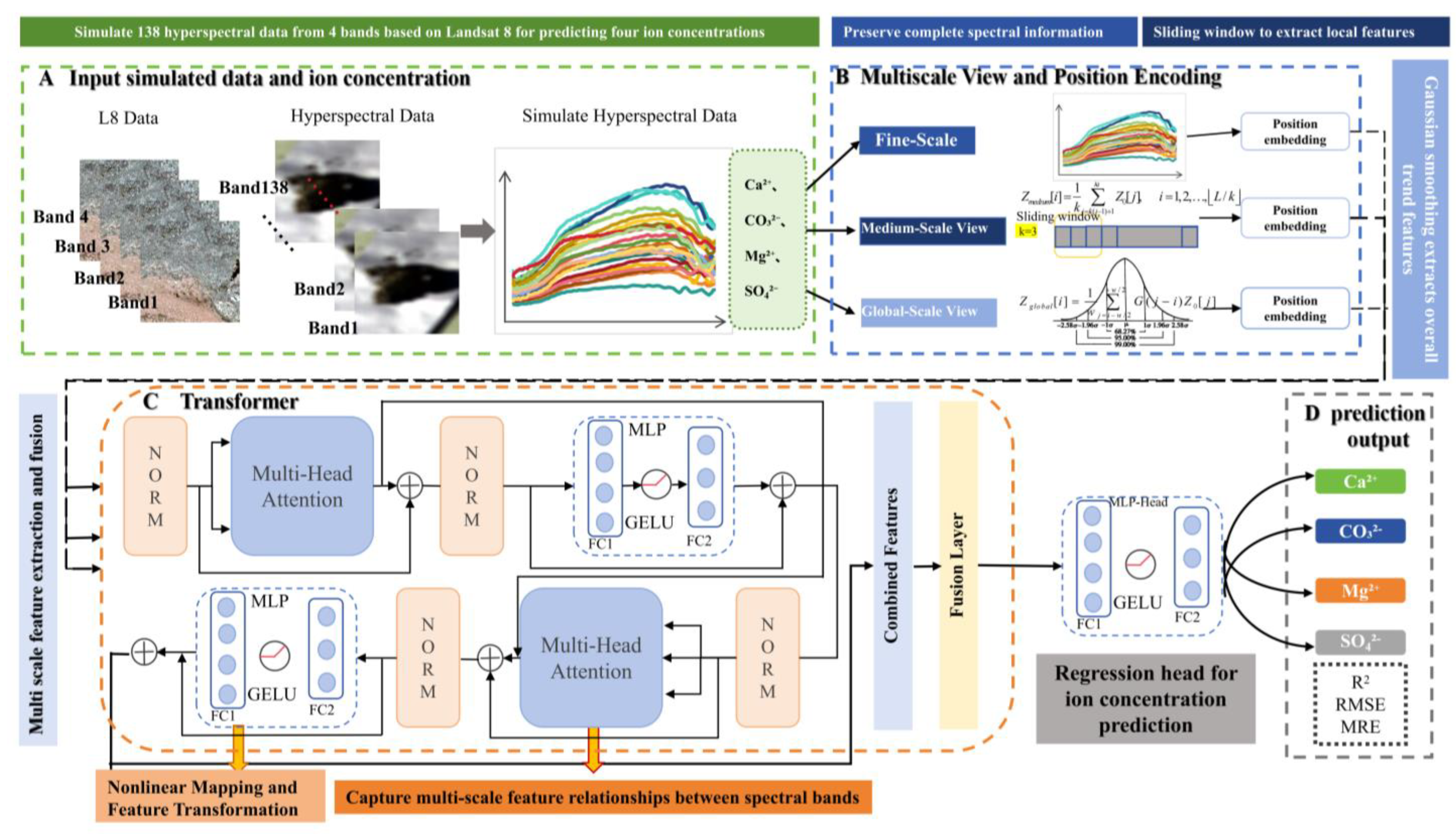
2.3. Hyperspectral Data Reconstruction Method
2.4. Soil Water-Soluble Ion Inversion Model MSATransformer
- Fine-Scale View: This view retains the original embedded sequence , i.e.,
- Medium-Scale View: This view is generated by performing sliding window down-sampling on , where the window size is k. It is defined as shown in Equation (4):where k is the window size (in this study, k = 3), and the downsampled dimension after this operation is .
- Global-Scale View: The global view is obtained by applying Gaussian smoothing to to capture the global features. It is defined as shown in Equation (5):where represents the Gaussian kernel weights, and is the window size (in this study, = 7).
2.5. Model Evaluation
3. Results
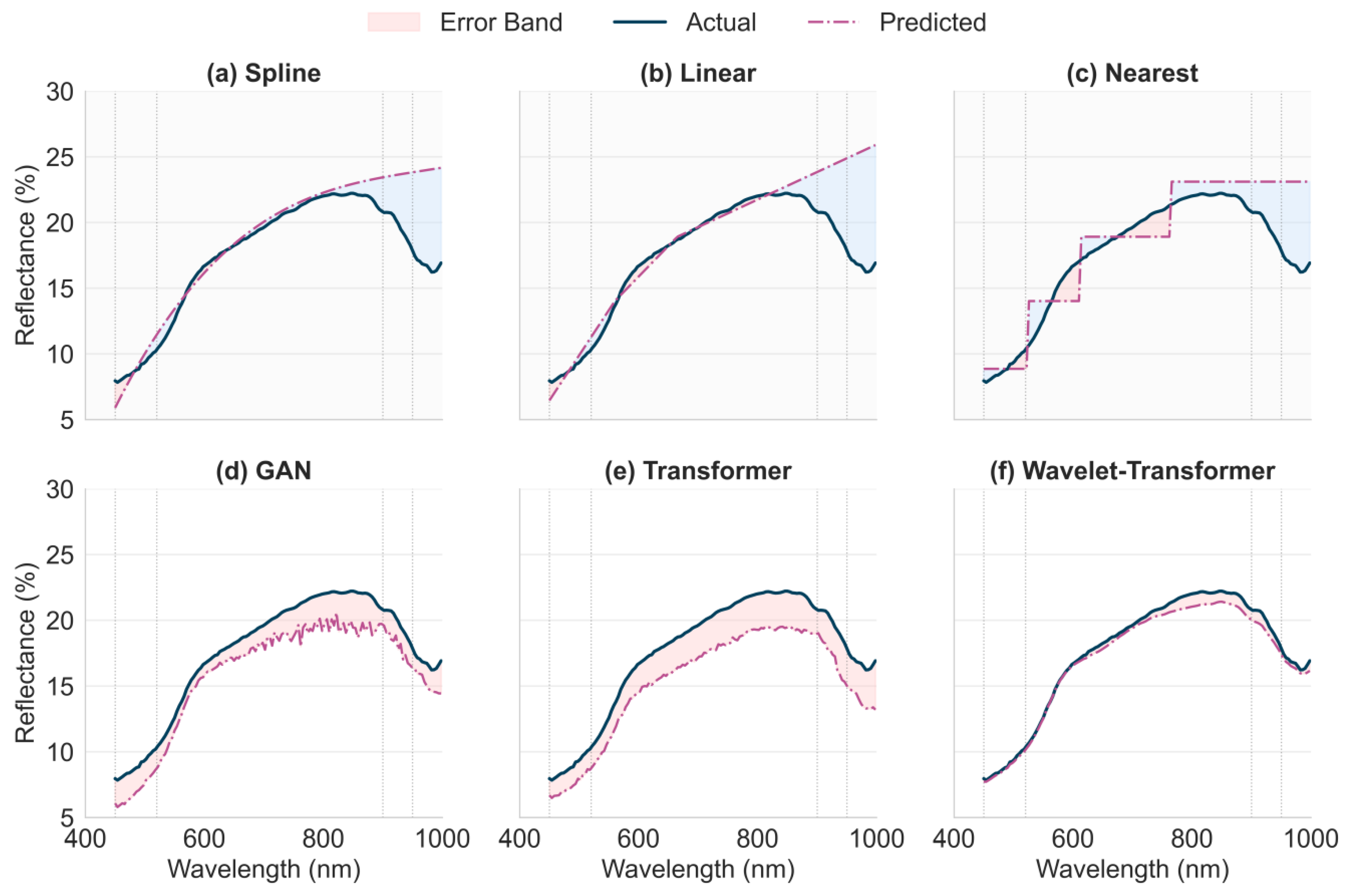
3.1. Comparison of Reconstructed Ground-Based Hyperspectral Data with Measured Hyperspectral Data
3.2. Inversion Accuracy Analysis of Water-Soluble Ions in Agricultural Soils
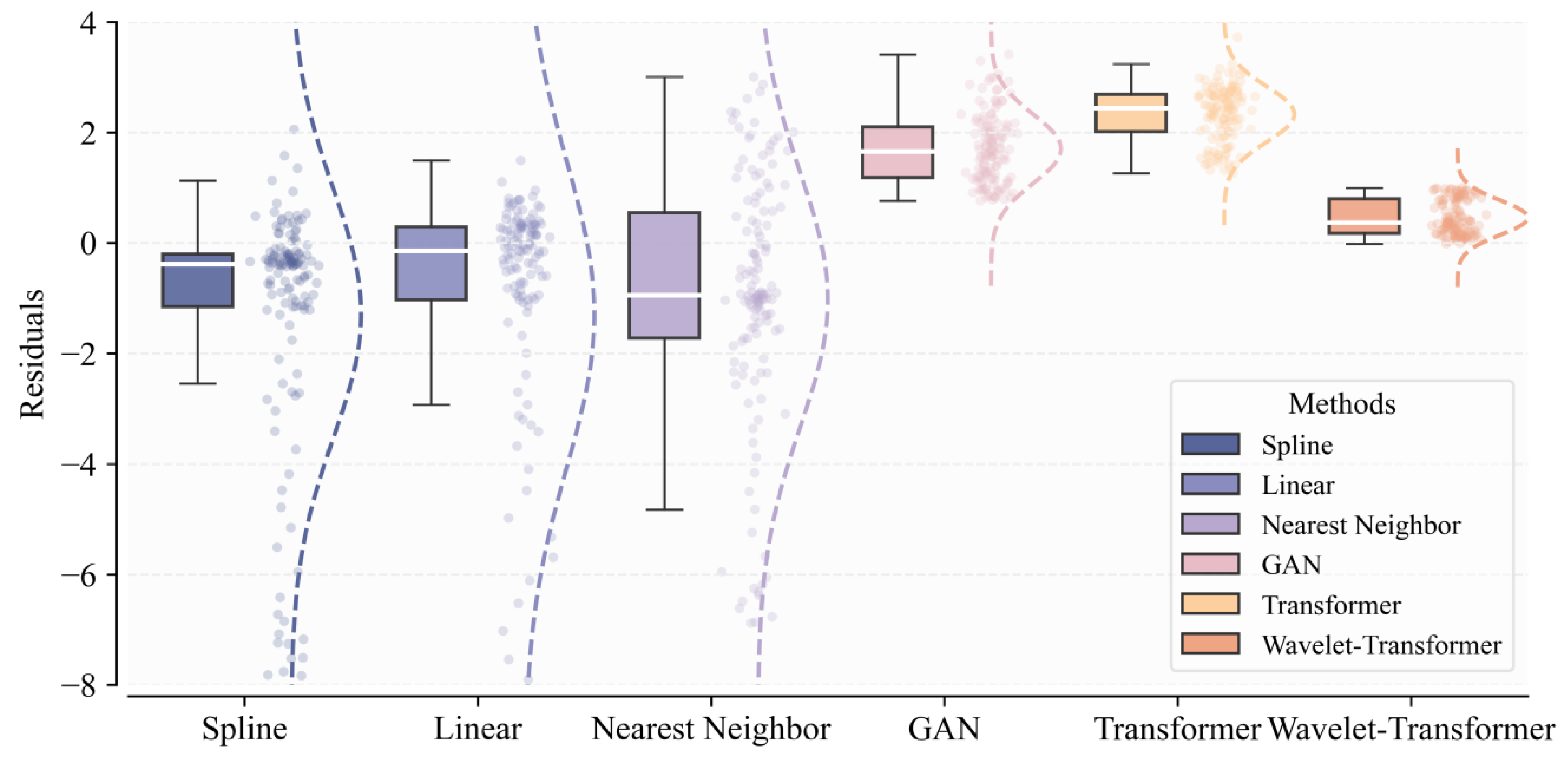
3.3. Residual Structure Analysis of Water-Soluble Ion Inversion Based on MSI and HSI
3.4. Comparative Analysis of Models
4. Discussion
4.1. Comparison of Reconstructed Hyperspectral Data with Real Data
4.2. Model Comparison
4.3. Soil Water-Soluble Ion Inversion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| XGBoost | eXtreme Gradient Boosting |
| RMSE | Root Mean Square Error |
| PLS | Partial least squares |
| CNN | Convolutional Neural Networks |
| GAN | Generative Adversarial Networks |
| PLSR | Partial least squares regression |
| BP | Back Propagation |
| RSD | Relative Standard Deviation |
| MSATransformer | Multi-Head Self-Attention Transformer |
| MSE | Mean Squared Error |
| MLP | Multilayer perceptron |
| GPS | Global Positioning System |
| RF | Random Forest |
References
- Muller, S.J.; Van Niekerk, A. Identification of WorldView-2 Spectral and Spatial Factors in Detecting Salt Accumulation in Cultivated Fields. Geoderma 2016, 273, 1–11. [Google Scholar] [CrossRef]
- Li, T.; Liu, T.; Wang, Y.; Li, X.; Gu, Y. Spectral Reconstruction Network From Multispectral Images to Hyperspectral Images: A Multitemporal Case. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Zhang, Z.; Chen, H.; Li, X.; Wang, M.; Chai, H. Quantitatively Estimating Main Soil Water-Soluble Salt Ions Content Based on Visible-near Infrared Wavelength Selected Using GC, SR and VIP. PeerJ 2019, 7, e6310. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Ma, S.; Liu, T.; Yao, S.; Li, S.; Gao, Y. Integrating UAV-Based Multispectral Data and Transfer Learning for Soil Moisture Prediction in the Black Soil Region of Northeast China. Agronomy 2025, 15, 759. [Google Scholar] [CrossRef]
- Jiang, C.; Zhao, J.; Li, G. Integration of Vis–NIR Spectroscopy and Machine Learning Techniques to Predict Eight Soil Parameters in Alpine Regions. Agronomy 2023, 13, 2816. [Google Scholar] [CrossRef]
- Guo, H.; Wu, F.; Yang, K.; Yang, Z.; Chen, Z.; Chen, D.; Xiao, R. Sentinel-2 Multispectral Satellite Remote Sensing Retrieval of Soil Cu Content Changes at Different pH Levels. Agronomy 2024, 14, 2182. [Google Scholar] [CrossRef]
- Nadporozhskaya, M.; Kovsh, N.; Paolesse, R.; Lvova, L. Recent Advances in Chemical Sensors for Soil Analysis: A Review. Chemosensors 2022, 10, 35. [Google Scholar] [CrossRef]
- Singh, H.; Northup, B.K.; Rice, C.W.; Prasad, P.V.V. Biochar Applications Influence Soil Physical and Chemical Properties, Microbial Diversity, and Crop Productivity: A Meta-Analysis. Biochar 2022, 4, 8. [Google Scholar] [CrossRef]
- Pan, Z.; Tong, Y.; Hou, J.; Zheng, J.; Kang, Y.; Wang, Y.; Cao, C. Hole Irrigation Process Simulation Using a Soil Water Dynamical Model with Parameter Inversion Method. Agric. Water Manag. 2021, 245, 106542. [Google Scholar] [CrossRef]
- Nevison, C.; Hu, L.; Ogle, S.M.; Keyser, A.; Lan, X.; McKain, K. Midwestern N2O Emissions Linked at Regional Scales to Remotely Sensed Soil Moisture in a North American Inversion. Glob. Biogeochem. Cycles 2025, 39, e2024GB008418. [Google Scholar] [CrossRef]
- Ranjbar, S.; Zarei, A.; Hasanlou, M.; Akhoondzadeh, M.; Amini, J.; Amani, M. Machine Learning Inversion Approach for Soil Parameters Estimation over Vegetated Agricultural Areas Using a Combination of Water Cloud Model and Calibrated Integral Equation Model. J. Appl. Rem. Sens. 2021, 15, 018503. [Google Scholar] [CrossRef]
- Dragonetti, G.; Farzamian, M.; Basile, A.; Monteiro Santos, F.; Coppola, A. In Situ Estimation of Soil Hydraulic and Hydrodispersive Properties by Inversion of Electromagnetic Induction Measurements and Soil Hydrological Modeling. Hydrol. Earth Syst. Sci. 2022, 26, 5119–5136. [Google Scholar] [CrossRef]
- Cao, Q.; Yang, G.; Duan, D.; Chen, L.; Wang, F.; Xu, B.; Zhao, C.; Niu, F. Combining Multispectral and Hyperspectral Data to Estimate Nitrogen Status of Tea Plants (Camellia sinensis (L.) O. Kuntze) under Field Conditions. Comput. Electron. Agric. 2022, 198, 107084. [Google Scholar] [CrossRef]
- Lu, H.; Qiao, D.; Li, Y.; Wu, S.; Deng, L. Fusion of China ZY-1 02D Hyperspectral Data and Multispectral Data: Which Methods Should Be Used? Remote Sens. 2021, 13, 2354. [Google Scholar] [CrossRef]
- Talone, M.; Zibordi, G.; Pitarch, J. On the Application of AERONET-OC Multispectral Data to Assess Satellite-Derived Hyperspectral Rrs. IEEE Geosci. Remote Sens. Lett. 2024, 21, 1–5. [Google Scholar] [CrossRef]
- Vaglio Laurin, G.; Puletti, N.; Hawthorne, W.; Liesenberg, V.; Corona, P.; Papale, D.; Chen, Q.; Valentini, R. Discrimination of Tropical Forest Types, Dominant Species, and Mapping of Functional Guilds by Hyperspectral and Simulated Multispectral Sentinel-2 Data. Remote Sens. Environ. 2016, 176, 163–176. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, B.; Xu, W.; Liu, S.; Lan, Y.; Zhang, L. Investigating the Impact of Hyperspectral Reconstruction Techniques on the Quantitative Inversion of Rice Physiological Parameters: A Case Study Using the MST++ Model. J. Integr. Agric. 2024, 24, 2540–2557. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, F.; Hu, G.; Ganjurjav, H.; Wu, R.; Gao, Q. Evaluation of Machine Learning Models for Estimating Grassland Pasture Yield Using Landsat-8 Imagery. Agronomy 2024, 14, 2984. [Google Scholar] [CrossRef]
- Datta, D.; Paul, M.; Murshed, M.; Teng, S.W.; Schmidtke, L. Comparative Analysis of Machine and Deep Learning Models for Soil Properties Prediction from Hyperspectral Visual Band. Environments 2023, 10, 77. [Google Scholar] [CrossRef]
- Zhang, D.; Su, X.; Cui, Z. Assessment of Land Degradation in Different Land Uses by Modeling Soil Salinity and Soil Erodibility Coupled Vis-NIR Spectroscopy and Machine Learning Model. Infrared Phys. Technol. 2025, 148, 105835. [Google Scholar] [CrossRef]
- Zhao, S.; Ayoubi, S.; Mousavi, S.R.; Mireei, S.A.; Shahpouri, F.; Wu, S.; Chen, C.; Zhao, Z.; Tian, C. Integrating Proximal Soil Sensing Data and Environmental Variables to Enhance the Prediction Accuracy for Soil Salinity and Sodicity in a Region of Xinjiang Province, China. J. Environ. Manag. 2024, 364, 121311. [Google Scholar] [CrossRef] [PubMed]
- Chlouveraki, E.; Katsenios, N.; Efthimiadou, A.; Lazarou, E.; Kounani, K.; Papakonstantinou, E.; Vlachakis, D.; Kasimati, A.; Zafeiriou, I.; Espejo-Garcia, B.; et al. Estimation of Soil Properties Using Hyperspectral Imaging and Machine Learning. Smart Agric. Technol. 2025, 10, 100790. [Google Scholar] [CrossRef]
- Bouslihim, Y.; Bouasria, A. Potential of EnMAP Hyperspectral Imagery for Regional-Scale Soil Organic Matter Mapping. Remote Sens. 2025, 17, 1600. [Google Scholar] [CrossRef]
- Vanguri, R.; Laneve, G.; Hościło, A. Mapping Forest Tree Species and Its Biodiversity Using EnMAP Hyperspectral Data along with Sentinel-2 Temporal Data: An Approach of Tree Species Classification and Diversity Indices. Ecol. Indic. 2024, 167, 112671. [Google Scholar] [CrossRef]
- Rossi, F.; Mirzaei, S.; Marrone, L.; Misbah, K.; Tricomi, A.; Casa, R.; Pignatti, S.; Laneve, G. Agricultural Soil Properties Mapping from PRISMA and EnMap Data: Exploiting Multitemporal Bare Soil Approaches. In Proceedings of the 13th EARSeL Workshop on Imaging Spectroscopy, Valencia, Spain, 16–18 April 2024. [Google Scholar] [CrossRef]
- Farzamian, M.; Bouksila, F.; Paz, A.M.; Santos, F.M.; Zemni, N.; Slama, F.; Ben Slimane, A.; Selim, T.; Triantafilis, J. Landscape-Scale Mapping of Soil Salinity with Multi-Height Electromagnetic Induction and Quasi-3d Inversion in Saharan Oasis, Tunisia. Agric. Water Manag. 2023, 284, 108330. [Google Scholar] [CrossRef]
- Badola, A.; Panda, S.K.; Roberts, D.A.; Waigl, C.F.; Bhatt, U.S.; Smith, C.W.; Jandt, R.R. Hyperspectral Data Simulation (Sentinel-2 to AVIRIS-NG) for Improved Wildfire Fuel Mapping, Boreal Alaska. Remote Sens. 2021, 13, 1693. [Google Scholar] [CrossRef]
- Wang, Y.; Yuan, F.; Cammarano, D.; Liu, X.; Tian, Y.; Zhu, Y.; Cao, W.; Cao, Q. Integrating Machine Learning with Spatial Analysis for Enhanced Soil Interpolation: Balancing Accuracy and Visualization. Smart Agric. Technol. 2025, 11, 101032. [Google Scholar] [CrossRef]
- Deng, L.; Sun, J.; Chen, Y.; Lu, H.; Duan, F.; Zhu, L.; Fan, T. M2H-Net: A Reconstruction Method For Hyperspectral Remotely Sensed Imagery. ISPRS J. Photogramm. Remote Sens. 2021, 173, 323–348. [Google Scholar] [CrossRef]
- Paul, S.; Nagesh Kumar, D. Transformation of Multispectral Data to Quasi-Hyperspectral Data Using Convolutional Neural Network Regression. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3352–3368. [Google Scholar] [CrossRef]
- Kaur, H.; Pham, N.; Fomel, S. Seismic Data Interpolation Using Deep Learning with Generative Adversarial Networks. Geophys. Prospect. 2021, 69, 307–326. [Google Scholar] [CrossRef]
- Lins, H.A.; Freitas Souza, M.D.; Batista, L.P.; Rodrigues, L.L.L.D.S.; Da Silva, F.D.; Fernandes, B.C.C.; De Melo, S.B.; Das Chagas, P.S.F.; Silva, D.V. Artificial Intelligence for Herbicide Recommendation: Case Study for the Use of Clomazone in Brazilian Soils. Smart Agric. Technol. 2024, 9, 100699. [Google Scholar] [CrossRef]
- Peng, J.; Ji, W.; Ma, Z.; Li, S.; Chen, S.; Zhou, L.; Shi, Z. Predicting Total Dissolved Salts and Soluble Ion Concentrations in Agricultural Soils Using Portable Visible Near-Infrared and Mid-Infrared Spectrometers. Biosyst. Eng. 2016, 152, 94–103. [Google Scholar] [CrossRef]
- Srivastava, R.; Sethi, M.; Yadav, R.K.; Bundela, D.S.; Singh, M.; Chattaraj, S.; Singh, S.K.; Nasre, R.A.; Bishnoi, S.R.; Dhale, S.; et al. Visible-Near Infrared Reflectance Spectroscopy for Rapid Characterization of Salt-Affected Soil in the Indo-Gangetic Plains of Haryana, India. J. Indian Soc. Remote Sens. 2017, 45, 307–315. [Google Scholar] [CrossRef]
- Shao, W.; Guan, Q.; Tan, Z.; Luo, H.; Li, H.; Sun, Y.; Ma, Y. Application of BP—ANN Model in Evaluation of Soil Quality in the Arid Area, Northwest China. Soil Tillage Res. 2021, 208, 104907. [Google Scholar] [CrossRef]
- Kashi, H.; Emamgholizadeh, S.; Ghorbani, H. Estimation of Soil Infiltration and Cation Exchange Capacity Based on Multiple Regression, ANN (RBF, MLP), and ANFIS Models. Commun. Soil Sci. Plant Anal. 2014, 45, 1195–1213. [Google Scholar] [CrossRef]
- Yang, Y.; Li, H.; Sun, M.; Liu, X.; Cao, L. A Study on Hyperspectral Soil Moisture Content Prediction by Incorporating a Hybrid Neural Network into Stacking Ensemble Learning. Agronomy 2024, 14, 2054. [Google Scholar] [CrossRef]
- Zheng, W.; Zheng, K.; Gao, L.; Zhangzhong, L.; Lan, R.; Xu, L.; Yu, J. GRU–Transformer: A Novel Hybrid Model for Predicting Soil Moisture Content in Root Zones. Agronomy 2024, 14, 432. [Google Scholar] [CrossRef]
- Wang, G.; Xu, B.; Tang, P.; Shi, H.; Tian, D.; Zhang, C.; Ren, J.; Li, Z. Modeling and Evaluating Soil Salt and Water Transport in a Cultivated Land–Wasteland–Lake System of Hetao, Yellow River Basin’s Upper Reaches. Sustainability 2022, 14, 14410. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, J.; Tang, Y. Estimation and Inversion of Soil Heavy Metal Arsenic (As) Based on UAV Hyperspectral Platform. Microchem. J. 2024, 207, 112027. [Google Scholar] [CrossRef]
- Xing, Y.; Song, Q.; Cheng, G. Benefit of Interpolation in Nearest Neighbor Algorithms. SIAM J. Math. Data Sci. 2022, 4, 935–956. [Google Scholar] [CrossRef]
- Adiban, M.; Siniscalchi, S.M.; Salvi, G. A Step-by-Step Training Method for Multi Generator GANs with Application to Anomaly Detection and Cybersecurity. Neurocomputing 2023, 537, 296–308. [Google Scholar] [CrossRef]
- Ahmad, Z.; Jaffri, Z.U.A.; Chen, M.; Bao, S. Understanding GANs: Fundamentals, Variants, Training Challenges, Applications, and Open Problems. Multimed Tools Appl. 2024, 84, 10347–10423. [Google Scholar] [CrossRef]
- Chokwitthaya, C.; Collier, E.; Zhu, Y.; Mukhopadhyay, S. Improving Prediction Accuracy in Building Performance Models Using Generative Adversarial Networks (GANs). In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; IEEE: Piscataway, NJ, USA; pp. 1–9. [Google Scholar]
- Pothapragada, I.S.; Sujatha, R. GANs for Data Augmentation with Stacked CNN Models and XAI for Interpretable Maize Yield Prediction. Smart Agric. Technol. 2025, 11, 100992. [Google Scholar] [CrossRef]
- Gao, Y.; Ruan, Y. Interpretable Deep Learning Model for Building Energy Consumption Prediction Based on Attention Mechanism. Energy Build. 2021, 252, 111379. [Google Scholar] [CrossRef]
- Cao, L.; Sun, M.; Yang, Z.; Jiang, D.; Yin, D.; Duan, Y. A Novel Transformer-CNN Approach for Predicting Soil Properties from LUCAS Vis-NIR Spectral Data. Agronomy 2024, 14, 1998. [Google Scholar] [CrossRef]
- Panuntun, I.A.; Jamaluddin, I.; Chen, Y.-N.; Lai, S.-N.; Fan, K.-C. LinkNet-Spectral-Spatial-Temporal Transformer Based on Few-Shot Learning for Mangrove Loss Detection with Small Dataset. Remote Sens. 2024, 16, 1078. [Google Scholar] [CrossRef]
- Afzaal, H.; Rude, D.; Farooque, A.A.; Randhawa, G.S.; Schumann, A.W.; Krouglicof, N. Improved Crop Row Detection by Employing Attention-Based Vision Transformers and Convolutional Neural Networks with Integrated Depth Modeling for Precise Spatial Accuracy. Smart Agric. Technol. 2025, 11, 100934. [Google Scholar] [CrossRef]
- Jiang, W.; Liu, C.; He, K. Intra-Task Mutual Attention Based Vision Transformer for Few-Shot Learning. IEEE Trans. Circuits Syst. Video Technol. 2025, 1. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, S.; Chen, J.; Chen, B.; Wang, X.; Hao, D.; Sun, L. Rice Yield Prediction and Model Interpretation Based on Satellite and Climatic Indicators Using a Transformer Method. Remote Sens. 2022, 14, 5045. [Google Scholar] [CrossRef]
- Wang, Y.; Zha, Y. Comparison of Transformer, LSTM and Coupled Algorithms for Soil Moisture Prediction in Shallow-Groundwater-Level Areas with Interpretability Analysis. Agric. Water Manag. 2024, 305, 109120. [Google Scholar] [CrossRef]
- Chen, J.; Xu, K.; Ning, Y.; Jiang, L.; Xu, Z. CRTED: Few-Shot Object Detection via Correlation-RPN and Transformer Encoder–Decoder. Electronics 2024, 13, 1856. [Google Scholar] [CrossRef]
- Wu, Z.; Liu, Z.; Lin, J.; Lin, Y.; Han, S. Lite Transformer with Long-Short Range Attention 2020. arXiv 2020, arXiv:2004.11886. [Google Scholar]
- Zheng, W.; Lu, S.; Yang, Y.; Yin, Z.; Yin, L. Lightweight Transformer Image Feature Extraction Network. PeerJ Comput. Sci. 2024, 10, e1755. [Google Scholar] [CrossRef] [PubMed]
- Mehta, S.; Ghazvininejad, M.; Iyer, S.; Zettlemoyer, L.; Hajishirzi, H. DeLighT: Deep and Light-Weight Transformer 2021. arXiv 2008, arXiv:2008.00623. [Google Scholar]
- Li, Q.; Guo, X.; Chen, L.; Li, Y.; Yuan, D.; Dai, B.; Wang, S. Investigating the Spectral Characteristic and Humification Degree of Dissolved Organic Matter in Saline-Alkali Soil Using Spectroscopic Techniques. Front. Earth Sci. 2017, 11, 76–84. [Google Scholar] [CrossRef]
- Tuv, E. Feature Selection with Ensembles, Artificial Variables, and Redundancy Elimination. J. Mach. Learn. Res. 2009, 10, 1341–1366. [Google Scholar]
- Hu, Y.; Deng, X.; Lan, Y.; Chen, X.; Long, Y.; Liu, C. Detection of Rice Pests Based on Self-Attention Mechanism and Multi-Scale Feature Fusion. Insects 2023, 14, 280. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Wang, S.; Wang, B.; Zhang, X.; Wang, X.; Zhao, Y. Enhanced Window-Based Self-Attention with Global and Multi-Scale Representations for Remote Sensing Image Super-Resolution. Remote Sens. 2024, 16, 2837. [Google Scholar] [CrossRef]
- Kara, A. Multi-Scale Deep Neural Network Approach with Attention Mechanism for Remaining Useful Life Estimation. Comput. Ind. Eng. 2022, 169, 108211. [Google Scholar] [CrossRef]
- Han, X.; Yu, J.; Luo, J.; Sun, W. Hyperspectral and Multispectral Image Fusion Using Cluster-Based Multi-Branch BP Neural Networks. Remote Sens. 2019, 11, 1173. [Google Scholar] [CrossRef]
- Liang, Y. Research on Soil Moisture Inversion Method Based on GA-BP Neural Network Model. Int. J. Remote Sens. 2019, 40, 2087–2103. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, X.; Yang, Y.; Cao, J.; Yin, L.; Zhang, B. Enhancing Soil Organic Carbon Prediction in Coastal Farmlands Using Multi-Source Remote Sensing Data and Machine Learning. Smart Agric. Technol. 2025, 11, 101059. [Google Scholar] [CrossRef]
- Mba, P.C.; Busoye, O.M.; Ajayi, J.T.; Njoku, J.N.; Nwakanma, C.I.; Asem-Hiablie, S.; Mallipeddi, R.; Park, T.; Uyeh, D.D. Estimation of Physico-Chemical Properties of Soil Using Machine Learning. Smart Agric. Technol. 2024, 9, 100679. [Google Scholar] [CrossRef]
- Qi, C.; Zhou, N.; Hu, T.; Wu, M.; Chen, Q.; Wang, H.; Zhang, K.; Lin, Z. Prediction of Copper Contamination in Soil across EU Using Spectroscopy and Machine Learning: Handling Class Imbalance Problem. Smart Agric. Technol. 2025, 10, 100728. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, L.; Zhao, J.; Hu, X.; Ma, X. Application of Hyperspectral Technology Combined With Bat Algorithm-AdaBoost Model in Field Soil Nutrient Prediction. IEEE Access 2022, 10, 100286–100299. [Google Scholar] [CrossRef]
- Zou, P.; Yang, J.; Fu, J.; Liu, G.; Li, D. Artificial Neural Network and Time Series Models for Predicting Soil Salt and Water Content. Agric. Water Manag. 2010, 97, 2009–2019. [Google Scholar] [CrossRef]
- Yang, G.; Tang, H.; Ding, M.; Sebe, N.; Ricci, E. Transformer-Based Attention Networks for Continuous Pixel-Wise Prediction. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; IEEE: New York, NY, USA; pp. 16249–16259. [Google Scholar]
- Hailu, B.; Mehari, H. Impacts of Soil Salinity/Sodicity on Soil-Water Relations and Plant Growth in Dry Land Areas: A Review. J. Nat. Sci. Res 2021, 12, 3. [Google Scholar] [CrossRef]
- Lao, C.; Chen, J.; Zhang, Z.; Chen, Y.; Ma, Y.; Chen, H.; Gu, X.; Ning, J.; Jin, J.; Li, X. Predicting the Contents of Soil Salt and Major Water-Soluble Ions with Fractional-Order Derivative Spectral Indices and Variable Selection. Comput. Electron. Agric. 2021, 182, 106031. [Google Scholar] [CrossRef]
- Liu, R.; Jia, K.; Li, H.; Zhang, J. Using Unmanned Aerial Vehicle Data to Improve Satellite Inversion: A Study on Soil Salinity. Land 2024, 13, 1438. [Google Scholar] [CrossRef]
- Song, Y.; Gao, M.; Wang, J. Inversion of Salinization in Multilayer Soils and Prediction of Water Demand for Salt Regulation in Coastal Region. Agric. Water Manag. 2024, 301, 108970. [Google Scholar] [CrossRef]
- Zou, Z.; Wang, Q.; Wu, Q.; Li, M.; Zhen, J.; Yuan, D.; Zhou, M.; Xu, C.; Wang, Y.; Zhao, Y.; et al. Inversion of Heavy Metal Content in Soil Using Hyperspectral Characteristic Bands-Based Machine Learning Method. J. Environ. Manag. 2024, 355, 120503. [Google Scholar] [CrossRef] [PubMed]

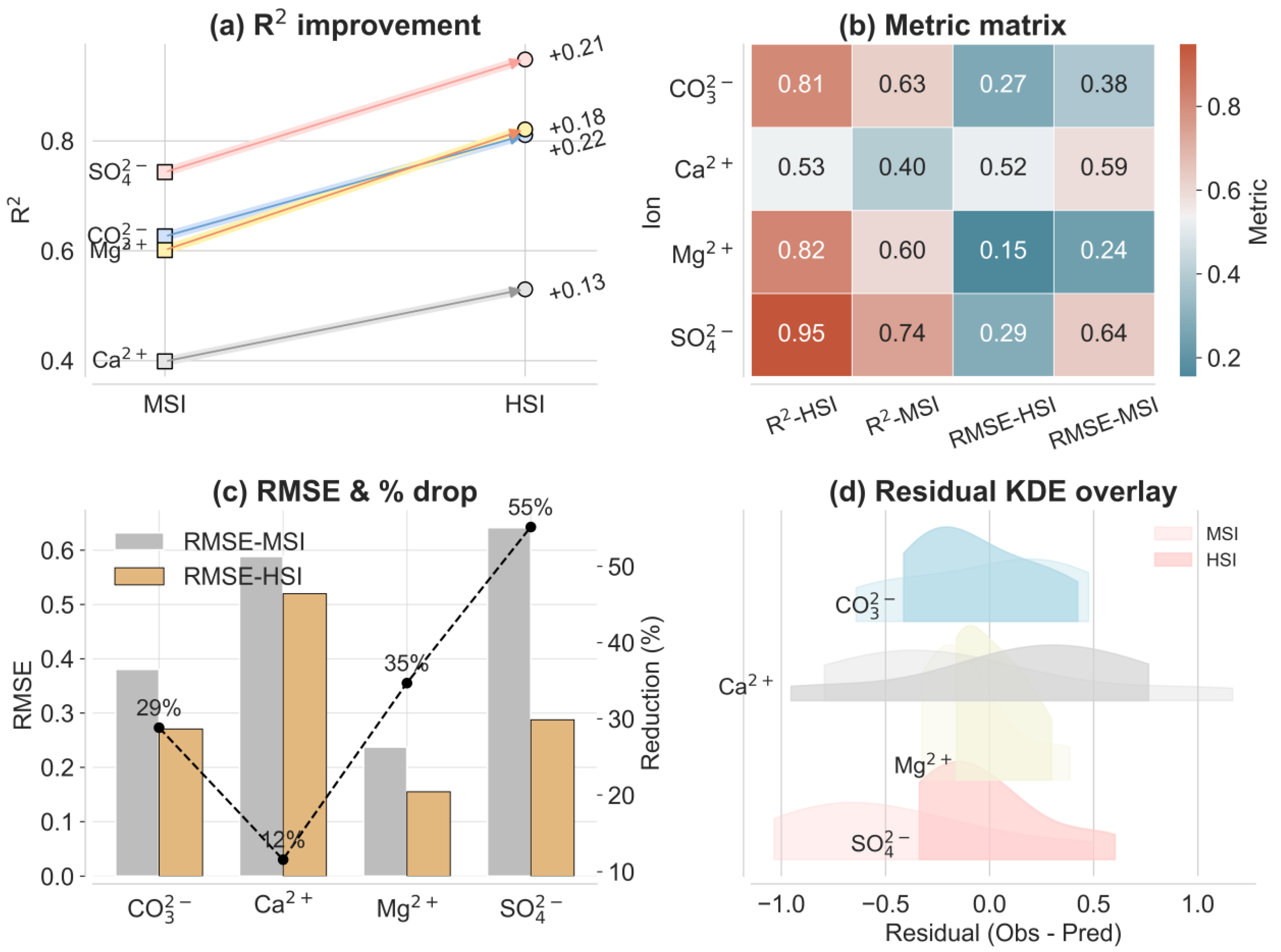
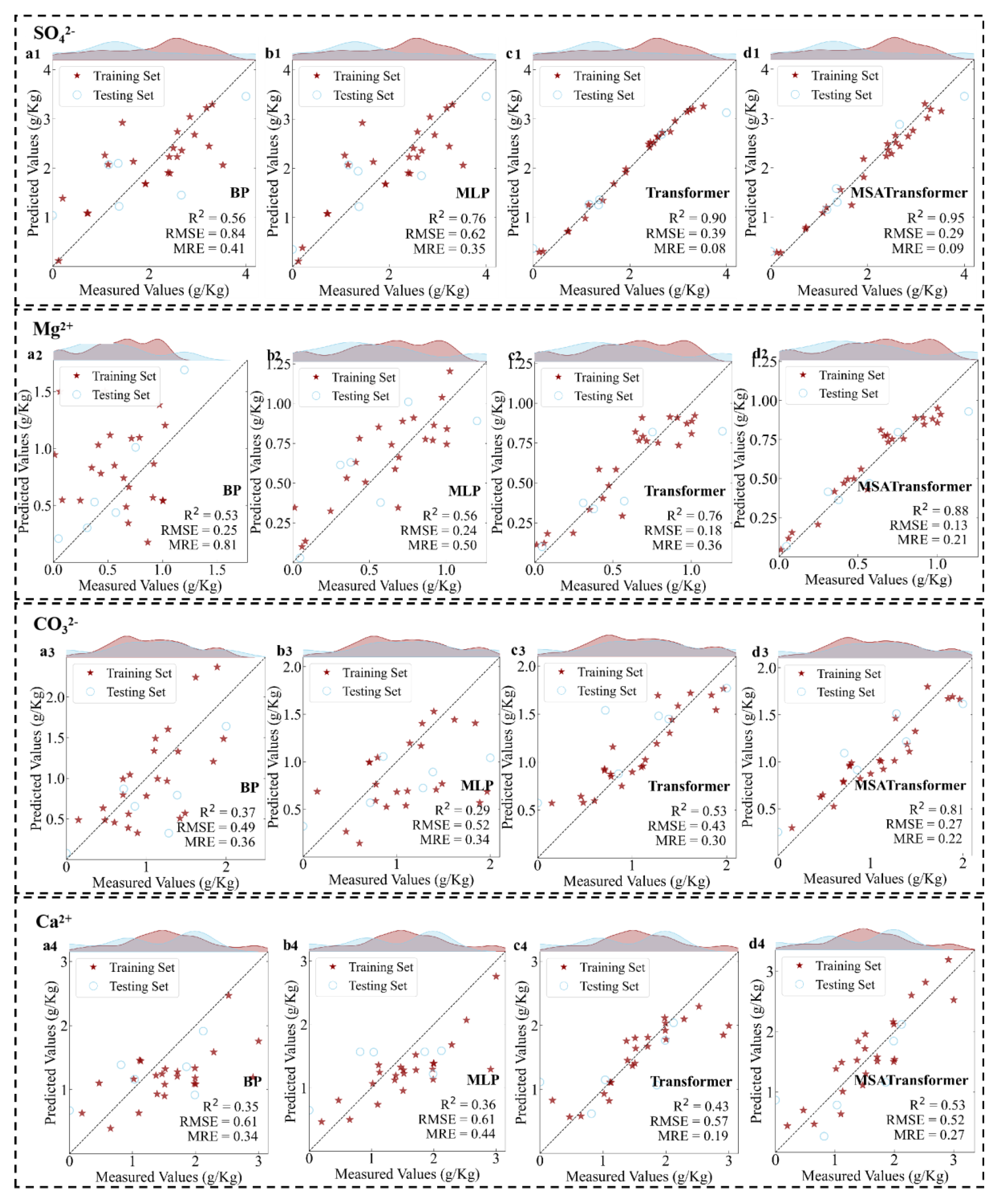
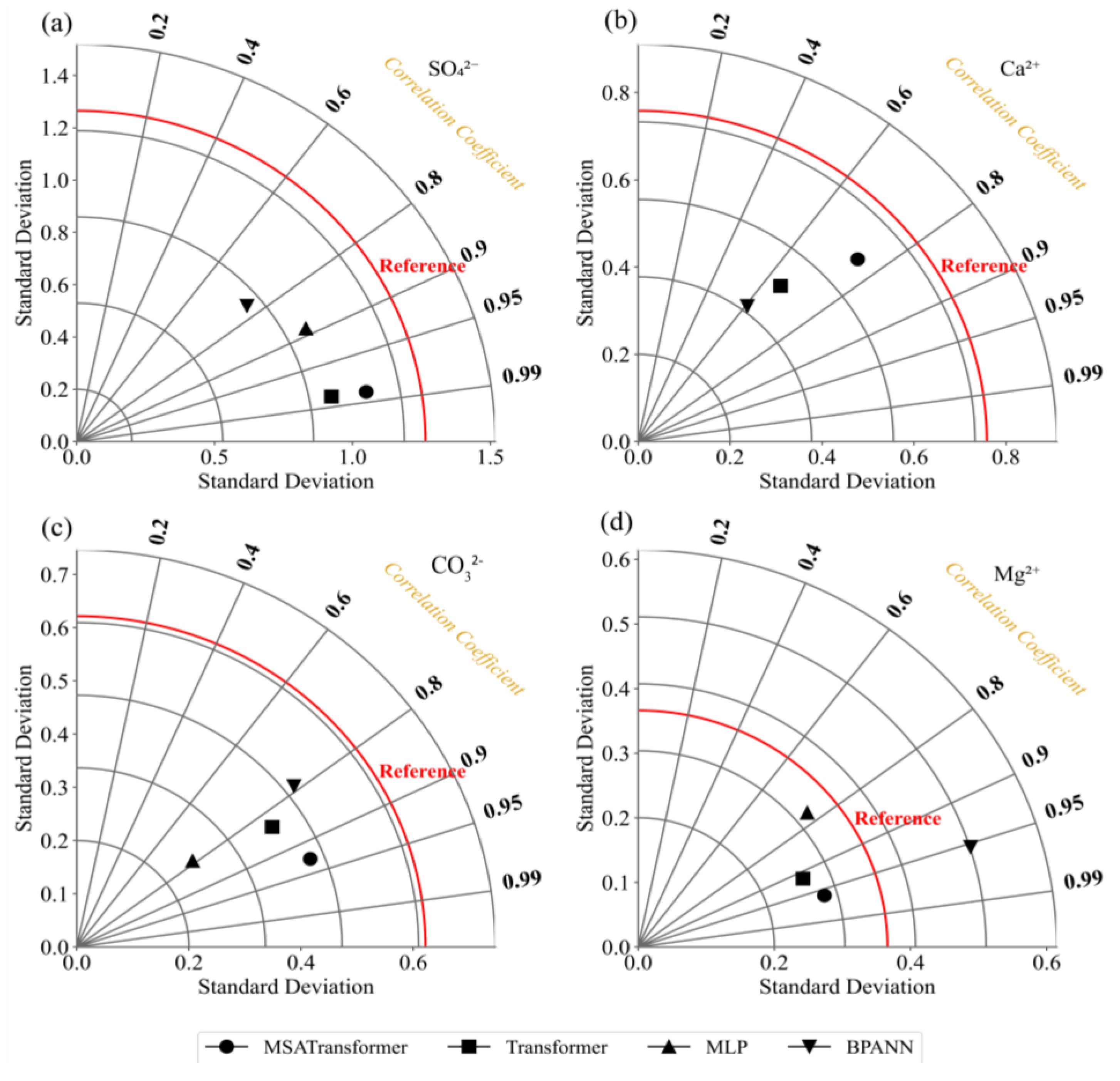
| Ions | Mean (g/kg) | Median (g/kg) | SD (g/kg) | MAD (g/kg) | Best-Fit Distribution (Shape, Scale) | Skewness | Shapiro–Wilk p |
|---|---|---|---|---|---|---|---|
| Ca2+ | 1.53 | 1.52 | 0.72 | 0.61 | Weibull (1.36, 1.60) | −0.07 | 0.91 |
| CO32− | 1.07 | 1.09 | 0.51 | 0.42 | Weibull (1.38, 1.12) | 0.03 | 0.76 |
| Mg2+ | 0.61 | 0.72 | 0.31 | 0.27 | Weibull (1.78, 0.67) | −0.23 | 0.45 |
| SO42− | 2.03 | 2.39 | 1.01 | 0.75 | Weibull (1.18, 2.06) | −0.23 | 0.45 |
| Method | R2 | MSE |
|---|---|---|
| Spline Interpolation | 0.67 | 6.38 |
| Linear Interpolation | 0.65 | 6.67 |
| Nearest Neighbor Interpolation | 0.52 | 9.30 |
| GAN | 0.83 | 3.29 |
| Transformer | 0.71 | 5.68 |
| Wavelet-Transformer | 0.98 | 0.31 |
| Ion | Pearson r | p-Value |
|---|---|---|
| Ca2+ | 0.93 | 0.02 |
| CO32− | 0.94 | <0.01 |
| Mg2+ | 0.96 | <0.01 |
| SO42− | 0.98 | <0.01 |
| Ion | MSI | HSI | ||||||
|---|---|---|---|---|---|---|---|---|
| Bias | σ | Skewness | Kurtosis | Bias | σ | Skewness | Kurtosis | |
| Ca2+ | 0.11 | 0.63 | –1.12 | 2.99 | −0.13 | 0.55 | 0.96 | 2.90 |
| CO32− | 0.01 | 0.42 | 0.32 | 1.60 | 0.06 | 0.29 | −0.52 | 1.86 |
| Mg2+ | 0.09 | 0.24 | −1.19 | 3.11 | −0.01 | 0.17 | −0.51 | 1.84 |
| SO42− | 0.44 | 0.51 | −0.82 | 2.46 | 0.02 | 0.31 | −1.03 | 2.82 |
| SO42− | CO32− | Ca2+ | Mg2+ | ||||
|---|---|---|---|---|---|---|---|
| Actual | Predicted | Actual | Predicted | Actual | Predicted | Actual | Predicted |
| 2.66 | 2.88 | 0.86 | 0.91 | 1.98 | 1.84 | 0.75 | 0.79 |
| 0 | 0.31 | 2.01 | 1.81 | 0.81 | 0.26 | 0.05 | 0.06 |
| 1.36 | 1.58 | 1.28 | 1.51 | 1.85 | 1.16 | 0.31 | 0.42 |
| 4 | 3.45 | 0.11 | 0.25 | 2.12 | 2.12 | 1.2 | 0.92 |
| 1.37 | 1.31 | 1.38 | 1.21 | 1.03 | 0.78 | 0.57 | 0.47 |
| 1.16 | 1.15 | 0.72 | 1.09 | 0 | 0.86 | 0.37 | 0.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Zhang, S.; Gao, J.; Wang, B.; Fang, K.; Liu, L.; Lv, S.; Zhang, Q. Soil Water-Soluble Ion Inversion via Hyperspectral Data Reconstruction and Multi-Scale Attention Mechanism: A Remote Sensing Case Study of Farmland Saline–Alkali Lands. Agronomy 2025, 15, 1779. https://doi.org/10.3390/agronomy15081779
Liu M, Zhang S, Gao J, Wang B, Fang K, Liu L, Lv S, Zhang Q. Soil Water-Soluble Ion Inversion via Hyperspectral Data Reconstruction and Multi-Scale Attention Mechanism: A Remote Sensing Case Study of Farmland Saline–Alkali Lands. Agronomy. 2025; 15(8):1779. https://doi.org/10.3390/agronomy15081779
Chicago/Turabian StyleLiu, Meichen, Shengwei Zhang, Jing Gao, Bo Wang, Kedi Fang, Lu Liu, Shengwei Lv, and Qian Zhang. 2025. "Soil Water-Soluble Ion Inversion via Hyperspectral Data Reconstruction and Multi-Scale Attention Mechanism: A Remote Sensing Case Study of Farmland Saline–Alkali Lands" Agronomy 15, no. 8: 1779. https://doi.org/10.3390/agronomy15081779
APA StyleLiu, M., Zhang, S., Gao, J., Wang, B., Fang, K., Liu, L., Lv, S., & Zhang, Q. (2025). Soil Water-Soluble Ion Inversion via Hyperspectral Data Reconstruction and Multi-Scale Attention Mechanism: A Remote Sensing Case Study of Farmland Saline–Alkali Lands. Agronomy, 15(8), 1779. https://doi.org/10.3390/agronomy15081779





