The Genome Era of Forage Selection: Current Status and Future Directions for Perennial Ryegrass Breeding and Evaluation

Abstract

Perennial ryegrass (Lolium perenne L.) is a cornerstone forage species in temperate dairy systems worldwide, valued for its high yield potential, nutritive quality, and grazing recovery. However, current regional evaluation systems face challenges in accurately assessing complex traits like seasonal dry matter yield due to polygenic nature, environmental variability, and lengthy evaluation cycles. This review examines the evolution of perennial ryegrass evaluation systems, from regional frameworks—like Australia’s Forage Value Index (AU-FVI), New Zealand’s Forage Value Index (NZ-FVI), and Ireland’s Pasture Profit Index (PPI)—to advanced genomic prediction (GP) approaches. We discuss prominent breeding frameworks—F2 family, Half-sib family, and Synthetic Population—and their integration with high-throughput genotyping technologies. Statistical models for GP are compared, including marker-based, kernel-based, and non-parametric approaches, highlighting their strengths in capturing genetic complexity. Key research efforts include representative genotyping approaches for heterozygous populations, disentangling endophyte–host interactions, extending prediction to additional economically important traits, and modeling genotype-by-environment (G × E) interactions. The integration of multi-omics data, advanced phenotyping technologies, and environmental modeling offers promising avenues for enhancing prediction accuracy under changing environmental conditions. By discussing the combination of regional evaluation systems with GP, this review provides comprehensive insights for enhancing perennial ryegrass breeding and evaluation programs, ultimately supporting sustainable productivity of the dairy industry in the face of climate challenges.

1. Perennial Ryegrass

Perennial ryegrass (Lolium perenne L.) is a cornerstone forage species in the dairy industry. It has fibrous roots and narrow blades and is densely tillered to form swards under grazing [1,2]. Native to Europe, Asia, and northern Africa, the species has been introduced worldwide and thrives under diverse climatic conditions [1,3,4,5,6,7]. Coupling a high yield [8,9,10,11], sufficient nutritive profile [12,13,14,15,16], and rapid recovery rate post grazing [17,18], perennial ryegrass has been the primary perennial grass species sown in grazed dairy systems across temperate regions of the world.

2. Regional Evaluation Systems

The assessment of perennial ryegrass agronomic performance is primarily on traits that directly impact livestock productivity and farm profitability. Dry matter yield (DMY) determines feed availability, while nutritive traits such as metabolizable energy (ME) [12,13], crude protein [14,19], water-soluble carbohydrates [14,16,19], and digestibility [14,15,19,20] influence milk production and feed efficiency.

In Australia, perennial ryegrass forms the backbone of the forage supply for dairy farms, particularly in the temperate region of southeastern Australia (including Victoria, Tasmania, and South Australia), collectively contributing 80.4% of the national milk production [5,10,21]. However, over 60 commercial cultivars are available on the market and exhibit significant variations in performance [13,22]. As such, an Australian Forage Value Index (AU-FVI) was developed to evaluate cultivar performance independently and guide farmers in selecting the most profitable options. The AU-FVI assesses pasture performance across five seasonal periods—Autumn, Winter, Early Spring, Late Spring, and Summer—and incorporates regional economic values to provide ratings [10,23]. Recent developments have expanded the AU-FVI to include ME, enhancing its ability to evaluate nutritional value [12].

New Zealand’s Forage Value Index (NZ-FVI) adopts a similar economic index approach to rate perennial ryegrass cultivars across four dairy regions based on seasonal DMY [24], wherein farm system modeling revealed substantial economic differences between highest and lowest ranked cultivars, ranging from NZD 556–863/ha/year depending on dairy regions [11]. A recent study investigated environmental variation and identified two distinct mega-environments—the upper North Island and the rest of New Zealand—providing a more accurate estimation of the regional economic values [11]. However, translating performance advantages demonstrated in small-plot trials to commercial farm settings remains challenging, as NZ farmlet studies showed such differences cannot consistently result in measurable gains in pasture yields, suggesting the need for more representative farm-scale data [11,25].

Ireland’s Pasture Profit Index (PPI) provides a more comprehensive evaluation framework by assigning economic values (EUR/ha/year) to traits including seasonal DMY, silage production, and nutritive parameters [9]. The economic values had proven remarkably consistent when tested across different farming systems, milk prices, and management intensities, with rank correlations between scenarios ranging from 0.90 to 1.0. This high consistency allows farmers to select cultivars that will deliver stable economic returns in farm-scale pastures while guiding breeders on economically important traits [9].

Notably, perennial ryegrass DMY is the primary focus in all regional evaluation systems because it represents the most economically important trait for farmers and serves as the fundamental selection criterion in breeding programs aimed at improving pasture productivity. However, the reliable evaluation of such traits depends heavily on the breeding frameworks.

3. Beeding Frameworks

Evaluation varies based on the agronomic traits of interest and local field trial designs employed within breeding approaches. Three primary frameworks—F2 family, Half-Sib family, and Synthetic Population frameworks—are widely adopted in perennial ryegrass breeding, each offering distinct advantages when evaluating diverse traits.

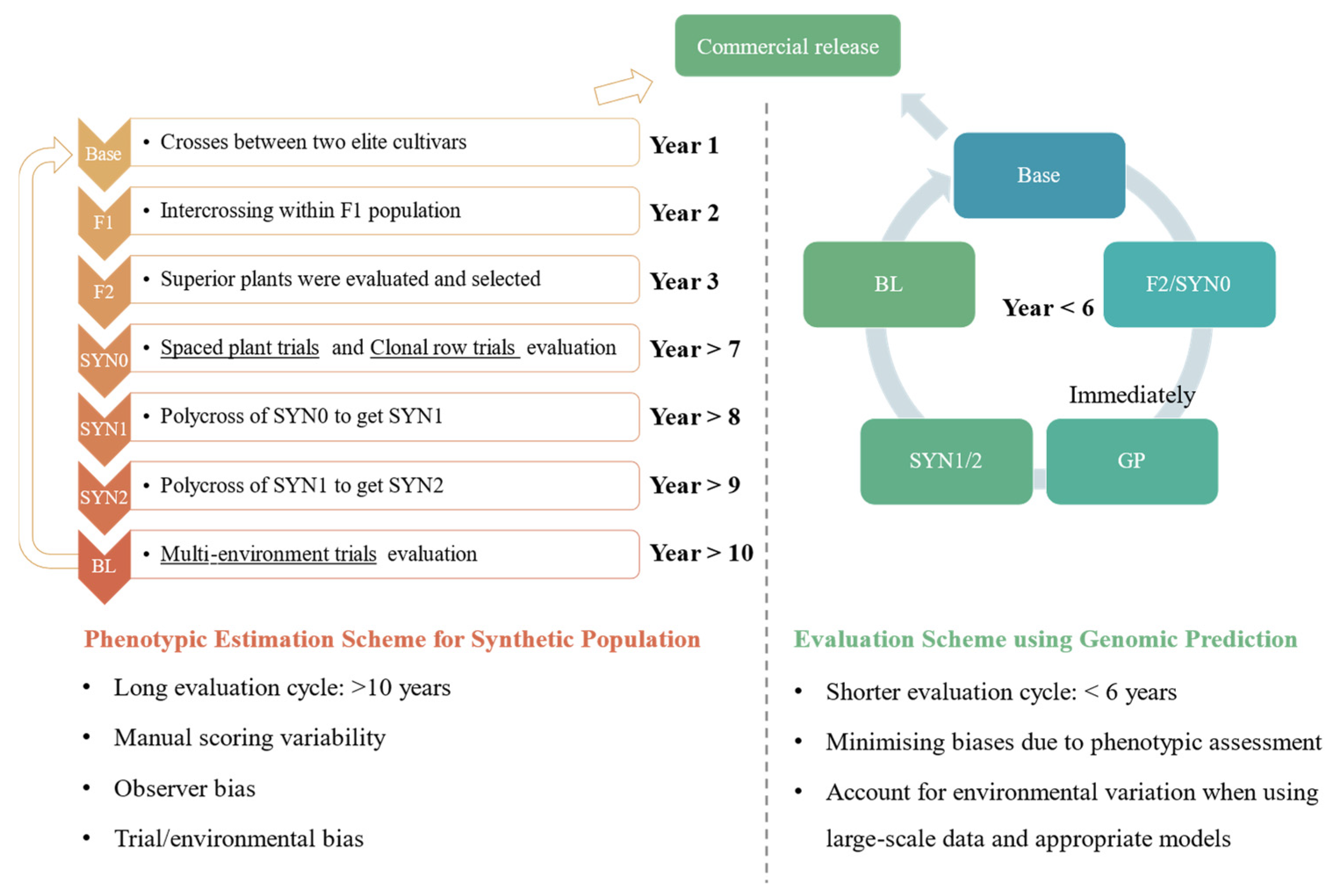
3.1. F2 Family Framework

The F2 family framework follows a structured evaluation process [19,26,27,28]. This approach begins with the selection of two superior parents based on multi-year spaced plant trials. The selected parents are crossed to produce F1 progeny, which remains heterozygous due to the outcrossing nature of ryegrass. These F1 individuals undergo random mating to generate F2 families, which are evaluated in sward trials for key agronomic traits such as yield and forage quality.

The F2 family evaluation framework is effective in assessing polygenic traits, and the ability to develop synthetic varieties from selected F2 families allows for faster cultivar development [19,26,27,28].

3.2. Half-Sib Family Framework

The half-sib framework provides an alternative evaluation strategy by focusing on maternal lines. This approach involves controlled polycrossing, where maternal plants are pollinated by multiple surrounding pollen donors [16,29,30], resulting in each plant within a half-sib family sharing the same maternal genetic material but with different paternal contributions.

The framework allows for identifying elite maternal plants through multi-staged family row trials to select superior half-sib families via progeny testing to assess traits such as herbage accumulation and nutritive quality [15,29]. For instance, Faville et al. evaluated 517 half-sib families in row trials, enabling precise evaluation of maternal lines [29].

3.3. Synthetic Population Framework

The synthetic population framework (Figure 1) manages genetic diversity by intercrossing multiple parents, ensuring high levels of heterozygosity, which is beneficial for long-term genetic improvement and trait stability across different environments [31].

However, this framework requires long evaluation cycles [31,32,33]. The process begins with controlled crosses between two elite ryegrass cultivars to generate an F1 population, which is then intercrossed to produce the F2 generation. These F2 plants undergo evaluation through spaced plant trials and clonal row trials to assess key agronomic traits. The most promising plants then undergo multiple rounds of polycrossing to generate synthetic populations, which may ultimately be released as commercial cultivars or advanced further in the breeding cycle.

3.4. Limitation of Phenotypic Evaluation

Each evaluation framework used in forage breeding presents distinct advantages in measuring plant performance. However, assessing complex traits remains challenging that are controlled by many genes (i.e., polygenic) and susceptible to environmental fluctuations, making phenotypic estimates biased to local trial conditions [10,11,22,24,25,29,31,32,33,34,35,36,37].

Differences in locations, climatic conditions, soil fertility, trial plot size, harvest intervals, and scoring methodologies often lead to inconsistent evaluation across different breeding programs. This inconsistency complicates the direct comparison of trait evaluation across environments and protocols [10,11,24,25,29,33,36].

Furthermore, traditional phenotypic selection remains resource-intensive, requiring repeated manual measurements across seasons and years, with high labor and financial costs [32,33,36]. This restricts the scale of evaluation and slows down genetic gain per breeding cycle.

These limitations inherent in the traditional phenotypic evaluation emphasize the need for integrating high throughput genotyping and advanced statistical models that account for environmental variation to select superior genotypes across diverse environments [38,39].

4. Technological Advancements in Genetic-Phenotypic Association Studies

4.1. Marker-Assisted Selection

The late 20th century witnessed the emergence of marker-assisted selection (MAS), by exploiting linkage disequilibrium (LD) patterns between markers and quantitative trait loci (QTLs), such as genome-wide association studies (GWAS) and QTL mapping [40,41,42,43,44,45,46,47,48,49].

The evolution of marker technologies, including restriction fragment length polymorphism (RFLP) markers [50,51], polymerase chain reaction (PCR)-based random amplified polymorphic deoxyribonucleic acid (DNA) markers [52], amplified fragment length polymorphism (AFLP) markers [53], and simple sequence repeats (SSRs) [54] established a foundation for molecular-based evaluation. Recently, single nucleotide polymorphisms (SNPs) [55,56,57] have enabled polymorphism to have a greater chance of being the causal agent of QTLs and make it possible to evaluate traits controlled by multiple QTLs [44,58,59].

Despite the advances, MAS faced challenges in estimating the traits controlled by numerous markers with individually non-significant but collectively significant effects; perennial ryegrass DMY is such a trait [20,33,46,58,60,61,62,63], necessitating the development of high-throughput genotyping approaches.

4.2. Advancements in High-Throughput Genotyping Technologies

High-throughput sequencing technologies have revolutionized genotyping strategy. The application of SNP arrays represented an early breakthrough [64,65], while restriction enzyme-based genotyping-by-sequencing (GBS) improved genotyping resolution through denser marker discovery by fragmenting the entire genome [29,57,66,67].

Further, GBS transcriptomics (GBS-t) targets expressed genomic regions rather than random fragments. This approach provides higher marker density in functionally relevant regions and more consistent coverage across samples with diverse genetic backgrounds. GBS-t has proven effective, with acceptable missing data rates, while focusing on biologically relevant genomic regions in several crop species [66].

Costs of high-throughput genotyping have decreased alongside technical improvements, enabling practical implementation in large-scale genotyping studies. A primary reduction was through multiplexing processes like sample pooling [29,64,65,66]. This could reduce costs by up to 60% while maintaining genotyping accuracy [65,66]. This advance builds upon reducing the use of sequencing reagents and other consumables. Streamlined library preparation methods further improve efficiency by optimizing laboratory workflows and minimizing processing time [29,64,65,66,68].

4.3. Genomic Prediction

Genomic prediction (GP) represents a transformative advancement in genetic evaluation, initially proposed by Meuwissen et al. [69]. Unlike conventional marker-assisted selection, which relies on the identification and utilization of a few genetic loci associated with major QTLs, GP leverages genome-wide molecular markers to capture both major and minor genetic effects. This approach allows for the prediction of complex polygenic traits, which are governed by many loci with small effects, without the need to identify specific causal variants.

The accuracy and robustness of GP hinge on its underlying statistical assumptions. Fundamentally, GP models assume additive genetic effects, whereby each marker contributes independently and additively to the phenotype, and the cumulative genetic value is expressed as the linear sum of these individual effects. A prediction can be implemented based on either pedigree information or genome-wide marker similarity. Pedigree-based genetic evaluations mainly assume related individuals share genetic materials inherited from common ancestors (Identity by Descent, IBD), where offspring phenotypes are predicted as approximately half of the parents’ genetic potential due to the random inheritance of genome segments during meiosis [63]. In contrast, similarity-based GP measures genetic similarity between individuals based on markers across the whole genome (Identity by State, IBS), regardless of their ancestral origin [36,63,69,70,71,72]. By capturing more precise relationship coefficients than the generalized assumptions in pedigree-based methods and combining with advanced statistical methodology, GP has enabled more accurate prediction than pedigree-based methods [36,63,69,70,71,72].

The effectiveness of GP in trait estimation has been demonstrated in various species. In dairy cattle, the USDA demonstrated its reliability in evaluating genetic merit [73,74]. In crop species, GP proved effective, as example studies in soybean [75] and wheat [76] showed high accuracy in trait prediction. The development of reference-free approaches has enabled GP application in non-model species like switchgrass [77]. These achievements across diverse species demonstrate the versatility of GP, suggesting strong potential for effective application in perennial ryegrass.

The applications of GP in perennial ryegrass have been reported in several traits. For traits with high heritability, such as heading date, GP yielded high predictive accuracies, ranging from 0.75 to 0.90 [14,26]. In addition, GP has shown strong potential in predicting nutritive traits such as crude protein content, water-soluble carbohydrates, and digestibility when leveraging optimal numbers of genome-wide markers [14,15,32,36,78].

Notably, recent research has extended the application of GP to the complex trait of DMY, which has traditionally posed challenges due to its low-to-moderate heritability and high sensitivity to environmental variation. In a recent study, GP was employed alongside large-scale, multi-harvest, multi-site (MHMS) field trial data and dense genotyping datasets comprising over 85 k high-quality SNPs to assess DMY across diverse Australian environments [38].

Nevertheless, achieving reliable GPs in perennial ryegrass requires continued efforts to identify optimal statistical models, incorporate non-additive effects, and refine training population design to maximize prediction accuracy and genetic gain.

5. Statistical Models for Genomic Prediction

Statistical models for GP vary in their approaches to estimating genetic effects and predicting trait performance. These models (

Table 1. Summary of genomic prediction models promising for perennial ryegrass performance estimation.

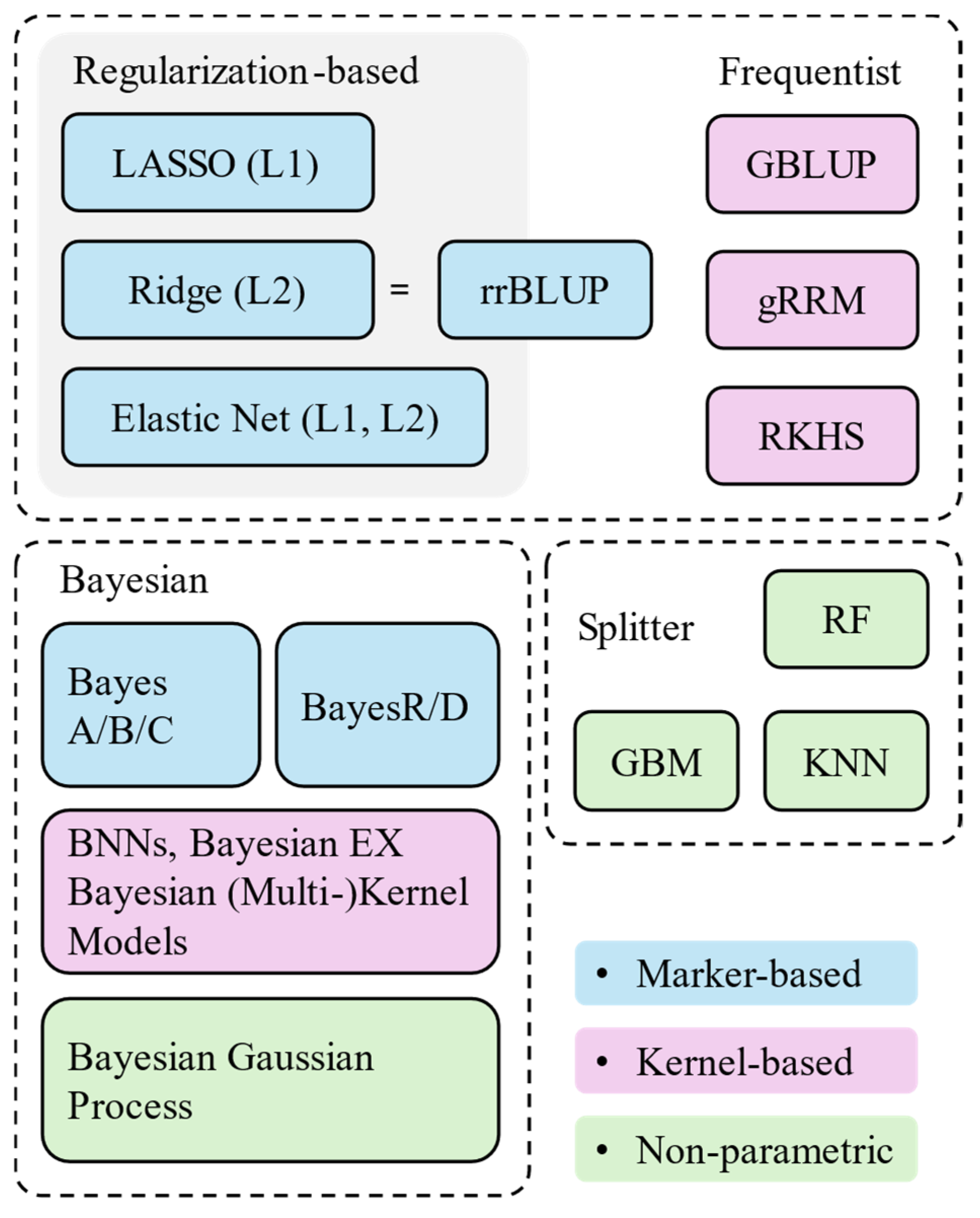
Model	Structures	Assumptions	Frameworks	Applications
LASSO	+ L1 penalty: ${‖\mathit{y}-\mu -\mathit{M}\mathit{\alpha }‖}^2+\lambda {‖\mathit{\alpha }‖}_1$	Linear additive marker effects; unified variances across markers	Sparse Marker-Based; Frequentist	High-dimensional additive genotyping data, feature selection [79]
Ridge regression	+ L2 penalty: ${‖\mathit{y}-\mu -\mathit{M}\mathit{\alpha }‖}^2+\lambda {‖\mathit{\alpha }‖}_2^2$; this is mathematically equivalent to $\mathit{\alpha }\sim \mathcal{N}\left(0,{\mathsf{\sigma }}^2\right)$	Linear additive marker effects; unified variances across markers	Dense Marker-Base; Frequentist	Traits with additive effects per marker, also called rrBLUP [20,29,30,31,47,57,68]; when markers are SNPs, also called snpBLUP
Elastic Net	+ L1 and L2 penalties	Linear additive marker effects; unified variances across markers	Sparse Marker-Base; Frequentist	Correlated markers with additive effects per marker
GBLUP	Variance components are in a genomic relationship matrix ($\mathit{G}$). Coefficients are solved by Henderson mixed model equation [80].	Linear association between genetic markers and phenotypes	Kernel-Based; Frequentist	Traits with linear additive effects; computational efficiency [15,26,28,29,30,32,38,79,81,82]. The basic GBLUP uses a genomic relationship matrix (GRM) [83]. When the GRM is expanded with Legendre polynomials to model environmental variances, it becomes a genomic random regression model (gRRM) [19].
RKHS	Akin to GBLUP but uses non-linear kernel $\mathit{K}$.	Non-linear association between markers and phenotypes	Kernel-Based; Frequentist	Traits with non-linear effects and epistatic interactions [16,79]
BayesA/B/C	$\mathrm{P}\left({\mathsf{\alpha }}_k=0\right)=\mathsf{\pi }\mathrm{ }$ $\mathrm{P}\left({\mathsf{\alpha }}_k\sim \mathcal{N}\left(0,{\mathsf{\sigma }}_k^2\right)\right)=1-\mathsf{\pi }\mathrm{ }$	Linear additive marker effects; Variances can be marker-specific (${\mathsf{\sigma }}_k\sim {\mathsf{\chi }}^{-2}\left(\mathsf{\nu },\mathrm{s}\right)$) or unified	Marker-Based: Dense when $\mathsf{\pi }=0$, Sparse when $\mathsf{\pi }\ne 0$; Bayesian	Traits with flexible genetic architecture [14,15,68,79,84]
BayesR/D	$\mathrm{P}\left({\mathsf{\alpha }}_k=0\right)={\mathit{\pi }}_0\mathrm{ }$ $\mathrm{P}\left({\mathsf{\alpha }}_k\sim \mathcal{N}\left(0,{\mathsf{\sigma }}_i^2\right)\right)={\mathit{\pi }}_i$, where ${\sum }_{i=0}{\mathit{\pi }}_i\mathrm{ }=1$	Linear additive marker effects with flexible shrinkage across multiple effect sizes; marker-specific variances	Sparse Marker-Based; Bayesian	Traits with mixed levels of effect sizes
Bayesian EX	General-purpose Bayesian framework: $\mathit{\alpha }\sim \mathrm{P}\mathrm{r}\mathrm{i}\mathrm{o}\mathrm{r}\left(\mathit{\alpha }\right)$, where	Linear additive marker effects; prior choice determines shrinkage or sparsity level	Marker-Based; Bayesian	Flexible prior choices for traits with additive effects per marker. The prior could be Gaussian (Bayesian Ridge) [79], Laplace (Bayesian LASSO) [68,79], or other distributions.
Bayesian Neural Networks (BNNs)	Network learns $f(\mathit{M};\mathit{W})\approx \mathit{y}$, mapping from markers $\mathit{M}$ to phenotypes $\mathit{y}$ via weights $\mathit{W}$.	Flexible marker effects; Implicit variance components	Marker-Based; Bayesian	Flexible genetic associations [79]
Bayesian Kernel Models	Flexible kernel $\mathit{K}$ is derived from the markers $\mathit{M}$ to account for genetic variance components, $f\left(\mathit{K}\right)$ then estimates genetic effects.	Flexible genotype similarities; predefined variance components	Kernel-Based; Bayesian	Traits with non-linear genetic associations. When combining multiple kernels: $f\left(\mathit{K}\right)={\sum }_m{f}_m\left({\mathit{K}}_m\right)$, it becomes a Bayesian Multikernel Model.
Bayesian Gaussian Process	$f\left(\mathit{\alpha }\right)\sim \mathcal{G}\mathcal{P}\left(\mu \left(\mathit{\alpha }\right),\mathit{K}\right)$	Flexible genotype similarities; stochastic variance components	Non-parametric; Kernel-Based; Bayesian	Traits requiring uncertainty quantification in genetic relationships.
Random Forest (RF)	${\widehat{y}}_t\left(\mathit{y},M\right)$ is trained on bootstrapped samples based on certain splitting criteria. RF parallelly aggregates tree predictions: ${\widehat{\mathit{y}}}_{\mathrm{RF}}={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T{\widehat{y}}_t$.	Similarity-based prediction: patterns among similar data points provide higher prediction reliability	Non-parametric; Tree-Based Splitter	Non-linear additive prediction; noisy datasets with missing data; marker interactions [20,28,29,31,57,68]
Gradient Boosting Machines (GBM)	GBM sequentially corrects tree predictions: ${\widehat{\mathit{y}}}_{GBM,t}={\widehat{y}}_{GBM,t-1}+\eta \cdot {\widehat{h}}_t$, where ${\widehat{h}}_t$ is negative gradient of the loss function in each tree, $\eta$ is the learning rate.	Similarity-based prediction	Non-parametric; Tree-Based Splitter	Non-linear prediction [20]
K-Nearest Neighbours (KNN)	Predicts based on $k$ closest training samples in the marker feature space: ${\widehat{y}}_{KNN}={\displaystyle \frac{1}{k}}{\sum }_{i=1}^K{y}_i$ where $i$ indexes the $K$ nearest neighbours.	Similarity-based prediction	Non-parametric; Splitter	Non-linear prediction [20]

and Figure 2) can be broadly categorized into parametric approaches (marker-based and kernel-based regression models) and non-parametric approaches that adapt to data patterns during the training process.

5.1. Marker-Based Models

Marker-based regression models directly associate genetic markers with the traits in a linear way:

$$\mathit{y}=\mu +\mathit{M}\mathit{\alpha }+\mathit{ϵ}$$

where $\mu$ denotes the overall mean, $\mathit{M}\mathit{\alpha }$ accounts for marker effects, and $\mathit{ϵ}$ represents residuals.

Marker-based models vary in their assumptions about marker effect distributions from normal distribution to flexible mixed distributions. For instance, the assumptions can be connected through L2 regularization in ridge regression, which is equivalent to assuming normally distributed marker effects in a Best Linear Unbiased Prediction (BLUP) framework (called rrBLUP) [20,29,30,31,47,57,68]. Furthermore, the LASSO and Elastic Net approaches are alternative regularization strategies, with LASSO utilizing L1 regularization and Elastic Net combining both L1 and L2 penalties. These methods have proven effective in performance estimation when handling polygenic traits with sparse marker associations [68,85]. Bayesian approaches, such as BayesA, BayesB, etc., provide probabilistic frameworks by incorporating flexible prior distributions for marker effects [15,68,79,84,86]. For example, Arojju et al. demonstrated that the Bayesian Lasso method achieved a predictive ability of 0.52 for crown rust resistance in perennial ryegrass [68].

5.2. Kernel-Based Models

Another type of prediction model estimates agronomic performances based on variance components through kernel functions $f\left(\mathit{K}\right)$ derived from genetic markers $\mathit{M}$. Wherein, BLUP, using the kernel derived from genomic data, i.e., GBLUP, has emerged as a powerful approach for predicting random genotypic coefficients [28,29,68,79,86]. In general, these models follow a Linear Mixed Model (LMM) framework:

$$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{Z}\mathit{u}+\mathit{ϵ}$$

where $\mathit{X}\mathit{\beta }$ accounts for known fixed effects (e.g., environmental or year-specific effects), $\mathit{Z}\mathit{u}$ represents random genetic effects, and $\mathit{ϵ}$ denotes residual effects following a normal distribution ($\mathit{ϵ}\sim \mathcal{N}\left(0,{\sigma }_{\epsilon }^2\right)$). The variance components are estimated utilizing restricted maximum likelihood [87], and the prediction can be calculated via Henderson’s mixed model equations [80].

The genetic variance components $\mathrm{V}\mathrm{a}\mathrm{r}\left(\mathit{u}\right)$ are often approximated using the Genomic Relationship Matrix (GRM) among genotypes. The calculation of GRM varies based on marker assumptions but commonly follows $\mathit{G}=\mathit{M}{\mathit{M}}^{\prime }/\mathit{c}$, where $\mathit{c}$ is a generic scaling factor [63]. When using the VanRaden GRM [83], which assumes Hardy–Weinberg equilibrium of the populations, GBLUP is mathematically equivalent to rrBLUP, as both assume independent and identically distributed (IID) marker effects with zero mean and constant variance [63]. For instance, Zhu et al. applied a GBLUP model using a GRM derived from ~86 k SNPs to predict dry matter yield of perennial ryegrass across 23 multi-environment trials, achieving a 12.7% improvement in predictive accuracy over the baseline model without genomic data [38].

The robustness of kernel-based models can be further enhanced by incorporating non-linear environmental kernels [19]. Taking Reproducing Kernel Hilbert Space (RKHS) as an example, it could capture non-additive genetic effects, such as epistatic effects, to enhance the predictive ability [16,79,88].

5.3. Non-Parametric Models

In addition, models that do not pre-define but dynamically adjust parameters during the modeling process are featured as non-parametric models. Random Forest (RF) is one such model and has emerged as an alternative in GP. Its successful implementation was reported in several perennial ryegrass prediction studies due to its ability to handle non-linear relationships and perform automatic feature selection [20,28,29,31,57,68]. For instance, in a Lolium perenne breeding study, RF achieved a prediction accuracy of 0.45 for dry matter digestibility, outperforming BLUP [20]. Other non-parametric approaches, such as Gradient Boosting Machines and K-Nearest Neighbors, were also explored for perennial ryegrass GP, demonstrating comparable efficiency [20].

5.4. Model Selection and Optimization Strategies

Implementing GP for perennial ryegrass requires a strategic alignment of statistical models with the biological complexity. One of the core decisions involves selecting appropriate statistical models. Among various GP models, GBLUP remains a preferred choice due to its high predictive accuracy and computational efficiency [15,16,20,26,27,28,29,30,32,38,39,78,79,81,82].

Equally important is the choice of cross-validation strategy, which influences the assessment of model adaptability. Random K-fold Cross-Validation is widely used for initial model evaluation, wherein the dataset is randomly divided into K subsets, with K-1 subsets used as training data and the remaining subset as validation data [26,27,31,32,78,89,90,91,92]. While this approach provides a general assessment of model robustness, it may overestimate prediction accuracy when the same populations are represented in both the training and validation sets [38,39,78,89,93].

Population-specific cross-validation addresses such limitations by partitioning data based on population structure. This strategy has been reported to provide more reliable genomic estimated breeding values (GEBVs) in untested populations [15,20,29,38,39,94].

Cross-validation can also be tailored to the traits of interest, particularly when considering multi-trait GP. For instance, different cross-validation schemes were employed to evaluate scenarios of primary and secondary traits [16], highlighting how the inclusion of correlated secondary traits can influence predictive ability.

Therefore, effective GP requires integrating both appropriate statistical models and validation techniques adapted to the prediction scenarios to ensure reliable estimation of perennial ryegrass [39].

5.5. Refinement of Genomic Prediction Models

Although GP models are promising, several factors should be considered for practical implementation. The effectiveness of GP is often influenced by genomic dissimilarity between training and target populations, with prediction accuracy declining when applied across distinct populations or breeding cycles. This challenge is particularly relevant for perennial ryegrass, given its diverse genetic background and complex breeding history [65,95,96,97].

Studies have shown accuracy decay between distinct populations or over generations [20,26,30,68,82,98]. The impact can be quantified by [99,100]:

$$r=\sqrt{{\displaystyle \frac{N{h}^2}{N{h}^2+Me}}}$$

where $N$ is the number of individuals in the training population; $h^2$ is the heritability of the trait; and $Me$ is the number of independent chromosome segments, which is related to effective population size and genome length.

This formula was later extended to account for more complex scenarios. For instance, Wientjes et al. [101] modified it to account for cross-population prediction: $r_g={cor}_{g}r$, where ${cor}_g$ represents the genetic correlation between the reference population and the selection candidates. However, Brard et al. [102] argued that various formulas only provide upper bounds of accuracy, and actual performance is usually lower due to factors not considered in the theoretical frameworks.

Training population size remains another factor affecting prediction accuracy, where increasing the training population size could improve prediction performance [99,100]. Additionally, trait heritability and selection intensity interact to determine the model’s long-term predictive ability [32,82,99,100,103]. For perennial ryegrass breeding programs utilizing synthetic populations [31], regular model updating and careful management of selection pressure would be necessary to maintain prediction accuracy across breeding cycles.

Alternative models may be considered when non-additive genetic effects are significant, such as RF for non-linear interactions or Bayesian models when prior genetic knowledge is available [20,31,68,79]. Additionally, reducing SNP sets, while maintaining predictive ability, is required to develop cost-effective genotyping assays to make the routine implementation of GS practical [15,29].

For practical implementation, comprehensive consideration of appropriate statistical models, cross-validation strategies, and genotyping data quality [14,16,27,30,31,32,79,84,86,104] are essential for reliable genomic estimation of perennial ryegrass performance.

6. Research Gaps and Future Research Directions

6.1. Requirements for Representative Genotyping Approaches

Perennial ryegrass is a self-incompatible, outcrossing species that relies on polycrossing and lacks breeding history documentation, leading to heterozygosity bias and complicating the application of GP. Without representative genotyping strategies, the genotypic data obtained may fail to accurately capture the allelic spectrum within breeding populations, thereby reducing the reliability of GP [64,72,83,84,93,98,99,105,106,107]. Polyploidy further complicates marker-trait associations and makes conventional discrete encoded genotyping less effective [14,78,84].

Recent technological advances offer promising alternatives. One such approach is the integration of pooled sequencing with target capture assay [65,66,78,97]. Pooled sequencing allows for genotyping at the population level from multiple individuals into fewer sequencing libraries, thus reducing sequencing costs and mitigating individual-level sampling bias [65,66,78,97]. Furthermore, target capture, which selectively amplifies specific genomic regions using pre-designed probes [66], increases the coverage of genetic variants across heterozygous loci. When combined, these methods shift genotyping from discrete genotype calls to continuous allele frequency, reducing errors associated with variant misclassification.

Despite these methodological improvements, cross-platform incompatibility and the restricted availability of raw genomic data—often due to proprietary or commercial constraints—remain significant barriers to data integration and reuse. Addressing these challenges requires the adoption of advanced computational tools, including machine learning-based algorithms capable of harmonizing heterogeneous datasets, thereby supporting a comprehensive understanding of genomic relationships among ryegrass cultivars across studies [97].

6.2. Endophyte Symbiotic Impacts

Endophytes impact host agronomic performance through complex biological interactions, such as host compatibility, metabolic trade-offs, and alkaloid biosynthesis pathways [108,109,110,111]. These compounds can enhance plant stress resistance but may impose metabolic costs or negatively affect animal health [108,109,110]. As such, the selection of endophytes in ryegrass breeding must consider both plant productivity and animal safety [97].

Recent insights from Zhu et al. emphasized the need to improve the fairness of endophyte-ryegrass performance evaluations, particularly under the constraints of imbalanced datasets [97]. Due to commercial restrictions, certain endophytes are typically tested only within proprietary host cultivars, making it difficult to model endophyte impacts on host genetic effects. To address this, Zhu demonstrated that treating endophytes as fixed effects in statistical models provided distinct estimates of their contributions to DMY. To enable more balanced evaluations, they also suggested that future research explore biologically separating and recombining endophytes and ryegrass lines and conducting independent assessments of endophytes and ryegrasses across breeding programs. These approaches could help reduce confounding and support more robust prediction of untested combinations.

Together, these findings underscore the importance of integrating both statistical and biological perspectives to improve the understanding of endophyte–ryegrass interactions and optimize pasture productivity.

6.3. Extension to Broader Agronomic Trait Profiling

While the current studies mainly focused on DMY, extending the GP framework to other economically important traits would facilitate a more comprehensive evaluation system for perennial ryegrass. Nutritive characteristics [13,15], persistence [7,19], and stress tolerance [68,112,113,114,115] are critical factors that collectively determine the profitability of the dairy industry and other livestock systems where perennial ryegrass is a key pasture species. Multi-trait GP has been shown to improve modeling efficiency by leveraging correlations between traits, such as incorporating water-soluble carbohydrates to improve prediction accuracy for DMY [16].

Persistence can influence long-term productivity in perennial ryegrass pastures. Bornhofen showed that random regression models effectively capture temporal genetic variations across multiple harvests and years [19]. The models revealed how persistence traits change as plants age, enabling the estimation of both persistence and productivity [19].

Stress tolerance, including resistance to abiotic and biotic factors, remains another evaluation objective and has been studied using GP to improve resistance to crown rust [68]. By integrating multiple traits into a single prediction framework, evaluation systems can better align with industry needs, ultimately enhancing the sustainability of ryegrass-based dairy systems.

6.4. Integration of Multi-Omics Data to Improve Performance Estimation

Multi-omics approaches could facilitate trait estimation by integrating diverse biological layers: genomics serves as the base layer when associating QTLs with phenotypic variation [27,31,38,39,47,79,97,116], transcriptomics might reveal the regulation mechanisms [117,118,119,120,121], and proteomics could examine functional molecules such as cellular activities linked to photosynthetic efficiency and carbon allocation [122,123], while metabolomics might offer insights into the plant’s physiological state by profiling molecules in biomass-controlling pathways [124,125]. Such integrated multi-omics studies could provide a systematic understanding of how genetic potential translates into phenotypic performance under varying conditions.

6.5. Advancement in Phenotypic Data Collection

Phenotyping is a crucial step in trait estimation for perennial ryegrass, and its advancements may greatly improve the efficiency of trait data collection.

Sensing technologies using drones and specialized sensors could enable high-throughput measurements of plant growth, canopy structure, and physiological status [126,127,128,129]. Implementing these approaches also requires advanced image processing and time-series analysis methods to extract valid phenotypic traits from these high-dimensional data [128,130,131]. Additionally, the development of non-destructive techniques would allow for more frequent measurements without compromising plant performance [132,133]. These advancements would be particularly promising for capturing seasonal variations more accurately [129,134].

6.6. Integrating Environmental Data and Modeling Climate Adaptation

Genotype-by-environment (G × E) interactions are widespread in perennial ryegrass and significantly affect cultivar rankings across dairy farming environments, presenting a major challenge to the reliability of regional evaluation systems [11,22,37,38,39,135,136]. These interactions are driven by locational, temporal, and management-related environmental variability. For example, it was reported that water content could influence root development and overall plant growth across different locations [135]. Substantial cultivar ranking changes across soil moisture levels have also been observed [11], emphasizing the importance of accounting for environmental factors that present locational variation. Temporal variation often occurs on seasonal timescales and is linked to temperature patterns [22,37,38,39,136,137,138]. This variability can alter performance, complicating consistent estimation [22,37]. Similarly, management practices, such as irrigation [139,140] or grazing intensity [18], could also introduce performance variation.

Addressing the complex sources of phenotypic variation in perennial ryegrass requires comprehensive MHMS field trial data to capture temporal and spatial variability [37,38,39,141]. Recent research has demonstrated that the integration of advanced statistical models and MHMS data significantly improves prediction accuracy and underscores the potential of GP for environment-specific cultivar selection [37,38,39].

Several modeling frameworks have been developed to account for G × E interactions. The Factor Analytic (FA) model simplifies the variance–covariance structure across sites, capturing heterogeneous genetic variances and improving predictive performance in large-scale trials [37,38,39,142,143]. The Additive Main Effects and Multiplicative Interaction Model (AMMI) represents another well-accepted approach that models the variances of additive main effects using principal component analysis as interaction variance components. This enables separating systematic variation from noise while providing visual interpretation through GGE (genotype plus genotype-by-environment) biplots, making it valuable for identifying stable genotypes across environments [61,144,145]. The Reaction Norm Model extends GP by modeling phenotypic responses as functions of environmental gradients using higher-order covariates [19]. This approach directly incorporates environmental variabilities into genomic models, allowing for a more precise prediction under variable environmental conditions.

Furthermore, emerging machine learning techniques, such as recurrent neural networks (RNNs) and long short-term memory (LSTM) architectures, offer the potential for capturing temporal dependencies in multi-harvest datasets. These models maintain the memory of prior states, making them well-suited for modeling seasonal fluctuations [146,147,148].

Furthermore, the crop growth model (CGM) offers a mechanistic approach to simulate plant development by incorporating genetic and environmental variables [149]. Different from fitting environmental variation as variance components, CGM accounts for G × E interactions by mechanistically modeling how plants respond to the environments [149,150,151,152,153]. This is a process-based simulation that translates external factors into physiological responses within the plant. The simulated physiological processes may include photosynthesis, respiration, biomass partitioning and accumulation, and phenological development [149,150,154,155,156,157,158,159]. These processes allow CGMs to predict crop performance, such as perennial ryegrass, across diverse environments based on genotype-specific parameters.

As climate change introduces increasing unpredictability, including temperature extremes, droughts, and salinity stress [160,161,162,163], there is a pressing need to extend prediction models beyond historical data. The integration of G × E-enhanced GP with CGMs could facilitate cultivar performance predictions, supporting anticipatory breeding strategies [149,150,159,164]. CGMs can simulate physiological responses to environmental variables that include projected climate data [165,166]. By using G × E-enhanced GP results as response variables and CGM simulations as predictors, breeders could develop a framework that predicts cultivar performance under future climate scenarios and before implementing actual field trials [39,150,165,166].

This integrated approach could also refine mega-environment classification, which may shift with ongoing climate change. Incorporating time-series environmental data into the prediction could enable dynamic updates to mega-environment boundaries and help identify climate-resilient cultivars for future conditions. Ultimately, combining genomic, environmental, and physiological data will enable the optimization of forage breeding under increasingly variable agricultural conditions.

6.7. Effective Communication and Implementation

Translating cutting-edge research into practical farm decision-making requires strategic implementation through existing evaluation frameworks (Figure 3). While GP offers powerful capabilities for developing superior varieties, successful adoption requires effective communication that bridges the gap between researchers and industry stakeholders.

Understanding GP and statistical models presents initial barriers to adoption. Clarification of both capabilities and limitations is essential, particularly regarding G × E interactions and environmental data requirements for robust predictions. Industry implementation must address forage-specific challenges including representative genotyping protocols [65,66], endophyte interaction complexities [108,109,110], and commercial data sensitivity concerns [97].

Integration of GP outputs with regional evaluation systems including AU-FVI, NZ-FVI, and PPI would provide a viable pathway for assessing cultivar performance [9,10,11]. This integration would enable stakeholders to evaluate performance within a genomic-unified system, facilitating more informed decision-making.

Developing user-friendly interface tools that simplify complex modeling outputs into actionable breeding decisions would enhance industry uptake. Advanced visualization tools are suggested to present statistical outputs through intuitive graphics or interactive dashboards, allowing stakeholders to explore data without requiring deep statistical knowledge. However, the effective utilization of these tools will still require structured training opportunities to ensure that stakeholders can confidently interpret and apply GP outputs in their decision-making processes. Recently, multimodal large language model-based AI systems have emerged as promising interfaces for helping industry stakeholders understand GP principles and interpret complex outputs. For example, farmers and breeders could use AI-powered tools to quickly grasp technical concepts and statistical interpretations, such as understanding GGE biplots through conversational interfaces that explain the relationships between genotypes, environments, and their interactions in plain language. These AI assistants could serve as accessible entry points for stakeholders to engage with GP concepts without requiring extensive statistical training.

The economic implications of implementing GP can be better understood by articulating them to industry stakeholders through cost-benefit analyses. These analyses may demonstrate how GP reduces traditional evaluation cycle length and accelerates genetic gain (Figure 1 and [32,33,36,104]), thereby justifying the initial investment required for GP infrastructure. Comparative studies showing the economic advantages of genomic selection over conventional breeding approaches would help build a compelling case for industry adoption.

Fostering collaborative networks among researchers, breeders, and practitioners is vital for successful GP implementation. These collaborative networks would facilitate knowledge exchange and create feedback loops to improve prediction models continuously and could be formalized through industry-led initiatives or public-private partnerships to ensure the sustainability and effectiveness of GP implementation in perennial ryegrass breeding programs.

7. Conclusions

This review traced the evolution from traditional phenotypic evaluation frameworks to genomic prediction approaches in perennial ryegrass breeding systems. The cornerstone role of perennial ryegrass in global dairy production necessitates reliable performance evaluation, particularly for economically important traits like seasonal dry matter yield.

High-throughput genotyping technologies combined with advanced statistical models represents a fundamental shift in cultivar evaluation paradigms. Representative genotyping data that accounts for the self-incompatible and heterogeneous nature of perennial ryegrass have significantly advanced prediction ability while potentially reducing evaluation timeframes [32,33,36,38,39,70,104].

The comparative review of statistical models, from marker-based approaches to kernel-based and non-parametric methods, provides guidance for model selection aligned with ryegrass genetic complexities. Recent critical explorations include an improved understanding of endophyte impacts on performance estimation, extension to other economically important traits beyond DMY, and sophisticated G × E interaction modeling. However, research gaps remain in multi-omics integration, automated phenotyping methodologies, and environmental modeling enhancement—all essential for maintaining prediction accuracy under evolving climate conditions.

The pathway to practical implementation lies in integrating GP with established cultivar evaluation systems, particularly through AU-FVI, NZ-FVI, and PPI frameworks. Success requires coordinated collaboration among research institutions, breeding companies, and stakeholders to achieve continued model refinement and strategic communication. Through this approach, GP technology can fundamentally enhance perennial ryegrass breeding effectiveness, ultimately contributing to more sustainable and productive global pasture systems under climate variability challenges.