Abstract
In order to analyze the relationship between hyperspectral image and soybean canopy nitrogen content in the field, and to establish a prediction model for soybean canopy nitrogen content with few parameters and a simple structure, hyperspectral image data and corresponding nitrogen content data of soybean canopy at different growth periods under different fertilization treatments were acquired. Three spectral characteristic variables selection methods, including correlation coefficient analysis, stepwise regression, and spectral index analysis, were used to determine the spectral characteristic variables that are closely related to the soybean canopy nitrogen content. The predictive models for soybean canopy nitrogen content based on spectral characteristic variables were established using a multiple linear regression algorithm. On this basis, the established prediction models for soybean canopy nitrogen content were compared and analyzed, and the optimal prediction model for soybean canopy nitrogen content was determined. To verify the applicability of prediction models for soybean canopy nitrogen content, a spatial distribution map of soybean canopy nitrogen content at the regional scale was drawn based on unmanned aerial vehicle (UAV) hyperspectral imaging data at the flowering and seed filling stages of soybean in the experimental area, and the spatial distribution of soybean nitrogen content was statistically analyzed. The results show the following: (1) Soybean canopy spectral reflectance was highly significantly negatively correlated with soybean canopy nitrogen content in the range of 450–729 nm, and highly significantly positively correlated in the range of 756–774 nm, with the largest positive correlation coefficient of 0.2296 at 765 nm and the largest absolute value of negative correlation coefficient of −0.8908 at 630 nm. (2) The predictive model for soybean canopy nitrogen content based on three optimal spectral indices, NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555), was optimal, with R2 of 0.9063 and 0.91566 and RMSE of 3.3229 and 3.2219 for the calibration and prediction set, respectively. (3) Based on the established optimal prediction model for soybean canopy nitrogen content combined with the UAV hyperspectral image data, spatial distribution maps of soybean nitrogen content at the flowering and seed filling stages were generated, and the R2 between soybean nitrogen content in the spatial distribution map and the ground measured value was 0.93906, the RMSE was 3.6476, and the average relative error was 9.5676%, which indicates that the model had higher prediction accuracy and applicability. (4) The overall results show that the optimal prediction model for soybean canopy nitrogen content established based on hyperspectral imaging data has the characteristics of few parameters, a simple structure, and strong applicability, which provides a new method for realizing rapid, dynamic, and non-destructive monitoring of soybean nutritional status on the regional scale and provides a decision-making basis for precision fertilization management during soybean growth.
1. Introduction
Soybean (Glycine max (L.) Merrill) is one of the world’s important food, oil, and feeding crops. Due to the richness of soybean in a variety of nutrients, it has a very wide range of uses, such as medicinal, health care, and so on. Thus, soybean has received widespread attention worldwide [1,2]. At present, there is a huge gap between China’ s soybean production and consumption demand. In order to alleviate the contradiction between the supply and demand of soybeans in China, measures such as scientific fertilization and optimized planting of soybeans have been used. These measures have not only improved the yield and quality of soybeans in China but also contributed to the sustainable development of China’s soybean industry and the stabilization of the agricultural economy [3].
Nitrogen is an important component of protein, nucleic acid, phospholipid, chlorophyll and certain hormones in soybean plants, and it is also one of the most important factors limiting the growth and high yield of soybean [4]. The rapid and effective monitoring of the nitrogen content during soybean growth is an important prerequisite and foundation for guiding soybean fertilization and achieving the high quality and high yield of soybean. Traditional monitoring methods of nitrogen content (such as Kjeldahl nitrogen determination) need to be conducted via laboratory chemical analysis after collecting samples in the field [5]. These methods have the disadvantages of a long detection period, complicated operation, and strong destructiveness. It is difficult to realize the spatial and temporal continuous dynamic monitoring of nitrogen content using traditional methods. It is also unable to meet the practical needs of modern precision agriculture for the rapid, real-time, non-destructive, large-area detection of nitrogen content in soybean [6].
The spectroscopy analysis technique is a technical system for analyzing and researching the structure and chemical composition of substances using their spectral characteristics [7,8]. The technique has the features of fast speed, high efficiency, low cost, large amount of information, and non-destructive operation [9,10,11]. It has become a hot spot in precision agriculture research in recent years, such that crop nutrient information is rapidly detected using the spectroscopy analysis technique [12,13]. The surplus and deficit of crop nutrient status will lead to a series of changes in leaf color, thickness, shape, structure, etc., and will be shown in crop spectral reflectance characteristics, which is the basis for the detection and diagnosis of crop nutrient content using the spectroscopy analysis technique [14]. At present, the key indicators of crop nutrition monitoring mainly include nitrogen content and the nitrogen balance index (NBI). Among them, nitrogen content is a central parameter directly reflecting the nitrogen nutritional status of crops, which can not only be used as a diagnostic indicator of crop growth status [15] but also provide a scientific basis for precise nitrogen application in the field. The NBI, as the ratio of chlorophyll and flavonoids, is an important fluorescence stress parameter that can dynamically reflect crop growth information and avoid the lag of fertilizer effects when evaluating the efficiency of nitrogen fertilizer absorption [16]. Since nitrogen content is directly related to the physiological and metabolic processes of crops, a large number of scholars have carried out research on the detection of crop nitrogen content based on the spectroscopy analysis technique. These studies mainly focus on the screening and construction of nitrogen-sensitive and vegetation indices. For example, Schlemmer et al. found that the red-edge chlorophyll index (CIred edge) was able to more accurately assess maize nitrogen content, and the coefficient of determination of the maize nitrogen content prediction model constructed on the basis of CIred edge was 0.87 [17]. Tang et al. constructed an NTRI model based on the first derivative spectroscopy in the 680~750 nm band, with R2 of 0.83 in the prediction set, RMSE of 0.11% in the validation set, and RE of 9.6%, which would provide reliable technological support for the intelligent fertilization of drip-irrigated maize in arid zones [18]. Liu et al. established the VI3-WOA-ELM model based on hyperspectral technology, which exhibited excellent performance, with R2 of 0.812, RMSE of 0.011 mg/g, and RPD of 2.3323 in the validation set, providing an effective method for the hyperspectral monitoring of anthocyanins [19]. In the rapid, real-time, non-destructive detection of soybean nitrogen content, scholars have attempted to carry out research on the detection of soybean nitrogen content based on spectroscopic techniques using a variety of data processing and modeling methods (linear and nonlinear). Zhang et al. established a predictive model for quantitative nitrogen content of soybean leaves based on DOSC-RF-PLS with an Rp2 of 0.9466 using hyperspectral imaging combined with chemometrics, which provides an efficient non-destructive method for crop nitrogen nutrient monitoring [20]. Tang et al. constructed an accurate prediction model of soybean leaf nitrogen content (LNC) using hyperspectral technology combined with a random forest (RF) model (R2 = 0.854) and established a nitrogen dilution curve based on chlorophyll content and the optimal spectral index (FDRI) to quantitatively diagnose the nitrogen nutritional status (NNI) of soybeans [21]. Chen et al., based on hyperspectral reflectance, constructed an LNC estimation model using a Continuous Wavelet Transform (CWT), which had optimal accuracy (RMSE = 0.6132, relative error 13.2%) and was better than the traditional vegetation index and UVE-PLS method. It provided an effective means of non-destructive monitoring of nitrogen nutrition in soybean leaves [22]. However, the existing models constructed based on the spectroscopy technique usually had problems of too many variables or complex modeling processes, with which it is difficult to effectively explain the actual relationship between modeled variables. In terms of the practical needs of the remote sensing monitoring of crop physiology and ecology, there is an urgent need to establish a regression model with streamlined parameters and a simple structure that has universal applicability and application value.
Hence, the specific objectives of the research were (1) to establish a predictive model for soybean canopy nitrogen content with streamlined parameters and a simple structure; (2) to verify the reliability and applicability of the optimum prediction model established; and (3) to provide methodological and data support for the monitoring of crop nutrient status on a large scale. In this study, in order to achieve these objectives, the relationship between soybean canopy spectral reflectance and canopy nitrogen content was analyzed. The optimal prediction model for soybean canopy nitrogen content was determined using multiple data extraction algorithms combined with multiple linear regression (MLR) models. The spatial distribution map of soybean nitrogen content in the study area was generated based on unmanned aerial vehicle (UAV) hyperspectral imaging data and the optimal prediction model of soybean canopy nitrogen content at the flowering and bulging stages in the experimental area. On this basis, the reliability of the optimal prediction model was verified by combining the ground-based measured canopy nitrogen content data.
2. Materials and Methods
2.1. Experimental Materials
The experiment was conducted from June to October 2017 in the experimental base of the National Engineering Research Centre of Intelligent Equipment for Agriculture, Xiaotangshan Town, Changping District, Beijing, China (116°44′ E, 40°18′ N). This area has a warm-temperate continental semi-humid and semi-arid monsoon climate, with an average annual temperature of 11.8 °C, an average annual frost-free period of 203 days, average annual sunshine hours of 2816 h, and an average annual precipitation of 584 mm. The previous crop was wheat, the soil type was alluvial soil, and it was irrigated by sprinkler irrigation. The nature of the soil is shown in Table 1. The experimental base has 2500 acres of land, owns a variety of models of soybean seeding, fertilizing, and harvesting machinery, and has professional agronomists to assist in carrying out experiments. The specific experimental location is shown in Figure 1.

Table 1.
The nature of the soil in the field.
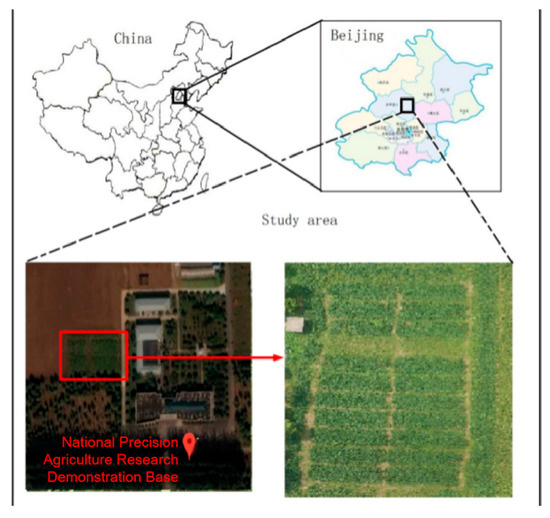
Figure 1.
Experimental field in National Engineering Research Centre of Intelligent Equipment for Agriculture.
In this study, the soybean variety of Zhonghuang 13, bred by the Chinese Academy of Agricultural Sciences, was selected as the experiment material. The soybean seeds were seeded on 16 June 2017, with seed spacing of 15 cm, row spacing of 45 cm, seeding depth of 5 cm, and seeding amount of 79.5 kg/hm2. Plant density of 180,000 plants/hm2 was retained when soybean grew to the three-leaf stage. In this study, the L934 orthogonal experiment design (4 factors 3 levels, 9 experiments) was used for the fertilizers stress experiment of nitrogen, phosphate, and potassium [23]. In this study, 9 orthogonal experiments were used to replace 27 (three-factor, three-level) full factorial experiments. Compared with the full factorial design, the L934 orthogonal experiment design significantly improved the efficiency of the multifactorial experiments in the field by reducing the number of experiments. The coding table of the fertilization factor level is shown in Table 2.

Table 2.
The coding table of the fertilization factor level in the field.
Based on the principle of the L934 orthogonal experiment design, 9 fertilization gradients were set up, another control group (no fertilization) was also set up, and finally 10 fertilization treatment groups were set up. Each fertilization treatment was repeated four times, and the whole experimental area was divided into 20 plots. The length of each experimental plot was 5 m, and the width was 3 m. In order to prevent the impact of interregional fertility loss on the experiment, a row buffer of 0.5 m was set up between the plots. Urea (46.4%), calcium dihydrogen phosphate (12%), and potassium sulfate (50%) were used as nitrogen, phosphate, and potassium fertilizers, respectively. The fertilization design scheme for each treatment is shown in Table 3 [24,25,26].

Table 3.
Design table of the orthogonal regression experiment in the field.
In order to avoid the influence of uneven terrain, uneven fertility, and other factors, the experimental plots were arranged in a completely randomized distribution, and the distribution of experimental spots is shown in Figure 2.
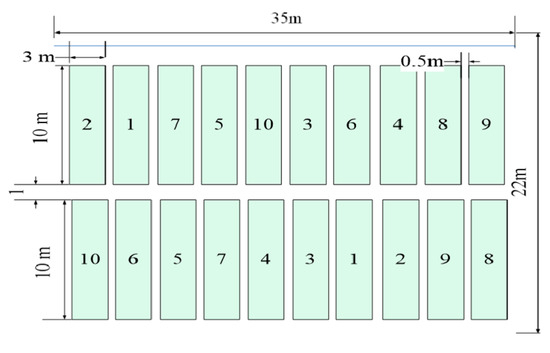
Figure 2.
Field distribution of soybean experimental plots. Note: 1–10 are the processing numbers of fertilization treatment, and 0.5 m is the width of the protective barrier between treatments.
2.2. Hyperspectral Imaging Data Acquisition
2.2.1. Hyperspectral Imaging Data Acquisition of Soybean at Canopy Scale
A visible–near-infrared hyperspectral imaging system (Image-λ-V10E-LU, Beijing Zhuo Li Han Guang Instrument Limited Company, Beijing, China) was used to collect the hyperspectral imaging data of the soybean canopy. The system is shown in Figure 3. The imaging spectrometer has a spectral range of 400~1000 nm, a spectral resolution of 2.8 nm, and a field of view of 25°. Since the system uses a passive light source (natural light) for spectral imaging, sunny days were selected during the experimental period, and hyperspectral imaging data acquisition was conducted from 10:00 to 14:00 on sunny days. During the measurement, the imaging spectrometer was fixed on the scanning platform at a distance of 1.5 m from the soybean canopy, and the imaging area of the system was 0.6 m2. The exposure time was set to 6 ms, and the linear scanning speed was set to 2.25 cm/s; to ensure the stability of the measurement data, the hyperspectral camera was preheated for 30 min in advance of the acquisition. The data were collected using a random sampling method, where soybean plants representative of plot growth were selected for canopy hyperspectral imaging data collection in each of the 20 plots. In order to reduce the influence of instrument sensitivity and light source change on hyperspectral imaging data, a standard whiteboard (a rectangular white board composed of polytetrafluoroethylene material) and dark current had to be corrected during each measurement. The calibration process was carried out according to Formula (1) as follows:

Figure 3.
Hyperspectral imaging acquisition system on canopy scale.
In the formula, denotes the original hyperspectral imaging data of soybean leaves, denotes whiteboard data captured with the light turned on, denotes current data obtained through covering the lens without illumination, and R (reflectance of raw spectra) denotes the corrected hyperspectral imaging data of soybean leaves.
2.2.2. UAV Hyperspectral Imaging Data Acquisition
An eight-rotor electric UAV platform carrying a UHD185 airborne hyperspectral imaging spectrometer (Cubert, Lise-Meitner-Straße 8·89081 Ulm, Germany) was used for hyperspectral image data acquisition in the research area. The UAV acquisition platform is shown in Figure 4. The UHD185 utilized a frame-type imaging method with a short integration time, which can obtain a hyperspectral imaging cube of the imaging area within 0.001 s. This efficient data acquisition method effectively avoided the compression and stretching phenomenon of hyperspectral images during UAV flight [27]. The UHD185 had a spectral range of 450–950 nm. The spectral channels were 125 with a spectral sampling interval of 4 nm. The UAV hyperspectral imaging data acquisition was set up with a flight altitude of 50 m, a total mass of 4.4 kg, a flight mass of 6000–11,000 g, a battery of LiPo (6S, 10,000–20,000 mAh, min.15 C), a size of 460 mm × 511 mm × 305 mm, a flight speed of 5 m/s, a flight time of 20 min, and a heading and sidetrack overlap of 80% and 60%, respectively. The ground spatial resolution (GSD) resulting from these settings was 3.2 cm. When the UAV acquired images, spectral correction was performed using a standard whiteboard (a rectangular white board composed of polytetrafluoroethylene material, reflectance of 100%) and blackboard (dark current, reflectance of 0%).

Figure 4.
Hyperspectral imaging collection platform for unmanned aerial vehicle (UAV).
Since the spectral resolutions between soybean canopy hyperspectral images and UAV hyperspectral images were different, a data normalization algorithm was used to preprocess the spectral data acquired from the canopy and UAV to ensure the consistency of the spectral data [28,29]. In this study, the resampling method was used to ensure that both the canopy spectral data and the UAV spectral data were acquired at 1 nm data intervals [30,31].
2.3. Determination and Data Division of Soybean Nitrogen Content
In this study, all canopy leaves within the field of view of the canopy hyperspectral camera were clipped. These leaves were placed in a plastic Ziplock bag and marked as one sample with a marker. A total of 159 soybean samples were collected from the four growth stages of soybean seedling, flowering, podding, and seed filling. The nitrogen content of the four growth stages was analyzed as shown in Figure 5.
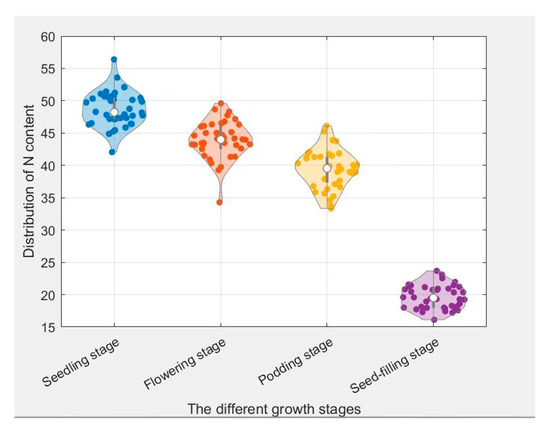
Figure 5.
Statistical analysis of nitrogen content in different growth stages.
The soybean samples were brought back to the laboratory for drying, weighing, and crushing. Chemical values of soybean canopy nitrogen content were determined using an AA3 continuous flow analyzer (Auto Analyzer 3 System, SEAL Analytical GmbH, Wrexham, UK). Afterwards, three times standard deviation was used to remove the outliers from the samples, and it was found that 6 outlier samples existed in the samples [20]. Finally, 153 samples were retained for the prediction model construction of soybean canopy nitrogen content. The Kennard–Stone (K-S) classification algorithm was used in this study to divide the soybean samples into a calibration set and a prediction set according to the ratio of 3:1 (as shown in Table 4).

Table 4.
Statistics of soybean canopy nitrogen content in the calibration and prediction sets.
2.4. Selection Method of Spectral Characteristic Variables
In this study, the correlation coefficient method [32], stepwise regression method [33], and spectral index method [34] were used to extract the spectral characteristic variables that were closely related to soybean nitrogen content. The variables were named spectral features. The spectral indices included the normalized spectral index (NDSI), ratio spectral index (RSI), and difference spectral index (DSI), with the expressions of (Rλ1 − Rλ2)/(Rλ1 + Rλ2), Rλ1/Rλ2 and (Rλ1 − Rλ2)/Rλ2, respectively. Rλ1 and Rλ2 were the spectral data in the acquired hyperspectral imaging data of soybean.
2.5. Model Construction
Multiple linear regression (MLR) is a commonly used modeling and analytical method in NIR spectral analysis [35,36]. This algorithm is an extension and expansion of unary linear regression, which is used to model the relationship between two or more independent variables and the dependent variable [37]. Since MLR uses a combination of multiple independent variables, its prediction of the dependent variable is better than the prediction result of a single independent variable. Thus, MLR has greater application in the modeling and analysis process. In this study, the prediction models for soybean nutrient content based on spectral features were established using MLR. The specific expression of MLR is as follows:
In the expression, X is the collected spectral matrix, n is the number of samples, m is the number of wavelength points, Y is the concentration matrix of soybean canopy nitrogen content, p is the number of sample group points, B is the matrix of regression coefficients, and E is the random error matrix.
2.6. Model Evaluation
The performances of the established MLR prediction models were evaluated using the decision coefficient (R2) and root mean square error (RMSE). The range of R2 was 0~1. A better model should have higher values of R2, and a lower value of RMSE [38]. The specific expressions of R2 and RMSE are as follows:
In the expression, is the measured value of soybean canopy nitrogen content in the i-th sample, is the measured mean value of soybean canopy nitrogen content, is the predicted value of soybean canopy nitrogen content in the i-th sample, is the predicted mean value of soybean canopy nitrogen content, and n is the number of samples.
3. Results
3.1. Correlation Analysis Between Spectral Reflectance and Soybean Canopy Nitrogen Content
Pearson correlation analysis was performed between canopy spectral reflectance and measured soybean canopy nitrogen content. Then, correlation curves were obtained, as shown in Figure 6. The spectral reflectance of soybean canopy was negatively correlated with soybean canopy nitrogen content in the spectral range of 450~738 nm and 890~900 nm, while the spectral reflectance of soybean canopy was positively correlated with soybean canopy nitrogen content in the spectral range of 738~890 nm. During the spectral range of 450~729 nm and 756~774 nm, the spectral reflectance of soybean canopy was significantly correlated with soybean canopy nitrogen content (p < 0.01). Among them, the spectral reflectance of soybean canopy in the range of 450~729 nm was significantly negatively correlated with soybean canopy nitrogen content (p < 0.01), and the spectral reflectance of soybean canopy in the range of 756~774 nm was significantly positively correlated with soybean canopy nitrogen content (p < 0.01). In the spectral range where the correlation coefficients showed a significant positive correlation, the correlation coefficient between the spectral reflectance of soybean canopy and the soybean canopy nitrogen content achieved the maximum value at 765 nm with a correlation coefficient of 0.2296. In the spectral range where the correlation coefficients showed a significant negative correlation, three valleys existed in the spectral ranges of 450~534 nm, 534~668 nm, and 669~738 nm. The extreme values were obtained at 513 nm, 630 nm, and 678 nm with a correlation coefficient of −0.8364, −0.8908, and −0.8790, respectively. Therefore, 513 nm, 630 nm, 678 nm, and 765 nm were selected as the sensitive characteristic variables for the analysis of soybean canopy spectral reflectance and soybean canopy nitrogen content.
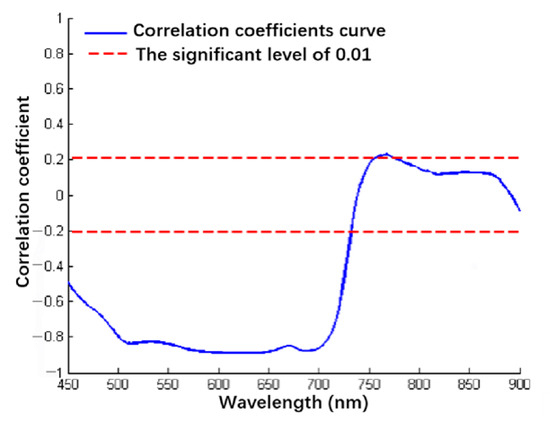
Figure 6.
Correlation curve between reflectance spectra and nitrogen content of soybean canopy. Note: The red dashed line represents the significant level (p < 0.01). The blue solid curve is the correlation coefficients curve between the spectral reflectance of soybean canopy and the soybean canopy nitrogen content.
3.2. Stepwise Regression Analysis Between Spectral Reflectance and Soybean Canopy Nitrogen Content
The stepwise regression algorithm is an important method in multiple regression analysis that can effectively eliminate the independent variables containing multicollinearity and maximize the reservation of variables with the greatest explanatory power and most importance [39]. In this study, the canopy spectral reflectance in the range of 450~900 nm was used as the independent variable, and the soybean canopy nitrogen content was used as the dependent variable. The stepwise regression algorithm was operated to obtain the characteristic spectral variables that were closely related to soybean canopy nitrogen content, as shown in Table 5. A total of seven characteristic variables were selected, and the order in which each variable was selected into the regression equation was 633 nm, 531 nm, 573 nm, 513 nm, 618 nm, 690 nm, and 459 nm. The contribution of each variable to the variation in soybean canopy nitrogen content is shown in Figure 7. When the regression model contained one variable of 633 nm, the regression model was able to explain 78.639% of the variation in soybean canopy nitrogen content. When the regression model contained two variables of 633 nm and 531 nm, the regression model could reasonably explain 82.7848% of the variation in soybean canopy nitrogen content, and the regression model’s adjusted coefficient of determination increased by 5.272%. When the regression model contained three variables of 633 nm, 531 nm, and 573 nm, the regression model could explain 84.4892% of the variation in soybean canopy nitrogen content, and the regression model’s adjusted coefficient of determination increased by 2.546%. Similarly, when the regression model included four, five, six, and seven variables, the regression model’s adjusted coefficient of determination increased by 2.485%, 3.157%, 2.284%, and 1.002%, respectively. It can be found that when the regression model included more than four variables, the overall trend for the adjusted coefficient of determination was decreased. Finally, four variables of 633 nm, 531 nm, 573 nm, and 513 nm were selected as the characteristic variables for the analysis of soybean canopy nitrogen content [40,41].

Table 5.
MLR prediction model for nitrogen content of soybean based on sensitive wavelengths selected using correlation coefficient method.
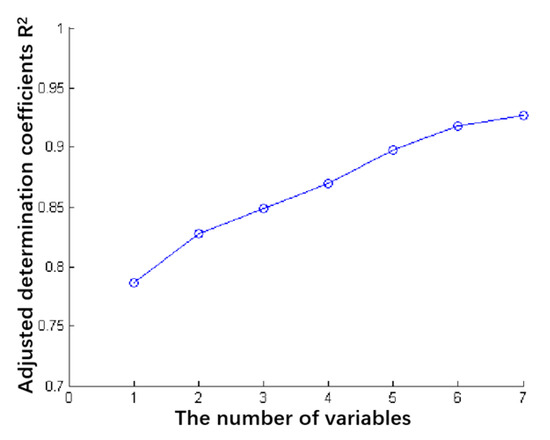
Figure 7.
Scotter plot of variable number and adjusted determination coefficient of estimation models at canopy scale.
3.3. Spectral Index Construction and Correlation Analysis for Soybean Canopy Nitrogen Content
In order to select the sensitive spectral index variables that were related to the soybean canopy nitrogen content, the contours of correlation coefficients between soybean canopy nitrogen content and the NDSI, RSI, and DSI were established, respectively (as shown in Figure 8). As can be observed from Figure 7, the contours of the NDSI and DSI were symmetric along the diagonal, while the contour of the RSI was asymmetric along the diagonal. In the visible range of 450–750 nm, the contours of the NDSI and DSI were symmetric along the diagonal, which reflected the strong reflective properties of chlorophyll in the green band (495–570 nm), while the contour of the RSI was asymmetric along the diagonal, which might be related to the difference between the absorption of carotenoids in the blue-violet band (450–495 nm) and that of chlorophyll on the red side (670–750 nm) [42]. The correlation coefficients between soybean canopy nitrogen content and the NDSI were greater than 0.8 in the spectral combinations of 450~498 nm and 471~519 nm, 450~594 nm and 540~696 nm, and 468~735 nm and 642~900 nm. Among them, NDSI(R552,R555) is in the green band, and its high sensitivity originates from the reflection peak of green light by chlorophyll. NDSI(R552,R555) had the highest correlation coefficient with a correlation coefficient value of 0.9500 (Figure 8a). In order to effectively analyze the sensitive index variables between soybean canopy nitrogen content and the RSI, the contours of the RSI were divided into two parts along the diagonal. Above the diagonal, the correlation coefficients between soybean canopy nitrogen content and the RSI were greater than 0.8 in the spectral combination regions of 450~498 nm and 474~528 nm, 450~594 nm and 549~702 nm, and 489~732 nm and 639~900 nm. Below the diagonal, the correlation coefficients between soybean canopy nitrogen content and the RSI were greater than 0.8 in the spectral combination regions of 489~519 nm and 450~501 nm, 546~696 nm and 450~594 nm, and 645~900 nm and 468~735 nm. Among them, RSI(R537,R573) spans the green-yellow band (537–573 nm), and its asymmetry reflects the absorption properties of the photosynthetic pigment complex. RSI(R537,R573) had the highest correlation coefficient with soybean canopy nitrogen content, and the correlation coefficient value was 0.9513 (Figure 8b). In Figure 8c, the correlation coefficients between soybean canopy nitrogen content and the RSI were greater than 0.8 in the spectral combination regions of 450~639 nm and 474~708 nm, and 702~732 nm and 720~780 nm. Among them, DSI(R540,R555) is within the green-yellow transition band (540––555 nm), and its high sensitivity originates from the synergistic effect of chlorophyll and carotenoids. The maximum value of the correlation coefficient between DSI(R540,R555) and soybean canopy nitrogen content was 0.9203. The correlation coefficient values of NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) were all above 0.9, which indicates that these spectral indices can be used as sensitive spectral variables to characterize the soybean canopy nitrogen content.
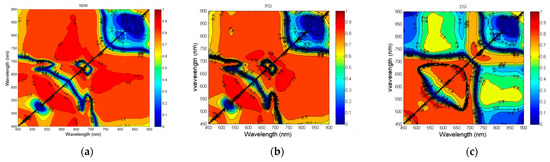
Figure 8.
Contours of correlation coefficients between nitrogen content and NDSI, RSI, and DSI, respectively, at canopy scale: (a) contour of correlation coefficient between nitrogen content and NDSI at canopy scale; (b) contour of correlation coefficient between nitrogen content and RSI at canopy scale; (c) contour of correlation coefficient between nitrogen content and DSI at canopy scale.
3.4. Construction and Validation of Prediction Model for Soybean Canopy Nitrogen Content
Based on the sensitive spectral characteristic variables selected using the correlation coefficient method, stepwise regression method, and spectral index method, the prediction models for soybean canopy nitrogen content were established combining the MLR algorithm. The modeling results are shown in Table 6. As can be seen from the table, the MLR model for soybean canopy nitrogen content based on NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) was the best, with the largest determination coefficient of 0.9063, and the smallest root mean square error of 3.3229. The performances of the MLR model established by RSI(R537,R573) was slightly worse than the best model, whereas the multiple linear regression model based on 513 nm, 630 nm, 678 nm, and 765 nm, which were selected with the correlation coefficient algorithm, had the lowest accuracy, with a coefficient of determination and root mean square error of 0.8280 and 4.5012, respectively. Based on the analysis of regression coefficients of MLR equations, the order of importance of variables in Equation (5) was R630, R687, R513, and R765; the order of importance of variables in Equation (6) was R531, R573, R513, and R633; and the order of importance of variables in Equation (10) was NDSI(R552,R555), DSI(R540,R555), and RSI(R537,R573).

Table 6.
Prediction models for soybean canopy nitrogen content.
In order to verify the performance of the soybean canopy nitrogen content prediction models established by spectral characteristic variables (selected using the correlation coefficient method, stepwise regression method, and spectral index method), 38 samples of the prediction set were used for the examination, and the results of the validation are shown in Figure 8. The red solid line is the 1:1 regression line, and the black dashed line is the line of the fitting equation between the measured and predicted soybean canopy nitrogen content. When the predicted and measured values of soybean canopy nitrogen content are closer to the 1:1 regression line, it indicates that the prediction models for soybean canopy nitrogen content had a better prediction performance. As can be seen from Figure 9, the decision coefficients of the prediction models for the prediction set established based on spectral characteristic variables (selected using the correlation coefficient method, stepwise regression method and spectral index method) are all above 0.85. The validation accuracy and fitting results of the prediction set are better. It is shown that the models based on the three spectral selection methods were able to achieve effective prediction for soybean canopy nitrogen content. The result based on NDSI(R552, R555), RSI(R537, R573), and DSI(R540, R555) had the best performance for soybean canopy nitrogen content in the prediction set, with a maximum determination coefficient of 0.91566 and a minimum root mean square of 3.2219. The determination coefficient improved by 4.2394% and 2.6582% compared to that the correlation coefficient method and stepwise regression method, respectively. This indicates that the validation result based on the characteristic variables selected using spectral index method was better than that of the correlation coefficients method and the stepwise regression method, which is consistent with the modeling results. The results show that the characteristic spectral variables selected using the spectral index method are closely related to soybean canopy nitrogen content. Hence, the multiple linear regression model based on NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) was selected as the most suitable method for the prediction of soybean canopy nitrogen content, and the model equation was (10).
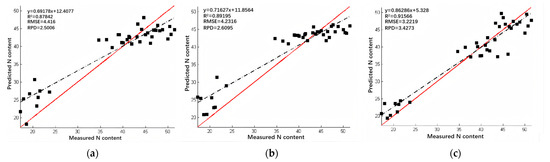
Figure 9.
Validation result for soybean canopy nitrogen content (a) based on sensitive wavelengths selected with correlation coefficient method at canopy scale; (b) based on sensitive wavelengths selected with stepwise regression method at canopy scale; and (c) based on vegetation index of NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) selected at canopy scale. Note: The red solid line is the 1:1 regression line, and the black dashed line is the line of the fitting equation between the measured and predicted soybean canopy nitrogen content.
3.5. Spatial Inversion and Accuracy Evaluation of Soybean Nitrogen Content Based on UAV Hyperspectral Imagery
To test the adaptability of the established soybean canopy nitrogen content prediction model, the soybean nitrogen content value corresponding to each pixel point in the UAV image was calculated based on the acquired UAV hyperspectral image and the determined optimal soybean canopy nitrogen content prediction model. The spatial distributions of soybean nitrogen content at the flowering and seed filling stage were obtained as shown in Figure 10. In comparing the spatial distribution maps of nitrogen content at the flowering and seed filling stages of soybean, it can be seen that the nitrogen content at the flowering stage of soybean was significantly higher than that at the seed filling stage. With the continuous advancement of soybean fertility, the nitrogen content of soybean plants decreased significantly, which is consistent with the changes in nitrogen content of the canopy of the plant in the process of soybean growth.
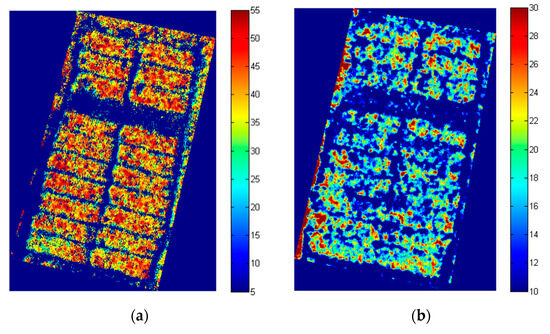
Figure 10.
Spatial distribution maps of nitrogen content of soybean at different stages: (a) spatial distribution maps of nitrogen content of soybean at flowering stage; (b) spatial distribution maps of nitrogen content of soybean at seed filling stage.
The data were collected at the flowering and seed filling stages using a random sampling method, where soybean plants representative of plot growth were selected for the determination of chemical values of canopy nitrogen content in each of the 20 plots. Forty measured values of soybean nitrogen content in the field and forty predicted soybean nitrogen content at corresponding locations in the spatial distribution map were used for comparison, and the result is shown in Figure 11. Most of the sample points were distributed near the 1:1 line, and the determination coefficient was 0.93906, the root mean square error was 3.6476, and the mean relative error was 9.5676%. This indicates a strong agreement between the spatial distribution maps of soybean nitrogen content and the measured soybean nitrogen content. And the result shows that the soybean nitrogen content prediction model established based on NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) could also be used for the prediction of soybean nitrogen content at the UAV scale, which is of great significance for realizing the rapid, dynamic, and non-destructive monitoring of the nutritional status of soybeans in a small area, laying a research basis for the fine management of nitrogen fertilizer during the growth process of soybean.
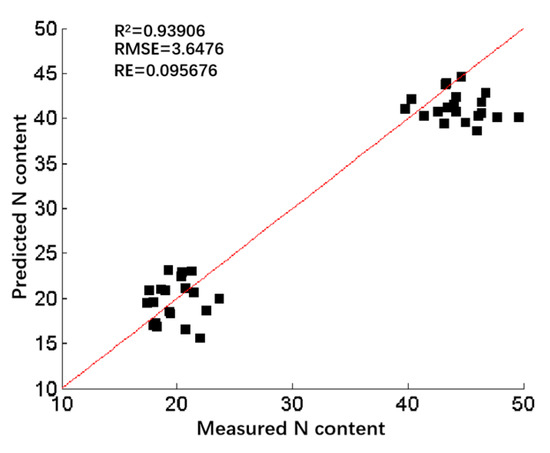
Figure 11.
Comparison of nitrogen content between the prediction value of the spatial distribution map and measured value.
4. Discussion
Some shortcomings in the detection of plant nutrient information existed in the current crop nutrient diagnostic methods. For example, traditional nutrient diagnostic methods, such as the appearance diagnosis method and chemical diagnosis method, have great limitations and lag in practical applications [43,44,45]. The nutrient diagnostic model established based on hyperspectral technology has the problems of variable redundancy and modeling complexity, making it difficult to effectively explain the actual relationships among variables [46]. Therefore, in this study, the spectral characteristic variables that were closely related to the soybean canopy nitrogen content were selected using the correlation coefficient analysis method, stepwise regression method, and spectral index method. And a prediction model for soybean nitrogen content with few parameters and a simple structure was proposed using multiple linear regression. The model equation was (10). The coefficient of determination R2 of the model in the prediction of soybean nitrogen content was 0.93906. The model was characterized by its simplicity and applicability, which provided a new method for the spatial prediction of soybean nutritional status and dynamic monitoring of growth status, and then provided a scientific basis for precise fertilization management decisions during soybean growth.
In terms of model accuracy, Guo et al. developed a prediction model for potato canopy nitrogen content using the hyperspectral index method with a model accuracy coefficient of determination of 0.84 [47]. Wang et al. used UAV remote sensing data combined with the random forest algorithm to establish a prediction model for rice nitrogen content, and the model’s determination coefficient was 0.77 [48]. Wang et al. established a prediction model for rice canopy nitrogen content using UAV hyperspectral technology, and the model’s determination coefficient was 0.881 [49]. The accuracy of the detection model for soybean canopy nitrogen content established in this study was slightly higher than that of the nitrogen content detection models established in other studies. On the one hand, it may be that the spectral characteristic variables selected with the spectral index method in this study, which were closely related to soybean canopy nitrogen content, minimized redundant variables. These selected variables improved the model prediction performance, simplifying the model complexity at the same time. On the other hand, it may be that the spectral index method (NDSI, RSI, DSI) in this study was able to capture more accurately the combination of spectral variables reflecting the soybean canopy nitrogen content, and these selected combinations of spectral variables further improved the predictive ability of the prediction model for soybean canopy nitrogen content.
In this study, the spatial distribution map of soybean canopy nitrogen content was drawn by combining UAV hyperspectral images with an optimal prediction model. The map could clearly present the spatial variability characteristics of nitrogen in the field, which could be transformed into a variable fertilization prescription map by combining it with expert knowledge. The variable fertilization prescription map could provide a decision-making basis for precision fertilization management during soybean growth.
In this study, a prediction model for soybean nitrogen content with a simple structure and few parameters was established using soybean canopy hyperspectral data combined with spectral indices, and the adaptability of the model was verified to validate the reliability of the model. This study provides methods and data support for nitrogen content and nutrition detection in other crops. However, in this study, soybean growth data in a single year were collected, and the adaptability of the model developed in this study would be further verified with different years and locations in subsequent studies.
5. Conclusions
- (1)
- In this study, the correlation between soybean canopy spectral reflectance and soybean canopy nitrogen content was analyzed. It was found that the soybean canopy spectral reflectance was significantly negatively correlated with the soybean canopy nitrogen content in the spectral range of 450~738 nm (p < 0.01), and the soybean canopy spectral reflectance was significantly positively correlated with the soybean canopy nitrogen content in the spectral range of 756~774 nm (p < 0.01). The negative correlation coefficients achieved extreme values at 513 nm, 630 nm, and 678 nm, which were −0.8364, −0.8908, and −0.8790, respectively.
- (2)
- After comparing the performance of the correlation coefficient method, stepwise regression method, and spectral index method in selecting the spectral characteristic variables closely related to soybean canopy nitrogen content, it was found that the spectral characteristic variables of NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) were closely related to the soybean canopy nitrogen content. The prediction model for soybean canopy nitrogen content based on NDSI(R552,R555), RSI(R537,R573), and DSI(R540,R555) was optimal, with a determination coefficient and root mean square error of 0.9063 and 3.3229 for the calibration set, respectively, and of 0.91566 and 3.2219 for the prediction set, respectively.
- (3)
- To demonstrate the adaptability of the established prediction model with few parameters and a simple structure for soybean canopy nitrogen content, spatial distribution maps for soybean nitrogen content at the flowering and seed filling stages were generated based on the UAV hyperspectral image. Forty measurements of soybean nitrogen content in the field were used to compare with the predicted values at the corresponding locations in the distribution map of soybean nitrogen content. It was found that the predicted values of the spatial distribution map of soybean nitrogen content had good consistency with the measured values, with a coefficient of determination, root mean square error, and mean relative error of 0.93906, 3.6476, and 9.5676%, respectively. This shows that the established prediction model for soybean canopy nitrogen content had high prediction accuracy and reliability. In addition, the results of spatial calculation for soybean nitrogen content in UAV images were basically consistent with the measured nitrogen content on the ground. This shows that the soybean nitrogen content model established in this study could be used for the inversion of nitrogen content at the UAV scale, which is of great significance for realizing the rapid, dynamic, and non-destructive monitoring of soybean nitrogen nutrient nutritional status at regional scale, and provides a research foundation for the fine management of nitrogen fertilizer during the growth process of soybean.
Author Contributions
Conceptualization, Y.Z. and Y.W.; methodology, Y.Z. and M.G.; supervision, L.W. and F.Z.; validation, M.G.; formal analysis, Y.Z. and M.G.; investigation, L.W., Y.W., X.C. and P.L.; resources, Y.Z. and F.Z.; data curation, Y.Z., M.G. and Y.W.; writing—original draft preparation, Y.Z.; writing—review and editing, Y.Z., M.G., P.L. and S.A.; visualization, Y.Z.; project administration, Y.Z., F.Z. and X.C.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Henan Provincial Science and Technology Research Project (No. 252102521059, No. 242102111185), Postgraduate Education Reform and QualityImprovement Project of Henan Province (YJS2025SZ18), Young Backbone Teachers Program of Henan University of Science and Technology (Grant No. 13450009), and the National Natural Science Foundation of China (No. 32202096).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the editor and reviewers for their assistance and valuable comments.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ma, Y.; Kan, G.; Zhang, X.; Wang, Y.; Zhang, W.; Du, H.; Yu, D. Quantitative Trait Loci (QTL) Mapping for Glycinin and β-Conglycinin Contents in Soybean (Glycine max L. Merr.). J. Agric. Food Chem. 2016, 64, 3473–3483. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, J.; Wu, X.; Chen, Q.; Lu, B.; Dai, C. Detection of viability of soybean seed based on fluorescence hyperspectra and CARS-SVM-AdaBoost model. J. Food Process. Preserv. 2019, 43, e14238. [Google Scholar] [CrossRef]
- Bureau of Statistics of the China. China Statistical Yearbook; China Statistics Press: Beijing, China, 2022.
- Hong, G.; Han, M.; Ikram, U. Analysis of Metabolomic Changes in Lettuce Leaves under Low Nitrogen and Phosphorus Deficiencies Stresses. Agriculture 2020, 10, 406. [Google Scholar] [CrossRef]
- Zhang, L.; Song, X.; Niu, Y.; Zhang, H.; Wang, A.; Zhu, Y.; Zhu, X.; Chen, L.; Zhu, Q. Estimating Winter Wheat Plant Nitrogen Content by Combining Spectral and Texture Features Based on a Low-Cost UAV RGB System throughout the Growing Season. Agriculture 2024, 14, 456. [Google Scholar] [CrossRef]
- Zhang, Y.K.; Luo, B.; Pan, D.Y.; Song, P.; Lu, W.C.; Wang, C.; Zhao, C.J. Estimation of Canopy Nitrogen Content of Soybean Crops Based on Fractional Differential Algorithm. Spectrosc. Spectr. Anal. 2018, 38, 3221–3230. [Google Scholar]
- Lu, W.Z.; Yuan, H.F.; Xu, G.T. Modern Techniques of Near Infrared Spectroscopy; China Petrochemical Press: Beijing, China, 2000. [Google Scholar]
- Wu, X.; Liang, X.; Wang, Y.; Wu, B.; Sun, J. Non-Destructive Techniques for the Analysis and Evaluation of Meat Quality and Safety: A Review. Foods 2022, 11, 3713. [Google Scholar] [CrossRef]
- Zhang, Y.; Sun, J.; Li, J.; Wu, X.; Dai, C. Quantitative Analysis of Cadmium Content in Tomato Leaves Based on Hyperspectral Image and Feature Selection. Appl. Eng. Agric. 2018, 34, 789–798. [Google Scholar] [CrossRef]
- Wang, F.; Lin, H.; Xu, P.; Bi, X.; Sun, L. Egg Freshness Evaluation Using Transmission and Reflection of NIR Spectroscopy Coupled Multivariate Analysis. Foods 2021, 10, 2176. [Google Scholar] [CrossRef]
- Muhammad, Z.; Muhammad, A.; Md, H.M.; Shujat, A.; Ou, Q.; Huan, L. Application of benchtop NIR spectroscopy coupled with multivariate analysis for rapid prediction of antioxidant properties of walnut (Juglans regia). Food Chem. 2021, 359, 129928. [Google Scholar]
- Guo, Z.; Wang, M.; Wu, J.; Tao, F.; Chen, Q.; Wang, Q.; Zou, X. Quantitative assessment of zearalenone in maize using multivariate algorithms coupled to Raman spectroscopy. Food Chem. 2019, 286, 282–288. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, X.; He, C.; Wu, B.; Zhang, S.; Sun, J. Near-infrared spectroscopy combined with fuzzy improved direct linear discriminant analysis for nondestructive discrimination of chrysanthemum tea varieties. Foods 2024, 13, 1439. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Y.; Li, Z.; Huang, X.; Shen, T.; Zou, X. Simultaneous and nondestructive diagnostics of nitrogen/magnesium/potassium-deficient cucumber leaf based on chlorophyll density distribution features. Biosyst. Eng. 2021, 212, 458–467. [Google Scholar] [CrossRef]
- Sun, X.; Wang, F.; Zhao, X.; Xie, W.; Guo, X. The estimation modeI of rice leaf nitrogen concentration based on canopy spectrum and BP neural network. Chin. J. Agric. Resour. Reg. Plan. 2019, 40, 35–44. [Google Scholar]
- Yu, H.; Qian, X. Study on the lag time of nitrogen efficiency of maize under different water and fertilizer coupling modes. Tillage Cultiv. 2012, 3–4. Available online: https://link.cnki.net/doi/10.13605/j.cnki.52-1065/s.2012.01.006 (accessed on 25 April 2025).
- Schlemmer, M.; Gitelson, A.; Schepers, J.; Ferguson, R.; Peng, Y.; Shanahan, J.; Rundquist, D. Remote estimation of nitrogen and chlorophyll contents in maize at leaf and canopy levels. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 47–54. [Google Scholar] [CrossRef]
- Tang, Y.; Li, F.; Hu, Y.; Yu, K. NTRI: A novel spectral index for developing a precise nitrogen diagnosis model across pre- and post-anthesis stages of maize plants. Field Crops Res. 2025, 325, 109829. [Google Scholar] [CrossRef]
- Liu, C.; Yu, H.; Liu, Y.; Zhang, L.; Li, D.; Zhang, J.; Sui, Y. Prediction of anthocyanin content in purple-leaf lettuce based on spectral features and optimized extreme learning machine algorithm. Agronomy 2024, 14, 2915. [Google Scholar] [CrossRef]
- Zhang, Y.; Guan, M.; Wang, L.; Cui, X.; Li, T.; Zhang, F. In Situ Nondestructive Detection of Nitrogen Content in Soybean Leaves Based on Hyperspectral Imaging Technology. Agronomy 2024, 14, 806. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, X.; Xiang, Y.; Liang, J.; Guo, J.; Li, W.; Zhang, F. Application of hyperspectral technology for leaf function monitoring and nitrogen nutrient diagnosis in soybean (Glycine max L.) production systems on the Loess Plateau of China. Eur. J. Agron. 2024, 154, 127098. [Google Scholar] [CrossRef]
- Chen, J.; Li, F.; Wang, R.; Fan, Y.; Raza, M.A.; Liu, Q.; Yang, W. Estimation of nitrogen and carbon content from soybean leaf reflectance spectra using wavelet analysis under shade stress. Comput. Electron. Agric. 2019, 156, 482–489. [Google Scholar] [CrossRef]
- Zheng, W.; Rui, G.; Wen, L.; Yong, N.; De, J. Effects of nitrogen, phosphorus and potassium fertilizers on dry matter accumulation and yield of soybean. Soybean Sci. 2008, 27, 588–592+598. [Google Scholar]
- Limin, H. Effects of formula application of nitrogen, phosphorus and potassium fertilizers on soybean yield and economic benefits. Misc. Crops 2003, 174–175. [Google Scholar]
- Shan, H. Research on Spectral Estimation of Soybean Nitrogen Nutrition Under Different Nitrogen Levels and Cropping Patterns. Ph.D. Thesis, Sichuan Agricultural University, Sichuan, China, 2015. [Google Scholar]
- Shu, W.; Yong, M.; Yong, J. Effect of optimized fertilization of nitrogen, phosphorus and potassium on the yield of summer soybean. Soybean Sci. Technol. 2009, 37–41. [Google Scholar]
- Tsakiridis, N.L.; Samarinas, N.; Kokkas, S.; Kalopesa, E.; Tziolas, N.V.; Zalidis, G.C. In situ grape ripeness estimation via hyperspectral imaging and deep autoencoders. Comput. Electron. Agric. 2023, 212, 108098. [Google Scholar] [CrossRef]
- Herold, M.; Roberts, D.A.; Gardner, M.E.; Dennison, P.E. Spectrometry for urban area remote sensing—Development and analysis of a spectral library from 350 to 2400 nm. Remote Sens. Environ. 2004, 91, 304–319. [Google Scholar] [CrossRef]
- XU, X.G.; ZHAO, C.J.; WANG, J.H.; Li, C.J.; Yang, X.D. Nitrogen content monitoring of barley leaves based on new visible-near-infrared spectral characteristics and optimal combination principle. J. Infrared Millim. Waves 2013, 32, 351–358. [Google Scholar] [CrossRef]
- Chunrui, G.; Hao, L.; Jiachen, W.; Xin, Z.; Kunming, H.; Xiaoyan, S. Combined use of spectral resampling and machine learning algorithms to estimate soybean leaf chlorophyll. Comput. Electron. Agric. 2024, 218, 108675. [Google Scholar]
- Yachun, M.; Jie, W.; Wang, C.; Ruibo, D.; Shijia, W.; Yanhua, F.; Mengyuan, X. Research on fusion algorithm based on the imaging spectrum of saddle mountain type iron ore. Spectrosc. Spectr. Anal. 2024, 44, 2620–2625. [Google Scholar]
- Shuangya, W.; Nan, S.; Junwei, L.; Qianwen, G.; Huibing, Y.; Zhiqiang, G. Estimating Chlorophyll Fluorescence Parameters of Rice (Oryza sativa L.) Based on Spectrum Transformation and a Joint Feature Extraction Algorithm. Agronomy 2023, 13, 337. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Li, P.P.; Sun, D.M.; Mao, H.P. Rapid detection method of total nitrogen content in organic matrix based on characteristic spectrum extraction. J. Agric. Mach. 2011, 42, 175–177+192. [Google Scholar]
- Hu, S.; Bao, Y. L. Phenotypic feature extraction of spring wheat based on UAV hyperspectral remote sensing. Agric. Technol. 2024, 44, 1–5. [Google Scholar]
- Liu, K.; Chen, X.; Li, L.; Chen, H.; Ruan, X.; Liu, W. A consensus successive projections algorithm–multiple linear regression method for analyzing near infrared spectra. Anal. Chim. Acta 2015, 858, 16–23. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Barbin, D.; Elmasry, G.; Sun, D.; Allen, P. Potential of hyperspectral imaging and pattern recognition for categorization and authentication of red meat. Innov. Food Sci. Emerg. Technol. 2012, 16, 316–325. [Google Scholar] [CrossRef]
- Du, Z.; Hu, Y.; Buttar, A.N. Analysis of mechanical properties for tea stem using grey relational analysis coupled with multiple linear regression. Sci. Hortic. 2020, 260, 108886. [Google Scholar] [CrossRef]
- Zeng, P.Z.; Wang, W.; Yuan, M.X.; Yang, F.Z. Inverse study on canopy nitrogen content of apple trees based on UAV remote sensing. Shandong Agric. Sci. 2024, 56, 167–173. [Google Scholar] [CrossRef]
- Sun, R. Research on Remote Sensing Monitoring of Wheat Leaf Rust Based on Near-Earth Hyperspectral and Unmanned Aerial Imagery. Ph.D. Thesis, Yangzhou University, Yangzhou, China. Available online: https://link.cnki.net/doi/10.27441/d.cnki.gyzdu.2021.000559 (accessed on 24 April 2025).
- Jianfu, C.; Yunkai, Y.; Hongyu, F.; Mingzhi, X.; Xin, J.; Liaoao, W. Estimation of nitrogen content in ramie leaves based on multi-scale hyperspectral technology. Shandong Agric. Sci. 2025, 57, 165–171. [Google Scholar]
- WenFeng, H.; WeiHao, T.; Chuang, L. Estimation of nitrogen content in rubber tree leaves based on near-infrared spectroscopy and hybrid learning framework. Spectrosc. Spectr. Anal. 2023, 43, 2050–2058. [Google Scholar]
- Faxu, G. Research on estimation of potato canopy water and nitrogen parameters based on UAV hyperspectral remote sensing. Ph.D. Thesis, Gansu Agricultural University, Gansu, China, 2024. [Google Scholar]
- Jinyang, L.; Meiqing, L.; Hanping, M.; Wenjing, Z. Diagnosis of potassium nutrition level in Solanum lycopersicum based on electrical impedance. Biosyst. Eng. 2016, 147, 130–138. [Google Scholar] [CrossRef]
- Zhu, W.; Li, J.; Li, L.; Wang, A.; Wei, X.; Mao, H. Nondestructive diagnostics of soluble sugar, total nitrogen and their ratio of tomato leaves in greenhouse by polarized spectra–hyperspectral data fusion. Int. J. Agric. Biol. Eng. 2020, 13, 189–197. [Google Scholar] [CrossRef]
- Xiao, Z.; Pei, W.; Han, M.; Hong, G.; Qing, L. Detection of the nutritional status of phosphorus in lettuce using THz time-domain spectroscopy. Eng. Agric. 2021, 41, 599–608. [Google Scholar]
- Jin, L.; Xu, Y.; Qiao, W.; Chu, Z.; Yong, H. Predictive modeling of nitrogen content in citrus plant leaves by hyperspectral imaging. Spectrosc. Spectr. Anal. 2014, 34, 212–216. [Google Scholar]
- Guo, F.; Feng, Q.; Yang, S.; Yang, W. Estimation of Potato Canopy Nitrogen Content Based on Hyperspectral Index Optimization. Agronomy 2023, 13, 1693. [Google Scholar] [CrossRef]
- Wang, Y.W.; Ma, X.; Tan, S.Y.; Jia, X.N.; Chen, J.Y.; Qin, Y.J.; Hu, X.H.; Zheng, H.W. Multimodal data fusion of unmanned aircraft remote sensing and ground observation for inversion of rice nitrogen content. J. Agric. Eng. 2024, 40, 100–109. [Google Scholar]
- Wang, B. Inversion of Nitrogen Content in Rice Canopy Based on UAV Hyperspectral Imagery. Ph.D. Thesis, Chengdu University of Technology, Chengdu, China, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).