Bayesian Ensemble Model with Detection of Potential Misclassification of Wax Bloom in Blueberry Images
Abstract
1. Introduction
- A shallow Bayesian–CNN ensemble is used to classify blueberry images according to its wax bloom content. It is shown that the Bayesian approach can better model the classification image problem for small networks despite the increase in the number of parameters included for training.
- A statistical module for estimating the final output of an ensemble set from the Bayesian architecture is proposed. Two metrics are explored: the distance between Gaussian mixture models (divergence between probability functions) and the relationship between the estimated probability of the classes using a quantile comparison approach.
- The method is evaluated for a Blueberry data set where the images are classified according to the wax bloom content of the blueberries [56]. To further validate the proposed method, state-of-the-art methods for combining the outputs of the Bayesian ensemble and detecting potential misclassification are implemented and used for comparison.
2. Materials and Methods
2.1. Blueberry Database
2.2. Shallow Bayesian–CNN Model
2.3. Binary Output Estimation and Potential Misclassification Detection
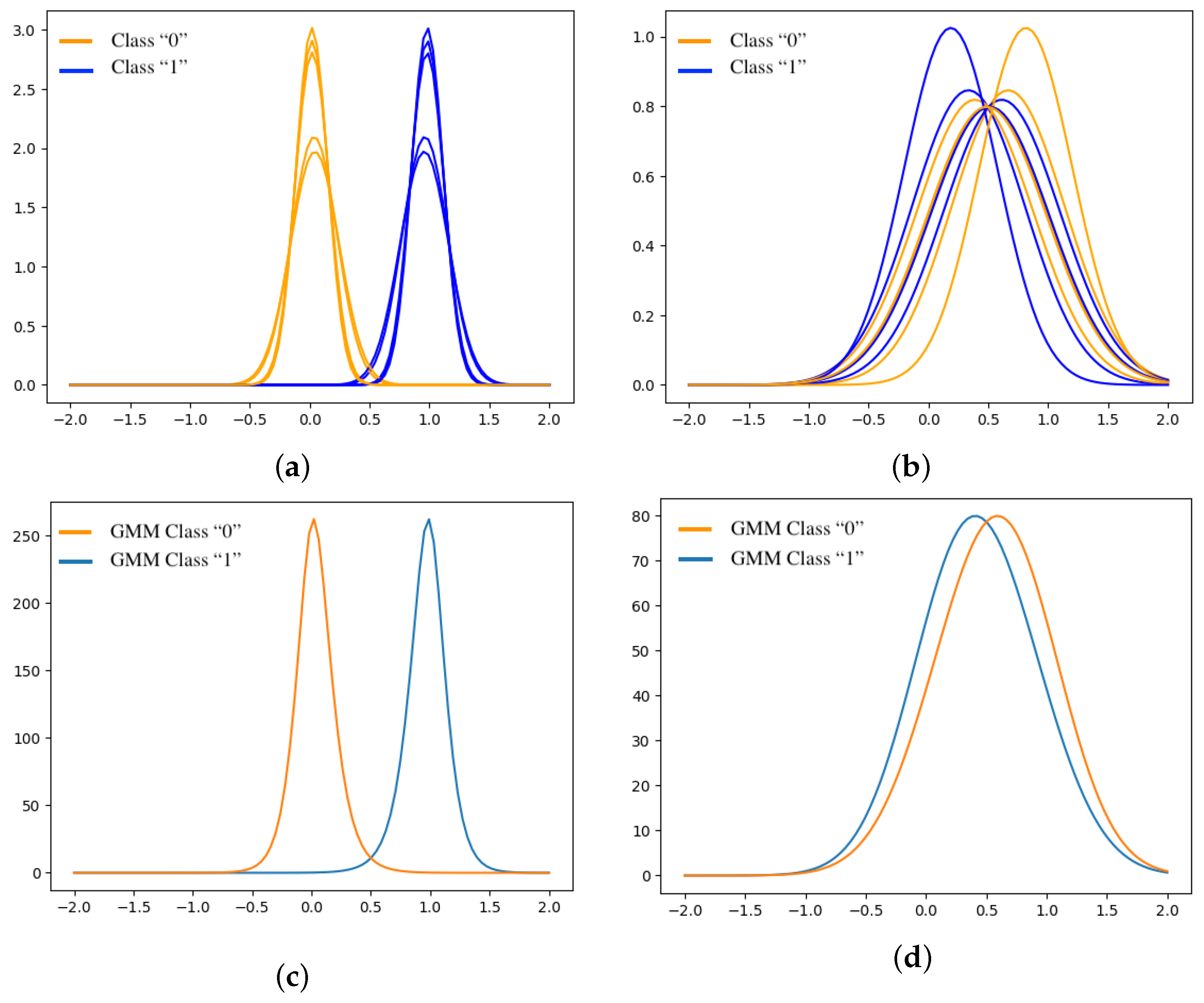
2.3.1. Euclidean Distance ( ) Between Gaussian Mixture Models
2.3.2. Quantile-to-Quantile Relationship Between Classes
2.4. Implementation Details: Software and Hardware
3. Experiments and Results
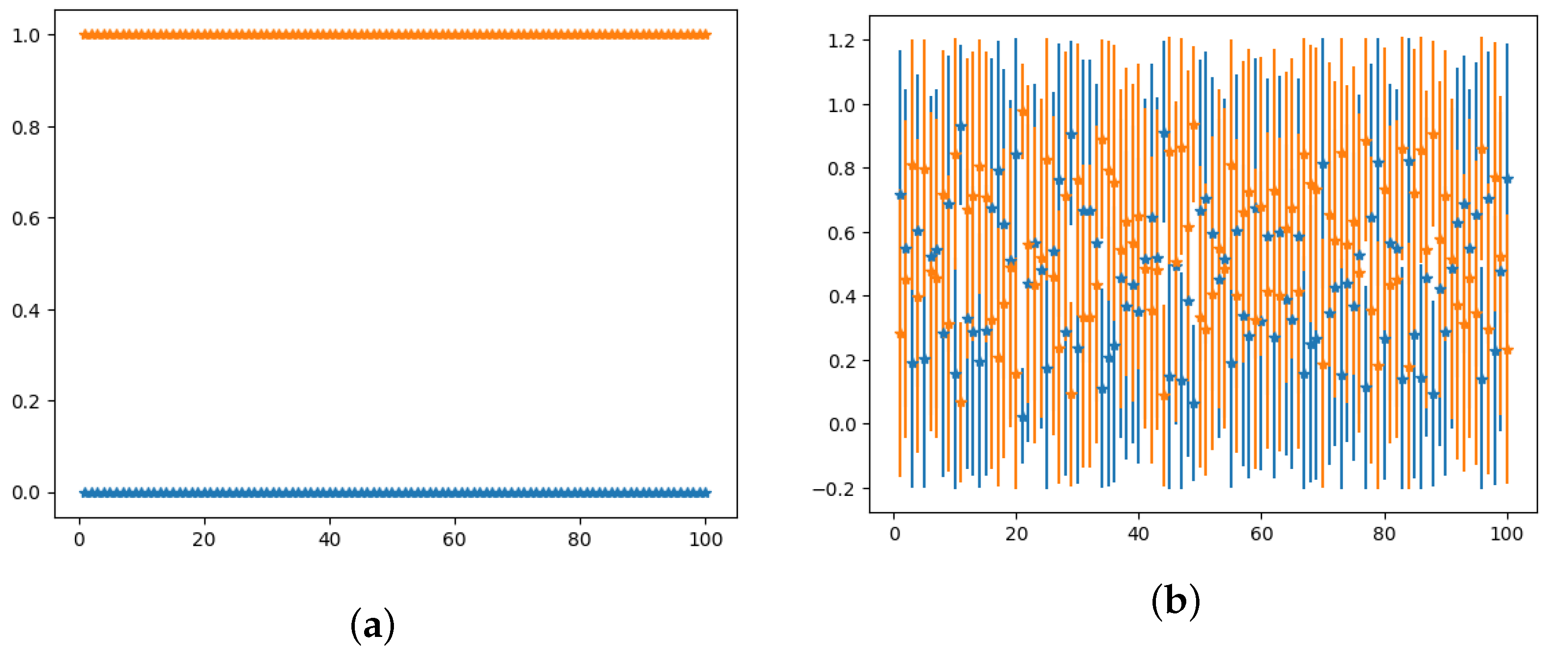
3.1. Bayesian–CNN Ensemble Model
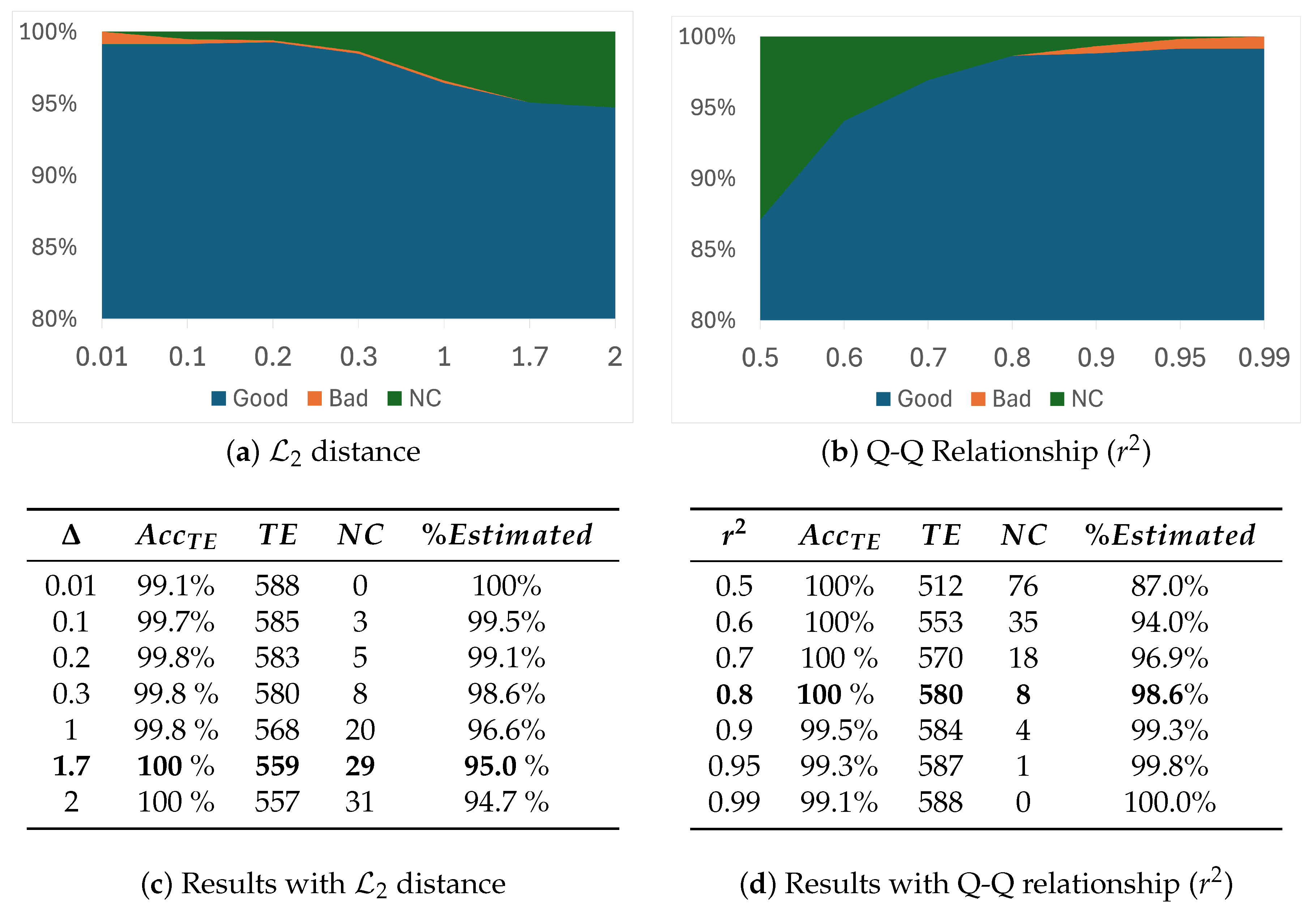
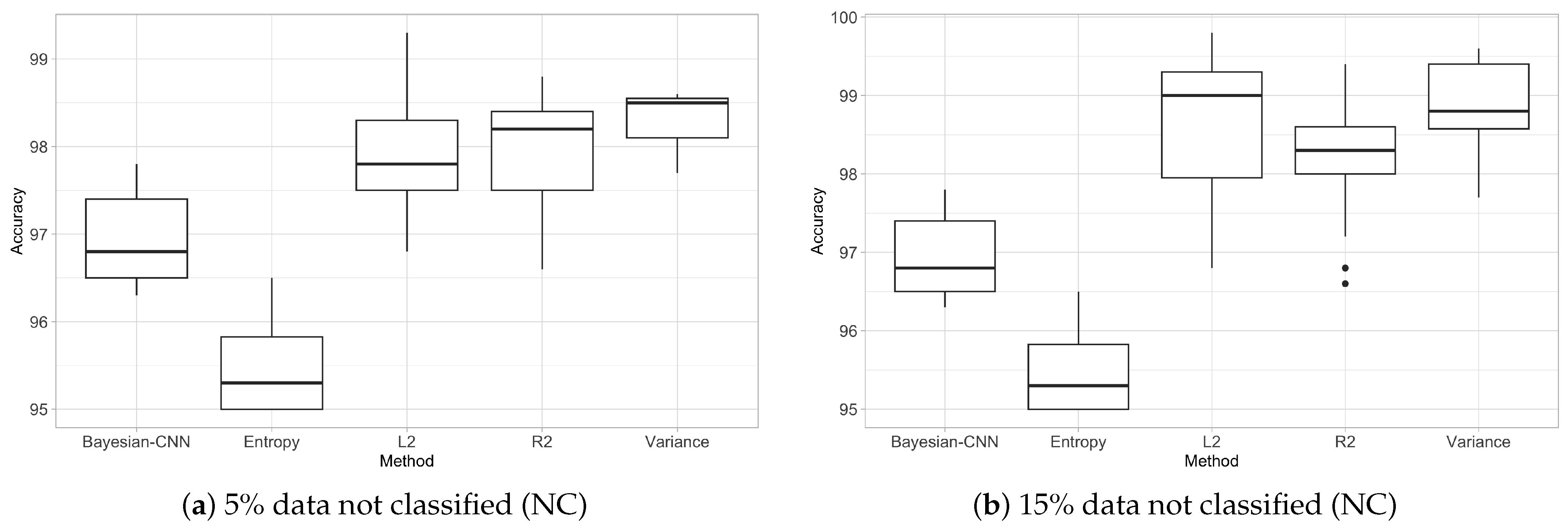
3.2. Potential Misclassification Detection Metrics
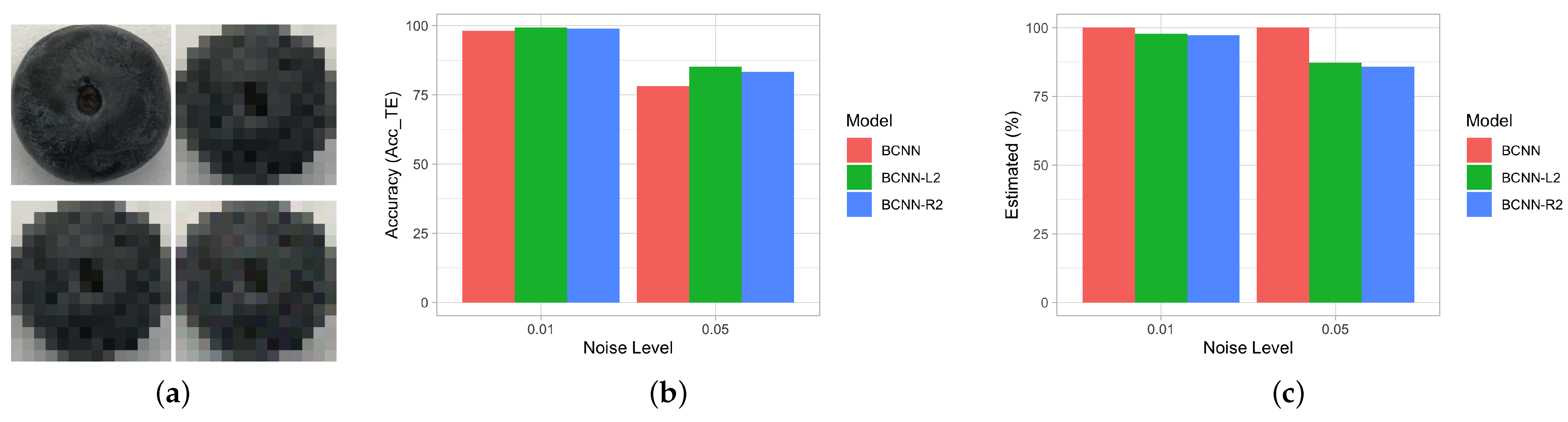
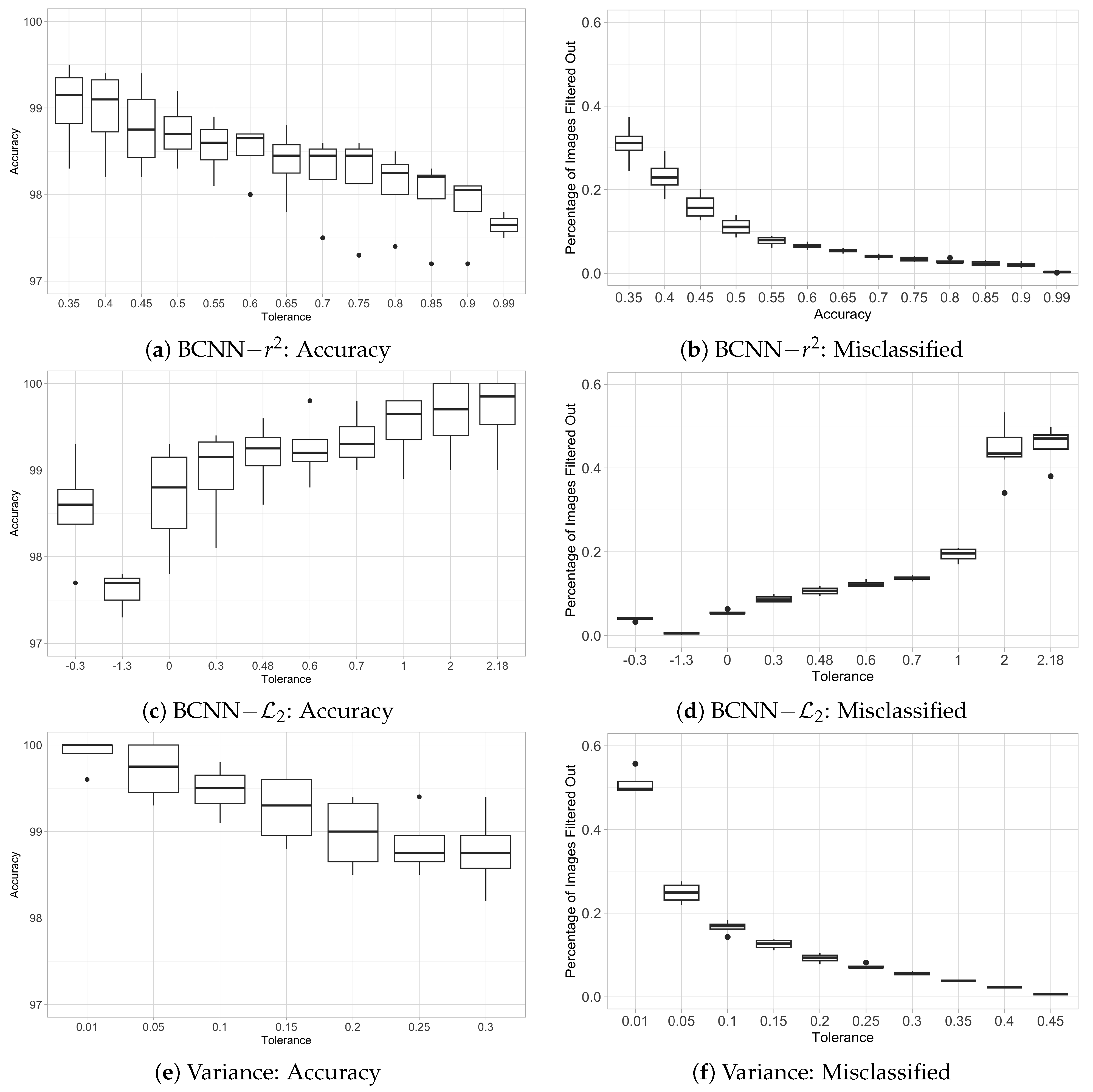
3.3. Trade-Off Between Accuracy and Number of Non-Classified Images (Filtered Out)
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ML | Machine Learning |
| DL | Deep Learning |
| BCNN | Bayesian Convolutional Neural Network |
| DL | Distillation Knowledge |
| CNN | Convolutional Neural Network |
| TP | True Positive |
| TN | True Negative |
| FP | False Positive |
| FN | False Negative |
| Normal (Gaussian) distribution | |
| Divergence between probability density functions ( distance) | |
| Coefficient of determination |
References
- Kalt, W.; Cassidy, A.; Howard, L.R.; Krikorian, R.; Stull, A.J.; Tremblay, F.; Zamora-Ros, R. Recent Research on the Health Benefits of Blueberries and Their Anthocyanins. Adv. Nutr. 2020, 11, 224–236. [Google Scholar] [CrossRef]
- Huamán, R.; Soto, F.; Ríos, A.; Paredes, E. International market concentration of fresh blueberries in the period 2001–2020. Humanit. Soc. Sci. Commun. 2023, 10, 967. [Google Scholar] [CrossRef]
- Mainland, C.M.; Frederick, V. Coville and the History of North American Highbush Blueberry Culture. Int. J. Fruit Sci. 2012, 12, 4–13. [Google Scholar] [CrossRef]
- Lobos, G.A.; Bravo, C.; Valdés, M.; Graell, J.; Lara Ayala, I.; Beaudry, R.M.; Moggia, C. Within-plant variability in blueberry (Vaccinium corymbosum L.): Matur. Harvest Position Canopy Influ. Fruit Firmness Harvest Postharvest. Postharvest Biol. Technol. 2018, 146, 26–35. [Google Scholar] [CrossRef]
- Ktenioudaki, A.; O’Donnell, C.P.; Emond, J.P.; do Nascimento Nunes, M.C. Blueberry supply chain: Critical steps impacting fruit quality and application of a boosted regression tree model to predict weight loss. Postharvest Biol. Technol. 2021, 179, 111590. [Google Scholar] [CrossRef]
- Funes, C.F.; Escobar, L.; Kirschbaum, D. Occurrence and population fluctuations of Drosophila suzukii (Diptera: Drosophilidae) in blueberry crops of subtropical Argentina. Acta Hortic. 2023, 1357, 257–264. [Google Scholar] [CrossRef]
- Yan, Y.; Castellarin, S.D. Blueberry water loss is related to both cuticular wax composition and stem scar size. Postharvest Biol. Technol. 2022, 188, 111907. [Google Scholar] [CrossRef]
- Chu, W.; Gao, H.; Chen, H.; Fang, X.; Zheng, Y. Effects of cuticular wax on the postharvest quality of blueberry fruit. Food Chem. 2018, 239, 68–74. [Google Scholar] [CrossRef]
- Loypimai, P.; Paewboonsom, S.; Damerow, L.; Blanke, M.M. The wax bloom on blueberry: Application of luster sensor technology to assess glossiness and the effect of polishing as a fruit quality parameter. J. Appl. Bot. Food Qual. 2017, 90, 158. [Google Scholar] [CrossRef]
- Gill, H.S.; Murugesan, G.; Mehbodniya, A.; Sekhar Sajja, G.; Gupta, G.; Bhatt, A. Fruit type classification using deep learning and feature fusion. Comput. Electron. Agric. 2023, 211, 107990. [Google Scholar] [CrossRef]
- Sa, I.; Ge, Z.; Dayoub, F.; Upcroft, B.; Perez, T.; McCool, C. DeepFruits: A Fruit Detection System Using Deep Neural Networks. Sensors 2016, 16, 1222. [Google Scholar] [CrossRef] [PubMed]
- Bargoti, S.; Underwood, J. Deep fruit detection in orchards. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 3626–3633. [Google Scholar] [CrossRef]
- Castro, W.; Oblitas, J.; De-La-Torre, M.; Cotrina, C.; Bazán, K.; Avila-George, H. Classification of Cape Gooseberry Fruit According to its Level of Ripeness Using Machine Learning Techniques and Different Color Spaces. IEEE Access 2019, 7, 27389–27400. [Google Scholar] [CrossRef]
- Pacheco, W.; López, F. Tomato classification according to organoleptic maturity (coloration) using machine learning algorithms K-NN, MLP, and K-Means Clustering. In Proceedings of the 2019 XXII Symposium on Image, Signal Processing and Artificial Vision (STSIVA), Bucaramanga, Colombia, 24–26 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Chen, S.; Aditya, S.; Sivakumar, N.; Dcunha, S.; Qu, C.; Taylor, C.J.; Das, J.; Kumar, V. Robust Fruit Counting: Combining Deep Learning, Tracking, and Structure from Motion. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1045–1052. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, K.; Yang, L.; Zhang, D. Fruit detection for strawberry harvesting robot in non-structural environment based on Mask-RCNN. Comput. Electron. Agric. 2019, 163, 104846. [Google Scholar]
- Gupta, S.; Tripathi, A.K. Fruit and vegetable disease detection and classification: Recent trends, challenges, and future opportunities. Eng. Appl. Artif. Intell. 2024, 133, 108260. [Google Scholar] [CrossRef]
- Li, Z.; Xu, R.; Li, C.; Munoz, P.; Takeda, F.; Leme, B. In-field blueberry fruit phenotyping with a MARS-PhenoBot and customized BerryNet. Comput. Electron. Agric. 2025, 232, 110057. [Google Scholar] [CrossRef]
- Gai, R.; Gao, J.; Xu, G. HPPEM: A High-Precision Blueberry Cluster Phenotype Extraction Model Based on Hybrid Task Cascade. Agronomy 2024, 14, 1178. [Google Scholar] [CrossRef]
- Altalak, M.; uddin, M.A.; Alajmi, A.; Rizg, A. Smart Agriculture Applications Using Deep Learning Technologies: A Survey. Appl. Sci. 2022, 12, 5919. [Google Scholar] [CrossRef]
- Seng, K.P.; Ang, L.; Schmidtke, L.M.; Rogiers, S.Y. Computer Vision and Machine Learning for Viticulture Technology. IEEE Access 2018, 6, 67494–67510. [Google Scholar] [CrossRef]
- Li, H.; Lee, W.S.; Wang, K. Identifying blueberry fruit of different growth stages using natural outdoor color images. Comput. Electron. Agric. 2014, 106, 91–101. [Google Scholar] [CrossRef]
- Yang, C.; Lee, W.S.; Gader, P. Hyperspectral band selection for detecting different blueberry fruit maturity stages. Comput. Electron. Agric. 2014, 109, 23–31. [Google Scholar] [CrossRef]
- Ahmad, A.; Saraswat, D.; El Gamal, A. A survey on using deep learning techniques for plant disease diagnosis and recommendations for development of appropriate tools. Smart Agric. Technol. 2023, 3, 100083. [Google Scholar] [CrossRef]
- Barbole, D.K.; Jadhav, P.M.; Patil, S.B. A Review on Fruit Detection and Segmentation Techniques in Agricultural Field. In Proceedings of the Second International Conference on Image Processing and Capsule Networks, Bangkok, Thailand, 27–28 May 2021; pp. 269–288. [Google Scholar] [CrossRef]
- Yang, B.; Xu, Y. Applications of deep-learning approaches in horticultural research: A review. Hortic. Res. 2021, 8, 123. [Google Scholar] [CrossRef]
- Zhu, L.; Spachos, P.; Pensini, E.; Plataniotis, K.N. Deep learning and machine vision for food processing: A survey. Curr. Res. Food Sci. 2021, 4, 233–249. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Zhang, Y.; Du, J.; Guo, X.; Wen, W.; Gu, S.; Wang, J.; Fan, J. Crop Phenomics: Current Status and Perspectives. Front. Plant Sci. 2019, 10, 714. [Google Scholar] [CrossRef]
- Yang, W.; Feng, H.; Zhang, X.; Zhang, J.; Doonan, J.H.; Batchelor, W.D.; Xiong, L.; Yan, J. Crop Phenomics and High-Throughput Phenotyping: Past Decades, Current Challenges, and Future Perspectives. Mol. Plant 2020, 13, 187–214. [Google Scholar] [CrossRef]
- Rossi, R.; Leolini, C.; Costafreda-Aumedes, S.; Leolini, L.; Bindi, M.; Zaldei, A.; Moriondo, M. Performances Evaluation of a Low-Cost Platform for High-Resolution Plant Phenotyping. Sensors 2020, 20, 3150. [Google Scholar] [CrossRef]
- Tausen, M.; Clausen, M.; Moeskjær, S.; Shihavuddin, A.; Dahl, A.B.; Janss, L.; Andersen, S.U. Greenotyper: Image-Based Plant Phenotyping Using Distributed Computing and Deep Learning. Front. Plant Sci. 2020, 11, 1181. [Google Scholar] [CrossRef]
- Quiroz, I.A.; Alférez, G.H. Image recognition of Legacy blueberries in a Chilean smart farm through deep learning. Comput. Electron. Agric. 2020, 168, 105044. [Google Scholar] [CrossRef]
- Feng, W.; Liu, M.; Sun, Y.; Wang, S.; Wang, J. The Use of a Blueberry Ripeness Detection Model in Dense Occlusion Scenarios Based on the Improved YOLOv9. Agronomy 2024, 14, 1860. [Google Scholar] [CrossRef]
- Ni, X.; Takeda, F.; Jiang, H.; Yang, W.Q.; Saito, S.; Li, C. A deep learning-based web application for segmentation and quantification of blueberry internal bruising. Comput. Electron. Agric. 2022, 201, 107200. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Y.; Li, C.; Yang, F. Fully convolutional networks for blueberry bruising and calyx segmentation using hyperspectral transmittance imaging. Biosyst. Eng. 2020, 192, 159–175. [Google Scholar] [CrossRef]
- Ni, X.; Li, C.; Jiang, H.; Takeda, F. Deep learning image segmentation and extraction of blueberry fruit traits associated with harvestability and yield. Hortic. Res. 2020, 7, 110. [Google Scholar] [CrossRef]
- Gonzalez, S.; Arellano, C.; Tapia, J.E. Deepblueberry: Quantification of Blueberries in the Wild Using Instance Segmentation. IEEE Access 2019, 7, 105776–105788. [Google Scholar] [CrossRef]
- Ni, X.; Li, C.; Jiang, H.; Takeda, F. Three-dimensional photogrammetry with deep learning instance segmentation to extract berry fruit harvestability traits. ISPRS J. Photogramm. Remote Sens. 2021, 171, 297–309. [Google Scholar] [CrossRef]
- Tan, K.; Lee, W.S.; Gan, H.; Wang, S. Recognising blueberry fruit of different maturity using histogram oriented gradients and colour features in outdoor scenes. Biosyst. Eng. 2018, 176, 59–72. [Google Scholar] [CrossRef]
- MacEachern, C.B.; Esau, T.J.; Schumann, A.W.; Hennessy, P.J.; Zaman, Q.U. Detection of fruit maturity stage and yield estimation in wild blueberry using deep learning convolutional neural networks. Smart Agric. Technol. 2023, 3, 100099. [Google Scholar] [CrossRef]
- Ropelewska, E.; Koniarski, M. A novel approach to authentication of highbush and lowbush blueberry cultivars using image analysis, traditional machine learning and deep learning algorithms. Eur. Food Res. Technol. 2024, 251, 193–204. [Google Scholar] [CrossRef]
- Niedbała, G.; Kurek, J.; Świderski, B.; Wojciechowski, T.; Antoniuk, I.; Bobran, K. Prediction of Blueberry (Vaccinium corymbosum L.) Yield Based on Artificial Intelligence Methods. Agriculture 2022, 12, 2089. [Google Scholar] [CrossRef]
- Chan, C.; Nelson, P.R.; Hayes, D.J.; Zhang, Y.J.; Hall, B. Predicting Water Stress in Wild Blueberry Fields Using Airborne Visible and Near Infrared Imaging Spectroscopy. Remote Sens. 2021, 13, 1425. [Google Scholar] [CrossRef]
- Hennessy, P.J.; Esau, T.J.; Schumann, A.W.; uz Zaman, Q.; Corscadden, K.W.; Farooque, A.A. Evaluation of Cameras and Image Distance for CNN-Based Weed Detection in Wild Blueberry. Smart Agric. Technol. 2021, 2, 100030. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, M.; Zhai, G. Application of Deep Learning Architectures for Accurate and Rapid Detection of Internal Mechanical Damage of Blueberry Using Hyperspectral Transmittance Data. Sensors 2018, 18, 1126. [Google Scholar] [CrossRef] [PubMed]
- Barbosa Júnior, M.R.; dos Santos, R.G.; de Azevedo Sales, L.; Vargas, R.B.S.; Deltsidis, A.; de Oliveira, L.P. Image-based and ML-driven analysis for assessing blueberry fruit quality. Heliyon 2025, 11, e42288. [Google Scholar] [CrossRef]
- Fan, S.; Li, C.; Huang, W.; Chen, L. Data Fusion of Two Hyperspectral Imaging Systems with Complementary Spectral Sensing Ranges for Blueberry Bruising Detection. Sensors 2018, 18, 4463. [Google Scholar] [CrossRef]
- Moggia, C.; Graell, J.; Lara, I.; Schmeda-Hirschmann, G.; Thomas-Valdés, S.; Lobos, G.A. Fruit characteristics and cuticle triterpenes as related to postharvest quality of highbush blueberries. Sci. Hortic. 2016, 211, 449–457. [Google Scholar] [CrossRef]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A review of uncertainty quantification in deep learning: Techniques, applications and challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Milosevic, M.; Ciric, V.; Milentijevic, I. Network Intrusion Detection Using Weighted Voting Ensemble Deep Learning Model. In Proceedings of the 2024 11th International Conference on Electrical, Electronic and Computing Engineering (IcETRAN), Nis, Serbia, 3–6 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, J.; Li, F.; Ye, F. An Ensemble-based Network Intrusion Detection Scheme with Bayesian Deep Learning. In Proceedings of the ICC 2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Abdullah, A.A.; Hassan, M.M.; Mustafa, Y.T. Leveraging Bayesian deep learning and ensemble methods for uncertainty quantification in image classification: A ranking-based approach. Heliyon 2024, 10, e24188. [Google Scholar] [CrossRef] [PubMed]
- Al-Majed, R.; Hussain, M. Entropy-Based Ensemble of Convolutional Neural Networks for Clothes Texture Pattern Recognition. Appl. Sci. 2024, 14, 10730. [Google Scholar] [CrossRef]
- Njieutcheu Tassi, C.R. Bayesian Convolutional Neural Network: Robustly Quantify Uncertainty for Misclassifications Detection. In Proceedings of the Pattern Recognition and Artificial Intelligence, Istanbul, Turkey, 22–23 December 2019; Djeddi, C., Jamil, A., Siddiqi, I., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 118–132. [Google Scholar]
- Joshi, P.; Dhar, R. EpICC: A Bayesian neural network model with uncertainty correction for a more accurate classification of cancer. Sci. Rep. 2022, 12, 14628. [Google Scholar] [CrossRef]
- Hofmann, N. Bloom Detection in Blueberry Images Using Neural Networks. Master’s Thesis, School of Bussines, Universidad Adolfo Ibañez, Santiago, Chile, 2021. (database available upon request). [Google Scholar]
- Jian, B.; Vemuri, B.C. Robust Point Set Registration Using Gaussian Mixture Models. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1633–1645. [Google Scholar] [CrossRef]
- Arellano, C.; Dahyot, R. Robust ellipse detection with Gaussian mixture models. Pattern Recognit. 2016, 58, 12–26. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, 7–9 May 2015; Conference Track Proceedings. Bengio, Y., LeCun, Y., Eds.; Computational and Biological Learning Society: Wisconsin, WI, USA, 2005. [Google Scholar]
- Howard, A.G.; Zhu, M.; Chen, B.; Kalenichenko, D.; Wang, W.; Weyand, T.; Andreetto, M.; Adam, H. MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications. arXiv 2017, arXiv:1704.04861. [Google Scholar]
- Lecun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, X.; Lei, X.; Wu, C. A novel deep LeNet-5 convolutional neural network model for image recognition. Comput. Sci. Inf. Syst. 2022, 19, 1463–1480. [Google Scholar] [CrossRef]




| Model | Parameters | Accuracy | Image Resolution |
|---|---|---|---|
| VGG16 [59] | 134,268,738 | 99.2% | 224 × 224 |
| MobileNet [60] | 5,148,154 | 98.4% | 224 × 224 |
| LeNet [61,62] | 44,046 | 98.0% | 28 × 28 |
| Proposed BCNN | 1052 | 96.9% | 14 × 14 |
| CNN | 1426 | 92.0% | 14 × 14 |
| Noise Level | Model | % | ||
|---|---|---|---|---|
| Original data set | BCNN-mean | - | ||
| BCNN-Entropy [53] | 97.8% | - | ||
| BCNN- | 29 | |||
| BCNN- | 8 | |||
| BCNN-Variance [55] | 43 | |||
| Added noise (0.01) | BCNN-mean | - | ||
| BCNN-Entropy [53] | - | |||
| BCNN- | 13 | |||
| BCNN- | 16 | |||
| BCNN-Variance [55] | 51 | |||
| Added noise (0.05) | BCNN-mean | - | ||
| BCNN-Entropy [53] | - | |||
| BCNN- | 75 | |||
| BCNN- | 84 | |||
| BCNN-Variance [55] | 199 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arellano, C.; Sagredo, K.; Muñoz, C.; Govan, J. Bayesian Ensemble Model with Detection of Potential Misclassification of Wax Bloom in Blueberry Images. Agronomy 2025, 15, 809. https://doi.org/10.3390/agronomy15040809
Arellano C, Sagredo K, Muñoz C, Govan J. Bayesian Ensemble Model with Detection of Potential Misclassification of Wax Bloom in Blueberry Images. Agronomy. 2025; 15(4):809. https://doi.org/10.3390/agronomy15040809
Chicago/Turabian StyleArellano, Claudia, Karen Sagredo, Carlos Muñoz, and Joseph Govan. 2025. "Bayesian Ensemble Model with Detection of Potential Misclassification of Wax Bloom in Blueberry Images" Agronomy 15, no. 4: 809. https://doi.org/10.3390/agronomy15040809
APA StyleArellano, C., Sagredo, K., Muñoz, C., & Govan, J. (2025). Bayesian Ensemble Model with Detection of Potential Misclassification of Wax Bloom in Blueberry Images. Agronomy, 15(4), 809. https://doi.org/10.3390/agronomy15040809







