Additionally, this paper presents a leader-based sparrow optimization algorithm to tackle the issues of non-optimal paths and poor smoothness. This method ensures rapid convergence while accommodating curvature constraints, enabling an optimization process with varying priorities. Consequently, the optimized path achieves the maximum curvature constraint and optimal path length. HPS-RRT* exhibits the following innovative features:
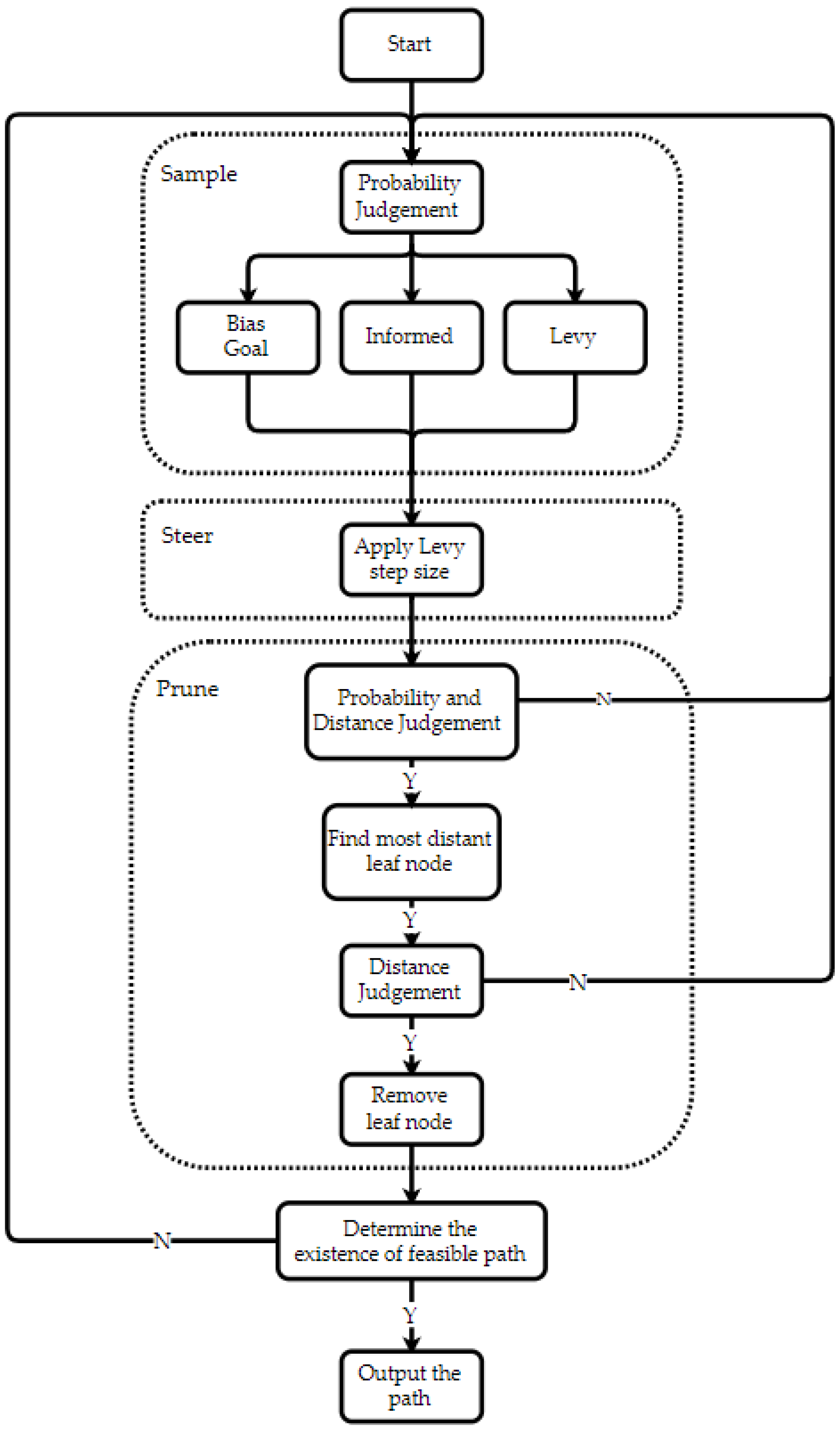
3.1. Hybrid Sampling Strategy
The traditional RRT* algorithm is characterized by slow convergence, blindness, and a tendency to become trapped in local optima. To address these shortcomings, HPS-RRT employs a hybrid sampling strategy that probabilistically selects from different sampling methods to balance their respective strengths and weaknesses. The sampling strategies utilized in HPS-RRT* are outlined in
Table 2:
As shown in
Table 2, each sampling strategy has its advantages and disadvantages.
The Bias-goal strategy includes a certain probability of directly selecting the goal point as a sample during the sampling process, allowing for a quicker approach to the target. However, this method is prone to becoming trapped in local optima and has lower search efficiency in complex and diverse environments.
Inspired by the Informed-RRT* algorithm, the Informed strategy narrows the sampling space during exploration. It focuses on the starting point and the node closest to the goal, constructing an ellipse with a semi-major axis of twice the distance between these two points. The sampling process within this ellipse is as follows:
Here, and represent the axis value of , and and represent the axis value of .
- 3.
Sample within a horizontally oriented ellipse with the same semi-major and semi-minor axes as the constructed ellipse;
- 4.
Apply the rotation matrix to the sampled points matrix to rotate it into the constructed ellipse, resulting in the actual sampled point coordinates, as given by the following formula:
where
represents the coordinates of the sampled points,
is the corresponding rotation matrix, and
denotes the coordinates of the points within the horizontal ellipse.
This sampling strategy utilizes a smaller, effective sampling space, improving search efficiency and optimizing the path. However, frequent computations can consume significant computational resources, placing certain demands on the processing platform. Additionally, the strategy exhibits poor adaptability in complex obstacle regions, making it challenging to find feasible paths.
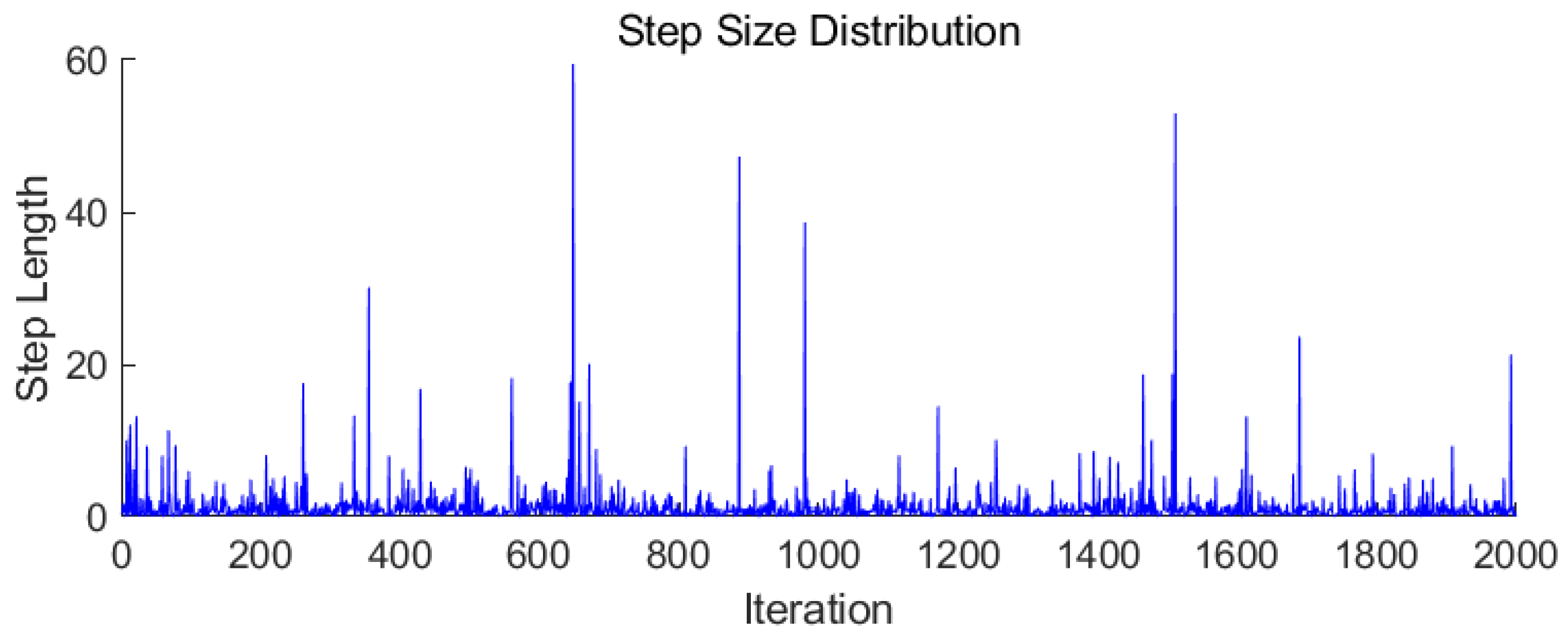
Lévy sampling is a sampling strategy that follows a Lévy distribution, characterized by its heavy-tailed probability distribution. In sampling, it manifests as frequent small-range samples interspersed with occasional large-range samples, a process known as the Lévy flight strategy. The sampling procedure is as follows:
The Lévy sampling strategy enhances algorithm adaptability in complex environments through localized sampling. Additionally, occasional large-range sampling helps to mitigate local optima, improving global optimality; however, it exhibits poor performance in local optimization.
Each sampling strategy has its advantages and disadvantages. The HPS-RRT* algorithm balances these by probabilistically selecting different sampling strategies at each step, allowing it to enhance path quality and adaptability in complex environments while maintaining convergence speed.
3.3. Leaf Prune
In the RRT* algorithm, each node connection is retained throughout the exploration process, which may lead to tree growth in incorrect or suboptimal directions. This can decrease exploration efficiency and increase the time required for path planning. To address this issue, HPS-RRT* introduces a pruning strategy inspired by ecological mechanisms in natural tree growth, such as apical dominance and lower branch degradation. This strategy aims to optimize the algorithm’s exploration and convergence performance. The specific process is outlined as follows:
When connecting a new node , if it is closer to the target than the nearest node , a pruning decision is initiated.
After meeting certain probabilistic criteria, the process proceeds, simulating the uncertainty in tree growth.
The farthest node from , labeled , is identified, and the distance to is calculated.
If this distance exceeds half of the direct distance from the start point to the target, the node is eliminated, simulating the degradation or wilting of lower leaves.
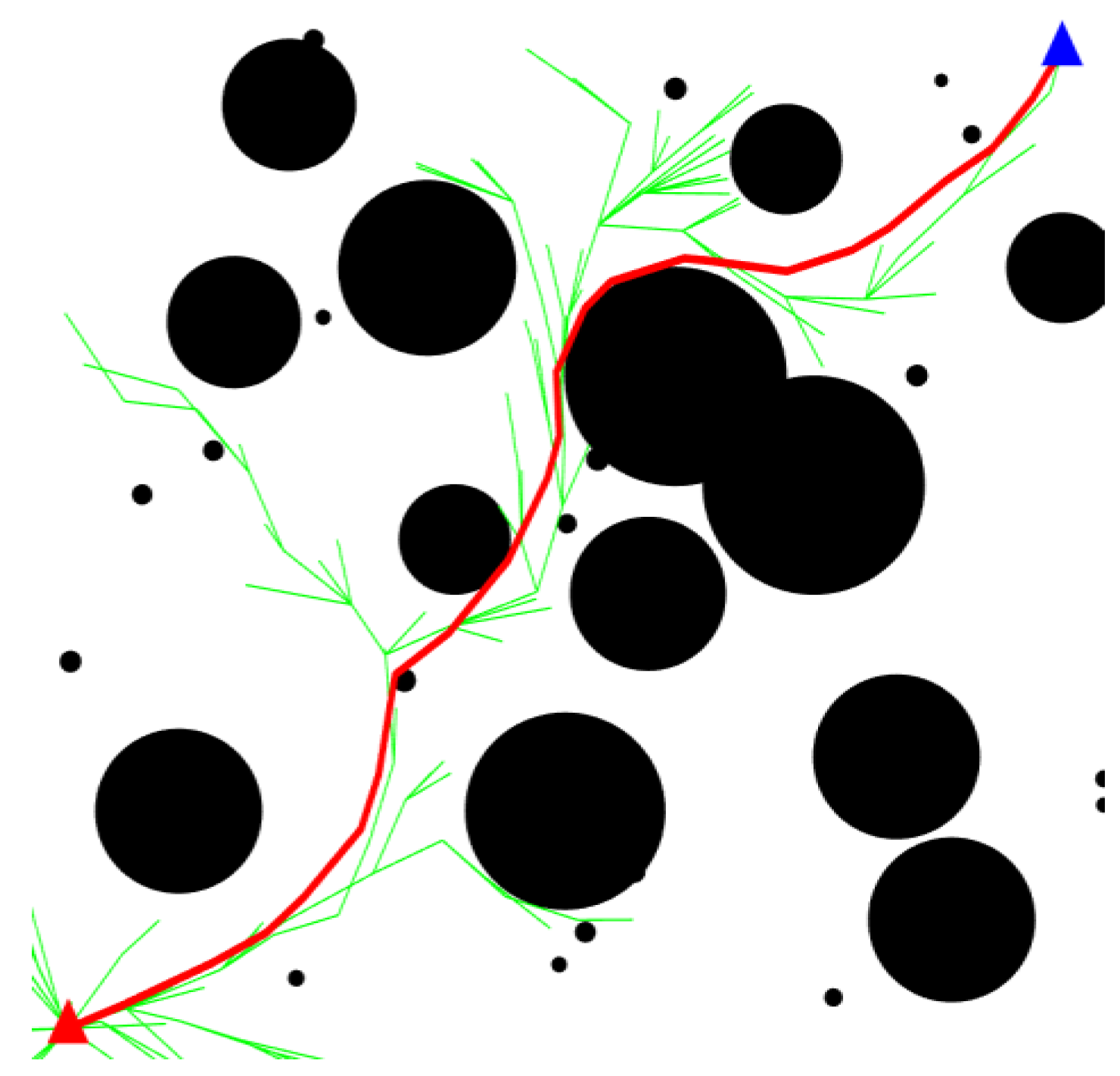
This strategy ensures stable tree growth during the initial exploration phase, allowing for comprehensive expansion and preventing premature convergence to local optima. In the later stages, as the tree approaches the target point, the pruning mechanism gradually directs the tree toward the target, reducing ineffective branches and enhancing algorithm efficiency. By removing nodes that are distant from the target, unnecessary search areas can be effectively minimized, conserving computational resources. The resultant effect is illustrated in
Figure 6.
In
Figure 6,
represents the new node,
denotes the nearest point to the target before connecting the new node,
is the farthest node from
,
indicates the starting point, and
signifies the target point. Distances
a and
b correspond to the distances from
and
to the target, respectively. The circular shapes represent nodes, solid lines indicate actual connections, and dashed lines illustrate the pruning operation.
From the diagram, it can be observed that when
b <
a and the distance and probability criteria are satisfied, a pruning operation is performed. The farthest node
from
and its connecting segments are pruned, as indicated by the dashed lines in
Figure 6.
This visually demonstrates that the overall trend of the tree after pruning is more aligned with the target point, akin to the growth of terminal buds in branches. This improvement enhances the convergence rate during node expansion, directing the expansion closer to the target point and reducing the exploration of erroneous directions.
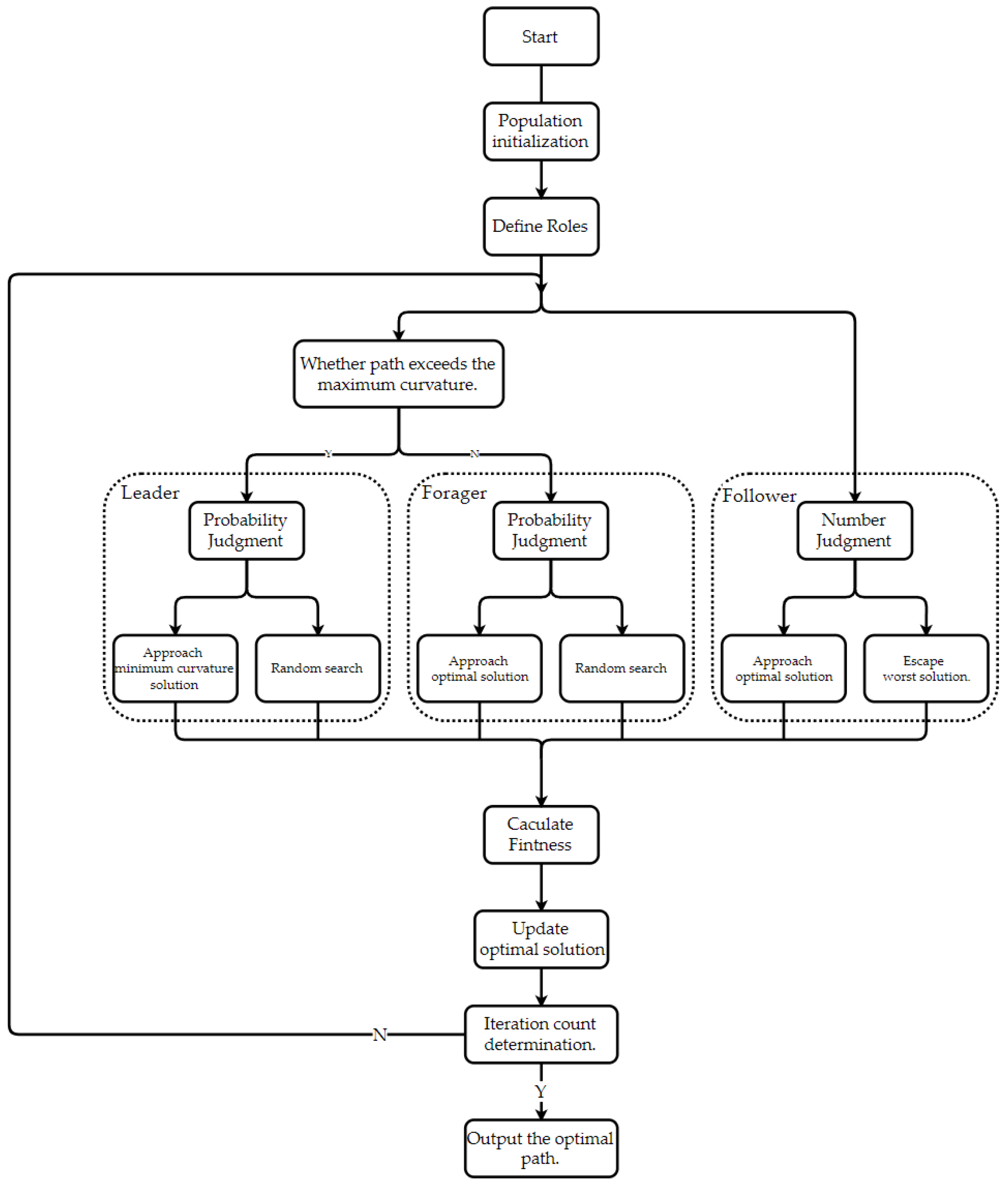
3.4. Leader-Based Sparrow Optimization Algorithm
Conventional RRT or RRT* algorithms often yield paths that are unsuitable for tracking by tracked robots in orchards. Some paths exhibit large curvature, failing to meet the maximum turning radius requirements of the tracked robots, which hinders effective tracking performance. Additionally, the generated paths are typically excessively long and not globally optimal, leading to increased operational costs and reduced efficiency for agricultural robots. This paper proposes an optimization strategy based on vehicle kinematic constraints—the improved sparrow search algorithm—to address this issue.
The sparrow search algorithm, as a heuristic swarm intelligence optimization method, is widely applied in various optimization scenarios. Its core idea is to simulate the foraging and anti-predation behaviors of sparrows, leveraging the collaboration and division of labor among individual members of the population to achieve effective global search and avoid local optima. In the conventional sparrow search algorithm, there are typically two roles: foragers and followers. Foragers are responsible for approaching the global optimum and enhancing solution diversity through random searches, simulating the foraging process of sparrows. On the other hand, followers focus on tracking the optimal solution while escaping from the worst solution, mimicking the anti-predation behavior and cooperative functionality of sparrows [
29]. The sparrow search algorithm is characterized by strong global search capability, fast convergence speed, and fewer parameters that are easy to adjust. The general procedure is as follows:
Initialize the sparrow population;
Assign roles to the sparrows;
Execute functions based on assigned roles;
Calculate fitness and update the optimal solution;
Check if the maximum iteration count is reached; if so, output the optimal solution; otherwise, return to step 3 for further iterations.
In path optimization, two key metrics require significant attention: the maximum curvature (or smoothness) of the path, which affects its suitability for actual navigation tasks and is critical for the tracking performance of the robot, and the path length, where shorter paths can reduce navigation time costs and enhance operational efficiency. In conventional sparrow search algorithm implementations, optimizing both maximum curvature and path length simultaneously may lead to paths with a greater maximum curvature after optimization compared to before. Additionally, while traditional path smoothing algorithms, such as B-spline optimization, can create smoother paths, they often overlook changes in path length, potentially resulting in an optimized path that is longer than the original. To comprehensively consider the two performance metrics mentioned above, ensuring that the maximum curvature of the path meets the robot’s movement requirements while achieving a shorter and safer path, HPS-RRT* employs an improved sparrow search algorithm.
The HPS-RRT* algorithm integrates and enhances the sparrow search algorithm for path optimization by innovatively proposing a leader-based sparrow optimization algorithm. This approach aims to optimize curvature while ensuring path optimality. The optimization process is shown in
Figure 7:
At the beginning of the optimization loop, the sparrow optimization algorithm calculates the fitness value based on the current path length and maximum curvature. The formula is as follows:
where
and
represent the penalty weights,
denotes the path length, and
indicates the maximum curvature of the path.
Next, a population of sparrows is randomly initialized, where this initialization involves applying random perturbations to the control points of the existing path. This process yields sparrows with diverse solutions, which are then categorized into different roles proportionally.
During each optimization iteration, the algorithm checks whether the current path meets the maximum curvature constraint to ensure feasibility. If the constraint is not satisfied, the leader mechanism is triggered. In this case, the leader assumes the role of the forager with a certain probability, guiding the population towards the solution with minimal curvature or conducting a random search.
The adjustment of control points in the path optimization can be expressed by the following formula:
In this context, represents the original control points, while denotes the optimized control points. The parameter is a random number between 0 and 1, which should be adjusted according to the size of the map and the path. indicates the direction of the solution with the minimum curvature and represents a random direction. Finally, p is a random probability between 0 and 1.
The leader mechanism effectively reduces the maximum curvature of the path, enhances path smoothness, and maintains solution diversity during the optimization process, thereby preventing convergence to local optima.
If the path satisfies the constraints, the forager will converge towards the optimal solution with a certain probability or explore in a random direction. This can be expressed by the following formula:
Here, represents the original control points, and denotes the optimized control points. is a random number between 0 and 1, indicates the direction of the current optimal solution, represents a random direction, and p is a random probability between 0 and 1.
The forager’s search allows the population to explore to a certain extent while simultaneously seeking the optimal solution, thereby enhancing the diversity of solutions.
The followers will either converge toward the optimal solution or evade danger by moving away from the worst solution. This can be expressed by the following formula:
Here, represents the original control points, while denotes the optimized control points. is a random number between 0 and 1, indicates the direction of the current optimal solution, represents the direction to escape from the worst solution, and p is a random probability between 0 and 1.
The followers are responsible for maintaining the stability of the population’s trend, with half of them approaching the optimal solution and the other half escaping the worst solution. This leads to an overall improvement in the population’s direction.
At the end of each iteration, the fitness of each sparrow in the population is calculated, and the optimal and worst solutions are updated, continuing until the maximum number of iterations is reached.
The final optimized path obtained through the above optimization process achieves optimality while satisfying curvature constraints. The sparrow optimization algorithm demonstrates significant advantages in convergence speed and global optimization compared to traditional algorithms such as SA and PSO. Additionally, the improved sparrow optimization algorithm features a prioritized optimization process that allows for flexible expansion and differentiated optimization of various path characteristics to meet diverse path requirements.
This algorithm has significant advantages over traditional path smoothing optimization methods, such as B-spline optimization, which often struggles to balance path length requirements and safety, leading to higher collision risks with obstacles. The improved sparrow optimization algorithm effectively addresses this issue by simultaneously optimizing path smoothness and globally optimizing path length to achieve an overall optimal solution.