Simulation and Experiment for Retractable Four-Point Flexible Gripper for Grape Picking End-Effector

Abstract

To address the automation of table grape harvesting, a clamping and cutting integrated, four-point flexible end-effector is designed, based on the biological and mechanical characteristics of grapes. The clamping device is validated in regard to force closure requirements using a force spiral. On this basis, a finite element model of the grape pedicel–blade system is established, and dynamic simulations of pedicel cutting are conducted using ANSYS 2021/LS-DYNA. The simulation results indicate that when the pedicel diameter is 10 mm, the maximum shear stress is 1.515 MPa. A kinematic simulation of the clamping device is performed using ADAMS, producing a contact force curve between the end effector’s finger joints and the grape during the clamping process. The simulation results show that the peak contact force of 11 N is lower than the critical rupture force of the grape (24.79 N), satisfying the requirements for flexible, low-damage harvesting. Furthermore, to address the vulnerability of grapes, a contact-force control system is designed, employing a position–speed–torque three-loop control strategy. Pressure sensors integrated into the four clamping fingers provide real-time feedback to adjust the contact force, ensuring precise clamping control. Finally, a physical prototype of the end effector and controller is developed, and harvesting trials are conducted in a vineyard. The harvesting success rate reaches 96.7%, with an average harvesting time of 13.7 s per trial. The grape cluster damage and berry drop rates are 3.2% and 2.8%, respectively, meeting the expected design requirements.

1. Introduction

China is one of the world’s largest producers of table grapes, accounting for approximately 50% of global production. Table grapes are cultivated ata large scale across most regions of China and they have become a highly efficient cash crop [1]. While modern agriculture is undergoing a transformation towards intelligence and mechanization, the automation level in the harvesting of table grapes—a fruit with high economic value and extensive cultivation—lags significantly behind other production stages. This gap has emerged as a critical bottleneck constraining both industrial efficiency and quality consistency. This has become one of the key constraints affecting industry efficiency and quality stability. Currently, table grape harvesting primarily relies on manual labor. This approach is not only labor-intensive and inefficient but is also hampered by a shortage of specialized workers. Furthermore, the high variability inherent in manual operations often leads to issues such as berry bruising and detachment, thereby compromising postharvest marketability and the consumer experience [2,3,4,5]. With the diminishing demographic dividend, the harvesting robots have evolved from exploratory research to a practical necessity [6,7,8,9,10].

Compared to fruits such as apples and citrus, grapes possess a more complex biological structure: they are tightly arranged, exhibit diverse shapes, and have delicate skins [11]. Current end-effectors for harvesting robots are mainly classified into three types: suction cup-based, soft-finger-based, and mesh-enveloping end-effectors. Yuseung Jo et al. designed a suction cup-based soft gripper to adapt to the contour and surface characteristics of cucumbers, achieving a harvesting success rate of 86.2% with a fruit damage rate of 4.7% [12]. Francesco Visentin et al. developed a flexible, sensor-equipped gripper suitable for harvesting small fruits like strawberries. In laboratory experiments, the harvesting success rate was 82% [13]. Goulart, Chen, and others implemented a soft gripper based on the Fin-Ray structure, utilizing two-finger, three-finger, and multi-finger configurations to achieve constant force gripping for fruits of varying sizes [14]. Xu Y et al. designed a three-finger mechanical gripper with adjustable angles, suitable for harvesting spherical or cylindrical fruits such as cherries, loquats, and cucumbers [15], and Xiong et al. developed a tomato harvesting robot based on 3D vision, equipped with a two-finger flexible gripper. In indoor tomato harvesting trials, the success rate was nearly 96.8%, but in actual farm environments, the average success rate was only 53.6% [16]. Vrochidou et al. designed an end-effector comprising a pair of flexible clamping fingers with a parallel blade for grape harvesting [17,18], though its subsequent practical performance has not been documented. Du Jincai et al. proposed an end-effector with curved rigid fingers [19]; however, this design struggles to precisely control the grasping force on grape clusters, often leading to fruit skin damage or berry detachment. In summary, suction cup-based systems are suitable for fruits with smooth surfaces [20]; soft bionic grippers are flexible and cause minimal damage to the fruit but are mainly used for small, lightweight fruits [21,22]; and mesh-enveloping systems are suitable for fruits with simple structures [23]. However, given the irregular shape and large mass of grape clusters, unstable clamping often occurs with these instruments.

In terms of control strategies, various methods have been introduced to improve clamping stability and operational flexibility, such as PID and fuzzy control. Cao D et al. installed thin-film force sensors inside a mushroom clamping device and utilized PID algorithms to achieve precise clamping force control, thus protecting the mushrooms from damage [24]. Zixu Li et al. employed fuzzy PID control to enhance the stability and speed of the grasping force for kiwi fruit, reducing the system response time to 1.08 s [25]. Shan Haiyong et al. adopted a control strategy that was “primarily automatic with manual assistance” [26], enhancing operational safety and accuracy. Yang Lei designed trapezoidal acceleration/deceleration, fuzzy PID-based position, and a velocity synchronization control algorithm to improve the success rate [27]. Although related studies have achieved initial progress and have effectively improved the response speed and stability of the control systems, there is still a lack of research and experimental validation regarding an efficient and low-damage end-effect or specifically designed for harvesting table grapes, considering their unique biomechanical characteristics.

To address this challenge, this study aimed to develop an end-effector system to reduce grape damage and improve the success rate during robotic harvesting. To achieve this, we designed an end-effector with a four-point convergent flexible clamping mechanism. Our methodology included a comprehensive analysis of the mechanical properties of grape bunches, conducted dynamic simulations of stem cutting using ANSYS/LS-DYNA, and performed contact force simulations with ADAMS. Furthermore, we designed a real-time contact force control system based on a position–speed–torque triple closed-loop control strategy. The results demonstrate that the four-point convergent flexible clamping structure ensures uniform force distribution and stable lifting of grape bunches. The implemented control system successfully provided real-time feedback on contact force. Field tests validated the system’s performance, achieving a high harvesting success rate of 96.7% while maintaining a low damage rate of only 3.2%.

2. Materials and Methods

2.1. Biological and Mechanical Property Analysis of Table Grapes

Biological and mechanical properties were measured for three grape varieties: Kyoho, Rose, and Red Globe. The results are summarized in

Table 1. Biological properties measurement data fortable grapes.

Parameter	Grape Cluster Length/mm	Grape Cluster Equatorial Diameter/mm	Mass/g	Pedicel Diameter/mm
Kyoho Grape	140~245	100~200	300~1600	5.8~10
Rose Grape	130~200	90~190	320~1300	4.6~9.5
Red Globe	180~290	100~180	400~2000	5.3~10.8

.

Transverse and longitudinal compression tests on individual grape berries were conducted using a desktop electronic universal testing machine from BosinTech Industrial Development Co., Ltd. (Shanghai, China) to determine the maximum critical rupture force. Shear tests were performed on grape pedicels to obtain the shear force and shear strength, as summarized in

Table 2. Mechanical properties measurement data of table grapes.

Property	Kyoho Grape	Rose Grape	Red Globe Grape
Lateral Compression Critical Rupture Force/N	31.59	27.96	34.54
Longitudinal Compression Critical Rupture Force/N	27.86	25.79	29.51
Pedicel Shear Force/N	88.75	85.37	92.36
Shear Strength/MPa	1.387	1.349	1.426

.

The weight of a grape typically ranges from 0.3 to 2 kg, and the critical rupture force for a grape is between 25.79 and 34.54 N. The condition for the stable clamping of the grape, ensuring it does not fall, is when the gravitational force G of the grape equals the static frictional force between the grape and the four-point clamping end-effector fingers. This means the minimum contact force F_min of a single finger must satisfy Equation (1). Taking a 2 kg grape as an example, with a static friction coefficient of µ =0.6, the minimum contact force F_min is 8.34 N. Therefore, the initial threshold for stable clamping without damaging the grape is determined to be 11 N.

$$F_{\min }\ge {\displaystyle \frac{G}{4\mu }}$$

(1)

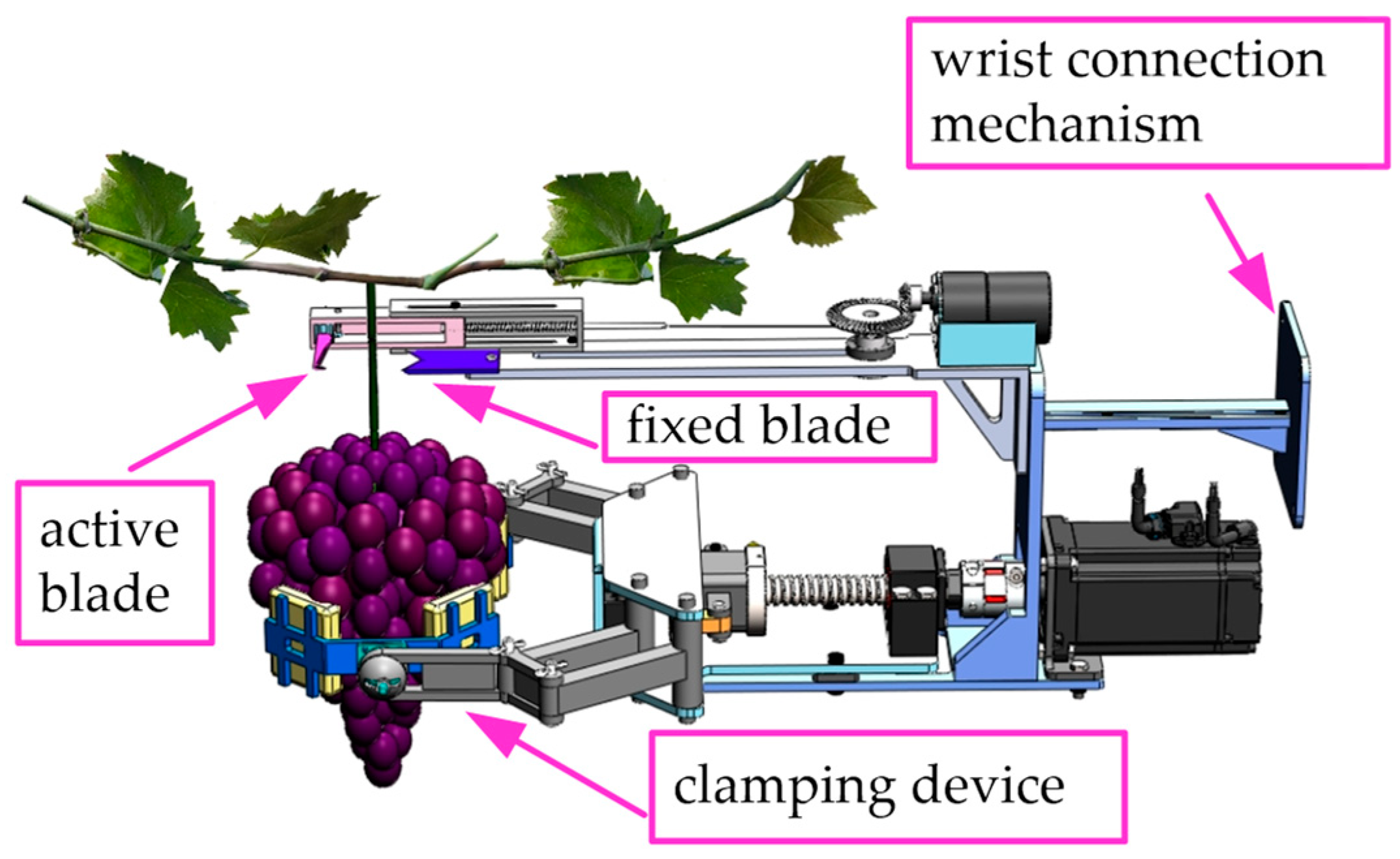
2.2. End-Effector Design Scheme

Due to the variations in the grape growing environment, there are significant differences in the size and shape of grape clusters. This paper proposes a retractable four-point flexible clamping end-effector for grape harvesting, consisting of a clamping device, a cutting device, and a wrist connection mechanism, as shown in Figure 1. The linkage mechanism and four-point gripping end-effector are constructed from PLA material to provide essential structural support. A layer of flexible silicone padding is attached to the inner surface of the gripping device, which enhances friction while reducing compression on the fruit skin. In the clamping device, four pressure sensors are installed on the four fingers of the four-point clamping end-effector to measure the contact force between the clamping device’s fingers and the grape in real time.

The clamping device is connected to the four-point fixed-angle end effector and linkage mechanism via a horizontal limit spherical universal joint, allowing the four-point clamping end to adjust its angle within the plane of the grape cluster’s equatorial surface. This ensures that the clamping surface remains perpendicular to the central axis of the grape cluster’s equatorial plane, enabling adaptations to grape clusters of different shapes. The cutting device uses a retractable structure in combination with a movable and fixed blade to complete the pedicel cutting and grape cluster separation. Figure 2 illustrates the workflow breakdown of the end-effector.

The end-effector is connected to the robotic arm via the wrist connection mechanism. After the RealSense 435 Depth camera (Intel Corporation, Santa Clara, CA, USA) locates the target grape, the robotic arm guides the harvesting device to the grape cluster’s position (Figure 2a). The end-effector continues to advance, and the moving blade of the cutting device makes contact with the grape pedicel. At this point, the contact force between the moving blade and the pedicel gradually increases, causing the torsion spring to compress due to the reaction force from the pedicel. The moving blade is progressively retracted into the blade casing (Figure 2b). Once the grape pedicel reaches the cutting range, the torsion spring resets to its initial uncompressed state, and the clamping device moves toward the center of the grape cluster. The clamping device gradually closes until the grape cluster is stably held. During this process, the ball-and-socket limit mechanism adjusts the angle adaptively according to the shape and orientation of the grape, ensuring that the four-point clamping end remains perpendicular to the line connecting the grape’s centroid and radius, maintaining force closure during the clamping process (Figure 2c). When the clamping device is stably holding the grape cluster, the moving blade begins to cut in cooperation with the fixed blade, severing the pedicel (Figure 2d). After the cutting operation is finished, the robotic arm guides the harvesting device to the unloading position, completing a single harvesting cycle.

2.3. Clamping Device Force Closure Analysis

To verify the stability of the clamping device under complex operating conditions, a static model based on force spiral theory is constructed to analyze the constraints on the contact forces and the criteria for force closure. The stability of the clamping device under various external forces is then validated. A coordinate system is established with the centroid of the grape cluster as the origin, and the grape cluster is simplified as a cylinder. The contact points between the fingers and the grape cluster model are labeled as $C_i$ (where i = 1, 2, 3, and 4). The central angle between adjacent contact points is denoted as θ (for i = 1 to 4). A local coordinate system is defined by the normal, tangential, and axial basis vectors ${\mathbf{n}}_i$, ${\mathbf{t}}_i$, and ${\mathbf{o}}_i$ with the corresponding position vectors represented as ${\mathbf{r}}_i$. The object coordinate system and the contact point coordinate system are shown in Figure 3.

The contact force vector and the force spiral at each contact point are defined as ${\mathbf{f}}_i$ and ${\mathbf{w}}_i$, as shown in Equations (2) and (3), respectively. It is assumed that all the contact points lie on the same cross-section. The position vector from the centroid to the contact point is defined as ${\mathbf{r}}_i$, and the force spiral equilibrium equations are established as shown in Equations (4) and (5).

$${\mathbf{f}}_i=f_{n,i}{\mathbf{n}}_i+f_{t1,i}{\mathbf{t}}_i+f_{t2,i}{\mathbf{o}}_i$$

(2)

$${\mathbf{w}}_i=\left[\begin{array}{c}{\mathbf{f}}_i\\ {\mathbf{r}}_i\text{×}{\mathbf{f}}_i\end{array}\right]$$

(3)

$${\mathbf{r}}_i={\left[R\cos {\theta }_i,R\sin {\theta }_i,0\right]}^T$$

(4)

$${\displaystyle \sum _{i=1}^4{\mathbf{w}}_i+{\mathbf{w}}_{ext}=0}$$

(5)

where, ${\mathbf{f}}_i$ is contact force vector at the $i$-th contact point (N); ${\mathbf{n}}_i$ is the normal unit vector on the equatorial plane of the grape cluster at the $i$-th contact point; ${\mathbf{t}}_i$ is the unit vector along the major diameter direction of the grape cluster at the $i$-th contact point; ${\mathbf{o}}_i$ is the unit tangent vector on the equatorial plane of the grape cluster at the $i$-th contact point; ${\mathbf{w}}_i$ is the wrench of the contact force at the $i$-th contact point; ${\mathbf{r}}_i$ is the position vector of the $i$-th contact point (m); $R$ is the radius of the grape cluster (m); ${\theta }_i$ is the central angle of the $i$-th contact point (°); ${\mathbf{w}}_{ext}$ is the force spiral of gravity on the centroid; $f_{n,i}$ is the normal force component at the $i$-th contact point (N); $f_{t1,i}$ and $f_{t2,i}$ are the tangential frictional force components at the $i$-th contact point (N).

The contact forces are mapped to the object’s external force spiral using the grasp matrix $\mathbf{G}\in R^{6\times 12}$, as shown in Equation (6).

$$\mathbf{G}=\left[\begin{array}{cccc}{G}_1& G_2& G_3& G_4\end{array}\right]$$

(6)

By applying force spiral theory, the contact forces are mapped to the generalized force space of the system. The expanded calculations for $G_i$ and $R_i$ with block-wise expressions are shown in Equations (7) and (8), respectively.

$$G_i=\left[\begin{array}{c}{I}_3\\ R_i\end{array}\right]\cdot \left[\begin{array}{ccc}{n}_i& t_i& o_i\end{array}\right](i=1,\dots ,4)$$

(7)

$$G_i=\left[\begin{array}{c}{I}_3\\ R_i\end{array}\right]\cdot \left[\begin{array}{ccc}{n}_i& t_i& o_i\end{array}\right](i=1,\dots ,4)$$

(8)

where $I_3$ is the 3 × 3 identity matrix; $R_i\in R^{3\times 3}$ is the cross-product matrix constructed from the position vector; ${\mathbf{f}}_i$ is the contact force vector at the i contact point.

The necessary and sufficient conditions for the force closure of the clamping device are as follows [28]:

(1)

The grasp matrix must be full rank. The rank(G) = 6, ensuring that the force spiral space covers any disturbance direction (satisfying the completeness of the force spiral space).

(2)

The existence of internal points: A set of solutions exists that strictly satisfy $f_{n,i}$ > 0.

The singular value decomposition (SVD) of G is computed, as shown in Equation (9). The calculation results indicate that all 6 singular values are non-zero, and the grasp matrix is full rank, thus satisfying Condition (1).

$$G=U\Sigma V^{\top }$$

(9)

where $\Sigma$ is the singular value matrix.

The sufficiency of force closure relies on the solvability of the friction cone constraints. Each contact force ${\mathbf{f}}_i$ must satisfy the Coulomb friction constraint, as shown in Equation (10). According to Minkowski’s duality theorem, the generalized force spiral $w_{\mathrm{ext}}$ must lie within the polyhedral cone generated by the friction cone mapping. To convert the nonlinear inequality into linear constraints, an octagonal approximation is used. The friction cone is decomposed into 8 directions: $u_j={\left[\begin{array}{c}\cos {\alpha }_j,\sin {\alpha }_j,1/\mu \end{array}\right]}^T$, where ${\alpha }_j={45}^{°}\times j(j=0,1,\dots ,7)$. The contact forces are decomposed as shown in Equation (11), and the total force spiral equation is transformed into Equation (12). Using ${\lambda }_{i,j}\ge 0$ as variable, there are a total of 8 × 4 = 32 vectors.

$$\left\{\begin{array}{l}Gf=-w_{\mathrm{ext}}\hfill \\ f_{n,i}\ge 0\hfill \\ \sqrt{f_{t1,i}^2+f_{t2,i}^2}\le \mu f_{n,i}\hfill \end{array}\right.$$

(10)

$$f_i={\displaystyle \sum _{j=1}^8{\lambda }_{i,j}}{u}_j,{\lambda }_{i,j}\ge 0$$

(11)

$$Gf=-w_{\mathrm{ext}}\Rightarrow {\displaystyle \sum _{i=1}^4{\displaystyle \sum _{j=1}^8{G}_i}}{\lambda }_{i,j}{u}_j=-w_{\mathrm{ext}}$$

(12)

where $\mu$ is the friction coefficient between the grape fruit and the contact surface; $u_j$ is the directional vector of the linearized friction cone; ${\lambda }_{i,j}$ is the coefficient of the directional vector.

Using MATLAB 2020’s linprog function to solve Equation (11) and Constraint (10), we verify that the objective function has a feasible solution. Therefore, the clamping device satisfies force closure.

2.4. Contact Force Control System Design

To achieve flexible, low-damage harvesting of grape clusters, this study designs an integrated “Perception–Control–Execution” contact force control system, as shown in the Figure 4 below. The system uses the LAUNCHXL-F28069M microcontroller (Texas Instruments, Dallas, TX, USA) as the core controller, which drives the servo motor HC60A2A04030-SCA (Beijing Times Chaoqun Electric Appliance Technology Co., Ltd., Beijing, Chian) to perform the clamping action. Four RP-S40-LT resistive pressure sensors (Legact Technology Co., Ltd., Shenzhen, China) installed on the clamping fingers provide real-time feedback regarding the contact force. When this real-time contact force feedback reaches the preset threshold, the motor stops, achieving high-precision control of the clamping action.

3. Results and Discussion

3.1. Finite Element Simulation Analysis of Pedicel Cutting Based on ANSYS/LS-DYNA

3.1.1. Simulation Parameter Setup for Grape Pedicel–Blade System

To evaluate the performance of the cutting device, a finite element model of the grape pedicel–blade system is constructed using ANSYS/LS-DYNA. The pedicel diameter is defined as 10 mm, with a length of 60 mm. The moving blade adopts a 15° edge angle single-edged hook structure, while the fixed blade features a 30° edge angle with a V-shaped double-edged structure. A simplified model of the cutting device is shown in Figure 5.

The blade system uses the MAT_RIGID rigid-body material model, using 45# steel for the blade material. The density is 7.89 × 10⁻³ g/mm³, the elastic modulus is 2.06 × 10⁵ MPa, and the Poisson’s ratio is 0.269. Based on the actual mechanical behavior of the grape pedicel, the MAT_ELASTIC material model in LS-DYNA is used to describe the linear elastic mechanical properties of the pedicel. The specific parameters are shown in

Table 3. Grape pedicel parameters.

Material	Density/g·mm−3	Ea/MPa	Eb/MPa	Ec/MPa	vab	vac	vbc	Gab/MPa	Gac/MPa	Gbc/MPa
Pedicel	4.5 × 10−4	300	450	1.2 × 10−4	0.4	0.04	0.03	50	300	200

.

Based on the actual cutting scenario, all degrees-of-freedom constraints are applied to the upper and lower surfaces of the pedicel and the lower surface of the fixed blade, with only the displacement constraint in the x-direction being retained for the moving blade. A displacement of 31 mm is applied in the x-direction over a time range of 0~1 s. The contact between the blade system and the pedicel is defined using the CONTACT_ERODING_SURFACE_TO_SURFACE erosion contact algorithm. The viscous damping coefficient is set to 10, the penalty ratio factor is set to 100, and the soft constraint ratio factor is set to 10. The simulation is then solved.

3.1.2. Post-Processing and Simulation Result Analysis

After the solution is completed, the simulation results are visualized using the ANSYS post-processors POST1, POST26, and LS-PREPOST. The stress distribution contour map and the shear strength curve for the grape pedicel–blade system are plotted, as shown in Figure 6 and Figure 7.

From Figure 6 and Figure 7, it can be seen that the blade starts moving at 0 s and comes into contact with the grape pedicel at 0.5116 s, and the cutting stress gradually increases. At 0.6513 s, the maximum cutting stress reaches its peak value of 1.515 MPa. At 0.7951 s, the grape pedicel is severed. During the cutting process of the stem, the maximum shear stress generated was 1.515 MPa, which exceeds the actual cutting strength required to sever the stem as recorded in Table 2. This indicates that the moving and stationary blade cutting system can successfully cut the stem, and the cutting strength meets the requirements.

3.2. The Kinematic Simulation of the Clamping Device Based on ADAMS

To obtain the contact force curve between the clamping device and the grape cluster, a kinematic simulation of the clamping device is conducted using ADAMS. A simplified model of the clamping device gripping the grape cluster is shown in Figure 8.

The lead screw is structural steel, and the linkage support frame is composed of an aluminum alloy. Links 1–4 are made of PLA material (

Table 4. Material parameters of the clamping device.

Material	Density (g/cm3)	Modulus of Elasticity (GPa)	Poisson’s Ratio
aluminum alloy	2.7	70	0.33
structural steel	7.8	200	0.28
PLA	1.25	3.5	0.35
grape cluster	0.9	0.01	0.45

).

A contact model based on penalty functions is used for the interaction between the clamping device and the grape cluster, with the contact stiffness set to 2 N/m and damping values ranging from 0.05 to 0.2. After multiple simulation tests, where the damping coefficient is set approximately 0.2, the variation in the contact force and other behaviors is found to align more closely with the energy loss characteristics observed in the actual contact process. The simulation constraints applied are shown in

Table 5. Model constraints table.

Serial Number	Constraint Type	Constrained Components
1	Fixed Pair	Support Plate—Ground
2	Fixed Pair	Base Plate—Ball Screw
3	Fixed Pair	Finger—Link 3
4	Fixed Pair	Finger—Pressure Sensor
5	Fixed Pair	Pressure Sensor—Rubber
6	Revolute Pair	Link 1—Support Plate
7	Revolute Pair	Link 2—Support Plate
8	Revolute Pair	Link 1—Link 3
9	Revolute Pair	Link 2—Link 3
10	Revolute Pair	Link 1—Link 4
11	Revolute Pair	Link 4—Ball Nut
12	Prismatic Pair	Lead Screw—Ball Nut
13	Contact Constraint	Rubber—Grape Cluster

.

The driving source is applied to the prismatic pair between the ball nut and the ball screw. The displacement function is defined as follows: STEP(time, 0, 0, 4, 16) − STEP(time, 4, 0, 12, 32) + STEP(time, 12, 0, 16, 16). The velocity and displacement of the ball nut with respect to time are shown in Figure 9.

The simulation time is set to 16 s with 200 simulation steps. After running the simulation, the contact force curve between the clamping device and the grape is obtained, as shown in Figure 10.

In Figure 10, it can be seen that at 8.5 s, the sensor fixed at the front of the robotic arm’s finger contacts the clamping target. As the clamping force gradually increases, the force on the grape also increases. When the minimum contact force required for stable clamping is reached, the motor stops to ensure the stability of the finger’s gripping posture. At this point, the force curve peaks, and after brief fluctuations due to force feedback adjustments, it stabilizes at the peak value. At 10 s, the clamping force becomes constant at 11 N, which is lower than the grape’s critical rupture force of 24.79 N, meeting the harvesting requirements.

3.2.1. Contact Force Test Platform

To determine the optimal clamping force threshold, a contact force test platform is constructed to verify the sensor threshold. The contact force test platform consists of a host computer, a controller, and the clamping device, as shown in Figure 11. The installation position of the sensorare shown in Figure 11a. A flexible cushioning pad is installed above the sensors, as shown in Figure 11b.

Three sensor threshold calculation methods are proposed: the Mean Method, the Weighted Average Method, and the Root Mean Square (RMS) Method. The force values measured by the four sensors are denoted as $F_1$, $F_2$, $F_3$, and $F_4$. The calculation formulas for the three methods are shown in Equations (13), (14), and (15) respectively.

$$F_{\mathrm{avg}}={\displaystyle \frac{F_1+F_2+F_3+F_4}{4}}$$

(13)

$$\begin{array}{c}{F}_{\mathrm{WA}}={\omega }_1{F}_1+{\omega }_2{F}_2+{\omega }_3{F}_3+{\omega }_4{F}_4\\ {\omega }_1+{\omega }_2+{\omega }_3+{\omega }_4=1\end{array}$$

(14)

$$F_{RMS}=\sqrt{{\displaystyle \frac{F_1^2+F_2^2+F_3^2+F_4^2}{4}}}$$

(15)

where ${\omega }_1$, ${\omega }_2$, ${\omega }_3$, and ${\omega }_4$ are weights; the two largest pressure values are assigned a weight of 0.27, and the two smallest pressure values are assigned a weight of 0.22.

By applying the three calculation methods to the contact force test data, the mean, standard deviation, and error ratio (standard deviation/mean) are compared, as shown in

Table 6. Comparison of maximum trajectory deviation.

Calculation Method	Mean/N	Standard Deviation/N	Error Ratio (Standard Deviation/Mean)
$\mathrm{Mean}\mathrm{Method}{F}_{\mathrm{avg}}$	9.994	0.256	0.0256
$\mathrm{Weighted}\mathrm{Average}\mathrm{Method}{F}_{WA}$	9.753	0.255	0.0261
$\mathrm{Root}\mathrm{Mean}\mathrm{Square}\mathrm{Method}{F}_{RMS}$	10.001	0.254	0.0255

. Since the goal is to minimize the error and improve the stability of the calculation, the Root Mean Square (RMS) Method is selected for the sensor calculation method, with the contact force threshold set to 11 N.

3.2.2. Motor Three-Loop Control System Design

The Field-Oriented Control (FOC) strategy with $i_d$ = 0 is adopted, and in conjunction with the application scenario of the grape harvesting machine’s end-effector, a position–speed–torque three–loop control system is employed to achieve high-precision position control of the motor. This ensures stable gripping and unloading by the clamping device. The control block diagram for the motor is shown in Figure 12.

The workflow of the three-loop control system is expressed as follows:

(1)

Torque Loop: The three-phase stator currents are sampled via shunt resistors and transformed into d- and q-axis currents in the stationary reference frame. Under the $i_d$ = 0 control strategy, the q-axis current reference $i_q$ is generated by the speed loop controller. It is then compared with the measured $i_d$ and $i_q$ values, and the error signals are processed by the torque loop controller to generate compensated voltage signals. These signals are modulated via SVPWM to drive the three-phase inverter, thereby controlling the motor and forming the torque closed-loop control system.

(2)

Speed Loop: An incremental encoder measures the motor rotor speed in real time. The speed error is calculated by comparing this measured value with the output of the speed loop controller. This error is processed by the speed loop controller, whose output serves as the current reference for the torque loop, adjusting the motor torque to ensure smooth system operation and forming a nested dual closed-loop control system with the torque loop.

(3)

Position Loop: The motor’s current position is obtained by integrating the speed information measured by the encoder. The position error is calculated by comparing this value with the position reference. This error is processed by the position loop controller, which outputs the desired speed reference for the speed loop. This ensures the precise tracking of position commands and accurate control of the end-effector’s motion, constituting the overall position closed-loop control system.

Based on the control block diagram in Figure 12, a Simulink simulation model for the motor three-loop control is established in MATLAB, as shown in Figure 13.

After multiple simulations, the final three-loop motor control parameters are shown in

Table 7. Main component parameters of the tractor.

Parameter	Value
Torque Loop Kp	0.02
Torque Loop Ki	0.5
Speed Loop Kp	2
Speed Loop Ki	5
Position Loop Ki	80

.

The motor position control response curve under these parameters is shown in Figure 14. From Figure 14, it can be observed that when the rotor position is set to 1 rad, the motor rotor responds quickly, reaching the desired position within 0.2 s with no overshoot, and the steady-state error is minimal, meeting the requirements of the position loop control. After deploying the above parameters in the controller, the actual motor position response is shown in Figure 15.

From Figure 15, it can be observed that the actual motor response curve closely matches the simulation, with a rapid response within 0.25 s and minimal steady-state error. Therefore, these motor control parameters can effectively reflect the motor response state and, for the operational scenario of the clamping device’s movement, can meet the control requirements for the clamping device.

3.3. Prototype Fabrication and Field Testing

Based on the design and simulation analysis of the retractable four-point flexible clamping end-effector for grape harvesting, the prototype of the grape harvesting end-effector was developed and integrated into the grape-picking robot, as illustrated in Figure 16.

To evaluate the operational performance of the end-effector—including the harvesting success rate, fruit damage rate, and operational efficiency per time unit—as well as to assess the stability, durability, and environmental adaptability of the equipment, field tests were conducted at Mashan Vineyard in Jimo District, Qingdao City, Shandong Province, China. The vineyard features 10-year-old grapevines and is located on the northern slopes of Mashan, with a longitudinal slope of approximately 15 degrees and a transverse slope of about 5 degrees. The vines are arranged in a vertical trellising system suitable for mechanized management, with a row spacing of 180 cm and a trellis height of 170 cm.

The performance of the harvesting end-effector is evaluated based on the grape drop rate, rupture rate, and cutting time. Harvesting tests were conducted on Kyoho grapes, Rose grapes, and Red Globe grapes. The test indicators were the damage rate and drop rate of the grape clusters, with a total of 60 harvesting trials conducted. The calculation formulas are shown in Equations (17) and (18). The stratified statistical method was used in the experiments to ensure the representativeness and accuracy of the data. Vertical statistics were conducted within the same experimental area, testing three grapevines per group, while horizontal statistics were conducted by selecting grape clusters from the upper, middle, and lower levels of a single vine to reduce the impact of the fruit maturity and structure variation at different heights on the harvesting results.

$$P={\displaystyle \frac{N_{\mathbf{A}}-N_T}{N_{\mathbf{T}}}}\times 100\%$$

(16)

$$D={\displaystyle \frac{N_{\mathbf{S}}}{N_{\mathbf{T}}}}\times 100\%$$

(17)

where $P$ is the grape drop rate; $D$ is the grape rupture rate; $N_{\mathbf{T}}$ is the number of grapes before the harvesting test; $N_{\mathbf{A}}$ is the number of grapes after the harvesting test.

The harvesting steps are shown in Figure 17.

The above harvesting process is repeated with the same harvesting parameters, recording the number of grapes and the number of damaged grapes before and after harvesting. Grapes exhibiting compressed deformation or rupture are considered damaged. The stable clamping and successful cutting of the grape is considered a successful harvest. If the pedicel is not cut or the fruit slips off, the harvesting is considered a failure. The harvesting success drop rate, and rupture rates are calculated, and the test results are shown in

Table 8. Grape harvesting test data.

The Variety of Grapes	Test Count	Stable Grasp Count	Successful Cutting Count	Average Drop Rate/%	Average Rupture Rate/%	Average Harvest Time/s	Harvesting Success Rate/%
Kyoho	20	20	19	3.1	2.9	13.2	95
Rose	20	20	19	3.5	3	14.9	95
Red Globe	20	20	20	3	2.5	13	100
	total/60	total/60	total/58	average/3.2	average/2.8	average/13.7	average/96.7

.

As shown in Table 8, the average harvesting success rate in the trials reached 96.7%, with an average fruit drop rate of 3.2% and an average rupture rate of 2.8%, meeting the expected design requirements. The average time per harvesting cycle was 13.7 s, which includes the processes of moving to the target fruit, pedicel gathering, pedicel cutting, and fruit clamping.

3.4. Discussion

This section focuses on the pedicel cutting and flexible clamping processes. It includes simulations of the cutting performance of the cutting device, simulations of the contact force between the clamping device and the grape cluster, the design of a contact force control system, and comprehensive performance verification through vineyard harvesting trials. The results indicate the following:

(1)

In the ANSYS/LS-DYNA simulation of the pedicel cutting process, the pedicel is completely severed at 0.7951 s, with a peak cutting stress of 1.515 MPa, exceeding the measured pedicel shear strength of 1.349~1.426 MPa. This confirms the rationality of the blade structure design and its effective cutting capability. In the ADAMS contact force simulation, the peak contact force between the clamping fingers and the grape is 11 N, which is close to the preliminarily determined clamping threshold of 11 N for stable, non-damaging gripping. Moreover, it remains significantly below the grape’s critical compressive rupture force (25.79~34.54 N), confirming that the clamping process ensures cluster stability without inducing mechanical damage.

(2)

The contact force bench test further verifies that 11 N is an appropriate clamping threshold, and the Root Mean Square (RMS) method is selected as the optimal algorithm for processing the four-channel sensor data. For motor control, a position–speed–torque three-loop control strategy is implemented to achieve precise control of the clamping motor. Both the simulation and the empirical results show that when the rotor target position is set to 1 rad, the motor completes a rapid response within 0.2~0.25 s, with no noticeable overshoot and minimal steady-state errors. The control response error remains within ±0.2 s, indicating excellent dynamic responsiveness and robustness—meeting the real-time and stability requirements of the clamping control system.

(3)

The field tests of our prototype yielded key performance metrics, including a harvesting success rate of 96.7%, a cycle time of 13.7 s, a bruise rate of 2.8%, and a berry drop rate of 3.2%. Compared to existing studies, our system demonstrates a competitive performance, particularly in its balanced efficiency and low damage.

Regarding the harvesting success rate, our system (96.7%) performs slightly better than most reported values, which range from 83% (literature [11,26]) and 87.4% (literature [29]) to 92% (literature [30]) and 95% (literature [27]). This result indicates that our end-effector design is effective for the successful grasping and detachment of peduncles across different grape varieties.

In terms of operational efficiency, our cycle time of 13.7 s is slower than the 5.71 s reported in the literature [30], which identifies a clear goal for our next stage of improvement. It is noteworthy that while literature [30] achieved higher speed, our system maintained a higher success rate (96.7% vs. 92%) and a lower bruise rate (2.8% vs. 4.4%). This balance is crucial for practical applications, where both throughput and fruit quality are key considerations. Furthermore, our comprehensive damage assessment, which includes both bruising and berry drop, provides a more complete evaluation of harvesting quality compared to studies reporting only success rate and time.

A limitation of this discussion is that it was not possible to compare all damage metrics across all studies, as such data are not universally reported. Future work will focus on further optimizing the cycle time without compromising the high success and low damage rates, with an emphasis on improving operational stability.

(4)

The harvesting tests performed in this study involved a total of 60 samples across three grape varieties, with 20 samples per variety. The relatively small sample size may introduce some uncertainty in the test results. Our research team plans to expand the sample database and conduct more repeated trials in the next harvesting season to improve the certainty of the test outcomes.

(5)

However, numerous issues warrant further investigation. Significant room for improvement remains in the optimization of the end-effector, as instances of the incomplete severing of grape pedicels during field trials persist, leading to system halts that require manual intervention. Integrating technologies such as environmental perception systems and autonomous navigation could substantially enhance the harvesting performance and intelligence level of the robotic harvester.

In summary, this in-depth study of a grape harvesting end-effector not only verifies the feasibility and efficiency of flexible clamping and precise cutting in practical harvesting operations but also provides theoretical and technical support for the structural design, control strategy optimization, and system integration of intelligent fruit-harvesting equipment. It lays a solid foundation for the future promotion and application of automated harvesting technologies for a wide variety of fruits and vegetables.

4. Conclusions

To address the challenges of automated harvesting and table grapes’significant susceptibility to damage, this study focused on the biological and mechanical properties of grapes and proposed a retractable four-point flexible clamping end-effector. A position–speed–torque three-loop motor control strategy was adopted, with pressure sensors deployed on the four clamping fingers to establish a real-time contact force feedback control system. The performance of the end-effector evaluated in terms of the harvesting success rate, operational efficiency, and fruit damage rate, was comprehensively assessed through ANSYS/LS-DYNA and ADAMS simulations, contact force bench tests, and vineyard harvesting trials.

(1)

To address issues such as high clamping damage rates in automated grape harvesting, diverse grape varieties and shapes, and dispersed pedicel regions, a retractable four-point flexible clamping end-effector was proposed. The theoretical analysis confirmed that the clamping mechanism met force-closure requirements, and an optimal contact force threshold of 11 N was determined to ensure stable gripping without damaging the grapes.

(2)

Simulations conducted using ANSYS/LS-DYNA and ADAMS confirmed the cutting device’s effective capability to sever the pedicel and verified the rationality of the contact force applied by the clamping mechanism. The contact force bench testing further determines that a maximum contact force threshold of 11 N enables stable clamping without damaging the grape berries. A prototype was fabricated and tested in vineyard field trials, which demonstrated a harvesting success rate of 96.7%, with drop and rupture rates controlled within 3.2% and 2.8%, respectively. The average time per harvesting cycle was 13.7 s. The system exhibited strong adaptability and stability across different grape varieties.

This research provides key structural and control strategy support for the intelligent, flexible harvesting of diverse fruits and vegetables, laying both theoretical and practical foundations for the development and deployment of highly adaptable robust harvesting end-effectors.